Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-24T07:20:52.270Z Has data issue: false hasContentIssue false
  • English
  • Français

Volterra-type operators on the minimal Möbius-invariant space

Part of: Special classes of linear operators Spaces and algebras of analytic functions

Published online by Cambridge University Press:  13 June 2022

Huayou Xie ,
Junming Liu  and
Saminathan Ponnusamy Open the ORCID record for Saminathan Ponnusamy [Opens in a new window]
Huayou Xie
Affiliation:
Department of Mathematics, Sun Yat-sen University, Guangzhou 510275, P. R. China e-mail: xiehy33@mail2.sysu.edu.cn
Junming Liu*
Affiliation:
School of Mathematics and Statistics, Guangdong University of Technology, Guangzhou, Guangdong 510520, P. R. China
Saminathan Ponnusamy
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, Chennai 600036, India Department of Mathematics, Petrozavodsk State University, ul. Lenina 33, 185910 Petrozavodsk, Russia e-mail: samy@iitm.ac.in
*
Junming Liu is the corresponding author. e-mail: jmliu@gdut.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we mainly study operator-theoretic properties on the Besov space 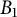$B_{1}$ on the unit disk. This space is the minimal Möbius-invariant space. First, we consider the boundedness of Volterra-type operators. Second, we prove that Volterra-type operators belong to the Deddens algebra of a composition operator. Third, we obtain estimates for the essential norm of Volterra-type operators. Finally, we give a complete characterization of the spectrum of Volterra-type operators.

Keywords

Volterra-type operatorsminimal Möbius-invariant spaceDeddens algebra

MSC classification

Primary: 47B38: Operators on function spaces (general)
Secondary: 30H25: Besov spaces and $Q_p$-spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 2 , June 2023 , pp. 509 - 524
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by NNSF of China (Grant Nos. 11801094 and 12126203).

References

Aleman, A. and Cima, J., An integral operator on ${H}^p$ and Hardy’s inequality . J. Anal. Math. 85(2001), 157–176.CrossRefGoogle Scholar
Aleman, A. and Constantin, O., Spectra of integration operators on weighted Bergman spaces . J. Anal. Math. 109(2009), 199–231.CrossRefGoogle Scholar
Aleman, A. and Siskakis, A., Integration operators on Bergman spaces . Indiana Univ. Math. J. 46(1997), no. 2, 337–356.10.1512/iumj.1997.46.1373CrossRefGoogle Scholar
Aleman, A. and Siskakis, A., An integral operator on ${H}^p$ . Complex Variables Theory Appl. 28(2001), no. 2, 149–158.10.1080/17476939508814844CrossRefGoogle Scholar
Arazy, J., Fisher, S. D., and Peetre, J., Möbius invariant function spaces . J. Reine Angew. Math. 363(1985), 110–145.Google Scholar
Bao, G. and Wulan, H., The minimal Möbius invariant space . Complex Var. Elliptic Equ. 59(2014), no. 2, 190–203.10.1080/17476933.2012.727408CrossRefGoogle Scholar
Blasco, O., Composition operators on the minimal space invariant under Möbius transformations . In: A. Carbery, P. Duren, D. Khavinson, and A. Siskakis (eds.), Complex and harmonic analysis, DEStech Publications, Lancaster, 2007, pp. 157–166.Google Scholar
Bonet, J., The spectrum of Volterra operators on Korenblum type spaces of analytic functions . Integr. Equ. Oper. Theory 91(2019), no. 5, Article no. 46, 16 pp.CrossRefGoogle Scholar
Colonna, F. and Li, S., Weighted composition operators from the minimal Möbius invariant space into the Bloch space . Mediterr. J. Math. 10(2013), no. 1, 395–409.CrossRefGoogle Scholar
Constantin, O., A Volterra-type integration operator on Fock spaces . Proc. Amer. Math. Soc. 47(2012), no. 12, 4247–4257.10.1090/S0002-9939-2012-11541-2CrossRefGoogle Scholar
Constantin, O. and Persson, A., The spectrum of Volterra-type integration operators on generalized Fock spaces . Bull. Lond. Math. Soc. 47(2015), no. 6, 958–963.Google Scholar
Conway, J., Functions of one complex variable. 2nd ed., Graduate Texts in Mathematics, 11, Springer, New York–Berlin, 1978.CrossRefGoogle Scholar
Čučković, Ž. and Paudyal, B., Invariant subspaces of the shift plus complex Volterra operator . J. Math. Anal. Appl. 426(2015), 1174–1181.CrossRefGoogle Scholar
Deddens, J., Another description of nest algebras. In: Hulbert space operators (Proc. Conf., Calif. State Univ., Long Beach, CA, 1977), Lecture Notes in Mathematics, 693, Springer, Berlin, 1978, pp. 77–86.Google Scholar
Duren, P., Theory of Hp spaces, Academic Press, New York, 1970.Google Scholar
Galanopoulos, P., Girela, D., and Peláez, J., Multipliers and integration operators on Dirichlet spaces . Trans. Amer. Math. Soc. 363(2011), no. 4, 1855–1886.CrossRefGoogle Scholar
Girela, D. and Merchán, N., Hankel matrices acting on the hardy space ${H}^1$ and on Dirichlet spaces . Rev. Mat. Complut. 32(2019), no. 3, 799–822.CrossRefGoogle Scholar
Girela, D. and Peláez, J., Carleson measures, multipliers and integration operators for spaces of Dirichlet type . J. Funct. Anal. 241(2006), no. 1, 334–358.CrossRefGoogle Scholar
Karaev, M. T. and Mustafayev, H. S., On some properties of Deddens algebras . Rocky Mountain J. Math. 33(2003), no. 3, 915–926.CrossRefGoogle Scholar
Lacruz, M., Invariant subspaces and Deddens algebras . Expo. Math. 33(2015), no. 1, 116–120.CrossRefGoogle Scholar
Lin, Q., Volterra type operators between Bloch type spaces and weighted Banach spaces . Integr. Equ. Oper. Theory 91(2019), no. 13, 20 pp.CrossRefGoogle Scholar
Lin, Q., Liu, J., and Wu, Y., Volterra type operators on ${S}_p(D)$ spaces . J. Math. Anal. Appl. 461(2018), no. 2, 1100–1114.CrossRefGoogle Scholar
Lin, Q., Liu, J., and Wu, Y., Strict singularity of Volterra type operators on hardy spaces . J. Math. Anal. Appl. 492(2020), no. 1, 9 pp.10.1016/j.jmaa.2020.124438CrossRefGoogle Scholar
Liu, J., Lou, Z., and Xiong, C., Essential norms of integral operators on spaces of analytic functions . Nonlinear Anal. 75(2012), no. 13, 5145–5156.CrossRefGoogle Scholar
Liu, J., Lou, Z., and Zhu, K., Embedding of Möbius invariant function spaces into tent spaces . J. Geom. Anal. 27(2017), no. 2, 1013–1028.CrossRefGoogle Scholar
Liu, X., Liu, Y., Xia, L., and Yu, Y., The essential norm of the integral type operators . Banach J. Math. Anal. 14(2020), no. 1, 181–202.CrossRefGoogle Scholar
Malman, B., Spectra of generalized Cesro operators acting on growth spaces . Integr. Equ. Oper. Theory 90(2018), no. 3, Article no. 26, 19 pp.10.1007/s00020-018-2448-4CrossRefGoogle Scholar
Mashreghi, J., The rate of increase of mean values of functions in hardy spaces . J. Aust. Math. Soc. 86(2009), no. 2, 199–204.CrossRefGoogle Scholar
Mengestie, T., On the spectrum of Volterra-type integral operators on Fock–Sobolev spaces . Complex Anal. Oper. Theory 11(2017), no. 6, 1451–1461.CrossRefGoogle Scholar
Mengestie, T., Spectral properties of Volterra-type integral operators on Fock–Sobolev spaces . J. Korean Math. Soc. 54(2017), no. 6, 1801–1816.Google Scholar
Miihkinen, S., Pau, J., Perälä, A., and Wang, M., Volterra type integration operators from Bergman spaces to Hardy spaces . J. Funct. Anal. 279(2020), no. 4, 32 pp.CrossRefGoogle Scholar
Mitsis, T. and Papadimitrakis, M., The essential norm of a composition operator on the minimal Möbius invariant space . Ann. Acad. Sci. Fenn. Math. 37(2012), no. 1, 203–214.10.5186/aasfm.2012.3714CrossRefGoogle Scholar
Ohno, S. and Pavlović, M., Weighted composition operators on the minimal Möbius invariant space . Bull. Korean Math. Soc. 51(2014), no. 4, 1187–1193.CrossRefGoogle Scholar
Petrovic, S., On the extended eigenvalues of some Volterra operators . Integr. Equ. Oper. Theory 57(2007), no. 4, 593–598.CrossRefGoogle Scholar
Petrovic, S., Deddens algebras and shift . Complex Anal. Oper. Theory 5(2011), no. 1, 253–259.CrossRefGoogle Scholar
Petrovic, S., Spectral radius algebras, Deddens algebras, and weighted shifts . Bull. Lond. Math. Soc. 43(2011), no. 3, 513–522.CrossRefGoogle Scholar
Petrovic, S. and Sievewright, D., Compact composition operators and Deddens algebras . Complex Anal. Oper. Theory 12(2018), no. 8, 1889–1901.10.1007/s11785-017-0689-xCrossRefGoogle Scholar
Pommerenke, C., Boundary behaviour of conformal maps, Grundlehren der Mathematischen Wissenschaften, 299, Springer, Berlin, 1992.CrossRefGoogle Scholar
Rättyä, J., n-th derivative characterisations, mean growth of derivatives and $F\left(p,q,s\right)$ . Bull. Aust. Math. Soc. 68(2003), no. 3, 405–421.10.1017/S0004972700037813CrossRefGoogle Scholar
Rudin, W., Functional analysis. 2nd ed. International Series in Pure and Applied Mathematics, McGraw-Hill, New York, 1991.Google Scholar
Shargorodsky, E., On the essential norms of Toeplitz operators with continuous symbols . J. Funct. Anal. 280(2021), no. 2, 108835.CrossRefGoogle Scholar
Sievewright, D., Deddens algebras for weighted shifts . Houst. J. Math. 41(2015), no. 3, 785–814.Google Scholar
Todorov, I., Bimodules over nest algebras and Deddens’ theorem . Proc. Amer. Math. Soc. 127(1999), no. 6, 1771–1780.CrossRefGoogle Scholar
Vukotić, D., The isoperimetric inequality and a theorem of Hardy and Littlewood . Amer. Math. Monthly 110(2003), no. 6, 532–536.CrossRefGoogle Scholar
Wulan, H. and Xiong, C., Composition operators on the minimal Möbius invariant space, Hilbert spaces of analytic functions, American Mathematical Society, Providence, RI, 2010.Google Scholar
Xiao, J. and Zhu, K., Volume integral means of holomorphic functions . Proc. Amer. Math. Soc. 139(2011), no. 4, 1455–1465.CrossRefGoogle Scholar
Zhao, R., On a general family of function spaces . Ann. Acad. Sci. Fenn. Math. Diss. (1996), no. 105, 56 pp.Google Scholar
Zhu, K., A class of Möbius invariant function spaces . Ill. J. Math. 51(2007), no. 3, 977–1002.Google Scholar