Search

Summary

This chapter develops some topology, the abstract geometry ofcloseness, that manages to capture properties of nearness withoutany appeal to distance. The previous chapter studied the shape ofthe linear continuum, focusing on what happens when one tries to cutor tear it in two. This chapter offers a qualitative generalizationof these ideas, about continuity and connectedness, but now withoutany metrics. The focus is on closed sets, boundaries, andeventually, continuous transformations and their fixed points,bringing ideas from analysis back to set theory. Concluding theoremsare proven about retractions and some lemmas about absolutelydisconnected space, leading to a parameterized version ofBrouwer’s fixed point theorem.

Assuming the Continuum Hypothesis, there is a compact, first countable, connected space of weight 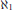${{\aleph }_{1}}$ with no totally disconnected perfect subsets. Each such space, however, may be destroyed by some proper forcing order which does not add reals.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

9 - Topology

Summary

First Countable Continua and Proper Forcing

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

9 - Topology

Summary

First Countable Continua and Proper Forcing