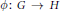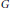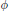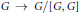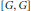An epimorphism 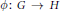 $\phi :\,G\,\to \,H$ of groups, where
$\phi :\,G\,\to \,H$ of groups, where 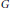 $G$ has rank
$G$ has rank  $n$, is called coessential if every (ordered) generating
$n$, is called coessential if every (ordered) generating  $n$-tuple of
$n$-tuple of  $H$ can be lifted along
$H$ can be lifted along 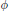 $\phi $ to a generating
$\phi $ to a generating  $n$-tuple for
$n$-tuple for 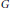 $G$. We discuss this property in the context of the category of groups, and establish a criterion for such a group
$G$. We discuss this property in the context of the category of groups, and establish a criterion for such a group 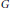 $G$ to have the property that its abelianization epimorphism
$G$ to have the property that its abelianization epimorphism 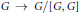 $G\,\to \,{G}/{[G,G]}\;$, where
$G\,\to \,{G}/{[G,G]}\;$, where 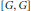 $[G,\,G]$ is the commutator subgroup, is coessential. We give an example of a family of 2-generator groups whose abelianization epimorphism is not coessential. This family also provides counterexamples to the generalized Andrews–Curtis conjecture.
$[G,\,G]$ is the commutator subgroup, is coessential. We give an example of a family of 2-generator groups whose abelianization epimorphism is not coessential. This family also provides counterexamples to the generalized Andrews–Curtis conjecture.