We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The asymptotic behavior of the Jaccard index in G(n, p), the classical Erdös–Rényi random graph model, is studied as n goes to infinity. We first derive the asymptotic distribution of the Jaccard index of any pair of distinct vertices, as well as the first two moments of this index. Then the average of the Jaccard indices over all vertex pairs in G(n, p) is shown to be asymptotically normal under an additional mild condition that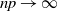 
$np\to\infty$ and 
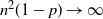$n^2(1-p)\to\infty$.
