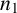1 results
BRANCHING TECHNIQUE FOR A BI-OBJECTIVE TWO-STAGE ASSIGNMENT PROBLEM
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 15 August 2022, pp. 183-204
-
- Article
- Export citation
-
We discuss a bi-objective two-stage assignment problem (BiTSAP) that aims at minimizing two objective functions: one comprising a nonlinear cost function defined explicitly in terms of assignment variables and the other a total completion time. A two-stage assignment problem deals with the optimal allocation of n jobs to n agents in two stages, where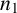
$n_1$
out of n jobs are primary jobs which constitute Stage-1 and the rest of the jobs are secondary jobs constituting Stage-2. The paper proposes an algorithm that seeks an optimal solution for a BiTSAP in terms of various efficient time-cost pairs. An algorithm for ranking all feasible assignments of a two-stage assignment problem in order of increasing total completion time is also presented. Theoretical justification and numerical illustrations are included to support the proposed algorithms.
