We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the complexities of isometry and isomorphism classes of separable Banach spaces in the Polish spaces of Banach spaces, recently introduced and investigated by the authors in [14]. We obtain sharp results concerning the most classical separable Banach spaces.
We prove that the infinite-dimensional separable Hilbert space is characterized as the unique separable infinite-dimensional Banach space whose isometry class is closed, and also as the unique separable infinite-dimensional Banach space whose isomorphism class is 
$F_\sigma $. For 
$p\in \left [1,2\right )\cup \left (2,\infty \right )$, we show that the isometry classes of 
$L_p[0,1]$ and 
$\ell _p$ are 
$G_\delta $-complete sets and 
$F_{\sigma \delta }$-complete sets, respectively. Then we show that the isometry class of 
$c_0$ is an 
$F_{\sigma \delta }$-complete set.
Additionally, we compute the complexities of many other natural classes of separable Banach spaces; for instance, the class of separable 
$\mathcal {L}_{p,\lambda +}$-spaces, for 
$p,\lambda \geq 1$, is shown to be a 
$G_\delta $-set, the class of superreflexive spaces is shown to be an 
$F_{\sigma \delta }$-set, and the class of spaces with local 
$\Pi $-basis structure is shown to be a 
$\boldsymbol {\Sigma }^0_6$-set. The paper is concluded with many open problems and suggestions for a future research.
Celebrating 100 years of the Banach contraction principle, we prove some fixed point theorems having all ingredients of the principle, but dealing with common fixed points of a contractive semigroup of nonlinear mappings acting in a modulated topological vector space. This research follows the ideas of the author’s recent papers [‘On modulated topological vector spaces and applications’, Bull. Aust. Math. Soc. 101 (2020), 325–332, and ‘Normal structure in modulated topological vector spaces’, Comment. Math. 60 (2020), 1–11]. Modulated topological vector spaces generalise, among others, Banach spaces and modular function spaces. The interest in modulars reflects the fact that the notions of ‘norm like’ but ‘noneuclidean’ (and not even necessarily convex) constructs to measure a level of proximity between complex objects are frequently used in science and technology. To prove our fixed point results in this setting, we introduce a new concept of Opial sets using analogies with the norm-weak and modular versions of the Opial property. As an example, the results of this work can be applied to spaces like 
$L^p$ for 
$p> 0 $, variable Lebesgue spaces 
$L^{p(\cdot )}$ where 
$1 \leq p(t) < + \infty $, Orlicz and Musielak–Orlicz spaces.
In this article, we study a generalized Bohr radius
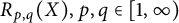$R_{p, q}(X), p, q\in [1, \infty )$
defined for a complex Banach space X. In particular, we determine the exact value of
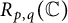$R_{p, q}(\mathbb {C})$
for the cases (i)
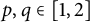$p, q\in [1, 2]$
, (ii)
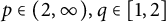$p\in (2, \infty ), q\in [1, 2]$
, and (iii)
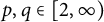$p, q\in [2, \infty )$
. Moreover, we consider an n-variable version
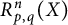$R_{p, q}^n(X)$
of the quantity
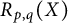$R_{p, q}(X)$
and determine (i)
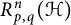$R_{p, q}^n(\mathcal {H})$
for an infinite-dimensional complex Hilbert space
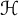$\mathcal {H}$
and (ii) the precise asymptotic value of
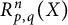$R_{p, q}^n(X)$
as
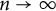$n\to \infty $
for finite-dimensional X. We also study the multidimensional analog of a related concept called the p-Bohr radius. To be specific, we obtain the asymptotic value of the n-dimensional p-Bohr radius for bounded complex-valued functions, and in the vector-valued case, we provide a lower estimate for the same, which is independent of n.
In this paper, we consider an equivalence relation on the space
$AP(\mathbb {R},X)$
of almost periodic functions with values in a prefixed Banach space X. In this context, it is known that the normality or Bochner-type property, which characterizes these functions, is based on the relative compactness of the family of translates. Now, we prove that every equivalence class is sequentially compact and the family of translates of a function belonging to this subspace is dense in its own class, i.e., the condition of almost periodicity of a function
$f\in AP(\mathbb {R},X)$
yields that every sequence of translates of f has a subsequence that converges to a function equivalent to f. This extends previous work by the same authors on the case of numerical almost periodic functions.
Non-amenability of 
${\mathcal {B}}(E)$ has been surprisingly difficult to prove for the classical Banach spaces, but is now known for E = ℓp and E = Lp for all 1 ⩽ p < ∞. However, the arguments are rather indirect: the proof for L1 goes via non-amenability of 
$\ell ^\infty ({\mathcal {K}}(\ell _1))$ and a transference principle developed by Daws and Runde (Studia Math., 2010).
In this note, we provide a short proof that 
${\mathcal {B}}(L_1)$ and some of its subalgebras are non-amenable, which completely bypasses all of this machinery. Our approach is based on classical properties of the ideal of representable operators on L1, and shows that 
${\mathcal {B}}(L_1)$ is not even approximately amenable.
Let 
${\mathcal{B}}_{n}(\unicode[STIX]{x1D6FA})$ be the set of Cowen–Douglas operators of index 
$n$ on a nonempty bounded connected open subset 
$\unicode[STIX]{x1D6FA}$ of 
$\mathbb{C}$. We consider the strong irreducibility of a class of Cowen–Douglas operators 
${\mathcal{F}}{\mathcal{B}}_{n}(\unicode[STIX]{x1D6FA})$ on Banach spaces. We show 
${\mathcal{F}}{\mathcal{B}}_{n}(\unicode[STIX]{x1D6FA})\subseteq {\mathcal{B}}_{n}(\unicode[STIX]{x1D6FA})$ and give some conditions under which an operator 
$T\in {\mathcal{F}}{\mathcal{B}}_{n}(\unicode[STIX]{x1D6FA})$ is strongly irreducible. All these results generalise similar results on Hilbert spaces.
Let 
$(X,+)$ be an Abelian group and 
$E$ be a Banach space. Suppose that 
$f:X\rightarrow E$ is a surjective map satisfying the inequality for some 
$$\begin{eqnarray}|\,\Vert f(x)-f(y)\Vert -\Vert f(x-y)\Vert \,|\leq {\it\varepsilon}\min \{\Vert f(x)-f(y)\Vert ^{p},\Vert f(x-y)\Vert ^{p}\}\end{eqnarray}$$
${\it\varepsilon}>0$, 
$p>1$ and for all 
$x,y\in X$. We prove that 
$f$ is an additive map. However, this result does not hold for 
$0<p\leq 1$. As an application, we show that if 
$f$ is a surjective map from a Banach space 
$E$ onto a Banach space 
$F$ so that for some 
${\it\epsilon}>0$ and 
$p>1$ whenever 
$$\begin{eqnarray}|\,\Vert f(x)-f(y)\Vert -\Vert f(u)-f(v)\Vert \,|\leq {\it\epsilon}\min \{\Vert f(x)-f(y)\Vert ^{p},\Vert f(u)-f(v)\Vert ^{p}\}\end{eqnarray}$$
$\Vert x-y\Vert =\Vert u-v\Vert$, then 
$f$ preserves equality of distance. Moreover, if 
$\dim E\geq 2$, there exists a constant 
$K\neq 0$ such that 
$Kf$ is an affine isometry. This improves a result of Vogt [‘Maps which preserve equality of distance’, Studia Math.45 (1973) 43–48].
