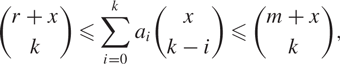2 results
Linear bounds on characteristic polynomials of matroids
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 168 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 10 January 2019, pp. 505-518
- Print publication:
- May 2020
-
- Article
- Export citation
-
Let χ(t) = a0tn – a1tn−1 + ⋯ + (−1)rartn−r be the chromatic polynomial of a graph, the characteristic polynomial of a matroid, or the characteristic polynomial of an arrangement of hyperplanes. For any integer k = 0, 1, …, r and real number x ⩾ k − r − 1, we obtain a linear bound of the coefficient sequence, that is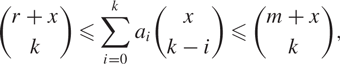
where m is the size of the graph, matroid, or hyperplane arrangement. It extends Whitney’s sign-alternating theorem, Meredith’s upper bound theorem, and Dowling and Wilson’s lower bound theorem on the coefficient sequence. In the end, we also propose a problem on the combinatorial interpretation of the above inequality.
\begin{align*} {r+x\choose k}\leqslant \sum_{i=0}^{k}a_{i}{x\choose k-i}\leqslant {m+x\choose k}, \end{align*}
Regions Cut by Arrangements of Topological Spheres
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 2 / 01 June 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-244
- Print publication:
- 01 June 1993
-
- Article
-
- You have access
- Export citation
