What parts of the classical descriptive set theory done in Polish spaces still hold for more general topological spaces, possibly T0 or T1, but not T2 (i.e. not Hausdorff)? This question has been addressed by Selivanov in a series of papers centred on algebraic domains. And recently it has been considered by de Brecht for quasi-Polish spaces, a framework that contains both countably based continuous domains and Polish spaces. In this paper, we present alternative unifying topological spaces, that we call approximation spaces. They are exactly the spaces for which player Nonempty has a stationary strategy in the Choquet game. A natural proper subclass of approximation spaces coincides with the class of quasi-Polish spaces. We study the Borel and Hausdorff difference hierarchies in approximation spaces, revisiting the work done for the other topological spaces. We also consider the problem of effectivization of these results.

We prove some results on the Wadge order on the space of sets of natural numbers endowed with Scott topology, and more generally, on omega-continuous domains. Using alternating decreasing chains we characterize the property of Wadge hardness for the classes of the Hausdorff difference hierarchy (iterated differences of open sets). A similar characterization holds for Wadge one-to-one and finite-to-one completeness. We consider the same questions for the effectivization of the Wadge relation. We also show that for the space of sets of natural numbers endowed with the Scott topology, in each class of the Hausdorff difference hierarchy there are two strictly increasing chains of Wadge degrees of sets properly in that class. The length of these chains is the rank of the considered class, and each element in one chain is incomparable with all the elements in the other chain.

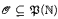We obtain a large class of significant examples of n-random reals (i.e., Martin-Löf random in oracle ∅(n−1)) à la Chaitin. Any such real is defined as the probability that a universal monotone Turing machine performing possibly infinite computations on infinite (resp. finite large enough, resp. finite self-delimited) inputs produces an output in a given set . In particular, we develop methods to transfer 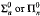many-one completeness results of index sets to n-randomness of associated probabilities.

We consider the question of randomness of the probability ΩU[X] that an optimal Turing machine U halts and outputs a string in a fixed set X. The main results are as follows:

• ΩU[X] is random whenever X is Σn0-complete or Πn0-complete for some n ≥ 2.

• However, for n ≥ 2, ΩU[X] is not n-random when X is Σn0 or Πn0. Nevertheless, there exists Δn+10 sets such that ΩU[X] is n-random.

• There are Δ20 sets X such that ΩU[X] is rational. Also, for every n ≥ 1, there exists a set X which is Δn+10 and Σn0-hard such that ΩU[X] is not random.

We also look at the range of ΩU as an operator. We prove that the set {ΩU[X]: X ⊆ 2≤ω} is a finite union of closed intervals. It follows that for any optimal machine U and any sufficiently small real r, there is a set X ⊆ 2≤ω recursive in ∅′ ⊕ r, such that ΩU[X] = r.

The same questions are also considered in the context of infinite computations, and lead to similar results.

We consider the four families of recognizable, synchronous, deterministic rational and rational subsets of a direct product of free monoids. They form a strict hierarchy and we investigate the following decision problem: given a relation in one of the families, does it belong to a smaller family? We settle the problem entirely when all monoids have a unique generator and fill some gaps in the general case. In particular, adapting a proof of Stearns, we show that it is recursively decidable whether or not a deterministic subset of an arbitrary number of free monoids is recognizable. Also we exhibit a single exponential algorithm for determining if a synchronous relation is recognizable.

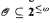Using possibly infinite computations on universal monotone Turing machines, we prove Martin-Löf randomness in ∅′ of the probability that the output be in some set under complexity assumptions about .

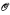We introduce a notion of syntactical truth predicate (s.t.p.) for the second order arithmetic PA2. An s.t.p. is a set T of closed formulas such that:

(i) T(t = u) if and only if the closed first order terms t and u are convertible, i.e., have the same value in the standard interpretation

(ii) T(A → B) if and only if (T(A) ⇒ T(B))

(iii) T(∀xA) if and only if (T(A[x ← t]) for any closed first order term t)

(iv) T(∀X A) if and only if (T(A[X ← ∆]) for any closed set definition ∆ = {x ∣ D(x)}).

S.t.p.'s can be seen as a counterpart to Tarski's notion of (model-theoretical) validity and have main model properties. In particular, their existence is equivalent to the existence of an ω-model of PA2, this fact being provable in PA2 with arithmetical comprehension only.

This paper is a contribution to the following natural problem in complexity theory:

(*) Is there a complexity theory for isomorphism types of recursive countable relational structures? I.e. given a recursive relational structure ℛ over the set N of nonnegative integers, is there a nontrivial lower bound for the time-space complexity of recursive structures isomorphic (resp. recursively isomorphic) to ℛ?

For unary recursive relations R, the answer is trivially negative: either R is finite or coinfinite or 〈N, R〉 is recursively isomorphic to 〈N, {x ϵ N: x is even}〉.

The general problem for relations with arity 2 (or greater) is open.

Related to this problem, a classical result (going back to S. C. Kleene [4], 1955) states that every recursive ordinal is in fact primitive recursive.

In [3] Patrick Dehornoy, using methods relevant to computer science, improves this result, showing that every recursive ordinal can be represented by a recursive total ordering over N which has linear deterministic time complexity relative to the binary representation of integers. As he notices, his proof applies to every recursive total order type α such that the isomorphism type of α is not changed if points are replaced by arbitrary finite nonempty subsets of consecutive points.

In this paper we extend Dehornoy's result to all recursive total orderings over N and get minimal complexity for both time and space simultaneously.