20 results
The emergence of bubble-induced scaling in thermal spectra in turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 958 / 10 March 2023
- Published online by Cambridge University Press:
- 27 February 2023, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
High humidity enhances the evaporation of non-aqueous volatile sprays
-
- Journal:
- Journal of Fluid Mechanics / Volume 956 / 10 February 2023
- Published online by Cambridge University Press:
- 02 February 2023, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Micro-droplet nucleation through solvent exchange in a turbulent buoyant jet
-
- Journal:
- Journal of Fluid Mechanics / Volume 943 / 25 July 2022
- Published online by Cambridge University Press:
- 06 June 2022, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Settling behaviour of thin curved particles in quiescent fluid and turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 922 / 10 September 2021
- Published online by Cambridge University Press:
- 16 July 2021, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterizing the turbulent drag properties of rough surfaces with a Taylor–Couette set-up
-
- Journal:
- Journal of Fluid Mechanics / Volume 919 / 25 July 2021
- Published online by Cambridge University Press:
- 01 June 2021, A45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kinematics and dynamics of freely rising spheroids at high Reynolds numbers
-
- Journal:
- Journal of Fluid Mechanics / Volume 912 / 10 April 2021
- Published online by Cambridge University Press:
- 09 February 2021, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double maxima of angular momentum transport in small gap
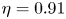 $\eta =0.91$ Taylor–Couette turbulence
$\eta =0.91$ Taylor–Couette turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 900 / 10 October 2020
- Published online by Cambridge University Press:
- 06 August 2020, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bubbly drag reduction using a hydrophobic inner cylinder in Taylor–Couette turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 883 / 25 January 2020
- Published online by Cambridge University Press:
- 29 November 2019, A61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Controlling secondary flow in Taylor–Couette turbulence through spanwise-varying roughness
-
- Journal:
- Journal of Fluid Mechanics / Volume 883 / 25 January 2020
- Published online by Cambridge University Press:
- 25 November 2019, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Drag reduction in boiling Taylor–Couette turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 881 / 25 December 2019
- Published online by Cambridge University Press:
- 24 October 2019, pp. 104-118
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Statistics, plumes and azimuthally travelling waves in ultimate Taylor–Couette turbulent vortices
-
- Journal:
- Journal of Fluid Mechanics / Volume 876 / 10 October 2019
- Published online by Cambridge University Press:
- 06 August 2019, pp. 733-765
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The influence of wall roughness on bubble drag reduction in Taylor–Couette turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 851 / 25 September 2018
- Published online by Cambridge University Press:
- 20 July 2018, pp. 436-446
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite-sized rigid spheres in turbulent Taylor–Couette flow: effect on the overall drag
-
- Journal:
- Journal of Fluid Mechanics / Volume 850 / 10 September 2018
- Published online by Cambridge University Press:
- 04 July 2018, pp. 246-261
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodically driven Taylor–Couette turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 846 / 10 July 2018
- Published online by Cambridge University Press:
- 10 May 2018, pp. 834-845
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental investigation of heat transport in homogeneous bubbly flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 845 / 25 June 2018
- Published online by Cambridge University Press:
- 20 April 2018, pp. 226-244
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turbulence strength in ultimate Taylor–Couette turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 836 / 10 February 2018
- Published online by Cambridge University Press:
- 11 December 2017, pp. 397-412
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Taylor–Couette turbulence at radius ratio
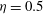 ${\it\eta}=0.5$: scaling, flow structures and plumes
${\it\eta}=0.5$: scaling, flow structures and plumes
-
- Journal:
- Journal of Fluid Mechanics / Volume 799 / 25 July 2016
- Published online by Cambridge University Press:
- 23 June 2016, pp. 334-351
-
- Article
- Export citation
Azimuthal velocity profiles in Rayleigh-stable Taylor–Couette flow and implied axial angular momentum transport
-
- Journal:
- Journal of Fluid Mechanics / Volume 774 / 10 July 2015
- Published online by Cambridge University Press:
- 09 June 2015, pp. 342-362
-
- Article
- Export citation
Optimal Taylor–Couette flow: radius ratio dependence
-
- Journal:
- Journal of Fluid Mechanics / Volume 747 / 25 May 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 1-29
-
- Article
- Export citation
Optimal Taylor–Couette turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 706 / 10 September 2012
- Published online by Cambridge University Press:
- 03 July 2012, pp. 118-149
-
- Article
- Export citation



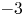
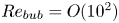
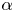
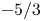
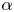
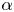
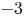
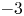
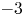

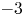
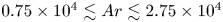

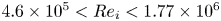
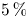
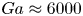

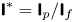
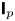

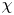
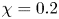
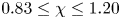
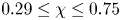
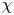
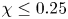
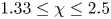
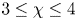
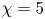
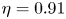
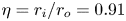
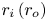
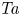
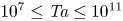
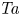
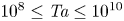
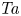
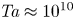
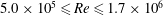

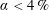
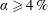
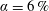

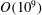
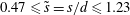
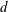
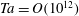

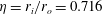
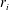

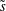
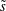
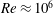


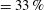
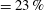
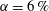
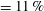
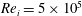
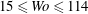
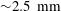
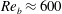

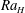
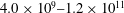
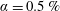
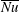
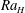

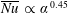
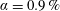
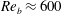
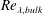
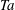
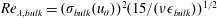
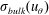
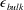

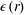
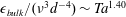
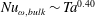
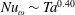
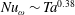
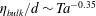
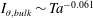
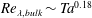
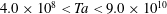
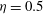
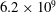
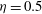
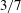
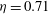
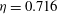
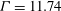
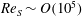
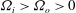
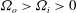
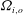
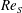
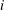

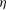
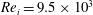
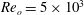
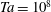
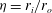
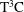
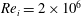
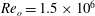
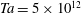
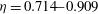
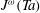
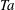
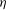
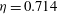
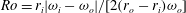
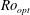
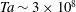
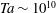
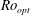
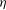
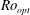
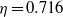 is experimentally studied. From global torque measurements, we analyse the dimensionless angular velocity flux
is experimentally studied. From global torque measurements, we analyse the dimensionless angular velocity flux 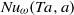 as a function of the Taylor number
as a function of the Taylor number 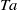 and the angular velocity ratio
and the angular velocity ratio 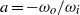 in the large-Taylor-number regime
in the large-Taylor-number regime 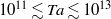 and well off the inviscid stability borders (Rayleigh lines)
and well off the inviscid stability borders (Rayleigh lines) 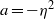 for co-rotation and
for co-rotation and 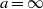 for counter-rotation. We analyse the data with the common power-law ansatz for the dimensionless angular velocity transport flux
for counter-rotation. We analyse the data with the common power-law ansatz for the dimensionless angular velocity transport flux 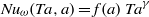 , with an amplitude
, with an amplitude 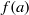 and an exponent
and an exponent 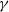 . The data are consistent with one effective exponent
. The data are consistent with one effective exponent 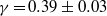 for all
for all  , but we discuss a possible
, but we discuss a possible  dependence in the co- and weakly counter-rotating regimes. The amplitude of the angular velocity flux
dependence in the co- and weakly counter-rotating regimes. The amplitude of the angular velocity flux 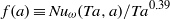 is measured to be maximal at slight counter-rotation, namely at an angular velocity ratio of
is measured to be maximal at slight counter-rotation, namely at an angular velocity ratio of 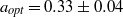 , i.e. along the line
, i.e. along the line 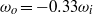 . This value is theoretically interpreted as the result of a competition between the destabilizing inner cylinder rotation and the stabilizing but shear-enhancing outer cylinder counter-rotation. With the help of laser Doppler anemometry, we provide angular velocity profiles and in particular identify the radial position
. This value is theoretically interpreted as the result of a competition between the destabilizing inner cylinder rotation and the stabilizing but shear-enhancing outer cylinder counter-rotation. With the help of laser Doppler anemometry, we provide angular velocity profiles and in particular identify the radial position 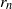 of the neutral line, defined by
of the neutral line, defined by 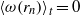 for fixed height
for fixed height  . For these large
. For these large 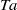 values, the ratio
values, the ratio 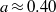 , which is close to
, which is close to 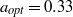 , is distinguished by a zero angular velocity gradient
, is distinguished by a zero angular velocity gradient 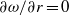 in the bulk. While for moderate counter-rotation
in the bulk. While for moderate counter-rotation 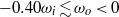 , the neutral line still remains close to the outer cylinder and the probability distribution function of the bulk angular velocity is observed to be monomodal. For stronger counter-rotation the neutral line is pushed inwards towards the inner cylinder; in this regime the probability distribution function of the bulk angular velocity becomes bimodal, reflecting intermittent bursts of turbulent structures beyond the neutral line into the outer flow domain, which otherwise is stabilized by the counter-rotating outer cylinder. Finally, a hypothesis is offered allowing a unifying view and consistent interpretation for all these various results.
, the neutral line still remains close to the outer cylinder and the probability distribution function of the bulk angular velocity is observed to be monomodal. For stronger counter-rotation the neutral line is pushed inwards towards the inner cylinder; in this regime the probability distribution function of the bulk angular velocity becomes bimodal, reflecting intermittent bursts of turbulent structures beyond the neutral line into the outer flow domain, which otherwise is stabilized by the counter-rotating outer cylinder. Finally, a hypothesis is offered allowing a unifying view and consistent interpretation for all these various results.