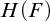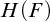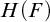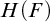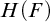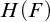2 results
INTERPRETING A FIELD IN ITS HEISENBERG GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 23 December 2021, pp. 1215-1230
- Print publication:
- September 2022
-
- Article
- Export citation
Some Results in Computability Theory
-
- Journal:
- Bulletin of Symbolic Logic / Volume 25 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 13 February 2020, pp. 452-453
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation