8 results
On the Maximum Number of Spanning Copies of an Orientation in a Tournament
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 06 June 2017, pp. 775-796
-
- Article
- Export citation
Large Feedback Arc Sets, High Minimum Degree Subgraphs, and Long Cycles in Eulerian Digraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 22 / Issue 6 / November 2013
- Published online by Cambridge University Press:
- 12 September 2013, pp. 859-873
-
- Article
- Export citation
Dense Graphs With a Large Triangle Cover Have a Large Triangle Packing
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 27 September 2012, pp. 952-962
-
- Article
- Export citation
Threshold Functions for H-factors
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 137-144
-
- Article
- Export citation
Packing Cliques in Graphs with Independence Number 2
-
- Journal:
- Combinatorics, Probability and Computing / Volume 16 / Issue 5 / September 2007
- Published online by Cambridge University Press:
- 01 September 2007, pp. 805-817
-
- Article
- Export citation
Families of Trees Decompose the Random Graph in an Arbitrary Way
-
- Journal:
- Combinatorics, Probability and Computing / Volume 13 / Issue 6 / November 2004
- Published online by Cambridge University Press:
- 03 November 2004, pp. 893-910
-
- Article
- Export citation
Dominating a Family of Graphs with Small Connected Subgraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 9 / Issue 4 / July 2000
- Published online by Cambridge University Press:
- 03 November 2000, pp. 309-313
-
- Article
- Export citation
Independent Transversals and Independent Coverings in Sparse Partite Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 01 March 1997, pp. 115-125
-
- Article
- Export citation

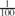
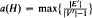 , where the maximum is taken over all subgraphs (
, where the maximum is taken over all subgraphs (