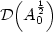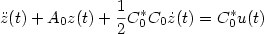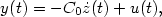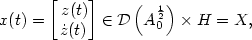7 results
Single input controllability of a simplified fluid-structure interaction model
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 23 February 2012, pp. 20-42
- Print publication:
- January 2013
-
- Article
- Export citation
On the null-controllability of diffusion equations
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 23 August 2010, pp. 1088-1100
- Print publication:
- October 2011
-
- Article
- Export citation
Uniformly exponentially stable approximations for a class of second order evolution equations: Application to LQR problems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 3 / July 2007
- Published online by Cambridge University Press:
- 05 June 2007, pp. 503-527
- Print publication:
- July 2007
-
- Article
- Export citation
How to get a conservative well-posed linear system out of thin air. Part I. Well-posedness and energy balance
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 9 / January 2003
- Published online by Cambridge University Press:
- 15 September 2003, pp. 247-273
- Print publication:
- January 2003
-
- Article
- Export citation
Simultaneous controllability in sharp time for two elastic strings
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 6 / 2001
- Published online by Cambridge University Press:
- 15 August 2002, pp. 259-273
- Print publication:
- 2001
-
- Article
- Export citation
Stabilization of second order evolution equations by a class of unbounded feedbacks
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 6 / 2001
- Published online by Cambridge University Press:
- 15 August 2002, pp. 361-386
- Print publication:
- 2001
-
- Article
- Export citation
Regularity of plate equations with control concentrated in interior curves
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 5 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1005-1025
- Print publication:
- 1997
-
- Article
- Export citation