Gerards and Seymour (see [10], p. 115) conjectured that if a graph has no odd complete minor of order l, then it is (l − 1)-colourable. This is an analogue of the well-known conjecture of Hadwiger, and in fact, this would immediately imply Hadwiger's conjecture. The current best-known bound for the chromatic number of graphs with no odd complete minor of order l is 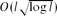 by the recent result by Geelen, Gerards, Reed, Seymour and Vetta [8], and by Kawarabayashi [12] later, independently. But it seems very hard to improve this bound since this would also improve the current best-known bound for the chromatic number of graphs with no complete minor of order l.
by the recent result by Geelen, Gerards, Reed, Seymour and Vetta [8], and by Kawarabayashi [12] later, independently. But it seems very hard to improve this bound since this would also improve the current best-known bound for the chromatic number of graphs with no complete minor of order l.
Motivated by this problem, in this note we show that there exists an absolute constant f(k) such that any graph G with no odd complete minor of order k admits a vertex partition V1, . . ., V496k such that each component in the subgraph induced on Vi (i ≥ 1) has at most f(k) vertices. When f(k) = 1, this is a colouring of G. Hence this is a relaxation of colouring in a sense, and this is the first result in this direction for the odd Hadwiger's conjecture.
Our proof is based on a recent decomposition theorem due to Geelen, Gerards, Reed, Seymour and Vetta [8], together with a connectivity result that forces a huge complete bipartite minor in large graphs by Böhme, Kawarabayashi, Maharry and Mohar [3].

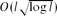 by the recent result by Geelen, Gerards, Reed, Seymour and Vetta [8], and by Kawarabayashi [12] later, independently. But it seems very hard to improve this bound since this would also improve the current best-known bound for the chromatic number of graphs with no complete minor of order
by the recent result by Geelen, Gerards, Reed, Seymour and Vetta [8], and by Kawarabayashi [12] later, independently. But it seems very hard to improve this bound since this would also improve the current best-known bound for the chromatic number of graphs with no complete minor of order 