45 results
EXPANDING THE REALS BY CONTINUOUS FUNCTIONS ADDS NO COMPUTATIONAL POWER
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 1083-1102
- Print publication:
- September 2023
-
- Article
- Export citation
COPYING ONE OF A PAIR OF STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1201-1214
- Print publication:
- September 2022
-
- Article
- Export citation
CODING IN GRAPHS AND LINEAR ORDERINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 673-690
- Print publication:
- June 2020
-
- Article
- Export citation
UNIFORM PROCEDURES IN UNCOUNTABLE STRUCTURES
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 529-550
- Print publication:
- June 2018
-
- Article
- Export citation
COMPUTING STRENGTH OF STRUCTURES RELATED TO THE FIELD OF REAL NUMBERS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 21 March 2017, pp. 137-150
- Print publication:
- March 2017
-
- Article
- Export citation
Computable structure theory using admissible recursion theory on ω1 using admissibility
-
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp 50-80
-
- Chapter
- Export citation
Isomorphism relations on computable structures
-
- Journal:
- The Journal of Symbolic Logic / Volume 77 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 12 March 2014, pp. 122-132
- Print publication:
- March 2012
-
- Article
- Export citation
Intrinsic bounds on complexity and definability at limit levels
-
- Journal:
- The Journal of Symbolic Logic / Volume 74 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1047-1060
- Print publication:
- September 2009
-
- Article
- Export citation
Spectra of Atomic Theories
-
- Journal:
- The Journal of Symbolic Logic / Volume 78 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1189-1198
- Print publication:
- December 2013
-
- Article
- Export citation
Turing computable embeddings
-
- Journal:
- The Journal of Symbolic Logic / Volume 72 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 12 March 2014, pp. 901-918
- Print publication:
- September 2007
-
- Article
- Export citation
Classification from a Computable Viewpoint
-
- Journal:
- Bulletin of Symbolic Logic / Volume 12 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 15 January 2014, pp. 191-218
- Print publication:
- June 2006
-
- Article
- Export citation
Computable trees of Scott rank ω1CK, and computable approximation
-
- Journal:
- The Journal of Symbolic Logic / Volume 71 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 12 March 2014, pp. 283-298
- Print publication:
- March 2006
-
- Article
- Export citation
Models of arithmetic: quantifiers and complexity
-
-
- Book:
- Reverse Mathematics 2001
- Published online:
- 31 March 2017
- Print publication:
- 02 March 2005, pp 271-280
-
- Chapter
- Export citation
Sequences of degrees associated with models of arithmetic
- from ARTICLES
-
-
- Book:
- Logic Colloquium '01
- Published online:
- 31 March 2017
- Print publication:
- 02 March 2005, pp 217-241
-
- Chapter
- Export citation
Bounding prime models
-
- Journal:
- The Journal of Symbolic Logic / Volume 69 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1117-1142
- Print publication:
- December 2004
-
- Article
- Export citation
Π11 relations and paths through
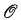
-
- Journal:
- The Journal of Symbolic Logic / Volume 69 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 12 March 2014, pp. 585-611
- Print publication:
- June 2004
-
- Article
- Export citation
Barwise: Infinitary Logic and Admissible Sets
-
- Journal:
- Bulletin of Symbolic Logic / Volume 10 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 15 January 2014, pp. 4-36
- Print publication:
- March 2004
-
- Article
- Export citation
Sequences of n-diagrams
-
- Journal:
- The Journal of Symbolic Logic / Volume 67 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1227-1247
- Print publication:
- September 2002
-
- Article
- Export citation
Minimality and completions of PA
-
- Journal:
- The Journal of Symbolic Logic / Volume 66 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1447-1457
- Print publication:
- September 2001
-
- Article
- Export citation
Computable Boolean algebras
-
- Journal:
- The Journal of Symbolic Logic / Volume 65 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1605-1623
- Print publication:
- December 2000
-
- Article
- Export citation

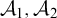
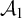
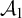
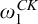
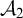
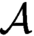
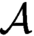
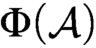
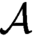
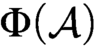
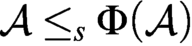
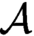
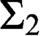
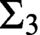
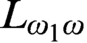
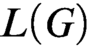
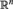
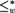
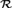
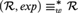
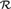
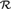
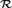
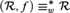
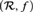
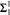 equivalence relations on hyperarithmetical subsets of
equivalence relations on hyperarithmetical subsets of 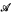 that is
that is 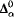 categorical, but not relatively
categorical, but not relatively 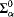 Scott family). We also show that for every computable limit ordinal
Scott family). We also show that for every computable limit ordinal 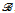 , the
, the 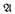 of
of 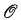
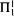 on a structure. We consider some examples of computable structures
on a structure. We consider some examples of computable structures 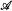 and intrinsically
and intrinsically 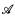 , the complete (elementary) diagram,
, the complete (elementary) diagram, 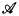 is a non-standard model of
is a non-standard model of 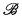 ):
): 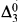 Boolean algebra need not have a computable copy (see also [T
Boolean algebra need not have a computable copy (see also [T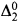 with certain added predicates can be embedded in one which is
with certain added predicates can be embedded in one which is 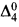 , at worst, and the same is true for a low
, at worst, and the same is true for a low