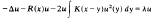4 results
Stabilization of a layered piezoelectric 3-D body by boundary dissipation
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 12 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 22 March 2006, pp. 198-215
- Print publication:
- April 2006
-
- Article
- Export citation
Decay rates of the solutions of nonlinear dispersive equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 124 / Issue 6 / 1994
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1231-1246
- Print publication:
- 1994
-
- Article
- Export citation
Propagation of classical solutions to the perturbed wave equation in a space of odd dimension
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 96 / Issue 3-4 / 1984
- Published online by Cambridge University Press:
- 14 November 2011, pp. 337-344
- Print publication:
- 1984
-
- Article
- Export citation
On regular solutions of a nonlinear equation of Choquard's type
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 86 / Issue 3-4 / 1980
- Published online by Cambridge University Press:
- 14 November 2011, pp. 291-301
- Print publication:
- 1980
-
- Article
- Export citation

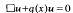 in ℝ
in ℝ