18 results
Turán problems in pseudorandom graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large cliques or cocliques in hypergraphs with forbidden order-size pairs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 286-299
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extremal problems for convex geometric hypergraphs and ordered hypergraphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 10 August 2020, pp. 1648-1666
- Print publication:
- December 2021
-
- Article
- Export citation
DISCRETE METRIC SPACES: STRUCTURE, ENUMERATION, AND 0-1 LAWS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 19 August 2019, pp. 1293-1325
- Print publication:
- December 2019
-
- Article
- Export citation
THE ERDŐS–SZEKERES PROBLEM AND AN INDUCED RAMSEY QUESTION
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 702-707
- Print publication:
- 2019
-
- Article
- Export citation
An Extremal Graph Problem with a Transcendental Solution
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 26 June 2018, pp. 303-324
-
- Article
- Export citation
Multicolour Sunflowers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 6 / November 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 974-987
-
- Article
- Export citation
Improved Bounds for the Ramsey Number of Tight Cycles Versus Cliques
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 08 March 2016, pp. 791-796
-
- Article
- Export citation
Perfect Packings in Quasirandom Hypergraphs II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 27 October 2015, pp. 595-611
-
- Article
- Export citation
On the Chromatic Thresholds of Hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 06 March 2015, pp. 172-212
-
- Article
- Export citation
EIGENVALUES AND LINEAR QUASIRANDOM HYPERGRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 14 January 2015, e2
-
- Article
-
- You have access
- Open access
- Export citation
Counting Independent Sets in Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 08 April 2014, pp. 539-550
-
- Article
- Export citation
The Turán Number of F3,3
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 29 November 2011, pp. 451-456
-
- Article
- Export citation
Erdős–Ko–Rado in Random Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 18 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 01 September 2009, pp. 629-646
-
- Article
- Export citation
Simplex Stability
-
- Journal:
- Combinatorics, Probability and Computing / Volume 18 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 441-454
-
- Article
- Export citation
When is an Almost Monochromatic K4 Guaranteed?
-
- Journal:
- Combinatorics, Probability and Computing / Volume 17 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 823-830
-
- Article
- Export citation
Rainbow Turán Problems
-
- Journal:
- Combinatorics, Probability and Computing / Volume 16 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 04 September 2006, pp. 109-126
-
- Article
- Export citation
Some Exact Results and New Asymptotics for Hypergraph Turán Numbers
-
- Journal:
- Combinatorics, Probability and Computing / Volume 11 / Issue 3 / May 2002
- Published online by Cambridge University Press:
- 10 July 2002, pp. 299-309
-
- Article
- Export citation

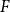
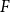
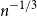
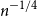
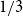
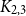
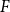
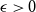

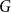
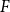
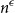
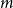
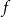
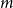
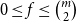
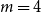
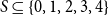
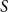
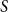
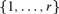
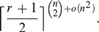
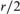
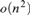
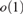
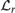
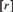
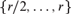
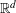
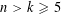
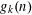
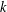
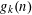
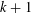

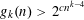
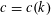
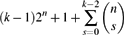
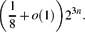
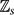
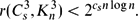
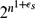
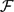
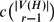
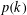
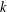
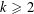
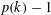
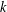
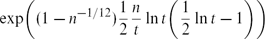
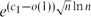
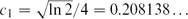
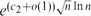
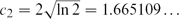
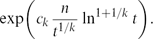
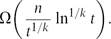
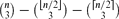 . This sharpens results of Zhou [9] and of the second author and Rödl [7].
. This sharpens results of Zhou [9] and of the second author and Rödl [7].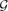
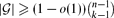 , then there is a vertex
, then there is a vertex 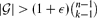 for any ϵ < 0 and
for any ϵ < 0 and 