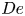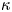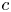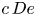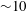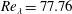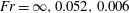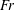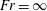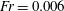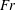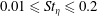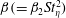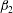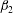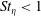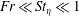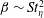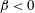75 results
Rotation of a fibre in simple shear flow of a dilute polymer solution
-
- Journal:
- Journal of Fluid Mechanics / Volume 976 / 10 December 2023
- Published online by Cambridge University Press:
- 28 November 2023, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The role of rolling resistance in the rheology of wizarding quidditch ball suspensions
-
- Journal:
- Journal of Fluid Mechanics / Volume 974 / 10 November 2023
- Published online by Cambridge University Press:
- 03 November 2023, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Collision efficiency of like-charged spheres settling in a quiescent environment
-
- Journal:
- Journal of Fluid Mechanics / Volume 968 / 10 August 2023
- Published online by Cambridge University Press:
- 04 August 2023, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of a self-propelled compound droplet
-
- Journal:
- Journal of Fluid Mechanics / Volume 952 / 10 December 2022
- Published online by Cambridge University Press:
- 24 November 2022, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Collision efficiency of non-Brownian spheres in a simple shear flow – the role of non-continuum hydrodynamic interactions
-
- Journal:
- Journal of Fluid Mechanics / Volume 950 / 10 November 2022
- Published online by Cambridge University Press:
- 19 October 2022, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Electroconvection near an ion-selective surface with Butler–Volmer kinetics
-
- Journal:
- Journal of Fluid Mechanics / Volume 930 / 10 January 2022
- Published online by Cambridge University Press:
- 11 November 2021, A26
-
- Article
- Export citation
Non-continuum tangential lubrication gas flow between two spheres
-
- Journal:
- Journal of Fluid Mechanics / Volume 920 / 10 August 2021
- Published online by Cambridge University Press:
- 04 June 2021, A2
-
- Article
- Export citation
Collision rate of bidisperse, hydrodynamically interacting spheres settling in a turbulent flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 912 / 10 April 2021
- Published online by Cambridge University Press:
- 04 February 2021, A5
-
- Article
- Export citation
Collision rate of bidisperse spheres settling in a compressional non-continuum gas flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 910 / 10 March 2021
- Published online by Cambridge University Press:
- 08 January 2021, A10
-
- Article
- Export citation
Electrophoresis in dilute polymer solutions
-
- Journal:
- Journal of Fluid Mechanics / Volume 884 / 10 February 2020
- Published online by Cambridge University Press:
- 05 December 2019, A9
-
- Article
- Export citation
The hydrodynamic lift of a slender, neutrally buoyant fibre in a wall-bounded shear flow at small Reynolds number
-
- Journal:
- Journal of Fluid Mechanics / Volume 879 / 25 November 2019
- Published online by Cambridge University Press:
- 19 September 2019, pp. 121-146
-
- Article
- Export citation
Slender body theory for particles with non-circular cross-sections with application to particle dynamics in shear flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 877 / 25 October 2019
- Published online by Cambridge University Press:
- 02 September 2019, pp. 1098-1133
-
- Article
- Export citation
The combined hydrodynamic and thermodynamic effects of immobilized proteins on the diffusion of mobile transmembrane proteins
-
- Journal:
- Journal of Fluid Mechanics / Volume 877 / 25 October 2019
- Published online by Cambridge University Press:
- 27 August 2019, pp. 648-681
-
- Article
- Export citation
The rapid distortion of two-way coupled particle-laden turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 877 / 25 October 2019
- Published online by Cambridge University Press:
- 19 August 2019, pp. 82-104
-
- Article
- Export citation
Inertial torques and a symmetry breaking orientational transition in the sedimentation of slender fibres
-
- Journal:
- Journal of Fluid Mechanics / Volume 875 / 25 September 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 576-596
-
- Article
- Export citation
Clustering of rapidly settling, low-inertia particle pairs in isotropic turbulence. Part 2. Comparison of theory and DNS
-
- Journal:
- Journal of Fluid Mechanics / Volume 871 / 25 July 2019
- Published online by Cambridge University Press:
- 22 May 2019, pp. 477-488
-
- Article
- Export citation
Clustering of rapidly settling, low-inertia particle pairs in isotropic turbulence. Part 1. Drift and diffusion flux closures
-
- Journal:
- Journal of Fluid Mechanics / Volume 871 / 25 July 2019
- Published online by Cambridge University Press:
- 22 May 2019, pp. 450-476
-
- Article
- Export citation
Clustering in Euler–Euler and Euler–Lagrange simulations of unbounded homogeneous particle-laden shear
-
- Journal:
- Journal of Fluid Mechanics / Volume 859 / 25 January 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 174-203
-
- Article
- Export citation
The effects of fluid transport on the creation of a dense cluster of activated fractures in a porous medium
-
- Journal:
- Journal of Fluid Mechanics / Volume 847 / 25 July 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 286-328
-
- Article
- Export citation
Controlling rotation and migration of rings in a simple shear flow through geometric modifications
-
- Journal:
- Journal of Fluid Mechanics / Volume 840 / 10 April 2018
- Published online by Cambridge University Press:
- 12 February 2018, pp. 379-407
-
- Article
- Export citation