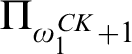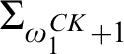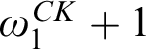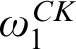7 results
STRUCTURAL HIGHNESS NOTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 1692-1724
- Print publication:
- December 2023
-
- Article
- Export citation
SCOTT COMPLEXITY OF COUNTABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1706-1720
- Print publication:
- December 2021
-
- Article
- Export citation
RELATIONSHIPS BETWEEN COMPUTABILITY-THEORETIC PROPERTIES OF PROBLEMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 47-71
- Print publication:
- March 2022
-
- Article
- Export citation
STRONG JUMP-TRACEABILITY
-
- Journal:
- Bulletin of Symbolic Logic / Volume 24 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 07 August 2018, pp. 147-164
- Print publication:
- June 2018
-
- Article
- Export citation
The finite intersection principle and genericity
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 160 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 26 November 2015, pp. 279-297
- Print publication:
- March 2016
-
- Article
- Export citation
CHARACTERIZING LOWNESS FOR DEMUTH RANDOMNESS
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 25 June 2014, pp. 526-560
- Print publication:
- June 2014
-
- Article
- Export citation
COMPUTING K-TRIVIAL SETS BY INCOMPLETE RANDOM SETS
-
- Journal:
- Bulletin of Symbolic Logic / Volume 20 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 13 May 2014, pp. 80-90
- Print publication:
- March 2014
-
- Article
- Export citation