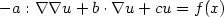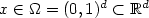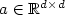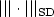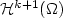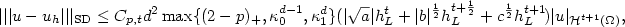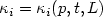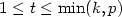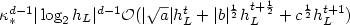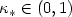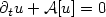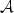16 results
Space-time variational saddle point formulations of Stokes and Navier–Stokes equations∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 24 April 2014, pp. 875-894
- Print publication:
- May 2014
-
- Article
- Export citation
Approximation by harmonic polynomials in star-shaped domains and exponential convergence of Trefftz hp-dGFEM∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 11 February 2014, pp. 727-752
- Print publication:
- May 2014
-
- Article
- Export citation
High order approximation of probabilistic shock profiles in hyperbolic conservation laws with uncertain initial data∗∗∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 3 / May 2013
- Published online by Cambridge University Press:
- 29 March 2013, pp. 807-835
- Print publication:
- May 2013
-
- Article
- Export citation
Contributors
-
-
- Book:
- Neuroimaging of Sleep and Sleep Disorders
- Published online:
- 05 March 2013
- Print publication:
- 07 March 2013, pp viii-xii
-
- Chapter
- Export citation
Sparse adaptive Taylor approximation algorithms for parametric and stochastic elliptic PDEs∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 29 November 2012, pp. 253-280
- Print publication:
- January 2013
-
- Article
- Export citation
Single Mode, Extreme Precision Doppler Spectrographs
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 8 / Issue S293 / August 2012
- Published online by Cambridge University Press:
- 29 April 2014, pp. 403-406
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
Contributors
-
-
- Book:
- Stroke Syndromes, 3ed
- Published online:
- 05 August 2012
- Print publication:
- 12 July 2012, pp vii-x
-
- Chapter
- Export citation
Contributors
-
-
- Book:
- Core Topics in Neuroanaesthesia and Neurointensive Care
- Published online:
- 05 December 2011
- Print publication:
- 13 October 2011, pp vii-x
-
- Chapter
- Export citation
Sparse tensor discretizations of high-dimensional parametric and stochastic PDEs*
-
- Journal:
- Acta Numerica / Volume 20 / May 2011
- Published online by Cambridge University Press:
- 28 April 2011, pp. 291-467
- Print publication:
- May 2011
-
- Article
- Export citation
Exponential convergence of hp quadrature for integral operators with Gevrey kernels
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 45 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 11 October 2010, pp. 387-422
- Print publication:
- May 2011
-
- Article
- Export citation
Sparse finite element approximation of high-dimensional transport-dominated diffusion problems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 42 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 30 July 2008, pp. 777-819
- Print publication:
- September 2008
-
- Article
- Export citation
Influence of deposition chamber pressure and substrate temperature on the properties of fluorescent blue and phosphorescent red OLED deposited by OVPD
-
- Journal:
- MRS Online Proceedings Library Archive / Volume 1003 / 2008
- Published online by Cambridge University Press:
- 20 February 2017, 1003-O02-24
- Print publication:
- 2008
-
- Article
- Export citation
Fast deterministic pricing of options on Lévy driven assets
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 37-71
- Print publication:
- January 2004
-
- Article
- Export citation
Numerical solution of parabolic equations in high dimensions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 93-127
- Print publication:
- January 2004
-
- Article
- Export citation
hp-FEM for three-dimensional elastic plates
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 4 / July 2002
- Published online by Cambridge University Press:
- 15 September 2002, pp. 597-630
- Print publication:
- July 2002
-
- Article
- Export citation
Two-scale FEM for homogenization problems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 4 / July 2002
- Published online by Cambridge University Press:
- 15 September 2002, pp. 537-572
- Print publication:
- July 2002
-
- Article
- Export citation