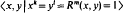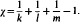38 results
Psychotropic medicines’ prevalence, patterns and effects on cognitive and physical function in older adults with intellectual disability in Ireland: longitudinal cohort study, 2009–2020
-
- Journal:
- BJPsych Open / Volume 10 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 01 February 2024, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Aid Triangle: Recognising the Human Dynamics of Dominance, Justice and Identity
-
- Journal:
- Journal of Pacific Rim Psychology / Volume 5 / Issue 1 / 01 August 2011
- Published online by Cambridge University Press:
- 23 February 2012, pp. 51-52
- Print publication:
- 01 August 2011
-
- Article
-
- You have access
- Export citation
Experiential Realism. By A. H. Johnson. London: George Allen & Unwin, New York: Humanities Press (Muirhead Library of Philosophy). 1973. pp. 443 $24.00.
-
- Journal:
- Dialogue: Canadian Philosophical Review / Revue canadienne de philosophie / Volume 13 / Issue 2 / June 1974
- Published online by Cambridge University Press:
- 09 June 2010, pp. 382-384
-
- Article
- Export citation
Thinking and Perceiving. By John W. Yolton. LaSalle, Illinois: Open Court Publishing Company. 1962, pp. xi, 161. $3.50.
-
- Journal:
- Dialogue: Canadian Philosophical Review / Revue canadienne de philosophie / Volume 2 / Issue 3 / December 1963
- Published online by Cambridge University Press:
- 09 June 2010, pp. 365-366
-
- Article
- Export citation
In Contact with the Physical World. By John Pennycuick. London: George Allen & Unwin; New York: Humanities Press. 1972. Pp. 150. $10.50.
-
- Journal:
- Dialogue: Canadian Philosophical Review / Revue canadienne de philosophie / Volume 11 / Issue 3 / September 1972
- Published online by Cambridge University Press:
- 09 June 2010, pp. 466-469
-
- Article
- Export citation
Analysis and Dialectic: Studies in the Logic of Foundation ProblemsJoseph J. Russell Nijhoff International Philosophy Series The Hague: Martinus Nijhoff, 1984. Pp. xxii, 464. $91.00
-
- Journal:
- Dialogue: Canadian Philosophical Review / Revue canadienne de philosophie / Volume 25 / Issue 3 / Autumn 1986
- Published online by Cambridge University Press:
- 13 April 2010, pp. 594-599
-
- Article
- Export citation
Commensurability classes of arithmetic Fuchsian surface groups of genus 2
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 148 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 28 September 2009, pp. 117-133
- Print publication:
- January 2010
-
- Article
- Export citation
A. J. Casson and S. A. Bleiler, Automorphisms of surfaces after Nielsen and Thurston (London Mathematical Society Student Texts 9, Cambridge University Press, Cambridge1988) 104 pp., cloth 0 521 34203 1, £20; paper 0 521 34985 0, £7.50.
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 34 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 20 January 2009, p. 167
-
- Article
-
- You have access
- Export citation
A. J. Beardon A primer on Riemann surfaces (London Mathematical Society Lecture Note Series 78, Cambridge University Press, 1984), 188 pp. £12.95.
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 28 / Issue 3 / October 1985
- Published online by Cambridge University Press:
- 20 January 2009, p. 425
-
- Article
-
- You have access
- Export citation
On discrete generalised triangle groups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 38 / Issue 3 / October 1995
- Published online by Cambridge University Press:
- 20 January 2009, pp. 397-412
-
- Article
-
- You have access
- Export citation
TORSION IN ARITHMETIC FUCHSIAN GROUPS
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 22 February 2006, pp. 14-30
- Print publication:
- February 2006
-
- Article
- Export citation
Previously treated oesophageal achalasia re-presenting with stridor
-
- Journal:
- The Journal of Laryngology & Otology / Volume 119 / Issue 3 / March 2005
- Published online by Cambridge University Press:
- 08 March 2006, pp. 237-238
- Print publication:
- March 2005
-
- Article
- Export citation
All Kleinian groups with two elliptic generators whose commutator is elliptic
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 135 / Issue 3 / November 2003
- Published online by Cambridge University Press:
- 24 October 2003, pp. 413-420
- Print publication:
- November 2003
-
- Article
- Export citation
Introduction arithmetic of Fuchsian groups
-
-
- Book:
- Topics on Riemann Surfaces and Fuchsian Groups
- Published online:
- 04 August 2010
- Print publication:
- 14 June 2001, pp 29-42
-
- Chapter
- Export citation
6 - Constructing hyperbolic manifolds
-
-
- Book:
- Computational and Geometric Aspects of Modern Algebra
- Published online:
- 06 July 2010
- Print publication:
- 15 June 2000, pp 78-86
-
- Chapter
- Export citation
INVARIANT TRACE-FIELDS AND QUATERNION ALGEBRAS OF POLYHEDRAL GROUPS
-
- Journal:
- Journal of the London Mathematical Society / Volume 58 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 01 December 1998, pp. 709-722
- Print publication:
- December 1998
-
- Article
- Export citation
Generating functions for finite group actions on surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 124 / Issue 1 / July 1998
- Published online by Cambridge University Press:
- 01 July 1998, pp. 21-49
- Print publication:
- July 1998
-
- Article
- Export citation
TWO-GENERATOR ARITHMETIC KLEINIAN GROUPS II
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 30 / Issue 3 / May 1998
- Published online by Cambridge University Press:
- 01 May 1998, pp. 258-266
- Print publication:
- May 1998
-
- Article
- Export citation
Minimum topological genus of compact bordered Klein surfaces admitting a prime-power automorphism
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 221-232
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation
Generalisations of Fibonacci numbers, groups and manifolds
-
-
- Book:
- Combinatorial and Geometric Group Theory, Edinburgh 1993
- Published online:
- 05 April 2013
- Print publication:
- 03 November 1994, pp 233-238
-
- Chapter
- Export citation