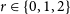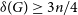10 results
Monochromatic paths and cycles in 2-edge-coloured graphs with large minimum degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 14 June 2021, pp. 109-122
-
- Article
- Export citation
Extremal problems for convex geometric hypergraphs and ordered hypergraphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 10 August 2020, pp. 1648-1666
- Print publication:
- December 2021
-
- Article
- Export citation
Adding Edges to Increase the Chromatic Number of a Graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 31 March 2016, pp. 592-594
-
- Article
- Export citation
Large Rainbow Matchings in Edge-Coloured Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 255-263
-
- Article
- Export citation
Minors in Graphs with High Chromatic Number
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 13 April 2011, pp. 513-518
-
- Article
- Export citation
Sizes of Induced Subgraphs of Ramsey Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 18 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 459-476
-
- Article
- Export citation
When is an Almost Monochromatic K4 Guaranteed?
-
- Journal:
- Combinatorics, Probability and Computing / Volume 17 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 823-830
-
- Article
- Export citation
Extremal Graphs for a Graph Packing Theorem of Sauer and Spencer
-
- Journal:
- Combinatorics, Probability and Computing / Volume 16 / Issue 3 / May 2007
- Published online by Cambridge University Press:
- 01 May 2007, pp. 409-416
-
- Article
- Export citation
On Sufficient Degree Conditions for a Graph to be $k$-linked
-
- Journal:
- Combinatorics, Probability and Computing / Volume 15 / Issue 5 / September 2006
- Published online by Cambridge University Press:
- 31 July 2006, pp. 685-694
-
- Article
- Export citation
On Two Conjectures on Packing of Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 14 / Issue 5-6 / November 2005
- Published online by Cambridge University Press:
- 11 October 2005, pp. 723-736
-
- Article
- Export citation