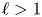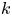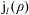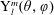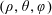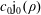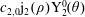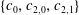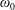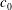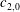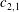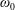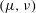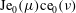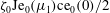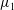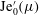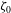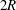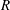17 results
Exact solutions of time-dependent oscillations in multipolar spherical vortices
-
- Journal:
- Journal of Fluid Mechanics / Volume 949 / 25 October 2022
- Published online by Cambridge University Press:
- 23 September 2022, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multipolar spherical and cylindrical vortices
-
- Journal:
- Journal of Fluid Mechanics / Volume 936 / 10 April 2022
- Published online by Cambridge University Press:
- 07 February 2022, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The persistence of balance in geophysical flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 570 / 10 January 2007
- Published online by Cambridge University Press:
- 14 October 2021, pp. 365-383
-
- Article
- Export citation
A stable precessing quasi-geostrophic vortex model with distributed potential vorticity
-
- Journal:
- Journal of Fluid Mechanics / Volume 890 / 10 May 2020
- Published online by Cambridge University Press:
- 02 March 2020, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A stable tripole vortex model in two-dimensional Euler flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 878 / 10 November 2019
- Published online by Cambridge University Press:
- 17 September 2019, R5
-
- Article
- Export citation
Exact solutions of asymmetric baroclinic quasi-geostrophic dipoles with distributed potential vorticity
-
- Journal:
- Journal of Fluid Mechanics / Volume 868 / 10 June 2019
- Published online by Cambridge University Press:
- 12 April 2019, R1
-
- Article
- Export citation
Azimuthal-mode solutions of two-dimensional Euler flows and the Chaplygin–Lamb dipole
-
- Journal:
- Journal of Fluid Mechanics / Volume 859 / 25 January 2019
- Published online by Cambridge University Press:
- 28 November 2018, R1
-
- Article
- Export citation
Isolated marginally stable geophysical vortices
-
- Journal:
- Journal of Fluid Mechanics / Volume 824 / 10 August 2017
- Published online by Cambridge University Press:
- 17 July 2017, R4
-
- Article
- Export citation
Elliptic and hyperbolic interior solutions of piecewise-constant potential vorticity geophysical vortices
-
- Journal:
- Journal of Fluid Mechanics / Volume 696 / 10 April 2012
- Published online by Cambridge University Press:
- 28 February 2012, pp. 301-318
-
- Article
- Export citation
The piecewise constant symmetric potential vorticity vortex in geophysical flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 614 / 10 November 2008
- Published online by Cambridge University Press:
- 16 October 2008, pp. 145-172
-
- Article
- Export citation
The origin of the stationary frontal wave packet spontaneously generated in rotating stratified vortex dipoles
-
- Journal:
- Journal of Fluid Mechanics / Volume 593 / 25 December 2007
- Published online by Cambridge University Press:
- 23 November 2007, pp. 359-383
-
- Article
- Export citation
Spiral patterns of inertia–gravity waves in geophysical flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 562 / 10 September 2006
- Published online by Cambridge University Press:
- 14 August 2006, pp. 73-82
-
- Article
- Export citation
Spontaneous generation of inertia–gravity wave packets by balanced geophysical flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 553 / 25 April 2006
- Published online by Cambridge University Press:
- 06 April 2006, pp. 107-117
-
- Article
- Export citation
Optimal potential vorticity balance of geophysical flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 521 / 25 December 2004
- Published online by Cambridge University Press:
- 13 December 2004, pp. 343-352
-
- Article
- Export citation
A balanced approach to modelling rotating stably stratified geophysical flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 488 / 10 July 2003
- Published online by Cambridge University Press:
- 02 July 2003, pp. 123-150
-
- Article
- Export citation
Vertical velocity in mesoscale geophysical flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 483 / 25 May 2003
- Published online by Cambridge University Press:
- 20 May 2003, pp. 199-223
-
- Article
- Export citation
An explicit potential-vorticity-conserving approach to modelling nonlinear internal gravity waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 458 / 10 May 2002
- Published online by Cambridge University Press:
- 23 May 2002, pp. 75-101
-
- Article
- Export citation