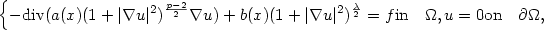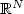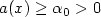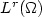2 results
Existence results for semilinear elliptic equations with some lack of coercivity
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 138 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 14 July 2008, pp. 569-595
- Print publication:
- June 2008
-
- Article
- Export citation
Uniqueness of renormalized solutions to nonlinear elliptic equations with a lower order term and right-hand side in L1(Ω)
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 8 / 2002
- Published online by Cambridge University Press:
- 15 August 2002, pp. 239-272
- Print publication:
- 2002
-
- Article
- Export citation