569 results
Assessment and Management of Eating Disorders at Community CAMHS in South Lanarkshire: A Quality Improvement Project
-
- Journal:
- BJPsych Open / Volume 10 / Issue S1 / June 2024
- Published online by Cambridge University Press:
- 01 August 2024, pp. S159-S160
-
- Article
-
- You have access
- Open access
- Export citation
How Are Inpatient Psychiatric Ward Rounds Understood in Research Literature? A Scoping Review
-
- Journal:
- BJPsych Open / Volume 10 / Issue S1 / June 2024
- Published online by Cambridge University Press:
- 01 August 2024, pp. S69-S70
-
- Article
-
- You have access
- Open access
- Export citation
Equally spaced squares and some impossible identities
-
- Journal:
- The Mathematical Gazette / Volume 108 / Issue 572 / July 2024
- Published online by Cambridge University Press:
- 23 August 2024, pp. 201-208
- Print publication:
- July 2024
-
- Article
- Export citation
Western Safflower Contracting Strategies
-
- Journal:
- Journal of Agricultural and Applied Economics / Volume 56 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. 216-233
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estranging the loop
-
- Journal:
- Finance and Society / Volume 6 / Issue 2 / 2020
- Published online by Cambridge University Press:
- 09 November 2023, pp. 146-147
-
- Article
-
- You have access
- Open access
- Export citation
Evaluation of appropriate transmission-based precautions for non-SARS-CoV-2 respiratory viruses
-
- Journal:
- Antimicrobial Stewardship & Healthcare Epidemiology / Volume 3 / Issue 1 / 2023
- Published online by Cambridge University Press:
- 31 October 2023, e193
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Various perspectives on a pair of simple inequalities for log x
-
- Journal:
- The Mathematical Gazette / Volume 107 / Issue 570 / November 2023
- Published online by Cambridge University Press:
- 11 October 2023, pp. 430-437
- Print publication:
- November 2023
-
- Article
- Export citation
Fourier coefficients of
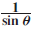 ${1 \over {\sin \,\theta }}$ and
${1 \over {\sin \,\theta }}$ and 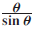 ${\theta\over {\sin \,\theta }}$
${\theta\over {\sin \,\theta }}$
-
- Journal:
- The Mathematical Gazette / Volume 107 / Issue 570 / November 2023
- Published online by Cambridge University Press:
- 11 October 2023, pp. 412-421
- Print publication:
- November 2023
-
- Article
- Export citation
On 107.27
-
- Journal:
- The Mathematical Gazette / Volume 107 / Issue 570 / November 2023
- Published online by Cambridge University Press:
- 11 October 2023, p. 549
- Print publication:
- November 2023
-
- Article
- Export citation
Outcomes of high-dose oral beta-lactam definitive therapy compared to fluoroquinolone or trimethoprim-sulfamethoxazole oral therapy for bacteremia secondary to a urinary tract infection
-
- Journal:
- Antimicrobial Stewardship & Healthcare Epidemiology / Volume 3 / Issue 1 / 2023
- Published online by Cambridge University Press:
- 08 September 2023, e148
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximating Lipschitz and continuous functions by polynomials; Jackson’s theorem
-
- Journal:
- The Mathematical Gazette / Volume 107 / Issue 569 / July 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 273-285
- Print publication:
- July 2023
-
- Article
- Export citation
Hardy’s inequality for averages
-
- Journal:
- The Mathematical Gazette / Volume 107 / Issue 568 / March 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 25-34
- Print publication:
- March 2023
-
- Article
- Export citation
Three-day ceftriaxone versus longer durations of therapy for inpatient treatment of uncomplicated urinary tract infection
-
- Journal:
- Antimicrobial Stewardship & Healthcare Epidemiology / Volume 2 / Issue 1 / 2022
- Published online by Cambridge University Press:
- 21 October 2022, e171
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
10 - Steady State Problems
-
- Book:
- Computational Aerodynamics
- Published online:
- 12 August 2022
- Print publication:
- 01 September 2022, pp 330-366
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Computational Aerodynamics
- Published online:
- 12 August 2022
- Print publication:
- 01 September 2022, pp xvii-xviii
-
- Chapter
- Export citation
Appendix F - Turbulence Models
-
- Book:
- Computational Aerodynamics
- Published online:
- 12 August 2022
- Print publication:
- 01 September 2022, pp 583-588
-
- Chapter
- Export citation
Dedication
-
- Book:
- Computational Aerodynamics
- Published online:
- 12 August 2022
- Print publication:
- 01 September 2022, pp vii-viii
-
- Chapter
- Export citation
2 - Mathematical Models of Fluid Flow
-
- Book:
- Computational Aerodynamics
- Published online:
- 12 August 2022
- Print publication:
- 01 September 2022, pp 10-41
-
- Chapter
- Export citation
Preface
-
- Book:
- Computational Aerodynamics
- Published online:
- 12 August 2022
- Print publication:
- 01 September 2022, pp xv-xvi
-
- Chapter
- Export citation
Appendix C - Polynomial Interpolation, Differentiation, and Integration
-
- Book:
- Computational Aerodynamics
- Published online:
- 12 August 2022
- Print publication:
- 01 September 2022, pp 527-543
-
- Chapter
- Export citation

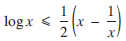
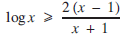
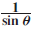
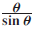
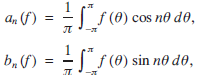
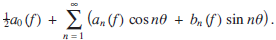
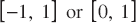 ), denote by
), denote by 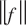 for
for 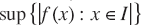 (the notation
(the notation 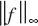 is often used). Uniform convergence of
is often used). Uniform convergence of 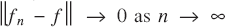 . Denote by
. Denote by 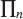 the space of polynomials of degree not more than
the space of polynomials of degree not more than