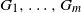1. Introduction and results
Mathematical modeling of complex networks aims to explain and reproduce characteristic properties of large real-world networks, such as power-law degree distributions and clustering. By clustering we refer to the tendency of nodes to cluster together by forming relatively small groups with a high density of ties within a group. Locally, in the vicinity of a vertex v, clustering can be measured by the probability that two randomly selected neighbors of v are adjacent. The average of these probabilities defines the local clustering coefficient of a network. Globally, the fraction of wedges (paths of length 2) that induce triangles defines the global clustering coefficient, which represents the probability that endpoints of a randomly selected wedge (friends of a friend) are adjacent. Clearly, nonvanishing clustering coefficients are connected to the abundance of triangles and other small and dense subgraphs. A natural and interesting question is to trace the relation between the clustering characteristics and the frequencies of various network motifs. We address this question by determining the distributional asymptotics of motif (subgraph) counts in a particular network model (community affiliation graph) that possesses the clustering property and a power-law degree distribution.
Another motivation for studying distributions of motif counts in complex network models comes from network science and its applications, where motif frequencies are used for parameter estimation [Reference Ambroise and Matias1, Reference Karjalainen, van Leeuwaarden and Leskelä16] and model evaluation [Reference Eikmeier, Ramani and Gleich8]. Moreover, motif frequencies tell of the structure, function, and similarities of real-world networks [Reference Benson, Gleich and Leskovec2, Reference Honey, Kötter, Breakspear and Sporns13, Reference Milo, Shen-Orr, Itzkovitz, Kashtan, Chlovskii and Alon19, Reference Ospina-Forero, Deane and Reinert20, Reference Shen-Orr, Milo, Mangan and Alon24]. In these contexts, it is important to understand the variability of the empirical statistics used in the methods. For example, the approach taken in [Reference Ugander, Backstrom and Kleinberg25, Reference van Leeuwaarden and Stegehuis27] was to compare empirical statistics from various datasets to their theoretical bounds. Here the knowledge of (asymptotic) distributions of respective motif counts facilitates statistical inference.
In the present paper we establish the normal and
![]() $\alpha$
-stable approximations of the numbers of k-cliques, k-cycles, and more general 2-connected subgraphs in a sparse network model defined by a superposition of Bernoulli random graphs [Reference Bloznelis and Leskelä6, Reference Yang and Leskovec28, Reference Yang and Leskovec29].
$\alpha$
-stable approximations of the numbers of k-cliques, k-cycles, and more general 2-connected subgraphs in a sparse network model defined by a superposition of Bernoulli random graphs [Reference Bloznelis and Leskelä6, Reference Yang and Leskovec28, Reference Yang and Leskovec29].
To the best of our knowledge this is the first systematic study of an
![]() $\alpha$
-stable approximation to subgraph counts in a theoretical model of a sparse affiliation network. We note that in the network model considered, the clustering property and the power-law degree distribution, the two basic properties of complex networks, are essential for an
$\alpha$
-stable approximation to subgraph counts in a theoretical model of a sparse affiliation network. We note that in the network model considered, the clustering property and the power-law degree distribution, the two basic properties of complex networks, are essential for an
![]() $\alpha$
-stable limit to emerge.
$\alpha$
-stable limit to emerge.
1.1. Network model
We start with the description of individual layers
![]() $G_1,\dots, G_m$
. Let (X, Q) be a random vector with values in
$G_1,\dots, G_m$
. Let (X, Q) be a random vector with values in
![]() $\{0,1,2, \dots\}\times [0,1]$
, and let
$\{0,1,2, \dots\}\times [0,1]$
, and let
![]() ${\mathcal G}=\{G(x,p)\colon x\in\{1,2\dots\}, \, p\in [0,1]\}$
be a family of Bernoulli random graphs independent of (X, Q). We set
${\mathcal G}=\{G(x,p)\colon x\in\{1,2\dots\}, \, p\in [0,1]\}$
be a family of Bernoulli random graphs independent of (X, Q). We set
![]() $[x]=\{1,2,\dots, x\}$
to be the vertex set of G(x, p). Recall that in G(x, p) every pair of vertices
$[x]=\{1,2,\dots, x\}$
to be the vertex set of G(x, p). Recall that in G(x, p) every pair of vertices
![]() $\{i,j\}\subset [x]$
is declared adjacent independently at random with probability p. For notational convenience we introduce the empty graph
$\{i,j\}\subset [x]$
is declared adjacent independently at random with probability p. For notational convenience we introduce the empty graph
![]() $G_{\emptyset}$
having no vertices and set
$G_{\emptyset}$
having no vertices and set
![]() $G(0,p)=G_{\emptyset}$
for any
$G(0,p)=G_{\emptyset}$
for any
![]() $p\in [0,1]$
. We define the mixture of Bernoulli random graphs G(X, Q) in a natural way: we first generate a random vector (X, Q) and then, given the instance (X, Q), we generate a Bernoulli random graph on X vertices with edge density Q. The individual layers
$p\in [0,1]$
. We define the mixture of Bernoulli random graphs G(X, Q) in a natural way: we first generate a random vector (X, Q) and then, given the instance (X, Q), we generate a Bernoulli random graph on X vertices with edge density Q. The individual layers
![]() $G_1,\dots, G_m$
are independent copies of G(X, Q).
$G_1,\dots, G_m$
are independent copies of G(X, Q).
In the next step we map the vertex sets of the layers
![]() $G_1,\dots, G_m$
to the set
$G_1,\dots, G_m$
to the set
![]() $V=\{1,\dots, n\}$
independently and uniformly at random. The union of mapped layers represents the community affiliation graph, which we denote by
$V=\{1,\dots, n\}$
independently and uniformly at random. The union of mapped layers represents the community affiliation graph, which we denote by
![]() $G_{[n,m]}$
. More rigorously, let
$G_{[n,m]}$
. More rigorously, let
![]() $(X_1,Q_1), (X_2,Q_2),\dots$
be a sequence of independent copies of (X, Q), and let
$(X_1,Q_1), (X_2,Q_2),\dots$
be a sequence of independent copies of (X, Q), and let
![]() ${\mathcal G}_i=\{G_i(x,p) \colon x\in{\mathbb N}, \, p\in [0,1]\}$
,
${\mathcal G}_i=\{G_i(x,p) \colon x\in{\mathbb N}, \, p\in [0,1]\}$
,
![]() $i=1,2,\dots$
, be independent copies of
$i=1,2,\dots$
, be independent copies of
![]() ${\mathcal G}$
. Given
${\mathcal G}$
. Given
![]() $X_1,\dots$
,
$X_1,\dots$
,
![]() $X_m$
, let
$X_m$
, let
![]() ${\mathcal V}_{n,i}={\mathcal V}_{n,i}(X_i)$
,
${\mathcal V}_{n,i}={\mathcal V}_{n,i}(X_i)$
,
![]() $1\le i\le m$
, be independent random subsets of [n] defined as follows. For
$1\le i\le m$
, be independent random subsets of [n] defined as follows. For
![]() $X_i\le n$
we select
$X_i\le n$
we select
![]() ${\mathcal V}_{n,i}$
uniformly at random from the class of subsets of [n] of size
${\mathcal V}_{n,i}$
uniformly at random from the class of subsets of [n] of size
![]() $X_i$
. For
$X_i$
. For
![]() $X_i\gt n$
we set
$X_i\gt n$
we set
![]() ${\mathcal V}_{n,i}=[n]$
. We write
${\mathcal V}_{n,i}=[n]$
. We write
![]() ${\tilde X}_i=|{\mathcal V}_{n,i}|=X_i\wedge n$
. Let
${\tilde X}_i=|{\mathcal V}_{n,i}|=X_i\wedge n$
. Let
![]() $G_{n,i}$
,
$G_{n,i}$
,
![]() $1\le i\le m$
, be independent random graphs with vertex sets
$1\le i\le m$
, be independent random graphs with vertex sets
![]() ${\mathcal V}_{n,i}$
defined as follows. We obtain
${\mathcal V}_{n,i}$
defined as follows. We obtain
![]() $G_{n,i}$
by a one-to-one mapping of vertices of
$G_{n,i}$
by a one-to-one mapping of vertices of
![]() $G_i({\tilde X}_i,Q_i)$
to the elements of
$G_i({\tilde X}_i,Q_i)$
to the elements of
![]() ${\mathcal V}_{n,i}$
and by retaining the adjacency relations of
${\mathcal V}_{n,i}$
and by retaining the adjacency relations of
![]() $G_i({\tilde X}_i,Q_i)$
. We denote by
$G_i({\tilde X}_i,Q_i)$
. We denote by
![]() ${\mathcal E}_{n,i}$
the edge set of
${\mathcal E}_{n,i}$
the edge set of
![]() $G_{n,i}$
. Finally, let
$G_{n,i}$
. Finally, let
![]() $G_{[n,m]}=(V, {\mathcal E})$
be the random graph with the vertex set
$G_{[n,m]}=(V, {\mathcal E})$
be the random graph with the vertex set
![]() $V=[n]$
and edge set
$V=[n]$
and edge set
![]() ${\mathcal E}={\mathcal E}_{n,1}\cup\cdots\cup {\mathcal E}_{n,m}$
. Therefore,
${\mathcal E}={\mathcal E}_{n,1}\cup\cdots\cup {\mathcal E}_{n,m}$
. Therefore,
![]() $G_{[n,m]}$
is the superposition of the layers (communities)
$G_{[n,m]}$
is the superposition of the layers (communities)
![]() $G_{n,1}, \dots, G_{n,m}$
.
$G_{n,1}, \dots, G_{n,m}$
.
The random graph
![]() $G_{[n,m]}$
represents a null model of the community affiliation graph model (AGM) introduced in [Reference Yang and Leskovec28, Reference Yang and Leskovec29], which has attracted considerable attention in the literature. It is worth mentioning that community memberships (i.e. the vertex sets of respective overlapping communities) in the AGM [Reference Yang and Leskovec28, Reference Yang and Leskovec29] are defined by a design that features non-negligible overlaps, whereas the null model
$G_{[n,m]}$
represents a null model of the community affiliation graph model (AGM) introduced in [Reference Yang and Leskovec28, Reference Yang and Leskovec29], which has attracted considerable attention in the literature. It is worth mentioning that community memberships (i.e. the vertex sets of respective overlapping communities) in the AGM [Reference Yang and Leskovec28, Reference Yang and Leskovec29] are defined by a design that features non-negligible overlaps, whereas the null model
![]() $G_{[n,m]}$
assumes that
$G_{[n,m]}$
assumes that
![]() ${\mathcal V}_{n,1},\dots, {\mathcal V}_{n,m}$
are located at random and, therefore, their overlaps are typically small. (In particular, for
${\mathcal V}_{n,1},\dots, {\mathcal V}_{n,m}$
are located at random and, therefore, their overlaps are typically small. (In particular, for
![]() ${\mathbb E}\, X\lt\infty$
and
${\mathbb E}\, X\lt\infty$
and
![]() $m=\Theta(n)$
the expected number of overlaps is linear in m as
$m=\Theta(n)$
the expected number of overlaps is linear in m as
![]() $n,m\to+\infty$
. Moreover, most of the overlaps are one-element sets.) We also mention that in the particular case where
$n,m\to+\infty$
. Moreover, most of the overlaps are one-element sets.) We also mention that in the particular case where
![]() $Q\equiv 1$
the random graph
$Q\equiv 1$
the random graph
![]() $G_{[n,m]}$
reduces to a union of randomly located cliques of variable sizes
$G_{[n,m]}$
reduces to a union of randomly located cliques of variable sizes
![]() ${\tilde X}_1,\dots, {\tilde X}_m$
. This model has been studied in the literature under the name ‘passive’ random intersection graph; see, e.g., [Reference Godehardt and Jaworski10].
${\tilde X}_1,\dots, {\tilde X}_m$
. This model has been studied in the literature under the name ‘passive’ random intersection graph; see, e.g., [Reference Godehardt and Jaworski10].
In the parameter regime
![]() $m=\Theta(n)$
as
$m=\Theta(n)$
as
![]() $m,n\to+\infty$
the random graph
$m,n\to+\infty$
the random graph
![]() $G_{[n,m]}$
admits a power-law degree distribution with tunable power-law exponent, a nonvanishing global clustering coefficient, and a tunable clustering spectrum [Reference Bloznelis and Leskelä6]. Moreover, it admits a limiting bidegree distribution with (stochastically dependent) power-law marginals, as shown in [Reference Bloznelis, Karjalainen and Leskelä7]. The present paper continues the study of the random graph
$G_{[n,m]}$
admits a power-law degree distribution with tunable power-law exponent, a nonvanishing global clustering coefficient, and a tunable clustering spectrum [Reference Bloznelis and Leskelä6]. Moreover, it admits a limiting bidegree distribution with (stochastically dependent) power-law marginals, as shown in [Reference Bloznelis, Karjalainen and Leskelä7]. The present paper continues the study of the random graph
![]() $G_{[n,m]}$
and focuses on the asymptotic distributions of (dense) subgraph counts.
$G_{[n,m]}$
and focuses on the asymptotic distributions of (dense) subgraph counts.
1.2. Results
Let
![]() $F=({\mathcal V}_F,{\mathcal E}_F)$
be a graph with vertex set
$F=({\mathcal V}_F,{\mathcal E}_F)$
be a graph with vertex set
![]() ${\mathcal V}_F$
and edge set
${\mathcal V}_F$
and edge set
![]() ${\mathcal E}_F$
. We write
${\mathcal E}_F$
. We write
![]() $v_F=|{\mathcal V}_F|$
and
$v_F=|{\mathcal V}_F|$
and
![]() $e_F=|{\mathcal E}_F|$
. We assume in what follows that F is 2-connected. That is, F is connected and, moreover, it stays connected even if we remove any one of its vertices. We call F balanced if
$e_F=|{\mathcal E}_F|$
. We assume in what follows that F is 2-connected. That is, F is connected and, moreover, it stays connected even if we remove any one of its vertices. We call F balanced if
![]() $e_F/v_F=\max\{e_H/v_H\colon H\subset F$
with
$e_F/v_F=\max\{e_H/v_H\colon H\subset F$
with
![]() $e_H\ge 1\}$
. For example, the cycle
$e_H\ge 1\}$
. For example, the cycle
![]() ${\mathcal C}_k$
and clique
${\mathcal C}_k$
and clique
![]() ${\mathcal K}_k$
(where k stands for the number of vertices) are 2-connected and balanced. Let
${\mathcal K}_k$
(where k stands for the number of vertices) are 2-connected and balanced. Let
![]() $N_F$
be the number of copies of F in G(X, Q). By a copy of F we mean a graph isomorphic to F. Denote by
$N_F$
be the number of copies of F in G(X, Q). By a copy of F we mean a graph isomorphic to F. Denote by
![]() $\sigma^2_F={\textrm{Var}}\, N_F$
the variance of
$\sigma^2_F={\textrm{Var}}\, N_F$
the variance of
![]() $N_F$
. We write
$N_F$
. We write
![]() $\sigma^2_F\lt\infty$
if the variance is finite and
$\sigma^2_F\lt\infty$
if the variance is finite and
![]() $\sigma^2_F=\infty$
otherwise. We use the shorthand notation
$\sigma^2_F=\infty$
otherwise. We use the shorthand notation
![]() $N_F^*\,:\!={\mathbb {E}}(N_F\mid X,Q) =a_F\binom{X}{v_F}Q^{e_F}$
, where
$N_F^*\,:\!={\mathbb {E}}(N_F\mid X,Q) =a_F\binom{X}{v_F}Q^{e_F}$
, where
![]() $a_F$
stands for the number of distinct copies of F in the complete graph on
$a_F$
stands for the number of distinct copies of F in the complete graph on
![]() $v_F$
vertices. We have, for example, that
$v_F$
vertices. We have, for example, that
![]() $N_{{\mathcal C}_k}^*=(X)_kQ^k/(2k)$
and
$N_{{\mathcal C}_k}^*=(X)_kQ^k/(2k)$
and
![]() $N_{{\mathcal K}_k}^*=(X)_kQ^{\binom{k}{2}}/k!$
. Here and below
$N_{{\mathcal K}_k}^*=(X)_kQ^{\binom{k}{2}}/k!$
. Here and below
![]() $(x)_k=x(x-1)\cdots(x-k+1)$
denotes the falling factorial. Furthermore, we have
$(x)_k=x(x-1)\cdots(x-k+1)$
denotes the falling factorial. Furthermore, we have
![]() ${\mathbb {E}}\, N_F={\mathbb {E}}\, N_F^*=a_F{\mathbb {E}}\big(\binom{X}{v_F}Q^{e_F}\big)$
.
${\mathbb {E}}\, N_F={\mathbb {E}}\, N_F^*=a_F{\mathbb {E}}\big(\binom{X}{v_F}Q^{e_F}\big)$
.
In Theorems 1 and 2 and Remark 4 below we consider a sequence of random graphs
![]() $\{G_{[n,m]}, n = 1,2,\dots\}$
, where
$\{G_{[n,m]}, n = 1,2,\dots\}$
, where
![]() $m = m_n$
satisfies
$m = m_n$
satisfies
![]() $m_n=\Theta(n)$
(i.e. both relations
$m_n=\Theta(n)$
(i.e. both relations
![]() $m_n=O(n)$
and
$m_n=O(n)$
and
![]() $n=O(m_n)$
hold) as
$n=O(m_n)$
hold) as
![]() $n\to+\infty$
. We often suppress the subscript n for notational simplicity.
$n\to+\infty$
. We often suppress the subscript n for notational simplicity.
Let
![]() ${\mathcal N}_F$
be the number of copies of F in
${\mathcal N}_F$
be the number of copies of F in
![]() $G_{[n,m]}$
. Our first result, Theorem 1, establishes the asymptotic normality of
$G_{[n,m]}$
. Our first result, Theorem 1, establishes the asymptotic normality of
![]() ${\mathcal N}_F$
.
${\mathcal N}_F$
.
Theorem 1.
Let
![]() $m,n\to+\infty$
and assume that
$m,n\to+\infty$
and assume that
![]() $m=\Theta(n)$
. Let F be a 2-connected graph with
$m=\Theta(n)$
. Let F be a 2-connected graph with
![]() $v_F\ge 3$
vertices. Assume that
$v_F\ge 3$
vertices. Assume that
![]() ${\mathbb {E}}\, X\lt\infty$
and
${\mathbb {E}}\, X\lt\infty$
and
![]() $0\lt \sigma^2_{F}\lt\infty$
. Assume, in addition, that
$0\lt \sigma^2_{F}\lt\infty$
. Assume, in addition, that
Then
![]() $({\mathcal N}_F-m{\mathbb {E}} N_F)/(\sigma_{F}\sqrt{m})$
converges in distribution to the standard normal distribution.
$({\mathcal N}_F-m{\mathbb {E}} N_F)/(\sigma_{F}\sqrt{m})$
converges in distribution to the standard normal distribution.
Remark 1. For a balanced graph F, the finite variance condition
![]() $\sigma_F^2\lt\infty$
is equivalent to the second moment condition
$\sigma_F^2\lt\infty$
is equivalent to the second moment condition
![]() ${\mathbb {E}}\big(N_F^*\big)^2\lt\infty$
. In particular, we have
${\mathbb {E}}\big(N_F^*\big)^2\lt\infty$
. In particular, we have
![]() $\sigma_F^2\lt\infty\Leftrightarrow {\mathbb {E}}(X^{2v_F}Q^{2e_F})\lt\infty$
.
$\sigma_F^2\lt\infty\Leftrightarrow {\mathbb {E}}(X^{2v_F}Q^{2e_F})\lt\infty$
.
Remark 2. In the special case where F is a clique on
![]() $k\ge 3$
vertices (
$k\ge 3$
vertices (
![]() $F={\mathcal K}_k$
), condition (1) can be replaced by
$F={\mathcal K}_k$
), condition (1) can be replaced by
where we write
![]() ${\hat r}\,:\!=\binom{r-1}{2}+1$
. Note that the moment condition (2) can be weaker than (1) for large k.
${\hat r}\,:\!=\binom{r-1}{2}+1$
. Note that the moment condition (2) can be weaker than (1) for large k.
The proofs of Theorem 1 and Remarks 1 and 2 are presented in Section 2. Let us briefly explain the result and conditions of Theorem 1. Let
![]() $N_{F,i}$
be the number of copies of F in
$N_{F,i}$
be the number of copies of F in
![]() $G(X_i,Q_i)$
, and define
$G(X_i,Q_i)$
, and define
![]() $S_F=N_{F,1}+\cdots+N_{F,m}$
. The first moment condition
$S_F=N_{F,1}+\cdots+N_{F,m}$
. The first moment condition
![]() ${\mathbb {E}}\, X\lt\infty$
and the assumption
${\mathbb {E}}\, X\lt\infty$
and the assumption
![]() $m=\Theta(n)$
ensure that, with high probability,
$m=\Theta(n)$
ensure that, with high probability,
![]() ${\tilde X}_i=X_i$
,
${\tilde X}_i=X_i$
,
![]() $1\le i\le m$
, i.e. the layer sizes do not need to be truncated. Next, from the fact that the typical overlap of two layers is either empty or a single-element set, we can deduce that (for 2-connected F) the principal contribution to the subgraph count
$1\le i\le m$
, i.e. the layer sizes do not need to be truncated. Next, from the fact that the typical overlap of two layers is either empty or a single-element set, we can deduce that (for 2-connected F) the principal contribution to the subgraph count
![]() ${\mathcal N}_F$
comes from the subgraph counts
${\mathcal N}_F$
comes from the subgraph counts
![]() $N_{F,i}$
of individual layers. Therefore we have
$N_{F,i}$
of individual layers. Therefore we have
![]() ${\mathcal N}_F\approx S_F$
. To make this approximation rigorous we introduce conditions (1) and (2) aimed at controlling the number of overlaps of different copies of F in
${\mathcal N}_F\approx S_F$
. To make this approximation rigorous we introduce conditions (1) and (2) aimed at controlling the number of overlaps of different copies of F in
![]() $G_{[n,m]}$
. The combinatorial origin of (1) and (2) is explained in Lemmas 1–4. Finally, the asymptotic normality of
$G_{[n,m]}$
. The combinatorial origin of (1) and (2) is explained in Lemmas 1–4. Finally, the asymptotic normality of
![]() ${\mathcal N}_F$
follows from the asymptotic normality of
${\mathcal N}_F$
follows from the asymptotic normality of
![]() $S_F$
. The latter is guaranteed by the second moment condition
$S_F$
. The latter is guaranteed by the second moment condition
![]() $\sigma_F^2\lt\infty$
.
$\sigma_F^2\lt\infty$
.
In the case where F is balanced and the random variable
![]() $N_F^*$
has an infinite second moment, we can obtain an
$N_F^*$
has an infinite second moment, we can obtain an
![]() $\alpha$
-stable limiting distribution for the subgraph count
$\alpha$
-stable limiting distribution for the subgraph count
![]() ${\mathcal N}_{F}$
. In Theorem 2 we assume that, for some
${\mathcal N}_{F}$
. In Theorem 2 we assume that, for some
![]() $a\gt 0$
and
$a\gt 0$
and
![]() $0\lt \alpha\lt 2$
, we have
$0\lt \alpha\lt 2$
, we have
Let
![]() $N_{F,i}^*={\mathbb {E}}(N_{F,i}\mid X_i, Q_i)$
,
$N_{F,i}^*={\mathbb {E}}(N_{F,i}\mid X_i, Q_i)$
,
![]() $1\le i\le m$
, be independent and identically distributed (i.i.d.) copies of
$1\le i\le m$
, be independent and identically distributed (i.i.d.) copies of
![]() $N_F^*$
, and put
$N_F^*$
, and put
![]() $S_F^*=N_{F,1}^*+\cdots+N_{F,m}^*$
. It is well known [Reference Gnedenko and Kolmogorov9, Theorem 2,
$S_F^*=N_{F,1}^*+\cdots+N_{F,m}^*$
. It is well known [Reference Gnedenko and Kolmogorov9, Theorem 2,
![]() $\S35$
] that the distribution of
$\S35$
] that the distribution of
![]() $m^{-1/\alpha}(S_F^*-B_m)$
converges to a stable distribution, say
$m^{-1/\alpha}(S_F^*-B_m)$
converges to a stable distribution, say
![]() $G_{\alpha,a}$
, which is defined by a and
$G_{\alpha,a}$
, which is defined by a and
![]() $\alpha$
. Here,
$\alpha$
. Here,
![]() $B_m=m{\mathbb {E}}\, N_F^*={\mathbb {E}}\, N_F$
for
$B_m=m{\mathbb {E}}\, N_F^*={\mathbb {E}}\, N_F$
for
![]() $1\lt\alpha \lt 2$
and
$1\lt\alpha \lt 2$
and
![]() $B_m\equiv 0$
for
$B_m\equiv 0$
for
![]() $0\lt \alpha\lt 1$
. For
$0\lt \alpha\lt 1$
. For
![]() $\alpha=1$
we have
$\alpha=1$
we have
![]() $B_m=c^{\star}_{\alpha,a}\ln m$
, where the constant
$B_m=c^{\star}_{\alpha,a}\ln m$
, where the constant
![]() $c^{\star}_{\alpha,a}\gt 0$
depends on a and
$c^{\star}_{\alpha,a}\gt 0$
depends on a and
![]() $\alpha$
.
$\alpha$
.
Our second result establishes an
![]() $\alpha$
-stable approximation to the distribution of
$\alpha$
-stable approximation to the distribution of
![]() ${\mathcal N}_F$
.
${\mathcal N}_F$
.
Theorem 2.
Let
![]() $n,m\to+\infty$
and assume that
$n,m\to+\infty$
and assume that
![]() $m=\Theta(n)$
. Let F be a balanced and 2-connected graph with
$m=\Theta(n)$
. Let F be a balanced and 2-connected graph with
![]() $v_F\ge 3$
vertices. Let
$v_F\ge 3$
vertices. Let
![]() $a\gt 0$
and
$a\gt 0$
and
![]() $0\lt \alpha\lt 2$
. Assume that
$0\lt \alpha\lt 2$
. Assume that
![]() ${\mathbb {E}} X\lt\infty$
and that (3) holds. Assume, in addition, that
${\mathbb {E}} X\lt\infty$
and that (3) holds. Assume, in addition, that
Then
![]() $({\mathcal N}_F-B_m)/m^{1/\alpha}$
converges in distribution to
$({\mathcal N}_F-B_m)/m^{1/\alpha}$
converges in distribution to
![]() $G_{\alpha,a}$
.
$G_{\alpha,a}$
.
Remark 3. In the special case where F is a clique on
![]() $k\ge 3$
vertices (
$k\ge 3$
vertices (
![]() $F={\mathcal K}_k$
), condition (4) can be replaced by
$F={\mathcal K}_k$
), condition (4) can be replaced by
where
![]() ${\hat r}=\binom{r-1}{2}+1$
.
${\hat r}=\binom{r-1}{2}+1$
.
The result of Theorem 2 is obtained by the approximations
![]() ${\mathcal N}_F\approx S_F$
and
${\mathcal N}_F\approx S_F$
and
![]() $S_F\approx S_F^*$
. To make the latter approximation rigorous we apply exponential large-deviation bounds [Reference Janson, Oleszkiewicz and Ruciński15] combined with Janson’s inequality [Reference Janson, Łuczak and Ruciński14, Theorem 2.14] to individual subgraph counts
$S_F\approx S_F^*$
. To make the latter approximation rigorous we apply exponential large-deviation bounds [Reference Janson, Oleszkiewicz and Ruciński15] combined with Janson’s inequality [Reference Janson, Łuczak and Ruciński14, Theorem 2.14] to individual subgraph counts
![]() $N_{F,i}$
conditionally given
$N_{F,i}$
conditionally given
![]() $(X_i,Q_i)$
; see Lemma 5. (At this step we use the assumption that F is balanced.) The
$(X_i,Q_i)$
; see Lemma 5. (At this step we use the assumption that F is balanced.) The
![]() $\alpha$
-stable limit of
$\alpha$
-stable limit of
![]() $S_F^*$
is now guaranteed by condition (3) and [Reference Gnedenko and Kolmogorov9, Theorem 2,
$S_F^*$
is now guaranteed by condition (3) and [Reference Gnedenko and Kolmogorov9, Theorem 2,
![]() $\S35$
].
$\S35$
].
We briefly comment on the technical conditions (1), (2), (4), and (5). The mixed moments defined there appear in our upper bounds on the expected number of overlaps of different copies of F in
![]() $G_{[n,m]}$
; see Lemmas 1 and 4 and inequality (10) in the proof below. We note that, for particular graphs F, the moment conditions (1), (2), (4), and (5) can be relaxed. For example, in the simplest case where
$G_{[n,m]}$
; see Lemmas 1 and 4 and inequality (10) in the proof below. We note that, for particular graphs F, the moment conditions (1), (2), (4), and (5) can be relaxed. For example, in the simplest case where
![]() $F={\mathcal K}_2$
such conditions are not needed at all.
$F={\mathcal K}_2$
such conditions are not needed at all.
Remark 4. Let
![]() $F={\mathcal K}_2$
. Let
$F={\mathcal K}_2$
. Let
![]() $n,m\to+\infty$
. Assume that
$n,m\to+\infty$
. Assume that
![]() $m=\Theta(n)$
and
$m=\Theta(n)$
and
![]() ${\mathbb {E}}\, X\lt\infty$
.
${\mathbb {E}}\, X\lt\infty$
.
-
(i) Assume that
 $0\lt \sigma_{{\mathcal K}_2}\lt\infty$
. Then
$0\lt \sigma_{{\mathcal K}_2}\lt\infty$
. Then
 $({\mathcal N}_{F}-m{\mathbb {E}} N_{F})/(\sigma_{F}\sqrt{m})$
converges in distribution to the standard normal distribution. Here,
$({\mathcal N}_{F}-m{\mathbb {E}} N_{F})/(\sigma_{F}\sqrt{m})$
converges in distribution to the standard normal distribution. Here,
 $\sigma_F^2={\textrm{Var}} \bigl(\binom{X}{2}Q\bigr)+{\mathbb {E}} \bigl(\binom{X}{2}Q(1-Q)\bigr)\lt\infty$
whenever
$\sigma_F^2={\textrm{Var}} \bigl(\binom{X}{2}Q\bigr)+{\mathbb {E}} \bigl(\binom{X}{2}Q(1-Q)\bigr)\lt\infty$
whenever
 ${\mathbb {E}}(X^4Q^2)\lt\infty$
.
${\mathbb {E}}(X^4Q^2)\lt\infty$
. -
(ii) Assume that, for some
 $a\gt 0$
and
$a\gt 0$
and
 $0.5\lt\alpha\lt 2$
, condition (3) holds. Then
$0.5\lt\alpha\lt 2$
, condition (3) holds. Then
 $({\mathcal N}_F-B_m)/m^{1/\alpha}$
converges in distribution to
$({\mathcal N}_F-B_m)/m^{1/\alpha}$
converges in distribution to
 $G_{\alpha,a}$
. We note that
$G_{\alpha,a}$
. We note that
 ${\mathbb {E}}\, X\lt\infty$
implies
${\mathbb {E}}\, X\lt\infty$
implies
 $\alpha\gt 0.5$
.
$\alpha\gt 0.5$
.
Let us examine Theorems 1 and 2 in the special case where the marginals X, Q of (X, Q) are independent and
![]() ${\mathbb {P}}\{Q\gt 0\}\gt 0$
. We first consider Theorem 1. The finite variance condition
${\mathbb {P}}\{Q\gt 0\}\gt 0$
. We first consider Theorem 1. The finite variance condition
![]() $\sigma_F^2\lt\infty$
of Theorem 1 reduces to the moment condition
$\sigma_F^2\lt\infty$
of Theorem 1 reduces to the moment condition
![]() ${\mathbb {E}}\, X^{2v_F}\lt\infty$
. Indeed, by the simple inequality
${\mathbb {E}}\, X^{2v_F}\lt\infty$
. Indeed, by the simple inequality
![]() $N_F\le (X)_{v_F}$
, we have that
$N_F\le (X)_{v_F}$
, we have that
![]() ${\mathbb {E}}\, X^{2v_F}\lt\infty\Rightarrow {\mathbb {E}}\, N_F^2\lt\infty\Rightarrow \sigma_F^2\lt\infty$
. On the other hand, by the variance identity
${\mathbb {E}}\, X^{2v_F}\lt\infty\Rightarrow {\mathbb {E}}\, N_F^2\lt\infty\Rightarrow \sigma_F^2\lt\infty$
. On the other hand, by the variance identity
![]() ${\textrm{Var}}\, N_F={\textrm{Var}}\, N_F^*+{\mathbb {E}}({\textrm{Var}}( N_F\mid X,Q))$
, we have that
${\textrm{Var}}\, N_F={\textrm{Var}}\, N_F^*+{\mathbb {E}}({\textrm{Var}}( N_F\mid X,Q))$
, we have that
![]() $\sigma_F^2\lt\infty\Rightarrow {\mathbb {E}} \big(N_F^*\big)^2\lt\infty$
, where the latter inequality (for independent X and Q) implies
$\sigma_F^2\lt\infty\Rightarrow {\mathbb {E}} \big(N_F^*\big)^2\lt\infty$
, where the latter inequality (for independent X and Q) implies
![]() ${\mathbb {E}}\, X^{2v_F}\lt\infty$
. Moreover, the moment condition
${\mathbb {E}}\, X^{2v_F}\lt\infty$
. Moreover, the moment condition
![]() ${\mathbb {E}}\, X^{2v_F}\lt\infty$
implies (1). Therefore, Theorem 1 establishes the asymptotic normality under the minimal second moment condition
${\mathbb {E}}\, X^{2v_F}\lt\infty$
implies (1). Therefore, Theorem 1 establishes the asymptotic normality under the minimal second moment condition
![]() $\sigma_F^2\lt\infty$
.
$\sigma_F^2\lt\infty$
.
We now turn to Theorem 2. For independent X and Q condition (3) of Theorem 2 is equivalent to the condition
where
![]() $\gamma=\alpha v_F$
and where b solves the equation
$\gamma=\alpha v_F$
and where b solves the equation
![]() $a=b(a_F/v_F!)^{\gamma/v_F}{\mathbb {E}}\, Q^{\gamma e_F/v_F}$
. Note that
$a=b(a_F/v_F!)^{\gamma/v_F}{\mathbb {E}}\, Q^{\gamma e_F/v_F}$
. Note that
![]() ${\mathbb {E}}\, X\lt\infty$
implies
${\mathbb {E}}\, X\lt\infty$
implies
![]() $\gamma\gt 1$
. Furthermore, the inequality
$\gamma\gt 1$
. Furthermore, the inequality
![]() $v_F\le e_F$
(which holds for any 2-connected F with
$v_F\le e_F$
(which holds for any 2-connected F with
![]() $v_F\ge 3$
) combined with
$v_F\ge 3$
) combined with
![]() $\gamma\gt 1$
implies
$\gamma\gt 1$
implies
![]() $\alpha e_F\gt 1$
. Observe that, for
$\alpha e_F\gt 1$
. Observe that, for
![]() $\alpha e_F\gt 1$
, condition (4) reads as
$\alpha e_F\gt 1$
, condition (4) reads as
![]() ${\mathbb {E}}\, X^{1+(v_F-1)(1-{1}/{\alpha e_F})}\lt\infty$
. In view of (6), the latter expectation is finite whenever
${\mathbb {E}}\, X^{1+(v_F-1)(1-{1}/{\alpha e_F})}\lt\infty$
. In view of (6), the latter expectation is finite whenever
We have arrived at the following corollary.
Corollary 1.
Let
![]() $n,m\to+\infty$
and assume that
$n,m\to+\infty$
and assume that
![]() $m=\Theta(n)$
. Let F be a 2-connected graph with
$m=\Theta(n)$
. Let F be a 2-connected graph with
![]() $v_F\ge 3$
vertices. Assume that X and Q are independent and
$v_F\ge 3$
vertices. Assume that X and Q are independent and
![]() ${\mathbb {P}}\{Q\gt 0\}\gt 0$
.
${\mathbb {P}}\{Q\gt 0\}\gt 0$
.
-
(i) If
 ${\mathbb {E}}\, X^{2v_F}\lt\infty$
then
${\mathbb {E}}\, X^{2v_F}\lt\infty$
then
 $({\mathcal N}_F-{\mathbb {E}}\, {\mathcal N}_F)/(\sigma_{F}\sqrt{m})$
converges in distribution to the standard normal distribution.
$({\mathcal N}_F-{\mathbb {E}}\, {\mathcal N}_F)/(\sigma_{F}\sqrt{m})$
converges in distribution to the standard normal distribution.
-
(ii) Let
 $b\gt 0$
and
$b\gt 0$
and
 $1\lt \gamma\lt 2v_F$
. Assume that (6) holds. Assume, in addition, that F is balanced and (7) holds, where
$1\lt \gamma\lt 2v_F$
. Assume that (6) holds. Assume, in addition, that F is balanced and (7) holds, where
 $\alpha=\gamma/v_F$
. Then
$\alpha=\gamma/v_F$
. Then
 $({\mathcal N}_F-B_m)/m^{1/\alpha}$
converges in distribution to
$({\mathcal N}_F-B_m)/m^{1/\alpha}$
converges in distribution to
 $G_{\alpha,a}$
. Here,
$G_{\alpha,a}$
. Here,
 $B_m$
and
$B_m$
and
 $G_{\alpha,a}$
are the same as in Theorem 2
, with
$G_{\alpha,a}$
are the same as in Theorem 2
, with
 $a=b(a_F/v_F!)^{\gamma/v_F}{\mathbb {E}}\, Q^{\gamma e_F/v_F}$
.
$a=b(a_F/v_F!)^{\gamma/v_F}{\mathbb {E}}\, Q^{\gamma e_F/v_F}$
.
It is relevant to mention that the moment condition
![]() ${\mathbb {E}}\, X\lt\infty$
together with the assumption
${\mathbb {E}}\, X\lt\infty$
together with the assumption
![]() $m=\nu n+o(n)$
for some
$m=\nu n+o(n)$
for some
![]() $\nu\gt 0$
(which is stronger than
$\nu\gt 0$
(which is stronger than
![]() $m=\Theta(n)$
), imply the existence of an asymptotic degree distribution of
$m=\Theta(n)$
), imply the existence of an asymptotic degree distribution of
![]() $G_{[n,m]}$
as
$G_{[n,m]}$
as
![]() $n,m\to+\infty$
. An asymptotic power-law degree distribution is obtained if we choose an appropriate distribution for the layer type (X, Q). Furthermore, under an additional moment condition
$n,m\to+\infty$
. An asymptotic power-law degree distribution is obtained if we choose an appropriate distribution for the layer type (X, Q). Furthermore, under an additional moment condition
![]() ${\mathbb {E}}\, X^3Q^2\lt\infty$
, the random graph
${\mathbb {E}}\, X^3Q^2\lt\infty$
, the random graph
![]() $G_{[n,m]}$
has a nonvanishing global clustering coefficient; see [Reference Bloznelis and Leskelä6]. Therefore, Theorems 1 and 2 establish the limit distributions of subgraph counts in a highly clustered complex network.
$G_{[n,m]}$
has a nonvanishing global clustering coefficient; see [Reference Bloznelis and Leskelä6]. Therefore, Theorems 1 and 2 establish the limit distributions of subgraph counts in a highly clustered complex network.
Finally, we discuss an important question about the relation between the community size X and strength Q. In Theorems 1 and 2, no assumption has been made about the stochastic dependence between the marginals X and Q of the bivariate random vector (X, Q) defining the random graph
![]() $G_{[n,m]}$
. Although we can simplify the model by assuming that X and Q are independent (as in Corollary 1), for network modeling purposes, various types of dependence between X and Q are of interest. For example, a negative correlation between X and Q would emphasise small strong communities and large weak communities, a pattern likely to occur in real networks with overlapping communities. Assuming that Q is proportional to a negative power of X, for example,
$G_{[n,m]}$
. Although we can simplify the model by assuming that X and Q are independent (as in Corollary 1), for network modeling purposes, various types of dependence between X and Q are of interest. For example, a negative correlation between X and Q would emphasise small strong communities and large weak communities, a pattern likely to occur in real networks with overlapping communities. Assuming that Q is proportional to a negative power of X, for example,
![]() $Q=\min\{1, bX^{-\beta}\}$
for some
$Q=\min\{1, bX^{-\beta}\}$
for some
![]() $\beta\ge 0$
and
$\beta\ge 0$
and
![]() $b\gt 0$
(cf. [Reference Yang and Leskovec28, Reference Yang and Leskovec29]), and we obtain a mathematically tractable network model admitting tunable power-law degree and bidegree distributions and a rich clustering spectrum [Reference Bloznelis and Leskelä6, Reference Bloznelis, Karjalainen and Leskelä7].
$b\gt 0$
(cf. [Reference Yang and Leskovec28, Reference Yang and Leskovec29]), and we obtain a mathematically tractable network model admitting tunable power-law degree and bidegree distributions and a rich clustering spectrum [Reference Bloznelis and Leskelä6, Reference Bloznelis, Karjalainen and Leskelä7].
1.3. Related work
Asymptotic distributions of subgraph counts in Bernoulli random graphs is a well-established area of research, see, e.g., [Reference Janson, Łuczak and Ruciński14, Reference Ruciński23] and references therein. For a recent development we refer to [Reference Bhattacharya, Chatterjee and Janson3, Reference Hladký, Pelekis and Šileikis12, Reference Kaur and Röllin17, Reference Privault and Serafin21, Reference Röllin22, Reference Zhang30]. A significant difference between the sparse Bernoulli random graphs and complex networks is that the former have no or very few copies of a triangle or a larger clique, while the latter often have abundant numbers of them. Since the global and local clustering coefficients are expressed in terms of counts of triangles and wedges, a rigorous asymptotic analysis of clustering coefficients reduces to that of the triangle counts and wedge counts. In particular, the bivariate asymptotic normality for triangle and wedge counts in a related sparse random intersection graph was shown in [Reference Bloznelis and Jaworski4], and related
![]() $\alpha$
-stable limits were established in [Reference Bloznelis and Kurauskas5]. Another line of research pursued in [Reference Gröhn, Karjalainen and Leskelä11, Reference Karjalainen, van Leeuwaarden and Leskelä16] addresses the concentration of subgraph counts in
$\alpha$
-stable limits were established in [Reference Bloznelis and Kurauskas5]. Another line of research pursued in [Reference Gröhn, Karjalainen and Leskelä11, Reference Karjalainen, van Leeuwaarden and Leskelä16] addresses the concentration of subgraph counts in
![]() $G_{[n,m]}$
. We also mention related work on local weak limits and subgraph counts: the results of [Reference Kurauskas18, Reference van der Hofstad, Komjáthy and Vadon26] imply the linear growth in n of the numbers of small dense subgraphs for a large class of sparse affiliation network models. Establishing the distributional asymptotics here is an interesting problem for future research. Another interesting question is about revoking the 2-connectivity and balancedness conditions on F in Theorems 1 and 2.
$G_{[n,m]}$
. We also mention related work on local weak limits and subgraph counts: the results of [Reference Kurauskas18, Reference van der Hofstad, Komjáthy and Vadon26] imply the linear growth in n of the numbers of small dense subgraphs for a large class of sparse affiliation network models. Establishing the distributional asymptotics here is an interesting problem for future research. Another interesting question is about revoking the 2-connectivity and balancedness conditions on F in Theorems 1 and 2.
The rest of the paper is organised as follows. In Section 2 we formulate and prove Theorems 1 and 2 and Remarks 1–4. We mention that the combinatorial Lemmas 2 and 3 and inequality (17) may be of independent interest.
2. Proofs
2.1. Notation
Before the proof we introduce some notation. Let
![]() ${\mathcal K}$
be the complete graph with vertex set
${\mathcal K}$
be the complete graph with vertex set
![]() $V=[n]$
so that
$V=[n]$
so that
![]() $G_{[n,m]}\subset {\mathcal K}$
. By
$G_{[n,m]}\subset {\mathcal K}$
. By
![]() ${\mathbb {E}}^*(\cdot)={\mathbb {E}}(\cdot\mid X, X_1,\dots, X_m,Q, Q_1,\dots, Q_m)$
we denote the conditional expectation given
${\mathbb {E}}^*(\cdot)={\mathbb {E}}(\cdot\mid X, X_1,\dots, X_m,Q, Q_1,\dots, Q_m)$
we denote the conditional expectation given
![]() $X, X_1,\dots, X_m,Q, Q_1,\dots, Q_m$
. Given F, for any positive sequences
$X, X_1,\dots, X_m,Q, Q_1,\dots, Q_m$
. Given F, for any positive sequences
![]() $\{a_n\}$
and
$\{a_n\}$
and
![]() $\{b_n\}$
we write
$\{b_n\}$
we write
![]() $a_n\asymp b_n$
(respectively
$a_n\asymp b_n$
(respectively
![]() $a_n\prec b_n$
) whenever, for sufficiently large n, we have
$a_n\prec b_n$
) whenever, for sufficiently large n, we have
![]() $c_1 \le a_n/b_n\le c_2$
(respectively
$c_1 \le a_n/b_n\le c_2$
(respectively
![]() $a_n\le c_2b_n$
), where constants
$a_n\le c_2b_n$
), where constants
![]() $0\lt c_1\lt c_2$
may only depend on F. For a sequence of random variables
$0\lt c_1\lt c_2$
may only depend on F. For a sequence of random variables
![]() $\{Y_n\}$
we write
$\{Y_n\}$
we write
![]() $Y_n=o_P(a_n)$
whenever
$Y_n=o_P(a_n)$
whenever
![]() $\lim_{n\to\infty}{\mathbb {P}}\{|Y_n|\lt\varepsilon|a_n|\}=1$
for any
$\lim_{n\to\infty}{\mathbb {P}}\{|Y_n|\lt\varepsilon|a_n|\}=1$
for any
![]() $\varepsilon\gt 0$
; and
$\varepsilon\gt 0$
; and
![]() $Y_n=O_P(a_n)$
if, for every
$Y_n=O_P(a_n)$
if, for every
![]() $\varepsilon\gt 0$
, there exists a constant
$\varepsilon\gt 0$
, there exists a constant
![]() $c_\varepsilon\gt 0$
such that
$c_\varepsilon\gt 0$
such that
![]() $\lim_{n\to\infty}{\mathbb {P}}\{|Y_n|\lt c_\varepsilon|a_n|\}\gt 1-\varepsilon$
.
$\lim_{n\to\infty}{\mathbb {P}}\{|Y_n|\lt c_\varepsilon|a_n|\}\gt 1-\varepsilon$
.
Recall that
![]() $N_F$
and
$N_F$
and
![]() $N_{F,i}$
denote the numbers of copies of F in G(X, Q) and
$N_{F,i}$
denote the numbers of copies of F in G(X, Q) and
![]() $G(X_i,Q_i)$
, respectively. Furthermore,
$G(X_i,Q_i)$
, respectively. Furthermore,
![]() $N_{F}^*={\mathbb {E}}(N_F\mid X,Q)$
,
$N_{F}^*={\mathbb {E}}(N_F\mid X,Q)$
,
![]() $N_{F,i}^*={\mathbb {E}}(N_{F,i}\mid X_i,Q_i)$
, and
$N_{F,i}^*={\mathbb {E}}(N_{F,i}\mid X_i,Q_i)$
, and
![]() $S_F=N_{F,1}+\cdots+N_{F,m}$
,
$S_F=N_{F,1}+\cdots+N_{F,m}$
,
![]() $S_F^*=N_{F,1}^*+\cdots+N_{F,m}^*$
. Note that
$S_F^*=N_{F,1}^*+\cdots+N_{F,m}^*$
. Note that
![]() $N_{F,i}^*={\mathbb {E}}^*(N_{F,i})$
and
$N_{F,i}^*={\mathbb {E}}^*(N_{F,i})$
and
![]() $S_F^*={\mathbb {E}}^*(S_F)$
. Finally, let
$S_F^*={\mathbb {E}}^*(S_F)$
. Finally, let
![]() ${\tilde N}_{F,i}$
be the number of copies of F in
${\tilde N}_{F,i}$
be the number of copies of F in
![]() $G_{n,i}$
, and let
$G_{n,i}$
, and let
![]() ${\tilde S}_F = {\tilde N}_{F,1}+\dots+{\tilde N}_{F,m}$
.
${\tilde S}_F = {\tilde N}_{F,1}+\dots+{\tilde N}_{F,m}$
.
We can identify the indices
![]() $1\le i\le m$
with colours, and assign (the edges of) each
$1\le i\le m$
with colours, and assign (the edges of) each
![]() $G_{n,i}$
the colour i. The coloured graph is denoted by
$G_{n,i}$
the colour i. The coloured graph is denoted by
![]() $G^{\star}_{n,i}$
. The union of coloured graphs
$G^{\star}_{n,i}$
. The union of coloured graphs
![]() $G^{\star}_{n,1}\cup\cdots\cup G^{\star}_{n,m}$
defines a multigraph, denoted by
$G^{\star}_{n,1}\cup\cdots\cup G^{\star}_{n,m}$
defines a multigraph, denoted by
![]() $G_{[n,m]}^{\star}$
, where parallel edges have different colours. Furthermore, each edge
$G_{[n,m]}^{\star}$
, where parallel edges have different colours. Furthermore, each edge
![]() $u\sim v$
of
$u\sim v$
of
![]() $G_{[n,m]}$
is assigned the set of colours that correspond to parallel edges of
$G_{[n,m]}$
is assigned the set of colours that correspond to parallel edges of
![]() $G^{\star}_{[n,m]}$
connecting u and v.
$G^{\star}_{[n,m]}$
connecting u and v.
A subgraph
![]() $H\subset G_{[n,m]}$
is called monochromatic if it is a subgraph of some
$H\subset G_{[n,m]}$
is called monochromatic if it is a subgraph of some
![]() $G_{n,i}$
and none of the edges of H are assigned more than one colour. Otherwise H is called polychromatic.
$G_{n,i}$
and none of the edges of H are assigned more than one colour. Otherwise H is called polychromatic.
![]() ${\mathcal N}_{F,M}$
and
${\mathcal N}_{F,M}$
and
![]() ${\mathcal N}_{F,P}$
stand for the numbers of monochromatic and polychromatic copies of F in
${\mathcal N}_{F,P}$
stand for the numbers of monochromatic and polychromatic copies of F in
![]() $G_{[n,m]}$
. A subgraph
$G_{[n,m]}$
. A subgraph
![]() $H^{\star}\subset G_{[n,m]}^{\star}$
is called monochromatic if it is a subgraph of some
$H^{\star}\subset G_{[n,m]}^{\star}$
is called monochromatic if it is a subgraph of some
![]() $G_{n,i}^{\star}$
. It is called polychromatic if it contains edges of different colours. Let
$G_{n,i}^{\star}$
. It is called polychromatic if it contains edges of different colours. Let
![]() ${\mathcal N}_{F,P}^{\star}$
be the number of polychromatic copies of F in
${\mathcal N}_{F,P}^{\star}$
be the number of polychromatic copies of F in
![]() $G_{[n,m]}^{\star}$
.
$G_{[n,m]}^{\star}$
.
Figure 1 depicts an instance of the overlay graph
![]() $G_{[5,3]}$
and respective multigraph
$G_{[5,3]}$
and respective multigraph
![]() $G^{\star}_{[5,3]}=G^{\star}_{5,1}\cup G^{\star}_{5,2}\cup G^{\star}_{5,3}$
, where
$G^{\star}_{[5,3]}=G^{\star}_{5,1}\cup G^{\star}_{5,2}\cup G^{\star}_{5,3}$
, where
![]() $G^{\star}_{5,i}$
has vertex set
$G^{\star}_{5,i}$
has vertex set
![]() ${\mathcal V}_{5,i}=\{i,i+1,i+2\}$
and edges labelled (coloured) i.
${\mathcal V}_{5,i}=\{i,i+1,i+2\}$
and edges labelled (coloured) i.
![]() $G^{\star}_{[5,3]}$
has three polychromatic and two monochromatic copies of
$G^{\star}_{[5,3]}$
has three polychromatic and two monochromatic copies of
![]() ${\mathcal K}_3$
(Figure 2), while
${\mathcal K}_3$
(Figure 2), while
![]() $G_{[5,3]}$
has two polychromatic copies of
$G_{[5,3]}$
has two polychromatic copies of
![]() ${\mathcal K}_3$
(induced by
${\mathcal K}_3$
(induced by
![]() $\{1,2,3\}$
and
$\{1,2,3\}$
and
![]() $\{2,3,4\}$
) and one monochromatic copy of
$\{2,3,4\}$
) and one monochromatic copy of
![]() ${\mathcal K}_3$
(induced by
${\mathcal K}_3$
(induced by
![]() $\{3,4,5\}$
).
$\{3,4,5\}$
).

Figure 1. Multigraph
![]() $G^{\star}_{[5,3]}$
and overlay graph
$G^{\star}_{[5,3]}$
and overlay graph
![]() $G_{[5,3]}$
.
$G_{[5,3]}$
.

Figure 2. Three polychromatic and two monochromatic copies of
![]() ${\mathcal K}_3$
in
${\mathcal K}_3$
in
![]() $G^{\star}_{[5,3]}$
.
$G^{\star}_{[5,3]}$
.
Given
![]() $H^{\star}=({\mathcal V}_{H^{\star}},{\mathcal E}_{H^{\star}})\subset G_{[n,m]}^{\star}$
, let
$H^{\star}=({\mathcal V}_{H^{\star}},{\mathcal E}_{H^{\star}})\subset G_{[n,m]}^{\star}$
, let
![]() $H_0\subset {\mathcal K}$
be the graph on the vertex set
$H_0\subset {\mathcal K}$
be the graph on the vertex set
![]() ${\mathcal V}_{H^{\star}}$
obtained from
${\mathcal V}_{H^{\star}}$
obtained from
![]() $H^{\star}$
as follows: two vertices of
$H^{\star}$
as follows: two vertices of
![]() $H_0$
are adjacent whenever they are joined by an edge in
$H_0$
are adjacent whenever they are joined by an edge in
![]() $H^{\star}$
. We call
$H^{\star}$
. We call
![]() $H_0$
the projection of
$H_0$
the projection of
![]() $H^{\star}$
. Note that there can be several monochromatic and/or polychromatic copies of F in
$H^{\star}$
. Note that there can be several monochromatic and/or polychromatic copies of F in
![]() $G_{[n,m]}^{\star}$
sharing the same projection
$G_{[n,m]}^{\star}$
sharing the same projection
![]() $F_0$
. We fix a copy
$F_0$
. We fix a copy
![]() $F_0$
of F in
$F_0$
of F in
![]() ${\mathcal K}$
and denote by
${\mathcal K}$
and denote by
![]() $h_F$
the expected number of polychromatic copies of F in
$h_F$
the expected number of polychromatic copies of F in
![]() $G^{\star}_{[n,m]}$
whose projection is
$G^{\star}_{[n,m]}$
whose projection is
![]() $F_0$
. By the symmetry of the random graph model
$F_0$
. By the symmetry of the random graph model
![]() $G^{\star}_{[n,m]}$
, the quantity
$G^{\star}_{[n,m]}$
, the quantity
![]() $h_F$
does not depend on the location of
$h_F$
does not depend on the location of
![]() $F_0$
in
$F_0$
in
![]() $\mathcal K$
. An expression of
$\mathcal K$
. An expression of
![]() $h_F$
in terms of mixed moments
$h_F$
in terms of mixed moments
![]() ${\mathbb {E}}(({\tilde X}_1)_sQ_1^{t})$
is given in (11) and (12).
${\mathbb {E}}(({\tilde X}_1)_sQ_1^{t})$
is given in (11) and (12).
2.2. Proofs
We first prove Theorems 1 and 2, and Remarks 2 and 3. Afterwards we prove Remarks 4 and 1.
We start with an outline of the proof of Theorems 1 and 2. We approximate
![]() ${\mathcal N}_F\approx {\tilde S}_F$
and
${\mathcal N}_F\approx {\tilde S}_F$
and
![]() ${\tilde S}_F\approx S_F$
. In the case where
${\tilde S}_F\approx S_F$
. In the case where
![]() ${\mathbb {E}}\, N_{F}^2\lt\infty$
we deduce the normal approximation to the sum
${\mathbb {E}}\, N_{F}^2\lt\infty$
we deduce the normal approximation to the sum
![]() $S_F$
(of i.i.d. random variables) by the standard central limit theorem. In the case where
$S_F$
(of i.i.d. random variables) by the standard central limit theorem. In the case where
![]() $N_F$
has an infinite variance we further approximate
$N_F$
has an infinite variance we further approximate
![]() $S_F\approx S_F^*$
and deduce the
$S_F\approx S_F^*$
and deduce the
![]() $\alpha$
-stable approximation by the generalised central limit theorem [Reference Gnedenko and Kolmogorov9, Theorem 2,
$\alpha$
-stable approximation by the generalised central limit theorem [Reference Gnedenko and Kolmogorov9, Theorem 2,
![]() $\S 35$
].
$\S 35$
].
Approximation
 ${\mathcal N}_F\approx {\tilde S}_F$
${\mathcal N}_F\approx {\tilde S}_F$
The approximation follows from the simple observation that
The inequalities
![]() ${\mathcal N}_{F,M}\le {\tilde S}_F$
and
${\mathcal N}_{F,M}\le {\tilde S}_F$
and
![]() ${\mathcal N}_{F,P}\le {\mathcal N}_{F,P}^{\star}$
are easy. To see why the inequality
${\mathcal N}_{F,P}\le {\mathcal N}_{F,P}^{\star}$
are easy. To see why the inequality
![]() ${\tilde S}_F\le {\mathcal N}_{F,M} + {\mathcal N}^{\star}_{F,P}$
holds true, let us inspect a pair
${\tilde S}_F\le {\mathcal N}_{F,M} + {\mathcal N}^{\star}_{F,P}$
holds true, let us inspect a pair
![]() $F_i\in G_{n,i}$
and
$F_i\in G_{n,i}$
and
![]() $F_j\in G_{n,j}$
of copies of
$F_j\in G_{n,j}$
of copies of
![]() $F=({\mathcal V}_F,{\mathcal E}_F)$
that share
$F=({\mathcal V}_F,{\mathcal E}_F)$
that share
![]() $t\,:\!=|{\mathcal E}_{F_i}\cap {\mathcal E}_{F_j}|\ge 1$
edges. Note that both copies
$t\,:\!=|{\mathcal E}_{F_i}\cap {\mathcal E}_{F_j}|\ge 1$
edges. Note that both copies
![]() $F_i$
and
$F_i$
and
![]() $F_j$
contribute to the sum
$F_j$
contribute to the sum
![]() ${\tilde S}_F$
, and neither contributes to the sum
${\tilde S}_F$
, and neither contributes to the sum
![]() ${\mathcal N}_{F,M}$
. In the case where
${\mathcal N}_{F,M}$
. In the case where
![]() $t\lt |{\mathcal E}_F|$
the pair gives rise to
$t\lt |{\mathcal E}_F|$
the pair gives rise to
![]() $2\cdot 2^{t}-2\ge 2$
polychromatic copies of F in
$2\cdot 2^{t}-2\ge 2$
polychromatic copies of F in
![]() $G^{\star}_{[n,m]}$
. In the case where
$G^{\star}_{[n,m]}$
. In the case where
![]() $t=|{\mathcal E}_F|$
(now
$t=|{\mathcal E}_F|$
(now
![]() $t\ge 3$
) the pair gives rise to
$t\ge 3$
) the pair gives rise to
![]() $2^t-2$
polychromatic copies of F in
$2^t-2$
polychromatic copies of F in
![]() $G^{\star}_{[n,m]}$
. Hence,
$G^{\star}_{[n,m]}$
. Hence,
![]() ${\tilde S}_F\le {\mathcal N}_{F,M}+{\mathcal N}^{\star}_{F,P}$
. From (8) we conclude that
${\tilde S}_F\le {\mathcal N}_{F,M}+{\mathcal N}^{\star}_{F,P}$
. From (8) we conclude that
In order to assess the accuracy of the approximation
![]() ${\mathcal N}_F\approx {\tilde S}_F$
we evaluate the expected value of
${\mathcal N}_F\approx {\tilde S}_F$
we evaluate the expected value of
![]() ${\mathcal N}_{F,P}^{\star}$
. We fix a copy of F in
${\mathcal N}_{F,P}^{\star}$
. We fix a copy of F in
![]() ${\mathcal K}$
, denoted
${\mathcal K}$
, denoted
![]() $F_0=({\mathcal V}_{0},{\mathcal E}_{0})\subset {\mathcal K}$
, with vertex set
$F_0=({\mathcal V}_{0},{\mathcal E}_{0})\subset {\mathcal K}$
, with vertex set
![]() ${\mathcal V}_0=\{1,\dots, v_F\}$
. Recall that
${\mathcal V}_0=\{1,\dots, v_F\}$
. Recall that
![]() $h_F$
denotes the expected number of polychromatic copies of F in
$h_F$
denotes the expected number of polychromatic copies of F in
![]() $G^{\star}_{[n,m]}$
whose projection is
$G^{\star}_{[n,m]}$
whose projection is
![]() $F_0$
. We have, by symmetry,
$F_0$
. We have, by symmetry,
Note that every polychromatic copy of F in
![]() $G^{\star}_{[n,m]}$
(say,
$G^{\star}_{[n,m]}$
(say,
![]() $F^{\star}\subset G^{\star}_{[n,m]}$
) whose projection is
$F^{\star}\subset G^{\star}_{[n,m]}$
) whose projection is
![]() $F_0$
is defined by a partition of the edge set
$F_0$
is defined by a partition of the edge set
![]() ${\mathcal E}_{0}$
into non-empty colour classes, say,
${\mathcal E}_{0}$
into non-empty colour classes, say,
![]() $B_1\cup\cdots\cup B_r={\mathcal E}_0$
, and a vector of distinct colours
$B_1\cup\cdots\cup B_r={\mathcal E}_0$
, and a vector of distinct colours
![]() $(i_1,\dots, i_r)\in [m]^r$
such that all the edges in
$(i_1,\dots, i_r)\in [m]^r$
such that all the edges in
![]() $B_j$
are of colour
$B_j$
are of colour
![]() $i_j$
(edges of
$i_j$
(edges of
![]() $B_j$
belong to
$B_j$
belong to
![]() $G^{\star}_{n,i_j}$
). Denote by
$G^{\star}_{n,i_j}$
). Denote by
![]() ${\tilde B}=(B_1,\dots, B_r)$
and
${\tilde B}=(B_1,\dots, B_r)$
and
![]() ${\tilde i}=(i_1,\dots, i_r)$
the partition and its colouring. The polychromatic subgraph
${\tilde i}=(i_1,\dots, i_r)$
the partition and its colouring. The polychromatic subgraph
![]() $F^{\star}$
defined by the pair
$F^{\star}$
defined by the pair
![]() $({\tilde B}, {\tilde i})$
is denoted
$({\tilde B}, {\tilde i})$
is denoted
![]() $F({\tilde B}, {\tilde i})$
. The probability that such a subgraph is present in
$F({\tilde B}, {\tilde i})$
. The probability that such a subgraph is present in
![]() $G_{[n,m]}^{\star}$
is
$G_{[n,m]}^{\star}$
is
 \begin{equation} h({\tilde B}, {\tilde i}) \,:\!= {\mathbb {P}}\Bigl\{ F({\tilde B}, {\tilde i}) \subset G_{[n,m]}^{\star} \Bigr\} = \prod_{j=1}^r\frac{1}{(n)_{v_j}} {\mathbb {E}} \Big( ({\tilde X}_{i_j})_{v_j}Q_{i_j}^{b_j} \Big).\end{equation}
\begin{equation} h({\tilde B}, {\tilde i}) \,:\!= {\mathbb {P}}\Bigl\{ F({\tilde B}, {\tilde i}) \subset G_{[n,m]}^{\star} \Bigr\} = \prod_{j=1}^r\frac{1}{(n)_{v_j}} {\mathbb {E}} \Big( ({\tilde X}_{i_j})_{v_j}Q_{i_j}^{b_j} \Big).\end{equation}
Here,
![]() $b_j\,:\!=|B_j|$
, and
$b_j\,:\!=|B_j|$
, and
![]() $v_j$
is the number of distinct vertices incident to edges from
$v_j$
is the number of distinct vertices incident to edges from
![]() $B_j$
. We have
$B_j$
. We have
 \begin{equation} h_F = {\mathbb {E}}\Bigg(\sum_{({\tilde B}, {\tilde i})}\textbf{1}_{\big\{F({\tilde B},{\tilde i})\in G_{[n,m]}^*\big\}}\Bigg) = \sum_{({\tilde B}, {\tilde i})} h({\tilde B}, {\tilde i}).\end{equation}
\begin{equation} h_F = {\mathbb {E}}\Bigg(\sum_{({\tilde B}, {\tilde i})}\textbf{1}_{\big\{F({\tilde B},{\tilde i})\in G_{[n,m]}^*\big\}}\Bigg) = \sum_{({\tilde B}, {\tilde i})} h({\tilde B}, {\tilde i}).\end{equation}
Here, the sum runs over all possible polychromatic copies
![]() $F^{\star}$
of F whose projection is
$F^{\star}$
of F whose projection is
![]() $F_0$
. We upper bound the quantity on the right of (12) in Lemmas 1 and 4 below.
$F_0$
. We upper bound the quantity on the right of (12) in Lemmas 1 and 4 below.
Approximation
 ${\tilde S}_F\approx S_F$
${\tilde S}_F\approx S_F$
For
![]() $1\le i\le m$
we couple
$1\le i\le m$
we couple
![]() $G({\tilde X}_i,Q_i)\subset G(X_i,Q_i)$
and
$G({\tilde X}_i,Q_i)\subset G(X_i,Q_i)$
and
![]() ${\tilde N}_{F,i}\le N_{F,i}$
so that
${\tilde N}_{F,i}\le N_{F,i}$
so that
![]() $G({\tilde X}_i,Q_i)\not= G(X_i,Q_i)$
and
$G({\tilde X}_i,Q_i)\not= G(X_i,Q_i)$
and
![]() ${\tilde N}_{F,i}\not= N_{F,i}$
whenever
${\tilde N}_{F,i}\not= N_{F,i}$
whenever
![]() $X_i\gt n$
. For
$X_i\gt n$
. For
![]() $m=O(n)$
, the event
$m=O(n)$
, the event
![]() ${\mathcal A}_n\,:\!=\{\max_{1\le i\le m}X_i\gt n\}$
has probability
${\mathcal A}_n\,:\!=\{\max_{1\le i\le m}X_i\gt n\}$
has probability
Hence,
![]() ${\mathbb {P}}\{{\tilde S}_F\not=S_F\}=o(1)$
. In (13) we used the fact that
${\mathbb {P}}\{{\tilde S}_F\not=S_F\}=o(1)$
. In (13) we used the fact that
![]() ${\mathbb {E}}\, X_1\lt \infty\Rightarrow{\mathbb {E}} \bigl(X_1\textbf{1}_{\{X_1\gt n\}}\bigr)=o(1)$
.
${\mathbb {E}}\, X_1\lt \infty\Rightarrow{\mathbb {E}} \bigl(X_1\textbf{1}_{\{X_1\gt n\}}\bigr)=o(1)$
.
Proof of Theorem 1 and Remark 2. By Lemma 1 (respectively, Lemma 4), we have
![]() $h_F=o(n^{0.5-v_F})$
. Invoking this bound in (10), we obtain
$h_F=o(n^{0.5-v_F})$
. Invoking this bound in (10), we obtain
![]() ${\mathcal N}_{F,P}^{\star}=o_P(\sqrt{m})$
. Next, from (9) we obtain that
${\mathcal N}_{F,P}^{\star}=o_P(\sqrt{m})$
. Next, from (9) we obtain that
![]() $({\mathcal N}_F-{\tilde S}_F)=o_P(\sqrt{m})$
. Then, an application of (13) shows that
$({\mathcal N}_F-{\tilde S}_F)=o_P(\sqrt{m})$
. Then, an application of (13) shows that
![]() $({\mathcal N}_F-S_F)=o_P(\sqrt{m})$
. Finally, we apply the classical central limit theorem to the sum of i.i.d. random variables
$({\mathcal N}_F-S_F)=o_P(\sqrt{m})$
. Finally, we apply the classical central limit theorem to the sum of i.i.d. random variables
![]() $S_F$
to get the asymptotic normality of
$S_F$
to get the asymptotic normality of
![]() $({\mathcal N}_F-m{\mathbb {E}} N_F)/ (\sigma_{F}\sqrt{m})$
.
$({\mathcal N}_F-m{\mathbb {E}} N_F)/ (\sigma_{F}\sqrt{m})$
.
Proof of Theorem 2 and Remark 3. By Lemma 1 (respectively, Lemma 4), we have
![]() $h_F=o(n^{({1}/{\alpha})-v_F})$
. Using this bound and proceeding as in the proof of Theorem 1, we obtain
$h_F=o(n^{({1}/{\alpha})-v_F})$
. Using this bound and proceeding as in the proof of Theorem 1, we obtain
![]() ${\mathcal N}_F=S_F+o_P(m^{1/\alpha})$
. Next, from the fact that the random variables
${\mathcal N}_F=S_F+o_P(m^{1/\alpha})$
. Next, from the fact that the random variables
![]() $N_{F,1}$
,
$N_{F,1}$
,
![]() $N_{F,2}$
,
$N_{F,2}$
,
![]() $\dots$
obey the power law (28) (see Lemma 5), we conclude that
$\dots$
obey the power law (28) (see Lemma 5), we conclude that
![]() $(S_F-B_m)/m^{1/\alpha}$
converges in distribution to
$(S_F-B_m)/m^{1/\alpha}$
converges in distribution to
![]() $G_{\alpha,a}$
[Reference Gnedenko and Kolmogorov9, Theorem 2,
$G_{\alpha,a}$
[Reference Gnedenko and Kolmogorov9, Theorem 2,
![]() $\S35$
]. Hence,
$\S35$
]. Hence,
![]() $({\mathcal N}_F-B_m)/m^{1/\alpha}$
converges in distribution to
$({\mathcal N}_F-B_m)/m^{1/\alpha}$
converges in distribution to
![]() $G_{\alpha,a}$
.
$G_{\alpha,a}$
.
Proof of Remark 4. We have
![]() ${\mathcal N}_{{\mathcal K}_2}=|{\mathcal E}|=|{\mathcal E}_{n,1}\cup\cdots\cup{\mathcal E}_{n,m}|$
and
${\mathcal N}_{{\mathcal K}_2}=|{\mathcal E}|=|{\mathcal E}_{n,1}\cup\cdots\cup{\mathcal E}_{n,m}|$
and
![]() ${\tilde S}_{{\mathcal K}_2}=\sum_{i=1}^n|{\mathcal E}_{n,i}|$
. By the inclusion–exclusion principle,
${\tilde S}_{{\mathcal K}_2}=\sum_{i=1}^n|{\mathcal E}_{n,i}|$
. By the inclusion–exclusion principle,
 \begin{equation} 0 \le \sum_{i=1}^m|{\mathcal E}_{n,i}|-|{\mathcal E}| \le \sum_{\{i,j\}\subset[m]}|{\mathcal E}_{n,i}\cap{\mathcal E}_{n,j}|. \end{equation}
\begin{equation} 0 \le \sum_{i=1}^m|{\mathcal E}_{n,i}|-|{\mathcal E}| \le \sum_{\{i,j\}\subset[m]}|{\mathcal E}_{n,i}\cap{\mathcal E}_{n,j}|. \end{equation}
We write
![]() $|{\mathcal E}_{n,i}\cap{\mathcal E}_{n,j}|=\sum_{\{u,v\}\subset V}\textbf{1}_{\{\{u,v\}\in {\mathcal E}_{n,i}\}} \textbf{1}_{\{\{u,v\}\in {\mathcal E}_{n,j}\}}$
and evaluate the conditional expectation
$|{\mathcal E}_{n,i}\cap{\mathcal E}_{n,j}|=\sum_{\{u,v\}\subset V}\textbf{1}_{\{\{u,v\}\in {\mathcal E}_{n,i}\}} \textbf{1}_{\{\{u,v\}\in {\mathcal E}_{n,j}\}}$
and evaluate the conditional expectation
To prove (i), in view of the identity
![]() $\sigma_{{\mathcal K}_2}^2 = {\textrm{Var}}\bigl(\binom{X}{2}Q\bigr) + {\mathbb {E}}\bigl(\binom{X}{2}Q(1-Q)\bigr)$
we have
$\sigma_{{\mathcal K}_2}^2 = {\textrm{Var}}\bigl(\binom{X}{2}Q\bigr) + {\mathbb {E}}\bigl(\binom{X}{2}Q(1-Q)\bigr)$
we have
![]() $\sigma_{{\mathcal K}_2}^2\lt\infty \Leftrightarrow {\mathbb {E}}\bigl(X^4Q^2\bigr)\lt \infty$
. Hence,
$\sigma_{{\mathcal K}_2}^2\lt\infty \Leftrightarrow {\mathbb {E}}\bigl(X^4Q^2\bigr)\lt \infty$
. Hence,
![]() $\sigma_{{\mathcal K}_2}^2\lt \infty$
implies
$\sigma_{{\mathcal K}_2}^2\lt \infty$
implies
![]() $\infty\gt{\mathbb {E}}(X^4Q^2)\ge ({\mathbb {E}}(X^2Q))^2$
, by Cauchy–Schwarz. Consequently, the expected value of the quantity on the right of (14) is
$\infty\gt{\mathbb {E}}(X^4Q^2)\ge ({\mathbb {E}}(X^2Q))^2$
, by Cauchy–Schwarz. Consequently, the expected value of the quantity on the right of (14) is
 \begin{equation*} {\mathbb {E}}\Bigg(\sum_{\{i,j\}\subset[m]}\bigg(\frac{({\tilde X}_i)_2Q_i({\tilde X}_j)_2Q_j}{2(n)_2}\bigg)\Bigg) = \binom{m}{2}\bigg(\frac{({\mathbb {E}}(({\tilde X}_1)_2Q_1))^2}{2(n)_2}\bigg) = O(1). \end{equation*}
\begin{equation*} {\mathbb {E}}\Bigg(\sum_{\{i,j\}\subset[m]}\bigg(\frac{({\tilde X}_i)_2Q_i({\tilde X}_j)_2Q_j}{2(n)_2}\bigg)\Bigg) = \binom{m}{2}\bigg(\frac{({\mathbb {E}}(({\tilde X}_1)_2Q_1))^2}{2(n)_2}\bigg) = O(1). \end{equation*}
Now, (14) implies
![]() ${\mathcal N}_{{\mathcal K}_2}={\tilde S}_{{\mathcal K}_2}+O_P(1)$
. Next, (13) implies
${\mathcal N}_{{\mathcal K}_2}={\tilde S}_{{\mathcal K}_2}+O_P(1)$
. Next, (13) implies
![]() $({\mathcal N}_{{\mathcal K}_2}-S_{{\mathcal K}_2})/(\sigma_{{\mathcal K}_2}\sqrt{m})=o_P(1)$
. Finally, the asymptotic normality of
$({\mathcal N}_{{\mathcal K}_2}-S_{{\mathcal K}_2})/(\sigma_{{\mathcal K}_2}\sqrt{m})=o_P(1)$
. Finally, the asymptotic normality of
![]() $({\mathcal N}_{{\mathcal K}_2} - m{\mathbb {E}} N_{{\mathcal K}_2})/(\sigma_{{\mathcal K}_2}\sqrt{m})$
follows by the classical central limit theorem applied to the sum
$({\mathcal N}_{{\mathcal K}_2} - m{\mathbb {E}} N_{{\mathcal K}_2})/(\sigma_{{\mathcal K}_2}\sqrt{m})$
follows by the classical central limit theorem applied to the sum
![]() $S_{{\mathcal K}_2}=\sum_{i\in[m]}N_{{\mathcal K}_2,i}$
.
$S_{{\mathcal K}_2}=\sum_{i\in[m]}N_{{\mathcal K}_2,i}$
.
To prove (ii), we have
![]() $N_{{\mathcal K}_2}^*=\binom{X}{2}Q$
. Observing that (3) implies
$N_{{\mathcal K}_2}^*=\binom{X}{2}Q$
. Observing that (3) implies
![]() ${\mathbb {P}}\{X^2\gt t\}\ge {\mathbb {P}}\{N_{{\mathcal K}_2}^*\gt t\}= (a+o(1))t^{-\alpha}$
, we obtain from the first moment condition
${\mathbb {P}}\{X^2\gt t\}\ge {\mathbb {P}}\{N_{{\mathcal K}_2}^*\gt t\}= (a+o(1))t^{-\alpha}$
, we obtain from the first moment condition
![]() ${\mathbb {E}}\, X\lt\infty$
that
${\mathbb {E}}\, X\lt\infty$
that
![]() $\alpha\gt 0.5$
.
$\alpha\gt 0.5$
.
Let R denote the quantity on the right of (14), and put
![]() $R^*={\mathbb {E}}^*R$
. We first show that
$R^*={\mathbb {E}}^*R$
. We first show that
![]() $R=o_P(m^{1/\alpha})$
. Note that
$R=o_P(m^{1/\alpha})$
. Note that
![]() $R^*\le 4m^{2/\alpha}n^{-2}T_*^2$
, where
$R^*\le 4m^{2/\alpha}n^{-2}T_*^2$
, where
![]() $T_*\,:\!=m^{-1/\alpha}\sum_{i\in[m]}N^*_{{\mathcal K}_2,i}$
. Given
$T_*\,:\!=m^{-1/\alpha}\sum_{i\in[m]}N^*_{{\mathcal K}_2,i}$
. Given
![]() $\varepsilon\in(0,1)$
, we have, for
$\varepsilon\in(0,1)$
, we have, for
![]() $A=\varepsilon m^{1/\alpha}$
and
$A=\varepsilon m^{1/\alpha}$
and
![]() $B=\varepsilon A$
,
$B=\varepsilon A$
,
Indeed,
![]() ${\mathbb {P}}\{R^*\gt B \}\le {\mathbb {P}}\big\{4m^{2/\alpha}n^{-2}T_*^2\gt B\big\} = {\mathbb {P}}\big\{4T_*^2\gt m^{-1/\alpha}n^2\varepsilon^2\big\}=o(1)$
, since
${\mathbb {P}}\{R^*\gt B \}\le {\mathbb {P}}\big\{4m^{2/\alpha}n^{-2}T_*^2\gt B\big\} = {\mathbb {P}}\big\{4T_*^2\gt m^{-1/\alpha}n^2\varepsilon^2\big\}=o(1)$
, since
![]() $m^{-1/\alpha}n^2{}\varepsilon^2\to+\infty$
for
$m^{-1/\alpha}n^2{}\varepsilon^2\to+\infty$
for
![]() $\alpha\gt 0.5$
and
$\alpha\gt 0.5$
and
![]() $T_*=O_P(1)$
by (3). Furthermore, by Markov’s inequality,
$T_*=O_P(1)$
by (3). Furthermore, by Markov’s inequality,
Clearly, (15) implies the bound
![]() $R=o_P(m^{1/\alpha})$
. Now, (14) implies
$R=o_P(m^{1/\alpha})$
. Now, (14) implies
![]() ${\mathcal N}_{{\mathcal K}_2}={\tilde S}_{{\mathcal K}_2}+o_P(m^{1/\alpha})$
. Next, (13) implies
${\mathcal N}_{{\mathcal K}_2}={\tilde S}_{{\mathcal K}_2}+o_P(m^{1/\alpha})$
. Next, (13) implies
![]() $({\mathcal N}_{{\mathcal K}_2}-S_{{\mathcal K}_2})m^{-1/\alpha}=o_P(1)$
. In the last step of the proof we show that
$({\mathcal N}_{{\mathcal K}_2}-S_{{\mathcal K}_2})m^{-1/\alpha}=o_P(1)$
. In the last step of the proof we show that
![]() $(S_{{\mathcal K}_2}-B_m)/m^{1/\alpha}$
converges in distribution to
$(S_{{\mathcal K}_2}-B_m)/m^{1/\alpha}$
converges in distribution to
![]() $G_{\alpha,a}$
using the same argument as in the proof of Theorem 2.
$G_{\alpha,a}$
using the same argument as in the proof of Theorem 2.
Proof of Remark 1. We have
![]() $\sigma_F^2={\textrm{Var}}\, N_F={\textrm{Var}}\, N_F^*+{\mathbb {E}} \big(\Delta_F^*\big)^2$
, where
$\sigma_F^2={\textrm{Var}}\, N_F={\textrm{Var}}\, N_F^*+{\mathbb {E}} \big(\Delta_F^*\big)^2$
, where
![]() $\Delta_F^*\,:\!=N_F-N_F^*$
. Therefore,
$\Delta_F^*\,:\!=N_F-N_F^*$
. Therefore,
![]() $\sigma_F^2\lt\infty\Rightarrow {\textrm{Var}}\, N_F^*\lt\infty \Rightarrow {\mathbb {E}} \big(N_F^*\big)^2\lt\infty$
. To prove that
$\sigma_F^2\lt\infty\Rightarrow {\textrm{Var}}\, N_F^*\lt\infty \Rightarrow {\mathbb {E}} \big(N_F^*\big)^2\lt\infty$
. To prove that
![]() ${\mathbb {E}} \big(N_F^*\big)^2\lt\infty\Rightarrow \sigma_F^2\lt\infty$
, it suffices to show that
${\mathbb {E}} \big(N_F^*\big)^2\lt\infty\Rightarrow \sigma_F^2\lt\infty$
, it suffices to show that
![]() ${\mathbb {E}} \big(\Delta_F^*\big)^2\lt\infty$
. By [Reference Janson, Łuczak and Ruciński14, Lemma 3.5], we have
${\mathbb {E}} \big(\Delta_F^*\big)^2\lt\infty$
. By [Reference Janson, Łuczak and Ruciński14, Lemma 3.5], we have
![]() ${\mathbb {E}}^*\big(\Delta_F^*\big)^2\prec\big(N_F^*\big)^2/{}\Phi_F(X,Q)$
, where
${\mathbb {E}}^*\big(\Delta_F^*\big)^2\prec\big(N_F^*\big)^2/{}\Phi_F(X,Q)$
, where
![]() $\Phi_F(X,Q)=\min_{H\subset F}X^{v_H}Q^{e_H}$
. Furthermore, from the inequality in (27), which holds for balanced F, we obtain
$\Phi_F(X,Q)=\min_{H\subset F}X^{v_H}Q^{e_H}$
. Furthermore, from the inequality in (27), which holds for balanced F, we obtain
 \begin{equation*} {\mathbb {E}}^*\big(\Delta_F^*\big)^2 \prec\frac{ \big(N_F^*\big)^2}{\min\Big\{\big(N_F^*\big)^{2/v_F},N_F^*\Big\}} = \max \Big\{ \big(N_F^*\big)^{2-2/v_F}, N_F^*\Big\} \le \max \big\{1, \big(N_F^*\big)^2\big\}. \end{equation*}
\begin{equation*} {\mathbb {E}}^*\big(\Delta_F^*\big)^2 \prec\frac{ \big(N_F^*\big)^2}{\min\Big\{\big(N_F^*\big)^{2/v_F},N_F^*\Big\}} = \max \Big\{ \big(N_F^*\big)^{2-2/v_F}, N_F^*\Big\} \le \max \big\{1, \big(N_F^*\big)^2\big\}. \end{equation*}
Hence,
![]() ${\mathbb {E}} \big(N_F^*\big)^2\lt\infty$
implies
${\mathbb {E}} \big(N_F^*\big)^2\lt\infty$
implies
![]() ${\mathbb {E}} \big(\Delta_F^*\big)^2={\mathbb {E}} \Big({\mathbb {E}}^*\big(\Delta_F^*\big)^2\Big)\lt\infty$
.
${\mathbb {E}} \big(\Delta_F^*\big)^2={\mathbb {E}} \Big({\mathbb {E}}^*\big(\Delta_F^*\big)^2\Big)\lt\infty$
.
2.3. Auxiliary lemmas
In Lemmas 1 and 4 we upper bound the quantities
![]() $h_F$
for 2-connected F and for
$h_F$
for 2-connected F and for
![]() $F={\mathcal K}_k$
, respectively. Clearly, the result of Lemma 1 applies to
$F={\mathcal K}_k$
, respectively. Clearly, the result of Lemma 1 applies to
![]() $F={\mathcal K}_k$
as well, but the bound of Lemma 4 is tighter for large k.
$F={\mathcal K}_k$
as well, but the bound of Lemma 4 is tighter for large k.
Lemma 1.
Let F be a 2-connected graph with
![]() $v_F\ge 3$
vertices. Let
$v_F\ge 3$
vertices. Let
![]() $n,m\to+\infty$
. Assume that
$n,m\to+\infty$
. Assume that
![]() $m=O(n)$
.
$m=O(n)$
.
In the proof we use the simple fact that, for any
![]() $s,t,\tau\gt 0$
, the moment condition
$s,t,\tau\gt 0$
, the moment condition
![]() ${\mathbb {E}} (X^sQ^t)\lt\infty$
implies
${\mathbb {E}} (X^sQ^t)\lt\infty$
implies
Write
![]() ${\tilde X}\,:\!=\min\{X,n\}$
. To see why (16) holds, choose
${\tilde X}\,:\!=\min\{X,n\}$
. To see why (16) holds, choose
![]() $0\lt \delta\lt\tau/(s+\tau)$
and split the expectation:
$0\lt \delta\lt\tau/(s+\tau)$
and split the expectation:
The inequalities
![]() ${\tilde X}\le n$
and
${\tilde X}\le n$
and
![]() ${\mathbb {E}} (X^sQ^t)\lt\infty$
imply
${\mathbb {E}} (X^sQ^t)\lt\infty$
imply
![]() $I_2 \le n^{\tau} {\mathbb {E}}\big(X^sQ^t\textbf{1}_{\{X\ge n^{\delta}\}}\big) = n^{\tau}\cdot o(1)$
, and the inequality
$I_2 \le n^{\tau} {\mathbb {E}}\big(X^sQ^t\textbf{1}_{\{X\ge n^{\delta}\}}\big) = n^{\tau}\cdot o(1)$
, and the inequality
![]() ${\tilde X}\le X$
implies
${\tilde X}\le X$
implies
![]() $I_1\le n^{\delta(s+\tau)}=o(n^\tau)$
.
$I_1\le n^{\delta(s+\tau)}=o(n^\tau)$
.
Proof of Lemma 1. The proofs of statements (i) and (ii) are identical. Therefore we only prove statement (i).
We start by establishing an auxiliary inequality, (17), which may be interesting in itself. Let
![]() $r\ge 2$
. Given a partition
$r\ge 2$
. Given a partition
![]() ${\tilde B}=(B_1,\dots, B_r)$
of the edge set
${\tilde B}=(B_1,\dots, B_r)$
of the edge set
![]() ${\mathcal E}_0$
of the graph
${\mathcal E}_0$
of the graph
![]() $F_0=({\mathcal V}_0,{\mathcal E}_0)$
, and given
$F_0=({\mathcal V}_0,{\mathcal E}_0)$
, and given
![]() $i\in [r]$
, let
$i\in [r]$
, let
![]() $V_i$
be the set of vertices incident to the edges from
$V_i$
be the set of vertices incident to the edges from
![]() $B_i$
. Let
$B_i$
. Let
![]() $\rho_i$
be the number of (connected) components of the graph
$\rho_i$
be the number of (connected) components of the graph
![]() $Z_i=(V_i,B_i)$
, and put
$Z_i=(V_i,B_i)$
, and put
![]() $v_i=|V_i|$
. We claim that
$v_i=|V_i|$
. We claim that
To establish the claim we consider the list
![]() $H_1,H_2,\dots, H_t$
of components of
$H_1,H_2,\dots, H_t$
of components of
![]() $Z_1,\dots,Z_r$
arranged in an arbitrary order. Here,
$Z_1,\dots,Z_r$
arranged in an arbitrary order. Here,
![]() $t\,:\!=\rho_1+\dots+\rho_r$
. Therefore, each graph
$t\,:\!=\rho_1+\dots+\rho_r$
. Therefore, each graph
![]() $H_i$
is a component of some
$H_i$
is a component of some
![]() $Z_j$
, and their union
$Z_j$
, and their union
![]() $H_1\cup\cdots\cup H_t=Z_1\cup\cdots\cup Z_r=F_0$
. Let us consider the sequence of graphs
$H_1\cup\cdots\cup H_t=Z_1\cup\cdots\cup Z_r=F_0$
. Let us consider the sequence of graphs
![]() ${\bar H}_j\,:\!= H_1\cup\cdots\cup H_{j}$
for
${\bar H}_j\,:\!= H_1\cup\cdots\cup H_{j}$
for
![]() $j=1,\dots, t-1$
. Let
$j=1,\dots, t-1$
. Let
![]() ${\bar \rho}_j$
and
${\bar \rho}_j$
and
![]() ${\bar v}_j$
denote the number of components and the number of vertices of
${\bar v}_j$
denote the number of components and the number of vertices of
![]() ${\bar H}_j$
. Let
${\bar H}_j$
. Let
![]() $v^{\prime}_j$
denote the number of vertices of
$v^{\prime}_j$
denote the number of vertices of
![]() $H_j$
. We use the observation that
$H_j$
. We use the observation that
Indeed,
![]() ${\bar \rho}_{j-1}={\bar \rho}_j$
means that the vertex set of (the connected graph)
${\bar \rho}_{j-1}={\bar \rho}_j$
means that the vertex set of (the connected graph)
![]() $H_j$
intersects with exactly one component of
$H_j$
intersects with exactly one component of
![]() ${\bar H}_{j-1}$
. Consequently,
${\bar H}_{j-1}$
. Consequently,
![]() $H_j$
and
$H_j$
and
![]() ${\bar H}_{j-1}$
have at least one common vertex and therefore (18) holds. Similarly,
${\bar H}_{j-1}$
have at least one common vertex and therefore (18) holds. Similarly,
![]() ${\bar \rho}_{j-1}-{\bar \rho}_j=y\gt 0$
means that the vertex set of
${\bar \rho}_{j-1}-{\bar \rho}_j=y\gt 0$
means that the vertex set of
![]() $H_j$
intersects with exactly
$H_j$
intersects with exactly
![]() $y+1$
different components of
$y+1$
different components of
![]() ${\bar H}_{j-1}$
. Consequently,
${\bar H}_{j-1}$
. Consequently,
![]() $H_j$
and
$H_j$
and
![]() ${\bar H}_{j-1}$
have at least
${\bar H}_{j-1}$
have at least
![]() $y+1$
common vertices and (18) holds again. The remaining case,
$y+1$
common vertices and (18) holds again. The remaining case,
![]() ${\bar \rho}_{j-1}-{\bar \rho}_j=-1$
, is realised by the configuration where the vertex sets of
${\bar \rho}_{j-1}-{\bar \rho}_j=-1$
, is realised by the configuration where the vertex sets of
![]() $H_j$
and
$H_j$
and
![]() ${\bar H}_{j-1}$
have no common elements. In this case (18) follows from the identity
${\bar H}_{j-1}$
have no common elements. In this case (18) follows from the identity
![]() ${\bar v}_j = {\bar v}_{j-1}+v^{\prime}_j$
.
${\bar v}_j = {\bar v}_{j-1}+v^{\prime}_j$
.
By summing the inequalities in (18), we obtain, using
![]() ${\bar \rho}_1=1$
, that
${\bar \rho}_1=1$
, that
![]() ${\bar v}_{t-1} \le v^{\prime}_1+\cdots+v^{\prime}_{t-1}+ {\bar \rho}_{t-1}-t+1$
. Note that, given
${\bar v}_{t-1} \le v^{\prime}_1+\cdots+v^{\prime}_{t-1}+ {\bar \rho}_{t-1}-t+1$
. Note that, given
![]() ${\bar H}_{t-1}$
with
${\bar H}_{t-1}$
with
![]() ${\bar \rho}_{t-1}$
components, the vertex set of
${\bar \rho}_{t-1}$
components, the vertex set of
![]() $H_{t}$
must intersect with each component in two or more points in order to make the union
$H_{t}$
must intersect with each component in two or more points in order to make the union
![]() ${\bar H}_{t-1}\cup H_t=F_0$
2-connected. Consequently, we have
${\bar H}_{t-1}\cup H_t=F_0$
2-connected. Consequently, we have
![]() ${\bar v}_t \le {\bar v}_{t-1}+v^{\prime}_t-2{\bar \rho}_{t-1}$
. Finally, we obtain
${\bar v}_t \le {\bar v}_{t-1}+v^{\prime}_t-2{\bar \rho}_{t-1}$
. Finally, we obtain
![]() $v_F = {\bar v}_t \le v_1^{\prime}{}+\cdots+v^{\prime}_t-{\bar \rho}_{t-1}-t+1$
. The claim follows from the identity
$v_F = {\bar v}_t \le v_1^{\prime}{}+\cdots+v^{\prime}_t-{\bar \rho}_{t-1}-t+1$
. The claim follows from the identity
![]() $v^{\prime}_1+\dots+v^{\prime}_t=v_1+\cdots+v_r$
and the inequality
$v^{\prime}_1+\dots+v^{\prime}_t=v_1+\cdots+v_r$
and the inequality
![]() ${\bar \rho}_{t-1}\ge 1$
.
${\bar \rho}_{t-1}\ge 1$
.
To prove statement (i), given
![]() $({\tilde B}, {\tilde i})$
, we obtain from (11) and (17) (recall the notation
$({\tilde B}, {\tilde i})$
, we obtain from (11) and (17) (recall the notation
![]() $b_j=|B_j|$
) that
$b_j=|B_j|$
) that
 \begin{equation*} h({\tilde B}, {\tilde i}) \le \frac{1}{n^{v_1+\dots+v_r}}\prod_{j=1}^r {\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big) \le \frac{1}{n^{v_F+\rho_1+\dots+\rho_r}} \prod_{j=1}^r {\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big). \end{equation*}
\begin{equation*} h({\tilde B}, {\tilde i}) \le \frac{1}{n^{v_1+\dots+v_r}}\prod_{j=1}^r {\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big) \le \frac{1}{n^{v_F+\rho_1+\dots+\rho_r}} \prod_{j=1}^r {\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big). \end{equation*}
Given
![]() ${\tilde B}=(B_1,\dots, B_r)$
, we estimate the sum over all possible colourings (there are
${\tilde B}=(B_1,\dots, B_r)$
, we estimate the sum over all possible colourings (there are
![]() $(m)_r$
of them):
$(m)_r$
of them):
 \begin{align*} \sum_{{\tilde i}}h({\tilde B},{\tilde i}) & \prec \frac{(m)_r}{n^{v_F+\rho_1+\dots+\rho_r}} \prod_{j=1}^r {\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big) \asymp n^{-v_F} \prod_{j=1}^r \frac{{\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big)}{n^{\rho_j-1}} \\ & = n^{0.5-v_F} \prod_{j=1}^r \frac{{\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big)}{n^{\rho_j-1+(b_j/(2e_F))}} = o\bigl(n^{0.5-v_F}\bigr). \end{align*}
\begin{align*} \sum_{{\tilde i}}h({\tilde B},{\tilde i}) & \prec \frac{(m)_r}{n^{v_F+\rho_1+\dots+\rho_r}} \prod_{j=1}^r {\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big) \asymp n^{-v_F} \prod_{j=1}^r \frac{{\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big)}{n^{\rho_j-1}} \\ & = n^{0.5-v_F} \prod_{j=1}^r \frac{{\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big)}{n^{\rho_j-1+(b_j/(2e_F))}} = o\bigl(n^{0.5-v_F}\bigr). \end{align*}
In the second-last identity we used
![]() $b_1+\dots+b_r=e_F$
, while the last bound follows by the chain of inequalities
$b_1+\dots+b_r=e_F$
, while the last bound follows by the chain of inequalities
 \begin{align*} n^{1-\rho_j}{\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big) & \le {\mathbb {E}}\big({\tilde X}^{v_j+1-\rho_j}Q^{b_j}\big) \le {\mathbb {E}}\big({\tilde X}^{v_j+1-\rho_j}Q^{v_j-\rho_j}\big) \\ & = o\big(n^{(v_j-\rho_j)/(2e_F)} \big) = o\big(n^{b_j/(2e_F)}\big). \end{align*}
\begin{align*} n^{1-\rho_j}{\mathbb {E}}\big({\tilde X}^{v_j}Q^{b_j}\big) & \le {\mathbb {E}}\big({\tilde X}^{v_j+1-\rho_j}Q^{b_j}\big) \le {\mathbb {E}}\big({\tilde X}^{v_j+1-\rho_j}Q^{v_j-\rho_j}\big) \\ & = o\big(n^{(v_j-\rho_j)/(2e_F)} \big) = o\big(n^{b_j/(2e_F)}\big). \end{align*}
Here, in the first step we used
![]() ${\tilde X}\le n$
; in the second step we used
${\tilde X}\le n$
; in the second step we used
![]() $Q\le 1$
and
$Q\le 1$
and
![]() $b_j\ge v_j-\rho_j$
(the latter inequality is based on the observation that any graph with
$b_j\ge v_j-\rho_j$
(the latter inequality is based on the observation that any graph with
![]() $v_j$
vertices and
$v_j$
vertices and
![]() $\rho_j$
components has at least
$\rho_j$
components has at least
![]() $v_j-\rho_j$
edges); the third step follows by (16) from the moment condition (1) applied to
$v_j-\rho_j$
edges); the third step follows by (16) from the moment condition (1) applied to
![]() $s=v_j-\rho_j$
; and the last step follows from the inequality
$s=v_j-\rho_j$
; and the last step follows from the inequality
![]() $b_j\ge v_j-\rho_j$
.
$b_j\ge v_j-\rho_j$
.
Finally, we conclude that
because the number of partitions
![]() ${\tilde B}$
of the edge set of a given graph F is always finite.
${\tilde B}$
of the edge set of a given graph F is always finite.
Before showing an upper bound for
![]() $h_F$
,
$h_F$
,
![]() $F={\mathcal K}_k$
, we introduce some notation. Given an integer
$F={\mathcal K}_k$
, we introduce some notation. Given an integer
![]() $b\ge 1$
, let
$b\ge 1$
, let
![]() $b^{\star}$
be the minimal number of vertices that a graph with b edges may have. Let
$b^{\star}$
be the minimal number of vertices that a graph with b edges may have. Let
![]() $H_b$
be such a graph. It has a simple structure described below. Let
$H_b$
be such a graph. It has a simple structure described below. Let
![]() $k_b\ge 2$
be the largest integer satisfying
$k_b\ge 2$
be the largest integer satisfying
![]() $b\ge \binom{k_b}{2}$
. Then
$b\ge \binom{k_b}{2}$
. Then
![]() $b={\binom{k_b}{2}} +\Delta_b$
for some integer
$b={\binom{k_b}{2}} +\Delta_b$
for some integer
![]() $0\le \Delta_b\le k_b-1$
. For
$0\le \Delta_b\le k_b-1$
. For
![]() $\Delta_b=0$
we have
$\Delta_b=0$
we have
![]() $b^{\star}=k_b$
and
$b^{\star}=k_b$
and
![]() $H_b={\mathcal K}_{b^{\star}}$
(clique on
$H_b={\mathcal K}_{b^{\star}}$
(clique on
![]() $b^{\star}=k_b$
vertices). For
$b^{\star}=k_b$
vertices). For
![]() $\Delta_b\gt 0$
, graph
$\Delta_b\gt 0$
, graph
![]() $H_b$
is a union of
$H_b$
is a union of
![]() ${\mathcal K}_{k_b}$
and a star
${\mathcal K}_{k_b}$
and a star
![]() ${\mathcal K}_{1, \Delta_b}$
such that all the vertices of the star except for the central vertex belong to the vertex set of
${\mathcal K}_{1, \Delta_b}$
such that all the vertices of the star except for the central vertex belong to the vertex set of
![]() ${\mathcal K}_{k_b}$
. In this case,
${\mathcal K}_{k_b}$
. In this case,
![]() $b^{\star}=k_b+1$
. In other words, we obtain
$b^{\star}=k_b+1$
. In other words, we obtain
![]() $H_b$
from
$H_b$
from
![]() ${\mathcal K}_{k_b+1}$
by deleting
${\mathcal K}_{k_b+1}$
by deleting
![]() $k_b-\Delta_b$
edges sharing a common endpoint. The next two lemmas establish useful properties of the function
$k_b-\Delta_b$
edges sharing a common endpoint. The next two lemmas establish useful properties of the function
![]() $b\to b^{\star}$
.
$b\to b^{\star}$
.
Lemma 2.
For integers
![]() $s\ge t\ge 1$
,
$s\ge t\ge 1$
,
Proof. We consider graphs
![]() $H_s$
and
$H_s$
and
![]() $H_t$
that have disjoint vertex sets so that the union
$H_t$
that have disjoint vertex sets so that the union
![]() $H_s\cup H_t$
has
$H_s\cup H_t$
has
![]() $s^{\star}+t^{\star}$
vertices.
$s^{\star}+t^{\star}$
vertices.
Note that for
![]() $t=1$
both sides of (20) are equal. In order to show (20) for
$t=1$
both sides of (20) are equal. In order to show (20) for
![]() $s\ge t\ge 2$
we consider the chain of neighbouring pairs
$s\ge t\ge 2$
we consider the chain of neighbouring pairs
In a step
![]() $(x,y)\to (x+1,y-1)$
we remove an edge from
$(x,y)\to (x+1,y-1)$
we remove an edge from
![]() $H_y$
and add it to
$H_y$
and add it to
![]() $H_x$
. A simple analysis of the step
$H_x$
. A simple analysis of the step
![]() $(H_x,H_y)\to (H_{x+1}, H_{y-1})$
shows that
$(H_x,H_y)\to (H_{x+1}, H_{y-1})$
shows that
We call a step
![]() $(x,y)\to(x+1,y-1)$
positive (respectively negative or neutral) if (23) (respectively (22) or (24)) holds. Therefore, as we move in (21) from left to right, every positive (negative) step decreases (increases) the total number of vertices in the union
$(x,y)\to(x+1,y-1)$
positive (respectively negative or neutral) if (23) (respectively (22) or (24)) holds. Therefore, as we move in (21) from left to right, every positive (negative) step decreases (increases) the total number of vertices in the union
![]() $H_x\cup H_y$
.
$H_x\cup H_y$
.
Let us now traverse (21) from right to left. We observe that the first non-neutral step encountered is positive (if we encounter a non-neutral step at all). Furthermore, after a negative step the first non-neutral step encountered is positive. Note that it may happen that the last non-neutral step encountered is negative. Therefore, the total number of positive steps is at least as large as the number of negative ones. This proves (20).
Lemma 3.
Let
![]() $k\ge 3$
and
$k\ge 3$
and
![]() $r\ge 2$
. Let
$r\ge 2$
. Let
![]() $B_1\cup\cdots\cup B_r$
be a partition of the edge set of the clique
$B_1\cup\cdots\cup B_r$
be a partition of the edge set of the clique
![]() ${\mathcal K}_k$
. Write
${\mathcal K}_k$
. Write
![]() $b_i=|B_i|$
,
$b_i=|B_i|$
,
![]() $1\le i\le r$
, and
$1\le i\le r$
, and
![]() $\varkappa=\binom{k}{2}$
. Then
$\varkappa=\binom{k}{2}$
. Then
Proof. The first inequality follows from (20) and the identity
![]() $b_1+\dots+b_r=\varkappa$
. The second inequality is simple. Indeed, for
$b_1+\dots+b_r=\varkappa$
. The second inequality is simple. Indeed, for
![]() $r\ge k$
the inequality follows from
$r\ge k$
the inequality follows from
![]() $2(r-1)\ge k+r-2$
and
$2(r-1)\ge k+r-2$
and
![]() $(\varkappa-(r-1))^{\star}\ge 2$
. For
$(\varkappa-(r-1))^{\star}\ge 2$
. For
![]() $r\le k-1$
we have
$r\le k-1$
we have
![]() $\varkappa-(r-1)\ge {\binom{k-1}{2}}+1$
and therefore
$\varkappa-(r-1)\ge {\binom{k-1}{2}}+1$
and therefore
![]() $(\varkappa-(r-1))^{\star}\ge k$
.
$(\varkappa-(r-1))^{\star}\ge k$
.
Now we are ready to bound
![]() $h_F$
for
$h_F$
for
![]() $F={\mathcal K}_k$
.
$F={\mathcal K}_k$
.
Lemma 4.
Let
![]() $k\ge 3$
,
$k\ge 3$
,
![]() $0\lt \alpha\le 2$
, and
$0\lt \alpha\le 2$
, and
![]() $A\gt 0$
. Let
$A\gt 0$
. Let
![]() $n,m\to+\infty$
. Assume that
$n,m\to+\infty$
. Assume that
![]() $m\le An$
. Let
$m\le An$
. Let
![]() $F={\mathcal K}_k$
. Then (5) implies the bound
$F={\mathcal K}_k$
. Then (5) implies the bound
![]() $h_F=o\big(n^{({1}/{\alpha})-k}\big)$
. Note that for
$h_F=o\big(n^{({1}/{\alpha})-k}\big)$
. Note that for
![]() $\alpha=2$
condition (5) is the same as (2).
$\alpha=2$
condition (5) is the same as (2).
Proof. For
![]() $F={\mathcal K}_k$
we have
$F={\mathcal K}_k$
we have
![]() $e_F=\binom{k}{2}$
. We observe that (5) implies
$e_F=\binom{k}{2}$
. We observe that (5) implies
Note that
![]() ${\hat s}=\binom{s-1}{2}+1$
is the smallest integer t such that
${\hat s}=\binom{s-1}{2}+1$
is the smallest integer t such that
![]() $t^{\star}=s$
. In particular, for any b with
$t^{\star}=s$
. In particular, for any b with
![]() $b^{\star}=s$
we have
$b^{\star}=s$
we have
![]() $b\ge {\hat s}$
. Therefore, given
$b\ge {\hat s}$
. Therefore, given
![]() $2\le s\le k$
, the moment condition
$2\le s\le k$
, the moment condition
![]() ${\mathbb {E}}\big(X^{s-{\hat s}/(\alpha\, e_F)}Q^{\hat s}\big) \lt \infty$
implies
${\mathbb {E}}\big(X^{s-{\hat s}/(\alpha\, e_F)}Q^{\hat s}\big) \lt \infty$
implies
![]() ${\mathbb {E}}\big(X^{s-b/(\alpha\, e_F)}Q^{b}\big) \lt \infty$
for any b satisfying
${\mathbb {E}}\big(X^{s-b/(\alpha\, e_F)}Q^{b}\big) \lt \infty$
for any b satisfying
![]() $b^{\star}=s$
. In this way, (5) yields (25).
$b^{\star}=s$
. In this way, (5) yields (25).
Let us bound
![]() $h_{{\mathcal K}_k}$
from above. Given a partition
$h_{{\mathcal K}_k}$
from above. Given a partition
![]() ${\tilde B}=(B_1,\dots, B_r)$
of the edge set
${\tilde B}=(B_1,\dots, B_r)$
of the edge set
![]() ${\mathcal E}_0$
of
${\mathcal E}_0$
of
![]() ${\mathcal K}_k=([k],{\mathcal E}_0)$
, let
${\mathcal K}_k=([k],{\mathcal E}_0)$
, let
![]() $v_j$
be the number of vertices incident to the edges from
$v_j$
be the number of vertices incident to the edges from
![]() $B_j$
and let
$B_j$
and let
![]() $b_j=|B_j|$
. For any vector
$b_j=|B_j|$
. For any vector
![]() ${\tilde i}=(i_1,\dots, i_r)$
of distinct colours,
${\tilde i}=(i_1,\dots, i_r)$
of distinct colours,
 \begin{equation*} h({\tilde B},{\tilde i}) \le \prod_{j=1}^r\frac{{\mathbb {E}}\bigl({\tilde X}^{v_j}Q^{b_j}\bigr)}{n^{v_j}} \le \prod_{j=1}^r\frac{{\mathbb {E}}\bigl({\tilde X}^{b_j^{\star}}Q^{b_j}\bigr)}{n^{b_j^{\star}}} \le \frac{1}{n^{k+r}} \prod_{j=1}^r {\mathbb {E}}\bigl({\tilde X}^{b_j^{\star}}Q^{b_j}\bigr). \end{equation*}
\begin{equation*} h({\tilde B},{\tilde i}) \le \prod_{j=1}^r\frac{{\mathbb {E}}\bigl({\tilde X}^{v_j}Q^{b_j}\bigr)}{n^{v_j}} \le \prod_{j=1}^r\frac{{\mathbb {E}}\bigl({\tilde X}^{b_j^{\star}}Q^{b_j}\bigr)}{n^{b_j^{\star}}} \le \frac{1}{n^{k+r}} \prod_{j=1}^r {\mathbb {E}}\bigl({\tilde X}^{b_j^{\star}}Q^{b_j}\bigr). \end{equation*}
Here, the first inequality follows from
![]() $({\tilde X})_t/(n)_t\le {\tilde X}^t/n^t$
, since
$({\tilde X})_t/(n)_t\le {\tilde X}^t/n^t$
, since
![]() ${\tilde X}\le n$
. The second inequality follows from the obvious inequality
${\tilde X}\le n$
. The second inequality follows from the obvious inequality
![]() $b_j^{\star}\le v_j$
and the fact that
$b_j^{\star}\le v_j$
and the fact that
![]() ${\tilde X}\le n$
. The last inequality follows from the inequality
${\tilde X}\le n$
. The last inequality follows from the inequality
![]() $b_1^{\star}+\cdots+b_r^{\star}\ge k+r$
of Lemma 3.
$b_1^{\star}+\cdots+b_r^{\star}\ge k+r$
of Lemma 3.
For each r-partition
![]() ${\tilde B}$
as above we bound the sum over all possible colourings
${\tilde B}$
as above we bound the sum over all possible colourings
![]() ${\tilde i}$
(there are
${\tilde i}$
(there are
![]() $(m)_r$
of them):
$(m)_r$
of them):
 \begin{equation} \sum_{{\tilde i}}h({\tilde B},{\tilde i}) \le \frac{(m)_r}{n^{k+r}} \prod_{j=1}^r {\mathbb {E}}\bigl({\tilde X}^{b_j^{\star}}Q^{b_j}\bigr) \le \frac{A^r}{n^k} \prod_{j=1}^r {\mathbb {E}}\bigl({\tilde X}^{b_j^{\star}}Q^{b_j}\bigr) = o(n^{({1}/{\alpha})-k}). \end{equation}
\begin{equation} \sum_{{\tilde i}}h({\tilde B},{\tilde i}) \le \frac{(m)_r}{n^{k+r}} \prod_{j=1}^r {\mathbb {E}}\bigl({\tilde X}^{b_j^{\star}}Q^{b_j}\bigr) \le \frac{A^r}{n^k} \prod_{j=1}^r {\mathbb {E}}\bigl({\tilde X}^{b_j^{\star}}Q^{b_j}\bigr) = o(n^{({1}/{\alpha})-k}). \end{equation}
In the very last step, with
![]() $e_F=b_1+\cdots+b_r=\binom{k}{2}$
, we used the bounds
$e_F=b_1+\cdots+b_r=\binom{k}{2}$
, we used the bounds
![]() ${\mathbb {E}}\big({\tilde X}^{b_j^{\star}}Q^{b_j}\big) = o\big(n^{{b_j}/{\alpha e_F}} \big)$
that follow from the moment conditions
${\mathbb {E}}\big({\tilde X}^{b_j^{\star}}Q^{b_j}\big) = o\big(n^{{b_j}/{\alpha e_F}} \big)$
that follow from the moment conditions
![]() ${\mathbb {E}}\big(X^{b_j^{\star}-({b_j}/{\alpha\, e_F})}Q^{b_j}\big) \lt \infty$
; see (25), via (16). Finally, proceeding as in (19), we obtain the desired bound
${\mathbb {E}}\big(X^{b_j^{\star}-({b_j}/{\alpha\, e_F})}Q^{b_j}\big) \lt \infty$
; see (25), via (16). Finally, proceeding as in (19), we obtain the desired bound
![]() $h_F=o\big(n^{({1}/{\alpha})-k}\big)$
from (26).
$h_F=o\big(n^{({1}/{\alpha})-k}\big)$
from (26).
2.4. Power-law tails
Recall that, given a graph
![]() $F=({\mathcal V}_F,{\mathcal E}_F)$
, we denote by
$F=({\mathcal V}_F,{\mathcal E}_F)$
, we denote by
![]() $v_F=|{\mathcal V}_F|$
the number of vertices and by
$v_F=|{\mathcal V}_F|$
the number of vertices and by
![]() $e_F=|{\mathcal E}_F|$
the number of edges. Let
$e_F=|{\mathcal E}_F|$
the number of edges. Let
![]() $\Psi_F=\Psi_F(n,p)=n^{v_F}p^{e_F}$
, and define
$\Psi_F=\Psi_F(n,p)=n^{v_F}p^{e_F}$
, and define
![]() $\Phi_F=\Phi_F(n,p) = \min_{H\subset F,\, e_H\ge 1}\Psi_H$
,
$\Phi_F=\Phi_F(n,p) = \min_{H\subset F,\, e_H\ge 1}\Psi_H$
,
![]() $m_F = \max_{H\subset F,\, e_H\ge 1}(e_H/v_H)$
. Here, the minimum/maximum is taken over all subgraphs
$m_F = \max_{H\subset F,\, e_H\ge 1}(e_H/v_H)$
. Here, the minimum/maximum is taken over all subgraphs
![]() $H\subset F$
with
$H\subset F$
with
![]() $e_H\ge 1$
. Recall that F is called balanced if
$e_H\ge 1$
. Recall that F is called balanced if
![]() $m_F=e_F/v_F$
. For a balanced F we have, for any
$m_F=e_F/v_F$
. For a balanced F we have, for any
![]() $H\subset F$
with
$H\subset F$
with
![]() $e_H\ge 1$
,
$e_H\ge 1$
,
![]() $\Psi_H = \bigl(np^{e_H/v_H}\bigr)^{v_H} \ge\bigl(np^{e_F/v_F}\bigr)^{v_H} = \Psi_F^{v_H/v_F}$
. Hence,
$\Psi_H = \bigl(np^{e_H/v_H}\bigr)^{v_H} \ge\bigl(np^{e_F/v_F}\bigr)^{v_H} = \Psi_F^{v_H/v_F}$
. Hence,
Lemma 5.
Let
![]() $a\gt 0$
and
$a\gt 0$
and
![]() $0\lt \alpha\lt 2$
. Assume that F is balanced, connected, and
$0\lt \alpha\lt 2$
. Assume that F is balanced, connected, and
![]() $v_F\ge 2$
. Assume that (3) holds. Then
$v_F\ge 2$
. Assume that (3) holds. Then
We remark that, for
![]() $0\lt \alpha\lt 2$
, the tail asymptotics (28) implies that
$0\lt \alpha\lt 2$
, the tail asymptotics (28) implies that
![]() $N_F$
belongs to the domain of attraction of an
$N_F$
belongs to the domain of attraction of an
![]() $\alpha$
-stable distribution. Indeed, the left tail of
$\alpha$
-stable distribution. Indeed, the left tail of
![]() $N_F$
vanishes since
$N_F$
vanishes since
![]() ${\mathbb {P}}\{N_F\ge 0\}=1$
. Therefore, the conditions of [Reference Gnedenko and Kolmogorov9, Theorem 2,
${\mathbb {P}}\{N_F\ge 0\}=1$
. Therefore, the conditions of [Reference Gnedenko and Kolmogorov9, Theorem 2,
![]() $\S35$
, Chapter 7] are satisfied.
$\S35$
, Chapter 7] are satisfied.
Proof. With a little abuse of notation we shall denote the conditional expectation and probability given (X, Q) by
![]() ${\mathbb {E}}^*$
and
${\mathbb {E}}^*$
and
![]() ${\mathbb {P}}^*$
. Furthermore, we write
${\mathbb {P}}^*$
. Furthermore, we write
![]() $k=v_F$
and
$k=v_F$
and
![]() $\Delta_F^* = N_F-N_F^*$
.
$\Delta_F^* = N_F-N_F^*$
.
To prove (28), we show that the contribution of
![]() $\Delta_F^*$
to the sum
$\Delta_F^*$
to the sum
![]() $N_F=N_F^*+\Delta_F^*$
is negligible compared to
$N_F=N_F^*+\Delta_F^*$
is negligible compared to
![]() $N_F^*$
and, therefore, the tail asymptotic (28) is determined by (3). For this purpose we apply exponential large-deviation bounds for subgraph counts in Bernoulli random graphs [Reference Janson, Łuczak and Ruciński14, Reference Janson, Oleszkiewicz and Ruciński15] (for
$N_F^*$
and, therefore, the tail asymptotic (28) is determined by (3). For this purpose we apply exponential large-deviation bounds for subgraph counts in Bernoulli random graphs [Reference Janson, Łuczak and Ruciński14, Reference Janson, Oleszkiewicz and Ruciński15] (for
![]() $F={\mathcal K}_2$
, we can apply Chernoff’s bounds).
$F={\mathcal K}_2$
, we can apply Chernoff’s bounds).
Given large
![]() $t\gt 0$
and small
$t\gt 0$
and small
![]() $\varepsilon\gt 0$
, introduce the event
$\varepsilon\gt 0$
, introduce the event
![]() ${\mathcal H} = \big\{-\varepsilon N_F^*\le \Delta_F^*\le \varepsilon t\big\}$
and split
${\mathcal H} = \big\{-\varepsilon N_F^*\le \Delta_F^*\le \varepsilon t\big\}$
and split
![]() ${\mathbb {P}}\{N_F\gt t\}$
:
${\mathbb {P}}\{N_F\gt t\}$
:
We first consider
![]() $P_1$
. Replacing
$P_1$
. Replacing
![]() $\Delta_F^*$
by its extreme values (on
$\Delta_F^*$
by its extreme values (on
![]() ${\mathcal H}$
) yields the inequalities
${\mathcal H}$
) yields the inequalities
We note that the right-hand side of this is at most
![]() ${\mathbb {P}}\big\{N_F^*\gt t(1-\varepsilon)\big\}$
, and the left-hand side is at least
${\mathbb {P}}\big\{N_F^*\gt t(1-\varepsilon)\big\}$
, and the left-hand side is at least
![]() ${\mathbb {P}}\big\{(1-\varepsilon)N_F^*\gt t\big\} - P_2^{\prime}-P_3^{\prime}$
, where
${\mathbb {P}}\big\{(1-\varepsilon)N_F^*\gt t\big\} - P_2^{\prime}-P_3^{\prime}$
, where
Hence, we have
Invoking the simple inequalities
![]() $P_2\le P_2^{\prime}$
and
$P_2\le P_2^{\prime}$
and
![]() $P_3^{\prime}\le P_3$
, we obtain, from (29) and (30), that
$P_3^{\prime}\le P_3$
, we obtain, from (29) and (30), that
We show below that, for any
![]() $0\lt \varepsilon\lt 1$
,
$0\lt \varepsilon\lt 1$
,
Note that (3) and (31) together with (32) imply (28). It remains to show (32).
To illustrate the argument for doing so, we first examine the simplest case, where
![]() $F={\mathcal K}_2$
. We apply Chernoff’s inequalities [Reference Janson, Łuczak and Ruciński14, (2.5), (2.6)] to
$F={\mathcal K}_2$
. We apply Chernoff’s inequalities [Reference Janson, Łuczak and Ruciński14, (2.5), (2.6)] to
![]() $\Delta^*_F$
conditionally given (X, Q). We have
$\Delta^*_F$
conditionally given (X, Q). We have
 \begin{align*} P_2^{\prime} & = {\mathbb {E}}\Big(\textbf{1}_{\{(1-\varepsilon)N_F^*\gt t\}}{\mathbb {P}}^*\big\{\Delta^*_F\lt -\varepsilon N^*_F\big\}\Big) \le {\mathbb {E}}\Big(\textbf{1}_{\{(1-\varepsilon)N_F^*\gt t\}}\textrm{e}^{-({\varepsilon^2}/{2})N_F^*}\Big) \\ & \le \exp\bigg\{{-}\frac{1}{2}\frac{\varepsilon^2}{1-\varepsilon}t\bigg\} = o(t^{-\alpha}); \\ P_3 & \le {\mathbb {E}}\big({\mathbb {P}}^*\big\{\Delta^*_F\gt \varepsilon t\big\}\big) \le {\mathbb {E}}\,\exp\bigg\{{-}\frac{\varepsilon^2 t^2}{2\big(N_F^*+\varepsilon t/3\big)}\bigg\} \\ & \le {\mathbb {P}}\Big\{N_F^*\gt t^{3/2}\Big\} + \exp\bigg\{{-}\frac{\varepsilon^2t^2}{2(t^{3/2}+\varepsilon t/3)}\bigg\} = o(t^{-\alpha}). \end{align*}
\begin{align*} P_2^{\prime} & = {\mathbb {E}}\Big(\textbf{1}_{\{(1-\varepsilon)N_F^*\gt t\}}{\mathbb {P}}^*\big\{\Delta^*_F\lt -\varepsilon N^*_F\big\}\Big) \le {\mathbb {E}}\Big(\textbf{1}_{\{(1-\varepsilon)N_F^*\gt t\}}\textrm{e}^{-({\varepsilon^2}/{2})N_F^*}\Big) \\ & \le \exp\bigg\{{-}\frac{1}{2}\frac{\varepsilon^2}{1-\varepsilon}t\bigg\} = o(t^{-\alpha}); \\ P_3 & \le {\mathbb {E}}\big({\mathbb {P}}^*\big\{\Delta^*_F\gt \varepsilon t\big\}\big) \le {\mathbb {E}}\,\exp\bigg\{{-}\frac{\varepsilon^2 t^2}{2\big(N_F^*+\varepsilon t/3\big)}\bigg\} \\ & \le {\mathbb {P}}\Big\{N_F^*\gt t^{3/2}\Big\} + \exp\bigg\{{-}\frac{\varepsilon^2t^2}{2(t^{3/2}+\varepsilon t/3)}\bigg\} = o(t^{-\alpha}). \end{align*}
In the last inequality we used the fact that
for
![]() $N_F^*\le t^{3/2}$
.
$N_F^*\le t^{3/2}$
.
Now we assume that
![]() $v_F\ge 3$
. In this case the proof of (32) is much more involved. In the proof we use often the fact [Reference Janson, Łuczak and Ruciński14, Lemma 3.5] that
$v_F\ge 3$
. In this case the proof of (32) is much more involved. In the proof we use often the fact [Reference Janson, Łuczak and Ruciński14, Lemma 3.5] that
We also use the simple relation
![]() $N_F^*\asymp a_F\Psi_F(X,Q)$
.
$N_F^*\asymp a_F\Psi_F(X,Q)$
.
To prove
![]() $P_2^{\prime}=o(t^{-\alpha})$
, given (X, Q) with
$P_2^{\prime}=o(t^{-\alpha})$
, given (X, Q) with
![]() $0\lt Q\lt 1$
(cases 0 and 1 are trivial), we apply Janson’s inequality [Reference Janson, Łuczak and Ruciński14, Theorem 2.14] to
$0\lt Q\lt 1$
(cases 0 and 1 are trivial), we apply Janson’s inequality [Reference Janson, Łuczak and Ruciński14, Theorem 2.14] to
![]() $p^*_{\varepsilon}\,:\!={\mathbb {P}}^*\big\{\Delta_F^*\lt -\varepsilon N_F^*\big\}$
. In what follows, we assume that the random graph G(X, Q) and complete graph
$p^*_{\varepsilon}\,:\!={\mathbb {P}}^*\big\{\Delta_F^*\lt -\varepsilon N_F^*\big\}$
. In what follows, we assume that the random graph G(X, Q) and complete graph
![]() ${\mathcal K}_{X}$
are both defined on the same vertex set of size X, and that
${\mathcal K}_{X}$
are both defined on the same vertex set of size X, and that
![]() $X\ge 1$
. Let
$X\ge 1$
. Let
 \begin{equation*} {\overline \delta} \,:\!= {\mathbb {E}}^*\bigl(N_F^2\bigr) - \delta, \qquad \delta \,:\!= \sum_{F^{\prime}\subset {\mathcal K}_{X}} \sum_{ \begin{subarray}{c} F^{\prime\prime}\subset {\mathcal K}_{X} \\ {\mathcal E}_{F^{\prime}}\cap {\mathcal E}_{F^{\prime\prime}}=\emptyset \end{subarray} }{\mathbb {E}}^* (\textbf{1}_{F^{\prime}}\textbf{1}_{F^{\prime\prime}}). \end{equation*}
\begin{equation*} {\overline \delta} \,:\!= {\mathbb {E}}^*\bigl(N_F^2\bigr) - \delta, \qquad \delta \,:\!= \sum_{F^{\prime}\subset {\mathcal K}_{X}} \sum_{ \begin{subarray}{c} F^{\prime\prime}\subset {\mathcal K}_{X} \\ {\mathcal E}_{F^{\prime}}\cap {\mathcal E}_{F^{\prime\prime}}=\emptyset \end{subarray} }{\mathbb {E}}^* (\textbf{1}_{F^{\prime}}\textbf{1}_{F^{\prime\prime}}). \end{equation*}
Here, the sum runs over ordered pairs (
![]() $F^{\prime}, F^{\prime\prime}$
) of subgraphs of
$F^{\prime}, F^{\prime\prime}$
) of subgraphs of
![]() ${\mathcal K}_{X}$
such that
${\mathcal K}_{X}$
such that
![]() $F^{\prime}$
and
$F^{\prime}$
and
![]() $F^{\prime\prime}$
are copies of F and their edge sets
$F^{\prime\prime}$
are copies of F and their edge sets
![]() ${\mathcal E}_{F^{\prime}}$
and
${\mathcal E}_{F^{\prime}}$
and
![]() ${\mathcal E}_{F^{\prime\prime}}$
are disjoint. Furthermore,
${\mathcal E}_{F^{\prime\prime}}$
are disjoint. Furthermore,
![]() $\textbf{1}_{F^{\prime}}$
stands for the indicator of the event that
$\textbf{1}_{F^{\prime}}$
stands for the indicator of the event that
![]() $F^{\prime}$
is present in G(X, Q). Janson’s inequality implies
$F^{\prime}$
is present in G(X, Q). Janson’s inequality implies
Next, we bound
![]() ${\bar \delta}$
from above. The (variance) identity
${\bar \delta}$
from above. The (variance) identity
![]() ${\mathbb {E}}^*(N_F^2)-\big(N_F^*\big)^2={\mathbb {E}}^*\big(\Delta_F^*\big)^2$
implies that
${\mathbb {E}}^*(N_F^2)-\big(N_F^*\big)^2={\mathbb {E}}^*\big(\Delta_F^*\big)^2$
implies that
Furthermore, using the observation that
![]() $V_{F^{\prime}}\cap V_{F^{\prime\prime}}=\emptyset$
implies
$V_{F^{\prime}}\cap V_{F^{\prime\prime}}=\emptyset$
implies
![]() ${\mathcal E}_{F^{\prime}}\cap {\mathcal E}_{F^{\prime\prime}}=\emptyset$
, and that the latter relation implies
${\mathcal E}_{F^{\prime}}\cap {\mathcal E}_{F^{\prime\prime}}=\emptyset$
, and that the latter relation implies
![]() ${\mathbb {E}}^* (\textbf{1}_{F^{\prime}}\textbf{1}_{F^{\prime\prime}}) = ({\mathbb {E}}^* \textbf{1}_{F^{\prime}})({\mathbb {E}}^*\textbf{1}_{F^{\prime\prime}})=Q^{2e_F}$
, we bound
${\mathbb {E}}^* (\textbf{1}_{F^{\prime}}\textbf{1}_{F^{\prime\prime}}) = ({\mathbb {E}}^* \textbf{1}_{F^{\prime}})({\mathbb {E}}^*\textbf{1}_{F^{\prime\prime}})=Q^{2e_F}$
, we bound
![]() $\delta$
from below:
$\delta$
from below:
 \begin{equation*} \delta \ge \sum_{F^{\prime}\subset {\mathcal K}_{X}} \sum_{ \begin{subarray}{c} F^{\prime\prime}\subset {\mathcal K}_{X} \\ V_{F^{\prime}}\cap V_{F^{\prime\prime}}=\emptyset \end{subarray} } {\mathbb {E}}^*(\textbf{1}_{F^{\prime}}\textbf{1}_{F^{\prime\prime}}) = a_F^2\binom{X}{k}\binom{X-k}{k}Q^{2e_F} = \frac{(X-k)_k}{(X)_k} \big(N_F^*\big)^2. \end{equation*}
\begin{equation*} \delta \ge \sum_{F^{\prime}\subset {\mathcal K}_{X}} \sum_{ \begin{subarray}{c} F^{\prime\prime}\subset {\mathcal K}_{X} \\ V_{F^{\prime}}\cap V_{F^{\prime\prime}}=\emptyset \end{subarray} } {\mathbb {E}}^*(\textbf{1}_{F^{\prime}}\textbf{1}_{F^{\prime\prime}}) = a_F^2\binom{X}{k}\binom{X-k}{k}Q^{2e_F} = \frac{(X-k)_k}{(X)_k} \big(N_F^*\big)^2. \end{equation*}
Then, we lower bound the fraction
and obtain that
![]() $\delta\ge \big(N_F^*\big)^2\big(1-k^2(X-k)^{-1}\big)$
. Invoking this bound in (35) we obtain
$\delta\ge \big(N_F^*\big)^2\big(1-k^2(X-k)^{-1}\big)$
. Invoking this bound in (35) we obtain
![]() ${\bar \delta} \le {\mathbb {E}}^*\big(\Delta_F^*\big)^2+\big(N_F^*\big)^2k^2(X-k)^{-1}$
. Hence, the ratio in the exponent of (34) satisfies
${\bar \delta} \le {\mathbb {E}}^*\big(\Delta_F^*\big)^2+\big(N_F^*\big)^2k^2(X-k)^{-1}$
. Hence, the ratio in the exponent of (34) satisfies
 \begin{equation} \frac{\big(N_F^*\big)^2}{{\bar\delta}} \ge \frac{\big(N_F^*\big)^2}{2\max\Big\{{\mathbb {E}}^*\big(\Delta_F^*\big)^2, \big(N_F^*\big)^2k^2(X-k)^{-1}\Big\}} = \frac12 \min\Bigg\{\frac{\big(N_F^*\big)^2} {{\mathbb {E}}^*\big(\Delta_F^*\big)^2},\frac{X-k}{k^2}\Bigg\}. \end{equation}
\begin{equation} \frac{\big(N_F^*\big)^2}{{\bar\delta}} \ge \frac{\big(N_F^*\big)^2}{2\max\Big\{{\mathbb {E}}^*\big(\Delta_F^*\big)^2, \big(N_F^*\big)^2k^2(X-k)^{-1}\Big\}} = \frac12 \min\Bigg\{\frac{\big(N_F^*\big)^2} {{\mathbb {E}}^*\big(\Delta_F^*\big)^2},\frac{X-k}{k^2}\Bigg\}. \end{equation}
We will show below that there exists
![]() $c_k\gt 0$
(independent of t) such that
$c_k\gt 0$
(independent of t) such that
![]() $N_F^*\gt t$
implies
$N_F^*\gt t$
implies
 \begin{equation} \frac{\big(N_F^*\big)^2} {{\mathbb {E}}^*\big(\Delta_F^*\big)^2}\gt c_kt^{2/k}. \end{equation}
\begin{equation} \frac{\big(N_F^*\big)^2} {{\mathbb {E}}^*\big(\Delta_F^*\big)^2}\gt c_kt^{2/k}. \end{equation}
We also note that
![]() $N_F^*\gt t$
implies
$N_F^*\gt t$
implies
![]() $X\gt (t/a_F)^{1/k}$
, using
$X\gt (t/a_F)^{1/k}$
, using
![]() $a_F\binom{X}{k} \ge a_F\binom{X}{k}Q^{e_F}=N_F^*$
). Therefore, on the event
$a_F\binom{X}{k} \ge a_F\binom{X}{k}Q^{e_F}=N_F^*$
). Therefore, on the event
![]() $N_F^*\gt t$
the right-hand side of (36) is at least
$N_F^*\gt t$
the right-hand side of (36) is at least
and this quantity scales as
![]() $t^{1/k}$
as
$t^{1/k}$
as
![]() $t\to+\infty$
. Finally, from (34), (36), and (38) we obtain that, on the event
$t\to+\infty$
. Finally, from (34), (36), and (38) we obtain that, on the event
![]() $N_F^*\gt t$
,
$N_F^*\gt t$
,
![]() $p_{\varepsilon}^* \le \textrm{e}^{-\varepsilon^2\Theta(t^{1/k})} = o(t^{-\alpha})$
as
$p_{\varepsilon}^* \le \textrm{e}^{-\varepsilon^2\Theta(t^{1/k})} = o(t^{-\alpha})$
as
![]() $t\to+\infty$
. We conclude that
$t\to+\infty$
. We conclude that
![]() $P_2^{\prime}=o(t^{-\alpha})$
. It remains to show (37). We observe that the inequalities
$P_2^{\prime}=o(t^{-\alpha})$
. It remains to show (37). We observe that the inequalities
![]() $N_F^*\le a_F\Psi_F(X,Q)$
and
$N_F^*\le a_F\Psi_F(X,Q)$
and
![]() $N_F^*\gt t$
imply
$N_F^*\gt t$
imply
![]() $\Psi_F(X,Q)\gt t/a_F\gt 1$
, where the last inequality holds for
$\Psi_F(X,Q)\gt t/a_F\gt 1$
, where the last inequality holds for
![]() $t\gt a_F$
. Then, (27) implies
$t\gt a_F$
. Then, (27) implies
![]() $\Phi_F(X,Q)\ge(\Psi_F(X,Q))^{2/k}$
, and (33) implies
$\Phi_F(X,Q)\ge(\Psi_F(X,Q))^{2/k}$
, and (33) implies
 \begin{equation*} \frac{\big(N_F^*\big)^2}{{\mathbb {E}}^*\big(\Delta_F^*\big)^2} \asymp \frac{\Phi_F(X,Q)}{1-Q} \ge \Phi_F(X,Q) \ge \Psi_F^{2/k}(X,Q) \ge (t/a_F)^{2/k}. \end{equation*}
\begin{equation*} \frac{\big(N_F^*\big)^2}{{\mathbb {E}}^*\big(\Delta_F^*\big)^2} \asymp \frac{\Phi_F(X,Q)}{1-Q} \ge \Phi_F(X,Q) \ge \Psi_F^{2/k}(X,Q) \ge (t/a_F)^{2/k}. \end{equation*}
To prove
![]() $P_3=o(t^{-\alpha})$
we apply exponential inequalities for upper tails of subgraph counts in Bernoulli random graphs [Reference Janson, Oleszkiewicz and Ruciński15]. For the reader’s convenience, we state the result from [Reference Janson, Oleszkiewicz and Ruciński15] that we will use. Let
$P_3=o(t^{-\alpha})$
we apply exponential inequalities for upper tails of subgraph counts in Bernoulli random graphs [Reference Janson, Oleszkiewicz and Ruciński15]. For the reader’s convenience, we state the result from [Reference Janson, Oleszkiewicz and Ruciński15] that we will use. Let
![]() $\Delta_F$
be the maximum degree of F. Let
$\Delta_F$
be the maximum degree of F. Let
 \begin{equation*} M_F(n,p) = \begin{cases} 1 & {\text{if }} p\lt n^{-1/m_F}, \\ \min_{H\subset F}\bigl(\Psi_H(n,p)\bigr)^{1/\alpha_H^*} & {\text{if }} n^{-1/m_F} \le p \le n^{-1/\Delta_F}, \\ n^2p^{\Delta_F} & {\text{if }} p \ge n^{-1/\Delta_F}. \end{cases} \end{equation*}
\begin{equation*} M_F(n,p) = \begin{cases} 1 & {\text{if }} p\lt n^{-1/m_F}, \\ \min_{H\subset F}\bigl(\Psi_H(n,p)\bigr)^{1/\alpha_H^*} & {\text{if }} n^{-1/m_F} \le p \le n^{-1/\Delta_F}, \\ n^2p^{\Delta_F} & {\text{if }} p \ge n^{-1/\Delta_F}. \end{cases} \end{equation*}
Here,
![]() $\alpha_H^*$
is the fractional independence number of a graph H [Reference Janson, Oleszkiewicz and Ruciński15]. We do not define the fractional independence number here as we only use the upper bound
$\alpha_H^*$
is the fractional independence number of a graph H [Reference Janson, Oleszkiewicz and Ruciński15]. We do not define the fractional independence number here as we only use the upper bound
![]() $\alpha_H^*\le v_H-1$
that holds for any H with
$\alpha_H^*\le v_H-1$
that holds for any H with
![]() $e_H\gt 0$
[Reference Janson, Oleszkiewicz and Ruciński15, (A.1)]. Let
$e_H\gt 0$
[Reference Janson, Oleszkiewicz and Ruciński15, (A.1)]. Let
![]() $\xi_F$
be the number of copies of F in G(n, p). By [Reference Janson, Oleszkiewicz and Ruciński15, Theorems 1.2 and 1.5], for any
$\xi_F$
be the number of copies of F in G(n, p). By [Reference Janson, Oleszkiewicz and Ruciński15, Theorems 1.2 and 1.5], for any
![]() $\eta\gt 0$
there exists
$\eta\gt 0$
there exists
![]() $c_{\eta, F}\gt 0$
such that, uniformly in p and
$c_{\eta, F}\gt 0$
such that, uniformly in p and
![]() $n\ge k$
(recall that
$n\ge k$
(recall that
![]() $k=v_F$
is the number of vertices of F),
$k=v_F$
is the number of vertices of F),
We will apply (39) to the number
![]() $N_F$
of copies of F in G(X, Q) conditionally given X, Q; see (43).
$N_F$
of copies of F in G(X, Q) conditionally given X, Q; see (43).
We write, for short,
![]() $s=\varepsilon t$
and estimate
$s=\varepsilon t$
and estimate
![]() $P_3\le {\mathbb {P}}\big\{\Delta_F^*\gt s\big\}$
. Let
$P_3\le {\mathbb {P}}\big\{\Delta_F^*\gt s\big\}$
. Let
![]() $\eta\gt 0$
. We split
$\eta\gt 0$
. We split
and estimate the probabilities
![]() $P_{31}$
and
$P_{31}$
and
![]() $P_{32}$
separately. The second probability,
$P_{32}$
separately. The second probability,
can be made negligibly small by choosing
![]() $\eta$
arbitrarily small.
$\eta$
arbitrarily small.
Now we upper bound the remaining probability
![]() $P_{31}$
. Introduce the events
$P_{31}$
. Introduce the events
and put
![]() ${\mathcal A}_2={\mathcal A}_{21}\cup{\mathcal A}_{22}$
(note that
${\mathcal A}_2={\mathcal A}_{21}\cup{\mathcal A}_{22}$
(note that
![]() $\Delta_F\ge 2m_F= 2e_F/v_F$
). We split
$\Delta_F\ge 2m_F= 2e_F/v_F$
). We split
and estimate
![]() ${\tilde P}_1$
and
${\tilde P}_1$
and
![]() ${\tilde P}_2$
separately.
${\tilde P}_2$
separately.
We first consider
![]() ${\tilde P}_1$
. The inequality
${\tilde P}_1$
. The inequality
![]() $Q\le X^{-1/m_F}$
implies
$Q\le X^{-1/m_F}$
implies
![]() $\Psi_F(X,Q)\le 1$
. Consequently, (27) implies
$\Psi_F(X,Q)\le 1$
. Consequently, (27) implies
![]() $\Phi_F(X,Q)\ge \Psi_F(X,Q)$
. The latter inequality, together with (33), imply
$\Phi_F(X,Q)\ge \Psi_F(X,Q)$
. The latter inequality, together with (33), imply
![]() ${\mathbb {E}}^* \big(\Delta_F^*\big)^2 \le c_k\Psi_F(X, Q)\le c_k$
for some
${\mathbb {E}}^* \big(\Delta_F^*\big)^2 \le c_k\Psi_F(X, Q)\le c_k$
for some
![]() $c_k\gt 0$
. Hence, on the event
$c_k\gt 0$
. Hence, on the event
![]() ${\mathcal A}_1$
we have
${\mathcal A}_1$
we have
![]() ${\mathbb {E}}^* \big(\Delta_F^*\big)^2\le c_k$
. Finally, by Markov’s inequality,
${\mathbb {E}}^* \big(\Delta_F^*\big)^2\le c_k$
. Finally, by Markov’s inequality,
Second, we consider
![]() ${\tilde P}_2$
. The inequality
${\tilde P}_2$
. The inequality
![]() $X^{-1/m_F}\lt Q$
implies
$X^{-1/m_F}\lt Q$
implies
![]() $\Psi_F(X,Q)\gt 1$
. For balanced F this yields
$\Psi_F(X,Q)\gt 1$
. For balanced F this yields
![]() $\Psi_H(X,Q)\gt 1$
for every
$\Psi_H(X,Q)\gt 1$
for every
![]() $H\subset F$
with
$H\subset F$
with
![]() $e_H\gt 0$
. Then, by using
$e_H\gt 0$
. Then, by using
![]() $\alpha^*_H\le v_H-1$
we obtain
$\alpha^*_H\le v_H-1$
we obtain
In the last step we used the fact that F is balanced once again. Hence, on the event
![]() ${\mathcal A}_{21}$
we have (recall that
${\mathcal A}_{21}$
we have (recall that
![]() $v_F=k$
)
$v_F=k$
)
We observe that (42) holds on the event
![]() ${\mathcal A}_{22}$
as well. Indeed, the inequality
${\mathcal A}_{22}$
as well. Indeed, the inequality
![]() $Q\ge X^{-1/\Delta_F}$
yields
$Q\ge X^{-1/\Delta_F}$
yields
![]() $M_F(X,Q)\ge X^2Q^{\Delta_F}\ge X$
. Now the inequality
$M_F(X,Q)\ge X^2Q^{\Delta_F}\ge X$
. Now the inequality
![]() $X^{v_F}\ge \Psi_F(X,Q)$
implies (42).
$X^{v_F}\ge \Psi_F(X,Q)$
implies (42).
From (39) and (42) we obtain the exponential bound
Let us bound
![]() ${\tilde P}_2$
from above. We fix a (large) number
${\tilde P}_2$
from above. We fix a (large) number
![]() $B\gt 0$
and introduce the events
$B\gt 0$
and introduce the events
![]() ${\mathcal B}_1=\big\{\Psi_F(X_1,Q_1)\gt B\ln^k s\big\}$
and
${\mathcal B}_1=\big\{\Psi_F(X_1,Q_1)\gt B\ln^k s\big\}$
and
![]() ${\mathcal B}_2=\big\{\Psi_F(X_1,Q_1)\le B\ln^k s\big\}$
. We then split
${\mathcal B}_2=\big\{\Psi_F(X_1,Q_1)\le B\ln^k s\big\}$
. We then split
![]() ${\tilde P}_2 = {\tilde P}_{21} + {\tilde P}_{22}$
,
${\tilde P}_2 = {\tilde P}_{21} + {\tilde P}_{22}$
,
![]() ${\tilde P}_{2i} = {\mathbb {P}}\big\{\Delta^*_F\gt \eta N_F^*, \Delta_F^*\gt s, {\mathcal A}_2,{\mathcal B}_i\big\}$
, and bound
${\tilde P}_{2i} = {\mathbb {P}}\big\{\Delta^*_F\gt \eta N_F^*, \Delta_F^*\gt s, {\mathcal A}_2,{\mathcal B}_i\big\}$
, and bound
![]() ${\tilde P}_{21}$
from above, using (43):
${\tilde P}_{21}$
from above, using (43):
 \begin{align} {\tilde P}_{21} & \le {\mathbb {P}}\big\{\Delta_F^*\gt \eta N_F^*, {\mathcal A}_2, {\mathcal B}_1\big\} = {\mathbb {E}} \left( \textbf{1}_{{\mathcal B}_1}\textbf{1}_{{\mathcal A}_2} {\mathbb {P}}^*\big\{\Delta_F^*\gt \eta N_F^*\big\}\right) \nonumber \\ & \le {\mathbb {E}}\Big(\textbf{1}_{{\mathcal B}_1} \exp\big\{{-}c_{\eta,F}(\Psi_H(X_1,Q_1))^{1/k}\big\}\Big) \le \textrm{e}^{-c_{\eta,F}B^{1/k}\ln s}. \end{align}
\begin{align} {\tilde P}_{21} & \le {\mathbb {P}}\big\{\Delta_F^*\gt \eta N_F^*, {\mathcal A}_2, {\mathcal B}_1\big\} = {\mathbb {E}} \left( \textbf{1}_{{\mathcal B}_1}\textbf{1}_{{\mathcal A}_2} {\mathbb {P}}^*\big\{\Delta_F^*\gt \eta N_F^*\big\}\right) \nonumber \\ & \le {\mathbb {E}}\Big(\textbf{1}_{{\mathcal B}_1} \exp\big\{{-}c_{\eta,F}(\Psi_H(X_1,Q_1))^{1/k}\big\}\Big) \le \textrm{e}^{-c_{\eta,F}B^{1/k}\ln s}. \end{align}
It remains to upper bound
![]() ${\tilde P}_{22}$
. The inequality
${\tilde P}_{22}$
. The inequality
![]() $\Psi_F(X,Q)\gt 1$
, which holds on the event
$\Psi_F(X,Q)\gt 1$
, which holds on the event
![]() ${\mathcal A}_2$
, implies (see (27))
${\mathcal A}_2$
, implies (see (27))
![]() $\Phi_F(X,Q)\ge (\Psi_F(X,Q))^{2/k}$
. Furthermore, (33) implies
$\Phi_F(X,Q)\ge (\Psi_F(X,Q))^{2/k}$
. Furthermore, (33) implies
![]() ${\mathbb {E}}^* \big(\Delta_F^*\big)^2 \le c_F(\Psi_F(X,Q))^{2-(2/k)}(1-Q)$
, where
${\mathbb {E}}^* \big(\Delta_F^*\big)^2 \le c_F(\Psi_F(X,Q))^{2-(2/k)}(1-Q)$
, where
![]() $c_F\gt 0$
depends only on F. Note that on the event
$c_F\gt 0$
depends only on F. Note that on the event
![]() ${\mathcal B}_2$
the right-hand side is upper bounded by
${\mathcal B}_2$
the right-hand side is upper bounded by
![]() $c_F(B\ln^k s)^{2-(2/k)}$
. Hence, by Markov’s inequality,
$c_F(B\ln^k s)^{2-(2/k)}$
. Hence, by Markov’s inequality,
Finally, we obtain
We complete the proof by showing that, for any
![]() $0\lt \varepsilon\lt 1$
, the probability
$0\lt \varepsilon\lt 1$
, the probability
![]() $P_3$
, which depends on
$P_3$
, which depends on
![]() $\varepsilon$
, satisfies
$\varepsilon$
, satisfies
![]() $P_3=o(t^{-\alpha})$
as
$P_3=o(t^{-\alpha})$
as
![]() $t\to+\infty$
. Recall that
$t\to+\infty$
. Recall that
![]() $s=\varepsilon t$
. We have, for any
$s=\varepsilon t$
. We have, for any
![]() $\eta\gt 0$
,
$\eta\gt 0$
,
 \begin{align*} \limsup_{t\to+\infty}t^{\alpha}P_3 & \le \limsup_{t\to+\infty} t^{\alpha}{\mathbb {P}}\big\{\Delta_F^*\gt \varepsilon t\big\} = \varepsilon^{-\alpha} \limsup_{s\to+\infty} s^{\alpha} {\mathbb {P}}\big\{\Delta_F^*\gt s\big\} \\ & \le \varepsilon^{-\alpha} \limsup_{s\to+\infty} s^{\alpha} \big({\tilde P}_1+{\tilde P}_{21}+{\tilde P}_{22}+P_{32}\big) \le (\eta/\varepsilon)^{\alpha}a. \end{align*}
\begin{align*} \limsup_{t\to+\infty}t^{\alpha}P_3 & \le \limsup_{t\to+\infty} t^{\alpha}{\mathbb {P}}\big\{\Delta_F^*\gt \varepsilon t\big\} = \varepsilon^{-\alpha} \limsup_{s\to+\infty} s^{\alpha} {\mathbb {P}}\big\{\Delta_F^*\gt s\big\} \\ & \le \varepsilon^{-\alpha} \limsup_{s\to+\infty} s^{\alpha} \big({\tilde P}_1+{\tilde P}_{21}+{\tilde P}_{22}+P_{32}\big) \le (\eta/\varepsilon)^{\alpha}a. \end{align*}
Hence,
![]() $\limsup_{t\to+\infty}t^{\alpha}P_3=0$
. The last inequality above follows from (40), (41), (44), and (45). Indeed, given
$\limsup_{t\to+\infty}t^{\alpha}P_3=0$
. The last inequality above follows from (40), (41), (44), and (45). Indeed, given
![]() $\eta\gt 0$
, we choose
$\eta\gt 0$
, we choose
![]() $B=B(\eta)$
(in (44) and (45)) large enough that
$B=B(\eta)$
(in (44) and (45)) large enough that
![]() $c_{\eta,F}B^{1/k}\gt 2$
. Then
$c_{\eta,F}B^{1/k}\gt 2$
. Then
![]() ${\tilde P}_{21}\le s^{-2}$
and
${\tilde P}_{21}\le s^{-2}$
and
![]() $\limsup_{s}s^{\alpha}{\tilde P}_{21}=0$
. We also mention the obvious relations
$\limsup_{s}s^{\alpha}{\tilde P}_{21}=0$
. We also mention the obvious relations
![]() $\limsup_{s}s^{\alpha}{\tilde P}_{1}=0$
and
$\limsup_{s}s^{\alpha}{\tilde P}_{1}=0$
and
![]() $\limsup_{s}s^{\alpha}{\tilde P}_{22}= 0$
.
$\limsup_{s}s^{\alpha}{\tilde P}_{22}= 0$
.
Funding information
JK was supported by the Magnus Ehrnrooth Foundation and Academy of Finland grant 346311 – Finnish Centre of Excellence in Randomness and Structures.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.