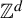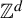1 Introduction
1.1 Overview
Theorems of Ambrose and Kakutani [Reference Ambrose1, Reference Ambrose and Kakutani2] established a connection between measure-preserving
![]() $\mathbb {Z}$
-actions and
$\mathbb {Z}$
-actions and
![]() $\mathbb {R}$
-flows by showing that any flow admits a cross-section and can be represented as a ‘flow under a function’. Their construction provides a foundation for the theory of Kakutani equivalence (also called monotone equivalence) [Reference Feldman7, Reference Katok11] on the one hand and the study of the possible ceiling functions in the ‘flow under a function’ representation [Reference Krengel16, Reference Rudolph21] on the other.
$\mathbb {R}$
-flows by showing that any flow admits a cross-section and can be represented as a ‘flow under a function’. Their construction provides a foundation for the theory of Kakutani equivalence (also called monotone equivalence) [Reference Feldman7, Reference Katok11] on the one hand and the study of the possible ceiling functions in the ‘flow under a function’ representation [Reference Krengel16, Reference Rudolph21] on the other.
The intuitive geometric picture of a ‘flow under a function’ does not generalize to
![]() $\mathbb {R}^{d}$
-flows for
$\mathbb {R}^{d}$
-flows for
![]() $d \ge 2$
. However, Katok [Reference Katok12] re-interpreted it in a way that can readily be adapted to the multidimensional set-up, calling flows appearing in this construction special flows. Despite their name, they are not so special, because, as shown in the same paper, every free ergodic measure-preserving
$d \ge 2$
. However, Katok [Reference Katok12] re-interpreted it in a way that can readily be adapted to the multidimensional set-up, calling flows appearing in this construction special flows. Despite their name, they are not so special, because, as shown in the same paper, every free ergodic measure-preserving
![]() $\mathbb {R}^{d}$
-flow is metrically isomorphic to a special flow. Similarly to the works of Ambrose and Kakutani, it opened up the study of multidimensional concepts of Kakutani equivalence [Reference del Junco and Rudolph5] and stimulated research on tilings of flows[Reference Kra, Quas and Şahin15, Reference Rudolph and Alexander22].
$\mathbb {R}^{d}$
-flow is metrically isomorphic to a special flow. Similarly to the works of Ambrose and Kakutani, it opened up the study of multidimensional concepts of Kakutani equivalence [Reference del Junco and Rudolph5] and stimulated research on tilings of flows[Reference Kra, Quas and Şahin15, Reference Rudolph and Alexander22].
Borel dynamics as a separate field goes back to the work of Weiss [Reference Weiss, Beals, Beck, Bellow and Hajian31] and has blossomed into a versatile branch of dynamical systems. The phase space here is a standard Borel space
![]() $(X, \mathcal {B})$
, that is, a set X with a
$(X, \mathcal {B})$
, that is, a set X with a
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {B}$
of Borel sets for some Polish topology on X. Some of the key ergodic theoretical results have their counterparts in Borel dynamics, although others do not generalize. For example, the Borel version of the Ambrose–Kakutani theorem on the existence of cross-sections in
$\mathcal {B}$
of Borel sets for some Polish topology on X. Some of the key ergodic theoretical results have their counterparts in Borel dynamics, although others do not generalize. For example, the Borel version of the Ambrose–Kakutani theorem on the existence of cross-sections in
![]() $\mathbb {R}$
-flows was proved by Wagh in [Reference Wagh30] showing that, just as in ergodic theory, all free Borel
$\mathbb {R}$
-flows was proved by Wagh in [Reference Wagh30] showing that, just as in ergodic theory, all free Borel
![]() $\mathbb {R}$
-flows emerge as ‘flows under a function’ over Borel
$\mathbb {R}$
-flows emerge as ‘flows under a function’ over Borel
![]() $\mathbb {Z}$
-actions. Likewise, Rudolph’s two-valued theorem [Reference Rudolph21] generalizes to the Borel framework [Reference Slutsky25]. The theory of Kakutani equivalence, on the other hand, exhibits a different phenomenon. Although it is a highly non-trivial equivalence relation among measure-preserving flows [Reference Gerber and Kunde9, Reference Ornstein, Rudolph and Weiss20], a descriptive set theoretical version of Kakutani equivalence collapses entirely [Reference Miller and Rosendal19].
$\mathbb {Z}$
-actions. Likewise, Rudolph’s two-valued theorem [Reference Rudolph21] generalizes to the Borel framework [Reference Slutsky25]. The theory of Kakutani equivalence, on the other hand, exhibits a different phenomenon. Although it is a highly non-trivial equivalence relation among measure-preserving flows [Reference Gerber and Kunde9, Reference Ornstein, Rudolph and Weiss20], a descriptive set theoretical version of Kakutani equivalence collapses entirely [Reference Miller and Rosendal19].
A considerable amount of work has been carried out to understand the Borel dynamics of
![]() $\mathbb {R}$
-flows, but relatively few things are known about multidimensional actions. This paper makes a contribution in this direction by showing that the analog of Katok’s special representation theorem does hold for free Borel
$\mathbb {R}$
-flows, but relatively few things are known about multidimensional actions. This paper makes a contribution in this direction by showing that the analog of Katok’s special representation theorem does hold for free Borel
![]() $\mathbb {R}^{d}$
-flows.
$\mathbb {R}^{d}$
-flows.
1.2 Structure of the paper
Constructions of orbit equivalent
![]() $\mathbb {R}^{d}$
-actions often rely on (essential) hyperfiniteness and use covers of orbits of the flow by coherent and exhaustive regions. This is the case for the aforementioned paper of Katok [Reference Katok12], and related approaches have been used in the descriptive set theoretical set-up as well (for example, [Reference Slutsky26]). Particular assumptions on such coherent regions, however, depend on the specific application. Section 2 summarizes a general language of partial actions, in which many of the aforementioned constructions can be formulated. As an application, we show that the orbit equivalence relation generated by a free
$\mathbb {R}^{d}$
-actions often rely on (essential) hyperfiniteness and use covers of orbits of the flow by coherent and exhaustive regions. This is the case for the aforementioned paper of Katok [Reference Katok12], and related approaches have been used in the descriptive set theoretical set-up as well (for example, [Reference Slutsky26]). Particular assumptions on such coherent regions, however, depend on the specific application. Section 2 summarizes a general language of partial actions, in which many of the aforementioned constructions can be formulated. As an application, we show that the orbit equivalence relation generated by a free
![]() $\mathbb {R}$
-flow can also be generated by a free action of any non-discrete and non-compact Polish group (see Theorem 2.6). This is in striking contrast with the actions of discrete groups, where a probability measure-preserving free
$\mathbb {R}$
-flow can also be generated by a free action of any non-discrete and non-compact Polish group (see Theorem 2.6). This is in striking contrast with the actions of discrete groups, where a probability measure-preserving free
![]() $\mathbb {Z}$
-action can be generated only by a free action of an amenable group.
$\mathbb {Z}$
-action can be generated only by a free action of an amenable group.
Section 3 does the technical work of constructing Lipschitz maps that are needed for Theorem 3.12, which shows, roughly speaking, that, up to an arbitrarily small bi-Lipschitz perturbation, any free
![]() $\mathbb {R}^{d}$
-flow admits an integer grid—a Borel cross-section invariant under the
$\mathbb {R}^{d}$
-flow admits an integer grid—a Borel cross-section invariant under the
![]() $\mathbb {Z}^{d}$
-action.
$\mathbb {Z}^{d}$
-action.
Finally, §4 discusses the descriptive set theoretical version of Katok’s special flow construction and shows, in Theorem 4.3, that, indeed, any free
![]() $\mathbb {R}^{d}$
-flow can be represented as a special flow generated by a bi-Lipschitz cocycle with Lipschitz constants arbitrarily close to
$\mathbb {R}^{d}$
-flow can be represented as a special flow generated by a bi-Lipschitz cocycle with Lipschitz constants arbitrarily close to
![]() $1$
. This provides a Borel version of Katok’s special representation theorem.
$1$
. This provides a Borel version of Katok’s special representation theorem.
2 Sequences of partial actions
We begin by discussing the framework of partial actions suitable for constructing orbit equivalent actions. Throughout this section, X denotes a standard Borel space.
2.1 Partial actions
Let G be a standard Borel group, that is, a group with a structure of a standard Borel space that makes group operations Borel. A partial G-action is a pair
![]() $(E, \phi )$
, where E is a Borel equivalence relation on X and
$(E, \phi )$
, where E is a Borel equivalence relation on X and
![]() $\phi : X \to G$
is a Borel map that is injective on each E-class:
$\phi : X \to G$
is a Borel map that is injective on each E-class:
![]() $\phi (x) \ne \phi (y)$
, whenever
$\phi (x) \ne \phi (y)$
, whenever
![]() $x E y$
. More precisely, we should call such
$x E y$
. More precisely, we should call such
![]() $(E, \phi )$
a partial free action. However, as we are mainly concerned with free actions in what follows, we choose to omit the adjective ‘free’ in the definition. The map
$(E, \phi )$
a partial free action. However, as we are mainly concerned with free actions in what follows, we choose to omit the adjective ‘free’ in the definition. The map
![]() $\phi $
itself may occasionally be referred to as a partial action when the equivalence relation is clear from the context.
$\phi $
itself may occasionally be referred to as a partial action when the equivalence relation is clear from the context.
The motivation for the name comes from the following observation. Consider the set
Injectivity of
![]() $\phi $
on E-classes ensures that, for each
$\phi $
on E-classes ensures that, for each
![]() $x \in X$
and
$x \in X$
and
![]() $g \in G$
, there is at most one
$g \in G$
, there is at most one
![]() $y \in X$
such that
$y \in X$
such that
![]() $(g,x,y) \in A_{\phi }$
. When such a y exists, we say that the action of g on x is defined and set
$(g,x,y) \in A_{\phi }$
. When such a y exists, we say that the action of g on x is defined and set
![]() $gx = y$
. Clearly,
$gx = y$
. Clearly,
![]() $(e,x, x) \in A_{\phi }$
for all
$(e,x, x) \in A_{\phi }$
for all
![]() $x \in X$
, and thus
$x \in X$
, and thus
![]() $ex=x$
; also,
$ex=x$
; also,
![]() $g_{2}(g_{1}x) = (g_{2}g_{1})x$
whenever all the terms are defined. The set
$g_{2}(g_{1}x) = (g_{2}g_{1})x$
whenever all the terms are defined. The set
![]() $A_{\phi }$
is a graph of a total action
$A_{\phi }$
is a graph of a total action
![]() $G \curvearrowright X$
if and only if, for each
$G \curvearrowright X$
if and only if, for each
![]() $x \in X$
and
$x \in X$
and
![]() $g \in G$
, there exists some
$g \in G$
, there exists some
![]() $y \in X$
such that
$y \in X$
such that
![]() $(g,x,y) \in A_{\phi }$
; in this case, the orbit equivalence relation generated by the action coincides with E.
$(g,x,y) \in A_{\phi }$
; in this case, the orbit equivalence relation generated by the action coincides with E.
Example 2.1. An easy way of getting a partial action is by restricting a total one. Suppose we have a free Borel action
![]() $G \curvearrowright X$
with the corresponding orbit equivalence relation
$G \curvearrowright X$
with the corresponding orbit equivalence relation
![]() $E_{G}$
and suppose that a Borel equivalence sub-relation
$E_{G}$
and suppose that a Borel equivalence sub-relation
![]() $E \subseteq E_{G}$
admits a Borel selector—a Borel E-invariant map
$E \subseteq E_{G}$
admits a Borel selector—a Borel E-invariant map
![]() $\pi : X \to X$
such that
$\pi : X \to X$
such that
![]() $x E \pi (x)$
for all
$x E \pi (x)$
for all
![]() $x \in X$
. If
$x \in X$
. If
![]() $\phi : X \to G$
is the map specified uniquely by the condition
$\phi : X \to G$
is the map specified uniquely by the condition
![]() $\phi (x) \pi (x) = x$
, then
$\phi (x) \pi (x) = x$
, then
![]() $(E, \phi )$
is a partial G-action.
$(E, \phi )$
is a partial G-action.
Sub-relations E as in Example 2.1 are often associated with cross-sections of actions of locally compact second countable (lcsc) groups.
2.2 Tessellations of lcsc group actions
Consider a free Borel action
![]() $G \curvearrowright X$
of an lcsc group. A cross-section of the action is a Borel set
$G \curvearrowright X$
of an lcsc group. A cross-section of the action is a Borel set
![]() $\mathcal {C} \subseteq X$
that intersects every orbit in a countable non-empty set. A cross-section
$\mathcal {C} \subseteq X$
that intersects every orbit in a countable non-empty set. A cross-section
![]() $\mathcal {C} \subseteq X$
is:
$\mathcal {C} \subseteq X$
is:
-
• discrete if
 $(Kx) \cap \mathcal {C}$
is finite for every
$(Kx) \cap \mathcal {C}$
is finite for every
 $x \in X$
and compact
$x \in X$
and compact
 $K \subseteq G$
;
$K \subseteq G$
; -
• U-lacunary, where
 $U \subseteq G$
is a neighborhood of the identity, if
$U \subseteq G$
is a neighborhood of the identity, if
 $Uc \cap \mathcal {C} = \{c\}$
for all
$Uc \cap \mathcal {C} = \{c\}$
for all
 $c \in \mathcal {C}$
;
$c \in \mathcal {C}$
; -
• lacunary if it is U-lacunary for some neighborhood of the identity U; and
-
• cocompact if
 $K\mathcal {C} = X$
for some compact
$K\mathcal {C} = X$
for some compact
 $K \subseteq G$
.
$K \subseteq G$
.
Let
![]() $\mathcal {C}$
be a lacunary cross-section for
$\mathcal {C}$
be a lacunary cross-section for
![]() $G \curvearrowright X$
, which exists by [Reference Kechris13, Corollary 1.2]. Any lcsc group G admits a compatible left-invariant proper metric [Reference Struble28], and any left-invariant metric d can be transferred to orbits owing to freeness of the action via
$G \curvearrowright X$
, which exists by [Reference Kechris13, Corollary 1.2]. Any lcsc group G admits a compatible left-invariant proper metric [Reference Struble28], and any left-invariant metric d can be transferred to orbits owing to freeness of the action via
![]() $\mathrm {dist}(x,y) = d(g,e)$
for the unique
$\mathrm {dist}(x,y) = d(g,e)$
for the unique
![]() $g \in G$
such that
$g \in G$
such that
![]() $gx = y$
. One can now define the so-called Voronoi tessellation of orbits by associating with each
$gx = y$
. One can now define the so-called Voronoi tessellation of orbits by associating with each
![]() $x \in X$
the closest point
$x \in X$
the closest point
![]() $\pi _{\mathcal {C}}(x) \in \mathcal {C}$
of the cross-section
$\pi _{\mathcal {C}}(x) \in \mathcal {C}$
of the cross-section
![]() $\mathcal {C}$
, as determined by
$\mathcal {C}$
, as determined by
![]() $\mathrm {dist}$
. Properness of the metric ensures that, for a ball
$\mathrm {dist}$
. Properness of the metric ensures that, for a ball
![]() $B_{R} \subseteq G$
of radius R,
$B_{R} \subseteq G$
of radius R,
![]() $B_{R} = \{g \in G : d(g,e) \le R\}$
, and, for any
$B_{R} = \{g \in G : d(g,e) \le R\}$
, and, for any
![]() $x \in X$
, the set
$x \in X$
, the set
![]() $\mathcal {C} \cap B_{R}x$
is finite. Indeed, there can be at most
$\mathcal {C} \cap B_{R}x$
is finite. Indeed, there can be at most
![]() $\unicode{x3bb} (B_{R +r})/ \unicode{x3bb} (B_{r})$
points in the intersection, where
$\unicode{x3bb} (B_{R +r})/ \unicode{x3bb} (B_{r})$
points in the intersection, where
![]() $\unicode{x3bb} $
is a Haar measure on the group and
$\unicode{x3bb} $
is a Haar measure on the group and
![]() $r> 0$
is so small that
$r> 0$
is so small that
![]() $B_{r}c \cap B_{r} c' = \varnothing $
whenever
$B_{r}c \cap B_{r} c' = \varnothing $
whenever
![]() $c, c' \in \mathcal {C}$
are distinct.
$c, c' \in \mathcal {C}$
are distinct.
Some care needs to be taken to address the possibility of having several closest points. For example, one may pick a Borel linear order on
![]() $\mathcal {C}$
and associated each x with the smallest closest point in the cross-section (see [Reference Slutsky23, §4] or [Reference Le Maître and Slutsky17, §B.2] for the specifics). In this way, we get a Borel equivalence relation
$\mathcal {C}$
and associated each x with the smallest closest point in the cross-section (see [Reference Slutsky23, §4] or [Reference Le Maître and Slutsky17, §B.2] for the specifics). In this way, we get a Borel equivalence relation
![]() $E_{\mathcal {C}} \subseteq E_{G}$
whose equivalence classes are the cells of the Voronoi tessellation:
$E_{\mathcal {C}} \subseteq E_{G}$
whose equivalence classes are the cells of the Voronoi tessellation:
![]() $x E_{\mathcal {C}} y$
if and only if
$x E_{\mathcal {C}} y$
if and only if
![]() $\pi _{\mathcal {C}}(x) = \pi _{\mathcal {C}}(y)$
.
$\pi _{\mathcal {C}}(x) = \pi _{\mathcal {C}}(y)$
.
Assumed freeness of the action
![]() $G \curvearrowright X$
allows a natural identification of each Voronoi cell with a subset of the acting group via the map
$G \curvearrowright X$
allows a natural identification of each Voronoi cell with a subset of the acting group via the map
![]() $\pi _{\mathcal {C}}^{-1}(c) \ni x \mapsto \phi _{\mathcal {C}}(x) \in G$
such that
$\pi _{\mathcal {C}}^{-1}(c) \ni x \mapsto \phi _{\mathcal {C}}(x) \in G$
such that
![]() $\phi _{\mathcal {C}}(x)c = x$
, which is exactly what the corresponding partial action from Example 2.1 does.
$\phi _{\mathcal {C}}(x)c = x$
, which is exactly what the corresponding partial action from Example 2.1 does.
Our intention is to use partial actions to define total actions, and the example above may seem like going ‘in the wrong direction’. The point, however, is that once we have a partial action
![]() $\phi : X \to G$
, we can compose it with an arbitrary Borel injection
$\phi : X \to G$
, we can compose it with an arbitrary Borel injection
![]() $f : G \to G$
to get a different partial action
$f : G \to G$
to get a different partial action
![]() $f\circ \phi $
. This pattern is typical in the sense that new partial actions are often constructed by modifying those obtained as restrictions of total actions.
$f\circ \phi $
. This pattern is typical in the sense that new partial actions are often constructed by modifying those obtained as restrictions of total actions.
2.3 Convergent sequences of partial actions
A total action can be defined whenever we have a sequence of partial actions that cohere in the appropriate sense. Let G be a standard Borel group. A sequence
![]() $(E_{n}, \phi _{n})$
,
$(E_{n}, \phi _{n})$
,
![]() $n \in \mathbb {N}$
, of partial G-actions on X is said to be convergent if it satisfies the following properties.
$n \in \mathbb {N}$
, of partial G-actions on X is said to be convergent if it satisfies the following properties.
-
• Monotonicity: equivalence relations
 $E_{n}$
form an increasing sequence, that is,
$E_{n}$
form an increasing sequence, that is,
 $E_{n} \subseteq E_{n+1}$
for all n.
$E_{n} \subseteq E_{n+1}$
for all n. -
• Coherence: for each n, the map
 $x \mapsto (\phi _{n}(x))^{-1}\phi _{n+1}(x)$
is
$x \mapsto (\phi _{n}(x))^{-1}\phi _{n+1}(x)$
is
 $E_{n}$
-invariant.
$E_{n}$
-invariant. -
• Exhaustiveness: for all
 $x \in X$
and all
$x \in X$
and all
 $g \in G$
, there exist n and
$g \in G$
, there exist n and
 $y \in X$
such that
$y \in X$
such that
 $xE_{n}y$
and
$xE_{n}y$
and
 $g\phi _{n}(x) = \phi _{n}(y)$
.
$g\phi _{n}(x) = \phi _{n}(y)$
.
With such a sequence, one can associate a free Borel (left) action
![]() $G \curvearrowright X$
, called the limit of
$G \curvearrowright X$
, called the limit of
![]() $(E_{n}, \phi _{n})_{n}$
, whose graph is
$(E_{n}, \phi _{n})_{n}$
, whose graph is
![]() $\bigcup _{n}A_{\phi _{n}}$
. Coherence ensures that the partial action defined by
$\bigcup _{n}A_{\phi _{n}}$
. Coherence ensures that the partial action defined by
![]() $\phi _{n+1}$
is an extension of the one given by
$\phi _{n+1}$
is an extension of the one given by
![]() $\phi _{n}$
. Indeed, if
$\phi _{n}$
. Indeed, if
![]() $xE_{n}y$
are such that
$xE_{n}y$
are such that
![]() $g\phi _{n}(x) = \phi _{n}(y)$
, then also
$g\phi _{n}(x) = \phi _{n}(y)$
, then also
![]() $x E_{n+1} y$
by monotonicity, and, using coherence,
$x E_{n+1} y$
by monotonicity, and, using coherence,
from which we get
![]() $A_{\phi _{n}} \subseteq A_{\phi _{n+1}}$
. If C is an
$A_{\phi _{n}} \subseteq A_{\phi _{n+1}}$
. If C is an
![]() $E_{n}$
-class and
$E_{n}$
-class and
![]() $s = (\phi _{n}(x))^{-1}\phi _{n+1}(x)$
for some
$s = (\phi _{n}(x))^{-1}\phi _{n+1}(x)$
for some
![]() $x \in C$
, then
$x \in C$
, then
![]() $\phi _{n+1}(C) = \phi _{n}(C)s$
, so the image
$\phi _{n+1}(C) = \phi _{n}(C)s$
, so the image
![]() $\phi _{n}(C)$
gets shifted on the right inside
$\phi _{n}(C)$
gets shifted on the right inside
![]() $\phi _{n+1}(C)$
. If we want to build a right action of the group, then
$\phi _{n+1}(C)$
. If we want to build a right action of the group, then
![]() $\phi _{n}(C)$
should be shifted on the left instead.
$\phi _{n}(C)$
should be shifted on the left instead.
Finally, exhaustiveness guarantees that
![]() $gx$
gets defined eventually: for all
$gx$
gets defined eventually: for all
![]() $g \in G$
and
$g \in G$
and
![]() $x \in X$
, there are n and
$x \in X$
, there are n and
![]() $y \in X$
such that
$y \in X$
such that
![]() $(g,x,y) \in A_{\phi _{n}}$
. It is straightforward to check that
$(g,x,y) \in A_{\phi _{n}}$
. It is straightforward to check that
![]() $\bigcup _{n}A_{\phi _{n}}$
is a graph of a total Borel action
$\bigcup _{n}A_{\phi _{n}}$
is a graph of a total Borel action
![]() $G \curvearrowright X$
. It is equally easy to check that the action is free, and that its orbits are precisely the equivalence classes of
$G \curvearrowright X$
. It is equally easy to check that the action is free, and that its orbits are precisely the equivalence classes of
![]() $\bigcup _{n}E_{n}$
.
$\bigcup _{n}E_{n}$
.
This framework, general as it is, delegates most of the complexity to the construction of maps
![]() $\phi _{n}$
. We illustrate these concepts on essentially hyperfinite actions of lcsc groups.
$\phi _{n}$
. We illustrate these concepts on essentially hyperfinite actions of lcsc groups.
2.4 Hyperfinite tessellations of lcsc group actions
In the context of §2.2, suppose that, furthermore, the restriction of the orbit equivalence relation
![]() $E_{G}$
onto the cross-section
$E_{G}$
onto the cross-section
![]() $\mathcal {C}$
is hyperfinite, that is, there is an increasing sequence of finite Borel equivalence relations
$\mathcal {C}$
is hyperfinite, that is, there is an increasing sequence of finite Borel equivalence relations
![]() $F_{n}$
on
$F_{n}$
on
![]() $\mathcal {C}$
such that
$\mathcal {C}$
such that
![]() $\bigcup _{n}F_{n} = E_{G}|_{\mathcal {C}}$
. We can use this sequence to define
$\bigcup _{n}F_{n} = E_{G}|_{\mathcal {C}}$
. We can use this sequence to define
![]() $xE_{n}y$
whenever
$xE_{n}y$
whenever
![]() $\pi _{\mathcal {C}}(x)F_{n}\pi _{\mathcal {C}}(y)$
, which yields an increasing sequence of Borel equivalence relations
$\pi _{\mathcal {C}}(x)F_{n}\pi _{\mathcal {C}}(y)$
, which yields an increasing sequence of Borel equivalence relations
![]() $E_{n}$
such that
$E_{n}$
such that
![]() $E_{G} = \bigcup _{n}E_{n}$
.
$E_{G} = \bigcup _{n}E_{n}$
.
The equivalence relations
![]() $F_{n}$
admit Borel transversals, that is, there are Borel sets
$F_{n}$
admit Borel transversals, that is, there are Borel sets
![]() $\mathcal {C}_{n}$
that pick exactly one point from each
$\mathcal {C}_{n}$
that pick exactly one point from each
![]() $F_{n}$
-class. As in §2.2, we may define
$F_{n}$
-class. As in §2.2, we may define
![]() $\phi _{n}(x) $
to be an element
$\phi _{n}(x) $
to be an element
![]() $g \in G$
such that
$g \in G$
such that
![]() $gc = x$
for the unique
$gc = x$
for the unique
![]() $c \in \mathcal {C}_{n}$
satisfying
$c \in \mathcal {C}_{n}$
satisfying
![]() $x E_{n}c$
. This gives a convergent sequence of partial G-actions
$x E_{n}c$
. This gives a convergent sequence of partial G-actions
![]() $(E_{n}, \phi _{n})_{n}$
whose limit is the original action
$(E_{n}, \phi _{n})_{n}$
whose limit is the original action
![]() $G \curvearrowright X$
.
$G \curvearrowright X$
.
2.5 Partial actions revisited
In practice, it is often more convenient to allow equivalence relations
![]() $E_{n}$
to be defined on proper subsets of X. Let
$E_{n}$
to be defined on proper subsets of X. Let
![]() $X_{n} \subseteq X$
,
$X_{n} \subseteq X$
,
![]() $n \in \mathbb {N}$
, be Borel subsets and suppose that, for each n,
$n \in \mathbb {N}$
, be Borel subsets and suppose that, for each n,
![]() $E_{n}$
is a Borel equivalence relation on
$E_{n}$
is a Borel equivalence relation on
![]() $X_{n}$
. We say that the sequence
$X_{n}$
. We say that the sequence
![]() $(E_{n})_{n}$
is monotone if the following conditions are satisfied for all
$(E_{n})_{n}$
is monotone if the following conditions are satisfied for all
![]() $m \le n$
.
$m \le n$
.
-
•
 $E_{m}|_{X_{m} \cap X_{n}} \subseteq E_{n}|_{X_{m} \cap X_{n}}$
.
$E_{m}|_{X_{m} \cap X_{n}} \subseteq E_{n}|_{X_{m} \cap X_{n}}$
. -
• If
 $x \in X_{m}\cap X_{n}$
, then the whole
$x \in X_{m}\cap X_{n}$
, then the whole
 $E_{m}$
-class of x is in
$E_{m}$
-class of x is in
 $X_{n}$
.
$X_{n}$
.
Partial action maps
![]() $\phi _{n} : X_{n} \to G$
, where, as earlier, G is a standard Borel group, need to satisfy the appropriate versions of coherence and exhaustiveness.
$\phi _{n} : X_{n} \to G$
, where, as earlier, G is a standard Borel group, need to satisfy the appropriate versions of coherence and exhaustiveness.
-
• Coherence:
 $X_{m} \cap X_{n} \ni x \mapsto (\phi _{m}(x))^{-1}\phi _{n}(x)$
is
$X_{m} \cap X_{n} \ni x \mapsto (\phi _{m}(x))^{-1}\phi _{n}(x)$
is
 $E_{m}$
-invariant for each
$E_{m}$
-invariant for each
 $m < n$
.
$m < n$
. -
• Exhaustiveness: for each
 $x \in X$
and
$x \in X$
and
 $g \in G$
, there exist n and
$g \in G$
, there exist n and
 $y \in X_{n}$
such that
$y \in X_{n}$
such that
 $x \in X_{n}$
,
$x \in X_{n}$
,
 $x E_{n}y$
and
$x E_{n}y$
and
 $g\phi _{n}(x) = \phi _{n}(y) $
.
$g\phi _{n}(x) = \phi _{n}(y) $
.
A sequence of partial G-actions
![]() $(X_{n},E_{n},\phi _{n})_{n}$
will be called convergent if it satisfies the above properties of monotonicity, coherence and exhaustiveness. Note that the condition
$(X_{n},E_{n},\phi _{n})_{n}$
will be called convergent if it satisfies the above properties of monotonicity, coherence and exhaustiveness. Note that the condition
![]() $\bigcup _{n}X_{n} = X$
follows from exhaustiveness, so sets
$\bigcup _{n}X_{n} = X$
follows from exhaustiveness, so sets
![]() $X_{n}$
must cover all of X.
$X_{n}$
must cover all of X.
Convergent sequences
![]() $(X_{n},E_{n},\phi _{n})_{n}$
define total actions, which can be easily seen by reducing this set-up to the notationally simpler one given in §2.3. To this end, extend
$(X_{n},E_{n},\phi _{n})_{n}$
define total actions, which can be easily seen by reducing this set-up to the notationally simpler one given in §2.3. To this end, extend
![]() $E_{n}$
to the equivalence relation
$E_{n}$
to the equivalence relation
![]() $\hat {E}_{n}$
on all of X by
$\hat {E}_{n}$
on all of X by
and also extend
![]() $\phi _{n}$
to
$\phi _{n}$
to
![]() $\hat {\phi }_{n} : X \to G$
by setting
$\hat {\phi }_{n} : X \to G$
by setting
![]() $\hat {\phi }_{n}(x) = \phi _{m}(x)$
for the maximal
$\hat {\phi }_{n}(x) = \phi _{m}(x)$
for the maximal
![]() $m \le n$
such that
$m \le n$
such that
![]() $x \in X_{m}$
or
$x \in X_{m}$
or
![]() $\hat {\phi }_{n}(x) = e$
if no such m exists. It is straightforward to check that
$\hat {\phi }_{n}(x) = e$
if no such m exists. It is straightforward to check that
![]() $(\hat {E}_{n}, \hat {\phi }_{n})_{n}$
is a convergent sequence of partial G-actions in the sense of §2.3. By the limit of the sequence of partial actions
$(\hat {E}_{n}, \hat {\phi }_{n})_{n}$
is a convergent sequence of partial G-actions in the sense of §2.3. By the limit of the sequence of partial actions
![]() $(X_{n}, E_{n}, \phi _{n})_{n}$
we mean the limit of
$(X_{n}, E_{n}, \phi _{n})_{n}$
we mean the limit of
![]() $(\hat {E}_{n}, \hat {\phi }_{n})_{n}$
as defined earlier.
$(\hat {E}_{n}, \hat {\phi }_{n})_{n}$
as defined earlier.
Remark 2.2. A variant of this generalized formulation, which we encounter in Proposition 2.4 below, occurs when sets
![]() $X_{n}$
are nested: that is,
$X_{n}$
are nested: that is,
![]() $X_{0} \subseteq X_{1} \subseteq X_{2} \subseteq \cdots $
. Monotonicity of equivalence relations then simplifies to
$X_{0} \subseteq X_{1} \subseteq X_{2} \subseteq \cdots $
. Monotonicity of equivalence relations then simplifies to
![]() $E_{0} \subseteq E_{1} \subseteq E_{2} \subseteq \cdots $
and coherence becomes equivalent to the
$E_{0} \subseteq E_{1} \subseteq E_{2} \subseteq \cdots $
and coherence becomes equivalent to the
![]() $E_{n}$
-invariant of maps
$E_{n}$
-invariant of maps
![]() $ X_{n} \ni x \mapsto (\phi _{n}(x))^{-1}\phi _{n+1}(x) \in G$
.
$ X_{n} \ni x \mapsto (\phi _{n}(x))^{-1}\phi _{n+1}(x) \in G$
.
As was mentioned above, it is easy to create new partial actions simply by composing a partial action
![]() $\phi : X \to G$
with some Borel bijection
$\phi : X \to G$
with some Borel bijection
![]() $f : G \to G$
(or
$f : G \to G$
(or
![]() $f : G \to H$
, if we choose to have values in a different group). However, an arbitrary bijection has no reason to preserve coherence and extra care is necessary to maintain it.
$f : G \to H$
, if we choose to have values in a different group). However, an arbitrary bijection has no reason to preserve coherence and extra care is necessary to maintain it.
Furthermore, in general, we need to apply different modifications f to different
![]() $E_{n}$
-classes, which naturally raises concern about how to ensure that construction is performed in a Borel way. In applications, the modification f applied to an
$E_{n}$
-classes, which naturally raises concern about how to ensure that construction is performed in a Borel way. In applications, the modification f applied to an
![]() $E_{n}$
-class C usually depends on the ‘shape’ of C and the
$E_{n}$
-class C usually depends on the ‘shape’ of C and the
![]() $E_{m}$
-classes it contains, but it does not depend on other
$E_{m}$
-classes it contains, but it does not depend on other
![]() $E_{n}$
-classes. If there are only countably many such ‘configurations’ of
$E_{n}$
-classes. If there are only countably many such ‘configurations’ of
![]() $E_{n}$
-classes, the resulting partial actions
$E_{n}$
-classes, the resulting partial actions
![]() $f \circ \phi $
will be Borel as long as we consistently apply the same modification whenever ‘configurations’ are the same. This idea can be formalized as follows.
$f \circ \phi $
will be Borel as long as we consistently apply the same modification whenever ‘configurations’ are the same. This idea can be formalized as follows.
2.6 Rational sequences of partial actions
Let
![]() $(E_{n}, \phi _{n})_{n}$
be a convergent sequence of partial actions on X. For an
$(E_{n}, \phi _{n})_{n}$
be a convergent sequence of partial actions on X. For an
![]() $E_{n}$
-class C, let
$E_{n}$
-class C, let
![]() $\mathcal {E}_{m}(C)$
denote the collection of
$\mathcal {E}_{m}(C)$
denote the collection of
![]() $E_{m}$
-classes contained in C. Given two
$E_{m}$
-classes contained in C. Given two
![]() $E_{n}$
-classes C and
$E_{n}$
-classes C and
![]() $C'$
, we denote by
$C'$
, we denote by
![]() $\phi _{n}(C) \equiv \phi _{n}(C')$
the existence for each
$\phi _{n}(C) \equiv \phi _{n}(C')$
the existence for each
![]() $m \le n$
of a bijection
$m \le n$
of a bijection
![]() $\mathcal {E}_{m}(C) \ni D \mapsto D' \in \mathcal {E}_{m}(C') $
such that
$\mathcal {E}_{m}(C) \ni D \mapsto D' \in \mathcal {E}_{m}(C') $
such that
![]() $\phi _{n}(D) = \phi _{n}(D')$
for all
$\phi _{n}(D) = \phi _{n}(D')$
for all
![]() $D \in \mathcal {E}_{m}(C)$
. The collection of images
$D \in \mathcal {E}_{m}(C)$
. The collection of images
![]() $\{\phi _{n}(D) : D \in \bigcup _{m\le n} \mathcal {E}_{m}(C) \}$
constitutes the ‘configuration’ of C referred to earlier.
$\{\phi _{n}(D) : D \in \bigcup _{m\le n} \mathcal {E}_{m}(C) \}$
constitutes the ‘configuration’ of C referred to earlier.
We say that the sequence
![]() $(E_{n}, \phi _{n})_{n}$
of partial actions is rational if, for each n, there exists a Borel
$(E_{n}, \phi _{n})_{n}$
of partial actions is rational if, for each n, there exists a Borel
![]() $E_{n}$
-invariant partition
$E_{n}$
-invariant partition
![]() $X = \bigsqcup _{k} Y_{k}$
such that, for each k, one has
$X = \bigsqcup _{k} Y_{k}$
such that, for each k, one has
![]() $\phi _{n}(C) \equiv \phi _{n}(C')$
for all
$\phi _{n}(C) \equiv \phi _{n}(C')$
for all
![]() $E_{n}$
-classes
$E_{n}$
-classes
![]() $C,C' \subseteq Y_{k}$
.
$C,C' \subseteq Y_{k}$
.
Remark 2.3. This concept of rationality applies verbatim to convergent sequences of partial actions
![]() $(X_{n},E_{n}, \phi _{n})_{n}$
, as described in §2.5. One can check that such a sequence is rational if and only if the sequence
$(X_{n},E_{n}, \phi _{n})_{n}$
, as described in §2.5. One can check that such a sequence is rational if and only if the sequence
![]() $(\hat {E}_{n},\hat {\phi }_{n})$
is rational.
$(\hat {E}_{n},\hat {\phi }_{n})$
is rational.
2.7 Generating the flow equivalence relation
As an application of the partial actions formalism, we show that any orbit equivalence relation given by a free Borel
![]() $\mathbb {R}$
-flow can also be generated by a free action of any non-discrete and non-compact Polish group. For this, we need the following representation of an
$\mathbb {R}$
-flow can also be generated by a free action of any non-discrete and non-compact Polish group. For this, we need the following representation of an
![]() $\mathbb {R}$
-flow as a limit of partial
$\mathbb {R}$
-flow as a limit of partial
![]() $\mathbb {R}$
-actions.
$\mathbb {R}$
-actions.
Proposition 2.4. Any free Borel
![]() $\mathbb {R}$
-flow on X can be represented as a limit of a convergent rational sequence of partial
$\mathbb {R}$
-flow on X can be represented as a limit of a convergent rational sequence of partial
![]() $\mathbb {R}$
-actions
$\mathbb {R}$
-actions
![]() $(X_{n},E_{n}, \phi _{n})_{n}$
such that:
$(X_{n},E_{n}, \phi _{n})_{n}$
such that:
-
(1) both
 $X_{n}$
and
$X_{n}$
and
 $E_{n}$
are increasing:
$E_{n}$
are increasing:
 $X_{0} \subseteq X_{1} \subseteq \cdots $
and
$X_{0} \subseteq X_{1} \subseteq \cdots $
and
 $E_{0} \subseteq E_{1} \subseteq \cdots $
(see Remark 2.2);
$E_{0} \subseteq E_{1} \subseteq \cdots $
(see Remark 2.2); -
(2) each
 $E_{n+1}$
-class contains finitely many
$E_{n+1}$
-class contains finitely many
 $E_{n}$
-classes;
$E_{n}$
-classes; -
(3) each
 $E_{0}$
-class has cardinality of continuum; and
$E_{0}$
-class has cardinality of continuum; and -
(4) for each
 $E_{n+1}$
-class C, the set
$E_{n+1}$
-class C, the set
 $C \setminus X_{n}$
has cardinality of continuum.
$C \setminus X_{n}$
has cardinality of continuum.
Proof. Any
![]() $\mathbb {R}$
-flow admits a rational
$\mathbb {R}$
-flow admits a rational
![]() $(-4,4)$
-lacunary cross-section (see [Reference Slutsky24, §2]), which we denote by
$(-4,4)$
-lacunary cross-section (see [Reference Slutsky24, §2]), which we denote by
![]() $\mathcal {C}$
. Rationality of the cross-section here means that the distance between any two points of
$\mathcal {C}$
. Rationality of the cross-section here means that the distance between any two points of
![]() $\mathcal {C}$
is a rational number. More generally, rationality of a cross-section
$\mathcal {C}$
is a rational number. More generally, rationality of a cross-section
![]() $\mathcal {C}$
for an
$\mathcal {C}$
for an
![]() $\mathbb {R}^{d}$
-action means that
$\mathbb {R}^{d}$
-action means that
![]() $r \in \mathbb {Q}^{d}$
whenever
$r \in \mathbb {Q}^{d}$
whenever
![]() $c + r = c'$
for some
$c + r = c'$
for some
![]() $c, c' \in \mathcal {C}$
. Let
$c, c' \in \mathcal {C}$
. Let
![]() $(E_{\mathcal {C}}, \phi _{\mathcal {C}})$
be the partial
$(E_{\mathcal {C}}, \phi _{\mathcal {C}})$
be the partial
![]() $\mathbb {R}$
-action as defined in §2.2. If D is an
$\mathbb {R}$
-action as defined in §2.2. If D is an
![]() $E_{\mathcal {C}}$
-class, then
$E_{\mathcal {C}}$
-class, then
![]() $\phi _{\mathcal {C}}(D)$
is an interval. For
$\phi _{\mathcal {C}}(D)$
is an interval. For
![]() $\epsilon> 0$
, let
$\epsilon> 0$
, let
![]() $D^{\epsilon }$
consist of those
$D^{\epsilon }$
consist of those
![]() $ x \in D$
such that
$ x \in D$
such that
![]() $\phi _{\mathcal {C}}(x)$
is at least
$\phi _{\mathcal {C}}(x)$
is at least
![]() $\epsilon $
away from the boundary points of
$\epsilon $
away from the boundary points of
![]() $\phi _{\mathcal {C}}(D)$
. In other words,
$\phi _{\mathcal {C}}(D)$
. In other words,
![]() $D^{\epsilon }$
is obtained by shrinking the class D by
$D^{\epsilon }$
is obtained by shrinking the class D by
![]() $\epsilon $
from each side.
$\epsilon $
from each side.
The restriction of the orbit equivalence relation onto
![]() $\mathcal {C}$
is hyperfinite. This fact is true in the much wider generality of actions of locally compact Abelian groups [Reference Cotton4]. Specifically for
$\mathcal {C}$
is hyperfinite. This fact is true in the much wider generality of actions of locally compact Abelian groups [Reference Cotton4]. Specifically for
![]() $\mathbb {R}$
-flows,
$\mathbb {R}$
-flows,
![]() $E|_{\mathcal {C}}$
is generated by the first return map—a Borel automorphism of
$E|_{\mathcal {C}}$
is generated by the first return map—a Borel automorphism of
![]() $\mathcal {C}$
that sends a point in
$\mathcal {C}$
that sends a point in
![]() $\mathcal {C}$
to the next one according to the order of the
$\mathcal {C}$
to the next one according to the order of the
![]() $\mathbb {R}$
-flow. The first return map is well defined and is invertible, except for the orbits, where
$\mathbb {R}$
-flow. The first return map is well defined and is invertible, except for the orbits, where
![]() $\mathcal {C}$
happens to have the maximal or the minimal point. The latter part of the space evidently admits a Borel selector and is, therefore, smooth; hence, it won’t affect hyperfiniteness of the equivalence relation. It remains to recall the standard fact that orbit equivalence relations of
$\mathcal {C}$
happens to have the maximal or the minimal point. The latter part of the space evidently admits a Borel selector and is, therefore, smooth; hence, it won’t affect hyperfiniteness of the equivalence relation. It remains to recall the standard fact that orbit equivalence relations of
![]() $\mathbb {Z}$
-actions are hyperfinite (see, for example, [Reference Dougherty, Jackson and Kechris6, Theorem 5.1]), and thus so is the restriction
$\mathbb {Z}$
-actions are hyperfinite (see, for example, [Reference Dougherty, Jackson and Kechris6, Theorem 5.1]), and thus so is the restriction
![]() $E|_{\mathcal {C}}$
.
$E|_{\mathcal {C}}$
.
In particular, we can represent the
![]() $\mathbb {R}$
-flow as the limit of a convergent sequence of partial actions
$\mathbb {R}$
-flow as the limit of a convergent sequence of partial actions
![]() $(E^{\prime }_{n}, \phi ^{\prime }_{n})_{n}$
, as described in §2.4. Note that
$(E^{\prime }_{n}, \phi ^{\prime }_{n})_{n}$
, as described in §2.4. Note that
![]() $(E^{\prime }_{n}, \phi ^{\prime }_{n})_{n}$
is necessarily rational by rationality of
$(E^{\prime }_{n}, \phi ^{\prime }_{n})_{n}$
is necessarily rational by rationality of
![]() $\mathcal {C}$
. Such a sequence satisfies items (2) and (3), but fails (4). We fix this by shrinking equivalence classes to achieve proper containment. Let
$\mathcal {C}$
. Such a sequence satisfies items (2) and (3), but fails (4). We fix this by shrinking equivalence classes to achieve proper containment. Let
![]() $(\epsilon _{n})_{n}$
be a strictly decreasing sequence of positive reals such that
$(\epsilon _{n})_{n}$
be a strictly decreasing sequence of positive reals such that
![]() $ 1> \epsilon _{0}$
and
$ 1> \epsilon _{0}$
and
![]() $\lim _{n}\epsilon _{n} = 0$
. Put
$\lim _{n}\epsilon _{n} = 0$
. Put
![]() $X^{\prime }_{n} = \bigcup D^{\epsilon _{n}}$
, where the union is taken over all
$X^{\prime }_{n} = \bigcup D^{\epsilon _{n}}$
, where the union is taken over all
![]() $E_{\mathcal {C}}$
-classes D. Note that sets
$E_{\mathcal {C}}$
-classes D. Note that sets
![]() $X^{\prime }_{n}$
fail to cover X, because the boundary points of any
$X^{\prime }_{n}$
fail to cover X, because the boundary points of any
![]() $E_{\mathcal {C}}$
-class do not belong to any of
$E_{\mathcal {C}}$
-class do not belong to any of
![]() $X^{\prime }_{n}$
. Put
$X^{\prime }_{n}$
. Put
![]() $Y = X \setminus \bigcup _{n} X^{\prime }_{n}$
and let
$Y = X \setminus \bigcup _{n} X^{\prime }_{n}$
and let
![]() $X_{n} = X^{\prime }_{n} \cup Y$
. Clearly,
$X_{n} = X^{\prime }_{n} \cup Y$
. Clearly,
![]() $(X_{n})_{n}$
is an increasing sequence of Borel sets and
$(X_{n})_{n}$
is an increasing sequence of Borel sets and
![]() $\bigcup _{n} X_{n} = X$
.
$\bigcup _{n} X_{n} = X$
.
Finally, set
![]() $E_{n} = E^{\prime }_{n}|_{X_{n}}$
and
$E_{n} = E^{\prime }_{n}|_{X_{n}}$
and
![]() $\phi _{n} : X_{n} \to \mathbb {R}$
to be
$\phi _{n} : X_{n} \to \mathbb {R}$
to be
![]() $\phi ^{\prime }_{n}|_{X_{n}}$
. The sequence
$\phi ^{\prime }_{n}|_{X_{n}}$
. The sequence
![]() $(X_{n},E_{n},\phi _{n})_{n}$
of partial
$(X_{n},E_{n},\phi _{n})_{n}$
of partial
![]() $\mathbb {R}$
-actions satisfies the conditions of the proposition.
$\mathbb {R}$
-actions satisfies the conditions of the proposition.
All non-smooth orbit equivalence relations produced by free Borel
![]() $\mathbb {R}$
-flows are Borel isomorphic to each other [Reference Kechris14, Theorem 3]. Theorem 2.6 shows that this orbit equivalence relation can also be generated by a free action of any non-compact and non-discrete Polish group.
$\mathbb {R}$
-flows are Borel isomorphic to each other [Reference Kechris14, Theorem 3]. Theorem 2.6 shows that this orbit equivalence relation can also be generated by a free action of any non-compact and non-discrete Polish group.
Let G be a group. We say that a set
![]() $A \subseteq G$
admits infinitely many disjoint right translates if there is a sequence
$A \subseteq G$
admits infinitely many disjoint right translates if there is a sequence
![]() $(g_{n})_{n}$
of elements of G such that
$(g_{n})_{n}$
of elements of G such that
![]() $Ag_{m} \cap Ag_{n} = \emptyset $
for all
$Ag_{m} \cap Ag_{n} = \emptyset $
for all
![]() $m \ne n$
.
$m \ne n$
.
Lemma 2.5. Let G be a non-compact Polish group. There exists a neighborhood of the identity
![]() $V \subseteq G$
such that, for any finite
$V \subseteq G$
such that, for any finite
![]() $F \subseteq G$
, the set
$F \subseteq G$
, the set
![]() $VF$
admits infinitely many disjoint right translates.
$VF$
admits infinitely many disjoint right translates.
Proof. We begin with the following characterization of compactness established independently by Solecki [Reference Solecki27, Lemma 1.2] and Uspenskij [Reference Uspenskij29]: a Polish group G is non-compact if and only if there exists a neighborhood of the identity
![]() $U \subseteq G$
such that
$U \subseteq G$
such that
![]() $F_{1}UF_{2} \ne G$
for all finite
$F_{1}UF_{2} \ne G$
for all finite
![]() $F_{1}, F_{2} \subseteq G$
. Let
$F_{1}, F_{2} \subseteq G$
. Let
![]() $V \subseteq G$
be a symmetric neighborhood of the identity such that
$V \subseteq G$
be a symmetric neighborhood of the identity such that
![]() $V^{2} \subseteq U$
. We claim that such a set V has the desired property. Pick a finite
$V^{2} \subseteq U$
. We claim that such a set V has the desired property. Pick a finite
![]() $F \subseteq G$
, set
$F \subseteq G$
, set
![]() $g_{0} = e$
and choose
$g_{0} = e$
and choose
![]() $g_{n}$
inductively as follows. Let
$g_{n}$
inductively as follows. Let
![]() $F_{1} = F^{-1}$
and
$F_{1} = F^{-1}$
and
![]() $F_{2,n} = F\cdot \{g_{k} : k < n\}$
. The defining property of U ensures existence of
$F_{2,n} = F\cdot \{g_{k} : k < n\}$
. The defining property of U ensures existence of
![]() $g_{n} \not \in F_{1}UF_{2,n}$
. Translates
$g_{n} \not \in F_{1}UF_{2,n}$
. Translates
![]() $(VFg_{n})_{n}$
are then pairwise disjoint, because if
$(VFg_{n})_{n}$
are then pairwise disjoint, because if
![]() $VFg_{m} \cap VFg_{n} \ne \emptyset $
for
$VFg_{m} \cap VFg_{n} \ne \emptyset $
for
![]() $m < n$
, then
$m < n$
, then
![]() $g_{n} \in F^{-1}V^{-1}VFg_{m} \subseteq F_{1}UF_{2,n}$
, which contradicts the construction.
$g_{n} \in F^{-1}V^{-1}VFg_{m} \subseteq F_{1}UF_{2,n}$
, which contradicts the construction.
Theorem 2.6. Let E be an orbit equivalence relation given by a free Borel
![]() $\mathbb {R}$
-flow on X. Any non-discrete, non-compact Polish group G admits a free Borel action
$\mathbb {R}$
-flow on X. Any non-discrete, non-compact Polish group G admits a free Borel action
![]() $G \curvearrowright X$
such that
$G \curvearrowright X$
such that
![]() $E_{G} = E$
.
$E_{G} = E$
.
Proof. Let
![]() $(X_{n}, E_{n}, \phi _{n})_{n}$
be a convergent sequence of partial
$(X_{n}, E_{n}, \phi _{n})_{n}$
be a convergent sequence of partial
![]() $\mathbb {R}$
-actions, as in Proposition 2.4, and let
$\mathbb {R}$
-actions, as in Proposition 2.4, and let
![]() $V \subseteq G$
be given by Lemma 2.5. Choose a countable dense
$V \subseteq G$
be given by Lemma 2.5. Choose a countable dense
![]() $(h_{n})_{n}$
in G so that
$(h_{n})_{n}$
in G so that
![]() $\bigcup _{n}Vh_{n} = G$
. Since the sequence of partial
$\bigcup _{n}Vh_{n} = G$
. Since the sequence of partial
![]() $\mathbb {R}$
-actions is rational, one may pick, for each n, a Borel
$\mathbb {R}$
-actions is rational, one may pick, for each n, a Borel
![]() $E_{n}$
-invariant partition
$E_{n}$
-invariant partition
![]() $X_{n} = \bigsqcup _{k}Y_{n,k}$
such that
$X_{n} = \bigsqcup _{k}Y_{n,k}$
such that
![]() $\phi _{n}(C) \equiv \phi _{n}(C')$
for all
$\phi _{n}(C) \equiv \phi _{n}(C')$
for all
![]() $E_{n}$
-classes
$E_{n}$
-classes
![]() $C,C' \subseteq Y_{n,k}$
. We construct a convergent sequence of partial G-actions
$C,C' \subseteq Y_{n,k}$
. We construct a convergent sequence of partial G-actions
![]() $(X_{n}, E_{n}, \psi _{n})_{n}$
such that, for each n and k, there exists a finite set
$(X_{n}, E_{n}, \psi _{n})_{n}$
such that, for each n and k, there exists a finite set
![]() $F \subseteq G$
such that
$F \subseteq G$
such that
![]() $\{h_{i} : i < n\} \subseteq F$
and
$\{h_{i} : i < n\} \subseteq F$
and
![]() $\psi _{n}(C) = VF$
for all
$\psi _{n}(C) = VF$
for all
![]() $E_{n}$
-classes
$E_{n}$
-classes
![]() $C \subseteq Y_{n,k}$
.
$C \subseteq Y_{n,k}$
.
For any
![]() $E_{0}$
-class C, both
$E_{0}$
-class C, both
![]() $\phi _{0}(C) \subseteq \mathbb {R}$
and
$\phi _{0}(C) \subseteq \mathbb {R}$
and
![]() $V \subseteq G$
are Borel sets of the same cardinality. Therefore, we may pick a Borel bijection
$V \subseteq G$
are Borel sets of the same cardinality. Therefore, we may pick a Borel bijection
![]() $f_{k} : \phi _{0}(C) \to V$
, where
$f_{k} : \phi _{0}(C) \to V$
, where
![]() $C \subseteq Y_{0,k}$
. For the base of the inductive construction, we set
$C \subseteq Y_{0,k}$
. For the base of the inductive construction, we set
![]() $\psi _{0}|_{Y_{k}} = f_{k}\circ \phi _{0}$
. Suppose that
$\psi _{0}|_{Y_{k}} = f_{k}\circ \phi _{0}$
. Suppose that
![]() $\psi _{m} : X_{m} \to G$
,
$\psi _{m} : X_{m} \to G$
,
![]() $m \le n$
, have been constructed.
$m \le n$
, have been constructed.
We now construct
![]() $\psi _{n+1}$
. Let C be an
$\psi _{n+1}$
. Let C be an
![]() $E_{n+1}$
-class and let
$E_{n+1}$
-class and let
![]() $D_{1}, \ldots , D_{l}$
be a complete list of
$D_{1}, \ldots , D_{l}$
be a complete list of
![]() $E_{n}$
-classes contained in C. By the inductive assumption, there are finite sets
$E_{n}$
-classes contained in C. By the inductive assumption, there are finite sets
![]() $F_{1}, \ldots , F_{l} \subseteq G$
such that
$F_{1}, \ldots , F_{l} \subseteq G$
such that
![]() $\psi _{n}(D_{i}) = VF_{i}$
. Let
$\psi _{n}(D_{i}) = VF_{i}$
. Let
![]() $\tilde {F} = \bigcup _{i \le l}F_{i}$
. By the choice of V, there are elements
$\tilde {F} = \bigcup _{i \le l}F_{i}$
. By the choice of V, there are elements
![]() $g_{1}, \ldots , g_{l} \in G$
such that
$g_{1}, \ldots , g_{l} \in G$
such that
![]() $V\tilde {F}g_{i}$
are pairwise disjoint for
$V\tilde {F}g_{i}$
are pairwise disjoint for
![]() $1 \le i \le l$
. Pick a finite
$1 \le i \le l$
. Pick a finite
![]() $F \subseteq G$
large enough so that
$F \subseteq G$
large enough so that
![]() $\tilde {F}g_{i} \subseteq F$
,
$\tilde {F}g_{i} \subseteq F$
,
![]() $\{h_{i} : i < n+1\} \subseteq F$
and
$\{h_{i} : i < n+1\} \subseteq F$
and
![]() $VF \setminus \bigcup _{i\le l}V\tilde {F}g_{i}$
has cardinality of continuum (the latter can be achieved, for example, by ensuring that one more disjoint translate of
$VF \setminus \bigcup _{i\le l}V\tilde {F}g_{i}$
has cardinality of continuum (the latter can be achieved, for example, by ensuring that one more disjoint translate of
![]() $V\tilde {F}$
is inside
$V\tilde {F}$
is inside
![]() $VF$
). Note that
$VF$
). Note that
![]() $\phi _{n+1}(C \setminus X_{n}) = \phi _{n+1}(C) \setminus \bigcup _{i\le l}\phi _{n+1}(D_{i})$
has cardinality of continuum by the properties guaranteed by Proposition 2.4. Pick any Borel bijection
$\phi _{n+1}(C \setminus X_{n}) = \phi _{n+1}(C) \setminus \bigcup _{i\le l}\phi _{n+1}(D_{i})$
has cardinality of continuum by the properties guaranteed by Proposition 2.4. Pick any Borel bijection
and define
![]() $\psi _{n+1}$
by the conditions
$\psi _{n+1}$
by the conditions
![]() $\psi _{n+1}|_{D_{i}} = \psi _{n}|_{D_{i}} \cdot g_{i}$
and
$\psi _{n+1}|_{D_{i}} = \psi _{n}|_{D_{i}} \cdot g_{i}$
and
![]() $\psi _{n+1}|_{C \setminus \bigcup _{i\le l}D_{i}} = f \circ \phi _{n+1}$
. As in the base case, the same modification f works for all
$\psi _{n+1}|_{C \setminus \bigcup _{i\le l}D_{i}} = f \circ \phi _{n+1}$
. As in the base case, the same modification f works for all
![]() $E_{n+1}$
-classes
$E_{n+1}$
-classes
![]() $C, C'$
such that
$C, C'$
such that
![]() $\phi _{n+1}(C) \equiv \phi _{n+1}(C')$
, which ensures Borelness of the construction.
$\phi _{n+1}(C) \equiv \phi _{n+1}(C')$
, which ensures Borelness of the construction.
It is now easy to check that
![]() $(X_{n}, E_{n},\psi _{n})_{n}$
is a convergent sequence of partial G-actions, and hence its limit is a free Borel action
$(X_{n}, E_{n},\psi _{n})_{n}$
is a convergent sequence of partial G-actions, and hence its limit is a free Borel action
![]() $G \curvearrowright X$
such that
$G \curvearrowright X$
such that
![]() $E_{G} = E$
.
$E_{G} = E$
.
Remark 2.7. Theorem 2.6 highlights the difference with actions of discrete groups, since a free Borel
![]() $\mathbb {Z}$
-action that preserves a finite measure cannot be generated by a free Borel action of a non-amenable group (see, for example, [Reference Zimmer32, Proposition 4.3.3] or [Reference Jackson, Kechris and Louveau10, Proposition 2.5(ii)]).
$\mathbb {Z}$
-action that preserves a finite measure cannot be generated by a free Borel action of a non-amenable group (see, for example, [Reference Zimmer32, Proposition 4.3.3] or [Reference Jackson, Kechris and Louveau10, Proposition 2.5(ii)]).
However, if we consider hyperfinite equivalence relations without any finite invariant measures, then we do have the analog for
![]() $\mathbb {Z}$
-actions. There exists a unique up to isomorphism, non-smooth, hyperfinite Borel equivalence relation without any finite invariant measures and it can be realized as an orbit equivalence relation of a free action of any infinite countable group [Reference Dougherty, Jackson and Kechris6, Proposition 11.2].
$\mathbb {Z}$
-actions. There exists a unique up to isomorphism, non-smooth, hyperfinite Borel equivalence relation without any finite invariant measures and it can be realized as an orbit equivalence relation of a free action of any infinite countable group [Reference Dougherty, Jackson and Kechris6, Proposition 11.2].
3 Lipschitz maps
Our goal in this section is to prove Theorem 3.12, which shows that any free Borel
![]() $\mathbb {R}^{d}$
-flow is bi-Lipschitz orbit equivalent to a flow with an integer grid. Sections 3.1–3.3 build the necessary tools to construct such an orbit equivalence. Verification of the Lipschitz conditions stated in the lemmas within these sections is straightforward and routine. Therefore, we omit the arguments for brevity.
$\mathbb {R}^{d}$
-flow is bi-Lipschitz orbit equivalent to a flow with an integer grid. Sections 3.1–3.3 build the necessary tools to construct such an orbit equivalence. Verification of the Lipschitz conditions stated in the lemmas within these sections is straightforward and routine. Therefore, we omit the arguments for brevity.
Recall that a map
![]() $f : X \to Y$
between metric spaces
$f : X \to Y$
between metric spaces
![]() $(X,d_{Y})$
and
$(X,d_{Y})$
and
![]() $(Y,d_{Y})$
is K-Lipschitz if
$(Y,d_{Y})$
is K-Lipschitz if
![]() $d_{Y}(f(x_{1}), f(x_{2})) \le K d_{X}(x_{1}, x_{2})$
for all
$d_{Y}(f(x_{1}), f(x_{2})) \le K d_{X}(x_{1}, x_{2})$
for all
![]() $x_{1}, x_{2} \in X$
, and it is
$x_{1}, x_{2} \in X$
, and it is
![]() $(K_{1},K_{2})$
-bi- Lipschitz if f is injective,
$(K_{1},K_{2})$
-bi- Lipschitz if f is injective,
![]() $K_{2}$
-Lipschitz and
$K_{2}$
-Lipschitz and
![]() $f^{-1}$
is
$f^{-1}$
is
![]() $K^{-1}_{1}$
-Lipschitz, which can equivalently be stated as
$K^{-1}_{1}$
-Lipschitz, which can equivalently be stated as
The Lipschitz constant of a Lipschitz map f is the smallest K with respect to which f is K-Lipschitz.
3.1 Linked sets
Given two Lipschitz maps
![]() $ f : A \to A' $
and
$ f : A \to A' $
and
![]() $ g : B \to B' $
that agree on the intersection
$ g : B \to B' $
that agree on the intersection
![]() $ A \cap B $
, the map
$ A \cap B $
, the map
![]() $ f \cup g : A \cup B \to A' \cup B' $
, in general, may not be Lipschitz. The following condition is sufficient to ensure that
$ f \cup g : A \cup B \to A' \cup B' $
, in general, may not be Lipschitz. The following condition is sufficient to ensure that
![]() $ f \cup g $
is Lipschitz with the Lipschitz constant bounded by the maximum of the constants of f and g.
$ f \cup g $
is Lipschitz with the Lipschitz constant bounded by the maximum of the constants of f and g.
Definition 3.1. Let
![]() $ (X, d) $
be a metric space and let
$ (X, d) $
be a metric space and let
![]() $ A, B \subseteq X $
be its subsets. We say that
$ A, B \subseteq X $
be its subsets. We say that
![]() $ A $
and
$ A $
and
![]() $ B $
are linked if, for all
$ B $
are linked if, for all
![]() $ x \in A $
and
$ x \in A $
and
![]() $ y \in B $
, there exists
$ y \in B $
, there exists
![]() $ z \in A \cap B $
such that
$ z \in A \cap B $
such that
![]() $ d(x,y) = d(x,z) + d(z, y) $
.
$ d(x,y) = d(x,z) + d(z, y) $
.
Lemma 3.2. Let
![]() $ (X, d) $
be a metric space, let
$ (X, d) $
be a metric space, let
![]() $ f : A \to A' $
,
$ f : A \to A' $
,
![]() $ g : B \to B' $
be
$ g : B \to B' $
be
![]() $ K $
-Lipschitz maps between subsets of X and suppose that
$ K $
-Lipschitz maps between subsets of X and suppose that
![]() $ f |_{A \cap B} = g |_{A \cap B} $
. If
$ f |_{A \cap B} = g |_{A \cap B} $
. If
![]() $ A $
and
$ A $
and
![]() $ B $
are linked, then
$ B $
are linked, then
![]() $ f \cup g : A \cup B \to A' \cup B' $
is
$ f \cup g : A \cup B \to A' \cup B' $
is
![]() $ K $
-Lipschitz.
$ K $
-Lipschitz.
Recall that a metric space
![]() $(X,d)$
is geodesic if, for all points
$(X,d)$
is geodesic if, for all points
![]() $x, y \in X$
, there exists a geodesic between them—an isometry
$x, y \in X$
, there exists a geodesic between them—an isometry
![]() $\tau : [0, d(x,y)] \to X$
such that
$\tau : [0, d(x,y)] \to X$
such that
![]() $\tau (0) = x$
and
$\tau (0) = x$
and
![]() $\tau (d(x,y)) = y$
. For geodesic metric spaces, closed sets
$\tau (d(x,y)) = y$
. For geodesic metric spaces, closed sets
![]() $ A, B \subseteq X $
are always linked whenever the boundary of one of them is contained in the other. The boundary of a set A will be denoted by
$ A, B \subseteq X $
are always linked whenever the boundary of one of them is contained in the other. The boundary of a set A will be denoted by
![]() $\partial A$
and
$\partial A$
and
![]() $\operatorname *{{\mathrm {int}}} A$
will stand for the interior of A.
$\operatorname *{{\mathrm {int}}} A$
will stand for the interior of A.
Lemma 3.3. Suppose that
![]() $ (X,d) $
is a geodesic metric space. If
$ (X,d) $
is a geodesic metric space. If
![]() $ A, B \subseteq X $
are closed and satisfy
$ A, B \subseteq X $
are closed and satisfy
![]() $ \partial A \subseteq B $
, then
$ \partial A \subseteq B $
, then
![]() $ A $
and
$ A $
and
![]() $ B $
are linked.
$ B $
are linked.
3.2 Inductive step
The following lemma encompasses the inductive step in the construction of the forthcoming Theorem 3.12.
Lemma 3.4. Let
![]() $(X,d)$
be a geodesic metric space and let
$(X,d)$
be a geodesic metric space and let
![]() $A \subseteq X$
be a closed set. Suppose that
$A \subseteq X$
be a closed set. Suppose that
![]() $(A_{i})_{i=1}^{n}$
are pairwise disjoint closed subsets of A and
$(A_{i})_{i=1}^{n}$
are pairwise disjoint closed subsets of A and
![]() $h_{i} : A_{i} \to A_{i}$
are
$h_{i} : A_{i} \to A_{i}$
are
![]() $(K_{1},K_{2})$
-bi-Lipschitz maps such that
$(K_{1},K_{2})$
-bi-Lipschitz maps such that
![]() $h_{i}|_{\partial A_{i}}$
is the identity map for each
$h_{i}|_{\partial A_{i}}$
is the identity map for each
![]() $1 \le i \le n$
. The map
$1 \le i \le n$
. The map
![]() $g : A \to A$
given by
$g : A \to A$
given by
 $$\begin{align*}g(x) = \begin{cases} h_{i}(x) & \textrm{ if}\ x \in A_{i},\\ x & \textrm{otherwise} \end{cases} \end{align*}$$
$$\begin{align*}g(x) = \begin{cases} h_{i}(x) & \textrm{ if}\ x \in A_{i},\\ x & \textrm{otherwise} \end{cases} \end{align*}$$
is
![]() $(K_{1},K_{2})$
-bi-Lipschitz.
$(K_{1},K_{2})$
-bi-Lipschitz.
3.3 Lipschitz shifts
Let
![]() $ (X, \lVert \cdot \rVert ) $
be a normed space and let
$ (X, \lVert \cdot \rVert ) $
be a normed space and let
![]() $A \subseteq X$
be a closed bounded subset. We begin with the following elementary and well-known observation regarding Lipschitz perturbations of the identity map.
$A \subseteq X$
be a closed bounded subset. We begin with the following elementary and well-known observation regarding Lipschitz perturbations of the identity map.
Lemma 3.5. If
![]() $\xi : A \to X$
is a K-Lipschitz map,
$\xi : A \to X$
is a K-Lipschitz map,
![]() $ K < 1$
, then
$ K < 1$
, then
![]() $ A \ni x \mapsto x + \xi (x) \in X$
is
$ A \ni x \mapsto x + \xi (x) \in X$
is
![]() $(1-K, 1+K)$
-bi-Lipschitz.
$(1-K, 1+K)$
-bi-Lipschitz.
For the rest of §3.3, we fix a vector
![]() $ v \in X $
and a real
$ v \in X $
and a real
![]() $ K> \|v\| $
. Let the function
$ K> \|v\| $
. Let the function
![]() $ f_{A, K, v} : A \to X $
be given by
$ f_{A, K, v} : A \to X $
be given by
where
![]() $d(x, \partial A)$
denotes the distance from x to the boundary of A. This function (as well as its variant, which will be introduced shortly) is
$d(x, \partial A)$
denotes the distance from x to the boundary of A. This function (as well as its variant, which will be introduced shortly) is
![]() $(1-K^{-1}\|v\|, 1+K^{-1}\|v\|)$
-bi-Lipschitz. To simplify the notation, we set
$(1-K^{-1}\|v\|, 1+K^{-1}\|v\|)$
-bi-Lipschitz. To simplify the notation, we set
![]() $\alpha ^{+} = 1 + K^{-1}\|v\|$
and
$\alpha ^{+} = 1 + K^{-1}\|v\|$
and
![]() $\alpha ^{-} = 1 - K^{-1}\|v\|$
.
$\alpha ^{-} = 1 - K^{-1}\|v\|$
.
Lemma 3.6. The function
![]() $f_{A,K,v}$
is an
$f_{A,K,v}$
is an
![]() $(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz homeomorphism onto A.
$(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz homeomorphism onto A.
Fix a real
![]() $L> 0$
and let
$L> 0$
and let
![]() $ A^{L} = \{x \in A : d(x, \partial A) \ge L \} $
be the set of those elements that are at least
$ A^{L} = \{x \in A : d(x, \partial A) \ge L \} $
be the set of those elements that are at least
![]() $ L $
units of distance away from the boundary of A.
$ L $
units of distance away from the boundary of A.
Lemma 3.7.
![]() $ f_{A,K,v}|_{A^{L}} = f_{A^{L},K,v} + LK^{-1} v $
and
$ f_{A,K,v}|_{A^{L}} = f_{A^{L},K,v} + LK^{-1} v $
and
![]() $ f_{A,K,v}(A^{L}) = A^{L} + LK^{-1}v $
.
$ f_{A,K,v}(A^{L}) = A^{L} + LK^{-1}v $
.
A truncated shift function
![]() $h_{A,K,v,L} : A \to X$
is defined by
$h_{A,K,v,L} : A \to X$
is defined by
 $$\begin{align*}h_{A,K,v,L}(x) = \begin{cases} f_{A,K,v}(x) & \text{for}\ x \in A \setminus A^{L}, \\ x + LK^{-1} v & \text{for}\ x \in A^{L}. \end{cases} \end{align*}$$
$$\begin{align*}h_{A,K,v,L}(x) = \begin{cases} f_{A,K,v}(x) & \text{for}\ x \in A \setminus A^{L}, \\ x + LK^{-1} v & \text{for}\ x \in A^{L}. \end{cases} \end{align*}$$
Lemma 3.8. The function
![]() $h_{A,K,v,L}$
is an
$h_{A,K,v,L}$
is an
![]() $(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz homeomorphism onto A.
$(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz homeomorphism onto A.
3.4 Lipschitz equivalence to grid flows
The maps
![]() $h_{A,K,v,L}$
can be used to show that any free Borel
$h_{A,K,v,L}$
can be used to show that any free Borel
![]() $\mathbb {R}^{d}$
-flow is bi-Lipschitz equivalent to a flow admitting an integer grid. This is the content of Theorem 3.12, but first we formulate the properties of partial actions needed for the construction. This is an adaption of the so-called unlayered toast construction announced in [Reference Gao, Jackson, Krohne and Seward8]. The proof given in [Reference Marks and Unger18, Appendix A] for
$\mathbb {R}^{d}$
-flow is bi-Lipschitz equivalent to a flow admitting an integer grid. This is the content of Theorem 3.12, but first we formulate the properties of partial actions needed for the construction. This is an adaption of the so-called unlayered toast construction announced in [Reference Gao, Jackson, Krohne and Seward8]. The proof given in [Reference Marks and Unger18, Appendix A] for
![]() $\mathbb {Z}^{d}$
-actions transfers to
$\mathbb {Z}^{d}$
-actions transfers to
![]() $\mathbb {R}^{d}$
-flows.
$\mathbb {R}^{d}$
-flows.
For the rest of the paper, we fix a norm
![]() $\| \cdot \|$
on
$\| \cdot \|$
on
![]() $\mathbb {R}^{d}$
and let
$\mathbb {R}^{d}$
and let
![]() $d(x,y) = \|x-y\|$
be the corresponding metric on
$d(x,y) = \|x-y\|$
be the corresponding metric on
![]() $\mathbb {R}^{d}$
. Recall that
$\mathbb {R}^{d}$
. Recall that
![]() $B_{R}(r) \subseteq \mathbb {R}^{d}$
denotes a closed ball of radius R centered at
$B_{R}(r) \subseteq \mathbb {R}^{d}$
denotes a closed ball of radius R centered at
![]() $r \in \mathbb {R}^{d}$
.
$r \in \mathbb {R}^{d}$
.
Lemma 3.9. Let
![]() $K> 0$
be a positive real. Any free
$K> 0$
be a positive real. Any free
![]() $\mathbb {R}^{d}$
-flow on a standard Borel space X is a limit of a rational convergent sequence of partial actions
$\mathbb {R}^{d}$
-flow on a standard Borel space X is a limit of a rational convergent sequence of partial actions
![]() $(X_{n}, E_{n}, \phi _{n})_{n}$
(see §2.5) such that, for each
$(X_{n}, E_{n}, \phi _{n})_{n}$
(see §2.5) such that, for each
![]() $E_{n}$
-class C:
$E_{n}$
-class C:
-
(1)
 $\phi _{n}(C)$
is a closed and bounded subset of
$\phi _{n}(C)$
is a closed and bounded subset of
 $\mathbb {R}^{d}$
and
$\mathbb {R}^{d}$
and
 $B_{K}(0) \subseteq \phi _{n}(C)$
;
$B_{K}(0) \subseteq \phi _{n}(C)$
; -
(2) the set of
 $E_{m}$
-classes,
$E_{m}$
-classes,
 $m \le n$
, contained in C is finite; and
$m \le n$
, contained in C is finite; and -
(3)
 $d(\phi _{n}(D), \partial \phi _{n}(C)) \ge K$
for any
$d(\phi _{n}(D), \partial \phi _{n}(C)) \ge K$
for any
 $E_{m}$
-class
$E_{m}$
-class
 $D $
such that
$D $
such that
 $D \subseteq C$
.
$D \subseteq C$
.
Before outlining the proof, we need to introduce some notation. Let
![]() $E_{1}, \ldots , E_{n}$
be equivalence relations on
$E_{1}, \ldots , E_{n}$
be equivalence relations on
![]() $X_{1}, \ldots , X_{n}$
, respectively. By
$X_{1}, \ldots , X_{n}$
, respectively. By
![]() $E_{1} \vee \cdots \vee E_{n}$
we mean the equivalence relation E on
$E_{1} \vee \cdots \vee E_{n}$
we mean the equivalence relation E on
![]() $\bigcup _{i \le n} X_{i}$
generated by
$\bigcup _{i \le n} X_{i}$
generated by
![]() $E_{i}$
, that is,
$E_{i}$
, that is,
![]() $x E y$
whenever there exist
$x E y$
whenever there exist
![]() $x_{1}, \ldots , x_{m}$
and, for each
$x_{1}, \ldots , x_{m}$
and, for each
![]() $ 1\le i \le m$
, there exists
$ 1\le i \le m$
, there exists
![]() $ 1 \le j(i) \le n$
such that
$ 1 \le j(i) \le n$
such that
![]() $x_{1} = x$
,
$x_{1} = x$
,
![]() $x_{m} = y$
and
$x_{m} = y$
and
![]() $x_{i} E_{j(i)} x_{i+1}$
for all
$x_{i} E_{j(i)} x_{i+1}$
for all
![]() $1 \le i < m$
.
$1 \le i < m$
.
If E is an equivalence relation on
![]() $Y \subseteq X$
and
$Y \subseteq X$
and
![]() $K> 0$
, we define the relation
$K> 0$
, we define the relation
![]() $E^{+K}$
on
$E^{+K}$
on
![]() $Y^{+K} = \{x \in X : \mathrm {dist}(x, y) \le K \textrm { for some } y \in Y\}$
by
$Y^{+K} = \{x \in X : \mathrm {dist}(x, y) \le K \textrm { for some } y \in Y\}$
by
![]() $x_{1} E^{+K} x_{2}$
if and only if there are
$x_{1} E^{+K} x_{2}$
if and only if there are
![]() $y_{1}, y_{2} \in Y$
such that
$y_{1}, y_{2} \in Y$
such that
![]() $\mathrm {dist}(x_{1},y_{1}) \le K $
,
$\mathrm {dist}(x_{1},y_{1}) \le K $
,
![]() $\mathrm {dist}(x_{2},y_{2}) \le K$
and
$\mathrm {dist}(x_{2},y_{2}) \le K$
and
![]() $y_{1} E y_{2}$
. Note that, in general,
$y_{1} E y_{2}$
. Note that, in general,
![]() $E^{+K}$
may not be an equivalence relation if two E-classes get connected after the ‘fattening’. However,
$E^{+K}$
may not be an equivalence relation if two E-classes get connected after the ‘fattening’. However,
![]() $E^{+K}$
is an equivalence relation if
$E^{+K}$
is an equivalence relation if
![]() $\mathrm {dist}(C_{1},C_{2})> 2K$
holds for all distinct E-classes
$\mathrm {dist}(C_{1},C_{2})> 2K$
holds for all distinct E-classes
![]() $C_{1}, C_{2}$
.
$C_{1}, C_{2}$
.
Proof of Lemma 3.9
One starts with a sufficiently fast-growing sequence of radii
![]() $a_{n}$
(for example,
$a_{n}$
(for example,
![]() $a_{n} = K1000^{n+1}$
is fast enough) and by choosing using [Reference Boykin, Jackson, Gao, Jackson and Zhang3] (see also [Reference Marks and Unger18, Lemma A.2]) a sequence of Borel
$a_{n} = K1000^{n+1}$
is fast enough) and by choosing using [Reference Boykin, Jackson, Gao, Jackson and Zhang3] (see also [Reference Marks and Unger18, Lemma A.2]) a sequence of Borel
![]() $B_{a_{n}}(0)$
-lacunary cross-sections
$B_{a_{n}}(0)$
-lacunary cross-sections
![]() $\mathcal {C}_{n} \subseteq X$
such that
$\mathcal {C}_{n} \subseteq X$
such that
where
![]() $\mathrm {dist}(x, \mathcal {C}_{n}) = \inf \{ \mathrm {dist}(x,c) : c \in \mathcal {C}_{n}\}$
and
$\mathrm {dist}(x, \mathcal {C}_{n}) = \inf \{ \mathrm {dist}(x,c) : c \in \mathcal {C}_{n}\}$
and
![]() $\text { there exists }^{\infty }$
stands for ‘there exist infinitely many’. We may assume, without loss of generality, that cross-sections
$\text { there exists }^{\infty }$
stands for ‘there exist infinitely many’. We may assume, without loss of generality, that cross-sections
![]() $\mathcal {C}_{n}$
are rational in the sense that if
$\mathcal {C}_{n}$
are rational in the sense that if
![]() $c_{1} + r = c_{2}$
for some
$c_{1} + r = c_{2}$
for some
![]() $c_{1}, c_{2} \in \bigcup _{n}\mathcal {C}_{n}$
, then
$c_{1}, c_{2} \in \bigcup _{n}\mathcal {C}_{n}$
, then
![]() $r \in \mathbb {Q}^{d}$
. This can be achieved by moving elements of
$r \in \mathbb {Q}^{d}$
. This can be achieved by moving elements of
![]() $\mathcal {C}_{n}$
by an arbitrarily small amount (see [Reference Slutsky24, Lemma 2.4]), which maintains the property given in equation (1). Rationality of cross-sections guarantees that the sequence of partial actions constructed below is rational.
$\mathcal {C}_{n}$
by an arbitrarily small amount (see [Reference Slutsky24, Lemma 2.4]), which maintains the property given in equation (1). Rationality of cross-sections guarantees that the sequence of partial actions constructed below is rational.
One now defines
![]() $X_{n}$
and
$X_{n}$
and
![]() $E_{n}$
inductively with the base
$E_{n}$
inductively with the base
![]() $X_{0} = \mathcal {C}_{0} + B_{a_{0}/10}(0)$
and with
$X_{0} = \mathcal {C}_{0} + B_{a_{0}/10}(0)$
and with
![]() $x E_{0} y$
if and only if there is
$x E_{0} y$
if and only if there is
![]() $c \in \mathcal {C}_{0}$
such that
$c \in \mathcal {C}_{0}$
such that
![]() $x, y \in c + B_{a_{0}/10}(0)$
. For the inductive step, begin with
$x, y \in c + B_{a_{0}/10}(0)$
. For the inductive step, begin with
![]() $\tilde {X}_{n} = \mathcal {C}_{n} + B_{a_{n}/10}(0) $
and
$\tilde {X}_{n} = \mathcal {C}_{n} + B_{a_{n}/10}(0) $
and
![]() $\tilde {E}_{n}$
being given analogously to the base case:
$\tilde {E}_{n}$
being given analogously to the base case:
![]() $x \tilde {E}_{n} y$
if and only if there is some
$x \tilde {E}_{n} y$
if and only if there is some
![]() $c \in \mathcal {C}_{n}$
such that
$c \in \mathcal {C}_{n}$
such that
![]() $\mathrm {dist}(x,c) \le a_{n}/10$
and
$\mathrm {dist}(x,c) \le a_{n}/10$
and
![]() $\mathrm {dist}(y,c) \le a_{n}/10$
. Set
$\mathrm {dist}(y,c) \le a_{n}/10$
. Set
![]() $E^{\prime }_{n} = \tilde {E}_{n} \vee E^{+K}_{n-1} \vee \cdots \vee E_{0}^{+K}$
and let
$E^{\prime }_{n} = \tilde {E}_{n} \vee E^{+K}_{n-1} \vee \cdots \vee E_{0}^{+K}$
and let
![]() $X^{\prime }_{n} = \tilde {X}_{n} \cup \bigcup _{i=0}^{n-1}X_{i}^{+K}$
be the domain of
$X^{\prime }_{n} = \tilde {X}_{n} \cup \bigcup _{i=0}^{n-1}X_{i}^{+K}$
be the domain of
![]() $E^{\prime }_{n}$
. Finally, let
$E^{\prime }_{n}$
. Finally, let
![]() $X_{n}$
be the
$X_{n}$
be the
![]() $E^{\prime }_{n}$
-saturation of
$E^{\prime }_{n}$
-saturation of
![]() $\tilde {X}_{n}$
, that is,
$\tilde {X}_{n}$
, that is,
![]() $x \in X_{n}$
if and only if there exists
$x \in X_{n}$
if and only if there exists
![]() $y \in \tilde {X}_{n}$
such that
$y \in \tilde {X}_{n}$
such that
![]() $x E^{\prime }_{n} y$
. Put
$x E^{\prime }_{n} y$
. Put
![]() $E_{n} = E^{\prime }_{n}|_{X_{n}}$
.
$E_{n} = E^{\prime }_{n}|_{X_{n}}$
.
An alternative description of an
![]() $E_{n}$
-class is as follows. We start with an
$E_{n}$
-class is as follows. We start with an
![]() $\tilde {E}_{n}$
-class
$\tilde {E}_{n}$
-class
![]() $C_{n}$
and join it first with all
$C_{n}$
and join it first with all
![]() $E^{+K}_{n-1}$
-classes D that intersect
$E^{+K}_{n-1}$
-classes D that intersect
![]() $C_{n}$
. Let the resulting
$C_{n}$
. Let the resulting
![]() $\tilde {E}_{n}\vee E^{+K}_{n-1}$
-class be denoted by
$\tilde {E}_{n}\vee E^{+K}_{n-1}$
-class be denoted by
![]() $C_{n-1}$
. Next, we add all
$C_{n-1}$
. Next, we add all
![]() $E^{+K}_{n-2}$
-classes that intersect
$E^{+K}_{n-2}$
-classes that intersect
![]() $C_{n-2}$
to produce an
$C_{n-2}$
to produce an
![]() $\tilde {E}_{n}\vee E^{+K}_{n-1} \vee E^{+K}_{n-2}$
-class
$\tilde {E}_{n}\vee E^{+K}_{n-1} \vee E^{+K}_{n-2}$
-class
![]() $C_{n-2}$
. The process terminates with an
$C_{n-2}$
. The process terminates with an
![]() $E_{n}$
-class
$E_{n}$
-class
![]() $C_{0}$
.
$C_{0}$
.
It is easy to check inductively that the diameter of any
![]() $E_{n}$
-class C satisfies
$E_{n}$
-class C satisfies
![]() $\mathrm {diam}(C) \le a_{n}/3$
and, therefore,
$\mathrm {diam}(C) \le a_{n}/3$
and, therefore,
![]() $\mathrm {dist}(C_{1}, C_{2}) \ge a_{n}/3 \gg 2K$
for all distinct
$\mathrm {dist}(C_{1}, C_{2}) \ge a_{n}/3 \gg 2K$
for all distinct
![]() $E_{n}$
-classes
$E_{n}$
-classes
![]() $C_{1},C_{2}$
by the lacunarity of
$C_{1},C_{2}$
by the lacunarity of
![]() $\mathcal {C}_{n}$
. The latter shows that
$\mathcal {C}_{n}$
. The latter shows that
![]() $E^{+K}_{n}$
is an equivalence relation on
$E^{+K}_{n}$
is an equivalence relation on
![]() $X_{n}^{+K}$
.
$X_{n}^{+K}$
.
Monotonicity of the sequence
![]() $(X_{n},E_{n})_{n}$
is evident from the construction. Equation (1) is crucial for establishing the fact that
$(X_{n},E_{n})_{n}$
is evident from the construction. Equation (1) is crucial for establishing the fact that
![]() $\bigcup _{n} X_{n} = X$
. Indeed, for each
$\bigcup _{n} X_{n} = X$
. Indeed, for each
![]() $x \in X$
, there exists some n such that
$x \in X$
, there exists some n such that
![]() $\mathrm {dist}(x, \mathcal {C}_{n}) < a_{n}/10$
and thus also
$\mathrm {dist}(x, \mathcal {C}_{n}) < a_{n}/10$
and thus also
![]() $x \in \tilde {X}_{n} \subseteq X_{n}$
.
$x \in \tilde {X}_{n} \subseteq X_{n}$
.
The maps
![]() $\phi _{n} : X_{n} \to \mathbb {R}^{d}$
, needed to specify partial
$\phi _{n} : X_{n} \to \mathbb {R}^{d}$
, needed to specify partial
![]() $\mathbb {R}^{d}$
-actions, are defined by the condition
$\mathbb {R}^{d}$
-actions, are defined by the condition
![]() $\phi _{n}(x)c = x$
for the unique
$\phi _{n}(x)c = x$
for the unique
![]() $c \in \mathcal {C}_{n}$
such that
$c \in \mathcal {C}_{n}$
such that
![]() $c E_{n} x$
. Note that
$c E_{n} x$
. Note that
![]() $d(\phi _{n}(D), \partial \phi _{n}(C)) \ge K$
for any
$d(\phi _{n}(D), \partial \phi _{n}(C)) \ge K$
for any
![]() $E_{m}$
-class D,
$E_{m}$
-class D,
![]() $m < n$
, that is contained in an
$m < n$
, that is contained in an
![]() $E_{n}$
-class C is a consequence of the fact that
$E_{n}$
-class C is a consequence of the fact that
![]() $D^{+K} \subseteq C $
by the construction. Therefore, the convergent sequence of partial actions
$D^{+K} \subseteq C $
by the construction. Therefore, the convergent sequence of partial actions
![]() $(X_{n},E_{n}, \phi _{n})_{n}$
satisfies the desired properties.
$(X_{n},E_{n}, \phi _{n})_{n}$
satisfies the desired properties.
Let
![]() $\mathfrak {F}_{1}$
and
$\mathfrak {F}_{1}$
and
![]() $\mathfrak {F}_{2}$
be free
$\mathfrak {F}_{2}$
be free
![]() $\mathbb {R}^{d}$
-flows on X that generate the same orbit equivalence relation,
$\mathbb {R}^{d}$
-flows on X that generate the same orbit equivalence relation,
![]() $E_{\mathfrak {F}_{1}} = E_{\mathfrak {F}_{2}}$
, and let
$E_{\mathfrak {F}_{1}} = E_{\mathfrak {F}_{2}}$
, and let
![]() $\rho = \rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}} : \mathbb {R}^{d} \times X \to \mathbb {R}^{d}$
be the associated cocycle map, defined for
$\rho = \rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}} : \mathbb {R}^{d} \times X \to \mathbb {R}^{d}$
be the associated cocycle map, defined for
![]() $x \in X$
and
$x \in X$
and
![]() $r \in \mathbb {R}^{d}$
by the condition
$r \in \mathbb {R}^{d}$
by the condition
![]() $x +_{2} r = x +_{1} \rho (r,x)$
. We say that the cocycle
$x +_{2} r = x +_{1} \rho (r,x)$
. We say that the cocycle
![]() $\rho $
is
$\rho $
is
![]() $(K_{1},K_{2})$
-bi-Lipschitz if such is the map
$(K_{1},K_{2})$
-bi-Lipschitz if such is the map
![]() $\rho (\,\cdot \, , x) : \mathbb {R}^{d} \to \mathbb {R}^{d}$
for all
$\rho (\,\cdot \, , x) : \mathbb {R}^{d} \to \mathbb {R}^{d}$
for all
![]() $x \in X$
: that is,
$x \in X$
: that is,
Since
![]() $\rho (r_{2},x) - \rho (r_{1},x) = \rho (r_{2} - r_{1},x +_{1} r_{1})$
, Lipschitz condition (2) for a cocycle can be equivalently and more concisely stated as
$\rho (r_{2},x) - \rho (r_{1},x) = \rho (r_{2} - r_{1},x +_{1} r_{1})$
, Lipschitz condition (2) for a cocycle can be equivalently and more concisely stated as
Remark 3.10. Note that cocycles
![]() $\rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}}$
and
$\rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}}$
and
![]() $\rho _{\mathfrak {F}_{2}, \mathfrak {F}_{1}}$
are connected via the identities
$\rho _{\mathfrak {F}_{2}, \mathfrak {F}_{1}}$
are connected via the identities
In particular, if
![]() $\rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}}$
is
$\rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}}$
is
![]() $(K_{1},K_{2})$
-bi-Lipschitz, then
$(K_{1},K_{2})$
-bi-Lipschitz, then
![]() $\rho _{\mathfrak {F}_{2}, \mathfrak {F}_{1}}$
is
$\rho _{\mathfrak {F}_{2}, \mathfrak {F}_{1}}$
is
![]() $(K_{2}^{-1}, K_{1}^{-1})$
-bi-Lipschitz.
$(K_{2}^{-1}, K_{1}^{-1})$
-bi-Lipschitz.
Definition 3.11. Let
![]() $\mathfrak {F}$
be a free
$\mathfrak {F}$
be a free
![]() $\mathbb {R}^{d}$
-flow on X. An integer grid for the flow
$\mathbb {R}^{d}$
-flow on X. An integer grid for the flow
![]() $\mathfrak {F}$
is a
$\mathfrak {F}$
is a
![]() $\mathbb {Z}^{d}$
-invariant Borel subset
$\mathbb {Z}^{d}$
-invariant Borel subset
![]() $Z \subseteq X$
whose intersection with each orbit of the flow is a
$Z \subseteq X$
whose intersection with each orbit of the flow is a
![]() $\mathbb {Z}^{d}$
-orbit. In other words,
$\mathbb {Z}^{d}$
-orbit. In other words,
![]() $Z + \mathbb {R}^{d} = X$
,
$Z + \mathbb {R}^{d} = X$
,
![]() $Z + \mathbb {Z}^{d} = Z$
and
$Z + \mathbb {Z}^{d} = Z$
and
![]() $z_{1}+ \mathbb {Z}^{d} = z_{2} + \mathbb {Z}^{d}$
for all
$z_{1}+ \mathbb {Z}^{d} = z_{2} + \mathbb {Z}^{d}$
for all
![]() $z_{1}, z_{2} \in Z$
such that
$z_{1}, z_{2} \in Z$
such that
![]() $z_{1}E_{\mathfrak {F}}z_{2}$
.
$z_{1}E_{\mathfrak {F}}z_{2}$
.
Not every flow admits an integer grid, but, as the following theorem shows, each flow is bi-Lipschitz equivalent to the one that does.
Theorem 3.12. Let
![]() $\mathfrak {F}_{1}$
be a free Borel
$\mathfrak {F}_{1}$
be a free Borel
![]() $\mathbb {R}^{d}$
-flow on X. For any
$\mathbb {R}^{d}$
-flow on X. For any
![]() $\alpha> 1$
, there exists a free Borel
$\alpha> 1$
, there exists a free Borel
![]() $\mathbb {R}^{d}$
-flow
$\mathbb {R}^{d}$
-flow
![]() $\mathfrak {F}_{2}$
on X that admits an integer grid, induces the same orbit equivalence as does
$\mathfrak {F}_{2}$
on X that admits an integer grid, induces the same orbit equivalence as does
![]() $\mathfrak {F}_{1}$
, that is,
$\mathfrak {F}_{1}$
, that is,
![]() $E_{\mathfrak {F}_{1}} = E_{\mathfrak {F}_{2}}$
, and whose associated cocycle
$E_{\mathfrak {F}_{1}} = E_{\mathfrak {F}_{2}}$
, and whose associated cocycle
![]() $\rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}}$
is
$\rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}}$
is
![]() $(\alpha ^{-1}, \alpha )$
-bi-Lipschitz.
$(\alpha ^{-1}, \alpha )$
-bi-Lipschitz.
Proof. Let R be so big that the ball
![]() $B_{R}(0) \subseteq \mathbb {R}^{d}$
satisfies
$B_{R}(0) \subseteq \mathbb {R}^{d}$
satisfies
![]() $\mathbb {Z}^{d} + B_{R}(0) = \mathbb {R}^{d}$
. Choose
$\mathbb {Z}^{d} + B_{R}(0) = \mathbb {R}^{d}$
. Choose
![]() $K> 0$
large enough to ensure that
$K> 0$
large enough to ensure that
![]() $\alpha ^{-} = 1 - K^{-1}R> \alpha ^{-1}$
and, therefore, also that
$\alpha ^{-} = 1 - K^{-1}R> \alpha ^{-1}$
and, therefore, also that
![]() $\alpha ^{+} = 1 + K^{-1}R < \alpha $
. Let
$\alpha ^{+} = 1 + K^{-1}R < \alpha $
. Let
![]() $(X_{n}, E_{n}, \phi _{n})_{n}$
be a rational convergent sequence of partial actions produced by Lemma 3.9 for the chosen value of K. For an
$(X_{n}, E_{n}, \phi _{n})_{n}$
be a rational convergent sequence of partial actions produced by Lemma 3.9 for the chosen value of K. For an
![]() $E_{n}$
-class C, let
$E_{n}$
-class C, let
![]() $C'$
denote the collection of all
$C'$
denote the collection of all
![]() $x \in C$
that are at least K-distance away from the boundary of C: that is,
$x \in C$
that are at least K-distance away from the boundary of C: that is,
If D is an
![]() $E_{m}$
-class such that
$E_{m}$
-class such that
![]() $D \subseteq C$
, then item (3) of Lemma 3.9 guarantees the inclusion
$D \subseteq C$
, then item (3) of Lemma 3.9 guarantees the inclusion
![]() $D \subseteq C'$
. Let
$D \subseteq C'$
. Let
![]() $X^{\prime }_{n} = \bigcup C'$
, where the union is taken over all
$X^{\prime }_{n} = \bigcup C'$
, where the union is taken over all
![]() $E_{n}$
-classes C, and set
$E_{n}$
-classes C, and set
![]() $E_{n}' = E_{n}|_{X^{\prime }_{n}}$
,
$E_{n}' = E_{n}|_{X^{\prime }_{n}}$
,
![]() $\phi ^{\prime }_{n}= \phi _{n}|_{X^{\prime }_{n}}$
. Note that
$\phi ^{\prime }_{n}= \phi _{n}|_{X^{\prime }_{n}}$
. Note that
![]() $(X^{\prime }_{n}, E^{\prime }_{n}, \phi ^{\prime }_{n})_{n}$
is a rational convergent sequence of partial actions whose limit is the flow
$(X^{\prime }_{n}, E^{\prime }_{n}, \phi ^{\prime }_{n})_{n}$
is a rational convergent sequence of partial actions whose limit is the flow
![]() $\mathfrak {F}_{1}$
. The flow
$\mathfrak {F}_{1}$
. The flow
![]() $\mathfrak {F}_{2}$
will be constructed as the limit of partial actions
$\mathfrak {F}_{2}$
will be constructed as the limit of partial actions
![]() $(X^{\prime }_{n},E^{\prime }_{n},\psi _{n})$
, where maps
$(X^{\prime }_{n},E^{\prime }_{n},\psi _{n})$
, where maps
![]() $\psi _{n}$
will be defined inductively and will satisfy
$\psi _{n}$
will be defined inductively and will satisfy
![]() $\psi _{n}(C') = \phi _{n}(C')$
for all
$\psi _{n}(C') = \phi _{n}(C')$
for all
![]() $E_{n}$
-classes C. The sets
$E_{n}$
-classes C. The sets
![]() $Z_{n} = \psi _{n}^{-1}(\mathbb {Z}^{d})$
will satisfy
$Z_{n} = \psi _{n}^{-1}(\mathbb {Z}^{d})$
will satisfy
![]() $Z_{m}\cap X^{\prime }_{n} \subseteq Z_{n}$
for
$Z_{m}\cap X^{\prime }_{n} \subseteq Z_{n}$
for
![]() $m \le n$
, and
$m \le n$
, and
![]() $Z = \bigcup _{n}Z_{n}$
will be an integer grid for
$Z = \bigcup _{n}Z_{n}$
will be an integer grid for
![]() $\mathfrak {F}_{2}$
.
$\mathfrak {F}_{2}$
.
For the base of the construction, set
![]() $\psi _{0} = \phi ^{\prime }_{0}$
and
$\psi _{0} = \phi ^{\prime }_{0}$
and
![]() $Z_{0} = \psi _{0}^{-1}(\mathbb {Z}^{d})$
. Next, consider a typical
$Z_{0} = \psi _{0}^{-1}(\mathbb {Z}^{d})$
. Next, consider a typical
![]() $E_{1}$
-class C with
$E_{1}$
-class C with
![]() $D_{1}, \ldots , D_{l}$
being a complete list of
$D_{1}, \ldots , D_{l}$
being a complete list of
![]() $E_{0}$
-classes contained in it (see Figure 1). Consider the set
$E_{0}$
-classes contained in it (see Figure 1). Consider the set
![]() $\tilde {Z}_{C'} = \phi _{1}^{-1}(\mathbb {Z}^{d}) \cap C'$
, which is the integer grid inside
$\tilde {Z}_{C'} = \phi _{1}^{-1}(\mathbb {Z}^{d}) \cap C'$
, which is the integer grid inside
![]() $C'$
(marked by dots in Figure 1). Each of the
$C'$
(marked by dots in Figure 1). Each of the
![]() $D_{i}$
-classes comes with the grid
$D_{i}$
-classes comes with the grid
![]() $\tilde {Z}_{D^{\prime }_{i}} = \psi _{0}^{-1}(\mathbb {Z}^{d})\cap D^{\prime }_{i}$
constructed at the previous stage (depicted by crosses in Figure 1). The coherence condition for partial actions guarantees existence of some
$\tilde {Z}_{D^{\prime }_{i}} = \psi _{0}^{-1}(\mathbb {Z}^{d})\cap D^{\prime }_{i}$
constructed at the previous stage (depicted by crosses in Figure 1). The coherence condition for partial actions guarantees existence of some
![]() $s_{i} \in \mathbb {R}^{d}$
,
$s_{i} \in \mathbb {R}^{d}$
,
![]() $i \le l$
, such that
$i \le l$
, such that

Figure 1 Construction of the integer grid.
In general, the grid
![]() $\tilde {Z}_{C'}$
does not contain
$\tilde {Z}_{C'}$
does not contain
![]() $\tilde {Z}_{D^{\prime }_{i}} $
, but, for each
$\tilde {Z}_{D^{\prime }_{i}} $
, but, for each
![]() $i \le l$
, we can find a vector
$i \le l$
, we can find a vector
![]() $v_{i} \in \mathbb {R}^{d}$
of norm
$v_{i} \in \mathbb {R}^{d}$
of norm
![]() $\|v_{i}\|\le R$
such that
$\|v_{i}\|\le R$
such that
![]() $\tilde {Z}_{D^{\prime }_{i}} +_{1} v_{i} \subseteq \tilde {Z}_{C'}$
. More precisely, we take for
$\tilde {Z}_{D^{\prime }_{i}} +_{1} v_{i} \subseteq \tilde {Z}_{C'}$
. More precisely, we take for
![]() $v_{i}$
any vector in
$v_{i}$
any vector in
![]() $B_{R}(0)$
such that
$B_{R}(0)$
such that
![]() $s_{i} + v_{i} \in \mathbb {Z}^{d}$
, which exists by the choice of R. Let
$s_{i} + v_{i} \in \mathbb {Z}^{d}$
, which exists by the choice of R. Let
![]() $h_{i} : \phi _{1}(D_{i}) \to \phi _{1}(D_{i})$
be the function
$h_{i} : \phi _{1}(D_{i}) \to \phi _{1}(D_{i})$
be the function
![]() $h_{\phi _{1}(D_{i}), K, v_{i}, K}$
, which is
$h_{\phi _{1}(D_{i}), K, v_{i}, K}$
, which is
![]() $(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz by Lemma 3.8. Finally, define
$(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz by Lemma 3.8. Finally, define
![]() $g_{1} : \phi _{1}(C') \to \phi _{1}(C')$
to be
$g_{1} : \phi _{1}(C') \to \phi _{1}(C')$
to be
 $$\begin{align*}g_{1}(r) = \begin{cases} h_{i}(r) & \textrm{if}\ r \in \phi_{1}(D_{i}),\\ r & \textrm{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}g_{1}(r) = \begin{cases} h_{i}(r) & \textrm{if}\ r \in \phi_{1}(D_{i}),\\ r & \textrm{otherwise}. \end{cases} \end{align*}$$
Lemma 3.4 has been tailored specifically to show that
![]() $g_{1}$
is
$g_{1}$
is
![]() $(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz. We set
$(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz. We set
![]() $\psi _{1}|_{C'} = g_{1} \circ \phi _{1}|_{C'}$
. Note that
$\psi _{1}|_{C'} = g_{1} \circ \phi _{1}|_{C'}$
. Note that
 $$ \begin{align}\begin{aligned} \psi_{1}(D^{\prime}_{i}) &= g_{1} \circ \phi_{1}(D^{\prime}_{i}) = h_{i} \circ \phi_{1}(D^{\prime}_{i}) = \phi_{1}(D^{\prime}_{i}) + KK^{-1}v_{i} \\ &= \phi_{0}(D^{\prime}_{i}) + s_{i} + v_{i} = \psi_{0}(D^{\prime}_{i}) + s_{i} + v_{i},\end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \psi_{1}(D^{\prime}_{i}) &= g_{1} \circ \phi_{1}(D^{\prime}_{i}) = h_{i} \circ \phi_{1}(D^{\prime}_{i}) = \phi_{1}(D^{\prime}_{i}) + KK^{-1}v_{i} \\ &= \phi_{0}(D^{\prime}_{i}) + s_{i} + v_{i} = \psi_{0}(D^{\prime}_{i}) + s_{i} + v_{i},\end{aligned} \end{align} $$
which validates coherence and, in view of
![]() $s_{i} + v_{i} \in \mathbb {Z}^{d}$
, gives
$s_{i} + v_{i} \in \mathbb {Z}^{d}$
, gives
![]() $\psi ^{-1}_{1}(\mathbb {Z}^{d}) \cap D^{\prime }_{i} = \psi _{0}^{-1}(\mathbb {Z}^{d}) \cap D^{\prime }_{i} $
for all
$\psi ^{-1}_{1}(\mathbb {Z}^{d}) \cap D^{\prime }_{i} = \psi _{0}^{-1}(\mathbb {Z}^{d}) \cap D^{\prime }_{i} $
for all
![]() $i \le l$
.
$i \le l$
.
Although we have provided the definition of
![]() $\psi _{1}$
on a single
$\psi _{1}$
on a single
![]() $E_{1}$
-class C, the same construction can be done in a Borel way across all
$E_{1}$
-class C, the same construction can be done in a Borel way across all
![]() $E_{1}$
-classes C using rationality of the sequence of partial actions in the same way as we did in Theorem 2.6. If we let
$E_{1}$
-classes C using rationality of the sequence of partial actions in the same way as we did in Theorem 2.6. If we let
![]() $Z_{1} = \psi _{1}^{-1}(\mathbb {Z}^{d})$
, then
$Z_{1} = \psi _{1}^{-1}(\mathbb {Z}^{d})$
, then
![]() $Z_{0} \cap X_{1} \subseteq Z_{1}$
by equation (4).
$Z_{0} \cap X_{1} \subseteq Z_{1}$
by equation (4).
The general inductive step is analogous. Suppose that we have constructed maps
![]() $\psi _{k}$
for
$\psi _{k}$
for
![]() $k \le n$
. An
$k \le n$
. An
![]() $E_{n+1}$
-class C contains finitely many subclasses
$E_{n+1}$
-class C contains finitely many subclasses
![]() $D_{1}, \ldots , D_{l}$
, where
$D_{1}, \ldots , D_{l}$
, where
![]() $D_{i}$
is an
$D_{i}$
is an
![]() $E_{m_{i}}$
-class,
$E_{m_{i}}$
-class,
![]() $m_{i} < n$
and no
$m_{i} < n$
and no
![]() $D_{i}$
is contained in a bigger
$D_{i}$
is contained in a bigger
![]() $E_{m}$
-class for some
$E_{m}$
-class for some
![]() $m_{i} < m < n$
. By coherence and the inductive assumption, there exist
$m_{i} < m < n$
. By coherence and the inductive assumption, there exist
![]() $s_{i} \in \mathbb {R}^{d}$
,
$s_{i} \in \mathbb {R}^{d}$
,
![]() $i \le l$
, such that
$i \le l$
, such that
Choose vectors
![]() $v_{i} \in B_{R}(0)$
to satisfy
$v_{i} \in B_{R}(0)$
to satisfy
![]() $s_{i} + v_{i} \in \mathbb {Z}^{d}$
, set
$s_{i} + v_{i} \in \mathbb {Z}^{d}$
, set
![]() $h_{i} : \phi _{n+1}(D_{i}) \to \phi _{n+1}(D_{i})$
to be
$h_{i} : \phi _{n+1}(D_{i}) \to \phi _{n+1}(D_{i})$
to be
![]() $h_{\phi _{n+1}(D_{i}), K, v_{i}, K}$
and define an
$h_{\phi _{n+1}(D_{i}), K, v_{i}, K}$
and define an
![]() $(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz function
$(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz function
![]() $g_{n+1}$
by
$g_{n+1}$
by
 $$\begin{align*}g_{n+1}(r) = \begin{cases} h_{i}(r) & \textrm{if}\ r \in \phi_{n+1}(D_{i}),\\ r & \textrm{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}g_{n+1}(r) = \begin{cases} h_{i}(r) & \textrm{if}\ r \in \phi_{n+1}(D_{i}),\\ r & \textrm{otherwise}. \end{cases} \end{align*}$$
Finally, set
![]() $\psi _{n+1}|_{C'} = g_{n+1} \circ \phi _{n+1}|_{C'} $
and extend this definition to a Borel map
$\psi _{n+1}|_{C'} = g_{n+1} \circ \phi _{n+1}|_{C'} $
and extend this definition to a Borel map
![]() $\psi _{n+1} : X^{\prime }_{n+1} \to \mathbb {R}^{d}$
using the rationality of the sequence of partial actions. Coherence of the maps
$\psi _{n+1} : X^{\prime }_{n+1} \to \mathbb {R}^{d}$
using the rationality of the sequence of partial actions. Coherence of the maps
![]() $(\psi _{k})_{k \le n+1}$
and the inclusion
$(\psi _{k})_{k \le n+1}$
and the inclusion
![]() $Z_{m}\cap X^{\prime }_{n+1} \subseteq Z_{n+1}$
for
$Z_{m}\cap X^{\prime }_{n+1} \subseteq Z_{n+1}$
for
![]() $m \le n+1$
follow from the analog of equation (4).
$m \le n+1$
follow from the analog of equation (4).
It remains to check the bi-Lipschitz condition for the resulting cocycle
![]() $\rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}}$
. It is easier to work with the cocycle
$\rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}}$
. It is easier to work with the cocycle
![]() $\rho _{\mathfrak {F}_{2}, \mathfrak {F}_{1}}$
, which, for
$\rho _{\mathfrak {F}_{2}, \mathfrak {F}_{1}}$
, which, for
![]() $x, x+r \in X^{\prime }_{n}$
, satisfies
$x, x+r \in X^{\prime }_{n}$
, satisfies
and is therefore
![]() $(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz, because so is
$(\alpha ^{-}, \alpha ^{+})$
-bi-Lipschitz, because so is
![]() $g_{n}$
. Hence,
$g_{n}$
. Hence,
![]() $\rho _{\mathfrak {F}_{2}, \mathfrak {F}_{1}}$
is also
$\rho _{\mathfrak {F}_{2}, \mathfrak {F}_{1}}$
is also
![]() $(\alpha ^{-1}, \alpha )$
-bi-Lipschitz, because
$(\alpha ^{-1}, \alpha )$
-bi-Lipschitz, because
![]() $\alpha ^{-1} < \alpha ^{-} < \alpha ^{+} < \alpha $
by the choice of K. Finally, we apply Remark 3.10 to conclude that
$\alpha ^{-1} < \alpha ^{-} < \alpha ^{+} < \alpha $
by the choice of K. Finally, we apply Remark 3.10 to conclude that
![]() $\rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}}$
is also
$\rho _{\mathfrak {F}_{1}, \mathfrak {F}_{2}}$
is also
![]() $(\alpha ^{-1}, \alpha )$
-bi-Lipschitz.
$(\alpha ^{-1}, \alpha )$
-bi-Lipschitz.
By restricting the action of
![]() $\mathfrak {F}_{2}$
onto the integer grid Z, we get the following corollary.
$\mathfrak {F}_{2}$
onto the integer grid Z, we get the following corollary.
Corollary 3.13. Let
![]() $\mathfrak {F}$
be a free Borel
$\mathfrak {F}$
be a free Borel
![]() $\mathbb {R}^{d}$
-flow on X. For any
$\mathbb {R}^{d}$
-flow on X. For any
![]() $\alpha> 1$
, there exist a cross-section
$\alpha> 1$
, there exist a cross-section
![]() $Z \subseteq X$
and a free
$Z \subseteq X$
and a free
![]() $\mathbb {Z}^{d}$
-action T on Z such that the cocycle
$\mathbb {Z}^{d}$
-action T on Z such that the cocycle
![]() $\rho = \rho _{\mathfrak {F}, T}: \mathbb {Z}^{d} \times X \to \mathbb {R}^{d}$
given by
$\rho = \rho _{\mathfrak {F}, T}: \mathbb {Z}^{d} \times X \to \mathbb {R}^{d}$
given by
![]() $T_{n}x = x + \rho (n,x)$
is
$T_{n}x = x + \rho (n,x)$
is
![]() $(\alpha ^{-1}, \alpha )$
-bi-Lipschitz.
$(\alpha ^{-1}, \alpha )$
-bi-Lipschitz.
4 Special representation theorem
The main goal of this section is to formulate and prove a Borel version of Katok’s special representation theorem [Reference Katok12] that connects free
![]() $\mathbb {R}^{d}$
-flows with free
$\mathbb {R}^{d}$
-flows with free
![]() $\mathbb {Z}^{d}$
-actions. We have already done most of the work in proving Theorem 3.12, and it is now a matter of defining special representations in the Borel context and connecting them to our earlier set-up.
$\mathbb {Z}^{d}$
-actions. We have already done most of the work in proving Theorem 3.12, and it is now a matter of defining special representations in the Borel context and connecting them to our earlier set-up.
4.1 Cocycles
Given a Borel action
![]() $G \curvearrowright X$
, a (Borel) cocycle with values in a group H is a (Borel) map
$G \curvearrowright X$
, a (Borel) cocycle with values in a group H is a (Borel) map
![]() $\rho : G \times X \to H$
that satisfies the cocycle identity: that is,
$\rho : G \times X \to H$
that satisfies the cocycle identity: that is,
We are primarily concerned with the Abelian groups
![]() $\mathbb {Z}^{d}$
and
$\mathbb {Z}^{d}$
and
![]() $\mathbb {R}^{d}$
in this section, so the cocycle identity will be written additively. A cocycle
$\mathbb {R}^{d}$
in this section, so the cocycle identity will be written additively. A cocycle
![]() $\rho : G \times X \to H$
is said to be injective if
$\rho : G \times X \to H$
is said to be injective if
![]() $\rho (g,x) \ne e_{H}$
for all
$\rho (g,x) \ne e_{H}$
for all
![]() $g \ne e_{G}$
and all
$g \ne e_{G}$
and all
![]() $x \in X$
, where
$x \in X$
, where
![]() $e_{G}$
and
$e_{G}$
and
![]() $e_{H}$
are the identity elements of the corresponding groups. Furthermore, suppose that the groups G and H are locally compact. We say that
$e_{H}$
are the identity elements of the corresponding groups. Furthermore, suppose that the groups G and H are locally compact. We say that
![]() $\rho $
escapes to infinity if, for all
$\rho $
escapes to infinity if, for all
![]() $x \in X$
,
$x \in X$
,
![]() $\lim _{g \to \infty }\rho (g,x) = +\infty $
in the sense that, for any compact
$\lim _{g \to \infty }\rho (g,x) = +\infty $
in the sense that, for any compact
![]() $K_{H} \subseteq H$
, there exists a compact
$K_{H} \subseteq H$
, there exists a compact
![]() $K_{G} \subseteq G$
such that
$K_{G} \subseteq G$
such that
![]() $\rho (g,x) \not \in K_{H}$
whenever
$\rho (g,x) \not \in K_{H}$
whenever
![]() $g \not \in K_{G}$
.
$g \not \in K_{G}$
.
Example 4.1. Suppose that
![]() $a_{H} : H \curvearrowright X$
and
$a_{H} : H \curvearrowright X$
and
![]() $a_{G} : G \curvearrowright Y$
,
$a_{G} : G \curvearrowright Y$
,
![]() $Y \subseteq X$
, are free actions of groups G and H on standard Borel spaces, and suppose that we have containment of orbit equivalence relations
$Y \subseteq X$
, are free actions of groups G and H on standard Borel spaces, and suppose that we have containment of orbit equivalence relations
![]() $E_{G} \subseteq E_{H}$
. For each
$E_{G} \subseteq E_{H}$
. For each
![]() $y \in Y$
and
$y \in Y$
and
![]() $g \in G$
, there exists a unique
$g \in G$
, there exists a unique
![]() $\rho _{a_{H},a_{G}}(g,y) \in H$
such that
$\rho _{a_{H},a_{G}}(g,y) \in H$
such that
![]() $a_{H}(\rho _{a_{H},a_{G}}(g,y),y) = a_{G}(g,y) $
. The map
$a_{H}(\rho _{a_{H},a_{G}}(g,y),y) = a_{G}(g,y) $
. The map
![]() $(g,y) \mapsto \rho _{a_{H},a_{G}}(g,y)$
is an injective Borel cocycle. We have already encountered two instances of this idea in §3.4.
$(g,y) \mapsto \rho _{a_{H},a_{G}}(g,y)$
is an injective Borel cocycle. We have already encountered two instances of this idea in §3.4.
4.2 Flow under a function
Borel
![]() $ \mathbb {R} $
-flows and
$ \mathbb {R} $
-flows and
![]() $ \mathbb {Z} $
-actions are tightly connected through the ‘flow under a function’ construction. Let
$ \mathbb {Z} $
-actions are tightly connected through the ‘flow under a function’ construction. Let
![]() $ T : Z \to Z $
be a free Borel automorphism of a standard Borel space and let
$ T : Z \to Z $
be a free Borel automorphism of a standard Borel space and let
![]() $ f : Z \to \mathbb {R}^{>0} $
be a positive Borel function. There is a natural definition of a flow
$ f : Z \to \mathbb {R}^{>0} $
be a positive Borel function. There is a natural definition of a flow
![]() $ \mathfrak {F} : \mathbb {R} \curvearrowright X $
on the space
$ \mathfrak {F} : \mathbb {R} \curvearrowright X $
on the space
![]() $ X = \{ (z, t) : z \in Z, 0 \le t < f(z)\} $
under the graph of
$ X = \{ (z, t) : z \in Z, 0 \le t < f(z)\} $
under the graph of
![]() $ f $
. The action
$ f $
. The action
![]() $ (z, t) + r $
for a positive
$ (z, t) + r $
for a positive
![]() $ r $
is defined by shifting the point
$ r $
is defined by shifting the point
![]() $ (z,t) $
by
$ (z,t) $
by
![]() $ r $
units upwards until the graph of
$ r $
units upwards until the graph of
![]() $ f $
is reached, jumping to the point
$ f $
is reached, jumping to the point
![]() $(Tz, 0)$
and then continuing to flow upwards until the graph of f at
$(Tz, 0)$
and then continuing to flow upwards until the graph of f at
![]() $Tz$
is reached, etc. More formally,
$Tz$
is reached, etc. More formally,
 $$ \begin{align*} (z, t) + r = \bigg(T^{k}z, t + r - \sum\limits_{i=0}^{k-1}f(T^{i}z)\bigg) \end{align*} $$
$$ \begin{align*} (z, t) + r = \bigg(T^{k}z, t + r - \sum\limits_{i=0}^{k-1}f(T^{i}z)\bigg) \end{align*} $$
for the unique
![]() $ k \ge 0 $
such that
$ k \ge 0 $
such that
![]() $ \sum _{i=0}^{k-1}f(T^{i}z) \le t + r < \sum _{i=0}^{k}f(T^{i}z) $
. For
$ \sum _{i=0}^{k-1}f(T^{i}z) \le t + r < \sum _{i=0}^{k}f(T^{i}z) $
. For
![]() $ r \le 0 $
, the action is defined by ‘flowing backward’, that is,
$ r \le 0 $
, the action is defined by ‘flowing backward’, that is,
 $$ \begin{align*} (z, t) + r = \bigg(T^{-k}z, t + r + \sum\limits_{i=1}^{k}f(T^{-i}z)\bigg) \end{align*} $$
$$ \begin{align*} (z, t) + r = \bigg(T^{-k}z, t + r + \sum\limits_{i=1}^{k}f(T^{-i}z)\bigg) \end{align*} $$
for
![]() $ k \ge 0 $
such that
$ k \ge 0 $
such that
![]() $ 0 \le t + r + \sum \nolimits _{i=1}^{k}f(T^{-i}z) < f(T^{-k}z) $
. The action is well defined provided that the fibers within the orbits of
$ 0 \le t + r + \sum \nolimits _{i=1}^{k}f(T^{-i}z) < f(T^{-k}z) $
. The action is well defined provided that the fibers within the orbits of
![]() $ T $
have infinite cumulative lengths: that is,
$ T $
have infinite cumulative lengths: that is,
 $$ \begin{align} \sum_{i=0}^{\infty}f(T^{i}z) = +\infty\quad \textrm{and} \quad \sum_{i=0}^{\infty}f(T^{-i}z) = +\infty\quad \textrm{for all } z \in Z. \end{align} $$
$$ \begin{align} \sum_{i=0}^{\infty}f(T^{i}z) = +\infty\quad \textrm{and} \quad \sum_{i=0}^{\infty}f(T^{-i}z) = +\infty\quad \textrm{for all } z \in Z. \end{align} $$
The appealing geometric picture of the ‘flow under a function’ does not generalize to higher dimensions, but it admits an interpretation as the so-called special flow construction suggested in [Reference Katok12].
4.3 Special flows
Let T be a free
![]() $\mathbb {Z}^{d}$
-action on a standard Borel space Z and let
$\mathbb {Z}^{d}$
-action on a standard Borel space Z and let
![]() $\rho : \mathbb {Z}^{d} \times Z \to \mathbb {R}^{d}$
be a Borel cocycle. One can construct a
$\rho : \mathbb {Z}^{d} \times Z \to \mathbb {R}^{d}$
be a Borel cocycle. One can construct a
![]() $\mathbb {Z}^{d}$
-action
$\mathbb {Z}^{d}$
-action
![]() $\hat {T}$
, the so-called principal
$\hat {T}$
, the so-called principal
![]() $\mathbb {R}^{d}$
-extension, defined on
$\mathbb {R}^{d}$
-extension, defined on
![]() $Z \times \mathbb {R}^{d}$
via
$Z \times \mathbb {R}^{d}$
via
![]() $\hat {T}_{n}(z, r) = (T_{n}z, r + \rho (n,z))$
. An easy application of the cocycle identity verifies axioms of the action. Although the action T will, typically, have complicated dynamics, the action
$\hat {T}_{n}(z, r) = (T_{n}z, r + \rho (n,z))$
. An easy application of the cocycle identity verifies axioms of the action. Although the action T will, typically, have complicated dynamics, the action
![]() $\hat {T}$
admits a Borel transversal as long as the cocycle
$\hat {T}$
admits a Borel transversal as long as the cocycle
![]() $\rho $
escapes to infinity.
$\rho $
escapes to infinity.
Lemma 4.2. If the cocycle
![]() $\rho $
satisfies
$\rho $
satisfies
![]() $\lim _{n \to \infty }\|\rho (n,z)\| = +\infty $
for all
$\lim _{n \to \infty }\|\rho (n,z)\| = +\infty $
for all
![]() $z \in Z$
, then the action
$z \in Z$
, then the action
![]() $\hat {T}$
has a Borel transversal.
$\hat {T}$
has a Borel transversal.
Proof. Let
![]() $Y_{k} = \{ (z, r) \in Z \times \mathbb {R}^{d} : \|r\| \le k\}$
. We claim that each orbit of
$Y_{k} = \{ (z, r) \in Z \times \mathbb {R}^{d} : \|r\| \le k\}$
. We claim that each orbit of
![]() $\hat {T}$
intersects
$\hat {T}$
intersects
![]() $Y_{k}$
in a finite (possibly empty) set. Indeed, cocycle values escaping to infinity yield, for any
$Y_{k}$
in a finite (possibly empty) set. Indeed, cocycle values escaping to infinity yield, for any
![]() $(z,r) \in Z \times \mathbb {R}^{d}$
, a number N so large that
$(z,r) \in Z \times \mathbb {R}^{d}$
, a number N so large that
![]() $\|r + \rho (n,z)\|> k$
whenever
$\|r + \rho (n,z)\|> k$
whenever
![]() $\|n\| \ge N$
. In particular,
$\|n\| \ge N$
. In particular,
![]() $\|n\| \ge N$
implies that
$\|n\| \ge N$
implies that
![]() $\hat {T}_{n}(z,r) = (T_{n}z, r + \rho (n,z)) \not \in Y_{k}$
. Hence, the intersection of the orbit of
$\hat {T}_{n}(z,r) = (T_{n}z, r + \rho (n,z)) \not \in Y_{k}$
. Hence, the intersection of the orbit of
![]() $(z,r)$
with
$(z,r)$
with
![]() $Y_{k}$
is finite.
$Y_{k}$
is finite.
Set
![]() $Y = \bigsqcup _{k \in \mathbb {N}} (Y_{k} \setminus \bigcup _{n \in \mathbb {Z}^{d}} \hat {T}_{n}Y_{k-1})$
. Each orbit of
$Y = \bigsqcup _{k \in \mathbb {N}} (Y_{k} \setminus \bigcup _{n \in \mathbb {Z}^{d}} \hat {T}_{n}Y_{k-1})$
. Each orbit of
![]() $\hat {T}$
intersects Y in a finite and necessarily non-empty set, so
$\hat {T}$
intersects Y in a finite and necessarily non-empty set, so
![]() $E_{\hat {T}}|_{Y}$
is a finite Borel equivalence relation. A Borel transversal for
$E_{\hat {T}}|_{Y}$
is a finite Borel equivalence relation. A Borel transversal for
![]() $E_{\hat {T}}|_{Y}$
is also a transversal for the action of
$E_{\hat {T}}|_{Y}$
is also a transversal for the action of
![]() $\hat {T}$
.
$\hat {T}$
.
Now, we assume that the cocycle
![]() $\rho $
satisfies the assumptions of Lemma 4.2 and
$\rho $
satisfies the assumptions of Lemma 4.2 and
![]() $X = (Z \times \mathbb {R}^{d})/E_{\hat {T}}$
, therefore, carries the structure of a standard Borel space as a push-forward of the factor map
$X = (Z \times \mathbb {R}^{d})/E_{\hat {T}}$
, therefore, carries the structure of a standard Borel space as a push-forward of the factor map
![]() $\pi : Z \times \mathbb {R}^{d} \to X$
, which sends a point to its
$\pi : Z \times \mathbb {R}^{d} \to X$
, which sends a point to its
![]() $E_{\hat {T}}$
-equivalence class.
$E_{\hat {T}}$
-equivalence class.
There is a natural
![]() $\mathbb {R}^{d}$
-flow
$\mathbb {R}^{d}$
-flow
![]() $\hat {\mathfrak {F}}$
on
$\hat {\mathfrak {F}}$
on
![]() $Z \times \mathbb {R}^{d}$
, which acts by shifting the second coordinate:
$Z \times \mathbb {R}^{d}$
, which acts by shifting the second coordinate:
![]() $(z,r) +_{\hat {\mathfrak {F}}} s = (z, r + s)$
. This flow commutes with the
$(z,r) +_{\hat {\mathfrak {F}}} s = (z, r + s)$
. This flow commutes with the
![]() $\mathbb {Z}^{d}$
-action
$\mathbb {Z}^{d}$
-action
![]() $\hat {T}$
and, therefore, projects onto the flow
$\hat {T}$
and, therefore, projects onto the flow
![]() $\mathfrak {F}$
on X given by the condition
$\mathfrak {F}$
on X given by the condition
![]() $\pi ((z,r) +_{\hat {\mathfrak {F}}} s) = \pi (z,r) +_{\mathfrak {F}} s$
. We say that
$\pi ((z,r) +_{\hat {\mathfrak {F}}} s) = \pi (z,r) +_{\mathfrak {F}} s$
. We say that
![]() $\mathfrak {F}$
is the special flow over T generated by the cocycle
$\mathfrak {F}$
is the special flow over T generated by the cocycle
![]() $\rho $
. Freeness of T implies freeness of
$\rho $
. Freeness of T implies freeness of
![]() $\mathfrak {F}$
.
$\mathfrak {F}$
.
The construction outlined above works just as well in the context of ergodic theory, where the space Z would be endowed with a finite measure
![]() $\nu $
preserved by the action T. The product of
$\nu $
preserved by the action T. The product of
![]() $\nu $
with the Lebesgue measure on
$\nu $
with the Lebesgue measure on
![]() $\mathbb {R}^{d}$
induces a measure
$\mathbb {R}^{d}$
induces a measure
![]() $\mu $
on X, which is preserved by the flow
$\mu $
on X, which is preserved by the flow
![]() $\mathfrak {F}$
. Furthermore,
$\mathfrak {F}$
. Furthermore,
![]() $\mu $
is finite provided the cocycle
$\mu $
is finite provided the cocycle
![]() $\rho $
is integrable in the sense of [Reference Katok12, Condition (J), pp. 122]. Katok’s special representation theorem asserts that, up to a null set, any free ergodic measure-preserving flow can be obtained via this process. Furthermore, the cocycle can be picked to be bi-Lipschitz with Lipschitz constants arbitrarily close to
$\rho $
is integrable in the sense of [Reference Katok12, Condition (J), pp. 122]. Katok’s special representation theorem asserts that, up to a null set, any free ergodic measure-preserving flow can be obtained via this process. Furthermore, the cocycle can be picked to be bi-Lipschitz with Lipschitz constants arbitrarily close to
![]() $1$
.
$1$
.
As will be shown shortly, such a representation result continues to hold in the framework of descriptive set theory, and every free Borel
![]() $\mathbb {R}^{d}$
-flow is Borel isomorphic to a special flow over some free Borel
$\mathbb {R}^{d}$
-flow is Borel isomorphic to a special flow over some free Borel
![]() $\mathbb {Z}^{d}$
-action. Moreover, just as in Katok’s original work, Theorem 4.3 provides some significant control on the cocycle that generates the flow, tightly coupling the dynamics of the
$\mathbb {Z}^{d}$
-action. Moreover, just as in Katok’s original work, Theorem 4.3 provides some significant control on the cocycle that generates the flow, tightly coupling the dynamics of the
![]() $\mathbb {Z}^{d}$
-action with the dynamics of the flow it produces. But, first, we re-interpret the construction in different terms.
$\mathbb {Z}^{d}$
-action with the dynamics of the flow it produces. But, first, we re-interpret the construction in different terms.
4.4 Flows generated by admissible cocycles
Let the map
![]() $ Z \ni z \mapsto (z,0) \in Z \times \{0\}$
be denoted by
$ Z \ni z \mapsto (z,0) \in Z \times \{0\}$
be denoted by
![]() $\iota $
. If the cocycle
$\iota $
. If the cocycle
![]() $\rho $
is injective, then
$\rho $
is injective, then
![]() $\pi \circ \iota : Z \to \pi (Z\times \{0\}) = Y$
is a bijection and Y intersects every orbit of
$\pi \circ \iota : Z \to \pi (Z\times \{0\}) = Y$
is a bijection and Y intersects every orbit of
![]() $\mathfrak {F}$
in a non-empty countable set. The
$\mathfrak {F}$
in a non-empty countable set. The
![]() $\mathbb {Z}^{d}$
-action T on Z can be transferred via
$\mathbb {Z}^{d}$
-action T on Z can be transferred via
![]() $\pi \circ \iota $
to give a free
$\pi \circ \iota $
to give a free
![]() $\mathbb {Z}^{d}$
-action
$\mathbb {Z}^{d}$
-action
![]() $T' = \pi \circ \iota \circ T \circ \iota ^{-1} \circ \pi ^{-1}$
on Y. Let
$T' = \pi \circ \iota \circ T \circ \iota ^{-1} \circ \pi ^{-1}$
on Y. Let
![]() $\rho ' = \rho _{T', \mathfrak {F}}: \mathbb {Z}^{d} \times Y \to \mathbb {R}^{d}$
be the cocycle of the action
$\rho ' = \rho _{T', \mathfrak {F}}: \mathbb {Z}^{d} \times Y \to \mathbb {R}^{d}$
be the cocycle of the action
![]() $\pi \circ \iota \circ T \circ \iota ^{-1} \circ \pi ^{-1}$
: that is,
$\pi \circ \iota \circ T \circ \iota ^{-1} \circ \pi ^{-1}$
: that is,
If
![]() $y = (\pi \circ \iota )(z)$
for
$y = (\pi \circ \iota )(z)$
for
![]() $z \in Z$
, then equation (6) translates into
$z \in Z$
, then equation (6) translates into
Since
![]() $\pi (T_{n}z, 0) = \pi (z, \rho (-n, T_{n}z)) = \pi (z, -\rho (n,z))$
, we conclude that
$\pi (T_{n}z, 0) = \pi (z, \rho (-n, T_{n}z)) = \pi (z, -\rho (n,z))$
, we conclude that
![]() $\rho '(n,y) = - \rho (n,z)$
, where
$\rho '(n,y) = - \rho (n,z)$
, where
![]() $y = (\pi \circ \iota ) (z)$
. In particular, Y is a discrete cross-section for the flow
$y = (\pi \circ \iota ) (z)$
. In particular, Y is a discrete cross-section for the flow
![]() $\mathfrak {F}$
precisely because
$\mathfrak {F}$
precisely because
![]() $\rho $
escapes to infinity.
$\rho $
escapes to infinity.
Conversely, if
![]() $\mathfrak {F}$
is any free
$\mathfrak {F}$
is any free
![]() $\mathbb {R}^{d}$
-flow on a standard Borel space X and if
$\mathbb {R}^{d}$
-flow on a standard Borel space X and if
![]() $Z \subseteq X$
is a discrete cross-section with a
$Z \subseteq X$
is a discrete cross-section with a
![]() $\mathbb {Z}^{d}$
-action T on it, then
$\mathbb {Z}^{d}$
-action T on it, then
![]() $\mathfrak {F}$
is isomorphic to the special flow over T generated by the (necessarily injective) cocycle
$\mathfrak {F}$
is isomorphic to the special flow over T generated by the (necessarily injective) cocycle
![]() $-\rho _{T,\mathfrak {F}}$
.
$-\rho _{T,\mathfrak {F}}$
.
We say that a cocycle
![]() $\rho $
is admissible if it is both injective and escapes to infinity. The discussion of the above two paragraphs can be summarized by saying that, up to a change of sign in the cocycles, representing a flow as a special flow generated by an admissible cocycle is the same thing as finding a free
$\rho $
is admissible if it is both injective and escapes to infinity. The discussion of the above two paragraphs can be summarized by saying that, up to a change of sign in the cocycles, representing a flow as a special flow generated by an admissible cocycle is the same thing as finding a free
![]() $\mathbb {Z}^{d}$
-action on a discrete cross-section of the flow.
$\mathbb {Z}^{d}$
-action on a discrete cross-section of the flow.
For instance, given any free
![]() $\mathbb {Z}^{d}$
-action T on Z, we may consider the admissible cocycle
$\mathbb {Z}^{d}$
-action T on Z, we may consider the admissible cocycle
![]() $\rho (n, z) = -n$
for all
$\rho (n, z) = -n$
for all
![]() $z \in Z$
and
$z \in Z$
and
![]() $n \in \mathbb {Z}^{d}$
. The set
$n \in \mathbb {Z}^{d}$
. The set
![]() $Y = \pi (Z \times \{0\})$
is then an integer grid for the flow
$Y = \pi (Z \times \{0\})$
is then an integer grid for the flow
![]() $\mathfrak {F}$
(in the sense of Definition 3.11). Conversely, any flow that admits an integer grid is isomorphic to a special flow generated by such a cocycle.
$\mathfrak {F}$
(in the sense of Definition 3.11). Conversely, any flow that admits an integer grid is isomorphic to a special flow generated by such a cocycle.
4.5 Special representation theorem
Restriction of the orbit equivalence relation of any
![]() $\mathbb {R}^{d}$
-flow onto a cross-section gives a hyperfinite equivalence relation [Reference Jackson, Kechris and Louveau10, Theorem 1.16], and therefore can be realized as an orbit equivalence relation by a free Borel
$\mathbb {R}^{d}$
-flow onto a cross-section gives a hyperfinite equivalence relation [Reference Jackson, Kechris and Louveau10, Theorem 1.16], and therefore can be realized as an orbit equivalence relation by a free Borel
![]() $\mathbb {Z}^{d}$
-action (as long as the restricted equivalence relation is aperiodic). Since any free flow admits a discrete (in fact, lacunary) aperiodic cross-section, it is isomorphic to a special flow over some action generated by some cocycle. In general, however, the structure of the
$\mathbb {Z}^{d}$
-action (as long as the restricted equivalence relation is aperiodic). Since any free flow admits a discrete (in fact, lacunary) aperiodic cross-section, it is isomorphic to a special flow over some action generated by some cocycle. In general, however, the structure of the
![]() $\mathbb {Z}^{d}$
-orbit and the corresponding orbit of the flow have little to do with each other. Theorem 3.12 and Corollary 3.13 allow us to improve on this and find a special representation generated by a bi-Lipschitz cocycle.
$\mathbb {Z}^{d}$
-orbit and the corresponding orbit of the flow have little to do with each other. Theorem 3.12 and Corollary 3.13 allow us to improve on this and find a special representation generated by a bi-Lipschitz cocycle.
For comparison, Katok’s theorem [Reference Katok12] can be formulated in the parlance of this section as follows.
Theorem. (Katok)
Pick some
![]() $\alpha> 1$
. Any free ergodic measure-preserving
$\alpha> 1$
. Any free ergodic measure-preserving
![]() $\mathbb {R}^{d}$
-flow on a standard Lebesgue space is isomorphic to a special flow over a free ergodic measure-preserving
$\mathbb {R}^{d}$
-flow on a standard Lebesgue space is isomorphic to a special flow over a free ergodic measure-preserving
![]() $\mathbb {Z}^{d}$
-action generated by an
$\mathbb {Z}^{d}$
-action generated by an
![]() $(\alpha ^{-1},\alpha )$
-bi-Lipschitz cocycle.
$(\alpha ^{-1},\alpha )$
-bi-Lipschitz cocycle.
As is the case with all ergodic theoretical results, isomorphism is understood to hold up to a set of measure zero. We conclude with a Borel version of Katok’s special representation theorem, which holds for all free Borel
![]() $\mathbb {R}^{d}$
-flows and establishes isomorphism on all orbits.
$\mathbb {R}^{d}$
-flows and establishes isomorphism on all orbits.
Theorem 4.3. Pick some
![]() $\alpha> 1$
. Any free Borel
$\alpha> 1$
. Any free Borel
![]() $\mathbb {R}^{d}$
-flow is isomorphic to a special flow over a free Borel
$\mathbb {R}^{d}$
-flow is isomorphic to a special flow over a free Borel
![]() $\mathbb {Z}^{d}$
-action generated by an
$\mathbb {Z}^{d}$
-action generated by an
![]() $(\alpha ^{-1},\alpha )$
-bi-Lipschitz cocycle.
$(\alpha ^{-1},\alpha )$
-bi-Lipschitz cocycle.
Proof. Let
![]() $\mathfrak {F}$
be a free Borel
$\mathfrak {F}$
be a free Borel
![]() $\mathbb {R}^{d}$
-flow on X. Corollary 3.13 gives a cross-section
$\mathbb {R}^{d}$
-flow on X. Corollary 3.13 gives a cross-section
![]() $Z \subseteq X$
and a
$Z \subseteq X$
and a
![]() $\mathbb {Z}^{d}$
-action T on it such that the cocycle
$\mathbb {Z}^{d}$
-action T on it such that the cocycle
![]() $\rho _{\mathfrak {F},T} : \mathbb {Z}^{d} \times X \to \mathbb {R}^{d}$
is
$\rho _{\mathfrak {F},T} : \mathbb {Z}^{d} \times X \to \mathbb {R}^{d}$
is
![]() $(\alpha ^{-1}, \alpha )$
-bi-Lipschitz. By the discussion in §4.4, this gives a representation of the flow as a special flow over T generated by the cocycle
$(\alpha ^{-1}, \alpha )$
-bi-Lipschitz. By the discussion in §4.4, this gives a representation of the flow as a special flow over T generated by the cocycle
![]() $-\rho _{\mathfrak {F},T}$
, which is also
$-\rho _{\mathfrak {F},T}$
, which is also
![]() $(\alpha ^{-1},\alpha )$
-bi-Lipschitz.
$(\alpha ^{-1},\alpha )$
-bi-Lipschitz.
Acknowledgement
The author was partially supported by NSF grant DMS-2153981