1. Introduction
In this work, we study the local and global existence and uniqueness of ‘non-Lipschitz’ solution for a class of abstract ordinary differential equations with state-dependent argument (SDA) of the form
The literature on differential equations with SDA is extensive and recent. To begin, we mention the pioneer work by Driver [Reference Driver6] that introduces and studies a class of neutral ordinary differential equations with state-dependent delay. Always in the context of ODEs with state-dependent delay, we mention the works [Reference Driver7, Reference Driver, LaSalle and Lefschtz8, Reference Enright and Hayashi11, Reference Enright and Hayashi12, Reference Grimm14, Reference Grimm15, Reference Jackiewicz27] and the excellent survey by Hartung et al. [Reference Hartung, Krisztin, Walther, Wu, Canada, Drabek and Fonda19]. For the case of ordinary differential equations with SDA similar to Equations (1.1)–(1.2), we cite the early papers by Cooke [Reference Cooke5], Dunkel [Reference Dunkel9], Eder [Reference Eder10] and Oberg [Reference Oberg36]. Concerning abstract problems with applications to Partial differential equations (PDEs), we cite the pioneer papers [Reference Gal13, Reference Hernandez, Prokopczyk and Ladeira24], our recent works [Reference Hernandez, Fernandes and Wu21, Reference Hernandez, Fernandes and Wu22, Reference Hernandez, Pierri and Wu23–Reference Hernandez and Wu.26] and the interesting papers [Reference Kosovalic, Chen and Wu28–Reference Krisztin and Rezounenko30, Reference Lv, Pei and Yuan34, Reference Lv, Rong and Yongzhen35].
To clarify the contributions of our paper to the field of abstract differential equations with SDA in infinite-dimensional spaces, it is convenient to include some comments about the associated literature. To begin, we note that in [Reference Gal13, Reference Hernandez, Prokopczyk and Ladeira24], possibly the first works on this type of problems, are introduced two different technical approaches, which have been extensively used in the literature. The existence of solution for a class of abstract differential equations with state-dependent ‘delay’ using the Schauder’s Fixed Point Theorem is studied in Hernandez et al. [Reference Hernandez, Prokopczyk and Ladeira24]. The existence and ‘uniqueness’ of solution for a problem similar to Equations (1.1)–(1.2) using the contraction mapping principle is studied in Ciprian [Reference Gal13]. The results in the interesting paper [Reference Gal13] are proved assuming a condition on the nonlinear term ![]() $F(\cdot)$ (see the condition H 3) , what can be understood as a ‘spatial regularizing property’. A simple manner to understand this observation is noting that the function
$F(\cdot)$ (see the condition H 3) , what can be understood as a ‘spatial regularizing property’. A simple manner to understand this observation is noting that the function ![]() $H(\cdot)$ in the example in [Reference Gal13] is a function defined from
$H(\cdot)$ in the example in [Reference Gal13] is a function defined from ![]() $L^{2}(\Omega)$ into
$L^{2}(\Omega)$ into ![]() $ W^{1}_{0}(\Omega)$. The approach in [Reference Gal13] was introduced to lead with the lack of the Lipschitz continuity of the map
$ W^{1}_{0}(\Omega)$. The approach in [Reference Gal13] was introduced to lead with the lack of the Lipschitz continuity of the map ![]() $u\mapsto u(\sigma(\cdot,u(\cdot)))$ in spaces of continuous functions. The aforementioned condition allowed the authors to work on a ‘space of Lipschitz functions’, where an inequality of the form
$u\mapsto u(\sigma(\cdot,u(\cdot)))$ in spaces of continuous functions. The aforementioned condition allowed the authors to work on a ‘space of Lipschitz functions’, where an inequality of the form
 \begin{eqnarray}
\parallel F( \cdot , u(\sigma(\cdot, u(\cdot)) )) &-& F( \cdot , v(\sigma(\cdot, v(\cdot)) )) \parallel_{C([0,b];X_{\alpha})} \hspace{1cm}\hspace{1cm} \hspace{1cm}\hspace{1cm}\nonumber\\ & \leq& [F]_{C_{Lip}} (1 + [v]_{C_{Lip}([0,b];X_{\alpha-1})} [\sigma]_{C_{\rm Lip}} )\nonumber \\ && \qquad \parallel u-v\parallel_{C([0,b]; X_{\alpha})}
\end{eqnarray}
\begin{eqnarray}
\parallel F( \cdot , u(\sigma(\cdot, u(\cdot)) )) &-& F( \cdot , v(\sigma(\cdot, v(\cdot)) )) \parallel_{C([0,b];X_{\alpha})} \hspace{1cm}\hspace{1cm} \hspace{1cm}\hspace{1cm}\nonumber\\ & \leq& [F]_{C_{Lip}} (1 + [v]_{C_{Lip}([0,b];X_{\alpha-1})} [\sigma]_{C_{\rm Lip}} )\nonumber \\ && \qquad \parallel u-v\parallel_{C([0,b]; X_{\alpha})}
\end{eqnarray}is satisfied. In this inequality, which ‘appear implicitly’ in the proof of [Reference Gal13, Theorem 2.2], X α is the domain of the fractional power ![]() $(-A)^{\alpha}$ of A endowed with the graph norm,
$(-A)^{\alpha}$ of A endowed with the graph norm, ![]() $X_{\alpha-1} $ is the dual space of
$X_{\alpha-1} $ is the dual space of ![]() $X_{1-\alpha}$ and
$X_{1-\alpha}$ and  $[F]_{C_{\rm Lip}}$,
$[F]_{C_{\rm Lip}}$,  $[v]_{C_{\rm Lip}([0,b];X_{\alpha-1})}$ and
$[v]_{C_{\rm Lip}([0,b];X_{\alpha-1})}$ and  $ [\sigma]_{C_{\rm Lip}}$ are the Lipschitz semi-norm of
$ [\sigma]_{C_{\rm Lip}}$ are the Lipschitz semi-norm of ![]() $F(\cdot)$,
$F(\cdot)$, ![]() $v(\cdot)$ and
$v(\cdot)$ and ![]() $\sigma(\cdot)$.
$\sigma(\cdot)$.
The approach in Ciprian [Reference Gal13] has been extensively used in the literature concerning the existence and uniqueness of a ‘Lipschitz’ solution for abstract problem with SDA, see, for example, [Reference Chadha and Bahuguna1–Reference Chadha and Pandey3, Reference Haloi, Bahuguna and Pandey16–Reference Haloi, Kumar and Pandey18, Reference Kumar, Pandey and Bahuguna31, Reference Kumar, Pandey and Bahuguna32]. A similar regularizing property is used by Rezounenko et al. in [Reference Krisztin and Rezounenko30, Reference Rezounenko38] to study the existence and ‘uniqueness’ of a ‘Lipschitz’ solution for abstract problems with state-dependent delay. Assuming, basically, that ![]() $F(\cdot)$ is a Lipschitz function from
$F(\cdot)$ is a Lipschitz function from ![]() $[0,a]\times X$ into X, in [Reference Hernández and Wu20–Reference Hernandez, Fernandes and Wu22, Reference Hernandez, Pierri and Wu23–Reference Hernandez and Wu.26], we also study the existence and uniqueness of a ‘Lipschitz’ solution for some different models of state-dependent delay differential equations.
$[0,a]\times X$ into X, in [Reference Hernández and Wu20–Reference Hernandez, Fernandes and Wu22, Reference Hernandez, Pierri and Wu23–Reference Hernandez and Wu.26], we also study the existence and uniqueness of a ‘Lipschitz’ solution for some different models of state-dependent delay differential equations.
In comparison to the early works [Reference Gal13, Reference Hernandez, Prokopczyk and Ladeira24] and the papers [Reference Chadha and Bahuguna1–Reference Chaudhary, Muslim and Pandey4, Reference Gal13, Reference Haloi, Bahuguna and Pandey16–Reference Haloi, Kumar and Pandey18, Reference Hernandez, Fernandes and Wu21, Reference Hernandez, Fernandes and Wu22, Reference Hernandez, Pierri and Wu23–Reference Hernandez and Wu.26, Reference Kumar, Pandey and Bahuguna31, Reference Kumar, Pandey and Bahuguna32], we present several novelties. To begin, we prove the existence and ‘uniqueness of a non-Lipschitz’ solution for Equations (1.1)–(1.2). In addition, to prove our results, we assume that the functions ![]() $F(\cdot)$ and
$F(\cdot)$ and ![]() $\sigma(\cdot)$ are L p-Lipschitz from
$\sigma(\cdot)$ are L p-Lipschitz from ![]() $[0,a]\times X_{\alpha}$ into X and from
$[0,a]\times X_{\alpha}$ into X and from ![]() $[0,a]\times X_{\alpha}$ into
$[0,a]\times X_{\alpha}$ into ![]() $[0,a]$, respectively, which simplify significantly the Condition H 3 in [Reference Gal13]. We remark that the class of L p-Lipschitz functions include the class of locally Lipschitz functions and that a L p-Lipschitz function is not necessarily a locally Lipschitz function (see Definition 2.1). We also study the local and global existence and uniqueness of solution and the existence of solution for the case
$[0,a]$, respectively, which simplify significantly the Condition H 3 in [Reference Gal13]. We remark that the class of L p-Lipschitz functions include the class of locally Lipschitz functions and that a L p-Lipschitz function is not necessarily a locally Lipschitz function (see Definition 2.1). We also study the local and global existence and uniqueness of solution and the existence of solution for the case ![]() $\sigma(0,x_{0}) \gt 0$, an interesting, non-trivial and unconsidered problem in the literature.
$\sigma(0,x_{0}) \gt 0$, an interesting, non-trivial and unconsidered problem in the literature.
This work has four sections. In the next section, we introduce some notation, concepts and results used in this paper. In particular, we include the concept of L p-Lipschitz functions, see Definition 2.1, and we present some simple examples, see Remark 2.1. In ![]() $\S$ 3, we study the local and global existence and uniqueness of mild solution assuming that
$\S$ 3, we study the local and global existence and uniqueness of mild solution assuming that ![]() $F(\cdot)$ and
$F(\cdot)$ and ![]() $\sigma(\cdot)$ are L p-Lipschitz functions. The local existence and uniqueness of solution for the case
$\sigma(\cdot)$ are L p-Lipschitz functions. The local existence and uniqueness of solution for the case ![]() $\sigma(0,x_{0})=0$ is established in Theorem 3.1 and Proposition 3.1. We observe that both results are proved working on spaces formed by functions in
$\sigma(0,x_{0})=0$ is established in Theorem 3.1 and Proposition 3.1. We observe that both results are proved working on spaces formed by functions in ![]() $ C ([0,b];X_{\alpha}) $, with α > 0, such that
$ C ([0,b];X_{\alpha}) $, with α > 0, such that  $\sup_{0 \lt \varepsilon \lt b} \varepsilon^{\theta}[u]_{C_{\rm Lip}([\varepsilon
,b];X_{\alpha})} \lt \infty,$ where
$\sup_{0 \lt \varepsilon \lt b} \varepsilon^{\theta}[u]_{C_{\rm Lip}([\varepsilon
,b];X_{\alpha})} \lt \infty,$ where  $[u]_{C_{\rm Lip}([\varepsilon ,b];X_{\alpha})}$ denotes the Lipschitz semi-norm of
$[u]_{C_{\rm Lip}([\varepsilon ,b];X_{\alpha})}$ denotes the Lipschitz semi-norm of ![]() $u(\cdot)$ on
$u(\cdot)$ on ![]() $[\varepsilon,b]$. From the ideas in the proofs of Theorem 3.1 and Proposition 3.1 are deduced several propositions and corollaries concerning the local and global existence and uniqueness of solution for the problems in Equations (1.1)–(1.2), see for example, Corollary 3.1, Corollary 3.2, Corollary 3.4 and Corollary 3.5. In
$[\varepsilon,b]$. From the ideas in the proofs of Theorem 3.1 and Proposition 3.1 are deduced several propositions and corollaries concerning the local and global existence and uniqueness of solution for the problems in Equations (1.1)–(1.2), see for example, Corollary 3.1, Corollary 3.2, Corollary 3.4 and Corollary 3.5. In ![]() $\S$ 3.2, we study the case
$\S$ 3.2, we study the case ![]() $\sigma(0,\varphi(0)) \gt 0$. This case, unconsidered in the associated literature, is particularly interesting because it is necessary to guarantee the existence of solution on some interval containing the interval
$\sigma(0,\varphi(0)) \gt 0$. This case, unconsidered in the associated literature, is particularly interesting because it is necessary to guarantee the existence of solution on some interval containing the interval ![]() $[0,\sigma(0,\varphi(0))]$. The existence of solution defined on
$[0,\sigma(0,\varphi(0))]$. The existence of solution defined on ![]() $[0,\infty)$ is studied in
$[0,\infty)$ is studied in ![]() $\S$ 4. Proposition 4.4 and Proposition 4.5 are deduced from the proofs of Theorem 3.1 and Proposition 3.1. The used approach in the other results of
$\S$ 4. Proposition 4.4 and Proposition 4.5 are deduced from the proofs of Theorem 3.1 and Proposition 3.1. The used approach in the other results of ![]() $\S$ 4 is different and based in the study of the existence and qualitative properties of maximal solutions. Finally, motivated by the applications in some recent works and by some PDEs arising in the theory of population dynamics, in
$\S$ 4 is different and based in the study of the existence and qualitative properties of maximal solutions. Finally, motivated by the applications in some recent works and by some PDEs arising in the theory of population dynamics, in ![]() $\S$ 5, we present some examples of PDEs with SDA.
$\S$ 5, we present some examples of PDEs with SDA.
2. Preliminaries
Let ![]() $(Z,\parallel \cdot\parallel _{Z})$ and
$(Z,\parallel \cdot\parallel _{Z})$ and ![]() $(W,\parallel \cdot \parallel _{W})$ be Banach spaces. In this work, for r > 0 and
$(W,\parallel \cdot \parallel _{W})$ be Banach spaces. In this work, for r > 0 and ![]() $z\in Z$, we use the symbol
$z\in Z$, we use the symbol ![]() $ B_{r}[z,Z] $ for the closed ball
$ B_{r}[z,Z] $ for the closed ball ![]() $ B_{r}[z,Z]=\{x\in Z; \parallel x-z\parallel_{Z}\leq r\} $. The open ball is denoted by
$ B_{r}[z,Z]=\{x\in Z; \parallel x-z\parallel_{Z}\leq r\} $. The open ball is denoted by ![]() $ B_{r}(z,Z). $ In addition, we use the notation
$ B_{r}(z,Z). $ In addition, we use the notation ![]() $ \mathcal{L}(Z,W)$ for the space of bounded linear operators from Z into W endowed with the uniform norm denoted by
$ \mathcal{L}(Z,W)$ for the space of bounded linear operators from Z into W endowed with the uniform norm denoted by ![]() $\parallel \cdot\parallel_{\mathcal{L}(Z,W) } $. For convenience, we write
$\parallel \cdot\parallel_{\mathcal{L}(Z,W) } $. For convenience, we write ![]() $\parallel \cdot\parallel_{\mathcal{L}(Z ) } $ in the place of
$\parallel \cdot\parallel_{\mathcal{L}(Z ) } $ in the place of ![]() $\parallel \cdot\parallel_{\mathcal{L}(Z,Z)} $ and
$\parallel \cdot\parallel_{\mathcal{L}(Z,Z)} $ and ![]() $\parallel \cdot\parallel $ for the norm
$\parallel \cdot\parallel $ for the norm ![]() $\parallel \cdot\parallel_{\mathcal{L}(X)} $. The spaces
$\parallel \cdot\parallel_{\mathcal{L}(X)} $. The spaces ![]() $C ([b,c];Z)$ and
$C ([b,c];Z)$ and ![]() $C_{\rm Lip}([b,c];Z)$ are usual, and their norms are denoted by
$C_{\rm Lip}([b,c];Z)$ are usual, and their norms are denoted by ![]() $\parallel \cdot\parallel_{C ([b,c];Z)}$ and
$\parallel \cdot\parallel_{C ([b,c];Z)}$ and  $\parallel \cdot\parallel_{C_{\rm Lip}([b,c];Z)}$, respectively. We remark that
$\parallel \cdot\parallel_{C_{\rm Lip}([b,c];Z)}$, respectively. We remark that  ${\parallel \cdot\parallel_{C_{\rm Lip}([b,c];Z)} =\parallel \cdot}\parallel_{C([b,c];Z)} +[ \cdot ]_{C_{\rm Lip}([b,c];Z)} $, where
${\parallel \cdot\parallel_{C_{\rm Lip}([b,c];Z)} =\parallel \cdot}\parallel_{C([b,c];Z)} +[ \cdot ]_{C_{\rm Lip}([b,c];Z)} $, where  $ [ \xi ]_{C_{\rm Lip}([b,c];Z)} = \sup_{t,s\in [b,c], t\neq s }\frac{\parallel \xi(s)-\xi(t)\parallel_{Z} }{\mid t-s\mid }$. In addition, we use the notation
$ [ \xi ]_{C_{\rm Lip}([b,c];Z)} = \sup_{t,s\in [b,c], t\neq s }\frac{\parallel \xi(s)-\xi(t)\parallel_{Z} }{\mid t-s\mid }$. In addition, we use the notation ![]() $C_{\rm Lip,loc}(Z;W)$ for the space formed by the functions
$C_{\rm Lip,loc}(Z;W)$ for the space formed by the functions ![]() $ G \in C(Z;W) $ such that
$ G \in C(Z;W) $ such that  $ [G ] _{C_{\rm lip}(B_{r}(0,Z);W ) } =\sup_{x\neq y, x,y\in B_{r}[0,Z]} \frac{\parallel G(x)-G(y)\parallel_{_{W}}}{\parallel x-y\parallel_{_{Z}}} \lt \infty$ for all r > 0.
$ [G ] _{C_{\rm lip}(B_{r}(0,Z);W ) } =\sup_{x\neq y, x,y\in B_{r}[0,Z]} \frac{\parallel G(x)-G(y)\parallel_{_{W}}}{\parallel x-y\parallel_{_{Z}}} \lt \infty$ for all r > 0.
As pointed, ![]() $A: D(A) \subset X\to X $ is the generator of an analytic C 0-semigroup
$A: D(A) \subset X\to X $ is the generator of an analytic C 0-semigroup ![]() $ (T(t))_{t\geq 0} $ on X. For simplicity, we assume that
$ (T(t))_{t\geq 0} $ on X. For simplicity, we assume that ![]() $0\in \rho(A)$. For η > 0, we use the notation
$0\in \rho(A)$. For η > 0, we use the notation ![]() $(-A)^{\eta}$ and X η for the η-fractional power of A and for the domain of
$(-A)^{\eta}$ and X η for the η-fractional power of A and for the domain of ![]() $(-A)^{\eta}$ endowed with the norm
$(-A)^{\eta}$ endowed with the norm ![]() $\parallel x\parallel_{\eta }=
\parallel (-A)^{\eta}x\parallel$. We also suppose that
$\parallel x\parallel_{\eta }=
\parallel (-A)^{\eta}x\parallel$. We also suppose that ![]() $C_{i}, C_{0,\eta}$ (
$C_{i}, C_{0,\eta}$ (![]() $i\in \mathbb{N}\cup\{0\}$,
$i\in \mathbb{N}\cup\{0\}$, ![]() $\eta\in (0,1)$) are positive such that
$\eta\in (0,1)$) are positive such that ![]() $\parallel A^{i}T(t)\parallel \leq C_{i}t^{-i}$ and
$\parallel A^{i}T(t)\parallel \leq C_{i}t^{-i}$ and ![]() $\parallel (-A)^{\eta}T(t)\parallel \leq C_{0,\eta}t^{-\eta}$ for all
$\parallel (-A)^{\eta}T(t)\parallel \leq C_{0,\eta}t^{-\eta}$ for all ![]() $t\in (0,a]$.
$t\in (0,a]$.
For positive numbers θ, α and b, we use the notation ![]() $C_{\rm Lip, \theta}((0,b];X_{\alpha})$ for the space
$C_{\rm Lip, \theta}((0,b];X_{\alpha})$ for the space
 \begin{equation*}
C_{\rm Lip, \theta}((0,b];X_{\alpha}) = \{u\in C ([0,b];X_{\alpha}) : {[u]_{C_{\rm Lip,\theta}((0,b];X_{\alpha})}}=\sup_{0 \lt \varepsilon \lt b} \varepsilon^{\theta}[u]_{C_{\rm Lip}([\varepsilon ,b];X_{\alpha})} \lt \infty \}, \nonumber
\end{equation*}
\begin{equation*}
C_{\rm Lip, \theta}((0,b];X_{\alpha}) = \{u\in C ([0,b];X_{\alpha}) : {[u]_{C_{\rm Lip,\theta}((0,b];X_{\alpha})}}=\sup_{0 \lt \varepsilon \lt b} \varepsilon^{\theta}[u]_{C_{\rm Lip}([\varepsilon ,b];X_{\alpha})} \lt \infty \}, \nonumber
\end{equation*}endowed with the norm ![]() $ \parallel \cdot \parallel_{C ( [0,b];X_{\alpha})}
$. In addition,
$ \parallel \cdot \parallel_{C ( [0,b];X_{\alpha})}
$. In addition, ![]() $ C_{\rm Lip, \theta,1}((0,\infty);X_{\alpha})$ is the space
$ C_{\rm Lip, \theta,1}((0,\infty);X_{\alpha})$ is the space
 \begin{equation*}
\{u\in C ([0,\infty);X_{\alpha}): u_{\mid_{_{[0,1]}}}\in {C_{\rm Lip,\theta}((0,1];X_{\alpha})}, u_{\mid_{[1,\infty)}}\in {C_{Lip}([1,\infty);X_{\alpha})} \}.
\end{equation*}
\begin{equation*}
\{u\in C ([0,\infty);X_{\alpha}): u_{\mid_{_{[0,1]}}}\in {C_{\rm Lip,\theta}((0,1];X_{\alpha})}, u_{\mid_{[1,\infty)}}\in {C_{Lip}([1,\infty);X_{\alpha})} \}.
\end{equation*}Concerning the problem
we remark that the function ![]() $u\in C ([0,b];X) $ given by
$u\in C ([0,b];X) $ given by  $ u(t) = T(t)x +\int_{0}^{t}T(t-s) \xi(s)\, {\rm d}s$, is called a mild solution of Equation (2.1) on
$ u(t) = T(t)x +\int_{0}^{t}T(t-s) \xi(s)\, {\rm d}s$, is called a mild solution of Equation (2.1) on ![]() $[0,b]$. A function
$[0,b]$. A function ![]() $v\in C ([0,b];X) $ is said to be a strict solution of Equation (2.1) on
$v\in C ([0,b];X) $ is said to be a strict solution of Equation (2.1) on ![]() $[0,b]$ (respectively, a classical solution of Equation (2.1) on
$[0,b]$ (respectively, a classical solution of Equation (2.1) on ![]() $[0,b]$) if
$[0,b]$) if ![]() $v\in C^{1}([0,b];X) \cap C([0,b];X_{1}) $ and
$v\in C^{1}([0,b];X) \cap C([0,b];X_{1}) $ and ![]() $v(\cdot)$ satisfies Equation (2.1) on
$v(\cdot)$ satisfies Equation (2.1) on ![]() $[0,b]$ (respectively,
$[0,b]$ (respectively, ![]() $v\in C^{1}((0,b];X) \cap C((0,b];X_{1}) $ and
$v\in C^{1}((0,b];X) \cap C((0,b];X_{1}) $ and ![]() $v(\cdot)$ satisfies Equation (2.1) on
$v(\cdot)$ satisfies Equation (2.1) on ![]() $(0,b]$).
$(0,b]$).
For convenience, we include the following result on regularity of mild solutions. In this result, for ![]() $\theta\in (0,1)$,
$\theta\in (0,1)$, ![]() $ C^{\theta}([0,b];Z)$ denotes the space formed by all the continuous functions
$ C^{\theta}([0,b];Z)$ denotes the space formed by all the continuous functions ![]() $\xi :[0,b]\mapsto Z$ such that
$\xi :[0,b]\mapsto Z$ such that  $[ \xi ]_{C^{\theta}([b,c];Z)} =
\sup_{t,s\in [b,c], t\neq s }\frac{\parallel \xi(s)-\xi(t)\parallel }{\mid
t-s\mid^{\theta}} $ is finite, endowed with the norm
$[ \xi ]_{C^{\theta}([b,c];Z)} =
\sup_{t,s\in [b,c], t\neq s }\frac{\parallel \xi(s)-\xi(t)\parallel }{\mid
t-s\mid^{\theta}} $ is finite, endowed with the norm  $ \parallel
\cdot\parallel_{C^{\theta}([b,c];Z)}=\parallel \cdot \parallel_{_{C([b,c];X)}}+[ \cdot
]_{C^{\theta}([b,c];Z)} $.
$ \parallel
\cdot\parallel_{C^{\theta}([b,c];Z)}=\parallel \cdot \parallel_{_{C([b,c];X)}}+[ \cdot
]_{C^{\theta}([b,c];Z)} $.
Lemma 2.1. Assume that ![]() $u\in C ([0,b];X) $ is the mild solution of Equation (2.1). If
$u\in C ([0,b];X) $ is the mild solution of Equation (2.1). If ![]() $ \gamma\in (0,1)$,
$ \gamma\in (0,1)$, ![]() $T(\cdot)x\in
C_{\rm Lip}([0,b];X_{\gamma})$ and
$T(\cdot)x\in
C_{\rm Lip}([0,b];X_{\gamma})$ and ![]() $\xi \in C([0,b];X)$, then
$\xi \in C([0,b];X)$, then ![]() $u\in
C^{1-\gamma}([0,b];X_{\gamma})$ and
$u\in
C^{1-\gamma}([0,b];X_{\gamma})$ and
 \begin{equation*} [u]_{C^{1-\gamma}([0,b];X_{\gamma}) }\leq [T(\cdot)x]_{C_{\rm Lip}([0,b];X_{\gamma})} b^{\gamma} +
\parallel \xi \parallel_{C([0,b];X)} \left(\frac{C_{1,1+\gamma} }{\gamma(1-\gamma)} + \frac{C_{0,\gamma} }{1-\gamma}\right). \end{equation*}
\begin{equation*} [u]_{C^{1-\gamma}([0,b];X_{\gamma}) }\leq [T(\cdot)x]_{C_{\rm Lip}([0,b];X_{\gamma})} b^{\gamma} +
\parallel \xi \parallel_{C([0,b];X)} \left(\frac{C_{1,1+\gamma} }{\gamma(1-\gamma)} + \frac{C_{0,\gamma} }{1-\gamma}\right). \end{equation*}For additional details on C 0-semigroups and the problem Equation (2.1), we cite [Reference Lunardi33, Reference Pazy37].
As noted in the introduction, our results on the existence and uniqueness of solutions are proved without assuming that ![]() $F(\cdot)$ and
$F(\cdot)$ and ![]() $\sigma(\cdot)$ are locally Lipschitz. From [Reference Hernandez, Fernandes and Wu22], we remark the next concept.
$\sigma(\cdot)$ are locally Lipschitz. From [Reference Hernandez, Fernandes and Wu22], we remark the next concept.
Definition 2.1. Let ![]() $ (Y_{i},\parallel \cdot\parallel_{Y_{i}} )$,
$ (Y_{i},\parallel \cdot\parallel_{Y_{i}} )$, ![]() $i=1,2,$ be Banach spaces and
$i=1,2,$ be Banach spaces and ![]() $p\geq 1$. We say that a function
$p\geq 1$. We say that a function ![]() $ P: [c,d]\times Y_{1}\mapsto Y_{2} $ is an L p-Lipschitz function if
$ P: [c,d]\times Y_{1}\mapsto Y_{2} $ is an L p-Lipschitz function if ![]() $P(t,\cdot):Y_{1}\mapsto Y_{2}$ is continuous
$P(t,\cdot):Y_{1}\mapsto Y_{2}$ is continuous ![]() $a.e.$ for
$a.e.$ for ![]() $t\in [c,d]$, there exists an integrable function
$t\in [c,d]$, there exists an integrable function ![]() $[P]_{(\cdot,\cdot)}:[c,d]\times [c,d] \to \mathbb{R}^{+} $ and a non-decreasing function
$[P]_{(\cdot,\cdot)}:[c,d]\times [c,d] \to \mathbb{R}^{+} $ and a non-decreasing function ![]() $ \mathcal{W} _{P}:\mathbb{R}^{+}\to \mathbb{R}^{+}$ such that
$ \mathcal{W} _{P}:\mathbb{R}^{+}\to \mathbb{R}^{+}$ such that ![]() $ [P]_{(t,\cdot)}\in L^{p}([c,t]; \mathbb{R}^{+})$ and
$ [P]_{(t,\cdot)}\in L^{p}([c,t]; \mathbb{R}^{+})$ and ![]() $ [P]_{(\cdot,c)}\in L^{p}([c,t]; \mathbb{R}^{+})$ for all
$ [P]_{(\cdot,c)}\in L^{p}([c,t]; \mathbb{R}^{+})$ for all ![]() $t\in (c,d]$ and
$t\in (c,d]$ and
for all ![]() $ x,y\in Y_{1}$ and
$ x,y\in Y_{1}$ and ![]() $ c\leq s\leq t\leq d.$ Next,
$ c\leq s\leq t\leq d.$ Next,  $L_{\rm Lip}^{p}([c,d]\times Y_{1}; Y_{2})$ denotes the set formed by this type of functions.
$L_{\rm Lip}^{p}([c,d]\times Y_{1}; Y_{2})$ denotes the set formed by this type of functions.
Remark 2.1. For completeness, we include some simple examples concerning Definition 2.1. Next, for p > 1, we use the notation p ʹ for the number ![]() $ p^\prime = {p}/({p-1}) $.
$ p^\prime = {p}/({p-1}) $.
(1) It is obvious that
 $ C_{\rm Lip}([0,a]\times Y_{1};Y_{2})\subset L^{p}_{\rm Lip}([0,a]\times Y_1; Y_{2})$ and that
$ C_{\rm Lip}([0,a]\times Y_{1};Y_{2})\subset L^{p}_{\rm Lip}([0,a]\times Y_1; Y_{2})$ and that  $ L^{p}_{\rm Lip}([0,a]\times Y_1; Y_{2})$ is a vectorial space.
$ L^{p}_{\rm Lip}([0,a]\times Y_1; Y_{2})$ is a vectorial space.(2) For p > 1, the function
 $f:[0,a]\mapsto \mathbb{R}$ given by
$f:[0,a]\mapsto \mathbb{R}$ given by  $f(t)= \sqrt[p]{t}$ belongs to
$f(t)= \sqrt[p]{t}$ belongs to  $ L^{q}_{\rm Lip}([0,a];\mathbb{R})$ for all
$ L^{q}_{\rm Lip}([0,a];\mathbb{R})$ for all  $q\in (1,p')$. In fact, for t > 0,
$q\in (1,p')$. In fact, for t > 0,  $ \mid f(t)-f(0)\mid \leq t^{\frac{1}{p}-1} t$ and from the mean value Theorem, it follows that
$ \mid f(t)-f(0)\mid \leq t^{\frac{1}{p}-1} t$ and from the mean value Theorem, it follows that  $ \mid f(t)-f(s)\mid \leq \frac{1}{p}s^{-(1-\frac{1}{p})} \mid t-s\mid $ for
$ \mid f(t)-f(s)\mid \leq \frac{1}{p}s^{-(1-\frac{1}{p})} \mid t-s\mid $ for  $0 \lt s\leq t \leq a$, which shows that
$0 \lt s\leq t \leq a$, which shows that  $f(\cdot)$ is a
$f(\cdot)$ is a  $L^{q}_{\rm Lip}$ function for
$L^{q}_{\rm Lip}$ function for  $q\in (1,p^\prime)$, with
$q\in (1,p^\prime)$, with  $[f]_{(t,s)}= \frac{1}{p}s^{-(1-\frac{1}{p})}$,
$[f]_{(t,s)}= \frac{1}{p}s^{-(1-\frac{1}{p})}$,  $[f]_{(t,0)}= t^{\frac{1}{p}-1}$ and
$[f]_{(t,0)}= t^{\frac{1}{p}-1}$ and  $[f]_{(0,0)}= 0 $.
$[f]_{(0,0)}= 0 $.(3) Let
 $ f\in L^{q}_{\rm Lip}([a,b]:\mathbb{R})$,
$ f\in L^{q}_{\rm Lip}([a,b]:\mathbb{R})$,  $G\in C(X;X)$ and assume that for all r > 0, there is
$G\in C(X;X)$ and assume that for all r > 0, there is  $L_{G}(r) \gt 0 $ such that
$L_{G}(r) \gt 0 $ such that  $\parallel G(x)-G(y)\parallel\leq L_{G}(r) \parallel x-y \parallel$ for all
$\parallel G(x)-G(y)\parallel\leq L_{G}(r) \parallel x-y \parallel$ for all  $x,y\in B_{r}[0,X]$. If
$x,y\in B_{r}[0,X]$. If  $ H(s,x)= f(t)G(x) $, for
$ H(s,x)= f(t)G(x) $, for  $ t, s\in [a,b]$ and
$ t, s\in [a,b]$ and  $x,y\in B_{r}[0,X]$, we note that
which shows that
$x,y\in B_{r}[0,X]$, we note that
which shows that \begin{eqnarray*}
\parallel H(t,x) &-& H(s,y)\parallel\\
&\leq& \parallel ( f(t )- f(s )) G(x)\parallel + \parallel f(s )( G(x)-G(y))\parallel \\
&\leq& [f]_{(t,s)} \mid t-s \mid \parallel G(x)\parallel + \mid f(s)\mid L_{G}(r)\parallel x-y\parallel\\
&\leq& [f]_{(t,s)} \mid t-s \mid (L_{G}(r)\parallel x\parallel+ \parallel G(0)\parallel ) + \parallel f\parallel_{C([a,b])}\\ && \quad \parallel L_{G}(r)\parallel x-y\parallel\\
&\leq& ( [f]_{(t,s)} + \parallel f\parallel_{C([a,b])} ) (L_{G}(r) r + \parallel G(0)\parallel + L_{G}(r))\\ && \quad ( \mid t-s \mid + \parallel x-y\parallel) ,
\end{eqnarray*}
\begin{eqnarray*}
\parallel H(t,x) &-& H(s,y)\parallel\\
&\leq& \parallel ( f(t )- f(s )) G(x)\parallel + \parallel f(s )( G(x)-G(y))\parallel \\
&\leq& [f]_{(t,s)} \mid t-s \mid \parallel G(x)\parallel + \mid f(s)\mid L_{G}(r)\parallel x-y\parallel\\
&\leq& [f]_{(t,s)} \mid t-s \mid (L_{G}(r)\parallel x\parallel+ \parallel G(0)\parallel ) + \parallel f\parallel_{C([a,b])}\\ && \quad \parallel L_{G}(r)\parallel x-y\parallel\\
&\leq& ( [f]_{(t,s)} + \parallel f\parallel_{C([a,b])} ) (L_{G}(r) r + \parallel G(0)\parallel + L_{G}(r))\\ && \quad ( \mid t-s \mid + \parallel x-y\parallel) ,
\end{eqnarray*} $ H\in L^{q}_{Lip}([a,b]\times X;X)$.
$ H\in L^{q}_{Lip}([a,b]\times X;X)$.(4) Assume that
 $ H (t,x)=\zeta(t) G(t,x)$, where
$ H (t,x)=\zeta(t) G(t,x)$, where  $G\in C_{\rm Lip}([0,a]\times X;X)$ and
$G\in C_{\rm Lip}([0,a]\times X;X)$ and  $\zeta\in C([0,a];\mathbb{R})$. Suppose that
$\zeta\in C([0,a];\mathbb{R})$. Suppose that  $\zeta(\cdot)$ is differentiable
$\zeta(\cdot)$ is differentiable  $a.e.$ on
$a.e.$ on  $[0,a]$, and there is a function
$[0,a]$, and there is a function  $\xi:[0,a]\times[0,a]\to\mathbb{R}^{+}$ such that
$\xi:[0,a]\times[0,a]\to\mathbb{R}^{+}$ such that  $ |\zeta(t)-\zeta(s)|\leq \zeta^\prime(\xi_{(t,s)})|t-s| $ and
$ |\zeta(t)-\zeta(s)|\leq \zeta^\prime(\xi_{(t,s)})|t-s| $ and  $ s\leq
\xi_{(s,t)}\leq t$ for all
$ s\leq
\xi_{(s,t)}\leq t$ for all  $ 0 \lt s\leq t \lt a $ and that the function
$ 0 \lt s\leq t \lt a $ and that the function  $[\zeta]_{(\cdot,\cdot)}=\zeta^\prime(\xi_{(\cdot,\cdot)})$ belongs to
$[\zeta]_{(\cdot,\cdot)}=\zeta^\prime(\xi_{(\cdot,\cdot)})$ belongs to  $L^{q}(U)$ for some q > 1, where
$L^{q}(U)$ for some q > 1, where  $U=\{(t,s)\in
[0,a]\times[0,a], s\leq t\}$. Then
$U=\{(t,s)\in
[0,a]\times[0,a], s\leq t\}$. Then  $H\in
L^{q}_{\rm Lip}([0,a]\times X;X)$ with
$H\in
L^{q}_{\rm Lip}([0,a]\times X;X)$ with  $[H]_{(t,s)}= [\zeta]_{(t,s)} +
\mid \xi(s) \mid $ and
$[H]_{(t,s)}= [\zeta]_{(t,s)} +
\mid \xi(s) \mid $ and  $ \mathcal{W }_{H}(r)= [G]_{\rm Lip}{ (a+r+1)}+ \parallel G(0,0)\parallel $.
$ \mathcal{W }_{H}(r)= [G]_{\rm Lip}{ (a+r+1)}+ \parallel G(0,0)\parallel $.(5) Assume that
 $H (t,x)=\zeta(t) G(t,x)$, where
$H (t,x)=\zeta(t) G(t,x)$, where  $G\in L^{q}_{\rm Lip}([0,a]\times X;X)$,
$G\in L^{q}_{\rm Lip}([0,a]\times X;X)$,  $\zeta\in L^{p}_{\rm Lip}([0,a] ;\mathbb{R})$ and
$\zeta\in L^{p}_{\rm Lip}([0,a] ;\mathbb{R})$ and  $ \frac{1}{p}+ \frac{1}{q}\leq 1$. If the functions
$ \frac{1}{p}+ \frac{1}{q}\leq 1$. If the functions  $G(\cdot)$ and
$G(\cdot)$ and  $\zeta(\cdot)$ are continuous, then
$\zeta(\cdot)$ are continuous, then  $H \in L^{\min\{p,q\}}_{\rm Lip}([0,a]\times X;X)$ with
$H \in L^{\min\{p,q\}}_{\rm Lip}([0,a]\times X;X)$ with  $[H ]_{(t,s)}= [G]_{(t,s)} ( [\zeta]_{(t,s)} + \parallel \zeta(s)\parallel ) $ and
$[H ]_{(t,s)}= [G]_{(t,s)} ( [\zeta]_{(t,s)} + \parallel \zeta(s)\parallel ) $ and  $ \mathcal{W }_{H }(r)= W_{G}(r) (a+r+1) $.
$ \mathcal{W }_{H }(r)= W_{G}(r) (a+r+1) $.
To work with  $ L^{q}_{\rm Lip}$ functions and SDA, it is convenient to include the following useful Lemma. We omit the proof.
$ L^{q}_{\rm Lip}$ functions and SDA, it is convenient to include the following useful Lemma. We omit the proof.
Lemma 2.2. Assume that  $ \sigma\in L^{q}_{\rm Lip}([0,a]\times X_{\alpha} ;[0,b]) $ for
$ \sigma\in L^{q}_{\rm Lip}([0,a]\times X_{\alpha} ;[0,b]) $ for ![]() $\alpha\geq 0$ and
$\alpha\geq 0$ and ![]() $0 \lt b\leq a$ and that
$0 \lt b\leq a$ and that ![]() $u,v \in C([0,b]; X_{\alpha} ) $.
$u,v \in C([0,b]; X_{\alpha} ) $.
(a) If
 $u\in C_{\rm Lip}([0,b]; X_{\alpha}) $, then
for all
$u\in C_{\rm Lip}([0,b]; X_{\alpha}) $, then
for all \begin{align*}
\parallel u ( \sigma(t+h,u(t+h))) &- u (\sigma(t ,u(t ))\parallel_{\alpha}\hspace{1cm}\hspace{1cm}\hspace{1cm} \hspace{1cm} \\
&\leq {[u ]_{C_{\rm Lip}([0,b];X_{\alpha})}} [\sigma]_{(t+h,t)}\mathcal{W}_{\sigma}(\rho_{1})(1+[u ]_{C_{\rm Lip}([0,b];X_{\alpha})}) h, \\
\!\!\!\!\!\parallel u (\sigma(t ,u(t ))- v (\sigma(t ,v(t )) \parallel_{\alpha} &\leq (1+[u]_{C_{\rm Lip}([0,b];X_{\alpha})}[\sigma]_{(t,t)} \mathcal{W}_{\sigma}(\rho_{2})) \parallel u-v \parallel_{C([0,b];X_{\alpha})}
\end{align*}
\begin{align*}
\parallel u ( \sigma(t+h,u(t+h))) &- u (\sigma(t ,u(t ))\parallel_{\alpha}\hspace{1cm}\hspace{1cm}\hspace{1cm} \hspace{1cm} \\
&\leq {[u ]_{C_{\rm Lip}([0,b];X_{\alpha})}} [\sigma]_{(t+h,t)}\mathcal{W}_{\sigma}(\rho_{1})(1+[u ]_{C_{\rm Lip}([0,b];X_{\alpha})}) h, \\
\!\!\!\!\!\parallel u (\sigma(t ,u(t ))- v (\sigma(t ,v(t )) \parallel_{\alpha} &\leq (1+[u]_{C_{\rm Lip}([0,b];X_{\alpha})}[\sigma]_{(t,t)} \mathcal{W}_{\sigma}(\rho_{2})) \parallel u-v \parallel_{C([0,b];X_{\alpha})}
\end{align*} $t,h\in [0,b]$ with
$t,h\in [0,b]$ with  $t+h\in [0,b]$, where
$t+h\in [0,b]$, where  $\rho_{1}= \parallel u\parallel_{C ([0,b];X_{\alpha})} $ and
$\rho_{1}= \parallel u\parallel_{C ([0,b];X_{\alpha})} $ and  $\rho_{2}=\max\{\parallel u\parallel_{C ([0,b];X_{\alpha})}, \parallel v\parallel_{C ([0,b];X_{\alpha})}\}$.
$\rho_{2}=\max\{\parallel u\parallel_{C ([0,b];X_{\alpha})}, \parallel v\parallel_{C ([0,b];X_{\alpha})}\}$.(b) If
 $u\in C^{\beta}([0,b];X_{\alpha})$ and
$u\in C^{\beta}([0,b];X_{\alpha})$ and  $\sigma(\cdot)$ is Lipschitz, then
$\sigma(\cdot)$ is Lipschitz, then  $u(\sigma(\cdot,\cdot))\in C^{\beta^{2}}([0,b];X_{\alpha})$ and
$u(\sigma(\cdot,\cdot))\in C^{\beta^{2}}([0,b];X_{\alpha})$ and
 \begin{eqnarray*}
{[u(\sigma(\cdot,\cdot)) ]_{C^{\beta^{2}}([0,b];X_{\alpha})}} \leq {[u ]_{C^{\beta}([0,b];X_{\alpha})}} [\sigma]_{C_{\rm Lip}}^{\beta}(b^{1-\beta}+[u ]_{C^{\beta}([0,b];X_{\alpha})})^{\beta} h^{\beta^{2}}.
\end{eqnarray*}
\begin{eqnarray*}
{[u(\sigma(\cdot,\cdot)) ]_{C^{\beta^{2}}([0,b];X_{\alpha})}} \leq {[u ]_{C^{\beta}([0,b];X_{\alpha})}} [\sigma]_{C_{\rm Lip}}^{\beta}(b^{1-\beta}+[u ]_{C^{\beta}([0,b];X_{\alpha})})^{\beta} h^{\beta^{2}}.
\end{eqnarray*}
3. Existence and uniqueness of solution
In this section, we study the local and global existence and uniqueness of solution for the problem (1.1)–(1.2). To begin, we introduce the following concepts of solution.
Definition 3.1. A function ![]() $u\in C([0,b];X)$,
$u\in C([0,b];X)$, ![]() $ 0 \lt b\leq a$, is called a mild solution of (1.1)–(1.2) on
$ 0 \lt b\leq a$, is called a mild solution of (1.1)–(1.2) on ![]() $[0,b]$ if
$[0,b]$ if ![]() $ u(0)=x_{0} $,
$ u(0)=x_{0} $, ![]() $\sigma(t,u(t))\in[0,b]$ for all
$\sigma(t,u(t))\in[0,b]$ for all ![]() $t\in [0,b]$ and
$t\in [0,b]$ and
 \begin{eqnarray*}
u(t) = T(t)x_{0} +\int_{0}^{t}T(t-s) F(s,u^{\sigma}(s))\, {\rm d}s,\qquad \forall\, t \in [0,b],
\end{eqnarray*}
\begin{eqnarray*}
u(t) = T(t)x_{0} +\int_{0}^{t}T(t-s) F(s,u^{\sigma}(s))\, {\rm d}s,\qquad \forall\, t \in [0,b],
\end{eqnarray*}where ![]() $ u^{\sigma} (\cdot)$ is the function
$ u^{\sigma} (\cdot)$ is the function ![]() $u^{\sigma}:[0,b]\mapsto X$ given by
$u^{\sigma}:[0,b]\mapsto X$ given by ![]() $u^{\sigma}(t)=u(\sigma(t,u(t)))$.
$u^{\sigma}(t)=u(\sigma(t,u(t)))$.
Definition 3.2. A function ![]() $u\in C([0,b];X)$,
$u\in C([0,b];X)$, ![]() $ b \gt 0 ,$ is said to be a classical solution of Equations (1.1)–(1.2) on
$ b \gt 0 ,$ is said to be a classical solution of Equations (1.1)–(1.2) on ![]() $[0,b]$ if
$[0,b]$ if ![]() $ u(0)=x_{0} $,
$ u(0)=x_{0} $,  $ u_{\mid_{(0,b]}} \in C((0,b];X_{1})\cap
C^{1}((0,b];X) $,
$ u_{\mid_{(0,b]}} \in C((0,b];X_{1})\cap
C^{1}((0,b];X) $, ![]() $\sigma(t,u(t))\in[0,b]$ for all
$\sigma(t,u(t))\in[0,b]$ for all ![]() $t\in [0,b]$ and
$t\in [0,b]$ and ![]() $u(\cdot)$ satisfies Equation (1.1) on
$u(\cdot)$ satisfies Equation (1.1) on ![]() $(0,b]$. If
$(0,b]$. If ![]() $u(\cdot)$ is a classical solution on
$u(\cdot)$ is a classical solution on ![]() $[0,b]$,
$[0,b]$,  $ u_{\mid_{[0,b]}} \in C([0,b];X_{1})\cap C^{1}([0,b];X) $ and
$ u_{\mid_{[0,b]}} \in C([0,b];X_{1})\cap C^{1}([0,b];X) $ and ![]() $u(\cdot)$ satisfies Equation (1.1) on
$u(\cdot)$ satisfies Equation (1.1) on ![]() $(0,b]$, then we say that
$(0,b]$, then we say that ![]() $u(\cdot)$ is a strict solution on
$u(\cdot)$ is a strict solution on ![]() $[0,b]$.
$[0,b]$.
To develop our studies, we include the next conditions.
 $ \bf H_{F,\sigma, a}^{q,r }(Y_{1} ; Y_{2}):$
$ \bf H_{F,\sigma, a}^{q,r }(Y_{1} ; Y_{2}):$ ![]() $(Y_{i},\parallel \cdot\parallel_{Y_{i}}) $,
$(Y_{i},\parallel \cdot\parallel_{Y_{i}}) $, ![]() $i=1,2,$ are Banach spaces, a > 0,
$i=1,2,$ are Banach spaces, a > 0, ![]() $ r,q\in [1,\infty]$,
$ r,q\in [1,\infty]$,  $ \frac{1}{q} + \frac{1}{r}\leq 1$,
$ \frac{1}{q} + \frac{1}{r}\leq 1$,  $ F\in L_{\rm Lip}^{q}( [0,a]\times Y_{1};Y_{2}) \cap C( [0,a]\times Y_{1};Y_{2})$ and
$ F\in L_{\rm Lip}^{q}( [0,a]\times Y_{1};Y_{2}) \cap C( [0,a]\times Y_{1};Y_{2})$ and ![]() $ \sigma(\cdot)$ belongs to
$ \sigma(\cdot)$ belongs to ![]() $ L_{\rm Lip}^{r }( [0,a]\times Y_{1} ;[0,a]) \cap C( [0,a]\times Y_{1} ;[0,a])$.
$ L_{\rm Lip}^{r }( [0,a]\times Y_{1} ;[0,a]) \cap C( [0,a]\times Y_{1} ;[0,a])$.
![]() $\bf \mathcal{H}_{{F}, a}(Y_{1} ; Y_{2}):$
$\bf \mathcal{H}_{{F}, a}(Y_{1} ; Y_{2}):$ ![]() $ (Y_{i},\parallel \cdot\parallel_{Y_{i}} )$,
$ (Y_{i},\parallel \cdot\parallel_{Y_{i}} )$, ![]() $i=1,2,$ are Banach spaces, a > 0, the function
$i=1,2,$ are Banach spaces, a > 0, the function ![]() $F(\cdot)$ belongs to
$F(\cdot)$ belongs to ![]() $ C([0,a]\times Y_{1};Y_{2})$, and there are integrable bounded functions
$ C([0,a]\times Y_{1};Y_{2})$, and there are integrable bounded functions ![]() $ \varrho_{i}:[0,a]\mapsto \mathbb{R}^{+}$,
$ \varrho_{i}:[0,a]\mapsto \mathbb{R}^{+}$, ![]() $i=1,2,$ and a non-decreasing function
$i=1,2,$ and a non-decreasing function ![]() $ \mathcal{K}_{F}:[0,\infty)\mapsto \mathbb{R}^{+}$ such that
$ \mathcal{K}_{F}:[0,\infty)\mapsto \mathbb{R}^{+}$ such that ![]() $ \parallel F(s,x) \parallel_{Y_{2}} \leq \mathcal{K}_{F}(\parallel x\parallel_{Y_{1} }) \varrho_{1}(s) +
\varrho_{2}(s) , $ for all
$ \parallel F(s,x) \parallel_{Y_{2}} \leq \mathcal{K}_{F}(\parallel x\parallel_{Y_{1} }) \varrho_{1}(s) +
\varrho_{2}(s) , $ for all ![]() $ s\in [0,a] $ and
$ s\in [0,a] $ and ![]() $ x \in Y_{1} $.
$ x \in Y_{1} $.
In order to work on spaces similar to ![]() $ C_{\rm Lip, \theta}((0,b];X_{\alpha})$ and to simplify the exposition, we introduce the following condition.
$ C_{\rm Lip, \theta}((0,b];X_{\alpha})$ and to simplify the exposition, we introduce the following condition.
Condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma }(Y_{1},Y_{2})$: the conditions
$\bf H_{F,\sigma, a}^{\alpha,\gamma }(Y_{1},Y_{2})$: the conditions  $\bf H_{F,\sigma, a}^{q,r }(Y_{1} ; Y_{2})$ and
$\bf H_{F,\sigma, a}^{q,r }(Y_{1} ; Y_{2})$ and ![]() $\bf \mathcal{H}_{F, a}(Y_{1} ; Y_{2})$ are satisfied,
$\bf \mathcal{H}_{F, a}(Y_{1} ; Y_{2})$ are satisfied, ![]() $0\leq\alpha \lt \gamma \lt 1+\alpha $, and there is a non-decreasing function
$0\leq\alpha \lt \gamma \lt 1+\alpha $, and there is a non-decreasing function ![]() $\xi\in C([0,a];\mathbb{R}^{+}) $ such that
$\xi\in C([0,a];\mathbb{R}^{+}) $ such that ![]() $0 \lt \xi(t)\leq \sigma(t,x)\leq t$ for all
$0 \lt \xi(t)\leq \sigma(t,x)\leq t$ for all ![]() $(t,x)\in (0,a]\times Y_{1} $ and the functions
$(t,x)\in (0,a]\times Y_{1} $ and the functions  $ \frac{[F]_{(\cdot+h,\cdot)}[\sigma]_{(\cdot+h,\cdot)} }{(t-\cdot)^\alpha \xi^{2(1+\alpha-\gamma) }(\cdot)} $ and
$ \frac{[F]_{(\cdot+h,\cdot)}[\sigma]_{(\cdot+h,\cdot)} }{(t-\cdot)^\alpha \xi^{2(1+\alpha-\gamma) }(\cdot)} $ and  $ \frac{[F]_{(\cdot, \cdot)} [\sigma]_{(\cdot,\cdot)}}{(t-\cdot)^{\alpha} \xi ^{1+\alpha-\gamma}(\cdot)} $ are integrable on
$ \frac{[F]_{(\cdot, \cdot)} [\sigma]_{(\cdot,\cdot)}}{(t-\cdot)^{\alpha} \xi ^{1+\alpha-\gamma}(\cdot)} $ are integrable on ![]() $[0,t]$ for all
$[0,t]$ for all ![]() $t\in [0,a]$ and h > 0 with
$t\in [0,a]$ and h > 0 with ![]() $t+h\leq a$.
$t+h\leq a$.
Remark 3.1. To avoid additional notation, independent of the spaces Y i, we use the same notation for the functions ![]() $[F]_{(\cdot,\cdot)}$,
$[F]_{(\cdot,\cdot)}$, ![]() $
[\sigma]_{(\cdot,\cdot)}$,
$
[\sigma]_{(\cdot,\cdot)}$, ![]() $\varrho_{i}(\cdot)$,
$\varrho_{i}(\cdot)$, ![]() $\mathcal{W}_{F}(\cdot)$,
$\mathcal{W}_{F}(\cdot)$, ![]() $ \mathcal{W}_{\sigma}$ and
$ \mathcal{W}_{\sigma}$ and ![]() $\xi(\cdot)$ in the conditions
$\xi(\cdot)$ in the conditions  $\bf H_{F,\sigma, a}^{q,r }(Y_{1} ; Y_{2})$ and
$\bf H_{F,\sigma, a}^{q,r }(Y_{1} ; Y_{2})$ and ![]() $\bf \mathcal{H}_{F, a}(Y_{1} ; Y_{2})$.
$\bf \mathcal{H}_{F, a}(Y_{1} ; Y_{2})$.
Notation 1.
If the condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma }(Y_{1},Y_{2})$ is satisfied and
$\bf H_{F,\sigma, a}^{\alpha,\gamma }(Y_{1},Y_{2})$ is satisfied and ![]() $\Lambda (\tau) =( 1+ {1 }/({ \xi^{1+\alpha-\gamma
}(\tau) }))$ for
$\Lambda (\tau) =( 1+ {1 }/({ \xi^{1+\alpha-\gamma
}(\tau) }))$ for ![]() $b\in (0,a]$ and r > 0, we use the following notation
$b\in (0,a]$ and r > 0, we use the following notation
 \begin{eqnarray*}
\Psi_{1}(b,r) &=& \parallel \varrho_{1}\parallel_{L^{\infty}([0,b])} \mathcal{K}_{F}(r) + \parallel \varrho_{2}\parallel_{L^{\infty}([0,b])}, \\
\Psi_{2}(b,r) &=& \parallel \varrho_{1}\parallel_{L^{1}([0,b])} \mathcal{K}_{F}(r) + \parallel \varrho_{2}\parallel_{L^{1}([0,b])}, \\
\Theta_{1}(b) &=& \sup_{t,h\in [0,b],t+h\leq b} \int_0^t [F]_{(\tau+h,\tau)} (1 + [\sigma]_{(\tau+h,\tau)}) \Lambda^{2}(\tau) \, {\rm d}\tau, \\
\Theta_{2}(b) &=& \int_0^b [F]_{(\tau,\tau)} (1 + [\sigma]_{(\tau,\tau)}) \Lambda (\tau)\, {\rm d}\tau , \\
\Theta_{3}(b) &=& \sup_{t,h\in [0,b],t+h\leq b} \int_0^t \frac{[F]_{(\tau+h,\tau)}}{(t-\tau)^{\alpha}} \left(1 + [\sigma]_{(\tau+h,\tau)}\right) \Lambda^{2} (\tau) \,{\rm d}\tau , \\
\Theta_{4}(b) &=& \sup_{t\in [0,b]} \int_0^t \frac{[F]_{(\tau,\tau)}}{(t-\tau)^{\alpha}} \left(1 + [\sigma]_{(\tau,\tau)}\right) \Lambda (\tau) \, {\rm d}\tau , \\
\Theta_{5}(b) &=& \sup_{t\in [0,b]} \int_0^t \frac{[F]_{(\tau,0)} }{(t-\tau)^{\alpha}}\, {\rm d}\tau.
\end{eqnarray*}
\begin{eqnarray*}
\Psi_{1}(b,r) &=& \parallel \varrho_{1}\parallel_{L^{\infty}([0,b])} \mathcal{K}_{F}(r) + \parallel \varrho_{2}\parallel_{L^{\infty}([0,b])}, \\
\Psi_{2}(b,r) &=& \parallel \varrho_{1}\parallel_{L^{1}([0,b])} \mathcal{K}_{F}(r) + \parallel \varrho_{2}\parallel_{L^{1}([0,b])}, \\
\Theta_{1}(b) &=& \sup_{t,h\in [0,b],t+h\leq b} \int_0^t [F]_{(\tau+h,\tau)} (1 + [\sigma]_{(\tau+h,\tau)}) \Lambda^{2}(\tau) \, {\rm d}\tau, \\
\Theta_{2}(b) &=& \int_0^b [F]_{(\tau,\tau)} (1 + [\sigma]_{(\tau,\tau)}) \Lambda (\tau)\, {\rm d}\tau , \\
\Theta_{3}(b) &=& \sup_{t,h\in [0,b],t+h\leq b} \int_0^t \frac{[F]_{(\tau+h,\tau)}}{(t-\tau)^{\alpha}} \left(1 + [\sigma]_{(\tau+h,\tau)}\right) \Lambda^{2} (\tau) \,{\rm d}\tau , \\
\Theta_{4}(b) &=& \sup_{t\in [0,b]} \int_0^t \frac{[F]_{(\tau,\tau)}}{(t-\tau)^{\alpha}} \left(1 + [\sigma]_{(\tau,\tau)}\right) \Lambda (\tau) \, {\rm d}\tau , \\
\Theta_{5}(b) &=& \sup_{t\in [0,b]} \int_0^t \frac{[F]_{(\tau,0)} }{(t-\tau)^{\alpha}}\, {\rm d}\tau.
\end{eqnarray*}Remark 3.2. Concerning the above conditions and notation, it is useful to make some observations. As pointed out in the introduction, an important contribution of our work is related to our studies and results about the existence and uniqueness of non-Lipschitz solution for the problem (1.1)–(1.2). Our different results about it, see, for example, Theorem 3.1, Proposition 3.1 and the associated corollaries, are proved using the contraction mapping principle on subsets of spaces of the form ![]() $
C_{\rm Lip, \theta}((0,b];X_{\beta})$ with
$
C_{\rm Lip, \theta}((0,b];X_{\beta})$ with ![]() $\beta\geq 0$ endowed with the uniform norm
$\beta\geq 0$ endowed with the uniform norm  $\parallel\cdot\parallel_{C([0,b];X_{\beta})}$, see, for instance, the space
$\parallel\cdot\parallel_{C([0,b];X_{\beta})}$, see, for instance, the space
 \begin{equation*}
S_{x_0} = \left\{ u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) : u(0)= x_{0},
\max\{ \parallel u \parallel_{C([0,b];X_{\alpha})}, [u]_{C_{\rm Lip,1+\alpha-\gamma} } \right\} \leq R \}
\end{equation*}
\begin{equation*}
S_{x_0} = \left\{ u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) : u(0)= x_{0},
\max\{ \parallel u \parallel_{C([0,b];X_{\alpha})}, [u]_{C_{\rm Lip,1+\alpha-\gamma} } \right\} \leq R \}
\end{equation*}in the proof of Theorem 3.1. Evidently, the use of the contraction mapping principle requires different estimates involving (directly or indirectly) the seminorm  $ [\cdot]_{C_{\rm Lip,1+\alpha-\gamma} }$. This simple fact is the justification for the introduction of the above conditions and the definitions of the functions
$ [\cdot]_{C_{\rm Lip,1+\alpha-\gamma} }$. This simple fact is the justification for the introduction of the above conditions and the definitions of the functions ![]() $\Theta_{i}(\cdot)$ in Notation 1. In particular, we observe that the definitions and the properties of the functions
$\Theta_{i}(\cdot)$ in Notation 1. In particular, we observe that the definitions and the properties of the functions ![]() $\Theta_{1}(\cdot)$ and
$\Theta_{1}(\cdot)$ and ![]() $\Theta_{4}(\cdot)$ are introduced to estimate the seminorm
$\Theta_{4}(\cdot)$ are introduced to estimate the seminorm  $[\Gamma u]_{C_{\rm Lip,1+\alpha-\gamma}
}$ and
$[\Gamma u]_{C_{\rm Lip,1+\alpha-\gamma}
}$ and ![]() $ \parallel \Gamma u - \Gamma v\parallel_{{C([0,b];X_{\alpha})}}$, respectively, where
$ \parallel \Gamma u - \Gamma v\parallel_{{C([0,b];X_{\alpha})}}$, respectively, where ![]() $\Gamma(\cdot)$ denotes the associated solution operator.
$\Gamma(\cdot)$ denotes the associated solution operator.
We divide the remainder of this section into four parts. To begin, we study the case in which ![]() $\bf \sigma(0,x_{0})=0$.
$\bf \sigma(0,x_{0})=0$.
3.1. The case  $\bf \sigma(0,x_{0})=0$
$\bf \sigma(0,x_{0})=0$
In this section, we establish and prove several results related to the existence and uniqueness of solution for the case ![]() $\bf
\sigma(0,x_{0})=0$. The ideas and the technical framework used to study this case are fundamental for the development of the next sections.
$\bf
\sigma(0,x_{0})=0$. The ideas and the technical framework used to study this case are fundamental for the development of the next sections.
To establish our first result, we need the next simple and useful lemma.
Lemma 3.1. For ![]() $0\leq\alpha \lt \gamma \lt 1+\alpha $ and
$0\leq\alpha \lt \gamma \lt 1+\alpha $ and ![]() $x_{0}\in X_{\gamma}$,
$x_{0}\in X_{\gamma}$,
 \begin{equation*} \parallel (-A)^{\alpha}T(t)x_{0}- (-A)^{\alpha}T(s)x_{0}\parallel \leq \frac{C_{0,1+\alpha-\gamma} }{s^{1+ \alpha-\gamma} } \parallel x_{0} \parallel_{\gamma}{ \mid t-s\mid}, \quad \forall
t \gt s \gt 0, \end{equation*}
\begin{equation*} \parallel (-A)^{\alpha}T(t)x_{0}- (-A)^{\alpha}T(s)x_{0}\parallel \leq \frac{C_{0,1+\alpha-\gamma} }{s^{1+ \alpha-\gamma} } \parallel x_{0} \parallel_{\gamma}{ \mid t-s\mid}, \quad \forall
t \gt s \gt 0, \end{equation*} ![]() $ T(\cdot)x_{0} \in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})$ and
$ T(\cdot)x_{0} \in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})$ and  $ {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}}\leq C_{0,1+\alpha-\gamma} \parallel x_{0} \parallel_{\gamma}$ for all a > 0.
$ {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}}\leq C_{0,1+\alpha-\gamma} \parallel x_{0} \parallel_{\gamma}$ for all a > 0.
Proof. We only note that for ![]() $ s\in (0,a]$ and
$ s\in (0,a]$ and ![]() $t\in (s,a]$,
$t\in (s,a]$,
 \begin{eqnarray*}
\parallel (-A)^{\alpha}T(t)x_{0}- (-A)^{\alpha}T(s)x_{0}\parallel
&\leq & \int_{s }^{t } \parallel (-A)^{1+\alpha-\gamma} T(\xi)(-A)^{\gamma} x_{0} \parallel\, {\rm d}\xi\\
& \leq & \int_{s }^{t } \frac{C_{0,1+\alpha-\gamma}}{\xi^{1+\alpha-\gamma}}\parallel (-A)^{\gamma} x_{0} \parallel\, {\rm d}\xi\\
& \leq & \frac{C_{0,1+\alpha-\gamma} }{s^{1+\alpha-\gamma} }\parallel (-A)^{\gamma} x_{0} \parallel \mid t-s\mid .
\end{eqnarray*}
\begin{eqnarray*}
\parallel (-A)^{\alpha}T(t)x_{0}- (-A)^{\alpha}T(s)x_{0}\parallel
&\leq & \int_{s }^{t } \parallel (-A)^{1+\alpha-\gamma} T(\xi)(-A)^{\gamma} x_{0} \parallel\, {\rm d}\xi\\
& \leq & \int_{s }^{t } \frac{C_{0,1+\alpha-\gamma}}{\xi^{1+\alpha-\gamma}}\parallel (-A)^{\gamma} x_{0} \parallel\, {\rm d}\xi\\
& \leq & \frac{C_{0,1+\alpha-\gamma} }{s^{1+\alpha-\gamma} }\parallel (-A)^{\gamma} x_{0} \parallel \mid t-s\mid .
\end{eqnarray*}We can now prove our first result on the existence and uniqueness of the solution for Equations (1.1)–(1.2).
Theorem 3.1. Suppose that the condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X_{\alpha})$ is satisfied, that the functions
$\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X_{\alpha})$ is satisfied, that the functions ![]() $ \Theta_{i} (\cdot) $,
$ \Theta_{i} (\cdot) $, ![]() $ i=1,2, $ are well defined and bounded and that
$ i=1,2, $ are well defined and bounded and that ![]() $x_{0}\in X_{\gamma}$ for some
$x_{0}\in X_{\gamma}$ for some ![]() $\gamma\in (\alpha, 1+\alpha)$. Then there exists a unique mild solution
$\gamma\in (\alpha, 1+\alpha)$. Then there exists a unique mild solution ![]() $u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of the problem (1.1)–(1.2) on
$u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of the problem (1.1)–(1.2) on ![]() $[0,b]$ for some
$[0,b]$ for some ![]() $0 \lt b\leq a$.
$0 \lt b\leq a$.
Proof. From Lemma 3.1, we can select  $R \gt C_{0}
\parallel x_{0}\parallel_{\alpha} +
{[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} $. From the assumptions and noting that
$R \gt C_{0}
\parallel x_{0}\parallel_{\alpha} +
{[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} $. From the assumptions and noting that ![]() $ \Psi_{2}( c,R)\to 0 $ and
$ \Psi_{2}( c,R)\to 0 $ and ![]() $ \Theta_{2}(c)\to 0$ as c → 0, we choose
$ \Theta_{2}(c)\to 0$ as c → 0, we choose ![]() $0 \lt b\leq a $ such that
$0 \lt b\leq a $ such that
 \begin{eqnarray}
C_{0 } \parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}} + C_{0 } \Psi_{2}(b,R)+ b^{1+\alpha-\gamma} C_{0} \Psi_{1}(b,R) && \nonumber\\
+ C_{0 } \mathcal{W}_{F,\sigma}(R) \left[ (1+R) ^{2} b^{1+\alpha-\gamma} \Theta_{1}(b) + (1+R) \Theta_{2}(b) \right] & \lt & R,
\end{eqnarray}
\begin{eqnarray}
C_{0 } \parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}} + C_{0 } \Psi_{2}(b,R)+ b^{1+\alpha-\gamma} C_{0} \Psi_{1}(b,R) && \nonumber\\
+ C_{0 } \mathcal{W}_{F,\sigma}(R) \left[ (1+R) ^{2} b^{1+\alpha-\gamma} \Theta_{1}(b) + (1+R) \Theta_{2}(b) \right] & \lt & R,
\end{eqnarray}where ![]() $\mathcal{W}_{F,\sigma}(R)=\mathcal{W}_{F }(R)(1+\mathcal{W}_{\sigma}(R))$, and we write
$\mathcal{W}_{F,\sigma}(R)=\mathcal{W}_{F }(R)(1+\mathcal{W}_{\sigma}(R))$, and we write  $ [\cdot ]_{C_{\rm Lip,1+\alpha-\gamma}} $ in place of
$ [\cdot ]_{C_{\rm Lip,1+\alpha-\gamma}} $ in place of  $ [\cdot]_{C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})} $.
$ [\cdot]_{C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})} $.
Let ![]() $S_{x_0} $ be the space
$S_{x_0} $ be the space
 \begin{equation*}
S_{x_0} = \left\{ u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) : u(0)= x_{0}, \max\{ \parallel u \parallel_{C([0,b];X_{\alpha})}, \, [u]_{C_{\rm Lip,1+\alpha-\gamma} } \right\} \leq R \},\nonumber
\end{equation*}
\begin{equation*}
S_{x_0} = \left\{ u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) : u(0)= x_{0}, \max\{ \parallel u \parallel_{C([0,b];X_{\alpha})}, \, [u]_{C_{\rm Lip,1+\alpha-\gamma} } \right\} \leq R \},\nonumber
\end{equation*}endowed with the metric ![]() $d(u,v)= \parallel u-v\parallel _{C([0,b];X_{\alpha})}
$ and
$d(u,v)= \parallel u-v\parallel _{C([0,b];X_{\alpha})}
$ and ![]() $\Gamma: S_{x_0} \mapsto C([0,b];X)$ be the map given by
$\Gamma: S_{x_0} \mapsto C([0,b];X)$ be the map given by
 \begin{eqnarray}
\Gamma u(t)= T (t) x_{0}+\int^t_0 T(t-s) F\left(s,u^{\sigma}(s)\right)\,{\rm d}s, \qquad \hbox{for}\ t\in [0,b].
\end{eqnarray}
\begin{eqnarray}
\Gamma u(t)= T (t) x_{0}+\int^t_0 T(t-s) F\left(s,u^{\sigma}(s)\right)\,{\rm d}s, \qquad \hbox{for}\ t\in [0,b].
\end{eqnarray} Let ![]() $ u \in S_{x_0} $. Noting that
$ u \in S_{x_0} $. Noting that ![]() $ x_0 \in X_{\alpha} $ and that
$ x_0 \in X_{\alpha} $ and that ![]() $ F(\cdot,u^{\sigma}(\cdot))\in C([0,b];X_{\alpha })$, it is trivial to see that
$ F(\cdot,u^{\sigma}(\cdot))\in C([0,b];X_{\alpha })$, it is trivial to see that ![]() $\Gamma u \in C([0,b];X_{\alpha}) $. In addition, from condition
$\Gamma u \in C([0,b];X_{\alpha}) $. In addition, from condition ![]() $\bf \mathcal{H}_{F, a}(X_{\alpha} ;X_{\alpha})$, we note that
$\bf \mathcal{H}_{F, a}(X_{\alpha} ;X_{\alpha})$, we note that
Using this estimate, for ![]() $t\in [ 0,b]$ we have that
$t\in [ 0,b]$ we have that
 \begin{eqnarray}
\parallel \Gamma u (t) \parallel _{\alpha} & \leq& \int_0^t C_{0} \parallel (-A)^{\alpha} F(\tau,u^{\sigma} (\tau)) \parallel \,{\rm d}\tau + C_{0} \parallel x_{0}\parallel _{\alpha} \nonumber\\
& \leq & C_{0} ( \parallel \varrho_{1}\parallel_{L^{1}([0,b])} \mathcal{K}_{F}(R) +\parallel \varrho_{2}\parallel_{L^{1}([0,b])} ) + C_{0} \parallel x_{0}\parallel _{\alpha} \nonumber\\
& \leq & C_{0} \Psi_{2}(b,R) + C_{0} \parallel x_{0}\parallel _{\alpha} \leq R .
\end{eqnarray}
\begin{eqnarray}
\parallel \Gamma u (t) \parallel _{\alpha} & \leq& \int_0^t C_{0} \parallel (-A)^{\alpha} F(\tau,u^{\sigma} (\tau)) \parallel \,{\rm d}\tau + C_{0} \parallel x_{0}\parallel _{\alpha} \nonumber\\
& \leq & C_{0} ( \parallel \varrho_{1}\parallel_{L^{1}([0,b])} \mathcal{K}_{F}(R) +\parallel \varrho_{2}\parallel_{L^{1}([0,b])} ) + C_{0} \parallel x_{0}\parallel _{\alpha} \nonumber\\
& \leq & C_{0} \Psi_{2}(b,R) + C_{0} \parallel x_{0}\parallel _{\alpha} \leq R .
\end{eqnarray} In addition, for ![]() $ s\in (0,b ) $ and
$ s\in (0,b ) $ and ![]() $ h\in (0,b] $ with
$ h\in (0,b] $ with ![]() $s+h\in ( 0,b]$, we note that
$s+h\in ( 0,b]$, we note that
 \begin{align}
\parallel F(s+h,u^{\sigma}(s+h)) &- F(s,u^{\sigma}(s))\parallel _{\alpha} \hspace{0.5cm} \nonumber\\
&\leq [F]_{(s+h,s)}\mathcal{W}_{F}(R) (h+ \parallel u^{\sigma}(s+h)-u^{\sigma}(s)\parallel_{\alpha}) \nonumber\\
&\leq [F]_{(s+h,s)}\mathcal{W}_{F}(R) \left(h+ \frac{[u ]_{ C_{\rm Lip,1+\alpha-\gamma} } }{ \xi^{1+\alpha-\gamma }(s) }\mathcal{W}_{\sigma}(R)[\sigma]_{(s+h,s)}\right. \nonumber \\ & \quad \left.\left(h + \frac{[u ]_{ C_{\rm Lip,1+\alpha-\gamma} }}{s^{1+\alpha-\gamma}} h\right) \right) \nonumber\\
&\leq [F]_{(s+h,s)}\mathcal{W}_{F}(R) \left(h+ \frac{R \mathcal{W}_{\sigma}(R)}{ \xi^{1+\alpha-\gamma }(s) }[\sigma]_{(s+h,s)} \left(h + \frac{R}{s^{1+\alpha-\gamma}} h\right) \right) \nonumber \\
&\leq \mathcal{W}_{F}(R) (1+\mathcal{W}_{\sigma}(R)) (1 + R)^{2} [F]_{(s+h,s)}\left(1+\frac{[\sigma]_{(s+h,s)} }{ \xi^{1+\alpha-\gamma }(s) }\right.\nonumber \\ & \quad\left.\left(1 + \frac{1 }{s^{1+\alpha-\gamma}} \right) \right) h \nonumber \\
&\leq \mathcal{W}_{F,\sigma}(R) (1 + R)^{2}
[F]_{(s+h,s)}(1+[\sigma]_{(s+h,s)})\left( 1+ \frac{1 }{ \xi^{1+\alpha-\gamma }(s) }\right. \nonumber \\ & \quad\left.\left(1 + \frac{1 }{s^{1+\alpha-\gamma}} \right)\right) h \nonumber \\
&\leq \mathcal{W}_{F,\sigma}(R) (1 + R)^{2}
[F]_{(s+h,s)}(1+[\sigma]_{(s+h,s)})\left( 1+ \frac{1 }{ \xi^{1+\alpha-\gamma }(s) }\right)\nonumber \\ &\quad\left( 1+ \frac{1 }{s^{1+\alpha-\gamma}} \right) h,
\end{align}
\begin{align}
\parallel F(s+h,u^{\sigma}(s+h)) &- F(s,u^{\sigma}(s))\parallel _{\alpha} \hspace{0.5cm} \nonumber\\
&\leq [F]_{(s+h,s)}\mathcal{W}_{F}(R) (h+ \parallel u^{\sigma}(s+h)-u^{\sigma}(s)\parallel_{\alpha}) \nonumber\\
&\leq [F]_{(s+h,s)}\mathcal{W}_{F}(R) \left(h+ \frac{[u ]_{ C_{\rm Lip,1+\alpha-\gamma} } }{ \xi^{1+\alpha-\gamma }(s) }\mathcal{W}_{\sigma}(R)[\sigma]_{(s+h,s)}\right. \nonumber \\ & \quad \left.\left(h + \frac{[u ]_{ C_{\rm Lip,1+\alpha-\gamma} }}{s^{1+\alpha-\gamma}} h\right) \right) \nonumber\\
&\leq [F]_{(s+h,s)}\mathcal{W}_{F}(R) \left(h+ \frac{R \mathcal{W}_{\sigma}(R)}{ \xi^{1+\alpha-\gamma }(s) }[\sigma]_{(s+h,s)} \left(h + \frac{R}{s^{1+\alpha-\gamma}} h\right) \right) \nonumber \\
&\leq \mathcal{W}_{F}(R) (1+\mathcal{W}_{\sigma}(R)) (1 + R)^{2} [F]_{(s+h,s)}\left(1+\frac{[\sigma]_{(s+h,s)} }{ \xi^{1+\alpha-\gamma }(s) }\right.\nonumber \\ & \quad\left.\left(1 + \frac{1 }{s^{1+\alpha-\gamma}} \right) \right) h \nonumber \\
&\leq \mathcal{W}_{F,\sigma}(R) (1 + R)^{2}
[F]_{(s+h,s)}(1+[\sigma]_{(s+h,s)})\left( 1+ \frac{1 }{ \xi^{1+\alpha-\gamma }(s) }\right. \nonumber \\ & \quad\left.\left(1 + \frac{1 }{s^{1+\alpha-\gamma}} \right)\right) h \nonumber \\
&\leq \mathcal{W}_{F,\sigma}(R) (1 + R)^{2}
[F]_{(s+h,s)}(1+[\sigma]_{(s+h,s)})\left( 1+ \frac{1 }{ \xi^{1+\alpha-\gamma }(s) }\right)\nonumber \\ &\quad\left( 1+ \frac{1 }{s^{1+\alpha-\gamma}} \right) h,
\end{align}and hence,
 \begin{align}
\parallel F(s+h,u^{\sigma}(s+h))-F(s,u^{\sigma}(s))\!\!\parallel_{\alpha}
\leq \mathcal{W}_{F,\sigma}(R) (1 + R)^{2}
[F]_{(s+h,s)}(1+[\sigma]_{(s+h,s)}) \Lambda^{2}(s) h .
\end{align}
\begin{align}
\parallel F(s+h,u^{\sigma}(s+h))-F(s,u^{\sigma}(s))\!\!\parallel_{\alpha}
\leq \mathcal{W}_{F,\sigma}(R) (1 + R)^{2}
[F]_{(s+h,s)}(1+[\sigma]_{(s+h,s)}) \Lambda^{2}(s) h .
\end{align} From Equation (3.6), for ![]() $t \in (0,b]$ and
$t \in (0,b]$ and ![]() $h\in [0,b]$ with
$h\in [0,b]$ with ![]() $t+h\in [0,b]$, we get
$t+h\in [0,b]$, we get
 \begin{align}
\parallel \Gamma u (t+h) &- \Gamma u (t)\parallel _\alpha \hspace{1cm} \nonumber\\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} + \int_0^h \parallel T( t+h-\tau ) \parallel \parallel F(\tau,u^{\sigma} (\tau)) \parallel_{\alpha} \, {\rm d}\tau \nonumber \\
& + \int_0^t C_{0 } \parallel F(\tau+h,u^\sigma(\tau+h)) - F(\tau,u^\sigma(\tau)) \parallel_{\alpha}\, {\rm d}\tau \nonumber \\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} + C_{0 }\left( \parallel \varrho_{1}\parallel_{L^{\infty}([0,b])} \mathcal{K}_{F}(R) +
\parallel \varrho_{2}\parallel_{L^{\infty}([0,b])} \right) h \nonumber\\
&+ \mathcal{W}_{F,\sigma}(R) (1 + R)^{2} C_{0 } \int_0^t
[F]_{(\tau+h,\tau)} (1+[\sigma]_{(\tau+h,\tau)}) \Lambda^{2}(\tau) h \,{\rm d}\tau \nonumber\\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} + C_{0 } \Psi_{1}(b,R) h + C_{0 } \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{1}(b) h ,
\end{align}
\begin{align}
\parallel \Gamma u (t+h) &- \Gamma u (t)\parallel _\alpha \hspace{1cm} \nonumber\\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} + \int_0^h \parallel T( t+h-\tau ) \parallel \parallel F(\tau,u^{\sigma} (\tau)) \parallel_{\alpha} \, {\rm d}\tau \nonumber \\
& + \int_0^t C_{0 } \parallel F(\tau+h,u^\sigma(\tau+h)) - F(\tau,u^\sigma(\tau)) \parallel_{\alpha}\, {\rm d}\tau \nonumber \\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} + C_{0 }\left( \parallel \varrho_{1}\parallel_{L^{\infty}([0,b])} \mathcal{K}_{F}(R) +
\parallel \varrho_{2}\parallel_{L^{\infty}([0,b])} \right) h \nonumber\\
&+ \mathcal{W}_{F,\sigma}(R) (1 + R)^{2} C_{0 } \int_0^t
[F]_{(\tau+h,\tau)} (1+[\sigma]_{(\tau+h,\tau)}) \Lambda^{2}(\tau) h \,{\rm d}\tau \nonumber\\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} + C_{0 } \Psi_{1}(b,R) h + C_{0 } \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{1}(b) h ,
\end{align}and hence,
 \begin{eqnarray}
[\Gamma u ]_{ C_{\rm Lip,1+\alpha-\gamma} } & \leq & [T(\cdot)x_0]_{ C_{Lip,1+\alpha-\gamma} }
+ C_{0 } b^{1+\alpha-\gamma} ( \Psi_{1}(b,R) + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{1}(b) ) \nonumber\\
& \leq & R.
\end{eqnarray}
\begin{eqnarray}
[\Gamma u ]_{ C_{\rm Lip,1+\alpha-\gamma} } & \leq & [T(\cdot)x_0]_{ C_{Lip,1+\alpha-\gamma} }
+ C_{0 } b^{1+\alpha-\gamma} ( \Psi_{1}(b,R) + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{1}(b) ) \nonumber\\
& \leq & R.
\end{eqnarray} From Equations (3.4) and (3.8), we conclude that ![]() $\Gamma(\cdot )$ is a
$\Gamma(\cdot )$ is a ![]() $\mathcal{S}_{x_0}$-valued function.
$\mathcal{S}_{x_0}$-valued function.
In order to estimate ![]() $ \parallel \Gamma u -\Gamma v \parallel_{C([0,b];X_{\alpha})} $, for
$ \parallel \Gamma u -\Gamma v \parallel_{C([0,b];X_{\alpha})} $, for ![]() $u,v\in \mathcal{S}_{x_0}$ and
$u,v\in \mathcal{S}_{x_0}$ and ![]() $s\in (0,b]$, we note that
$s\in (0,b]$, we note that
 \begin{align}
\!\parallel u^{\sigma}(s)- v^{\sigma}(s) \parallel_{\alpha}
& \leq \ \parallel u(\sigma(s,u(s))) - v(\sigma(s,u(s)))\parallel_{\alpha} + \parallel v(\sigma(s,u(s))) - v(\sigma(s,v(s)))\parallel_{\alpha} \nonumber \\
& \leq \ \parallel u-v\parallel_{C((0,b];X_{\alpha})} + \frac{[v]_{C_{\rm Lip,1+\alpha-\gamma }}}{\xi^{1+\alpha-\gamma} (s)} |\sigma(s,u(s)) - \sigma(s,v(s))| \nonumber \\
& \leq \ \parallel u-v\parallel _{C((0,b];X_{\alpha})} + \frac{R [\sigma]_{(s,s)}\mathcal{W}_{\sigma}(R)}{\xi^{1+\alpha-\gamma} (s)}\parallel u-v\parallel_{C((0,b];X_{\alpha})} \nonumber \\
& \leq \left( 1 + \frac{R[\sigma]_{(s,s)}\mathcal{W}_{\sigma}(R) }{\xi^{1+\alpha-\gamma} (s) } \right) \parallel u-v\parallel_{C((0,b];X_{\alpha})} \nonumber \\
& \leq (1+R [\sigma]_{(s,s)} \mathcal{W}_{\sigma}(R) )\left(1+ \frac{1}{\xi^{1+\alpha-\gamma} (s) } \right) \parallel u-v\parallel_{C((0,b];X_{\alpha})} \nonumber \\
& \leq (1+R) (1+ \mathcal{W}_{\sigma}(R)) (1 + [\sigma]_{(s,s)} ) \Lambda (s) \parallel u-v\parallel_{C((0,b];X_{\alpha})}.
\end{align}
\begin{align}
\!\parallel u^{\sigma}(s)- v^{\sigma}(s) \parallel_{\alpha}
& \leq \ \parallel u(\sigma(s,u(s))) - v(\sigma(s,u(s)))\parallel_{\alpha} + \parallel v(\sigma(s,u(s))) - v(\sigma(s,v(s)))\parallel_{\alpha} \nonumber \\
& \leq \ \parallel u-v\parallel_{C((0,b];X_{\alpha})} + \frac{[v]_{C_{\rm Lip,1+\alpha-\gamma }}}{\xi^{1+\alpha-\gamma} (s)} |\sigma(s,u(s)) - \sigma(s,v(s))| \nonumber \\
& \leq \ \parallel u-v\parallel _{C((0,b];X_{\alpha})} + \frac{R [\sigma]_{(s,s)}\mathcal{W}_{\sigma}(R)}{\xi^{1+\alpha-\gamma} (s)}\parallel u-v\parallel_{C((0,b];X_{\alpha})} \nonumber \\
& \leq \left( 1 + \frac{R[\sigma]_{(s,s)}\mathcal{W}_{\sigma}(R) }{\xi^{1+\alpha-\gamma} (s) } \right) \parallel u-v\parallel_{C((0,b];X_{\alpha})} \nonumber \\
& \leq (1+R [\sigma]_{(s,s)} \mathcal{W}_{\sigma}(R) )\left(1+ \frac{1}{\xi^{1+\alpha-\gamma} (s) } \right) \parallel u-v\parallel_{C((0,b];X_{\alpha})} \nonumber \\
& \leq (1+R) (1+ \mathcal{W}_{\sigma}(R)) (1 + [\sigma]_{(s,s)} ) \Lambda (s) \parallel u-v\parallel_{C((0,b];X_{\alpha})}.
\end{align} Using this inequality, for ![]() $t\in (0,b]$, it is easy to see that
$t\in (0,b]$, it is easy to see that
 \begin{align}
\parallel \Gamma u (t) &- \Gamma v (t)\parallel_{C([0,b];X_{\alpha})} \hspace{1cm} \nonumber\\
&\leq C_{0 } \mathcal{W}_{F }(R) \int^t_0 [F]_{(\tau,\tau)} \parallel u^{\sigma}(\tau)- v^{\sigma}(\tau)\parallel _{\alpha}\, {\rm d}\tau \nonumber\\
&\leq C_{0 } (1+R) \mathcal{W}_{F,\sigma}(R) \int_0^t [F]_{(\tau,\tau)} (1 + [\sigma]_{(\tau,\tau)} ) \Lambda (\tau) \,{\rm d}\tau \parallel u-v\parallel_{C((0,b];X_{\alpha})}\nonumber\\
&\leq C_{0 } (1+R) \mathcal{W}_{F,\sigma}(R) \Theta_{2}(b) \parallel u-v\parallel_{C([0,b];X_{\alpha})},
\end{align}
\begin{align}
\parallel \Gamma u (t) &- \Gamma v (t)\parallel_{C([0,b];X_{\alpha})} \hspace{1cm} \nonumber\\
&\leq C_{0 } \mathcal{W}_{F }(R) \int^t_0 [F]_{(\tau,\tau)} \parallel u^{\sigma}(\tau)- v^{\sigma}(\tau)\parallel _{\alpha}\, {\rm d}\tau \nonumber\\
&\leq C_{0 } (1+R) \mathcal{W}_{F,\sigma}(R) \int_0^t [F]_{(\tau,\tau)} (1 + [\sigma]_{(\tau,\tau)} ) \Lambda (\tau) \,{\rm d}\tau \parallel u-v\parallel_{C((0,b];X_{\alpha})}\nonumber\\
&\leq C_{0 } (1+R) \mathcal{W}_{F,\sigma}(R) \Theta_{2}(b) \parallel u-v\parallel_{C([0,b];X_{\alpha})},
\end{align} which implies, see Equation (3.1), that ![]() $\Gamma(\cdot)$ is a contraction from
$\Gamma(\cdot)$ is a contraction from ![]() $\mathcal{S}_{x_0} $ into
$\mathcal{S}_{x_0} $ into ![]() $\mathcal{S}_{x_0} $. Thus, there exists a unique mild solution
$\mathcal{S}_{x_0} $. Thus, there exists a unique mild solution ![]() $u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of the problem (1.1)–(1.2) on
$u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of the problem (1.1)–(1.2) on ![]() $[0,b]$.
$[0,b]$.
Remark 3.3. Let ![]() $u(\cdot)$ be the mild solution in Theorem 3.1 and
$u(\cdot)$ be the mild solution in Theorem 3.1 and ![]() $0 \lt \varepsilon \lt b$. From the definition of
$0 \lt \varepsilon \lt b$. From the definition of ![]() $
C_{Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $, it is obvious that
$
C_{Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $, it is obvious that ![]() $u_{\mid{[\varepsilon,b]}}\in C_{\rm Lip}([\varepsilon,b];X_{\alpha}) $ and
$u_{\mid{[\varepsilon,b]}}\in C_{\rm Lip}([\varepsilon,b];X_{\alpha}) $ and  $[u]_{C_{\rm Lip }([\varepsilon,b];X_{\alpha})}\leq [u]_{C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})}\varepsilon^{-(1+\alpha-\gamma)} $. Moreover, if
$[u]_{C_{\rm Lip }([\varepsilon,b];X_{\alpha})}\leq [u]_{C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})}\varepsilon^{-(1+\alpha-\gamma)} $. Moreover, if ![]() $\sigma(\cdot) $ is Lipschitz, by using that
$\sigma(\cdot) $ is Lipschitz, by using that ![]() $\sigma(t,x)\geq \xi(t) \geq \xi(\varepsilon) \gt 0$ for all
$\sigma(t,x)\geq \xi(t) \geq \xi(\varepsilon) \gt 0$ for all ![]() $t\in [\varepsilon,b]$ and Lemma 2.2, we obtain that
$t\in [\varepsilon,b]$ and Lemma 2.2, we obtain that
 \begin{equation*}[u^{\sigma}]_{C_{\rm Lip }([\varepsilon,b];X_{\alpha})}\leq {[u]_{C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})}} \xi^{-1}(\varepsilon) [\sigma]_{C_{\rm Lip}} (1+[u]_{C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})}\varepsilon^{-(1+\alpha-\gamma)} ) . \end{equation*}
\begin{equation*}[u^{\sigma}]_{C_{\rm Lip }([\varepsilon,b];X_{\alpha})}\leq {[u]_{C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})}} \xi^{-1}(\varepsilon) [\sigma]_{C_{\rm Lip}} (1+[u]_{C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})}\varepsilon^{-(1+\alpha-\gamma)} ) . \end{equation*} From the above, we have that ![]() $u_{\mid{[\varepsilon,b]}}$ and
$u_{\mid{[\varepsilon,b]}}$ and  $u^{\sigma}_{\mid{[\varepsilon,b]}}$ belongs to
$u^{\sigma}_{\mid{[\varepsilon,b]}}$ belongs to ![]() $ C_{\rm Lip}([\varepsilon,b];X_{\alpha}) $ for all
$ C_{\rm Lip}([\varepsilon,b];X_{\alpha}) $ for all ![]() $0 \lt \varepsilon \lt b$.
$0 \lt \varepsilon \lt b$.
Notation.
For convenience, in the remainder of this work, if non-confusion arise, we write simply  $ [\cdot ]_{C_{\rm Lip,1+\alpha-\gamma}} $ in place of
$ [\cdot ]_{C_{\rm Lip,1+\alpha-\gamma}} $ in place of  $ [\cdot]_{C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})} $.
$ [\cdot]_{C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})} $.
From the proof of Theorem 3.1, we infer the next results on the existence of solution defined on ![]() $[0,a]$.
$[0,a]$.
Corollary 3.1. Assume that the condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X_{\alpha})$ is satisfied that the functions
$\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X_{\alpha})$ is satisfied that the functions ![]() $ \Theta_{i} (\cdot) $,
$ \Theta_{i} (\cdot) $, ![]() $ i=1,2 $, are well defined and bounded and that
$ i=1,2 $, are well defined and bounded and that ![]() $x_{0}\in X_{\gamma}$. Let
$x_{0}\in X_{\gamma}$. Let ![]() $P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function given by
$P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function given by
 \begin{align*}
P_{a} (x) & = C_{0 }\parallel x_{0}\parallel_{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0 } \Psi_{2}(a,x) + C_{0 } \Psi_{1}( a,x) a^{1+\alpha-\gamma}\\
&+C_{0 } \mathcal{W}_{F,\sigma}(x) \left[ (1+x) ^{2} a^{1+\alpha-\gamma} \Theta_{1}(a) + (1+x) \Theta_{2}(a) \right] -x,
\end{align*}
\begin{align*}
P_{a} (x) & = C_{0 }\parallel x_{0}\parallel_{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0 } \Psi_{2}(a,x) + C_{0 } \Psi_{1}( a,x) a^{1+\alpha-\gamma}\\
&+C_{0 } \mathcal{W}_{F,\sigma}(x) \left[ (1+x) ^{2} a^{1+\alpha-\gamma} \Theta_{1}(a) + (1+x) \Theta_{2}(a) \right] -x,
\end{align*}where ![]() $\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. If
$\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. If ![]() $P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution
$P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution ![]() $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a]; X_{\alpha})$ of Equations (1.1)–(1.2) on
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a]; X_{\alpha})$ of Equations (1.1)–(1.2) on ![]() $[0,a]$.
$[0,a]$.
Proof. The condition ![]() $P_{a}(R) \lt 0$ implies that the inequality (3.1) is satisfied with ‘a’ in place ‘b’, which allows us to complete the proof arguing as in the proof of Theorem 3.1.
$P_{a}(R) \lt 0$ implies that the inequality (3.1) is satisfied with ‘a’ in place ‘b’, which allows us to complete the proof arguing as in the proof of Theorem 3.1.
If the functions ![]() $F(\cdot)$ and
$F(\cdot)$ and ![]() $\sigma(\cdot)$ are Lipschitz, we get the following:
$\sigma(\cdot)$ are Lipschitz, we get the following:
Corollary 3.2. Let the condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X_{\alpha})$ hold. Assume that
$\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X_{\alpha})$ hold. Assume that ![]() $ F(\cdot)$ and
$ F(\cdot)$ and ![]() $\sigma(\cdot)$ are Lipschitz, that
$\sigma(\cdot)$ are Lipschitz, that ![]() $ \Lambda^{2} (\cdot)$ is integrable on
$ \Lambda^{2} (\cdot)$ is integrable on ![]() $[0,a]$ and let
$[0,a]$ and let ![]() $P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function given by
$P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function given by
 \begin{align*}
P_{a} (x) & = C_{0 } \parallel x_{0}\parallel_{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0 } \Psi_{2}(a,x) + C_{0 } \Psi_{1}( a,x) a^{1+\alpha-\gamma}\\
& \quad + 2 [F]_{C_{\rm Lip}} (1+ [\sigma]_{C_{Lip}}) C_{0 } \left( (1+x) ^{2} a^{1+\alpha-\gamma}\parallel \Lambda^{2}\parallel_{L^{1}([0,a])}\right. \\
&\quad \left. + (1+x) \parallel \Lambda \parallel_{L^{1}([0,a])} \right) -x \\
&= \theta + (1+x) ^{2}\eta_{1} + (1+x) \eta_{2} -x .
\end{align*}
\begin{align*}
P_{a} (x) & = C_{0 } \parallel x_{0}\parallel_{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0 } \Psi_{2}(a,x) + C_{0 } \Psi_{1}( a,x) a^{1+\alpha-\gamma}\\
& \quad + 2 [F]_{C_{\rm Lip}} (1+ [\sigma]_{C_{Lip}}) C_{0 } \left( (1+x) ^{2} a^{1+\alpha-\gamma}\parallel \Lambda^{2}\parallel_{L^{1}([0,a])}\right. \\
&\quad \left. + (1+x) \parallel \Lambda \parallel_{L^{1}([0,a])} \right) -x \\
&= \theta + (1+x) ^{2}\eta_{1} + (1+x) \eta_{2} -x .
\end{align*} If ![]() $P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution
$P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution ![]() $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a];X)$ of the problem (1.1)–(1.2) on
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a];X)$ of the problem (1.1)–(1.2) on ![]() $[0,a]$. In particular, if
$[0,a]$. In particular, if ![]() $P(({1-2\eta_{1}-\eta_{2}})/{2\eta_{1}} ) \lt 0$ and
$P(({1-2\eta_{1}-\eta_{2}})/{2\eta_{1}} ) \lt 0$ and ![]() $P(\cdot)$ has a positive root, then there exists a unique mild solution
$P(\cdot)$ has a positive root, then there exists a unique mild solution ![]() $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a];X)$ of (1.1)–(1.2) on
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a];X)$ of (1.1)–(1.2) on ![]() $[0,a]$.
$[0,a]$.
Proof. The first assertion follows from Corollary 3.1 using ![]() $
\mathcal{W}_{F}(\theta)=\mathcal{W}_{\sigma}(\theta)=1$,
$
\mathcal{W}_{F}(\theta)=\mathcal{W}_{\sigma}(\theta)=1$,  $[F]_{(t,s)}=[F]_{C_{\rm Lip}} $ and
$[F]_{(t,s)}=[F]_{C_{\rm Lip}} $ and  $[\sigma]_{(t,s)}=[\sigma]_{C_{\rm Lip}}$. In addition, if
$[\sigma]_{(t,s)}=[\sigma]_{C_{\rm Lip}}$. In addition, if ![]() $P(({1-2\eta_{1}-\eta_{2}})/{2\eta_{1}} ) \lt 0$ and
$P(({1-2\eta_{1}-\eta_{2}})/{2\eta_{1}} ) \lt 0$ and ![]() $R_{1} \gt 0$ is a positive roof of
$R_{1} \gt 0$ is a positive roof of ![]() $P_{a}(\cdot)$, by noting that
$P_{a}(\cdot)$, by noting that ![]() $({1-2\eta_{1}-\eta_{2}})/{2\eta_{1}} $ is the global minimum point of
$({1-2\eta_{1}-\eta_{2}})/{2\eta_{1}} $ is the global minimum point of ![]() $P(\cdot)$, it follows that there exists R between
$P(\cdot)$, it follows that there exists R between ![]() $({1-2\eta_{1}-\eta_{2}})/{2\eta_{1}} $ and R 1 such that
$({1-2\eta_{1}-\eta_{2}})/{2\eta_{1}} $ and R 1 such that ![]() $P(R) \lt 0$, which allows us to prove the assertion.
$P(R) \lt 0$, which allows us to prove the assertion.
Remark 3.4. For convenience, in the remainder of this work, if the condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma}(Y_{1},Y_{2})$ is satisfied, we assume that the functions in Notation 1 are well defined and bounded.
$\bf H_{F,\sigma, a}^{\alpha,\gamma}(Y_{1},Y_{2})$ is satisfied, we assume that the functions in Notation 1 are well defined and bounded.
Concerning Corollary 3.3 below, which is an obvious consequence of Theorem 3.1, we alert that the objective of this result modifies some parts of the proof of Theorem 3.1 in order to develop our studies on the existence and uniqueness of solution on ![]() $[0,\infty)$ using the idea in Corollary 3.1. Specifically, we want to modify the definition of the map
$[0,\infty)$ using the idea in Corollary 3.1. Specifically, we want to modify the definition of the map ![]() $P_{a}(\cdot)$ in Corollary 3.1.
$P_{a}(\cdot)$ in Corollary 3.1.
Corollary 3.3. In addition to the conditions in Theorem 3.1, assume that ![]() $\Theta_{1}(c)\to 0$ as c → 0 and that
$\Theta_{1}(c)\to 0$ as c → 0 and that  $
C_{0} \parallel \varrho_{1}\parallel_{L^{\infty}([0,a])} \limsup_{r\to \infty} \frac{\mathcal{K}_{F}(r)}{r} \lt 1. $ Then there exists a unique mild solution
$
C_{0} \parallel \varrho_{1}\parallel_{L^{\infty}([0,a])} \limsup_{r\to \infty} \frac{\mathcal{K}_{F}(r)}{r} \lt 1. $ Then there exists a unique mild solution ![]() $u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of (1.1)–(1.2) on
$u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of (1.1)–(1.2) on ![]() $[0,b]$ for some
$[0,b]$ for some ![]() $0 \lt b\leq a$.
$0 \lt b\leq a$.
Proof. To begin, we select R > 0 such that
 \begin{align}
R & \gt C_{0} \parallel x_{0}\parallel_{\alpha}
+ [T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})} + C_{0} ( \parallel \varrho_{1}\parallel_{L^{\infty}([0,a])} \mathcal{K}_{F}(R)\nonumber\\
&\quad + \parallel \varrho_{2}\parallel_{L^{\infty}([0,a])} ) \nonumber\\
& = C_{0} \parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})} + C_{0} \Psi_{1} (a,R).
\end{align}
\begin{align}
R & \gt C_{0} \parallel x_{0}\parallel_{\alpha}
+ [T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})} + C_{0} ( \parallel \varrho_{1}\parallel_{L^{\infty}([0,a])} \mathcal{K}_{F}(R)\nonumber\\
&\quad + \parallel \varrho_{2}\parallel_{L^{\infty}([0,a])} ) \nonumber\\
& = C_{0} \parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})} + C_{0} \Psi_{1} (a,R).
\end{align} Using the assumptions on the functions ![]() $\Theta_{i}(\cdot)$ and the fact that
$\Theta_{i}(\cdot)$ and the fact that ![]() $ \Psi_{2}(c,R)\to 0 $ as c → 0, we select
$ \Psi_{2}(c,R)\to 0 $ as c → 0, we select ![]() $0 \lt b\leq \min\{a,1\}$ such that
$0 \lt b\leq \min\{a,1\}$ such that
 \begin{eqnarray}
C_{0 } \parallel x_{0}\parallel_{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0} \Psi_{1}(a,R)&& \nonumber\\
+ C_{0 } \Psi_{2}(b,R) + C_{0 } \mathcal{W}_{F,\sigma}(R) \left( (1+R) ^{2} \Theta_{1}(b) + (1+R) \Theta_{2}(b) \right) \lt R,
\end{eqnarray}
\begin{eqnarray}
C_{0 } \parallel x_{0}\parallel_{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0} \Psi_{1}(a,R)&& \nonumber\\
+ C_{0 } \Psi_{2}(b,R) + C_{0 } \mathcal{W}_{F,\sigma}(R) \left( (1+R) ^{2} \Theta_{1}(b) + (1+R) \Theta_{2}(b) \right) \lt R,
\end{eqnarray}where ![]() $\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$.
$\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$.
Let ![]() $ {S_{x_0}} $ and
$ {S_{x_0}} $ and ![]() $\Gamma(\cdot)$ be defined as in the proof of Theorem 3.1. A review of the proof of Theorem 3.1 allows us to infer that the inequalities (3.4) and (3.6) remain valid, which implies that
$\Gamma(\cdot)$ be defined as in the proof of Theorem 3.1. A review of the proof of Theorem 3.1 allows us to infer that the inequalities (3.4) and (3.6) remain valid, which implies that ![]() $\parallel \Gamma
u (t) \parallel _{\alpha} \leq R $ for all
$\parallel \Gamma
u (t) \parallel _{\alpha} \leq R $ for all ![]() $t\in
[0,b]$ and that
$t\in
[0,b]$ and that
 \begin{align}
[\Gamma u ]_{ C_{\rm Lip,1+\alpha-\gamma} } & \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } + b^{1+\alpha-\gamma} C_{0 } \Psi_{1}( b,x) + C_{0 } \mathcal{W}_{F,\sigma}(R)\nonumber\\& \quad (1+R) ^{2} b^{1+\alpha-\gamma} \Theta_{1}(b) \nonumber\\
&\leq [T(\cdot)x_0]_{ C_{Lip,1+\alpha-\gamma} } + C_{0 } \Psi_{1}( b,x) + C_{0 } \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{1}(b) \leq R
\end{align}
\begin{align}
[\Gamma u ]_{ C_{\rm Lip,1+\alpha-\gamma} } & \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } + b^{1+\alpha-\gamma} C_{0 } \Psi_{1}( b,x) + C_{0 } \mathcal{W}_{F,\sigma}(R)\nonumber\\& \quad (1+R) ^{2} b^{1+\alpha-\gamma} \Theta_{1}(b) \nonumber\\
&\leq [T(\cdot)x_0]_{ C_{Lip,1+\alpha-\gamma} } + C_{0 } \Psi_{1}( b,x) + C_{0 } \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{1}(b) \leq R
\end{align}because ![]() $0 \lt b \lt 1$. This proves that
$0 \lt b \lt 1$. This proves that ![]() $\Gamma (\cdot)$ is an
$\Gamma (\cdot)$ is an ![]() ${S_{x_0}}$-valued function. We also note that the estimates (3.9) and (3.10) are also satisfied, which allows us to infer that
${S_{x_0}}$-valued function. We also note that the estimates (3.9) and (3.10) are also satisfied, which allows us to infer that ![]() $\Gamma(\cdot)$ is a contraction. This allows us to finish the proof.
$\Gamma(\cdot)$ is a contraction. This allows us to finish the proof.
Corollary 3.4. Assume that the conditions in Corollary 3.3 are satisfied and let ![]() $P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function defined by
$P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function defined by
 \begin{align}
P_{a} (x) & = C_{0 } \parallel x_{0}\parallel_{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0} ( \Psi_{1}(a,x) +\Psi_{2}(a,{ x}) )\nonumber\\
& \quad + C_{0 } \mathcal{W}_{F,\sigma}(x) ( (1+x) ^{2} \Theta_{1}(a) + (1+x) \Theta_{2}(a)) -x,
\end{align}
\begin{align}
P_{a} (x) & = C_{0 } \parallel x_{0}\parallel_{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0} ( \Psi_{1}(a,x) +\Psi_{2}(a,{ x}) )\nonumber\\
& \quad + C_{0 } \mathcal{W}_{F,\sigma}(x) ( (1+x) ^{2} \Theta_{1}(a) + (1+x) \Theta_{2}(a)) -x,
\end{align}where ![]() $\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. If
$\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. If ![]() $P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution
$P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution ![]() $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a];X)$ of (1.1)–(1.2) on
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a];X)$ of (1.1)–(1.2) on ![]() $[0,a]$.
$[0,a]$.
Proof. If ![]() $a\leq 1$, from the definition of
$a\leq 1$, from the definition of ![]() $ P_{a}(\cdot)$, we have that the inequality (3.12) is satisfied with ‘a’ in place of ‘b’, which allows us to use the proof of Corollary 3.3 to prove the assertion.
$ P_{a}(\cdot)$, we have that the inequality (3.12) is satisfied with ‘a’ in place of ‘b’, which allows us to use the proof of Corollary 3.3 to prove the assertion.
Suppose a > 1. Let  $\widehat{S_{x_0} } $ be the space
$\widehat{S_{x_0} } $ be the space
 \begin{align}
\widehat{S_{x_0} } & =
\left\{ u\in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha}) : u(0)= x_{0}, \, \parallel u\parallel_{C ([0,a];X_{\alpha}) } \leq R,\, \right.\nonumber\\
& \hspace{1cm} \hspace{1cm}\hspace{1cm} \left. [u]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha}) } \leq R, [u]_{C_{\rm Lip} ([1,a];X_{\alpha}) } \leq R \right\}
\end{align}
\begin{align}
\widehat{S_{x_0} } & =
\left\{ u\in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha}) : u(0)= x_{0}, \, \parallel u\parallel_{C ([0,a];X_{\alpha}) } \leq R,\, \right.\nonumber\\
& \hspace{1cm} \hspace{1cm}\hspace{1cm} \left. [u]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha}) } \leq R, [u]_{C_{\rm Lip} ([1,a];X_{\alpha}) } \leq R \right\}
\end{align}endowed with the metric ![]() $d(u,v)= \parallel u-v\parallel _{C([0,a];X_{\alpha})}
$ and
$d(u,v)= \parallel u-v\parallel _{C([0,a];X_{\alpha})}
$ and  $\Gamma: \widehat{S_{x_0} } \mapsto C([0,a];X)$ be defined as in the proof of Theorem 3.1.
$\Gamma: \widehat{S_{x_0} } \mapsto C([0,a];X)$ be defined as in the proof of Theorem 3.1.
Using that ![]() $P_{a}(R) \lt 0$, it follows that the inequality (3.12) is satisfied. In addition, observing that the estimates (3.3) and (3.6) are satisfied with ‘a’ in place of ‘b’, it is easy to show that Equations (3.4) and (3.7) are also satisfied. In particular, from Equation (3.7), for
$P_{a}(R) \lt 0$, it follows that the inequality (3.12) is satisfied. In addition, observing that the estimates (3.3) and (3.6) are satisfied with ‘a’ in place of ‘b’, it is easy to show that Equations (3.4) and (3.7) are also satisfied. In particular, from Equation (3.7), for ![]() $t \in (0,a]$ and h > 0 with
$t \in (0,a]$ and h > 0 with ![]() $t+h\in [0,a]$, we have that
$t+h\in [0,a]$, we have that
 \begin{align}
\parallel \Gamma u (t+h) - \Gamma u (t)\parallel _\alpha
& \leq {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} \frac{h}{t^{1+\alpha-\gamma}} + C_{0 } \Psi_{1}( a,R) h \nonumber \\
& + \mathcal{W}_{F,\sigma}( R ) (1+R) ^{2} C_{0 } \Theta_{1}(a) h.
\end{align}
\begin{align}
\parallel \Gamma u (t+h) - \Gamma u (t)\parallel _\alpha
& \leq {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} \frac{h}{t^{1+\alpha-\gamma}} + C_{0 } \Psi_{1}( a,R) h \nonumber \\
& + \mathcal{W}_{F,\sigma}( R ) (1+R) ^{2} C_{0 } \Theta_{1}(a) h.
\end{align}Using this inequality, it is easy to see that
 \begin{align}
[\Gamma u ]_{ C_{\rm Lip,1+\alpha-\gamma} ((0,1];X_{\alpha})} & \leq {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0 } \Psi_{1}( a,R) \nonumber \\
& + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} C_{0 } \Theta_{1}(a) \leq R.
\end{align}
\begin{align}
[\Gamma u ]_{ C_{\rm Lip,1+\alpha-\gamma} ((0,1];X_{\alpha})} & \leq {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0 } \Psi_{1}( a,R) \nonumber \\
& + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} C_{0 } \Theta_{1}(a) \leq R.
\end{align} Moreover, from Equation (3.16), for ![]() $t\in [1,a]$ and h > 0 with
$t\in [1,a]$ and h > 0 with ![]() $t+h\in [1,a]$, we have that
$t+h\in [1,a]$, we have that
 \begin{align}
\parallel \Gamma u (t+h) - \Gamma u (t)\parallel _\alpha & \leq {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} h + C_{0 } \Psi_{1}( a,R) h
\end{align}
\begin{align}
\parallel \Gamma u (t+h) - \Gamma u (t)\parallel _\alpha & \leq {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} h + C_{0 } \Psi_{1}( a,R) h
\end{align} \begin{eqnarray}
&& + \mathcal{W}_{F,\sigma}( R ) (1+R) ^{2} C_{0 } \Theta_{1}(a) h ,
\end{eqnarray}
\begin{eqnarray}
&& + \mathcal{W}_{F,\sigma}( R ) (1+R) ^{2} C_{0 } \Theta_{1}(a) h ,
\end{eqnarray} \begin{align}
{{{[\Gamma u]_{C_{\rm Lip }([1,a];X_{\alpha}) }} }}&\nonumber\\
& \leq {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0 } \Psi_{1}( a,R) + \mathcal{W}_{F,\sigma}(R )\nonumber\\ & \quad(1+R) ^{2} C_{0,\alpha} \Theta_{1}(a) \leq R.
\end{align}
\begin{align}
{{{[\Gamma u]_{C_{\rm Lip }([1,a];X_{\alpha}) }} }}&\nonumber\\
& \leq {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0 } \Psi_{1}( a,R) + \mathcal{W}_{F,\sigma}(R )\nonumber\\ & \quad(1+R) ^{2} C_{0,\alpha} \Theta_{1}(a) \leq R.
\end{align} From Equations (3.17) and (3.20), it follows that ![]() $\Gamma(\cdot)$ is an
$\Gamma(\cdot)$ is an  $\widehat{S_{x_0} } $-valued function. Moreover, from the estimates in the last part of the proof of Theorem 3.1, we infer that Equations (3.9) and (3.10) are satisfied with ‘a’ in place of ‘b’, which shows that
$\widehat{S_{x_0} } $-valued function. Moreover, from the estimates in the last part of the proof of Theorem 3.1, we infer that Equations (3.9) and (3.10) are satisfied with ‘a’ in place of ‘b’, which shows that ![]() $\Gamma(\cdot)$ is a contraction. This completes the proof.
$\Gamma(\cdot)$ is a contraction. This completes the proof.
Considering the ideas in the proofs of the previous results, next we study the existence of solution for the case in which the condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X )$ is satisfied with α > 0 because the case in which the condition
$\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X )$ is satisfied with α > 0 because the case in which the condition  $\bf H_{F,\sigma, a}^{0,\gamma }(X ,X )$ holds follows from Theorem 3.1. For completeness, we include a short proof of the next results.
$\bf H_{F,\sigma, a}^{0,\gamma }(X ,X )$ holds follows from Theorem 3.1. For completeness, we include a short proof of the next results.
Proposition 3.1. Assume that the condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X )$ is satisfied with α > 0,
$\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X )$ is satisfied with α > 0, ![]() $x_{0}\in X_{\gamma}$ for some
$x_{0}\in X_{\gamma}$ for some ![]() $\gamma\in (\alpha, 1+\alpha )$ and
$\gamma\in (\alpha, 1+\alpha )$ and ![]() $ F(0,\cdot)\in C_{\rm Lip,loc}(X_{\alpha};X_{\alpha}) $. If
$ F(0,\cdot)\in C_{\rm Lip,loc}(X_{\alpha};X_{\alpha}) $. If ![]() $ \Theta_{4}(c)\to 0$ as c → 0, then there exists a unique mild solution
$ \Theta_{4}(c)\to 0$ as c → 0, then there exists a unique mild solution ![]() $u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of the problem (1.1)–(1.2) on
$u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of the problem (1.1)–(1.2) on ![]() $[0,b]$ for some
$[0,b]$ for some ![]() $0 \lt b\leq a$.
$0 \lt b\leq a$.
Proof. Let  $R \gt C_{0} \parallel x_{0}\parallel _{\alpha} +
[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})} $. Remarking that the functions
$R \gt C_{0} \parallel x_{0}\parallel _{\alpha} +
[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})} $. Remarking that the functions ![]() $ \Theta_{3}(\cdot),
\Theta_{5}(\cdot)$ are bounded on
$ \Theta_{3}(\cdot),
\Theta_{5}(\cdot)$ are bounded on ![]() $[0,a]$, from the assumption on
$[0,a]$, from the assumption on ![]() $
\Theta_{4}(\cdot)$, we can select
$
\Theta_{4}(\cdot)$, we can select ![]() $0 \lt b\leq a $ such that
$0 \lt b\leq a $ such that
 \begin{align}
C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} \nonumber\\
+ C_{0 } \max\{b, b^{1+\alpha-\gamma}\} ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2R [F(0,\cdot)]_{C_{\rm lip}(B_{R}(0,X_{\alpha});X_{\alpha})} ) & \nonumber\\ +
C_{0,\alpha} \mathcal{W}_{F }(R) b \Theta_{5} (b) + b^{1+\alpha-\gamma} C_{0,\alpha} \left( { \mathcal{W}_{F }(R) \Theta_{5}(b) } + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{3}(b) \right) \nonumber\\
+ C_{0,\alpha} \mathcal{W}_{F,\sigma}(R) (1+R) \Theta_{4}(b) \lt R,
\end{align}
\begin{align}
C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} \nonumber\\
+ C_{0 } \max\{b, b^{1+\alpha-\gamma}\} ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2R [F(0,\cdot)]_{C_{\rm lip}(B_{R}(0,X_{\alpha});X_{\alpha})} ) & \nonumber\\ +
C_{0,\alpha} \mathcal{W}_{F }(R) b \Theta_{5} (b) + b^{1+\alpha-\gamma} C_{0,\alpha} \left( { \mathcal{W}_{F }(R) \Theta_{5}(b) } + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{3}(b) \right) \nonumber\\
+ C_{0,\alpha} \mathcal{W}_{F,\sigma}(R) (1+R) \Theta_{4}(b) \lt R,
\end{align}where ![]() $\mathcal{W}_{F,\sigma}(R)=\mathcal{W}_{F }(R)(1+\mathcal{W}_{\sigma}(R))$.
$\mathcal{W}_{F,\sigma}(R)=\mathcal{W}_{F }(R)(1+\mathcal{W}_{\sigma}(R))$.
Let ![]() $ \mathcal{S}_{x_0} $ and
$ \mathcal{S}_{x_0} $ and ![]() $\Gamma(\cdot)$ be defined as in the proof of Theorem 3.1 and
$\Gamma(\cdot)$ be defined as in the proof of Theorem 3.1 and ![]() $u,v\in \mathcal{S}_{x_0} $. To begin, for
$u,v\in \mathcal{S}_{x_0} $. To begin, for ![]() $t\in [0,b]$, we note that
$t\in [0,b]$, we note that
 \begin{eqnarray}
\parallel (-A)^{\alpha} \Gamma u(t ) \parallel &\leq& \parallel T(t) x_{0}\parallel _{\alpha} + \int_0^t \parallel T(t-s) (-A)^{\alpha} F(0,x_{0}) \parallel \,{\rm d}\tau \nonumber\\
&& + \int_0^t \parallel T(t-s) (-A)^{\alpha} F(0,u^{\sigma} (\tau)) - (-A)^{\alpha} F(0,x_{0}) \parallel \, {\rm d}\tau \nonumber \\
&& + \int_0^t \parallel (-A)^{\alpha}T(t-s) ( F(\tau,u^{\sigma} (\tau)) - F(0,u^{\sigma} (\tau))) \parallel \, {\rm d}\tau \nonumber\\
& \leq & + C_{0} \parallel x_{0}\parallel _{\alpha} + C_{0 } b ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2R [F(0,\cdot)]_{C_{\rm lip}(B_{R}(0,X_{\alpha});X_{\alpha})} ) \nonumber\\
&& + \int_0^t \frac{C_{0,\alpha} }{(t -\tau)^\alpha} \mathcal{W}_{F }(R)[F]_{(\tau,0)}\tau \, {\rm d}\tau \nonumber\\
& \leq & + C_{0} \parallel x_{0}\parallel _{\alpha} + C_{0 } b ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2R [F(0,\cdot)]_{C_{\rm lip}(B_{R}(0,X_{\alpha});X_{\alpha})} ) \nonumber\\
&& + C_{0,\alpha} \mathcal{W}_{F }(R) b \Theta_{5}(b) \leq R,
\end{eqnarray}
\begin{eqnarray}
\parallel (-A)^{\alpha} \Gamma u(t ) \parallel &\leq& \parallel T(t) x_{0}\parallel _{\alpha} + \int_0^t \parallel T(t-s) (-A)^{\alpha} F(0,x_{0}) \parallel \,{\rm d}\tau \nonumber\\
&& + \int_0^t \parallel T(t-s) (-A)^{\alpha} F(0,u^{\sigma} (\tau)) - (-A)^{\alpha} F(0,x_{0}) \parallel \, {\rm d}\tau \nonumber \\
&& + \int_0^t \parallel (-A)^{\alpha}T(t-s) ( F(\tau,u^{\sigma} (\tau)) - F(0,u^{\sigma} (\tau))) \parallel \, {\rm d}\tau \nonumber\\
& \leq & + C_{0} \parallel x_{0}\parallel _{\alpha} + C_{0 } b ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2R [F(0,\cdot)]_{C_{\rm lip}(B_{R}(0,X_{\alpha});X_{\alpha})} ) \nonumber\\
&& + \int_0^t \frac{C_{0,\alpha} }{(t -\tau)^\alpha} \mathcal{W}_{F }(R)[F]_{(\tau,0)}\tau \, {\rm d}\tau \nonumber\\
& \leq & + C_{0} \parallel x_{0}\parallel _{\alpha} + C_{0 } b ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2R [F(0,\cdot)]_{C_{\rm lip}(B_{R}(0,X_{\alpha});X_{\alpha})} ) \nonumber\\
&& + C_{0,\alpha} \mathcal{W}_{F }(R) b \Theta_{5}(b) \leq R,
\end{eqnarray}which implies that ![]() $ \Gamma u\in C([0,b];X_{\alpha})$ and that
$ \Gamma u\in C([0,b];X_{\alpha})$ and that ![]() $ \parallel \Gamma u \parallel_{C([0,b];X_{\alpha})} \leq R$.
$ \parallel \Gamma u \parallel_{C([0,b];X_{\alpha})} \leq R$.
On the other hand, noting that the estimate (3.6) is satisfied and proceeding as in the estimates (3.22) and (3.7), for ![]() $t \in (0,b]$ and h > 0 with
$t \in (0,b]$ and h > 0 with ![]() $t+h\in [0,b]$, we get
$t+h\in [0,b]$, we get
 \begin{align}
\parallel \Gamma u (t+h) &- \Gamma u (t)\parallel _\alpha\nonumber\\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} + \int_0^h C_{0 }\parallel F(0,x_{0}) \parallel_{\alpha}\, {\rm d}\tau \nonumber \\
& \quad + \int_0^h C_{0 } \parallel F(0,u^{\sigma} (\tau)) - F(0,x_{0}) \parallel_{\alpha} \,{\rm d}\tau \nonumber \\
& \quad + \int_0^h \frac{C_{0,\alpha}}{(t+h-\tau)^\alpha}\parallel F(\tau,u^{\sigma} (\tau)) - F(0,u^{\sigma} (\tau)) \parallel\, {\rm d}\tau \nonumber \\
& \quad + \int_0^t \frac{C_{0,\alpha}}{(t-\tau)^\alpha}\parallel F(\tau+h,u^\sigma(\tau+h)) - F(\tau,u^\sigma(\tau)) \parallel\, {\rm d}\tau \nonumber \\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} +
C_{0}\parallel F(0,x_{0}) \parallel_{\alpha} h \nonumber \\
& \quad + C_{0 } [F(0,\cdot)]_{C_{\rm Lip}(B_{R}(0,X_{\alpha});X_{\alpha})} 2R h + \int_0^h \frac{C_{0,\alpha} }{(t+h-\tau)^\alpha}\mathcal{W}_{F}(R)[F]_{(\tau,0)}\tau \,{\rm d}\tau \nonumber \\
& \quad + \mathcal{W}_{F,\sigma}(R) (1 + R)^{2} C_{0,\alpha} \int_0^t
\frac{[F]_{(\tau+h,\tau)} }{(t -\tau)^\alpha} (1+[\sigma]_{(\tau+h,\tau)}) \Lambda^{2}(\tau) h \,{\rm d}\tau \nonumber \\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} +
C_{0} ( \parallel F(0,x_{0}) \parallel_{\alpha} \nonumber \\ & \quad+ [F(0,\cdot)]_{C_{\rm Lip}(B_{R}(0,X_{\alpha});X_{\alpha})} 2R) h \nonumber\\
& \quad + C_{0,\alpha} \mathcal{W}_{F}(R) \Theta_{5}(b) h + \mathcal{W}_{F,\sigma}(R) (1 + R)^{2} C_{0,\alpha} \Theta_{3}(b) h ,
\end{align}
\begin{align}
\parallel \Gamma u (t+h) &- \Gamma u (t)\parallel _\alpha\nonumber\\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} + \int_0^h C_{0 }\parallel F(0,x_{0}) \parallel_{\alpha}\, {\rm d}\tau \nonumber \\
& \quad + \int_0^h C_{0 } \parallel F(0,u^{\sigma} (\tau)) - F(0,x_{0}) \parallel_{\alpha} \,{\rm d}\tau \nonumber \\
& \quad + \int_0^h \frac{C_{0,\alpha}}{(t+h-\tau)^\alpha}\parallel F(\tau,u^{\sigma} (\tau)) - F(0,u^{\sigma} (\tau)) \parallel\, {\rm d}\tau \nonumber \\
& \quad + \int_0^t \frac{C_{0,\alpha}}{(t-\tau)^\alpha}\parallel F(\tau+h,u^\sigma(\tau+h)) - F(\tau,u^\sigma(\tau)) \parallel\, {\rm d}\tau \nonumber \\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} +
C_{0}\parallel F(0,x_{0}) \parallel_{\alpha} h \nonumber \\
& \quad + C_{0 } [F(0,\cdot)]_{C_{\rm Lip}(B_{R}(0,X_{\alpha});X_{\alpha})} 2R h + \int_0^h \frac{C_{0,\alpha} }{(t+h-\tau)^\alpha}\mathcal{W}_{F}(R)[F]_{(\tau,0)}\tau \,{\rm d}\tau \nonumber \\
& \quad + \mathcal{W}_{F,\sigma}(R) (1 + R)^{2} C_{0,\alpha} \int_0^t
\frac{[F]_{(\tau+h,\tau)} }{(t -\tau)^\alpha} (1+[\sigma]_{(\tau+h,\tau)}) \Lambda^{2}(\tau) h \,{\rm d}\tau \nonumber \\
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } \frac{h}{t^{1+\alpha-\gamma}} +
C_{0} ( \parallel F(0,x_{0}) \parallel_{\alpha} \nonumber \\ & \quad+ [F(0,\cdot)]_{C_{\rm Lip}(B_{R}(0,X_{\alpha});X_{\alpha})} 2R) h \nonumber\\
& \quad + C_{0,\alpha} \mathcal{W}_{F}(R) \Theta_{5}(b) h + \mathcal{W}_{F,\sigma}(R) (1 + R)^{2} C_{0,\alpha} \Theta_{3}(b) h ,
\end{align}and hence,
 \begin{align}
[\Gamma u ]_{ C_{\rm Lip,1+\alpha-\gamma} }
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } +
C_{0} b^{1+\alpha-\gamma} (\parallel F(0,x_{0}) \parallel_{\alpha}\nonumber \\ & \qquad+ [F(0,\cdot)]_{C_{\rm lip}(B_{R}(0,X_{\alpha});X_{\alpha})} 2R)\nonumber \\
& \quad b^{1+\alpha-\gamma} C_{0,\alpha} \left( \mathcal{W}_{F }(R) \Theta_{5}(b) + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{3}(b) \right) \leq R.
\end{align}
\begin{align}
[\Gamma u ]_{ C_{\rm Lip,1+\alpha-\gamma} }
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } +
C_{0} b^{1+\alpha-\gamma} (\parallel F(0,x_{0}) \parallel_{\alpha}\nonumber \\ & \qquad+ [F(0,\cdot)]_{C_{\rm lip}(B_{R}(0,X_{\alpha});X_{\alpha})} 2R)\nonumber \\
& \quad b^{1+\alpha-\gamma} C_{0,\alpha} \left( \mathcal{W}_{F }(R) \Theta_{5}(b) + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{3}(b) \right) \leq R.
\end{align} From Equations (3.22) and (3.24), it follows that ![]() $\Gamma(\cdot )$ has values in
$\Gamma(\cdot )$ has values in ![]() $\mathcal{S}_{x_0}$.
$\mathcal{S}_{x_0}$.
To finish, noting that the inequality (3.9) is satisfied and arguing as in the estimate (3.10), for ![]() $t\in (0,b]$, we get
$t\in (0,b]$, we get
 \begin{eqnarray}
\parallel \Gamma u (t) &-& \Gamma v (t)\parallel_{C([0,b];X_{\alpha})} \nonumber\\
&\leq& C_{0,\alpha} \mathcal{W}_{F }(R) \int^t_0\frac{[F]_{(\tau,\tau)}}{(t-\tau)^\alpha} \parallel u^{\sigma}(\tau)- v^{\sigma}(\tau)\parallel_{ \alpha}\, {\rm d}\tau \nonumber\\
&\leq& C_{0,\alpha} (1+R) \mathcal{W}_{F,\sigma}(R) \int_0^t \frac{[F]_{(\tau,\tau)}}{(t-\tau)^\alpha} (1 + [\sigma]_{(\tau,\tau)} ) \Lambda (\tau) \, {\rm d}\tau \parallel u-v\parallel_{C((0,b];X_{\alpha})}\nonumber\\
&\leq& C_{0,\alpha} (1+R) \mathcal{W}_{F,\sigma}(R) \Theta_{4}(b) \parallel u-v\parallel_{C([0,b];X_{\alpha})},
\end{eqnarray}
\begin{eqnarray}
\parallel \Gamma u (t) &-& \Gamma v (t)\parallel_{C([0,b];X_{\alpha})} \nonumber\\
&\leq& C_{0,\alpha} \mathcal{W}_{F }(R) \int^t_0\frac{[F]_{(\tau,\tau)}}{(t-\tau)^\alpha} \parallel u^{\sigma}(\tau)- v^{\sigma}(\tau)\parallel_{ \alpha}\, {\rm d}\tau \nonumber\\
&\leq& C_{0,\alpha} (1+R) \mathcal{W}_{F,\sigma}(R) \int_0^t \frac{[F]_{(\tau,\tau)}}{(t-\tau)^\alpha} (1 + [\sigma]_{(\tau,\tau)} ) \Lambda (\tau) \, {\rm d}\tau \parallel u-v\parallel_{C((0,b];X_{\alpha})}\nonumber\\
&\leq& C_{0,\alpha} (1+R) \mathcal{W}_{F,\sigma}(R) \Theta_{4}(b) \parallel u-v\parallel_{C([0,b];X_{\alpha})},
\end{eqnarray}which implies (see Equation (3.21)) that ![]() $\Gamma(\cdot)$ is a contraction on
$\Gamma(\cdot)$ is a contraction on ![]() $\mathcal{S}_{x_0} $ and that there exists a unique mild solution
$\mathcal{S}_{x_0} $ and that there exists a unique mild solution ![]() $u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of (1.1)–(1.2) on
$u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of (1.1)–(1.2) on ![]() $[0,b]$.
$[0,b]$.
Remark 3.5. Concerning the assumptions in the last result, assume that ![]() $F(t,x)= f(t)x_{0} + G(t,x) $, where
$F(t,x)= f(t)x_{0} + G(t,x) $, where  $ G\in L^{q}_{\rm Lip}([0,a]\times X_{\alpha};X )\cap C( [0,a]\times X_{\alpha};X )$ and
$ G\in L^{q}_{\rm Lip}([0,a]\times X_{\alpha};X )\cap C( [0,a]\times X_{\alpha};X )$ and  $f\in L^{q}_{\rm Lip}([0,a];\mathbb{R}) $. If
$f\in L^{q}_{\rm Lip}([0,a];\mathbb{R}) $. If ![]() $G(0,\cdot)\equiv 0 $ and
$G(0,\cdot)\equiv 0 $ and ![]() $f(0)\in\{0,1\}$, then
$f(0)\in\{0,1\}$, then ![]() $F(\cdot)$ verifies the conditions in Proposition 3.1.
$F(\cdot)$ verifies the conditions in Proposition 3.1.
On the other hand, concerning the condition on ![]() $ {
\Theta}_{4}(\cdot)$, it is interesting to note that integrability of the functions
$ {
\Theta}_{4}(\cdot)$, it is interesting to note that integrability of the functions  $ \tau\mapsto
\frac{[F]_{(\tau,\tau)}}{(t-\tau)^{\alpha}}
(1 + [\sigma]_{(\tau,\tau)}) \Lambda (\tau) $ on
$ \tau\mapsto
\frac{[F]_{(\tau,\tau)}}{(t-\tau)^{\alpha}}
(1 + [\sigma]_{(\tau,\tau)}) \Lambda (\tau) $ on ![]() $[0,t]$ does not implies that
$[0,t]$ does not implies that ![]() $
\Theta_{4}(b) \to 0 $ as b → 0. About it, assume that
$
\Theta_{4}(b) \to 0 $ as b → 0. About it, assume that ![]() $F(\cdot)$ and
$F(\cdot)$ and ![]() $\sigma(\cdot)$ are Lipschitz,
$\sigma(\cdot)$ are Lipschitz, ![]() $\alpha\in(0,1)$,
$\alpha\in(0,1)$, ![]() $\gamma=2\alpha $, and there is
$\gamma=2\alpha $, and there is ![]() $\beta\in (0,1)$ such that
$\beta\in (0,1)$ such that ![]() $\beta \tau\leq \xi(\tau)\leq \tau$ for all
$\beta \tau\leq \xi(\tau)\leq \tau$ for all ![]() $\tau\in [0,a]$. From the estimates
$\tau\in [0,a]$. From the estimates
 \begin{align*}
\parallel \frac{[F]_{(\cdot,\cdot)}}{(t-\cdot)^{\alpha}}& (1 + [\sigma]_{(\cdot,\cdot)}) \Lambda (\cdot) \parallel_{L^{1}([0,t])} \hspace{1cm}\hspace{0.5cm} \\
&\quad\leq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{\rm Lip}}\right) \int_{0}^{t} \frac{1 }{(t-\tau)^{\alpha} }\left(1+\frac{1}{\xi(\tau)^{1-\alpha}}\right)\,{\rm d}\tau \\
&\quad\leq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{Lip}}\right) \left( \frac{t^{1-\alpha}}{1-\alpha}+ \int_{\frac{t}{2}}^{t} \frac{{\rm d}\tau }{(t-\tau)^{\alpha} \left(\frac{\beta t}{2}\right)^{1-\alpha}}\right.\\ &\qquad \left.+ \int_{0}^{\frac{t}{2}} \frac{{\rm d}\tau }{\left(\frac{t}{2}\right)^{\alpha} (\beta\tau)^{1-\alpha}} \right) \\
&\quad \leq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{\rm Lip}}\right)\left(\frac{a^{1-\alpha}}{1-\alpha}+ \frac{1}{1-\alpha} \left(\frac{2}{\beta t}\right)^{1-\alpha}\left(\frac{t}{2}\right)^{1-\alpha}\right. \nonumber \\ & \qquad \left. + \left(\frac{2}{t}\right)^{\alpha}\frac{1}{\alpha} \left(\frac{\beta t}{2}\right)^{\alpha} \right)\\
&\quad \leq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{Lip}}\right)\left(
\frac{1}{1-\alpha}\left(a^{1-\alpha}+\frac{1}{\beta^{1-\alpha}}\right) +
\frac{\beta^{\alpha}}{\alpha } \right),
\\
\parallel \frac{[F]_{(\cdot,\cdot)}}{(t-\cdot)^{\alpha}} & \left(1 + [\sigma]_{(\cdot,\cdot)}\right) \Lambda (\cdot) \parallel_{L^{1}([0,t])}\geq
[F]_{C_{\rm Lip}} (1+ [\sigma]_{C_{\rm Lip}}) \int_{0}^{t} \frac{{\rm d}\tau }{(t-\tau)^{\alpha} \xi(\tau)^{1-\alpha}} \hspace{1cm}\hspace{0.5cm} \\
&\quad\geq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{Lip}}\right) \left( \int_{0}^{\frac{t}{2}}\frac{{\rm d}\tau }{(t-\tau)^{\alpha} \left(\frac{t}{2}\right)^{1-\alpha}} + \int_{\frac{t}{2}}^{t}\frac{{\rm d}\tau }{\left( \frac{t}{2}\right)^{\alpha} \tau^{1-\alpha} } \right)\\
&\quad \geq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{\rm Lip}}\right) \left( \frac{2^{1-\alpha}}{t
^{1-\alpha}}\frac{1}{1-\alpha}\left[t^{1-\alpha}- \left(\frac{t}{2}\right)^{1-\alpha}\right]\right.\\
& \qquad + \left.\left(\frac{2}{t}\right)^{\alpha}\frac{1}{\alpha}\left[ t^{\alpha}- \left(\frac{t}{2}\right)^{\alpha} \right]\right)
\\
& \quad \geq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{\rm Lip}}\right) \left[\frac{2^{1-\alpha}-1}{1-\alpha} +
\frac{2^{\alpha}-1}{\alpha}\right],
\end{align*}
\begin{align*}
\parallel \frac{[F]_{(\cdot,\cdot)}}{(t-\cdot)^{\alpha}}& (1 + [\sigma]_{(\cdot,\cdot)}) \Lambda (\cdot) \parallel_{L^{1}([0,t])} \hspace{1cm}\hspace{0.5cm} \\
&\quad\leq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{\rm Lip}}\right) \int_{0}^{t} \frac{1 }{(t-\tau)^{\alpha} }\left(1+\frac{1}{\xi(\tau)^{1-\alpha}}\right)\,{\rm d}\tau \\
&\quad\leq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{Lip}}\right) \left( \frac{t^{1-\alpha}}{1-\alpha}+ \int_{\frac{t}{2}}^{t} \frac{{\rm d}\tau }{(t-\tau)^{\alpha} \left(\frac{\beta t}{2}\right)^{1-\alpha}}\right.\\ &\qquad \left.+ \int_{0}^{\frac{t}{2}} \frac{{\rm d}\tau }{\left(\frac{t}{2}\right)^{\alpha} (\beta\tau)^{1-\alpha}} \right) \\
&\quad \leq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{\rm Lip}}\right)\left(\frac{a^{1-\alpha}}{1-\alpha}+ \frac{1}{1-\alpha} \left(\frac{2}{\beta t}\right)^{1-\alpha}\left(\frac{t}{2}\right)^{1-\alpha}\right. \nonumber \\ & \qquad \left. + \left(\frac{2}{t}\right)^{\alpha}\frac{1}{\alpha} \left(\frac{\beta t}{2}\right)^{\alpha} \right)\\
&\quad \leq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{Lip}}\right)\left(
\frac{1}{1-\alpha}\left(a^{1-\alpha}+\frac{1}{\beta^{1-\alpha}}\right) +
\frac{\beta^{\alpha}}{\alpha } \right),
\\
\parallel \frac{[F]_{(\cdot,\cdot)}}{(t-\cdot)^{\alpha}} & \left(1 + [\sigma]_{(\cdot,\cdot)}\right) \Lambda (\cdot) \parallel_{L^{1}([0,t])}\geq
[F]_{C_{\rm Lip}} (1+ [\sigma]_{C_{\rm Lip}}) \int_{0}^{t} \frac{{\rm d}\tau }{(t-\tau)^{\alpha} \xi(\tau)^{1-\alpha}} \hspace{1cm}\hspace{0.5cm} \\
&\quad\geq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{Lip}}\right) \left( \int_{0}^{\frac{t}{2}}\frac{{\rm d}\tau }{(t-\tau)^{\alpha} \left(\frac{t}{2}\right)^{1-\alpha}} + \int_{\frac{t}{2}}^{t}\frac{{\rm d}\tau }{\left( \frac{t}{2}\right)^{\alpha} \tau^{1-\alpha} } \right)\\
&\quad \geq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{\rm Lip}}\right) \left( \frac{2^{1-\alpha}}{t
^{1-\alpha}}\frac{1}{1-\alpha}\left[t^{1-\alpha}- \left(\frac{t}{2}\right)^{1-\alpha}\right]\right.\\
& \qquad + \left.\left(\frac{2}{t}\right)^{\alpha}\frac{1}{\alpha}\left[ t^{\alpha}- \left(\frac{t}{2}\right)^{\alpha} \right]\right)
\\
& \quad \geq
[F]_{C_{\rm Lip}} \left(1+ [\sigma]_{C_{\rm Lip}}\right) \left[\frac{2^{1-\alpha}-1}{1-\alpha} +
\frac{2^{\alpha}-1}{\alpha}\right],
\end{align*}we have that the function  $\frac{[F]_{(\cdot,\cdot)}}{(t-\cdot)^{\alpha}}
(1 + [\sigma]_{(\cdot,\cdot)}) \Lambda (\cdot) $ belongs to
$\frac{[F]_{(\cdot,\cdot)}}{(t-\cdot)^{\alpha}}
(1 + [\sigma]_{(\cdot,\cdot)}) \Lambda (\cdot) $ belongs to ![]() $ L^{1}([0,t]) $ for all
$ L^{1}([0,t]) $ for all ![]() $t\in [0,a]$, that
$t\in [0,a]$, that ![]() $ { \Theta}_{4}(\cdot) $ is bounded on
$ { \Theta}_{4}(\cdot) $ is bounded on ![]() $[0,a]$ and that
$[0,a]$ and that ![]() $ { \Theta}_{4}(c) $ does not converge to 0 as c → 0. We also note that similar observations hold concerning other results and functions, see for example, Proposition 4.6, Corollary 3.6 and Proposition 4.6.
$ { \Theta}_{4}(c) $ does not converge to 0 as c → 0. We also note that similar observations hold concerning other results and functions, see for example, Proposition 4.6, Corollary 3.6 and Proposition 4.6.
Similar to the corollaries associated to Theorem 3.1, from the proof of Proposition 3.1, we can prove the next results. We omit the proofs.
Corollary 3.5. Assume that the conditions  $ \bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X )$ is satisfied,
$ \bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X )$ is satisfied, ![]() $x_{0}\in X_{\gamma}$ for some
$x_{0}\in X_{\gamma}$ for some ![]() $\gamma\in (\alpha, 1+\alpha)$ and
$\gamma\in (\alpha, 1+\alpha)$ and ![]() $F(0,\cdot)\in C_{\rm Lip,loc}(X_{\alpha};X_{\alpha}) $.
$F(0,\cdot)\in C_{\rm Lip,loc}(X_{\alpha};X_{\alpha}) $.
(a) Let
 $P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function given by
where
$P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function given by
where \begin{align*}
P_{a} (x) & = C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} \\
& \quad + C_{0 } \max\{a, a^{1+\alpha-\gamma}\} ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2x [F(0,\cdot)]_{C_{\rm Lip}(B_{x}(0,X_{\alpha});X_{\alpha})} )
\\ & \quad+
C_{0,\alpha} \mathcal{W}_{F }(x) a \Theta_{5} (a)
+
a^{1+\alpha-\gamma} C_{0,\alpha} \left( { \mathcal{W}_{F }(x) \Theta_{5}(a) } + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \Theta_{3}(a) \right) \\ &
\quad + C_{0,\alpha} \mathcal{W}_{F,\sigma}(x) (1+x) \Theta_{4}(a) - x,
\end{align*}
\begin{align*}
P_{a} (x) & = C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} \\
& \quad + C_{0 } \max\{a, a^{1+\alpha-\gamma}\} ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2x [F(0,\cdot)]_{C_{\rm Lip}(B_{x}(0,X_{\alpha});X_{\alpha})} )
\\ & \quad+
C_{0,\alpha} \mathcal{W}_{F }(x) a \Theta_{5} (a)
+
a^{1+\alpha-\gamma} C_{0,\alpha} \left( { \mathcal{W}_{F }(x) \Theta_{5}(a) } + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \Theta_{3}(a) \right) \\ &
\quad + C_{0,\alpha} \mathcal{W}_{F,\sigma}(x) (1+x) \Theta_{4}(a) - x,
\end{align*} $\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. If
$\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. If  $P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution
$P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution  $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a]; X_{ \alpha})$ of (1.1)–(1.2) on
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a]; X_{ \alpha})$ of (1.1)–(1.2) on  $[0,a]$.
$[0,a]$.(b) Assume, in addition, that
 $ F\in C_{\rm Lip}([0,a]\times X_{\alpha};X)$ and
$ F\in C_{\rm Lip}([0,a]\times X_{\alpha};X)$ and  $\sigma \in C_{\rm Lip}([0,a]\times X_{\alpha};[0,a])$, and let
$\sigma \in C_{\rm Lip}([0,a]\times X_{\alpha};[0,a])$, and let  $P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function defined by
where
$P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function defined by
where \begin{align*}
P_{a} (x) & = C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} +
C_{0,\alpha} [F]_{C_{\rm Lip}} \frac{a^{2-\alpha}}{1-\alpha} \\
& \quad + C_{0 } \max\{a, a^{1+\alpha-\gamma}\} ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2x [F(0,\cdot)]_{C_{\rm Lip}(B_{x}(0,X_{\alpha});X_{\alpha})} ) \\
& \quad + C_{0,\alpha} a^{1+\alpha-\gamma} \left( { [F]_{C_{\rm Lip}} \frac{a^{1-\alpha}}{1-\alpha} }+ 2[F]_{C_{\rm Lip}} (1+ [\sigma]_{C_{\rm Lip}}) (1+x) ^{2} \widetilde{\Theta} _{3}(a) \right) \\
& \quad + 2 C_{0,\alpha} [F]_{C_{\rm Lip}} (1+ [\sigma]_{C_{\rm Lip}}) (1+x) \widetilde{\Theta} _{4} (a) -x ,
\end{align*}
\begin{align*}
P_{a} (x) & = C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} +
C_{0,\alpha} [F]_{C_{\rm Lip}} \frac{a^{2-\alpha}}{1-\alpha} \\
& \quad + C_{0 } \max\{a, a^{1+\alpha-\gamma}\} ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2x [F(0,\cdot)]_{C_{\rm Lip}(B_{x}(0,X_{\alpha});X_{\alpha})} ) \\
& \quad + C_{0,\alpha} a^{1+\alpha-\gamma} \left( { [F]_{C_{\rm Lip}} \frac{a^{1-\alpha}}{1-\alpha} }+ 2[F]_{C_{\rm Lip}} (1+ [\sigma]_{C_{\rm Lip}}) (1+x) ^{2} \widetilde{\Theta} _{3}(a) \right) \\
& \quad + 2 C_{0,\alpha} [F]_{C_{\rm Lip}} (1+ [\sigma]_{C_{\rm Lip}}) (1+x) \widetilde{\Theta} _{4} (a) -x ,
\end{align*} $
\widetilde{\Theta}_{3}(a) = \sup_{ t\in [0,a] } \int_0^t \frac{ \Lambda^{2}(\tau) }{(t-\tau)^{\alpha}}\,{\rm d}\tau
\nonumber $ and
$
\widetilde{\Theta}_{3}(a) = \sup_{ t\in [0,a] } \int_0^t \frac{ \Lambda^{2}(\tau) }{(t-\tau)^{\alpha}}\,{\rm d}\tau
\nonumber $ and  $ \widetilde{\Theta} _{4}(a) = \sup_{t\in [0,a] } \int_0^t \frac{ \Lambda (\tau) }{(t-\tau)^{\alpha}} \,{\rm d}\tau. $ If
$ \widetilde{\Theta} _{4}(a) = \sup_{t\in [0,a] } \int_0^t \frac{ \Lambda (\tau) }{(t-\tau)^{\alpha}} \,{\rm d}\tau. $ If  $P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution
$P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution  $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a]; X_{ \alpha})$ of the problem (1.1)–(1.2) on
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a]; X_{ \alpha})$ of the problem (1.1)–(1.2) on  $[0,a]$.
$[0,a]$.
Similar to the results in the first part of this section, to study the existence of solution on ![]() $[0,\infty)$ using the ideas in the proof of Proposition 3.1, it is convenient to introduce some modifications to the proof of this proposition. It is the objective of the next results.
$[0,\infty)$ using the ideas in the proof of Proposition 3.1, it is convenient to introduce some modifications to the proof of this proposition. It is the objective of the next results.
Corollary 3.6. Suppose that the conditions in Proposition 3.1 are satisfied and that ![]() $ \Theta_{i}(c)\to 0$ as c → 0 for
$ \Theta_{i}(c)\to 0$ as c → 0 for ![]() $i= 3,4,5$. Then there exists a unique mild solution
$i= 3,4,5$. Then there exists a unique mild solution ![]() $u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of (1.1)–(1.2) on
$u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha}) $ of (1.1)–(1.2) on ![]() $[0,b]$ for some
$[0,b]$ for some ![]() $0 \lt b\leq a$.
$0 \lt b\leq a$.
Proof. The proof follows combining the ideas in the proof of Corollary 3.3 and Proposition 3.1. For completeness, we include some details. To begin, we select R > 0 large enough such that
 \begin{equation*} R \gt C_{0}\parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}
.\end{equation*}
\begin{equation*} R \gt C_{0}\parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}
.\end{equation*} From the assumptions on the functions ![]() $ \Theta_{i}(\cdot)
$,
$ \Theta_{i}(\cdot)
$, ![]() $i= 3,4,5$, we select
$i= 3,4,5$, we select  $0 \lt b\leq \min\{a,1\}$ such that
$0 \lt b\leq \min\{a,1\}$ such that
 \begin{align*}
C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} \\
+ C_{0 } \max\{b, b^{1+\alpha-\gamma}\} ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2R \left[F(0,\cdot)\right]_{C_{\rm Lip}(B_{R}(0,X_{\alpha});X_{\alpha})} )
+ C_{0,\alpha} \mathcal{W}_{F }(R) b \Theta_{5} (b) \\
\!\!\!\!\! + C_{0,\alpha} \left( \mathcal{W}_{F }(R) \Theta_{5}(b) + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{3}(b) + \mathcal{W}_{F,\sigma}(R) (1+R) \Theta_{4}(b) \right) \lt R,
\end{align*}
\begin{align*}
C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} \\
+ C_{0 } \max\{b, b^{1+\alpha-\gamma}\} ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2R \left[F(0,\cdot)\right]_{C_{\rm Lip}(B_{R}(0,X_{\alpha});X_{\alpha})} )
+ C_{0,\alpha} \mathcal{W}_{F }(R) b \Theta_{5} (b) \\
\!\!\!\!\! + C_{0,\alpha} \left( \mathcal{W}_{F }(R) \Theta_{5}(b) + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{3}(b) + \mathcal{W}_{F,\sigma}(R) (1+R) \Theta_{4}(b) \right) \lt R,
\end{align*}and  $\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. Let
$\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. Let  $ \mathcal{S}_{x_0} $ and
$ \mathcal{S}_{x_0} $ and  $\Gamma(\cdot)$ be defined as in the proof of Theorem 3.1.
$\Gamma(\cdot)$ be defined as in the proof of Theorem 3.1.
Arguing as in the proof of Proposition 3.1, it is easy to see that  $ \Gamma u\in C([0,b];X_{\alpha})$ and that the inequalities (3.22) and (3.25) remain valid. In addition, noting that Equations (3.23) and (3.24) are satisfied, we obtain that
$ \Gamma u\in C([0,b];X_{\alpha})$ and that the inequalities (3.22) and (3.25) remain valid. In addition, noting that Equations (3.23) and (3.24) are satisfied, we obtain that
 \begin{align*}
[\Gamma u ]_{ C_{\rm Lip,1+\alpha-\gamma} }
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } +
C_{0} (\parallel F(0,x_{0}) \parallel_{\alpha} + [F(0,\cdot)]_{C_{\rm Lip}(B_{R}(0,X_{\alpha});X_{\alpha})} 2R) \\
& \quad C_{0,\alpha} \left( \mathcal{W}_{F }(R) \Theta_{5}(b) + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{3}(b) \right) \leq R
\end{align*}
\begin{align*}
[\Gamma u ]_{ C_{\rm Lip,1+\alpha-\gamma} }
& \leq [T(\cdot)x_0]_{ C_{\rm Lip,1+\alpha-\gamma} } +
C_{0} (\parallel F(0,x_{0}) \parallel_{\alpha} + [F(0,\cdot)]_{C_{\rm Lip}(B_{R}(0,X_{\alpha});X_{\alpha})} 2R) \\
& \quad C_{0,\alpha} \left( \mathcal{W}_{F }(R) \Theta_{5}(b) + \mathcal{W}_{F,\sigma}(R) (1+R) ^{2} \Theta_{3}(b) \right) \leq R
\end{align*}because  $0 \lt b \lt 1$. From the above remarks, we obtain that
$0 \lt b \lt 1$. From the above remarks, we obtain that  $\Gamma(\cdot)$ is a contraction on
$\Gamma(\cdot)$ is a contraction on  $\mathcal{S}_{x_0}$.
$\mathcal{S}_{x_0}$.
The proof of the next result follows arguing as in the proof of Corollary 3.4, but using the estimates in the proof of Proposition 3.1 in place of the estimates in the proof of Theorem 3.1. We omit the proof.
Corollary 3.7. Suppose that the condition  $ \bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X )$ is satisfied,
$ \bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X )$ is satisfied,  $x_{0}\in X_{\gamma}$ for some
$x_{0}\in X_{\gamma}$ for some  $\gamma\in (\alpha, 1+\alpha)$ and
$\gamma\in (\alpha, 1+\alpha)$ and  $F(0,\cdot)\in C_{\rm Lip,loc}(X_{\alpha};X_{\alpha}) $. Let
$F(0,\cdot)\in C_{\rm Lip,loc}(X_{\alpha};X_{\alpha}) $. Let  $P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function defined by
$P_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function defined by
 \begin{eqnarray}
P_{a} (x) & =& C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} \nonumber\\
&& + C_{0 } \max\{a, a^{1+\alpha-\gamma}\} ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2x [F(0,\cdot)]_{C_{\rm Lip}(B_{x}(0,X_{\alpha});X_{\alpha})} )
\nonumber\\ && +
C_{0,\alpha} \mathcal{W}_{F }(x) a \Theta_{5} (a)
+
C_{0,\alpha} \left( \mathcal{W}_{F }(x) \Theta_{5}(a) + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \Theta_{3}(a) \right) \nonumber\\ & &
+ C_{0,\alpha} \mathcal{W}_{F,\sigma}(x) (1+x) \Theta_{4}(a) - x,
\end{eqnarray}
\begin{eqnarray}
P_{a} (x) & =& C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} \nonumber\\
&& + C_{0 } \max\{a, a^{1+\alpha-\gamma}\} ( \parallel F(0,x_{0}) \parallel_{\alpha} + 2x [F(0,\cdot)]_{C_{\rm Lip}(B_{x}(0,X_{\alpha});X_{\alpha})} )
\nonumber\\ && +
C_{0,\alpha} \mathcal{W}_{F }(x) a \Theta_{5} (a)
+
C_{0,\alpha} \left( \mathcal{W}_{F }(x) \Theta_{5}(a) + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \Theta_{3}(a) \right) \nonumber\\ & &
+ C_{0,\alpha} \mathcal{W}_{F,\sigma}(x) (1+x) \Theta_{4}(a) - x,
\end{eqnarray}where  $\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. If
$\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. If  $P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution
$P_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution  $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a];{ X_{\alpha}})$ of (1.1)–(1.2) on
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a];{ X_{\alpha}})$ of (1.1)–(1.2) on  $[0,a]$. Moreover,
$[0,a]$. Moreover,  $ [u_{\mid_{[0,1]}} ]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha})}\leq R$ and
$ [u_{\mid_{[0,1]}} ]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha})}\leq R$ and  $ [u_{\mid_{[1,a]}}]_{C_{\rm Lip }([1,\infty);X_{\alpha})}\leq R$ if a > 1.
$ [u_{\mid_{[1,a]}}]_{C_{\rm Lip }([1,\infty);X_{\alpha})}\leq R$ if a > 1.
3.2. The case  $\bf \sigma(0,x_{0}) \gt 0$
$\bf \sigma(0,x_{0}) \gt 0$
The case  $\bf \sigma(0,x_{0}) \gt 0$ is qualitatively different to the case
$\bf \sigma(0,x_{0}) \gt 0$ is qualitatively different to the case  $\sigma(0,x_{0})=0$ because it is necessary to establish the existence of solution on an interval
$\sigma(0,x_{0})=0$ because it is necessary to establish the existence of solution on an interval  $[0,b]$ with
$[0,b]$ with  $b \gt \sigma(0,x_{0})$. Noting that this case is an unconsidered problem in the literature, next we study the existence and uniqueness of a Lipschitz mild solution (the case
$b \gt \sigma(0,x_{0})$. Noting that this case is an unconsidered problem in the literature, next we study the existence and uniqueness of a Lipschitz mild solution (the case  $ T(\cdot)x_{0}
\in C_{\rm Lip}([0,a];X_{\alpha})$) and of a non-Lipschitz mild solution (the case,
$ T(\cdot)x_{0}
\in C_{\rm Lip}([0,a];X_{\alpha})$) and of a non-Lipschitz mild solution (the case,  $ T(\cdot)x_{0} \in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})$).
$ T(\cdot)x_{0} \in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})$).
3.2.1. Existence of a non-Lipschitz solution, the case  $ T(\cdot)x_{0} \in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})$
$ T(\cdot)x_{0} \in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})$
The next result follows from the ideas in Theorem 3.1, see also Corollary 3.1.
Proposition 3.2. Assume that the conditions  $ \bf H_{F,\sigma, a}^{q,r }(X_{\alpha} ;X_{\alpha})$ and
$ \bf H_{F,\sigma, a}^{q,r }(X_{\alpha} ;X_{\alpha})$ and  $\bf \mathcal{H}_{F, a}(X_{\alpha} ;X_{\alpha})$ are satisfied,
$\bf \mathcal{H}_{F, a}(X_{\alpha} ;X_{\alpha})$ are satisfied,  $\sigma(\cdot)$ is Lipschitz,
$\sigma(\cdot)$ is Lipschitz,  $x_{0}\in X_{\gamma} $,
$x_{0}\in X_{\gamma} $,  $a \gt \sigma(0,x_{0}) \gt 0$ and there is a non-decreasing function
$a \gt \sigma(0,x_{0}) \gt 0$ and there is a non-decreasing function  $\xi\in C([0,b];\mathbb{R}^{+}) $ such that
$\xi\in C([0,b];\mathbb{R}^{+}) $ such that  $0 \lt \xi(t)\leq \min\{\sigma(t,x), t\}$ for all
$0 \lt \xi(t)\leq \min\{\sigma(t,x), t\}$ for all 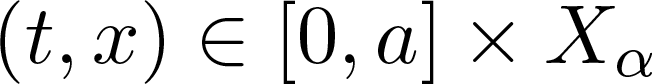 $(t,x)\in [0,a]\times X_{\alpha}$. Let
$(t,x)\in [0,a]\times X_{\alpha}$. Let  $P : [0,\infty)\times [0,a]\mapsto \mathbb{R} $ be the function given by
$P : [0,\infty)\times [0,a]\mapsto \mathbb{R} $ be the function given by
 \begin{eqnarray*}
P (x,s) & :=& C_{0 } \parallel x_{0}\parallel_{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0 } \Psi_{2}( s,x) + s^{1+\alpha-\gamma} C_{0 } \Psi_{1}( s,x)\\
&& + 2 \mathcal{W}_{F}(x) C_{0 } \left(1+[\sigma]_{C_{\rm Lip}}\right)\left( (1+x) ^{2} s^{1+\alpha-\gamma} \widehat{\Theta}_{1}(s) + (1+x) \widehat{\Theta}_{2}(s) \right) -x,
\end{eqnarray*}
\begin{eqnarray*}
P (x,s) & :=& C_{0 } \parallel x_{0}\parallel_{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + C_{0 } \Psi_{2}( s,x) + s^{1+\alpha-\gamma} C_{0 } \Psi_{1}( s,x)\\
&& + 2 \mathcal{W}_{F}(x) C_{0 } \left(1+[\sigma]_{C_{\rm Lip}}\right)\left( (1+x) ^{2} s^{1+\alpha-\gamma} \widehat{\Theta}_{1}(s) + (1+x) \widehat{\Theta}_{2}(s) \right) -x,
\end{eqnarray*}where  $
\widehat{\Theta}_{1}(s) = \sup_{t,h\in [0,s],t+h\leq s} \int_0^t [F]_{(\tau+h,\tau)}
\Lambda^{2}(\tau) \,{\rm d}\tau $ and
$
\widehat{\Theta}_{1}(s) = \sup_{t,h\in [0,s],t+h\leq s} \int_0^t [F]_{(\tau+h,\tau)}
\Lambda^{2}(\tau) \,{\rm d}\tau $ and  $
\widehat{\Theta} _{2}(s) = \int_0^s [F]_{(\tau,\tau)}
\Lambda (\tau) \,{\rm d}\tau $ and
$
\widehat{\Theta} _{2}(s) = \int_0^s [F]_{(\tau,\tau)}
\Lambda (\tau) \,{\rm d}\tau $ and  $\Lambda (\tau) =\left( 1+ \frac{1 }{ \xi^{1+\alpha-\gamma }(\tau) }\right)$. If there are
$\Lambda (\tau) =\left( 1+ \frac{1 }{ \xi^{1+\alpha-\gamma }(\tau) }\right)$. If there are  $b \gt \sigma(0,x_{0})$ and R > 0 such that
$b \gt \sigma(0,x_{0})$ and R > 0 such that  $P(R,b) \lt 0$ and
$P(R,b) \lt 0$ and  $ [\sigma]_{C_{\rm Lip}} ( b+ 2R ) + \sigma( 0 , x_{0}) \leq b$, then there exists a unique mild solution
$ [\sigma]_{C_{\rm Lip}} ( b+ 2R ) + \sigma( 0 , x_{0}) \leq b$, then there exists a unique mild solution  $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,b]; X_{\alpha})$ of (1.1)–(1.2) on
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,b]; X_{\alpha})$ of (1.1)–(1.2) on  $[0,b]$. In particular, if there is R > 0 such that
$[0,b]$. In particular, if there is R > 0 such that  $P(R,a) \lt 0$ and
$P(R,a) \lt 0$ and  $ [\sigma]_{C_{\rm Lip}} ( a+ R +\parallel x_{0} \parallel_{\alpha} ) + \sigma(0, x_{0}) \leq a$, then there exists a unique mild solution
$ [\sigma]_{C_{\rm Lip}} ( a+ R +\parallel x_{0} \parallel_{\alpha} ) + \sigma(0, x_{0}) \leq a$, then there exists a unique mild solution  $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a]; X_{\alpha})$ on
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a]; X_{\alpha})$ on  $[0,a]$.
$[0,a]$.
Proof. Assume  $P(R,b) \lt 0$. From the definition of
$P(R,b) \lt 0$. From the definition of  $P(\cdot)$, we have that the inequality (3.1) is satisfied. If
$P(\cdot)$, we have that the inequality (3.1) is satisfied. If  $\mathcal{S}_{x_0}$ is the set defined in the proof of Theorem 3.1 and
$\mathcal{S}_{x_0}$ is the set defined in the proof of Theorem 3.1 and  $u\in \mathcal{S}_{x_0}$, for
$u\in \mathcal{S}_{x_0}$, for  $s\in (0,b] $, we get
$s\in (0,b] $, we get
 \begin{eqnarray}
\sigma(s,u(s)) &\leq& \mid
\sigma(s,u(s)) -\sigma(0, x_{0})\mid + \sigma(0, x_{0}) \nonumber\\
&\leq& [\sigma]_{C_{\rm Lip}} (s+ \parallel u(s) - x_{0} \parallel_{\alpha}) + \sigma(0, x_{0}) \nonumber\\
&\leq& [\sigma]_{C_{\rm Lip}}(b+ \parallel u(s) \parallel_{\alpha} +\parallel x_{0} \parallel_{\alpha} ) + \sigma( 0 , x_{0}) \nonumber\\
&\leq& [\sigma]_{C_{\rm Lip}} ( b+ 2R ) + \sigma( 0 , x_{0}) \leq b ,
\end{eqnarray}
\begin{eqnarray}
\sigma(s,u(s)) &\leq& \mid
\sigma(s,u(s)) -\sigma(0, x_{0})\mid + \sigma(0, x_{0}) \nonumber\\
&\leq& [\sigma]_{C_{\rm Lip}} (s+ \parallel u(s) - x_{0} \parallel_{\alpha}) + \sigma(0, x_{0}) \nonumber\\
&\leq& [\sigma]_{C_{\rm Lip}}(b+ \parallel u(s) \parallel_{\alpha} +\parallel x_{0} \parallel_{\alpha} ) + \sigma( 0 , x_{0}) \nonumber\\
&\leq& [\sigma]_{C_{\rm Lip}} ( b+ 2R ) + \sigma( 0 , x_{0}) \leq b ,
\end{eqnarray}which implies that  $ \sigma(s,u(s))\in [0,b]$. From this fact, we have that the map
$ \sigma(s,u(s))\in [0,b]$. From this fact, we have that the map  $\Gamma (\cdot)$ in the proof of Theorem 3.1 is well defined on
$\Gamma (\cdot)$ in the proof of Theorem 3.1 is well defined on  $S_{x_{0}}$. Moreover, arguing as in the cited proof, we can show that
$S_{x_{0}}$. Moreover, arguing as in the cited proof, we can show that  $\Gamma (\cdot)$ is a contraction on
$\Gamma (\cdot)$ is a contraction on  $\mathcal{S}_{x_0}$, which implies that there exists a unique mild solution
$\mathcal{S}_{x_0}$, which implies that there exists a unique mild solution  $u\in \mathcal{S}_{x_0}$. The last assertion follows from the above remarks.
$u\in \mathcal{S}_{x_0}$. The last assertion follows from the above remarks.
3.2.2. Existence of a Lipschitz solution, the case  $ T(\cdot)x_{0} \in C_{\rm Lip}([0,a];X_{\alpha})$
$ T(\cdot)x_{0} \in C_{\rm Lip}([0,a];X_{\alpha})$
To develop the studies in this section, it is convenient to introduce some notation.
Notation 3.
In this section, we assume that the condition  $\bf H_{F,\sigma, a}^{q, r }(X_{\alpha} ;X) $ is satisfied, that the functions
$\bf H_{F,\sigma, a}^{q, r }(X_{\alpha} ;X) $ is satisfied, that the functions  $\frac{[F]_{(\cdot,0)}}{( t-\cdot)^{\alpha}}
(1+ [\sigma]_{(\cdot,0)}) $ and
$\frac{[F]_{(\cdot,0)}}{( t-\cdot)^{\alpha}}
(1+ [\sigma]_{(\cdot,0)}) $ and  $ \frac{[F]_{(\cdot+h,\cdot)}}{(t-\cdot)^{\alpha}} (1+[\sigma]_{(\cdot+h,\cdot)})$ are integrable on
$ \frac{[F]_{(\cdot+h,\cdot)}}{(t-\cdot)^{\alpha}} (1+[\sigma]_{(\cdot+h,\cdot)})$ are integrable on  $[0,t]$ for all
$[0,t]$ for all  $t\in [0,a]$ and we use the notation
$t\in [0,a]$ and we use the notation  $ \Phi_{i} $,
$ \Phi_{i} $,  $i=1,2$, for the functions
$i=1,2$, for the functions  $ \Phi_{i}: [0,a]\mapsto \mathbb{R}^{+}$,
$ \Phi_{i}: [0,a]\mapsto \mathbb{R}^{+}$,  $ i=1,2$, defined by
$ i=1,2$, defined by
 \begin{eqnarray}
\Phi_{1}(b)&:=& \sup_{t,h\in [0,b],t+h\leq b} \int^t_0 \frac{[F]_{(s+h,s)}}{(t-s)^{\alpha}} (1+[\sigma]_{(s+h,s)}) \, {\rm d}s,
\end{eqnarray}
\begin{eqnarray}
\Phi_{1}(b)&:=& \sup_{t,h\in [0,b],t+h\leq b} \int^t_0 \frac{[F]_{(s+h,s)}}{(t-s)^{\alpha}} (1+[\sigma]_{(s+h,s)}) \, {\rm d}s,
\end{eqnarray} \begin{eqnarray}
\Phi_{2}(b)&:= & \sup_{t\in [0,b]} \int^t_0 \frac{[F]_{(s,0)}}{( t-s)^{\alpha}}
(1+ [\sigma]_{(s,0)})\, {\rm d}s.
\end{eqnarray}
\begin{eqnarray}
\Phi_{2}(b)&:= & \sup_{t\in [0,b]} \int^t_0 \frac{[F]_{(s,0)}}{( t-s)^{\alpha}}
(1+ [\sigma]_{(s,0)})\, {\rm d}s.
\end{eqnarray}Proposition 3.3. Assume that the condition  $\bf H_{F,\sigma, a}^{q, r }(X_{\alpha} ;X) $ is satisfied,
$\bf H_{F,\sigma, a}^{q, r }(X_{\alpha} ;X) $ is satisfied,  $ T(\cdot)x_{0} \in C_{\rm Lip}([0,a];X_{\alpha})$,
$ T(\cdot)x_{0} \in C_{\rm Lip}([0,a];X_{\alpha})$,  $a \gt \sigma(0,x_{0}) \gt 0$ and that the function
$a \gt \sigma(0,x_{0}) \gt 0$ and that the function  $ F(0,\cdot) $ takes bounded set of X α into bounded sets of X α. Let
$ F(0,\cdot) $ takes bounded set of X α into bounded sets of X α. Let  $P :[0,\infty)\times [0,a]\mapsto\mathbb{R}$ be the function given by
$P :[0,\infty)\times [0,a]\mapsto\mathbb{R}$ be the function given by
 \begin{eqnarray*}
P (x,s) &:=&
[T (\cdot)x_{0}]_{C_{\rm Lip}([0,s];X_{\alpha})} + \sup_{y\in B_{\rho(x,s)}[0,X_{ \alpha}]} \parallel (-A)^{\alpha}{ T({ \cdot})} F(0,y) \parallel_{L^{\infty}([0,s];X)}\\ && + (1+ x)^{2}
\mathcal{W}_{F}(\rho(x,s)) (1+\mathcal{W}_{\sigma}(\rho(x,s))) C_{0,\alpha}\left( \Phi_{1}(s) + \Phi_{2}(s)\right) -x ,
\end{eqnarray*}
\begin{eqnarray*}
P (x,s) &:=&
[T (\cdot)x_{0}]_{C_{\rm Lip}([0,s];X_{\alpha})} + \sup_{y\in B_{\rho(x,s)}[0,X_{ \alpha}]} \parallel (-A)^{\alpha}{ T({ \cdot})} F(0,y) \parallel_{L^{\infty}([0,s];X)}\\ && + (1+ x)^{2}
\mathcal{W}_{F}(\rho(x,s)) (1+\mathcal{W}_{\sigma}(\rho(x,s))) C_{0,\alpha}\left( \Phi_{1}(s) + \Phi_{2}(s)\right) -x ,
\end{eqnarray*}where  $\rho(x,s)= x s + \parallel x_{0}\parallel_{\alpha} $. If there are
$\rho(x,s)= x s + \parallel x_{0}\parallel_{\alpha} $. If there are  $b \gt \sigma(0,x_{0})$ and R > 0 such that
$b \gt \sigma(0,x_{0})$ and R > 0 such that  $P(R,b) \lt 0$ and
$P(R,b) \lt 0$ and  $ 0 \leq \sigma(s, x)\leq b $ for all
$ 0 \leq \sigma(s, x)\leq b $ for all  $ s\in [0,b]$ and
$ s\in [0,b]$ and  $ \parallel x \parallel_{\alpha} \leq \rho(R,b) = R b + \parallel x_{0}\parallel_{\alpha} $, then there exists a unique mild solution
$ \parallel x \parallel_{\alpha} \leq \rho(R,b) = R b + \parallel x_{0}\parallel_{\alpha} $, then there exists a unique mild solution  $u\in C_{\rm Lip}([0,b];X_{\alpha})$ of the problem (1.1)–(1.2) on
$u\in C_{\rm Lip}([0,b];X_{\alpha})$ of the problem (1.1)–(1.2) on  $[0,b]$.
$[0,b]$.
Proof. From the assumptions on  $P(\cdot)$, we have that
$P(\cdot)$, we have that
 \begin{align}
[T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})} + \sup_{y\in B_{\rho(R, b)}[0,X_{ \alpha}]} \parallel (-A)^{\alpha} T(\cdot) F(0,y) \parallel_{L^{\infty}([0,b];X)} &
\nonumber\\ \!\!\!+ (1+ R )^{2}
\mathcal{W}_{F,\sigma}(\rho(R,b)) C_{0,\alpha}\left( \Phi_{1}(b) + \Phi_{2}(b)\right) & \lt R,
\end{align}
\begin{align}
[T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})} + \sup_{y\in B_{\rho(R, b)}[0,X_{ \alpha}]} \parallel (-A)^{\alpha} T(\cdot) F(0,y) \parallel_{L^{\infty}([0,b];X)} &
\nonumber\\ \!\!\!+ (1+ R )^{2}
\mathcal{W}_{F,\sigma}(\rho(R,b)) C_{0,\alpha}\left( \Phi_{1}(b) + \Phi_{2}(b)\right) & \lt R,
\end{align}where  $ \mathcal{W}_{F,\sigma}(\theta)=
\mathcal{W}_{F}(\theta) (1+\mathcal{W}_{\sigma}(\theta).$
$ \mathcal{W}_{F,\sigma}(\theta)=
\mathcal{W}_{F}(\theta) (1+\mathcal{W}_{\sigma}(\theta).$
Let  $\mathcal{S}(R,b) $ be the space
$\mathcal{S}(R,b) $ be the space
 \begin{equation*}\mathcal{S}(R,b)=\{u\in C([0,b];X_{ \alpha}) : u(0)=x_{0}, [u]_{C_{\rm Lip}([0,b];X_{\alpha})}\leq R \},\end{equation*}
\begin{equation*}\mathcal{S}(R,b)=\{u\in C([0,b];X_{ \alpha}) : u(0)=x_{0}, [u]_{C_{\rm Lip}([0,b];X_{\alpha})}\leq R \},\end{equation*}endowed with the metric  $d(u,v)=\parallel u-v\parallel _{C([0,b];X_{\alpha})}$ and
$d(u,v)=\parallel u-v\parallel _{C([0,b];X_{\alpha})}$ and  $\Gamma :\mathcal{S}(R,b)\mapsto C([0,b];X_{\alpha}) $, the function defined using Equation (3.2).
$\Gamma :\mathcal{S}(R,b)\mapsto C([0,b];X_{\alpha}) $, the function defined using Equation (3.2).
For  $u\in\mathcal{S}(R,b) $ and
$u\in\mathcal{S}(R,b) $ and  $t\in [0,b]$,
$t\in [0,b]$,  $\parallel u(t)\parallel_{\alpha} \leq \parallel u(t)-u(0)\parallel_{\alpha} + \parallel u(0)\parallel_{\alpha} \leq R b +\parallel x_{0} \parallel = \rho(R,b) $, which implies that
$\parallel u(t)\parallel_{\alpha} \leq \parallel u(t)-u(0)\parallel_{\alpha} + \parallel u(0)\parallel_{\alpha} \leq R b +\parallel x_{0} \parallel = \rho(R,b) $, which implies that  $ \sigma(t,u(t))\in [0,b]$ and that the functions
$ \sigma(t,u(t))\in [0,b]$ and that the functions  $u( \sigma(\cdot,u(\cdot)) )$ and
$u( \sigma(\cdot,u(\cdot)) )$ and  $\Gamma u(\cdot) $ are well defined.
$\Gamma u(\cdot) $ are well defined.
Let  $u,v\in \mathcal{S}(R,b)$. Proceeding as in the estimate (3.5) and remarking that
$u,v\in \mathcal{S}(R,b)$. Proceeding as in the estimate (3.5) and remarking that  $ \parallel u(s)\parallel_{ \alpha} \leq \rho(R,b) $ for all
$ \parallel u(s)\parallel_{ \alpha} \leq \rho(R,b) $ for all  $s\in [0,b]$, for
$s\in [0,b]$, for  $s,h\in [0,b] $ with
$s,h\in [0,b] $ with  $s+h\in[0,b]$, we get
$s+h\in[0,b]$, we get
 \begin{align}
\parallel F(s+h,u^{\sigma}(s+h))&-F(s,u^{\sigma}(s))\parallel \nonumber\\
&\leq
[F]_{(s+h,s)}\mathcal{W}_{F}(\rho(R,b)) (h+ \parallel u^{\sigma}(s+h)-u^{\sigma}(s)\parallel_{\alpha}) \nonumber \\ &\leq
[F]_{(s+h,s)}\mathcal{W}_{F}(\rho(R,b)) (h+ {[u ]_{C_{\rm Lip}([0,b];X_{\alpha})}} \mathcal{W}_{\sigma}(\rho(R,b))[\sigma]_{(s+h,s)}\nonumber \\ &\qquad (1+ {[u ]_{C_{\rm Lip}([0,b]; X_{\alpha})}})h) \nonumber \\
&\leq { [F]_{(s+h,s)}\mathcal{W}_{F}(\rho(R,b)) (1+R\mathcal{W}_{\sigma}(\rho(R,b))[\sigma]_{(s+h,s)}(1+R))) h } \nonumber \\
&\leq \mathcal{W}_{F}(\rho(R,b)) (1+\mathcal{W}_{\sigma}(\rho(R,b))) (1 + R)^{2} [F]_{(s+h,s)}(1+[\sigma]_{(s+h,s)}) h
\end{align}
\begin{align}
\parallel F(s+h,u^{\sigma}(s+h))&-F(s,u^{\sigma}(s))\parallel \nonumber\\
&\leq
[F]_{(s+h,s)}\mathcal{W}_{F}(\rho(R,b)) (h+ \parallel u^{\sigma}(s+h)-u^{\sigma}(s)\parallel_{\alpha}) \nonumber \\ &\leq
[F]_{(s+h,s)}\mathcal{W}_{F}(\rho(R,b)) (h+ {[u ]_{C_{\rm Lip}([0,b];X_{\alpha})}} \mathcal{W}_{\sigma}(\rho(R,b))[\sigma]_{(s+h,s)}\nonumber \\ &\qquad (1+ {[u ]_{C_{\rm Lip}([0,b]; X_{\alpha})}})h) \nonumber \\
&\leq { [F]_{(s+h,s)}\mathcal{W}_{F}(\rho(R,b)) (1+R\mathcal{W}_{\sigma}(\rho(R,b))[\sigma]_{(s+h,s)}(1+R))) h } \nonumber \\
&\leq \mathcal{W}_{F}(\rho(R,b)) (1+\mathcal{W}_{\sigma}(\rho(R,b))) (1 + R)^{2} [F]_{(s+h,s)}(1+[\sigma]_{(s+h,s)}) h
\end{align} \begin{eqnarray}
&\leq& \mathcal{W}_{F,\sigma}(\rho(R,b)) (1 + R)^{2}
[F]_{(s+h,s)}(1+[\sigma]_{(s+h,s)}) h .
\end{eqnarray}
\begin{eqnarray}
&\leq& \mathcal{W}_{F,\sigma}(\rho(R,b)) (1 + R)^{2}
[F]_{(s+h,s)}(1+[\sigma]_{(s+h,s)}) h .
\end{eqnarray}Moreover, proceeding as above, we obtain that
 \begin{eqnarray}
\parallel F(s,u^{\sigma}(s)) - F(0,u(\sigma(0,x_{0}))) \parallel
\leq (1+ R )^{2}\mathcal{W}_{F,\sigma}(\rho(R,b)) [F]_{(s,0)} (1+ [\sigma]_{(s,0)}) s .
\end{eqnarray}
\begin{eqnarray}
\parallel F(s,u^{\sigma}(s)) - F(0,u(\sigma(0,x_{0}))) \parallel
\leq (1+ R )^{2}\mathcal{W}_{F,\sigma}(\rho(R,b)) [F]_{(s,0)} (1+ [\sigma]_{(s,0)}) s .
\end{eqnarray} From the above inequalities, for  $ h,t\in [0,b]$ with
$ h,t\in [0,b]$ with  $t+h\in[0,b]$, we see that
$t+h\in[0,b]$, we see that
 \begin{align}
\parallel \Gamma u(t+h) &- \Gamma u(t)\parallel_{\alpha} \hspace{1cm} \nonumber\\
&\leq [T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})}h +
\int^{h}_0 \parallel (-A)^{\alpha}T(t+h-s) F(0,u(\sigma(0,x_{0}) )) \parallel \,{\rm d}s \nonumber\\
& \quad + \int^{h}_0 \parallel (-A)^{\alpha} T(t+h-s) \parallel \parallel F(s,u^{\sigma}(s)) - F(0,u(\sigma(0,x_{0}))) \parallel \,{\rm d}s \nonumber\\
& \quad + \int^{t}_0\parallel (-A)^{\alpha} T(t -s) \parallel \parallel F(s+h,u^{\sigma}(s+h))-F(s,u^{\sigma}(s))\parallel \,{\rm d}s \nonumber \\
&\leq [T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})}h + C_{0} \sup_{v\in \mathcal{S}(R,b) } \parallel (-A)^{\alpha}T(\cdot) F(0,v(\sigma(0,x_{0}) )) \nonumber\\ &\qquad \parallel_{L^{\infty}([0,b];X)} h \nonumber\\ & \quad + (1+ R)^{2}\mathcal{W}_{F,\sigma}(\rho(R,b)) C_{0,\alpha} ( \Phi_{1}(b) + \Phi_{2}(b) ) h \nonumber\\
&\leq [T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})}h + \sup_{y\in B_{\rho(R,b)}[0,X_{ \alpha}]} \parallel (-A)^{\alpha } T(\cdot) F(0,y) \parallel_{L^{\infty}([0,b];X)} h \nonumber\\ & \qquad + (1+ R)^{2}
\mathcal{W}_{F,\sigma}(\rho(R,b)) C_{0,\alpha} ( \Phi_{1}(b) +
\Phi_{2}(b) ) h,
\end{align}
\begin{align}
\parallel \Gamma u(t+h) &- \Gamma u(t)\parallel_{\alpha} \hspace{1cm} \nonumber\\
&\leq [T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})}h +
\int^{h}_0 \parallel (-A)^{\alpha}T(t+h-s) F(0,u(\sigma(0,x_{0}) )) \parallel \,{\rm d}s \nonumber\\
& \quad + \int^{h}_0 \parallel (-A)^{\alpha} T(t+h-s) \parallel \parallel F(s,u^{\sigma}(s)) - F(0,u(\sigma(0,x_{0}))) \parallel \,{\rm d}s \nonumber\\
& \quad + \int^{t}_0\parallel (-A)^{\alpha} T(t -s) \parallel \parallel F(s+h,u^{\sigma}(s+h))-F(s,u^{\sigma}(s))\parallel \,{\rm d}s \nonumber \\
&\leq [T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})}h + C_{0} \sup_{v\in \mathcal{S}(R,b) } \parallel (-A)^{\alpha}T(\cdot) F(0,v(\sigma(0,x_{0}) )) \nonumber\\ &\qquad \parallel_{L^{\infty}([0,b];X)} h \nonumber\\ & \quad + (1+ R)^{2}\mathcal{W}_{F,\sigma}(\rho(R,b)) C_{0,\alpha} ( \Phi_{1}(b) + \Phi_{2}(b) ) h \nonumber\\
&\leq [T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})}h + \sup_{y\in B_{\rho(R,b)}[0,X_{ \alpha}]} \parallel (-A)^{\alpha } T(\cdot) F(0,y) \parallel_{L^{\infty}([0,b];X)} h \nonumber\\ & \qquad + (1+ R)^{2}
\mathcal{W}_{F,\sigma}(\rho(R,b)) C_{0,\alpha} ( \Phi_{1}(b) +
\Phi_{2}(b) ) h,
\end{align}which implies that  $[\Gamma u]_{C_{\rm Lip}([0,b];X_{\alpha})}\leq R$. This shows that
$[\Gamma u]_{C_{\rm Lip}([0,b];X_{\alpha})}\leq R$. This shows that  $\Gamma(\cdot)$ is an
$\Gamma(\cdot)$ is an  $\mathcal{S}(R,b)$-valued function.
$\mathcal{S}(R,b)$-valued function.
To finish, using Lemma 2.2, for  $u,
v\in\mathcal{S}(R,b) $ and
$u,
v\in\mathcal{S}(R,b) $ and  $t\in [0,b]$, it is easy to see that
$t\in [0,b]$, it is easy to see that
 \begin{align}
\parallel \Gamma u(t ) &- \Gamma v(t)\parallel \nonumber\\
&\leq C_{0,\alpha} \mathcal{W}_{F}(\rho(R,b)) \int^t_0 \frac{ [F]_{(s ,s)}}{(t-s)^{\alpha}} \left( 1 +
R \mathcal{W}_{\sigma}(\rho(R,b)) [\sigma]_{(s ,s)}\right) \parallel u-v\parallel_{C([0,s];X_{\alpha})}\,{\rm d}s \nonumber \\
&\leq (1+R) \mathcal{W}_{F}(\rho(R,b)) (1+\mathcal{W}_{\sigma}(\rho(R,b))) C_{0,\alpha} \int^t_0 \frac{ [F]_{(s ,s)}}{(t-s)^{\alpha}} (1+ [\sigma]_{(s ,s)}) \,{\rm d}s\nonumber \\
& \quad \parallel u-v\parallel_{C([0,b];X_{\alpha})} \nonumber \\
&\leq (1+R) \mathcal{W}_{F,\sigma}(\rho(R,b)) C_{0,\alpha}
\Phi_{1}(b) \parallel u-v\parallel_{ C([0,b];X_{\alpha})},
\end{align}
\begin{align}
\parallel \Gamma u(t ) &- \Gamma v(t)\parallel \nonumber\\
&\leq C_{0,\alpha} \mathcal{W}_{F}(\rho(R,b)) \int^t_0 \frac{ [F]_{(s ,s)}}{(t-s)^{\alpha}} \left( 1 +
R \mathcal{W}_{\sigma}(\rho(R,b)) [\sigma]_{(s ,s)}\right) \parallel u-v\parallel_{C([0,s];X_{\alpha})}\,{\rm d}s \nonumber \\
&\leq (1+R) \mathcal{W}_{F}(\rho(R,b)) (1+\mathcal{W}_{\sigma}(\rho(R,b))) C_{0,\alpha} \int^t_0 \frac{ [F]_{(s ,s)}}{(t-s)^{\alpha}} (1+ [\sigma]_{(s ,s)}) \,{\rm d}s\nonumber \\
& \quad \parallel u-v\parallel_{C([0,b];X_{\alpha})} \nonumber \\
&\leq (1+R) \mathcal{W}_{F,\sigma}(\rho(R,b)) C_{0,\alpha}
\Phi_{1}(b) \parallel u-v\parallel_{ C([0,b];X_{\alpha})},
\end{align}which proves that  $\Gamma(\cdot)$ is a contraction on
$\Gamma(\cdot)$ is a contraction on  $
\mathcal{S}(R,b)$ and that there exists a unique mild solution
$
\mathcal{S}(R,b)$ and that there exists a unique mild solution  $u\in C_{\rm Lip}([0,b];X_{\alpha})$ of the problem (1.1)–(1.2) on
$u\in C_{\rm Lip}([0,b];X_{\alpha})$ of the problem (1.1)–(1.2) on  $[0,b]$.
$[0,b]$.
Corollary 3.8. Suppose that the condition  $\bf H_{F,\sigma, a}^{q, r }(X_{\alpha} ;X) $ is satisfied,
$\bf H_{F,\sigma, a}^{q, r }(X_{\alpha} ;X) $ is satisfied,  $\sigma(\cdot)$ is Lipschitz,
$\sigma(\cdot)$ is Lipschitz,  $ T(\cdot)x_{0} \in C_{\rm Lip}([0,a];X_{\alpha})$,
$ T(\cdot)x_{0} \in C_{\rm Lip}([0,a];X_{\alpha})$,  $a \gt \sigma(0,x_{0}) \gt 0$ and that
$a \gt \sigma(0,x_{0}) \gt 0$ and that  $ F(0,\cdot) $ takes bounded set of X α into bounded sets of X α. Let
$ F(0,\cdot) $ takes bounded set of X α into bounded sets of X α. Let  $P :[0,\infty)\times [0,a]\mapsto\mathbb{R}$ be the map defined by
$P :[0,\infty)\times [0,a]\mapsto\mathbb{R}$ be the map defined by
 \begin{eqnarray*}
P (x,s) &:=& [T (\cdot)x_{0}]_{C_{\rm Lip}([0,s];X_{\alpha})} + \sup_{y\in B_{\rho({ x},s)}[0,X_{ \alpha}]} \parallel (-A)^{\alpha} T(\cdot) F(0,y) \parallel_{L^{\infty}([0,s];X)} \\ && + 2(1+ x )^{2}
\mathcal{W}_{F}(\rho(x,s)) C_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip}}) \left( \widehat{\Phi}_{1}(s) + \widehat{\Phi}_{2}(s)\right) - x,
\end{eqnarray*}
\begin{eqnarray*}
P (x,s) &:=& [T (\cdot)x_{0}]_{C_{\rm Lip}([0,s];X_{\alpha})} + \sup_{y\in B_{\rho({ x},s)}[0,X_{ \alpha}]} \parallel (-A)^{\alpha} T(\cdot) F(0,y) \parallel_{L^{\infty}([0,s];X)} \\ && + 2(1+ x )^{2}
\mathcal{W}_{F}(\rho(x,s)) C_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip}}) \left( \widehat{\Phi}_{1}(s) + \widehat{\Phi}_{2}(s)\right) - x,
\end{eqnarray*}where  $
\widehat{\Phi} _{1}(c) := \sup_{t,h\in [0,c],t+h\leq c} \int^t_0 \frac{[F]_{(s+h,s)}}{(t-s)^{\alpha}} \,{\rm d}s $,
$
\widehat{\Phi} _{1}(c) := \sup_{t,h\in [0,c],t+h\leq c} \int^t_0 \frac{[F]_{(s+h,s)}}{(t-s)^{\alpha}} \,{\rm d}s $,  $ \widehat{\Phi} _{2}(c) := \sup_{t\in [0,c]} \int^t_0 \frac{[F]_{(s,0)}}{( t-s)^{\alpha}}
\,{\rm d}s$ and
$ \widehat{\Phi} _{2}(c) := \sup_{t\in [0,c]} \int^t_0 \frac{[F]_{(s,0)}}{( t-s)^{\alpha}}
\,{\rm d}s$ and  $\rho(x,s)= \parallel x_{0}\parallel_{\alpha} + x s$. If there are
$\rho(x,s)= \parallel x_{0}\parallel_{\alpha} + x s$. If there are  $b\in (\sigma(0,x_{0}),a]$ and R > 0 such that
$b\in (\sigma(0,x_{0}),a]$ and R > 0 such that  $P (R,b) \lt 0$ and
$P (R,b) \lt 0$ and  $[\sigma]_{C_{\rm Lip}}(1+ R)b + \sigma(0,x_{0}) \leq b$, then there exists a unique mild solution
$[\sigma]_{C_{\rm Lip}}(1+ R)b + \sigma(0,x_{0}) \leq b$, then there exists a unique mild solution  $u\in C_{\rm Lip}([0,b];X_{\alpha})$ of (1.1)–(1.2) on
$u\in C_{\rm Lip}([0,b];X_{\alpha})$ of (1.1)–(1.2) on  $[0,b]$.
$[0,b]$.
Proof. Let  $\mathcal{S}(R,b) $ and
$\mathcal{S}(R,b) $ and  $\Gamma (\cdot)$ be defined as in the proof of Proposition 3.3. For
$\Gamma (\cdot)$ be defined as in the proof of Proposition 3.3. For  $
u\in\mathcal{S}(R,b) $ and
$
u\in\mathcal{S}(R,b) $ and  $t\in [0,b]$,
$t\in [0,b]$,
 \begin{eqnarray*}
\mid \sigma(t,u(t))\mid &\leq& \mid \sigma(t,u(t))-\sigma(0,x_{0})) \mid + \sigma(0,x_{0})\\
&\leq& [\sigma]_{C_{\rm Lip}}(t + \parallel u(t)-x_{0}\parallel_{\alpha}) + \sigma(0,x_{0})\\
&\leq& [\sigma]_{C_{\rm Lip}}(1+ R)b+ \sigma(0,x_{0})\leq b,
\end{eqnarray*}
\begin{eqnarray*}
\mid \sigma(t,u(t))\mid &\leq& \mid \sigma(t,u(t))-\sigma(0,x_{0})) \mid + \sigma(0,x_{0})\\
&\leq& [\sigma]_{C_{\rm Lip}}(t + \parallel u(t)-x_{0}\parallel_{\alpha}) + \sigma(0,x_{0})\\
&\leq& [\sigma]_{C_{\rm Lip}}(1+ R)b+ \sigma(0,x_{0})\leq b,
\end{eqnarray*}which shows  $\sigma(t,u(t))\in [0,b]$ and that the functions
$\sigma(t,u(t))\in [0,b]$ and that the functions  $u(\sigma(\cdot,u(\cdot)))$ and
$u(\sigma(\cdot,u(\cdot)))$ and  $\Gamma u(\cdot)$ are well defined. From this fact, we can use the proof of Proposition 3.3 to prove the assertion.
$\Gamma u(\cdot)$ are well defined. From this fact, we can use the proof of Proposition 3.3 to prove the assertion.
The next result is an obvious consequence of Corollary 3.8.
Corollary 3.9. Assume  $F\in C_{\rm Lip}([0,a]\times X_{\alpha};X ) $,
$F\in C_{\rm Lip}([0,a]\times X_{\alpha};X ) $,  $\sigma \in
C_{\rm Lip}([0,a]\times X_{\alpha};[0,a] ) $,
$\sigma \in
C_{\rm Lip}([0,a]\times X_{\alpha};[0,a] ) $,  $ \sigma(0,x_{0}) \gt 0$,
$ \sigma(0,x_{0}) \gt 0$,  $ T(\cdot)x_{0} \in C_{\rm Lip}([0,a];X_{\alpha})$ and that
$ T(\cdot)x_{0} \in C_{\rm Lip}([0,a];X_{\alpha})$ and that  $
F(0,\cdot)\equiv 0 $. Let
$
F(0,\cdot)\equiv 0 $. Let  $P :[0,\infty)\times
[0,a]\mapsto\mathbb{R}$ be the function given by
$P :[0,\infty)\times
[0,a]\mapsto\mathbb{R}$ be the function given by
 \begin{eqnarray*}
P (x,s) :=
[T (\cdot)x_{0}]_{C_{\rm Lip}([0,s];X_{\alpha})} +
4[F]_{C_{\rm Lip}} (1+[\sigma]_{C_{\rm Lip}} ) C_{0,\alpha}
\frac{s^{1-\alpha}}{1-\alpha} (1+ x)^{2} -x .
\end{eqnarray*}
\begin{eqnarray*}
P (x,s) :=
[T (\cdot)x_{0}]_{C_{\rm Lip}([0,s];X_{\alpha})} +
4[F]_{C_{\rm Lip}} (1+[\sigma]_{C_{\rm Lip}} ) C_{0,\alpha}
\frac{s^{1-\alpha}}{1-\alpha} (1+ x)^{2} -x .
\end{eqnarray*} If there is  $b \gt \sigma(0,x_{0})$ and R > 0 such that
$b \gt \sigma(0,x_{0})$ and R > 0 such that  $P(R,b) \lt 0$ and
$P(R,b) \lt 0$ and  $ [\sigma]_{C_{\rm Lip}} ( b+ R ) + \sigma(0, x_{0}) \leq b$, then there exists a unique mild solution
$ [\sigma]_{C_{\rm Lip}} ( b+ R ) + \sigma(0, x_{0}) \leq b$, then there exists a unique mild solution  $u\in C_{\rm Lip}([0,b];X_{\alpha})$ of the problem (1.1)–(1.2) on
$u\in C_{\rm Lip}([0,b];X_{\alpha})$ of the problem (1.1)–(1.2) on  $[0,b]$.
$[0,b]$.
4. Existence and uniqueness of solution on  $[0,\infty)$
$[0,\infty)$
In the first part of this section, we study the existence of solution on  $[0,\infty)$ using the basic ideas in Corollary 3.4 and Corollary 3.5. In the second part, we use a different approach based in the study of the existence and qualitative properties of maximal solution. Next, we use use the notation
$[0,\infty)$ using the basic ideas in Corollary 3.4 and Corollary 3.5. In the second part, we use a different approach based in the study of the existence and qualitative properties of maximal solution. Next, we use use the notation  $ [T(\cdot)x_{0}]_{C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})} =\sup_{a \gt 0} {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}}$.
$ [T(\cdot)x_{0}]_{C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})} =\sup_{a \gt 0} {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}}$.
4.1. The case  $[T(\cdot)x_{0}]_{C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})} \lt \infty$
$[T(\cdot)x_{0}]_{C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})} \lt \infty$
To prove the results in this section, we assume that the conditions in Theorem 3.1 or the conditions in Proposition 3.1 are satisfied for all a > 0. For convenience, we introduce some notation.
Notation 4.
In this section, we assume  $F\in C([0,\infty)\times X_{\alpha};X)$ and
$F\in C([0,\infty)\times X_{\alpha};X)$ and  $\sigma \in C([0,\infty)\times X_{\alpha};[0,\infty))$. Depending on the result, next we assume that the condition
$\sigma \in C([0,\infty)\times X_{\alpha};[0,\infty))$. Depending on the result, next we assume that the condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X_{\alpha} )$ or that the condition
$\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X_{\alpha} )$ or that the condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X )$ is satisfied for all a > 0. Considering it, next we use the notation
$\bf H_{F,\sigma, a}^{\alpha,\gamma }(X_{\alpha},X )$ is satisfied for all a > 0. Considering it, next we use the notation  $ \Psi_{F,\sigma}(\cdot)$ and
$ \Psi_{F,\sigma}(\cdot)$ and  $\mathcal{W}_{F,\sigma}(\cdot)$ for the functions
$\mathcal{W}_{F,\sigma}(\cdot)$ for the functions  $ \Psi_{F,\sigma}(t,s):\{(t,s):t\geq s\geq 0 \} \times [0,\infty) \mapsto [0,\infty)$ and
$ \Psi_{F,\sigma}(t,s):\{(t,s):t\geq s\geq 0 \} \times [0,\infty) \mapsto [0,\infty)$ and  $\mathcal{W}_{F,\sigma}: [0,\infty) \mapsto [0,\infty) $ defined by
$\mathcal{W}_{F,\sigma}: [0,\infty) \mapsto [0,\infty) $ defined by  $
\Psi_{F,\sigma}(t,s ) = [F]_{(t,s)} (1+ [\sigma]_{(t,s)} ) \nonumber
$ and
$
\Psi_{F,\sigma}(t,s ) = [F]_{(t,s)} (1+ [\sigma]_{(t,s)} ) \nonumber
$ and  $\mathcal{W}_{F,\sigma}(x)=\mathcal{W}_{F }(x)(1+\mathcal{W}_{\sigma}(x))$. In addition, for b > 0 and x > 0, we consider the next notation.
$\mathcal{W}_{F,\sigma}(x)=\mathcal{W}_{F }(x)(1+\mathcal{W}_{\sigma}(x))$. In addition, for b > 0 and x > 0, we consider the next notation.
 \begin{eqnarray*}
\chi_{_{1},\infty}( x)&:=& \sup_{s\geq 0 } \parallel T(s) \parallel \parallel \varrho_{1}(\cdot)\mathcal{K}_{F}( x ) + \varrho_{2}(\cdot) \parallel_{L^{\infty}([0,\infty))} \\
\chi_{_{2}}(b,x)&:=& \sup_{t\in [0,b]} \parallel \parallel T(t-\cdot) \parallel \varrho_{1}(\cdot)\mathcal{K}_{F}( x ) + \varrho_{2}(\cdot) \parallel_{L^{1}([0,t])} \\
\vartheta_{1}(b)&:=& \sup\limits_{{ t,h\in [0,b], t+h\in [0,b]}} \parallel \parallel T(t-\cdot) \parallel \Psi_{F,\sigma}(\cdot+h,\cdot ) \Lambda ^{2}(\cdot) \parallel _{L^{1}([0,t])} ,
\\
\vartheta_{2}(b) &=& \sup_{t \in [0,b] } \parallel \parallel T(t-\cdot) \parallel \Psi_{F,\sigma}(\cdot ,\cdot ) \Lambda (\cdot) \parallel _{L^{1}([0,t])} , \\
\vartheta_{3}(b) &=& \sup_{t,h\in [0,b],t+h\leq b} \parallel \parallel(-A)^{\alpha}T(t-\cdot) \parallel \Psi_{F,\sigma}(\cdot +h ,\cdot ) ,
\Lambda^{2}(\cdot) \parallel_{L^{1}([0,t])}, \\
\vartheta_{4}(b) &=& \sup_{t \in [0,b] } \parallel \parallel(-A)^{\alpha}T(t-\cdot) \parallel
\Psi_{F,\sigma}(\cdot ,\cdot ) \Lambda (\cdot) \parallel_{L^{1}([0,t])} ,\\
\vartheta_{5}(b) &=& \sup_{t\in [0,b]} \parallel \parallel(-A)^{\alpha}T(t-\cdot) \parallel [F]_{(\cdot,0)} \parallel_{L^{1}([0,t])}, \\
\vartheta_{6}(b) &=& \sup_{t\in [0,b]} \int_0^t \parallel(-A)^{\alpha}T(t-\tau) \parallel [F]_{(\tau,0)} \tau \, {\rm d}\tau, \\
\chi_{_{2},\infty} (x) &:=& \sup_{b\geq 0}\chi_{_{2} }(b,x) , \qquad \vartheta_{i,\infty} :=
\sup_{b\geq 0} \vartheta_{i}(b) , \quad i=1,\ldots,6 .
\end{eqnarray*}
\begin{eqnarray*}
\chi_{_{1},\infty}( x)&:=& \sup_{s\geq 0 } \parallel T(s) \parallel \parallel \varrho_{1}(\cdot)\mathcal{K}_{F}( x ) + \varrho_{2}(\cdot) \parallel_{L^{\infty}([0,\infty))} \\
\chi_{_{2}}(b,x)&:=& \sup_{t\in [0,b]} \parallel \parallel T(t-\cdot) \parallel \varrho_{1}(\cdot)\mathcal{K}_{F}( x ) + \varrho_{2}(\cdot) \parallel_{L^{1}([0,t])} \\
\vartheta_{1}(b)&:=& \sup\limits_{{ t,h\in [0,b], t+h\in [0,b]}} \parallel \parallel T(t-\cdot) \parallel \Psi_{F,\sigma}(\cdot+h,\cdot ) \Lambda ^{2}(\cdot) \parallel _{L^{1}([0,t])} ,
\\
\vartheta_{2}(b) &=& \sup_{t \in [0,b] } \parallel \parallel T(t-\cdot) \parallel \Psi_{F,\sigma}(\cdot ,\cdot ) \Lambda (\cdot) \parallel _{L^{1}([0,t])} , \\
\vartheta_{3}(b) &=& \sup_{t,h\in [0,b],t+h\leq b} \parallel \parallel(-A)^{\alpha}T(t-\cdot) \parallel \Psi_{F,\sigma}(\cdot +h ,\cdot ) ,
\Lambda^{2}(\cdot) \parallel_{L^{1}([0,t])}, \\
\vartheta_{4}(b) &=& \sup_{t \in [0,b] } \parallel \parallel(-A)^{\alpha}T(t-\cdot) \parallel
\Psi_{F,\sigma}(\cdot ,\cdot ) \Lambda (\cdot) \parallel_{L^{1}([0,t])} ,\\
\vartheta_{5}(b) &=& \sup_{t\in [0,b]} \parallel \parallel(-A)^{\alpha}T(t-\cdot) \parallel [F]_{(\cdot,0)} \parallel_{L^{1}([0,t])}, \\
\vartheta_{6}(b) &=& \sup_{t\in [0,b]} \int_0^t \parallel(-A)^{\alpha}T(t-\tau) \parallel [F]_{(\tau,0)} \tau \, {\rm d}\tau, \\
\chi_{_{2},\infty} (x) &:=& \sup_{b\geq 0}\chi_{_{2} }(b,x) , \qquad \vartheta_{i,\infty} :=
\sup_{b\geq 0} \vartheta_{i}(b) , \quad i=1,\ldots,6 .
\end{eqnarray*}We can establish now the first result of this section.
Proposition 4.4. Assume that the conditions in Theorem 3.1 are satisfied for all a > 0, the functions  $ \varrho_{i}(\cdot)$ are bounded on
$ \varrho_{i}(\cdot)$ are bounded on  $[0,\infty)$,
$[0,\infty)$,  $ \vartheta_{i,\infty} \lt \infty $ and
$ \vartheta_{i,\infty} \lt \infty $ and  $ \chi_{_{i},\infty} (x) \lt \infty$ for
$ \chi_{_{i},\infty} (x) \lt \infty$ for  $i= 1,2$ and all x > 0. Let
$i= 1,2$ and all x > 0. Let  $ Q_{\infty} : [0,\infty)\mapsto\mathbb{R}$ be the function given by
$ Q_{\infty} : [0,\infty)\mapsto\mathbb{R}$ be the function given by
 \begin{eqnarray*}
Q_{\infty} (x ) & :=& C_{0} \parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})} +
( \chi_{_{1},\infty}(x) + \chi_{_{2},\infty}(x) ) \\
&& + \mathcal{W}_{F }(x ) (1+\mathcal{W}_{\sigma}(x)) \left( (1+x) ^{2} \vartheta_{1,\infty}
+ (1+x) \vartheta_{2,\infty} \right) -x .
\end{eqnarray*}
\begin{eqnarray*}
Q_{\infty} (x ) & :=& C_{0} \parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})} +
( \chi_{_{1},\infty}(x) + \chi_{_{2},\infty}(x) ) \\
&& + \mathcal{W}_{F }(x ) (1+\mathcal{W}_{\sigma}(x)) \left( (1+x) ^{2} \vartheta_{1,\infty}
+ (1+x) \vartheta_{2,\infty} \right) -x .
\end{eqnarray*} If  $Q_{\infty} (R ) \lt 0 $ for some R > 0, then there exists a unique mild solution
$Q_{\infty} (R ) \lt 0 $ for some R > 0, then there exists a unique mild solution  $u(\cdot)$ of (1.1)–(1.2) in
$u(\cdot)$ of (1.1)–(1.2) in  $ C_{\rm Lip, 1+\alpha-\gamma,1}((0,\infty);X_{\alpha}) $ such that
$ C_{\rm Lip, 1+\alpha-\gamma,1}((0,\infty);X_{\alpha}) $ such that  $ [ u_{\mid_{[0,1]}}]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha})}\leq R$ and
$ [ u_{\mid_{[0,1]}}]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha})}\leq R$ and  $ [u_{\mid_{[1,\infty)}} ]_{C_{\rm Lip }([1,\infty);X_{\alpha})}\leq R$.
$ [u_{\mid_{[1,\infty)}} ]_{C_{\rm Lip }([1,\infty);X_{\alpha})}\leq R$.
Proof. For a > 1, let  $ Q_{a}(\cdot)$ be the function
$ Q_{a}(\cdot)$ be the function  $Q_{a}
:[0,\infty) \mapsto\mathbb{R}$ given by
$Q_{a}
:[0,\infty) \mapsto\mathbb{R}$ given by
 \begin{eqnarray*}
Q_{a} (x ) & :=& C_{0} \parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})} + ( \chi_{_{1} }(a,x) + \chi_{_{2} }(a,x) )\\
&& + \mathcal{W}_{F }(x ) (1+\mathcal{W}_{\sigma}(x)) \left((1+x) ^{2} \vartheta_{1 }(a ) + (1+x) \vartheta_{2 }(a) \right) -x.
\end{eqnarray*}
\begin{eqnarray*}
Q_{a} (x ) & :=& C_{0} \parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})} + ( \chi_{_{1} }(a,x) + \chi_{_{2} }(a,x) )\\
&& + \mathcal{W}_{F }(x ) (1+\mathcal{W}_{\sigma}(x)) \left((1+x) ^{2} \vartheta_{1 }(a ) + (1+x) \vartheta_{2 }(a) \right) -x.
\end{eqnarray*} From the definition of  $Q_{a}(\cdot)$ and
$Q_{a}(\cdot)$ and  $Q_{\infty}(\cdot)$, we note that
$Q_{\infty}(\cdot)$, we note that  $ Q_{a} (x )\leq Q_{\infty}(x)$ for all x > 0, which implies that
$ Q_{a} (x )\leq Q_{\infty}(x)$ for all x > 0, which implies that  $ Q_{a} (R )\leq Q_{\infty}(R) \lt 0$. Moreover, using that
$ Q_{a} (R )\leq Q_{\infty}(R) \lt 0$. Moreover, using that  $ Q_{a} (R ) \lt 0$ and proceeding as in the proofs of Theorem 3.1 and Corollary 3.4, we can prove that there exists a ‘unique’ mild solution
$ Q_{a} (R ) \lt 0$ and proceeding as in the proofs of Theorem 3.1 and Corollary 3.4, we can prove that there exists a ‘unique’ mild solution  $ u_{\mid_{[0,1]}} \in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha}) $ of the problem (1.1)–(1.2) on
$ u_{\mid_{[0,1]}} \in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha}) $ of the problem (1.1)–(1.2) on  $[0,a]$ such that
$[0,a]$ such that  $ [ u^{a}_{\mid_{[0,1]}}]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha})}\leq R$ and
$ [ u^{a}_{\mid_{[0,1]}}]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha})}\leq R$ and  $ [ u^{a}_{\mid_{[1,a]}}]_{C_{\rm Lip }([1,a];X_{\alpha})}\leq R$. From the uniqueness of the solution
$ [ u^{a}_{\mid_{[1,a]}}]_{C_{\rm Lip }([1,a];X_{\alpha})}\leq R$. From the uniqueness of the solution  $u^{a}(\cdot)$, it follows that the function
$u^{a}(\cdot)$, it follows that the function  $u:[0,\infty)\mapsto X_{\alpha} $ defined by
$u:[0,\infty)\mapsto X_{\alpha} $ defined by  $u(t)=u^{a}(t)$ for
$u(t)=u^{a}(t)$ for  $t\in [0,a]$ is a mild solution of (1.1)–(1.2) on
$t\in [0,a]$ is a mild solution of (1.1)–(1.2) on  $[0,\infty)$. Moreover, from the above remarks and the proof of Corollary 3.4, we have that
$[0,\infty)$. Moreover, from the above remarks and the proof of Corollary 3.4, we have that  $ u\in C_{\rm Lip, 1+\alpha-\gamma,1}((0,\infty);X_{\alpha}) $, that
$ u\in C_{\rm Lip, 1+\alpha-\gamma,1}((0,\infty);X_{\alpha}) $, that  $ [ u_{\mid_{[0,1]}}]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha})}\leq R$ and that
$ [ u_{\mid_{[0,1]}}]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha})}\leq R$ and that  $ [ u_{\mid_{[0,\infty)}}]_{C_{\rm Lip }([1,\infty);X_{\alpha})}\leq R$. The proof is complete.
$ [ u_{\mid_{[0,\infty)}}]_{C_{\rm Lip }([1,\infty);X_{\alpha})}\leq R$. The proof is complete.
The proof of Proposition 4.4 is done combining the ideas in the proofs of Corollary 3.4 and Theorem 3.1. In a similar way, but using Corollary 3.7 and Proposition 3.1, we can prove the existence of a solution on  $[0,\infty)$ for the case in which
$[0,\infty)$ for the case in which  $F\in
C([0,\infty)\times X_{\alpha};X)$. In the next result, we assume that
$F\in
C([0,\infty)\times X_{\alpha};X)$. In the next result, we assume that  $F(0,\cdot)\in C_{\rm Lip,loc}(X_{\alpha};X_{\alpha}) $ and we use the next notation:
$F(0,\cdot)\in C_{\rm Lip,loc}(X_{\alpha};X_{\alpha}) $ and we use the next notation:
 \begin{align*}
\chi_{_{3}}(t) &:= \parallel (-A)^{\alpha}F(0,x_{0}) \parallel \int_0^t \parallel T(t-s) \parallel \,{\rm d}s , \qquad \chi_{_{3},\infty} =\sup_{t\geq 0} \chi_{_{3}}(t) ,\\
\chi_{_{4} }( t,x)&:= 2x [F(0,\cdot)]_{C_{\rm Lip}(B_{x}(0,X_{\alpha});X_{\alpha})} \int_0^t \parallel T(t-s) \parallel \,{\rm d}s\quad{\rm and} \quad \chi_{_{4},\infty}( x) = \sup_{t\geq 0}\chi_{_{4} }( t,x).
\end{align*}
\begin{align*}
\chi_{_{3}}(t) &:= \parallel (-A)^{\alpha}F(0,x_{0}) \parallel \int_0^t \parallel T(t-s) \parallel \,{\rm d}s , \qquad \chi_{_{3},\infty} =\sup_{t\geq 0} \chi_{_{3}}(t) ,\\
\chi_{_{4} }( t,x)&:= 2x [F(0,\cdot)]_{C_{\rm Lip}(B_{x}(0,X_{\alpha});X_{\alpha})} \int_0^t \parallel T(t-s) \parallel \,{\rm d}s\quad{\rm and} \quad \chi_{_{4},\infty}( x) = \sup_{t\geq 0}\chi_{_{4} }( t,x).
\end{align*}Proposition 4.5. Assume that the conditions in Proposition 3.1 are satisfied for all a > 0, that  $ \vartheta_{i,\infty} \lt \infty $ for
$ \vartheta_{i,\infty} \lt \infty $ for  $i= 3,4,5, 6$,
$i= 3,4,5, 6$,  $\chi_{_{3},\infty} \lt \infty $ and
$\chi_{_{3},\infty} \lt \infty $ and  $ \chi_{_{4},\infty}( x) \lt \infty $ for all x > 0, and let
$ \chi_{_{4},\infty}( x) \lt \infty $ for all x > 0, and let  $ Q_{\infty} : [0,\infty)\mapsto \mathbb{R}$ be the function given by
$ Q_{\infty} : [0,\infty)\mapsto \mathbb{R}$ be the function given by
 \begin{eqnarray*}
Q_{\infty} (x) & =& C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + ( \chi_{_{3},\infty} + \chi_{_{4},\infty}( x) ) \\ && +
\mathcal{W}_{F }(x) \vartheta_{6,\infty}
+ \left( { \mathcal{W}_{F }(x) \vartheta_{5,\infty} } + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \vartheta_{3,\infty} \right) \\
& & + \mathcal{W}_{F,\sigma}(x) (1+x) \vartheta_{4,\infty} - x,
\end{eqnarray*}
\begin{eqnarray*}
Q_{\infty} (x) & =& C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + ( \chi_{_{3},\infty} + \chi_{_{4},\infty}( x) ) \\ && +
\mathcal{W}_{F }(x) \vartheta_{6,\infty}
+ \left( { \mathcal{W}_{F }(x) \vartheta_{5,\infty} } + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \vartheta_{3,\infty} \right) \\
& & + \mathcal{W}_{F,\sigma}(x) (1+x) \vartheta_{4,\infty} - x,
\end{eqnarray*}where  $\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. If
$\mathcal{W}_{F,\sigma}(\theta)=\mathcal{W}_{F }(\theta)(1+\mathcal{W}_{\sigma}(\theta))$. If  $Q_{\infty}(R) \lt 0$ for some R > 0, then there exists a unique mild solution
$Q_{\infty}(R) \lt 0$ for some R > 0, then there exists a unique mild solution  $ u\in C_{\rm Lip, 1+\alpha-\gamma}((0,\infty); X_{\alpha})$ of (1.1)–(1.2) on
$ u\in C_{\rm Lip, 1+\alpha-\gamma}((0,\infty); X_{\alpha})$ of (1.1)–(1.2) on  $[0,\infty)$.
$[0,\infty)$.
Proof. To prove the assertion, we use the argument in the proof of Corollary 3.7 and Proposition 3.1. Let a > 0. Considering the definition of the function  $P_{a}(\cdot)$ in the proof of Corollary 3.7, see (3.26), we introduce the function
$P_{a}(\cdot)$ in the proof of Corollary 3.7, see (3.26), we introduce the function  $Q_{a} :[0,\infty) \mapsto\mathbb{R}$ defined by
$Q_{a} :[0,\infty) \mapsto\mathbb{R}$ defined by
 \begin{eqnarray*}
Q_{a} (x ) & :=& C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + ( \chi_{_{3} } (a) + \chi_{_{4}}(a, x) ) \\ && +
\mathcal{W}_{F }(x) \vartheta_{6,\infty} + \left( {\mathcal{W}_{F }(x) \vartheta_{5,\infty} } + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \vartheta_{3,\infty} \right) \\
& & + \mathcal{W}_{F,\sigma}(x) (1+x) \vartheta_{4,\infty}-x.
\end{eqnarray*}
\begin{eqnarray*}
Q_{a} (x ) & :=& C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + ( \chi_{_{3} } (a) + \chi_{_{4}}(a, x) ) \\ && +
\mathcal{W}_{F }(x) \vartheta_{6,\infty} + \left( {\mathcal{W}_{F }(x) \vartheta_{5,\infty} } + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \vartheta_{3,\infty} \right) \\
& & + \mathcal{W}_{F,\sigma}(x) (1+x) \vartheta_{4,\infty}-x.
\end{eqnarray*} Noting that  $Q_{a}(R) \leq Q_{\infty}(R) \lt 0 $ and that the term
$Q_{a}(R) \leq Q_{\infty}(R) \lt 0 $ and that the term  $ ( \chi_{_{3} } (a) + \chi_{_{4}}(a, x) ) $ has the same sense that the term
$ ( \chi_{_{3} } (a) + \chi_{_{4}}(a, x) ) $ has the same sense that the term  $ C_{0 } \max\{a, a^{1+\alpha-\gamma}\} ( \parallel
F(0,x_{0}) \parallel_{\alpha} + 2x
[F(0,\cdot)]_{C_{\rm Lip}(B_{x}(0,X_{\alpha});X_{\alpha})} ) $ in the definition of
$ C_{0 } \max\{a, a^{1+\alpha-\gamma}\} ( \parallel
F(0,x_{0}) \parallel_{\alpha} + 2x
[F(0,\cdot)]_{C_{\rm Lip}(B_{x}(0,X_{\alpha});X_{\alpha})} ) $ in the definition of  $P_{a}(\cdot)$, it follows that we can use the same argument in the proof of Corollary 3.7 to prove that there exists a unique mild solution
$P_{a}(\cdot)$, it follows that we can use the same argument in the proof of Corollary 3.7 to prove that there exists a unique mild solution  $u^{a} \in
C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha}) $ of the problem (1.1)–(1.2) on
$u^{a} \in
C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha}) $ of the problem (1.1)–(1.2) on  $[0,a]$ such that
$[0,a]$ such that  $
[u^{a}_{\mid_{[0,1]}}]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha})}\leq R$ and
$
[u^{a}_{\mid_{[0,1]}}]_{C_{\rm Lip,1+\alpha-\gamma}((0,1];X_{\alpha})}\leq R$ and  $ [u^{a}_{\mid_{[1,a]}}]_{C_{\rm Lip }([1,a];X_{\alpha})}\leq R$. To finish, we only note that the function
$ [u^{a}_{\mid_{[1,a]}}]_{C_{\rm Lip }([1,a];X_{\alpha})}\leq R$. To finish, we only note that the function  $u:[0,\infty)\mapsto
X_{\alpha} $ given by
$u:[0,\infty)\mapsto
X_{\alpha} $ given by  $u(t)=u^{a}(t)$ for
$u(t)=u^{a}(t)$ for  $t\in [0,a]$ satisfies the conditions in the assertion. We omit extra details.
$t\in [0,a]$ satisfies the conditions in the assertion. We omit extra details.
We believe it is interesting to make some observations concerning the viability of the assumptions in last propositions. For sake of brevity, we only consider an example related to Proposition 4.4. In the next example, we assume that  $\alpha\in (0,1)$ and there are
$\alpha\in (0,1)$ and there are  $ l\in \mathbb{N}$ and ɛ > 0 such that
$ l\in \mathbb{N}$ and ɛ > 0 such that  $t\geq \sigma(t,x)\geq t^{l}$ for all
$t\geq \sigma(t,x)\geq t^{l}$ for all  $(t,x)\in [0,1] \times
[0,\infty)$,
$(t,x)\in [0,1] \times
[0,\infty)$,  $ \sigma(t,x)\leq t$ for all
$ \sigma(t,x)\leq t$ for all  $(t,x)\in [0,\infty)
\times [0,\infty)$,
$(t,x)\in [0,\infty)
\times [0,\infty)$,  $\gamma=1+ \alpha-\varepsilon$ and
$\gamma=1+ \alpha-\varepsilon$ and  $ 1 - 2l\varepsilon \gt 0$.
$ 1 - 2l\varepsilon \gt 0$.
In addition to the above, we suppose  $F\in
C_{\rm Lip}([0,\infty)\times X;X)$,
$F\in
C_{\rm Lip}([0,\infty)\times X;X)$,  $\sigma\in C_{\rm Lip}([0,\infty)\times
X;[0,\infty) )$, that both functions are bounded and that the semigroup
$\sigma\in C_{\rm Lip}([0,\infty)\times
X;[0,\infty) )$, that both functions are bounded and that the semigroup  $ (T(t))_{t\geq 0} $ is uniformly exponentially stable. Specifically, we assume that there are β > 0 and constants
$ (T(t))_{t\geq 0} $ is uniformly exponentially stable. Specifically, we assume that there are β > 0 and constants  $D_{0,\theta} \gt 0$ such that
$D_{0,\theta} \gt 0$ such that  $\parallel (-A)^{\theta} T(t)\parallel \leq D_{0,\theta}
\,{\rm e}^{-\beta t}t^{-\theta} $ for all t > 0 and θ > 0. Under these conditions, we can assume that
$\parallel (-A)^{\theta} T(t)\parallel \leq D_{0,\theta}
\,{\rm e}^{-\beta t}t^{-\theta} $ for all t > 0 and θ > 0. Under these conditions, we can assume that  $\mathcal{W}_{F,\sigma}( x )\leq 2$,
$\mathcal{W}_{F,\sigma}( x )\leq 2$,  $
[F]_{(t,s)} (1+ [ \sigma]_{(t,s)})= [F]_{C_{\rm Lip} } (1+
[\sigma]_{C_{\rm Lip} } )$ for all
$
[F]_{(t,s)} (1+ [ \sigma]_{(t,s)})= [F]_{C_{\rm Lip} } (1+
[\sigma]_{C_{\rm Lip} } )$ for all  $t\geq s\geq 0$ and x > 0 and that
$t\geq s\geq 0$ and x > 0 and that  $\xi(s)=s^{l}$ for
$\xi(s)=s^{l}$ for  $s\in (0,1]$ and
$s\in (0,1]$ and  $\xi(s)=1$ for
$\xi(s)=1$ for  $s\geq 1 $.
$s\geq 1 $.
In order to estimate  $ \vartheta_{1,\infty}$, for t > 0 and h > 0, we note that
$ \vartheta_{1,\infty}$, for t > 0 and h > 0, we note that
 \begin{align*}
\int_{{0}}^{t} & \parallel T(t-s)\parallel \frac{[F]_{(s+h,s)} }{\zeta^{2(1+\alpha-\gamma)}(s) } (1 + [ \sigma]_{(s+h,s)})\, {\rm d}s \hspace{1cm}\hspace{1cm} \\
& \leq D_{0,0} [F]_{C_{\rm Lip} } (1+ [\sigma]_{C_{\rm Lip} } )
\int_{{0}}^{t} \frac{{\rm e}^{-\beta (t-s)}}{\xi^{2(1+\alpha-\gamma)}(s) } {\rm d}s \\
& \leq D_{0,0} [F]_{C_{\rm Lip} } (1+ [\sigma]_{C_{\rm Lip} } ) \left( \sup_{\tau \in [0,1]} \int_{0}^{\tau} \frac{{\rm d}s}{s^{2l\varepsilon}} + \sup_{\tau \in [1,\infty)} \int_{1}^{ \tau} {\rm e}^{-\beta (\tau-s)} \,{\rm d}s \right)\\
& \leq D_{0,0} [F]_{C_{\rm Lip} } (1+ [\sigma]_{C_{\rm Lip} } ) \left( \frac{1}{1-2l\varepsilon} + \frac{1}{\beta} \right),
\end{align*}
\begin{align*}
\int_{{0}}^{t} & \parallel T(t-s)\parallel \frac{[F]_{(s+h,s)} }{\zeta^{2(1+\alpha-\gamma)}(s) } (1 + [ \sigma]_{(s+h,s)})\, {\rm d}s \hspace{1cm}\hspace{1cm} \\
& \leq D_{0,0} [F]_{C_{\rm Lip} } (1+ [\sigma]_{C_{\rm Lip} } )
\int_{{0}}^{t} \frac{{\rm e}^{-\beta (t-s)}}{\xi^{2(1+\alpha-\gamma)}(s) } {\rm d}s \\
& \leq D_{0,0} [F]_{C_{\rm Lip} } (1+ [\sigma]_{C_{\rm Lip} } ) \left( \sup_{\tau \in [0,1]} \int_{0}^{\tau} \frac{{\rm d}s}{s^{2l\varepsilon}} + \sup_{\tau \in [1,\infty)} \int_{1}^{ \tau} {\rm e}^{-\beta (\tau-s)} \,{\rm d}s \right)\\
& \leq D_{0,0} [F]_{C_{\rm Lip} } (1+ [\sigma]_{C_{\rm Lip} } ) \left( \frac{1}{1-2l\varepsilon} + \frac{1}{\beta} \right),
\end{align*}which implies that  $
\vartheta_{1,\infty} \leq D_{0,0} [F]_{C_{\rm Lip} } (1+ [\sigma]_{C_{\rm Lip} } )\left( \frac{1}{1-2l\varepsilon} + \frac{1}{\beta} \right)$. In a similar way, we can prove that
$
\vartheta_{1,\infty} \leq D_{0,0} [F]_{C_{\rm Lip} } (1+ [\sigma]_{C_{\rm Lip} } )\left( \frac{1}{1-2l\varepsilon} + \frac{1}{\beta} \right)$. In a similar way, we can prove that  $
\vartheta_{2,\infty} \leq D_{0,0} [F]_{C_{\rm Lip} } (1+ [\sigma]_{C_{\rm Lip} } )\left( \frac{1}{1- l\varepsilon} + \frac{1}{\beta} \right)$. In addition, noting that
$
\vartheta_{2,\infty} \leq D_{0,0} [F]_{C_{\rm Lip} } (1+ [\sigma]_{C_{\rm Lip} } )\left( \frac{1}{1- l\varepsilon} + \frac{1}{\beta} \right)$. In addition, noting that  $F(\cdot)$ is bounded, we can assume that the functions
$F(\cdot)$ is bounded, we can assume that the functions  $\varrho_{i}(\cdot)$,
$\varrho_{i}(\cdot)$,  $i=1,2,$ are given by
$i=1,2,$ are given by  $\varrho_{1}(t)= \parallel F(\cdot,\cdot)\parallel_{C([0,\infty)\times X;X)}$ and
$\varrho_{1}(t)= \parallel F(\cdot,\cdot)\parallel_{C([0,\infty)\times X;X)}$ and  $\varrho_{2}(t)= 0$. From the above, for b > 0 and x > 0, we get
$\varrho_{2}(t)= 0$. From the above, for b > 0 and x > 0, we get
 \begin{align*}
\chi_{_{1,\infty}}( x)
&\leq D_{0,0}\parallel F(\cdot,\cdot)\parallel_{C([0,\infty)\times X;X)}, \\
\chi_{_{2},\infty} (x) &\leq D_{0,0} \sup_{t\in [0,b]} \int_{0}^{t} {\rm e}^{-\beta(t-s)}\,{\rm d}s\!\!\parallel F(\cdot,\cdot)\parallel_{C([0,\infty)\times X;X)} \leq \frac{D_{0,0} }{\beta} \parallel F(\cdot,\cdot)\parallel_{C([0,\infty)\times X;X)}.
\end{align*}
\begin{align*}
\chi_{_{1,\infty}}( x)
&\leq D_{0,0}\parallel F(\cdot,\cdot)\parallel_{C([0,\infty)\times X;X)}, \\
\chi_{_{2},\infty} (x) &\leq D_{0,0} \sup_{t\in [0,b]} \int_{0}^{t} {\rm e}^{-\beta(t-s)}\,{\rm d}s\!\!\parallel F(\cdot,\cdot)\parallel_{C([0,\infty)\times X;X)} \leq \frac{D_{0,0} }{\beta} \parallel F(\cdot,\cdot)\parallel_{C([0,\infty)\times X;X)}.
\end{align*} From Lemma 3.1, we also note that  $[T(\cdot)x_{0}]_{ C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})}\leq D_{0,1+\alpha-\gamma} \parallel (-A)^{\gamma}x_{0}\parallel$ if
$[T(\cdot)x_{0}]_{ C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})}\leq D_{0,1+\alpha-\gamma} \parallel (-A)^{\gamma}x_{0}\parallel$ if  $x_{0}\in D(A^{\gamma})$ for some
$x_{0}\in D(A^{\gamma})$ for some  $ \gamma\in (\alpha, \alpha + 1)$. From the above remarks, it follows that under the current conditions, the function
$ \gamma\in (\alpha, \alpha + 1)$. From the above remarks, it follows that under the current conditions, the function  $Q_{\infty}(\cdot)$ in Proposition 4.4 is well defined.
$Q_{\infty}(\cdot)$ in Proposition 4.4 is well defined.
4.2. Maximal and global solutions
In the previous results on the existence of solutions on  $[0,\infty)$, we use the ideas in the proof of Corollary 3.4 and Corollary 3.7. Next, we consider a different approach based on the study of the existence and qualitative properties of maximal solutions. This approach can be also used to study the global existence and uniqueness of a Lispchitz solution and is a novelty in this type of study. Considering the above comments, next we study separately the global existence of Lipschtz and non-Lipschitz solution.
$[0,\infty)$, we use the ideas in the proof of Corollary 3.4 and Corollary 3.7. Next, we consider a different approach based on the study of the existence and qualitative properties of maximal solutions. This approach can be also used to study the global existence and uniqueness of a Lispchitz solution and is a novelty in this type of study. Considering the above comments, next we study separately the global existence of Lipschtz and non-Lipschitz solution.
To establish and prove the next results, we include the following condition.
 \begin{align*}
\mathcal{H}_{F,\sigma,a}^{\alpha,\beta}: q\geq 1, \alpha \in (0,1), \beta\in (\alpha,1), F\in L^{q}_{\rm Lip}([0,a]\times X_{1};X_{\beta})\cap L^{q}_{\rm Lip}([0,a]\times X_{\alpha};X )\\
\mathrm{and}\ \sigma\in C_{\rm Lip}([0,a]\times X_{\alpha};\mathbb{R}^{+} ).
\end{align*}
\begin{align*}
\mathcal{H}_{F,\sigma,a}^{\alpha,\beta}: q\geq 1, \alpha \in (0,1), \beta\in (\alpha,1), F\in L^{q}_{\rm Lip}([0,a]\times X_{1};X_{\beta})\cap L^{q}_{\rm Lip}([0,a]\times X_{\alpha};X )\\
\mathrm{and}\ \sigma\in C_{\rm Lip}([0,a]\times X_{\alpha};\mathbb{R}^{+} ).
\end{align*}4.2.1. Existence and uniqueness of a Lipschitz solution on  $[0,\infty)$
$[0,\infty)$
To begin, we study the existence and qualitative properties of maximal solutions. In the next results, we assume that the condition  $ \bf H_{F,\sigma, a}^{q,r }(X_{\alpha} ;X)$ is satisfied and that
$ \bf H_{F,\sigma, a}^{q,r }(X_{\alpha} ;X)$ is satisfied and that  $\sigma(\cdot)$ is Lipschitz. In addition, for
$\sigma(\cdot)$ is Lipschitz. In addition, for  $c\in (0,a]$, we use the notation
$c\in (0,a]$, we use the notation  $\widehat{\Phi}_{i,c} $,
$\widehat{\Phi}_{i,c} $,  $i=1,2$, for the functions
$i=1,2$, for the functions  $\widehat{\Phi}_{i,c} : [c,a] \mapsto\mathbb{R} $ given by
$\widehat{\Phi}_{i,c} : [c,a] \mapsto\mathbb{R} $ given by
 \begin{equation*}
\widehat{\Phi}_{1,c}(d) = \sup_{t\in [c,d] } \int_c^t \frac{[F]_{(\tau,0)}}{(t-\tau)^\alpha} \,{\rm d}\tau \quad {\rm and} \quad \widehat{\Phi}_{2,c}(d) = \sup_{t,h\in [c,d],t+h\leq d} \int_c^t \frac{[F]_{(\tau+h,\tau)}}{(t-\tau)^\alpha } \,{\rm d}\tau.
\end{equation*}
\begin{equation*}
\widehat{\Phi}_{1,c}(d) = \sup_{t\in [c,d] } \int_c^t \frac{[F]_{(\tau,0)}}{(t-\tau)^\alpha} \,{\rm d}\tau \quad {\rm and} \quad \widehat{\Phi}_{2,c}(d) = \sup_{t,h\in [c,d],t+h\leq d} \int_c^t \frac{[F]_{(\tau+h,\tau)}}{(t-\tau)^\alpha } \,{\rm d}\tau.
\end{equation*}The proof of the next proposition follows from the proof of Proposition 3.3 or from the results in [Reference Hernandez, Fernandes and Wu22]. However, to develop our next results, it is convenient to include some details of the proof.
Proposition 4.6. Assume that the condition  $\bf H_{F,\sigma, a}^{q,r }(X_{\alpha} ;X)$ is satisfied, that
$\bf H_{F,\sigma, a}^{q,r }(X_{\alpha} ;X)$ is satisfied, that  $\sigma(\cdot)$ is Lipschitz,
$\sigma(\cdot)$ is Lipschitz,  $ T(\cdot)x_{0} \in C_{\rm Lip}([0,a];X_{\alpha})$,
$ T(\cdot)x_{0} \in C_{\rm Lip}([0,a];X_{\alpha})$,  $ F(0, x_{0}) \in X_{\alpha} $ and
$ F(0, x_{0}) \in X_{\alpha} $ and  $0\leq \sigma(s,x)\leq s$ for all
$0\leq \sigma(s,x)\leq s$ for all  $(s,x)\in [0,a]\times X_{\alpha}$. If
$(s,x)\in [0,a]\times X_{\alpha}$. If  $ \widehat{\Phi}_{1,0}(b) +\widehat{\Phi}_{2,0}(b) \to 0 $ as b → 0, then there exists a unique mild solution
$ \widehat{\Phi}_{1,0}(b) +\widehat{\Phi}_{2,0}(b) \to 0 $ as b → 0, then there exists a unique mild solution  $u\in C_{\rm Lip}([0,b];X_{\alpha})$ of (1.1)–(1.2) on
$u\in C_{\rm Lip}([0,b];X_{\alpha})$ of (1.1)–(1.2) on  $[0,b]$ for some
$[0,b]$ for some  $0 \lt b\leq a$.
$0 \lt b\leq a$.
Proof. Let  $R \gt [T (\cdot)x_{0}]_{C_{\rm Lip}([0,a];X_{\alpha})} + \parallel
T(\cdot) F(0,x_{0}) \parallel_{L^{\infty}([0,a];X_{\alpha} )} $ and
$R \gt [T (\cdot)x_{0}]_{C_{\rm Lip}([0,a];X_{\alpha})} + \parallel
T(\cdot) F(0,x_{0}) \parallel_{L^{\infty}([0,a];X_{\alpha} )} $ and  $0 \lt b\leq a $ such that
$0 \lt b\leq a $ such that
 \begin{eqnarray}
[T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha} )} + \parallel T(\cdot) F(0,x_{0}) \parallel_{L^{\infty}([0,a];X_{\alpha} )} && \nonumber\\
+ (1+ R )^{2} \mathcal{W}_{F}(\rho(R,b)){ \left(1+ [\sigma]_{C_{Lip} } \right)} C_{0,\alpha}\left( \widehat{\Phi}_{1,0}(b) +\widehat{\Phi}_{2,0}(b)\right) \lt R,
\end{eqnarray}
\begin{eqnarray}
[T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha} )} + \parallel T(\cdot) F(0,x_{0}) \parallel_{L^{\infty}([0,a];X_{\alpha} )} && \nonumber\\
+ (1+ R )^{2} \mathcal{W}_{F}(\rho(R,b)){ \left(1+ [\sigma]_{C_{Lip} } \right)} C_{0,\alpha}\left( \widehat{\Phi}_{1,0}(b) +\widehat{\Phi}_{2,0}(b)\right) \lt R,
\end{eqnarray}where  $ \rho(R,b):= R b + \parallel x_{0}\parallel_{\alpha} $. Let
$ \rho(R,b):= R b + \parallel x_{0}\parallel_{\alpha} $. Let  $\mathcal{S}(R,b) $ and
$\mathcal{S}(R,b) $ and  $\Gamma(\cdot)$ be defined as in the proof of Proposition 3.3.
$\Gamma(\cdot)$ be defined as in the proof of Proposition 3.3.
Let  $u,v\in \mathcal{S}(R,b)$ and
$u,v\in \mathcal{S}(R,b)$ and  $t,s\in [0,b]$. Noting that
$t,s\in [0,b]$. Noting that  $
\parallel u^{\sigma}(s)\parallel_{\alpha} \leq \parallel u^{\sigma}(s)-x_{0}\parallel_{\alpha}
+ \parallel x_{0}\parallel_{\alpha} \leq \rho(R,b)$ and that
$
\parallel u^{\sigma}(s)\parallel_{\alpha} \leq \parallel u^{\sigma}(s)-x_{0}\parallel_{\alpha}
+ \parallel x_{0}\parallel_{\alpha} \leq \rho(R,b)$ and that  $u(\sigma(0,x_{0}))=u(0)=x_0$, from the proof of Proposition 3.3, it is easy to infer that
$u(\sigma(0,x_{0}))=u(0)=x_0$, from the proof of Proposition 3.3, it is easy to infer that
 \begin{eqnarray*}
\parallel F(s+h,u^{\sigma}(s+h))-F(s,u^{\sigma}(s))\parallel &\leq & \mathcal{W}_{F}(\rho(R,b)) [F]_{(s+h,s)} (1 + R)^{2} (1+ [\sigma]_{C_{\rm Lip} }) h , \\
\parallel F(s,u^{\sigma}(s)) -F(0,{x_{0}}) \parallel &\leq & (1+ R )^{2}\mathcal{W}_{F}(\rho(R,b)) [F]_{(s,0)} (1+ [\sigma]_{C_{\rm Lip} } ) s ,
\end{eqnarray*}
\begin{eqnarray*}
\parallel F(s+h,u^{\sigma}(s+h))-F(s,u^{\sigma}(s))\parallel &\leq & \mathcal{W}_{F}(\rho(R,b)) [F]_{(s+h,s)} (1 + R)^{2} (1+ [\sigma]_{C_{\rm Lip} }) h , \\
\parallel F(s,u^{\sigma}(s)) -F(0,{x_{0}}) \parallel &\leq & (1+ R )^{2}\mathcal{W}_{F}(\rho(R,b)) [F]_{(s,0)} (1+ [\sigma]_{C_{\rm Lip} } ) s ,
\end{eqnarray*}for all  $s, h \in [0,b] $ with
$s, h \in [0,b] $ with  $s+h\in [0,b]$. From the above and arguing as in the proof of Proposition 3.3, see (3.34) and (3.35), for
$s+h\in [0,b]$. From the above and arguing as in the proof of Proposition 3.3, see (3.34) and (3.35), for  $ h,t\in [0,b]$ with
$ h,t\in [0,b]$ with  $t+h\in[0,b]$, we get
$t+h\in[0,b]$, we get
 \begin{align*}
\parallel \Gamma u(t+h) - \Gamma u(t)\parallel_{\alpha}
&\leq [T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})}h + \int^{h}_0 \parallel T(t+h-s) (-A)^{\alpha}F(0,x_{0} ) \parallel\,{\rm d}s \\
& \quad + \int^{h}_0 \parallel (-A)^{\alpha} T(t+h-s) \parallel \parallel F(s,u^{\sigma}(s)) - F(0,x_{0}) \parallel\, {\rm d}s \\
& \quad + \int^{t}_0\parallel (-A)^{\alpha} T(t-s) \parallel \parallel F(s+h,u^{\sigma}(s+h))\\ &\qquad-F(s,u^{\sigma}(s))\parallel \,{\rm d}s \\
&\leq [T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})}h + \parallel T(\cdot) F(0,x_{0}) \parallel_{L^{\infty}([0,a];X_{\alpha} )} h \\ & \quad + (1+ R )^{2}\mathcal{W}_{F}(\rho(R,b)) (1+ [\sigma]_{C_{\rm Lip} } ) ( \widehat{\Phi}_{1,0}(b) +\widehat{\Phi}_{2,0}(b))h \\
&\leq Rh,
\end{align*}
\begin{align*}
\parallel \Gamma u(t+h) - \Gamma u(t)\parallel_{\alpha}
&\leq [T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})}h + \int^{h}_0 \parallel T(t+h-s) (-A)^{\alpha}F(0,x_{0} ) \parallel\,{\rm d}s \\
& \quad + \int^{h}_0 \parallel (-A)^{\alpha} T(t+h-s) \parallel \parallel F(s,u^{\sigma}(s)) - F(0,x_{0}) \parallel\, {\rm d}s \\
& \quad + \int^{t}_0\parallel (-A)^{\alpha} T(t-s) \parallel \parallel F(s+h,u^{\sigma}(s+h))\\ &\qquad-F(s,u^{\sigma}(s))\parallel \,{\rm d}s \\
&\leq [T (\cdot)x_{0}]_{C_{\rm Lip}([0,b];X_{\alpha})}h + \parallel T(\cdot) F(0,x_{0}) \parallel_{L^{\infty}([0,a];X_{\alpha} )} h \\ & \quad + (1+ R )^{2}\mathcal{W}_{F}(\rho(R,b)) (1+ [\sigma]_{C_{\rm Lip} } ) ( \widehat{\Phi}_{1,0}(b) +\widehat{\Phi}_{2,0}(b))h \\
&\leq Rh,
\end{align*}and
 \begin{align}
\parallel \Gamma u(t ) - \Gamma v(t)\parallel
&\leq C_{0,\alpha} \mathcal{W}_{F}(\rho(R,b)) \int^t_0 \frac{ [F]_{(s ,s)}}{(t-s)^{\alpha}} ( 1 +
R [\sigma]_{C_{\rm Lip} } ) \parallel u-v\parallel_{C([0,s];X_{\alpha})} \,{\rm d}s \nonumber \\
&\leq (1+R) \mathcal{W}_{F}(\rho(R,b)) C_{0,\alpha} (1+
[\sigma]_{C_{\rm Lip} } ) \widehat{\Phi}_{2,0}(b) \parallel u-v\parallel_{
C([0,b];X_{\alpha})} ,
\end{align}
\begin{align}
\parallel \Gamma u(t ) - \Gamma v(t)\parallel
&\leq C_{0,\alpha} \mathcal{W}_{F}(\rho(R,b)) \int^t_0 \frac{ [F]_{(s ,s)}}{(t-s)^{\alpha}} ( 1 +
R [\sigma]_{C_{\rm Lip} } ) \parallel u-v\parallel_{C([0,s];X_{\alpha})} \,{\rm d}s \nonumber \\
&\leq (1+R) \mathcal{W}_{F}(\rho(R,b)) C_{0,\alpha} (1+
[\sigma]_{C_{\rm Lip} } ) \widehat{\Phi}_{2,0}(b) \parallel u-v\parallel_{
C([0,b];X_{\alpha})} ,
\end{align}which shows that  $\Gamma(\cdot) $ is a contraction from
$\Gamma(\cdot) $ is a contraction from  $\mathcal{S}(R,b) $ into
$\mathcal{S}(R,b) $ into  $\mathcal{S}(R,b) $. This completes the proof.
$\mathcal{S}(R,b) $. This completes the proof.
In order to use the condition  $\bf \mathcal{H}_{F,\sigma,a}^{\alpha,\beta} $, we remark the next result on strict solution.
$\bf \mathcal{H}_{F,\sigma,a}^{\alpha,\beta} $, we remark the next result on strict solution.
Proposition 4.7. [Reference Hernandez, Fernandes and Wu22, Proposition 3.2] Assume that the conditions in Proposition 4.6 are satisfied,  $x_{0}\in D(A)$ and let
$x_{0}\in D(A)$ and let  $u(\cdot)$ be the mild solution in Proposition 4.6. If
$u(\cdot)$ be the mild solution in Proposition 4.6. If  $ \parallel [F]_{(s,\cdot)}\parallel_{L^{1}([s-\mu,s])} \to 0 $ as
$ \parallel [F]_{(s,\cdot)}\parallel_{L^{1}([s-\mu,s])} \to 0 $ as  $\mu\downarrow 0$ uniformly for s in bounded subsets of
$\mu\downarrow 0$ uniformly for s in bounded subsets of  $[0,a]$, or
$[0,a]$, or  $ \sup_{s\in [0,a]}
\parallel [F]_{(s,\cdot)}\parallel_{L^{q}([0,a])} $ is finite, or
$ \sup_{s\in [0,a]}
\parallel [F]_{(s,\cdot)}\parallel_{L^{q}([0,a])} $ is finite, or  $ F\in C_{\rm Lip} ([0,a]\times ; X_{\alpha}: X ) $, then
$ F\in C_{\rm Lip} ([0,a]\times ; X_{\alpha}: X ) $, then  $u(\cdot )$ is a strict solution of (1.1)–(1.2) on
$u(\cdot )$ is a strict solution of (1.1)–(1.2) on  $ [ 0 ,b] $.
$ [ 0 ,b] $.
The next result is concerning the existence of a maximal strict solution.
Proposition 4.8. Assume that the assumptions in Proposition 4.6 and that the condition  $\bf \mathcal{H}_{F,\sigma,a}^{\alpha,\beta} $ are satisfied. Suppose in addition,
$\bf \mathcal{H}_{F,\sigma,a}^{\alpha,\beta} $ are satisfied. Suppose in addition,  $x_{0}\in D(A)$,
$x_{0}\in D(A)$,  $\lim_{d\downarrow c} \widehat{\Phi}_{i,c}(d)=0 $ for
$\lim_{d\downarrow c} \widehat{\Phi}_{i,c}(d)=0 $ for  $i=1,2 $ and every c > 0 and that
$i=1,2 $ and every c > 0 and that  $F(\cdot)$ satisfies some of the conditions in Proposition 4.7. Then there exists a unique maximal strict solution
$F(\cdot)$ satisfies some of the conditions in Proposition 4.7. Then there exists a unique maximal strict solution  $u\in C(I_{\max};X_{\alpha})$ of (1.1)–(1.2). Moreover,
$u\in C(I_{\max};X_{\alpha})$ of (1.1)–(1.2). Moreover,  $ I_{\max}=[0,a]$ if
$ I_{\max}=[0,a]$ if  $[ u]_{C_{\rm Lip}(I_{\max};X_{\alpha})} $ is finite.
$[ u]_{C_{\rm Lip}(I_{\max};X_{\alpha})} $ is finite.
Proof. Let  $u\in C_{\rm Lip}( [0,b];X_{\alpha})$ be the mild solution in the Proposition 4.6, R be the number in the proof of the cited result and assume b < a. To begin, we study the existence and uniqueness of solution for the problem
$u\in C_{\rm Lip}( [0,b];X_{\alpha})$ be the mild solution in the Proposition 4.6, R be the number in the proof of the cited result and assume b < a. To begin, we study the existence and uniqueness of solution for the problem
Noting that  $u(\cdot)$ is a strict solution on
$u(\cdot)$ is a strict solution on  $[0,b]$, see Proposition 4.7, from condition
$[0,b]$, see Proposition 4.7, from condition  $\bf \mathcal{
H}_{F,\sigma,a}^{\alpha,\beta}$, we obtain that
$\bf \mathcal{
H}_{F,\sigma,a}^{\alpha,\beta}$, we obtain that  $
F(\cdot,u(\cdot))\in C ([0,b];X_{\beta}) $. Using this fact, we have that
$
F(\cdot,u(\cdot))\in C ([0,b];X_{\beta}) $. Using this fact, we have that
 \begin{align}
\parallel (- A)^{1+\alpha}u(b) \parallel
&\leq
\ \parallel (- A)^{1+\alpha} T(b) x_{0} \parallel +
\int_{0}^{b} \parallel (- A)^{1 + \alpha-\beta} T(b-s) \parallel \parallel (- A)^{\beta}\nonumber \\ & \qquad F(s,u^{\sigma}(s)) \parallel \,{\rm d}s \nonumber\\
&\leq
\ \parallel (- A)^{1+\alpha} T(b) x_{0} \parallel + \int_{0}^{b} \frac{ C_{ 0 ,1+\alpha-\beta} }{( b-s)^{1+\alpha-\beta}} \parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C([0,b];X_{\beta})} \,{\rm d}s
\nonumber\\
&\leq \ \parallel (- A)^{1+\alpha} T(b) x_{0} \parallel + \parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C([0,b];X_{\beta})} C_{ 0 ,1+\alpha-\beta} \frac{b^{\beta-\alpha } }{\beta-\alpha} ,
\end{align}
\begin{align}
\parallel (- A)^{1+\alpha}u(b) \parallel
&\leq
\ \parallel (- A)^{1+\alpha} T(b) x_{0} \parallel +
\int_{0}^{b} \parallel (- A)^{1 + \alpha-\beta} T(b-s) \parallel \parallel (- A)^{\beta}\nonumber \\ & \qquad F(s,u^{\sigma}(s)) \parallel \,{\rm d}s \nonumber\\
&\leq
\ \parallel (- A)^{1+\alpha} T(b) x_{0} \parallel + \int_{0}^{b} \frac{ C_{ 0 ,1+\alpha-\beta} }{( b-s)^{1+\alpha-\beta}} \parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C([0,b];X_{\beta})} \,{\rm d}s
\nonumber\\
&\leq \ \parallel (- A)^{1+\alpha} T(b) x_{0} \parallel + \parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C([0,b];X_{\beta})} C_{ 0 ,1+\alpha-\beta} \frac{b^{\beta-\alpha } }{\beta-\alpha} ,
\end{align}which implies that  $ u(b)\in D((- A)^{1 + \alpha} ) $.
$ u(b)\in D((- A)^{1 + \alpha} ) $.
From the above,  $T(\cdot-b)u(b)\in C_{\rm Lip}([b,a];X_{\alpha})$ and
$T(\cdot-b)u(b)\in C_{\rm Lip}([b,a];X_{\alpha})$ and  $ F(b , u^{\sigma}(b) )\in X_{\alpha}$, which allows us to use the same argument of the proof of Proposition 4.6 to study the existence of solution for the problem (4.38)–(4.39). Let
$ F(b , u^{\sigma}(b) )\in X_{\alpha}$, which allows us to use the same argument of the proof of Proposition 4.6 to study the existence of solution for the problem (4.38)–(4.39). Let
 \begin{equation*}R_{1} \gt R+ [T (\cdot-b )u(b)]_{C_{\rm Lip}([b,a];X_{\alpha})} + \parallel T(\cdot) F(b , u^{\sigma}(b) )\parallel_{L^{\infty}([0,a];X_{\alpha})}.\end{equation*}
\begin{equation*}R_{1} \gt R+ [T (\cdot-b )u(b)]_{C_{\rm Lip}([b,a];X_{\alpha})} + \parallel T(\cdot) F(b , u^{\sigma}(b) )\parallel_{L^{\infty}([0,a];X_{\alpha})}.\end{equation*} From the assumptions on the functions  $ \widehat{\Phi}_{i,b}(\cdot)$,
$ \widehat{\Phi}_{i,b}(\cdot)$,  $i=1,2$, there exists δ > 0 such that
$i=1,2$, there exists δ > 0 such that
 \begin{eqnarray}
R+ [T (\cdot-b )u(b)]_{C_{\rm Lip}([b,a];X_{\alpha})} + \parallel T(\cdot) F(b , u^{\sigma}(b) )\parallel_{L^{\infty}([0,a];X_{\alpha})} &&
\nonumber\\ + (1+ R_{1} )^{2}
\mathcal{W}_{F}(\rho(R_{1})) C_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip} } )\left( \widehat{\Phi}_{1,b}(b+\delta) + \widehat{\Phi}_{2,b}(b+\delta)\right) \lt R_{1},
\end{eqnarray}
\begin{eqnarray}
R+ [T (\cdot-b )u(b)]_{C_{\rm Lip}([b,a];X_{\alpha})} + \parallel T(\cdot) F(b , u^{\sigma}(b) )\parallel_{L^{\infty}([0,a];X_{\alpha})} &&
\nonumber\\ + (1+ R_{1} )^{2}
\mathcal{W}_{F}(\rho(R_{1})) C_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip} } )\left( \widehat{\Phi}_{1,b}(b+\delta) + \widehat{\Phi}_{2,b}(b+\delta)\right) \lt R_{1},
\end{eqnarray}where  $ \rho(R_{1}):= R_{1} a + \parallel u(b)\parallel_{\alpha} $. Proceeding as in the proof of Proposition 4.6, we define the space
$ \rho(R_{1}):= R_{1} a + \parallel u(b)\parallel_{\alpha} $. Proceeding as in the proof of Proposition 4.6, we define the space
 \begin{equation*}\mathcal{S}(R_{1},b+\delta)=\{v\in C([ 0 ,b+\delta ];X): v_{\mid_{[0,b]}}=u , [v]_{C_{\rm Lip}([ b,b+\delta ];X_{\alpha})}\leq R_{1} \},\end{equation*}
\begin{equation*}\mathcal{S}(R_{1},b+\delta)=\{v\in C([ 0 ,b+\delta ];X): v_{\mid_{[0,b]}}=u , [v]_{C_{\rm Lip}([ b,b+\delta ];X_{\alpha})}\leq R_{1} \},\end{equation*}endowed with the metric  $d(w,v)=\parallel w-v\parallel _{C([ b,b+\delta ];X_{\alpha})}$. In addition, we define the map
$d(w,v)=\parallel w-v\parallel _{C([ b,b+\delta ];X_{\alpha})}$. In addition, we define the map  $\Gamma: \mathcal{S}(R_{1},b+\delta)\to C([ 0 ,b+\delta ];X)$ by
$\Gamma: \mathcal{S}(R_{1},b+\delta)\to C([ 0 ,b+\delta ];X)$ by  $\Gamma v(t)=u(t)$ for
$\Gamma v(t)=u(t)$ for  $t\in [0,b]$ and
$t\in [0,b]$ and
 \begin{equation*} \Gamma v(t)= T (t-b) u(b) +\int^t_b T(t-s) F\left(s,v^{\sigma}(s)\right)\,{\rm d}s, \qquad {\rm for}\ t\in [ b,b+\delta ]. \end{equation*}
\begin{equation*} \Gamma v(t)= T (t-b) u(b) +\int^t_b T(t-s) F\left(s,v^{\sigma}(s)\right)\,{\rm d}s, \qquad {\rm for}\ t\in [ b,b+\delta ]. \end{equation*} Arguing as in the proof of Proposition 4.6, we can prove that  $\Gamma(\cdot)$ is a contraction, which implies that there exists a unique mild solution
$\Gamma(\cdot)$ is a contraction, which implies that there exists a unique mild solution  $v\in C_{\rm Lip}([0,b+\delta
]; X_{\alpha}) $ of (4.38)–(4.39). Moreover, using Proposition 4.7, it is easy to infer that
$v\in C_{\rm Lip}([0,b+\delta
]; X_{\alpha}) $ of (4.38)–(4.39). Moreover, using Proposition 4.7, it is easy to infer that  $v(\cdot) $ is the unique X α-valued Lipschitz strict solution of (1.1)–(1.2) on
$v(\cdot) $ is the unique X α-valued Lipschitz strict solution of (1.1)–(1.2) on  $[0,b+\delta]$.
$[0,b+\delta]$.
From the above remarks and the Zorn’s Lemma, we infer that there exists a unique maximal ‘locally Lipschitz’ strict solution  $w\in C ( I_{\max};X_{\alpha})$ of Equations (1.1)–(1.2).
$w\in C ( I_{\max};X_{\alpha})$ of Equations (1.1)–(1.2).
To complete the proof, assume  $b_{x_{0}} = \sup I_{\max} \lt a
$ and that
$b_{x_{0}} = \sup I_{\max} \lt a
$ and that  $[w]_{C_{\rm Lip} ( I_{\max};X_{\alpha})} \lt \infty$. Using that
$[w]_{C_{\rm Lip} ( I_{\max};X_{\alpha})} \lt \infty$. Using that 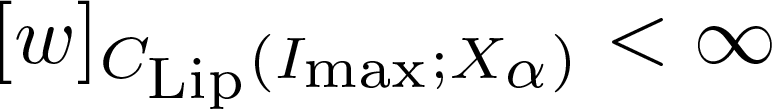 $[w]_{C_{\rm Lip} ( I_{\max};X_{\alpha})} \lt \infty$, it follows that X α-
$[w]_{C_{\rm Lip} ( I_{\max};X_{\alpha})} \lt \infty$, it follows that X α- $\lim_{t\to b_{x_{0}}} w(t) $ exists and it is easy to see that the function
$\lim_{t\to b_{x_{0}}} w(t) $ exists and it is easy to see that the function  $\overline{w} :[0,b_{x_{0}}]\mapsto X_{\alpha}$ defined by
$\overline{w} :[0,b_{x_{0}}]\mapsto X_{\alpha}$ defined by  $\overline{w}(\theta)=w(\theta)$ for
$\overline{w}(\theta)=w(\theta)$ for  $\theta \lt b_{x_{0}} $ and
$\theta \lt b_{x_{0}} $ and  $\overline{w}(b_{x_{0}})=\lim_{t\to b_{x_{0}} }w(t) $ is a mild solution of Equations (1.1)–(1.2) on
$\overline{w}(b_{x_{0}})=\lim_{t\to b_{x_{0}} }w(t) $ is a mild solution of Equations (1.1)–(1.2) on  $[0,b_{x_{0}}]$ and that
$[0,b_{x_{0}}]$ and that  $\overline{w}\in C_{\rm Lip}([0,b_{x_{0}} ];X_{\alpha})$. Moreover, from Proposition 4.7, we have that
$\overline{w}\in C_{\rm Lip}([0,b_{x_{0}} ];X_{\alpha})$. Moreover, from Proposition 4.7, we have that  $w(\cdot)$ is also a strict solution on
$w(\cdot)$ is also a strict solution on  $[0,b_{x_{0}}]$. Noting that
$[0,b_{x_{0}}]$. Noting that  $w(\cdot)$ is a maximal locally X α-valued Lipschitz strict solution, we infer that
$w(\cdot)$ is a maximal locally X α-valued Lipschitz strict solution, we infer that  $\overline{w}(\cdot)=w(\cdot)$ and that
$\overline{w}(\cdot)=w(\cdot)$ and that  $I_{\max}=[0,b_{x_{0}}]$. Using now the condition
$I_{\max}=[0,b_{x_{0}}]$. Using now the condition  $\bf \mathcal{
H}_{F,\sigma,a}^{\alpha,\beta}$ and proceeding as in the estimative (4.40), we obtain that
$\bf \mathcal{
H}_{F,\sigma,a}^{\alpha,\beta}$ and proceeding as in the estimative (4.40), we obtain that  $w(b_{x_{0}})\in
X_{1+\alpha} $ and
$w(b_{x_{0}})\in
X_{1+\alpha} $ and  $F(b_{x_{0}}, w^{\sigma}(b_{x_{0}}))\in
X_{\beta}\subset X_{\alpha}$.
$F(b_{x_{0}}, w^{\sigma}(b_{x_{0}}))\in
X_{\beta}\subset X_{\alpha}$.
From the above,  $T(\cdot-b_{x_{0}})u(b_{x_{0}})\in C_{\rm Lip}([b_{x_{0}},a];X_{\alpha})$ and
$T(\cdot-b_{x_{0}})u(b_{x_{0}})\in C_{\rm Lip}([b_{x_{0}},a];X_{\alpha})$ and  $F(b_{x_{0}}, w^{\sigma}(b_{x_{0}}))\in X_{\beta}\subset X_{\alpha}$, which allows us to use the argument in the first part of this proof to prove that there exists
$F(b_{x_{0}}, w^{\sigma}(b_{x_{0}}))\in X_{\beta}\subset X_{\alpha}$, which allows us to use the argument in the first part of this proof to prove that there exists  $\delta_{1} \gt 0$ and a unique strict solution
$\delta_{1} \gt 0$ and a unique strict solution  $z\in C_{\rm Lip}([0,b_{x_{0}}+\delta_{1}];X_{\alpha})$ of (1.1)–(1.2) such that
$z\in C_{\rm Lip}([0,b_{x_{0}}+\delta_{1}];X_{\alpha})$ of (1.1)–(1.2) such that  $z(\cdot)=w(\cdot)$ on
$z(\cdot)=w(\cdot)$ on  $I_{\max}$, which is absurd because
$I_{\max}$, which is absurd because  $w((\cdot)$ is a maximal solution. This proves that
$w((\cdot)$ is a maximal solution. This proves that  $b_{x_{0}}=a$ if
$b_{x_{0}}=a$ if  $[w]_{C_{\rm Lip} ( I_{\max};X_{\alpha})} \lt \infty$. The proof is complete.
$[w]_{C_{\rm Lip} ( I_{\max};X_{\alpha})} \lt \infty$. The proof is complete.
In the next result, we establish the existence of an X α-Lipschitz strict solution on  $[0,a]$.
$[0,a]$.
Proposition 4.9. Suppose the conditions in Proposition 4.8 hold. If  $x_{0}\in D((-A)^{1+\alpha})$ and
$x_{0}\in D((-A)^{1+\alpha})$ and  $ F(\cdot)$ is Lipschitz, then there exists a unique strict solution
$ F(\cdot)$ is Lipschitz, then there exists a unique strict solution  $u\in C_{\rm Lip}
([0,a];X_{\alpha})$ of (1.1)–(1.2).
$u\in C_{\rm Lip}
([0,a];X_{\alpha})$ of (1.1)–(1.2).
Proof. Let  $u\in C (I_{\max};X_{\alpha})$ be the unique maximal strict solution in Proposition 4.8 and
$u\in C (I_{\max};X_{\alpha})$ be the unique maximal strict solution in Proposition 4.8 and  $b_{x_{0}}=\sup I_{\max}$. For
$b_{x_{0}}=\sup I_{\max}$. For  $t\in I_{\max} $, we have that
$t\in I_{\max} $, we have that
 \begin{align*}
\parallel (-A)^{\alpha}u (t) \parallel &\leq
C_{0} \parallel (-A)^{\alpha} x_{0} \parallel + \int_{0}^{t} \frac{C_{0,\alpha} }{(t-s)^{\alpha}}\parallel F(s,u^{\sigma}(s))-F(s, 0 ) \parallel\, {\rm d}s \nonumber\\ &\quad + \parallel F(\cdot, 0 ) \parallel_{C([0,b_{x_{0}});X)} C_{0,\alpha}
\frac{b_{x_{0}}^{1-\alpha} }{1-\alpha} \nonumber\\
&\leq
C_{0} \parallel (-A)^{\alpha} x_{0} \parallel + C_{0,\alpha} [F]_{C_{\rm Lip} } \int_{0}^{t} \frac{\parallel u\parallel_{C([0,s);X_{\alpha})} }{(t-s)^{\alpha}} \,{\rm d}s \nonumber\\ &
\quad + \parallel F(\cdot, 0 )\parallel_{C([0,b_{x_{0}});X)} C_{0,\alpha}
\frac{b_{x_{0}}^{1-\alpha} }{1-\alpha} ,\nonumber
\end{align*}
\begin{align*}
\parallel (-A)^{\alpha}u (t) \parallel &\leq
C_{0} \parallel (-A)^{\alpha} x_{0} \parallel + \int_{0}^{t} \frac{C_{0,\alpha} }{(t-s)^{\alpha}}\parallel F(s,u^{\sigma}(s))-F(s, 0 ) \parallel\, {\rm d}s \nonumber\\ &\quad + \parallel F(\cdot, 0 ) \parallel_{C([0,b_{x_{0}});X)} C_{0,\alpha}
\frac{b_{x_{0}}^{1-\alpha} }{1-\alpha} \nonumber\\
&\leq
C_{0} \parallel (-A)^{\alpha} x_{0} \parallel + C_{0,\alpha} [F]_{C_{\rm Lip} } \int_{0}^{t} \frac{\parallel u\parallel_{C([0,s);X_{\alpha})} }{(t-s)^{\alpha}} \,{\rm d}s \nonumber\\ &
\quad + \parallel F(\cdot, 0 )\parallel_{C([0,b_{x_{0}});X)} C_{0,\alpha}
\frac{b_{x_{0}}^{1-\alpha} }{1-\alpha} ,\nonumber
\end{align*}and using that the function  $s\to \parallel u\parallel_{C([0,s);X_{\alpha})} $ is non-decreasing, we obtain that
$s\to \parallel u\parallel_{C([0,s);X_{\alpha})} $ is non-decreasing, we obtain that
 \begin{align}
\parallel u\parallel_{C([0,t);X_{\alpha})} &\leq
C_{0} \parallel (-A)^{\alpha} x_{0} \parallel + C_{0,\alpha} [F]_{C_{\rm Lip} } \int_{0}^{t} \frac{\parallel u\parallel_{C([0,s);X_{\alpha})} }{(t-s)^{\alpha}} \,{\rm d}s \nonumber\\ &
\quad + \parallel F(\cdot, 0 )\parallel_{C([0,b_{x_{0}});X)} C_{0,\alpha}
\frac{b_{x_{0}}^{1-\alpha} }{1-\alpha} ,
\end{align}
\begin{align}
\parallel u\parallel_{C([0,t);X_{\alpha})} &\leq
C_{0} \parallel (-A)^{\alpha} x_{0} \parallel + C_{0,\alpha} [F]_{C_{\rm Lip} } \int_{0}^{t} \frac{\parallel u\parallel_{C([0,s);X_{\alpha})} }{(t-s)^{\alpha}} \,{\rm d}s \nonumber\\ &
\quad + \parallel F(\cdot, 0 )\parallel_{C([0,b_{x_{0}});X)} C_{0,\alpha}
\frac{b_{x_{0}}^{1-\alpha} }{1-\alpha} ,
\end{align}which implies (see [Reference Ye, Gao and Ding39]) that  $ \parallel u \parallel_{C ( I_{\max} ;X_{\alpha})} \lt \infty$.
$ \parallel u \parallel_{C ( I_{\max} ;X_{\alpha})} \lt \infty$.
We estimate now  $\parallel Au \parallel_{C( I_{\max} ;X)} $. From Lemma 2.1 and Lemma 2.2, we infer that
$\parallel Au \parallel_{C( I_{\max} ;X)} $. From Lemma 2.1 and Lemma 2.2, we infer that  $u\in
C^{1-\alpha}( I_{\max} ;X_{\alpha})$ and
$u\in
C^{1-\alpha}( I_{\max} ;X_{\alpha})$ and  $u^{\sigma}\in C^{(1-\alpha)^{2}}(
I_{\max} ;X_{\alpha})$. From the above, for
$u^{\sigma}\in C^{(1-\alpha)^{2}}(
I_{\max} ;X_{\alpha})$. From the above, for  $t\in I_{\max} $, we get
$t\in I_{\max} $, we get
 \begin{align}
\parallel A u (t) \parallel &\leq
C_{0} \parallel A x_{0} \parallel + \int_{0}^{t} \parallel A T(t-s) \parallel \parallel F(s,u^{\sigma}(s))- F(t,u^{\sigma}(t)) \parallel\ {\rm d}s\nonumber\\ &
\quad \parallel A \int_{0}^{t} T(t-s) F(t,u^{\sigma}(t)) \, {\rm d}s \parallel \nonumber\\
&\leq
C_{0} \parallel A x_{0} \parallel +
\int_{0}^{t} \frac{ C_{1}[F]_{C_{\rm Lip} } }{(t-s)} ( (t-s) + [u^{\sigma}]_{C^{(1-\alpha)^{2}}(I_{\max};X_{\alpha})}(t-s)^{(1-\alpha)^{2}} )\,{\rm d}s \nonumber\\ & \quad +
\parallel T(t) F(t,u^{\sigma}(t)) - F(t,u^{\sigma}(t)) \parallel \nonumber\\
&\leq
C_{0} \parallel A x_{0} \parallel + C_{1}[F]_{C_{\rm Lip} } b_{x_{0}} + C_{1}[F]_{C_{\rm Lip} } [u^{\sigma}]_{C^{(1-\alpha)^{2}}(I_{\max};X_{\alpha})} \frac{b_{x_{0}}^{ (1-\alpha)^{2}} }{ (1-\alpha)^{2}} \nonumber\\ & \quad + (C_{0}+1) \parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C([0,b_{x_{0}});X)} ,
\end{align}
\begin{align}
\parallel A u (t) \parallel &\leq
C_{0} \parallel A x_{0} \parallel + \int_{0}^{t} \parallel A T(t-s) \parallel \parallel F(s,u^{\sigma}(s))- F(t,u^{\sigma}(t)) \parallel\ {\rm d}s\nonumber\\ &
\quad \parallel A \int_{0}^{t} T(t-s) F(t,u^{\sigma}(t)) \, {\rm d}s \parallel \nonumber\\
&\leq
C_{0} \parallel A x_{0} \parallel +
\int_{0}^{t} \frac{ C_{1}[F]_{C_{\rm Lip} } }{(t-s)} ( (t-s) + [u^{\sigma}]_{C^{(1-\alpha)^{2}}(I_{\max};X_{\alpha})}(t-s)^{(1-\alpha)^{2}} )\,{\rm d}s \nonumber\\ & \quad +
\parallel T(t) F(t,u^{\sigma}(t)) - F(t,u^{\sigma}(t)) \parallel \nonumber\\
&\leq
C_{0} \parallel A x_{0} \parallel + C_{1}[F]_{C_{\rm Lip} } b_{x_{0}} + C_{1}[F]_{C_{\rm Lip} } [u^{\sigma}]_{C^{(1-\alpha)^{2}}(I_{\max};X_{\alpha})} \frac{b_{x_{0}}^{ (1-\alpha)^{2}} }{ (1-\alpha)^{2}} \nonumber\\ & \quad + (C_{0}+1) \parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C([0,b_{x_{0}});X)} ,
\end{align}which implies that  $ \parallel Au\parallel_{C( I_{\max} ;X)} \lt \infty $.
$ \parallel Au\parallel_{C( I_{\max} ;X)} \lt \infty $.
Using now the condition  $\bf \mathcal{H}_{F,\sigma,a}^{
\alpha,\beta}$, we have that
$\bf \mathcal{H}_{F,\sigma,a}^{
\alpha,\beta}$, we have that  $\parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C( I_{\max} ;X_{\beta})} \lt \infty $, and noting that
$\parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C( I_{\max} ;X_{\beta})} \lt \infty $, and noting that  $\beta \gt \alpha$, we get
$\beta \gt \alpha$, we get
 \begin{align}
\parallel (-A)^{1+\alpha} u (t) \parallel &\leq
C_{0} \parallel (-A)^{1+\alpha} x_{0} \parallel + \int_{0}^{t} \parallel (-A)^{1+\alpha-\beta}T(t-s) \parallel\nonumber \\ & \qquad \parallel (-A)^{\beta} F(s,u^{\sigma}(s))\parallel \, {\rm d}s\nonumber\\ &\leq
C_{0} \parallel (-A)^{1+\alpha} x_{0} \parallel + \parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C( I_{\max} ;X_{\beta})} C_{1+\alpha-\beta}\frac{a^{\beta-\alpha} }{\beta-\alpha} ,
\end{align}
\begin{align}
\parallel (-A)^{1+\alpha} u (t) \parallel &\leq
C_{0} \parallel (-A)^{1+\alpha} x_{0} \parallel + \int_{0}^{t} \parallel (-A)^{1+\alpha-\beta}T(t-s) \parallel\nonumber \\ & \qquad \parallel (-A)^{\beta} F(s,u^{\sigma}(s))\parallel \, {\rm d}s\nonumber\\ &\leq
C_{0} \parallel (-A)^{1+\alpha} x_{0} \parallel + \parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C( I_{\max} ;X_{\beta})} C_{1+\alpha-\beta}\frac{a^{\beta-\alpha} }{\beta-\alpha} ,
\end{align}which shows that  $u(\cdot)$ is an
$u(\cdot)$ is an  $X_{1+\alpha}$-valued function and that
$X_{1+\alpha}$-valued function and that  $\parallel A u \parallel_{C( I_{\max} ;X_{\alpha})} \lt \infty$. Using the previous estimates and that
$\parallel A u \parallel_{C( I_{\max} ;X_{\alpha})} \lt \infty$. Using the previous estimates and that  $u^\prime(\cdot)$ is a strict solution, we obtain that
$u^\prime(\cdot)$ is a strict solution, we obtain that
which implies that  $[u]_{C_{\rm Lip} ( I_{\max} ;X_{\alpha})} $ is finite and that
$[u]_{C_{\rm Lip} ( I_{\max} ;X_{\alpha})} $ is finite and that  $ I_{\max} =[0,a]$, see Proposition 4.8.
$ I_{\max} =[0,a]$, see Proposition 4.8.
The next result is an immediate consequence of Proposition 4.9.
4.2.2. Existence and uniqueness of non-Lipschitz solutions on  $[0,\infty)$
$[0,\infty)$
The results in this section follow combining Proposition 4.8, Proposition 4.9 and Remark 3.3. In Proposition 4.10 below, we use the ideas in the proof of Proposition 4.8.
Proposition 4.10. Suppose the conditions in Theorem 3.1 hold. Assume that the condition  $\bf \mathcal{H}_{F,\sigma,a}^{\alpha,\beta}$ is satisfied,
$\bf \mathcal{H}_{F,\sigma,a}^{\alpha,\beta}$ is satisfied,  $x_{0}\in D(A)$,
$x_{0}\in D(A)$,  $\lim_{d\downarrow c} \widehat{\Phi}_{i,c}(d)=0 $,
$\lim_{d\downarrow c} \widehat{\Phi}_{i,c}(d)=0 $,  $i=1,2, $ for every
$i=1,2, $ for every  $a \gt c \gt 0$ and that
$a \gt c \gt 0$ and that  $F(\cdot)$ satisfies some of the conditions in Proposition 4.7. Then there exists a unique maximal classical solution
$F(\cdot)$ satisfies some of the conditions in Proposition 4.7. Then there exists a unique maximal classical solution  $u\in C(I_{max};X_{\alpha}) $ such that
$u\in C(I_{max};X_{\alpha}) $ such that  $u_{\mid_{(0,c]}}\in C_{\rm Lip,1+\alpha-\gamma}( (0,c];X_{\alpha}) $ and
$u_{\mid_{(0,c]}}\in C_{\rm Lip,1+\alpha-\gamma}( (0,c];X_{\alpha}) $ and  $u_{\mid_{[\varepsilon, d]}}\in C_{\rm Lip}( [\varepsilon,d];X_{\alpha}) $ for all
$u_{\mid_{[\varepsilon, d]}}\in C_{\rm Lip}( [\varepsilon,d];X_{\alpha}) $ for all  $0 \lt \varepsilon\leq c $ and
$0 \lt \varepsilon\leq c $ and  $ d \lt b_{x_{0}} =\sup I_{\max} \leq a$. Moreover, if
$ d \lt b_{x_{0}} =\sup I_{\max} \leq a$. Moreover, if  $[ u]_{C_{\rm Lip}([c,b_{x_{0}}) ;X_{\alpha})} \lt \infty$ for some
$[ u]_{C_{\rm Lip}([c,b_{x_{0}}) ;X_{\alpha})} \lt \infty$ for some  $0 \lt c \lt b_{x_{0}}$, then
$0 \lt c \lt b_{x_{0}}$, then  $ I_{\max}=[0,a]$.
$ I_{\max}=[0,a]$.
Proof. Let  $u\in C_{\rm Lip,1+\alpha-\gamma}( (0,b];X_{\alpha}) $ be the mild solution in Theorem 3.1. From Remark 3.3, we note that
$u\in C_{\rm Lip,1+\alpha-\gamma}( (0,b];X_{\alpha}) $ be the mild solution in Theorem 3.1. From Remark 3.3, we note that  $u_{\mid_{\left[\frac{b}{2},b\right]}}\in
C_{\rm Lip}([\frac{b}{2},b];X_{\alpha})$, which in turn implies that
$u_{\mid_{\left[\frac{b}{2},b\right]}}\in
C_{\rm Lip}([\frac{b}{2},b];X_{\alpha})$, which in turn implies that  $u^{\sigma}_{\mid_{\left[\frac{b}{2},b\right]}}\in
C_{\rm Lip}([\frac{b}{2},b];X_{\alpha})$. Moreover, it is easy to see that
$u^{\sigma}_{\mid_{\left[\frac{b}{2},b\right]}}\in
C_{\rm Lip}([\frac{b}{2},b];X_{\alpha})$. Moreover, it is easy to see that  $u_{\mid_{\left[\xi\left( \frac{b}{2} \right),b\right]}}$ is a mild solution of the problem
$u_{\mid_{\left[\xi\left( \frac{b}{2} \right),b\right]}}$ is a mild solution of the problem
 \begin{align}
w^\prime(t)&= Aw(t)+ F(t,w(\sigma(t,w(t)))), \qquad t\in \left[\frac{b}{2} , b \right],
\end{align}
\begin{align}
w^\prime(t)&= Aw(t)+ F(t,w(\sigma(t,w(t)))), \qquad t\in \left[\frac{b}{2} , b \right],
\end{align} \begin{align}
w(s) &= u(s),\qquad s\in \left[\xi\left( \frac{b}{2} \right), \frac{b}{2} \right].
\end{align}
\begin{align}
w(s) &= u(s),\qquad s\in \left[\xi\left( \frac{b}{2} \right), \frac{b}{2} \right].
\end{align} Let  $\rho(b):=\parallel u\parallel_{C([0,b];X_{\alpha})}$. For
$\rho(b):=\parallel u\parallel_{C([0,b];X_{\alpha})}$. For  $t\in \left( \frac{b}{2},b \right]$, we see that
$t\in \left( \frac{b}{2},b \right]$, we see that
 \begin{align}
\parallel A u(t)\parallel & \leq \ \parallel AT \left(t-\frac{b}{2}\right) u\left(\frac{b}{2}\right)\parallel +
\int^t_{\frac{b}{2}} \parallel A T(t-s) \parallel F (s,u^{\sigma}(s) ) - F (t,u^{\sigma}(t) ) )\parallel \, {\rm d}s\nonumber\\
& \quad + \parallel A\int^t_{\frac{b}{2}} T(t-s) F (t,u^{\sigma}(t) ) \parallel \,{\rm d}s \nonumber\\
& \leq \quad \parallel AT \left(t-\frac{b}{2}\right) u\left(\frac{b}{2}\right)\parallel +
\int^t_{\frac{b}{2}} \frac{C_{1}\mathcal{W}_{F}(\rho(b))}{(t-s)} [F]_{(t,s)}\nonumber \\ & \qquad\left(1+ [u^{\sigma}]_{C_{\rm Lip}\left(\left[ \frac{b}{2} ,b\right];X_{\alpha}\right)}\right)(t-s) \, {\rm d}s \nonumber\\
& \quad + \parallel T(t)F (t,u^{\sigma}(t) )- F (t,u^{\sigma}(t) )\parallel \nonumber\\
& \leq \quad \parallel AT \left(t-\frac{b}{2}\right) u\left(\frac{b}{2}\right)\parallel +
C_{1} \mathcal{W}_{F}(\rho(b)) \parallel [F]_{(t,\cdot)}\parallel_{L^{1}([0,t])}\nonumber \\ &\qquad \left(1+ [u^{\sigma}]_{C_{\rm Lip}\left(\left[ \frac{b}{2} ,b\right];X_{\alpha}\right)}\right) \nonumber\\
& \quad + (C_{0}+1) \parallel F (t,u^{\sigma}(t) ) \parallel
\end{align}
\begin{align}
\parallel A u(t)\parallel & \leq \ \parallel AT \left(t-\frac{b}{2}\right) u\left(\frac{b}{2}\right)\parallel +
\int^t_{\frac{b}{2}} \parallel A T(t-s) \parallel F (s,u^{\sigma}(s) ) - F (t,u^{\sigma}(t) ) )\parallel \, {\rm d}s\nonumber\\
& \quad + \parallel A\int^t_{\frac{b}{2}} T(t-s) F (t,u^{\sigma}(t) ) \parallel \,{\rm d}s \nonumber\\
& \leq \quad \parallel AT \left(t-\frac{b}{2}\right) u\left(\frac{b}{2}\right)\parallel +
\int^t_{\frac{b}{2}} \frac{C_{1}\mathcal{W}_{F}(\rho(b))}{(t-s)} [F]_{(t,s)}\nonumber \\ & \qquad\left(1+ [u^{\sigma}]_{C_{\rm Lip}\left(\left[ \frac{b}{2} ,b\right];X_{\alpha}\right)}\right)(t-s) \, {\rm d}s \nonumber\\
& \quad + \parallel T(t)F (t,u^{\sigma}(t) )- F (t,u^{\sigma}(t) )\parallel \nonumber\\
& \leq \quad \parallel AT \left(t-\frac{b}{2}\right) u\left(\frac{b}{2}\right)\parallel +
C_{1} \mathcal{W}_{F}(\rho(b)) \parallel [F]_{(t,\cdot)}\parallel_{L^{1}([0,t])}\nonumber \\ &\qquad \left(1+ [u^{\sigma}]_{C_{\rm Lip}\left(\left[ \frac{b}{2} ,b\right];X_{\alpha}\right)}\right) \nonumber\\
& \quad + (C_{0}+1) \parallel F (t,u^{\sigma}(t) ) \parallel
\end{align}which implies that  $u(t)\in D(A)$ for all
$u(t)\in D(A)$ for all  $t\in ( \frac{b}{2},b ] $. Moreover, noting that the same argument can be used on
$t\in ( \frac{b}{2},b ] $. Moreover, noting that the same argument can be used on  $[\frac{b}{3},b]$, we infer that
$[\frac{b}{3},b]$, we infer that  $u\left(\frac{b}{2}\right)\in D(A)$ and that
$u\left(\frac{b}{2}\right)\in D(A)$ and that
 \begin{align*}
\parallel A u \parallel_{C([\frac{b}{2},b ];X)} &\leq C_{0} \parallel A u\left(\frac{b}{2}\right)\parallel +
C_{1} \mathcal{W}_{F}(\rho(b)) \sup_{t\in [0,a]} \parallel [F]_{(t,\cdot)}\parallel_{L^{1}([0,t])}\\ & \qquad \left(1+ [u^{\sigma}]_{C_{\rm Lip}\left(\left[ \frac{b}{2} ,b\right];X_{\alpha}\right)}\right)\\
& \quad + (C_{0}+1) \parallel F (\cdot,u^{\sigma}(\cdot) ) \parallel_{C([\frac{b}{2},b ];X)}.
\end{align*}
\begin{align*}
\parallel A u \parallel_{C([\frac{b}{2},b ];X)} &\leq C_{0} \parallel A u\left(\frac{b}{2}\right)\parallel +
C_{1} \mathcal{W}_{F}(\rho(b)) \sup_{t\in [0,a]} \parallel [F]_{(t,\cdot)}\parallel_{L^{1}([0,t])}\\ & \qquad \left(1+ [u^{\sigma}]_{C_{\rm Lip}\left(\left[ \frac{b}{2} ,b\right];X_{\alpha}\right)}\right)\\
& \quad + (C_{0}+1) \parallel F (\cdot,u^{\sigma}(\cdot) ) \parallel_{C([\frac{b}{2},b ];X)}.
\end{align*} From the above and the condition  $\bf \mathcal{H}_{F,\sigma,a}^{\alpha,\beta}$, we obtain that
$\bf \mathcal{H}_{F,\sigma,a}^{\alpha,\beta}$, we obtain that  $F(\cdot,u^{\sigma}(\cdot))_{\mid_{\left[\frac{b}{2},b\right] }}\in C( [\frac{b}{2},b];X_{\beta}) $. Using this fact and proceeding as in the estimate (4.44), for
$F(\cdot,u^{\sigma}(\cdot))_{\mid_{\left[\frac{b}{2},b\right] }}\in C( [\frac{b}{2},b];X_{\beta}) $. Using this fact and proceeding as in the estimate (4.44), for  $t\in [\frac{b}{2},b],$ we see that
$t\in [\frac{b}{2},b],$ we see that
 \begin{align}
\parallel (-A)^{1+\alpha} u (b) \parallel &\leq
\ \parallel (-A)^{1+\alpha} T\left( \frac{b}{2}\right) u\left(\frac{b}{2}\right) \parallel \,\, \nonumber\\
& \qquad +
\int_{\frac{b}{2}}^{b} \parallel (-A)^{1+\alpha-\beta}T(b-s) \parallel \parallel (-A)^{\beta} F(s,u^{\sigma}(s)) \parallel \, {\rm d}s
\nonumber\\ &\leq \parallel (-A)^{1+\alpha} T\left( \frac{b}{2}\right) u\left(\frac{b}{2}\right) \parallel + \parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C( [\frac{b}{2},b] ;X_{\beta})} C_{1+\alpha-\beta}\frac{ b ^{\beta-\alpha} }{\beta-\alpha} , \hspace{0.5cm}
\end{align}
\begin{align}
\parallel (-A)^{1+\alpha} u (b) \parallel &\leq
\ \parallel (-A)^{1+\alpha} T\left( \frac{b}{2}\right) u\left(\frac{b}{2}\right) \parallel \,\, \nonumber\\
& \qquad +
\int_{\frac{b}{2}}^{b} \parallel (-A)^{1+\alpha-\beta}T(b-s) \parallel \parallel (-A)^{\beta} F(s,u^{\sigma}(s)) \parallel \, {\rm d}s
\nonumber\\ &\leq \parallel (-A)^{1+\alpha} T\left( \frac{b}{2}\right) u\left(\frac{b}{2}\right) \parallel + \parallel F(\cdot,u^{\sigma}(\cdot))\parallel_{C( [\frac{b}{2},b] ;X_{\beta})} C_{1+\alpha-\beta}\frac{ b ^{\beta-\alpha} }{\beta-\alpha} , \hspace{0.5cm}
\end{align}which shows that  $u(b)\in X_{1+\alpha} $.
$u(b)\in X_{1+\alpha} $.
From the above,  $T(\cdot-b)u(b)\in C_{\rm Lip}([b,a];X_{\alpha})$ and
$T(\cdot-b)u(b)\in C_{\rm Lip}([b,a];X_{\alpha})$ and  $F(b,u^{\sigma}(b))\in X_{\alpha}$, and arguing as in the proof of Proposition 4.8, we can prove that there exists a maximal locally X α-Lipschitz strict solution
$F(b,u^{\sigma}(b))\in X_{\alpha}$, and arguing as in the proof of Proposition 4.8, we can prove that there exists a maximal locally X α-Lipschitz strict solution  $v\in C(
I_{\max};X_{\alpha} ) $, with
$v\in C(
I_{\max};X_{\alpha} ) $, with  $I_{\max}\subset [\xi(b),a]$, of the problem
$I_{\max}\subset [\xi(b),a]$, of the problem
Defining  $z:[0,b]\cup I_{\max}\mapsto X_{\alpha}$ by
$z:[0,b]\cup I_{\max}\mapsto X_{\alpha}$ by  $z(\theta)=u(\theta)$ for
$z(\theta)=u(\theta)$ for  $\theta\in [0, b ]$ and
$\theta\in [0, b ]$ and  $z(\theta)=v(\theta)$ for
$z(\theta)=v(\theta)$ for  $\theta\in I_{\max}$, we obtain a maximal classical solution of the problem (1.1)–(1.2) in
$\theta\in I_{\max}$, we obtain a maximal classical solution of the problem (1.1)–(1.2) in  $C_{\rm Lip, 1+\alpha-\gamma}([0,b]\cup
I_{\max};X_{\alpha})$.
$C_{\rm Lip, 1+\alpha-\gamma}([0,b]\cup
I_{\max};X_{\alpha})$.
We complete this section with the following two results.
Proposition 4.11. If the conditions in Proposition 4.10 are satisfied and  $ F(\cdot)$,
$ F(\cdot)$,  $\sigma(\cdot)$ are Lipschitz, then there exists a unique classical solution
$\sigma(\cdot)$ are Lipschitz, then there exists a unique classical solution  $u\in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha}) $ of (1.1)–(1.2).
$u\in C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha}) $ of (1.1)–(1.2).
Proof. The assertion follows from the proof of Proposition 4.10. We only note that under the current conditions, from Proposition 4.9, it is possible to infer that the maximal strict solution  $v(\cdot)$ of the problem (4.49)–(4.50) belongs to
$v(\cdot)$ of the problem (4.49)–(4.50) belongs to  $C_{\rm Lip}[ \xi\left( \frac{b}{2} \right),a ] ;X_{\alpha}) $, which implies that the maximal classical solution
$C_{\rm Lip}[ \xi\left( \frac{b}{2} \right),a ] ;X_{\alpha}) $, which implies that the maximal classical solution  $z(\cdot)$ is defined on the whole interval
$z(\cdot)$ is defined on the whole interval  $[0,a]$.
$[0,a]$.
The next corollary is an immediate consequence of Proposition 4.11.
5. Examples
In this section, we study the existence of solutions for some PDEs with SDA. Next, A is the Laplacian operator with domain  $ D(A)= H^{2}(\Omega)\cap H_{0}^{1}(\Omega)$ in
$ D(A)= H^{2}(\Omega)\cap H_{0}^{1}(\Omega)$ in  $X=L^{2}(\Omega)$, where
$X=L^{2}(\Omega)$, where  $\Omega\subset \mathbb{R}^{N}$ is an open bounded set with smooth boundary. It is well known that A is the generator of an analytic C 0-semigroup
$\Omega\subset \mathbb{R}^{N}$ is an open bounded set with smooth boundary. It is well known that A is the generator of an analytic C 0-semigroup  $ (T(t))_{t\geq 0} $ on X. Next, for the semigroup
$ (T(t))_{t\geq 0} $ on X. Next, for the semigroup  $ (T(t))_{t\geq 0} $, we adopt all the notation used in the previous sections.
$ (T(t))_{t\geq 0} $, we adopt all the notation used in the previous sections.
Motivated by the theory of differential equations associated to the Fisher–Kolmogoroff equation, see for example [Reference Hernandez, Wu and Chadha25, Example 1]; next we study the diffusion type problem
 $\sigma(t,y)=\mu(t)\varrho(\parallel y \parallel ) $ for t > 0 and
$\sigma(t,y)=\mu(t)\varrho(\parallel y \parallel ) $ for t > 0 and  $y\in X$,
$y\in X$,  $ \mu \in C_{\rm Lip}([0,a] ; (0,a] )$,
$ \mu \in C_{\rm Lip}([0,a] ; (0,a] )$,  $\varrho \in C_{\rm Lip}([0,\infty);[\delta,\infty))$ for some
$\varrho \in C_{\rm Lip}([0,\infty);[\delta,\infty))$ for some  $1 \gt \delta \gt 0$ and
$1 \gt \delta \gt 0$ and  $\zeta\in C([0,a];\mathbb{R})$ is the function in the fourth example of Remark 2.1.
$\zeta\in C([0,a];\mathbb{R})$ is the function in the fourth example of Remark 2.1.
To represent the problem (5.1)–(5.3) in the form (1.1)–(1.2), we select  $\alpha\in (0,1)$ such that
$\alpha\in (0,1)$ such that  $ X_{\alpha} \hookrightarrow C(\Omega)$ and we define the map
$ X_{\alpha} \hookrightarrow C(\Omega)$ and we define the map  $F:[0,a]\times X_{\alpha}\to X $ by
$F:[0,a]\times X_{\alpha}\to X $ by  $F(t,u)(x)=\zeta(t)u(x)[1-u(x)] .$ From the previous assumptions, it is obvious that
$F(t,u)(x)=\zeta(t)u(x)[1-u(x)] .$ From the previous assumptions, it is obvious that  $\sigma(\cdot)$ is Lipschitz. To show that
$\sigma(\cdot)$ is Lipschitz. To show that  $F\in L_{\rm Lip}^{q}( [0,a]\times X_{\alpha} ;X) $, we use the notation
$F\in L_{\rm Lip}^{q}( [0,a]\times X_{\alpha} ;X) $, we use the notation  $\parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} $ and
$\parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} $ and  $ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha};X)} $ for the norm of the inclusion map from X α into
$ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha};X)} $ for the norm of the inclusion map from X α into  $C(\Omega;\mathbb{R}^{n})$ and from X α into X. For r > 0,
$C(\Omega;\mathbb{R}^{n})$ and from X α into X. For r > 0,  $0\leq s \lt t\leq a $ and
$0\leq s \lt t\leq a $ and  $ u,v \in B_r[0,X_{\alpha}]$, we get
$ u,v \in B_r[0,X_{\alpha}]$, we get
 \begin{align*}
\parallel F(t,u) &- F(s,v) \parallel \\
&\leq \ \mid \zeta(t) -\zeta(s) \mid \parallel u (1 - u) \parallel + \mid \zeta(s) \mid \parallel u - v - (u^2 - v^2 ) \parallel \\
&\leq [\zeta]_{(t,s)}|t-s| (1+ \parallel u\parallel_{C(\Omega)} ) \parallel u \parallel +
\mid \zeta(s)\mid \parallel u -v\parallel\\&\qquad ( 1 + \parallel u\parallel_{C(\Omega)} +\parallel v\parallel_{C(\Omega)} ) \\
&\leq [\zeta]_{(t,s)}|t-s|
(1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))}\parallel u\parallel_{{\alpha}} ) \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha};X)} \parallel u \parallel_{\alpha} \\
& \qquad +
\mid \zeta(s)\mid \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; X)} \parallel u -v\parallel_{\alpha} ( 1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} (\parallel u\parallel_{\alpha} +\parallel v\parallel_{\alpha} )) \\
&\leq [\zeta]_{(t,s)}|t-s|
(1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))}r ) \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; X)}r \\
& \qquad +
\mid \zeta(s)\mid \parallel u -v\parallel_{\alpha} \parallel\parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha};X)} ( 1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} 2 r ) \\
&\leq ( [\zeta]_{(t,s)} + \mid \zeta(s)\mid )
\parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; X)}(1+ 2 \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} )(1+r)^2\\ & \qquad (|t-s|+ \parallel u -v\parallel_{\alpha}) .
\end{align*}
\begin{align*}
\parallel F(t,u) &- F(s,v) \parallel \\
&\leq \ \mid \zeta(t) -\zeta(s) \mid \parallel u (1 - u) \parallel + \mid \zeta(s) \mid \parallel u - v - (u^2 - v^2 ) \parallel \\
&\leq [\zeta]_{(t,s)}|t-s| (1+ \parallel u\parallel_{C(\Omega)} ) \parallel u \parallel +
\mid \zeta(s)\mid \parallel u -v\parallel\\&\qquad ( 1 + \parallel u\parallel_{C(\Omega)} +\parallel v\parallel_{C(\Omega)} ) \\
&\leq [\zeta]_{(t,s)}|t-s|
(1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))}\parallel u\parallel_{{\alpha}} ) \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha};X)} \parallel u \parallel_{\alpha} \\
& \qquad +
\mid \zeta(s)\mid \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; X)} \parallel u -v\parallel_{\alpha} ( 1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} (\parallel u\parallel_{\alpha} +\parallel v\parallel_{\alpha} )) \\
&\leq [\zeta]_{(t,s)}|t-s|
(1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))}r ) \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; X)}r \\
& \qquad +
\mid \zeta(s)\mid \parallel u -v\parallel_{\alpha} \parallel\parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha};X)} ( 1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} 2 r ) \\
&\leq ( [\zeta]_{(t,s)} + \mid \zeta(s)\mid )
\parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; X)}(1+ 2 \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} )(1+r)^2\\ & \qquad (|t-s|+ \parallel u -v\parallel_{\alpha}) .
\end{align*} This shows that  $F(\cdot)$ belongs to
$F(\cdot)$ belongs to  $ L_{\rm Lip}^{q}( [0,a]\times X_{\alpha} ;X)$ with
$ L_{\rm Lip}^{q}( [0,a]\times X_{\alpha} ;X)$ with  $ [F]_{(t,s)} = ( [\zeta]_{(t,s)} + \mid \zeta(s)\mid ) $ and
$ [F]_{(t,s)} = ( [\zeta]_{(t,s)} + \mid \zeta(s)\mid ) $ and  $\mathcal{W}_{F}(r)=3
(1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} + \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; X)})^{2} (1+r)^2 $. Moreover, from the definition of
$\mathcal{W}_{F}(r)=3
(1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} + \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; X)})^{2} (1+r)^2 $. Moreover, from the definition of  $F(\cdot)$, it is easy to see that
$F(\cdot)$, it is easy to see that  $\parallel F(t,u) \parallel \leq \mid \zeta(t) \mid \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha};X)} (r + r^{2})$, and hence, the condition
$\parallel F(t,u) \parallel \leq \mid \zeta(t) \mid \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha};X)} (r + r^{2})$, and hence, the condition  $\bf \mathcal{H}_{F, a}(X_{\alpha} ;X)$ is satisfied with
$\bf \mathcal{H}_{F, a}(X_{\alpha} ;X)$ is satisfied with  $ \mathcal{ K}_{F}(x) = \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha};X)} (x + x^{2}) $,
$ \mathcal{ K}_{F}(x) = \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha};X)} (x + x^{2}) $,  $\varrho_{1}(t) =\zeta(t)$ and
$\varrho_{1}(t) =\zeta(t)$ and  $\varrho_{2}(t) =0$. In addition, from the current assumptions, we can assume that the functions
$\varrho_{2}(t) =0$. In addition, from the current assumptions, we can assume that the functions  $\xi(\cdot)$ and
$\xi(\cdot)$ and  $ \Lambda(\cdot)$ in condition
$ \Lambda(\cdot)$ in condition  $\bf H_{F,\sigma, a}^{\alpha,\gamma }(Y_{1},Y_{2})$ and Notation 1 are given by
$\bf H_{F,\sigma, a}^{\alpha,\gamma }(Y_{1},Y_{2})$ and Notation 1 are given by  $\xi(t)= \mu(t) {\delta}$ and
$\xi(t)= \mu(t) {\delta}$ and  $ \Lambda (\tau) =( 1+ \frac{1}{(\delta \mu(\tau) )^{1+\alpha-\gamma }}).$ From the above remarks, we have that the conditions
$ \Lambda (\tau) =( 1+ \frac{1}{(\delta \mu(\tau) )^{1+\alpha-\gamma }}).$ From the above remarks, we have that the conditions  $\bf H_{F,\sigma, a}^{q,r }(X_{\alpha} ;X)$ and
$\bf H_{F,\sigma, a}^{q,r }(X_{\alpha} ;X)$ and  $\bf \mathcal{H}_{F, a}(X_{\alpha} ;X)$ are satisfied. Moreover, for the sake of simplicity, next we assume that
$\bf \mathcal{H}_{F, a}(X_{\alpha} ;X)$ are satisfied. Moreover, for the sake of simplicity, next we assume that  $ \mu ^{-2(1+\alpha-\gamma) } \in L^{p}([0,a])$ for some p > 1 and for all a > 0. In this case, we have that the functions
$ \mu ^{-2(1+\alpha-\gamma) } \in L^{p}([0,a])$ for some p > 1 and for all a > 0. In this case, we have that the functions  $ \Lambda(\cdot)$ and
$ \Lambda(\cdot)$ and  $ \Lambda^{2}(\cdot)$ also belongs to
$ \Lambda^{2}(\cdot)$ also belongs to  $ L^{p}([0,a])$ for all a > 0.
$ L^{p}([0,a])$ for all a > 0.
Remark 5.1. In the remainder of this section, we use the same functions  $\zeta(\cdot)$,
$\zeta(\cdot)$,  $\sigma(\cdot)$,
$\sigma(\cdot)$,  $\mu(\cdot)$ and
$\mu(\cdot)$ and  $\varrho(\cdot) $ introduced above.
$\varrho(\cdot) $ introduced above.
In Proposition 5.1 below, we said that  $u \in C([0,b]; X)$ is a mild solution of (5.1)–(5.3) on
$u \in C([0,b]; X)$ is a mild solution of (5.1)–(5.3) on  $[0,b]$ if
$[0,b]$ if  $u(\cdot)$ is a mild solution of the associated problem (1.1)–(1.2). A similar nomenclature is used for the other examples of this section.
$u(\cdot)$ is a mild solution of the associated problem (1.1)–(1.2). A similar nomenclature is used for the other examples of this section.
Proposition 5.1. Assume that the above conditions are satisfied,  $ x_{0}\in X_{\gamma}$ for some
$ x_{0}\in X_{\gamma}$ for some  $\gamma \in (\alpha,\alpha+1) $ and
$\gamma \in (\alpha,\alpha+1) $ and  $ x_{0} [1-x_{0}] \in X_{\alpha} $.
$ x_{0} [1-x_{0}] \in X_{\alpha} $.
(a) Let a > 0. If
 $\frac{1}{p}+\frac{1}{q}+ \frac{1}{\tau(q,p)} =1$,
$\frac{1}{p}+\frac{1}{q}+ \frac{1}{\tau(q,p)} =1$,  $ 1-\alpha {\tau(q,p)} \gt 0$,
$ 1-\alpha {\tau(q,p)} \gt 0$,  $ \sup_{t,h\in [0,a],t+h\leq a} \parallel [\zeta]_{(\cdot+h,\cdot)} \parallel_{L^{q}( [0,t])} \lt \infty$ and
$ \sup_{t,h\in [0,a],t+h\leq a} \parallel [\zeta]_{(\cdot+h,\cdot)} \parallel_{L^{q}( [0,t])} \lt \infty$ and  $\zeta(0)=0$, then there exists a unique mild solution
$\zeta(0)=0$, then there exists a unique mild solution  $u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})$ of (5.1)–(5.3) for some b > 0.
$u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})$ of (5.1)–(5.3) for some b > 0.(b) Suppose that the conditions in (a) are satisfied and let
 $Q_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function defined by
where(5.4)
$Q_{a} : [0,\infty)\mapsto \mathbb{R} $ be the function defined by
where(5.4) \begin{align}
Q_{a} (x) & =
C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} +
C_{0,\alpha} a\overline{\Theta}_{5}(a)
\end{align}(5.5)
\begin{align}
Q_{a} (x) & =
C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} +
C_{0,\alpha} a\overline{\Theta}_{5}(a)
\end{align}(5.5) \begin{align}
& +
a^{1+\alpha-\gamma} C_{0,\alpha} \left( \mathcal{W}_{F}(x) \overline{\Theta}_{5}(a) + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \overline{\Theta}_{3}(a) \right)
\end{align}(5.6)
\begin{align}
& +
a^{1+\alpha-\gamma} C_{0,\alpha} \left( \mathcal{W}_{F}(x) \overline{\Theta}_{5}(a) + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \overline{\Theta}_{3}(a) \right)
\end{align}(5.6) \begin{align}
& + C_{0,\alpha} \mathcal{W}_{F,\sigma}(x) (1+x) \overline{\Theta}_{4}(a) -x ,
\end{align}(5.7)and
\begin{align}
& + C_{0,\alpha} \mathcal{W}_{F,\sigma}(x) (1+x) \overline{\Theta}_{4}(a) -x ,
\end{align}(5.7)and \begin{align}
\overline{\Theta}_{3} (a) &= C_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip}}) \parallel \Lambda ^{2} \parallel_{L^{p}([0,a])} \sup_{t,h\in [0,a],t+h\leq a} \parallel [\zeta]_{(\cdot+h,\cdot)} + \zeta (\cdot) \parallel_{L^{q}([0,a])}\Psi , \nonumber \\
\overline{\Theta}_{4} (a) &= C_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip}}) \parallel \Lambda (\cdot) \parallel_{L^{p}([0,a])} (\parallel [\zeta]_{(\cdot,\cdot)} + \zeta (\cdot) \parallel_{L^{q}([0,a])})\Psi , \nonumber\\
\overline{\Theta}_{5}(b) &= C_{0,\alpha} \parallel [\zeta]_{(\cdot,0)}\parallel_{L^{q}([0,a])} a^{\frac{1}{q^\prime}-\alpha}{[1-q^\prime\alpha]^{-\frac{1}{q^\prime}}} ,
\end{align}
\begin{align}
\overline{\Theta}_{3} (a) &= C_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip}}) \parallel \Lambda ^{2} \parallel_{L^{p}([0,a])} \sup_{t,h\in [0,a],t+h\leq a} \parallel [\zeta]_{(\cdot+h,\cdot)} + \zeta (\cdot) \parallel_{L^{q}([0,a])}\Psi , \nonumber \\
\overline{\Theta}_{4} (a) &= C_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip}}) \parallel \Lambda (\cdot) \parallel_{L^{p}([0,a])} (\parallel [\zeta]_{(\cdot,\cdot)} + \zeta (\cdot) \parallel_{L^{q}([0,a])})\Psi , \nonumber\\
\overline{\Theta}_{5}(b) &= C_{0,\alpha} \parallel [\zeta]_{(\cdot,0)}\parallel_{L^{q}([0,a])} a^{\frac{1}{q^\prime}-\alpha}{[1-q^\prime\alpha]^{-\frac{1}{q^\prime}}} ,
\end{align} $ \Psi = {a^{\frac{1}{\tau(q,p)}- \alpha}}{[1- \tau(q,p)\alpha]^{-\frac{1}{\tau(q,p)}}} $. If
$ \Psi = {a^{\frac{1}{\tau(q,p)}- \alpha}}{[1- \tau(q,p)\alpha]^{-\frac{1}{\tau(q,p)}}} $. If  $Q_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution
$Q_{a}(R) \lt 0$ for some R > 0, then there exists a unique mild solution  $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a];X_{\alpha})$ of (5.1)–(5.3) on
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,a];X_{\alpha})$ of (5.1)–(5.3) on  $[0,a]$.
$[0,a]$.(c) Suppose that the conditions in (a) are satisfied for all a > 0, that there exists β > 0 such that for all
 $\theta\geq 0$, there is
$\theta\geq 0$, there is  $D_{0,\theta} \gt 0$ such that
$D_{0,\theta} \gt 0$ such that  $\parallel (-A)^{\theta} T(t)\parallel \leq D_{0,\theta} {\rm e}^{-\beta t}t^{-\theta} $ for all t > 0 and that
are finite. Let
$\parallel (-A)^{\theta} T(t)\parallel \leq D_{0,\theta} {\rm e}^{-\beta t}t^{-\theta} $ for all t > 0 and that
are finite. Let \begin{align*}
{\overline{\vartheta}}_{3,\infty} &= D_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip}}) \sup_{b \gt 0, t,h\in [0,b], t+h\leq b } \parallel \frac{{\rm e}^{-\beta(t-\cdot) }}{(t-\cdot)^{\alpha}} \Lambda^{2}(\cdot) ( [\zeta]_{(\cdot+h,\cdot)} + \zeta (\cdot) ) \parallel_{L^{1}([0,t])} , \\
\overline{\vartheta}_{4,\infty} &= D_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip}})
\sup_{t \geq 0 } \parallel \frac{{\rm e}^{-\beta(t-\cdot) }}{(t-\cdot)^{\alpha}} \Lambda (\cdot) ( [\zeta]_{(\cdot ,\cdot)} + \zeta (\cdot) ) \parallel_{L^{1}([0,t])}, \\
\overline{\vartheta}_{ 5,\infty} &= D_{0,\alpha} \sup_{b \gt 0, t\in [0,b]} \parallel \frac{{\rm e}^{-\beta(t-\cdot) }}{(t-\cdot)^{\alpha}} [F]_{(\cdot,0)} \parallel_{L^{1}([0,t])}, \\
\overline{\vartheta}_{6,\infty} &= D_{0,\alpha} \sup_{b \gt 0, t\in [0,b]} \int_0^t \frac{{\rm e}^{-\beta(t-\tau) }}{(t-\tau)^{\alpha}} [F]_{(\tau,0)} \tau \, {\rm d}\tau
\end{align*}
\begin{align*}
{\overline{\vartheta}}_{3,\infty} &= D_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip}}) \sup_{b \gt 0, t,h\in [0,b], t+h\leq b } \parallel \frac{{\rm e}^{-\beta(t-\cdot) }}{(t-\cdot)^{\alpha}} \Lambda^{2}(\cdot) ( [\zeta]_{(\cdot+h,\cdot)} + \zeta (\cdot) ) \parallel_{L^{1}([0,t])} , \\
\overline{\vartheta}_{4,\infty} &= D_{0,\alpha} (1+ [\sigma]_{C_{\rm Lip}})
\sup_{t \geq 0 } \parallel \frac{{\rm e}^{-\beta(t-\cdot) }}{(t-\cdot)^{\alpha}} \Lambda (\cdot) ( [\zeta]_{(\cdot ,\cdot)} + \zeta (\cdot) ) \parallel_{L^{1}([0,t])}, \\
\overline{\vartheta}_{ 5,\infty} &= D_{0,\alpha} \sup_{b \gt 0, t\in [0,b]} \parallel \frac{{\rm e}^{-\beta(t-\cdot) }}{(t-\cdot)^{\alpha}} [F]_{(\cdot,0)} \parallel_{L^{1}([0,t])}, \\
\overline{\vartheta}_{6,\infty} &= D_{0,\alpha} \sup_{b \gt 0, t\in [0,b]} \int_0^t \frac{{\rm e}^{-\beta(t-\tau) }}{(t-\tau)^{\alpha}} [F]_{(\tau,0)} \tau \, {\rm d}\tau
\end{align*} $Q_{\infty} : [0,\infty)\mapsto \mathbb{R} $ be the function given by
(5.8)
$Q_{\infty} : [0,\infty)\mapsto \mathbb{R} $ be the function given by
(5.8) \begin{align}
\overline{Q}_{\infty} (x) & = C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + \overline{\vartheta}_{6,\infty} \nonumber\\
& + \left( \overline{\vartheta}_{5 ,\infty} + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \overline{\vartheta}_{3 ,\infty} \right) + \mathcal{W}_{F,\sigma}(x) (1+x) \overline{\vartheta}_{4 ,\infty} -x .
\end{align}
\begin{align}
\overline{Q}_{\infty} (x) & = C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip,1+\alpha-\gamma}((0,a];X_{\alpha})}} + \overline{\vartheta}_{6,\infty} \nonumber\\
& + \left( \overline{\vartheta}_{5 ,\infty} + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \overline{\vartheta}_{3 ,\infty} \right) + \mathcal{W}_{F,\sigma}(x) (1+x) \overline{\vartheta}_{4 ,\infty} -x .
\end{align}If
 $ \overline{Q}_{\infty} (R) \lt 0$ for some R > 0, then there exists a unique mild solution
$ \overline{Q}_{\infty} (R) \lt 0$ for some R > 0, then there exists a unique mild solution  $u\in C ((0,\infty);X)$ of the problem (5.1)–(5.3) on
$u\in C ((0,\infty);X)$ of the problem (5.1)–(5.3) on  $[0,\infty)$ such that
$[0,\infty)$ such that  $u\in C_{\rm Lip,1 +\alpha-\gamma}((0,\infty); X_{\alpha})$.
$u\in C_{\rm Lip,1 +\alpha-\gamma}((0,\infty); X_{\alpha})$.
Proof. The assertions follow from Proposition 3.1, Corollary 3.5 and Proposition 4.5, respectively. Concerning (a), we only note that
 \begin{align*}
{\Theta}_{4}(b) &\leq \sup_{t\in [0,b]} \int_0^t \frac{[F]_{(\tau,\tau)}}{(t-\tau)^{\alpha}} (1 + [\sigma]_{(\tau,\tau)}) \Lambda (\tau) \, {\rm d}\tau \\
&\leq (1 + [\sigma]_{C_{\rm Lip}}) \parallel [F]_{(\cdot,\cdot)}\parallel_{L^{q}([0,a])} \parallel\Lambda(\cdot)\parallel_{L^{p}([0,a])} \frac{b^{\frac{1}{\tau(q,p)}- \alpha} }{\left[1-\frac{\alpha }{\tau(q,p)}\right]^{\frac{1}{\tau(q,p)}}} \to 0 \ \hbox{as}\ b\to 0.
\end{align*}
\begin{align*}
{\Theta}_{4}(b) &\leq \sup_{t\in [0,b]} \int_0^t \frac{[F]_{(\tau,\tau)}}{(t-\tau)^{\alpha}} (1 + [\sigma]_{(\tau,\tau)}) \Lambda (\tau) \, {\rm d}\tau \\
&\leq (1 + [\sigma]_{C_{\rm Lip}}) \parallel [F]_{(\cdot,\cdot)}\parallel_{L^{q}([0,a])} \parallel\Lambda(\cdot)\parallel_{L^{p}([0,a])} \frac{b^{\frac{1}{\tau(q,p)}- \alpha} }{\left[1-\frac{\alpha }{\tau(q,p)}\right]^{\frac{1}{\tau(q,p)}}} \to 0 \ \hbox{as}\ b\to 0.
\end{align*} The assertion in (b) follows from the first assertion in Corollary 3.5 noting that  $ P_{a}(x)\leq Q_{a}(x)$ for all x > 0. Similarly, the last assertion follows from Proposition 4.5 noting that
$ P_{a}(x)\leq Q_{a}(x)$ for all x > 0. Similarly, the last assertion follows from Proposition 4.5 noting that  $ Q_{\infty}(x)\leq
\overline{Q}_{\infty} (x) $ for all x > 0. We omit additional details.
$ Q_{\infty}(x)\leq
\overline{Q}_{\infty} (x) $ for all x > 0. We omit additional details.
To establish the next result, we assume that N = 1, that  $(-A)^{\frac{1}{2}}=\frac{\partial}{\partial _{x}} $ and that
$(-A)^{\frac{1}{2}}=\frac{\partial}{\partial _{x}} $ and that  $D((-A)^{\frac{1}{2}})= H^{1}_{0}(\Omega)$. In this case,
$D((-A)^{\frac{1}{2}})= H^{1}_{0}(\Omega)$. In this case,  $F\in
L_{\rm Lip}^{q}( [0,a]\times X_{\alpha} ; X_{\alpha} ) $ for
$F\in
L_{\rm Lip}^{q}( [0,a]\times X_{\alpha} ; X_{\alpha} ) $ for  $\alpha=
\frac{1}{2}$ and using the norm
$\alpha=
\frac{1}{2}$ and using the norm  $\parallel x\parallel_{\alpha} = \parallel
(-A)^{\alpha}x\parallel$, it is easy to see that
$\parallel x\parallel_{\alpha} = \parallel
(-A)^{\alpha}x\parallel$, it is easy to see that
 \begin{align*}
\parallel F(t,u) &- F(s,v) \parallel_{\alpha} \hspace{1cm} \\
& \leq ( [\zeta]_{(t,s)} + \mid \zeta(s)\mid )
(2r^{2}+5r+1) (1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} ) (|t-s|+ \parallel u -v\parallel_{\alpha}).
\end{align*}
\begin{align*}
\parallel F(t,u) &- F(s,v) \parallel_{\alpha} \hspace{1cm} \\
& \leq ( [\zeta]_{(t,s)} + \mid \zeta(s)\mid )
(2r^{2}+5r+1) (1+ \parallel i_{c}\parallel_{\mathcal{L}(X_{\alpha}; C(\Omega))} ) (|t-s|+ \parallel u -v\parallel_{\alpha}).
\end{align*}for  $0\leq s \lt t\leq a $ and
$0\leq s \lt t\leq a $ and  $ u,v \in B_r[0,X_{\alpha}]$.
$ u,v \in B_r[0,X_{\alpha}]$.
Proposition 5.2. Assume  $\alpha=\frac{1}{2}$ and
$\alpha=\frac{1}{2}$ and  $ x_{0}\in X_{\gamma}$ for some
$ x_{0}\in X_{\gamma}$ for some  $\gamma \in (\alpha,\alpha+1) $.
$\gamma \in (\alpha,\alpha+1) $.
(a) Let a > 0. If
 $\frac{1}{p}+\frac{1}{q} \leq 1$ and
(5.9)for some
$\frac{1}{p}+\frac{1}{q} \leq 1$ and
(5.9)for some \begin{eqnarray}
\Xi(c)= \sup_{d\in [0,c], t,h\in [0,d],t+h\leq d} \parallel [\zeta]_{(\cdot+h,\cdot)}\parallel_{L^{q}([0,t])} \lt \infty,
\end{eqnarray}
\begin{eqnarray}
\Xi(c)= \sup_{d\in [0,c], t,h\in [0,d],t+h\leq d} \parallel [\zeta]_{(\cdot+h,\cdot)}\parallel_{L^{q}([0,t])} \lt \infty,
\end{eqnarray} $0 \lt c\leq a$, then there exists a unique mild solution
$0 \lt c\leq a$, then there exists a unique mild solution  $u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})$ of (5.1)–(5.3) for some b > 0.
$u\in C_{\rm Lip,1+\alpha-\gamma}((0,b];X_{\alpha})$ of (5.1)–(5.3) for some b > 0.(b) Assume
 $ T(\cdot)x_{0}\in C_{\rm Lip}([0,a];X_{\alpha})$,
$ T(\cdot)x_{0}\in C_{\rm Lip}([0,a];X_{\alpha})$,  $ 1-\alpha q^\prime \gt 0$ and that Equation (5.9) is satisfied. Then there exists a unique mild solution
$ 1-\alpha q^\prime \gt 0$ and that Equation (5.9) is satisfied. Then there exists a unique mild solution  $u\in C_{\rm Lip}([0,b];X_{\alpha})$ of (5.1)–(5.3) on
$u\in C_{\rm Lip}([0,b];X_{\alpha})$ of (5.1)–(5.3) on  $[0,b]$ for some b > 0.
$[0,b]$ for some b > 0.
Proof. The assertion in (a) follows from Theorem 3.1 noting that the condition (5.9) implies  $\Theta_{1}(d) \lt \Xi(c)\parallel \Lambda^{2}\parallel_{L^{p}([0,c])} \lt \infty$ for all d < c and that
$\Theta_{1}(d) \lt \Xi(c)\parallel \Lambda^{2}\parallel_{L^{p}([0,c])} \lt \infty$ for all d < c and that
 \begin{eqnarray*}
{\Theta}_{2}(b) \leq \sup_{t\in [0,b]} \int_0^t [F]_{(\tau,\tau)}
(1 + [\sigma]_{(\tau,\tau)}) \Lambda (\tau) \, {\rm d}\tau \leq (1 + [\sigma]_{C_{\rm Lip}}) \parallel [F]_{(\cdot,\cdot)} \Lambda(\cdot)\parallel_{L^{1}([0,b])} \to 0\,
\end{eqnarray*}
\begin{eqnarray*}
{\Theta}_{2}(b) \leq \sup_{t\in [0,b]} \int_0^t [F]_{(\tau,\tau)}
(1 + [\sigma]_{(\tau,\tau)}) \Lambda (\tau) \, {\rm d}\tau \leq (1 + [\sigma]_{C_{\rm Lip}}) \parallel [F]_{(\cdot,\cdot)} \Lambda(\cdot)\parallel_{L^{1}([0,b])} \to 0\,
\end{eqnarray*}as b → 0 because  $ \frac{1}{p}+\frac{1}{q} \leq 1$. Concerning (b), we note that
$ \frac{1}{p}+\frac{1}{q} \leq 1$. Concerning (b), we note that
 \begin{align}
\widehat{\Phi}_{1}(b) & \leq (1 + [\sigma]_{C_{\rm Lip}}) \int_0^b{ \frac{( [\zeta]_{(s,0)} + \mid \zeta(0)\mid )}{(t-s)^{\alpha}} }\,{\rm d}\tau \nonumber\\
&\leq (1 + [\sigma]_{C_{\rm Lip}}) ( \parallel \zeta(\cdot,0)\parallel_{L^{q}([0,b])} + \mid \zeta(0)\mid) {b^{\frac{1}{q^\prime}-\alpha }}{[1-q^\prime\alpha]^{-\frac{1}{q^\prime}} } \to 0,
\nonumber\\
\widehat{\Phi}_{2}(b) & \leq (1 + [\sigma]_{C_{\rm Lip}}) \sup_{t,h\in [0,b],t+h\leq b} \int_0^t { \frac{( [\zeta]_{(s+h,s)} + \mid \zeta(s)\mid ) }{(t-s)^{\alpha}}
}\, {\rm d}\tau \nonumber\\
& \leq (1 + [\sigma]_{C_{\rm Lip}}) ( \Xi(b) + \parallel \zeta\parallel_{L^{q}( [0,b])}) {b^{\frac{1}{q^\prime}-\alpha }}{[1-q^\prime\alpha]^{-\frac{1}{q^\prime}} } \to 0
\end{align}
\begin{align}
\widehat{\Phi}_{1}(b) & \leq (1 + [\sigma]_{C_{\rm Lip}}) \int_0^b{ \frac{( [\zeta]_{(s,0)} + \mid \zeta(0)\mid )}{(t-s)^{\alpha}} }\,{\rm d}\tau \nonumber\\
&\leq (1 + [\sigma]_{C_{\rm Lip}}) ( \parallel \zeta(\cdot,0)\parallel_{L^{q}([0,b])} + \mid \zeta(0)\mid) {b^{\frac{1}{q^\prime}-\alpha }}{[1-q^\prime\alpha]^{-\frac{1}{q^\prime}} } \to 0,
\nonumber\\
\widehat{\Phi}_{2}(b) & \leq (1 + [\sigma]_{C_{\rm Lip}}) \sup_{t,h\in [0,b],t+h\leq b} \int_0^t { \frac{( [\zeta]_{(s+h,s)} + \mid \zeta(s)\mid ) }{(t-s)^{\alpha}}
}\, {\rm d}\tau \nonumber\\
& \leq (1 + [\sigma]_{C_{\rm Lip}}) ( \Xi(b) + \parallel \zeta\parallel_{L^{q}( [0,b])}) {b^{\frac{1}{q^\prime}-\alpha }}{[1-q^\prime\alpha]^{-\frac{1}{q^\prime}} } \to 0
\end{align}as b → 0, which implies that the conditions in Proposition 4.6 are satisfied and allows us to finish the proof.
The next example is related the diffusive Nicholson’s blowflies equation, see [Reference Hernandez, Pierri and Wu23] for additional details. Consider the differential equation
 \begin{align}
u^\prime(t,x)&= \Delta u(t,x)+\zeta(t)\int_{\Omega}u(\sigma(t,u(t)),y )g(x,y)\,{\rm d}y , \qquad (t,x) \in [0,a]\times \Omega ,
\end{align}
\begin{align}
u^\prime(t,x)&= \Delta u(t,x)+\zeta(t)\int_{\Omega}u(\sigma(t,u(t)),y )g(x,y)\,{\rm d}y , \qquad (t,x) \in [0,a]\times \Omega ,
\end{align} $\sigma(\cdot)$ and
$\sigma(\cdot)$ and  $\zeta(\cdot) $ are the functions in the problem (5.1)–(5.3),
$\zeta(\cdot) $ are the functions in the problem (5.1)–(5.3),  $x_{0}\in X $ and
$x_{0}\in X $ and  $g\in L^{2}(\Omega\times \Omega;\mathbb{R} )$.
$g\in L^{2}(\Omega\times \Omega;\mathbb{R} )$.
To study this problem, we define  $F:[0,a]\times X \mapsto X$ by
$F:[0,a]\times X \mapsto X$ by  $ F(t,x)(y)= \zeta(t) \int_{\Omega} x(z)g(y,z)\,{\rm d}z $. For
$ F(t,x)(y)= \zeta(t) \int_{\Omega} x(z)g(y,z)\,{\rm d}z $. For  $0 \lt s\leq t\leq a$
$0 \lt s\leq t\leq a$  $x,y \in B_{r}[0,X]$, it is easy to see that
$x,y \in B_{r}[0,X]$, it is easy to see that  $ \parallel F(t,x) \parallel
\leq L_{g} \mid \zeta (t)\mid r $ and
$ \parallel F(t,x) \parallel
\leq L_{g} \mid \zeta (t)\mid r $ and
where  $L_{g}= \left(\int_{\Omega} \int_{\Omega} g^{2}(\xi,\eta) \,{\rm d}\xi \,{\rm d} \eta \right)^{\frac{1}{2}}$. Thus,
$L_{g}= \left(\int_{\Omega} \int_{\Omega} g^{2}(\xi,\eta) \,{\rm d}\xi \,{\rm d} \eta \right)^{\frac{1}{2}}$. Thus,  $ F\in L_{\rm Lip}^{q}( [0,a]\times X ;X)$ with
$ F\in L_{\rm Lip}^{q}( [0,a]\times X ;X)$ with  $ [F]_{(t,s)} = ( [\zeta]_{(t,s)} + \mid \zeta(s)\mid ) $ and
$ [F]_{(t,s)} = ( [\zeta]_{(t,s)} + \mid \zeta(s)\mid ) $ and  $\mathcal{W}_{F}(r)= (r+1)L_{g} $, and the condition
$\mathcal{W}_{F}(r)= (r+1)L_{g} $, and the condition  $\bf \mathcal{H}_{{F}, a}(X ; X) $ is satisfied with
$\bf \mathcal{H}_{{F}, a}(X ; X) $ is satisfied with  $ \varrho_{1}(t)= \mid \zeta (t)\mid$,
$ \varrho_{1}(t)= \mid \zeta (t)\mid$,  $ \varrho_{2}(t)= 0$ and
$ \varrho_{2}(t)= 0$ and  $ \mathcal{K}_{F}(x) =
L_{g} x $.
$ \mathcal{K}_{F}(x) =
L_{g} x $.
From the results in the previous sections we have the next one.
Proposition 5.3. Assume that the above conditions concerning the problem (5.11)–(5.13) are satisfied and that  $x_{0}\in X_{\gamma}$ for some
$x_{0}\in X_{\gamma}$ for some  $\gamma\in (0,1)$.
$\gamma\in (0,1)$.
(a) If
 $\frac{1}{p}+\frac{1}{q} \leq 1$ and the condition in Equation (5.9) is satisfied, then there exists a unique mild solution
$\frac{1}{p}+\frac{1}{q} \leq 1$ and the condition in Equation (5.9) is satisfied, then there exists a unique mild solution  $u\in C_{\rm Lip,1-\gamma}((0,b];X)$ for some b > 0.
$u\in C_{\rm Lip,1-\gamma}((0,b];X)$ for some b > 0.(b) Assume
 $ \zeta \in C ([0,a];\mathbb{R})$,
$ \zeta \in C ([0,a];\mathbb{R})$,  $\frac{1}{p}+\frac{1}{q} \leq 1$,
$\frac{1}{p}+\frac{1}{q} \leq 1$,  $ \Xi(a) \lt \infty$ (see Equation (5.9)) and let
$ \Xi(a) \lt \infty$ (see Equation (5.9)) and let  $P :[0,\infty)\mapsto\mathbb{R}$ be the function defined by
$P :[0,\infty)\mapsto\mathbb{R}$ be the function defined by
 \begin{align*}
P_{a} (x) &= C_{0 } \parallel x_{0}\parallel + {[T(\cdot)x_{0}]_{C_{\rm Lip,1 -\gamma}((0,a];X )}} + C_{0 } L_{g} ( \parallel \zeta \parallel_{L^{1}([0,a])}\\ &\qquad + \parallel \zeta \parallel_{L^{\infty}([0,a])} a^{1 -\gamma} ) x \\ & +
2 C_{0 } \mathcal{W}_{F }(x) (1+ [\sigma]_{C_{\rm Lip}}) (1+x) ^{2} a^{1 -\gamma} \sup_{t,h\in [0,a],t+h\in [0,a]} \int_{0}^{t} ( [\zeta]_{(\tau+h,\tau)} \\ &\qquad + \mid \zeta (\tau)\mid ) \Lambda^{2}(\tau) \,{\rm d}\tau
\\ &\quad +
2 C_{0 } \mathcal{W}_{F }(x)(1+ [\sigma]_{C_{\rm Lip}})
(1+x) \int_{0}^{a} ( [\zeta]_{(\tau,\tau)} + \zeta (\tau)) \Lambda (\tau) \,{\rm d}\tau -x.
\end{align*}
\begin{align*}
P_{a} (x) &= C_{0 } \parallel x_{0}\parallel + {[T(\cdot)x_{0}]_{C_{\rm Lip,1 -\gamma}((0,a];X )}} + C_{0 } L_{g} ( \parallel \zeta \parallel_{L^{1}([0,a])}\\ &\qquad + \parallel \zeta \parallel_{L^{\infty}([0,a])} a^{1 -\gamma} ) x \\ & +
2 C_{0 } \mathcal{W}_{F }(x) (1+ [\sigma]_{C_{\rm Lip}}) (1+x) ^{2} a^{1 -\gamma} \sup_{t,h\in [0,a],t+h\in [0,a]} \int_{0}^{t} ( [\zeta]_{(\tau+h,\tau)} \\ &\qquad + \mid \zeta (\tau)\mid ) \Lambda^{2}(\tau) \,{\rm d}\tau
\\ &\quad +
2 C_{0 } \mathcal{W}_{F }(x)(1+ [\sigma]_{C_{\rm Lip}})
(1+x) \int_{0}^{a} ( [\zeta]_{(\tau,\tau)} + \zeta (\tau)) \Lambda (\tau) \,{\rm d}\tau -x.
\end{align*}If there is R > 0 such that
 $P_{a}(R) \lt 0$, then there exists a unique mild solution
$P_{a}(R) \lt 0$, then there exists a unique mild solution  $u\in C_{\rm Lip,1-\gamma}((0,a];X )$ of the problem (5.11)–(5.13).
$u\in C_{\rm Lip,1-\gamma}((0,a];X )$ of the problem (5.11)–(5.13).(c) Suppose that
 $\parallel T(s)\parallel \leq C_{0}$ for all s > 0,
$\parallel T(s)\parallel \leq C_{0}$ for all s > 0,  $\zeta \in C ([0,\infty);\mathbb{R}) $ and that
are finite. Let
$\zeta \in C ([0,\infty);\mathbb{R}) $ and that
are finite. Let \begin{align*}
\chi_{_{1},\infty}(x) &= C_{0 } L_{g} \parallel \zeta \parallel_{L^{\infty}([0,\infty))}x , \qquad \chi_{_{2},\infty} = C_{0 } L_{g} \parallel \zeta \parallel_{L^{1}([0,\infty))} x \\
\vartheta_{1,\infty} &= (1+ [\sigma]_{C_{\rm Lip}}) \sup_{b \gt 0, t,h \gt 0, t+h \in [0,b]}\int_{{0}}^{t}\parallel T(t-s)\parallel ( [\zeta]_{(s+h,s)}\\ & \qquad +\mid \zeta(s)\mid ) \Lambda^{2} (s) \,{\rm d}s, \\
\vartheta_{2,\infty} &= (1+ [\sigma]_{C_{\rm Lip}}) \sup_{t \gt 0}\int_{{0}}^{t} \parallel T(t-s)\parallel ( [\zeta]_{(s ,s)} +\mid \zeta(s)\mid ) \Lambda (s) \,{\rm d}s
\end{align*}
\begin{align*}
\chi_{_{1},\infty}(x) &= C_{0 } L_{g} \parallel \zeta \parallel_{L^{\infty}([0,\infty))}x , \qquad \chi_{_{2},\infty} = C_{0 } L_{g} \parallel \zeta \parallel_{L^{1}([0,\infty))} x \\
\vartheta_{1,\infty} &= (1+ [\sigma]_{C_{\rm Lip}}) \sup_{b \gt 0, t,h \gt 0, t+h \in [0,b]}\int_{{0}}^{t}\parallel T(t-s)\parallel ( [\zeta]_{(s+h,s)}\\ & \qquad +\mid \zeta(s)\mid ) \Lambda^{2} (s) \,{\rm d}s, \\
\vartheta_{2,\infty} &= (1+ [\sigma]_{C_{\rm Lip}}) \sup_{t \gt 0}\int_{{0}}^{t} \parallel T(t-s)\parallel ( [\zeta]_{(s ,s)} +\mid \zeta(s)\mid ) \Lambda (s) \,{\rm d}s
\end{align*} $P_{\infty} :[0,\infty)\mapsto\mathbb{R}$ be the function given by
$P_{\infty} :[0,\infty)\mapsto\mathbb{R}$ be the function given by
 \begin{align*}
P_{\infty} (x ) & := C_{0} \parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})} + ( \chi_{_{1},\infty}(x) + \chi_{_{2},\infty}(x) )\\
& + 2 \mathcal{W}_{F }(x ) \left( (1+x) ^{2} \vartheta_{1,\infty}
+ (1+x) \vartheta_{2,\infty} \right) -x .
\end{align*}
\begin{align*}
P_{\infty} (x ) & := C_{0} \parallel x_{0}\parallel_{\alpha} + [T(\cdot)x_{0}]_{C_{\rm Lip, 1+\alpha-\gamma}((0,\infty);X_{\alpha})} + ( \chi_{_{1},\infty}(x) + \chi_{_{2},\infty}(x) )\\
& + 2 \mathcal{W}_{F }(x ) \left( (1+x) ^{2} \vartheta_{1,\infty}
+ (1+x) \vartheta_{2,\infty} \right) -x .
\end{align*}If there is R > 0 such that
 $P(R) \lt 0$, then there exists a unique mild solution
$P(R) \lt 0$, then there exists a unique mild solution  $ u\in C_{Lip, 1-\gamma}((0,\infty); X )$ of the problem (5.11)–(5.13).
$ u\in C_{Lip, 1-\gamma}((0,\infty); X )$ of the problem (5.11)–(5.13).(d) Assume
 $\zeta(0)=0$, that
$\zeta(0)=0$, that  $(T(t))_{t\geq 0} $ verify the conditions in item (c) of Proposition 5.1 and that
are finite. Let
$(T(t))_{t\geq 0} $ verify the conditions in item (c) of Proposition 5.1 and that
are finite. Let \begin{align*}
\vartheta_{3,\infty} &= (1+ [\sigma]_{C_{\rm Lip}}) \sup_{b \gt 0, t,h\in [0,b] ,t+h\leq b } \int_{{0}}^{t} \frac{{\rm e}^{-\beta(t-s) }}{(t-s)^{\alpha}} ( [\zeta]_{(s+h,s)} +\mid \zeta(s)\mid ) \Lambda^{2}(s) \, {\rm d}s , \\
\vartheta_{4,\infty} &= (1+ [\sigma]_{C_{\rm Lip}}) \sup_{t \gt 0} \parallel \frac{{\rm e}^{-\beta(t-\cdot) }}{(t-\cdot)^{\alpha}}
( [\zeta]_{(\cdot ,\cdot)} +\mid \zeta(\cdot)\mid ) \Lambda (\cdot) \parallel_{L^{1}([0,t])} , \\
\vartheta_{ 5,\infty} &= \sup_{b \gt 0, t\in [0,b]} \parallel \frac{{\rm e}^{-\beta(t-\cdot) }}{(t-\cdot)^{\alpha}} [\zeta]_{(\cdot,0)} \parallel_{L^{1}([0,t])}, \\
\vartheta_{6,\infty} &= \sup_{b \gt 0, t\in [0,b]} \int_0^t \frac{{\rm e}^{-\beta(t-\tau) }}{(t-\tau)^{\alpha}} [\zeta]_{(\tau,0)} \tau \,{\rm d}\tau
\end{align*}
\begin{align*}
\vartheta_{3,\infty} &= (1+ [\sigma]_{C_{\rm Lip}}) \sup_{b \gt 0, t,h\in [0,b] ,t+h\leq b } \int_{{0}}^{t} \frac{{\rm e}^{-\beta(t-s) }}{(t-s)^{\alpha}} ( [\zeta]_{(s+h,s)} +\mid \zeta(s)\mid ) \Lambda^{2}(s) \, {\rm d}s , \\
\vartheta_{4,\infty} &= (1+ [\sigma]_{C_{\rm Lip}}) \sup_{t \gt 0} \parallel \frac{{\rm e}^{-\beta(t-\cdot) }}{(t-\cdot)^{\alpha}}
( [\zeta]_{(\cdot ,\cdot)} +\mid \zeta(\cdot)\mid ) \Lambda (\cdot) \parallel_{L^{1}([0,t])} , \\
\vartheta_{ 5,\infty} &= \sup_{b \gt 0, t\in [0,b]} \parallel \frac{{\rm e}^{-\beta(t-\cdot) }}{(t-\cdot)^{\alpha}} [\zeta]_{(\cdot,0)} \parallel_{L^{1}([0,t])}, \\
\vartheta_{6,\infty} &= \sup_{b \gt 0, t\in [0,b]} \int_0^t \frac{{\rm e}^{-\beta(t-\tau) }}{(t-\tau)^{\alpha}} [\zeta]_{(\tau,0)} \tau \,{\rm d}\tau
\end{align*} $P_{\infty} : [0,\infty)\mapsto \mathbb{R} $ be the function defined by
(5.14)
$P_{\infty} : [0,\infty)\mapsto \mathbb{R} $ be the function defined by
(5.14) \begin{align}
P_{\infty} (x) & = C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip , 1+\alpha-\gamma}((0,\infty);X_{\alpha})}} +
\vartheta_{6,\infty}
\nonumber\\
& \quad + \left( \vartheta_{5 ,\infty} + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \vartheta_{3 ,\infty} \right) + \mathcal{W}_{F,\sigma}(x) (1+x) \vartheta_{4 ,\infty} -x .
\end{align}
\begin{align}
P_{\infty} (x) & = C_{0} \parallel x_{0}\parallel _{\alpha} + {[T(\cdot)x_{0}]_{C_{\rm Lip , 1+\alpha-\gamma}((0,\infty);X_{\alpha})}} +
\vartheta_{6,\infty}
\nonumber\\
& \quad + \left( \vartheta_{5 ,\infty} + \mathcal{W}_{F,\sigma}(x) (1+x) ^{2} \vartheta_{3 ,\infty} \right) + \mathcal{W}_{F,\sigma}(x) (1+x) \vartheta_{4 ,\infty} -x .
\end{align}If
 $P_{\infty}(R) \lt 0$ for some R > 0, then there exists a mild solution
$P_{\infty}(R) \lt 0$ for some R > 0, then there exists a mild solution  $ u\in C_{\rm Lip, 1-\gamma}((0,\infty); X_{\alpha} )$ of the problem (5.11)–(5.13).
$ u\in C_{\rm Lip, 1-\gamma}((0,\infty); X_{\alpha} )$ of the problem (5.11)–(5.13).
Acknowledgements
The authors wish to thank the referees and the editor responsible for this paper for their valuable comments and suggestions.
Competing Interest
This work was developed during the visit of A.Z.’s to the São Paulo University, São Paulo, Brazil. This visit was supported by the Higher Education Commission of Pakistan under the HEC Post-Doctoral Fellowships Programme (Phase III)-Batch I. The other authors declare none.



































































































