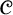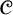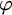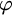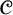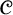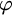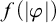1 Introduction
Many classes of graphs can be defined by a finite set of forbidden induced finite subgraphs. One of the simplest examples is the class of graphs of bounded degree. Let
![]() $d\ge 1$
and let the set
$d\ge 1$
and let the set
![]() $\mathscr {F}_d$
consist of all graphs with vertex set
$\mathscr {F}_d$
consist of all graphs with vertex set
![]() $\{1, \ldots , d+2\}$
and maximum degree
$\{1, \ldots , d+2\}$
and maximum degree
![]() $d+1$
. Then a graph G has degree at most d if and only if no graph in
$d+1$
. Then a graph G has degree at most d if and only if no graph in
![]() $\mathscr {F}_d$
is isomorphic to an induced subgraph of G. Less trivial examples include classes of graphs of small vertex cover (attributed to Lovász [Reference Fellows12]), of bounded tree-depth [Reference Ding7], and of bounded shrub-depth [Reference Ganian, Hlinený, Nesetril, Obdrzálek, de Mendez and Ramadurai16]. As a matter of fact, understanding forbidden induced subgraphs for those graph classes is an important question in structural graph theory [Reference Dvorák, Giannopoulou and Thilikos10, Reference Gajarský and Kreutzer14, Reference Ganian, Hlinený, Nesetril, Obdrzálek and Ossona de Mendez15, Reference Zaslavsky28]. However, a straightforward adaptation of a result in [Reference Fellows and Langston13] shows that it is in general impossible to compute the forbidden induced subgraphs from a description of classes of finite graphs by Turing machines.
$\mathscr {F}_d$
is isomorphic to an induced subgraph of G. Less trivial examples include classes of graphs of small vertex cover (attributed to Lovász [Reference Fellows12]), of bounded tree-depth [Reference Ding7], and of bounded shrub-depth [Reference Ganian, Hlinený, Nesetril, Obdrzálek, de Mendez and Ramadurai16]. As a matter of fact, understanding forbidden induced subgraphs for those graph classes is an important question in structural graph theory [Reference Dvorák, Giannopoulou and Thilikos10, Reference Gajarský and Kreutzer14, Reference Ganian, Hlinený, Nesetril, Obdrzálek and Ossona de Mendez15, Reference Zaslavsky28]. However, a straightforward adaptation of a result in [Reference Fellows and Langston13] shows that it is in general impossible to compute the forbidden induced subgraphs from a description of classes of finite graphs by Turing machines.
Łoś [Reference Łoś19] and Tarski [Reference Tarski26] proved the first so-called preservation theorem of classical model theory. In its simplest form it says for classes of graphs that the class ![]() of finite and infinite graphs that are models of a sentence
of finite and infinite graphs that are models of a sentence
![]() $\varphi $
of first-order logic (FO) is closed under induced subgraphs (or, that
$\varphi $
of first-order logic (FO) is closed under induced subgraphs (or, that
![]() $\varphi $
is preserved under induced subgraphs) if and only if there is a universal FO-sentence
$\varphi $
is preserved under induced subgraphs) if and only if there is a universal FO-sentence
![]() $\mu $
with
$\mu $
with ![]() . Recall that a universal sentence
. Recall that a universal sentence
![]() $\mu $
is a sentence of the form
$\mu $
is a sentence of the form
![]() $\forall x_1 \ldots \forall x_k\, \mu _0$
, where
$\forall x_1 \ldots \forall x_k\, \mu _0$
, where
![]() $\mu _0$
is quantifier-free.
$\mu _0$
is quantifier-free.
For a class
![]() $\mathscr {F}$
of graphs let
$\mathscr {F}$
of graphs let ![]() consist of all graphs that do not contain an induced subgraph isomorphic to a graph in
consist of all graphs that do not contain an induced subgraph isomorphic to a graph in
![]() $\mathscr {F}$
. For any class
$\mathscr {F}$
. For any class
![]() $\mathscr {C}$
of graphs closed under isomorphism and under induced subgraphs we have
$\mathscr {C}$
of graphs closed under isomorphism and under induced subgraphs we have ![]() where
where
![]() $\mathscr {F}$
consists of all graphs not in
$\mathscr {F}$
consists of all graphs not in
![]() $\mathscr {C}$
. Observe that
$\mathscr {C}$
. Observe that
![]() $\mathscr {F}$
is an infinite class that contains infinite graphs if
$\mathscr {F}$
is an infinite class that contains infinite graphs if
![]() $\mathscr {C}$
is not the class of all graphs (later on we only will consider
$\mathscr {C}$
is not the class of all graphs (later on we only will consider ![]() for sets
for sets
![]() $ \mathscr {F}$
).
$ \mathscr {F}$
).
It is folklore (see, e.g., [Reference McKee20]) that for a class
![]() $\mathscr {C}$
of graphs its definability by a universal sentence of first-order logic is equivalent to its characterization by finitely many forbidden induced finite subgraphs, i.e., equivalent to
$\mathscr {C}$
of graphs its definability by a universal sentence of first-order logic is equivalent to its characterization by finitely many forbidden induced finite subgraphs, i.e., equivalent to ![]() for some finite set
for some finite set
![]() $\mathscr {F}$
of finite graphs. In fact, for a universal sentence
$\mathscr {F}$
of finite graphs. In fact, for a universal sentence
![]() $\mu :=\forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
$\mu :=\forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
![]() $\mu _0$
we have (see Proposition 2.2)
$\mu _0$
we have (see Proposition 2.2)
Here for any FO-sentence
![]() $\varphi $
and
$\varphi $
and
![]() $k\ge 1$
by
$k\ge 1$
by
![]() $\mathscr {F}_k(\varphi )$
we denote the class of graphs that are models of
$\mathscr {F}_k(\varphi )$
we denote the class of graphs that are models of
![]() $\neg \varphi $
and whose universe is
$\neg \varphi $
and whose universe is
![]() $\{1, \ldots , \ell \}$
for some
$\{1, \ldots , \ell \}$
for some
![]() $\ell $
with
$\ell $
with
![]() $1\le \ell \le k$
. Clearly,
$1\le \ell \le k$
. Clearly,
![]() $\mathscr {F}_k(\varphi )$
is finite.
$\mathscr {F}_k(\varphi )$
is finite.
We say that a class
![]() $\mathscr {C}$
of finite and infinite graphs is definable by a finite set of forbidden induced finite subgraphs if there is a finite set
$\mathscr {C}$
of finite and infinite graphs is definable by a finite set of forbidden induced finite subgraphs if there is a finite set
![]() $\mathscr {F}$
of finite graphs such that
$\mathscr {F}$
of finite graphs such that ![]() . Hence the Łoś–Tarski Theorem (for classes of graphs) can be restated in the form:
. Hence the Łoś–Tarski Theorem (for classes of graphs) can be restated in the form:
For a class
![]() $\mathscr {C}$
of finite and infinite graphs the following are equivalent:
$\mathscr {C}$
of finite and infinite graphs the following are equivalent:
-
(i)
 $\mathscr {C}$
is closed under induced subgraphs and FO-axiomatizable.
$\mathscr {C}$
is closed under induced subgraphs and FO-axiomatizable. -
(ii)
 $\mathscr {C}$
is axiomatizable by a universal sentence.
$\mathscr {C}$
is axiomatizable by a universal sentence. -
(iii)
 $\mathscr {C}$
is definable by a finite set of forbidden induced finite subgraphs.
$\mathscr {C}$
is definable by a finite set of forbidden induced finite subgraphs.
This version of the Łoś–Tarski Theorem is already contained, at least implicitly, in the article [Reference Vaught27] of Vaught published in 1954.
Clearly (1) implies ![]() where
where ![]() and
and ![]() denote the class of finite graphs in
denote the class of finite graphs in ![]() and in
and in ![]() , respectively. Hence the equivalence between (ii) and (iii) holds too if we only consider classes of finite graphs.
, respectively. Hence the equivalence between (ii) and (iii) holds too if we only consider classes of finite graphs.
Note that we have repeatedly mentioned that in the Łoś–Tarski Theorem graphs are allowed to be infinite. This is not merely a technicality. In [Reference Chen and Flum3], to obtain the forbidden induced subgraph characterization of graphs of bounded shrub-depth using the Łoś–Tarski Theorem, one simple but vital step is to extend the notion of shrub-depth to infinite graphs. Indeed, Tait [Reference Tait25] exhibited a class
![]() $\mathscr {C}$
of finite structures (which might be understood as colored directed graphs) that is closed under induced substructures and FO-axiomatizable. Yet,
$\mathscr {C}$
of finite structures (which might be understood as colored directed graphs) that is closed under induced substructures and FO-axiomatizable. Yet,
![]() $\mathscr {C}$
is not definable by any universal sentence, thus cannot be characterized by a finite set of forbidden induced finite substructures. In [Reference Alechina and Gurevich1] the authors present a class
$\mathscr {C}$
is not definable by any universal sentence, thus cannot be characterized by a finite set of forbidden induced finite substructures. In [Reference Alechina and Gurevich1] the authors present a class
![]() $\mathscr {C}$
of finite directed graphs with loops with the same properties, i.e.,
$\mathscr {C}$
of finite directed graphs with loops with the same properties, i.e.,
![]() $\mathscr {C}$
is closed under induced substructures and FO-axiomatizable (even by a sentence without equality) but not axiomatizable by a universal sentence. Of course, the class
$\mathscr {C}$
is closed under induced substructures and FO-axiomatizable (even by a sentence without equality) but not axiomatizable by a universal sentence. Of course, the class
![]() $\mathscr {C}'$
of graphs in
$\mathscr {C}'$
of graphs in
![]() $\mathscr {C}$
is closed under induced subgraphs but
$\mathscr {C}$
is closed under induced subgraphs but
![]() $\mathscr {C}'$
is axiomatizable by a universal sentence (as
$\mathscr {C}'$
is axiomatizable by a universal sentence (as
![]() $\mathscr {C}'$
is empty).
$\mathscr {C}'$
is empty).
The first result of this paper strengthens the preceding “negative results” to graphs; more precisely we show the following theorem:
Theorem 1.1. There is a class
![]() $\mathscr {C}$
of finite graphs that is closed under induced subgraphs and
$\mathscr {C}$
of finite graphs that is closed under induced subgraphs and
![]() $\mathrm{FO}$
-axiomatizable but not definable by a finite set of forbidden induced finite subgraphs (i.e., there is no finite set
$\mathrm{FO}$
-axiomatizable but not definable by a finite set of forbidden induced finite subgraphs (i.e., there is no finite set
![]() $\mathscr {F}$
of finite graphs such that
$\mathscr {F}$
of finite graphs such that ![]() ).
).
Even though we are interested in structural and algorithmic results for classes of finite graphs, we see that in order to apply the Łoś–Tarski Theorem for such purposes we have to consider classes of finite and infinite graphs. Hence, in this paper “graph” means finite or infinite graph. As in the preceding result we mention it explicitly if we only consider finite graphs.
Complementing Theorem 1.1 we show that it is even undecidable whether a given FO-definable class of finite graphs that is closed under induced subgraphs can be characterized by a finite set of forbidden induced finite subgraphs. More precisely, we prove:
Theorem 1.2. There is no algorithm that for any
![]() $\mathrm{FO}$
-sentence
$\mathrm{FO}$
-sentence
![]() $\varphi $
such that
$\varphi $
such that ![]() is closed under induced subgraphs decides whether
is closed under induced subgraphs decides whether
![]() $\varphi $
is equivalent to a universal sentence on finite graphs.
$\varphi $
is equivalent to a universal sentence on finite graphs.
For a first-order definable class of graphs closed under induced subgraphs, often it is preferable to have an explicit construction of a finite set of forbidden induced finite subgraphs. This however turns out to be difficult for many natural classes of graphs. Let us consider the k-vertex cover problem for a constant
![]() $k\ge 1$
. It asks whether a given graph has a vertex cover (i.e., a set of vertices that contains at least one endpoint of every edge) of size at most k. The class of all yes-instances of this problem, finite and infinite, is closed under induced subgraphs and FO-axiomatizable by the FO-sentence
$k\ge 1$
. It asks whether a given graph has a vertex cover (i.e., a set of vertices that contains at least one endpoint of every edge) of size at most k. The class of all yes-instances of this problem, finite and infinite, is closed under induced subgraphs and FO-axiomatizable by the FO-sentence

where ![]() axiomatizes the class of graphs. Hence, by the Łoś–Tarski Theorem there is a universal sentence
axiomatizes the class of graphs. Hence, by the Łoś–Tarski Theorem there is a universal sentence
![]() $\mu $
equivalent to
$\mu $
equivalent to
![]() $\varphi ^k_{\text {VC}}$
. As the reader will notice, it is by no means trivial to find such a
$\varphi ^k_{\text {VC}}$
. As the reader will notice, it is by no means trivial to find such a
![]() $\mu $
. On the other hand, using the Completeness Theorem, we eventually will get such a
$\mu $
. On the other hand, using the Completeness Theorem, we eventually will get such a
![]() $\mu $
. Then we can extract corresponding forbidden induced subgraphs from
$\mu $
. Then we can extract corresponding forbidden induced subgraphs from
![]() $\mu $
as in (1). For the reader familiar with parameterized complexity [Reference Downey and Fellows8], to get a
$\mu $
as in (1). For the reader familiar with parameterized complexity [Reference Downey and Fellows8], to get a
![]() $\mu $
we can alternatively use that a graph with vertex cover of size at most k admits a kernel with at most
$\mu $
we can alternatively use that a graph with vertex cover of size at most k admits a kernel with at most
![]() $k^2$
edges. Observe that this approach involves the co-NP-hard problem of deciding whether an input graph does not contain a vertex cover of size at most k.
$k^2$
edges. Observe that this approach involves the co-NP-hard problem of deciding whether an input graph does not contain a vertex cover of size at most k.
By [Reference Ding7], also the class of finite graphs of tree-depth at most k is definable by a finite set of forbidden induced finite subgraphs. However, forbidden induced subgraphs are only known for
![]() $k\le 3$
[Reference Dvorák, Giannopoulou and Thilikos10].
$k\le 3$
[Reference Dvorák, Giannopoulou and Thilikos10].
We prove two “negative” results that explain the hardness of constructing forbidden induced subgraphs.
Theorem 1.3. There is no algorithm that for any
![]() $\mathrm{FO}$
-sentence
$\mathrm{FO}$
-sentence
![]() $\varphi $
which is equivalent to a universal sentence
$\varphi $
which is equivalent to a universal sentence
![]() $\mu $
on finite graphs computes such a
$\mu $
on finite graphs computes such a
![]() $\mu $
. Or equivalently, there is no algorithm that for any
$\mu $
. Or equivalently, there is no algorithm that for any
![]() $\mathrm{FO}$
-sentence
$\mathrm{FO}$
-sentence
![]() $\varphi $
such that
$\varphi $
such that
for a finite set
![]() $\mathscr {F}$
of finite graphs computes such an
$\mathscr {F}$
of finite graphs computes such an
![]() $\mathscr {F}$
.
$\mathscr {F}$
.
Theorem 1.4. Let
![]() $f: \mathbb N\to \mathbb N$
be a computable function. Then there is a class
$f: \mathbb N\to \mathbb N$
be a computable function. Then there is a class
![]() $\mathscr {C}$
of finite graphs and an
$\mathscr {C}$
of finite graphs and an
![]() $\mathrm{FO}$
-sentence
$\mathrm{FO}$
-sentence
![]() $\varphi $
such that
$\varphi $
such that
![]() $:$
$:$
-
(i)
 .
. -
(ii)
 for some universal sentence
for some universal sentence
 $\mu $
, in particular
$\mu $
, in particular
 $\mathscr {C}$
is closed under induced subgraphs.
$\mathscr {C}$
is closed under induced subgraphs. -
(iii) For every universal sentence
 $\mu $
with
$\mu $
with  we have
we have
 $|\mu |\ge f(|\varphi |)$
.
$|\mu |\ge f(|\varphi |)$
.
Theorem 1.3 significantly strengthens the aforementioned result of [Reference Fellows and Langston13]: even if a class
![]() $\mathscr {C}$
of finite graphs definable by a finite set of forbidden induced finite subgraphs is given by an
$\mathscr {C}$
of finite graphs definable by a finite set of forbidden induced finite subgraphs is given by an
![]() $\mathrm{FO}$
-sentence
$\mathrm{FO}$
-sentence
![]() $\varphi $
with
$\varphi $
with ![]() , instead of a (much more powerful) Turing machine deciding
, instead of a (much more powerful) Turing machine deciding
![]() $\mathscr {C}$
, we still cannot compute an appropriate finite set of forbidden induced finite subgraphs for
$\mathscr {C}$
, we still cannot compute an appropriate finite set of forbidden induced finite subgraphs for
![]() $\mathscr {C}$
from
$\mathscr {C}$
from
![]() $\varphi $
. On top of it, Theorem 1.4 implies that the size of forbidden subgraphs for
$\varphi $
. On top of it, Theorem 1.4 implies that the size of forbidden subgraphs for
![]() $\mathscr {C}$
cannot be bounded by any computable function in terms of the size of
$\mathscr {C}$
cannot be bounded by any computable function in terms of the size of
![]() $\varphi $
. There is an important precursor for Theorem 1.4:
$\varphi $
. There is an important precursor for Theorem 1.4:
Theorem 1.5 (Gurevich’s Theorem [Reference Gurevich17]).
Let
![]() $f:\mathbb N\to \mathbb N$
be computable. Then there is an
$f:\mathbb N\to \mathbb N$
be computable. Then there is an
![]() $\mathrm{FO}$
-sentence
$\mathrm{FO}$
-sentence
![]() $\varphi $
such that the class
$\varphi $
such that the class ![]() of models of
of models of
![]() $\varphi $
is closed under induced substructures but for every universal sentence
$\varphi $
is closed under induced substructures but for every universal sentence
![]() $\mu $
with
$\mu $
with ![]() we have
we have
![]() $|\mu |\ge f(|\varphi |)$
.
$|\mu |\ge f(|\varphi |)$
.
Hence, Theorem 1.4 can be viewed as the graph-theoretic version of Theorem 1.5.
Besides its importance in graph theory, Theorem 1.4 is also relevant in the context of algorithmic model theory. For algorithmic applications, the Łoś–Tarski theorem provides a normal form (i.e., a universal sentence) for any FO-sentence preserved under induced substructures. In [Reference Dawar, Grohe, Kreutzer and Schweikardt5, Theorem 6.1], it is shown that on labelled trees there is no elementary bound on the length of the equivalent universal sentence in terms of the original one. We should point out that Theorem 1.4 is not comparable to this result, since our lower bound is uncomputable (and thus, much higher than non-elementary) while the classes of graphs we construct in the proof are dense (thus very far from trees).
Our technical contributions
For every vocabulary it is well-known that the class of structures of this vocabulary is FO-interpretable in the class of graphs (see, for example, [Reference Ebbinghaus and Flum11]). Hence one might expect that Theorems 1.1 and 1.4 can be derived easily from Tait’s Theorem and Gurevich’s Theorem using the standard FO-interpretations. However, an easy analysis shows that those interpretations yield classes of graphs that are not closed under induced subgraphs. So we introduce the notion of strongly existential interpretation that translates any class of structures preserved under induced substructures and relevant to our investigations to a class of graphs closed under induced subgraphs. A lot of care is needed to construct strongly existential interpretations.
Related research
Let us briefly mention some further results related to the Łoś–Tarski Theorem. Essentially one could divide them into three categories (a), (b), and (c).
-
(a) The positive results showing that for certain classes
 $\mathscr {C}$
of finite structures the analogue of the Łoś–Tarski Theorem holds if we restrict to structures in
$\mathscr {C}$
of finite structures the analogue of the Łoś–Tarski Theorem holds if we restrict to structures in
 $\mathscr {C}$
. For example, this is the case if
$\mathscr {C}$
. For example, this is the case if
 $\mathscr {C}$
is the class of all finite structures of tree-width at most k for some
$\mathscr {C}$
is the class of all finite structures of tree-width at most k for some
 $k\in \mathbb N$
[Reference Atserias, Dawar and Grohe2] or if
$k\in \mathbb N$
[Reference Atserias, Dawar and Grohe2] or if
 $\mathscr {C}$
is the class of all finite structures whose hypergraph satisfies certain properties [Reference Duris9].
$\mathscr {C}$
is the class of all finite structures whose hypergraph satisfies certain properties [Reference Duris9]. -
(b) Both just mentioned papers contain also negative results, i.e., classes for which the analogue of the Łoś–Tarski Theorem fails. For example, in [Reference Atserias, Dawar and Grohe2] this is shown for the class of finite planar graphs, a class not axiomatizable in FO (cf. Remark 5.7(b)).
-
(c) The third category contains generalizations of the Łoś–Tarski Theorem or of its failure on finite structures. For example, in [Reference Sankaran, Adsul and Chakraborty24] the authors for every
 $k\in \mathbb N$
derive a preservation theorem for
$k\in \mathbb N$
derive a preservation theorem for
 $\Sigma _2$
-sentences of the form
$\Sigma _2$
-sentences of the form
 $\exists x_1\ldots \exists x_k\,\mu $
with universal
$\exists x_1\ldots \exists x_k\,\mu $
with universal
 $\mu $
. For
$\mu $
. For
 $k= 0$
it coincides with the Łoś–Tarski Theorem; see Remark 3.5 for the precise statement. The paper [Reference Lopez18] contains a further extension of the Łoś–Tarski Theorem. In [Reference Dawar and Sankaran6] the authors show that for every
$k= 0$
it coincides with the Łoś–Tarski Theorem; see Remark 3.5 for the precise statement. The paper [Reference Lopez18] contains a further extension of the Łoś–Tarski Theorem. In [Reference Dawar and Sankaran6] the authors show that for every
 $n\ge 1$
there is a
$n\ge 1$
there is a
 $\Pi _{2n+ 1}$
-sentence whose class of finite models is closed under induced substructures and that is not equivalent to a
$\Pi _{2n+ 1}$
-sentence whose class of finite models is closed under induced substructures and that is not equivalent to a
 $\Sigma _{2n+ 1}$
-sentence in the finite.
$\Sigma _{2n+ 1}$
-sentence in the finite.
Most classical preservation theorems fail in the finite (see [Reference Rossman21] for an exception). The question whether a preservation theorem fails for finite graphs is specially relevant for the Łoś–Tarski Theorem due to its connection to forbidden induced subgraphs.
Organization of this paper
In Section 2 we fix some notation and recall or derive some results about universal sentences we need in this paper. In Section 3 we include a proof of Tait’s result (essentially as done in [Reference Alechina and Gurevich1]). Moreover, we prove a technical result (Proposition 3.11) that is an important tool in the proof of Gurevich’s Theorem. We introduce the concept of strongly existential interpretation in Section 4 and show that the results of the preceding section remain true under such interpretations. We present an appropriate strongly existential interpretation for graphs (in Section 5). Hence, we get the results of Section 3 for graphs. In Section 6 we first derive Gurevich’s Theorem and apply our interpretations to get the corresponding results for graphs. Finally, in Section 7, we prove that various problems related to our results are undecidable.
This paper is the full version of our conference paper [Reference Chen and Flum4].
2 Preliminaries
We denote by
![]() $\mathbb N$
the set of natural numbers greater or equal to 0. For
$\mathbb N$
the set of natural numbers greater or equal to 0. For
![]() $n\in \mathbb N$
let
$n\in \mathbb N$
let
![]() $[n]:= \{1, 2, \ldots , n\}$
.
$[n]:= \{1, 2, \ldots , n\}$
.
2.1 First-order logic FO
A vocabulary
![]() $\tau $
is a finite set of relation symbols. Each relation symbol has an arity. A structure
$\tau $
is a finite set of relation symbols. Each relation symbol has an arity. A structure
![]() $\mathcal A$
of vocabulary
$\mathcal A$
of vocabulary
![]() $\tau $
, or
$\tau $
, or
![]() $\tau $
-structure, consists of a (finite or infinite) nonempty set A, called the universe of
$\tau $
-structure, consists of a (finite or infinite) nonempty set A, called the universe of
![]() $\mathcal A$
, and of an interpretation
$\mathcal A$
, and of an interpretation
![]() $R^{\mathcal A}\subseteq A^r$
of each r-ary relation symbol
$R^{\mathcal A}\subseteq A^r$
of each r-ary relation symbol
![]() $R\in \tau $
. If
$R\in \tau $
. If
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal B$
are
$\mathcal B$
are
![]() $\tau $
-structures, then
$\tau $
-structures, then
![]() $\mathcal A$
is a substructure of
$\mathcal A$
is a substructure of
![]() $\mathcal B$
, denoted by
$\mathcal B$
, denoted by
![]() $\mathcal A\subseteq \mathcal B$
, if
$\mathcal A\subseteq \mathcal B$
, if
![]() $A\subseteq B$
and
$A\subseteq B$
and
![]() $R^{\mathcal A}\subseteq R^{\mathcal B}$
, and
$R^{\mathcal A}\subseteq R^{\mathcal B}$
, and
![]() $\mathcal A$
is an induced substructure of
$\mathcal A$
is an induced substructure of
![]() $\mathcal B$
, denoted by
$\mathcal B$
, denoted by
![]() $\mathcal A\subseteq _{\text {ind}} \mathcal B$
, if
$\mathcal A\subseteq _{\text {ind}} \mathcal B$
, if
![]() $A\subseteq B$
and
$A\subseteq B$
and
![]() $R^{\mathcal A}= R^{\mathcal B}\cap A^r$
, where r is the arity of R. A substructure
$R^{\mathcal A}= R^{\mathcal B}\cap A^r$
, where r is the arity of R. A substructure
![]() $\mathcal A$
of
$\mathcal A$
of
![]() $\mathcal B$
is proper if
$\mathcal B$
is proper if
![]() $\mathcal A \ne \mathcal B $
. By
$\mathcal A \ne \mathcal B $
. By ![]()
![]() we denote the class of all (of all finite)
we denote the class of all (of all finite)
![]() $\tau $
-structures.
$\tau $
-structures.
If we speak of a class of structures, we assume that it is closed under isomorphism. On the other hand, note that every nonempty set of structures does not have this closure property.
Formulas
![]() $\varphi $
of first-order logic FO of vocabulary
$\varphi $
of first-order logic FO of vocabulary
![]() $\tau $
are built up from atomic formulas
$\tau $
are built up from atomic formulas
![]() $x_1= x_2$
and
$x_1= x_2$
and
![]() $Rx_1 \ldots x_r$
(where
$Rx_1 \ldots x_r$
(where
![]() $R\in \tau $
is of arity r and
$R\in \tau $
is of arity r and
![]() $x_1, x_2, \ldots , x_r$
are variables) using the boolean connectives
$x_1, x_2, \ldots , x_r$
are variables) using the boolean connectives
![]() $\neg $
,
$\neg $
,
![]() $\wedge $
, and
$\wedge $
, and
![]() $\vee $
and the universal
$\vee $
and the universal
![]() $\forall $
and existential
$\forall $
and existential
![]() $\exists $
quantifiers. A relation symbol R is positive (negative) in
$\exists $
quantifiers. A relation symbol R is positive (negative) in
![]() $\varphi $
if all atomic subformulas
$\varphi $
if all atomic subformulas
![]() $R\ldots $
in
$R\ldots $
in
![]() $\varphi $
appear in the scope of an even (odd) number of negation symbols. By the notation
$\varphi $
appear in the scope of an even (odd) number of negation symbols. By the notation
![]() $\varphi (\bar x)$
with
$\varphi (\bar x)$
with
![]() $\bar x= x_1, \ldots , x_e$
we indicate that the variables free in
$\bar x= x_1, \ldots , x_e$
we indicate that the variables free in
![]() $\varphi $
are among
$\varphi $
are among
![]() $x_1, \ldots , x_e$
. If
$x_1, \ldots , x_e$
. If
![]() $\mathcal A$
is a
$\mathcal A$
is a
![]() $\tau $
-structure and
$\tau $
-structure and
![]() $a_1, \ldots , a_e\in A$
, then
$a_1, \ldots , a_e\in A$
, then
![]() $\mathcal A\models \varphi (a_1, \ldots , a_e)$
means that
$\mathcal A\models \varphi (a_1, \ldots , a_e)$
means that
![]() $\varphi (\bar x)$
holds in
$\varphi (\bar x)$
holds in
![]() $\mathcal A$
if
$\mathcal A$
if
![]() $x_i$
is interpreted by
$x_i$
is interpreted by
![]() $a_i$
for
$a_i$
for
![]() $i\in [e]$
.
$i\in [e]$
.
A sentence is a formula without free variables. For a sentence
![]() $\varphi $
we denote by
$\varphi $
we denote by ![]() the class of models of
the class of models of
![]() $\varphi $
and
$\varphi $
and ![]() is its subclass consisting of the finite models of
is its subclass consisting of the finite models of
![]() $\varphi $
. Sentences
$\varphi $
. Sentences
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are equivalent if
$\psi $
are equivalent if ![]() and finitely equivalent if
and finitely equivalent if ![]() .
.
2.2 Graphs
Let
![]() $\tau _E:= \{E\}$
with binary E. For all
$\tau _E:= \{E\}$
with binary E. For all
![]() $\tau _E$
-structures we use the notation
$\tau _E$
-structures we use the notation
![]() $G= (V(G), E(G))$
common in graph theory. Here
$G= (V(G), E(G))$
common in graph theory. Here
![]() $V(G)$
, the universe of G, is the set of vertices, and
$V(G)$
, the universe of G, is the set of vertices, and
![]() $E(G)$
, the interpretation of the relation symbol E, is the set of edges. The
$E(G)$
, the interpretation of the relation symbol E, is the set of edges. The
![]() $\tau _E$
-structure
$\tau _E$
-structure
![]() $G = (V(G), E(G))$
is a directed graph if
$G = (V(G), E(G))$
is a directed graph if
![]() $E(G)$
does not contain loops, i.e.,
$E(G)$
does not contain loops, i.e.,
![]() $(v,v)\notin E(G)$
for all
$(v,v)\notin E(G)$
for all
![]() $v\in V(G)$
. If moreover
$v\in V(G)$
. If moreover
![]() $(u,v)\in E(G)$
implies
$(u,v)\in E(G)$
implies
![]() $(v,u)\in E(G)$
for all pairs
$(v,u)\in E(G)$
for all pairs
![]() $(u,v)$
, then G is an (undirected) graph. We denote by
$(u,v)$
, then G is an (undirected) graph. We denote by ![]() and
and ![]() the class of graphs and the class of finite graphs, respectively. Furthermore, for an
the class of graphs and the class of finite graphs, respectively. Furthermore, for an
![]() ${\text {FO}}[\tau _E]$
-sentence
${\text {FO}}[\tau _E]$
-sentence
![]() $\varphi $
by
$\varphi $
by ![]() and
and ![]() we denote the class of graphs (and the class of finite graphs) that are models of
we denote the class of graphs (and the class of finite graphs) that are models of
![]() $\varphi $
.
$\varphi $
.
2.3 Universal sentences and forbidden induced substructures
An FO-formula is universal if it is built up from atomic and negated atomic formulas by means of the connectives
![]() $\wedge $
and
$\wedge $
and
![]() $\vee $
and the universal quantifier
$\vee $
and the universal quantifier
![]() $\forall $
. Often we say that a formula containing, for example, the connective
$\forall $
. Often we say that a formula containing, for example, the connective
![]() $\to $
is universal if by replacing
$\to $
is universal if by replacing
![]() $\varphi \to \psi $
by
$\varphi \to \psi $
by
![]() $\neg \varphi \vee \psi $
(and “simple manipulations”) we get an equivalent universal formula. Every universal sentence
$\neg \varphi \vee \psi $
(and “simple manipulations”) we get an equivalent universal formula. Every universal sentence
![]() $\mu $
is equivalent to a sentence
$\mu $
is equivalent to a sentence
![]() $\mu '$
of the form
$\mu '$
of the form
![]() $\forall x_1\ldots \forall x_k\, \mu ^{\prime }_0$
for some
$\forall x_1\ldots \forall x_k\, \mu ^{\prime }_0$
for some
![]() $k\ge 1$
and some quantifier-free
$k\ge 1$
and some quantifier-free
![]() $\mu ^{\prime }_0$
; moreover the length
$\mu ^{\prime }_0$
; moreover the length
![]() $|\mu '|$
of
$|\mu '|$
of
![]() $\mu '$
is at most
$\mu '$
is at most
![]() $|\mu |$
. If in the definition of universal formula we replace the universal quantifier by the existential one, we get the definition of an existential formula.
$|\mu |$
. If in the definition of universal formula we replace the universal quantifier by the existential one, we get the definition of an existential formula.
One easily verifies that the class of models of a set of universal sentence is closed under induced substructures. As already mentioned in the Introduction for classes of graphs, Łoś [Reference Łoś19] and Tarski [Reference Tarski26] proved the following theorem:
Theorem 2.1 (Łoś–Tarski Theorem).
Let
![]() $\tau $
be a vocabulary and
$\tau $
be a vocabulary and
![]() $\varphi $
an
$\varphi $
an
![]() ${\mathrm{FO}}[\tau ]$
-sentence. Then
${\mathrm{FO}}[\tau ]$
-sentence. Then ![]() is closed under induced substructures if and only if
is closed under induced substructures if and only if
![]() $\varphi $
is equivalent to a universal sentence.
$\varphi $
is equivalent to a universal sentence.
We first recall the relationship between the axiomatizability of a class of structures by a universal sentence and its definability by a finite set of forbidden finite induced substructures. We fix a vocabulary
![]() $\tau $
. Let
$\tau $
. Let
![]() $\mathscr {F}$
be a set of
$\mathscr {F}$
be a set of
![]() $\tau $
-structures and denote by
$\tau $
-structures and denote by ![]() and
and ![]() the class of structures (of finite structures) that do not contain an induced substructure isomorphic to a structure in
the class of structures (of finite structures) that do not contain an induced substructure isomorphic to a structure in
![]() $\mathscr {F}$
. Clearly for sets
$\mathscr {F}$
. Clearly for sets
![]() $\mathscr {F}$
and
$\mathscr {F}$
and
![]() $\mathscr {F}'$
of
$\mathscr {F}'$
of
![]() $\tau $
-structures we have
$\tau $
-structures we have
Furthermore, for a class
![]() $\mathscr {C}$
of
$\mathscr {C}$
of
![]() $\tau $
-structures closed under induced substructures one easily verifies that
$\tau $
-structures closed under induced substructures one easily verifies that
We have put the corresponding
![]() $\mathscr {F}$
’s in brackets as they are not sets but classes. However for
$\mathscr {F}$
’s in brackets as they are not sets but classes. However for
![]() $\mathscr {C}_{\text {fin}} $
we can repair this by considering only structures whose universe is an initial segment of natural numbers, i.e.,
$\mathscr {C}_{\text {fin}} $
we can repair this by considering only structures whose universe is an initial segment of natural numbers, i.e.,
So we see that for every class of finite structures a denumerable set
![]() $ \mathscr {F}$
suffices. When is a finite
$ \mathscr {F}$
suffices. When is a finite
![]() $ \mathscr {F}$
enough?
$ \mathscr {F}$
enough?
We say that a class
![]() $\mathscr {C}$
of
$\mathscr {C}$
of
![]() $\tau $
-structures (of finite
$\tau $
-structures (of finite
![]() $\tau $
-structures) is definable by a finite set of forbidden induced finite substructures if there is a finite set
$\tau $
-structures) is definable by a finite set of forbidden induced finite substructures if there is a finite set
![]() $\mathscr {F}$
of finite structures such that
$\mathscr {F}$
of finite structures such that ![]()
![]() . Recall that
. Recall that
![]() $\tau _E= \{E\}$
with binary E. The sentences
$\tau _E= \{E\}$
with binary E. The sentences
axiomatize the classes of directed graphs and of graphs, respectively. Define the
![]() $\tau _E$
-structures
$\tau _E$
-structures
![]() $H_0=\big (V(H_0), E(H_0)\big )$
and
$H_0=\big (V(H_0), E(H_0)\big )$
and
![]() $H_1= \big (V(H_1), E({H_1})\big )$
by
$H_1= \big (V(H_1), E({H_1})\big )$
by
Then ![]() and
and ![]() are the class of directed graphs and the class of graphs, respectively, i.e.,
are the class of directed graphs and the class of graphs, respectively, i.e., ![]() and
and ![]() .
.
The following result (Proposition 2.2) generalizes this simple fact and establishes the equivalence between axiomatizability by a universal sentence and definability by a finite set of forbidden induced finite substructures. For an arbitrary vocabulary
![]() $\tau $
, an
$\tau $
, an
![]() ${\text {FO}}[\tau ]$
-sentence
${\text {FO}}[\tau ]$
-sentence
![]() $\varphi $
, and
$\varphi $
, and
![]() $k\ge 1$
let
$k\ge 1$
let
Thus,
![]() $\mathscr {F}_k(\varphi )$
is, up to isomorphism, the class of structures with at most k elements that fail to be a model of
$\mathscr {F}_k(\varphi )$
is, up to isomorphism, the class of structures with at most k elements that fail to be a model of
![]() $\varphi $
. Note that
$\varphi $
. Note that
![]() $\mathscr {F}_1(\varphi _{\text {DG}})= \{H_0\}$
. By (2) and (3) we have
$\mathscr {F}_1(\varphi _{\text {DG}})= \{H_0\}$
. By (2) and (3) we have

Proposition 2.2. For a class
![]() $\mathscr {C}$
of
$\mathscr {C}$
of
![]() $\tau $
-structures and
$\tau $
-structures and
![]() $k\ge 1$
the statements (i) and (ii) are equivalent.
$k\ge 1$
the statements (i) and (ii) are equivalent.
-
(i)
 for some universal sentence
for some universal sentence
 $\mu := \forall x_1\ldots \forall x_k\, \mu _0$
with quantifier-free
$\mu := \forall x_1\ldots \forall x_k\, \mu _0$
with quantifier-free
 $\mu _0$
.
$\mu _0$
. -
(ii)
 for some finite set
for some finite set
 $\mathscr {F}$
of structures, all of at most k elements.
$\mathscr {F}$
of structures, all of at most k elements.
If (i) holds for
![]() $\mu $
, then
$\mu $
, then ![]() .
.
The main step of the proof of (ii)
![]() $\Rightarrow $
(i) is contained in the following lemma.
$\Rightarrow $
(i) is contained in the following lemma.
Lemma 2.3. Let
![]() $\mathcal A$
be a finite
$\mathcal A$
be a finite
![]() $\tau $
-structure and
$\tau $
-structure and
![]() $k:= |A|$
. There is a universal sentence
$k:= |A|$
. There is a universal sentence
![]() $\mu _{\mathcal A\not \to }= \forall x_1\ldots \forall x_k\, \mu _0$
with quantifier-free
$\mu _{\mathcal A\not \to }= \forall x_1\ldots \forall x_k\, \mu _0$
with quantifier-free
![]() $\mu _0$
such that for every
$\mu _0$
such that for every
![]() $\tau $
-structure
$\tau $
-structure
![]() $\mathcal B$
,
$\mathcal B$
,
i.e.,
Proof Let
![]() $A= \{a_1,\ldots , a_k\}$
. Let
$A= \{a_1,\ldots , a_k\}$
. Let
![]() $\delta (x_1,\ldots , x_k)$
be the conjunction of all literals (i.e., atomic or negated atomic formulas)
$\delta (x_1,\ldots , x_k)$
be the conjunction of all literals (i.e., atomic or negated atomic formulas)
![]() $\lambda (x_1, \ldots , x_k)$
such that
$\lambda (x_1, \ldots , x_k)$
such that
![]() $\mathcal A\models \lambda (a_1, \ldots , a_k)$
. Then for every
$\mathcal A\models \lambda (a_1, \ldots , a_k)$
. Then for every
![]() $\tau $
-structure
$\tau $
-structure
![]() $\mathcal B$
and
$\mathcal B$
and
![]() $b_1, \ldots , b_k\in B$
we have
$b_1, \ldots , b_k\in B$
we have
 $$ \begin{align*} \mathcal B\models \delta(b_1, \ldots, b_k) \iff & \text{ the clauses}\ \pi(a_i)= b_i\ \text{for}\ i\in[k]\ \text{define} \\ & \qquad \text{an isomorphism from}\ \mathcal A\ \text{onto}\ [b_1,\ldots, b_k]^{\mathcal B} \end{align*} $$
$$ \begin{align*} \mathcal B\models \delta(b_1, \ldots, b_k) \iff & \text{ the clauses}\ \pi(a_i)= b_i\ \text{for}\ i\in[k]\ \text{define} \\ & \qquad \text{an isomorphism from}\ \mathcal A\ \text{onto}\ [b_1,\ldots, b_k]^{\mathcal B} \end{align*} $$
(recall that
![]() $[b_1,\ldots , b_k]^{\mathcal B}$
denotes the substructure of
$[b_1,\ldots , b_k]^{\mathcal B}$
denotes the substructure of
![]() $\mathcal B$
induced on
$\mathcal B$
induced on
![]() $\{b_1,\ldots , b_k \}$
). Thus we can set
$\{b_1,\ldots , b_k \}$
). Thus we can set
Proof of Proposition 2.2
(ii)
![]() $\Rightarrow $
(i): Let
$\Rightarrow $
(i): Let ![]() for some finite set
for some finite set
![]() $\mathscr {F}$
of structures, all of at most k elements. If
$\mathscr {F}$
of structures, all of at most k elements. If
![]() $\mathscr {F}$
is empty, then
$\mathscr {F}$
is empty, then ![]() . Otherwise, by (ii) and (5),
. Otherwise, by (ii) and (5),

As the conjunction of finitely many universal sentences of the form
![]() $\forall x_1\ldots \forall x_\ell \,\mu _0$
with quantifier-free sentence
$\forall x_1\ldots \forall x_\ell \,\mu _0$
with quantifier-free sentence
![]() $\mu _0$
and with
$\mu _0$
and with
![]() $\ell \le k$
is equivalent to such a sentence, we get the desired result.
$\ell \le k$
is equivalent to such a sentence, we get the desired result.
(i)
![]() $\Rightarrow $
(ii): Let
$\Rightarrow $
(ii): Let ![]() for
for
![]() $\mu $
as in (i). Then
$\mu $
as in (i). Then ![]() is closed under induced substructures and hence,
is closed under induced substructures and hence, ![]() by (4). Now assume that
by (4). Now assume that
![]() $\mathcal A\notin \mathscr {C}$
. Then
$\mathcal A\notin \mathscr {C}$
. Then
![]() $\mathcal A\models \neg \mu $
and hence there are
$\mathcal A\models \neg \mu $
and hence there are
![]() $a_1, \ldots , a_k\in A$
with
$a_1, \ldots , a_k\in A$
with
![]() $\mathcal A\models \neg \mu _0(a_1, \ldots , a_k)$
. For
$\mathcal A\models \neg \mu _0(a_1, \ldots , a_k)$
. For
![]() $\mathcal B:= [a_1, \ldots , a_k]^{\mathcal A}$
we have
$\mathcal B:= [a_1, \ldots , a_k]^{\mathcal A}$
we have
![]() $\mathcal B\models \neg \mu _0(a_1,\ldots , a_k)$
(as
$\mathcal B\models \neg \mu _0(a_1,\ldots , a_k)$
(as
![]() $\mu _0$
is quantifier-free) and thus,
$\mu _0$
is quantifier-free) and thus,
![]() $\mathcal B\models \neg \mu $
. Therefore,
$\mathcal B\models \neg \mu $
. Therefore,
![]() $\mathcal B$
is isomorphic to a structure in
$\mathcal B$
is isomorphic to a structure in
![]() $\mathscr {F}_k(\mu )$
and therefore,
$\mathscr {F}_k(\mu )$
and therefore, ![]() .
.
Corollary 2.4. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\tau $
-sentence and
$\tau $
-sentence and
![]() $k\ge 1$
. Then
$k\ge 1$
. Then

By (2) and (4) we get the following corollaries:
Corollary 2.5. If ![]() for some universal
for some universal
![]() $\mu $
and some
$\mu $
and some
![]() $k\ge 1$
, then
$k\ge 1$
, then ![]() for all
for all
![]() $\ell \ge k$
.
$\ell \ge k$
.
Corollary 2.6. It is decidable whether two universal sentences are equivalent.
Proof Let
![]() $\mu $
and
$\mu $
and
![]() $\mu '$
be universal sentences. W.l.o.g. we may assume that
$\mu '$
be universal sentences. W.l.o.g. we may assume that
![]() $\mu = \forall x_1\ldots \forall x_k\, \mu _0$
and
$\mu = \forall x_1\ldots \forall x_k\, \mu _0$
and
![]() $\mu '= \forall x_1\ldots \forall x_\ell \, \mu ^{\prime }_0$
with
$\mu '= \forall x_1\ldots \forall x_\ell \, \mu ^{\prime }_0$
with
![]() $1\le k\le \ell $
and quantifier-free
$1\le k\le \ell $
and quantifier-free
![]() $\mu _0$
and
$\mu _0$
and
![]() $\mu ^{\prime }_0$
. By Corollaries 2.4 and 2.5, we have
$\mu ^{\prime }_0$
. By Corollaries 2.4 and 2.5, we have
Thus
![]() $\mu $
and
$\mu $
and
![]() $\mu '$
are equivalent if and only if
$\mu '$
are equivalent if and only if
![]() $\mathscr {F}_\ell (\mu )= \mathscr {F}_\ell (\mu ')$
. The right-hand side of this equivalence is clearly decidable.
$\mathscr {F}_\ell (\mu )= \mathscr {F}_\ell (\mu ')$
. The right-hand side of this equivalence is clearly decidable.
The last equivalence of the preceding proof shows the following:
Corollary 2.7. For universal sentences
![]() $\mu $
and
$\mu $
and
![]() $\mu '$
we have
$\mu '$
we have
The next result generalizes this corollary.
Lemma 2.8. Let
![]() $\Phi $
be a set of universal sentences and
$\Phi $
be a set of universal sentences and
![]() $\nu $
a
$\nu $
a
![]() $\Pi _2$
-sentence, i.e., a sentence of the form
$\Pi _2$
-sentence, i.e., a sentence of the form
![]() $\forall x_1\ldots \forall x_k\exists y_1\ldots \exists y_\ell \, \nu _0$
for some
$\forall x_1\ldots \forall x_k\exists y_1\ldots \exists y_\ell \, \nu _0$
for some
![]() $k, \ell \in \mathbb N$
and some quantifier-free
$k, \ell \in \mathbb N$
and some quantifier-free
![]() $\nu _0$
.
$\nu _0$
.
If
![]() $\Phi \models _{\text {fin}} \nu $
, then
$\Phi \models _{\text {fin}} \nu $
, then
![]() $\Phi \models \nu $
and thus there exists a finite
$\Phi \models \nu $
and thus there exists a finite
![]() $\Phi _0\subseteq \Phi $
with
$\Phi _0\subseteq \Phi $
with
![]() $\Phi _0\models _{\text {fin}} \nu $
.
$\Phi _0\models _{\text {fin}} \nu $
.
Proof If not
![]() $\Phi \models \nu $
, then there is a (finite or infinite) structure
$\Phi \models \nu $
, then there is a (finite or infinite) structure
![]() $\mathcal A$
with
$\mathcal A$
with
![]() $\mathcal A\models \Phi \cup \{\neg \nu \}$
. Note that
$\mathcal A\models \Phi \cup \{\neg \nu \}$
. Note that
![]() $\neg \nu $
is equivalent to a sentence of the form
$\neg \nu $
is equivalent to a sentence of the form
with universal
![]() $\mu $
. Choose elements
$\mu $
. Choose elements
![]() $a_1,\ldots , a_k$
with
$a_1,\ldots , a_k$
with
![]() $\mathcal A \models \mu (a_1,\ldots , a_k)$
. Then
$\mathcal A \models \mu (a_1,\ldots , a_k)$
. Then
![]() $\mathcal B:=[a_1,\ldots , a_k]^{\mathcal A}$
is a model of
$\mathcal B:=[a_1,\ldots , a_k]^{\mathcal A}$
is a model of
![]() $\Phi \cup \{\neg \nu \}$
and thus shows
$\Phi \cup \{\neg \nu \}$
and thus shows
![]() $\Phi \not \models _{\text {fin}} \nu $
.
$\Phi \not \models _{\text {fin}} \nu $
.
As the class of all at most countable
![]() $\tau $
-structures shows, not every class closed under induced substructures is the class of models of a set of universal sentences. In contrast, for classes of finite structures, we have the following:
$\tau $
-structures shows, not every class closed under induced substructures is the class of models of a set of universal sentences. In contrast, for classes of finite structures, we have the following:
Lemma 2.9. Let
![]() $\mathscr {C}$
be a class of finite
$\mathscr {C}$
be a class of finite
![]() $\tau $
-structures closed under induced substructures and define the set of universal sentences
$\tau $
-structures closed under induced substructures and define the set of universal sentences
![]() $\Phi _{\mathscr {C}}$
by
$\Phi _{\mathscr {C}}$
by
Then,
Proof The first equality immediately follows from (3) using the closure of
![]() $\mathscr {C}$
under induced substructures and the second equality follows from (5).
$\mathscr {C}$
under induced substructures and the second equality follows from (5).
We use the two preceding results to prove (see [Reference Gurevich17]):
Theorem 2.10 (Compton’s Theorem).
Let
![]() $\mathscr {C}$
be a class of finite
$\mathscr {C}$
be a class of finite
![]() $\tau $
-structures closed under induced substructures and
$\tau $
-structures closed under induced substructures and
![]() $\mathrm{FO}$
-axiomatizable by a
$\mathrm{FO}$
-axiomatizable by a
![]() $\Pi _2$
-sentence
$\Pi _2$
-sentence
![]() $\nu $
. Then
$\nu $
. Then
![]() $\mathscr {C}$
is already axiomatizable by a universal sentence.
$\mathscr {C}$
is already axiomatizable by a universal sentence.
Proof By assumption and the preceding lemma, we have ![]() , in particular,
, in particular,
![]() $\Phi _{\mathscr {C}}\models _{\text {fin}}\nu $
. By Lemma 2.8 there is a finite subset
$\Phi _{\mathscr {C}}\models _{\text {fin}}\nu $
. By Lemma 2.8 there is a finite subset
![]() $\Phi _0$
of
$\Phi _0$
of
![]() $\Phi _{\mathscr {C}}$
such that
$\Phi _{\mathscr {C}}$
such that
![]() $\Phi _0\models _{\text {fin}} \nu $
. Thus,
$\Phi _0\models _{\text {fin}} \nu $
. Thus,
Hence,
![]() $\mathscr {C}$
is axiomatizable by the conjunction of the sentences in
$\mathscr {C}$
is axiomatizable by the conjunction of the sentences in
![]() $\Phi _0$
, a universal sentence.
$\Phi _0$
, a universal sentence.
Recall that our main goal is to find a class of finite graphs with the properties (a)–(c).
-
(a) The class is closed under induced subgraphs.
-
(b) The class is FO-axiomatizable (by a single sentence).
-
(c) The class is not FO-axiomatizable by a universal sentence.
Compton’s Theorem tells us that w.r.t. the quantifier prefix the simplest possible FO-axiomatization of such a class is by a
![]() $\Sigma _2$
-sentence, i.e., by a sentence of the form
$\Sigma _2$
-sentence, i.e., by a sentence of the form
![]() $\exists x_1\ldots \exists x_k\forall y_1\ldots \forall y_\ell \, \rho $
with
$\exists x_1\ldots \exists x_k\forall y_1\ldots \forall y_\ell \, \rho $
with
![]() $k,\ell \in \mathbb N$
and quantifier-free
$k,\ell \in \mathbb N$
and quantifier-free
![]() $\rho $
.
$\rho $
.
The following consequence of Corollary 2.2 will be used in the next section.
Corollary 2.11. Let
![]() $m,k\in \mathbb N$
with
$m,k\in \mathbb N$
with
![]() $m> k$
and let
$m> k$
and let
![]() $\psi _0$
and
$\psi _0$
and
![]() $\psi _1$
be
$\psi _1$
be
![]() ${\mathrm{FO}}[\tau ]$
-sentences. Assume that
${\mathrm{FO}}[\tau ]$
-sentences. Assume that
![]() $\mathcal A$
is a finite model of
$\mathcal A$
is a finite model of
![]() $\psi _0\wedge \psi _1$
with at least m elements and all its induced substructures with at most k elements are models of
$\psi _0\wedge \psi _1$
with at least m elements and all its induced substructures with at most k elements are models of
![]() $\psi _0\wedge \neg \psi _1$
. Then
$\psi _0\wedge \neg \psi _1$
. Then
![]() $\psi _0\wedge \neg \psi _1$
is not finitely equivalent to a universal sentence of the form
$\psi _0\wedge \neg \psi _1$
is not finitely equivalent to a universal sentence of the form
![]() $\mu := \forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
$\mu := \forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
![]() $\mu _0$
.
$\mu _0$
.
Proof As there is no universal sentence
![]() $\mu $
as above for
$\mu $
as above for
![]() $k= 0$
, we can assume
$k= 0$
, we can assume
![]() $k\ge 1$
. For a contradiction assume
$k\ge 1$
. For a contradiction assume ![]() for
for
![]() $\mu := \forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
$\mu := \forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
![]() $\mu _0$
. As
$\mu _0$
. As ![]() by Proposition 2.2, we get (applying the finite equivalence of
by Proposition 2.2, we get (applying the finite equivalence of
![]() $\psi _0\wedge \neg \psi _1$
and
$\psi _0\wedge \neg \psi _1$
and
![]() $\mu $
to obtain the last equality)
$\mu $
to obtain the last equality)
However, by the assumptions the structure
![]() $\mathcal A$
is not contained in
$\mathcal A$
is not contained in ![]() but in the class
but in the class ![]() .
.
Remark 2.12. Let
![]() $\mathscr {C}$
be a class of
$\mathscr {C}$
be a class of
![]() $\tau $
-structures closed under induced substructures. For an
$\tau $
-structures closed under induced substructures. For an
![]() ${\text {FO}}[\tau ]$
-sentence
${\text {FO}}[\tau ]$
-sentence
![]() $\varphi $
we set
$\varphi $
we set ![]() . We say that the Łoś-Tarski Theorem holds for
. We say that the Łoś-Tarski Theorem holds for
![]() $\mathscr {C}$
if for every
$\mathscr {C}$
if for every
![]() ${\text {FO}}[\tau ]$
-sentence
${\text {FO}}[\tau ]$
-sentence
![]() $\varphi $
such that the class
$\varphi $
such that the class ![]() is closed under induced substructures there is a universal sentence
is closed under induced substructures there is a universal sentence
![]() $\mu $
such that
$\mu $
such that ![]() . The following holds:
. The following holds:
Let
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {C}'$
be classes of
$\mathscr {C}'$
be classes of
![]() $\tau $
-structures closed under induced substructures with
$\tau $
-structures closed under induced substructures with
![]() $\mathscr {C}'\subseteq \mathscr {C}$
. Furthermore assume that there is a universal sentence
$\mathscr {C}'\subseteq \mathscr {C}$
. Furthermore assume that there is a universal sentence
![]() $\mu _0$
such that
$\mu _0$
such that ![]() . If the Łoś–Tarski Theorem holds for
. If the Łoś–Tarski Theorem holds for
![]() $\mathscr {C}$
, then it holds for
$\mathscr {C}$
, then it holds for
![]() $\mathscr {C}'$
, too.
$\mathscr {C}'$
, too.
In fact, for every
![]() ${\text {FO}}[\tau ]$
-sentence
${\text {FO}}[\tau ]$
-sentence
![]() $\varphi $
we have
$\varphi $
we have ![]() . Hence, if
. Hence, if ![]() is closed under induced substructures, then by assumption there is a universal
is closed under induced substructures, then by assumption there is a universal
![]() $\mu $
such that
$\mu $
such that ![]() . Therefore,
. Therefore, ![]() .
.
However, as examples mentioned in the Introduction show, in general the failure of the Łoś–Tarski Theorem on a class does not imply its failure on every subclass.
3 Basic ideas underlying the classical results
This section contains a proof of Tait’s Theorem telling us that the analogue of the Łoś–Tarski-Theorem fails if we only consider finite structures. Afterwards we refine the argument to derive a generalization, namely Proposition 3.11, which is a key result to get Gurevich’s Theorem.
Our counterexample to the Łoś–Tarski-Theorem on finite structures essentially is the one given by Alechina and Gurevich in [Reference Alechina and Gurevich1], which in turn simplifies the one given by Gurevich and Shelah in [Reference Gurevich17]. All these counterexamples use the main idea of the original counterexample due to Tait [Reference Tait25].
We consider the vocabulary
![]() $\tau _0:= \{<, U_{\text {min}}, U_{\text {max}}, S\}$
, where
$\tau _0:= \{<, U_{\text {min}}, U_{\text {max}}, S\}$
, where
![]() $<$
and S (the “successor relation”) are binary relation symbols and
$<$
and S (the “successor relation”) are binary relation symbols and
![]() $U_{\text {min}}$
and
$U_{\text {min}}$
and
![]() $U_{\text {max}}$
are unary.
$U_{\text {max}}$
are unary.
Let
![]() $\varphi _0$
be the conjunction of the universal sentences:
$\varphi _0$
be the conjunction of the universal sentences:
-
–
 $\forall x \neg x< x$
,
$\forall x \neg x< x$
,
 $\forall x\forall y (x<y\vee x=y\vee y<x)$
,
$\forall x\forall y (x<y\vee x=y\vee y<x)$
,
 $\forall x\forall y\forall z ((x<y\wedge y<z)\to x<z)$
, i.e., “
$\forall x\forall y\forall z ((x<y\wedge y<z)\to x<z)$
, i.e., “
 $<$
is an ordering.”
$<$
is an ordering.” -
–
 $\forall x\forall y\big (U_{\text {min}}\, x\to (x=y\vee x<y)\big )$
, i.e., “every element in
$\forall x\forall y\big (U_{\text {min}}\, x\to (x=y\vee x<y)\big )$
, i.e., “every element in
 $U_{\text {min}}$
is a minimum w.r.t.
$U_{\text {min}}$
is a minimum w.r.t.
 $<$
.”
$<$
.” -
–
 $\forall x\forall y\big (U_{\text {max}}\, x\to (x=y\vee y<x)\big )$
, i.e., “every element in
$\forall x\forall y\big (U_{\text {max}}\, x\to (x=y\vee y<x)\big )$
, i.e., “every element in
 $U_{\text {max}}$
is a maximum w.r.t.
$U_{\text {max}}$
is a maximum w.r.t.
 $<$
.”
$<$
.” -
–
 $\forall x\forall y(Sxy\to x<y).$
$\forall x\forall y(Sxy\to x<y).$
-
–
 $\forall x\forall y\forall z((x<y\wedge y<z)\to \neg Sxz)$
.
$\forall x\forall y\forall z((x<y\wedge y<z)\to \neg Sxz)$
.
Note that in models of
![]() $\varphi _0$
there is at most one element in
$\varphi _0$
there is at most one element in
![]() $U_{\text {min}}$
, at most one in
$U_{\text {min}}$
, at most one in
![]() $U_{\text {max}}$
, and that S is a subset of the successor relation w.r.t.
$U_{\text {max}}$
, and that S is a subset of the successor relation w.r.t.
![]() $<$
. We call the models of
$<$
. We call the models of
![]() $\varphi _0\ \tau _0$
-orderings.
$\varphi _0\ \tau _0$
-orderings.
For a vocabulary
![]() $\tau $
with
$\tau $
with
![]() $<\in \tau $
and
$<\in \tau $
and
![]() $\tau $
-structures
$\tau $
-structures
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal B$
we write
$\mathcal B$
we write
![]() $\mathcal B\subseteq _< \mathcal A$
and say that
$\mathcal B\subseteq _< \mathcal A$
and say that
![]() $\mathcal B$
is a
$\mathcal B$
is a
![]() $<$
-substructure of
$<$
-substructure of
![]() $\mathcal A$
if
$\mathcal A$
if
![]() $\mathcal B$
is a substructure of
$\mathcal B$
is a substructure of
![]() $\mathcal A$
with
$\mathcal A$
with
![]() $<^{\mathcal B}= <^{\mathcal A}\cap \, (B\times B)$
.
$<^{\mathcal B}= <^{\mathcal A}\cap \, (B\times B)$
.
We remark that the relation symbols
![]() $U_{\text {min}}, \ U_{\text {max}}$
, and S are negative in
$U_{\text {min}}, \ U_{\text {max}}$
, and S are negative in
![]() $\varphi _0$
. Therefore we have the following:
$\varphi _0$
. Therefore we have the following:
Lemma 3.1. Let
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal B$
be
$\mathcal B$
be
![]() $\tau _0$
-structures with
$\tau _0$
-structures with
![]() $\mathcal B\subseteq _< \mathcal A$
. If
$\mathcal B\subseteq _< \mathcal A$
. If
![]() $\mathcal A\models \varphi _0$
, then
$\mathcal A\models \varphi _0$
, then
![]() $\mathcal B\models \varphi _0$
.
$\mathcal B\models \varphi _0$
.
Let
We call models of
![]() $\varphi _0\wedge \varphi _1$
complete
$\varphi _0\wedge \varphi _1$
complete
![]() $\tau _0$
-orderings. Clearly, for every
$\tau _0$
-orderings. Clearly, for every
![]() $k\ge 1$
there is a unique, up to isomorphism, complete
$k\ge 1$
there is a unique, up to isomorphism, complete
![]() $\tau _0$
-ordering with exactly k elements. The next lemma shows that all its proper
$\tau _0$
-ordering with exactly k elements. The next lemma shows that all its proper
![]() $<$
-substructures are models of
$<$
-substructures are models of
![]() $\varphi _0\wedge \neg \varphi _1$
.
$\varphi _0\wedge \neg \varphi _1$
.
Lemma 3.2. Let
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal B$
be
$\mathcal B$
be
![]() $\tau _0$
-structures. Assume that
$\tau _0$
-structures. Assume that
![]() $\mathcal A\models \varphi _0$
and
$\mathcal A\models \varphi _0$
and
![]() $\mathcal B$
is a finite
$\mathcal B$
is a finite
![]() $<$
-substructure of
$<$
-substructure of
![]() $\mathcal A$
that is a model of
$\mathcal A$
that is a model of
![]() $\varphi _1$
. Then
$\varphi _1$
. Then
![]() $\mathcal B= \mathcal A$
(in particular,
$\mathcal B= \mathcal A$
(in particular,
![]() $\mathcal A\models \varphi _1$
).
$\mathcal A\models \varphi _1$
).
Proof By the previous lemma we know that
![]() $\mathcal B\models \varphi _0$
. Let
$\mathcal B\models \varphi _0$
. Let
![]() $B:= \{b_1, \ldots , b_n\}$
. As
$B:= \{b_1, \ldots , b_n\}$
. As
![]() $<^{\mathcal B}$
is an ordering, we may assume that
$<^{\mathcal B}$
is an ordering, we may assume that
As
![]() $\mathcal B\models (\varphi _0\wedge \varphi _1)$
, we have
$\mathcal B\models (\varphi _0\wedge \varphi _1)$
, we have
![]() $U_{\text {min}}^{\mathcal B} b_1$
,
$U_{\text {min}}^{\mathcal B} b_1$
,
![]() $U_{\text {max}}^{\mathcal B} b_n$
, and
$U_{\text {max}}^{\mathcal B} b_n$
, and
![]() $S^{\mathcal B} b_ib_{i+1}$
for
$S^{\mathcal B} b_ib_{i+1}$
for
![]() $i\in [n-1]$
. As
$i\in [n-1]$
. As
![]() $\mathcal B\subseteq \mathcal A$
, everywhere we can replace the upper index
$\mathcal B\subseteq \mathcal A$
, everywhere we can replace the upper index
![]() $^{\mathcal B}$
by
$^{\mathcal B}$
by
![]() $^{\mathcal A}$
.
$^{\mathcal A}$
.
We show
![]() $A= B$
(then
$A= B$
(then
![]() $\mathcal A= \mathcal B$
follows from
$\mathcal A= \mathcal B$
follows from
![]() $\mathcal A\models \varphi _0$
): Let
$\mathcal A\models \varphi _0$
): Let
![]() $a\in A$
. By
$a\in A$
. By
![]() $\mathcal A\models \varphi _0$
, we have
$\mathcal A\models \varphi _0$
, we have
![]() $b_1\le ^{\mathcal A} a\le ^{\mathcal A} b_n$
. Let
$b_1\le ^{\mathcal A} a\le ^{\mathcal A} b_n$
. Let
![]() $i\in [n]$
be maximal with
$i\in [n]$
be maximal with
![]() $b_i \le ^{\mathcal A} a$
. If
$b_i \le ^{\mathcal A} a$
. If
![]() $i= n$
, then
$i= n$
, then
![]() $b_n= a$
. Otherwise,
$b_n= a$
. Otherwise,
![]() $b_i\le ^{\mathcal A} a<^{\mathcal A} b_{i+1}$
. As
$b_i\le ^{\mathcal A} a<^{\mathcal A} b_{i+1}$
. As
![]() $S^{\mathcal A} b_ib_{i+1}$
, we see that
$S^{\mathcal A} b_ib_{i+1}$
, we see that
![]() $b_i= a$
(by the last conjunct of
$b_i= a$
(by the last conjunct of
![]() $\varphi _0$
).
$\varphi _0$
).
Corollary 3.3. Every finite proper
![]() $<$
-substructure of a model of
$<$
-substructure of a model of
![]() $\varphi _0\wedge \varphi _1$
is a model of
$\varphi _0\wedge \varphi _1$
is a model of
![]() $\varphi _0\wedge \neg \varphi _1$
.
$\varphi _0\wedge \neg \varphi _1$
.
The Łoś–Tarski Theorem does not remain valid when restricted to finite structures. In fact, the class of finite
![]() $\tau _0$
-orderings that are not complete is closed under induced substructures but not axiomatizable by a universal sentence:
$\tau _0$
-orderings that are not complete is closed under induced substructures but not axiomatizable by a universal sentence:
Theorem 3.4 (Tait’s Theorem).
The class ![]() is closed under
is closed under
![]() $<$
-substructures (and hence, closed under induced substructures) but
$<$
-substructures (and hence, closed under induced substructures) but
![]() $\varphi _0\wedge \neg \varphi _1$
is not finitely equivalent to a universal sentence.Footnote
1
$\varphi _0\wedge \neg \varphi _1$
is not finitely equivalent to a universal sentence.Footnote
1
By Compton’s Theorem (Theorem 2.10) the sentence
![]() $\varphi _0\wedge \neg \varphi _1$
is not even equivalent to a
$\varphi _0\wedge \neg \varphi _1$
is not even equivalent to a
![]() $\Pi _2$
-sentence. However, note that
$\Pi _2$
-sentence. However, note that
![]() $\varphi _0\wedge \neg \varphi _1$
is (equivalent to) a
$\varphi _0\wedge \neg \varphi _1$
is (equivalent to) a
![]() $\Sigma _2$
-sentence.
$\Sigma _2$
-sentence.
Proof of Theorem 3.4
![]() is closed under
is closed under
![]() $<$
-substructures: If
$<$
-substructures: If
![]() $\mathcal A\models \varphi _0\wedge \neg \varphi _1$
and
$\mathcal A\models \varphi _0\wedge \neg \varphi _1$
and
![]() $\mathcal B$
is a finite
$\mathcal B$
is a finite
![]() $<$
-substructure of
$<$
-substructure of
![]() $\mathcal A$
, then
$\mathcal A$
, then
![]() $\mathcal B\models \varphi _0$
(by Lemma 3.1). If
$\mathcal B\models \varphi _0$
(by Lemma 3.1). If
![]() $\mathcal B\models \neg \varphi _1$
, we are done. If
$\mathcal B\models \neg \varphi _1$
, we are done. If
![]() $\mathcal B\models \varphi _1$
, then
$\mathcal B\models \varphi _1$
, then
![]() $\mathcal A\models \varphi _1$
by Lemma 3.2, which contradicts our assumption
$\mathcal A\models \varphi _1$
by Lemma 3.2, which contradicts our assumption
![]() $\mathcal A\models \neg \varphi _1$
.
$\mathcal A\models \neg \varphi _1$
.
Let
![]() $k\in \mathbb N$
. It is clear that there is a finite model
$k\in \mathbb N$
. It is clear that there is a finite model
![]() $\mathcal A$
of
$\mathcal A$
of
![]() $\varphi _0\wedge \varphi _1$
with at least
$\varphi _0\wedge \varphi _1$
with at least
![]() $k+1$
elements. By Corollary 3.3 every proper induced substructure of
$k+1$
elements. By Corollary 3.3 every proper induced substructure of
![]() $\mathcal A$
is a model of
$\mathcal A$
is a model of
![]() $\varphi _0\wedge \neg \varphi _1$
. Therefore, by Corollary 2.11, the sentence
$\varphi _0\wedge \neg \varphi _1$
. Therefore, by Corollary 2.11, the sentence
![]() $\varphi _0\wedge \neg \varphi _1$
is not finitely equivalent to a universal sentence of the form
$\varphi _0\wedge \neg \varphi _1$
is not finitely equivalent to a universal sentence of the form
![]() $\forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
$\forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
![]() $\mu _0$
. As k was arbitrary, we get our claim.
$\mu _0$
. As k was arbitrary, we get our claim.
Remark 3.5. As ![]() is closed under induced substructures but
is closed under induced substructures but
![]() $\varphi _0\wedge \neg \varphi _1$
is not finitely equivalent and hence not equivalent to a universal sentence, the class
$\varphi _0\wedge \neg \varphi _1$
is not finitely equivalent and hence not equivalent to a universal sentence, the class ![]() of finite and infinite models of
of finite and infinite models of
![]() $\varphi _0\wedge \neg \varphi _1$
is not closed under induced substructures. Nevertheless, as
$\varphi _0\wedge \neg \varphi _1$
is not closed under induced substructures. Nevertheless, as
![]() $\varphi _0\wedge \neg \varphi _1$
is equivalent to a
$\varphi _0\wedge \neg \varphi _1$
is equivalent to a
![]() $\Sigma _2$
-sentence, a result in [Reference Sankaran, Adsul and Chakraborty24] tells us that this class has a “local Łoś–Tarski property.” More precisely, for
$\Sigma _2$
-sentence, a result in [Reference Sankaran, Adsul and Chakraborty24] tells us that this class has a “local Łoś–Tarski property.” More precisely, for
![]() $k\in \mathbb N$
we say that a class
$k\in \mathbb N$
we say that a class
![]() $\mathscr {C}$
of
$\mathscr {C}$
of
![]() $\tau $
-structures has k-cores if for every
$\tau $
-structures has k-cores if for every
![]() $\mathcal A\in \mathscr {C}$
there is a subset C of A of at most k elements such that every induced substructure
$\mathcal A\in \mathscr {C}$
there is a subset C of A of at most k elements such that every induced substructure
![]() $\mathcal B$
of
$\mathcal B$
of
![]() $\mathcal A$
with
$\mathcal A$
with
![]() $C\subseteq B$
is in the class
$C\subseteq B$
is in the class
![]() $\mathscr {C}$
. Note that
$\mathscr {C}$
. Note that ![]() has 2-cores. In fact, let
has 2-cores. In fact, let
![]() $\mathcal A$
be in this class. If
$\mathcal A$
be in this class. If
![]() $\mathcal A\models \neg \forall x\forall y(x<y \to \exists z Sxz)$
, then set
$\mathcal A\models \neg \forall x\forall y(x<y \to \exists z Sxz)$
, then set
![]() $C= \{a,b \}$
where
$C= \{a,b \}$
where
![]() $a<^{\mathcal A}b$
and for all
$a<^{\mathcal A}b$
and for all
![]() $a'\in A$
not
$a'\in A$
not
![]() $S^{\mathcal A}aa'$
. If
$S^{\mathcal A}aa'$
. If
![]() $\mathcal A\models \forall x\forall y(x<y \to \exists z Sxz)$
, then choose as C the empty set.
$\mathcal A\models \forall x\forall y(x<y \to \exists z Sxz)$
, then choose as C the empty set.
In [Reference Sankaran, Adsul and Chakraborty24] the authors showed: Let
![]() $k\in \mathbb N$
and
$k\in \mathbb N$
and
![]() $\mathscr {C}$
be an FO-axiomatizable class of
$\mathscr {C}$
be an FO-axiomatizable class of
![]() $\tau $
-structures. Then
$\tau $
-structures. Then
![]() $\mathscr {C}$
has k-cores if and only if
$\mathscr {C}$
has k-cores if and only if
![]() $\mathscr {C}$
is axiomatizable by a
$\mathscr {C}$
is axiomatizable by a
![]() $\Sigma _2$
-sentence of the form
$\Sigma _2$
-sentence of the form
![]() $\exists x_1\ldots \exists x_k\,\mu $
with universal
$\exists x_1\ldots \exists x_k\,\mu $
with universal
![]() $\mu $
. Note that for
$\mu $
. Note that for
![]() $k= 0$
we get the Łoś–Tarski Theorem.
$k= 0$
we get the Łoś–Tarski Theorem.
We turn to a refinement of Theorem 3.4 that will be helpful to get Gurevich’s Theorem.
Definition 3.6.
-
(a) Let
 $\tau $
be obtained from the vocabulary
$\tau $
be obtained from the vocabulary
 $\tau _0$
by adding finitely many relation symbols “in pairs,” the standard R together with its complement
$\tau _0$
by adding finitely many relation symbols “in pairs,” the standard R together with its complement
 $R^{{\text {comp}}}$
(intended as the complement of R). The symbols R and
$R^{{\text {comp}}}$
(intended as the complement of R). The symbols R and
 $R^{{\text {comp}}}$
have the same arity and for our purposes we can restrict ourselves to unary or binary relation symbols (even though all results can be generalized to arbitrary arities). We briefly say that
$R^{{\text {comp}}}$
have the same arity and for our purposes we can restrict ourselves to unary or binary relation symbols (even though all results can be generalized to arbitrary arities). We briefly say that
 $\tau $
is obtained from
$\tau $
is obtained from
 $\tau _0$
by adding pairs.
$\tau _0$
by adding pairs. -
(b) Let
 $\tau $
be obtained from
$\tau $
be obtained from
 $\tau _0$
by adding pairs. We say that
$\tau _0$
by adding pairs. We say that
 $\varphi _{0\tau }\in {\text {FO}}[\tau ]$
is an extension of
$\varphi _{0\tau }\in {\text {FO}}[\tau ]$
is an extension of
 $\varphi _0$
(where
$\varphi _0$
(where
 $\varphi _0$
is as above) if it is a universal sentence such that:
$\varphi _0$
is as above) if it is a universal sentence such that:-
(i) the sentence
 $\varphi _0$
is a conjunct of
$\varphi _0$
is a conjunct of
 $\varphi _{0\tau }$
,
$\varphi _{0\tau }$
, -
(ii) the sentence
 $\bigwedge _{R \text { standard}}\forall \bar x(\neg R\bar x\vee \neg R^{{\text {comp}}}\bar x)$
is a conjunct of
$\bigwedge _{R \text { standard}}\forall \bar x(\neg R\bar x\vee \neg R^{{\text {comp}}}\bar x)$
is a conjunct of
 $\varphi _{0\tau }$
,
$\varphi _{0\tau }$
, -
(iii) besides
 $<$
all relation symbols are negative in
$<$
all relation symbols are negative in
 $\varphi _{0\tau }$
(if this is not the case for some new R or
$\varphi _{0\tau }$
(if this is not the case for some new R or
 $R^{{\text {comp}}}$
, the idea is to replace any positive occurrence of R or
$R^{{\text {comp}}}$
, the idea is to replace any positive occurrence of R or
 $R^{{\text {comp}}}$
by
$R^{{\text {comp}}}$
by
 $\neg R^{{\text {comp}}}$
and
$\neg R^{{\text {comp}}}$
and
 $\neg R$
, respectively). For instance, we replace a subformula
$\neg R$
, respectively). For instance, we replace a subformula  $$ \begin{align*} x<y \wedge R xy \ \ \ \text{by} \ \ x<y \wedge \neg R^{{\text{comp}}} xy. \end{align*} $$
$$ \begin{align*} x<y \wedge R xy \ \ \ \text{by} \ \ x<y \wedge \neg R^{{\text{comp}}} xy. \end{align*} $$
-
-
(c) Let
 $\tau $
be obtained from
$\tau $
be obtained from
 $\tau _0$
by adding pairs. Then we set where
$\tau _0$
by adding pairs. Then we set where $$ \begin{align*} \varphi_{1\tau}:= \varphi_1\wedge\bigwedge_{R \text{ standard}} \forall \bar x(R\bar x\vee R^{{\text{comp}}}\bar x), \end{align*} $$
$$ \begin{align*} \varphi_{1\tau}:= \varphi_1\wedge\bigwedge_{R \text{ standard}} \forall \bar x(R\bar x\vee R^{{\text{comp}}}\bar x), \end{align*} $$
 $\varphi _1$
is as above see (6).
$\varphi _1$
is as above see (6).
For a
![]() $\tau $
-structure
$\tau $
-structure
![]() $\mathcal B$
with
$\mathcal B$
with
![]() $\mathcal B\models \varphi _{0\tau }\wedge \varphi _{1\tau }$
we have
$\mathcal B\models \varphi _{0\tau }\wedge \varphi _{1\tau }$
we have
 $$\begin{align*}\mathcal B\models\bigwedge_{R \text{ standard}} \Big(\forall \bar x(\neg R\bar x\vee \neg R^{{\text{comp}}}\bar x) \wedge \forall \bar x(R\bar x\vee R^{{\text{comp}}}\bar x)\Big). \end{align*}$$
$$\begin{align*}\mathcal B\models\bigwedge_{R \text{ standard}} \Big(\forall \bar x(\neg R\bar x\vee \neg R^{{\text{comp}}}\bar x) \wedge \forall \bar x(R\bar x\vee R^{{\text{comp}}}\bar x)\Big). \end{align*}$$
Hence, for standard
![]() $R\in \tau $
of arity r, we have
$R\in \tau $
of arity r, we have
Now we derive the analogues of Lemma 3.1—Theorem 3.4 essentially by the same proofs. In all these results the vocabulary
![]() $\tau $
is obtained from
$\tau $
is obtained from
![]() $\tau _0$
by adding pairs and
$\tau _0$
by adding pairs and
![]() $\varphi _{0\tau }$
is an extension of
$\varphi _{0\tau }$
is an extension of
![]() $\varphi _0$
.
$\varphi _0$
.
Lemma 3.7. If
![]() $\mathcal B\subseteq _< \mathcal A$
and
$\mathcal B\subseteq _< \mathcal A$
and
![]() $\mathcal A\models \varphi _{0\tau }$
, then
$\mathcal A\models \varphi _{0\tau }$
, then
![]() $\mathcal B\models \varphi _{0\tau }$
.
$\mathcal B\models \varphi _{0\tau }$
.
Proof By Definition 3.6, the sentence
![]() $\varphi _{0\tau }$
is universal and all relation symbols distinct from
$\varphi _{0\tau }$
is universal and all relation symbols distinct from
![]() $<$
are negative in
$<$
are negative in
![]() $\varphi _{0\tau }$
.
$\varphi _{0\tau }$
.
Lemma 3.8. Assume that
![]() $\mathcal A\models \varphi _{0\tau }$
and that a finite
$\mathcal A\models \varphi _{0\tau }$
and that a finite
![]() $<$
-substructure
$<$
-substructure
![]() $\mathcal B$
of
$\mathcal B$
of
![]() $\mathcal A$
is a model of
$\mathcal A$
is a model of
![]() $\varphi _{1\tau }$
. Then
$\varphi _{1\tau }$
. Then
![]() $\mathcal B= \mathcal A$
in particular,
$\mathcal B= \mathcal A$
in particular,
![]() $\mathcal A\models \varphi _{1\tau }$
.
$\mathcal A\models \varphi _{1\tau }$
.
Proof Let
![]() $\mathcal A\upharpoonright \tau _0$
and
$\mathcal A\upharpoonright \tau _0$
and
![]() $\mathcal B\upharpoonright \tau _0$
be the
$\mathcal B\upharpoonright \tau _0$
be the
![]() $\tau _0$
-structures obtained from
$\tau _0$
-structures obtained from
![]() $\mathcal A$
and from
$\mathcal A$
and from
![]() $\mathcal B$
by removing all relations in
$\mathcal B$
by removing all relations in
![]() $\tau \setminus \tau _0$
. By Lemma 3.2 we know that
$\tau \setminus \tau _0$
. By Lemma 3.2 we know that
![]() $\mathcal B\upharpoonright \tau _0= \mathcal A\upharpoonright \tau _0$
. Furthermore,
$\mathcal B\upharpoonright \tau _0= \mathcal A\upharpoonright \tau _0$
. Furthermore,
![]() $\mathcal B\models \varphi _{0\tau }$
by the previous lemma; thus,
$\mathcal B\models \varphi _{0\tau }$
by the previous lemma; thus,
![]() $\mathcal B\models \varphi _{0\tau }\wedge \varphi _{1\tau }$
. Hence, by (7),
$\mathcal B\models \varphi _{0\tau }\wedge \varphi _{1\tau }$
. Hence, by (7),
![]() $(R^{{\text {comp}}})^{\mathcal B}$
is the complement of
$(R^{{\text {comp}}})^{\mathcal B}$
is the complement of
![]() $R^{\mathcal B}$
for standard R. Clearly,
$R^{\mathcal B}$
for standard R. Clearly,
![]() $R^{\mathcal B}\subseteq R^{\mathcal A}$
and
$R^{\mathcal B}\subseteq R^{\mathcal A}$
and
![]() $(R^{{\text {comp}}})^{\mathcal B}\subseteq (R^{{\text {comp}}})^{\mathcal A}$
. As
$(R^{{\text {comp}}})^{\mathcal B}\subseteq (R^{{\text {comp}}})^{\mathcal A}$
. As
![]() $A= B$
and
$A= B$
and
![]() $\mathcal A$
is a model of the sentence
$\mathcal A$
is a model of the sentence
![]() $\bigwedge _{R \text { standard}}\forall \bar x(\neg R\bar x\vee \neg R^{{\text {comp}}}\bar x)$
, we get
$\bigwedge _{R \text { standard}}\forall \bar x(\neg R\bar x\vee \neg R^{{\text {comp}}}\bar x)$
, we get
![]() $R^{\mathcal B}= R^{\mathcal A}$
and
$R^{\mathcal B}= R^{\mathcal A}$
and
![]() $(R^{{\text {comp}}})^{\mathcal B}= (R^{{\text {comp}}})^{\mathcal A}$
.
$(R^{{\text {comp}}})^{\mathcal B}= (R^{{\text {comp}}})^{\mathcal A}$
.
Corollary 3.9. Every proper
![]() $<$
-substructure of a finite model of
$<$
-substructure of a finite model of
![]() $\varphi _{0\tau }\wedge \varphi _{1\tau }$
is a model of
$\varphi _{0\tau }\wedge \varphi _{1\tau }$
is a model of
![]() $\varphi _{0\tau }\wedge \neg \varphi _{1\tau }$
.
$\varphi _{0\tau }\wedge \neg \varphi _{1\tau }$
.
By replacing in the proof of Tait’s Theorem the use of Lemma 3.1, Lemma 3.2, and Corollary 3.3 by Lemma 3.7, Lemma 3.8, and Corollary 3.9, respectively, we get the following:
Lemma 3.10. The class ![]() is closed under
is closed under
![]() $<$
-substructures (and hence, closed under induced substructures) but
$<$
-substructures (and hence, closed under induced substructures) but
![]() $\varphi _{0\tau }\wedge \neg \varphi _{1\tau }$
is not finitely equivalent to a universal sentence.
$\varphi _{0\tau }\wedge \neg \varphi _{1\tau }$
is not finitely equivalent to a universal sentence.
Perhaps the reader will ask why we do not introduce for
![]() $<$
the “complement relation symbol”
$<$
the “complement relation symbol”
![]() $<^{\text {comp}}$
and add the corresponding conjuncts to
$<^{\text {comp}}$
and add the corresponding conjuncts to
![]() $\varphi _{0\tau }$
and
$\varphi _{0\tau }$
and
![]() $\varphi _{1\tau }$
(or, to
$\varphi _{1\tau }$
(or, to
![]() $\varphi _0$
and
$\varphi _0$
and
![]() $\varphi _1$
) in order to get a result of the type of Lemma 3.8 (or already of the type of Lemma 3.2) where we can replace “
$\varphi _1$
) in order to get a result of the type of Lemma 3.8 (or already of the type of Lemma 3.2) where we can replace “
![]() $ <$
-substructure” by “substructure.” The reader will realize that corresponding proofs of
$ <$
-substructure” by “substructure.” The reader will realize that corresponding proofs of
![]() $B= A$
break down.
$B= A$
break down.
The next proposition, the core of the proof of Gurevich’s Theorem, provides a uniform way to construct FO-sentences that are only equivalent to universal sentences of large size.
Proposition 3.11. Again let
![]() $\tau $
be obtained from
$\tau $
be obtained from
![]() $\tau _0$
by adding pairs and
$\tau _0$
by adding pairs and
![]() $\varphi _{0\tau }$
be an extension of
$\varphi _{0\tau }$
be an extension of
![]() $\varphi _0$
. Let
$\varphi _0$
. Let
![]() $m\ge 1$
and
$m\ge 1$
and
![]() $\gamma $
be an
$\gamma $
be an
![]() ${\mathrm{FO}}[\tau ]$
-sentence such that
${\mathrm{FO}}[\tau ]$
-sentence such that
For
![]() $ \chi := \varphi _{0\tau }\wedge (\varphi _{1\tau }\to \neg \gamma ) $
the statements (a) and (b) hold.
$ \chi := \varphi _{0\tau }\wedge (\varphi _{1\tau }\to \neg \gamma ) $
the statements (a) and (b) hold.
-
(a) The class
 is closed under
is closed under
 $<$
-substructures.
$<$
-substructures. -
(b) If
 $\mu :=\forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
$\mu :=\forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
 $\mu _0$
is finitely equivalent to
$\mu _0$
is finitely equivalent to
 $\chi $
, then
$\chi $
, then
 $k\ge m$
.
$k\ge m$
.
Proof (a) Let
![]() $\mathcal A\models \chi $
and
$\mathcal A\models \chi $
and
![]() $\mathcal B\subseteq _< \mathcal A$
. Thus,
$\mathcal B\subseteq _< \mathcal A$
. Thus,
![]() $\mathcal B\models \varphi _{0\tau }$
. If
$\mathcal B\models \varphi _{0\tau }$
. If
![]() $\mathcal B\not \models \varphi _{1\tau }$
, we are done. Assume
$\mathcal B\not \models \varphi _{1\tau }$
, we are done. Assume
![]() $\mathcal B \models \varphi _{1\tau }$
. In case B is infinite, by (8) we know that
$\mathcal B \models \varphi _{1\tau }$
. In case B is infinite, by (8) we know that
![]() $\mathcal B$
is a model of
$\mathcal B$
is a model of
![]() $\neg \gamma $
and hence of
$\neg \gamma $
and hence of
![]() $\chi $
. Otherwise, B is finite; then
$\chi $
. Otherwise, B is finite; then
![]() $\mathcal B= \mathcal A$
(by Lemma 3.8) and thus,
$\mathcal B= \mathcal A$
(by Lemma 3.8) and thus,
![]() $\mathcal B\models \chi $
.
$\mathcal B\models \chi $
.
(b) According to (8) there is a finite model
![]() $\mathcal A$
of
$\mathcal A$
of
![]() $\varphi _{0\tau }\wedge \varphi _{1\tau }\wedge \gamma $
, i.e., of
$\varphi _{0\tau }\wedge \varphi _{1\tau }\wedge \gamma $
, i.e., of
![]() $\varphi _{0\tau }\wedge \neg (\varphi _{1\tau }\to \neg \gamma )$
, with at least m elements. By Corollary 3.9 every proper induced substructure of
$\varphi _{0\tau }\wedge \neg (\varphi _{1\tau }\to \neg \gamma )$
, with at least m elements. By Corollary 3.9 every proper induced substructure of
![]() $\mathcal A$
is not a model of
$\mathcal A$
is not a model of
![]() $\varphi _{1\tau }$
and therefore, it is a model of
$\varphi _{1\tau }$
and therefore, it is a model of
![]() $\varphi _{0\tau }\wedge (\varphi _{1\tau }\to \neg \gamma )$
. Hence by Corollary 2.11,
$\varphi _{0\tau }\wedge (\varphi _{1\tau }\to \neg \gamma )$
. Hence by Corollary 2.11,
![]() $\varphi _{0\tau }\wedge (\varphi _{1\tau }\to \neg \gamma )$
is not finitely equivalent to a universal sentence of the form
$\varphi _{0\tau }\wedge (\varphi _{1\tau }\to \neg \gamma )$
is not finitely equivalent to a universal sentence of the form
![]() $\mu :=\forall x_1\ldots \forall x_k\,\mu _0$
with
$\mu :=\forall x_1\ldots \forall x_k\,\mu _0$
with
![]() $k< m$
and quantifier-free
$k< m$
and quantifier-free
![]() $\mu _0$
.
$\mu _0$
.
Remark 3.12. We can strengthen the statement (b) of the preceding proposition to:
If the
![]() $\Pi _2$
-sentence
$\Pi _2$
-sentence
![]() $\nu = \forall x_1\ldots \forall x_k\exists y_1\ldots \exists y_\ell \; \nu _0$
with quantifier-free
$\nu = \forall x_1\ldots \forall x_k\exists y_1\ldots \exists y_\ell \; \nu _0$
with quantifier-free
![]() $\nu _0$
is finitely equivalent to
$\nu _0$
is finitely equivalent to
![]() $\chi $
, then
$\chi $
, then
![]() $k\ge m$
.
$k\ge m$
.
In fact, assume that ![]() with
with
![]() $\nu $
as above. We first show that k cannot be 0. In fact, if
$\nu $
as above. We first show that k cannot be 0. In fact, if
![]() $k= 0$
, then
$k= 0$
, then
![]() $\nu $
is an existential sentence. By assumption there is a finite model
$\nu $
is an existential sentence. By assumption there is a finite model
![]() $\mathcal A$
of
$\mathcal A$
of
![]() $\varphi _{0\tau }\wedge \varphi _{1\tau }\wedge \gamma $
with at least m elements. Obtain the
$\varphi _{0\tau }\wedge \varphi _{1\tau }\wedge \gamma $
with at least m elements. Obtain the
![]() $\tau $
-structure
$\tau $
-structure
![]() $\mathcal B$
from
$\mathcal B$
from
![]() $\mathcal A$
by setting
$\mathcal A$
by setting
![]() $U_{\text {min}}^{\mathcal B}= U_{\text {max}}^{\mathcal B}=\emptyset $
. Clearly, then
$U_{\text {min}}^{\mathcal B}= U_{\text {max}}^{\mathcal B}=\emptyset $
. Clearly, then
![]() $\mathcal B\models \neg \varphi _{1\tau }$
and
$\mathcal B\models \neg \varphi _{1\tau }$
and
![]() $\mathcal B\models \varphi _{0\tau }$
as
$\mathcal B\models \varphi _{0\tau }$
as
![]() $U_{\text {min}}$
and
$U_{\text {min}}$
and
![]() $U_{\text {max}}$
are negative in
$U_{\text {max}}$
are negative in
![]() $\varphi _{0\tau }$
. Hence,
$\varphi _{0\tau }$
. Hence,
![]() $\mathcal B\models \chi $
and thus,
$\mathcal B\models \chi $
and thus,
![]() $\mathcal B\models \nu $
. Let
$\mathcal B\models \nu $
. Let
![]() $\mathcal C$
be a finite extension of
$\mathcal C$
be a finite extension of
![]() $\mathcal B$
(i.e.,
$\mathcal B$
(i.e.,
![]() $\mathcal B$
is an induced substructure of
$\mathcal B$
is an induced substructure of
![]() $\mathcal C$
) with an element c such that
$\mathcal C$
) with an element c such that
![]() $(c,c)\in <^{\mathcal C}$
. Then,
$(c,c)\in <^{\mathcal C}$
. Then,
![]() $\mathcal C\models \nu $
as
$\mathcal C\models \nu $
as
![]() $\nu $
is existential. However,
$\nu $
is existential. However,
![]() $\mathcal C\models \neg \varphi _{0\tau }$
as
$\mathcal C\models \neg \varphi _{0\tau }$
as
![]() $<^{\mathcal C}$
is not an ordering. Thus,
$<^{\mathcal C}$
is not an ordering. Thus,
![]() $\mathcal C\models \neg \chi $
, a contradiction.
$\mathcal C\models \neg \chi $
, a contradiction.
So we know that
![]() $k\ge 1$
and now show that
$k\ge 1$
and now show that ![]() implies
implies
![]() $k\ge m$
. For a contradiction assume
$k\ge m$
. For a contradiction assume
![]() $k< m$
. By (8) there is a finite model
$k< m$
. By (8) there is a finite model
![]() $\mathcal A$
of
$\mathcal A$
of
![]() $\varphi _{0\tau }\wedge \varphi _{1\tau }\wedge \gamma $
with at least m elements. Then
$\varphi _{0\tau }\wedge \varphi _{1\tau }\wedge \gamma $
with at least m elements. Then
![]() $\mathcal A\not \models \nu $
. Hence there are
$\mathcal A\not \models \nu $
. Hence there are
![]() $a_1,\ldots , a_k\in A$
with
$a_1,\ldots , a_k\in A$
with
![]() $\mathcal A\models \neg \exists y_1\ldots \exists y_\ell \, \nu _0(a_1, \ldots , a_k)$
. Then
$\mathcal A\models \neg \exists y_1\ldots \exists y_\ell \, \nu _0(a_1, \ldots , a_k)$
. Then
![]() $\mathcal B\models \neg \exists y_1 \ldots \exists y_\ell \, \nu _0(a_1,\ldots , a_k)$
, where
$\mathcal B\models \neg \exists y_1 \ldots \exists y_\ell \, \nu _0(a_1,\ldots , a_k)$
, where
![]() $\mathcal B:= [a_1, \ldots , a_k]^{\mathcal A}$
is the substructure of
$\mathcal B:= [a_1, \ldots , a_k]^{\mathcal A}$
is the substructure of
![]() $\mathcal A$
induced by
$\mathcal A$
induced by
![]() $a_1, \ldots , a_k$
. Hence,
$a_1, \ldots , a_k$
. Hence,
![]() $\mathcal B\not \models \nu $
and therefore,
$\mathcal B\not \models \nu $
and therefore,
![]() $\mathcal B\not \models \varphi _{0\tau }\wedge \neg \varphi _{1\tau }$
. As
$\mathcal B\not \models \varphi _{0\tau }\wedge \neg \varphi _{1\tau }$
. As
![]() $k< m$
, the structure
$k< m$
, the structure
![]() $\mathcal B$
is a proper induced substructure of
$\mathcal B$
is a proper induced substructure of
![]() $\mathcal A$
. Thus,
$\mathcal A$
. Thus,
![]() $\mathcal B\models \varphi _{0\tau }\wedge \neg \varphi _{1\tau }$
by Corollary 3.9, a contradiction.
$\mathcal B\models \varphi _{0\tau }\wedge \neg \varphi _{1\tau }$
by Corollary 3.9, a contradiction.
4 The general machinery: strongly existential interpretations
We show that appropriate interpretations preserve the validity of Tait’s theorem and of the statement of Proposition 3.11. Later on these interpretations will allow us to get versions of the results for graphs.
Let
![]() $\tau _E:= \{E\}$
with binary E. As already remarked in the Preliminaries for all
$\tau _E:= \{E\}$
with binary E. As already remarked in the Preliminaries for all
![]() $\tau _E$
-structures we use the notation
$\tau _E$
-structures we use the notation
![]() $G= (V(G), E(G))$
common in graph theory.
$G= (V(G), E(G))$
common in graph theory.
Let
![]() $\tau $
be obtained from
$\tau $
be obtained from
![]() $\tau _0$
by adding pairs. Furthermore, let
$\tau _0$
by adding pairs. Furthermore, let
![]() $I:=(\varphi _{\text {uni}}, (\varphi _T)_{T\in \tau })$
be an interpretation of width
$I:=(\varphi _{\text {uni}}, (\varphi _T)_{T\in \tau })$
be an interpretation of width
![]() $2$
(we only need this case) of
$2$
(we only need this case) of
![]() $\tau $
-structures in
$\tau $
-structures in
![]() $\tau _E$
-structures. This means that
$\tau _E$
-structures. This means that
![]() $\varphi _{\text {uni}}$
and the
$\varphi _{\text {uni}}$
and the
![]() $\varphi _T $
’s are
$\varphi _T $
’s are
![]() ${\text {FO}}[\tau _E]$
-formulas with
${\text {FO}}[\tau _E]$
-formulas with
![]() $\varphi _{\text {uni}} =\varphi _{\text {uni}}(x_1, x_2)$
,
$\varphi _{\text {uni}} =\varphi _{\text {uni}}(x_1, x_2)$
,
![]() $\varphi _T= \varphi _T(x_1, x_2)$
for every unary relation symbol
$\varphi _T= \varphi _T(x_1, x_2)$
for every unary relation symbol
![]() $T\in \tau $
, and
$T\in \tau $
, and
![]() ${\varphi _T=\varphi _T(x_1, x_2, y_1, y_2)}$
for every binary relation symbol
${\varphi _T=\varphi _T(x_1, x_2, y_1, y_2)}$
for every binary relation symbol
![]() $T\in \tau $
.
$T\in \tau $
.
Then for every
![]() $\tau _E$
-structure G we set
$\tau _E$
-structure G we set
If
![]() $O_I(G)\ne \emptyset $
, i.e., if
$O_I(G)\ne \emptyset $
, i.e., if
![]() $G\models \exists \bar x\varphi _{\text {uni}}(\bar x)$
, then the interpretation I assigns to G a
$G\models \exists \bar x\varphi _{\text {uni}}(\bar x)$
, then the interpretation I assigns to G a
![]() $\tau $
-structure with universe
$\tau $
-structure with universe
![]() $O_I(G)$
, which we denote by
$O_I(G)$
, which we denote by
![]() $\mathcal O_I(G)$
Footnote
2
, given by:
$\mathcal O_I(G)$
Footnote
2
, given by:
-
–
 $T^{O_I(G)}:= \big \{\bar a\in O_I(G) {\;\big |\;} G \models \varphi _T(\bar a) \big \}$
for unary
$T^{O_I(G)}:= \big \{\bar a\in O_I(G) {\;\big |\;} G \models \varphi _T(\bar a) \big \}$
for unary
 $T\in \tau .$
$T\in \tau .$
-
–
 $T^{O_I(G)}:= \big \{(\bar a,\bar b)\in O_I(G)\times O_I(G) {\;\big |\;} G \models \varphi _T(\bar a, \bar b)\big \}$
for binary
$T^{O_I(G)}:= \big \{(\bar a,\bar b)\in O_I(G)\times O_I(G) {\;\big |\;} G \models \varphi _T(\bar a, \bar b)\big \}$
for binary
 $T\in \tau $
.
$T\in \tau $
.
As the interpretation I is of width
![]() $2$
, we have
$2$
, we have
Recall that for every sentence
![]() $\varphi \in {\text {FO}}[\tau ]$
there is a sentence
$\varphi \in {\text {FO}}[\tau ]$
there is a sentence
![]() $\varphi ^I \in {\text {FO}}[\tau _E]$
such that for all
$\varphi ^I \in {\text {FO}}[\tau _E]$
such that for all
![]() $\tau _E$
-structures G with
$\tau _E$
-structures G with
![]() $G\models \exists \bar x\varphi _{\text {uni}}(\bar x)$
we have
$G\models \exists \bar x\varphi _{\text {uni}}(\bar x)$
we have
For example, for the sentence
![]() $\varphi = \forall x\forall y\, Txy$
we have
$\varphi = \forall x\forall y\, Txy$
we have
Furthermore there is a constant
![]() $c_I\in \mathbb N$
such that for all
$c_I\in \mathbb N$
such that for all
![]() $\varphi \in {\text {FO}}[\tau ]$
,
$\varphi \in {\text {FO}}[\tau ]$
,
From time to time we will make use of the following lemma.
Lemma 4.1. Let
![]() $I:= \big (\varphi _{\text {uni}}, (\varphi _T)_{T\in \tau }\big )$
be an interpretation of
$I:= \big (\varphi _{\text {uni}}, (\varphi _T)_{T\in \tau }\big )$
be an interpretation of
![]() $\tau $
-structures in
$\tau $
-structures in
![]() $\tau _E$
-structures. For
$\tau _E$
-structures. For
![]() $\tau $
-sentences
$\tau $
-sentences
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
,
$\psi _2$
,
and the same implication holds if we restrict to finite structures, i.e.,

If for every finite
![]() $\tau $
-structure
$\tau $
-structure
![]() $\mathcal A$
there is a finite graph G with
$\mathcal A$
there is a finite graph G with
![]() $\mathcal O_I(G)\cong \mathcal A$
, then
$\mathcal O_I(G)\cong \mathcal A$
, then

Proof The implications in (12) and (13) follow immediately from (10). We still have to show the implication from right to left in (14). So let
![]() $\mathcal A$
be a finite
$\mathcal A$
be a finite
![]() $\tau $
-structure. By assumption there is a finite graph G with
$\tau $
-structure. By assumption there is a finite graph G with
![]() $\mathcal O_I(G)\cong \mathcal A$
. As
$\mathcal O_I(G)\cong \mathcal A$
. As
![]() $A\ne \emptyset $
, we have
$A\ne \emptyset $
, we have
![]() $G\models \neg \forall \bar x\neg \varphi _{\text {uni}}(\bar x)$
. By the equality on the right-hand side, thus we know that
$G\models \neg \forall \bar x\neg \varphi _{\text {uni}}(\bar x)$
. By the equality on the right-hand side, thus we know that
![]() $\big (G\models {\psi _1}^I\iff G\models {\psi _2}^I\big )$
. Hence, by (10),
$\big (G\models {\psi _1}^I\iff G\models {\psi _2}^I\big )$
. Hence, by (10), ![]() .
.
Definition 4.2. Let
![]() $\tau $
be obtained from
$\tau $
be obtained from
![]() $\tau _0$
by adding pairs. An interpretation I of
$\tau _0$
by adding pairs. An interpretation I of
![]() $\tau $
-structures in
$\tau $
-structures in
![]() $\tau _E$
-structures is strongly existential if all formulas of I (i.e.,
$\tau _E$
-structures is strongly existential if all formulas of I (i.e.,
![]() $\varphi _T$
for
$\varphi _T$
for
![]() $T\in \tau $
and
$T\in \tau $
and
![]() $\varphi _{\text {uni}}$
) are existential and in addition
$\varphi _{\text {uni}}$
) are existential and in addition
![]() $\varphi _<$
is quantifier-free.
$\varphi _<$
is quantifier-free.
Lemma 4.3. Let
![]() $\tau $
be obtained from
$\tau $
be obtained from
![]() $\tau _0$
by adding pairs and let
$\tau _0$
by adding pairs and let
![]() $\varphi _{0\tau }$
be an extension of
$\varphi _{0\tau }$
be an extension of
![]() $\varphi _0$
. Then for every strongly existential interpretation I the sentence
$\varphi _0$
. Then for every strongly existential interpretation I the sentence
![]() ${\varphi _{0\tau }}^I$
is (equivalent to) a universal sentence.
${\varphi _{0\tau }}^I$
is (equivalent to) a universal sentence.
Proof The claim holds as all relation symbols distinct from
![]() $<$
are negative in
$<$
are negative in
![]() $\varphi _{0\tau }$
. For example, for
$\varphi _{0\tau }$
. For example, for
![]() $\varphi := \forall x\forall y \big (U_{\text {min}}\, x\to (x=y\vee x<y)\big )$
, we have
$\varphi := \forall x\forall y \big (U_{\text {min}}\, x\to (x=y\vee x<y)\big )$
, we have
The following result shows that strongly existential interpretations transform induced subgraphs into
![]() $<$
-substructures; this will be crucial to transfer the results of the preceding section to graphs.
$<$
-substructures; this will be crucial to transfer the results of the preceding section to graphs.
Lemma 4.4. Assume that I is strongly existential. Then for all
![]() $\tau _E$
-structures G and H with
$\tau _E$
-structures G and H with
![]() $H\subseteq _{\text {ind}} G$
and
$H\subseteq _{\text {ind}} G$
and
![]() $O_I(H)\ne \emptyset $
, we have
$O_I(H)\ne \emptyset $
, we have
![]() $\mathcal O_I(H) \subseteq _< \mathcal O_I(G)$
.
$\mathcal O_I(H) \subseteq _< \mathcal O_I(G)$
.
Proof As
![]() $\varphi _{\text {uni}}$
is existential, we have
$\varphi _{\text {uni}}$
is existential, we have
![]() $O_I(H)\subseteq O_I(G)$
. Let
$O_I(H)\subseteq O_I(G)$
. Let
![]() $T\in \tau $
be distinct from
$T\in \tau $
be distinct from
![]() $<$
and
$<$
and
![]() $\bar b\in T^{\mathcal O_I(H)}$
. Then
$\bar b\in T^{\mathcal O_I(H)}$
. Then
![]() $H\models \varphi _T(\bar b)$
. As
$H\models \varphi _T(\bar b)$
. As
![]() $\varphi _T$
is existential,
$\varphi _T$
is existential,
![]() $G\models \varphi _T(\bar b)$
and thus,
$G\models \varphi _T(\bar b)$
and thus,
![]() $\bar b\in T^{\mathcal O_I(G)}$
. Moreover, for
$\bar b\in T^{\mathcal O_I(G)}$
. Moreover, for
![]() $\bar b, \bar b'\in O_I(H)$
we have
$\bar b, \bar b'\in O_I(H)$
we have
 $$ \begin{align*} \bar b<^{\mathcal O_I(H)}\bar b' & \iff H\models \varphi_<(\bar b,\bar b') \\ & \iff G\models \varphi_<(\bar b,\bar b') \qquad \text{(as}\ H\subseteq_{\text{ind}} G\ \text{and}\ \varphi_<\ \text{is quantifier-free)} \\ & \iff \bar b<^{\mathcal O_I(G)}\bar b'. \end{align*} $$
$$ \begin{align*} \bar b<^{\mathcal O_I(H)}\bar b' & \iff H\models \varphi_<(\bar b,\bar b') \\ & \iff G\models \varphi_<(\bar b,\bar b') \qquad \text{(as}\ H\subseteq_{\text{ind}} G\ \text{and}\ \varphi_<\ \text{is quantifier-free)} \\ & \iff \bar b<^{\mathcal O_I(G)}\bar b'. \end{align*} $$
Putting all together we see that
![]() $\mathcal O_I(H)\subseteq _< \mathcal O_I(G)$
.
$\mathcal O_I(H)\subseteq _< \mathcal O_I(G)$
.
Corollary 4.5. Assume I is strongly existential and let
![]() $\psi $
be a
$\psi $
be a
![]() $\tau $
-sentence. If
$\tau $
-sentence. If ![]() (resp.
(resp. ![]() ) is closed under
) is closed under
![]() $<$
-substructures, then
$<$
-substructures, then ![]() (resp.
(resp. ![]() ) is closed under induced substructures.
) is closed under induced substructures.
Proof Let G and H be
![]() $\tau _E$
-structures,
$\tau _E$
-structures,
![]() $H\subseteq _{\text {ind}} G$
, and
$H\subseteq _{\text {ind}} G$
, and
![]() $G\models \forall \bar x\neg \varphi _{\text {uni}}(\bar x)\vee \psi ^I$
. If
$G\models \forall \bar x\neg \varphi _{\text {uni}}(\bar x)\vee \psi ^I$
. If
![]() $H\models \forall \bar x\neg \varphi _{\text {uni}}(\bar x)$
, we are done. Otherwise, also
$H\models \forall \bar x\neg \varphi _{\text {uni}}(\bar x)$
, we are done. Otherwise, also
![]() $G\not \models \forall \bar x\neg \varphi _{\text {uni}}(\bar x)$
and thus,
$G\not \models \forall \bar x\neg \varphi _{\text {uni}}(\bar x)$
and thus,
![]() $G\models \psi ^I$
. Hence,
$G\models \psi ^I$
. Hence,
![]() $\mathcal O_I(G)\models \psi $
and
$\mathcal O_I(G)\models \psi $
and
![]() $\mathcal O_I(H) \subseteq _< \mathcal O_I(G)$
by the previous lemma. Therefore, by assumption,
$\mathcal O_I(H) \subseteq _< \mathcal O_I(G)$
by the previous lemma. Therefore, by assumption,
![]() $\mathcal O_I(H)\models \psi $
and thus,
$\mathcal O_I(H)\models \psi $
and thus,
![]() $H\models \psi ^I$
.
$H\models \psi ^I$
.
We obtain from Lemma 3.8 the corresponding result in our framework.
Lemma 4.6. Let I be strongly existential and let
![]() $\varphi _{0\tau }$
be an extension of
$\varphi _{0\tau }$
be an extension of
![]() $\varphi _0$
. Assume that the
$\varphi _0$
. Assume that the
![]() $\tau _E$
-structure G is a model of
$\tau _E$
-structure G is a model of
![]() ${\varphi _{0\tau }}^I$
and that
${\varphi _{0\tau }}^I$
and that
![]() $H\subseteq _{\text {ind}} G$
with finite
$H\subseteq _{\text {ind}} G$
with finite
![]() $O_I(H)$
, is a model of
$O_I(H)$
, is a model of
![]() ${\varphi _{1\tau }}^I$
. Then
${\varphi _{1\tau }}^I$
. Then
![]() $\mathcal O_I(H)= \mathcal O_I(G)$
and
$\mathcal O_I(H)= \mathcal O_I(G)$
and
![]() $G\models {\varphi _{1\tau }}^I$
.
$G\models {\varphi _{1\tau }}^I$
.
Proof As
![]() $H\models {\varphi _{1\tau }}^I$
, we have
$H\models {\varphi _{1\tau }}^I$
, we have
![]() $H\models (\exists x\, U_{\text {min}}\, x)^I$
holds and thus,
$H\models (\exists x\, U_{\text {min}}\, x)^I$
holds and thus,
![]() $O_I(H)\ne \emptyset $
. Therefore,
$O_I(H)\ne \emptyset $
. Therefore,
![]() $\mathcal O_I(H)\subseteq _< \mathcal O_I(G)$
by Lemma 4.4. By assumption and (10),
$\mathcal O_I(H)\subseteq _< \mathcal O_I(G)$
by Lemma 4.4. By assumption and (10),
![]() $\mathcal O_I(G)\models \varphi _{0\tau }$
and
$\mathcal O_I(G)\models \varphi _{0\tau }$
and
![]() $\mathcal O_I(H)\models \varphi _{1\tau }$
. As
$\mathcal O_I(H)\models \varphi _{1\tau }$
. As
![]() $O_I(H)$
is finite, Lemma 3.8 implies
$O_I(H)$
is finite, Lemma 3.8 implies
![]() $\mathcal O_I(H)= \mathcal O_I(G)$
, and in particular
$\mathcal O_I(H)= \mathcal O_I(G)$
, and in particular
![]() $\mathcal O_I(G)\models \varphi _{1\tau }$
. Hence,
$\mathcal O_I(G)\models \varphi _{1\tau }$
. Hence,
![]() $G\models {\varphi _{1\tau }}^I$
by (10).
$G\models {\varphi _{1\tau }}^I$
by (10).
We now prove for strongly existential interpretations two results, Proposition 4.7 corresponds to Tait’s Theorem (Theorem 3.4) and Proposition 4.8 corresponds to Proposition 3.11 (relevant to Gurevich’s Theorem).
Proposition 4.7. Assume that the interpretation I of
![]() $\tau _0$
-structures in
$\tau _0$
-structures in
![]() $\tau _E$
-structures is strongly existential. Furthermore, assume that for every finite complete
$\tau _E$
-structures is strongly existential. Furthermore, assume that for every finite complete
![]() $\tau _0$
-ordering
$\tau _0$
-ordering
![]() $\mathcal A$
, i.e.,
$\mathcal A$
, i.e.,
![]() $\mathcal A\models \varphi _0\wedge \varphi _1$
, there is a finite graph G with
$\mathcal A\models \varphi _0\wedge \varphi _1$
, there is a finite graph G with
![]() $\mathcal O_I(G)\cong \mathcal A$
. Then for
$\mathcal O_I(G)\cong \mathcal A$
. Then for
the class ![]() is closed under induced subgraphs, but
is closed under induced subgraphs, but
![]() $\varphi $
is not equivalent to a universal sentence in finite graphs.
$\varphi $
is not equivalent to a universal sentence in finite graphs.
Proof By Theorem 3.4, we know that ![]() is closed under
is closed under
![]() $<$
-substructures. Hence,
$<$
-substructures. Hence, ![]() is closed under induced subgraphs by Corollary 4.5.
is closed under induced subgraphs by Corollary 4.5.
Now we show that for every
![]() $k\ge 1$
the sentence
$k\ge 1$
the sentence
![]() $\varphi $
is not equivalent in finite graphs to a sentence of the form
$\varphi $
is not equivalent in finite graphs to a sentence of the form
![]() $\mu = \forall z_1\ldots \forall z_k\,\mu _0$
with quantifier-free
$\mu = \forall z_1\ldots \forall z_k\,\mu _0$
with quantifier-free
![]() $\mu _0$
. Let
$\mu _0$
. Let
![]() $\mathcal A:= \big (A, <^{\mathcal A}, U_{\text {min}}^{\mathcal A}, U_{\text {max}}^{\mathcal A}, S^{\mathcal A}\big )$
be a complete
$\mathcal A:= \big (A, <^{\mathcal A}, U_{\text {min}}^{\mathcal A}, U_{\text {max}}^{\mathcal A}, S^{\mathcal A}\big )$
be a complete
![]() $\tau _0$
-ordering with at least
$\tau _0$
-ordering with at least
![]() $k^2+1$
elements. In particular,
$k^2+1$
elements. In particular,
![]() $\mathcal A\models \varphi _0\wedge \varphi _1$
. By assumption there is a finite graph G such that
$\mathcal A\models \varphi _0\wedge \varphi _1$
. By assumption there is a finite graph G such that
![]() $\mathcal O_I(G)\cong \mathcal A$
. Then
$\mathcal O_I(G)\cong \mathcal A$
. Then
![]() $\mathcal O_I(G)\models \varphi _0\wedge \varphi _1$
, hence,
$\mathcal O_I(G)\models \varphi _0\wedge \varphi _1$
, hence,
![]() $G\models {\varphi _0}^I\wedge {\varphi _1}^I$
. Thus
$G\models {\varphi _0}^I\wedge {\varphi _1}^I$
. Thus
![]() $G\models \neg \varphi $
. As
$G\models \neg \varphi $
. As
![]() $|O_I(G)|= |A|\ge k^2+ 1$
, the graph G must contain more than k vertices by (9).
$|O_I(G)|= |A|\ge k^2+ 1$
, the graph G must contain more than k vertices by (9).
We want to show that every induced subgraph of G with at most k vertices is a model of
![]() $\varphi $
. Then the result follows from Corollary 2.11 for
$\varphi $
. Then the result follows from Corollary 2.11 for ![]() and
and
![]() $\psi _1:=\exists \bar x \varphi _{\text {uni}}(\bar x)\wedge {\varphi _1}^I$
.
$\psi _1:=\exists \bar x \varphi _{\text {uni}}(\bar x)\wedge {\varphi _1}^I$
.
So let H be an induced subgraph of G with at most k vertices. Clearly,
![]() $H\models {\varphi _{0}}^I$
. If
$H\models {\varphi _{0}}^I$
. If
![]() $H\models \forall \bar x \neg \varphi _{\text {uni}}(\bar x)$
or
$H\models \forall \bar x \neg \varphi _{\text {uni}}(\bar x)$
or
![]() $H\models \neg {\varphi _{1}}^I$
, we are done. Otherwise
$H\models \neg {\varphi _{1}}^I$
, we are done. Otherwise
![]() $O_I(H)\ne \emptyset $
and
$O_I(H)\ne \emptyset $
and
![]() $H\models {\varphi _{1}}^I$
. Then, Lemma 4.6 implies
$H\models {\varphi _{1}}^I$
. Then, Lemma 4.6 implies
![]() $O_I(H)=O_I(G)$
. Recall
$O_I(H)=O_I(G)$
. Recall
![]() $|V(H)|\le k$
, so
$|V(H)|\le k$
, so
![]() $O_I(H)$
has at most
$O_I(H)$
has at most
![]() $k^2$
elements by (9), a contradiction as
$k^2$
elements by (9), a contradiction as
![]() $|O_I(G)|\ge k^2+1$
.
$|O_I(G)|\ge k^2+1$
.
Proposition 4.8. Let
![]() $\tau $
be obtained from
$\tau $
be obtained from
![]() $\tau _0$
by adding pairs and let
$\tau _0$
by adding pairs and let
![]() $\varphi _{0\tau }$
be an extension of
$\varphi _{0\tau }$
be an extension of
![]() $\varphi _0$
. Assume that I is a strongly existential interpretation of
$\varphi _0$
. Assume that I is a strongly existential interpretation of
![]() $\tau $
-structures in
$\tau $
-structures in
![]() $\tau _E$
-structures with the property that for every finite
$\tau _E$
-structures with the property that for every finite
![]() $\tau $
-structure
$\tau $
-structure
![]() $\mathcal A$
that is a model of
$\mathcal A$
that is a model of
![]() $\varphi _{0\tau }\wedge \varphi _{1\tau }$
there is a finite graph G with
$\varphi _{0\tau }\wedge \varphi _{1\tau }$
there is a finite graph G with
![]() $\mathcal O_I(G)\cong \mathcal A$
and
$\mathcal O_I(G)\cong \mathcal A$
and
![]() $G\models \psi $
.
$G\models \psi $
.
Let
![]() $m\ge 1$
and
$m\ge 1$
and
![]() $\gamma $
be an
$\gamma $
be an
![]() ${\mathrm{FO}}[\tau ]$
-sentence such that
${\mathrm{FO}}[\tau ]$
-sentence such that
For
the statements (a) and (b) hold.
-
(a) The class
 is closed under induced subgraphs.
is closed under induced subgraphs. -
(b) If
 $\mu := \forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
$\mu := \forall x_1\ldots \forall x_k\,\mu _0$
with quantifier-free
 $\mu _0$
is equivalent in finite graphs to
$\mu _0$
is equivalent in finite graphs to
 $\rho $
, then
$\rho $
, then
 $k^2\ge m$
.
$k^2\ge m$
.
Proof Again (a) follows from Proposition 3.11(a) by Corollary 4.5.
(b) By (15) there is a finite model
![]() $\mathcal A$
of
$\mathcal A$
of
![]() $\varphi _{0\tau }\wedge \varphi _{1\tau }\wedge \gamma $
with at least m elements. By assumption there is a finite graph G with
$\varphi _{0\tau }\wedge \varphi _{1\tau }\wedge \gamma $
with at least m elements. By assumption there is a finite graph G with
![]() $\mathcal O_I(G)\cong \mathcal A$
and
$\mathcal O_I(G)\cong \mathcal A$
and
![]() $G\models \psi $
. Clearly,
$G\models \psi $
. Clearly,
![]() $G\models \neg \forall \bar x\neg \varphi _{\text {uni}}(\bar x)$
and
$G\models \neg \forall \bar x\neg \varphi _{\text {uni}}(\bar x)$
and
![]() $G\models (\varphi _{0\tau }\wedge \varphi _{1\tau }\wedge \gamma )^I$
. Hence,
$G\models (\varphi _{0\tau }\wedge \varphi _{1\tau }\wedge \gamma )^I$
. Hence,
![]() $G\models \neg \rho $
. Assume that
$G\models \neg \rho $
. Assume that
![]() $k^2< m$
. We want to show that every induced subgraph of G with at most k elements is a model of
$k^2< m$
. We want to show that every induced subgraph of G with at most k elements is a model of
![]() $\rho $
. Then the claim (b) follows from Corollary 2.11 (with
$\rho $
. Then the claim (b) follows from Corollary 2.11 (with
![]() $\psi _0:=\forall x\, x=x$
and
$\psi _0:=\forall x\, x=x$
and
![]() $\psi _1:= \neg \rho $
).
$\psi _1:= \neg \rho $
).
So let H be an induced subgraph of G with at most k elements. Clearly,
![]() $H\models {\varphi _{0\tau }}^I$
. If
$H\models {\varphi _{0\tau }}^I$
. If
![]() $H\models \forall \bar x\neg \varphi _{\text {uni}}(\bar x)$
or
$H\models \forall \bar x\neg \varphi _{\text {uni}}(\bar x)$
or
![]() $H\models \neg {\varphi _{1\tau }}^I$
, we are done. Otherwise
$H\models \neg {\varphi _{1\tau }}^I$
, we are done. Otherwise
![]() $O_I(H)\ne \emptyset $
and
$O_I(H)\ne \emptyset $
and
![]() $H\models {\varphi _{1\tau }}^I$
. Then,
$H\models {\varphi _{1\tau }}^I$
. Then,
![]() $O_I(H)= O_I(G)$
by Lemma 4.6. This leads to a contradiction, as
$O_I(H)= O_I(G)$
by Lemma 4.6. This leads to a contradiction, as
![]() $O_I(H)$
has at most
$O_I(H)$
has at most
![]() $k^2$
elements by (10), while
$k^2$
elements by (10), while
![]() $O_I(G)$
has m elements and we assumed
$O_I(G)$
has m elements and we assumed
![]() $k^2< m$
.
$k^2< m$
.
Remark 4.9. (a) The result corresponding to Remark 3.12 is valid for Proposition 4.7 too.
(b) By Compton’s Theorem (Theorem 2.10) the sentence
![]() $\forall \bar x\neg \varphi _{\text {uni}}(\bar x) \vee \big (\varphi _0\wedge \neg \varphi _1\big )^I$
is not equivalent to a
$\forall \bar x\neg \varphi _{\text {uni}}(\bar x) \vee \big (\varphi _0\wedge \neg \varphi _1\big )^I$
is not equivalent to a
![]() $\Pi _2$
-sentence. However,
$\Pi _2$
-sentence. However,
![]() $\forall \bar x\neg \varphi _{\text {uni}}(\bar x) \vee \big (\varphi _0\wedge \neg \varphi _1\big )^I$
itself is equivalent to a
$\forall \bar x\neg \varphi _{\text {uni}}(\bar x) \vee \big (\varphi _0\wedge \neg \varphi _1\big )^I$
itself is equivalent to a
![]() $\Sigma _2$
-sentence. In fact, as all relation symbols besides
$\Sigma _2$
-sentence. In fact, as all relation symbols besides
![]() $<$
are negative in
$<$
are negative in
![]() $\varphi _0$
, the sentence
$\varphi _0$
, the sentence
![]() ${\varphi _0}^I$
is universal. Moreover, as
${\varphi _0}^I$
is universal. Moreover, as
![]() $U_{\text {min}}$
,
$U_{\text {min}}$
,
![]() $U_{\text {max}}$
, and S are positive in
$U_{\text {max}}$
, and S are positive in
![]() $\varphi _1$
, the sentence
$\varphi _1$
, the sentence
![]() ${\varphi _1}^I$
(as
${\varphi _1}^I$
(as
![]() $\varphi _1$
) is equivalent to a
$\varphi _1$
) is equivalent to a
![]() $\Pi _2$
-sentence. Hence
$\Pi _2$
-sentence. Hence
![]() $\forall \bar x\neg \varphi _{\text {uni}}(\bar x) \vee \big (\varphi _0\wedge \neg \varphi _1\big )^I$
is equivalent to a
$\forall \bar x\neg \varphi _{\text {uni}}(\bar x) \vee \big (\varphi _0\wedge \neg \varphi _1\big )^I$
is equivalent to a
![]() $\Sigma _2$
-sentence.
$\Sigma _2$
-sentence.
5 Tait’s Theorem for finite graphs
We present strongly existential interpretations that allow us to get Tait’s Theorem for graphs in this section and Gurevich’s Theorem for graphs in Section 6.
We first introduce a further concept. Let G be a graph and
![]() $a,b\in V(G)$
. For
$a,b\in V(G)$
. For
![]() $r,s\ge 3$
a path from vertex a to vertex b of length r with an s-ear is a path between a and b with a cycle of length s; one vertex of this cycle is adjacent to the vertex adjacent to b on the path; path and cycle have no vertex in common. Figure 1 is a path from a to b of length
$r,s\ge 3$
a path from vertex a to vertex b of length r with an s-ear is a path between a and b with a cycle of length s; one vertex of this cycle is adjacent to the vertex adjacent to b on the path; path and cycle have no vertex in common. Figure 1 is a path from a to b of length
![]() $6$
with a
$6$
with a
![]() $4$
-ear.
$4$
-ear.

Figure 1 A path of length 6 with a
![]() $4$
-ear.
$4$
-ear.
Lemma 5.1. For
![]() $r,s\ge 3$
there are quantifier-free formulas
$r,s\ge 3$
there are quantifier-free formulas
![]() $\varphi _{c,r}(x, \bar z)$
and
$\varphi _{c,r}(x, \bar z)$
and
![]() $\varphi _{pe,r,s}(x, y, \bar z, \bar w)$
such that for all graphs G we have
$\varphi _{pe,r,s}(x, y, \bar z, \bar w)$
such that for all graphs G we have
![]() $:$
$:$
-
(a)
 $G\models \varphi _{c,r}(a, \bar u)\iff \bar u$
is a cycle of length r containing a.
$G\models \varphi _{c,r}(a, \bar u)\iff \bar u$
is a cycle of length r containing a. -
(b)
 $G\models \varphi _{pe,r,s}(a,b,\bar u,\bar v)\iff \bar u$
is path from a to b of length r with the s-ear
$G\models \varphi _{pe,r,s}(a,b,\bar u,\bar v)\iff \bar u$
is path from a to b of length r with the s-ear
 $\bar v$
.
$\bar v$
.
Proof (a) We can take as
![]() $\varphi _{c,r}(x, z_1,\ldots , z_r)$
the formula
$\varphi _{c,r}(x, z_1,\ldots , z_r)$
the formula
(b) We can take as
![]() $\varphi _{pe,r,s}(x, y, z_0,\ldots , z_r, w_1, \ldots , w_s)$
the formula
$\varphi _{pe,r,s}(x, y, z_0,\ldots , z_r, w_1, \ldots , w_s)$
the formula
 $$ \begin{align*} x= z_0 \wedge y=z_r\wedge \bigwedge_{0\le i<r-1}Ez_iz_{i+1} \wedge \bigwedge_{0\le i< j\le r}&\neg z_i= z_j \wedge \bigwedge_{0\le i\le r,\ j\in[s]}\neg z_i=w_j \\ & \wedge\bigvee_{i\in [s]} (\varphi_{c,s}(w_i,w_1,\ldots, w_s) \wedge Ez_{r-1}w_i). \end{align*} $$
$$ \begin{align*} x= z_0 \wedge y=z_r\wedge \bigwedge_{0\le i<r-1}Ez_iz_{i+1} \wedge \bigwedge_{0\le i< j\le r}&\neg z_i= z_j \wedge \bigwedge_{0\le i\le r,\ j\in[s]}\neg z_i=w_j \\ & \wedge\bigvee_{i\in [s]} (\varphi_{c,s}(w_i,w_1,\ldots, w_s) \wedge Ez_{r-1}w_i). \end{align*} $$
To understand better how we obtain the desired interpretation we first assign to every complete
![]() $\tau _0$
-ordering
$\tau _0$
-ordering
![]() $\mathcal A$
, i.e., to every model of
$\mathcal A$
, i.e., to every model of
![]() $\varphi _0\wedge \varphi _1$
, a
$\varphi _0\wedge \varphi _1$
, a
![]() $\tau _E$
-structure
$\tau _E$
-structure
![]() $G:= G(\mathcal A)$
that is a graph.
$G:= G(\mathcal A)$
that is a graph.
In a first step we extend
![]() $\mathcal A$
to a
$\mathcal A$
to a
![]() $\tau ^*_0$
-structure
$\tau ^*_0$
-structure
![]() $\mathcal A^*$
, where
$\mathcal A^*$
, where
![]() $\tau ^*_0:= \tau _0\cup \{B,C, L, F\}$
in the following way. Here
$\tau ^*_0:= \tau _0\cup \{B,C, L, F\}$
in the following way. Here
![]() $B,C$
are unary and
$B,C$
are unary and
![]() $L,F$
are binary relation symbols.
$L,F$
are binary relation symbols.
For every original (or, basic) element a, i.e., for every
![]() $a\in A$
, we introduce a new element
$a\in A$
, we introduce a new element
![]() $a'$
, the companion of a. We set
$a'$
, the companion of a. We set
-
–
 $A^*:= A\cup \{a' \mid a\in A\}$
,
$A^*:= A\cup \{a' \mid a\in A\}$
, -
–
 $B^{\mathcal A^*}:= A$
,
$B^{\mathcal A^*}:= A$
,
 $C^{\mathcal A^*}:= \{a' \mid a\in A\}$
,
$C^{\mathcal A^*}:= \{a' \mid a\in A\}$
, -
–
 $L^{\mathcal A^*}:= \big \{(a,a'){\;\big |\;} a\in A\big \}, \qquad F^{\mathcal A^*}:= \big \{(a',b),(b,a') {\;\big |\;} a,b\in A,\ a<^{\mathcal A} b\big \}$
.
$L^{\mathcal A^*}:= \big \{(a,a'){\;\big |\;} a\in A\big \}, \qquad F^{\mathcal A^*}:= \big \{(a',b),(b,a') {\;\big |\;} a,b\in A,\ a<^{\mathcal A} b\big \}$
.
Note that the relation F is irreflexive and symmetric, i.e.,
![]() $\big (A^*,F^{\mathcal A^*}\big )$
is already a graph, which is illustrated by Figure 2. Observe that F contains the whole information of the ordering
$\big (A^*,F^{\mathcal A^*}\big )$
is already a graph, which is illustrated by Figure 2. Observe that F contains the whole information of the ordering
![]() $<^{\mathcal A}$
up to isomorphism.
$<^{\mathcal A}$
up to isomorphism.

Figure 2 Turning an ordering to the relation F.
We use
![]() $\mathcal A^*$
to define the desired graph
$\mathcal A^*$
to define the desired graph
![]() $G= G(\mathcal A)$
. The vertex set
$G= G(\mathcal A)$
. The vertex set
![]() $V(G)$
contains the elements of
$V(G)$
contains the elements of
![]() $A^*$
and the edge relation
$A^*$
and the edge relation
![]() $E(G)$
contains
$E(G)$
contains
![]() $F^{\mathcal A^*}$
. Furthermore G contains just all the vertices and edges required by the “gadgets” introduced by the following clauses:
$F^{\mathcal A^*}$
. Furthermore G contains just all the vertices and edges required by the “gadgets” introduced by the following clauses:
-
– To
 $a\in U_{\text {min}}^{\mathcal A}$
we add a cycle of length
$a\in U_{\text {min}}^{\mathcal A}$
we add a cycle of length
 $5$
through a, all the other vertices of the cycle are new, i.e., not in
$5$
through a, all the other vertices of the cycle are new, i.e., not in
 $A^*$
.
$A^*$
. -
– To
 $a\in U_{\text {max}}^{\mathcal A}$
we add a cycle of length
$a\in U_{\text {max}}^{\mathcal A}$
we add a cycle of length
 $7$
through a, all the other vertices of the cycle are new.
$7$
through a, all the other vertices of the cycle are new. -
– To
 $a\in B^{\mathcal A^*}$
we add a cycle of length
$a\in B^{\mathcal A^*}$
we add a cycle of length
 $9$
through a, all the other vertices of the cycle are new.
$9$
through a, all the other vertices of the cycle are new. -
– To
 $a\in C^{\mathcal A^*}$
we add a cycle of length
$a\in C^{\mathcal A^*}$
we add a cycle of length
 $11$
through a, all the other vertices of the cycle are new.
$11$
through a, all the other vertices of the cycle are new. -
– To
 $(a,b)\in S^{\mathcal A}$
we add a path from a to b of length
$(a,b)\in S^{\mathcal A}$
we add a path from a to b of length
 $17$
with a
$17$
with a
 $13$
-ear consisting of new vertices (besides a and b).
$13$
-ear consisting of new vertices (besides a and b). -
– To
 $(a,a')\in L^{\mathcal A^*}$
we add a path from a to
$(a,a')\in L^{\mathcal A^*}$
we add a path from a to
 $a'$
of length
$a'$
of length
 $17$
with a
$17$
with a
 $15$
-ear consisting of new vertices (besides a and
$15$
-ear consisting of new vertices (besides a and
 $a'$
).
$a'$
).
Hereby we meant by “add a cycle” or “add a path with an ear” that we only add the edges required by the corresponding formulas in Lemma 5.1.
To ease the discussion, we divide cycles in
![]() $G\ (= G(\mathcal A))$
into four categories.
$G\ (= G(\mathcal A))$
into four categories.
[F-cycle] These are the cycles in
![]() $\big (A^*,F^{\mathcal A^*}\big )$
, i.e., the cycles using only edges of
$\big (A^*,F^{\mathcal A^*}\big )$
, i.e., the cycles using only edges of
![]() $F^{\mathcal A^*}$
.
$F^{\mathcal A^*}$
.
[T-cycle] For every
![]() $T\in \big \{U_{{\text {min}}}, U_{{\text {max}}}, B, C\big \}$
and
$T\in \big \{U_{{\text {min}}}, U_{{\text {max}}}, B, C\big \}$
and
![]() $a\in T^{\mathcal A}$
the cycle introduced for a is a T-cycle.
$a\in T^{\mathcal A}$
the cycle introduced for a is a T-cycle.
[ear-cycle] These are the cycles that are the ears on the gadgets introduced for the pairs of the relations
![]() $S^{\mathcal A^*}$
and
$S^{\mathcal A^*}$
and
![]() $L^{\mathcal A^*}$
.
$L^{\mathcal A^*}$
.
[mixed-cycle] All the other cycles are mixed.
For example, we get a mixed cycle if we start with
![]() $a_2$
,
$a_2$
,
![]() $a^{\prime }_0$
,
$a^{\prime }_0$
,
![]() $a_1$
in Figure 2 and then add the path introduced for
$a_1$
in Figure 2 and then add the path introduced for
![]() $(a_1, a_2)\in S^{\mathcal A}$
(ignoring the ear).
$(a_1, a_2)\in S^{\mathcal A}$
(ignoring the ear).
A number of observations for these types of cycles are in order.
Lemma 5.2.
-
(i) All the F-cycles are of even length.
-
(ii) Every
 $U_{{\text {min}}}$
-,
$U_{{\text {min}}}$
-,
 $U_{{\text {max}}}$
-, B-, and C-cycle is of length
$U_{{\text {max}}}$
-, B-, and C-cycle is of length
 $5$
,
$5$
,
 $7$
,
$7$
,
 $9$
, and
$9$
, and
 $11$
, respectively.
$11$
, respectively. -
(iii) Every ear-cycle is of length
 $13$
or
$13$
or
 $15$
.
$15$
. -
(iv) Every mixed-cycle neither uses new vertices of any T-cycle for
 $T\in \big \{U_{{\text {min}}}, U_{{\text {max}}}, B, C\big \}$
nor any vertex of any ear-cycle.
$T\in \big \{U_{{\text {min}}}, U_{{\text {max}}}, B, C\big \}$
nor any vertex of any ear-cycle. -
(v) Every mixed-cycle has length at least
 $17$
.
$17$
.
Proof (i) follows easily from the fact that
![]() $\big (A^*,F^{\mathcal A^*}\big )$
is a bipartite graph; (ii) and (iii) are trivial. For (iv) assume that a mixed-cycle uses a new vertex b of a T-cycle
$\big (A^*,F^{\mathcal A^*}\big )$
is a bipartite graph; (ii) and (iii) are trivial. For (iv) assume that a mixed-cycle uses a new vertex b of a T-cycle
![]() $\mathcal C$
introduced for some
$\mathcal C$
introduced for some
![]() $a\in T^{\mathcal A^*}$
, where
$a\in T^{\mathcal A^*}$
, where
![]() $T\in \big \{U_{{\text {min}}}, U_{{\text {max}}}, B, C\big \}$
. As
$T\in \big \{U_{{\text {min}}}, U_{{\text {max}}}, B, C\big \}$
. As
![]() $\mathcal C$
is mixed, it must contain a vertex
$\mathcal C$
is mixed, it must contain a vertex
![]() $c\notin T^{\mathcal A^*}$
. To reach b from c the mixed cycle must pass through a and hence must contain one of the two segments of
$c\notin T^{\mathcal A^*}$
. To reach b from c the mixed cycle must pass through a and hence must contain one of the two segments of
![]() $\mathcal C$
between b and a. Therefore, in order for the mixed-cycle to go back from b to c, it must also use the other segment of
$\mathcal C$
between b and a. Therefore, in order for the mixed-cycle to go back from b to c, it must also use the other segment of
![]() $\mathcal C$
between a and b. This means that it must be the T-cycle
$\mathcal C$
between a and b. This means that it must be the T-cycle
![]() $\mathcal C$
itself, instead of a mixed one. A similar argument shows that mixed cycles do not contain vertices of any ear-cycle.
$\mathcal C$
itself, instead of a mixed one. A similar argument shows that mixed cycles do not contain vertices of any ear-cycle.
To prove (v), let
![]() $\mathcal C$
be a mixed-cycle. By (iv),
$\mathcal C$
be a mixed-cycle. By (iv),
![]() $\mathcal C$
must contain all vertices of a (at least one) path introduced for a pair
$\mathcal C$
must contain all vertices of a (at least one) path introduced for a pair
![]() $(a,a')\in L^{\mathcal A*}$
or
$(a,a')\in L^{\mathcal A*}$
or
![]() $(a,b)\in S^{\mathcal A^*}$
(ignoring the ear). As these paths have length
$(a,b)\in S^{\mathcal A^*}$
(ignoring the ear). As these paths have length
![]() $17$
, we get our claim.
$17$
, we get our claim.
We want to recover
![]() $\mathcal A$
(up to isomorphism) from
$\mathcal A$
(up to isomorphism) from
![]() $G(\mathcal A)$
by means of a strongly existential interpretation. Let G be any graph. First we define a
$G(\mathcal A)$
by means of a strongly existential interpretation. Let G be any graph. First we define a
![]() $\tau _0$
-structure
$\tau _0$
-structure
![]() $\mathcal O(G)$
, possibly the “empty structure” (and then we show that
$\mathcal O(G)$
, possibly the “empty structure” (and then we show that
![]() $\mathcal O(G)=\mathcal O_I(G)$
for some strongly existential interpretation I). For the definitions of “cycle” and of “path with ear” see Lemma 5.1.
$\mathcal O(G)=\mathcal O_I(G)$
for some strongly existential interpretation I). For the definitions of “cycle” and of “path with ear” see Lemma 5.1.
-
–
 $O(G):= \big \{(a_1,a_2)\in V(G)\times V(G) {\;\big |\;} a_1\ \text {is a member of a cycle of length}\ 9, a_2\ \text {is a member} \text {of a cycle of length}\ 11, \text {and there is a path from}\ a_1\ \text{to}\ a_2\ \text {of}\\ \text{length}\ 17\ \text {with a}\ 15\text {-ear}\big \}$
$O(G):= \big \{(a_1,a_2)\in V(G)\times V(G) {\;\big |\;} a_1\ \text {is a member of a cycle of length}\ 9, a_2\ \text {is a member} \text {of a cycle of length}\ 11, \text {and there is a path from}\ a_1\ \text{to}\ a_2\ \text {of}\\ \text{length}\ 17\ \text {with a}\ 15\text {-ear}\big \}$
-
–
 $<^{\mathcal O(G)}:= \big \{((a_1,a_2), (b_1,b_2)) \in O(G)\times O(G) {\;\big |\;} \{a_2,b_1\}\in E(G)\big \}$
$<^{\mathcal O(G)}:= \big \{((a_1,a_2), (b_1,b_2)) \in O(G)\times O(G) {\;\big |\;} \{a_2,b_1\}\in E(G)\big \}$
-
–
 $U_{\text {min}}^{\mathcal O(G)}:= \big \{(a_1,a_2)\in O(G){\;\big |\;} a_1\ \text {is a member of a cycle of length}\ 5 \big \}$
$U_{\text {min}}^{\mathcal O(G)}:= \big \{(a_1,a_2)\in O(G){\;\big |\;} a_1\ \text {is a member of a cycle of length}\ 5 \big \}$
-
–
 $U_{\text {max}}^{\mathcal O(G)}:= \big \{(a_1,a_2) \in O(G){\;\big |\;} a_1\ \text {is a member of a cycle of length}\ 7\big \}$
$U_{\text {max}}^{\mathcal O(G)}:= \big \{(a_1,a_2) \in O(G){\;\big |\;} a_1\ \text {is a member of a cycle of length}\ 7\big \}$
-
–
 $S^{\mathcal O(G)}:= \big \{((a_1,a_2),(b_1,b_2))\in O(G)\times O(G) \mid \text {there is a path from}\ a_1\ \text {to}\ b_1 \text {of length}\ 17\ \text {with a}\ 13\text {-ear} \big \}$
.
$S^{\mathcal O(G)}:= \big \{((a_1,a_2),(b_1,b_2))\in O(G)\times O(G) \mid \text {there is a path from}\ a_1\ \text {to}\ b_1 \text {of length}\ 17\ \text {with a}\ 13\text {-ear} \big \}$
.
Lemma 5.3. For every complete
![]() $\tau _0$
-ordering
$\tau _0$
-ordering
![]() $\mathcal A$
we have
$\mathcal A$
we have
![]() $\mathcal O(G(\mathcal A))\cong \mathcal A$
.
$\mathcal O(G(\mathcal A))\cong \mathcal A$
.
Proof Let
![]() $G:= G(\mathcal A)$
and
$G:= G(\mathcal A)$
and
![]() $\mathcal A^+:= \mathcal O(G)$
. We claim that the mapping
$\mathcal A^+:= \mathcal O(G)$
. We claim that the mapping
![]() $h: A\to A^+$
defined by
$h: A\to A^+$
defined by
is an isomorphism from
![]() $\mathcal A$
to
$\mathcal A$
to
![]() $\mathcal A^+$
. To that end, we first prove that
$\mathcal A^+$
. To that end, we first prove that
which implies that h is well defined and a bijection. For every
![]() $a\in A$
it is easy to see that
$a\in A$
it is easy to see that
![]() $(a, a')\in O(G) \ (= A^+)$
. For the converse, let
$(a, a')\in O(G) \ (= A^+)$
. For the converse, let
![]() $(a_1, a_2)\in O(G)$
. In particular,
$(a_1, a_2)\in O(G)$
. In particular,
![]() $a_1$
is a member of a cycle of length
$a_1$
is a member of a cycle of length
![]() $9$
. By Lemma 5.2, this must be a B-cycle that contains some
$9$
. By Lemma 5.2, this must be a B-cycle that contains some
![]() $a\in A$
. Using the same argument,
$a\in A$
. Using the same argument,
![]() $a_2$
is a member of a C-cycle that contains a vertex
$a_2$
is a member of a C-cycle that contains a vertex
![]() $b'$
being the companion of some
$b'$
being the companion of some
![]() $b\in A$
. Furthermore, there is a path from
$b\in A$
. Furthermore, there is a path from
![]() $a_1$
to
$a_1$
to
![]() $a_2$
of length
$a_2$
of length
![]() $17$
with a
$17$
with a
![]() $15$
-ear. The
$15$
-ear. The
![]() $15$
-ear is a cycle of length
$15$
-ear is a cycle of length
![]() $15$
. Again by Lemma 5.2 this cycle is an ear-cycle that belongs to the gadget we introduced for some
$15$
. Again by Lemma 5.2 this cycle is an ear-cycle that belongs to the gadget we introduced for some
![]() $(c,c')\in L^{\mathcal A^*}$
with
$(c,c')\in L^{\mathcal A^*}$
with
![]() $c\in A$
. Then it is easy to see that
$c\in A$
. Then it is easy to see that
![]() $a= c= b$
. This finishes the proof that h is a bijection from A to
$a= c= b$
. This finishes the proof that h is a bijection from A to
![]() $A^+$
.
$A^+$
.
Similarly, we can prove that h preserves all the relations.
We show that we can obtain
![]() $\mathcal O(G)$
from G by a strongly existential FO-interpretation I of width 2. We set
$\mathcal O(G)$
from G by a strongly existential FO-interpretation I of width 2. We set
Here
![]() $\eta (x,x',\bar x,\bar x',\bar z, \bar w)$
is the formula
$\eta (x,x',\bar x,\bar x',\bar z, \bar w)$
is the formula
that expresses “
![]() $\bar x$
is a cycle of length
$\bar x$
is a cycle of length
![]() $9$
containing x,
$9$
containing x,
![]() $\bar x'$
is a cycle of length
$\bar x'$
is a cycle of length
![]() $11$
containing
$11$
containing
![]() $x'$
, and
$x'$
, and
![]() $\bar z$
is a path from x to
$\bar z$
is a path from x to
![]() $x'$
of length
$x'$
of length
![]() $17$
with the
$17$
with the
![]() $15$
-ear
$15$
-ear
![]() $\bar w$
.” Furthermore we define:
$\bar w$
.” Furthermore we define:
-
–
 $\varphi _<(x,x',y,y'):= Ex'y$
,
$\varphi _<(x,x',y,y'):= Ex'y$
, -
–
 $\varphi _{U_{\text {min}}}(x,x'):= \exists \bar z\, \varphi _{c,5}(x,\bar z)$
,
$\varphi _{U_{\text {min}}}(x,x'):= \exists \bar z\, \varphi _{c,5}(x,\bar z)$
, -
–
 $\varphi _{U_{\text {max}}}(x,x'):= \exists \bar z\, \varphi _{c,7}(x,\bar z)$
,
$\varphi _{U_{\text {max}}}(x,x'):= \exists \bar z\, \varphi _{c,7}(x,\bar z)$
, -
–
 $\varphi _S(x,x',y,y'):= \exists \bar z \exists \bar w \varphi _{pe,17,13}(x,y,\bar z,\bar w)$
.
$\varphi _S(x,x',y,y'):= \exists \bar z \exists \bar w \varphi _{pe,17,13}(x,y,\bar z,\bar w)$
.
Then we have the following:
Lemma 5.4.
![]() $I:= (\varphi _{\text {uni}}, \varphi _<, \varphi _{U_{\text {min}}}, \varphi _{U_{\text {max}}}, \varphi _S)$
is a strongly existential interpretation of
$I:= (\varphi _{\text {uni}}, \varphi _<, \varphi _{U_{\text {min}}}, \varphi _{U_{\text {max}}}, \varphi _S)$
is a strongly existential interpretation of
![]() $\tau _0$
-structures in
$\tau _0$
-structures in
![]() $\tau _E$
-structures. For every complete
$\tau _E$
-structures. For every complete
![]() $\tau _0$
-ordering
$\tau _0$
-ordering
![]() $\mathcal A$
we have
$\mathcal A$
we have
![]() $\mathcal O_I(G(\mathcal A))= \mathcal O(G(\mathcal A))$
and hence, by Lemma 5.3,
$\mathcal O_I(G(\mathcal A))= \mathcal O(G(\mathcal A))$
and hence, by Lemma 5.3,
We get from Proposition 4.7:
Theorem 5.5 (Tait’s Theorem for graphs).
There is a
![]() $\tau _E$
-sentence
$\tau _E$
-sentence
![]() $\varphi $
such that
$\varphi $
such that ![]() , the class of finite graphs that are models of
, the class of finite graphs that are models of
![]() $\varphi $
, is closed under induced subgraphs but
$\varphi $
, is closed under induced subgraphs but
![]() $\varphi $
is not equivalent to a universal sentence in finite graphs.
$\varphi $
is not equivalent to a universal sentence in finite graphs.
In this section we presented a strongly existential interpretation of
![]() $\tau _0$
-structures in
$\tau _0$
-structures in
![]() $\tau _E$
-structures (more precisely, in graphs) and applied it to finite complete
$\tau _E$
-structures (more precisely, in graphs) and applied it to finite complete
![]() $\tau _0$
-orderings, i.e., to models of
$\tau _0$
-orderings, i.e., to models of
![]() $\varphi _0\wedge \varphi _1$
. A straightforward generalization of the preceding proofs allows us to show the following result for vocabularies obtained from
$\varphi _0\wedge \varphi _1$
. A straightforward generalization of the preceding proofs allows us to show the following result for vocabularies obtained from
![]() $\tau _0$
by adding pairs. We shall use it in Section 6.
$\tau _0$
by adding pairs. We shall use it in Section 6.
Lemma 5.6. Let
![]() $\tau $
be obtained from
$\tau $
be obtained from
![]() $\tau _0$
by adding pairs. There is a strongly existential interpretation
$\tau _0$
by adding pairs. There is a strongly existential interpretation
![]() $I\ (=I_\tau )$
that for every extension
$I\ (=I_\tau )$
that for every extension
![]() $\varphi _{0\tau }$
of
$\varphi _{0\tau }$
of
![]() $\varphi _0$
assigns to every
$\varphi _0$
assigns to every
![]() $\tau $
-structure
$\tau $
-structure
![]() $\mathcal A$
that is a model of
$\mathcal A$
that is a model of
![]() $\varphi _{0\tau }\wedge \varphi _{1\tau }$
a graph
$\varphi _{0\tau }\wedge \varphi _{1\tau }$
a graph
![]() $G(\mathcal A)$
with
$G(\mathcal A)$
with
![]() $\mathcal O_I(G(\mathcal A))\cong \mathcal A$
. For finite
$\mathcal O_I(G(\mathcal A))\cong \mathcal A$
. For finite
![]() $\mathcal A$
the graph
$\mathcal A$
the graph
![]() $G(\mathcal A)$
is finite.
$G(\mathcal A)$
is finite.
Proof We get the graph
![]() $G(\mathcal A)$
as in the case
$G(\mathcal A)$
as in the case
![]() $\tau := \tau _0$
: For the elements of new unary relations we add cycles such that the lengths of the cycles are odd and distinct for distinct unary relations in
$\tau := \tau _0$
: For the elements of new unary relations we add cycles such that the lengths of the cycles are odd and distinct for distinct unary relations in
![]() $\tau $
. Let c be the maximal length of these cycles. Then we add paths with ears to the tuples of binary relations as above. For distinct binary relations the ears should have distinct length and again this length should be odd and greater than c. On the other hand, the length of added new paths can be the same for all binary relations but should be greater than the length of all the cycles.
$\tau $
. Let c be the maximal length of these cycles. Then we add paths with ears to the tuples of binary relations as above. For distinct binary relations the ears should have distinct length and again this length should be odd and greater than c. On the other hand, the length of added new paths can be the same for all binary relations but should be greater than the length of all the cycles.
Remark 5.7. (a) Let ![]() be the class of finite directed graphs. Then
be the class of finite directed graphs. Then ![]() , the class of finite graphs, is a subclass of
, the class of finite graphs, is a subclass of
![]() $\mathscr {C}$
closed under induced substructures and definable in
$\mathscr {C}$
closed under induced substructures and definable in
![]() $\mathscr {C}$
by the universal sentence
$\mathscr {C}$
by the universal sentence
![]() $\forall x \forall y(Exy\to Eyx)$
. As the Łoś–Tarski Theorem fails for the class of finite graphs, it fails for the class of directed graphs by Remark 2.12.
$\forall x \forall y(Exy\to Eyx)$
. As the Łoś–Tarski Theorem fails for the class of finite graphs, it fails for the class of directed graphs by Remark 2.12.
(b) Let ![]() be the class of finite planar graphs, a subclass of
be the class of finite planar graphs, a subclass of ![]() closed under induced subgraphs. As mentioned in the Introduction, in [Reference Atserias, Dawar and Grohe2] it is shown that the Łoś–Tarski Theorem fails for
closed under induced subgraphs. As mentioned in the Introduction, in [Reference Atserias, Dawar and Grohe2] it is shown that the Łoś–Tarski Theorem fails for ![]() . As
. As ![]() is not axiomatizable in
is not axiomatizable in ![]() by a universal sentence, not even by a first-order sentence, we do not get the failure of the Łoś–Tarski Theorem for the class of finite graphs (i.e., Theorem 5.5) by applying the result of Remark 2.12. We show that
by a universal sentence, not even by a first-order sentence, we do not get the failure of the Łoś–Tarski Theorem for the class of finite graphs (i.e., Theorem 5.5) by applying the result of Remark 2.12. We show that ![]() for a finite set
for a finite set
![]() $\mathscr {F}$
of finite graphs (or, equivalently,
$\mathscr {F}$
of finite graphs (or, equivalently, ![]() for a universal
for a universal
![]() $\mu $
) leads to a contradiction. Let k be the maximum size of the set of vertices of graphs in
$\mu $
) leads to a contradiction. Let k be the maximum size of the set of vertices of graphs in
![]() $\mathscr {F}$
. Let G be the graph obtained from the clique
$\mathscr {F}$
. Let G be the graph obtained from the clique
![]() $K_5$
of five vertices by subdividing each edge
$K_5$
of five vertices by subdividing each edge
![]() $k+1$
times. Clearly,
$k+1$
times. Clearly, ![]() . However, every subgraph of G induced on at most k vertices is planar. Hence,
. However, every subgraph of G induced on at most k vertices is planar. Hence, ![]() .
.
(c) Let
![]() $\tau $
be any vocabulary with at least one at least binary relation T. Then the Łoś–Tarski Theorem fails for the class
$\tau $
be any vocabulary with at least one at least binary relation T. Then the Łoś–Tarski Theorem fails for the class ![]() , the class of all finite
, the class of all finite
![]() $\tau $
-structures. By Remark 2.12 it suffices to show the existence of a universally definable subclass
$\tau $
-structures. By Remark 2.12 it suffices to show the existence of a universally definable subclass
![]() $\mathscr {C}'$
of
$\mathscr {C}'$
of
![]() $\mathscr {C}$
which “essentially is the class of graphs.” We set
$\mathscr {C}$
which “essentially is the class of graphs.” We set
and let
![]() $\mathscr {C}'$
be
$\mathscr {C}'$
be ![]() .
.
If
![]() $\tau $
only contains unary relation symbols, the Łoś–Tarski Theorem holds for
$\tau $
only contains unary relation symbols, the Łoś–Tarski Theorem holds for ![]() . It is easy to see for an
. It is easy to see for an
![]() ${\text {FO}}(\tau )$
-sentence
${\text {FO}}(\tau )$
-sentence
![]() $\varphi $
that the closure under induced substructures of
$\varphi $
that the closure under induced substructures of ![]() implies that of
implies that of ![]() .
.
6 Gurevich’s Theorem
The following discussion will eventually lead to a proof of Gurevich’s Theorem, i.e., Theorem 1.5. Our proof essentially follows Gurevich’s proof in [Reference Gurevich17], but it contains some elements of Rossman’s proof of the same result in [Reference Rossman22].Footnote 3 Afterwards we show that it remains true if we restrict ourselves to graphs.
Our main tool is Proposition 3.11: the goal is to construct a formula
![]() $\gamma $
satisfying (8) and whose size is much smaller than the number m. Basically
$\gamma $
satisfying (8) and whose size is much smaller than the number m. Basically
![]() $\gamma $
will describe a very long computation of a Turing machine on a short input. We fix a universal Turing machine M operating on a one-way infinite tape, the tape alphabet is
$\gamma $
will describe a very long computation of a Turing machine on a short input. We fix a universal Turing machine M operating on a one-way infinite tape, the tape alphabet is
![]() $\{0, 1\}$
, where
$\{0, 1\}$
, where
![]() $0$
is also considered as blank and Q is the set of states of M. The initial state is
$0$
is also considered as blank and Q is the set of states of M. The initial state is
![]() $q_0$
and
$q_0$
and
![]() $q_h$
is the halting state; thus
$q_h$
is the halting state; thus
![]() $q_0, q_h\in Q$
and we assume that
$q_0, q_h\in Q$
and we assume that
![]() $q_0\ne q_h$
. An instruction of M has the form
$q_0\ne q_h$
. An instruction of M has the form
where
![]() $q, p\in Q$
,
$q, p\in Q$
,
![]() $a,b\in \{0, 1\}$
and
$a,b\in \{0, 1\}$
and
![]() $d\in \{-1, 0, 1\}$
. It indicates that if M is in state q and the head of M reads an a, then M changes to state p, the head replaces a by b and moves to the left (if
$d\in \{-1, 0, 1\}$
. It indicates that if M is in state q and the head of M reads an a, then M changes to state p, the head replaces a by b and moves to the left (if
![]() $d= -1$
), stays still (if
$d= -1$
), stays still (if
![]() $d= 0$
), or moves to the right (if
$d= 0$
), or moves to the right (if
![]() $d= 1$
). In order to describe computations of M by FO-formulas we introduce binary predicates
$d= 1$
). In order to describe computations of M by FO-formulas we introduce binary predicates
![]() $H_q(x,t)$
for
$H_q(x,t)$
for
![]() $q\in Q$
to indicate that at time t the machine M is in state q and the head scans cell x, and a binary predicate
$q\in Q$
to indicate that at time t the machine M is in state q and the head scans cell x, and a binary predicate
![]() $C_0(x,t)$
to indicate that the content of cell x at time t is 0.
$C_0(x,t)$
to indicate that the content of cell x at time t is 0.
The vocabulary
![]() $\tau _M$
is obtained from
$\tau _M$
is obtained from
![]() $\tau _0$
by adding pairs (see Definition 3.6(a)),
$\tau _0$
by adding pairs (see Definition 3.6(a)),
Intuitively,
![]() $H_q^{\text {comp}}(x,t)$
says that “at time t the machine is not in state q or the head does not scan cell x;” and
$H_q^{\text {comp}}(x,t)$
says that “at time t the machine is not in state q or the head does not scan cell x;” and
![]() $C_0^{\text {comp}}(x,t)$
says that “at time t the content of cell x is (not 0 and thus is) 1.” Sometimes we write
$C_0^{\text {comp}}(x,t)$
says that “at time t the content of cell x is (not 0 and thus is) 1.” Sometimes we write
![]() $C_1$
instead of
$C_1$
instead of
![]() $C_0^{\text {comp}}$
(e.g., below in
$C_0^{\text {comp}}$
(e.g., below in
![]() $\varphi _2$
if
$\varphi _2$
if
![]() $a= 1$
or
$a= 1$
or
![]() $b= 0$
).
$b= 0$
).
Let
![]() $\varphi _0$
and
$\varphi _0$
and
![]() $\varphi _1$
be the sentences already introduced in Section 3. For
$\varphi _1$
be the sentences already introduced in Section 3. For
![]() $w\in \{0, 1\}^*$
the sentence
$w\in \{0, 1\}^*$
the sentence
![]() $\varphi _{0w}$
will be an extension of
$\varphi _{0w}$
will be an extension of
![]() $\varphi _0$
(compare Definition 3.6(b)). Hence,
$\varphi _0$
(compare Definition 3.6(b)). Hence,
![]() $\varphi _{0w}$
will be a universal sentence and all relations symbols besides
$\varphi _{0w}$
will be a universal sentence and all relations symbols besides
![]() $<$
are negative in
$<$
are negative in
![]() $\varphi _{0w}$
; in particular, it contains as conjuncts
$\varphi _{0w}$
; in particular, it contains as conjuncts
![]() $\varphi _0$
and
$\varphi _0$
and
Finally,
![]() $\varphi _{0w}$
will contain the following sentences
$\varphi _{0w}$
will contain the following sentences
![]() $\varphi _2$
and
$\varphi _2$
and
![]() $\varphi _w$
as conjuncts. The sentence
$\varphi _w$
as conjuncts. The sentence
![]() $\varphi _2$
describes one computation step. It contains for each instruction of M one conjunct. For example, the instruction
$\varphi _2$
describes one computation step. It contains for each instruction of M one conjunct. For example, the instruction
![]() $qapb1$
contributes the conjunct
$qapb1$
contributes the conjunct
 $$ \begin{align*} \forall x \forall x'\forall t \forall t' \forall y \Big(\big(H_{q}&(x,t) \wedge C_a (x,t) \wedge S(x,x')\wedge S(t,t')\big) \\ \to \Big( &(\neg C_{1-b}(x,t') \wedge \neg H^{\text{comp}} _{p}(x',t')) \\ & \wedge (y\ne x'\to \bigwedge_{r\in Q}\neg H_r(y,t')) \\ & \wedge (y\ne x\to((C_0(y,t)\to \neg C^{\text{comp}}_0(y,t')) \wedge (C^{\text{comp}}_0(y,t)\to\neg C_0(y,t'))))\Big)\Big). \end{align*} $$
$$ \begin{align*} \forall x \forall x'\forall t \forall t' \forall y \Big(\big(H_{q}&(x,t) \wedge C_a (x,t) \wedge S(x,x')\wedge S(t,t')\big) \\ \to \Big( &(\neg C_{1-b}(x,t') \wedge \neg H^{\text{comp}} _{p}(x',t')) \\ & \wedge (y\ne x'\to \bigwedge_{r\in Q}\neg H_r(y,t')) \\ & \wedge (y\ne x\to((C_0(y,t)\to \neg C^{\text{comp}}_0(y,t')) \wedge (C^{\text{comp}}_0(y,t)\to\neg C_0(y,t'))))\Big)\Big). \end{align*} $$
For
![]() $w\in \{0, 1\}^*$
the sentence
$w\in \{0, 1\}^*$
the sentence
![]() $\varphi _w$
describes the initial configuration of M with input w (if
$\varphi _w$
describes the initial configuration of M with input w (if
![]() $w= w_1\ldots w_{|w|}$
, the first
$w= w_1\ldots w_{|w|}$
, the first
![]() $|w|$
cells (if present) contain
$|w|$
cells (if present) contain
![]() $w_1, \ldots , w_{|w|}$
, the remaining cells contain
$w_1, \ldots , w_{|w|}$
, the remaining cells contain
![]() $0$
, and the head scans the first cell in the starting state
$0$
, and the head scans the first cell in the starting state
![]() $q_0$
). Taking into account that models of
$q_0$
). Taking into account that models of
![]() $\varphi _0\wedge \varphi _1$
might contain less than
$\varphi _0\wedge \varphi _1$
might contain less than
![]() $|w|$
elements, as
$|w|$
elements, as
![]() $\varphi _w$
we can take the conjunction of
$\varphi _w$
we can take the conjunction of
-
–
 $\forall x_1\ldots \forall x_{|w|}\big ((U_{\text {min}}\, x_1\to \neg C_{1-w_1}(x_1,x_1)) \\[2mm] {\hspace {2.3cm}}\wedge \bigwedge _{i\in [|w|-1]}(S{x_i}x_{i+1} \to \neg C_{1-w_{i+1}}(x_{i+1},x_1)) \big )$
$\forall x_1\ldots \forall x_{|w|}\big ((U_{\text {min}}\, x_1\to \neg C_{1-w_1}(x_1,x_1)) \\[2mm] {\hspace {2.3cm}}\wedge \bigwedge _{i\in [|w|-1]}(S{x_i}x_{i+1} \to \neg C_{1-w_{i+1}}(x_{i+1},x_1)) \big )$
-
–
 $\forall x_1\ldots \forall x_{|w|}\forall x\big ((U_{\text {min}}\, x_1\wedge \bigwedge _{i\in [|w|-1]}S{x_i}x_{i+1}\wedge x_{|w|}<x)\to \neg C^{\text {comp}}_{0}(x,x_1)\big )$
$\forall x_1\ldots \forall x_{|w|}\forall x\big ((U_{\text {min}}\, x_1\wedge \bigwedge _{i\in [|w|-1]}S{x_i}x_{i+1}\wedge x_{|w|}<x)\to \neg C^{\text {comp}}_{0}(x,x_1)\big )$
-
–
 $\forall x\forall y\big (U_{\text {min}}\, x\to (\neg H_{q_0}^{\text {comp}}(x,x)\wedge (y\ne x\to \bigwedge _{q\in Q}\neg H_q(y,x)))\big )$
.
$\forall x\forall y\big (U_{\text {min}}\, x\to (\neg H_{q_0}^{\text {comp}}(x,x)\wedge (y\ne x\to \bigwedge _{q\in Q}\neg H_q(y,x)))\big )$
.
Note that besides
![]() $<$
all relation symbols of
$<$
all relation symbols of
![]() $\tau _M$
are negative in
$\tau _M$
are negative in
![]() $\varphi _{0w}$
. We set
$\varphi _{0w}$
. We set
![]() $\varphi _{1M}:=\varphi _{1\tau _M}$
; recall that by Definition 3.6(c),
$\varphi _{1M}:=\varphi _{1\tau _M}$
; recall that by Definition 3.6(c),
Let
![]() $w\in \{0,1\}^*$
and
$w\in \{0,1\}^*$
and
![]() $r\in \mathbb N$
. Furthermore, let
$r\in \mathbb N$
. Furthermore, let
![]() $\mathcal A$
be a
$\mathcal A$
be a
![]() $\tau _M$
-structure where
$\tau _M$
-structure where
![]() $<^{\mathcal A}$
is an ordering and
$<^{\mathcal A}$
is an ordering and
![]() $|A|\ge r+1$
. Let
$|A|\ge r+1$
. Let
![]() $a_0, \ldots , a_r$
be the first
$a_0, \ldots , a_r$
be the first
![]() $r+1$
elements of
$r+1$
elements of
![]() $<^{\mathcal A}$
. Assume that M on the input
$<^{\mathcal A}$
. Assume that M on the input
![]() $w\in \{0, 1\}^*$
runs at least r steps. We say that
$w\in \{0, 1\}^*$
runs at least r steps. We say that
![]() $\mathcal A$
correctly encodes r steps of the computation of M on w if for
$\mathcal A$
correctly encodes r steps of the computation of M on w if for
![]() $i,j$
with
$i,j$
with
![]() $0\le i,j\le r$
,
$0\le i,j\le r$
,
and for
![]() $q\in Q$
,
$q\in Q$
,
Lemma 6.1. Let
![]() $w\in \{0, 1\}^*$
and
$w\in \{0, 1\}^*$
and
![]() $r\in \mathbb N$
.
$r\in \mathbb N$
.
-
(a) Let
 $\mathcal A\models \varphi _{0w}\wedge \varphi _{1M}$
and
$\mathcal A\models \varphi _{0w}\wedge \varphi _{1M}$
and
 $r+1\le |A|$
(this holds if A is infinite). If M on w runs at least r steps, then
$r+1\le |A|$
(this holds if A is infinite). If M on w runs at least r steps, then
 $\mathcal A$
correctly encodes r steps of the computation of M on w.
$\mathcal A$
correctly encodes r steps of the computation of M on w. -
(b) There is a finite model of
 $\varphi _{0w}\wedge \varphi _{1M}$
with
$\varphi _{0w}\wedge \varphi _{1M}$
with
 $r+1$
elements. If M runs at least r steps, then this model is unique up to isomorphism.
$r+1$
elements. If M runs at least r steps, then this model is unique up to isomorphism.
Proof (a) holds by the definitions of
![]() $\varphi _{0w}$
and
$\varphi _{0w}$
and
![]() $\varphi _{1M}$
. For (b) let
$\varphi _{1M}$
. For (b) let
![]() $A=\{a_0, \ldots , a_r\}$
with pairwise distinct
$A=\{a_0, \ldots , a_r\}$
with pairwise distinct
![]() $a_i$
’s. Assume first that M on w runs at least r steps. We can interpret (17) and (18) as defining relations
$a_i$
’s. Assume first that M on w runs at least r steps. We can interpret (17) and (18) as defining relations
![]() $C_0^{\mathcal A}$
and
$C_0^{\mathcal A}$
and
![]() $H_q^{\mathcal A}$
on A equipped with the “natural” ordering and its corresponding relations
$H_q^{\mathcal A}$
on A equipped with the “natural” ordering and its corresponding relations
![]() $U_{{\text {min}}}$
,
$U_{{\text {min}}}$
,
![]() $U_{{\text {max}}}$
, and S. If furthermore we let
$U_{{\text {max}}}$
, and S. If furthermore we let
![]() $(C^{\text {comp}}_0)^{\mathcal A}$
and
$(C^{\text {comp}}_0)^{\mathcal A}$
and
![]() $(H_q^{\text {comp}})^{\mathcal A}$
be the complements in
$(H_q^{\text {comp}})^{\mathcal A}$
be the complements in
![]() $A\times A$
of
$A\times A$
of
![]() $C_0^{\mathcal A}$
and
$C_0^{\mathcal A}$
and
![]() $H_q^{\mathcal A}$
, respectively, we get a model of
$H_q^{\mathcal A}$
, respectively, we get a model of
![]() $\varphi _{0w}\wedge \varphi _{1M}$
with
$\varphi _{0w}\wedge \varphi _{1M}$
with
![]() $r+1$
elements. By (a), this model is unique up to isomorphism.
$r+1$
elements. By (a), this model is unique up to isomorphism.
If M on input w halts, say in
![]() $h(w)$
steps, with
$h(w)$
steps, with
![]() $h(w)< r$
, we get a model
$h(w)< r$
, we get a model
![]() $\mathcal A$
of
$\mathcal A$
of
![]() $\varphi _{0w}\wedge \varphi _{1M}$
with
$\varphi _{0w}\wedge \varphi _{1M}$
with
![]() $A= \{0, 1, \ldots , r\}$
, for example “by repeating the configuration reached after
$A= \{0, 1, \ldots , r\}$
, for example “by repeating the configuration reached after
![]() $h(w)$
steps”. This means, if T is any of the relations
$h(w)$
steps”. This means, if T is any of the relations
![]() $C_0,H_q,C_0^{\text {comp}}, H_q^{\text {comp}}$
, we set for j with
$C_0,H_q,C_0^{\text {comp}}, H_q^{\text {comp}}$
, we set for j with
![]() $h(w)<j\le r$
and
$h(w)<j\le r$
and
![]() $i=0,\ldots , r$
,
$i=0,\ldots , r$
,
Let
![]() $\gamma _M$
be a sentence expressing that “M reaches the halting state
$\gamma _M$
be a sentence expressing that “M reaches the halting state
![]() $q_h$
in exactly ‘
$q_h$
in exactly ‘
![]() ${\text {max}}$
’ steps,” e.g., we let
${\text {max}}$
’ steps,” e.g., we let
![]() $\gamma _M$
be
$\gamma _M$
be
As a consequence of the preceding lemma, we obtain the following:
Corollary 6.2. Let
![]() $w\in \{0,1\}^*$
and set
$w\in \{0,1\}^*$
and set
-
(a) If M on w does not halt, then
 $\pi _w$
has no finite model.
$\pi _w$
has no finite model. -
(b) Assume M on w eventually halts, say in
 $h(w)$
steps. Then
$h(w)$
steps. Then
 $\pi _w$
has a unique model up to isomorphism. This model is finite and has exactly
$\pi _w$
has a unique model up to isomorphism. This model is finite and has exactly
 $h(w)+1$
elements.
$h(w)+1$
elements.
We set
Applying Proposition 3.11 to part (b) of the preceding corollary, we get the following:
Lemma 6.3. Let M on w halt in
![]() $h(w)$
steps. Then
$h(w)$
steps. Then
![]() $:$
$:$
-
(a)
 is closed under
is closed under
 $<$
-substructures.
$<$
-substructures. -
(b) If
 $\chi _w$
is finitely equivalent to a universal sentence
$\chi _w$
is finitely equivalent to a universal sentence
 $\mu $
, then
$\mu $
, then
 $|\mu | \ge h(w)+1$
.
$|\mu | \ge h(w)+1$
.
Now we show the following version of Gurevich’s Theorem.
Theorem 6.4. Let
![]() $f: \mathbb N\to \mathbb N$
be a computable function. Then there is a
$f: \mathbb N\to \mathbb N$
be a computable function. Then there is a
![]() $w\in \{0,1\}^*$
such that
$w\in \{0,1\}^*$
such that ![]() is closed under
is closed under
![]() $<$
-substructures (and hence equivalent to a universal sentence) but
$<$
-substructures (and hence equivalent to a universal sentence) but
![]() $\chi _w$
is not finitely equivalent to a universal sentence of length less than
$\chi _w$
is not finitely equivalent to a universal sentence of length less than
![]() $f(|\chi _w|)$
.
$f(|\chi _w|)$
.
Note that by Corollary 2.7 the conclusion of this theorem is only apparently stronger than “
![]() $\chi _w$
is not equivalent to a universal sentence of length less than
$\chi _w$
is not equivalent to a universal sentence of length less than
![]() $f(|\chi _w|)$
.” A similar remark applies to Theorem 6.6.
$f(|\chi _w|)$
.” A similar remark applies to Theorem 6.6.
Proof of Theorem 6.4
By the previous lemma it suffices to find a
![]() $w\in \{0,1\}^*$
such that M on input w halts in
$w\in \{0,1\}^*$
such that M on input w halts in
![]() $h(w)$
steps with
$h(w)$
steps with
W.l.o.g. we assume that f is increasing. An analysis of the formula
![]() $\chi _{w}$
shows that for some
$\chi _{w}$
shows that for some
![]() $c_M\in \mathbb N$
we have for all
$c_M\in \mathbb N$
we have for all
![]() $w\in \{0,1\}^*$
,
$w\in \{0,1\}^*$
,
We define
![]() $g:\mathbb N\to \mathbb N$
by
$g:\mathbb N\to \mathbb N$
by
Let
![]() $M_0$
be a Turing machine computing g, more precisely, the function
$M_0$
be a Turing machine computing g, more precisely, the function
![]() $1^k\mapsto 1^{g(k)}$
. We code
$1^k\mapsto 1^{g(k)}$
. We code
![]() $M_0$
and
$M_0$
and
![]() $1^k$
by a
$1^k$
by a
![]() $\{0, 1\}$
-string
$\{0, 1\}$
-string
![]() $\textit {code}(M_0,1^k)$
such that M on
$\textit {code}(M_0,1^k)$
such that M on
![]() $\textit {code}(M_0,1^k)$
simulates the computation of
$\textit {code}(M_0,1^k)$
simulates the computation of
![]() $M_0$
on
$M_0$
on
![]() $1^k$
.
$1^k$
.
Choose the least k such that for
![]() $w:= \textit {code}(M_0,1^k)$
we have
$w:= \textit {code}(M_0,1^k)$
we have
The universal Turing machine M on input w computes
![]() $1^{g(k)}$
and thus runs at least
$1^{g(k)}$
and thus runs at least
![]() $g(k)$
steps, say, exactly
$g(k)$
steps, say, exactly
![]() $h(w)$
steps. By (21) and (22)
$h(w)$
steps. By (21) and (22)
Finally we prove Gurevich’s Theorem for graphs. For
![]() $\tau := \tau _M$
let I be an interpretation according to Lemma 5.6. For
$\tau := \tau _M$
let I be an interpretation according to Lemma 5.6. For
![]() $w\in \{0, 1\}^*$
we consider the sentence
$w\in \{0, 1\}^*$
we consider the sentence
That is, for
![]() $G\models \rho _w$
, either the graph G interprets an “empty
$G\models \rho _w$
, either the graph G interprets an “empty
![]() $\tau _M$
-structure,” or a
$\tau _M$
-structure,” or a
![]() $\tau _M$
-structure that is a model of
$\tau _M$
-structure that is a model of
![]() $\chi _w$
. If M halts in
$\chi _w$
. If M halts in
![]() $h(w)$
steps on input w, then
$h(w)$
steps on input w, then
![]() $\varphi _{0w}\wedge \varphi _{1M}\wedge \gamma _M$
has no infinite model but a finite model with
$\varphi _{0w}\wedge \varphi _{1M}\wedge \gamma _M$
has no infinite model but a finite model with
![]() $h(w)+1$
elements by Corollary 6.2(b). Hence, by Proposition 4.8 we get the following analogue of Lemma 6.3.
$h(w)+1$
elements by Corollary 6.2(b). Hence, by Proposition 4.8 we get the following analogue of Lemma 6.3.
Lemma 6.5. Let M on input w halt in
![]() $h(w)$
steps. Then
$h(w)$
steps. Then
![]() $:$
$:$
-
(a)
 , the class of graphs that are models of
, the class of graphs that are models of
 $\rho _w$
, is closed under induced subgraphs.
$\rho _w$
, is closed under induced subgraphs. -
(b) If
 $\rho _w$
is equivalent in the class of finite graphs to the universal sentence
$\rho _w$
is equivalent in the class of finite graphs to the universal sentence
 $\mu $
, then
$\mu $
, then
 $|\mu |^2 \ge h(w)$
.
$|\mu |^2 \ge h(w)$
.
Theorem 6.6 (Gurevich’s Theorem for graphs).
Let
![]() $f:\mathbb N\to \mathbb N$
be a computable function. Furthermore, let
$f:\mathbb N\to \mathbb N$
be a computable function. Furthermore, let
![]() $\rho _w$
be defined by (23), where I is an interpretation for
$\rho _w$
be defined by (23), where I is an interpretation for
![]() $\tau := \tau _M$
according to Lemma 5.6. Then there is a
$\tau := \tau _M$
according to Lemma 5.6. Then there is a
![]() $w\in \{0,1\}^*$
such that
$w\in \{0,1\}^*$
such that ![]() is closed under induced subgraphs (and hence equivalent in the class of graphs to a universal sentence) but
is closed under induced subgraphs (and hence equivalent in the class of graphs to a universal sentence) but
![]() $\rho _w$
is not equivalent in the class of finite graphs to a universal sentence of length less than
$\rho _w$
is not equivalent in the class of finite graphs to a universal sentence of length less than
![]() $f(|\rho _w|)$
.
$f(|\rho _w|)$
.
Proof Again we assume that f is increasing. By the previous lemma it suffices to find a
![]() $w\in \{0,1\}^*$
such that M on input w halts in
$w\in \{0,1\}^*$
such that M on input w halts in
![]() $h(w)$
steps with
$h(w)$
steps with
There is a
![]() $c\in \mathbb N$
, which depends on I but not on w, such that for
$c\in \mathbb N$
, which depends on I but not on w, such that for
![]() $c_I$
as in (11) and
$c_I$
as in (11) and
![]() $c_M$
as in (21) we have for
$c_M$
as in (21) we have for
![]() $d_M:= c+ c_I\cdot c_M$
,
$d_M:= c+ c_I\cdot c_M$
,
We define
![]() $g:\mathbb N\to \mathbb N$
by
$g:\mathbb N\to \mathbb N$
by
and then proceed as in the proof of Theorem 6.4. Let
![]() $M_0$
be a Turing machine computing the function
$M_0$
be a Turing machine computing the function
![]() $1^k\mapsto 1^{g(k)}$
. We code
$1^k\mapsto 1^{g(k)}$
. We code
![]() $M_0$
and
$M_0$
and
![]() $1^k$
by a
$1^k$
by a
![]() $\{0, 1\}$
-string
$\{0, 1\}$
-string
![]() $\textit {code}(M_0,1^k)$
such that M on
$\textit {code}(M_0,1^k)$
such that M on
![]() $\textit {code}(M_0,1^k)$
simulates the computation of
$\textit {code}(M_0,1^k)$
simulates the computation of
![]() $M_0$
on
$M_0$
on
![]() $1^k$
.
$1^k$
.
Choose the least k such that for
![]() $w:= \textit {code}(M_0,1^k)$
we have
$w:= \textit {code}(M_0,1^k)$
we have
The universal Turing machine M on input w computes
![]() $1^{g(k)}$
and thus runs at least
$1^{g(k)}$
and thus runs at least
![]() $g(k)$
steps, say, exactly
$g(k)$
steps, say, exactly
![]() $h(w)$
steps. We have
$h(w)$
steps. We have
Remark 6.7. Using previous remarks (Remarks 3.12 and 4.9) one can even show that for every computable function
![]() $f: \mathbb N\to \mathbb N$
the sentence
$f: \mathbb N\to \mathbb N$
the sentence
![]() $\chi _w$
is not finitely equivalent to a
$\chi _w$
is not finitely equivalent to a
![]() $\Pi _2$
-sentence of length less than
$\Pi _2$
-sentence of length less than
![]() $f(|\chi _w|)$
and the sentence
$f(|\chi _w|)$
and the sentence
![]() $\rho _w$
is not finitely equivalent in graphs to a
$\rho _w$
is not finitely equivalent in graphs to a
![]() $\Pi _2$
-sentence of length less than
$\Pi _2$
-sentence of length less than
![]() $f(|\chi _w|)$
. Moreover,
$f(|\chi _w|)$
. Moreover,
![]() $\chi _w$
and
$\chi _w$
and
![]() $\rho _w$
are equivalent to
$\rho _w$
are equivalent to
![]() $\Sigma _2$
-sentences. To verify this note that in models of
$\Sigma _2$
-sentences. To verify this note that in models of
![]() $\varphi _{0w}$
the sentence
$\varphi _{0w}$
the sentence
![]() $\gamma _M$
is equivalent to
$\gamma _M$
is equivalent to
and hence equivalent to a
![]() $\Sigma _2$
and to a
$\Sigma _2$
and to a
![]() $\Pi _2$
-sentence. One easily verifies that the same holds for
$\Pi _2$
-sentence. One easily verifies that the same holds for
![]() $\gamma _M^I$
.
$\gamma _M^I$
.
7 Some undecidable problems
In this section we show that various problems related to the results of the preceding sections are undecidable. Among others, these results explain why it might be hard, in fact impossible in general, to algorithmically obtain forbidden induced subgraphs for various classes of graphs.
A simple application of Gurevich’s Theorem for graphs yields:
Proposition 7.1. There is no algorithm that applied to any
![]() ${\mathrm{FO}}[\tau _E]$
-sentence
${\mathrm{FO}}[\tau _E]$
-sentence
![]() $\varphi $
decides whether the class
$\varphi $
decides whether the class ![]() is closed under induced subgraphs.
is closed under induced subgraphs.
Proof Assume
![]() $\mathbb A$
is such an algorithm. By the Completeness Theorem there is an algorithm
$\mathbb A$
is such an algorithm. By the Completeness Theorem there is an algorithm
![]() $\mathbb B$
that assigns to every sentence
$\mathbb B$
that assigns to every sentence
![]() $\varphi $
such that
$\varphi $
such that ![]() is closed under induced subgraphs a universal sentence equivalent to
is closed under induced subgraphs a universal sentence equivalent to
![]() $\varphi $
in graphs. Define the function g by
$\varphi $
in graphs. Define the function g by
 $$\begin{align*}g(\varphi):= \begin{cases} 0, & \text{if}\ \mathbb A\ \text{rejects}\ \varphi, \\ m, & \mathbb B\text{ needs}\ m\text{ steps to produce a universal sentence equivalent to}\ \varphi\ \text{in graphs,} \end{cases} \end{align*}$$
$$\begin{align*}g(\varphi):= \begin{cases} 0, & \text{if}\ \mathbb A\ \text{rejects}\ \varphi, \\ m, & \mathbb B\text{ needs}\ m\text{ steps to produce a universal sentence equivalent to}\ \varphi\ \text{in graphs,} \end{cases} \end{align*}$$
and set
![]() $f(k):= {\text {max}}\{g(\varphi )\mid |\varphi |\le k\}$
. Then f would contradict Theorem 6.6.
$f(k):= {\text {max}}\{g(\varphi )\mid |\varphi |\le k\}$
. Then f would contradict Theorem 6.6.
Corollary 7.2. There is no algorithm that applied to any
![]() ${\mathrm{FO}}[\tau _E]$
-sentence
${\mathrm{FO}}[\tau _E]$
-sentence
![]() $\varphi $
either reports that
$\varphi $
either reports that ![]() is not closed under induced subgraphs or it computes for
is not closed under induced subgraphs or it computes for ![]() a finite set of forbidden induced finite subgraphs.
a finite set of forbidden induced finite subgraphs.
Proof Otherwise we could use this algorithm as a decision algorithm for the previous result.
The following proposition is the analogue of Proposition 7.1 for classes of finite graphs. We state it for
![]() ${\text {FO}}[\tau _E]$
-sentences and graphs even though we prove it for
${\text {FO}}[\tau _E]$
-sentences and graphs even though we prove it for
![]() ${\text {FO}}[\tau _M]$
-sentences. One gets the version for graphs using the machinery we developed in previous sections similarly as we get Corollary 7.5 along the lines of the proof of Proposition 7.4.
${\text {FO}}[\tau _M]$
-sentences. One gets the version for graphs using the machinery we developed in previous sections similarly as we get Corollary 7.5 along the lines of the proof of Proposition 7.4.
We write
![]() $M: w\mapsto \infty $
for the universal Turing machine M and a word
$M: w\mapsto \infty $
for the universal Turing machine M and a word
![]() $w\in \{0, 1\}^*$
if M on input w does not halt. We make use of the sentences
$w\in \{0, 1\}^*$
if M on input w does not halt. We make use of the sentences
![]() $\varphi _{0w}$
,
$\varphi _{0w}$
,
![]() $\varphi _{1M}$
, and
$\varphi _{1M}$
, and
![]() $\gamma _M$
defined in the previous section.
$\gamma _M$
defined in the previous section.
Proposition 7.3. There is no algorithm that applied to any
![]() ${\mathrm{FO}}[\tau _E]$
-sentence
${\mathrm{FO}}[\tau _E]$
-sentence
![]() $\varphi $
decides whether the class
$\varphi $
decides whether the class ![]() is closed under induced subgraphs.
is closed under induced subgraphs.
Proof For the universal Turing machine M and a word
![]() $w\in \{0, 1\}^*$
consider the sentence
$w\in \{0, 1\}^*$
consider the sentence
introduced in Corollary 6.2. Then
In fact, if
![]() $M: w\mapsto \infty $
, then
$M: w\mapsto \infty $
, then ![]() (see Corollary 6.2(a)), hence
(see Corollary 6.2(a)), hence ![]() is trivially closed under induced substructures. If M on input w halts after
is trivially closed under induced substructures. If M on input w halts after
![]() $h(w)$
steps, then, up to isomorphism, there is a unique model
$h(w)$
steps, then, up to isomorphism, there is a unique model
![]() $\mathcal A_w$
of
$\mathcal A_w$
of
![]() $\pi _w$
and it has
$\pi _w$
and it has
![]() $h(w)+ 1$
elements (see Corollary 6.2(b)). Take an induced substructure of
$h(w)+ 1$
elements (see Corollary 6.2(b)). Take an induced substructure of
![]() $\mathcal A_w$
with
$\mathcal A_w$
with
![]() $h(w)$
elements (note that
$h(w)$
elements (note that
![]() $h(w)\ge 1$
). Hence this substructure is not a model of
$h(w)\ge 1$
). Hence this substructure is not a model of
![]() $\pi _w$
and thus
$\pi _w$
and thus ![]() is not closed under induced substructures. As the halting problem for every universal Turing machine is not decidable, by (27) we get our claim.
is not closed under induced substructures. As the halting problem for every universal Turing machine is not decidable, by (27) we get our claim.
Proposition 7.4. There is no algorithm that applied to any
![]() ${\mathrm{FO}}[\tau _M]$
-sentence that is finitely equivalent to a universal sentence computes such a universal sentence.
${\mathrm{FO}}[\tau _M]$
-sentence that is finitely equivalent to a universal sentence computes such a universal sentence.
Proof Assume that there exists such an algorithm
![]() $\mathbb A$
. It suffices to show for every
$\mathbb A$
. It suffices to show for every
![]() $w\in \{0, 1\}^*$
the statements (a) and (b) for
$w\in \{0, 1\}^*$
the statements (a) and (b) for
defined in (20).
-
(a)
 for some universal
for some universal
 $\mu $
.
$\mu $
. -
(b)
 .
.
Then we can decide the halting problem for M by checking whether the universal sentence produced by the claimed algorithm
![]() $\mathbb A$
is finitely equivalent to the universal sentence
$\mathbb A$
is finitely equivalent to the universal sentence
![]() $\varphi _{0w}$
. This can be decided effectively by Corollaries 2.6 and 2.7, which leads to a contradiction.
$\varphi _{0w}$
. This can be decided effectively by Corollaries 2.6 and 2.7, which leads to a contradiction.
If M halts on w, say in
![]() $h(w)$
steps, then we get (a) by Lemma 6.3(a) and the Łoś–Tarski Theorem. Furthermore, by Corollary 6.2(b) we know that there is a finite structure with
$h(w)$
steps, then we get (a) by Lemma 6.3(a) and the Łoś–Tarski Theorem. Furthermore, by Corollary 6.2(b) we know that there is a finite structure with
![]() $h(w)+1$
elements that is a model of
$h(w)+1$
elements that is a model of
![]() $\varphi _{0w}\wedge \varphi _{1M}\wedge \gamma _M$
and thus of
$\varphi _{0w}\wedge \varphi _{1M}\wedge \gamma _M$
and thus of
![]() $\varphi _{0w}\wedge \neg \chi _w$
. Hence this structure is a model of
$\varphi _{0w}\wedge \neg \chi _w$
. Hence this structure is a model of
![]() $\varphi _{0w}\wedge \neg \mu $
. In particular,
$\varphi _{0w}\wedge \neg \mu $
. In particular,
![]() $\mu $
(and hence,
$\mu $
(and hence,
![]() $\chi _w$
) is not finitely equivalent to
$\chi _w$
) is not finitely equivalent to
![]() $\varphi _{0w}$
. Thus, also (b) holds if M halts on w.
$\varphi _{0w}$
. Thus, also (b) holds if M halts on w.
If
![]() $M: w\to \infty $
, then we show that
$M: w\to \infty $
, then we show that ![]() (this implies (a) and (b) in this case). Clearly,
(this implies (a) and (b) in this case). Clearly, ![]() . Now let
. Now let
![]() $\mathcal A$
be a finite model of
$\mathcal A$
be a finite model of
![]() $\varphi _{0w} $
. If
$\varphi _{0w} $
. If
![]() $\mathcal A\not \models \varphi _{1M}$
, then
$\mathcal A\not \models \varphi _{1M}$
, then
![]() $\mathcal A\models \chi _w$
. Otherwise
$\mathcal A\models \chi _w$
. Otherwise
![]() $\mathcal A \models \varphi _{1M}$
and then
$\mathcal A \models \varphi _{1M}$
and then
![]() $\mathcal A$
correctly represents the first
$\mathcal A$
correctly represents the first
![]() $|A|-1$
steps of the computation of M on w by Lemma 6.1. Thus
$|A|-1$
steps of the computation of M on w by Lemma 6.1. Thus
![]() $\mathcal A$
is a model of
$\mathcal A$
is a model of
![]() $\neg \gamma _M$
as M does not halt on w. Therefore,
$\neg \gamma _M$
as M does not halt on w. Therefore,
![]() $\mathcal A$
is a model of
$\mathcal A$
is a model of
![]() $\chi _w$
.
$\chi _w$
.
Corollary 7.5. There is no algorithm that applied to any
![]() ${\mathrm{FO}}[\tau _E]$
-sentence
${\mathrm{FO}}[\tau _E]$
-sentence
![]() $\varphi $
such that
$\varphi $
such that ![]() has a finite set of forbidden induced finite subgraphs computes such a set.
has a finite set of forbidden induced finite subgraphs computes such a set.
Proof Equivalently we show that there is no algorithm that applied to any
![]() ${\text {FO}}[\tau _E]$
-sentence
${\text {FO}}[\tau _E]$
-sentence
![]() $\varphi $
such that
$\varphi $
such that ![]() for some universal sentence
for some universal sentence
![]() $\mu $
computes such a
$\mu $
computes such a
![]() $\mu $
.
$\mu $
.
For graphs let
![]() $I\ (=I_{\tau _M})$
be a strongly existential interpretation of
$I\ (=I_{\tau _M})$
be a strongly existential interpretation of
![]() $\tau _M$
-structures in graphs according to Lemma 5.6. For
$\tau _M$
-structures in graphs according to Lemma 5.6. For
![]() $w\in \{0, 1\}^*$
we consider the sentence
$w\in \{0, 1\}^*$
we consider the sentence
defined in (23) and show (a’) and (b’), the analogues of (a) and (b) of the preceding proof.
-
(a’)
 for some universal
for some universal
 $\mu $
.
$\mu $
. -
(b’)
 .
.
Then we get the claim of the corollary arguing as in the previous proof.
(a’) holds by Lemma 6.5(a).
By Lemma 5.6 for every finite
![]() $\tau _M$
-structure
$\tau _M$
-structure
![]() $\mathcal A$
there is a finite graph G with
$\mathcal A$
there is a finite graph G with
![]() $\mathcal O_I(G)\cong \mathcal A$
. Therefore,
$\mathcal O_I(G)\cong \mathcal A$
. Therefore,

Observe that Corollary 7.5 is precisely Theorem 1.3 as stated in the Introduction. Finally we prove Theorem 1.2, which is equivalent to the following result.
Theorem 7.6. There is no algorithm that applied to an
![]() ${\mathrm{FO}}[\tau _E]$
-sentence
${\mathrm{FO}}[\tau _E]$
-sentence
![]() $\varphi $
such that
$\varphi $
such that ![]() is closed under induced subgraphs decides whether there is a finite set
is closed under induced subgraphs decides whether there is a finite set
![]() $\mathscr {F}$
of finite graphs such that
$\mathscr {F}$
of finite graphs such that
Proof Again we prove the corresponding result for
![]() $\tau _M$
-sentences and
$\tau _M$
-sentences and
![]() $\tau _M$
-structures and leave it to the reader to translate it to graphs as in the previous proof. That is, we show:
$\tau _M$
-structures and leave it to the reader to translate it to graphs as in the previous proof. That is, we show:
There is no algorithm that applied to an
![]() ${\text {FO}}[\tau _M]$
-sentence
${\text {FO}}[\tau _M]$
-sentence
![]() $\varphi $
such that
$\varphi $
such that ![]() is closed under induced substructures decides whether there is a finite set
is closed under induced substructures decides whether there is a finite set
![]() $\mathscr {F}$
of
$\mathscr {F}$
of
![]() $\tau _M$
-structures such that
$\tau _M$
-structures such that
For
![]() $w\in \{0, 1\}^*$
set
$w\in \{0, 1\}^*$
set
It suffices to show that ![]() is closed under induced substructures and that
is closed under induced substructures and that
Assume first that
![]() $M: w\to \infty $
. Then
$M: w\to \infty $
. Then
![]() $\varphi _{0w}\wedge \varphi _{1M}\wedge \gamma _M$
has no finite model by Lemma 6.1(a) and the definition (19) of
$\varphi _{0w}\wedge \varphi _{1M}\wedge \gamma _M$
has no finite model by Lemma 6.1(a) and the definition (19) of
![]() $\gamma _M$
. Therefore,
$\gamma _M$
. Therefore, ![]() . By Lemma 6.1(b) the sentence
. By Lemma 6.1(b) the sentence
![]() $\varphi _{0w}\wedge \neg \varphi _{1M}$
has arbitrarily large finite models. Recall that
$\varphi _{0w}\wedge \neg \varphi _{1M}$
has arbitrarily large finite models. Recall that
![]() $\varphi _{0w}$
is an extension of
$\varphi _{0w}$
is an extension of
![]() $\varphi _0$
and
$\varphi _0$
and
![]() $\varphi _{1M}= \varphi _{1\tau _M}$
(see (16)). Hence, by Lemma 3.10, we know that
$\varphi _{1M}= \varphi _{1\tau _M}$
(see (16)). Hence, by Lemma 3.10, we know that ![]() is closed under induced substructures but not finitely equivalent to a universal sentence.
is closed under induced substructures but not finitely equivalent to a universal sentence.
Now assume that M on input w halts in
![]() $h(w)$
steps. Then Corollary 6.2(b) guarantees that there is a unique model
$h(w)$
steps. Then Corollary 6.2(b) guarantees that there is a unique model
![]() $\mathcal A_w$
of
$\mathcal A_w$
of
![]() $\varphi _{0w}\wedge \varphi _{1M}\wedge \gamma _M$
; moreover,
$\varphi _{0w}\wedge \varphi _{1M}\wedge \gamma _M$
; moreover,
![]() ${|A_w|= h(w)+1}$
. We present a finite set
${|A_w|= h(w)+1}$
. We present a finite set
![]() $\mathscr {F}$
of finite
$\mathscr {F}$
of finite
![]() $\tau _M$
-structures such that
$\tau _M$
-structures such that
As
![]() $\varphi _{0w}$
is universal, there is a finite set
$\varphi _{0w}$
is universal, there is a finite set
![]() $\mathscr {F}_0$
of finite
$\mathscr {F}_0$
of finite
![]() $\tau _M$
-structures such that
$\tau _M$
-structures such that
We define the sets
![]() $\mathscr {F}_1$
and
$\mathscr {F}_1$
and
![]() $\mathscr {F}_2$
as follows: For every
$\mathscr {F}_2$
as follows: For every
![]() $\tau _M$
-structure
$\tau _M$
-structure
![]() $\mathcal B$
,
$\mathcal B$
,
Here
![]() $\varphi ^*_{1M}$
is obtained from
$\varphi ^*_{1M}$
is obtained from
![]() $\varphi _{1M}$
by replacing the conjunct
$\varphi _{1M}$
by replacing the conjunct
![]() $\varphi _1$
see (6) by
$\varphi _1$
see (6) by
The difference is that
![]() $\varphi ^*_1$
does not require the set
$\varphi ^*_1$
does not require the set
![]() $U_{{\text {max}}}$
to be nonempty. Hence,
$U_{{\text {max}}}$
to be nonempty. Hence,
![]() $\varphi ^*_{1M}$
is the conjunction of
$\varphi ^*_{1M}$
is the conjunction of
![]() $\varphi ^*_1$
with
$\varphi ^*_1$
with
Note that Lemma 6.1(a) remains true if in its statement we replace
![]() $\varphi _{1M}$
by
$\varphi _{1M}$
by
![]() $\varphi ^*_{1M}$
.
$\varphi ^*_{1M}$
.
For
![]() $\mathscr {F}:= \mathscr {F}_0\cup \mathscr {F}_1\cup \mathscr {F}_2$
we show (28). Assume first that a finite structure
$\mathscr {F}:= \mathscr {F}_0\cup \mathscr {F}_1\cup \mathscr {F}_2$
we show (28). Assume first that a finite structure
![]() $\mathcal C$
is a model of
$\mathcal C$
is a model of
![]() $\alpha _w$
. In particular,
$\alpha _w$
. In particular,
![]() $\mathcal C\models \varphi _{0w}$
and therefore,
$\mathcal C\models \varphi _{0w}$
and therefore,
![]() $\mathcal C$
has no induced substructure isomorphic to a structure in
$\mathcal C$
has no induced substructure isomorphic to a structure in
![]() $\mathscr {F}_0$
.
$\mathscr {F}_0$
.
Now, for a contradiction suppose that
![]() $\mathcal B$
is an induced substructure of
$\mathcal B$
is an induced substructure of
![]() $\mathcal C$
isomorphic to a structure in
$\mathcal C$
isomorphic to a structure in
![]() $\mathscr {F}_1$
. Then
$\mathscr {F}_1$
. Then
![]() $\mathcal B\models \varphi _{1M}$
and thus, by Lemma 3.8,
$\mathcal B\models \varphi _{1M}$
and thus, by Lemma 3.8,
![]() $\mathcal C= \mathcal B$
. As
$\mathcal C= \mathcal B$
. As
![]() $\mathcal C\models \alpha _w$
, we get
$\mathcal C\models \alpha _w$
, we get
![]() $\mathcal C\models \varphi _{0w}\wedge \varphi _{1M}\wedge \gamma _M$
. Hence,
$\mathcal C\models \varphi _{0w}\wedge \varphi _{1M}\wedge \gamma _M$
. Hence,
![]() $\mathcal C\cong \mathcal A_w$
, a contradiction, as on the one hand
$\mathcal C\cong \mathcal A_w$
, a contradiction, as on the one hand
![]() $|C|= |B|\le h(w)$
and on the other hand
$|C|= |B|\le h(w)$
and on the other hand
![]() $|C|= |A_w|= h(w)+1$
.
$|C|= |A_w|= h(w)+1$
.
Next we show that
![]() $\mathcal C$
has no induced substructure
$\mathcal C$
has no induced substructure
![]() $\mathcal B$
isomorphic to a structure in
$\mathcal B$
isomorphic to a structure in
![]() $\mathscr {F}_2$
. As
$\mathscr {F}_2$
. As
![]() $\mathcal B\models \varphi _{0w}\wedge \varphi ^*_{1M}$
and has
$\mathcal B\models \varphi _{0w}\wedge \varphi ^*_{1M}$
and has
![]() $h(w)+2$
elements, the first
$h(w)+2$
elements, the first
![]() $h(w)+1$
elements of
$h(w)+1$
elements of
![]() $\mathcal B$
correctly encode the first
$\mathcal B$
correctly encode the first
![]() $h(w)$
steps of the computation of M on w, hence the full computation. As
$h(w)$
steps of the computation of M on w, hence the full computation. As
![]() $|B|= h(w)+2$
, this contradicts
$|B|= h(w)+2$
, this contradicts
![]() $\mathcal B\models \forall t \forall t' \big (t<t'\to \forall y\neg H_{q_h}(y,t)\big )$
.
$\mathcal B\models \forall t \forall t' \big (t<t'\to \forall y\neg H_{q_h}(y,t)\big )$
.
As the final step let ![]() . We show that
. We show that
![]() $\mathcal C\models \alpha _w$
. As any structure in
$\mathcal C\models \alpha _w$
. As any structure in
![]() $\mathcal C$
does not contain structures in
$\mathcal C$
does not contain structures in
![]() $\mathscr {F}_0$
as induced substructures, we see that
$\mathscr {F}_0$
as induced substructures, we see that
![]() $\mathcal C\models \varphi _{0w}$
. If
$\mathcal C\models \varphi _{0w}$
. If
![]() $\mathcal C\not \models \varphi _{1M}$
, we are done.
$\mathcal C\not \models \varphi _{1M}$
, we are done.
Recall that by Lemma 6.1(a) (more precisely, by the extension of Lemma 6.1(a) mentioned above) for finite models
![]() $\mathcal B$
of
$\mathcal B$
of
![]() $\varphi _{0w}\wedge \varphi ^*_{1M}$
we know:
$\varphi _{0w}\wedge \varphi ^*_{1M}$
we know:
-
(a) if
 $|B|\le h(w)+1$
, then
$|B|\le h(w)+1$
, then
 $\mathcal B$
encodes
$\mathcal B$
encodes
 $|B|- 1$
steps of the computation of M on w,
$|B|- 1$
steps of the computation of M on w, -
(b) if
 $|B|> h(w)+1$
, then the first
$|B|> h(w)+1$
, then the first
 $h(w)+1$
elements in the ordering
$h(w)+1$
elements in the ordering
 $<^{\mathcal B}$
correctly encode the (full) computation of M on w.
$<^{\mathcal B}$
correctly encode the (full) computation of M on w.
Now assume that
![]() $\mathcal C\models \varphi _{1M}$
, then (a) and (b) apply to
$\mathcal C\models \varphi _{1M}$
, then (a) and (b) apply to
![]() $\mathcal C$
. As no structure in
$\mathcal C$
. As no structure in
![]() $\mathscr {F}_1$
is isomorphic to an induced substructure of
$\mathscr {F}_1$
is isomorphic to an induced substructure of
![]() $\mathcal C$
, we see that
$\mathcal C$
, we see that
![]() $|C|\ge h(w)+1$
. But
$|C|\ge h(w)+1$
. But
![]() $\mathcal C$
cannot have more than
$\mathcal C$
cannot have more than
![]() $h(w)+1$
elements, as otherwise the substructure of
$h(w)+1$
elements, as otherwise the substructure of
![]() $\mathcal C$
induced on the first
$\mathcal C$
induced on the first
![]() $h(w)+2$
elements would be isomorphic to a structure
$h(w)+2$
elements would be isomorphic to a structure
![]() $\mathcal B$
in
$\mathcal B$
in
![]() $\mathscr {F}_2$
, a contradiction. Hence,
$\mathscr {F}_2$
, a contradiction. Hence,
![]() $|C|= h(w)+1$
and thus,
$|C|= h(w)+1$
and thus,
![]() $\mathcal C\models \alpha _w$
.
$\mathcal C\models \alpha _w$
.
Remark 7.7. Mainly using Remark 6.7 one easily verifies that in all results but Proposition 7.3 of this section we can replace:
by
In Proposition 7.3 we have to replace it by:
as
![]() $\varphi _{1M}$
(and
$\varphi _{1M}$
(and
![]() $\varphi ^I_{1M}$
) are
$\varphi ^I_{1M}$
) are
![]() $\Pi _2$
-sentences.
$\Pi _2$
-sentences.
7.1 Open problem
The main result of this paper shows that the analogue of the Łoś–Tarski Theorem fails for the class of finite graphs. That is, there exist FO-axiomatizable classes of finite graphs closed under induced subgraphs that are not definable by a finite set of forbidden induced subgraphs. Often in graph theory one considers subgraphs instead of induced subgraphs. It is known that FO-axiomatizable classes of finite and infinite graphs are closed under subgraphs if and only if they are definable by a finite set of forbidden finite subgraphs. However, to the best of our knowledge it is still open whether FO-axiomatizable classes of finite graphs closed under subgraphs are definable by a finite set of forbidden subgraphs.
Acknowledgment
We thank Abhisekh Sankaran for mentioning to the first author the question of whether Tait’s Theorem generalizes to graphs (see also [Reference Sankaran23]).
Funding
The collaboration of the authors is funded by the Sino-German Center for Research Promotion (GZ 1518). Yijia Chen is supported by the National Natural Science Foundation of China (Project 62372291). He also likes to express his gratitude to Hong Xu and Liqun Zhang for offering a very cordial working environment at Fudan through the difficult year of 2020.