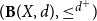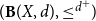1. Introduction
A quasi-metric on a nonempty set X is a map
![]() $d: X\times X\longrightarrow[0,+\infty]$
satisfying:
$d: X\times X\longrightarrow[0,+\infty]$
satisfying:
![]() $d(x,x)=0$
;
$d(x,x)=0$
;
![]() $d(x,z)\leq d(x,y)+d(y,z)$
; and
$d(x,z)\leq d(x,y)+d(y,z)$
; and
![]() $d(x,y)=d(y,x)=0$
implies
$d(x,y)=d(y,x)=0$
implies
![]() $x=y$
. The pair (X,d) is then called a quasi-metric space. One motivation of domain theory is to study the properties of spaces and provide them with suitable computational models (Abramsky and Jung, Reference Abramsky and Jung1994, Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003). The space of formal balls
$x=y$
. The pair (X,d) is then called a quasi-metric space. One motivation of domain theory is to study the properties of spaces and provide them with suitable computational models (Abramsky and Jung, Reference Abramsky and Jung1994, Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003). The space of formal balls
![]() ${\bf B}(X,d)$
of a quasi-metric space (X,d) is probably the single most important artifact (Edalat and Heckmann, Reference Edalat and Heckmann1998, Weihrauch and Schreiber, Reference Weihrauch and Schreiber1981). Formal balls were introduced by Weihrauch and Schreiber (Weihrauch and Schreiber, Reference Weihrauch and Schreiber1981). Edalat and Heckmann proved that a metric space is complete if and only if its poset of formal balls is a domain, and then they showed why formal balls were so important in the metric case (Edalat and Heckmann, Reference Edalat and Heckmann1998). It is natural to ask whether the links between domain theory and quasi-metric space theory can be established in the style of Edalat and Heckmann. There are five important parallel theories in the setting of quasi-metric spaces and the formal ball model:
${\bf B}(X,d)$
of a quasi-metric space (X,d) is probably the single most important artifact (Edalat and Heckmann, Reference Edalat and Heckmann1998, Weihrauch and Schreiber, Reference Weihrauch and Schreiber1981). Formal balls were introduced by Weihrauch and Schreiber (Weihrauch and Schreiber, Reference Weihrauch and Schreiber1981). Edalat and Heckmann proved that a metric space is complete if and only if its poset of formal balls is a domain, and then they showed why formal balls were so important in the metric case (Edalat and Heckmann, Reference Edalat and Heckmann1998). It is natural to ask whether the links between domain theory and quasi-metric space theory can be established in the style of Edalat and Heckmann. There are five important parallel theories in the setting of quasi-metric spaces and the formal ball model:
-
(1) [Romaguera–Valero Theorem] A quasi-metric space (X,d) is Smyth-complete if and only if
 $({\bf B}(X,d),\leq^{d^{+}}\!)$
is a continuous dcpo and its way-below relation is the relation
$({\bf B}(X,d),\leq^{d^{+}}\!)$
is a continuous dcpo and its way-below relation is the relation
 $\prec$
, defined by
$\prec$
, defined by
 $(x,r)\prec (y,s)$
if and only if
$(x,r)\prec (y,s)$
if and only if
 $d(x,y)< r-s$
(Romaguera and Valero, Reference Romaguera and Valero2010).
$d(x,y)< r-s$
(Romaguera and Valero, Reference Romaguera and Valero2010). -
(2) [Kostanek–Waszkiewicz Theorem] A quasi-metric space (X,d) is Yoneda-complete if and only if
 $({\bf B}(X,d),\leq^{d^{+}}\!)$
is a dcpo (Kostanek and Waszkiewicz, Reference Kostanek and Waszkiewicz2011).
$({\bf B}(X,d),\leq^{d^{+}}\!)$
is a dcpo (Kostanek and Waszkiewicz, Reference Kostanek and Waszkiewicz2011). -
(3) A quasi-metric space (X,d) is continuous Yoneda-complete if and only if
 $({\bf B}(X,d),\leq^{d^{+}}\!)$
is a domain (Goubault-Larrecq and Ng, Reference Goubault-Larrecq and Ng2017).
$({\bf B}(X,d),\leq^{d^{+}}\!)$
is a domain (Goubault-Larrecq and Ng, Reference Goubault-Larrecq and Ng2017). -
(4) A quasi-metric space (X,d) is algebraic Yoneda-complete if and only if
 $({\bf B}(X,d), \leq^{d^{+}}\!)$
is a domain with basis
$({\bf B}(X,d), \leq^{d^{+}}\!)$
is a domain with basis
 $\{(x,r)\mid x$
is finite
$\{(x,r)\mid x$
is finite
 $\}$
(Ali-Akbari et al. Reference Ali-Akbari, Honari, Pourmahdian and Rezaii2009).
$\}$
(Ali-Akbari et al. Reference Ali-Akbari, Honari, Pourmahdian and Rezaii2009). -
(5) A Yoneda-complete quasi-metric space (X,d) is quasi-continuous if and only if
 $({\bf B}(X,d),\leq^{d^{+}}\!)$
is a quasi-continuous domain with a fin basis of
$({\bf B}(X,d),\leq^{d^{+}}\!)$
is a quasi-continuous domain with a fin basis of
 $\{\{(x,s)\mid x\in G\}\mid G\in\mathcal{P}_{f}(X),s\in[0,+\infty)\}$
, where
$\{\{(x,s)\mid x\in G\}\mid G\in\mathcal{P}_{f}(X),s\in[0,+\infty)\}$
, where
 $\mathcal{P}_{f}(X)$
is the set of all nonempty finite subsets of X (Ng and Ho, Reference Ng and Ho2019).
$\mathcal{P}_{f}(X)$
is the set of all nonempty finite subsets of X (Ng and Ho, Reference Ng and Ho2019).
It is obvious from the above statements that we research on quasi-metric spaces and their spaces of formal balls, mostly focused on Yoneda-complete spaces, but those should have a meaning even in noncomplete spaces. One question arises naturally: can we give a characterization of properties of a non-Yoneda-complete quasi-metric space in terms of some order-theoretic properties of its poset of formal balls. Our objective is to answer this question. In this paper, we propose the notion of local Yoneda-complete quasi-metric spaces using the domain-theoretic properties of the poset of formal balls and prove that a quasi-metric space is local Yoneda-complete if and only if every local net has a d-limit.
Quasi-metric space unifies the metric space and partially ordered set, and this structure has been extensively studied by several people (Bonsangue et al. Reference Bonsangue, Van Breugel and Rutten1998, Lawvere, Reference Lawvere1973). Similar to the classical completion of metric spaces and posets, Smyth completions and Yoneda completions of quasi-metric spaces are fundamental in the study of quasi-metric spaces (Bonsangue et al. Reference Bonsangue, Van Breugel and Rutten1998; Künzi and Schellekens Reference Künzi and Schellekens2002; Vickers Reference Vickers2005). Smyth provided that there exists an idempotent Smyth completion to every quasi-metric space (Smyth, Reference Smyth1987). Künzi and Schellekens (Reference Künzi and Schellekens2002) prove that every quasi-metric space has a Yoneda completion. However, the fact remains that this Yoneda completion is not idempotent in general. In Ng and Ho (Reference Ng and Ho2017), Ng and Ho showed that every quasi-metric space (X,d) has an idempotent Yoneda completion via dcpo completion of
![]() ${\bf B}(X,d)$
. After seeing that every quasi-metric space has a Smyth completion and Yoneda completion, one may ask: whether every quasi-metric space has a local Yoneda completion. In this paper, we shall provide a positive answer, that is, we prove that every quasi-metric space has a local Yoneda completion.
${\bf B}(X,d)$
. After seeing that every quasi-metric space has a Smyth completion and Yoneda completion, one may ask: whether every quasi-metric space has a local Yoneda completion. In this paper, we shall provide a positive answer, that is, we prove that every quasi-metric space has a local Yoneda completion.
2. Quasi-Metric Spaces
Let (X,d) be a quasi-metric space,
![]() $(x_{i})_{i\in I,\sqsubseteq}$
be a net, and
$(x_{i})_{i\in I,\sqsubseteq}$
be a net, and
![]() $x\in X$
. If for all
$x\in X$
. If for all
![]() $y\in X$
, it holds that
$y\in X$
, it holds that
![]() $d(x,y)=\limsup d(x_{i},y)$
, then
$d(x,y)=\limsup d(x_{i},y)$
, then
![]() $x\in X$
is called a d-limit of
$x\in X$
is called a d-limit of
![]() $(x_{i})_{i\in I,\sqsubseteq}$
, denoted by
$(x_{i})_{i\in I,\sqsubseteq}$
, denoted by
![]() $x=\lim_{d} x_{i}$
. A net
$x=\lim_{d} x_{i}$
. A net
![]() $(x_{i},r_{i})_{i\in I,\sqsubseteq}$
in
$(x_{i},r_{i})_{i\in I,\sqsubseteq}$
in
![]() $X\times [0,+\infty)$
is Cauchy-weighted in (X,d) if
$X\times [0,+\infty)$
is Cauchy-weighted in (X,d) if
![]() $\bigwedge_{i\in I}r_{i}=0$
, and for each
$\bigwedge_{i\in I}r_{i}=0$
, and for each
![]() $i, i^{'}\in I$
, whenever
$i, i^{'}\in I$
, whenever
![]() $i\sqsubseteq i^{'}$
,
$i\sqsubseteq i^{'}$
,
![]() $d(x_{i}, x_{i^{'}})\leq r_{i}-r_{i^{'}}$
. For any Cauchy-weighted net
$d(x_{i}, x_{i^{'}})\leq r_{i}-r_{i^{'}}$
. For any Cauchy-weighted net
![]() $(x_{i},r_{i})_{i\in I,\sqsubseteq}$
in (X,d),
$(x_{i},r_{i})_{i\in I,\sqsubseteq}$
in (X,d),
![]() $x\in X$
is a d-limit of the Cauchy net
$x\in X$
is a d-limit of the Cauchy net
![]() $(x_{i})_{i\in I,\sqsubseteq}$
if and only if for any
$(x_{i})_{i\in I,\sqsubseteq}$
if and only if for any
![]() $y\in X$
, it holds that
$y\in X$
, it holds that
![]() $d(x,y)=\bigvee_{i\in I}(d(x_{i},y)-r_{i})$
.
$d(x,y)=\bigvee_{i\in I}(d(x_{i},y)-r_{i})$
.
Definition 1 (Ng and Ho Reference Ng and Ho2017). Let (X,d) and
![]() $(X^{'}\!,d^{'})$
be two quasi-metric spaces, and
$(X^{'}\!,d^{'})$
be two quasi-metric spaces, and
![]() $f: X\longrightarrow X^{'}$
be a mapping. We say that f is
$f: X\longrightarrow X^{'}$
be a mapping. We say that f is
-
(1) limit-continuous if it preserves Cauchy nets and their existing d-limits;
-
(2) Y-continuous if it is limit-continuous and nonexpansive, that is, for any
 $x,y\in X$
,
$x,y\in X$
,
 $d^{'}(f(x),f(y))\leq d(x,y)$
.
$d^{'}(f(x),f(y))\leq d(x,y)$
.
Definition 2 (Goubault-Larrecq Reference Goubault-Larrecq2013). Let (X,d) be a quasi-metric space. Define
![]() ${\bf B}(X,d)=X\times[0,+\infty)$
. We call the elements of
${\bf B}(X,d)=X\times[0,+\infty)$
. We call the elements of
![]() ${\bf B}(X,d)$
formal balls. On
${\bf B}(X,d)$
formal balls. On
![]() ${\bf B}(X,d)$
, we can define a quasi-metric
${\bf B}(X,d)$
, we can define a quasi-metric
![]() $d^{+}$
as follows:
$d^{+}$
as follows:
and as a result the induced order
![]() $\leq^{d^{+}}$
defined by
$\leq^{d^{+}}$
defined by
Unless otherwise stated, throughout the paper, whenever an order is mentioned in the context of
![]() ${\bf B}(X,d)$
, it is to be interpreted with respect to the induced order
${\bf B}(X,d)$
, it is to be interpreted with respect to the induced order
![]() $\leq^{d^{+}}$
on
$\leq^{d^{+}}$
on
![]() ${\bf B}(X,d)$
.
${\bf B}(X,d)$
.
A quasi-metric space (X,d) is standard if and only if, for every directed family of formal balls
![]() $(x_{i},r_{i})_{i\in I}$
, for every
$(x_{i},r_{i})_{i\in I}$
, for every
![]() $s\in [0,+\infty)$
,
$s\in [0,+\infty)$
,
![]() $(x_{i},r_{i})_{i\in I}$
has a supremum in
$(x_{i},r_{i})_{i\in I}$
has a supremum in
![]() ${\bf B}(X,d)$
if and only if
${\bf B}(X,d)$
if and only if
![]() $(x_{i},r_{i}+s)_{i\in I}$
has a supremum in
$(x_{i},r_{i}+s)_{i\in I}$
has a supremum in
![]() ${\bf B}(X,d)$
.
${\bf B}(X,d)$
.
Let (X,d) be a quasi-metric space. A directed family
![]() $(x_{i},r_{i})_{i\in I}$
in
$(x_{i},r_{i})_{i\in I}$
in
![]() ${\bf B}(X,d)$
is translational complete if for any
${\bf B}(X,d)$
is translational complete if for any
![]() $a\in[\!-\bigwedge_{i\in I}r_{i},+\infty)$
,
$a\in[\!-\bigwedge_{i\in I}r_{i},+\infty)$
,
![]() $\bigvee_{i\in I}(x_{i},r_{i}+a)$
exists.
$\bigvee_{i\in I}(x_{i},r_{i}+a)$
exists.
Remark 3. Let (X,d) be a quasi-metric space. If
![]() $(x_{i},r_{i})_{i\in I}$
is a translational complete directed family in
$(x_{i},r_{i})_{i\in I}$
is a translational complete directed family in
![]() ${\bf B}(X,d)$
and has supremum (x,r), then
${\bf B}(X,d)$
and has supremum (x,r), then
![]() $(x_{i},r_{i}+a)_{i\in I}$
is a translational complete directed family in
$(x_{i},r_{i}+a)_{i\in I}$
is a translational complete directed family in
![]() ${\bf B}(X,d)$
and has supremum
${\bf B}(X,d)$
and has supremum
![]() $(x,r+a)$
for any
$(x,r+a)$
for any
![]() $a\in[\!-\bigwedge_{i\in I}r_{i},+\infty)$
.
$a\in[\!-\bigwedge_{i\in I}r_{i},+\infty)$
.
Let (X,d) and
![]() $(X^{'}\!,d^{'})$
be two quasi-metric spaces. A map
$(X^{'}\!,d^{'})$
be two quasi-metric spaces. A map
![]() $g: {\bf B}(X,d)\longrightarrow {\bf B}(X^{'}\!,d^{'})$
is Y-Scott continuous if it preserves the suprema of translational complete directed families.
$g: {\bf B}(X,d)\longrightarrow {\bf B}(X^{'}\!,d^{'})$
is Y-Scott continuous if it preserves the suprema of translational complete directed families.
Proposition 4 (Ng and Ho Reference Ng and Ho2017). Let (X,d) and
![]() $(X^{'}\!,d^{'})$
be two quasi-metric spaces, and
$(X^{'}\!,d^{'})$
be two quasi-metric spaces, and
![]() $f: X\longrightarrow X^{'}$
be a mapping. Define a mapping
$f: X\longrightarrow X^{'}$
be a mapping. Define a mapping
![]() ${\bf B}(f): {\bf B}(X,d)\longrightarrow {\bf B}(X^{'}\!,d^{'})$
as follows:
${\bf B}(f): {\bf B}(X,d)\longrightarrow {\bf B}(X^{'}\!,d^{'})$
as follows:
Then f is Y-continuous if and only if
![]() ${\bf B}(f)$
is a Y-Scott continuous map.
${\bf B}(f)$
is a Y-Scott continuous map.
Definition 5 (Ng and Ho Reference Ng and Ho2017). Let (X,d) be a quasi-metric space. A subset C of
![]() ${\bf B}(X,d)$
is called g-closed if it is
${\bf B}(X,d)$
is called g-closed if it is
-
(1) downward closed with respect to
 $\leq^{d^{+}}$
;
$\leq^{d^{+}}$
; -
(2) closed under the existing suprema of translational complete directed families, that is, whenever
 $(x_{i},r_{i})_{i\in I}\subseteq C$
is a translational complete directed family that has supremum (x,r), then (x,r) belongs to C.
$(x_{i},r_{i})_{i\in I}\subseteq C$
is a translational complete directed family that has supremum (x,r), then (x,r) belongs to C.
We denote the collection of all g-closed subsets of
![]() ${\bf B}(X,d)$
by
${\bf B}(X,d)$
by
![]() $\Gamma_{g}({\bf B}(X,d))$
. Then
$\Gamma_{g}({\bf B}(X,d))$
. Then
![]() $\Gamma_{g}({\bf B}(X,d))$
is a co-topology on
$\Gamma_{g}({\bf B}(X,d))$
is a co-topology on
![]() ${\bf B}(X,d)$
, that is, the family
${\bf B}(X,d)$
, that is, the family
is a topology, called the g-topology on
![]() ${\bf B}(X,d)$
. For any subset E of B(X,d), let
${\bf B}(X,d)$
. For any subset E of B(X,d), let
![]() $cl_{g}(E)$
denote the g-closure of E. Define the Hausdorf-f-Hoare quasi-metric
$cl_{g}(E)$
denote the g-closure of E. Define the Hausdorf-f-Hoare quasi-metric
![]() $d_{\mathcal{H}}$
on
$d_{\mathcal{H}}$
on
![]() $\Gamma_{g}({\bf B}(X,d))$
by
$\Gamma_{g}({\bf B}(X,d))$
by
![]() $d_{\mathcal{H}}(A,B)=\bigvee_{(a,m)\in A}\bigwedge_{(c,r)\in B}d^{+}((a,m),(c,r)).$
Then
$d_{\mathcal{H}}(A,B)=\bigvee_{(a,m)\in A}\bigwedge_{(c,r)\in B}d^{+}((a,m),(c,r)).$
Then
![]() $d_{\mathcal{H}}(A,B)=0$
if and only if
$d_{\mathcal{H}}(A,B)=0$
if and only if
![]() $A\subseteq B$
.
$A\subseteq B$
.
Remark 6. Let (X,d) be a Yoneda-complete quasi-metric space. Then C is a g-closed set if and only if C is a Scott closed set.
Let
![]() $\alpha: \Gamma_{g}({\bf B}(X,d))\longrightarrow[0,+\infty]$
,
$\alpha: \Gamma_{g}({\bf B}(X,d))\longrightarrow[0,+\infty]$
,
![]() $C\longmapsto \bigwedge_{(x,r)\in C}r$
. Call
$C\longmapsto \bigwedge_{(x,r)\in C}r$
. Call
![]() $\alpha(C)$
the aperture of C. Let
$\alpha(C)$
the aperture of C. Let
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $C+t=\{(c,t+s)\mid (c,s)\in C\}$
. Then
$C+t=\{(c,t+s)\mid (c,s)\in C\}$
. Then
![]() $C+t$
is a g-closed set. Let
$C+t$
is a g-closed set. Let
![]() $r\leq\alpha(C)$
and
$r\leq\alpha(C)$
and
![]() $C-r=\{(c,s-r)\mid (c,s)\in C\}$
. Then
$C-r=\{(c,s-r)\mid (c,s)\in C\}$
. Then
![]() $C-r$
is a g-closed set.
$C-r$
is a g-closed set.
Proposition 7 (Ng and Ho Reference Ng and Ho2017). Let (X,d) be a quasi-metric space and
![]() $E\subseteq {\bf B}(X,d)$
. Then
$E\subseteq {\bf B}(X,d)$
. Then
![]() $cl_{g}(E)=cl_{g}(E-\alpha(E))+\alpha(E)$
.
$cl_{g}(E)=cl_{g}(E-\alpha(E))+\alpha(E)$
.
Definition 8 (Mislove Reference Mislove1999). A poset P is called a local dcpo if every directed subset of P with an upper bound has a least upper bound.
3. Local Yoneda-Complete Quasi-Metric Spaces
Definition 9. Let (X,d) be a quasi-metric space. Then (X,d) is called local Yoneda-complete if the following conditions are satisfied:
-
(1) whenever a directed family
 $(x_{i},r_{i})_{i\in I}$
in
$(x_{i},r_{i})_{i\in I}$
in
 ${\bf B}(X,d)$
has supremum (x,r), then
${\bf B}(X,d)$
has supremum (x,r), then
 $r=\bigwedge_{i\in I}r_{i}$
;
$r=\bigwedge_{i\in I}r_{i}$
; -
(2)
 ${\bf B}(X,d)$
is a local dcpo.
${\bf B}(X,d)$
is a local dcpo.
Remark 10. (1) Let (X,d) be a Yoneda-complete quasi-metric space. Then (X,d) is a local Yoneda-complete quasi-metric space. But the converse may not be true as shown by Examples 11 (1) and (2).
(2) The conditions (1) and (2) in Definition 9 are independent as shown by Examples 11 (2) and (3).
Example 11. (1)
![]() $([0,+\infty),d)$
is local Yoneda-complete, not Yoneda-complete, where
$([0,+\infty),d)$
is local Yoneda-complete, not Yoneda-complete, where
![]() $d: [0,+\infty)\times [0,+\infty)\longrightarrow[0,+\infty]$
as follows:
$d: [0,+\infty)\times [0,+\infty)\longrightarrow[0,+\infty]$
as follows:
 \begin{eqnarray*} d(x,y)=\left\{ \begin{array}{l@{\quad}l} 0,&{x\le y,}\\ {x - y,} & {y < x.}\end{array}\right. \end{eqnarray*}
\begin{eqnarray*} d(x,y)=\left\{ \begin{array}{l@{\quad}l} 0,&{x\le y,}\\ {x - y,} & {y < x.}\end{array}\right. \end{eqnarray*}
In fact, the map
![]() $(x,r)\longmapsto (x\!-\!r,-r)$
defines an order isomorphism from
$(x,r)\longmapsto (x\!-\!r,-r)$
defines an order isomorphism from
![]() ${\bf B}([0,+\infty),d)$
onto
${\bf B}([0,+\infty),d)$
onto
![]() $C=\{(a,b)\in\mathbb{R}\times(\!-\infty,0]\mid a\geq b\}$
ordered component-wise. Since C is a local dcpo, we have that
$C=\{(a,b)\in\mathbb{R}\times(\!-\infty,0]\mid a\geq b\}$
ordered component-wise. Since C is a local dcpo, we have that
![]() ${\bf B}([0,+\infty),d)$
is a local dcpo. Let
${\bf B}([0,+\infty),d)$
is a local dcpo. Let
![]() $(x_{i},r_{i})_{i\in I}$
be a directed family in
$(x_{i},r_{i})_{i\in I}$
be a directed family in
![]() ${\bf B}([0,+\infty),d)$
with supremum (x,r). Then
${\bf B}([0,+\infty),d)$
with supremum (x,r). Then
![]() $\bigvee\limits_{i\in I}^{C}(x_{i}\!-\!r_{i},-r_{i})=(x-r,-r)$
, and thus
$\bigvee\limits_{i\in I}^{C}(x_{i}\!-\!r_{i},-r_{i})=(x-r,-r)$
, and thus
![]() $\bigvee_{i\in I}(\!-r_{i})=-r$
. Hence,
$\bigvee_{i\in I}(\!-r_{i})=-r$
. Hence,
![]() $r=\bigwedge_{i\in I}r_{i}$
. So we conclude that
$r=\bigwedge_{i\in I}r_{i}$
. So we conclude that
![]() $([0,+\infty),d)$
is local Yoneda-complete. Obviously, C is not a dcpo. Then
$([0,+\infty),d)$
is local Yoneda-complete. Obviously, C is not a dcpo. Then
![]() ${\bf B}([0,+\infty),d)$
is not a dcpo, and thus
${\bf B}([0,+\infty),d)$
is not a dcpo, and thus
![]() $([0,+\infty),d)$
is not Yoneda-complete.
$([0,+\infty),d)$
is not Yoneda-complete.
(2) Every poset
![]() $(X,\leq)$
can be seen as a quasi-metric space by letting
$(X,\leq)$
can be seen as a quasi-metric space by letting
 \begin{eqnarray*} d_{\leq}(x,y)=\left\{ \begin{array}{l@{\quad}l} 0,&{x\leq y,}\\ +\infty,&{\rm otherwise}.\end{array}\right. \end{eqnarray*}
\begin{eqnarray*} d_{\leq}(x,y)=\left\{ \begin{array}{l@{\quad}l} 0,&{x\leq y,}\\ +\infty,&{\rm otherwise}.\end{array}\right. \end{eqnarray*}
On formal balls
![]() $(x,r)\leq^{d_{\leq}\!{^{+}}}(y,s)$
if and only if
$(x,r)\leq^{d_{\leq}\!{^{+}}}(y,s)$
if and only if
![]() $x\leq y$
and
$x\leq y$
and
![]() $r\geq s$
. So
$r\geq s$
. So
![]() $(x,r)\longmapsto (x,-r)$
defines an order isomorphism from
$(x,r)\longmapsto (x,-r)$
defines an order isomorphism from
![]() ${\bf B}(X,d_{\leq})$
onto
${\bf B}(X,d_{\leq})$
onto
![]() $X\times(\!-\infty,0]$
ordered component-wise. Obviously,
$X\times(\!-\infty,0]$
ordered component-wise. Obviously,
![]() $(X,d_{\leq})$
satisfies the condition (1) in Definition 9. This implies that
$(X,d_{\leq})$
satisfies the condition (1) in Definition 9. This implies that
![]() $(X,d_{\leq})$
is a local Yoneda-complete quasi-metric space if and only if X is a local dcpo. Since
$(X,d_{\leq})$
is a local Yoneda-complete quasi-metric space if and only if X is a local dcpo. Since
![]() $\mathbb{N}$
is a local dcpo, not a dcpo, we have that
$\mathbb{N}$
is a local dcpo, not a dcpo, we have that
![]() $(\mathbb{N}, d_{\preceq})$
is local Yoneda-complete, not Yoneda-complete, where
$(\mathbb{N}, d_{\preceq})$
is local Yoneda-complete, not Yoneda-complete, where
![]() $\mathbb{N}$
denotes the set of natural numbers with the usual order
$\mathbb{N}$
denotes the set of natural numbers with the usual order
![]() $\preceq$
. Moreover, let
$\preceq$
. Moreover, let
![]() $X=\mathbb{N}\cup\{\omega_{1},\omega_{2}\}$
, and let the partial order
$X=\mathbb{N}\cup\{\omega_{1},\omega_{2}\}$
, and let the partial order
![]() $\leq$
on X as follows:
$\leq$
on X as follows:
![]() $\bullet$
for
$\bullet$
for
![]() $x\in\mathbb{N}$
,
$x\in\mathbb{N}$
,
![]() $x\leq \omega_{1},\omega_{2}$
;
$x\leq \omega_{1},\omega_{2}$
;
![]() $\bullet$
$\bullet$
![]() $\omega_{1}\leq\omega_{1}$
,
$\omega_{1}\leq\omega_{1}$
,
![]() $\omega_{2}\leq\omega_{2}$
;
$\omega_{2}\leq\omega_{2}$
;
![]() $\bullet$
for
$\bullet$
for
![]() $x,y\in \mathbb{N}$
,
$x,y\in \mathbb{N}$
,
![]() $x\leq y$
if and only if
$x\leq y$
if and only if
![]() $x\preceq y$
.
$x\preceq y$
.
That is, we add
![]() $\omega_{1},\omega_{2}$
above all elements in
$\omega_{1},\omega_{2}$
above all elements in
![]() $\mathbb{N}$
. Then X is not a local dcpo, and thus
$\mathbb{N}$
. Then X is not a local dcpo, and thus
![]() $(X,d_{\leq})$
does not satisfy the condition (2) in Definition 9.
$(X,d_{\leq})$
does not satisfy the condition (2) in Definition 9.
(3) Let
![]() $X=\{0\}\cup\{\frac{1}{2^{m}}\mid m\in\mathbb{N}_{+}\}$
and d on
$X=\{0\}\cup\{\frac{1}{2^{m}}\mid m\in\mathbb{N}_{+}\}$
and d on
![]() $X\times X$
which is defined as follows:
$X\times X$
which is defined as follows:
 \begin{eqnarray*} d(x,y)=\left\{ \begin{array}{l@{\quad}l} 0,&{x=y,}\\+\infty,&{x<y,}\\\sqrt{2},&{0=y<x,}\\ x-y,&{0<y<x,}\end{array}\right. \end{eqnarray*}
\begin{eqnarray*} d(x,y)=\left\{ \begin{array}{l@{\quad}l} 0,&{x=y,}\\+\infty,&{x<y,}\\\sqrt{2},&{0=y<x,}\\ x-y,&{0<y<x,}\end{array}\right. \end{eqnarray*}
where
![]() $\mathbb{N}_{+}$
denotes the set of all positive integers. Then (X,d) is a quasi-metric space. Let
$\mathbb{N}_{+}$
denotes the set of all positive integers. Then (X,d) is a quasi-metric space. Let
![]() $(x,r), (y,s)\in {\bf B}(X,d)$
. If
$(x,r), (y,s)\in {\bf B}(X,d)$
. If
![]() $(x,r)\leq^{d{^{+}}}(y,s)$
, then
$(x,r)\leq^{d{^{+}}}(y,s)$
, then
![]() $d(x,y)\leq r-s$
, and thus
$d(x,y)\leq r-s$
, and thus
![]() $x\geq y$
. First, we shall prove that
$x\geq y$
. First, we shall prove that
![]() ${\bf B}(X,d)$
is a local dcpo. Let
${\bf B}(X,d)$
is a local dcpo. Let
![]() $(x_{i},r_{i})_{i\in I}$
be a directed family in
$(x_{i},r_{i})_{i\in I}$
be a directed family in
![]() ${\bf B}(X,d)$
with an upper bound (x,r). Then
${\bf B}(X,d)$
with an upper bound (x,r). Then
![]() $d(x_{i},x)\leq r_{i}\!-\!r$
for any
$d(x_{i},x)\leq r_{i}\!-\!r$
for any
![]() $i\in I$
. There are three cases:
$i\in I$
. There are three cases:
Case 1. There exists
![]() $i_{0}\in I$
such that
$i_{0}\in I$
such that
![]() $x_{i_{0}}=0$
. Let
$x_{i_{0}}=0$
. Let
![]() $J=\{i\in I\mid (x_{i_{0}},r_{i_{0}})\leq^{d{^{+}}} (x_{i},r_{i})\}$
. Then
$J=\{i\in I\mid (x_{i_{0}},r_{i_{0}})\leq^{d{^{+}}} (x_{i},r_{i})\}$
. Then
![]() $(x_{j},r_{j})_{j\in J}$
is a cofinal subset of
$(x_{j},r_{j})_{j\in J}$
is a cofinal subset of
![]() $(x_{i},r_{i})_{i\in I}$
. Obviously,
$(x_{i},r_{i})_{i\in I}$
. Obviously,
![]() $\bigvee_{j\in J} (x_{j},r_{j})=(0,\bigwedge_{i\in I}r_{i})$
. Then
$\bigvee_{j\in J} (x_{j},r_{j})=(0,\bigwedge_{i\in I}r_{i})$
. Then
![]() $\bigvee_{i\in I}(x_{i},r_{i})=(0,\bigwedge_{i\in I}r_{i})$
.
$\bigvee_{i\in I}(x_{i},r_{i})=(0,\bigwedge_{i\in I}r_{i})$
.
Case 2.
![]() $x_{i}\neq 0$
for any
$x_{i}\neq 0$
for any
![]() $i\in I$
and
$i\in I$
and
![]() $\bigwedge_{i\in I}x_{i}=0$
. Since (x,r) is an upper bound of
$\bigwedge_{i\in I}x_{i}=0$
. Since (x,r) is an upper bound of
![]() $(x_{i},r_{i})_{i\in I}$
, we have that
$(x_{i},r_{i})_{i\in I}$
, we have that
![]() $x\leq x_{i}$
for any
$x\leq x_{i}$
for any
![]() $i\in I$
. Then
$i\in I$
. Then
![]() $x=0$
, and thus
$x=0$
, and thus
![]() $r+\sqrt{2}\leq r_{i}$
for any
$r+\sqrt{2}\leq r_{i}$
for any
![]() $i\in I$
. Hence
$i\in I$
. Hence
![]() $(\bigwedge_{i\in I}r_{i})-\sqrt{2}\geq0$
. Obviously,
$(\bigwedge_{i\in I}r_{i})-\sqrt{2}\geq0$
. Obviously,
![]() $(x_{i},r_{i})\leq^{d{^{+}}}(0,(\bigwedge_{i\in I}r_{i})-\sqrt{2})$
for any
$(x_{i},r_{i})\leq^{d{^{+}}}(0,(\bigwedge_{i\in I}r_{i})-\sqrt{2})$
for any
![]() $i\in I$
. Let (y,s) be an upper bound of
$i\in I$
. Let (y,s) be an upper bound of
![]() $(x_{i},r_{i})_{i\in I}$
in
$(x_{i},r_{i})_{i\in I}$
in
![]() ${\bf B}(X,d)$
. Then
${\bf B}(X,d)$
. Then
![]() $y\leq x_{i}$
for any
$y\leq x_{i}$
for any
![]() $i\in I$
, and thus
$i\in I$
, and thus
![]() $y=0$
. This implies
$y=0$
. This implies
![]() $\sqrt{2}+s\leq\bigwedge_{i\in I}r_{i}$
, that is
$\sqrt{2}+s\leq\bigwedge_{i\in I}r_{i}$
, that is
![]() $d(0,0)\leq (\bigwedge_{i\in I}r_{i})-\sqrt{2}-s$
, and hence
$d(0,0)\leq (\bigwedge_{i\in I}r_{i})-\sqrt{2}-s$
, and hence
![]() $(0,(\bigwedge_{i\in I}r_{i})-\sqrt{2})\leq^{d{^{+}}}(y,s)$
. Therefore,
$(0,(\bigwedge_{i\in I}r_{i})-\sqrt{2})\leq^{d{^{+}}}(y,s)$
. Therefore,
![]() $\bigvee_{i\in I}(x_{i},r_{i})=(0,(\bigwedge_{i\in I}r_{i})-\sqrt{2})$
. In particular,
$\bigvee_{i\in I}(x_{i},r_{i})=(0,(\bigwedge_{i\in I}r_{i})-\sqrt{2})$
. In particular,
![]() $(\frac{1}{2^{m}},\frac{1}{2^{m}}+\sqrt{2})_{m\in\mathbb{N}}$
is a directed family in
$(\frac{1}{2^{m}},\frac{1}{2^{m}}+\sqrt{2})_{m\in\mathbb{N}}$
is a directed family in
![]() ${\bf B}(X,d)$
and has an upper bound (0,0). So we conclude that
${\bf B}(X,d)$
and has an upper bound (0,0). So we conclude that
![]() $\bigvee_{m\in\mathbb{N}}(\frac{1}{2^{m}},\frac{1}{2^{m}}+\sqrt{2})=(0,0)$
.
$\bigvee_{m\in\mathbb{N}}(\frac{1}{2^{m}},\frac{1}{2^{m}}+\sqrt{2})=(0,0)$
.
Case 3.
![]() $x_{i}\neq 0$
for any
$x_{i}\neq 0$
for any
![]() $i\in I$
and
$i\in I$
and
![]() $\bigwedge_{i\in I}x_{i}\neq0$
. Then there exists
$\bigwedge_{i\in I}x_{i}\neq0$
. Then there exists
![]() $m\in \mathbb{N}$
such that
$m\in \mathbb{N}$
such that
![]() $\bigwedge_{i\in I}x_{i}=\frac{1}{2^{m}}$
, and thus there exists
$\bigwedge_{i\in I}x_{i}=\frac{1}{2^{m}}$
, and thus there exists
![]() $i_{1}\in I$
such that
$i_{1}\in I$
such that
![]() $x_{i_{1}}=\frac{1}{2^{m}}$
. For all i in I, there exists
$x_{i_{1}}=\frac{1}{2^{m}}$
. For all i in I, there exists
![]() $j\in I$
such that
$j\in I$
such that
![]() $(x_{i},r_{i})$
,
$(x_{i},r_{i})$
,
![]() $(x_{i_{1}},r_{i_{1}})\leq^{d{^{+}}}(x_{j},r_{j})$
, and thus
$(x_{i_{1}},r_{i_{1}})\leq^{d{^{+}}}(x_{j},r_{j})$
, and thus
![]() $x_{j}=\frac{1}{2^{m}}$
. So we conclude that
$x_{j}=\frac{1}{2^{m}}$
. So we conclude that
![]() $d(x_{i},\frac{1}{2^{m}})\leq r_{i}-r_{j}\leq r_{i}-\bigwedge_{i\in I}r_{i}$
. This shows that
$d(x_{i},\frac{1}{2^{m}})\leq r_{i}-r_{j}\leq r_{i}-\bigwedge_{i\in I}r_{i}$
. This shows that
![]() $(\frac{1}{2^{m}},\bigwedge_{i\in I}r_{i})$
is an upper bound of
$(\frac{1}{2^{m}},\bigwedge_{i\in I}r_{i})$
is an upper bound of
![]() $(x_{i},r_{i})_{i\in I}$
. Let (y,s) be an upper bound of
$(x_{i},r_{i})_{i\in I}$
. Let (y,s) be an upper bound of
![]() $(x_{i},r_{i})_{i\in I}$
in
$(x_{i},r_{i})_{i\in I}$
in
![]() ${\bf B}(X,d)$
. Then
${\bf B}(X,d)$
. Then
![]() $d(x_{i},y)\leq r_{i}-s$
for any
$d(x_{i},y)\leq r_{i}-s$
for any
![]() $i\in I$
. For all k in I, there exists
$i\in I$
. For all k in I, there exists
![]() $k_{0}\in I$
such that
$k_{0}\in I$
such that
![]() $(x_{k},r_{k}), (x_{i_{1}},r_{i_{1}})\leq^{d{^{+}}} (x_{k_{0}},r_{k_{0}})$
, and thus
$(x_{k},r_{k}), (x_{i_{1}},r_{i_{1}})\leq^{d{^{+}}} (x_{k_{0}},r_{k_{0}})$
, and thus
![]() $x_{k_{0}}=\frac{1}{2^{m}}$
and
$x_{k_{0}}=\frac{1}{2^{m}}$
and
![]() $r_{k_{0}}\leq r_{k}$
. So we conclude that
$r_{k_{0}}\leq r_{k}$
. So we conclude that
![]() $d(\frac{1}{2^{m}},y)\leq r_{k_{0}}-s\leq r_{k}-s$
. This implies
$d(\frac{1}{2^{m}},y)\leq r_{k_{0}}-s\leq r_{k}-s$
. This implies
![]() $d(\frac{1}{2^{m}},y)+s\leq \bigwedge_{i\in I}r_{i}$
. Hence,
$d(\frac{1}{2^{m}},y)+s\leq \bigwedge_{i\in I}r_{i}$
. Hence,
![]() $(\frac{1}{2^{m}},\bigwedge_{i\in I}r_{i})\leq^{d{^{+}}} (y,s)$
. Therefore,
$(\frac{1}{2^{m}},\bigwedge_{i\in I}r_{i})\leq^{d{^{+}}} (y,s)$
. Therefore,
![]() $\bigvee_{i\in I}(x_{i},r_{i})=(\frac{1}{2^{m}},\bigwedge_{i\in I}r_{i})$
.
$\bigvee_{i\in I}(x_{i},r_{i})=(\frac{1}{2^{m}},\bigwedge_{i\in I}r_{i})$
.
Consequently,
![]() ${\bf B}(X,d)$
is a local dcpo. Yet since
${\bf B}(X,d)$
is a local dcpo. Yet since
![]() $\bigvee_{m\in\mathbb{N}}(\frac{1}{2^{m}},\frac{1}{2^{m}}+\sqrt{2})=(0,0)$
as shown in Case 2 and
$\bigvee_{m\in\mathbb{N}}(\frac{1}{2^{m}},\frac{1}{2^{m}}+\sqrt{2})=(0,0)$
as shown in Case 2 and
![]() $\bigwedge_{m\in\mathbb{N}}(\frac{1}{2^{m}}+\sqrt{2})=\sqrt{2}$
, we have that (X,d) does not satisfy the condition (1) in Definition 9.
$\bigwedge_{m\in\mathbb{N}}(\frac{1}{2^{m}}+\sqrt{2})=\sqrt{2}$
, we have that (X,d) does not satisfy the condition (1) in Definition 9.
Proposition 12. A metric space (X,d) is local Yoneda-complete if and only if (X,d) is complete.
Proof. Sufficiency. Let (X,d) be a complete metric space. Then (X,d) is a Yoneda-complete metric space, and thus (X,d) is local Yoneda-complete.
Necessity. Let (X,d) be a local Yoneda-complete metric space. We shall prove that
![]() ${\bf B}(X,d)$
is a dcpo. Let
${\bf B}(X,d)$
is a dcpo. Let
![]() $(x_{i},r_{i})_{i\in I}$
be a directed family in
$(x_{i},r_{i})_{i\in I}$
be a directed family in
![]() ${\bf B}(X,d)$
and let
${\bf B}(X,d)$
and let
![]() $r_{\infty}=\bigwedge_{i\in I}r_{i}$
. Then there exists
$r_{\infty}=\bigwedge_{i\in I}r_{i}$
. Then there exists
![]() $(y_{n},s_{n})\in(x_{i},r_{i})_{i\in I}$
such that
$(y_{n},s_{n})\in(x_{i},r_{i})_{i\in I}$
such that
![]() $s_{n}<r_{\infty}+\frac{1}{n}$
for any
$s_{n}<r_{\infty}+\frac{1}{n}$
for any
![]() $n\in \mathbb{N}_{+}$
, where
$n\in \mathbb{N}_{+}$
, where
![]() $\mathbb{N}_{+}$
denotes the set of all positive integers. Let
$\mathbb{N}_{+}$
denotes the set of all positive integers. Let
![]() $(x_{1},r_{1})=(y_{1},s_{1})$
. For any
$(x_{1},r_{1})=(y_{1},s_{1})$
. For any
![]() $n>1$
, let
$n>1$
, let
![]() $(x_{n},r_{n})$
be an upper bound of
$(x_{n},r_{n})$
be an upper bound of
![]() $(y_{n},s_{n})$
and
$(y_{n},s_{n})$
and
![]() $(x_{n-1},r_{n-1})$
. Then
$(x_{n-1},r_{n-1})$
. Then
![]() $(x_{1},r_{1})\leq^{d{^{+}}}(x_{2},r_{2})\leq^{d{^{+}}}\cdot\cdot\cdot\leq^{d{^{+}}}(x_{n},r_{n})\leq^{d{^{+}}}\cdot\cdot\cdot,$
and thus
$(x_{1},r_{1})\leq^{d{^{+}}}(x_{2},r_{2})\leq^{d{^{+}}}\cdot\cdot\cdot\leq^{d{^{+}}}(x_{n},r_{n})\leq^{d{^{+}}}\cdot\cdot\cdot,$
and thus
![]() $\cdot\cdot\cdot \leq r_{n}\leq r_{n-1}\leq\cdot\cdot\cdot\leq r_{2}\leq r_{1}$
. For a fixed
$\cdot\cdot\cdot \leq r_{n}\leq r_{n-1}\leq\cdot\cdot\cdot\leq r_{2}\leq r_{1}$
. For a fixed
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $n_{0}\in \mathbb{N}_{+}$
such that
$n_{0}\in \mathbb{N}_{+}$
such that
![]() $r_{n}-r_{m}<\varepsilon$
for any
$r_{n}-r_{m}<\varepsilon$
for any
![]() $n_{0}\leq n\leq m$
. For all n in
$n_{0}\leq n\leq m$
. For all n in
![]() $\mathbb{N}_{+}$
, there exists
$\mathbb{N}_{+}$
, there exists
![]() $l\in \mathbb{N}_{+}$
such that
$l\in \mathbb{N}_{+}$
such that
![]() $n_{0},n\leq l$
, and by symmetry
$n_{0},n\leq l$
, and by symmetry
![]() $d(x_{l},x_{n_{0}})\leq r_{n_{0}}-r_{l}<\varepsilon$
, and thus
$d(x_{l},x_{n_{0}})\leq r_{n_{0}}-r_{l}<\varepsilon$
, and thus
![]() $d(x_{n},x_{n_{0}})\leq d(x_{n},x_{l})+d(x_{l},x_{n_{0}})< r_{n}-r_{l}+\varepsilon\leq r_{n}+\varepsilon.$
Hence
$d(x_{n},x_{n_{0}})\leq d(x_{n},x_{l})+d(x_{l},x_{n_{0}})< r_{n}-r_{l}+\varepsilon\leq r_{n}+\varepsilon.$
Hence
![]() $(x_{n},r_{n}+\varepsilon)\leq^{d{^{+}}} (x_{n_{0}},0)$
. So we conclude that
$(x_{n},r_{n}+\varepsilon)\leq^{d{^{+}}} (x_{n_{0}},0)$
. So we conclude that
![]() $(x_{n_{0}},0)$
is an upper bound of the directed family
$(x_{n_{0}},0)$
is an upper bound of the directed family
![]() $(x_{n},r_{n}+\varepsilon)_{n\in\mathbb{N}_{+}}$
. By hypothesis, we have that
$(x_{n},r_{n}+\varepsilon)_{n\in\mathbb{N}_{+}}$
. By hypothesis, we have that
![]() $\bigvee_{n\in\mathbb{N}_{+}}(x_{n},r_{n}+\varepsilon)$
exists, denoted by (x,r). Then
$\bigvee_{n\in\mathbb{N}_{+}}(x_{n},r_{n}+\varepsilon)$
exists, denoted by (x,r). Then
![]() $r=\bigwedge_{n\in\mathbb{N}_{+}}(r_{n}+\varepsilon)$
. Obviously,
$r=\bigwedge_{n\in\mathbb{N}_{+}}(r_{n}+\varepsilon)$
. Obviously,
![]() $(x,r-\varepsilon)$
is an upper bound of
$(x,r-\varepsilon)$
is an upper bound of
![]() $(x_{n},r_{n})_{n\in\mathbb{N}_{+}}$
. Let (y,s) be an upper bound of
$(x_{n},r_{n})_{n\in\mathbb{N}_{+}}$
. Let (y,s) be an upper bound of
![]() $(x_{n},r_{n})_{n\in\mathbb{N}_{+}}$
. Then
$(x_{n},r_{n})_{n\in\mathbb{N}_{+}}$
. Then
![]() $(x_{n},r_{n}+\varepsilon)\leq^{d{^{+}}}(y,s+\varepsilon)$
for any
$(x_{n},r_{n}+\varepsilon)\leq^{d{^{+}}}(y,s+\varepsilon)$
for any
![]() $n\in\mathbb{N}_{+}$
, and thus
$n\in\mathbb{N}_{+}$
, and thus
![]() $(x,r)\leq^{d{^{+}}}(y,s+\varepsilon)$
. Hence
$(x,r)\leq^{d{^{+}}}(y,s+\varepsilon)$
. Hence
![]() $(x,r-\varepsilon)\leq^{d{^{+}}}(y,s)$
, and so we conclude that
$(x,r-\varepsilon)\leq^{d{^{+}}}(y,s)$
, and so we conclude that
![]() $\bigvee_{n\in\mathbb{N}_{+}}(x_{n},r_{n})=(x,r-\varepsilon)$
. Let
$\bigvee_{n\in\mathbb{N}_{+}}(x_{n},r_{n})=(x,r-\varepsilon)$
. Let
![]() $i\in I$
. Then there exists
$i\in I$
. Then there exists
![]() $(z_{n},t_{n})\in (x_{i},r_{i})_{i\in I}$
such that
$(z_{n},t_{n})\in (x_{i},r_{i})_{i\in I}$
such that
![]() $(x_{n},r_{n}),(x_{i},r_{i})\leq^{d{^{+}}}(z_{n},t_{n})$
for any
$(x_{n},r_{n}),(x_{i},r_{i})\leq^{d{^{+}}}(z_{n},t_{n})$
for any
![]() $n\in \mathbb{N}_{+}$
. Hence
$n\in \mathbb{N}_{+}$
. Hence
 \begin{align*}\begin{array}{lll}d(x_{i},x)\leq d(x_{i},z_{n})+d(z_{n},x_{n})+d(x_{n},x)&\leq& r_{i}-t_{n}+r_{n}-t_{n}+r_{n}-(r-\varepsilon)\\[3pt]&=&r_{i}-(r-\varepsilon)+2(r_{n}-t_{n})\\[3pt]&\leq&r_{i}-(r-\varepsilon)+2(r_{n}-r_{\infty})\\[3pt]&<&r_{i}-(r-\varepsilon)+\frac{2}{n}.\end{array}\end{align*}
\begin{align*}\begin{array}{lll}d(x_{i},x)\leq d(x_{i},z_{n})+d(z_{n},x_{n})+d(x_{n},x)&\leq& r_{i}-t_{n}+r_{n}-t_{n}+r_{n}-(r-\varepsilon)\\[3pt]&=&r_{i}-(r-\varepsilon)+2(r_{n}-t_{n})\\[3pt]&\leq&r_{i}-(r-\varepsilon)+2(r_{n}-r_{\infty})\\[3pt]&<&r_{i}-(r-\varepsilon)+\frac{2}{n}.\end{array}\end{align*}
This implies
![]() $d(x_{i},x)\leq r_{i}-(r-\varepsilon)$
. Then
$d(x_{i},x)\leq r_{i}-(r-\varepsilon)$
. Then
![]() $(x_{i},r_{i})\leq^{d{^{+}}}(x,r-\varepsilon)$
, and thus
$(x_{i},r_{i})\leq^{d{^{+}}}(x,r-\varepsilon)$
, and thus
![]() $(x,r-\varepsilon)$
is an upper bound of
$(x,r-\varepsilon)$
is an upper bound of
![]() $(x_{i},r_{i})_{i\in I}$
. Suppose that (z,t) is an upper bound of
$(x_{i},r_{i})_{i\in I}$
. Suppose that (z,t) is an upper bound of
![]() $(x_{i},r_{i})_{i\in I}$
. Then (z,t) is an upper bound of
$(x_{i},r_{i})_{i\in I}$
. Then (z,t) is an upper bound of
![]() $(x_{n},r_{n})_{n\in\mathbb{N}_{+}}$
, and thus
$(x_{n},r_{n})_{n\in\mathbb{N}_{+}}$
, and thus
![]() $(x,r-\varepsilon)\leq^{d{^{+}}}(z,t)$
. Hence,
$(x,r-\varepsilon)\leq^{d{^{+}}}(z,t)$
. Hence,
![]() $\bigvee_{i\in I}(x_{i},r_{i})=(x,r-\varepsilon)$
. This shows that
$\bigvee_{i\in I}(x_{i},r_{i})=(x,r-\varepsilon)$
. This shows that
![]() ${\bf B}(X,d)$
is a dcpo. Therefore, (X,d) is complete.
${\bf B}(X,d)$
is a dcpo. Therefore, (X,d) is complete.
Definition 13. Let (X,d) be a quasi-metric space, and
![]() $(x_{i})_{i\in I,\sqsubseteq}$
be a net. If there exists
$(x_{i})_{i\in I,\sqsubseteq}$
be a net. If there exists
![]() $(r_{i})_{i\in I,\sqsubseteq}\subseteq[0,+\infty)$
such that
$(r_{i})_{i\in I,\sqsubseteq}\subseteq[0,+\infty)$
such that
![]() $(x_{i},r_{i})_{i\in I,\sqsubseteq}$
is a monotone net in
$(x_{i},r_{i})_{i\in I,\sqsubseteq}$
is a monotone net in
![]() ${\bf B}(X,d)$
and has an upper bound, then
${\bf B}(X,d)$
and has an upper bound, then
![]() $(x_{i})_{i\in I,\sqsubseteq}$
is called a local net.
$(x_{i})_{i\in I,\sqsubseteq}$
is called a local net.
Theorem 14. Let (X,d) be a quasi-metric space. Then every local net has a d-limit if and only if (X,d) is a local Yoneda-complete quasi-metric space.
Proof. Necessity. Let (X,d) be a quasi-metric space where every local net has a d-limit. We start by proving part (2) of Definition 9. Let
![]() $(x_{i},r_{i})_{i\in I}$
be a directed family in
$(x_{i},r_{i})_{i\in I}$
be a directed family in
![]() ${\bf B}(X,d)$
with an upper bound. Define a preorder
${\bf B}(X,d)$
with an upper bound. Define a preorder
![]() $\sqsubseteq$
on I as follows:
$\sqsubseteq$
on I as follows:
Then
![]() $(x_{i},r_{i})_{i\in I,\sqsubseteq}$
is a monotone net in
$(x_{i},r_{i})_{i\in I,\sqsubseteq}$
is a monotone net in
![]() ${\bf B}(X,d)$
and has an upper bound, and thus
${\bf B}(X,d)$
and has an upper bound, and thus
![]() $(x_{i})_{i\in I,\sqsubseteq}$
is a local net. Hence, the net
$(x_{i})_{i\in I,\sqsubseteq}$
is a local net. Hence, the net
![]() $(x_{i})_{i\in I,\sqsubseteq}$
has a d-limit y. This implies
$(x_{i})_{i\in I,\sqsubseteq}$
has a d-limit y. This implies
![]() $\bigwedge_{i\in I}\bigvee_{j\in I,i\sqsubseteq j}d(x_{j},y)=0$
. Then for all
$\bigwedge_{i\in I}\bigvee_{j\in I,i\sqsubseteq j}d(x_{j},y)=0$
. Then for all
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $i_{0}\in I$
such that
$i_{0}\in I$
such that
![]() $\bigvee_{j\in I,i_{0}\sqsubseteq j}d(x_{j},y)<\varepsilon$
. Let
$\bigvee_{j\in I,i_{0}\sqsubseteq j}d(x_{j},y)<\varepsilon$
. Let
![]() $i\in I$
. Then there exists
$i\in I$
. Then there exists
![]() $j\in I$
such that
$j\in I$
such that
![]() $i, i_{0}\sqsubseteq j$
, and thus
$i, i_{0}\sqsubseteq j$
, and thus
 $$\begin{array}{lll}d(x_{i},y)\leq d(x_{i},x_{j})+d(x_{j},y)&\leq& r_{i}-r_{j}+d(x_{j},y)\\[3pt]&\leq& r_{i}-\bigwedge_{i\in I}r_{i}+d(x_{j},y)\\[3pt]&<&r_{i}-\bigwedge_{i\in I}r_{i}+\varepsilon.\end{array}$$
$$\begin{array}{lll}d(x_{i},y)\leq d(x_{i},x_{j})+d(x_{j},y)&\leq& r_{i}-r_{j}+d(x_{j},y)\\[3pt]&\leq& r_{i}-\bigwedge_{i\in I}r_{i}+d(x_{j},y)\\[3pt]&<&r_{i}-\bigwedge_{i\in I}r_{i}+\varepsilon.\end{array}$$
So we conclude that
![]() $d(x_{i},y)\leq r_{i}-\bigwedge_{i\in I}r_{i}$
. Hence,
$d(x_{i},y)\leq r_{i}-\bigwedge_{i\in I}r_{i}$
. Hence,
![]() $(y,\bigwedge_{i\in I}r_{i})$
is an upper bound of
$(y,\bigwedge_{i\in I}r_{i})$
is an upper bound of
![]() $(x_{i},r_{i})_{i\in I}$
. Let (z,s) be an upper bound of
$(x_{i},r_{i})_{i\in I}$
. Let (z,s) be an upper bound of
![]() $(x_{i},r_{i})_{i\in I}$
. Then
$(x_{i},r_{i})_{i\in I}$
. Then
![]() $d(x_{i},z)\leq r_{i}-s$
for any
$d(x_{i},z)\leq r_{i}-s$
for any
![]() $i\in I$
, and thus
$i\in I$
, and thus
![]() $s\leq\bigwedge_{i\in I}r_{i}$
. Since
$s\leq\bigwedge_{i\in I}r_{i}$
. Since
![]() $d(y,z)=\bigwedge_{i\in I}\bigvee_{j\in I,i\sqsubseteq j}d(x_{j},z)\leq\bigwedge_{i\in I}\bigvee_{j\in I,i\sqsubseteq j}(r_{j}-s)\leq\bigwedge_{i\in I}(r_{i}-s)=(\bigwedge_{i\in I}r_{i})-s$
, we have that
$d(y,z)=\bigwedge_{i\in I}\bigvee_{j\in I,i\sqsubseteq j}d(x_{j},z)\leq\bigwedge_{i\in I}\bigvee_{j\in I,i\sqsubseteq j}(r_{j}-s)\leq\bigwedge_{i\in I}(r_{i}-s)=(\bigwedge_{i\in I}r_{i})-s$
, we have that
![]() $(y,\bigwedge_{i\in I}r_{i})\leq^{d{^{+}}}(z,s)$
. This shows that
$(y,\bigwedge_{i\in I}r_{i})\leq^{d{^{+}}}(z,s)$
. This shows that
![]() $\bigvee_{i\in I}(x_{i},r_{i})=(y,\bigwedge_{i\in I}r_{i})$
. Part (1) of Definition 9 is then a trivial consequence. Therefore, (X,d) is a local Yoneda-complete quasi-metric space.
$\bigvee_{i\in I}(x_{i},r_{i})=(y,\bigwedge_{i\in I}r_{i})$
. Part (1) of Definition 9 is then a trivial consequence. Therefore, (X,d) is a local Yoneda-complete quasi-metric space.
Sufficiency. Let (X,d) be a local Yoneda-complete quasi-metric space, and let
![]() $(x_{i})_{i\in I,\sqsubseteq}$
be a local net. Then, there exists
$(x_{i})_{i\in I,\sqsubseteq}$
be a local net. Then, there exists
![]() $(r_{i})_{i\in I,\sqsubseteq}\subseteq[0,+\infty)$
such that
$(r_{i})_{i\in I,\sqsubseteq}\subseteq[0,+\infty)$
such that
![]() $(x_{i},r_{i})_{i\in I,\sqsubseteq}$
is a monotone net in
$(x_{i},r_{i})_{i\in I,\sqsubseteq}$
is a monotone net in
![]() ${\bf B}(X,d)$
and has an upper bound, and thus
${\bf B}(X,d)$
and has an upper bound, and thus
![]() $(x_{i},r_{i})_{i\in I}$
is a directed family in
$(x_{i},r_{i})_{i\in I}$
is a directed family in
![]() ${\bf B}(X,d)$
and has an upper bound. Hence
${\bf B}(X,d)$
and has an upper bound. Hence
![]() $\bigvee_{i\in I}(x_{i},r_{i})$
exists, denoted by (x,r). By hypothesis, we have that
$\bigvee_{i\in I}(x_{i},r_{i})$
exists, denoted by (x,r). By hypothesis, we have that
![]() $r=\bigwedge_{i\in I}r_{i}$
. Then
$r=\bigwedge_{i\in I}r_{i}$
. Then
![]() $(x_{i},r_{i}-\bigwedge_{i\in I}r_{i})_{i\in I,\sqsubseteq}$
is a Cauchy-weighted net and
$(x_{i},r_{i}-\bigwedge_{i\in I}r_{i})_{i\in I,\sqsubseteq}$
is a Cauchy-weighted net and
![]() $\bigvee_{i\in I}(x_{i},r_{i}-\bigwedge_{i\in I}r_{i})=(x,0)$
. Next, we shall prove that x is the d-limit of
$\bigvee_{i\in I}(x_{i},r_{i}-\bigwedge_{i\in I}r_{i})=(x,0)$
. Next, we shall prove that x is the d-limit of
![]() $(x_{i})_{i\in I,\sqsubseteq}$
. For any
$(x_{i})_{i\in I,\sqsubseteq}$
. For any
![]() $z\in X$
, since
$z\in X$
, since
![]() $d(x_{i},z)\leq d(x_{i},x)+d(x,z)\leq r_{i}-\bigwedge_{i\in I}r_{i}+d(x,z)$
for any
$d(x_{i},z)\leq d(x_{i},x)+d(x,z)\leq r_{i}-\bigwedge_{i\in I}r_{i}+d(x,z)$
for any
![]() $i\in I$
, we have that
$i\in I$
, we have that
![]() $d(x_{i},z)-r_{i}\leq d(x,z)-\bigwedge_{i\in I}r_{i}$
for any
$d(x_{i},z)-r_{i}\leq d(x,z)-\bigwedge_{i\in I}r_{i}$
for any
![]() $i\in I$
. Obviously,
$i\in I$
. Obviously,
![]() $\bigvee_{i\in I}(d(x_{i},z)-r_{i})$
exists, denoted by s. Then
$\bigvee_{i\in I}(d(x_{i},z)-r_{i})$
exists, denoted by s. Then
![]() $s\leq d(x,z)-\bigwedge_{i\in I}r_{i}$
. Suppose that
$s\leq d(x,z)-\bigwedge_{i\in I}r_{i}$
. Suppose that
![]() $s<d(x,z)-\bigwedge_{i\in I}r_{i}$
. Then
$s<d(x,z)-\bigwedge_{i\in I}r_{i}$
. Then
![]() $s<+\infty$
. Since
$s<+\infty$
. Since
![]() $d(x_{i},z)-r_{i}\leq s$
for any
$d(x_{i},z)-r_{i}\leq s$
for any
![]() $i\in I$
, we have that
$i\in I$
, we have that
![]() $d(x_{i},z)\leq r_{i}+s$
for any
$d(x_{i},z)\leq r_{i}+s$
for any
![]() $i\in I$
. Then
$i\in I$
. Then
![]() $(x_{i},r_{i}+s)\leq^{d{^{+}}}(z,0)$
for any
$(x_{i},r_{i}+s)\leq^{d{^{+}}}(z,0)$
for any
![]() $i\in I$
, and thus
$i\in I$
, and thus
![]() $\bigvee_{i\in I}(x_{i},r_{i}+s)$
exists, denoted by
$\bigvee_{i\in I}(x_{i},r_{i}+s)$
exists, denoted by
![]() $(y,\bigwedge_{i\in I}r_{i}+s)$
. Hence
$(y,\bigwedge_{i\in I}r_{i}+s)$
. Hence
![]() $y=x$
, that is
$y=x$
, that is
![]() $\bigvee_{i\in I}(x_{i},r_{i}+s)=(x,\bigwedge_{i\in I}r_{i}+s)$
. This implies
$\bigvee_{i\in I}(x_{i},r_{i}+s)=(x,\bigwedge_{i\in I}r_{i}+s)$
. This implies
![]() $(x,\bigwedge_{i\in I}r_{i}+s)\leq^{d{^{+}}}(z,0)$
. Then
$(x,\bigwedge_{i\in I}r_{i}+s)\leq^{d{^{+}}}(z,0)$
. Then
![]() $d(x,z)\leq\bigwedge_{i\in I}r_{i}+s$
, which is a contradiction. So we conclude that
$d(x,z)\leq\bigwedge_{i\in I}r_{i}+s$
, which is a contradiction. So we conclude that
![]() $s=d(x,z)-\bigwedge_{i\in I}r_{i}$
. Therefore,
$s=d(x,z)-\bigwedge_{i\in I}r_{i}$
. Therefore,
![]() $d(x,z)=\bigvee_{i\in I}(d(x_{i},z)-r_{i})+\bigwedge_{i\in I}r_{i}=\bigvee_{i\in I}(d(x_{i},z)-r_{i}+\bigwedge_{i\in I}r_{i})$
. This shows that x is the d-limit of
$d(x,z)=\bigvee_{i\in I}(d(x_{i},z)-r_{i})+\bigwedge_{i\in I}r_{i}=\bigvee_{i\in I}(d(x_{i},z)-r_{i}+\bigwedge_{i\in I}r_{i})$
. This shows that x is the d-limit of
![]() $(x_{i})_{i\in I,\sqsubseteq}$
.
$(x_{i})_{i\in I,\sqsubseteq}$
.
Proposition 15. Every local Yoneda-complete quasi-metric space is standard.
Proof. Let (X,d) be a local Yoneda-complete quasi-metric space and let
![]() $(x_{i},r_{i})_{i\in I}$
be a directed family in
$(x_{i},r_{i})_{i\in I}$
be a directed family in
![]() ${\bf B}(X,d)$
. By Lemma 7.4.25 of Goubault-Larrecq (Reference Goubault-Larrecq2013) and Theorem 14, we have that (x,r) is the supremum of
${\bf B}(X,d)$
. By Lemma 7.4.25 of Goubault-Larrecq (Reference Goubault-Larrecq2013) and Theorem 14, we have that (x,r) is the supremum of
![]() $(x_{i},r_{i})_{i\in I}$
if and only if x is the d-limit of
$(x_{i},r_{i})_{i\in I}$
if and only if x is the d-limit of
![]() $(x_{i})_{i\in I,\sqsubseteq}$
and
$(x_{i})_{i\in I,\sqsubseteq}$
and
![]() $r=\bigwedge_{i\in I}r_{i}$
. For any
$r=\bigwedge_{i\in I}r_{i}$
. For any
![]() $s\in [0,+\infty)$
, then the existence of a supremum is equivalent for
$s\in [0,+\infty)$
, then the existence of a supremum is equivalent for
![]() $(x_{i},r_{i})_{i\in I}$
and for
$(x_{i},r_{i})_{i\in I}$
and for
![]() $(x_{i},r_{i}+s)_{i\in I}$
, both being equivalent to the existence of a d-limit of the net
$(x_{i},r_{i}+s)_{i\in I}$
, both being equivalent to the existence of a d-limit of the net
![]() $(x_{i})_{i\in I,\sqsubseteq}$
. Therefore, (X,d) is standard.
$(x_{i})_{i\in I,\sqsubseteq}$
. Therefore, (X,d) is standard.
4. The Local Yoneda Completions of Quasi-Metric Spaces
Definition 16. A local Yoneda completion of a quasi-metric space (X,d) is a local Yoneda-complete quasi-metric space
![]() $(\hat{X},\hat{d})$
, together with a Y-continuous map
$(\hat{X},\hat{d})$
, together with a Y-continuous map
![]() $\tau: X\longrightarrow\hat{X}$
, such that for any local Yoneda-complete quasi-metric space
$\tau: X\longrightarrow\hat{X}$
, such that for any local Yoneda-complete quasi-metric space
![]() $(X^{'}\!,e)$
and Y-continuous map
$(X^{'}\!,e)$
and Y-continuous map
![]() $f: X\longrightarrow X^{'}$
, there exists a unique Y-continuous map
$f: X\longrightarrow X^{'}$
, there exists a unique Y-continuous map
![]() $\hat{f}:\hat{X}\longrightarrow X^{'}$
such that
$\hat{f}:\hat{X}\longrightarrow X^{'}$
such that
![]() $f=\hat{f}\circ\tau$
, i.e., the following diagram commutes:
$f=\hat{f}\circ\tau$
, i.e., the following diagram commutes:

Definition 17. Let (X,d) be a quasi-metric space. A subset A of
![]() ${\bf B}(X,d)$
is called a local g-set if for any Y-continuous function
${\bf B}(X,d)$
is called a local g-set if for any Y-continuous function
![]() $f: X\longrightarrow X^{'}$
mapping into a local Yoneda complete quasi-metric space
$f: X\longrightarrow X^{'}$
mapping into a local Yoneda complete quasi-metric space
![]() $(X^{'}\!,d^{'})$
, there exists a unique
$(X^{'}\!,d^{'})$
, there exists a unique
![]() $(y_{A},r_{A})\in {\bf B}(X^{'}\!,d^{'})$
such that
$(y_{A},r_{A})\in {\bf B}(X^{'}\!,d^{'})$
such that
![]() $cl_{g}({\bf B}(f)(A))=\mathord{\downarrow}\hspace{0.05em}(y_{A},r_{A})$
.
$cl_{g}({\bf B}(f)(A))=\mathord{\downarrow}\hspace{0.05em}(y_{A},r_{A})$
.
Proposition 18. Let (X,d) be a quasi-metric space, and A be a local g-set satisfying
![]() $\alpha(A)=0$
. If
$\alpha(A)=0$
. If
![]() $(Y,d^{'})$
is a local Yoneda complete quasi-metric space and
$(Y,d^{'})$
is a local Yoneda complete quasi-metric space and
![]() $f: X\longrightarrow Y$
is a Y-continuous function, then there exists a unique
$f: X\longrightarrow Y$
is a Y-continuous function, then there exists a unique
![]() $(y_{A},r_{A})\in {\bf B}(Y\!,d^{'})$
such that
$(y_{A},r_{A})\in {\bf B}(Y\!,d^{'})$
such that
![]() $cl_{g}({\bf B}(f)(A))=\mathord{\downarrow}\hspace{0.05em}(y_{A},r_{A})$
and
$cl_{g}({\bf B}(f)(A))=\mathord{\downarrow}\hspace{0.05em}(y_{A},r_{A})$
and
![]() $r_{A}=0$
.
$r_{A}=0$
.
Proof. By Definition 17, we only need to prove that
![]() $r_{A}=0$
. Let
$r_{A}=0$
. Let
![]() $(y,s)\in cl_{g}({\bf B}(f)(A))$
. Then
$(y,s)\in cl_{g}({\bf B}(f)(A))$
. Then
![]() $(y,s)\leq^{d^{'}{^{+}}}(y_{A},r_{A})$
, and thus
$(y,s)\leq^{d^{'}{^{+}}}(y_{A},r_{A})$
, and thus
![]() $r_{A}\leq s$
. Hence
$r_{A}\leq s$
. Hence
![]() $r_{A}\leq \alpha(cl_{g}({\bf B}(f)(A)))\leq \alpha(A)=0$
, that is,
$r_{A}\leq \alpha(cl_{g}({\bf B}(f)(A)))\leq \alpha(A)=0$
, that is,
![]() $r_{A}=0$
.
$r_{A}=0$
.
Let
![]() $\tilde{X}=\{A\subseteq {\bf B}(X,d)\mid A\mbox{ is a $g$-closed set satisfying }\alpha(A)=0\}$
, where the notion of g-closed sets is introduced in Definition 5. Define a mapping
$\tilde{X}=\{A\subseteq {\bf B}(X,d)\mid A\mbox{ is a $g$-closed set satisfying }\alpha(A)=0\}$
, where the notion of g-closed sets is introduced in Definition 5. Define a mapping
![]() $\tilde{d}=d_{\mathcal{H}}\mid_{\tilde{X}\times\tilde{X}}:\tilde{X}\times\tilde{X}\longrightarrow[0,+\infty]$
as follows:
$\tilde{d}=d_{\mathcal{H}}\mid_{\tilde{X}\times\tilde{X}}:\tilde{X}\times\tilde{X}\longrightarrow[0,+\infty]$
as follows:
Then
![]() $(\tilde{X},\tilde{d})$
is a Yoneda-complete quasi-metric space (see Ng and Ho Reference Ng and Ho2017). We write
$(\tilde{X},\tilde{d})$
is a Yoneda-complete quasi-metric space (see Ng and Ho Reference Ng and Ho2017). We write
Then
![]() $\hat{X}\subseteq\tilde{X}.$
Define the mapping
$\hat{X}\subseteq\tilde{X}.$
Define the mapping
![]() $\hat{d}$
as the restriction of
$\hat{d}$
as the restriction of
![]() $\tilde{d}$
to
$\tilde{d}$
to
![]() $\hat{X}\times\hat{X}$
. Then
$\hat{X}\times\hat{X}$
. Then
![]() $(\hat{X},\hat{d})$
is a quasi-metric space.
$(\hat{X},\hat{d})$
is a quasi-metric space.
Proposition 19.
Let (X,d) be a quasi-metric space, and
![]() $(A_{i_{1}},r_{i_{1}}), (A_{i_{2}},r_{i_{2}})\in {\bf B}(\tilde{X},\tilde{d})$
. Then
$(A_{i_{1}},r_{i_{1}}), (A_{i_{2}},r_{i_{2}})\in {\bf B}(\tilde{X},\tilde{d})$
. Then
![]() $(A_{i_{1}},r_{i_{1}})\leq^{\tilde{d}{^{+}}}(A_{i_{2}},r_{i_{2}})$
if and only if
$(A_{i_{1}},r_{i_{1}})\leq^{\tilde{d}{^{+}}}(A_{i_{2}},r_{i_{2}})$
if and only if
![]() $A_{i_{1}}+r_{i_{1}}\subseteq A_{i_{2}}+r_{i_{2}}$
.
$A_{i_{1}}+r_{i_{1}}\subseteq A_{i_{2}}+r_{i_{2}}$
.
Proof. This immediately follows from Ng and Ho (Reference Ng and Ho2017, Lemma 3.14).
Proposition 20.
Let (X,d) be a quasi-metric space, and
![]() $(A_{i},r_{i})_{i\in I}$
be a directed family in
$(A_{i},r_{i})_{i\in I}$
be a directed family in
![]() ${\bf B}(\tilde{X},\tilde{d})$
. Then
${\bf B}(\tilde{X},\tilde{d})$
. Then
![]() $\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
.
$\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
.
Proof. Obviously,
![]() $cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))$
is a g-closed set. Since
$cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))$
is a g-closed set. Since
 $$\begin{array}{lll}\alpha(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})))&\leq&\alpha(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\\&=&\bigwedge_{i\in I}\alpha(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})\\&=&\bigwedge_{i\in I}(r_{i}-\bigwedge_{i\in I}r_{i})\\&=&0,\end{array}$$
$$\begin{array}{lll}\alpha(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})))&\leq&\alpha(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\\&=&\bigwedge_{i\in I}\alpha(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})\\&=&\bigwedge_{i\in I}(r_{i}-\bigwedge_{i\in I}r_{i})\\&=&0,\end{array}$$
we have that
![]() $cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\in\tilde{X}$
. Since
$cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\in\tilde{X}$
. Since
![]() $(A_{i},r_{i})\leq^{\tilde{d}{^{+}}}(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
for any
$(A_{i},r_{i})\leq^{\tilde{d}{^{+}}}(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
for any
![]() $i\in I$
, we have that
$i\in I$
, we have that
![]() $(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
is an upper bound of
$(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
is an upper bound of
![]() $(A_{i},r_{i})_{i\in I}$
in
$(A_{i},r_{i})_{i\in I}$
in
![]() ${\bf B}(\tilde{X},\tilde{d})$
. Let (B,s) be an upper bound of
${\bf B}(\tilde{X},\tilde{d})$
. Let (B,s) be an upper bound of
![]() $(A_{i},r_{i})_{i\in I}$
in
$(A_{i},r_{i})_{i\in I}$
in
![]() ${\bf B}(\tilde{X},\tilde{d})$
. Then
${\bf B}(\tilde{X},\tilde{d})$
. Then
![]() $(A_{i},r_{i})\leq^{\tilde{d}{^{+}}} (B,s)$
for any
$(A_{i},r_{i})\leq^{\tilde{d}{^{+}}} (B,s)$
for any
![]() $i\in I$
, and thus
$i\in I$
, and thus
![]() $A_{i}+r_{i}\subseteq B+s$
for any
$A_{i}+r_{i}\subseteq B+s$
for any
![]() $i\in I$
. So we conclude that
$i\in I$
. So we conclude that
![]() $\bigcup_{i\in I}(A_{i}+r_{i})\subseteq B+s$
, and hence
$\bigcup_{i\in I}(A_{i}+r_{i})\subseteq B+s$
, and hence
![]() $cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}))\subseteq B+s.$
Since
$cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}))\subseteq B+s.$
Since
![]() $\alpha(\bigcup_{i\in I}(A_{i}+r_{i}))=\bigwedge_{i\in I}r_{i}$
, it follows from Proposition 7 that
$\alpha(\bigcup_{i\in I}(A_{i}+r_{i}))=\bigwedge_{i\in I}r_{i}$
, it follows from Proposition 7 that
![]() $cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}))=cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))+\bigwedge_{i\in I}r_{i}.$
Therefore,
$cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}))=cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))+\bigwedge_{i\in I}r_{i}.$
Therefore,
![]() $cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))+\bigwedge_{i\in I}r_{i}\subseteq B+s$
, whence
$cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))+\bigwedge_{i\in I}r_{i}\subseteq B+s$
, whence
![]() $(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})\leq^{\tilde{d}{^{+}}}(B,s)$
by Proposition 19. Therefore,
$(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})\leq^{\tilde{d}{^{+}}}(B,s)$
by Proposition 19. Therefore,
![]() $\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
.
$\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
.
Next, we show that the sub-poset
![]() ${\bf B}(\hat{X},\hat{d})$
of
${\bf B}(\hat{X},\hat{d})$
of
![]() ${\bf B}(\tilde{X},\tilde{d})$
is closed under least upper bounds of bounded directed families.
${\bf B}(\tilde{X},\tilde{d})$
is closed under least upper bounds of bounded directed families.
Proposition 21.
Let (X,d) be a quasi-metric space, and
![]() $(A_{i},r_{i})_{i\in I}$
be a directed family in
$(A_{i},r_{i})_{i\in I}$
be a directed family in
![]() ${\bf B}(\hat{X},\hat{d})$
with an upper bound (A,r). Then
${\bf B}(\hat{X},\hat{d})$
with an upper bound (A,r). Then
![]() $\bigvee\limits_{i\in I}^{{\bf B}(\hat{X},\hat{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
.
$\bigvee\limits_{i\in I}^{{\bf B}(\hat{X},\hat{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
.
Proof. Let
![]() $(A_{i},r_{i})_{i\in I}$
be a directed family in
$(A_{i},r_{i})_{i\in I}$
be a directed family in
![]() $B(\hat{X},\hat{d})$
with an upper bound (A,r). Then
$B(\hat{X},\hat{d})$
with an upper bound (A,r). Then
![]() $(A_{i},r_{i})_{i\in I}$
is a directed family in
$(A_{i},r_{i})_{i\in I}$
is a directed family in
![]() $B(\tilde{X},\tilde{d})$
. By Proposition 20,
$B(\tilde{X},\tilde{d})$
. By Proposition 20,
![]() $\bigvee\limits_{i\in I}^{B(\tilde{X},\tilde{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
holds. Next, we shall prove that
$\bigvee\limits_{i\in I}^{B(\tilde{X},\tilde{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
holds. Next, we shall prove that
![]() $cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\in \hat{X}$
. It suffices to prove that
$cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\in \hat{X}$
. It suffices to prove that
![]() $cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))$
is a local g-set. Let
$cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))$
is a local g-set. Let
![]() $(Y,d^{'})$
be a local Yoneda-complete quasi-metric space and
$(Y,d^{'})$
be a local Yoneda-complete quasi-metric space and
![]() $f: X\longrightarrow Y$
be a Y-continuous function. Then there exists a unique
$f: X\longrightarrow Y$
be a Y-continuous function. Then there exists a unique
![]() $(y_{A_{i}},r_{A_{i}})\in B(Y,d^{'})$
such that
$(y_{A_{i}},r_{A_{i}})\in B(Y,d^{'})$
such that
![]() $cl_{g}({\bf B}(f)(A_{i}))=\mathord{\downarrow}\hspace{0.05em}(y_{A_{i}},r_{A_{i}})$
and
$cl_{g}({\bf B}(f)(A_{i}))=\mathord{\downarrow}\hspace{0.05em}(y_{A_{i}},r_{A_{i}})$
and
![]() $r_{A_{i}}=0$
for any
$r_{A_{i}}=0$
for any
![]() $i\in I$
, and there exists a unique
$i\in I$
, and there exists a unique
![]() $(y_{A},r_{A})\in B(Y,d^{'})$
such that
$(y_{A},r_{A})\in B(Y,d^{'})$
such that
![]() $cl_{g}({\bf B}(f)(A))=\mathord{\downarrow}\hspace{0.05em}(y_{A},r_{A})$
and
$cl_{g}({\bf B}(f)(A))=\mathord{\downarrow}\hspace{0.05em}(y_{A},r_{A})$
and
![]() $r_{A}=0$
. Let
$r_{A}=0$
. Let
![]() $i_{1},i_{2}\in I$
. Then there exists
$i_{1},i_{2}\in I$
. Then there exists
![]() $i_{3}\in I$
such that
$i_{3}\in I$
such that
![]() $(A_{i_{1}},r_{i_{1}}), (A_{i_{2}},r_{i_{2}})\leq^{\hat{d}{^{+}}}(A_{i_{3}},r_{i_{3}})$
, and thus
$(A_{i_{1}},r_{i_{1}}), (A_{i_{2}},r_{i_{2}})\leq^{\hat{d}{^{+}}}(A_{i_{3}},r_{i_{3}})$
, and thus
![]() $A_{i_{1}}+r_{i_{1}}\subseteq A_{i_{3}}+r_{i_{3}}$
and
$A_{i_{1}}+r_{i_{1}}\subseteq A_{i_{3}}+r_{i_{3}}$
and
![]() $A_{i_{2}}+r_{i_{2}}\subseteq A_{i_{3}}+r_{i_{3}}$
. Hence
$A_{i_{2}}+r_{i_{2}}\subseteq A_{i_{3}}+r_{i_{3}}$
. Hence
![]() $cl_{g}({\bf B}(f)(A_{i_{1}}+r_{i_{1}}))\subseteq cl_{g}({\bf B}(f)(A_{i_{3}}+r_{i_{3}}))$
and
$cl_{g}({\bf B}(f)(A_{i_{1}}+r_{i_{1}}))\subseteq cl_{g}({\bf B}(f)(A_{i_{3}}+r_{i_{3}}))$
and
![]() $cl_{g}({\bf B}(f)(A_{i_{2}}+r_{i_{2}}))\subseteq cl_{g}({\bf B}(f)(A_{i_{3}}+r_{i_{3}}))$
. By Proposition 7, we have that
$cl_{g}({\bf B}(f)(A_{i_{2}}+r_{i_{2}}))\subseteq cl_{g}({\bf B}(f)(A_{i_{3}}+r_{i_{3}}))$
. By Proposition 7, we have that
![]() $cl_{g}({\bf B}(f)(A_{i}+r_{i}))=cl_{g}({\bf B}(f)(A_{i}))+r_{i}$
for any
$cl_{g}({\bf B}(f)(A_{i}+r_{i}))=cl_{g}({\bf B}(f)(A_{i}))+r_{i}$
for any
![]() $i\in I$
. Then
$i\in I$
. Then
![]() $cl_{g}({\bf B}(f)(A_{i_{1}}))+r_{i_{1}}\subseteq cl_{g}({\bf B}(f)(A_{i_{3}}))+r_{i_{3}}$
and
$cl_{g}({\bf B}(f)(A_{i_{1}}))+r_{i_{1}}\subseteq cl_{g}({\bf B}(f)(A_{i_{3}}))+r_{i_{3}}$
and
![]() $cl_{g}({\bf B}(f)(A_{i_{2}}))+r_{i_{2}}\subseteq cl_{g}({\bf B}(f)(A_{i_{3}}))+r_{i_{3}}$
, and thus
$cl_{g}({\bf B}(f)(A_{i_{2}}))+r_{i_{2}}\subseteq cl_{g}({\bf B}(f)(A_{i_{3}}))+r_{i_{3}}$
, and thus
![]() $\mathord{\downarrow}\hspace{0.05em}(y_{A_{i_{1}}},0)+r_{i_{1}}\subseteq\mathord{\downarrow}\hspace{0.05em}(y_{A_{i_{3}}},0)+r_{i_{3}}$
and
$\mathord{\downarrow}\hspace{0.05em}(y_{A_{i_{1}}},0)+r_{i_{1}}\subseteq\mathord{\downarrow}\hspace{0.05em}(y_{A_{i_{3}}},0)+r_{i_{3}}$
and
![]() $\mathord{\downarrow}\hspace{0.05em}(y_{A_{i_{2}}},0)+r_{i_{2}}\subseteq\mathord{\downarrow}\hspace{0.05em}(y_{A_{i_{3}}},0)+r_{i_{3}}$
. Hence
$\mathord{\downarrow}\hspace{0.05em}(y_{A_{i_{2}}},0)+r_{i_{2}}\subseteq\mathord{\downarrow}\hspace{0.05em}(y_{A_{i_{3}}},0)+r_{i_{3}}$
. Hence
![]() $(y_{A_{i_{1}}},r_{i_{1}}), (y_{A_{i_{2}}},r_{i_{2}})\leq^{d^{'}{^{+}}}(y_{A_{i_{3}}},r_{i_{3}})$
, and so we conclude that
$(y_{A_{i_{1}}},r_{i_{1}}), (y_{A_{i_{2}}},r_{i_{2}})\leq^{d^{'}{^{+}}}(y_{A_{i_{3}}},r_{i_{3}})$
, and so we conclude that
![]() $(y_{A_{i}},r_{i})_{i\in I}$
is a directed family in
$(y_{A_{i}},r_{i})_{i\in I}$
is a directed family in
![]() ${\bf B}(Y,d^{'})$
. Similarly, we can check that
${\bf B}(Y,d^{'})$
. Similarly, we can check that
![]() $(y_{A},r)$
is an upper bound of
$(y_{A},r)$
is an upper bound of
![]() $(y_{A_{i}},r_{i})_{i\in I}$
. Since
$(y_{A_{i}},r_{i})_{i\in I}$
. Since
![]() $(Y,d^{'})$
is a local Yoneda-complete quasi-metric space, we have that
$(Y,d^{'})$
is a local Yoneda-complete quasi-metric space, we have that
![]() $\bigvee_{i\in I}(y_{A_{i}},r_{i})$
exists. Then
$\bigvee_{i\in I}(y_{A_{i}},r_{i})$
exists. Then
![]() $(y_{A_{i}},r_{i}-\bigwedge_{i\in I}r_{i})_{i\in I}$
is a directed family in
$(y_{A_{i}},r_{i}-\bigwedge_{i\in I}r_{i})_{i\in I}$
is a directed family in
![]() $B(Y,d^{'})$
and has an upper bound, hence there exists
$B(Y,d^{'})$
and has an upper bound, hence there exists
![]() $b\in Y$
such that
$b\in Y$
such that
![]() $\bigvee_{i\in I}(y_{A_{i}},r_{i}-\bigwedge_{i\in I}r_{i})=(b,0)$
. This implies
$\bigvee_{i\in I}(y_{A_{i}},r_{i}-\bigwedge_{i\in I}r_{i})=(b,0)$
. This implies
![]() ${\bf B}(f)(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\subseteq\mathord{\downarrow}\hspace{0.05em} (b,0)$
. Let B be a g-closed set satisfying
${\bf B}(f)(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\subseteq\mathord{\downarrow}\hspace{0.05em} (b,0)$
. Let B be a g-closed set satisfying
![]() ${\bf B}(f)(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\subseteq B$
. Then
${\bf B}(f)(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\subseteq B$
. Then
![]() $(y_{A_{i}},r_{i}-\bigwedge_{i\in I}r_{i})\in B$
for any
$(y_{A_{i}},r_{i}-\bigwedge_{i\in I}r_{i})\in B$
for any
![]() $i\in I$
. Obviously,
$i\in I$
. Obviously,
![]() $(y_{A_{i}},r_{i}-\bigwedge_{i\in I}r_{i})_{i\in I}$
is a translational complete directed set. Then
$(y_{A_{i}},r_{i}-\bigwedge_{i\in I}r_{i})_{i\in I}$
is a translational complete directed set. Then
![]() $\bigvee_{i\in I}(y_{A_{i}},r_{i}-\bigwedge_{i\in I}r_{i})=(b,0)\in B$
, and thus
$\bigvee_{i\in I}(y_{A_{i}},r_{i}-\bigwedge_{i\in I}r_{i})=(b,0)\in B$
, and thus
![]() $\mathord{\downarrow}\hspace{0.05em}(b,0)\subseteq B$
. Hence,
$\mathord{\downarrow}\hspace{0.05em}(b,0)\subseteq B$
. Hence,
![]() $cl_{g}({\bf B}(f)(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})))=\mathord{\downarrow}\hspace{0.05em}(b,0)$
. This shows that
$cl_{g}({\bf B}(f)(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})))=\mathord{\downarrow}\hspace{0.05em}(b,0)$
. This shows that
![]() $cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\in \hat{X}$
. Therefore,
$cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\in \hat{X}$
. Therefore,
![]() $\bigvee\limits_{i\in I}^{{\bf B}(\hat{X},\hat{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
.
$\bigvee\limits_{i\in I}^{{\bf B}(\hat{X},\hat{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
.
Let
![]() $\mathcal{A}\subseteq\tilde{X}$
.
$\mathcal{A}\subseteq\tilde{X}$
.
![]() $\mathcal{A}$
satisfies Condition
$\mathcal{A}$
satisfies Condition
![]() $(\!\ast\!)$
if, whenever for any directed family
$(\!\ast\!)$
if, whenever for any directed family
![]() $(A_{i},r_{i})_{i\in I}$
in
$(A_{i},r_{i})_{i\in I}$
in
![]() ${\bf B}(\mathcal{A},d_{\mathcal{H}}\mid_{\mathcal{A}\times \mathcal{A}})$
with an upper bound (Z,t), then
${\bf B}(\mathcal{A},d_{\mathcal{H}}\mid_{\mathcal{A}\times \mathcal{A}})$
with an upper bound (Z,t), then
 $$\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})\in {\bf B}(\mathcal{A},d_{\mathcal{H}}\mid_{\mathcal{A}\times \mathcal{A}}\!).$$
$$\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})\in {\bf B}(\mathcal{A},d_{\mathcal{H}}\mid_{\mathcal{A}\times \mathcal{A}}\!).$$
Proposition 21 means that
![]() $\hat{X}$
satisfies Condition
$\hat{X}$
satisfies Condition
![]() $(\!\ast\!)$
. Let
$(\!\ast\!)$
. Let
![]() $\Psi(X)=\{\mathord{\downarrow}\hspace{0.05em}(x,0)\mid x\in X\}$
, and
$\Psi(X)=\{\mathord{\downarrow}\hspace{0.05em}(x,0)\mid x\in X\}$
, and
Define the mapping
![]() $d_{L}$
as the restriction of
$d_{L}$
as the restriction of
![]() $\tilde{d}$
to
$\tilde{d}$
to
![]() $cl_{L}(\Psi(X))$
. Then
$cl_{L}(\Psi(X))$
. Then
![]() $(cl_{L}(\Psi(X)),d_{L})$
is a quasi-metric space.
$(cl_{L}(\Psi(X)),d_{L})$
is a quasi-metric space.
Proposition 22. Let (X,d) be a quasi-metric space. Then
![]() $(cl_{L}(\Psi(X)),d_{L})$
is a local Yoneda-complete quasi-metric space.
$(cl_{L}(\Psi(X)),d_{L})$
is a local Yoneda-complete quasi-metric space.
Proof. We start by proving part (2) of Definition 9. Let
![]() $(A_{i},r_{i})_{i\in I}$
be a directed family in
$(A_{i},r_{i})_{i\in I}$
be a directed family in
![]() ${\bf B}(cl_{L}(\Psi(X)),d_{L})$
with an upper bound. If
${\bf B}(cl_{L}(\Psi(X)),d_{L})$
with an upper bound. If
![]() $\mathcal{A}\subseteq\tilde{X}$
with
$\mathcal{A}\subseteq\tilde{X}$
with
![]() $\Psi(X)\subseteq\mathcal{A}$
satisfies Condition
$\Psi(X)\subseteq\mathcal{A}$
satisfies Condition
![]() $(\!\ast\!)$
, then
$(\!\ast\!)$
, then
![]() $(A_{i},r_{i})_{i\in I}$
is a directed family in
$(A_{i},r_{i})_{i\in I}$
is a directed family in
![]() ${\bf B}(\mathcal{A},d_{\mathcal{H}}\mid_{\mathcal{A}\times \mathcal{A}}\!)$
and has an upper bound. So we conclude that
${\bf B}(\mathcal{A},d_{\mathcal{H}}\mid_{\mathcal{A}\times \mathcal{A}}\!)$
and has an upper bound. So we conclude that
![]() $\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})\in {\bf B}(\mathcal{A},d_{L})$
. By Proposition 20, we have that
$\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})\in {\bf B}(\mathcal{A},d_{L})$
. By Proposition 20, we have that
![]() $\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
. Then
$\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
. Then
![]() $cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\in \mathcal{A}$
, and thus
$cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\in \mathcal{A}$
, and thus
![]() $cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\in cl_{L}(\Psi(X))$
. Hence
$cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\in cl_{L}(\Psi(X))$
. Hence
![]() $\bigvee_{i\in I}\limits^{{\bf B}(cl_{L}(\Psi(X)),d_{L})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
. Part (1) of Definition 9 is then a trivial consequence. Therefore,
$\bigvee_{i\in I}\limits^{{\bf B}(cl_{L}(\Psi(X)),d_{L})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i})$
. Part (1) of Definition 9 is then a trivial consequence. Therefore,
![]() $(cl_{L}(\Psi(X)),d_{L})$
is a local Yoneda-complete quasi-metric space.
$(cl_{L}(\Psi(X)),d_{L})$
is a local Yoneda-complete quasi-metric space.
Proposition 23. Let (X,d) be a quasi-metric space. Define a mapping
![]() $\zeta: X\longrightarrow cl_{L}(\Psi(X))$
as follows:
$\zeta: X\longrightarrow cl_{L}(\Psi(X))$
as follows:
Then
![]() $\zeta$
is a Y-continuous mapping.
$\zeta$
is a Y-continuous mapping.
Proof. Let
![]() $(x,r),(y,s)\in {\bf B}(X,d)$
satisfying
$(x,r),(y,s)\in {\bf B}(X,d)$
satisfying
![]() $(x,r)\leq^{d{^{+}}}(y,s)$
. Then
$(x,r)\leq^{d{^{+}}}(y,s)$
. Then
![]() $d(x,y)\leq r-s$
. If
$d(x,y)\leq r-s$
. If
![]() $(a,m)\in\mathord{\downarrow}\hspace{0.05em}(x,0)$
, then
$(a,m)\in\mathord{\downarrow}\hspace{0.05em}(x,0)$
, then
![]() $d^{+}((a,m),(x,0))=0$
, and thus
$d^{+}((a,m),(x,0))=0$
, and thus
Hence
![]() $\bigvee\limits_{(a,m)\in\mathord{\downarrow}\hspace{0.05em}(x,0)}\bigwedge\limits_{(b,n)\in\mathord{\downarrow}\hspace{0.05em}(y,0)}d^{+}((a,m),(b,n))\leq r-s$
. So we conclude that
$\bigvee\limits_{(a,m)\in\mathord{\downarrow}\hspace{0.05em}(x,0)}\bigwedge\limits_{(b,n)\in\mathord{\downarrow}\hspace{0.05em}(y,0)}d^{+}((a,m),(b,n))\leq r-s$
. So we conclude that
Therefore,
![]() $(\mathord{\downarrow}\hspace{0.05em}(x,0),r)\leq^{{d_{L}}\!{^{+}}}(\mathord{\downarrow}\hspace{0.05em}(y,0),s)$
. This shows that
$(\mathord{\downarrow}\hspace{0.05em}(x,0),r)\leq^{{d_{L}}\!{^{+}}}(\mathord{\downarrow}\hspace{0.05em}(y,0),s)$
. This shows that
![]() ${\bf B}(\zeta)(x,r)\leq^{{d_{L}}\!{^{+}}} {\bf B}(\zeta)(y,s).$
${\bf B}(\zeta)(x,r)\leq^{{d_{L}}\!{^{+}}} {\bf B}(\zeta)(y,s).$
Let
![]() $(x_{i},r_{i})_{i\in I}$
be a translational complete directed family in
$(x_{i},r_{i})_{i\in I}$
be a translational complete directed family in
![]() ${\bf B}(X,d)$
with supremum (x,r). Then
${\bf B}(X,d)$
with supremum (x,r). Then
![]() $r=\bigwedge_{i\in I}r_{i}$
, and
$r=\bigwedge_{i\in I}r_{i}$
, and
![]() $(\mathord{\downarrow}\hspace{0.05em}(x_{i},0),r_{i})_{i\in I}$
is a directed family in
$(\mathord{\downarrow}\hspace{0.05em}(x_{i},0),r_{i})_{i\in I}$
is a directed family in
![]() ${\bf B}(cl_{L}(\Psi(X)),d_{L})$
. Since
${\bf B}(cl_{L}(\Psi(X)),d_{L})$
. Since
![]() $(x_{i},r_{i})\leq^{d{^{+}}} (x,r)$
for any
$(x_{i},r_{i})\leq^{d{^{+}}} (x,r)$
for any
![]() $i\in I$
, we have that
$i\in I$
, we have that
![]() $(\mathord{\downarrow}\hspace{0.05em}(x_{i},0),r_{i})\leq^{{d_{L}}\!{^{+}}}(\mathord{\downarrow}\hspace{0.05em}(x,0),r)$
for any
$(\mathord{\downarrow}\hspace{0.05em}(x_{i},0),r_{i})\leq^{{d_{L}}\!{^{+}}}(\mathord{\downarrow}\hspace{0.05em}(x,0),r)$
for any
![]() $i\in I$
. Let
$i\in I$
. Let
![]() $(B,s)\in {\bf B}(cl_{L}(\Psi(X)),d_{L})$
such that
$(B,s)\in {\bf B}(cl_{L}(\Psi(X)),d_{L})$
such that
![]() $(\mathord{\downarrow}\hspace{0.05em}(x_{i},0),r_{i})\leq^{{d_{L}}\!{^{+}}} (B,s)$
for any
$(\mathord{\downarrow}\hspace{0.05em}(x_{i},0),r_{i})\leq^{{d_{L}}\!{^{+}}} (B,s)$
for any
![]() $i\in I$
. Then
$i\in I$
. Then
![]() $s\leq\bigwedge_{i\in I}r_{i}$
, and
$s\leq\bigwedge_{i\in I}r_{i}$
, and
![]() $(x_{i},r_{i})\in B+s$
for any
$(x_{i},r_{i})\in B+s$
for any
![]() $i\in I$
. Since
$i\in I$
. Since
![]() $B+s$
is a g-closed set, we have that
$B+s$
is a g-closed set, we have that
![]() $(x,r)\in B+s$
. Then
$(x,r)\in B+s$
. Then
![]() $(x,r-s)\in B$
, and thus
$(x,r-s)\in B$
, and thus
![]() $\mathord{\downarrow}\hspace{0.05em}(x,r-s)\subseteq B$
. Therefore,
$\mathord{\downarrow}\hspace{0.05em}(x,r-s)\subseteq B$
. Therefore,
![]() $(\mathord{\downarrow}\hspace{0.05em}(x,0),r)\leq^{{d_{L}}\!{^{+}}} (B,s)$
. So we conclude that
$(\mathord{\downarrow}\hspace{0.05em}(x,0),r)\leq^{{d_{L}}\!{^{+}}} (B,s)$
. So we conclude that
![]() $\bigvee\limits_{i\in I}^{{\bf B}(cl_{L}(\Psi(X)),d_{L})}(\mathord{\downarrow}\hspace{0.05em}(x_{i},0),r_{i})=(\mathord{\downarrow}\hspace{0.05em}(x,0),r)$
. This shows that
$\bigvee\limits_{i\in I}^{{\bf B}(cl_{L}(\Psi(X)),d_{L})}(\mathord{\downarrow}\hspace{0.05em}(x_{i},0),r_{i})=(\mathord{\downarrow}\hspace{0.05em}(x,0),r)$
. This shows that
![]() ${\bf B}(\zeta)$
is Y-Scott continuous, and hence
${\bf B}(\zeta)$
is Y-Scott continuous, and hence
![]() $\zeta$
is a Y-continuous mapping.
$\zeta$
is a Y-continuous mapping.
Proposition 24.
Let (X,d) be a quasi-metric space. Then
![]() $\hat{X}=cl_{L}(\Psi(X))$
.
$\hat{X}=cl_{L}(\Psi(X))$
.
Proof. By Proposition 21, we have that
![]() $\hat{X}$
satisfies Condition
$\hat{X}$
satisfies Condition
![]() $(\!\ast\!)$
. Obviously,
$(\!\ast\!)$
. Obviously,
![]() $\Psi(X)\subseteq\hat{X}$
. Then
$\Psi(X)\subseteq\hat{X}$
. Then
![]() $cl_{L}(\Psi(X))\subseteq\hat{X}$
. Let
$cl_{L}(\Psi(X))\subseteq\hat{X}$
. Let
![]() $A\in\hat{X}$
. By Proposition 22, we have that
$A\in\hat{X}$
. By Proposition 22, we have that
![]() $(cl_{L}(\Psi(X)),d_{L})$
is a local Yoneda-complete quasi-metric space. It follows from Proposition 23 that there exists
$(cl_{L}(\Psi(X)),d_{L})$
is a local Yoneda-complete quasi-metric space. It follows from Proposition 23 that there exists
![]() $(M,s)\in {\bf B}(cl_{L}(\Psi(X)),d_{L})$
such that
$(M,s)\in {\bf B}(cl_{L}(\Psi(X)),d_{L})$
such that
![]() $cl_{g}({\bf B}(\zeta)(A))=\mathord{\downarrow}\hspace{0.05em}(M,s)$
. Then
$cl_{g}({\bf B}(\zeta)(A))=\mathord{\downarrow}\hspace{0.05em}(M,s)$
. Then
![]() $s=0$
and
$s=0$
and
![]() $A\subseteq M$
. Let
$A\subseteq M$
. Let
Then
![]() $\mathcal{B}$
is a g-closed subset of
$\mathcal{B}$
is a g-closed subset of
![]() ${\bf B}(cl_{L}(\Psi(X)),d_{L})$
. Since
${\bf B}(cl_{L}(\Psi(X)),d_{L})$
. Since
![]() ${\bf B}(\zeta)(A)\subseteq\mathcal{B}$
, we have that
${\bf B}(\zeta)(A)\subseteq\mathcal{B}$
, we have that
![]() $cl_{g}({\bf B}(\zeta)(A))\subseteq\mathcal{B}$
. Then
$cl_{g}({\bf B}(\zeta)(A))\subseteq\mathcal{B}$
. Then
![]() $(M,0)\in\mathcal{B}$
, and thus
$(M,0)\in\mathcal{B}$
, and thus
![]() $d_{\mathcal{H}}(M,A)=0$
. So we conclude that
$d_{\mathcal{H}}(M,A)=0$
. So we conclude that
![]() $M\subseteq A$
. Therefore,
$M\subseteq A$
. Therefore,
![]() $M=A\in cl_{L}(\Psi(X))$
. This shows that
$M=A\in cl_{L}(\Psi(X))$
. This shows that
![]() $\hat{X}=cl_{L}(\Psi(X))$
.
$\hat{X}=cl_{L}(\Psi(X))$
.
Corollary 25. Let (X,d) be a quasi-metric space. Then
![]() $(\hat{X},\hat{d})$
is a local Yoneda-complete quasi-metric space.
$(\hat{X},\hat{d})$
is a local Yoneda-complete quasi-metric space.
Proof. Immediately from Propositions 22 and 24.
Proposition 26.
Let (X,d),
![]() $(X^{'}\!,d^{'})$
be two quasi-metric spaces, and
$(X^{'}\!,d^{'})$
be two quasi-metric spaces, and
![]() $f: X\longrightarrow X^{'}\!$
be a function. Then
$f: X\longrightarrow X^{'}\!$
be a function. Then
![]() ${\bf B}(f)$
is a Y-Scott continuous map if and only if
${\bf B}(f)$
is a Y-Scott continuous map if and only if
![]() ${\bf B}(f)$
is continuous with respect to the g-topology.
${\bf B}(f)$
is continuous with respect to the g-topology.
Proof. Only-if direction. Let C be a g-closed subset of
![]() ${\bf B}(X^{'}\!,d^{'})$
. Then
${\bf B}(X^{'}\!,d^{'})$
. Then
![]() $({\bf B}(f))^{-1}(C)$
is downward closed. Let
$({\bf B}(f))^{-1}(C)$
is downward closed. Let
![]() $(x_{i},r_{i})_{i\in I}$
be a translational complete directed family in
$(x_{i},r_{i})_{i\in I}$
be a translational complete directed family in
![]() $({\bf B}(f))^{-1}(C)$
with supremum (x,r). Then
$({\bf B}(f))^{-1}(C)$
with supremum (x,r). Then
![]() $(f(x_{i}),r_{i})_{i\in I}\subseteq C$
. Since
$(f(x_{i}),r_{i})_{i\in I}\subseteq C$
. Since
![]() ${\bf B}(f)$
is a Y-Scott continuous map, we have that
${\bf B}(f)$
is a Y-Scott continuous map, we have that
![]() $(f(x_{i}),r_{i})_{i\in I}$
is a translational complete directed family in
$(f(x_{i}),r_{i})_{i\in I}$
is a translational complete directed family in
![]() ${\bf B}(X^{'}\!,d^{'})$
, and
${\bf B}(X^{'}\!,d^{'})$
, and
![]() $\bigvee_{i\in I}(f(x_{i}),r_{i})={\bf B}(f)(x,r)=(f(x),r)$
. Then
$\bigvee_{i\in I}(f(x_{i}),r_{i})={\bf B}(f)(x,r)=(f(x),r)$
. Then
![]() $(f(x),r)\in C$
, and thus
$(f(x),r)\in C$
, and thus
![]() $(x,r)\in({\bf B}(f))^{-1}(C)$
. Therefore,
$(x,r)\in({\bf B}(f))^{-1}(C)$
. Therefore,
![]() $({\bf B}(f))^{-1}(C)$
is a g-closed set. This shows that
$({\bf B}(f))^{-1}(C)$
is a g-closed set. This shows that
![]() ${\bf B}(f)$
is continuous with respect to the g-topology.
${\bf B}(f)$
is continuous with respect to the g-topology.
If direction. Let
![]() $(x_{1},r_{1}), (x_{2},r_{2})\in {\bf B}(X,d)$
satisfying
$(x_{1},r_{1}), (x_{2},r_{2})\in {\bf B}(X,d)$
satisfying
![]() $(x_{1},r_{1})\leq^{d^{+}}(x_{2},r_{2})$
. Clearly,
$(x_{1},r_{1})\leq^{d^{+}}(x_{2},r_{2})$
. Clearly,
![]() $(f(x_{2}),r_{2})\in\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2})$
, and therefore,
$(f(x_{2}),r_{2})\in\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2})$
, and therefore,
![]() $(x_{2},r_{2})\in({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2}))$
. Since
$(x_{2},r_{2})\in({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2}))$
. Since
![]() $\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2})$
is a g-closed set, so is
$\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2})$
is a g-closed set, so is
![]() $({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2}))$
. Thus,
$({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2}))$
. Thus,
![]() $(x_{1},r_{1})\in({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2})),$
which implies
$(x_{1},r_{1})\in({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2})),$
which implies
![]() $(f(x_{1}), r_{1})\in\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2})$
, whence
$(f(x_{1}), r_{1})\in\mathord{\downarrow}\hspace{0.05em}(f(x_{2}),r_{2})$
, whence
![]() $(f(x_{1}),r_{1})\leq^{d^{'}\!{^{+}}}(f(x_{2}),r_{2})$
.
$(f(x_{1}),r_{1})\leq^{d^{'}\!{^{+}}}(f(x_{2}),r_{2})$
.
Let
![]() $(x_{i},r_{i})_{i\in I}$
be a translational complete directed family in
$(x_{i},r_{i})_{i\in I}$
be a translational complete directed family in
![]() ${\bf B}(X,d)$
with supremum (x,r). Then
${\bf B}(X,d)$
with supremum (x,r). Then
![]() $(f(x_{i}),r_{i})\leq^{d^{'}\!{^{+}}}(f(x),r)$
for any
$(f(x_{i}),r_{i})\leq^{d^{'}\!{^{+}}}(f(x),r)$
for any
![]() $i\in I$
. Let (y,s) be an upper bound of
$i\in I$
. Let (y,s) be an upper bound of
![]() $(f(x_{i}),r_{i})_{i\in I}$
. Then
$(f(x_{i}),r_{i})_{i\in I}$
. Then
![]() $(f(x_{i}),r_{i})\in\mathord{\downarrow}\hspace{0.05em}(y,s)$
for any
$(f(x_{i}),r_{i})\in\mathord{\downarrow}\hspace{0.05em}(y,s)$
for any
![]() $i\in I$
, and thus
$i\in I$
, and thus
![]() $(x_{i},r_{i})\in({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(y,s))$
for any
$(x_{i},r_{i})\in({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(y,s))$
for any
![]() $i\in I$
. Obviously,
$i\in I$
. Obviously,
![]() $\mathord{\downarrow}\hspace{0.05em}(y,s)$
is a g-closed set. Then
$\mathord{\downarrow}\hspace{0.05em}(y,s)$
is a g-closed set. Then
![]() $({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(y,s))$
is a g-closed set, and thus
$({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(y,s))$
is a g-closed set, and thus
![]() $(x,r)\in({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(y,s))$
, that is,
$(x,r)\in({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(y,s))$
, that is,
![]() $(f(x),r)\leq^{d^{'}\!{^{+}}}(y,s)$
. Therefore,
$(f(x),r)\leq^{d^{'}\!{^{+}}}(y,s)$
. Therefore,
![]() $\bigvee_{i\in I}(f(x_{i}),r_{i})=(f(x),r)$
. This implies that
$\bigvee_{i\in I}(f(x_{i}),r_{i})=(f(x),r)$
. This implies that
![]() $(f(x_{i}),r_{i})_{i\in I}$
is a translational complete directed family in
$(f(x_{i}),r_{i})_{i\in I}$
is a translational complete directed family in
![]() ${\bf B}(X^{'}\!,d^{'})$
. So we conclude that
${\bf B}(X^{'}\!,d^{'})$
. So we conclude that
![]() ${\bf B}(f)$
is a Y-Scott continuous map.
${\bf B}(f)$
is a Y-Scott continuous map.
Theorem 27. Let (X,d) be a quasi-metric space. Then
![]() $(\hat{X},\hat{d})$
is the local Yoneda completion of (X,d).
$(\hat{X},\hat{d})$
is the local Yoneda completion of (X,d).
Proof. Let
![]() $(X^{'}\!,d^{'})$
be a local Yoneda-complete quasi-metric space, and
$(X^{'}\!,d^{'})$
be a local Yoneda-complete quasi-metric space, and
![]() $f: X\longrightarrow X^{'}$
be a Y-continuous mapping. For all A in
$f: X\longrightarrow X^{'}$
be a Y-continuous mapping. For all A in
![]() $\hat{X}$
, there exists a unique
$\hat{X}$
, there exists a unique
![]() $(y_{A},r_{A})\in {\bf B}(X^{'}\!,d^{'})$
such that
$(y_{A},r_{A})\in {\bf B}(X^{'}\!,d^{'})$
such that
![]() $cl_{g}({\bf B}(f)(A))=\mathord{\downarrow}\hspace{0.05em}(y_{A},r_{A})$
and
$cl_{g}({\bf B}(f)(A))=\mathord{\downarrow}\hspace{0.05em}(y_{A},r_{A})$
and
![]() $r_{A}=0$
. Define a mapping
$r_{A}=0$
. Define a mapping
![]() $f^{\ast}: \hat{X}\longrightarrow X^{'}\!$
as follows:
$f^{\ast}: \hat{X}\longrightarrow X^{'}\!$
as follows:
Then
![]() $f^{\ast}$
is well-defined.
$f^{\ast}$
is well-defined.
Claim 1.
![]() $f^{\ast}\circ \zeta=f$
.
$f^{\ast}\circ \zeta=f$
.
Let
![]() $x\in X$
. Then
$x\in X$
. Then
![]() $f^{\ast}(\zeta(x))=f^{\ast}(\mathord{\downarrow}\hspace{0.05em}(x,0))$
. Since
$f^{\ast}(\zeta(x))=f^{\ast}(\mathord{\downarrow}\hspace{0.05em}(x,0))$
. Since
we have that
![]() $f^{\ast}(\mathord{\downarrow}\hspace{0.05em}(x,0))=f(x)$
. Then
$f^{\ast}(\mathord{\downarrow}\hspace{0.05em}(x,0))=f(x)$
. Then
![]() $f^{\ast}\circ \zeta=f$
.
$f^{\ast}\circ \zeta=f$
.
Claim 2.
![]() $f^{\ast}$
is a Y-continuous mapping.
$f^{\ast}$
is a Y-continuous mapping.
To prove this claim, we show that
![]() ${\bf B}(f^{\ast})$
is Y-Scott continuous and then use Proposition 4. Let
${\bf B}(f^{\ast})$
is Y-Scott continuous and then use Proposition 4. Let
![]() $(B_{1},r),(B_{2},s)\in {\bf B}(\hat{X},\hat{d})$
satisfying
$(B_{1},r),(B_{2},s)\in {\bf B}(\hat{X},\hat{d})$
satisfying
![]() $(B_{1},r)\leq^{\hat{d}{^{+}}}(B_{2},s)$
. Then
$(B_{1},r)\leq^{\hat{d}{^{+}}}(B_{2},s)$
. Then
![]() $B_{1}+r\subseteq B_{2}+s$
, and thus
$B_{1}+r\subseteq B_{2}+s$
, and thus
![]() $B_{1}+r-s\subseteq B_{2}$
. Therefore,
$B_{1}+r-s\subseteq B_{2}$
. Therefore,
![]() ${\bf B}(f)(B_{1}+r-s)\subseteq {\bf B}(f)(B_{2})$
, and so we conclude that
${\bf B}(f)(B_{1}+r-s)\subseteq {\bf B}(f)(B_{2})$
, and so we conclude that
![]() $cl_{g}({\bf B}(f)(B_{1}+r-s))\subseteq cl_{g}({\bf B}(f)(B_{2}))$
. Since
$cl_{g}({\bf B}(f)(B_{1}+r-s))\subseteq cl_{g}({\bf B}(f)(B_{2}))$
. Since
![]() $cl_{g}({\bf B}(f)(B_{1}))=\mathord{\downarrow}\hspace{0.05em}(y_{B_{1}},0), cl_{g}({\bf B}(f)(B_{2}))=\mathord{\downarrow}\hspace{0.05em}(y_{B_{2}},0)$
, and
$cl_{g}({\bf B}(f)(B_{1}))=\mathord{\downarrow}\hspace{0.05em}(y_{B_{1}},0), cl_{g}({\bf B}(f)(B_{2}))=\mathord{\downarrow}\hspace{0.05em}(y_{B_{2}},0)$
, and
![]() $cl_{g}({\bf B}(f)(B_{1}+r-s))=cl_{g}({\bf B}(f)(B_{1}))+(r-s),$
we have that
$cl_{g}({\bf B}(f)(B_{1}+r-s))=cl_{g}({\bf B}(f)(B_{1}))+(r-s),$
we have that
![]() $(y_{B_{1}},r-s)\leq^{d^{'}\!{^{+}}}(y_{B_{2}},0)$
. Then
$(y_{B_{1}},r-s)\leq^{d^{'}\!{^{+}}}(y_{B_{2}},0)$
. Then
![]() $d^{'}(y_{B_{1}},y_{B_{2}})\leq r-s$
. This shows that
$d^{'}(y_{B_{1}},y_{B_{2}})\leq r-s$
. This shows that
![]() ${\bf B}(f^{\ast})(B_{1},r)\leq^{d^{'}\!{^{+}}} {\bf B}(f^{\ast})(B_{2},s)$
.
${\bf B}(f^{\ast})(B_{1},r)\leq^{d^{'}\!{^{+}}} {\bf B}(f^{\ast})(B_{2},s)$
.
Let
![]() $(A_{i},r_{i})_{i\in I}$
be a translational complete directed family in
$(A_{i},r_{i})_{i\in I}$
be a translational complete directed family in
![]() ${\bf B}(\hat{X},\hat{d})$
satisfying
${\bf B}(\hat{X},\hat{d})$
satisfying
![]() $\bigvee\limits_{i\in I}^{{\bf B}(\hat{X},\hat{d})}(A_{i},r_{i})$
exists. By Proposition 21, we have that
$\bigvee\limits_{i\in I}^{{\bf B}(\hat{X},\hat{d})}(A_{i},r_{i})$
exists. By Proposition 21, we have that
![]() $\bigvee\limits_{i\in I}^{{\bf B}(\hat{X},\hat{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i}).$
Next, we shall prove that
$\bigvee\limits_{i\in I}^{{\bf B}(\hat{X},\hat{d})}(A_{i},r_{i})=(cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})),\bigwedge_{i\in I}r_{i}).$
Next, we shall prove that
 $${\bf B}(f^{\ast})(\bigvee\limits_{i\in I}^{{\bf B}(\hat{X},\hat{d})}(A_{i},r_{i}))=\bigvee\limits_{i\in I}^{{\bf B}(X^{'}\!,d^{'})}{\bf B}(f^{\ast})(A_{i},r_{i}),$$
$${\bf B}(f^{\ast})(\bigvee\limits_{i\in I}^{{\bf B}(\hat{X},\hat{d})}(A_{i},r_{i}))=\bigvee\limits_{i\in I}^{{\bf B}(X^{'}\!,d^{'})}{\bf B}(f^{\ast})(A_{i},r_{i}),$$
that is,
![]() $(f^{\ast}(A),\bigwedge_{i\in I}r_{i})=\bigvee\limits_{i\in I}^{{\bf B}(X^{'}\!,d^{'})}(f^{\ast}(A_{i}),r_{i}),$
where
$(f^{\ast}(A),\bigwedge_{i\in I}r_{i})=\bigvee\limits_{i\in I}^{{\bf B}(X^{'}\!,d^{'})}(f^{\ast}(A_{i}),r_{i}),$
where
![]() $A=cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))$
. Since
$A=cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))$
. Since
![]() $(A_{i},r_{i})\leq^{\hat{d}{^{+}}}(A,\bigwedge_{i\in I}r_{i})$
for any
$(A_{i},r_{i})\leq^{\hat{d}{^{+}}}(A,\bigwedge_{i\in I}r_{i})$
for any
![]() $i\in I$
, we have that
$i\in I$
, we have that
![]() $(f^{\ast}(A_{i}),r_{i})\leq^{d^{'}\!{^{+}}}(f^{\ast}(A),\bigwedge_{i\in I}r_{i})$
and
$(f^{\ast}(A_{i}),r_{i})\leq^{d^{'}\!{^{+}}}(f^{\ast}(A),\bigwedge_{i\in I}r_{i})$
and
![]() $(f^{\ast}(A_{i}),r_{i})_{i\in I}$
is a directed set. Since
$(f^{\ast}(A_{i}),r_{i})_{i\in I}$
is a directed set. Since
![]() $(X^{'}\!,d^{'})$
is a local Yoneda-complete quasi-metric space, we have that
$(X^{'}\!,d^{'})$
is a local Yoneda-complete quasi-metric space, we have that
![]() $\bigvee\limits_{i\in I}^{{\bf B}(X^{'}\!,d^{'})}{\bf B}(f^{\ast})(A_{i},r_{i})$
exists, denoted by
$\bigvee\limits_{i\in I}^{{\bf B}(X^{'}\!,d^{'})}{\bf B}(f^{\ast})(A_{i},r_{i})$
exists, denoted by
![]() $(y,\bigwedge_{i\in I}r_{i})$
. Thus
$(y,\bigwedge_{i\in I}r_{i})$
. Thus
![]() $(y,\bigwedge_{i\in I}r_{i})\leq^{d^{'}\!{^{+}}}(f^{\ast}(A),\bigwedge_{i\in I}r_{i})$
, which implies
$(y,\bigwedge_{i\in I}r_{i})\leq^{d^{'}\!{^{+}}}(f^{\ast}(A),\bigwedge_{i\in I}r_{i})$
, which implies
![]() $d^{'}\!{^{+}}(y,f^{\ast}(A))=0$
.
$d^{'}\!{^{+}}(y,f^{\ast}(A))=0$
.
Since
![]() $(f^{\ast}(A_{i}),r_{i})\leq^{d^{'}\!{^{+}}} (y,\bigwedge_{i\in I}r_{i})$
, we have that
$(f^{\ast}(A_{i}),r_{i})\leq^{d^{'}\!{^{+}}} (y,\bigwedge_{i\in I}r_{i})$
, we have that
![]() $(f^{\ast}(A_{i}),r_{i}-\bigwedge_{i\in I}r_{i})\leq^{d^{'}\!{^{+}}} (y,0)$
for any
$(f^{\ast}(A_{i}),r_{i}-\bigwedge_{i\in I}r_{i})\leq^{d^{'}\!{^{+}}} (y,0)$
for any
![]() $i\in I$
. From this, we may conclude
$i\in I$
. From this, we may conclude
 $$\begin{array}{lll}{\bf B}(f)(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})&\subseteq cl_{g}({\bf B}(f)(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\\&=cl_{g}({\bf B}(f)(A_{i}))+r_{i}-\bigwedge_{i\in I}r_{i}\\&=\mathord{\downarrow}\hspace{0.05em}(f^{\ast}(A_{i}),0)+r_{i}-\bigwedge_{i\in I}r_{i}\\&=\mathord{\downarrow}\hspace{0.05em}(f^{\ast}(A_{i}),r_{i}-\bigwedge_{i\in I}r_{i})\\&\subseteq \mathord{\downarrow}\hspace{0.05em}(y,0)\end{array}$$
$$\begin{array}{lll}{\bf B}(f)(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i})&\subseteq cl_{g}({\bf B}(f)(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\\&=cl_{g}({\bf B}(f)(A_{i}))+r_{i}-\bigwedge_{i\in I}r_{i}\\&=\mathord{\downarrow}\hspace{0.05em}(f^{\ast}(A_{i}),0)+r_{i}-\bigwedge_{i\in I}r_{i}\\&=\mathord{\downarrow}\hspace{0.05em}(f^{\ast}(A_{i}),r_{i}-\bigwedge_{i\in I}r_{i})\\&\subseteq \mathord{\downarrow}\hspace{0.05em}(y,0)\end{array}$$
for any
![]() $i\in I$
. Since
$i\in I$
. Since
![]() ${\bf B}(f)$
is a Y-Scott continuous mapping, it follows from Proposition 26 that
${\bf B}(f)$
is a Y-Scott continuous mapping, it follows from Proposition 26 that
![]() $({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(y,0))$
is a g-closed set. Hence,
$({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(y,0))$
is a g-closed set. Hence,
![]() $A=cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\subseteq({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(y,0))$
, and thus
$A=cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))\subseteq({\bf B}(f))^{-1}(\mathord{\downarrow}\hspace{0.05em}(y,0))$
, and thus
![]() $cl_{g}({\bf B}(f)(A))\subseteq\mathord{\downarrow}\hspace{0.05em}(y,0)$
. By the definition of
$cl_{g}({\bf B}(f)(A))\subseteq\mathord{\downarrow}\hspace{0.05em}(y,0)$
. By the definition of
![]() $f^{\ast}$
, this implies
$f^{\ast}$
, this implies
![]() $\mathord{\downarrow}\hspace{0.05em}(f^{\ast}(A),0)\subseteq\mathord{\downarrow}\hspace{0.05em}(y,0)$
, and therefore,
$\mathord{\downarrow}\hspace{0.05em}(f^{\ast}(A),0)\subseteq\mathord{\downarrow}\hspace{0.05em}(y,0)$
, and therefore,
![]() $(f^{\ast}(A),0)\leq^{{d^{'}}\!{^{+}}}(y,0)$
, which implies
$(f^{\ast}(A),0)\leq^{{d^{'}}\!{^{+}}}(y,0)$
, which implies
![]() $d^{'}\!{^{+}}(f^{\ast}(A),y)=0$
. Together with
$d^{'}\!{^{+}}(f^{\ast}(A),y)=0$
. Together with
![]() $d^{'}\!{^{+}}(y,f^{\ast}(A))=0$
from above,
$d^{'}\!{^{+}}(y,f^{\ast}(A))=0$
from above,
![]() $f^{\ast}(A)=y$
follows. Therefore,
$f^{\ast}(A)=y$
follows. Therefore,
![]() $\bigvee\limits_{i\in I}^{{\bf B}(X^{'}\!,d^{'})}(f^{\ast}(A_{i}),r_{i})=(f^{\ast}(A),\bigwedge_{i\in I}r_{i})$
. Hence
$\bigvee\limits_{i\in I}^{{\bf B}(X^{'}\!,d^{'})}(f^{\ast}(A_{i}),r_{i})=(f^{\ast}(A),\bigwedge_{i\in I}r_{i})$
. Hence
![]() $f^{\ast}$
is a Y-continuous mapping.
$f^{\ast}$
is a Y-continuous mapping.
Claim 3.
![]() $f^{\ast}$
is a unique Y-continuous mapping such that
$f^{\ast}$
is a unique Y-continuous mapping such that
![]() $f^{\ast}\circ \zeta=f$
.
$f^{\ast}\circ \zeta=f$
.
Suppose that there exists a Y-continuous mapping
![]() $g:\hat{X}\longrightarrow X^{'}\!$
such that
$g:\hat{X}\longrightarrow X^{'}\!$
such that
![]() $g\circ\zeta=f$
. Let
$g\circ\zeta=f$
. Let
![]() $\mathcal{C}=\{A\in\hat{X}\mid f^{\ast}(A)=g(A)\}$
. Then
$\mathcal{C}=\{A\in\hat{X}\mid f^{\ast}(A)=g(A)\}$
. Then
![]() $\mathcal{C}\subseteq \hat{X}\subseteq\tilde{X}$
and
$\mathcal{C}\subseteq \hat{X}\subseteq\tilde{X}$
and
![]() $\Psi(X)\subseteq \mathcal{C}$
. Next, we shall prove that
$\Psi(X)\subseteq \mathcal{C}$
. Next, we shall prove that
![]() $\mathcal{C}$
satisfies the Condition
$\mathcal{C}$
satisfies the Condition
![]() $(\!\ast\!)$
. Let
$(\!\ast\!)$
. Let
![]() $(A_{i},r_{i})_{i\in I}$
be a directed family in
$(A_{i},r_{i})_{i\in I}$
be a directed family in
![]() ${\bf B}(\mathcal{C},d_{\mathcal{H}}\mid_{\mathcal{C}\times \mathcal{C}})$
with an upper bound (B,s). By Propositions 20 and 21, we have that
${\bf B}(\mathcal{C},d_{\mathcal{H}}\mid_{\mathcal{C}\times \mathcal{C}})$
with an upper bound (B,s). By Propositions 20 and 21, we have that
![]() $\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})=(A,\bigwedge_{i\in I}r_{i})$
and
$\bigvee\limits_{i\in I}^{{\bf B}(\tilde{X},\tilde{d})}(A_{i},r_{i})=(A,\bigwedge_{i\in I}r_{i})$
and
![]() $A\in\hat{X}$
, where
$A\in\hat{X}$
, where
![]() $A=cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))$
. Obviously,
$A=cl_{g}(\bigcup_{i\in I}(A_{i}+r_{i}-\bigwedge_{i\in I}r_{i}))$
. Obviously,
![]() $(A_{i},r_{i}-\bigwedge_{i\in I}r_{i})_{i\in I,\sqsubseteq}$
is a Cauchy weighted net in
$(A_{i},r_{i}-\bigwedge_{i\in I}r_{i})_{i\in I,\sqsubseteq}$
is a Cauchy weighted net in
![]() ${\bf B}(\hat{X},\hat{d})$
. Let
${\bf B}(\hat{X},\hat{d})$
. Let
![]() $Z\in \hat{X}$
. Then,
$Z\in \hat{X}$
. Then,
![]() $\hat{d}(A_{i},Z)\leq\hat{d}(A_{i},A)+\hat{d}(A,Z)\leq r_{i}-\bigwedge_{i\in I}r_{i}+\hat{d}(A,Z)$
for any
$\hat{d}(A_{i},Z)\leq\hat{d}(A_{i},A)+\hat{d}(A,Z)\leq r_{i}-\bigwedge_{i\in I}r_{i}+\hat{d}(A,Z)$
for any
![]() $i\in I$
, and thus
$i\in I$
, and thus
![]() $\hat{d}(A_{i},Z)-r_{i}+\bigwedge_{i\in I}r_{i}\leq\hat{d}(A,Z)$
for any
$\hat{d}(A_{i},Z)-r_{i}+\bigwedge_{i\in I}r_{i}\leq\hat{d}(A,Z)$
for any
![]() $i\in I$
. Let s be an upper bound of
$i\in I$
. Let s be an upper bound of
![]() $(\hat{d}(A_{i},Z)-r_{i}+\bigwedge_{i\in I}r_{i})_{i\in I}$
. If
$(\hat{d}(A_{i},Z)-r_{i}+\bigwedge_{i\in I}r_{i})_{i\in I}$
. If
![]() $s=+\infty$
, then
$s=+\infty$
, then
![]() $\hat{d}(A,Z)\leq s$
. If
$\hat{d}(A,Z)\leq s$
. If
![]() $s<+\infty$
, then
$s<+\infty$
, then
![]() $\hat{d}(A_{i},Z)-r_{i}+\bigwedge_{i\in I}r_{i}\leq s$
for any
$\hat{d}(A_{i},Z)-r_{i}+\bigwedge_{i\in I}r_{i}\leq s$
for any
![]() $i\in I$
, and thus
$i\in I$
, and thus
![]() $\hat{d}(A_{i},Z)\leq s+r_{i}-\bigwedge_{i\in I}r_{i}$
for any
$\hat{d}(A_{i},Z)\leq s+r_{i}-\bigwedge_{i\in I}r_{i}$
for any
![]() $i\in I$
. Hence,
$i\in I$
. Hence,
![]() $(A_{i},r_{i}+s)\leq^{\hat{d}{^{+}}}(Z,\bigwedge_{i\in I}r_{i})$
for any
$(A_{i},r_{i}+s)\leq^{\hat{d}{^{+}}}(Z,\bigwedge_{i\in I}r_{i})$
for any
![]() $i\in I$
, and so we conclude that
$i\in I$
, and so we conclude that
![]() $(A,\bigwedge_{i\in I}r_{i}+s)\leq^{\hat{d}{^{+}}}(Z,\bigwedge_{i\in I}r_{i})$
. This implies
$(A,\bigwedge_{i\in I}r_{i}+s)\leq^{\hat{d}{^{+}}}(Z,\bigwedge_{i\in I}r_{i})$
. This implies
![]() $\hat{d}(A,Z)\leq s$
. Therefore,
$\hat{d}(A,Z)\leq s$
. Therefore,
![]() $\bigvee_{i\in I}(\hat{d}(A_{i},Z)-r_{i}+\bigwedge_{i\in I}r_{i})=\hat{d}(A,Z)$
. By Lemma 2.6 (i) of Ng and Ho (Reference Ng and Ho2017), A is the d-limit of
$\bigvee_{i\in I}(\hat{d}(A_{i},Z)-r_{i}+\bigwedge_{i\in I}r_{i})=\hat{d}(A,Z)$
. By Lemma 2.6 (i) of Ng and Ho (Reference Ng and Ho2017), A is the d-limit of
![]() $(A_{i})_{i\in I}$
. Since
$(A_{i})_{i\in I}$
. Since
![]() $f^{\ast}$
and g are Y-continuous, we have that
$f^{\ast}$
and g are Y-continuous, we have that
![]() $f^{\ast}(A)=f^{\ast}(\lim_{d}A_{i})=\lim_{d}f^{\ast}(A_{i})=\lim_{d}g(A_{i})=g(\lim_{d}A_{i})=g(A).$
So we conclude
$f^{\ast}(A)=f^{\ast}(\lim_{d}A_{i})=\lim_{d}f^{\ast}(A_{i})=\lim_{d}g(A_{i})=g(\lim_{d}A_{i})=g(A).$
So we conclude
![]() $A\in \mathcal{C}$
. It follows from Proposition 24 that
$A\in \mathcal{C}$
. It follows from Proposition 24 that
![]() $\hat{X}=cl_{L}(\Psi(X))=\mathcal{C}$
, and therefore
$\hat{X}=cl_{L}(\Psi(X))=\mathcal{C}$
, and therefore
![]() $f^{\ast}=g$
.
$f^{\ast}=g$
.
Consequently,
![]() $(\hat{X},\hat{d})$
is the local Yoneda completion of (X,d).
$(\hat{X},\hat{d})$
is the local Yoneda completion of (X,d).
Acknowledgments
The authors would like to thank the referee for the numerous and very helpful suggestions that have improved this paper substantially.