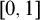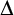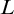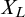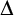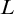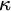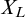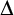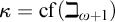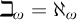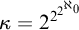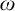1 Introduction
Throughout,
![]() $\kappa $
denotes a regular uncountable cardinal. A ladder system over a stationary subset S of
$\kappa $
denotes a regular uncountable cardinal. A ladder system over a stationary subset S of
![]() $\kappa $
is a sequence
$\kappa $
is a sequence
![]() ${\vec L}=\langle A_\delta \mathrel {|} \delta \in S\rangle $
such that each
${\vec L}=\langle A_\delta \mathrel {|} \delta \in S\rangle $
such that each
![]() $A_\delta $
is a cofinal subset of
$A_\delta $
is a cofinal subset of
![]() $\delta $
. It is
$\delta $
. It is
![]() $\xi $
-bounded iff
$\xi $
-bounded iff
![]() $\operatorname {\mathrm {otp}}(A_\delta )\le \xi $
for all
$\operatorname {\mathrm {otp}}(A_\delta )\le \xi $
for all
![]() $\delta \in S$
. The corresponding topological space
$\delta \in S$
. The corresponding topological space
![]() $X_{\vec L}$
has underlying set
$X_{\vec L}$
has underlying set
![]() $(\kappa \times \{0\})\cup (S\times \{1\})$
with all points in
$(\kappa \times \{0\})\cup (S\times \{1\})$
with all points in
![]() $(\kappa \times \{0\})$
being isolated and, for every
$(\kappa \times \{0\})$
being isolated and, for every
![]() $\delta \in S$
, the neighborhoods of
$\delta \in S$
, the neighborhoods of
![]() $(\delta ,1)$
consisting of sets of the form
$(\delta ,1)$
consisting of sets of the form
![]() $(A\times \{0\})\cup \{(\delta ,1)\}$
for some A an end segment of
$(A\times \{0\})\cup \{(\delta ,1)\}$
for some A an end segment of
![]() $A_\delta $
.
$A_\delta $
.
A topological space X is a
![]() $\Delta $
-space (resp. countably metacompact) iff for very decreasing sequence
$\Delta $
-space (resp. countably metacompact) iff for very decreasing sequence
![]() $\langle D_n\mathrel {|} n<\omega \rangle $
of subsets of X (resp. closed subsets of X) with empty intersection, there is a decreasing sequence
$\langle D_n\mathrel {|} n<\omega \rangle $
of subsets of X (resp. closed subsets of X) with empty intersection, there is a decreasing sequence
![]() $\langle U_n\mathrel {|} n<\omega \rangle $
of open subsets of X with empty intersection such that
$\langle U_n\mathrel {|} n<\omega \rangle $
of open subsets of X with empty intersection such that
![]() $D_n\subseteq U_n$
for all
$D_n\subseteq U_n$
for all
![]() $n<\omega $
.
$n<\omega $
.
It is well-known that the product of two normal topological spaces need not be normal, but what about the product of a normal space X and the unit interval
![]() $[0,1]$
? It is a classical theorem of Dowker [Reference Dowker8] that the product
$[0,1]$
? It is a classical theorem of Dowker [Reference Dowker8] that the product
![]() $X\times [0,1]$
is again normal iff X is countably metacompact, hence the importance of this notion. The notion of a
$X\times [0,1]$
is again normal iff X is countably metacompact, hence the importance of this notion. The notion of a
![]() $\Delta $
-space is due to Knight [Reference Knight17].
$\Delta $
-space is due to Knight [Reference Knight17].
In a recent paper by Leiderman and Szeptycki [Reference Leiderman and Szeptycki19], a systematic study of
![]() $\Delta $
-spaces is carried out, motivated by the
$\Delta $
-spaces is carried out, motivated by the
![]() $C_p$
-theory of such spaces (see [Reference Ka̧kol and Leiderman16, Theorem 2.1]). Section 5 of [Reference Leiderman and Szeptycki19] is dedicated to the study of spaces of the form
$C_p$
-theory of such spaces (see [Reference Ka̧kol and Leiderman16, Theorem 2.1]). Section 5 of [Reference Leiderman and Szeptycki19] is dedicated to the study of spaces of the form
![]() $X_{\vec L}$
. It is proved that in
$X_{\vec L}$
. It is proved that in
![]() $\textsf {{ZFC}}$
there is an
$\textsf {{ZFC}}$
there is an
![]() $\omega $
-bounded ladder system
$\omega $
-bounded ladder system
![]() ${\vec L}$
over
${\vec L}$
over
![]() $\aleph _1$
for which
$\aleph _1$
for which
![]() $X_{\vec L}$
is countably metacompact, that under Martin’s axiom all
$X_{\vec L}$
is countably metacompact, that under Martin’s axiom all
![]() $\omega $
-bounded ladder systems
$\omega $
-bounded ladder systems
![]() ${\vec L}$
over
${\vec L}$
over
![]() $\aleph _1$
satisfy that
$\aleph _1$
satisfy that
![]() $X_{\vec L}$
is countably metacompact, and that in the forcing extension after adding a single Cohen real, there exists an
$X_{\vec L}$
is countably metacompact, and that in the forcing extension after adding a single Cohen real, there exists an
![]() $\omega $
-bounded ladder system
$\omega $
-bounded ladder system
![]() ${\vec L}$
over
${\vec L}$
over
![]() $\aleph _1$
for which the space
$\aleph _1$
for which the space
![]() $X_{\vec L}$
is not a
$X_{\vec L}$
is not a
![]() $\Delta $
-space. At the end of that section, Problem 5.11 asks whether there is a
$\Delta $
-space. At the end of that section, Problem 5.11 asks whether there is a
![]() $\textsf {{ZFC}}$
example of a ladder system
$\textsf {{ZFC}}$
example of a ladder system
![]() ${\vec L}$
over some cardinal
${\vec L}$
over some cardinal
![]() $\kappa $
whose corresponding space
$\kappa $
whose corresponding space
![]() $X_{\vec L}$
is not countably metacompact, hence not a
$X_{\vec L}$
is not countably metacompact, hence not a
![]() $\Delta $
-space. We answer this question in the affirmative, as follows.
$\Delta $
-space. We answer this question in the affirmative, as follows.
Theorem A. For
![]() $\kappa :=\operatorname {\mathrm {cf}}(\beth _{\omega +1})$
there are co-boundedly many regular cardinals
$\kappa :=\operatorname {\mathrm {cf}}(\beth _{\omega +1})$
there are co-boundedly many regular cardinals
![]() $\mu <\beth _\omega $
such that
$\mu <\beth _\omega $
such that
![]() $E^\kappa _\mu :=\{\delta <\kappa \mathrel {|} \operatorname {\mathrm {cf}}(\delta )=\mu \}$
carries a
$E^\kappa _\mu :=\{\delta <\kappa \mathrel {|} \operatorname {\mathrm {cf}}(\delta )=\mu \}$
carries a
![]() $\mu $
-bounded ladder system
$\mu $
-bounded ladder system
![]() ${\vec L}$
such that
${\vec L}$
such that
![]() $X_{\vec L}$
is not countably metacompact.
$X_{\vec L}$
is not countably metacompact.
Theorem A fits into a well-known programme of obtaining analogues in
![]() $\textsf {{ZFC}}$
of statements which are undecidable at small cardinals. Often times, the price is that these results concern higher cardinals and it suggests the fruitfulness of an asymptotic viewpoint to statements in infinite combinatorics. So, here the Leiderman–Szeptycki consistency result for
$\textsf {{ZFC}}$
of statements which are undecidable at small cardinals. Often times, the price is that these results concern higher cardinals and it suggests the fruitfulness of an asymptotic viewpoint to statements in infinite combinatorics. So, here the Leiderman–Szeptycki consistency result for
![]() $\kappa =\aleph _1$
is obtained in
$\kappa =\aleph _1$
is obtained in
![]() $\textsf {{ZFC}}$
at
$\textsf {{ZFC}}$
at
![]() $\kappa =\operatorname {\mathrm {cf}}(2^\lambda )$
, where
$\kappa =\operatorname {\mathrm {cf}}(2^\lambda )$
, where
![]() $\lambda :=\sup \{2^{\aleph _0},2^{2^{\aleph _0}},2^{2^{2^{\aleph _0}}},\ldots \}$
. The proof builds heavily on Shelah’s contributions to this programme, where he previously showed that refined forms of Jensen’s results for Gödel’s constructible universe [Reference Jensen15] hold asymptotically in any universe of set theory. This includes refined forms of the
$\lambda :=\sup \{2^{\aleph _0},2^{2^{\aleph _0}},2^{2^{2^{\aleph _0}}},\ldots \}$
. The proof builds heavily on Shelah’s contributions to this programme, where he previously showed that refined forms of Jensen’s results for Gödel’s constructible universe [Reference Jensen15] hold asymptotically in any universe of set theory. This includes refined forms of the
![]() $\textsf {{GCH}}$
[Reference Shelah25], of the square principle [Reference Shelah24] and of the diamond principle [Reference Shelah26]. These refined results often state that a desired phenomenon holds at all but some indispensable small set of ‘bad’ cardinals, and typically, these ‘bad’ cardinals include
$\textsf {{GCH}}$
[Reference Shelah25], of the square principle [Reference Shelah24] and of the diamond principle [Reference Shelah26]. These refined results often state that a desired phenomenon holds at all but some indispensable small set of ‘bad’ cardinals, and typically, these ‘bad’ cardinals include
![]() $\aleph _0$
(see, for instance, [Reference Cummings, Foreman and Magidor6, Theorem 3.5], [Reference Shelah27, Section 2], and [Reference Abraham and Magidor1, Lemma 8.13], the latter two highlighting the role played by
$\aleph _0$
(see, for instance, [Reference Cummings, Foreman and Magidor6, Theorem 3.5], [Reference Shelah27, Section 2], and [Reference Abraham and Magidor1, Lemma 8.13], the latter two highlighting the role played by
![]() $\aleph _1$
-complete ideals having well-defined rank functions). In our context, this raises the question whether a ladder system
$\aleph _1$
-complete ideals having well-defined rank functions). In our context, this raises the question whether a ladder system
![]() $\vec L$
as in Theorem A may be obtained to concentrate at points of countable cofinality, thereby ensuring that the corresponding space
$\vec L$
as in Theorem A may be obtained to concentrate at points of countable cofinality, thereby ensuring that the corresponding space
![]() $X_{\vec L}$
be first countable. The next two theorems provide sufficient conditions beyond
$X_{\vec L}$
be first countable. The next two theorems provide sufficient conditions beyond
![]() $\textsf {{ZFC}}$
for an affirmative answer.
$\textsf {{ZFC}}$
for an affirmative answer.
The first theorem yields a ladder system of interest from a weak arithmetic hypothesis, the failure of which is consistent [Reference Foreman and Woodin11], but has a very high consistency strength.Footnote 1
Theorem B. If there exists an infinite cardinal
![]() $\lambda $
such that
$\lambda $
such that
![]() $\kappa :=2^{2^{2^{\lambda }}}$
is a finite successor of
$\kappa :=2^{2^{2^{\lambda }}}$
is a finite successor of
![]() $\lambda $
, then
$\lambda $
, then
![]() $E^\kappa _\omega $
carries an
$E^\kappa _\omega $
carries an
![]() $\omega $
-bounded ladder system
$\omega $
-bounded ladder system
![]() $\vec L$
for which
$\vec L$
for which
![]() $X_{\vec L}$
is not countably metacompact.
$X_{\vec L}$
is not countably metacompact.
In particular, if
![]() $2^{2^{2^{\aleph _0}}}<\aleph _\omega $
, then the conclusion holds for
$2^{2^{2^{\aleph _0}}}<\aleph _\omega $
, then the conclusion holds for
![]() $\kappa :=2^{2^{2^{\aleph _0}}}$
.
$\kappa :=2^{2^{2^{\aleph _0}}}$
.
The second theorem yields a ladder system of interest from the existence of a particular type of a Souslin tree.
Theorem C. If there exists a (resp. coherent)
![]() $\kappa $
-Souslin tree, then there exists a ladder system
$\kappa $
-Souslin tree, then there exists a ladder system
![]() $\vec L$
over some stationary subset of
$\vec L$
over some stationary subset of
![]() $\kappa $
(resp. over
$\kappa $
(resp. over
![]() $E^\kappa _\omega $
) for which
$E^\kappa _\omega $
) for which
![]() $X_{\vec L}$
is not countably metacompact.
$X_{\vec L}$
is not countably metacompact.
Note that in Theorems A, B, and C, the cardinal
![]() $\kappa $
was not defined in terms of the
$\kappa $
was not defined in terms of the
![]() $\aleph $
-hierarchy. This is not a coincidence, as a simple generalisation of [Reference Balogh, Eisworth, Gruenhage, Pavlov and Szeptycki3, Claim 1] implies that for any ordinal
$\aleph $
-hierarchy. This is not a coincidence, as a simple generalisation of [Reference Balogh, Eisworth, Gruenhage, Pavlov and Szeptycki3, Claim 1] implies that for any ordinal
![]() $\alpha $
, upon forcing Martin’s axiom together with the continuum being greater than
$\alpha $
, upon forcing Martin’s axiom together with the continuum being greater than
![]() $\aleph _\alpha $
, for every
$\aleph _\alpha $
, for every
![]() $\omega $
-bounded ladder system
$\omega $
-bounded ladder system
![]() $\vec L$
over a stationary subset of
$\vec L$
over a stationary subset of
![]() $E^\kappa _\omega $
,
$E^\kappa _\omega $
,
![]() $X_{\vec L}$
is countably metacompact.
$X_{\vec L}$
is countably metacompact.
Ultimately, our proofs of Theorems A and B go through a diamond-type principle on ladder systems studied by Shelah under various names (see [Reference Shelah26, Reference Shelah27]): middle diamond, super black box,
![]() $\operatorname {\mathrm {Ps}}_1$
. We opt for the following nomenclature.
$\operatorname {\mathrm {Ps}}_1$
. We opt for the following nomenclature.
Definition 1. For a ladder system
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
over some stationary
$\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
over some stationary
![]() $S\subseteq \kappa $
and a cardinal
$S\subseteq \kappa $
and a cardinal
![]() $\theta $
,
$\theta $
,
![]() $\diamondsuit (\vec L,\theta )$
asserts the existence of a sequence
$\diamondsuit (\vec L,\theta )$
asserts the existence of a sequence
![]() $\langle f_\delta \mathrel {|} \delta \in S\rangle $
such that:
$\langle f_\delta \mathrel {|} \delta \in S\rangle $
such that:
-
• for every
 $\delta \in S$
,
$\delta \in S$
,
 $f_\delta $
is a function from
$f_\delta $
is a function from
 $A_\delta $
to
$A_\delta $
to
 $\theta $
;
$\theta $
; -
• for every function
 $f:\kappa \rightarrow \theta $
, there are stationarily many
$f:\kappa \rightarrow \theta $
, there are stationarily many
 $\delta \in S$
such that
$\delta \in S$
such that
 $f \mathbin {\upharpoonright } A_\delta =f_\delta $
.
$f \mathbin {\upharpoonright } A_\delta =f_\delta $
.
Note that Jensen’s diamond principle
![]() $\diamondsuit (S)$
is simply
$\diamondsuit (S)$
is simply
![]() $\diamondsuit (\vec L,2)$
for the degenerate ladder system
$\diamondsuit (\vec L,2)$
for the degenerate ladder system
![]() $\vec L=\langle \delta \mathrel {|} \delta \in S\rangle $
. In [Reference Shelah26], Shelah proved that
$\vec L=\langle \delta \mathrel {|} \delta \in S\rangle $
. In [Reference Shelah26], Shelah proved that
![]() $\diamondsuit (\vec L,\mu )$
holds in
$\diamondsuit (\vec L,\mu )$
holds in
![]() $\textsf {{ZFC}}$
for various ladder systems
$\textsf {{ZFC}}$
for various ladder systems
![]() $\vec L$
and cardinals
$\vec L$
and cardinals
![]() $\mu $
. A central case reads as follows.
$\mu $
. A central case reads as follows.
Fact 2 (Shelah).
Suppose that
![]() $\Lambda \le \lambda $
is a pair of uncountable cardinals such that
$\Lambda \le \lambda $
is a pair of uncountable cardinals such that
![]() $\Lambda $
is a strong limit. Denote
$\Lambda $
is a strong limit. Denote
![]() $\kappa := \operatorname {\mathrm {cf}}(2^\lambda )$
. Then, for co-boundedly many regular cardinals
$\kappa := \operatorname {\mathrm {cf}}(2^\lambda )$
. Then, for co-boundedly many regular cardinals
![]() $\mu <\Lambda $
, there exists a
$\mu <\Lambda $
, there exists a
![]() $\mu $
-bounded ladder system
$\mu $
-bounded ladder system
![]() $\vec C=\langle C_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
with each
$\vec C=\langle C_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
with each
![]() $C_\delta $
a club in
$C_\delta $
a club in
![]() $\delta $
such that
$\delta $
such that
![]() $\diamondsuit (\vec C, \mu )$
holds.Footnote
2
$\diamondsuit (\vec C, \mu )$
holds.Footnote
2
That Fact 2 should have applications in set-theoretic topology was anticipated ever since [Reference Shelah26] was written, and yet Theorem A is the first application.
At the beginning of this paper, we shall give an accessible proof of Fact 2. Our motivation for doing so is twofold. First, this will pave the way for the proof of Theorem B. Second, ladder systems are a rich source of examples and counterexamples in set-theoretic topology (see, for example, [Reference Nikosh20]), and weak diamonds have proved to be useful in studying abstract elementary classes (see, for example, [Reference Baldwin2]), so we hope that this paper will help popularise this result of Shelah and its variations. In particular, we expect the next theorem to find further applications.
Theorem D. Suppose that
![]() $\aleph _\omega $
is a strong limit. For every positive integer n, for all infinite cardinals
$\aleph _\omega $
is a strong limit. For every positive integer n, for all infinite cardinals
![]() $\mu \le \theta <\aleph _\omega $
, there are a cardinal
$\mu \le \theta <\aleph _\omega $
, there are a cardinal
![]() $\kappa <\aleph _\omega $
, a
$\kappa <\aleph _\omega $
, a
![]() $\mu $
-bounded ladder system
$\mu $
-bounded ladder system
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
and a map
$\vec L=\langle A_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
and a map
![]() $g:\kappa \rightarrow \theta $
such that for every function
$g:\kappa \rightarrow \theta $
such that for every function
![]() $f:[\kappa ]^n\rightarrow \theta $
, there are stationarily many
$f:[\kappa ]^n\rightarrow \theta $
, there are stationarily many
![]() $\delta \in E^\kappa _\mu $
such that
$\delta \in E^\kappa _\mu $
such that
![]() $f"[A_\delta ]^n=\{g(\delta )\}$
.
$f"[A_\delta ]^n=\{g(\delta )\}$
.
1.1 Organisation of this paper
In Section 2 we include a proof of Fact 2 and some variants. This section is written at a slower pace hoping to introduce readers to the basic construction of diamonds on ladder systems. The reader we have in mind here is a topologist or a model-theorist who is not necessarily familiar with Shelah’s revised
![]() $\textsf {{GCH}}$
and the approachability ideal. While the results here are due to Shelah or can be extracted from [Reference Shelah26], some of the proofs make use of ideas and concepts from recent papers of the authors of this paper.
$\textsf {{GCH}}$
and the approachability ideal. While the results here are due to Shelah or can be extracted from [Reference Shelah26], some of the proofs make use of ideas and concepts from recent papers of the authors of this paper.
In Section 3 we prepare the ground for Theorem B, and we prove Theorem D which is of independent interest. Here, we shall assume the reader is comfortable with the content of Section 2.
Section 4 is focused on topological applications of diamonds on ladder systems and our other main results. In particular, the proof of Theorems A, B, and C will be found there.
1.2 Notation and conventions
The set of all infinite regular cardinals below
![]() $\kappa $
is denoted by
$\kappa $
is denoted by
![]() $\operatorname {\mathrm {Reg}}(\kappa )$
. For a set X, we write
$\operatorname {\mathrm {Reg}}(\kappa )$
. For a set X, we write
![]() $[X]^{\kappa }$
for the collection of all subsets of X of size
$[X]^{\kappa }$
for the collection of all subsets of X of size
![]() $\kappa $
. The collections
$\kappa $
. The collections
![]() $[X]^{\le \kappa }$
and
$[X]^{\le \kappa }$
and
![]() $[X]^{<\kappa }$
are defined similarly. In the specific case when X is a set of ordinals and n is an integer
$[X]^{<\kappa }$
are defined similarly. In the specific case when X is a set of ordinals and n is an integer
![]() $\ge 2$
, we will identify
$\ge 2$
, we will identify
![]() $[X]^n$
with the set of ordered tuples
$[X]^n$
with the set of ordered tuples
![]() $(\alpha _1,\ldots ,\alpha _n)$
where
$(\alpha _1,\ldots ,\alpha _n)$
where
![]() $\alpha _1<\cdots <\alpha _n$
are all from X. For a set of ordinals A, we write
$\alpha _1<\cdots <\alpha _n$
are all from X. For a set of ordinals A, we write
![]() $\operatorname {\mathrm {acc}}(A) := \{\alpha \in A \mathrel {|} \sup (A \cap \alpha ) = \alpha> 0\}$
and
$\operatorname {\mathrm {acc}}(A) := \{\alpha \in A \mathrel {|} \sup (A \cap \alpha ) = \alpha> 0\}$
and
![]() $\operatorname {\mathrm {nacc}}(A) := A \setminus \operatorname {\mathrm {acc}}(A)$
. For cardinals
$\operatorname {\mathrm {nacc}}(A) := A \setminus \operatorname {\mathrm {acc}}(A)$
. For cardinals
![]() $\theta $
and
$\theta $
and
![]() $\mu $
,
$\mu $
,
![]() $\theta ^{+\mu }$
denotes the
$\theta ^{+\mu }$
denotes the
![]() $\mu {\text {th}}$
cardinal after
$\mu {\text {th}}$
cardinal after
![]() $\theta $
: so if
$\theta $
: so if
![]() $\theta = \aleph _\alpha $
, then
$\theta = \aleph _\alpha $
, then
![]() $\theta ^{+\mu }= \aleph _{\alpha +\mu }$
. The map
$\theta ^{+\mu }= \aleph _{\alpha +\mu }$
. The map
![]() $\alpha \mapsto \beth _\alpha $
is defined by recursion on the class of ordinals, setting
$\alpha \mapsto \beth _\alpha $
is defined by recursion on the class of ordinals, setting
![]() $\beth _0:=\aleph _0$
,
$\beth _0:=\aleph _0$
,
![]() $\beth _{\alpha +1}:=2^{\beth _\alpha }$
and
$\beth _{\alpha +1}:=2^{\beth _\alpha }$
and
![]() $\beth _\alpha :=\bigcup _{\beta <\alpha }\beth _\beta $
for every infinite limit ordinal
$\beth _\alpha :=\bigcup _{\beta <\alpha }\beth _\beta $
for every infinite limit ordinal
![]() $\alpha $
.
$\alpha $
.
2 Diamonds on ladder systems
2.1 Motivation
Diamonds on ladder systems have already found deep applications in algebra [Reference Shelah28, Reference Shelah29], but in view of the overall limited number of applications thus far, we would like to further motivate this concept by recalling an application to model theory and mentioning a natural strengthening of it that is still an open problem.
To start, note that Definition 1 concerns itself with guessing one-dimensional colourings
![]() $f: \kappa \rightarrow \theta $
, but in the same way one may also wish to guess higher-dimensional colourings f with
$f: \kappa \rightarrow \theta $
, but in the same way one may also wish to guess higher-dimensional colourings f with
![]() $\operatorname {\mathrm {dom}}(f)=[\kappa ]^2$
or even
$\operatorname {\mathrm {dom}}(f)=[\kappa ]^2$
or even
![]() $\operatorname {\mathrm {dom}}(f)={}^{<\omega }\kappa $
. Here is a concrete variation:
$\operatorname {\mathrm {dom}}(f)={}^{<\omega }\kappa $
. Here is a concrete variation:
Definition 2.1. For a ladder system
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
over some stationary
$\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
over some stationary
![]() $S\subseteq \kappa $
and a cardinal
$S\subseteq \kappa $
and a cardinal
![]() $\theta $
,
$\theta $
,
![]() $\diamondsuit ^{<\omega }(\vec L,\theta )$
asserts the existence of a sequence
$\diamondsuit ^{<\omega }(\vec L,\theta )$
asserts the existence of a sequence
![]() $\langle f_\delta \mathrel {|} \delta \in S\rangle $
such that:
$\langle f_\delta \mathrel {|} \delta \in S\rangle $
such that:
-
• for every
 $\delta \in S$
,
$\delta \in S$
,
 $f_\delta $
is a function from
$f_\delta $
is a function from
 ${}^{<\omega }A_\delta $
to
${}^{<\omega }A_\delta $
to
 $\theta $
;
$\theta $
; -
• for every function
 $f:{}^{< \omega }\kappa \rightarrow \theta $
, there are stationarily many
$f:{}^{< \omega }\kappa \rightarrow \theta $
, there are stationarily many
 $\delta \in S$
such that
$\delta \in S$
such that
 $f \mathbin {\upharpoonright } {}^{<\omega }A_\delta =f_\delta $
.
$f \mathbin {\upharpoonright } {}^{<\omega }A_\delta =f_\delta $
.
One of the reasons for the interest in higher-dimensional variations of Definition 1 is provided by the following application.
Fact 2.2 (Shelah [Reference Shelah26, Theorem 0.1]).
Suppose that
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
is a ladder system over some stationary
$\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
is a ladder system over some stationary
![]() $S\subseteq \kappa $
and
$S\subseteq \kappa $
and
![]() $\tau $
is an infinite cardinal such that
$\tau $
is an infinite cardinal such that
![]() $\diamondsuit ^{<\omega }(\vec L,2^\tau )$
holds.
$\diamondsuit ^{<\omega }(\vec L,2^\tau )$
holds.
Then, for every relational language
![]() $\mathcal L$
of size at most
$\mathcal L$
of size at most
![]() $\tau $
, there is a sequence
$\tau $
, there is a sequence
![]() $\langle M_\delta \mathrel {|} \delta \in S\rangle $
of
$\langle M_\delta \mathrel {|} \delta \in S\rangle $
of
![]() $\mathcal L$
-structures such that for every
$\mathcal L$
-structures such that for every
![]() $\mathcal L$
-structure M with carrier set
$\mathcal L$
-structure M with carrier set
![]() $\kappa $
, for stationarily-many
$\kappa $
, for stationarily-many
![]() $\delta \in S$
,
$\delta \in S$
,
![]() $M_\delta $
is a substructure of M with carrier set
$M_\delta $
is a substructure of M with carrier set
![]() $A_\delta $
.
$A_\delta $
.
The application is rather straightforward. Let
![]() $\mathcal L$
be a relational language with relational symbols
$\mathcal L$
be a relational language with relational symbols
![]() $\langle R_i \mathrel {|} i< \tau \rangle $
. The hypothesis of
$\langle R_i \mathrel {|} i< \tau \rangle $
. The hypothesis of
![]() $\diamondsuit ^{<\omega }(\vec L,2^\tau )$
provides us with a sequence
$\diamondsuit ^{<\omega }(\vec L,2^\tau )$
provides us with a sequence
![]() $\langle f_\delta \mathrel {|} \delta \in S\rangle $
where for every
$\langle f_\delta \mathrel {|} \delta \in S\rangle $
where for every
![]() $\delta \in S$
,
$\delta \in S$
,
![]() $f_\delta : {}^{< \omega }A_\delta \rightarrow {}^\tau 2$
, and such that for every function
$f_\delta : {}^{< \omega }A_\delta \rightarrow {}^\tau 2$
, and such that for every function
![]() $f:{}^{< \omega }\kappa \rightarrow {}^\tau 2$
, the set
$f:{}^{< \omega }\kappa \rightarrow {}^\tau 2$
, the set
![]() $\{\delta \in S\mathrel {|} f_\delta =f \mathbin {\upharpoonright } {}^{< \omega }A_\delta \}$
is stationary.
$\{\delta \in S\mathrel {|} f_\delta =f \mathbin {\upharpoonright } {}^{< \omega }A_\delta \}$
is stationary.
For every
![]() $\delta \in S$
, let
$\delta \in S$
, let
![]() $M_\delta $
be the structure with carrier set
$M_\delta $
be the structure with carrier set
![]() $A_\delta $
and relations given as follows: for a finite tuple
$A_\delta $
and relations given as follows: for a finite tuple
![]() $\langle \alpha _0,\ldots ,\alpha _{n-1}\rangle \in {}^{< \omega }A_\delta $
and an index
$\langle \alpha _0,\ldots ,\alpha _{n-1}\rangle \in {}^{< \omega }A_\delta $
and an index
![]() $i<\tau $
,
$i<\tau $
,
Now given an
![]() $\mathcal L$
-structure
$\mathcal L$
-structure
![]() $M= \langle \kappa , R_i \rangle _{i< \tau }$
, define a function
$M= \langle \kappa , R_i \rangle _{i< \tau }$
, define a function
![]() $f:{}^{< \omega }\kappa \rightarrow \mathcal {}^\tau 2$
by letting
$f:{}^{< \omega }\kappa \rightarrow \mathcal {}^\tau 2$
by letting
Then it is clear that
![]() $M_\delta $
is a substructure of M whenever
$M_\delta $
is a substructure of M whenever
![]() $f_\delta = f \mathbin {\upharpoonright } {}^{< \omega }A_\delta $
.
$f_\delta = f \mathbin {\upharpoonright } {}^{< \omega }A_\delta $
.
Remark 2.3. As indicated by Shelah in [Reference Shelah26, Section 0], obtaining diamonds on ladder systems which would allow for strengthening of Fact 2.2 by requiring the
![]() $M_\delta $
’s to be elementary substructures of M is one of the key open problems in this area.
$M_\delta $
’s to be elementary substructures of M is one of the key open problems in this area.
As for the matter of when
![]() $\diamondsuit ^{<\omega }(\vec L,\theta )$
or other higher-dimensional variants hold, we leave to the interested reader the task of translating the arguments from the upcoming subsection to their purpose with the assurance that no extra ingenuity is required. As the differences are minor we have chosen to focus on the most transparent case.
$\diamondsuit ^{<\omega }(\vec L,\theta )$
or other higher-dimensional variants hold, we leave to the interested reader the task of translating the arguments from the upcoming subsection to their purpose with the assurance that no extra ingenuity is required. As the differences are minor we have chosen to focus on the most transparent case.
2.2 Results
In this subsection, we reproduce some results from [Reference Shelah26] with the goal of proving Fact 2 and laying the groundwork for Section 3.
We start by considering two (one-dimensional) generalisations of
![]() $\diamondsuit (\vec L,\theta )$
and a generalisation of the Devlin–Shelah weak diamond principle
$\diamondsuit (\vec L,\theta )$
and a generalisation of the Devlin–Shelah weak diamond principle
![]() $\Phi $
[Reference Devlin and Shelah7].
$\Phi $
[Reference Devlin and Shelah7].
Definition 2.4. Suppose that
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
is a ladder system over some stationary
$\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
is a ladder system over some stationary
![]() $S\subseteq \kappa $
, and that
$S\subseteq \kappa $
, and that
![]() $\mu ,\theta $
are cardinals greater than
$\mu ,\theta $
are cardinals greater than
![]() $1$
.
$1$
.
-
•
 $\diamondsuit ^*(\vec L,\mu ,\theta )$
asserts the existence of a sequence
$\diamondsuit ^*(\vec L,\mu ,\theta )$
asserts the existence of a sequence
 $\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
such that:
$\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
such that:-
– for every
 $\delta \in S$
,
$\delta \in S$
,
 $|\mathcal P_\delta |<\mu $
;
$|\mathcal P_\delta |<\mu $
; -
– for every function
 $f:\kappa \rightarrow \theta $
, there are club many
$f:\kappa \rightarrow \theta $
, there are club many
 $\delta \in S$
such that
$\delta \in S$
such that
 $f \mathbin {\upharpoonright } A_\delta \in \mathcal P_\delta $
.
$f \mathbin {\upharpoonright } A_\delta \in \mathcal P_\delta $
.
-
-
•
 $\diamondsuit (\vec L,\mu ,\theta )$
asserts the existence of a sequence
$\diamondsuit (\vec L,\mu ,\theta )$
asserts the existence of a sequence
 $\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
such that:
$\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
such that:-
– for every
 $\delta \in S$
,
$\delta \in S$
,
 $|\mathcal P_\delta |<\mu $
;
$|\mathcal P_\delta |<\mu $
; -
– for every function
 $f:\kappa \rightarrow \theta $
, there are stationarily many
$f:\kappa \rightarrow \theta $
, there are stationarily many
 $\delta \in S$
such that
$\delta \in S$
such that
 $f \mathbin {\upharpoonright } A_\delta \in \mathcal P_\delta $
.
$f \mathbin {\upharpoonright } A_\delta \in \mathcal P_\delta $
.
-
-
•
 $\Phi (\vec L,\mu ,\theta )$
asserts that for every function
$\Phi (\vec L,\mu ,\theta )$
asserts that for every function
 $F:(\bigcup _{\delta \in S}{}^{A_\delta }\mu )\rightarrow \theta $
, there exists a function
$F:(\bigcup _{\delta \in S}{}^{A_\delta }\mu )\rightarrow \theta $
, there exists a function
 $g:S\rightarrow \theta $
such that, for every function
$g:S\rightarrow \theta $
such that, for every function
 $f:\kappa \rightarrow \mu $
, there are stationarily many
$f:\kappa \rightarrow \mu $
, there are stationarily many
 $\delta \in S$
such that
$\delta \in S$
such that
 $F(f \mathbin {\upharpoonright } A_\delta )= g(\delta )$
.
$F(f \mathbin {\upharpoonright } A_\delta )= g(\delta )$
.
We encourage the reader to determine the monotonicity properties of the above principles; another easy exercise is to verify that for every ladder system
![]() $\vec L$
over a subset of
$\vec L$
over a subset of
![]() $\kappa $
and every cardinal
$\kappa $
and every cardinal
![]() $\mu $
,
$\mu $
,
![]() $\diamondsuit ^*(\vec L, \mu ^\kappa , \mu )$
holds.
$\diamondsuit ^*(\vec L, \mu ^\kappa , \mu )$
holds.
Note that for
![]() $\kappa $
a successor cardinal, the principle
$\kappa $
a successor cardinal, the principle
![]() $\diamondsuit ^*(S)$
is simply
$\diamondsuit ^*(S)$
is simply
![]() $\diamondsuit ^*(\vec L,\kappa ,2)$
for the degenerate ladder system
$\diamondsuit ^*(\vec L,\kappa ,2)$
for the degenerate ladder system
![]() $\vec L=\langle \delta \mathrel {|} \delta \in S\rangle $
. Also note that
$\vec L=\langle \delta \mathrel {|} \delta \in S\rangle $
. Also note that
![]() $\diamondsuit ^*(\vec L,\mu ,\theta )\implies \diamondsuit (\vec L,\mu ,\theta )$
and
$\diamondsuit ^*(\vec L,\mu ,\theta )\implies \diamondsuit (\vec L,\mu ,\theta )$
and
![]() $\diamondsuit (\vec L,\theta )\iff \diamondsuit (\vec L,2,\theta )$
. Less immediate from these two observations, but clear after expanding the definitions is that
$\diamondsuit (\vec L,\theta )\iff \diamondsuit (\vec L,2,\theta )$
. Less immediate from these two observations, but clear after expanding the definitions is that
![]() $\diamondsuit (\vec L,\mu )\implies \Phi (\vec L,\mu ,\theta )$
for any cardinal
$\diamondsuit (\vec L,\mu )\implies \Phi (\vec L,\mu ,\theta )$
for any cardinal
![]() $\theta $
. This implication admits a converse, as follows.
$\theta $
. This implication admits a converse, as follows.
Lemma 2.5. Suppose that
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
is a
$\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
is a
![]() $\xi $
-bounded ladder system over some stationary
$\xi $
-bounded ladder system over some stationary
![]() $S\subseteq \kappa $
. If
$S\subseteq \kappa $
. If
![]() $\Phi (\vec L,\mu ,\mu ^{|\xi |})$
holds, then so does
$\Phi (\vec L,\mu ,\mu ^{|\xi |})$
holds, then so does
![]() $\diamondsuit ( \vec L, \mu )$
.
$\diamondsuit ( \vec L, \mu )$
.
Proof Denote
![]() $\theta :=\mu ^{|\xi |}$
. Let
$\theta :=\mu ^{|\xi |}$
. Let
![]() $\vec h = \langle h_\tau \mathrel {|} \tau < \theta \rangle $
be some enumeration of
$\vec h = \langle h_\tau \mathrel {|} \tau < \theta \rangle $
be some enumeration of
![]() ${}^\xi \mu $
. For every
${}^\xi \mu $
. For every
![]() $\delta \in S$
, fix an injection
$\delta \in S$
, fix an injection
![]() $\psi _\delta : A_\delta \rightarrow \xi $
. Fix a function
$\psi _\delta : A_\delta \rightarrow \xi $
. Fix a function
![]() $F:(\bigcup _{\delta \in S}{}^{A_\delta }\mu )\rightarrow \theta $
such that for all
$F:(\bigcup _{\delta \in S}{}^{A_\delta }\mu )\rightarrow \theta $
such that for all
![]() $\delta \in S$
and
$\delta \in S$
and
![]() $\bar f: A_\delta \rightarrow \mu $
,
$\bar f: A_\delta \rightarrow \mu $
,
Now, assuming that
![]() $\Phi (\vec L, \mu , \theta )$
holds, we may fix a function
$\Phi (\vec L, \mu , \theta )$
holds, we may fix a function
![]() $g: S \rightarrow \theta $
such that for every function
$g: S \rightarrow \theta $
such that for every function
![]() $f:\kappa \rightarrow \mu $
, the set
$f:\kappa \rightarrow \mu $
, the set
![]() $\{\delta \in S\mathrel {|} F(f \mathbin {\upharpoonright } A_\delta )= g(\delta )\}$
is stationary in
$\{\delta \in S\mathrel {|} F(f \mathbin {\upharpoonright } A_\delta )= g(\delta )\}$
is stationary in
![]() $\kappa $
.
$\kappa $
.
For every
![]() $\delta \in S$
, let
$\delta \in S$
, let
![]() $f_\delta :=h_{g(\delta )}\circ \psi _\delta $
. We claim that
$f_\delta :=h_{g(\delta )}\circ \psi _\delta $
. We claim that
![]() $\langle f_\delta \mathrel {|} \delta \in S\rangle $
witnesses that
$\langle f_\delta \mathrel {|} \delta \in S\rangle $
witnesses that
![]() $\diamondsuit (\vec L,\mu )$
holds. Indeed, given
$\diamondsuit (\vec L,\mu )$
holds. Indeed, given
![]() $f: \kappa \rightarrow \mu $
, consider the stationary set
$f: \kappa \rightarrow \mu $
, consider the stationary set
![]() $S':=\{\delta \in S\mathrel {|} F(f \mathbin {\upharpoonright } A_\delta )= g(\delta )\}$
. For every
$S':=\{\delta \in S\mathrel {|} F(f \mathbin {\upharpoonright } A_\delta )= g(\delta )\}$
. For every
![]() $\delta \in S'$
, it is the case that
$\delta \in S'$
, it is the case that
as sought.
We can at this stage describe the structure of the proof of Fact 2 given below. To start, in Lemma 2.9 we establish an instance of the principle
![]() $\diamondsuit ^*(\vec L, \ldots )$
. The caveat here is that the second parameter, the width of the diamond sequence, will be rather large. Using this very wide diamond and an instance of a colouring principle which is established in Lemma 2.8, we will then in Lemma 2.10 derive an instance of the principle
$\diamondsuit ^*(\vec L, \ldots )$
. The caveat here is that the second parameter, the width of the diamond sequence, will be rather large. Using this very wide diamond and an instance of a colouring principle which is established in Lemma 2.8, we will then in Lemma 2.10 derive an instance of the principle
![]() $\Phi (\vec L, \mu , \theta )$
. Crucially for us here, the parameter
$\Phi (\vec L, \mu , \theta )$
. Crucially for us here, the parameter
![]() $\theta $
, the number of colours, will be large. Finally, we will use Lemma 2.5 to obtain a narrow diamond sequence on the ladder system. The details are in Corollary 2.12.
$\theta $
, the number of colours, will be large. Finally, we will use Lemma 2.5 to obtain a narrow diamond sequence on the ladder system. The details are in Corollary 2.12.
The upcoming proof of Fact 2 will make multiple uses of Shelah’s revised GCH theorem [Reference Shelah25] that was briefly mentioned in the paper’s introduction. To state it, we shall need the following definition.
Definition 2.6. For cardinals
![]() $\theta \le \lambda $
:
$\theta \le \lambda $
:
-
•
 $\lambda ^{[\theta ]}$
stands for the least size of a subfamily
$\lambda ^{[\theta ]}$
stands for the least size of a subfamily
 $\mathcal A\subseteq [\lambda ]^{\le \theta }$
satisfying that every element of
$\mathcal A\subseteq [\lambda ]^{\le \theta }$
satisfying that every element of
 $[\lambda ]^\theta $
is the union of less than
$[\lambda ]^\theta $
is the union of less than
 $\theta $
many sets from
$\theta $
many sets from
 $\mathcal A$
;
$\mathcal A$
; -
•
 $m(\lambda ,\theta )$
stands for the least size of a subfamily
$m(\lambda ,\theta )$
stands for the least size of a subfamily
 $\mathcal A\subseteq [\lambda ]^{\theta }$
satisfying that for every
$\mathcal A\subseteq [\lambda ]^{\theta }$
satisfying that for every
 $b\in [\lambda ]^\theta $
, there is an
$b\in [\lambda ]^\theta $
, there is an
 $a\in \mathcal A$
with
$a\in \mathcal A$
with
 $|a\cap b|=\theta $
.
$|a\cap b|=\theta $
.
Note that for
![]() $\theta $
a regular cardinal,
$\theta $
a regular cardinal,
![]() $m(\lambda ,\theta )\le \lambda ^{[\theta ]}$
.
$m(\lambda ,\theta )\le \lambda ^{[\theta ]}$
.
Fact 2.7 (Shelah’s RGCH [Reference Shelah25]).
For every pair
![]() $\Lambda \le \lambda $
of uncountable cardinals such that
$\Lambda \le \lambda $
of uncountable cardinals such that
![]() $\Lambda $
is a strong limit, for co-boundedly many
$\Lambda $
is a strong limit, for co-boundedly many
![]() $\theta \in \operatorname {\mathrm {Reg}}(\Lambda )$
,
$\theta \in \operatorname {\mathrm {Reg}}(\Lambda )$
,
![]() $\lambda ^{[\theta ]}=\lambda $
.
$\lambda ^{[\theta ]}=\lambda $
.
As a warm up, we prove the following lemma that may be extracted from the proof of [Reference Shelah26, Claim 1.11]. It concerns the principle
![]() ${{{\sf onto}}}(\ldots )$
that was recently introduced in the paper [Reference Inamdar and Rinot13] by the second and third authors.
${{{\sf onto}}}(\ldots )$
that was recently introduced in the paper [Reference Inamdar and Rinot13] by the second and third authors.
Lemma 2.8. Suppose that
![]() $\theta ,\lambda $
are infinite cardinals such that
$\theta ,\lambda $
are infinite cardinals such that
![]() $2^\theta \le m(\lambda ,\theta )=\lambda $
.
$2^\theta \le m(\lambda ,\theta )=\lambda $
.
Then
![]() ${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\theta )$
holds, i.e., there is a colouring
${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\theta )$
holds, i.e., there is a colouring
![]() $c:\lambda \times 2^\lambda \rightarrow \theta $
such that, for every
$c:\lambda \times 2^\lambda \rightarrow \theta $
such that, for every
![]() $B\in [2^\lambda ]^{\lambda ^+}$
,Footnote
3
there exists an
$B\in [2^\lambda ]^{\lambda ^+}$
,Footnote
3
there exists an
![]() $\alpha <\lambda $
such that
$\alpha <\lambda $
such that
![]() $c[\{\alpha \}\times B]=\theta $
.
$c[\{\alpha \}\times B]=\theta $
.
Proof Let
![]() $\mathcal A$
be a witness for
$\mathcal A$
be a witness for
![]() $m(\lambda ,\theta )=\lambda $
. The next claim is of independent interest. It may be proved using elementary submodels, but we give a more elementary (for the reason of avoiding elementary submodels) proof due to Ido Feldman.
$m(\lambda ,\theta )=\lambda $
. The next claim is of independent interest. It may be proved using elementary submodels, but we give a more elementary (for the reason of avoiding elementary submodels) proof due to Ido Feldman.
Claim 2.8.1. For every
![]() $\mathcal H\subseteq {}^\lambda 2$
of size
$\mathcal H\subseteq {}^\lambda 2$
of size
![]() $\lambda ^+$
, there exists an
$\lambda ^+$
, there exists an
![]() $a\in \mathcal A$
such that the set
$a\in \mathcal A$
such that the set
![]() $\{h \mathbin {\upharpoonright } a \mathrel {|} h \in \mathcal H\}$
has size at least
$\{h \mathbin {\upharpoonright } a \mathrel {|} h \in \mathcal H\}$
has size at least
![]() $\theta $
.
$\theta $
.
Proof (Feldman)
For two distinct functions
![]() $g,h\in {}^\lambda 2$
, denote
$g,h\in {}^\lambda 2$
, denote
Now, let a family
![]() $\mathcal H\subseteq {}^\lambda 2$
of size
$\mathcal H\subseteq {}^\lambda 2$
of size
![]() $\lambda ^+$
be given.
$\lambda ^+$
be given.
![]() $\blacktriangleright $
If there exists a function
$\blacktriangleright $
If there exists a function
![]() $g:\lambda \rightarrow 2$
such that
$g:\lambda \rightarrow 2$
such that
![]() $D(g):=\{ \Delta (g,h)\mathrel {|} h\in \mathcal H\setminus \{g\}\}$
has size greater than or equal to
$D(g):=\{ \Delta (g,h)\mathrel {|} h\in \mathcal H\setminus \{g\}\}$
has size greater than or equal to
![]() $\theta $
, then pick
$\theta $
, then pick
![]() $a\in \mathcal A$
such that
$a\in \mathcal A$
such that
![]() $|a\cap D(g)|=\theta $
, and for each
$|a\cap D(g)|=\theta $
, and for each
![]() $\delta \in a\cap D(g)$
, pick some
$\delta \in a\cap D(g)$
, pick some
![]() $h_\delta \in \mathcal H$
such that
$h_\delta \in \mathcal H$
such that
![]() $\Delta (g,h_\delta )=\delta $
. Then
$\Delta (g,h_\delta )=\delta $
. Then
![]() $\delta \mapsto h_\delta \mathbin {\upharpoonright } a$
is injective over
$\delta \mapsto h_\delta \mathbin {\upharpoonright } a$
is injective over
![]() $a\cap D(g)$
.
$a\cap D(g)$
.
![]() $\blacktriangleright $
Otherwise, for every
$\blacktriangleright $
Otherwise, for every
![]() $g:\lambda \rightarrow 2$
, let
$g:\lambda \rightarrow 2$
, let
![]() $\pi _g:\operatorname {\mathrm {otp}}(D(g))\rightarrow D(g)$
be the increasing enumeration of
$\pi _g:\operatorname {\mathrm {otp}}(D(g))\rightarrow D(g)$
be the increasing enumeration of
![]() $D(g)$
, so that
$D(g)$
, so that
![]() $\bar g:=g\circ \pi _g$
is an element of
$\bar g:=g\circ \pi _g$
is an element of
![]() ${}^{<\theta }2$
. As
${}^{<\theta }2$
. As
![]() $2^{<\theta }\le 2^\theta \le \lambda $
, we may find
$2^{<\theta }\le 2^\theta \le \lambda $
, we may find
![]() $g\neq h$
in
$g\neq h$
in
![]() $\mathcal H$
such that
$\mathcal H$
such that
![]() $\bar g=\bar h$
. Consider
$\bar g=\bar h$
. Consider
![]() $\delta :=\Delta (g,h)$
. Then
$\delta :=\Delta (g,h)$
. Then
![]() ${\delta \in D(g)\cap D(h)}$
. In addition, since
${\delta \in D(g)\cap D(h)}$
. In addition, since
![]() $g \mathbin {\upharpoonright }\delta =h \mathbin {\upharpoonright }\delta $
,
$g \mathbin {\upharpoonright }\delta =h \mathbin {\upharpoonright }\delta $
,
![]() $D(g)\cap \delta =D(h)\cap \delta $
. In particular, for
$D(g)\cap \delta =D(h)\cap \delta $
. In particular, for
![]() $\xi :=\operatorname {\mathrm {otp}}(D(g)\cap \delta )$
, we get that
$\xi :=\operatorname {\mathrm {otp}}(D(g)\cap \delta )$
, we get that
![]() $\pi _g(\xi )=\delta =\pi _h(\xi )$
and hence
$\pi _g(\xi )=\delta =\pi _h(\xi )$
and hence
![]() $g(\delta )=\bar g(\xi )=\bar h(\xi )=h(\delta )$
, contradicting the definition of
$g(\delta )=\bar g(\xi )=\bar h(\xi )=h(\delta )$
, contradicting the definition of
![]() $\delta $
. So this case does not exist.
$\delta $
. So this case does not exist.
For each
![]() $a \in \mathcal A$
, let
$a \in \mathcal A$
, let
![]() $\mathcal G^a$
be the collection of all functions
$\mathcal G^a$
be the collection of all functions
![]() $g:{}^a\theta \rightarrow \theta $
such that
$g:{}^a\theta \rightarrow \theta $
such that
Clearly,
![]() $|\mathcal G^a|=2^\theta \le \lambda $
. For each
$|\mathcal G^a|=2^\theta \le \lambda $
. For each
![]() $g\in \mathcal G^a$
, we lift g to a function
$g\in \mathcal G^a$
, we lift g to a function
![]() $\hat g:{}^\lambda \theta \rightarrow \theta $
by letting
$\hat g:{}^\lambda \theta \rightarrow \theta $
by letting
Now, let
![]() $\langle g_\alpha \mathrel {|} \alpha < \lambda \rangle $
be an injective enumeration of
$\langle g_\alpha \mathrel {|} \alpha < \lambda \rangle $
be an injective enumeration of
![]() $\{\hat g\mathrel {|} a \in \mathcal A,\, g \in \mathcal G^a\}$
, and let
$\{\hat g\mathrel {|} a \in \mathcal A,\, g \in \mathcal G^a\}$
, and let
![]() $\langle h_\beta \mathrel {|} \beta <2^\lambda \rangle $
be an injective enumeration of
$\langle h_\beta \mathrel {|} \beta <2^\lambda \rangle $
be an injective enumeration of
![]() ${}^\lambda 2$
. Define a colouring
${}^\lambda 2$
. Define a colouring
![]() $c:\lambda \times 2^\lambda \rightarrow \theta $
via
$c:\lambda \times 2^\lambda \rightarrow \theta $
via
![]() $c(\alpha ,\beta ):=g_\alpha (h_\beta )$
. To see that c is as sought, let
$c(\alpha ,\beta ):=g_\alpha (h_\beta )$
. To see that c is as sought, let
![]() $B\in [2^\lambda ]^{\lambda ^+}$
. By Claim 2.8.1, pick
$B\in [2^\lambda ]^{\lambda ^+}$
. By Claim 2.8.1, pick
![]() $a\in \mathcal A$
such that
$a\in \mathcal A$
such that
![]() $\{ h_\beta \mathbin {\upharpoonright } a\mathrel {|} \beta \in B\}$
has size at least
$\{ h_\beta \mathbin {\upharpoonright } a\mathrel {|} \beta \in B\}$
has size at least
![]() $\theta $
. Pick
$\theta $
. Pick
![]() $B'\subseteq B$
of order type
$B'\subseteq B$
of order type
![]() $\theta $
on which
$\theta $
on which
![]() $\beta \mapsto h_\beta \mathbin {\upharpoonright } a$
is injective. It follows that we may define a function
$\beta \mapsto h_\beta \mathbin {\upharpoonright } a$
is injective. It follows that we may define a function
![]() $g:{}^a\theta \rightarrow \theta $
in
$g:{}^a\theta \rightarrow \theta $
in
![]() $\mathcal G^a$
via
$\mathcal G^a$
via
 $$ \begin{align*}g(f):=\begin{cases}\operatorname{\mathrm{otp}}(B'\cap\beta),&\text{if }\beta \in B' \text{ and }f= h_\beta \mathbin{\upharpoonright} a,\\ 0,&\text{otherwise}.\end{cases}\end{align*} $$
$$ \begin{align*}g(f):=\begin{cases}\operatorname{\mathrm{otp}}(B'\cap\beta),&\text{if }\beta \in B' \text{ and }f= h_\beta \mathbin{\upharpoonright} a,\\ 0,&\text{otherwise}.\end{cases}\end{align*} $$
Pick
![]() $\alpha <\lambda $
such that
$\alpha <\lambda $
such that
![]() $\hat g=g_\alpha $
. Then,
$\hat g=g_\alpha $
. Then,
![]() $c[\{\alpha \}\times B']=\theta $
.
$c[\{\alpha \}\times B']=\theta $
.
Our next step is proving the following lemma that is easily extracted from the beginning of the proof of [Reference Shelah26, Claim 1.10]. It uses two fine approximations in
![]() $\textsf {{ZFC}}$
of Gödel’s constructible universe: the revised
$\textsf {{ZFC}}$
of Gödel’s constructible universe: the revised
![]() $\textsf {{GCH}}$
theorem and the approachability ideal
$\textsf {{GCH}}$
theorem and the approachability ideal
![]() $I[\kappa ]$
.
$I[\kappa ]$
.
Lemma 2.9. Suppose that
![]() $\Lambda \le \lambda $
is a pair of uncountable cardinals such that
$\Lambda \le \lambda $
is a pair of uncountable cardinals such that
![]() $\Lambda $
is a strong limit. Denote
$\Lambda $
is a strong limit. Denote
![]() $\kappa := \operatorname {\mathrm {cf}}(2^\lambda )$
. Then, for co-boundedly many
$\kappa := \operatorname {\mathrm {cf}}(2^\lambda )$
. Then, for co-boundedly many
![]() $\mu \in \operatorname {\mathrm {Reg}}(\Lambda )$
, there is a
$\mu \in \operatorname {\mathrm {Reg}}(\Lambda )$
, there is a
![]() $\mu $
-bounded C-sequence
$\mu $
-bounded C-sequence
![]() $\vec C$
over some stationary
$\vec C$
over some stationary
![]() $S\subseteq E^\kappa _\mu $
such that
$S\subseteq E^\kappa _\mu $
such that
![]() $\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
holds.
$\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
holds.
Proof We start with the following claim which guides our choice of
![]() $\mu $
.
$\mu $
.
Claim 2.9.1. There is a co-bounded set of
![]() $\mu \in \operatorname {\mathrm {Reg}}(\Lambda )$
such that for every cardinal
$\mu \in \operatorname {\mathrm {Reg}}(\Lambda )$
such that for every cardinal
![]() $\varkappa < 2^\lambda $
,
$\varkappa < 2^\lambda $
,
![]() $\varkappa ^{[\mu ]} < 2^\lambda $
.
$\varkappa ^{[\mu ]} < 2^\lambda $
.
Proof By Fact 2.7, for every
![]() $\varkappa \in [\Lambda ,2^\lambda )$
, there is a cardinal
$\varkappa \in [\Lambda ,2^\lambda )$
, there is a cardinal
![]() $\epsilon _\varkappa < \Lambda $
such that for every
$\epsilon _\varkappa < \Lambda $
such that for every
![]() $\mu \in \operatorname {\mathrm {Reg}}(\Lambda )\setminus \epsilon _\varkappa $
,
$\mu \in \operatorname {\mathrm {Reg}}(\Lambda )\setminus \epsilon _\varkappa $
,
![]() $\varkappa ^{[\mu ]}=\varkappa $
. Now, as
$\varkappa ^{[\mu ]}=\varkappa $
. Now, as
![]() $\operatorname {\mathrm {cf}}(2^\lambda )>\lambda \ge \Lambda $
, it follows that there is
$\operatorname {\mathrm {cf}}(2^\lambda )>\lambda \ge \Lambda $
, it follows that there is
![]() $\Gamma $
, an unbounded subset of cardinals in
$\Gamma $
, an unbounded subset of cardinals in
![]() $2^\lambda $
, and a cardinal
$2^\lambda $
, and a cardinal
![]() $\epsilon < \Lambda $
such that for every
$\epsilon < \Lambda $
such that for every
![]() $\varkappa \in \Gamma $
,
$\varkappa \in \Gamma $
,
![]() $\epsilon _\varkappa < \epsilon $
. In particular, for every
$\epsilon _\varkappa < \epsilon $
. In particular, for every
![]() $\mu \in \operatorname {\mathrm {Reg}}(\Lambda ) \setminus \epsilon $
, for every
$\mu \in \operatorname {\mathrm {Reg}}(\Lambda ) \setminus \epsilon $
, for every
![]() $\varkappa \in \Gamma $
,
$\varkappa \in \Gamma $
,
![]() ${\varkappa ^{[\mu ]} = \varkappa < 2^\lambda }$
. This, combined with the observation that for any cardinals
${\varkappa ^{[\mu ]} = \varkappa < 2^\lambda }$
. This, combined with the observation that for any cardinals
![]() $\varkappa _0< \varkappa _1$
and cardinal
$\varkappa _0< \varkappa _1$
and cardinal
![]() $\mu $
,
$\mu $
,
![]() $\varkappa _0^{[\mu ]} \leq \varkappa _1^{[\mu ]}$
, verifies the claim.
$\varkappa _0^{[\mu ]} \leq \varkappa _1^{[\mu ]}$
, verifies the claim.
Let
![]() $\mu $
be any cardinal in the co-bounded subset of
$\mu $
be any cardinal in the co-bounded subset of
![]() $\operatorname {\mathrm {Reg}}(\Lambda )$
given by the claim. Hereafter, all we shall need to assume about
$\operatorname {\mathrm {Reg}}(\Lambda )$
given by the claim. Hereafter, all we shall need to assume about
![]() $\mu $
is that it is a regular cardinal smaller than
$\mu $
is that it is a regular cardinal smaller than
![]() $\lambda $
and
$\lambda $
and
![]() $m(\varkappa ,\mu )<2^\lambda $
for all
$m(\varkappa ,\mu )<2^\lambda $
for all
![]() $\varkappa <2^\lambda $
. As
$\varkappa <2^\lambda $
. As
![]() $\mu ^+\le \lambda <\kappa $
, by [Reference Shelah24, Claim 1.2 and Lemma 1.4], there exists a stationary
$\mu ^+\le \lambda <\kappa $
, by [Reference Shelah24, Claim 1.2 and Lemma 1.4], there exists a stationary
![]() $S\subseteq E^\kappa _\mu $
that lies in
$S\subseteq E^\kappa _\mu $
that lies in
![]() $I[\kappa ]$
. By possibly intersecting S with some club, this means that there exists a
$I[\kappa ]$
. By possibly intersecting S with some club, this means that there exists a
![]() $\mu $
-bounded C-sequence
$\mu $
-bounded C-sequence
![]() $\vec C=\langle C_\delta \mathrel {|} \delta \in S\rangle $
satisfying the following weak coherence property: for every pair
$\vec C=\langle C_\delta \mathrel {|} \delta \in S\rangle $
satisfying the following weak coherence property: for every pair
![]() $\gamma <\delta $
of ordinals from S, for all
$\gamma <\delta $
of ordinals from S, for all
![]() $\beta \in \operatorname {\mathrm {nacc}}(C_{\gamma })\cap \operatorname {\mathrm {nacc}}(C_\delta )$
,
$\beta \in \operatorname {\mathrm {nacc}}(C_{\gamma })\cap \operatorname {\mathrm {nacc}}(C_\delta )$
,
![]() $C_{\gamma }\cap \beta =C_\delta \cap \beta $
. We shall prove that
$C_{\gamma }\cap \beta =C_\delta \cap \beta $
. We shall prove that
![]() $\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
holds.
$\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
holds.
To this end, we fix the following objects:
-
(i) Let
 $h: \kappa \rightarrow 2^\lambda $
be increasing and cofinal.
$h: \kappa \rightarrow 2^\lambda $
be increasing and cofinal. -
(ii) Let
 $\mathcal C:= \{C_\delta \cap \beta \mathrel {|} \delta \in S, \beta \in \operatorname {\mathrm {nacc}}(C_\delta )\}$
, so that
$\mathcal C:= \{C_\delta \cap \beta \mathrel {|} \delta \in S, \beta \in \operatorname {\mathrm {nacc}}(C_\delta )\}$
, so that
 $|\mathcal C| =\kappa $
and it consists of sets of size less than
$|\mathcal C| =\kappa $
and it consists of sets of size less than
 $\mu $
.
$\mu $
. -
(iii) Let
 $T:= \{f \mathrel {|} \exists C \in \mathcal C\, [f \in {}^C(2^\lambda )]\}$
. For each
$T:= \{f \mathrel {|} \exists C \in \mathcal C\, [f \in {}^C(2^\lambda )]\}$
. For each
 $C \in \mathcal C$
, since
$C \in \mathcal C$
, since
 $|C|<\mu <\lambda $
, it is the case that
$|C|<\mu <\lambda $
, it is the case that
 $2^\lambda \leq |{}^C(2^\lambda )| \leq (2^\lambda )^{|C|} = 2^\lambda $
. As
$2^\lambda \leq |{}^C(2^\lambda )| \leq (2^\lambda )^{|C|} = 2^\lambda $
. As
 $|\mathcal C| = \kappa $
, we conclude that
$|\mathcal C| = \kappa $
, we conclude that
 $|T| =2^\lambda $
.
$|T| =2^\lambda $
. -
(iv) Let
 $\langle f_i \mathrel {|} i< 2^\lambda \rangle $
be an enumeration of T.
$\langle f_i \mathrel {|} i< 2^\lambda \rangle $
be an enumeration of T. -
(v) For
 $\delta < \kappa $
, denote
$\delta < \kappa $
, denote
 $T_{< \delta }:= \{f_i \mathrel {|} i < h(\delta )\}$
, so that
$T_{< \delta }:= \{f_i \mathrel {|} i < h(\delta )\}$
, so that
 $|T_{<\delta }|<2^\lambda $
.
$|T_{<\delta }|<2^\lambda $
.
For every
![]() $\delta \in S$
, let
$\delta \in S$
, let
We shall show that the sequence
![]() $\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
is a witness for
$\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
is a witness for
![]() $\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
. We begin by estimating its width. Implicit in the upcoming proof are the ‘tree powers’ from the hypotheses of [Reference Shelah26, Claim 1.10].
$\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
. We begin by estimating its width. Implicit in the upcoming proof are the ‘tree powers’ from the hypotheses of [Reference Shelah26, Claim 1.10].
Claim 2.9.2. Let
![]() $\delta \in S$
. Then
$\delta \in S$
. Then
![]() $|\mathcal P_\delta | < 2^\lambda $
.
$|\mathcal P_\delta | < 2^\lambda $
.
Proof Consider the set
![]() $Q_\delta := \{g \in T_{<\delta } \mathrel {|} \exists \beta \in \operatorname {\mathrm {nacc}}(C_\delta )\,[g \in {}^{C_\delta \cap \beta }h(\delta )]\}$
. For every
$Q_\delta := \{g \in T_{<\delta } \mathrel {|} \exists \beta \in \operatorname {\mathrm {nacc}}(C_\delta )\,[g \in {}^{C_\delta \cap \beta }h(\delta )]\}$
. For every
![]() $f\in \mathcal P_\delta $
,
$f\in \mathcal P_\delta $
,
![]() $b_f:=\{q \in Q_\delta \mathrel {|} q \subseteq f\}$
is nothing but
$b_f:=\{q \in Q_\delta \mathrel {|} q \subseteq f\}$
is nothing but
![]() $\{ f \mathbin {\upharpoonright }\beta \mathrel {|} \beta \in \operatorname {\mathrm {nacc}}(C_\delta )\}$
. So from
$\{ f \mathbin {\upharpoonright }\beta \mathrel {|} \beta \in \operatorname {\mathrm {nacc}}(C_\delta )\}$
. So from
![]() $\operatorname {\mathrm {otp}}(C_\delta )=\operatorname {\mathrm {cf}}(\delta )=\mu $
, we infer that
$\operatorname {\mathrm {otp}}(C_\delta )=\operatorname {\mathrm {cf}}(\delta )=\mu $
, we infer that
![]() $(b_f,{\subseteq })$
is order-isomorphic to
$(b_f,{\subseteq })$
is order-isomorphic to
![]() $(\mu ,{\in })$
, satisfying that
$(\mu ,{\in })$
, satisfying that
![]() $\bigcup b=f$
for every
$\bigcup b=f$
for every
![]() $b\in [b_f]^\mu $
. In particular,
$b\in [b_f]^\mu $
. In particular,
![]() $|b_f\cap b_{f'}|<\mu $
for all
$|b_f\cap b_{f'}|<\mu $
for all
![]() $f\neq f'$
from
$f\neq f'$
from
![]() $\mathcal P_\delta $
.
$\mathcal P_\delta $
.
Set
![]() $\varkappa :=|Q_\delta |$
. As
$\varkappa :=|Q_\delta |$
. As
![]() $\varkappa \le |T_{<\delta }|<2^\lambda $
, the choice of
$\varkappa \le |T_{<\delta }|<2^\lambda $
, the choice of
![]() $\mu $
ensures that
$\mu $
ensures that
![]() $m(\varkappa ,\mu )<2^\lambda $
. In particular, we may fix a subfamily
$m(\varkappa ,\mu )<2^\lambda $
. In particular, we may fix a subfamily
![]() $\mathcal A_\delta \subseteq [Q_\delta ]^\mu $
of size less than
$\mathcal A_\delta \subseteq [Q_\delta ]^\mu $
of size less than
![]() $2^\lambda $
such that, for every
$2^\lambda $
such that, for every
![]() $f\in \mathcal P_\delta $
, there exists
$f\in \mathcal P_\delta $
, there exists
![]() $a_f\in \mathcal A_\delta $
with
$a_f\in \mathcal A_\delta $
with
![]() $|a_f\cap b_f|=\mu $
. Then
$|a_f\cap b_f|=\mu $
. Then
![]() $f\mapsto a_f$
forms an injection from
$f\mapsto a_f$
forms an injection from
![]() $\mathcal P_\delta $
to
$\mathcal P_\delta $
to
![]() $\mathcal A_\delta $
, so that
$\mathcal A_\delta $
, so that
![]() $|\mathcal P_\delta |<2^\lambda $
.
$|\mathcal P_\delta |<2^\lambda $
.
We are left with verifying that
![]() $\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
has the required guessing property. So let
$\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
has the required guessing property. So let
![]() $f: \kappa \rightarrow {}2^\lambda $
. Let
$f: \kappa \rightarrow {}2^\lambda $
. Let
![]() $D\subseteq \kappa $
be a club such that
$D\subseteq \kappa $
be a club such that
![]() $\delta \in D$
implies that:
$\delta \in D$
implies that:
-
(i) for every
 $\beta < \delta $
,
$\beta < \delta $
,
 $f(\beta ) < h(\delta )$
;
$f(\beta ) < h(\delta )$
; -
(ii) for every
 $\beta < \delta $
, for every
$\beta < \delta $
, for every
 $\delta '\in S$
such that
$\delta '\in S$
such that
 $\beta \in \operatorname {\mathrm {nacc}}(C_{\delta '})$
, we have
$\beta \in \operatorname {\mathrm {nacc}}(C_{\delta '})$
, we have
 $f \mathbin {\upharpoonright } (C_{\delta '}\cap \beta ) \in T_{< \delta }$
.
$f \mathbin {\upharpoonright } (C_{\delta '}\cap \beta ) \in T_{< \delta }$
.
Here we use the weak coherence property of
![]() $\vec C$
to ensure that the requirement in (ii) can indeed be satisfied. Now suppose that
$\vec C$
to ensure that the requirement in (ii) can indeed be satisfied. Now suppose that
![]() $\delta \in D$
. Then for every
$\delta \in D$
. Then for every
![]() $\beta \in \operatorname {\mathrm {nacc}}(C_\delta )$
,
$\beta \in \operatorname {\mathrm {nacc}}(C_\delta )$
,
![]() $f \mathbin {\upharpoonright } (C_\delta \cap \beta ) \in T_{< \delta }$
and
$f \mathbin {\upharpoonright } (C_\delta \cap \beta ) \in T_{< \delta }$
and
![]() $\operatorname {\mathrm {Im}}(f \mathbin {\upharpoonright } (C_\delta \cap \beta )) \subseteq h(\delta )$
. So indeed
$\operatorname {\mathrm {Im}}(f \mathbin {\upharpoonright } (C_\delta \cap \beta )) \subseteq h(\delta )$
. So indeed
![]() $f \mathbin {\upharpoonright } C_\delta \in \mathcal P_\delta $
.
$f \mathbin {\upharpoonright } C_\delta \in \mathcal P_\delta $
.
The last step is proving the next lemma that we extracted from the end of the proof of [Reference Shelah26, Claim 1.10]. The new ingredient here is the use of the principle
![]() ${{{\sf onto}}}(\ldots )$
. It generalizes Kunen’s lemma [Reference Kunen18, Theorem 7.14] that
${{{\sf onto}}}(\ldots )$
. It generalizes Kunen’s lemma [Reference Kunen18, Theorem 7.14] that
![]() $\diamondsuit ^-$
implies
$\diamondsuit ^-$
implies
![]() $\diamondsuit $
which amounts to the case
$\diamondsuit $
which amounts to the case
![]() $\omega _1=\kappa =\lambda ^+=2^\lambda =\theta $
, using [Reference Inamdar and Rinot13, Lemma 8.3(1)].
$\omega _1=\kappa =\lambda ^+=2^\lambda =\theta $
, using [Reference Inamdar and Rinot13, Lemma 8.3(1)].
Lemma 2.10. Suppose that
![]() $:$
$:$
-
•
 $\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
is a ladder system over some stationary
$\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
is a ladder system over some stationary
 $S\subseteq \kappa ;$
$S\subseteq \kappa ;$
-
•
 $\diamondsuit (\vec L,2^\lambda ,2^\lambda )$
holds with
$\diamondsuit (\vec L,2^\lambda ,2^\lambda )$
holds with
 $\lambda <\kappa ;$
$\lambda <\kappa ;$
-
•
 ${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\theta )$
holds.
${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\theta )$
holds.
Then
![]() $\Phi (\vec L,2^\lambda ,\theta )$
holds.
$\Phi (\vec L,2^\lambda ,\theta )$
holds.
Proof Fix a bijection
![]() $\psi :{}^\lambda (2^\lambda )\leftrightarrow 2^\lambda $
. For every
$\psi :{}^\lambda (2^\lambda )\leftrightarrow 2^\lambda $
. For every
![]() $\alpha <\lambda $
, define a map
$\alpha <\lambda $
, define a map
![]() $\psi _\alpha :2^\lambda \rightarrow 2^\lambda $
via
$\psi _\alpha :2^\lambda \rightarrow 2^\lambda $
via
The point is that for every function
![]() $\sigma :\lambda \rightarrow 2^\lambda $
and every
$\sigma :\lambda \rightarrow 2^\lambda $
and every
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
For every
![]() $x\subseteq \kappa $
, for every map
$x\subseteq \kappa $
, for every map
![]() $\eta :x\rightarrow 2^\lambda $
, for every
$\eta :x\rightarrow 2^\lambda $
, for every
![]() $\alpha <\lambda $
, we let
$\alpha <\lambda $
, we let
![]() $\eta ^\alpha :=\psi _\alpha \circ \eta $
, so
$\eta ^\alpha :=\psi _\alpha \circ \eta $
, so
![]() $\eta _\alpha : x \rightarrow 2^\lambda $
as well.
$\eta _\alpha : x \rightarrow 2^\lambda $
as well.
Now, let
![]() $F:(\bigcup _{\delta \in S}{}^{A_\delta }2^\lambda )\rightarrow \theta $
be given. Let
$F:(\bigcup _{\delta \in S}{}^{A_\delta }2^\lambda )\rightarrow \theta $
be given. Let
![]() $\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
be a witness for
$\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
be a witness for
![]() $\diamondsuit (\vec L,2^\lambda ,2^\lambda )$
. Without loss of generality, we may assume that for every
$\diamondsuit (\vec L,2^\lambda ,2^\lambda )$
. Without loss of generality, we may assume that for every
![]() $\delta \in S$
, each element of
$\delta \in S$
, each element of
![]() $\mathcal P_\delta $
is a function from
$\mathcal P_\delta $
is a function from
![]() $A_\delta $
to
$A_\delta $
to
![]() $2^\lambda $
. In particular, for all
$2^\lambda $
. In particular, for all
![]() $\delta \in S$
,
$\delta \in S$
,
![]() $\eta \in \mathcal P_\delta $
, and
$\eta \in \mathcal P_\delta $
, and
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $\eta ^\alpha $
is a map from
$\eta ^\alpha $
is a map from
![]() $A_\delta $
to
$A_\delta $
to
![]() $2^\lambda $
so that
$2^\lambda $
so that
![]() $F(\eta ^\alpha )$
is a well-defined ordinal less than
$F(\eta ^\alpha )$
is a well-defined ordinal less than
![]() $\theta $
. In other words, for all
$\theta $
. In other words, for all
![]() $\delta \in S$
and
$\delta \in S$
and
![]() $\eta \in \mathcal P_\delta $
,
$\eta \in \mathcal P_\delta $
,
is a map from
![]() $\lambda $
to
$\lambda $
to
![]() $\theta $
.
$\theta $
.
Claim 2.10.1. Let
![]() $\delta \in S$
. There exists a function
$\delta \in S$
. There exists a function
![]() $g_\delta :\lambda \rightarrow \theta $
such that, for every
$g_\delta :\lambda \rightarrow \theta $
such that, for every
![]() $\eta \in \mathcal P_\delta $
, there exists an
$\eta \in \mathcal P_\delta $
, there exists an
![]() $\alpha <\lambda $
with
$\alpha <\lambda $
with
![]() $h_\eta (\alpha )= g_\delta (\alpha )$
.
$h_\eta (\alpha )= g_\delta (\alpha )$
.
Proof Fix a witness
![]() $c:\lambda \times 2^\lambda \rightarrow \theta $
to
$c:\lambda \times 2^\lambda \rightarrow \theta $
to
![]() ${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\theta )$
. Notice that for every
${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\theta )$
. Notice that for every
![]() $\eta \in \mathcal P_\delta $
, the set
$\eta \in \mathcal P_\delta $
, the set
![]() $B_\eta :=\{\beta <2^\lambda \mathrel {|} \forall \alpha <\lambda \,[h_\eta (\alpha )\neq c(\alpha ,\beta )]\}$
has size no more than
$B_\eta :=\{\beta <2^\lambda \mathrel {|} \forall \alpha <\lambda \,[h_\eta (\alpha )\neq c(\alpha ,\beta )]\}$
has size no more than
![]() $\lambda $
, since otherwise, by the choice of c, we may pick an
$\lambda $
, since otherwise, by the choice of c, we may pick an
![]() $\alpha <\lambda $
such that
$\alpha <\lambda $
such that
![]() $c[\{\alpha \}\times B_\eta ]=\theta $
, and in particular,
$c[\{\alpha \}\times B_\eta ]=\theta $
, and in particular,
![]() $h_\eta (\alpha ) \in c[\{\alpha \}\times B_\eta ]$
. Now, as
$h_\eta (\alpha ) \in c[\{\alpha \}\times B_\eta ]$
. Now, as
![]() $|\mathcal P_\delta |<2^\lambda $
, it follows that we may pick
$|\mathcal P_\delta |<2^\lambda $
, it follows that we may pick
![]() $\beta \in 2^\lambda \setminus \bigcup _{\eta \in \mathcal P_\delta }B_\eta $
. Define
$\beta \in 2^\lambda \setminus \bigcup _{\eta \in \mathcal P_\delta }B_\eta $
. Define
![]() $g_\delta :\lambda \rightarrow \theta $
via
$g_\delta :\lambda \rightarrow \theta $
via
![]() $g_\delta (\alpha ):=c(\alpha ,\beta )$
. Then
$g_\delta (\alpha ):=c(\alpha ,\beta )$
. Then
![]() $g_\delta $
is as sought.
$g_\delta $
is as sought.
Switching the roles of
![]() $\delta $
and
$\delta $
and
![]() $\alpha $
in the preceding claim, we may fix a sequence
$\alpha $
in the preceding claim, we may fix a sequence
![]() $\langle g_\alpha :S\rightarrow \theta \mathrel {|} \alpha <\lambda \rangle $
such that, for every
$\langle g_\alpha :S\rightarrow \theta \mathrel {|} \alpha <\lambda \rangle $
such that, for every
![]() $\delta \in S$
, for every
$\delta \in S$
, for every
![]() $\eta \in \mathcal P_\delta $
, there exists an
$\eta \in \mathcal P_\delta $
, there exists an
![]() $\alpha <\lambda $
with
$\alpha <\lambda $
with
![]() $h_\eta (\alpha )= g_\alpha (\delta )$
.
$h_\eta (\alpha )= g_\alpha (\delta )$
.
Claim 2.10.2. There exists an
![]() $\alpha <\lambda $
such that for every function
$\alpha <\lambda $
such that for every function
![]() $f:\kappa \rightarrow 2^\lambda $
, the following set is stationary in
$f:\kappa \rightarrow 2^\lambda $
, the following set is stationary in
![]() $\kappa :$
$\kappa :$
Proof Suppose not. Then, for every
![]() $\alpha <\lambda $
, we may fix a function
$\alpha <\lambda $
, we may fix a function
![]() $f_\alpha :\kappa \rightarrow 2^\lambda $
and a club
$f_\alpha :\kappa \rightarrow 2^\lambda $
and a club
![]() $D_\alpha \subseteq \kappa $
disjoint from
$D_\alpha \subseteq \kappa $
disjoint from
![]() $\{\delta \in S\mathrel {|} F(f_\alpha \mathbin {\upharpoonright } A_\delta )=g_\alpha (\delta )\}$
. Define a map
$\{\delta \in S\mathrel {|} F(f_\alpha \mathbin {\upharpoonright } A_\delta )=g_\alpha (\delta )\}$
. Define a map
![]() $\eta :\kappa \rightarrow 2^\lambda $
via:
$\eta :\kappa \rightarrow 2^\lambda $
via:
Now, as
![]() $\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
witnesses
$\langle \mathcal P_\delta \mathrel {|} \delta \in S\rangle $
witnesses
![]() $\diamondsuit (\vec L,2^\lambda ,2^\lambda )$
, we may pick
$\diamondsuit (\vec L,2^\lambda ,2^\lambda )$
, we may pick
![]() $\delta \in \bigcap _{\alpha <\lambda }D_\alpha \cap S$
such that
$\delta \in \bigcap _{\alpha <\lambda }D_\alpha \cap S$
such that
![]() $\bar \eta :=\eta \mathbin {\upharpoonright } A_\delta $
is in
$\bar \eta :=\eta \mathbin {\upharpoonright } A_\delta $
is in
![]() $\mathcal P_\delta $
. For every
$\mathcal P_\delta $
. For every
![]() $\alpha <\lambda $
, recall that
$\alpha <\lambda $
, recall that
![]() $\bar \eta ^\alpha $
is defined as
$\bar \eta ^\alpha $
is defined as
![]() $\psi _\alpha \circ \bar \eta $
, so that, for every
$\psi _\alpha \circ \bar \eta $
, so that, for every
![]() $\gamma \in A_\delta $
,
$\gamma \in A_\delta $
,
That is, for every
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $\bar \eta ^\alpha =f_\alpha \mathbin {\upharpoonright } A_\delta $
. As
$\bar \eta ^\alpha =f_\alpha \mathbin {\upharpoonright } A_\delta $
. As
![]() $\bar \eta \in \mathcal P_\delta $
, we may pick some
$\bar \eta \in \mathcal P_\delta $
, we may pick some
![]() $\alpha <\lambda $
such that
$\alpha <\lambda $
such that
![]() $h_{\bar \eta }(\alpha )=g_\alpha (\delta )$
. But, by the definition of
$h_{\bar \eta }(\alpha )=g_\alpha (\delta )$
. But, by the definition of
![]() $h_{\bar \eta }$
,
$h_{\bar \eta }$
,
Altogether,
contradicting the fact that
![]() $\delta \in D_\alpha \cap S$
.
$\delta \in D_\alpha \cap S$
.
This completes the proof.
Remark 2.11. Straight-forward adjustments to the preceding proof establish the following. Suppose that
![]() $\diamondsuit (\vec L,\mu ,2^\lambda )$
holds for a given ladder system
$\diamondsuit (\vec L,\mu ,2^\lambda )$
holds for a given ladder system
![]() $\vec L$
over a stationary subset of
$\vec L$
over a stationary subset of
![]() $\kappa $
, and a given cardinal
$\kappa $
, and a given cardinal
![]() $\lambda <\kappa $
. For every cardinal
$\lambda <\kappa $
. For every cardinal
![]() $\theta $
, if
$\theta $
, if
![]() ${{{\sf onto}}}(\{\lambda \},J,\theta )$
holds for some
${{{\sf onto}}}(\{\lambda \},J,\theta )$
holds for some
![]() $\mu $
-complete proper ideal J over
$\mu $
-complete proper ideal J over
![]() $\mu $
, then so does
$\mu $
, then so does
![]() $\Phi (\vec L,2^\lambda ,\theta )$
. For a list of sufficient conditions for
$\Phi (\vec L,2^\lambda ,\theta )$
. For a list of sufficient conditions for
![]() ${{{\sf onto}}}(\{\lambda \},J,\theta )$
to hold, see the appendix of [Reference Inamdar and Rinot14].
${{{\sf onto}}}(\{\lambda \},J,\theta )$
to hold, see the appendix of [Reference Inamdar and Rinot14].
On another front, note that the principles
![]() $\diamondsuit (\vec L, \mu , \theta )$
and
$\diamondsuit (\vec L, \mu , \theta )$
and
![]() $\Phi (\vec L, \mu , \theta )$
can be strengthened by adding an extra parameter I, an ideal on
$\Phi (\vec L, \mu , \theta )$
can be strengthened by adding an extra parameter I, an ideal on
![]() $\kappa $
extending
$\kappa $
extending
![]() $\operatorname {\mathrm {NS}}_\kappa \mathbin {\upharpoonright } S$
. In each case, the set of good guesses
$\operatorname {\mathrm {NS}}_\kappa \mathbin {\upharpoonright } S$
. In each case, the set of good guesses
![]() $\delta $
is now required to be a set in
$\delta $
is now required to be a set in
![]() $I^+$
instead of merely a stationary subset of S. We leave to the interested reader to verify that most of the results in this section hold for these strengthenings for I any
$I^+$
instead of merely a stationary subset of S. We leave to the interested reader to verify that most of the results in this section hold for these strengthenings for I any
![]() $\lambda ^+$
-complete ideal on
$\lambda ^+$
-complete ideal on
![]() $\kappa $
extending
$\kappa $
extending
![]() $\operatorname {\mathrm {NS}}_\kappa \mathbin {\upharpoonright } S$
. The only change that needs to be made is that the second hypothesis of Lemma 2.10 will now require
$\operatorname {\mathrm {NS}}_\kappa \mathbin {\upharpoonright } S$
. The only change that needs to be made is that the second hypothesis of Lemma 2.10 will now require
![]() $\diamondsuit ^*(\vec L, 2^\lambda , 2^\lambda )$
instead of
$\diamondsuit ^*(\vec L, 2^\lambda , 2^\lambda )$
instead of
![]() $\diamondsuit (\vec L, 2^\lambda , 2^\lambda )$
, which is what Lemma 2.8 produces anyway.
$\diamondsuit (\vec L, 2^\lambda , 2^\lambda )$
, which is what Lemma 2.8 produces anyway.
We are now in a condition to prove Fact 2.
Corollary 2.12. Suppose that
![]() $\Lambda \le \lambda $
is a pair of uncountable cardinals such that
$\Lambda \le \lambda $
is a pair of uncountable cardinals such that
![]() $\Lambda $
is a strong limit. Denote
$\Lambda $
is a strong limit. Denote
![]() $\kappa := \operatorname {\mathrm {cf}}(2^\lambda )$
. Then, for co-boundedly many regular cardinals
$\kappa := \operatorname {\mathrm {cf}}(2^\lambda )$
. Then, for co-boundedly many regular cardinals
![]() $\mu <\Lambda $
, there exists a
$\mu <\Lambda $
, there exists a
![]() $\mu $
-bounded C-sequence
$\mu $
-bounded C-sequence
![]() $\vec C$
over a stationary
$\vec C$
over a stationary
![]() $S\subseteq E^\kappa _\mu $
such that
$S\subseteq E^\kappa _\mu $
such that
![]() $\diamondsuit (\vec C \mathbin {\upharpoonright } S', \mu )$
holds for every stationary
$\diamondsuit (\vec C \mathbin {\upharpoonright } S', \mu )$
holds for every stationary
![]() $S'\subseteq S$
.
$S'\subseteq S$
.
Proof By Lemma 2.9, for co-boundedly many
![]() $\mu \in \operatorname {\mathrm {Reg}}(\Lambda )$
, there is a
$\mu \in \operatorname {\mathrm {Reg}}(\Lambda )$
, there is a
![]() $\mu $
-bounded C-sequence
$\mu $
-bounded C-sequence
![]() $\vec C$
over some stationary
$\vec C$
over some stationary
![]() $S\subseteq E^\kappa _\mu $
such that
$S\subseteq E^\kappa _\mu $
such that
![]() $\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
holds. In particular,
$\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
holds. In particular,
![]() $\diamondsuit (\vec C \mathbin {\upharpoonright } S', 2^\lambda , 2^\lambda )$
holds for any given stationary
$\diamondsuit (\vec C \mathbin {\upharpoonright } S', 2^\lambda , 2^\lambda )$
holds for any given stationary
![]() $S'\subseteq S$
. By Fact 2.7, we may fix
$S'\subseteq S$
. By Fact 2.7, we may fix
![]() $\theta \in \operatorname {\mathrm {Reg}}(\Lambda )$
above
$\theta \in \operatorname {\mathrm {Reg}}(\Lambda )$
above
![]() $2^\mu $
such that
$2^\mu $
such that
![]() $\lambda ^{[\theta ]}=\lambda $
. As
$\lambda ^{[\theta ]}=\lambda $
. As
![]() $\Lambda $
is a strong limit,
$\Lambda $
is a strong limit,
![]() $2^\theta <\Lambda \le \lambda $
. Thus, by Lemma 2.8,
$2^\theta <\Lambda \le \lambda $
. Thus, by Lemma 2.8,
![]() ${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\theta )$
holds. Now, let
${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\theta )$
holds. Now, let
![]() $S'\subseteq S$
be stationary. By Lemma 2.10,
$S'\subseteq S$
be stationary. By Lemma 2.10,
![]() $\Phi (\vec C \mathbin {\upharpoonright } S',2^\lambda ,\theta )$
holds. In particular,
$\Phi (\vec C \mathbin {\upharpoonright } S',2^\lambda ,\theta )$
holds. In particular,
![]() $\Phi (\vec C \mathbin {\upharpoonright } S',\mu ,2^\mu )$
holds. Then, by Lemma 2.5,
$\Phi (\vec C \mathbin {\upharpoonright } S',\mu ,2^\mu )$
holds. Then, by Lemma 2.5,
![]() $\diamondsuit (\vec C \mathbin {\upharpoonright } S', \mu )$
holds.
$\diamondsuit (\vec C \mathbin {\upharpoonright } S', \mu )$
holds.
Before concluding this section, we would like to briefly describe an additional configuration which provide narrow diamonds over a ladder system. Above, we used Shelah’s beautiful revised GCH theorem, Fact 2.7, to obtain instances of cardinals
![]() $\theta \leq \lambda $
such that
$\theta \leq \lambda $
such that
![]() $m(\lambda , \theta ) = \lambda $
. The following folklore fact provides other instances (see the proof of [Reference Burke and Magidor5, Lemma 5.12]).
$m(\lambda , \theta ) = \lambda $
. The following folklore fact provides other instances (see the proof of [Reference Burke and Magidor5, Lemma 5.12]).
Fact 2.13. For all infinite cardinals
![]() $\theta \le \lambda < \theta ^{+\operatorname {\mathrm {cf}}(\theta )}$
,
$\theta \le \lambda < \theta ^{+\operatorname {\mathrm {cf}}(\theta )}$
,
![]() $m(\lambda , \theta ) = \lambda $
holds.
$m(\lambda , \theta ) = \lambda $
holds.
Using Fact 2.13 we can trace through the proofs of this section to obtain the following theorem. The reader may first consider Corollary 2.15 which deals with the simplest case of the theorem, where
![]() $\mu := \aleph _0$
, in which case
$\mu := \aleph _0$
, in which case
![]() $\mu ^{+\mu }= \aleph _\omega $
.
$\mu ^{+\mu }= \aleph _\omega $
.
Theorem 2.14. Suppose that
![]() $\mu $
is an infinite regular cardinal, and
$\mu $
is an infinite regular cardinal, and
![]() $\lambda $
is a cardinal such that
$\lambda $
is a cardinal such that
![]() $\mu <2^\mu <2^{2^\mu }\le \lambda <2^\lambda <\mu ^{+\mu }$
. Then
$\mu <2^\mu <2^{2^\mu }\le \lambda <2^\lambda <\mu ^{+\mu }$
. Then
![]() $\kappa := 2^\lambda $
is a regular cardinal admitting a
$\kappa := 2^\lambda $
is a regular cardinal admitting a
![]() $\mu $
-bounded C-sequence
$\mu $
-bounded C-sequence
![]() $\vec C$
over a stationary
$\vec C$
over a stationary
![]() $S\subseteq E^\kappa _\mu $
such that
$S\subseteq E^\kappa _\mu $
such that
![]() $\diamondsuit (\vec C \mathbin {\upharpoonright } S', \mu )$
holds for every stationary
$\diamondsuit (\vec C \mathbin {\upharpoonright } S', \mu )$
holds for every stationary
![]() $S'\subseteq S$
.
$S'\subseteq S$
.
Proof Let
![]() $\alpha <\mu $
be such that
$\alpha <\mu $
be such that
![]() $\kappa =\mu ^{+\alpha }$
. If
$\kappa =\mu ^{+\alpha }$
. If
![]() $\kappa $
were to be singular, then
$\kappa $
were to be singular, then
![]() $\operatorname {\mathrm {cf}}(2^\lambda )=\operatorname {\mathrm {cf}}(\alpha )<\mu <\lambda $
, contradicting Konig’s lemma. So
$\operatorname {\mathrm {cf}}(2^\lambda )=\operatorname {\mathrm {cf}}(\alpha )<\mu <\lambda $
, contradicting Konig’s lemma. So
![]() $\kappa $
is regular. Next, as
$\kappa $
is regular. Next, as
![]() $2^\lambda <\mu ^{+\mu }$
, for every cardinal
$2^\lambda <\mu ^{+\mu }$
, for every cardinal
![]() $\varkappa \in [\mu ,2^\lambda )$
, it is the case that
$\varkappa \in [\mu ,2^\lambda )$
, it is the case that
![]() $\mu \le \varkappa <\mu ^{+\mu }$
, and so Fact 2.13 implies that
$\mu \le \varkappa <\mu ^{+\mu }$
, and so Fact 2.13 implies that
![]() $m(\varkappa , \mu ) = \varkappa <2^\lambda $
. As made clear right after Claim 2.9.1, we then get a
$m(\varkappa , \mu ) = \varkappa <2^\lambda $
. As made clear right after Claim 2.9.1, we then get a
![]() $\mu $
-bounded C-sequence
$\mu $
-bounded C-sequence
![]() $\vec C$
over some stationary
$\vec C$
over some stationary
![]() $S\subseteq E^\kappa _\mu $
such that
$S\subseteq E^\kappa _\mu $
such that
![]() $\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
holds. In particular,
$\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
holds. In particular,
![]() $\diamondsuit (\vec C \mathbin {\upharpoonright } S', 2^\lambda , 2^\lambda )$
holds for any given stationary
$\diamondsuit (\vec C \mathbin {\upharpoonright } S', 2^\lambda , 2^\lambda )$
holds for any given stationary
![]() $S'\subseteq S$
. Now let
$S'\subseteq S$
. Now let
![]() $\theta := 2^\mu $
. As
$\theta := 2^\mu $
. As
![]() $\mu <\theta <\lambda <\mu ^{+\mu }$
, it is the case that
$\mu <\theta <\lambda <\mu ^{+\mu }$
, it is the case that
![]() $\theta <\lambda <\theta ^{+\theta }$
, so Fact 2.13 implies that
$\theta <\lambda <\theta ^{+\theta }$
, so Fact 2.13 implies that
![]() $m(\lambda ,\theta )=\lambda $
. Then, by Lemma 2.8,
$m(\lambda ,\theta )=\lambda $
. Then, by Lemma 2.8,
![]() ${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\theta )$
holds. Then, by Lemma 2.10,
${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\theta )$
holds. Then, by Lemma 2.10,
![]() $\Phi (\vec C \mathbin {\upharpoonright } S',2^\lambda ,\theta )$
holds. In particular,
$\Phi (\vec C \mathbin {\upharpoonright } S',2^\lambda ,\theta )$
holds. In particular,
![]() $\Phi (\vec C,\mu ,2^\mu )$
holds. Then, by Lemma 2.5,
$\Phi (\vec C,\mu ,2^\mu )$
holds. Then, by Lemma 2.5,
![]() $\diamondsuit ( \vec C \mathbin {\upharpoonright } S', \mu )$
holds.
$\diamondsuit ( \vec C \mathbin {\upharpoonright } S', \mu )$
holds.
Corollary 2.15. For every
![]() $n\in [3,\omega )$
such that
$n\in [3,\omega )$
such that
![]() $\beth _n<\aleph _\omega $
, there is an
$\beth _n<\aleph _\omega $
, there is an
![]() $\omega $
-bounded C-sequence
$\omega $
-bounded C-sequence
![]() $\vec C$
over
$\vec C$
over
![]() $E^{\beth _n}_\omega $
such that
$E^{\beth _n}_\omega $
such that
![]() $\diamondsuit (\vec C, \omega )$
holds. In particular, if
$\diamondsuit (\vec C, \omega )$
holds. In particular, if
![]() $\kappa :=2^{2^{2^{\aleph _0}}}$
is smaller than
$\kappa :=2^{2^{2^{\aleph _0}}}$
is smaller than
![]() $\aleph _\omega $
, then there is an
$\aleph _\omega $
, then there is an
![]() $\omega $
-bounded C-sequence
$\omega $
-bounded C-sequence
![]() $\vec C$
over
$\vec C$
over
![]() $E^\kappa _\omega $
such that
$E^\kappa _\omega $
such that
![]() $\diamondsuit (\vec C, \omega )$
holds.
$\diamondsuit (\vec C, \omega )$
holds.
Remark 2.16. With a bit more work, one can show that if
![]() $\aleph _\omega $
is a strong limit, then for every uncountable cardinal
$\aleph _\omega $
is a strong limit, then for every uncountable cardinal
![]() $\mu <\aleph _\omega $
, there is a finite set
$\mu <\aleph _\omega $
, there is a finite set
![]() $\Theta \subseteq \aleph _\omega $
such that for every cardinal
$\Theta \subseteq \aleph _\omega $
such that for every cardinal
![]() $\lambda $
with
$\lambda $
with
![]() $\operatorname {\mathrm {cf}}(\lambda )\notin \Theta $
, there exists a
$\operatorname {\mathrm {cf}}(\lambda )\notin \Theta $
, there exists a
![]() $\mu $
-bounded C-sequence
$\mu $
-bounded C-sequence
![]() $\vec C$
over
$\vec C$
over
![]() $E^{\lambda ^+}_\mu $
such that
$E^{\lambda ^+}_\mu $
such that
![]() $\diamondsuit (\vec C, \mu )$
holds. This is obtained by developing stepping up methods which allow for transferring diamonds on ladder systems from smaller cardinals to larger cardinals.
$\diamondsuit (\vec C, \mu )$
holds. This is obtained by developing stepping up methods which allow for transferring diamonds on ladder systems from smaller cardinals to larger cardinals.
Having discussed the methods from the preceding remark and its limitations with Jing Zhang, the following question emerged:
Question 2.17 (Zhang).
Suppose that
![]() $\aleph _\omega $
is a strong limit and
$\aleph _\omega $
is a strong limit and
![]() $\square _{\aleph _\omega }$
holds. Does there exist a cardinal
$\square _{\aleph _\omega }$
holds. Does there exist a cardinal
![]() $\mu <\aleph _\omega $
, and a
$\mu <\aleph _\omega $
, and a
![]() $\mu $
-bounded ladder system
$\mu $
-bounded ladder system
![]() $\vec L$
over a nonreflecting stationary subset of
$\vec L$
over a nonreflecting stationary subset of
![]() $E^{\aleph _{\omega +1}}_\mu $
such that
$E^{\aleph _{\omega +1}}_\mu $
such that
![]() $\diamondsuit (\vec L, \mu )$
holds?
$\diamondsuit (\vec L, \mu )$
holds?
3 Club guessing with diamonds
The main result of this section concerns the following n-dimensional version of Definition 1. The main technical result, Theorem 3.5, additionally incorporates club guessing into the ladder system on which diamond holds.
Definition 3.1. For a ladder system
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
over some stationary
$\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
over some stationary
![]() ${S\subseteq \kappa }$
a cardinal
${S\subseteq \kappa }$
a cardinal
![]() $\theta $
and a positive integer n,
$\theta $
and a positive integer n,
![]() $\diamondsuit ^{n}(\vec L,\theta )$
asserts the existence of a sequence
$\diamondsuit ^{n}(\vec L,\theta )$
asserts the existence of a sequence
![]() $\langle f_\delta \mathrel {|} \delta \in S\rangle $
such that:
$\langle f_\delta \mathrel {|} \delta \in S\rangle $
such that:
-
• for every
 $\delta \in S$
,
$\delta \in S$
,
 $f_\delta $
is a function from
$f_\delta $
is a function from
 $[A_\delta ]^n$
to
$[A_\delta ]^n$
to
 $\theta $
;
$\theta $
; -
• for every function
 $f:[\kappa ]^n\rightarrow \theta $
, there are stationarily many
$f:[\kappa ]^n\rightarrow \theta $
, there are stationarily many
 $\delta \in S$
such that
$\delta \in S$
such that
 $f \mathbin {\upharpoonright } [A_\delta ]^n=f_\delta $
.
$f \mathbin {\upharpoonright } [A_\delta ]^n=f_\delta $
.
Remark 3.2. One may also consider the variation of
![]() $\diamondsuit ^{n}(\vec L,\theta )$
where the functions above are of the form
$\diamondsuit ^{n}(\vec L,\theta )$
where the functions above are of the form
![]() $f_\delta :{}^{n}A_\delta \rightarrow \theta $
and these serve to guess a function
$f_\delta :{}^{n}A_\delta \rightarrow \theta $
and these serve to guess a function
![]() $f:{}^n\kappa \rightarrow \theta $
. However, in case
$f:{}^n\kappa \rightarrow \theta $
. However, in case
![]() $\theta $
is infinite the two are easily seen to be equivalent.
$\theta $
is infinite the two are easily seen to be equivalent.
The main corollary to the results of this section is the following, which proves Theorem D.
Corollary 3.3. Suppose that
![]() $\aleph _\omega $
is a strong limit. For every positive integer n, for all infinite cardinals
$\aleph _\omega $
is a strong limit. For every positive integer n, for all infinite cardinals
![]() $\mu \le \theta <\aleph _\omega $
, there are a cardinal
$\mu \le \theta <\aleph _\omega $
, there are a cardinal
![]() $\kappa <\aleph _\omega $
, and a
$\kappa <\aleph _\omega $
, and a
![]() $\mu $
-bounded ladder system
$\mu $
-bounded ladder system
![]() $\vec L$
over
$\vec L$
over
![]() $E^\kappa _\mu $
such that
$E^\kappa _\mu $
such that
![]() $\diamondsuit ^n(\vec L,\theta )$
holds and is moreover witnessed by a sequence
$\diamondsuit ^n(\vec L,\theta )$
holds and is moreover witnessed by a sequence
![]() $\langle f_\delta \mathrel {|} \delta \in S\rangle $
consisting of constant maps.
$\langle f_\delta \mathrel {|} \delta \in S\rangle $
consisting of constant maps.
Proof By Theorem 3.5, taking
![]() $\Omega :=\omega $
.
$\Omega :=\omega $
.
Towards the proof of Theorem 3.5, we shall need the following strong variation of Lemma 2.8.
Lemma 3.4. Suppose that
![]() $\theta ,\lambda $
are infinite cardinals such that
$\theta ,\lambda $
are infinite cardinals such that
![]() $\lambda ^\theta =\lambda $
. Then there is a proper
$\lambda ^\theta =\lambda $
. Then there is a proper
![]() $\theta ^+$
-complete ideal I over
$\theta ^+$
-complete ideal I over
![]() $\lambda $
such that
$\lambda $
such that
![]() ${{{\sf onto}}}(I^+,[2^\lambda ]^{<\theta },\theta )$
holds. That is, there is a colouring
${{{\sf onto}}}(I^+,[2^\lambda ]^{<\theta },\theta )$
holds. That is, there is a colouring
![]() $c:\lambda \times 2^\lambda \rightarrow \theta $
satisfying that for all
$c:\lambda \times 2^\lambda \rightarrow \theta $
satisfying that for all
![]() $A\in I^+$
and
$A\in I^+$
and
![]() $B\in [2^\lambda ]^\theta $
, there exists an
$B\in [2^\lambda ]^\theta $
, there exists an
![]() $\alpha \in A$
such that
$\alpha \in A$
such that
![]() $c[\{\alpha \}\times B]=\theta $
.
$c[\{\alpha \}\times B]=\theta $
.
Proof As
![]() $\lambda ^\theta =\lambda $
, by the Engelking–Karlowicz theorem, [Reference Engelking and Karłowicz9], we may fix a sequence
$\lambda ^\theta =\lambda $
, by the Engelking–Karlowicz theorem, [Reference Engelking and Karłowicz9], we may fix a sequence
![]() $\vec f=\langle f_\alpha \mathrel {|} \alpha <\lambda \rangle $
of functions from
$\vec f=\langle f_\alpha \mathrel {|} \alpha <\lambda \rangle $
of functions from
![]() $2^\lambda $
to
$2^\lambda $
to
![]() $\lambda $
such that for every function
$\lambda $
such that for every function
![]() $g:x\rightarrow \lambda $
with
$g:x\rightarrow \lambda $
with
![]() $x\in [2^\lambda ]^\theta $
, there exists an
$x\in [2^\lambda ]^\theta $
, there exists an
![]() $\alpha <\lambda $
such that
$\alpha <\lambda $
such that
![]() $g\subseteq f_\alpha $
. Let us identify a useful feature of
$g\subseteq f_\alpha $
. Let us identify a useful feature of
![]() $\vec f$
.
$\vec f$
.
Claim 3.4.1. For every sequence
![]() $\langle B_i \mathrel {|} i< \theta \rangle $
of elements of
$\langle B_i \mathrel {|} i< \theta \rangle $
of elements of
![]() $[2^\lambda ]^\theta $
, for some
$[2^\lambda ]^\theta $
, for some
![]() $\alpha < \lambda $
, for every
$\alpha < \lambda $
, for every
![]() $i< \theta $
,
$i< \theta $
,
![]() $f_\alpha [B_i] = \theta $
.
$f_\alpha [B_i] = \theta $
.
Proof Let
![]() $\langle B_i \mathrel {|} i< \theta \rangle $
a sequence of elements of
$\langle B_i \mathrel {|} i< \theta \rangle $
a sequence of elements of
![]() $[2^\lambda ]^\theta $
be given. First, let
$[2^\lambda ]^\theta $
be given. First, let
![]() $\langle B^*_i \mathrel {|} i< \theta \rangle $
be a sequence of pairwise disjoint sets such that for each
$\langle B^*_i \mathrel {|} i< \theta \rangle $
be a sequence of pairwise disjoint sets such that for each
![]() $i< \theta $
,
$i< \theta $
,
![]() $B^*_i \in [B_i]^\theta $
. Then let
$B^*_i \in [B_i]^\theta $
. Then let
![]() $x:= \bigcup _{i< \theta }B^*_i$
, and let
$x:= \bigcup _{i< \theta }B^*_i$
, and let
![]() $g:x \rightarrow \lambda $
be such that for each
$g:x \rightarrow \lambda $
be such that for each
![]() $\beta \in x$
,
$\beta \in x$
,
![]() $g(\beta ) = \xi $
iff for some
$g(\beta ) = \xi $
iff for some
![]() $i< \theta $
,
$i< \theta $
,
![]() $\beta \in B^*_i$
and
$\beta \in B^*_i$
and
![]() $\operatorname {\mathrm {otp}}(B^*_i \cap \beta ) = \xi $
. Then if
$\operatorname {\mathrm {otp}}(B^*_i \cap \beta ) = \xi $
. Then if
![]() $\alpha < \lambda $
is such that
$\alpha < \lambda $
is such that
![]() $g \subseteq f_\alpha $
, then for every
$g \subseteq f_\alpha $
, then for every
![]() $i< \theta $
we have that
$i< \theta $
we have that
![]() $f_\alpha [B_i] = \theta $
.
$f_\alpha [B_i] = \theta $
.
Now let I denote the collection of all
![]() $A\subseteq \lambda $
for which there exists
$A\subseteq \lambda $
for which there exists
![]() $\mathcal B\in [[2^\lambda ]^\theta ]^\theta $
such that, for every
$\mathcal B\in [[2^\lambda ]^\theta ]^\theta $
such that, for every
![]() $\alpha \in A$
, for some
$\alpha \in A$
, for some
![]() $B\in \mathcal B$
it is the case that
$B\in \mathcal B$
it is the case that
![]() $f_\alpha [B]\neq \theta $
. It is clear that I is a
$f_\alpha [B]\neq \theta $
. It is clear that I is a
![]() $\theta ^+$
-complete ideal over
$\theta ^+$
-complete ideal over
![]() $\lambda $
and it is proper by Claim 3.4.1. Now pick
$\lambda $
and it is proper by Claim 3.4.1. Now pick
![]() $c:\lambda \times 2^\lambda \rightarrow \theta $
such that
$c:\lambda \times 2^\lambda \rightarrow \theta $
such that
![]() $c(\alpha ,\beta )=f_\alpha (\beta )$
whenever
$c(\alpha ,\beta )=f_\alpha (\beta )$
whenever
![]() $f_\alpha (\beta )<\theta $
. Then c and I are as sought.
$f_\alpha (\beta )<\theta $
. Then c and I are as sought.
The next theorem deals with getting a witness for
![]() $\diamondsuit ^n(\vec L,\theta )$
from Definition 3.1 with several additional features. First, the local functions
$\diamondsuit ^n(\vec L,\theta )$
from Definition 3.1 with several additional features. First, the local functions
![]() $\langle f_\delta \mathrel {|} \delta \in S\rangle $
witnessing
$\langle f_\delta \mathrel {|} \delta \in S\rangle $
witnessing
![]() $\diamondsuit ^n(\vec L,\theta )$
are the simplest possible: they are constant maps—see the function g in Clause (1) below. Second, the sequence
$\diamondsuit ^n(\vec L,\theta )$
are the simplest possible: they are constant maps—see the function g in Clause (1) below. Second, the sequence
![]() $\langle S_j\mathrel {|} j<\kappa \rangle $
of Clause (2) shows that we have
$\langle S_j\mathrel {|} j<\kappa \rangle $
of Clause (2) shows that we have
![]() $\kappa $
-many disjoint stationary sets each of which carries the desired diamond. This is motivated by results such as [Reference Rinot, Shalev and Todorcevic22, Theorem A.1] that uses a guessing principle with
$\kappa $
-many disjoint stationary sets each of which carries the desired diamond. This is motivated by results such as [Reference Rinot, Shalev and Todorcevic22, Theorem A.1] that uses a guessing principle with
![]() $\mu $
many pairwise disjoint active parts to construct
$\mu $
many pairwise disjoint active parts to construct
![]() $2^\mu $
many pairwise nonhomeomorphic Dowker spaces. Unlike the usual diamond and some of its variants (see, for example, [Reference Brodsky and Rinot4, Theorem 3.7] and [Reference Fernandes, Moreno and Rinot10, Lemma 3.19]) that abstractly admit a partition into
$2^\mu $
many pairwise nonhomeomorphic Dowker spaces. Unlike the usual diamond and some of its variants (see, for example, [Reference Brodsky and Rinot4, Theorem 3.7] and [Reference Fernandes, Moreno and Rinot10, Lemma 3.19]) that abstractly admit a partition into
![]() $\kappa $
many active parts, here we do not know of such a partition theorem, hence the explicit inclusion of Clause (2). One possible explanation for the lack of a partition theorem is that for cardinals
$\kappa $
many active parts, here we do not know of such a partition theorem, hence the explicit inclusion of Clause (2). One possible explanation for the lack of a partition theorem is that for cardinals
![]() $\mu <\theta <\kappa $
, the collection corresponding to the failure of diamond on
$\mu <\theta <\kappa $
, the collection corresponding to the failure of diamond on
![]() $\mu $
-bounded ladder systems for
$\mu $
-bounded ladder systems for
![]() $\theta $
-colourings does not form a
$\theta $
-colourings does not form a
![]() $\kappa $
-complete ideal which prevents the use of standard non-saturation results such as Ulam’s theorem and its generalisations [Reference Inamdar and Rinot13].
$\kappa $
-complete ideal which prevents the use of standard non-saturation results such as Ulam’s theorem and its generalisations [Reference Inamdar and Rinot13].
The third feature of the next theorem is motivated by the study of relative club guessing and can be most concisely expressed as
![]() $\operatorname {\mathrm {CG}}_\mu (E^\kappa _\mu ,T,\kappa )$
in the sense of [Reference Inamdar and Rinot12, Definition 2.2]. To make our explanation self-contained, notice that the
$\operatorname {\mathrm {CG}}_\mu (E^\kappa _\mu ,T,\kappa )$
in the sense of [Reference Inamdar and Rinot12, Definition 2.2]. To make our explanation self-contained, notice that the
![]() $\delta \in S_j$
below not only guesses the global function f on the set
$\delta \in S_j$
below not only guesses the global function f on the set
![]() $[B_\delta ]^n$
, but additionally, given a club
$[B_\delta ]^n$
, but additionally, given a club
![]() $D\subseteq \kappa $
we ensure that
$D\subseteq \kappa $
we ensure that
![]() $\delta $
simultaneously guesses the club D relative to T, that is,
$\delta $
simultaneously guesses the club D relative to T, that is,
![]() $B_\delta \subseteq D \cap T$
. For more on the utility of this feature, we refer the reader to [Reference Inamdar and Rinot12].
$B_\delta \subseteq D \cap T$
. For more on the utility of this feature, we refer the reader to [Reference Inamdar and Rinot12].
When reading the next theorem for the first time, the reader may want to begin by considering the case when
![]() $n=1$
and
$n=1$
and
![]() $\Omega =\mu =\theta =\omega $
, so that
$\Omega =\mu =\theta =\omega $
, so that
![]() $\kappa =2^{2^{2^{\aleph _0}}}$
.
$\kappa =2^{2^{2^{\aleph _0}}}$
.
Theorem 3.5. Suppose that n is a positive integer,
![]() $\Omega ,\mu \le \theta $
are infinite cardinals with
$\Omega ,\mu \le \theta $
are infinite cardinals with
![]() $\mu $
regular,
$\mu $
regular,
![]() $\kappa :=\beth _{n+2}(\theta )$
is smaller than
$\kappa :=\beth _{n+2}(\theta )$
is smaller than
![]() $\Omega ^{+\omega }$
, and
$\Omega ^{+\omega }$
, and
![]() $T\subseteq \kappa $
is stationary. Then there are
$T\subseteq \kappa $
is stationary. Then there are
![]() $:$
$:$
-
(1) a map
 $g:E^\kappa _\mu \rightarrow \theta $
,
$g:E^\kappa _\mu \rightarrow \theta $
, -
(2) a partition
 $\langle S_j\mathrel {|} j<\kappa \rangle $
of
$\langle S_j\mathrel {|} j<\kappa \rangle $
of
 $E^\kappa _\mu $
into stationary sets, and
$E^\kappa _\mu $
into stationary sets, and -
(3) a
 $\mu $
-bounded ladder system
$\mu $
-bounded ladder system
 $\vec L=\langle B_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
,
$\vec L=\langle B_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
,
such that for every club
![]() $D\subseteq \kappa $
, for every function
$D\subseteq \kappa $
, for every function
![]() $f:[\kappa ]^n\rightarrow \theta $
, for every
$f:[\kappa ]^n\rightarrow \theta $
, for every
![]() $j<\kappa $
, there is a
$j<\kappa $
, there is a
![]() $\delta \in S_j$
such that
$\delta \in S_j$
such that
![]() $B_\delta \subseteq D\cap T$
and
$B_\delta \subseteq D\cap T$
and
![]() $f"[B_\delta ]^n=\{g(\delta )\}$
.
$f"[B_\delta ]^n=\{g(\delta )\}$
.
Proof By the Erdős–Rado theorem, the cardinal
![]() $\chi :=(\beth _{n-1}(\theta ))^+$
satisfies
$\chi :=(\beth _{n-1}(\theta ))^+$
satisfies
![]() $\chi \rightarrow (\mu )^n_\theta $
. Put
$\chi \rightarrow (\mu )^n_\theta $
. Put
![]() $\sigma :=2^{<\chi }$
and
$\sigma :=2^{<\chi }$
and
![]() $\lambda :=2^\sigma $
. Consequently,
$\lambda :=2^\sigma $
. Consequently,
![]() $\sigma = \beth _n(\theta )$
,
$\sigma = \beth _n(\theta )$
,
![]() $\lambda = \beth _{n+1}(\theta )$
, and
$\lambda = \beth _{n+1}(\theta )$
, and
![]() $\kappa = \beth _{n+2}(\theta ) = 2^\lambda $
. Altogether,
$\kappa = \beth _{n+2}(\theta ) = 2^\lambda $
. Altogether,
Fix an
![]() $m<\omega $
such that
$m<\omega $
such that
![]() $\kappa =\lambda ^{+m+1}$
and let
$\kappa =\lambda ^{+m+1}$
and let
![]() $\Lambda :=\lambda ^{+m}$
, so that
$\Lambda :=\lambda ^{+m}$
, so that
![]() $\lambda \leq \Lambda $
. Note that Hausdorff’s lemma implies that
$\lambda \leq \Lambda $
. Note that Hausdorff’s lemma implies that
![]() $\Lambda ^\sigma =\Lambda <\kappa $
. In addition, since
$\Lambda ^\sigma =\Lambda <\kappa $
. In addition, since
![]() $\lambda ^\sigma =\lambda $
, Lemma 3.4 provides us with a
$\lambda ^\sigma =\lambda $
, Lemma 3.4 provides us with a
![]() $\sigma ^+$
-complete proper ideal I over
$\sigma ^+$
-complete proper ideal I over
![]() $\lambda $
such that
$\lambda $
such that
![]() ${{{\sf onto}}}(I^+,[\kappa ]^{<\sigma },\sigma )$
holds.
${{{\sf onto}}}(I^+,[\kappa ]^{<\sigma },\sigma )$
holds.
Claim 3.5.1. There exists a
![]() $\chi $
-bounded C-sequence
$\chi $
-bounded C-sequence
![]() $\langle C_\rho \mathrel {|} \rho \in R\rangle $
such that
$\langle C_\rho \mathrel {|} \rho \in R\rangle $
such that
![]() $:$
$:$
-
•
 $R\subseteq \operatorname {\mathrm {acc}}(\kappa )\cap E^\kappa _{\le \chi }$
is stationary
$R\subseteq \operatorname {\mathrm {acc}}(\kappa )\cap E^\kappa _{\le \chi }$
is stationary
 $;$
$;$
-
• for every
 $\rho \in R$
, for every
$\rho \in R$
, for every
 $\delta \in \operatorname {\mathrm {acc}}(C_\rho )$
,
$\delta \in \operatorname {\mathrm {acc}}(C_\rho )$
,
 $\delta \in R$
and
$\delta \in R$
and
 $C_\delta =C_\rho \cap \delta ;$
$C_\delta =C_\rho \cap \delta ;$
-
• for every club
 $D\subseteq \kappa $
, for every
$D\subseteq \kappa $
, for every
 $\varepsilon <\kappa $
, there exists a
$\varepsilon <\kappa $
, there exists a
 $\rho \in R\cap E^\kappa _{\chi }$
such that
$\rho \in R\cap E^\kappa _{\chi }$
such that
 $\operatorname {\mathrm {nacc}}(C_\rho )\subseteq D\cap T$
and
$\operatorname {\mathrm {nacc}}(C_\rho )\subseteq D\cap T$
and
 $\min (C_\rho )\ge \varepsilon $
.
$\min (C_\rho )\ge \varepsilon $
.
Proof The proof is similar to that of [Reference Shelah23, Lemma 2]. As
![]() $\kappa =\Lambda ^+$
and
$\kappa =\Lambda ^+$
and
![]() $\Lambda ^\chi =\Lambda $
, for every
$\Lambda ^\chi =\Lambda $
, for every
![]() $\rho \in \operatorname {\mathrm {acc}}(\kappa )\cap E^\kappa _{\le \chi }$
we may let
$\rho \in \operatorname {\mathrm {acc}}(\kappa )\cap E^\kappa _{\le \chi }$
we may let
![]() $\langle C_{\rho ,j}\mathrel {|} j<\Lambda \rangle $
be an enumeration of all clubs in
$\langle C_{\rho ,j}\mathrel {|} j<\Lambda \rangle $
be an enumeration of all clubs in
![]() $\rho $
of order-type no more than
$\rho $
of order-type no more than
![]() $\chi $
. In addition, using
$\chi $
. In addition, using
![]() $\Lambda ^\chi =\Lambda $
, by the Engelking–Karlowicz theorem, we may fix a sequence
$\Lambda ^\chi =\Lambda $
, by the Engelking–Karlowicz theorem, we may fix a sequence
![]() $\vec f=\langle f_i\mathrel {|} i<\Lambda \rangle $
of functions from
$\vec f=\langle f_i\mathrel {|} i<\Lambda \rangle $
of functions from
![]() $\kappa $
to
$\kappa $
to
![]() $\Lambda $
such that for every function
$\Lambda $
such that for every function
![]() $g:x\rightarrow \Lambda $
with
$g:x\rightarrow \Lambda $
with
![]() $x\in [\kappa ]^\chi $
, there exists an
$x\in [\kappa ]^\chi $
, there exists an
![]() $i<\Lambda $
such that
$i<\Lambda $
such that
![]() $g\subseteq f_i$
. Denote
$g\subseteq f_i$
. Denote
![]() $C_\rho ^i:=C_{\rho ,f_i(\rho )}$
. Clearly, for every
$C_\rho ^i:=C_{\rho ,f_i(\rho )}$
. Clearly, for every
![]() $i<\Lambda $
,
$i<\Lambda $
,
![]() $\vec C^i:=\langle C_\rho ^i\mathrel {|} \rho \in \operatorname {\mathrm {acc}}(\kappa )\cap E^\kappa _{\le \chi }\rangle $
is a
$\vec C^i:=\langle C_\rho ^i\mathrel {|} \rho \in \operatorname {\mathrm {acc}}(\kappa )\cap E^\kappa _{\le \chi }\rangle $
is a
![]() $\chi $
-bounded C-sequence.
$\chi $
-bounded C-sequence.
We claim that there exists an
![]() $i<\Lambda $
such that for every club
$i<\Lambda $
such that for every club
![]() $D\subseteq \kappa $
, for every
$D\subseteq \kappa $
, for every
![]() $\varepsilon <\kappa $
, there exists a
$\varepsilon <\kappa $
, there exists a
![]() $\rho \in R\cap E^\kappa _{\chi }$
such that:
$\rho \in R\cap E^\kappa _{\chi }$
such that:
-
(1)
 $\operatorname {\mathrm {nacc}}(C_\rho ^i)\subseteq D\cap T$
;
$\operatorname {\mathrm {nacc}}(C_\rho ^i)\subseteq D\cap T$
; -
(2)
 $\min (C^i_\rho )\ge \varepsilon $
$\min (C^i_\rho )\ge \varepsilon $
-
(3) for every
 $\delta \in \operatorname {\mathrm {acc}}(C^i_\rho )$
,
$\delta \in \operatorname {\mathrm {acc}}(C^i_\rho )$
,
 $C^i_\delta =C^i_\rho \cap \delta $
.
$C^i_\delta =C^i_\rho \cap \delta $
.
Indeed, otherwise, for each
![]() $i<\Lambda $
, we may fix a club
$i<\Lambda $
, we may fix a club
![]() $D_i\subseteq \kappa $
and some
$D_i\subseteq \kappa $
and some
![]() $\varepsilon _i<\kappa $
such that for every
$\varepsilon _i<\kappa $
such that for every
![]() $\rho \in R\cap E^\kappa _\chi $
, either (1) fails for
$\rho \in R\cap E^\kappa _\chi $
, either (1) fails for
![]() $D_i$
or (2) fails for
$D_i$
or (2) fails for
![]() $\varepsilon _i$
or (3) fails. Let
$\varepsilon _i$
or (3) fails. Let
![]() $D:=\bigcap _{i<\Lambda }D_i$
and
$D:=\bigcap _{i<\Lambda }D_i$
and
![]() $\varepsilon :=\sup _{i<\Lambda }\varepsilon _i$
. As T is stationary, we may now fix some
$\varepsilon :=\sup _{i<\Lambda }\varepsilon _i$
. As T is stationary, we may now fix some
![]() $\rho \in E^\kappa _\chi $
above
$\rho \in E^\kappa _\chi $
above
![]() $\varepsilon $
such that
$\varepsilon $
such that
![]() $D\cap T$
is cofinal in
$D\cap T$
is cofinal in
![]() $\rho $
. Fix a club C in
$\rho $
. Fix a club C in
![]() $\rho $
of order-type
$\rho $
of order-type
![]() $\chi $
such that
$\chi $
such that
![]() $\operatorname {\mathrm {nacc}}(C)\subseteq D\cap T$
and
$\operatorname {\mathrm {nacc}}(C)\subseteq D\cap T$
and
![]() $\min (C)=\varepsilon $
. Pick a function
$\min (C)=\varepsilon $
. Pick a function
![]() $g:\operatorname {\mathrm {acc}}(C)\cup \{\rho \}\rightarrow \Lambda $
such that
$g:\operatorname {\mathrm {acc}}(C)\cup \{\rho \}\rightarrow \Lambda $
such that
![]() $g(\delta )=j$
implies
$g(\delta )=j$
implies
![]() $C\cap \delta =C_{\delta ,j}$
. Pick an
$C\cap \delta =C_{\delta ,j}$
. Pick an
![]() $i<\Lambda $
such that
$i<\Lambda $
such that
![]() $g\subseteq f_i$
. This implies that
$g\subseteq f_i$
. This implies that
and for
![]() $\delta \in \operatorname {\mathrm {acc}}(C)$
,
$\delta \in \operatorname {\mathrm {acc}}(C)$
,
Then we arrive at the following contradiction:
-
(i)
 $\operatorname {\mathrm {nacc}}(C_\rho ^i)= \operatorname {\mathrm {nacc}}(C)\subseteq D\cap T\subseteq D_i\cap T$
;
$\operatorname {\mathrm {nacc}}(C_\rho ^i)= \operatorname {\mathrm {nacc}}(C)\subseteq D\cap T\subseteq D_i\cap T$
; -
(ii)
 $\min (C^i_\rho )=\min (C)=\varepsilon \ge \varepsilon _i$
;
$\min (C^i_\rho )=\min (C)=\varepsilon \ge \varepsilon _i$
; -
(iii) for every
 $\delta \in \operatorname {\mathrm {acc}}(C^i_\rho )$
,
$\delta \in \operatorname {\mathrm {acc}}(C^i_\rho )$
,
 $C^i_\delta =C\cap \delta =C^i_\rho \cap \delta $
.
$C^i_\delta =C\cap \delta =C^i_\rho \cap \delta $
.
Thus, pick
![]() $i<\Lambda $
such that for every club
$i<\Lambda $
such that for every club
![]() $D\subseteq \kappa $
, for every
$D\subseteq \kappa $
, for every
![]() $\varepsilon <\kappa $
, there exists a
$\varepsilon <\kappa $
, there exists a
![]() $\rho \in R\cap E^\kappa _{\chi }$
such that (1)–(3) holds. Set
$\rho \in R\cap E^\kappa _{\chi }$
such that (1)–(3) holds. Set
Then
![]() $\langle C^i_\rho \mathrel {|} \rho \in R\rangle $
is as sought.
$\langle C^i_\rho \mathrel {|} \rho \in R\rangle $
is as sought.
Let
![]() $\langle C_\rho \mathrel {|} \rho \in R\rangle $
be given by the claim. It follows that the set
$\langle C_\rho \mathrel {|} \rho \in R\rangle $
be given by the claim. It follows that the set
is cofinal in
![]() $\kappa $
. For every
$\kappa $
. For every
![]() $j<\kappa $
, let
$j<\kappa $
, let
![]() $\mathcal E(j)$
denote the unique
$\mathcal E(j)$
denote the unique
![]() $\varepsilon \in \mathcal E$
to satisfy
$\varepsilon \in \mathcal E$
to satisfy
![]() $\operatorname {\mathrm {otp}}(\mathcal E\cap \varepsilon )=j$
, and then let:
$\operatorname {\mathrm {otp}}(\mathcal E\cap \varepsilon )=j$
, and then let:
-
•
 $R_j:=\{\rho \in R\cap E^\kappa _\chi \mathrel {|} \min (C_\rho )=\mathcal E(j)\}$
, and
$R_j:=\{\rho \in R\cap E^\kappa _\chi \mathrel {|} \min (C_\rho )=\mathcal E(j)\}$
, and -
•
 $S_j:=\bigcup \{ \operatorname {\mathrm {acc}}(C_\rho )\mathrel {|} \rho \in R_j\}\cap E^\kappa _\mu $
.
$S_j:=\bigcup \{ \operatorname {\mathrm {acc}}(C_\rho )\mathrel {|} \rho \in R_j\}\cap E^\kappa _\mu $
.
The sets in
![]() $\langle S_j\mathrel {|} j<\kappa \rangle $
are pairwise disjoint, since for
$\langle S_j\mathrel {|} j<\kappa \rangle $
are pairwise disjoint, since for
![]() $j < j'< \kappa $
we have that
$j < j'< \kappa $
we have that
![]() $\mathcal E(j) \neq \mathcal E(j')$
, and by the coherence property of
$\mathcal E(j) \neq \mathcal E(j')$
, and by the coherence property of
![]() $\langle C_\rho \mathrel {|} \rho \in R\rangle $
. Also, for every
$\langle C_\rho \mathrel {|} \rho \in R\rangle $
. Also, for every
![]() ${j< \kappa }$
and every club
${j< \kappa }$
and every club
![]() $D \subseteq \kappa $
there is a
$D \subseteq \kappa $
there is a
![]() $\rho \in R_j \cap E^\kappa _\chi $
such that
$\rho \in R_j \cap E^\kappa _\chi $
such that
![]() $\operatorname {\mathrm {nacc}}(C_\rho ) \subseteq ^* D$
, and hence
$\operatorname {\mathrm {nacc}}(C_\rho ) \subseteq ^* D$
, and hence
![]() $\operatorname {\mathrm {acc}}(C_\rho ) \cap D\cap E^\kappa _\mu \neq \emptyset $
as
$\operatorname {\mathrm {acc}}(C_\rho ) \cap D\cap E^\kappa _\mu \neq \emptyset $
as
![]() $\mu <\chi $
. It follows that
$\mu <\chi $
. It follows that
![]() $\langle S_j\mathrel {|} j<\kappa \rangle $
is a partition into stationary sets of some subset S of
$\langle S_j\mathrel {|} j<\kappa \rangle $
is a partition into stationary sets of some subset S of
![]() $E^\kappa _\mu $
.
$E^\kappa _\mu $
.
For each
![]() $\delta \in S$
, let
$\delta \in S$
, let
and note that
For each
![]() $\delta \in S$
, since
$\delta \in S$
, since
![]() $\operatorname {\mathrm {otp}}(C_\delta )\le \chi $
but
$\operatorname {\mathrm {otp}}(C_\delta )\le \chi $
but
![]() $\operatorname {\mathrm {cf}}(\delta )=\mu <\chi $
, it is the case that
$\operatorname {\mathrm {cf}}(\delta )=\mu <\chi $
, it is the case that
![]() $\operatorname {\mathrm {otp}}(C_\delta )<\chi $
. Combining this with
$\operatorname {\mathrm {otp}}(C_\delta )<\chi $
. Combining this with
![]() $\theta \cdot 2^{<\chi }=\sigma $
, let us also fix an enumeration
$\theta \cdot 2^{<\chi }=\sigma $
, let us also fix an enumeration
![]() $\langle (\tau _{\delta ,i},B_{\delta ,i})\mathrel {|} i<\sigma \rangle $
of all pairs
$\langle (\tau _{\delta ,i},B_{\delta ,i})\mathrel {|} i<\sigma \rangle $
of all pairs
![]() $(\tau ,B)$
such that
$(\tau ,B)$
such that
![]() $\tau <\theta $
and B is a cofinal subset of
$\tau <\theta $
and B is a cofinal subset of
![]() $\operatorname {\mathrm {nacc}}(C_\delta )$
of order type
$\operatorname {\mathrm {nacc}}(C_\delta )$
of order type
![]() $\mu $
.
$\mu $
.
Moving on, as
![]() $\kappa =2^\lambda =\theta ^\lambda $
, let us fix a bijection
$\kappa =2^\lambda =\theta ^\lambda $
, let us fix a bijection
![]() $\psi :{}^\lambda \theta \leftrightarrow \kappa $
. For every
$\psi :{}^\lambda \theta \leftrightarrow \kappa $
. For every
![]() $\alpha <\lambda $
, define a map
$\alpha <\lambda $
, define a map
![]() $\psi _\alpha :\kappa \rightarrow \theta $
via
$\psi _\alpha :\kappa \rightarrow \theta $
via
For every subset
![]() $C\subseteq \kappa $
, for every map
$C\subseteq \kappa $
, for every map
![]() $\eta :[C]^n\rightarrow \kappa $
, for every
$\eta :[C]^n\rightarrow \kappa $
, for every
![]() $\alpha <\lambda $
, we let
$\alpha <\lambda $
, we let
![]() $\eta ^\alpha :=\psi _\alpha \circ \eta $
, so that
$\eta ^\alpha :=\psi _\alpha \circ \eta $
, so that
![]() $\eta ^\alpha $
is a function from
$\eta ^\alpha $
is a function from
![]() $[C]^n$
to
$[C]^n$
to
![]() $\theta $
. We say that
$\theta $
. We say that
![]() $f:[C]^n\rightarrow \theta $
is good iff there is some cofinal subset
$f:[C]^n\rightarrow \theta $
is good iff there is some cofinal subset
![]() $H\subseteq \operatorname {\mathrm {nacc}}(C)$
such that
$H\subseteq \operatorname {\mathrm {nacc}}(C)$
such that
![]() $f \mathbin {\upharpoonright }[H]^n$
is constant.
$f \mathbin {\upharpoonright }[H]^n$
is constant.
Let
![]() $\delta \in S$
and
$\delta \in S$
and
![]() $\eta \in \mathcal P_\delta $
. So, for some
$\eta \in \mathcal P_\delta $
. So, for some
![]() $\epsilon \in C_\delta $
,
$\epsilon \in C_\delta $
,
![]() $\eta : [C_\delta \setminus \epsilon ]^n \rightarrow \delta $
. As
$\eta : [C_\delta \setminus \epsilon ]^n \rightarrow \delta $
. As
![]() $\operatorname {\mathrm {Im}}(\eta )\subseteq \kappa $
, for every
$\operatorname {\mathrm {Im}}(\eta )\subseteq \kappa $
, for every
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $\eta ^\alpha :[C_\delta \setminus \epsilon ]^n\rightarrow \theta $
, so we let
$\eta ^\alpha :[C_\delta \setminus \epsilon ]^n\rightarrow \theta $
, so we let
![]() $A_\eta :=\{\alpha <\lambda \mathrel {|} \eta ^\alpha \text { is good}\}$
. Pick a map
$A_\eta :=\{\alpha <\lambda \mathrel {|} \eta ^\alpha \text { is good}\}$
. Pick a map
![]() $h_\eta :\lambda \rightarrow \sigma $
such that for every
$h_\eta :\lambda \rightarrow \sigma $
such that for every
![]() $\alpha \in A_\eta $
,
$\alpha \in A_\eta $
,
![]() $i:=h_\eta (\alpha )$
satisfies that
$i:=h_\eta (\alpha )$
satisfies that
![]() $B_{\delta ,i}$
is a cofinal subset of
$B_{\delta ,i}$
is a cofinal subset of
![]() $\operatorname {\mathrm {nacc}}(C_\delta \setminus \epsilon )$
for which
$\operatorname {\mathrm {nacc}}(C_\delta \setminus \epsilon )$
for which
![]() $\eta ^\alpha \mathbin {\upharpoonright }[B_{\delta ,i}]^n$
is constant with value
$\eta ^\alpha \mathbin {\upharpoonright }[B_{\delta ,i}]^n$
is constant with value
![]() $\tau _{\delta ,i}$
.
$\tau _{\delta ,i}$
.
Claim 3.5.2. Let
![]() $\delta \in S$
. There exists a function
$\delta \in S$
. There exists a function
![]() $g_\delta :\lambda \rightarrow \sigma $
such that, for every
$g_\delta :\lambda \rightarrow \sigma $
such that, for every
![]() $\eta \in \mathcal P_\delta $
with
$\eta \in \mathcal P_\delta $
with
![]() $A_\eta \in I^+$
, there exists an
$A_\eta \in I^+$
, there exists an
![]() $\alpha \in A_\eta $
with
$\alpha \in A_\eta $
with
![]() $h_\eta (\alpha )= g_\delta (\alpha )$
.
$h_\eta (\alpha )= g_\delta (\alpha )$
.
Proof Fix a colouring
![]() $c:\lambda \times \kappa \rightarrow \sigma $
witnessing
$c:\lambda \times \kappa \rightarrow \sigma $
witnessing
![]() ${{{\sf onto}}}(I^+,[\kappa ]^{<\sigma },\sigma )$
. Let
${{{\sf onto}}}(I^+,[\kappa ]^{<\sigma },\sigma )$
. Let
![]() $\eta \in \mathcal P_\delta $
such that
$\eta \in \mathcal P_\delta $
such that
![]() $A_\eta \in I^+$
. Note that the set
$A_\eta \in I^+$
. Note that the set
![]() $B_\eta :=\{\beta <\kappa \mathrel {|} \forall \alpha \in A_\eta \,[h_\eta (\alpha )\neq c(\alpha ,\beta )]\}$
has size less than
$B_\eta :=\{\beta <\kappa \mathrel {|} \forall \alpha \in A_\eta \,[h_\eta (\alpha )\neq c(\alpha ,\beta )]\}$
has size less than
![]() $\sigma $
. Indeed, otherwise,
$\sigma $
. Indeed, otherwise,
![]() $B_\eta \in [\kappa ]^{\sigma }$
, and so since
$B_\eta \in [\kappa ]^{\sigma }$
, and so since
![]() $A_\eta \in I^+$
, we may pick an
$A_\eta \in I^+$
, we may pick an
![]() $\alpha \in A_\eta $
such that
$\alpha \in A_\eta $
such that
![]() $c[\{\alpha \}\times B_\eta ]=\sigma $
, and in particular,
$c[\{\alpha \}\times B_\eta ]=\sigma $
, and in particular,
![]() $h_\eta (\alpha ) \in c[\{\alpha \}\times B_\eta ]$
.
$h_\eta (\alpha ) \in c[\{\alpha \}\times B_\eta ]$
.
As
![]() $|\mathcal P_\delta |<\kappa $
, it follows that we may pick
$|\mathcal P_\delta |<\kappa $
, it follows that we may pick
![]() $\beta \in \kappa \setminus \bigcup \{B_\eta \mathrel {|} \eta \in \mathcal P_\delta \ \&\ A_\eta \in I^+\}$
. Define
$\beta \in \kappa \setminus \bigcup \{B_\eta \mathrel {|} \eta \in \mathcal P_\delta \ \&\ A_\eta \in I^+\}$
. Define
![]() $g_\delta :\lambda \rightarrow \sigma $
via
$g_\delta :\lambda \rightarrow \sigma $
via
![]() $g_\delta (\alpha ):=c(\alpha ,\beta )$
. Then
$g_\delta (\alpha ):=c(\alpha ,\beta )$
. Then
![]() $g_\delta $
is as sought.
$g_\delta $
is as sought.
Let
![]() $\langle g_\delta \mathrel {|} \delta \in S\rangle $
be given by the preceding claim.
$\langle g_\delta \mathrel {|} \delta \in S\rangle $
be given by the preceding claim.
Claim 3.5.3. Let
![]() $j<\kappa $
. There exists an
$j<\kappa $
. There exists an
![]() $\alpha <\lambda $
such that for every function
$\alpha <\lambda $
such that for every function
![]() $f:[\kappa ]^n\rightarrow \theta $
, for every club
$f:[\kappa ]^n\rightarrow \theta $
, for every club
![]() $D\subseteq \kappa $
, there is a
$D\subseteq \kappa $
, there is a
![]() $\delta \in S_j$
such that
$\delta \in S_j$
such that
![]() $B_{\delta ,g_\delta (\alpha )}\subseteq D\cap T$
and
$B_{\delta ,g_\delta (\alpha )}\subseteq D\cap T$
and
![]() $f"[B_{\delta ,g_\delta (\alpha )}]^n=\{\tau _{\delta ,g_\delta (\alpha )}\}$
.
$f"[B_{\delta ,g_\delta (\alpha )}]^n=\{\tau _{\delta ,g_\delta (\alpha )}\}$
.
Proof Suppose not. Then, for every
![]() $\alpha <\lambda $
, we may fix a function
$\alpha <\lambda $
, we may fix a function
![]() $f_\alpha :[\kappa ]^n\rightarrow \theta $
and a club
$f_\alpha :[\kappa ]^n\rightarrow \theta $
and a club
![]() $D_\alpha \subseteq \kappa $
such that for every
$D_\alpha \subseteq \kappa $
such that for every
![]() $\delta \in S_j$
, either
$\delta \in S_j$
, either
![]() $B_{\delta ,g_\delta (\alpha )}\nsubseteq D_\alpha \cap T$
or
$B_{\delta ,g_\delta (\alpha )}\nsubseteq D_\alpha \cap T$
or
![]() $f_\alpha "[B_{\delta ,g_\delta (\alpha )}]^n\neq \{\tau _{\delta ,g_\delta (\alpha )}\}$
. Using that
$f_\alpha "[B_{\delta ,g_\delta (\alpha )}]^n\neq \{\tau _{\delta ,g_\delta (\alpha )}\}$
. Using that
![]() $\psi :{}^\lambda \theta \leftrightarrow \kappa $
is a bijection define a map
$\psi :{}^\lambda \theta \leftrightarrow \kappa $
is a bijection define a map
![]() $\eta :[\kappa ]^n\rightarrow \kappa $
via:
$\eta :[\kappa ]^n\rightarrow \kappa $
via:
Consider the club
![]() $D:=\{\delta \in \bigcap _{\alpha <\lambda }D_\alpha \mathrel {|} \eta "[\delta ]^n\subseteq \delta \}$
. Pick
$D:=\{\delta \in \bigcap _{\alpha <\lambda }D_\alpha \mathrel {|} \eta "[\delta ]^n\subseteq \delta \}$
. Pick
![]() $\rho \in R_j$
and a large enough
$\rho \in R_j$
and a large enough
![]() $\epsilon \in C_\rho $
such that
$\epsilon \in C_\rho $
such that
![]() $\operatorname {\mathrm {nacc}}(C_\rho \setminus \epsilon )\subseteq D\cap T$
. As
$\operatorname {\mathrm {nacc}}(C_\rho \setminus \epsilon )\subseteq D\cap T$
. As
![]() $\operatorname {\mathrm {otp}}(\operatorname {\mathrm {nacc}}(C_\rho \setminus \epsilon ))=\chi $
, recalling that
$\operatorname {\mathrm {otp}}(\operatorname {\mathrm {nacc}}(C_\rho \setminus \epsilon ))=\chi $
, recalling that
![]() $\chi \rightarrow (\mu )^n_\theta $
holds, for every
$\chi \rightarrow (\mu )^n_\theta $
holds, for every
![]() $\alpha <\lambda $
, we may pick a subset
$\alpha <\lambda $
, we may pick a subset
![]() $H_\alpha \subseteq \operatorname {\mathrm {nacc}}(C_\rho \setminus \epsilon )$
of order-type
$H_\alpha \subseteq \operatorname {\mathrm {nacc}}(C_\rho \setminus \epsilon )$
of order-type
![]() $\mu $
such that
$\mu $
such that
![]() $f_\alpha \mathbin {\upharpoonright }[H_\alpha ]^n$
is constant, and clearly
$f_\alpha \mathbin {\upharpoonright }[H_\alpha ]^n$
is constant, and clearly
![]() $\delta _\alpha :=\sup (H_\alpha )$
is an element of
$\delta _\alpha :=\sup (H_\alpha )$
is an element of
![]() $\operatorname {\mathrm {acc}}(C_\rho \setminus \epsilon )\cap E^\kappa _\mu $
, and hence of
$\operatorname {\mathrm {acc}}(C_\rho \setminus \epsilon )\cap E^\kappa _\mu $
, and hence of
![]() $S_j\cap D$
too. As
$S_j\cap D$
too. As
![]() $|C_\rho |=\chi \le \sigma $
and I is a proper
$|C_\rho |=\chi \le \sigma $
and I is a proper
![]() $\sigma ^+$
-complete ideal on
$\sigma ^+$
-complete ideal on
![]() $\lambda $
, let us now pick a
$\lambda $
, let us now pick a
![]() $\delta \in S_j\cap D$
such that
$\delta \in S_j\cap D$
such that
![]() $A^*:=\{\alpha <\lambda \mathrel {|} \delta _\alpha =\delta \}$
is in
$A^*:=\{\alpha <\lambda \mathrel {|} \delta _\alpha =\delta \}$
is in
![]() $I^+$
.
$I^+$
.
Since
![]() $\delta \in \operatorname {\mathrm {acc}}(C_\rho )$
, it is the case that
$\delta \in \operatorname {\mathrm {acc}}(C_\rho )$
, it is the case that
![]() $C_\delta =C_\rho \cap \delta $
, and hence, for every
$C_\delta =C_\rho \cap \delta $
, and hence, for every
![]() $\alpha \in A^*$
,
$\alpha \in A^*$
,
![]() $H_\alpha $
witnesses that
$H_\alpha $
witnesses that
![]() $f_\alpha \mathbin {\upharpoonright }[C_\delta \setminus \epsilon ]^n$
is good.
$f_\alpha \mathbin {\upharpoonright }[C_\delta \setminus \epsilon ]^n$
is good.
Since
![]() $\delta \in D$
, we know that
$\delta \in D$
, we know that
![]() $\bar \eta :=\eta \mathbin {\upharpoonright }[C_\delta \setminus \epsilon ]^n$
is in
$\bar \eta :=\eta \mathbin {\upharpoonright }[C_\delta \setminus \epsilon ]^n$
is in
![]() $\mathcal P_\delta $
. For every
$\mathcal P_\delta $
. For every
![]() $\alpha <\lambda $
, recall that
$\alpha <\lambda $
, recall that
![]() $\bar \eta ^\alpha $
is defined as
$\bar \eta ^\alpha $
is defined as
![]() $\psi _\alpha \circ \bar \eta $
, so that, for every
$\psi _\alpha \circ \bar \eta $
, so that, for every
![]() $(\gamma _1,\ldots ,\gamma _n)\in [C_\delta \setminus \epsilon ]^n$
,
$(\gamma _1,\ldots ,\gamma _n)\in [C_\delta \setminus \epsilon ]^n$
,
That is,
![]() $\bar \eta ^\alpha =f_\alpha \mathbin {\upharpoonright }[C_\delta \setminus \epsilon ]^n$
for every
$\bar \eta ^\alpha =f_\alpha \mathbin {\upharpoonright }[C_\delta \setminus \epsilon ]^n$
for every
![]() $\alpha <\lambda $
, so
$\alpha <\lambda $
, so
![]() $A_{\bar \eta }$
is equal to
$A_{\bar \eta }$
is equal to
![]() $\{\alpha <\lambda \mathrel {|} f_\alpha \mathbin {\upharpoonright }[C_\delta \setminus \epsilon ]^n\text { is good}\}$
and it covers the
$\{\alpha <\lambda \mathrel {|} f_\alpha \mathbin {\upharpoonright }[C_\delta \setminus \epsilon ]^n\text { is good}\}$
and it covers the
![]() $I^+$
-set
$I^+$
-set
![]() $A^*$
, and hence
$A^*$
, and hence
![]() $A_{\bar \eta }\in I^+$
. Recalling that
$A_{\bar \eta }\in I^+$
. Recalling that
![]() $g_\delta $
was given to us by Claim 3.5.2, we may now pick an
$g_\delta $
was given to us by Claim 3.5.2, we may now pick an
![]() $\alpha \in A_{\bar \eta }$
with
$\alpha \in A_{\bar \eta }$
with
![]() $h_{\bar \eta }(\alpha )= g_\delta (\alpha )$
. By the definition of
$h_{\bar \eta }(\alpha )= g_\delta (\alpha )$
. By the definition of
![]() $h_{\bar \eta }$
, this means that
$h_{\bar \eta }$
, this means that
![]() $B_{\delta ,g_\delta (\alpha )}$
is a cofinal subset of
$B_{\delta ,g_\delta (\alpha )}$
is a cofinal subset of
![]() $\operatorname {\mathrm {nacc}}(C_\delta \setminus \epsilon )$
for which
$\operatorname {\mathrm {nacc}}(C_\delta \setminus \epsilon )$
for which
![]() $\bar \eta ^\alpha \mathbin {\upharpoonright }[B_{\delta ,g_\delta (\alpha )}]^n$
is constant with value
$\bar \eta ^\alpha \mathbin {\upharpoonright }[B_{\delta ,g_\delta (\alpha )}]^n$
is constant with value
![]() $\tau _{\delta ,g_\delta (\alpha )}$
. But
$\tau _{\delta ,g_\delta (\alpha )}$
. But
and
![]() $\bar \eta ^\alpha \mathbin {\upharpoonright } [B_{\delta ,g_\delta (\alpha )}]^n=f_\alpha \mathbin {\upharpoonright } [B_{\delta ,g_\delta (\alpha )}]^n$
, contradicting the choice of
$\bar \eta ^\alpha \mathbin {\upharpoonright } [B_{\delta ,g_\delta (\alpha )}]^n=f_\alpha \mathbin {\upharpoonright } [B_{\delta ,g_\delta (\alpha )}]^n$
, contradicting the choice of
![]() $D_\alpha $
and
$D_\alpha $
and
![]() $f_\alpha $
.
$f_\alpha $
.
For every
![]() $j<\kappa $
, let
$j<\kappa $
, let
![]() $\alpha _j<\lambda $
be given by the preceding claim, and then for every
$\alpha _j<\lambda $
be given by the preceding claim, and then for every
![]() $\delta \in S_j$
, let
$\delta \in S_j$
, let
![]() $B_\delta :=B_{\delta ,g_\delta (\alpha _j)}$
and
$B_\delta :=B_{\delta ,g_\delta (\alpha _j)}$
and
![]() $g(\delta ):=\tau _{\delta ,g_\delta (\alpha _j)}$
. Then
$g(\delta ):=\tau _{\delta ,g_\delta (\alpha _j)}$
. Then
![]() $\langle B_\delta \mathrel {|} \delta \in S\rangle $
,
$\langle B_\delta \mathrel {|} \delta \in S\rangle $
,
![]() $\langle S_j\mathrel {|} j<\kappa \rangle $
and
$\langle S_j\mathrel {|} j<\kappa \rangle $
and
![]() $g:E^\kappa _\mu \rightarrow \theta $
are as sought modulo the fact that
$g:E^\kappa _\mu \rightarrow \theta $
are as sought modulo the fact that
![]() $S=\bigcup _{j<\kappa }S_j$
may possibly be a proper subset of
$S=\bigcup _{j<\kappa }S_j$
may possibly be a proper subset of
![]() $E^\kappa _\mu $
, but this can be mitigated by allocating all the left-out points to
$E^\kappa _\mu $
, but this can be mitigated by allocating all the left-out points to
![]() $S_0$
and defining
$S_0$
and defining
![]() $B_\delta $
and
$B_\delta $
and
![]() $g(\delta )$
arbitrarily over these points.
$g(\delta )$
arbitrarily over these points.
Remark 3.6. An inspection of the preceding proof shows that if
![]() $n>1$
, then we may as well take
$n>1$
, then we may as well take
![]() $\sigma $
to be
$\sigma $
to be
![]() $\chi $
since in this case,
$\chi $
since in this case,
![]() $\theta \cdot \chi ^\mu =\chi $
. Thus, for
$\theta \cdot \chi ^\mu =\chi $
. Thus, for
![]() $n>1$
, the proof yields the same conclusion for
$n>1$
, the proof yields the same conclusion for
![]() $\kappa :=\beth _2((\beth _{n-1}(\theta ))^+)$
(instead of
$\kappa :=\beth _2((\beth _{n-1}(\theta ))^+)$
(instead of
![]() $\beth _{n+2}(\theta )$
) assuming it is smaller than
$\beth _{n+2}(\theta )$
) assuming it is smaller than
![]() $\Omega ^{+\omega }$
.
$\Omega ^{+\omega }$
.
Remark 3.7. In the special case
![]() $\mu =\theta $
, assuming
$\mu =\theta $
, assuming
![]() $\diamondsuit (E^\kappa _\mu )$
, it is possible to arrange a
$\diamondsuit (E^\kappa _\mu )$
, it is possible to arrange a
![]() $\mu $
-bounded ladder system
$\mu $
-bounded ladder system
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
and a sequence
$\vec L=\langle A_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
and a sequence
![]() $\langle f_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
witnessing
$\langle f_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
witnessing
![]() $\diamondsuit ^n(\vec L, \theta )$
as in Definition 3.1 such that, for some ‘wild’ function
$\diamondsuit ^n(\vec L, \theta )$
as in Definition 3.1 such that, for some ‘wild’ function
![]() $f:[\kappa ]^n\rightarrow \theta $
, for every
$f:[\kappa ]^n\rightarrow \theta $
, for every
![]() $\delta $
in the stationary set
$\delta $
in the stationary set
![]() $\{\delta \in E^\kappa _\mu \mathrel {|} f \mathbin {\upharpoonright } [A_\delta ]^n = f_\delta \}$
, it is the case that
$\{\delta \in E^\kappa _\mu \mathrel {|} f \mathbin {\upharpoonright } [A_\delta ]^n = f_\delta \}$
, it is the case that
![]() $f \mathbin {\upharpoonright }[A_\delta ]^n$
is a bijection. For the purposes of our application in Corollary 4.7 however this is no good, and we need at least a small portion of the Ramsey-theoretic feature provided by the function g of Theorem 3.5. The reason can be gleaned from considering the negation of Clause (3) of Fact 4.2.
$f \mathbin {\upharpoonright }[A_\delta ]^n$
is a bijection. For the purposes of our application in Corollary 4.7 however this is no good, and we need at least a small portion of the Ramsey-theoretic feature provided by the function g of Theorem 3.5. The reason can be gleaned from considering the negation of Clause (3) of Fact 4.2.
We conclude this section with pointing out that similar to Remark 2.16, by using standard stepping up methods one can transfer Corollary 3.3 to
![]() $\aleph _{\omega +1}$
, as follows.
$\aleph _{\omega +1}$
, as follows.
Corollary 3.8. Suppose that
![]() $\aleph _\omega $
is a strong limit. For every positive integer n and every
$\aleph _\omega $
is a strong limit. For every positive integer n and every
![]() $\theta <\aleph _\omega $
, there exist a ladder system
$\theta <\aleph _\omega $
, there exist a ladder system
![]() $\vec L=\langle A_\delta \mathrel {|} \delta <\aleph _{\omega +1}\rangle $
and a function
$\vec L=\langle A_\delta \mathrel {|} \delta <\aleph _{\omega +1}\rangle $
and a function
![]() $g:\aleph _{\omega +1}\rightarrow \theta $
such that for every function
$g:\aleph _{\omega +1}\rightarrow \theta $
such that for every function
![]() $f:[\aleph _{\omega +1}]^n\rightarrow \theta $
, for every uncountable cardinal
$f:[\aleph _{\omega +1}]^n\rightarrow \theta $
, for every uncountable cardinal
![]() $\mu <\aleph _\omega $
,
$\mu <\aleph _\omega $
,
![]() $\{\delta \in E^{\aleph _{\omega +1}}_\mu \mathrel {|} f"[A_\delta ]^n=\{g(\delta )\}\}$
is a reflecting stationary set.
$\{\delta \in E^{\aleph _{\omega +1}}_\mu \mathrel {|} f"[A_\delta ]^n=\{g(\delta )\}\}$
is a reflecting stationary set.
4 Ladder systems and topological spaces
In this section, we give the first topological application of diamonds on ladder systems to topology. While not stated explicitly so far, we shall want the topological spaces constructed in this paper to at least be Hausdorff. Thus, we shall need the following folklore fact.
Fact 4.1. For a ladder system
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
, all of following are equivalent
$\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
, all of following are equivalent
![]() $:$
$:$
-
(1)
 $X_{\vec L}$
is Hausdorff
$X_{\vec L}$
is Hausdorff
 $;$
$;$
-
(2)
 $X_{\vec L}$
is Hausdorff and regular
$X_{\vec L}$
is Hausdorff and regular
 $;$
$;$
-
(3) for every pair
 $\gamma <\delta $
of ordinals from S,
$\gamma <\delta $
of ordinals from S,
 $\sup (A_\gamma \cap A_\delta )<\gamma $
.
$\sup (A_\gamma \cap A_\delta )<\gamma $
.
In particular, if
![]() $\vec L$
is
$\vec L$
is
![]() $\omega $
-bounded, then
$\omega $
-bounded, then
![]() $X_{\vec L}$
is Hausdorff and regular. More generally, for every
$X_{\vec L}$
is Hausdorff and regular. More generally, for every
![]() $\mu $
-bounded ladder system
$\mu $
-bounded ladder system
![]() $\vec L$
over a subset of
$\vec L$
over a subset of
![]() $E^\kappa _\mu $
, it is the case that
$E^\kappa _\mu $
, it is the case that
![]() $X_{\vec L}$
is Hausdorff and regular. A second basic fact will be needed. Namely, by [Reference Leiderman and Szeptycki19, Proposition 4.1] and a straight-forward generalisation of [Reference Balogh, Eisworth, Gruenhage, Pavlov and Szeptycki3, Claim 1], we have the following characterisation.
$X_{\vec L}$
is Hausdorff and regular. A second basic fact will be needed. Namely, by [Reference Leiderman and Szeptycki19, Proposition 4.1] and a straight-forward generalisation of [Reference Balogh, Eisworth, Gruenhage, Pavlov and Szeptycki3, Claim 1], we have the following characterisation.
Fact 4.2. For a ladder system
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
, all of following are equivalent
$\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
, all of following are equivalent
![]() $:$
$:$
-
(1)
 $X_{\vec L}$
is a
$X_{\vec L}$
is a
 $\Delta $
-space
$\Delta $
-space
 $;$
$;$
-
(2)
 $X_{\vec L}$
is countably metacompact
$X_{\vec L}$
is countably metacompact
 $;$
$;$
-
(3) For every function
 $g:S \rightarrow \omega $
, there is a function
$g:S \rightarrow \omega $
, there is a function
 $f: \kappa \rightarrow \omega $
, such that, for every
$f: \kappa \rightarrow \omega $
, such that, for every
 $\delta \in S$
,
$\delta \in S$
,
 $\sup \{\alpha \in A_\delta \mathrel {|} f(\alpha ) \leq g(\delta )\} <\delta $
.
$\sup \{\alpha \in A_\delta \mathrel {|} f(\alpha ) \leq g(\delta )\} <\delta $
.
Remark 4.3. The above characterisation makes it clear that an
![]() $\omega $
-bounded ladder system
$\omega $
-bounded ladder system
![]() $\vec L$
over
$\vec L$
over
![]() $\omega _1$
for which
$\omega _1$
for which
![]() $X_{\vec L}$
is not countably metacompact can be constructed from a gallery of hypotheses. To mention just two, by [Reference Brodsky and Rinot4, Theorem 3.7] such a ladder system exists assuming
$X_{\vec L}$
is not countably metacompact can be constructed from a gallery of hypotheses. To mention just two, by [Reference Brodsky and Rinot4, Theorem 3.7] such a ladder system exists assuming
![]() $\clubsuit $
, and by the proof of [Reference Rinot, Shalev and Todorcevic22, Corollary 4.6] such a ladder system exists assuming
$\clubsuit $
, and by the proof of [Reference Rinot, Shalev and Todorcevic22, Corollary 4.6] such a ladder system exists assuming
![]() $\diamondsuit (\mathfrak b)$
.
$\diamondsuit (\mathfrak b)$
.
Lemma 4.4. Suppose that
![]() $\mu <\kappa $
is a pair of regular uncountable cardinals, and that
$\mu <\kappa $
is a pair of regular uncountable cardinals, and that
![]() $\vec L$
is a
$\vec L$
is a
![]() $\mu $
-bounded ladder system over
$\mu $
-bounded ladder system over
![]() $E^\kappa _\mu $
such that
$E^\kappa _\mu $
such that
![]() $\Phi (\vec L,\omega ,\omega )$
holds. Then
$\Phi (\vec L,\omega ,\omega )$
holds. Then
![]() $X_{\vec L}$
is a regular Hausdorff space that is not countably metacompact.
$X_{\vec L}$
is a regular Hausdorff space that is not countably metacompact.
Proof Since
![]() $\vec L$
is a
$\vec L$
is a
![]() $\mu $
-bounded ladder system over
$\mu $
-bounded ladder system over
![]() $E^\kappa _\mu $
, Fact 4.1 implies that
$E^\kappa _\mu $
, Fact 4.1 implies that
![]() $X_{\vec L}$
is regular and Hausdorff. Write
$X_{\vec L}$
is regular and Hausdorff. Write
![]() $\vec L$
as
$\vec L$
as
![]() $\langle A_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
. Define a function
$\langle A_\delta \mathrel {|} \delta \in E^\kappa _\mu \rangle $
. Define a function
![]() $F:(\bigcup _{\delta \in S}{}^{A_\delta }\omega )\rightarrow \omega $
by letting for all
$F:(\bigcup _{\delta \in S}{}^{A_\delta }\omega )\rightarrow \omega $
by letting for all
![]() $\delta \in S$
and
$\delta \in S$
and
![]() $ f:A_\delta \rightarrow \omega $
,
$ f:A_\delta \rightarrow \omega $
,
Since
![]() $\Phi (\vec L,\omega ,\omega )$
holds, we may now fix a function
$\Phi (\vec L,\omega ,\omega )$
holds, we may now fix a function
![]() $g:S\rightarrow \omega $
such that, for every function
$g:S\rightarrow \omega $
such that, for every function
![]() $f:\kappa \rightarrow \omega $
, there are stationarily many
$f:\kappa \rightarrow \omega $
, there are stationarily many
![]() $\delta \in S$
such that
$\delta \in S$
such that
![]() $F(f \mathbin {\upharpoonright } A_\delta )= g(\delta )$
. In particular, for every function
$F(f \mathbin {\upharpoonright } A_\delta )= g(\delta )$
. In particular, for every function
![]() $f:\kappa \rightarrow \omega $
there are stationarily many
$f:\kappa \rightarrow \omega $
there are stationarily many
![]() $\delta \in S$
such that
$\delta \in S$
such that
![]() $\sup \{\alpha \in A_\delta \mathrel {|} f(\alpha ) =g(\delta )\} =\delta $
. So, by Fact 4.2,
$\sup \{\alpha \in A_\delta \mathrel {|} f(\alpha ) =g(\delta )\} =\delta $
. So, by Fact 4.2,
![]() $X_{\vec L}$
is not countably metacompact.
$X_{\vec L}$
is not countably metacompact.
We are now ready to prove Theorem A. Indeed, it follows by taking
![]() $\Lambda =\lambda =\beth _\omega $
in the next theorem.
$\Lambda =\lambda =\beth _\omega $
in the next theorem.
Corollary 4.5. Suppose that
![]() $\Lambda \le \lambda $
is a pair of uncountable cardinals such that
$\Lambda \le \lambda $
is a pair of uncountable cardinals such that
![]() $\Lambda $
is a strong limit. Denote
$\Lambda $
is a strong limit. Denote
![]() $\kappa := \operatorname {\mathrm {cf}}(2^\lambda )$
. Then there are co-boundedly many
$\kappa := \operatorname {\mathrm {cf}}(2^\lambda )$
. Then there are co-boundedly many
![]() $\mu \in \operatorname {\mathrm {Reg}}(\Lambda )$
such that
$\mu \in \operatorname {\mathrm {Reg}}(\Lambda )$
such that
![]() $E^\kappa _\mu $
carries a
$E^\kappa _\mu $
carries a
![]() $\mu $
-bounded ladder system
$\mu $
-bounded ladder system
![]() ${\vec L}$
such that
${\vec L}$
such that
![]() $X_{\vec L}$
is a regular Hausdorff space that is not countably metacompact.
$X_{\vec L}$
is a regular Hausdorff space that is not countably metacompact.
Proof By Corollary 2.12, there are co-boundedly many uncountable
![]() $\mu \in \operatorname {\mathrm {Reg}}(\Lambda )$
, for which there exists a
$\mu \in \operatorname {\mathrm {Reg}}(\Lambda )$
, for which there exists a
![]() $\mu $
-bounded ladder system
$\mu $
-bounded ladder system
![]() $\vec L$
over
$\vec L$
over
![]() $E^\kappa _\mu $
such that
$E^\kappa _\mu $
such that
![]() $\diamondsuit (\vec L, \omega )$
holds, in particular,
$\diamondsuit (\vec L, \omega )$
holds, in particular,
![]() $\Phi (\vec L, \omega ,\omega )$
holds. Now, appeal to Lemma 4.4.
$\Phi (\vec L, \omega ,\omega )$
holds. Now, appeal to Lemma 4.4.
Theorem 4.6. If
![]() $\kappa :=2^{2^{\aleph _1}}$
is smaller than
$\kappa :=2^{2^{\aleph _1}}$
is smaller than
![]() $\aleph _{\omega _1}$
, then there exists an
$\aleph _{\omega _1}$
, then there exists an
![]() $\omega _1$
-bounded ladder system
$\omega _1$
-bounded ladder system
![]() $\vec L$
over
$\vec L$
over
![]() $E^\kappa _{\omega _1}$
for which
$E^\kappa _{\omega _1}$
for which
![]() $X_{\vec L}$
is a regular Hausdorff space that is not countably metacompact.
$X_{\vec L}$
is a regular Hausdorff space that is not countably metacompact.
Proof Denote
![]() $\mu :=\aleph _1$
and
$\mu :=\aleph _1$
and
![]() $\lambda :=2^\mu $
. Note that
$\lambda :=2^\mu $
. Note that
![]() $\aleph _1<\lambda <\operatorname {\mathrm {cf}}(\kappa )\le \kappa <\aleph _{\omega _1}$
and hence
$\aleph _1<\lambda <\operatorname {\mathrm {cf}}(\kappa )\le \kappa <\aleph _{\omega _1}$
and hence
![]() $\kappa $
is regular. As
$\kappa $
is regular. As
![]() $2^\lambda <\mu ^{+\mu }$
, for every cardinal
$2^\lambda <\mu ^{+\mu }$
, for every cardinal
![]() $\varkappa \in [\mu ,2^\lambda )$
, it is the case that
$\varkappa \in [\mu ,2^\lambda )$
, it is the case that
![]() $\mu \le \varkappa <\mu ^{+\mu }$
, and so Fact 2.13 implies that
$\mu \le \varkappa <\mu ^{+\mu }$
, and so Fact 2.13 implies that
![]() $m(\varkappa , \mu ) = \varkappa <2^\lambda $
. As made clear right after Claim 2.9.1, we then get a
$m(\varkappa , \mu ) = \varkappa <2^\lambda $
. As made clear right after Claim 2.9.1, we then get a
![]() $\mu $
-bounded C-sequence
$\mu $
-bounded C-sequence
![]() $\vec C$
over some stationary
$\vec C$
over some stationary
![]() $S\subseteq E^\kappa _\mu $
such that
$S\subseteq E^\kappa _\mu $
such that
![]() $\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
holds. In particular, there is a
$\diamondsuit ^*(\vec C, 2^\lambda , 2^\lambda )$
holds. In particular, there is a
![]() $\mu $
-bounded C-sequence
$\mu $
-bounded C-sequence
![]() $\vec C$
over
$\vec C$
over
![]() $E^\kappa _\mu $
such that
$E^\kappa _\mu $
such that
![]() $\diamondsuit (\vec C, 2^\lambda , 2^\lambda )$
holds. As
$\diamondsuit (\vec C, 2^\lambda , 2^\lambda )$
holds. As
![]() $\lambda ^\mu =\lambda $
, Lemma 2.8 implies that
$\lambda ^\mu =\lambda $
, Lemma 2.8 implies that
![]() ${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\mu )$
holds. Then, by Lemma 2.10,
${{{\sf onto}}}(\{\lambda \},[2^\lambda ]^{\le \lambda },\mu )$
holds. Then, by Lemma 2.10,
![]() $\Phi (\vec C,2^\lambda ,\mu )$
holds. Now, appeal to Lemma 4.4.
$\Phi (\vec C,2^\lambda ,\mu )$
holds. Now, appeal to Lemma 4.4.
We are also in a condition to prove Theorem B.
Corollary 4.7. If
![]() $\kappa :=2^{2^{2^{\aleph _0}}}$
is smaller than
$\kappa :=2^{2^{2^{\aleph _0}}}$
is smaller than
![]() $\aleph _\omega $
, then there exists an
$\aleph _\omega $
, then there exists an
![]() $\omega $
-bounded ladder system
$\omega $
-bounded ladder system
![]() $\vec L$
over
$\vec L$
over
![]() $E^\kappa _{\omega }$
for which
$E^\kappa _{\omega }$
for which
![]() $X_{\vec L}$
is a regular Hausdorff space that is not countably metacompact.
$X_{\vec L}$
is a regular Hausdorff space that is not countably metacompact.
Proof Suppose that
![]() $\kappa :=2^{2^{2^{\aleph _0}}}$
is smaller than
$\kappa :=2^{2^{2^{\aleph _0}}}$
is smaller than
![]() $\aleph _\omega $
. Appealing to Theorem 3.5 with
$\aleph _\omega $
. Appealing to Theorem 3.5 with
![]() $(n,\Omega ,\mu ,\theta ):=(1,\omega ,\omega ,\omega )$
, we obtain an
$(n,\Omega ,\mu ,\theta ):=(1,\omega ,\omega ,\omega )$
, we obtain an
![]() $\omega $
-bounded ladder system
$\omega $
-bounded ladder system
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in E^\kappa _\omega \rangle $
and a map
$\vec L=\langle A_\delta \mathrel {|} \delta \in E^\kappa _\omega \rangle $
and a map
![]() $g:\kappa \rightarrow \omega $
such that for every function
$g:\kappa \rightarrow \omega $
such that for every function
![]() $f:\kappa \rightarrow \omega $
, there are stationarily many
$f:\kappa \rightarrow \omega $
, there are stationarily many
![]() $\delta \in E^\kappa _\omega $
such that
$\delta \in E^\kappa _\omega $
such that
![]() $f" A_\delta =\{g(\delta )\}$
. Since
$f" A_\delta =\{g(\delta )\}$
. Since
![]() $\vec L$
is a
$\vec L$
is a
![]() $\mu $
-bounded ladder system over
$\mu $
-bounded ladder system over
![]() $E^\kappa _\mu $
, Fact 4.1 implies that
$E^\kappa _\mu $
, Fact 4.1 implies that
![]() $X_{\vec L}$
is regular and Hausdorff. In addition, by Fact 4.2,
$X_{\vec L}$
is regular and Hausdorff. In addition, by Fact 4.2,
![]() $X_{\vec L}$
is not countably metacompact.
$X_{\vec L}$
is not countably metacompact.
We conclude this paper by providing a proof of Theorem C. The definition of a regressive tree may be found in [Reference Rinot and Shalev21, Definition 2.14], and the fact that coherent trees are regressive is easily shown.
Theorem 4.8. If there exists a
![]() $\kappa $
-Souslin tree
$\kappa $
-Souslin tree
![]() $\mathbf T$
, then there exists a ladder system
$\mathbf T$
, then there exists a ladder system
![]() $\vec L$
over some stationary subset of
$\vec L$
over some stationary subset of
![]() $\kappa $
for which
$\kappa $
for which
![]() $X_{\vec L}$
is a regular Hausdorff space that is not countably metacompact. If the tree
$X_{\vec L}$
is a regular Hausdorff space that is not countably metacompact. If the tree
![]() $\mathbf T$
is regressive, then
$\mathbf T$
is regressive, then
![]() $\operatorname {\mathrm {dom}}(\vec L)=E^\kappa _\omega $
so that
$\operatorname {\mathrm {dom}}(\vec L)=E^\kappa _\omega $
so that
![]() $X_{\vec L}$
is moreover first countable.
$X_{\vec L}$
is moreover first countable.
Proof By [Reference Rinot and Shalev21, Theorem 2.29], the existence of a
![]() $\kappa $
-Souslin tree
$\kappa $
-Souslin tree
![]() $\mathbf T$
implies that
$\mathbf T$
implies that
![]() $\clubsuit _{\operatorname {\mathrm {AD}}}(\mathcal S,1,1)$
holds for some
$\clubsuit _{\operatorname {\mathrm {AD}}}(\mathcal S,1,1)$
holds for some
![]() $\kappa $
-sized pairwise disjoint family
$\kappa $
-sized pairwise disjoint family
![]() $\mathcal S$
of stationary subsets of
$\mathcal S$
of stationary subsets of
![]() $\kappa $
. Denote
$\kappa $
. Denote
![]() $S:=\biguplus \mathcal S$
. By [Reference Rinot and Shalev21, Corollary 2.25(2)], if
$S:=\biguplus \mathcal S$
. By [Reference Rinot and Shalev21, Corollary 2.25(2)], if
![]() $\mathbf T$
is regressive, then we may moreover secure that
$\mathbf T$
is regressive, then we may moreover secure that
![]() $S=E^\kappa _\omega $
. As
$S=E^\kappa _\omega $
. As
![]() $\mathcal S$
is infinite, let
$\mathcal S$
is infinite, let
![]() $\langle S_n\mathrel {|} n<\omega \rangle $
be a partition of S in such a way that each
$\langle S_n\mathrel {|} n<\omega \rangle $
be a partition of S in such a way that each
![]() $S_n$
covers some set from
$S_n$
covers some set from
![]() $\mathcal S$
, so that
$\mathcal S$
, so that
![]() $\clubsuit _{\operatorname {\mathrm {AD}}}(\{S_n\mathrel {|} n<\omega \},1,1)$
holds. Finally, the latter means that there exists a ladder system
$\clubsuit _{\operatorname {\mathrm {AD}}}(\{S_n\mathrel {|} n<\omega \},1,1)$
holds. Finally, the latter means that there exists a ladder system
![]() $\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
such that the following two hold:
$\vec L=\langle A_\delta \mathrel {|} \delta \in S\rangle $
such that the following two hold:
-
(i) for every cofinal
 $A\subseteq \kappa $
, for every
$A\subseteq \kappa $
, for every
 $n<\omega $
, there exists a
$n<\omega $
, there exists a
 $\delta \in S_n$
such that
$\delta \in S_n$
such that
 $\sup (A_\delta \cap A)=\delta $
;
$\sup (A_\delta \cap A)=\delta $
; -
(ii) for every pair
 $\gamma <\delta $
of ordinals from S,
$\gamma <\delta $
of ordinals from S,
 $\sup (A_{\gamma }\cap A_{\delta })<\gamma $
.
$\sup (A_{\gamma }\cap A_{\delta })<\gamma $
.
Now letting
![]() $g:S\rightarrow \omega $
describe the partition of S, we get that for every function
$g:S\rightarrow \omega $
describe the partition of S, we get that for every function
![]() $f: \kappa \rightarrow \omega $
, by picking
$f: \kappa \rightarrow \omega $
, by picking
![]() $n<\omega $
such that
$n<\omega $
such that
![]() $A:=f^{-1}\{n\}$
is cofinal in
$A:=f^{-1}\{n\}$
is cofinal in
![]() $\kappa $
, we may find
$\kappa $
, we may find
![]() $\delta \in S_n$
such that
$\delta \in S_n$
such that
![]() $\sup (A_\delta \cap A)=\delta $
, and hence
$\sup (A_\delta \cap A)=\delta $
, and hence
![]() $\sup \{\alpha \in A_\delta \mathrel {|} f(\alpha ) =g(\delta )\} =\delta $
. So Clause (i) implies that
$\sup \{\alpha \in A_\delta \mathrel {|} f(\alpha ) =g(\delta )\} =\delta $
. So Clause (i) implies that
![]() $X_{\vec L}$
is not countably metacompact by Fact 4.2, and Clause (ii) ensures that
$X_{\vec L}$
is not countably metacompact by Fact 4.2, and Clause (ii) ensures that
![]() $X_{\vec L}$
is a regular Hausdorff space by Fact 4.1.
$X_{\vec L}$
is a regular Hausdorff space by Fact 4.1.
Acknowledgments
We thank Ido Feldman for the combinatorial proof of Claim 2.8.1. We thank Jing Zhang for a discussion on this paper and in particular for isolating Question 2.17. We thank the referee for their feedback.
Funding
The first author was supported by the European Research Council (Grant No. ERC-2018-StG 802756). The second author was supported by the Israel Science Foundation (Grant No. 665/20). The third author was partially supported by the Israel Science Foundation (Grant No. 203/22) and by the European Research Council (Grant No. ERC-2018-StG 802756).