In [1, Chapter 3, Section 2], we collected together results we had previously obtained relating to the question of which positive integers m were Lucasian, that is, factors of some Lucas number Ln. We pointed out that the behaviors of odd and even numbers m were quite different. Thus, for example, 2 and 4 are both Lucasian but 8 is not; for the sequence of residue classes mod 8 of the Lucas numbers, n ⩾ 0, reads
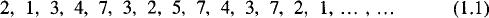
and thus does not contain the residue class 0*. On the other hand, it is a striking fact that, if the odd number s is Lucasian, then so are all of its positive powers.