Introduction
Large outlet glaciers and ice streams are the primary means by which ice is transported from the interior of Antarctica to the ocean (e.g. Reference Rignot and ThomasRignot and Thomas, 2002). These glaciers are known to change speed on a range of timescales, ranging from days (Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003) to decades (Reference Joughin, Rignot, Rosanova, Lucchitta and BohlanderJoughin and others, 2003; Reference Stearns, Jezek and van der VeenStearns and others, 2005) to centuries (Reference Retzlaff, Lord and BentleyRetzlaff and others, 1993; Reference Hulbe and FahnestockHulbe and Fahnestock, 2007). As a result of these flow changes, many glaciers are now driving negative mass imbalances in West Antarctica (Reference Shepherd, Wingham and RignotShepherd and others, 2004; Reference ThomasThomas, 2004) and the Antarctic Peninsula (Reference Pritchard and VaughanPritchard and Vaughan, 2007). Changes in flow speed are often a glacier’s dynamic response to climate-related perturbations at its seaward margin (Reference Payne, Vieli, Shepherd, Wingham and RignotPayne and others, 2004; Reference RignotScambos and others, 2004; Reference Nick, Vieli, Howat and JoughinNick and others, 2009), although other mechanisms related to changes in subglacial hydrology might also play a role in speed increases (Reference Stearns, Smith and HamiltonStearns and others, 2008; Reference Van de WalVan de Wal and others, 2008).
The East Antarctic ice sheet (EAIS) is the largest reservoir of fresh water on Earth, with ~50m of sea-level rise equivalent. Current mass-balance estimates vary from –1 to +67km3 a–1 (Reference Shepherd and WinghamShepherd and Wingham, 2007; Reference RignotRignot and others, 2008), and while most of the growth is driven by enhanced snowfall over the ice-sheet interior (Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005), near-coastal imbalances have been linked to ice dynamics (Reference Rignot and JacobsRignot and Jacobs, 2002). Recent results from the Gravity Recovery and Climate Experiment (GRACE) suggest some ice mass loss in the coastal regions of the EAIS, but spatial aliasing makes it difficult to resolve the behavior of individual catchment basins (Reference Chen, Wilson, Blankenship and TapleyChen and others, 2009; Reference WuWu and others, 2010). Because outlet glacier speeds exert a major control on ice-sheet mass balance and modulate ice-sheet contributions to sea-level rise, it is essential that their sensitivity to a range of dynamic processes is properly understood and incorporated into prognostic ice-sheet models.
Model studies (Reference Dupont and AlleyDupont and Alley, 2005) suggest that glaciers with high driving stresses, large basal drag and minimal side drag (such as those draining through the Transantarctic Mountains) are more sensitive to changes in buttressing than other outlet glaciers. Consequently, modest thinning or retreat of the Ross Ice Shelf might initiate an adjustment in the flow speeds of Transantarctic Mountain outlet glaciers (Reference Gagliardini, Durand, Zwinger, Hindmarsh and Le MeurGagliardini and others, 2010). Recent observations (Reference Stearns, Smith and HamiltonStearns and others, 2008) also show that these glaciers are sensitive to varying inputs of subglacial water. These characteristics motivate the need for a better understanding of Transantarctic Mountain outlet glacier dynamics and mass balance.
Most of what is known about East Antarctic outlet glaciers draining into the Ross Ice Shelf has been gleaned from limited field programs in the early 1960s (Reference SwithinbankSwithinbank, 1963), aerial photogrammetry from the late 1970s (Reference BrecherBrecher, 1982) and recent satellite remote-sensing studies (Reference Frezzotti, Capra and VittuariFrezzotti and others, 1998; Reference Rignot and ThomasRignot and Thomas, 2002; Reference Schenk, Csatho, van der Veen, Brecher, Ahn and YoonSchenk and others, 2005; Reference StearnsStearns, 2007). There have been no detailed, high-resolution field studies of the kind that have focused on the Siple Coast ice streams and Amundsen Sea embayment of West Antarctica. As a result, we have an incomplete understanding of many key details of the current configuration and dynamics of these glaciers, and are ill-equipped to model their response to potential future forcings.
Here the mass balance is estimated for four glaciers draining ice from the EAIS through the Transantarctic Mountains into the Ross Sea embayment: David Glacier (75.3˚S, 162˚E), Mulock Glacier (79˚S, 160.5˚E), Byrd Glacier (80˚S, 160˚E) and Nimrod Glacier (82.5˚S, 160.2˚E) (Fig. 1). Together, these glaciers drain ~1. 53±106 km2 of East Antarctica. With the exception of David Glacier, they discharge ice into the Ross Ice Shelf. Remote-sensing observations are used to map changes in ice flow and surface elevation, and ultimately to compute the mass balance of each glacier using the input–output method.

Fig. 1. Catchment boundaries for East Antarctic outlet glaciers studied in this paper, overlaid on a portion of the 1997 RADARSAT mosaic (Jezek and others, 2002). Together, these glaciers drain ~1.53±106km2 (or 12% by area) of the Antarctic ice sheet.
Data and Methods
Spatially extensive and multitemporal glaciological observations are limited for most Transantarctic Mountain outlet glaciers due to challenging field logistics and, until recently, sparse satellite coverage south of ~81.5˚S. Here, imagery from the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER), which became available in 2000, is used to derive ice-velocity and surface-elevation maps over four Transantarctic Mountain glaciers. Landsat Thematic Mapper (TM), Landsat Enhanced TM+ (ETM+), Advanced Land Observing Satellite (ALOS) and Système Probatoire pour l’Observation de la Terre (SPOT) (Reference Korona, Berthier, Bernard, Rémy and ThouvenotKorona and others, 2009) imagery, where available, is used to extend the spatial and temporal coverage of the data. The images used in this study are listed in the Appendix.
Velocity
The ASTER sensor is well suited for mapping glaciers at high latitudes because it images at high resolution (15m pixel size in the visible/near-infrared (VNIR) bands) with coverage to ~84˚N/S. To obtain ice velocities, a cross-correlation technique (Reference Rignot and ThomasScambos and others, 1992) is applied to sequential images to track the displacement of surface features such as crevasses. Cloud-free, co-registered and orthorectified image pairs are ingested to the software, and operator-controlled settings are used to maximize the statistical cross-correlation, based on variable flow speeds of each subsetted image. All the images are orthorectified using a reference digital elevation model (DEM), specifically chosen for each glacier based on adequate coverage of the glacier and surrounding mountains (which are needed for tie points). In many cases, the reference DEM is a mosaic of a few ASTER DEMs acquired on the same day.
The ASTER instrument’s across-track, off-nadir scene acquisition capability (∓24˚) in the VNIR introduces an image geometry change that must be considered during scene selection. Over regions of rugged relief, such as the Transantarctic Mountains, the pointing angles of sequential images must be within 3˚to maintain similar geometric characteristics (Reference Stearns and HamiltonStearns and Hamilton, 2007). If the pointing angle difference is >3˚, panoramic distortion inhibits cross-correlation.
The measured displacements of surface features have several sources of uncertainty originating from image orthorectification, co-registration and application of the feature-matching technique. Orthorectification using the ASTER DEM translates the DEM errors onto the orthorectified image. Reference KääbKääb (2002) reports a 10m ground position error for rough terrain in the Swiss Alps, which is smaller than the 30m position error found by Reference StearnsStearns (2007) for East Greenland. Velocity errors are variable because of the different time separation of each image pair, but in all cases they are small in comparison to the observed speeds (Reference StearnsStearns, 2007).
Archival velocity measurements exist for some of the glaciers in this study. In 1960–62, Reference SwithinbankSwithinbank (1963) measured surface displacement on Mulock, Byrd and Nimrod glaciers, using traditional theodolite observations. Surveys of each glacier consisted of one transverse profile, with 6–21 surveyed points. Reference BrecherBrecher (1982) used aerial photographs of Byrd Glacier, acquired on 6 December 1978 and 31 January 1979, to calculate the displacement of 472 points on the glacier trunk. Velocity measurements on David Glacier derived from remote-sensing and field-based GPS were collected between 1990 and 1994 by Reference Frezzotti, Capra and VittuariFrezzotti and others (1998). Synthetic aperture radar interferometry (InSAR) was also used to measure ice velocities of David, Byrd and Mulock glaciers in 1997 (Reference RignotRignot, 2002; Reference Rignot and ThomasRignot and Thomas, 2002; Reference Wuite, Jezek, Wu, Farness and CarandeWuite and others, 2009).
Elevation data
Surface elevation maps are produced from stereo ASTER imagery using the Japanese ASTER Science Team procedure described by Reference Fujisada, Bailey, Kelly, Hara and AbramsFujisada and others (2005) and Reference Stearns and HamiltonStearns and Hamilton (2007). The ASTER sensor collects a stereo image-pair using two telescopes in visible band 3: a nadir-viewing telescope (3N) and a backward-looking telescope (3B). The individual ASTER scenes are converted to DEMs through processing of the stereo bands to epipolar geometry, and parallax-matching using commercial software, SILCAST (Reference Fujisada, Bailey, Kelly, Hara and AbramsFujisada and others, 2005). Products generated using identical procedures can be ordered from the NASA/US Geological Survey (USGS) Land Processes Distributed Active Archive Center (LP DAAC) at https://wist.echo.nasa.gov.api/. The final DEM product is referenced to the Earth Gravitational Model 1996 (EGM96) geoid, and has a grid spacing of 15 m.
DEM uncertainties are from a combination of systematic errors, and random errors due to satellite positioning, image acquisition geometry and atmospheric conditions. Each DEM was tested for a systematic bias with respect to other DEMs of the same glacier; detected biases were removed. Calculated random errors contribute to a root-mean-square (rms) error of one pixel, based on a comparison of elevation differences in static regions (Reference StearnsStearns, 2007). This error is consistent with Reference Fujisada, Bailey, Kelly, Hara and AbramsFujisada and others (2005), who report a DEM vertical accuracy of 20m with 95% confidence (2σ). In extremely rugged mountain regions, uncertainties in absolute elevations can be quite large (~60m rms), but uncertainties in relative elevations, important for surface elevation change and volume loss estimates, are usually much smaller (Reference KääbKääb, 2002; Reference Stearns and HamiltonStearns and Hamilton, 2007). An error of 30m is assigned to the ASTER DEMs, as long as quality-control tests over static regions (mountains) show only minor elevation differences between DEMs (Reference StearnsStearns, 2007).
Accumulation rates
Snow accumulation is one of the most difficult mass-balance parameters to constrain (Reference EisenEisen and others, 2008). There are <100 in situ surface mass-balance measurements in the catchment areas of the four outlet glaciers studied here, an area of ~1.53Ø106 km2. These observations cover a range of time periods and are of variable quality. Several efforts have been made to incorporate the in situ measurements into continental-scale compilations using remote sensing, atmospheric reanalyses and statistical modeling (Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others, 1999; Reference Arthern, Winebrenner and VaughanArthern and others, 2006; Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others, 2006). This study uses the results from these three compilations to calculate the catchment-specific mass balance. Both Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999) and Reference Arthern, Winebrenner and VaughanArthern and others (2006) use satellite microwave radiometry (6.9 and 35 GHz, respectively) to extend the spatial distribution of surface measurements across the ice sheet. Thermal microwaves are emitted from the uppermost layers of the firn, but the actual depth depends on firn properties and the sensor wavelength, meaning the accumulation rates are unlikely to be averaged over a consistent time period. In comparison, Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others (2006) use a regional atmospheric climate model, RACMO2/ANT, for the period 1980–2004, calibrated by field measurements, to produce their surface mass-balance map. RACMO2/ANT does parameterize sublimation, but snowdrift is not included (Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others, 2006). Reference Lenaerts, van den Broeke, van de Berg, van Meijgaard and Kuipers MunnekeLenaerts and others (in press) performed RACMO simulations using the European Centre for Medium-Range Weather Forecasts’ (ECMWF) newest reanalysis dataset: ERA-Interim (1989–2009). ERA-Interim decreases precipitation inland compared to ERA-40, which was used by Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others (2006). Moreover, the model by J. Lenaerts and others (unpublished information) includes snowdrift physics and yields very different accumulation values over the Antarctic plateau.
Catchment area
To compute mass balance, the size of the catchment basins over which snow accumulation occurs must be known. Catchment basins are delineated manually by mapping changes in surface slope on the OSU DEM of Antarctica (Reference Jezek, Liu, Zhao and LiJezek and others, 1999; Reference Liu, Jezek and LiLiu and others, 1999) and tracing flowlines and stripes on RADARSAT imagery. Reference Price and WhillansPrice and Whillans (1998) assign an uncertainty of 9% to catchment basin areas, using traditional surveying techniques. The use of higher-resolution satellite-derived DEMs and imagery leads to improved catchment basin delineation; in this case, an uncertainty of 5% is applied. The catchment areas used in this study are within 3% of corresponding dimensions delineated in other studies (Reference Frezzotti, Capra and VittuariFrezzotti and others, 1998; Reference Rignot and JacobsRignot and Jacobs, 2002; Reference Rignot and ThomasRignot and Thomas, 2002).
Grounding line
The grounding line for each glacier was determined from a combination of surface slope flattening and reduction in driving stress (from ~300 kPa to <10 kPa) (Reference StearnsStearns, 2007). Misplacing the grounding line will introduce an uncertainty into the computed discharge flux. The error is quantified as the difference between this study’s grounding line location and grounding lines determined by surface flexure (Reference Rignot and JacobsRignot and Jacobs, 2002; Reference Brunt, Fricker, Padman, Scambos and O’NeelBrunt and others, 2010) and a combination of photoclinometry and laser altimetry (Reference BindschadlerBindschadler and others, 2011). Grounding lines are shown as being orthogonal to ice flow, which is probably a simplification of their actual curvilinear shape. However, this simplification is unlikely to substantially alter the calculated outgoing flux, since flow speeds near the margins are much slower.
Mass balance
The mass budget approach compares catchment–wide accumulation rates with ice flux across the grounding line. For a glacier in balance,
in which accumulation rate, ḃ, is integrated over the catchment area. The basal melt rate, ṁ , is integrated over the zone of glacier sliding, and the depth–averaged velocity, ū, is integrated across the width of the grounding line. Ice discharge across the flux gate is referred to as fluxout throughout the text. The depth-averaged velocity is calculated using measured values of surface velocity u s,
where n = 3, and B is the stiffness parameter set to 500 kPa a–1/3 (appropriate for ice at –15˚C (Reference Whillans, Chen, van der Veen and HughesWhillans and others, 1989)), H is ice thickness, g is the gravitational acceleration (9.81ms–2), α is the surface slope and S f is the shape factor at the grounding line (equal to the cross-sectional area divided by the product of the perimeter and ice thickness).
Ice thickness
Ice thickness at the grounding line, which is needed to determine fluxout, is traditionally calculated from hydrostatic equilibrium, following
in which h is the ice surface elevation above sea level, and ρ ice and ρ water are the densities of ice (900–917 kgm–3) and sea water (1027–1030 kgm–3), respectively. Calculated ice thicknesses vary by <12% between the maximum and minimum density values.
In reality, the column-averaged density across the grounding line will not be 917 kgm–3, but will include a layer of less-dense firn (Reference Van den Broeke, van de Berg and van MeijgaardVan den Broeke and others, 2008). A firn depth correction of 16m is applied, following values cited in Van den Broeke and others (2008). This correction reduces the thickness values by ≤2%. A 1σ error of 100m is applied to the ice thickness estimates, which accounts for uncertainties in grounding line location, density determination and firn compaction (this is comparable to errors applied to BEDMAP values (Reference Lythe and VaughanLythe and others, 2001)).
Basal melt
Mass loss from basal melting arises from the conduction of geothermal heat into the ice and frictional energy dissipation at the bed. Melt rates could only be calculated for areas covered by the velocity maps, and yielded values ranging from 6mmw.e. a–1 for Mulock Glacier to 260 mmw.e. a–1 for Byrd Glacier (Reference StearnsStearns, 2007). This variability is a function of different flow speeds, and magnitudes of driving stress and basal drag (Mulock Glacier has a comparatively low driving stress).
Results
David Glacier
David Glacier (75.3˚S, 162˚E) drains ice from northern Victoria Land through the Transantarctic Mountains and into the Ross Sea (Fig. 2a). It is the only glacier in this study that is not buttressed by the Ross Ice Shelf, but rather feeds into the Drygalski Ice Tongue. The ice tongue extends ~90 km into a polynya in Terra Nova Bay, which is kept free of sea ice by the force and persistence of katabatic winds (Reference Kurtz and BromwichKurtz and Bromwich, 1983). Earlier work shows that flow speeds on David Glacier increase almost linearly from the grounding line to the front of the Drygalski Ice Tongue (Reference FrezzottiFrezzotti, 1993; Reference Frezzotti, Tabacco and ZirizzottiFrezzotti and others, 2000; Reference Wuite, Jezek, Wu, Farness and CarandeWuite and others, 2009), which is consistent with the results from this study (Fig. 2b).

Fig. 2. David Glacier. (a) ASTER satellite image from 12 December 2004. David Cauldron is the steep drop to the left of the image. Ice flow is from left to right. The grounding line position (identified by Reference RignotRignot (2002) and this study) is shown in black; the velocity profile used in Figure 3 is shown in white. (b) Ice velocity (m a–1) determined from an ASTER image pair (17 January 2001/14 October 2001) and gridded to 1 km. (c) Surface topography (m) derived from the ASTER image in (a) and gridded to 1 km. The valley walls have been masked out.
The trunk of David Glacier begins as ice flows over David Cauldron, a bedrock step that is evident in both satellite imagery (Fig. 2a) and surface topography (Fig. 2c). The glacier loses 400–500m of elevation in David Cauldron, which causes a rapid, but isolated, flow acceleration (Fig. 2b). Down-flow of David Cauldron, the surface slope flattens and ice flow decreases. The glacier accelerates again as the tributary joins the main trunk. Throughout the trunk of David Glacier, flow speeds are much slower at the lateral margins, indicating the influence of lateral drag from the rock walls (Fig. 2b).
Reference RignotRignot (2002) located the grounding line at the base of David Cauldron (Fig. 2a), based on tidal flexure detected using interferometry. Reference Frezzotti, Capra and VittuariFrezzotti and others (1998) had previously placed the grounding line ~15 km down-flow of David Cauldron, based on an analysis of tidal cycles in GPS observations carried out at eight locations along the glacier and the Drygalski Ice Tongue. The analysis of ASTER DEM slope changes places the grounding line near the Reference RignotRignot (2002) position.
ASTER-derived velocities (2001–06) are compared with earlier results from Landsat TM images (Reference Frezzotti, Capra and VittuariFrezzotti and others, 1998), radar imagery from 1991 to 2000 (Reference Wuite, Jezek, Wu, Farness and CarandeWuite and others, 2009), and several GPS sites surveyed in 1991 and 1994 (Reference Frezzotti, Capra and VittuariFrezzotti and others, 1998) (Fig. 3). Flow speeds are generally within the respective errors, suggesting no significant changes in speed over the 16 year period. Ice velocity in 1990 is slightly higher (Fig. 3) than in subsequent years, particularly at the foot of David Cauldron, but with the current time series it is difficult to assess the cause or significance of this possible change in speed.

Fig. 3. David Glacier ice velocity derived from field surveys and repeat Landsat (Reference Frezzotti, Capra and VittuariFrezzotti and others, 1998) and ASTER images for five epochs along the white profile line in Figure 2a (x=0 is near David Cauldron; ice flow is from left to right). The solid black curve shows velocities derived from Landsat TM imagery (Reference Frezzotti, Capra and VittuariFrezzotti and others, 1998); the stars represent 1991–94 GPS velocities (Reference Frezzotti, Capra and VittuariFrezzotti and others, 1998). Error bars for each image pair are shown in the legend (dates are mm/dd/yyyy).
Existing mass-budget estimates for David Glacier indicate that it is close to zero balance (Reference FrezzottiFrezzotti, 1993; Reference Frezzotti, Tabacco and ZirizzottiFrezzotti and others, 2000; Reference RignotRignot, 2002), with small differences in the estimates, probably arising from variability in the way that catchment-wide accumulation rates were quantified. The estimated fluxout derived in this study (9.28∓0.88 Gt a–1) is comparable to that estimated by Reference Frezzotti, Tabacco and ZirizzottiFrezzotti and others (2000) (9.1∓0.9 Gt a–1). Some mass-balance estimates (using snow-accumulation rates derived from historical snow-pit stratigraphy) suggest a large positive balance of 19.6 Gt a–1 (Reference Giovinetto and BentleyGiovinetto and Bentley, 1985) and 25.5 Gt a–1 (Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others, 1999) for David Glacier. These positive balances are not supported by surface elevation observations (Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005; Reference Wingham, Shepherd, Muir and MarshallWingham and others, 2006; Reference HelsenHelsen and others, 2008; Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009) or GRACE estimates (Reference RamillienRamillien and others, 2006; Reference Chen, Wilson, Blankenship and TapleyChen and others, 2009), which suggest near-zero mass balance in this region.
Mulock Glacier
Mulock Glacier (79˚S, 160.5˚E) drains the largest catchment basin between David and Byrd Glaciers (Fig. 4c). It is buttressed by the Ross Ice Shelf, and drains 5.23∓0.59 Gt a–1 of ice from East Antarctica into the ice shelf. The net balance of Mulock Glacier (1.91∓0.84 Gt a–1) suggests that it is roughly in balance with its catchment-wide accumulation; a finding consistent with Reference Rignot and ThomasRignot and Thomas (2002).

Fig. 4. Mulock Glacier. (a) ASTER satellite image from 23 November 2002. Ice flow is from left to right. The grounding line position is shown in black; the velocity profile used in Figure 3 is shown in white. (b) Ice velocity (m a–1) from an ASTER image pair (20 October 2001/23 November 2002), gridded to 1 km spacing. (c) Surface topography (m) derived from the ASTER image in (a) and gridded to 1 km spacing.
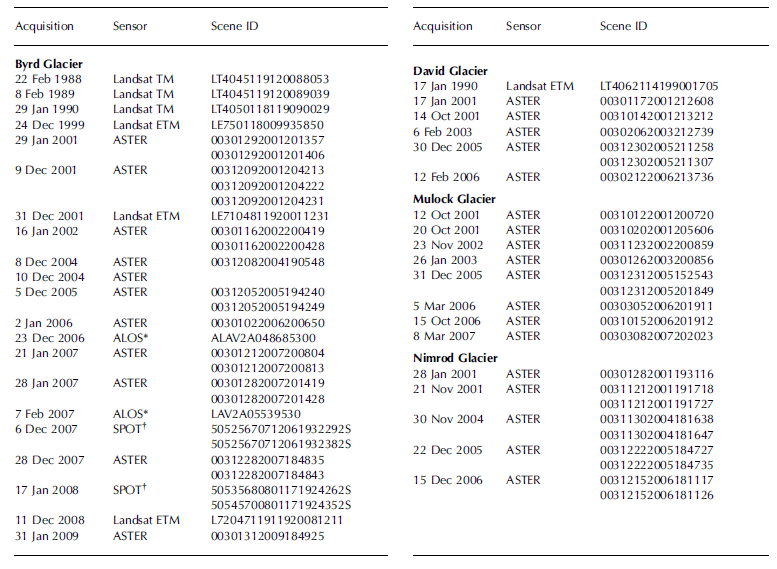
The main trunk of Mulock Glacier is ~60km long (Fig. 4a) and undergoes a ~800m drop in elevation from the edge of the EAIS to the grounding line where it enters the Ross Ice Shelf (Fig. 4c). The ASTER-derived DEM shows large changes in surface concavity, which are most likely a function of flow across an overdeepened basin. Ice flow accelerates to accommodate discharge through a constriction in the fjord, and again as ice flows over a step into the Ross Ice Shelf (Fig. 4b). The sharp peak in velocity ~50 km down the flowline (Fig. 5) is probably due to the increase in surface slope observed in the ASTER DEMs (Fig. 4c). The location of the grounding line is determined on the basis of crevasse patterns (Fig. 4a), ice flow (Fig. 5) and surface-elevation changes (Fig. 4c).
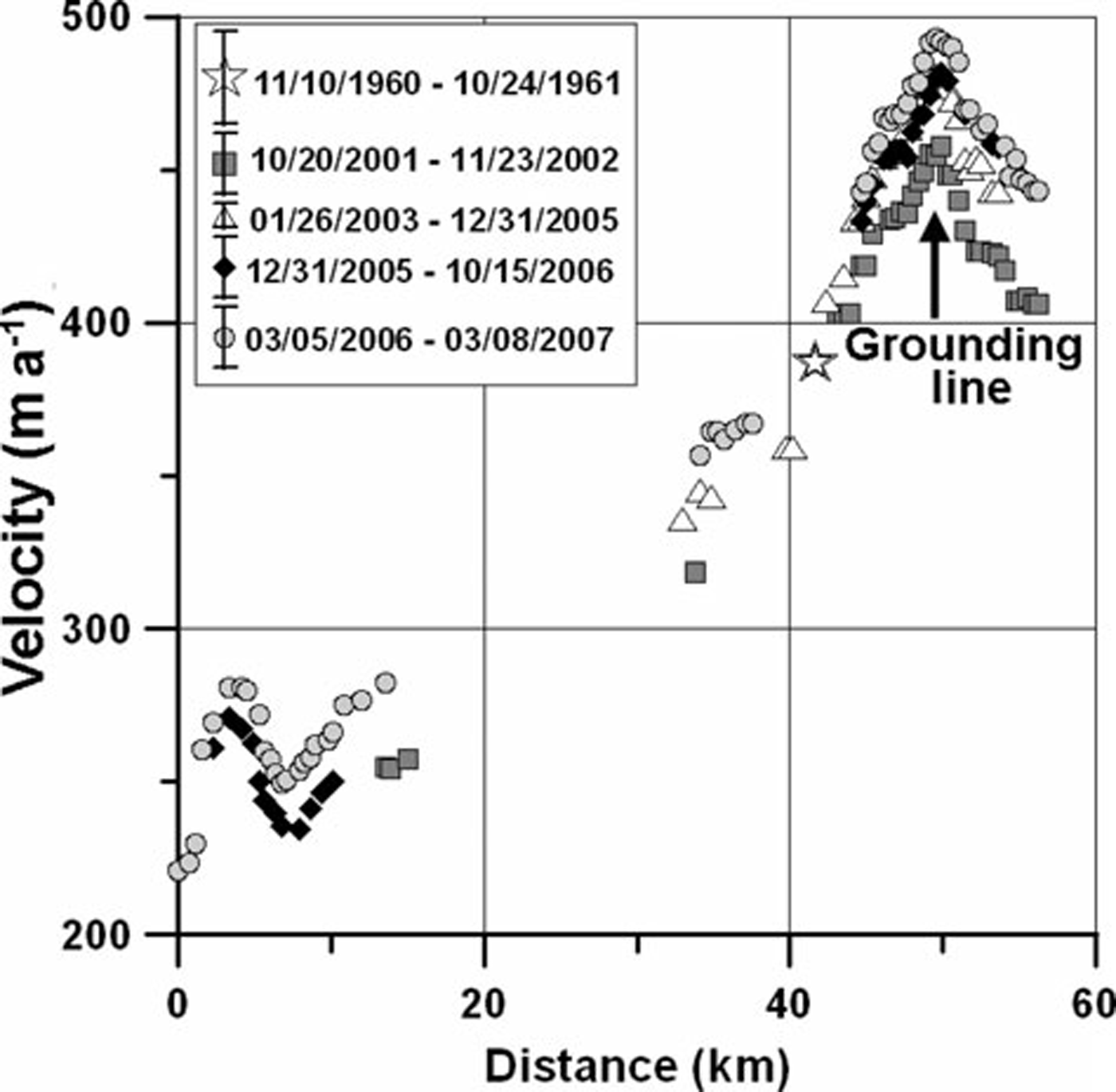
Fig. 5. Mulock Glacier ice velocity derived from repeat ASTER images for four epochs along the white line in Figure 4a. The star denotes repeat geodetic measurements by Reference SwithinbankSwithinbank (1963). Error bars for each image pair are shown in the legend (dates are mm/dd/yyyy).
Geodetic measurements from 1960–61 yielded ice velocities of ~387ma–1 along the grounded center line of the glacier (Fig. 5) (Reference SwithinbankSwithinbank, 1963). Results from repeat feature tracking, while not overlapping the same location, imply comparable ice speeds, 40 years after the Reference SwithinbankSwithinbank (1963) study (Fig. 5). The more recent pattern of satellite image-derived velocities shows a gradual acceleration at the grounding line from 457±10ma–1 in 2001–02, to 481± 8ma–1 in 2003–05, to 493±20ma–1 in 2006–07. If the velocity increases are real, dynamic thinning should be detected along the length of the glacier: the uncertainties in the ASTER DEMs are too large to currently detect this effect (Reference StearnsStearns, 2007), but slight thinning (~–3cma–1) is detected in firn-corrected maps of elevation change (Reference HelsenHelsen and others, 2008).
Byrd Glacier
Byrd Glacier (80˚S, 160˚E) has one of the largest catchment basins in Antarctica (1 101 725 km2), delivers 22.32± 1.72 Gt a–1 of ice into the Ross Ice Shelf, and sustains rapid flow speeds in excess of 800 ma–1. Prolonged changes in the flow dynamics of Byrd Glacier will have an impact on the mass balance of a significant portion of East Antarctica and might also affect the stability of the Ross Ice Shelf (Reference Gagliardini, Durand, Zwinger, Hindmarsh and Le MeurGagliardini and others, 2010).
A ~10 km wide grounding zone was first identified by Reference Hughes and FastookHughes and Fastook (1981), who used traditional surveying techniques to detect tidal fluctuations at 15 surface elevation markers along the center line of Byrd Glacier (Fig. 6). Instead of a sharp grounding line, their data implied a gradual shift from floating to grounded ice (Reference Hughes and FastookHughes and Fastook, 1981). The grounding line might be prone to up-glacier retreat because of high basal melt rates (12–15ma–1) along the floating part of Byrd Glacier (Reference Kenneally and HughesKenneally and Hughes, 2004), a process that has been observed on other glaciers with floating tongues (Reference RignotRignot, 2001; Reference Rignot and JacobsRignot and Jacobs, 2002). In this study, the grounding line is identified (Fig. 6a) on the basis of changes in surface velocity (Fig. 7) and surface concavity (Fig. 6c). This grounding line is near the middle of the grounding zone identified by Reference Hughes and FastookHughes and Fastook (1981) and Reference BindschadlerBindschadler and others (2011) (dashed line in Fig. 6a).

Fig. 6. Byrd Glacier. (a) Landsat satellite image from 20 January 1990. Ice flow is from left to right. The grounding line position is shown in black (solid line; located by this study), along with the grounding line identified by Reference BindschadlerBindschadler and others (2011) (dashed line); the velocity profile used in Figure 7 is shown in white. (b) Ice velocity (m a–1) from an ASTER image pair (5 December 2005/28 January 2007), gridded to 1 km spacing. (c) Surface topography (m) derived from an ASTER image on 29 January 2001 and gridded to 1 km.
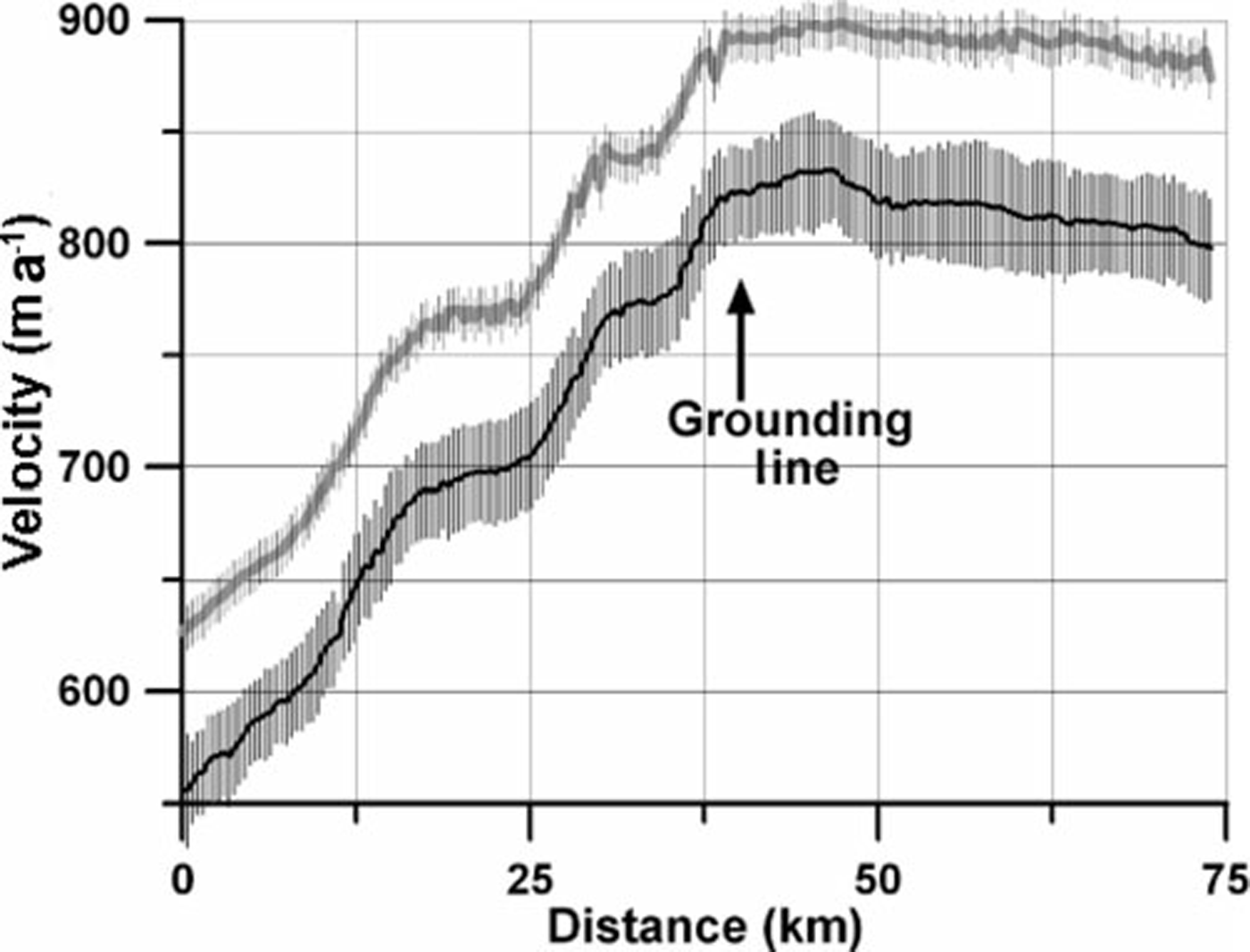
Fig. 7. Byrd Glacier ice velocity along the profile shown in Figure 6a. The thin black line represents the mean of seven pre-2005 ice velocity measurements (Reference Stearns, Smith and HamiltonStearns and others, 2008), with the vertical lines representing the standard deviation. The thicker grey curve represents the mean of ice velocity measurements (from four independent image pairs), derived during December 2005 and February 2007, when ice velocity was at its highest; the vertical lines represent the standard deviation.
The spatial pattern of ice velocity (Fig. 6b) can be explained by along-flow changes in surface topography (Fig. 7c). Ice velocity increases steadily along-flow in response to increases in surface slope (Fig. 7c). It peaks near the grounding line, and is concentrated towards the northern margin of the glacier. The velocity begins to decrease where linear flow switches to diverging shelf flow as the floating ice enters the Ross Ice Shelf.
Measurements from geodetic surveys (Reference SwithinbankSwithinbank, 1963), repeat photogrammetry (Reference BrecherBrecher, 1982) and satellite imaging techniques imply that flow speeds did not change between 1960 and 2005 (Fig. 7). Feature tracking performed on ASTER images acquired between December 2005 and January 2007 show accelerated flow speeds of ~80ma–1 (Reference Stearns, Smith and HamiltonStearns and others, 2008). The speed-up extends from the floating tongue to >75km inland (Fig. 7). The acceleration, which began in late 2005, coincided with the inferred drainage of two subglacial lakes, located 200 km up-flow of the grounding line (Reference Stearns, Smith and HamiltonStearns and others, 2008). Based on Ice, Cloud and land Elevation Satellite (ICESat) observations, the lakes began refilling in late 2007; at the same time Byrd Glacier returned to its pre-acceleration speed. The discrete shift in flow speeds is illustrated in Figure 7.
There is currently no observed thinning on the grounded portion of Byrd Glacier, according to the differencing of ASTER DEMs. Reference Schenk, Csatho, van der Veen, Brecher, Ahn and YoonSchenk and others (2005) detect thinning of 10–30m on the floating part of the glacier by comparing 1978 elevations from photogrammetry (Reference BrecherBrecher, 1982) with 2004 elevations from ICESat. Assuming a constant rate of change, an elevation change of 2.4–7.2m is expected during the 2005–07 glacier speed-up, but this elevation change is too small to be detected with ASTER DEMs. Localized thinning exists in some parts of the Byrd catchment (Reference Wingham, Shepherd, Muir and MarshallWingham and others, 2006; Reference HelsenHelsen and others, 2008; Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009), and thickening is found in other regions (Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005; Reference Wingham, Shepherd, Muir and MarshallWingham and others, 2006), but both trends are small and were determined using altimetry data that pre-date the acceleration of Byrd. Catchment-wide estimates suggest overall balance (Reference Wingham, Shepherd, Muir and MarshallWingham and others, 2006; Reference HelsenHelsen and others, 2008; Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009), although in each study only a fraction of the whole catchment contained data. Results from GRACE show no apparent mass change in this region of East Antarctica (Reference RamillienRamillien and others, 2006; Reference Chen, Wilson, Blankenship and TapleyChen and others, 2009).
Nimrod Glacier
Nimrod Glacier (82.5˚S, 160.2˚E) consists of two tributaries which merge ~50 km from the Ross Ice Shelf (Fig. 8a). The contour plots in Figure 8 show ice velocity and surface elevation gridded to 1 km. The DEM of Nimrod Glacier reveals steep slopes on the tributaries and flatter gradients farther down-glacier. Valley walls reduce the width of the glacier by ~45% just below the confluence of the tributaries. This sudden narrowing causes a noticeable increase in velocity from ~400ma–1 to ~600ma–1 (Fig. 8a). Velocity decreases as the glacier widens and its slope decreases in the down-flow direction (Fig. 8c).

Fig. 8. Nimrod Glacier. (a) ASTER satellite image from 21 November 2001, with the grounding line (black line) and velocity profile (white line) for Figure 9 overlain. Ice flow is from left to right. (b) Ice velocity (m a–1) from an ASTER image pair (28 January 2001/ 21 November 2001), gridded to 1 km. (c) Surface topography (m) derived from the ASTER image in (a) and gridded to 1 km.
There is no detectable change in ice speed on Nimrod Glacier. Reference SwithinbankSwithinbank (1963) conducted geodetic measurements on the floating portion of Nimrod Glacier in 1960–61. His results are not significantly different (Fig. 9) from velocity measurements derived from an ASTER image pair on 30 November 2004/15 December 2006, which is the only pair to overlap with his survey line. Ice velocity does not appear to change between 2001 and 2006, except for a slight acceleration from 238±13ma–1 to 264∓11 ma–1 at the grounding line (Fig. 9).
Fig. 9. Nimrod Glacier ice velocity derived from repeat geodetic measurements in 1960–61 by Reference SwithinbankSwithinbank (1963) and ASTER imagery from 2001 to 2006. Grounding line, derived from changes in ASTER-derived surface slopes, is at x≈30 . Error bars for each image pair are shown in the legend (dates are mm/dd/yyyy).
The surface elevation of the grounded portion of Nimrod Glacier did not change from 2000 to 2006 (Reference StearnsStearns, 2007). Past the grounding line, there appears to be slight (12.6∓4.7 ma–1) thinning between 2000 and 2006. The net mass balance of Nimrod Glacier is 0.88∓0.39 Gt a–1, suggesting it is roughly in balance with its catchment-wide accumulation.
Mass balance
The mass-balance estimates for each glacier basin are listed in Table 1. Accumulation rates, b, are from the surface mass-balance compilation of Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others (2006).
Table 1. Mass-balance results using accumulation estimates from Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others (2006). Areas in parentheses are catchment areas. The year refers to the velocity data used to calculate fluxes. Variables are defined in Equation (1). The bottom two rows list mass-balance estimates derived from this study (Ṁ Stearns) and Reference Rignot and ThomasRignot and Thomas (2002) (Ṁ Rignot). The Reference Rignot and ThomasRignot and Thomas (2002) study did not include Nimrod Glacier (NA = not available)
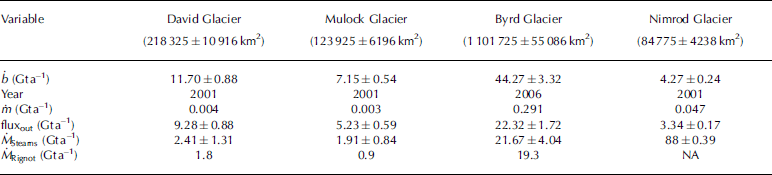
The mass-balance results for David, Mulock and Nimrod glaciers all seem reasonable, given the general consistency in flow speed over the past few decades (Reference SwithinbankSwithinbank, 1963; Reference FrezzottiFrezzotti, 1993) and the lack of large elevation changes in the altimetry record (Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005; Reference Wingham, Shepherd, Muir and MarshallWingham and others, 2006). The large positive balance for Byrd Glacier is a surprise; possible explanations are considered in the next section.
Discussion
The input–output method of computing mass balance is sensitive to spatial variations in accumulation rate. Antarctic accumulation rate compilations rely on an irregular, low-density distribution of surface mass-balance measurements to guide the interpolation of low-resolution model output (Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others, 2006) or remote-sensing observations (Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others, 1999; Reference Arthern, Winebrenner and VaughanArthern and others, 2006). For the ~1.5±106 km2 catchment areas of David, Mulock, Byrd and Nimrod glaciers, there are <100 field measurements, and derived accumulation maps show large inter-map variability. The effect of inter-map variability is explored in Table 2 by assuming that each glacier is in steady state and then computing balance velocities (ū balance) required to discharge the mass prescribed by different compilations.
Table 2. Balance velocity (ū balance) estimates derived from three surface mass-balance compilations, compared to observed velocities (ūobserved). The fluxout for Byrd Glacier is estimated using velocities derived in 2006
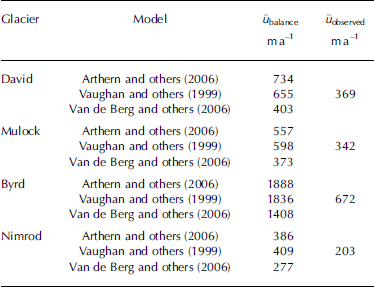
Observed velocities (in Table 2) are those derived from remote-sensing techniques described in the text. Balance velocities based on the Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999) and Reference Arthern, Winebrenner and VaughanArthern and others (2006) accumulation rates are similar to one another, but consistently infer higher velocities than those observed. The differences in balance velocity are a function of the methods used to produce the compilations. Both Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999) and Arthern and others (2006) use satellite microwave radiometry (6.9 and 35 GHz, respectively) to extend the spatial distribution of surface measurements. Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others (2006) use a regional climate model, calibrated by field measurements, to produce their surface mass-balance map.
Table 2 shows that balance velocities computed using accumulation rates from Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others (2006) consistently come closest to the observed velocities. The higher balance velocities required by the Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999) and Reference Arthern, Winebrenner and VaughanArthern and others (2006) datasets imply that these compilations overestimate catchment-wide accumulation rates, at least in this part of Antarctica. Reference Le Brocq, Payne and VieliLe Brocq and others (2010) note the reverse seems to be the case on a continent-wide basis, i.e. Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others (2006) produce higher accumulations than Vaughan and others (1999) and Reference Arthern, Winebrenner and VaughanArthern and others (2006).
In addition, Reference MagandMagand and others (2007) suggest that, for a sector of East Antarctica from 90˚E to 180˚E, >40% of the point measurements that constrain the surface mass-balance compilations are unreliable due to lack of quality control and measurement accuracy. Regional accumulation rates change significantly when the unreliable data points are removed (Reference MagandMagand and others, 2007). The greatest change is above 3000 m, where there is a 20–30% reduction (Reference MagandMagand and others, 2007) in snow accumulation from the original compilations of Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999), Reference Arthern, Winebrenner and VaughanArthern and others (2006) and Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others (2006).
Discrepancies between ground-based measurements and accumulation compilation maps have been quantified for David Glacier basin, where Reference Frezzotti, Urbini, Proposito, Scarchilli and GandolfiFrezzotti and others (2007) found wind-driven sublimation can account for 20–75% of solid precipitation in high-slope areas. Similarly, preliminary results from a 2005 overland traverse in East Antarctica suggest that field–based measurements are 30–40% lower (personal communication from D. Dixon, 2008) than estimates by Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999) and Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others (2006) in the same area. While differences between isolated field measurements and coarse-resolution continent-scale compilations are to be expected (Reference Arthern, Winebrenner and VaughanArthern and others, 2006), consistent and large discrepancies between independent compilations denote caution should be used when estimating the mass balance of individual drainage basins. Wind-driven ablation is an important mass loss process in most of East Antarctica (Reference Scarchilli, Frezzotti, Grigioni, De Silvestri, Agnoletto and DolciScarchilli and others, 2010); this parameter is also difficult to quantify in surface accumulation maps. It is likely that accumulation overestimates, particularly in low-accumulation regions like East Antarctica, are due to the lack of constraints on wind-driven processes. A new model-based compilation (Reference Lenaerts, van den Broeke, van de Berg, van Meijgaard and Kuipers MunnekeLenaerts and others, in press), which accounts for snowdrift physics, reveals generally smaller snow accumulation values on the East Antarctic plateau.
Other possible explanations for the calculated imbalance of Byrd Glacier are explored below, but none of them are as plausible as the aforementioned overestimates in accumulation rate.
-
1. The calculated mass gain (21.67∓4.04 Gt a–1; Table 1) would be viable if Byrd Glacier were thickening at a rate of ~6 cma–1 throughout its catchment. Satellite radar altimetry maps for the period 1992–2003 show slight thickening (0.0–0.4 cma–1) in parts of the Byrd catchment (Reference Davis and FergusonDavis and Ferguson, 2004; Reference Wingham, Shepherd, Muir and MarshallWingham and others, 2006), but this is well below the inferred rate mentioned above. Reference Davis, Li, McConnell, Frey and HannaDavis and others (2005) infer an increase in snowfall in several East Antarctic catchments between the early and late 1990s, by comparing radar altimetry measurements in 1992, 1995 and 2000. However, the Byrd Glacier catchment has a net thinning of –1.0± 1.2 cma–1 in that study (Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005). Their overall thinning, which is enhanced at the margins, is also detected with ICESat elevation change estimates (Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009). An analysis of repeat ASTER DEMs over Byrd shows no elevation change, although the uncertainties are large.
-
2. In order to accommodate the large ḃ suggested in the compilations, Byrd Glacier would need to be flowing almost twice as fast as currently measured (Table 2). In Table 1, the mass balance of Byrd Glacier is reported using velocities derived during its speed-up (Reference Stearns, Smith and HamiltonStearns and others, 2008), not during the time of steady flow. This is to show that, even when Byrd Glacier accelerated by 80 ma–1, it did not flow fast enough to get rid of the snow accumulation estimated from various surface mass-balance compilations. The positive mass imbalance, using pre-acceleration velocities, is even larger (23.63∓4.02 Gt a–1). There is no evidence in the velocity record (1963–2004; Fig. 7) of an earlier phase of sustained and enhanced ice discharge, suggesting that the glacier was in steady state with catchment accumulation during this time period.
-
3. An erroneously high catchment-wide accumulation rate could be the result of an overestimated catchment area. In this study, the Byrd Glacier catchment basin was delineated using a continental DEM (Reference Liu, Jezek and LiLiu and others, 1999) and RADARSATimagery to map the ice divides and flow directions. The catchment basin area, estimated to be 1 101 725∓55 086 km2, is consistent with an estimate of 1 070 400km2 by Reference Rignot and ThomasRignot and Thomas (2002). Given an average ḃ value of 400 mma–1 (Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others, 2006), the Byrd catchment would need to be less than two-thirds its size (~600 000 km2) to be in steady state with its calculated fluxout.
-
4. An inaccurate ice thickness at the grounding line could lead to an underestimated fluxout component of the balance equation, and a calculated positive imbalance. However, the flux gate would need to be almost twice as large (71.3km2, and not 34.3 km2) in order for Byrd Glacier to be in balance with the prescribed accumulation rates; since the fjord walls do not accommodate widening, this would mean 1350m thicker ice, which is clearly implausible.
The simplest explanation for Byrd Glacier’s calculated imbalance is that a small overestimate in accumulation rate leads to a large error in mass input when scaled to the glacier’s large catchment.
Conclusions
Outlet glaciers flowing through the Transantarctic Mountains are important pathways for ice to drain from the EAIS into the Ross Ice Shelf. Mass balance computed using the flux method indicates small positive balances for David (2.41∓1.31 Gt a–1), Mulock (1.91∓0.84 Gt a–1) and Nimrod (0.88∓0.39 Gt a–1) glaciers (Table 1). These results are consistent with Reference Rignot and ThomasRignot and Thomas (2002) for all but David Glacier, where Reference Rignot and ThomasRignot and Thomas (2002) estimate a negative balance of 2Gt a–1. This difference is probably due to discrepancies in surface accumulation estimates. The results also highlight a large imbalance for Byrd Glacier (21.67∓4.04 Gt a–1) which is likely due to overestimated catchment-wide accumulation rates. In order to improve basin-wide mass-balance estimates, additional accumulation and ice thickness measurements are needed.
Acknowledgements
This work is an extension of work that L.A.S. did as part of her PhD thesis at the University of Maine. G.S. Hamilton provided invaluable support throughout the project. This work was supported by NASA’s Cryospheric Sciences Program through NNG04-GK39G (G.S. Hamilton) and a NASA Earth Systems Science Fellowship (L.A.S.). I thank C. Swithinbank for providing raw data and maps from his 1961 Antarctic field season; B. Lucchitta and T. Hughes for providing Landsat TM4 scenes of Byrd Glacier; and W.-J. van de Berg and J. Lenaerts for generously sharing their modeled surface mass-balance data for this study. Two anonymous reviewers and associate editor D. van As provided comments which greatly improved the manuscript.
Appendix
Images used in this paper.