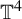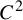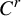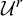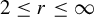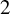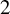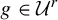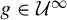1 Introduction and results
Shub introduced in [Reference Shub and Chillingworth26] an example of a diffeomorphism on
$\mathbb T^4$
which is very important in smooth dynamics: it is the first example of a diffeomorphism which is robustly transitive and it is not uniformly hyperbolic. Later, Mañé [Reference Mañé19] also built an example of a robustly transitive but non-hyperbolic diffeomorphism, this time on
${\mathbb T}^3$
. Both examples belong to the class of partially hyperbolic diffeomorphisms, Shub’s example has center dimension 2, while Mañe’s example has center dimension 1 (for the definition of partial hyperbolicity, see §1.1).
There are many works addressing further properties of Mañe’s examples, and there is a fairly good understanding of their dynamics. The Shub’s example was also studied, but mainly under the restrictive condition that the center bundle has a dominated splitting into two one-dimensional sub-bundles. In this paper, we are interested in the general Shub’s examples, in particular, we do not assume that the maps admit a further domination of the center bundle. This lack of further domination makes it an interesting class of maps, because we cannot use one-dimensional techniques; however, we will see that we may have enough hyperbolicity within these systems to obtain a good understanding of their ergodic properties.
In this paper, we will consider a slightly more general class than the original setting of the Shub’s example, a precise definition is the following.
1.1 Shub class
Definition 1.1. A diffeomorphism
$f: M\to M$
is called partially hyperbolic if the tangent bundle admits a continuous
$Df$
-invariant splitting
$TM = E^s \oplus E^c\oplus E^u$
such that there exist continuous functions
$0<\unicode{x3bb} _s(x)<\unicode{x3bb} _c^-(x)\leq \unicode{x3bb} _c^+(x)<\unicode{x3bb} _u(x)$
, with
$\unicode{x3bb} _s(x)<1<\unicode{x3bb} _u(x)$
, satisfying the following conditions:
-
(1)
$\|Df(x)v^s\|\leq \unicode{x3bb} _s(x)$
; -
(2)
$\unicode{x3bb} _c^-(x) \leq \|Df(x) v^c\| \leq \unicode{x3bb} _c^+(x)$
; -
(3)
$\| Df(x) v^u\|\geq \unicode{x3bb} _u(x)$
,
for every
$x\in M$
and unit vectors
$v^i \in E^i(x)(i = s, c, u$
).
A partially hyperbolic diffeomorphism is called dynamically coherent if there exist invariant foliations
${\mathcal F}^{cs}$
and
${\mathcal F}^{cu}$
tangent to
$E^{cs} = E^c \oplus E^s$
and
$E^{cu} = E^c \oplus E^u$
. In this case,
${\mathcal F}^{cs}$
is subfoliated by the stable and central foliations
${\mathcal F}^s$
and
${\mathcal F}^c$
, while
${\mathcal F}^{cu}$
is subfoliated by the unstable and center foliations
${\mathcal F}^u$
and
${\mathcal F}^c$
.
Let
$A, B$
be two linear Anosov automorphisms on
${\mathbb T}^2$
such that
$1<|\unicode{x3bb} _B|<|\unicode{x3bb} _A|$
, where
$\unicode{x3bb} _A$
and
$\unicode{x3bb} _B$
are the unstable eigenvalues of A and B. Then
$f_{A,B}: {\mathbb T}^2\times {\mathbb T}^2 \to {\mathbb T}^2\times {\mathbb T}^2 $
$$ \begin{align*}f_{A,B}(x,y)=(A(x),B(y))\end{align*} $$
is an Anosov automorphism, which can also be seen as a partially hyperbolic diffeomorphism with two-dimensional center bundle, and one-dimensional stable and unstable bundles.
Definition 1.2. Let
$\operatorname {PH}_{A,B}$
be the set of partially hyperbolic diffeomorphisms isotopic to
$f_{A,B}$
, all of them having the same dimension (that is, one dimension) of the stable and unstable bundle, and let
$\operatorname {PH}_{A,B}^0$
be the connected component of
$\operatorname {PH}_{A,B}$
containing
$f_{A,B}$
.
It is easy to see that
$\operatorname {PH}_{A,B}^0$
is an open set of diffeomorphisms of
${\mathbb T}^4$
. The following proposition is known.
Proposition 1.3. (Fisher, Potrie, and Sambarino [Reference Fisher, Potrie and Sambarino11])
If
$f\in \operatorname {PH}_{A,B}^0$
, then f is dynamically coherent and admits a center foliation where all central leaves are
$C^1$
two-dimensional tori, and f is center leaf conjugate to
$f_{A,B}$
.
Definition 1.4. The Shub class
$\mathcal {SH}\subset \bigcup _{1<\unicode{x3bb} _B<\unicode{x3bb} _A}\operatorname {PH}_{A,B}^0$
is the set of partially hyperbolic diffeomorphisms f of
${\mathbb T}^4$
such that f belongs to some
$\operatorname {PH}_{A,B}^0$
and there exists a fixed point
$p_f=f(p_f)\in {\mathbb T}^4$
, such that
$f\mid _{{\mathcal F}^c_{f}(p_f)}$
is an Anosov diffeomorphism, where
${\mathcal F}^c_{f}(p_f)$
is the (fixed) center leaf passing through
$p_f$
. Also let
$$ \begin{align*} \mathcal {SH}^r:=\{f\in\mathcal {SH}:\ f \mbox{ is } C^r\},\quad r\geq 1. \end{align*} $$
Although this part will not be used in the proof, through analyzing the induced map on the fundamental group, it is easy to show that
$f\mid _{{\mathcal F}^c_f(p_f\!)}$
is topological conjugate to B. Shub proved the following.
Theorem 1.5. (Shub [Reference Shub and Chillingworth26])
$\mathcal {SH}$
is
$C^1$
open and every
$f\in \mathcal {SH}$
is transitive.
Shub proved this result for some specific examples, but the proof can be adapted for the Shub class of diffeomorphisms with minor modifications. In this article, we consider the class of Shub diffeomorphisms which also satisfy some bunching conditions.
Definition 1.6. The bunched Shub class
$\mathcal {SH}^r_b$
is the set of partially hyperbolic diffeomorphisms
$f\in \mathcal {SH}^r$
which also satisfy the following bunching conditions:
-
(a) global bunching,
(1) -
(b) stronger local bunching at the fixed center leaf
${\mathcal F}^c_f(p_f\!)$
, (2)and(3)
Clearly,
$\mathcal {SH}^r_b$
is a
$C^1$
open set.
Remark 1.7. The condition in equation (1) implies (see [Reference Pugh, Shub and Wilkinson24]) that if f is
$C^2$
, then the stable and unstable bundles are
$C^1$
when restricted to the center-stable and center-unstable leaves, and, as a consequence, the strong stable and strong unstable holonomies between the center leaves are of class
$C^1$
(when restricted to the center-stable respectively center-unstable leaves). We will see later that, in fact, these holonomies depend continuously in the
$C^1$
topology with respect to the points (or the center leaves) and with respect to the map f (in the
$C^2$
topology).
Remark 1.8. The condition in equation (2) is the standard 2-bunching condition, and [Reference Hirsch, Pugh and Shub13] implies that if f is
$C^2$
, then
${\mathcal F}^c_f(p_f\!)$
,
${\mathcal F}^{cs}_f(p_f\!)$
, and
${\mathcal F}^{cu}_f(p_f\!)$
are of class
$C^2$
. If the central bounds are symmetric, or
$\unicode{x3bb} _c^-\unicode{x3bb} _c^+=1$
, then it is equivalent to the global bunching condition in equation (1).
The condition in equation (3) gives us better regularity of the strong foliations corresponding to the fixed Anosov leaf
${\mathcal F}^c_f(p_f\!)$
. In particular, if f is
$C^3$
, then the strong stable foliation
${\mathcal F}^s_f$
restricted to the center-stable manifold
${\mathcal F}^{cs}_f(p_f\!)$
is of class
$C^2$
, and the strong unstable foliation
${\mathcal F}^u_f$
restricted to the center-unstable manifold
${\mathcal F}^{cu}_f(p_f\!)$
is also of class
$C^2$
(see [Reference Pugh, Shub and Wilkinson24]).
1.2 Results
The homoclinic intersections between hyperbolic periodic points were first observed by Poincaré, and, since then, they play an important role in the theory of dynamical systems. Smale [Reference Smale27] used them to define homoclinic classes.
Definition 1.9. Given two hyperbolic periodic points
$p, q$
of the diffeomorphism f, with the same stable index, we say that they are homoclinically related if their stable and unstable manifolds intersect transversally:
$$ \begin{align} W^s(p)\pitchfork W^u(q)\neq \emptyset \quad\text{and}\quad W^s(q)\pitchfork W^u(p)\neq \emptyset. \end{align} $$
We say that
$\mathrm {Orb}(p)$
and
$\mathrm {Orb}(q)$
are homoclinically related if
$$ \begin{align} W^s(\mathrm{Orb}(p))\pitchfork W^u(\mathrm{Orb}(q))\neq \emptyset \quad\text{and}\quad W^s(\mathrm{Orb}(q))\pitchfork W^u(\mathrm{Orb}(p))\neq \emptyset. \end{align} $$
This is an equivalence relation between hyperbolic periodic orbits. The homoclinic class of
$\mathrm {Orb}(p)$
,
$HC(\mathrm {Orb}(p))$
, is the closure of the equivalence class of
$\mathrm {Orb}(p)$
.
For diffeomorphisms in the Shub class, the center bundle may not admit a dominated splitting, which means that the diffeomorphisms may not have a dominated splitting of index 2. If a diffeomorphism has no dominated splitting of index 2, it seems unexpected that any two hyperbolic points of stable index
$2$
are homoclinically related to each other. Indeed, the sizes of stable and unstable manifolds of the hyperbolic periodic points are non-uniform, and the intersection in equation (5) can be empty. However, even if the intersection is non-empty, the intersection may not be transverse, because of the lack of domination (see [Reference Pujals and Sambarino25]).
The main result of this paper is the following.
Theorem A. For any
$2\leq r\leq \infty $
, there exists a
$C^2$
open and
$C^r$
dense subset
${\mathcal U}^r\subset \mathcal {SH}^r_b$
, such that for any
$f\in {\mathcal U}^r$
, holds the following: every pair of hyperbolic periodic points of f with stable index
$2$
are homoclinically related.
As a consequence, any diffeomorphism
$f\in {\mathcal U}^r$
admits a unique homoclinic class associated to the hyperbolic periodic points of index
$2$
. Denote by
$p_f$
a hyperbolic fixed point of
$f\in {\mathcal U}^r$
.
Corollary B. For any
$f\in {\mathcal U}^r$
, f admits a unique homoclinic class
$H(p_f,f)$
associated to the hyperbolic periodic points of index
$2$
, and the homoclinic class coincides with the ambient manifold.
For a continuous potential
$\phi $
and a continuous map f, an f-invariant probability measure
$\mu $
is called an equilibrium measure for the potential
$\phi $
, if
$$ \begin{align*}h_\mu(f) + \int \phi\, d\mu = P_{\mathrm{top}}(\phi),\end{align*} $$
where
$P_{\mathrm {top}}(\phi ) := \sup _{\nu \in {\mathcal M}_e(f)}\{h_\nu (f) + \int \phi \,d\nu \}$
.
The equilibrium states do not necessarily exist. Assuming entropy expansiveness, Bowen [Reference Bowen4] proved the equilibrium states do exist. It was shown by Liao, Viana, and Yang [Reference Liao, Viana and Yang18] that any diffeomorphism away from homoclinic tangencies is entropy expansive. Yomdin [Reference Yomdin31] (see also Buzzi [Reference Buzzi6]) proved also that for any
$C^\infty $
diffeomorphism, equilibrium states always exist.
The uniqueness of equilibrium states is a more subtle problem. Recently, Climenhaga and Thompson [Reference Climenhaga and Thompson9] (see also Pacifico, Yang, and Yang [Reference Pacifico, Yang and Yang23]) gave a criterion based on Bowen property and specification. Another method used by Buzzi, Crovisier, and Sarig [Reference Buzzi, Crovisier and Sarig7] (see also Ben Ovadia [Reference Ben Ovadia2, Reference Ben Ovadia3]) is based on the use of the homoclinic class of measures.
Definition 1.10. Suppose f is a
$C^r$
diffeomorphism for some
$r>1$
. For two ergodic hyperbolic measures
$\mu _1$
and
$\mu _2$
of f, we write
$\mu _1 \preceq \mu _2$
if and only if there exist measurable sets
$A_1, A_2 \subset M$
with
$\mu _i(A_i)> 0$
such that for any
$x_1\in A_1$
and
$x_2\in A_2$
, the manifolds
$W^u(x_1)$
and
$W^s (x_2)$
have a point of transverse intersection.
Here,
$\mu _1$
,
$\mu _2$
are homoclinically related if
$\mu _1 \preceq \mu _2$
and
$\mu _2\preceq \mu _1$
. We write
$\mu _1 \overset {h}{\sim } \mu _2$
. The set of ergodic measures homoclinically related to a hyperbolic ergodic measure
$\mu $
is called the measured homoclinic class of
$\mu $
.
Remark 1.11. The homoclinic relation is an equivalence relation, moreover, two atomic measures supported on two periodic orbits are homoclinically related if and only if the two periodic orbits are hyperbolic and homoclinically related.
We have the following theorem. For a discussion on the index of hyperbolic measures, see §§2.3 and 2.4.
Theorem C. For any
$f\in {\mathcal U}^r$
, all the hyperbolic ergodic measures of index
$2$
are homoclinically related. Let
$\phi :{\mathbb T}^4\rightarrow \mathbb R$
be any Hölder potential function with
$\max _{x,y\in {\mathbb T}^4}\|\phi (x)-\phi (y)\|<\log \unicode{x3bb} _B$
, where
$f\in \operatorname {PH}_{A,B}^0$
, then f admits at most one equilibrium state for the potential
$\phi $
. In particular, every
$f\in {\mathcal U}^r$
admits at most one measure of maximal entropy.
A direct consequence of [Reference Buzzi6, Reference Yomdin31] is the following.
Corollary D. Every
$f\in {\mathcal U}^{\infty }\cap \operatorname {PH}_{A,B}^0$
admits a unique equilibrium state for every Hölder potential satisfying
$\max _{x,y\in {\mathbb T}^4}\|\phi (x)-\phi (y)\|<\log \unicode{x3bb} _B$
. In particular, every
${f\in {\mathcal U}^{\infty }}$
admits a unique measure of maximal entropy.
For Shub’s example, some similar results were obtained under some extra assumptions. For instance, by Newhouse and Young [Reference Newhouse and Young21] and Carvalho and Pérez [Reference Carvalho and Pérez8], with the extra assumption that within the center foliation there exists a one-dimensional invariant sub-foliation, and by Álvarez [Reference Álvarez1], assuming that the center bundle admits a further dominated splitting. For other partially hyperbolic diffeomorphisms on
$\mathbb T^4$
, there are results on the uniqueness of u-Gibbs states in [Reference Crovisier, Obata and Poletti10, Reference Obata22].
2 Preliminaries
2.1 Stable and unstable holonomies between center leaves
As we mentioned before, the condition in equation (1) implies that the holonomies between the center leafs are uniformly
$C^1$
. In fact, there exists a continuity of the holonomies in the
$C^1$
topology. If
$y\in {\mathcal F}^u_f(x)$
, let us denote by
$h_{f,x,y}^u:{\mathcal F}^c_f(x)\rightarrow {\mathcal F}^c_f(y)$
the unstable holonomy between the two center leaves. Since it is of class
$C^1$
, the derivative
$Dh_{f,x,y}^u$
induces a continuous map between the unit tangent bundles
$Dh_{f,x,y*}^u:T^1{\mathcal F}^c_f(x)\rightarrow T^1{\mathcal F}^c_f(y)$
.
Lemma 2.1.
$Dh_{f,x,y*}^u$
is continuous with respect to
$f\in \mathcal {SH}^2_b$
(the
$C^2$
topology) and
$x,y\in {\mathbb T}^4,\ \ y\in {\mathcal F}^u_f(x)$
. The same holds for the stable holonomy.
Remark 2.2. The continuity in Lemma 2.1 means that if
$f_n$
converges to f in the
$C^2$
topology,
$x_n$
converges to x in
${\mathbb T}^4$
, and
$y_n\in {\mathcal F}^u_{f_n, loc}(x_n)$
converges to y, then
$Dh_{f_n,x_n,y_n*}^u$
converges uniformly to
$Dh_{f,x,y*}^u$
. The proof requires only the weaker global condition in equation (1).
Remark 2.3. Since, in our case, the stable and unstable bundles are one-dimensional, one could approach the continuity question using the classical ordinary differential equation (ODE) theory of the regularity of solutions with respect to the initial conditions and parameters. We prefer to present a different proof which constructs the projectivized holonomies as unstable foliations of the projectivization of f along the center bundle.
Proof. Let
$T^1{\mathbb T}^4$
be the unit tangent bundle of
${\mathbb T}^4$
(which can be identified with
${\mathbb T}^4\times \mathbb S^3$
) with
$Df_*$
being the
$C^1$
diffeomorphism induced by f. We will consider the central unit tangent bundle
$S_f:=\bigcup _{x\in {\mathbb T}^4}S(f,x)$
, where
$S(f,x)=T_x^1{\mathcal F}^c_f(x)$
is the unit circle in
$E^c_f(x)$
. Then,
$S_f$
is a Hölder submanifold of
$T^1{\mathbb T}^4$
invariant under
$Df_*$
, which is also a Hölder bundle over
${\mathbb T}^4$
.
We claim that there exists a continuous unstable foliation on
$S_f$
and that
$Dh_{f,x,y*}^u$
is exactly the unstable holonomy for this foliation between the transversals
$T^1{\mathcal F}^c_f(x)$
and
$T^1{\mathcal F}^c_f(y)$
. We apply the standard construction of the local unstable leaves as the invariant section of a bundle contraction map (see [Reference Hirsch, Pugh and Shub13] for example), with a minor difficulty arising from the lack of smoothness.
For any
$x,y\in {\mathbb T}^4$
, we define the
$\pi _{f,y,x}:E^c_f(y)\rightarrow E^c_f(x)$
as the projection parallel to
$E^s_f(x)\oplus E^u_f(x)$
. The maps
$\pi _{f,y,x}$
depend continuously on
$x,y\in {\mathbb T}^4$
and f (in the
$C^1$
topology). For x close to y, this is invertible and close to the identity, and its projectivization
$\pi _{f,x,y*}$
is bi-Lipschitz with Lipschitz constant close to 1.
For
$\delta>0$
and
$x\in {\mathbb T}^4$
, let
$\alpha _{f,x}:[-\delta ,\delta ]\rightarrow {\mathcal F}^u_f(x)$
be the length parameterization of the local unstable manifold of f at x. Since the unstable foliation is orientable and depends continuously in the
$C^1$
topology with respect to x and f, we have that
$\alpha _{f,x}$
is continuous in x and f (in the
$C^1$
topology).
For any
$\delta>0$
, there exists
$\epsilon _{\delta }>0$
such that for any
$x,y$
such that
$d(x,y)<\delta $
, we have:
-
•
$\|\pi _{f,y,x}^{\pm 1}-\mathrm {Id}\|<\epsilon _{\delta }$
; -
•
$\pi _{f,y,x*}^{\pm 1}$
is bi-Lipschitz with constant
$(1+\epsilon _{\delta })$
; -
•
$(1+\epsilon _{\delta })^{-1}\unicode{x3bb} _c^-(x)<\unicode{x3bb} _c^-(y)\leq \unicode{x3bb} _c^+(y)<(1+\epsilon _{\delta })\unicode{x3bb} _c^+(x)$
. -
• If furthermore
$y\in {\mathcal F}^u_{f,\delta }(x)$
, then
$d_u(f(x),f(y))\geq (1+\epsilon _{\delta })^{-1}\unicode{x3bb} _u(x)d_u(x,y)$
, where
$d_u$
is the distance along the unstable leaves.
We can choose
$\epsilon _{\delta }$
independent of f in a
$C^1$
neighborhood and
$\lim _{\delta \rightarrow 0}\epsilon _{\delta }=0$
.
Now we will construct the bundle with the candidates for the local unstable manifolds in
$S_f\:\!$
. Consider
$\delta>0$
(small) to be specified later. Let
$$ \begin{align*} B=\bigg\{\sigma:[-\delta,\delta])\rightarrow \mathbb R:\ \sigma(0)=0,\ \bigg|\frac{\sigma(t)}{t}\bigg|<\infty\bigg\} \end{align*} $$
be the Banach space of functions
$\sigma $
bounded for the norm
$$ \begin{align*} \|\sigma\|=\sup_{t\in [-\delta,\delta]}\bigg|\frac{\sigma(t)}{t}\bigg|. \end{align*} $$
Then,
$$ \begin{align*} V(f):=S_f\times B \end{align*} $$
is a continuous (in fact, Hölder) Banach bundle over
$S_f$
.
Remark 2.4. The maps
$\sigma $
are candidates for unstable manifolds in
$S_f$
in the following sense. For any
$(x,v)\in S_f$
and
$\sigma \in B$
, we can define a section
$\tilde \sigma :{\mathcal F}^u_{f,\delta }(x)\rightarrow S_f$
in the following way:
$$ \begin{align*} \tilde\sigma(y):=\pi_{f,y,x*}^{-1}(v+\sigma(\alpha_{f,x}^{-1}(y)))\in S(f,y). \end{align*} $$
The graph of this section
$\tilde \sigma $
is a natural candidate for the local unstable manifold in
${(x,v)\in S_f}\:\!$
. We construct it as a fixed point of the natural graph transformation.
Let
$T:V(f)\rightarrow V(f)$
be the bundle map which fibers over
$Df_*$
on
$S_f$
and is given by
$$ \begin{align*} T\sigma_{(x,v)}(t)&=(\pi_{f,f(y(t)),f(x)}\circ Df(y(t))\circ\pi_{f,y(t),x}^{-1})_*(v+\sigma(\alpha_{f,x}^{-1}(y(t))))\\ &\quad-Df(x)_*(v),\\ y(t)&=f^{-1}\circ\alpha_{f,f(x)}(t). \end{align*} $$
One can check that in fact T is defined in such a way so that we have
$\tilde {T\sigma }=Df_*\tilde \sigma $
. Let us check that T is a continuous bundle map on
$V(f)$
, which is also a fiber contraction.
Claim 1. If
$\sigma \in B$
, then
$T\sigma _{(x,v)}\in B$
.
Proof. Remember that
$y(t)=f^{-1}\circ \alpha _{f,f(x)}(t)$
, and let us denote
$$ \begin{align*} G(t):=(\pi_{f,f(y(t)),f(x)}\circ Df(y(t))\circ\pi_{f,x,y}^{-1}). \end{align*} $$
Observe that
$G(t)_*$
is Lipschitz with the Lipschitz constant
Also,
Then,
where in the last line, we used the inequality
$$ \begin{align*} \bigg\|\frac a{\|a\|}-\frac b{\|b\|}\bigg\|\leq\bigg\|\frac a{\|a\|}-\frac a{\|b\|}\bigg\|+\bigg\|\frac a{\|b\|}-\frac b{\|b\|}\bigg\|\leq\frac 2{\|b\|}\|a-b\|. \end{align*} $$
Let us remark that if
$v\in E^c_f(x)$
, then
$\pi _{f,f(y(t)),f(x)}\circ Df(x)\circ \pi _{f,y,x}^{-1}(v)=Df(x)(v)$
, because the partially hyperbolic splitting is invariant under
$Df$
. Then,
Finally, we obtain the desired bound:
Claim 2. T is a fiber contraction.
Proof. We have
Now all we have to do is to choose
$\delta $
small enough so that
$\epsilon _{\delta }$
is close enough to zero so that we have
Claims 1 and 2 show that we are in the conditions of the invariant section theorem from [Reference Hirsch, Pugh and Shub13], so there exists a unique bounded continuous invariant section.
From [Reference Pugh, Shub and Wilkinson24], we know that the unstable holonomy along center leaves is uniformly differentiable. The projectivization of the derivative of this local holonomy will then correspond to a bounded invariant section for the transfer operator T, so it has to coincide with the unique continuous invariant section constructed above. This concludes the proof of the continuity of
$Dh^u_{f,x,y*}$
with respect to the points
$x,y$
(we proved it for
$d(x,y)<\delta $
, but this can be easily extended to larger distances).
If
$f_n$
converges to f, then
$S_{f_n}$
converges to
$S_f$
(this can be made explicit by projecting
$E_{f_n}^c$
to
$E^c_f$
parallel to
$E_f^s\oplus E_f^u$
for example). One can check that the corresponding transfer operators
$T_{f_n}$
also converge to
$T_f$
. Since the invariant section is continuous with respect to the bundle map, we obtain the continuity of
$Dh^u_{f,x,y*}$
with respect to f.
Remark 2.5. We gave the proof for our special setting, but the proof can be adapted to general partially hyperbolic diffeomorphisms in higher dimensions. We used that
$Df$
is Lipschitz to show that the transfer operator T verifies the conditions of the invariant section theorem. The proof can be adapted for f of class
$C^{1+\alpha }$
and the stronger bunching condition
$\unicode{x3bb} _s(x)^{\alpha }<{\unicode{x3bb} _c^-(x)}/{\unicode{x3bb} _c^+(x)}\leq {\unicode{x3bb} _c^+(x)}/{\unicode{x3bb} _c^-(x)}<\unicode{x3bb} _u(x)^{\alpha }$
, using the norm
$\|\sigma \|=\sup _{t\in [-\delta ,\delta ]}|{\sigma (t)}/{t^{\alpha }}|$
. Once one obtains the bounded invariant section for the projectivization
$Df_*$
on
$S_f$
, using the boundness of the Jacobian, one could try to obtain the differentiability of the stable/unstable holonomy along center leaves.
2.2 Homoclinic holonomies
Let
$f\in \mathcal {SH}^2_b$
and
$p_f$
be the fixed point such that
$f\mid _{{\mathcal F}^c_f(p_f\!)}$
is Anosov. We will drop the index f when it is not necessary to specify the dependence on the map f. From [Reference Hirsch, Pugh and Shub13] and the bunching conditions, we know that
${\mathcal F}^c(p), {\mathcal F}^{cu}(p)$
and
${\mathcal F}^{cs}(p)$
are
$C^2$
submanifolds. Assume that q is a homoclinic point of
$W^c(p)$
, that is,
$q\in {\mathcal F}^{cu}(p)\cap {\mathcal F}^{cs}(p)$
, then
$W^c(q)$
is also
$C^2$
as a connected component of the intersection of the transverse
$C^2$
submanifolds
${\mathcal F}^{cu}(p)$
and
${\mathcal F}^{cs}(p)$
. We can define the stable holonomy
$h_{p,q}^s:{\mathcal F}^c(p)\rightarrow {\mathcal F}^c(q)$
and the unstable holonomy
$h_{q,p}^u:{\mathcal F}^c(q)\rightarrow {\mathcal F}^c(p)$
, and they are both of class
$C^1$
. Then
$\tilde h_q:=h_{q,p}^u\circ h_{p,q}^s:{\mathcal F}^c(p)\rightarrow {\mathcal F}^c(p)$
is a
$C^1$
diffeomorphism, so it induces a
$C^0$
map on the unit tangent bundle
$T^1{\mathcal F}^c(p)$
which we denote by
$D\tilde h_{q*}$
.
Let
$\tilde v^s(x)$
be the unit vector tangent in
$x\in {\mathcal F}^c(p)$
to the stable bundle of
$f\mid _{{\mathcal F}^c(p)}$
(we fix an orientation). Since
$f\mid _{{\mathcal F}^c(p)}$
is a
$C^2$
Anosov map on a
$C^2$
surface, we have that
$\tilde v^s:{\mathcal F}^c(p)\rightarrow T^1{\mathcal F}^c(p)$
is
$C^1$
. We define the map
$\tilde g_{q}:{\mathcal F}^c(p)\rightarrow T^1{\mathcal F}^c(p)$
,
$$ \begin{align} \tilde g_{q}(x):=D\tilde h_{q*}(\tilde v^s(h_q^{-1}(x)))=\frac{D\tilde h_q(h_q^{-1}(x))\tilde v^s(h_q^{-1}(x))}{\|D\tilde h_q(h_q^{-1}(x))\tilde v^s(h_q^{-1}(x))\|}. \end{align} $$
Remark 2.6. In fact, we consider the stable foliation of
$f\mid _{{\mathcal F}^c(p)}$
inside the leaf
${\mathcal F}^c(p)$
, we first push it forward using the stable holonomy
$h_{p,q}^s$
to the leaf
${\mathcal F}^c(q)$
, and then we push it again using the unstable holonomy
$h_{q,p}^u$
back to the leaf
${\mathcal F}^c(p)$
. Then
$\tilde g_{q}(x)$
is in fact the unit tangent vector in x to this new foliation.
If furthermore
$f\in \mathcal {SH}^3_b$
, then the stable and unstable holonomies along the fixed center-stable leaf
$W^{cs}(p)$
and respectively the fixed center-unstable leaf
$W^{cu}(p)$
are
$C^2$
, so, in this case,
$D\tilde h_{q*}$
and
$\tilde g_q$
are in fact
$C^1$
.
If the map
$f'$
is
$C^2$
close to f, then the fixed Anosov center leaf
${\mathcal F}^c(p)$
and its homoclinic center leaf
${\mathcal F}^c(q)$
will have continuations
${\mathcal F}^c_{f'}(p(f'))$
and
${\mathcal F}^c_{f'}(q(f'))$
. Then we obtain the continuations of the stable holonomy
$h_{p(f'),q(f'),f'}^s:{\mathcal F}^c_{f'}(p(f'))\rightarrow {\mathcal F}^c_{f'}(q(f'))$
and the unstable holonomy
$h_{q(f'),p(f'),f'}^u:{\mathcal F}^c_{f'}(q(f'))\rightarrow {\mathcal F}^c_{f'}(p(f'))$
; they are
$C^1$
maps and depend continuously in the
$C^1$
topology with respect to
$f'$
(in the
$C^2$
topology). We also have a continuation of the homoclinic holonomy
$\tilde h_{q(f'),f'}:{\mathcal F}^c_{f'}(p(f'))\rightarrow {\mathcal F}^c_{f'}(p(f'))$
and also the continuation
$\tilde g_{q(f'),f'}:{\mathcal F}^c_{f'}(p(f'))\rightarrow T^1{\mathcal F}^c_{f'}(p(f'))$
, which is continuous both with respect to
$x\in {\mathcal F}^c_{f'}(p(f'))$
and with respect to
$f'\in \mathcal {SH}^2_b$
(in the
$C^2$
topology).
2.3 Hyperbolic measures
Let
$\mu $
be an ergodic measure of a diffeomorphism f, then by the theorem of Oseledets, for
$\mu $
-almost every point
$x\in M$
, there exist
$k(\mu )\in \mathbb {N}$
, real numbers
$\unicode{x3bb} _1(\mu )>\cdots \unicode{x3bb} _k(\mu )$
, and an invariant splitting
${T_xM=E^1(x)\oplus \cdots }\oplus E^k(x)$
of the tangent bundle at x, depending measurably on the point, such that
$\lim _{n\to \pm \infty } ({1}/{n})\log \|Df^n_x(v)\|=\unicode{x3bb} _j(\mu )$
for all
$0\neq v\in E^j(x)$
. The real numbers
$\unicode{x3bb} _j(\mu )$
are the Lyapunov exponents of
$\mu $
. We say that the ergodic measure
$\mu $
is hyperbolic if all the Lyapunov exponents of
$\mu $
are non-zero.
Theorem 2.7. (Katok’s horseshoe theorem [Reference Katok14])
For any
$f\in \mathrm {Diff}^r(M)$
,
$r>1$
and any hyperbolic ergodic measure
$\mu $
, there exists a hyperbolic periodic point p, such that
$\mu \overset {h}{\sim } \delta _{\mathrm {Orb}(p)}$
, where
$\delta _{\mathrm {Orb}(p)}$
is the ergodic measure supported on the orbit
$\mathrm {Orb}(p)$
.
If a diffeomorphism f admits a dominated splitting, then the Oseledet’s splitting must be subordinated to the dominated splitting. In particular, since every
$f\in \mathcal {SH}$
is partially hyperbolic on
$\mathbb {T}^4$
, then for any ergodic measure
$\mu $
of f, its biggest Lyapunov exponent is positive (
$\unicode{x3bb} ^u>0$
) and its associated Oseledet’s bundle is tangent to the strong unstable bundle
$E^u$
of f. A similar result holds for the minimal Lyapunov exponent
$\unicode{x3bb} ^s<0$
with its associated Oseledet’s bundle tangent to the strong stable bundle
$E^s$
. There are also two center Lyapunov exponents (counted with multiplicity)
$\unicode{x3bb} ^c_1\geq \unicode{x3bb} ^c_2$
whose associated Oseledet’s bundles are tangent to the center bundle
$E^c$
of f.
2.4 Criterion of uniqueness of equilibrium state
Definition 2.8. Let
$\mu $
be an ergodic hyperbolic measure of a diffeomorphism f. The stable index of
$\mu $
is the number of negative Lyapunov exponents, counted with multiplicity.
Proposition 2.9. Let
$f: M \to M$
be a
$C^r$
diffeomorphism
$r> 1$
,
$\phi :M\rightarrow \mathbb R$
be a Hölder potential, and p a hyperbolic periodic point. Then there is at most one equilibrium state for
$\phi $
which is homoclinically related to
$\delta _{Orb(p)}$
, and its support coincides with
$\mathrm {HC}(Orb(p))$
.
Proof. This is explained in [Reference Ben Ovadia3, Theorem 2.4] and [Reference Buzzi, Crovisier and Sarig7, §1.6]. See also [Reference Ben Ovadia2] and [Reference Buzzi, Crovisier and Sarig7, Corollary 3.3].
2.5 Hyperbolicity of equilibrium states
If
$f\in \operatorname {PH}_{A,B}^0$
, then standard results of Franks and Manning [Reference Franks12, Reference Manning20] imply that f is semi-conjugate to
$f_{A,B}$
, that is, there exists a continuous surjection
$h : \mathbb {T}^4\to \mathbb {T}^4$
homotopic to the identity such that
$f_{A,B}\circ h=h\circ f$
. By the Ledrappier–Walters variational principle [Reference Ledrappier and Walters16], we have
For any invariant probability measure
$\mu $
of f, we say that a measurable partition
$\xi $
is
$\mu $
adapted (sub-ordinated) to
${\mathcal F}^u$
if the following conditions are satisfied:
-
• there is
$r_0> 0$
such that
$\xi (x) \subset B^{{\mathcal F}^u}_{r_0}(x)$
for
$\mu $
almost every x, where
$B^{{\mathcal F}^u}_{r_0}(x)$
is a ball of
${\mathcal F}^u(x)$
with radius
$r_0$
; -
•
$\xi (x)$
contains an open neighborhood of x inside
${\mathcal F}^u(x)$
; -
•
$\xi $
is increasing, that is, for
$\mu $
almost every x,
$\xi (x)\subset f(\xi (f^{-1}(x)))$
.
The existence of such a partition was provided by [Reference Ledrappier and Strelcyn15] (see also [Reference Ledrappier and Young17, Reference Yang30]). The partial entropy of
$\mu $
along the expanding foliation
${\mathcal F}^u$
is defined by
$$ \begin{align*}h_\mu(f, {\mathcal F}^u) = H_\mu(f^{-1}\xi \mid \xi).\end{align*} $$
The definition of the partial entropy does not depend on the choice of the partition.
The following two lemmas are important for our further discussion.
Lemma 2.10. If
$f\in \operatorname {PH}_{A,B}^0$
, then
$h_\mu (f,{\mathcal F}^u)\leq \log \unicode{x3bb} _A$
.
Proof. Denote by
${\mathcal F}^c_f$
the center foliation of f. By Proposition 1.3, the projection map
$\pi ^c_f$
along the center foliation induces a topological Anosov homeomorphism
$\overline {f}$
on the quotient space
$\overline {{\mathbb T}}^2_f={\mathbb T}^4/{\mathcal F}^c_f$
, which is topological conjugate to A, so we may in fact identify
$\overline {{\mathbb T}}^2_f$
with
${\mathbb T}^2$
and
$\overline {f}$
with A.
Denote by
${\mathcal F}^s_A$
(respectively
${\mathcal F}^u_A$
) the stable (respectively unstable) foliation of A. The projection map
$\pi ^c_f$
maps each center unstable leaf
${\mathcal F}^{cu}$
of f to an unstable leaf
${\mathcal F}^u_A$
of A. In particular,
$\pi ^c_f$
maps every unstable leaf
${\mathcal F}^u$
of f to an unstable leaf
${\mathcal F}^u_A$
of A. Proposition 1.3 implies that all the hypotheses of Tahzibi and Yang [Reference Tahzibi and Yang28, Theorem A] are satisfied (see also [Reference Álvarez1, §2.5]), and this implies that
$h_\mu (f,{\mathcal F}^u)\leq h_{{\mathrm {top}}}(A)=\log \unicode{x3bb} _A$
.
The following lemma is a generalization of [Reference Álvarez1, Theorem A].
Lemma 2.11. Let
$f\in \operatorname {PH}_{A,B}^0$
be a
$C^r$
diffeomorphism,
$r>1$
, and
$\mu $
an ergodic invariant measure of f with
$h_\mu (f)> \log \unicode{x3bb} _A$
. Then
$\mu $
is a hyperbolic ergodic measure of f with stable index
$2$
, that is,
$\unicode{x3bb} ^c_1>0>\unicode{x3bb} ^c_2$
.
Proof. We will show that
$\unicode{x3bb} ^c_1>0$
. To prove that
$\unicode{x3bb} ^c_2<0$
, one only needs to consider the diffeomorphism
$f^{-1}$
instead of diffeomorphism f.
Suppose by contradiction that
$\unicode{x3bb} ^c_1\leq 0$
. The entropy formula of Ledrappier and Young (see [Reference Brown5, Reference Ledrappier and Strelcyn15]) implies that
$h_\mu (f)=h_\mu (f,{\mathcal F}^u)$
.
Combining with the previous lemma, we obtain that
$h_\mu (f)\leq \log \unicode{x3bb} _A$
, which is a contradiction with the hypothesis that
$h_\mu (f)>\log \unicode{x3bb} _A$
. The proof is complete.
3 Proof of Theorem A
3.1 Definition of
$\mathcal U^r$
and plan of the proof
Let us define the open set
$\mathcal U^r$
which is the candidate for the set
$\mathcal U^r$
in Theorem A. We recall that p is a fixed point for
$f\in \mathcal {SH}^r_b$
, and the restriction of f to the center leaf
${\mathcal F}^c(p)$
is Anosov. Here, q is a homoclinic point of
${\mathcal F}^c(p)$
if
$q\in {\mathcal F}^{cu}(p)\cap {\mathcal F}^{cs}(p)$
. The map
$\tilde g_q:{\mathcal F}^c(p)\rightarrow T^1{\mathcal F}^c(p)$
is defined by equation (6), and represents in fact the unit tangent vector to the foliation obtained by pushing the stable foliation of
$f\mid _{{\mathcal F}^c(p)}$
along the homoclinic loop corresponding to q.
Definition 3.1. Let
$\mathcal U_s^r\subset \mathcal {SH}^r_b$
,
$$ \begin{align} \mathcal U_s^r&=\{f\in \mathcal {SH}^r_b: \text{ for all } x\in {\mathcal F}^c(p), \text{ there exists } q \mbox{ homoclinic to }{\mathcal F}^c(p)\nonumber\\ &\qquad\mbox{such that } \tilde g_{q}(x)\neq \pm\tilde v^s(x)\}. \end{align} $$
In a similar way, we define
$\mathcal U_u^r$
. Let
$\mathcal U^r=\mathcal U_s^r\cap \mathcal U_u^r$
.
The definition of
$\mathcal U_s^r$
is given, in fact, by a transversality condition. What we ask is that the stable foliation of
$f\mid _{{\mathcal F}^c(p)}$
and its pushed forward by holonomies along homoclinic loops are transverse.
To prove Theorem A, we will have to show the following three facts:
-
(1) the set
$\mathcal U^r$
is
$C^2$
open; -
(2) the set
$\mathcal U^r$
is
$C^r$
dense; -
(3) the set
$\mathcal U^r$
verifies the conclusion of Theorem A, in other words, if
$f\in \mathcal U^r$
, then any two hyperbolic periodic points of f of index 2 are homoclinically related.
Consequently, the proof of Theorem A is divided into the following three propositions.
Proposition 3.2.
$\mathcal U^r$
is
$C^2$
open.
Proof. An immediate consequence of the compactness of
${\mathcal F}^c(p)$
and of the fact that the stable and unstable holonomies depend continuously in the
$C^1$
topology with respect to the points (see Remark 1.7) is the following lemma.
Lemma 3.3. Let
$f\in \mathcal {SH}^r_b$
. Then
$f\in \mathcal U_s^r$
if and only if there exist
$q_1,q_2,\ldots q_k$
homoclinic points of
${\mathcal F}^c(p)$
such that the image of
$\tilde g_{q_1}\times \tilde g_{q_2}\times \cdots \times \tilde g_{q_k}$
is disjoint from the image of
$\pm \tilde v^{s^k}$
.
However, the holonomies along the center leaves depend continuously in the
$C^1$
topology with respect to the map f (in
$C^2$
topology), so the images of
$\tilde g_{q_1}\times \tilde g_{q_2}\times \cdots \times \tilde g_{q_k}$
and
$\pm \tilde v^{s^k}$
depend continuously on the map f. Since these images are compact, this concludes the
$C^2$
openness of
$\mathcal U_s^r$
. The proof for
$\mathcal U_u^r$
is similar, so
$\mathcal U^r=\mathcal U_s^r\cap \mathcal U_u^r$
is
$C^2$
open.
Proposition 3.4.
$\mathcal U^r$
is
$C^r$
dense.
We will give the proof of the proposition in §3.2.
Proposition 3.5. If
$f\in \mathcal U^r$
, then any two hyperbolic periodic points of f of index 2 are homoclinically related.
We will give the proof of the proposition in §3.3. As we mentioned before, the proof of these three propositions will imply Theorem A.
3.2 Proof of
$C^r$
density
We will show that
$\mathcal U_s^r$
is
$C^r$
dense in
$\mathcal {SH}^r_b$
, the proof for
$\mathcal U_u^r$
is similar. Then
$\mathcal U^r$
will be
$C^r$
dense as the intersection of two
$C^r$
open dense sets.
The main perturbation result which we will use is the following lemma.
Lemma 3.6. Let
$f\in \mathcal {SH}^3_b$
. Let q be a homoclinic point of the fixed Anosov leaf
${\mathcal F}^c(p)$
. Then we have the following.
-
(1) For any
$C^2$
family
$(\phi _T)$
, where
$T\in \mathbb R^n$
is a parameter, of perturbations of the identity on
$\mathbb T^4$
(in other words,
$\phi _{0^n}=\mathrm {Id}_{\mathbb T^4}$
), supported in a neighborhood of
${\mathcal F}^c(q)$
disjoint from all the other iterates
$f^k({\mathcal F}^c(q)),\ k\in \mathbb Z\setminus \{0\}$
, the map
$(T,x)\mapsto \tilde g_{q(f\circ \phi _T),f\circ \phi _T}(x)$
is
$C^1$
on
$[-\delta ,\delta ]^n\times {\mathcal F}^c(p)$
for some
$\delta>0$
. -
(2) For any
$x_0\in {\mathcal F}^c(p)$
and any
$r_0>0$
, there exists a
$C^{\infty }$
family
$(\phi _t)_{t\in [-\delta ,\delta ]}$
of (volume-preserving) perturbations of the identity on
$\mathbb T^4$
, supported in
$B(y_0,r_0)$
where
$y_0:=h_{p,q}^u(x_0)\in {\mathcal F}^c(q)$
, such that (9)
$$ \begin{align} \frac{\partial}{\partial t}\tilde g_{q(f\circ\phi_t),f\circ\phi_t}(x)\mid_{(x,t)=(x_0,0)}\neq 0. \end{align} $$
Proof.
Part (1). Since
${\mathcal F}^c(p)$
is compact, it is enough to prove that
$\tilde g_{q(f\circ \phi _T),f\circ \phi _T}(x)$
is
$C^1$
in
$(x,T)$
in a small neighborhood of every point
$(x_0,0^n)\in {\mathcal F}^c(p)\times \mathbb R^n$
.
Let
$x_0\in {\mathcal F}^c(p)$
and denote
$y_0=h_{p,q}^u(x_0)\in {\mathcal F}^c(q)$
,
$y_1=f(y_0)\in {\mathcal F}^c(f(q))$
,
$z_1=h_{f(q),p}^s(y_1)\in {\mathcal F}^c(p)$
, and
$z_0=f^{-1}(z_1)\in {\mathcal F}^c(p)$
. The f-invariance of the stable holonomy implies that
$h_{q,p}^s(y_0)=z_0$
, or
$\tilde h_q(z_0)=x_0$
.
Let
$\psi _p:\mathbb T^2\rightarrow {\mathcal F}^c(p)$
be a
$C^2$
embedding,
$a_0=\psi _p^{-1}(x_0),\ b_0=\psi _p^{-1}(z_0)$
. Let
$I_{\delta }=[-\delta ,\delta ]$
. There exist
$C^2$
foliations charts of
${\mathcal F}^s$
(respectively
${\mathcal F}^u$
) on a small neighborhood of
$y_1$
(respectively
$y_0$
) inside
${\mathcal F}^{cs}(p)$
(respectively
${\mathcal F}^{cu}(p)$
):
$$ \begin{align*} &\alpha^s:B^c_{y_1}\times I_{\delta}\rightarrow B^{cs}_{y_1}, \alpha^s(\cdot,0)=\mathrm{Id}_{{\mathcal F}^c_{\mathrm{loc}}(y_1)}, \alpha^s(\{y\}\times I_{\delta})={\mathcal F}^s_{\mathrm{loc}}(y)\quad \text{for all } y\in B^c_{y_1};\\ &\alpha ^u:B^c_{y_0}\times I_{\delta}\rightarrow B^{cu}_{y_0}, \alpha^u(\cdot,0)=\mathrm{Id}_{{\mathcal F}^c_{\mathrm{loc}}(y_0)}, \alpha^u(\{y\}\times I_{\delta})={\mathcal F}^u_{\mathrm{loc}}(y)\quad \text{for all } y\in B^c_{y_0}, \end{align*} $$
where
$B_x^*$
denotes a small ball centered in x inside
${\mathcal F}^*(x)$
. Define the
$C^2$
maps
$$ \begin{align*} &\beta^s:B_{b_0}\times I_{\delta}\rightarrow B^{cs}_{y_1},\ \beta^s(b,s)=\alpha^s(h^s_{p,f(q)}(f(\psi_p(b))),s);\\ &\beta ^u:B_{a_0}\times I_{\delta}\rightarrow B^{cu}_{y_0},\ \beta^u(a,r)=\alpha^u(h_{p,q}^u(\psi_p(a)),r), \end{align*} $$
where
$B_x$
is a small ball centered at x in
$\mathbb T^2$
.
We know that the support of
$\phi _T$
does not intersect
$f^k({\mathcal F}^{cs}_{\mathrm {loc}}(y_1)) \text { for all } k\geq 0$
and
$f^l({\mathcal F}^{cu}_{\mathrm {loc}}(y_0)) \text { for all } l<0$
. This implies that
${\mathcal F}^{cs}_{\mathrm {loc}}(y_1)$
remains a local center-stable leaf for
$f_T:=f\circ \phi _T$
for all T,
$\beta ^s(a,\cdot )$
remain parameterizations of the strong stable manifolds inside
${\mathcal F}^{cs}_{\mathrm {loc}}(y_i)$
,
${\mathcal F}^{cs}_{\mathrm {loc}}(y_1)$
remains inside
${\mathcal F}^{cs}(p)$
and the stable holonomy between
${\mathcal F}^c(p)$
and
${\mathcal F}^{cs}_{\mathrm {loc}}(y_1)$
is unchanged. A similar statement holds for
${\mathcal F}^{cu}_{\mathrm {loc}}(y_0)$
.
The maps
$f_T$
do change the center leaves
${\mathcal F}^c(q)$
, we have that
${\mathcal F}^c(q(f_T),f_T)=f^{-1}({\mathcal F}^s_{\mathrm {loc}}({\mathcal F}^c(y_1)))\cap {\mathcal F}^u_{\mathrm {loc}}({\mathcal F}^c(y_0))$
. We can in fact compute implicitly the homoclinic stable–unstable holonomy
$\tilde h_{q(f_T), f_T}$
in a neighborhood of
$z_0$
in the following way:
$$ \begin{align*} \psi_p(a)=\tilde h_{q(f_T),f_T}(\psi_p(b)) &\! \iff h^u_{p,q(f_T),f_T}(\psi_p(a))=h^s_{p,q(f_T),f_T}(\psi_p(b))\\ &\! \iff h^u_{p,q(f_T),f_T}(\psi_p(a))=f_T^{-1}(h^s_{p,q(f_T),f_T}(f(\psi_p(b)))\\ &\!\iff \beta^u(a,r)=f_T^{-1}(\beta^s(b,s)) \quad\mbox{for some } r,s\in I_{\delta}\\ &\!\iff \phi_T(\beta^u(a,r))=f^{-1}(\beta^s(b,s)) \quad\mbox{for some } r,s\in I_{\delta}. \end{align*} $$
In conclusion, denoting
$h_T=\psi _p^{-1}\circ \tilde h_{q(f_T),f_T}\circ \psi _p$
(the map
$\tilde h_{q(f_T),f_T}$
in the chart
$\psi _p$
), we have
$$ \begin{align} a=h_T(b)\!\iff \phi_T(\beta^u(a,r))=f^{-1}(\beta^s(b,s)) \quad\mbox{for some } r,s\in I_{\delta}. \end{align} $$
We choose a
$C^{\infty }$
chart
$\psi _q:B_{y_0}\rightarrow \mathbb R^4$
(can also be volume preserving) such that:
-
•
$\psi _q(y_0)=0^4$
; -
•
$D\psi _q(y_0)(E^c(q_0))=\mathrm {span}\{e_1,e_2\}$
; -
•
$D\psi _q(y_0)(E^u(q_0))=\mathrm {span}\{e_3\}$
; -
•
$D\psi _q(y_0)(E^s(q_0))=\mathrm {span}\{e_4\}$
.
Let
$E:B_{a_0}\times B_{b_0}\times I_{\delta }^{n+2}\rightarrow \mathbb R^4$
,
$$ \begin{align} E(a,b,r,s,T)=\psi_q(\phi_T(\beta^u(a,r)))-\psi_q(f^{-1}(\beta^s(b,s))). \end{align} $$
We have that E is
$C^2$
and
$E(a_0,b_0,0,0,0^n)=\psi _q(y_0)-\psi _q(f^{-1}(y_1))=0$
.
Claim.
${\partial E}/{\partial (b,r,s)}(a_0,b_0,0,0,0^n)$
is invertible.
Proof. We observe that since
$\alpha ^s$
is a diffeomorphism such that
$\alpha ^s(\{y\}\times I_{\delta })={\mathcal F}^s_{\mathrm {loc}}(y)$
, we have that
$D\alpha ^s(y,0)\cdot {\partial }/{\partial s}$
is a non-zero vector in
$E^s(y)$
. Since
$Df$
preserves
$E^s$
, and
$D\psi _q(y_0)$
takes
$E^s(q_0)$
to the line generated by
$e_4$
, we have that
$DE(a_0,b_0,0,0,0^n)$
takes the line generated by
${\partial }/{\partial s}$
isomorphically to the line generated by
$e_4$
.
A similar argument shows that
$DE(a_0,b_0,0,0,0^n)$
takes the line generated by
${\partial }/{\partial r}$
isomorphically to the line generated by
$e_3$
(remember that
$\phi _{0^n}=\mathrm {Id}_{\mathbb T^4}$
).
Now let us analyze the action of
$DE(a_0,b_0,0,0,0^n)$
on the two-dimensional space
$T_{b_0}B_{b_0}$
. It is not hard to see that
$D\beta ^s(b_0,0)$
takes
$T_{b_0}B_{b_0}$
isomorphically to
$E^c(y_1)$
. Since
$Df$
preserves
$E^c$
and
$D\psi _q(y_0)$
takes
$E^c(q_0)$
to the plane generated by
$e_1$
and
$e_2$
, we have that
$DE(a_0,b_0,0,0,0^n)$
takes
$T_{b_0}B_{b_0}$
isomorphically to the plane generated by
$e_1$
and
$e_2$
. This concludes the proof of the claim.
Now let us finish the proof of the first part of the lemma. The implicit function theorem gives us the existence of a
$C^2$
function
$H:B_{a_0}\times I_{\delta }^n\rightarrow B_{b_0}\times I_{\delta }^2$
,
$H(a,T)=(h(a,T), r(a,T),s(a,T))$
such that
$E(a,h(a,T),r(a,T),s(a,T),T)=0$
(eventually by making smaller the balls and the intervals). Then the map
$h_T(a)=h(a,T)$
is
$C^2$
in both variables, which means that
$\tilde h_{q(f_T), f_T}(x)$
is
$C^2$
in both variables, and then
$\tilde g_{q(f\circ \phi _T),f\circ \phi _T}(x)$
is
$C^1$
in both variables. This finishes the proof of the first part.
Part (2). We will use the same notation from part (1). Let
$\rho :\mathbb R^4\rightarrow [0,\infty )$
be a smooth bump function supported on a small ball centered at the origin, and constantly equal to one near the origin. The family
$\phi _t:\mathbb T^4\rightarrow \mathbb T^4$
is defined as
$$ \begin{align*} \phi_t:=\psi_{q}^{-1}\circ (R_{\rho t}\times \mathrm{Id}_{\mathbb R^2})\circ\psi_q, \end{align*} $$
where
$R_t$
is the rotation of angle t in
$\mathbb R^2$
. Assume that the support of
$\rho $
is small enough so that the support of
$\phi _t$
is inside
$B(y_0,r_0)$
and disjoint of all the other iterates of
$W^c(q)$
. From part (1), we have
$$ \begin{align} E(a,b,r,s,t)=(R_{\rho t}\times \mathrm{Id}|{\mathbb R^2})(\psi_q(\beta^u(a,r)))-\psi_q(f^{-1}(\beta^s(b,s))). \end{align} $$
We will compute
$DE(a_0,b_0,0,0,t)$
. Observe that
$L_b:=DE(a_0,b_0,0,0,t)\mid _{T_{b_0}B_{b_0}}:T_{b_0}B_{B_0}\!\rightarrow \text {span}\{e_1,e_2\}$
and
$L_s:=DE(a_0,b_0,0,0,t)\mid _{\text {span}\{{\partial }/{\partial s}\}}:\text {span}\{\partial /{\partial s}\}\!\rightarrow \text {span}\{e_4\}$
are isomorphisms independent of t. Since
$D(R_{\rho t}\times \mathrm {Id}_{\mathbb R^2})$
keeps
$e_3$
invariant, we have that also
$L_r:=DE(a_0,b_0,0,0,t)\mid _{\text {span}\{{\partial }/{\partial r}\}}:\text {span}\{\partial /{\partial r}\}\rightarrow \text {span}\{e_3\}$
is also an isomorphism independent of t, and
$$ \begin{align*} \frac{\partial E}{\partial(b,r,s)}(a_0,b_0,0,0,t)=L_b\times L_r\times L_s. \end{align*} $$
From equation (12), we can compute
$$ \begin{align*} DE(a_0,b_0,0,0,t)\mid_{T_{a_0}B_{a_0}}=R_t\circ L_a:T_{a_0}B_{a_0}\rightarrow \text{span}\{e_1,e_2\}, \end{align*} $$
where
$L_a:=DE(a_0,b_0,0,0,0)\mid _{T_{a_0}B_{a_0}}:T_{a_0}B_{a_0}\rightarrow \text {span}\{e_1,e_2\}$
is an isomorphism. From the implicit function theorem, we deduce that
$$ \begin{align} Dh_t(a_0)=L_b^{-1}\circ R_t\circ L_a. \end{align} $$
Define
$g:B_{a_0}\times I_{\delta }\rightarrow \mathbb T^1$
,
$$ \begin{align*} g(a,t):=D\psi_p^{-1}(a)_*\tilde g_{q(f\circ\phi_t),f\circ\phi_t}(\psi(a))=\frac{Dh_t(a)(v^s(a))}{\|Dh_t(a)(v^s(a))\|}, \end{align*} $$
where
$D\psi _p^{-1}(a)_*$
is the diffeomorphism induced by
$D\psi _p^{-1}(a)$
on the unit tangent bundles and
$v^s(a)=D\psi _p^{-1}(a)(\tilde v^s(\psi _p(a)))$
. In other words,
$g(\cdot ,t)$
is in fact the map
$\tilde g_{q(f\circ \phi _t),f\circ \phi _t}$
seen in the chart
$\psi _p$
which identifies
$W^c(p)$
with
$\mathbb T^2$
and the unit tangent spaces to
$W^c(p)$
with
$\mathbb T^1$
. To prove equation (9), it is enough to show that
$$ \begin{align*} \frac{\partial}{\partial t}g(a,t)\mid_{(a,t)=(a_0,0)}\neq 0, \end{align*} $$
which in turns is equivalent to the fact that
$Dh_0(a_0)(v^s(a_0))$
and
${\partial }/{\partial t}Dh_t(a_0)(v^s(a_0))|_{t=0}$
are not collinear. Using equation (13), we obtain
$Dh_0(a_0)(v^s(a_0))=L_b^{-1}\circ L_a(v^s(a_0))$
and
${\partial }/{\partial t}Dh_t(a_0)(v^s(a_0))\mid _{t=0}=L_b^{-1}\circ R_{{\pi }/2}\circ L_a(v^s(a_0))$
, which are clearly non-collinear since
$L_a$
and
$L_b$
are isomorphisms while
$v^s(a_0)$
is non-zero. This finishes the proof of part (2).
Now let us prove Proposition 3.4.
Proof of Proposition 3.4
Let
$f\in \mathcal {SH}^r_b$
. We need to find maps in
$\mathcal U^r_s$
arbitrarily
$C^r$
close to f. Since the
$C^{\infty }$
maps are dense in the
$C^r$
maps in the
$C^r$
topology (even inside the volume preserving class), we can assume that f is
$C^{\infty }$
.
Choose
$q_1,q_2,q_3$
homoclinic points of
${\mathcal F}^c(p)$
such that the orbits of the homoclinic leaves
${\mathcal F}^c(q_i)$
are mutually disjoint,
$i\in \{1,2,3\}$
.
For any
$x\in {\mathcal F}^c(p)$
and any
$1\leq i\leq 3$
, there exists
$r_{x,i}>0$
such that if
$y_i:=h_{p,q_i}^u(x)\in {\mathcal F}^c(q_i)$
, then the ball
$B(y_i,r_{x,i})$
is disjoint from
${\mathcal F}^c(p)$
, from all the iterates
$f^k({\mathcal F}^c(q_i))\text { for all } k\neq 0$
, and from all the iterates of
${\mathcal F}^c(q_j)$
,
$j\neq i$
. Applying Lemma 3.6 part (2), we obtain the family of perturbations
$\phi _{t,x,i}$
such that the derivative of
$\tilde g_{q_i,f\circ \phi _{t,x,i}}$
with respect to t in
$(x,0)$
does not vanish. By the continuity of the derivative, there exists a neighborhood
$U_{x,i}$
of x such that
$({\partial }/{\partial t})\tilde g_{q_i,f\circ \phi _{t,x,i}}$
is non-zero on
$\overline U_{x,i}\times \{0\}$
.
Let
$U_x=\bigcap _{i=1}^3U_{x,i}$
. By compactness of
${\mathcal F}^c(p)$
, there exist finitely many
$x^1,x^2,\ldots x^K\in {\mathcal F}^c(p)$
such that
${\mathcal F}^c(p)=\bigcup _{j=1}^KU_{x^j}$
.
Let us fix some notation. Denote
$$ \begin{align*} T=(t_i^j)_{1\leq i\leq 3, 1\leq j\leq K} = (T_i)_{1\leq i\leq 3}=(T^j)_{1\leq j\leq K}\in I^{3K}:=[-\delta,\delta]^{3K}, \end{align*} $$
with
$T_i=(t_i^j)_{1\leq j\leq K}\in I^K$
,
$i\in \{1,2,3\}$
and
$T^j=(t_i^j)_{1\leq i\leq 3}\in I^3$
,
$j\in \{1,2,\ldots K\}$
.
For every
$1\leq i\leq 3$
, we let
$\phi _i:\mathbb T^4\times I^K\rightarrow \mathbb T^4$
given by
$$ \begin{align} \phi_i(\cdot, T_i)=\phi_{t_i^1,x^1,i}\circ\phi_{t_i^2,x^2,i}\circ\cdots\circ\phi_{t_i^K,x^K,i}\quad \text{for all } T_i\in I^K. \end{align} $$
We define
$\phi ,\ F:\mathbb T^4\times I^{3K}\rightarrow \mathbb T^4$
,
$$ \begin{align*} \phi(\cdot,T)=\phi_T(\cdot)&:= \phi_1(\cdot, T_1)\circ\phi_2(\cdot,T_2)\circ \phi_3(\cdot,T_3),\\ F(\cdot,T)=F_T(\cdot)&:= f\circ\phi_T. \end{align*} $$
The maps
$\phi _i$
,
$\phi $
, and F have the following properties:
-
(1)
$\phi _i$
,
$\phi $
, and F are of class
$C^{\infty }$
on
$(x,T)$
; -
(2)
$\phi _i$
is a small perturbation of the identity on a small neighborhood of
${\mathcal F}^c(q_i)$
, in particular, it leaves the other homoclinic orbits of
${\mathcal F}^c(q_j)$
unchanged for
$j\neq i$
; -
(3)
$F_T$
is equal to f on a neighborhood of
${\mathcal F}^c(p)$
, so it does not change
${\mathcal F}^c(p)$
and the function
$\tilde v^s$
.
Let
$V_j=\psi _p^{-1}(U_{x^j})$
, where
$\psi _p:\mathbb T^2\rightarrow {\mathcal F}^c(p)$
is the
$C^2$
embedding. For every
$1\leq i\leq~3$
, define
$g_i:\mathbb T^2\times I^{3K}\rightarrow \mathbb T^1$
,
$$ \begin{align*} g_i(x,T)=D\psi_p^{-1}(x)_*\tilde g_{q_i(f_T),f_T}(\psi_p(x)). \end{align*} $$
In other words,
$g_i(\cdot ,T)$
is again the map
$\tilde g_{q_i(f_T),f_T}$
seen in the chart
$\psi _p$
which identifies
${\mathcal F}^c(p)$
with
$\mathbb T^2$
and the unit tangent spaces
$T^1{\mathcal F}^c(p)$
with
$\mathbb T^1$
. Lemma 3.6 part (1) tells us that
$g_i$
is
$C^1$
with respect to
$(x,T)\in \mathbb T^2\times I^{3K}$
(maybe for a smaller interval I). Furthermore,
$$ \begin{align} \frac{\partial g_i}{\partial t_i^j}(x,T)\neq 0\quad \text{for all } (x,T)\in \overline V_j\times\{0\}^{3K}, \text{ for all } 1\leq j\leq K. \end{align} $$
However, because for
$l\neq i$
, the perturbation
$\phi _l$
does not touch the orbit of
${\mathcal F}^c(q_i)$
, we have
$$ \begin{align} \frac{\partial g_i}{\partial t_l^j}(x,T)= 0\quad \text{for all } (x,T), \text{ for all } l\neq i, \text{ for all } 1\leq j\leq K. \end{align} $$
Define
$G:\mathbb T^2\times I^{3K}\rightarrow \mathbb T^3$
$$ \begin{align} G(x,T)=(g_1(x,T),g_2(x,T),g_3(x,T)). \end{align} $$
Again, G is
$C^1$
in
$(x,T)\in \mathbb T^2\times I^{3K}$
. Equations (15) and (16) tell us that for every
$1\leq j\leq K$
, we have
$$ \begin{align*} \det\bigg(\frac{\partial G}{\partial T^j}(x,T)\bigg)=\det\bigg(\frac {\partial g_i}{\partial t_i^j}(x,T)\bigg)=\prod_{i=1}^3\frac {\partial g_i}{\partial t_i^j}(x,T)\neq 0\quad \text{for all } (x,T)\in \overline V_j\times\{0\}^{3K}. \end{align*} $$
From the compactness of
$\overline V_j$
and the
$C^1$
continuity of G with respect to T, there exists
$J\subset I$
with
$0\in J$
such that, for all
$1\leq j\leq K$
, we have
$$ \begin{align} \det\bigg(\frac{\partial G}{\partial T^j}(x,T)\bigg)\neq 0\quad \text{ for all } (x,T)\in V_j\times J^{3K}, \end{align} $$
and since every point from
$\mathbb T^2$
is inside some
$V_j$
, we conclude that G has maximal rank at every point in
$\mathbb T^2\times J^{3K}$
.
Remember that
$v^s:\mathbb T^2\rightarrow \mathbb T^1$
is the
$C^1$
map given by
$v^s(x)=D\psi _p^{-1}(x)_*\tilde v^s(\psi (x))$
. Let
$A:=\{(x,T)\in \mathbb T^2\times J^{3K}:\ G(x,T)\in \{-v^s(x),v^s(x)\}^3\}$
and
$B=\pi _2(A)$
, where
$\pi _2$
is the projection from
$\mathbb T^2\times J^{3K}$
on the T component in
$J^{3K}$
.
A simple consequence of the above definitions is the fact that if
$T\notin B$
, then
$f_T\in \mathcal U_s^r$
. To finish the proof of the density of
$\mathcal U_s^r$
, we have to find T arbitrarily close to
$0^{NK}$
such that
$T\notin B$
. We will prove in fact that B has Lebesgue measure zero in
$J^{3K}$
.
It is enough to show this for
$B_1=\pi _2(A_1)$
, where
$A_1=\{(x,T)\in \mathbb T^2\times J^{3K}:\ G(x,T)=v^s(x)^3\}$
, the other combinations of
$\pm v^s$
work similarly. Let
$H(x, T)=G(x,T)-v^s(x)^3$
, this is a
$C^1$
map from
$\mathbb T^2\times J^{3K}$
to
$\mathbb T^3$
. Equation (18) tells us that H has maximal rank equal to 3 at every point (
$v^s$
is independent of T), so
$H^{-1}(0^3)$
is a
$C^1$
submanifold of codimension 3 (or dimension
$3K-1$
) inside
$\mathbb T^2\times J^{3K}$
. Since
$\pi _2\mid _{H^{-1}(0^3)}:H^{-1}(0^3)\rightarrow J^{3K}$
is a
$C^1$
map, Sard’s theorem tells us that the image
$B_1$
has Lebesgue measure zero.
This implies that we can find arbitrarily small
$T\notin B$
, which finishes the proof of the
$C^r$
density of
$\mathcal U_s^r$
.
3.3 Proof of Proposition 3.5
Proof. We first remark that, because of the transitivity of the homoclinic relation, it is enough to show that every hyperbolic periodic point of index 2 of
$f\in \mathcal U^r$
is homoclinically related to the fixed point p of the hyperbolic fixed leaf
${\mathcal F}^c(p)$
.
Let x be a hyperbolic point of
$f\in \mathcal U^r$
of index 2. Let
$\tilde v^u(x)$
be the unit tangent vector to the weak unstable direction inside
$T_x{\mathcal F}^c(x)$
. The strong unstable manifold
${\mathcal F}^u(x)$
must accumulate on the fixed hyperbolic leaf
${\mathcal F}^c(p)$
, so there exists a sequence of homoclinic points
$p_n\in {\mathcal F}^u(x)\cap {\mathcal F}^s_{\mathrm {loc}}({\mathcal F}^c(p))$
such that
$\lim _{n\rightarrow \infty }p_n=p_0\in {\mathcal F}^c(p)$
. If for some
$p_n$
we have that
$Dh^u_{x,p_n*}(\tilde v^u(x))\neq \pm Dh^s_{p,p_n*}(\tilde v^s(h^{s^{-1}}_{p,p_n}(p_n)))$
, then the two-dimensional unstable manifold of x,
$W^u(x)$
, intersects
${\mathcal F}^c(p_n)$
in a
$C^1$
curve locally transverse to the weak stable foliation inside
${\mathcal F}^c(p_n)$
(which is then pushed forward by the stable holonomy of the weak stable foliation in
${\mathcal F}^c(p)$
). Since the two-dimensional global stable manifold of p,
$W^s(p)$
, is dense inside the weak stable foliation of
${\mathcal F}^c(p_n)$
, we obtain a transverse homoclinic intersection from x to p.
Suppose that
$W^u(x)\cap W^s(p)=\emptyset $
. The above argument implies that
$$ \begin{align*} Dh^u_{x,p_n*}(\tilde v^u)=\pm Dh^s_{p,p_n*}(\tilde v^s(h^{s^{-1}}_{p,p_n}(p_n)))\quad \mbox{for all } n\in\mathbb N. \end{align*} $$
Since
$f\in \mathcal U^r$
, there exists a homoclinic point q of
${\mathcal F}^c(p)$
such that
$\tilde g_q(p_0)\neq \pm \tilde v^s(p_0)\in T^1{\mathcal F}^c(p)$
. Let
$q_0:=h^u_{p,q}(p_0)$
, consider the strong unstable holonomy
$h^u_{\mathrm {loc}}:{\mathcal F}^{cs}_{\mathrm {loc}}(p_0)\rightarrow {\mathcal F}^{cs}_{\mathrm {loc}}(q_0)$
, and let
$q_n:=h^u_{\mathrm {loc}}(p_n)\in {\mathcal F}^{cs}_{\mathrm {loc}}(q_0)$
. Then,
$q_n\rightarrow q_0$
. The lack of homoclinic relations between x and p implies that also
$$ \begin{align*} Dh^u_{x,q_n*}(\tilde v^u)=\pm Dh^s_{p,q_n*}(\tilde v^s(h^{s^{-1}}_{p,q_n}(q_n)))\quad \mbox{for all } n\in\mathbb N. \end{align*} $$
Since
$h_{x,q_n}^u=h_{p_n,q_n}^u\circ h_{x,p_n}^u$
, we obtain that
$$ \begin{align*} Dh^s_{p,q_n*}(\tilde v^s(h^{s^{-1}}_{p,q_n}(q_n)))=\pm Dh^u_{p_n,q_n*}\circ Dh^s_{p,p_n*}(\tilde v^s(h^{s^{-1}}_{p,p_n}(p_n))). \end{align*} $$
Using the continuity of
$\tilde v^s$
and of
$Dh^{s,u}$
, we can pass to the limit and obtain that
$$ \begin{align*} Dh^s_{p,q*}(\tilde v^s(h^{s^{-1}}_{p,q}(q_0)))=\pm Dh^u_{p,q*}(\tilde v^s(p_0)), \end{align*} $$
or
$\tilde g_q(p_0)=\pm \tilde v^s(p_0)$
, which is a contradiction.
The proof of the intersection of the global stable manifold of x with the global unstable manifold of p is similar. This concludes the proof.
Now, as we explained in §3.1, the proof of Theorem A is concluded by this last proposition.
4 Proof of Corollary B
We have to show that for any
$f\in \mathcal U^r$
, the transverse homoclinic intersections of the invariant manifolds of the fixed hyperbolic point
$p_f$
are dense in
${\mathbb T}^4$
. The proof uses the same ideas from the proof of Proposition 3.5.
Let
$f\in \mathcal U^r$
, and p be the hyperbolic fixed point of f (for simplicity, we will drop the index f in the following arguments). Let U be an open set in
${\mathbb T}^4$
. Since
$W^u(p)\cap W^s({\mathcal F}^c(p))$
is dense in
${\mathbb T}^4$
, choose
$x\in W^u(p)\cap W^s({\mathcal F}^c(p))$
such that
$B(x,\delta )\subset U$
for some
$\delta>0$
. If
$Dh^s_{p,x*}(\tilde v^s(h^s_{x,p}(x)))\notin T_xW^u(p)$
, then clearly there is a transverse homoclinic intersection between
$W^s(p)$
and
$W^u(p)$
arbitrarily close to x.
Suppose that
$v:=Dh^s_{p,x*}(\tilde v^s(h^s_{x,p}(x)))\in T_xW^u(p)$
. Then there exists a subsequence
$n_k\rightarrow \infty $
and
$(p_0,v_0)\in T^1{\mathcal F}^c(p)$
such that
$Df^{n_k}_*(x,v)\rightarrow (p_0,\tilde v^s(p_0))$
. There exists a homoclinic point q of
${\mathcal F}^c(p)$
such that
$\tilde g_q(p_0)\neq \pm \tilde v^s(p_0)\in T^1{\mathcal F}^c(p)$
. We consider again the strong unstable holonomy
$h^u_{\mathrm {loc}}:{\mathcal F}^{cs}_{\mathrm {loc}}(p_0)\rightarrow {\mathcal F}^{cs}_{\mathrm {loc}}(q_0)$
and let
$q_k:=h^u_{\mathrm {loc}}(f^{n_k}(x))\in {\mathcal F}^{cs}_{\mathrm {loc}}(q_0)$
, where
$q_0:=h^u_{p,q}(p_0)$
. We have that
$$ \begin{align*} Dh^s_{p,q*}(\tilde v^s(h^{s^{-1}}_{p,q}(q_0)))\neq\pm Dh^u_{p,q*}(\tilde v^s(p_0)), \end{align*} $$
and by continuity, for all k large enough, we have
$$ \begin{align*} Dh^s_{p,q_k*}(\tilde v^s(h^{s^{-1}}_{p,q_k}(q_k)))\neq\pm Dh^u_{f^{n_k}(x),q_k*}(\tilde v^s(f^{n_k}(x))). \end{align*} $$
Iterating by
$f^{-n_k}$
and denoting
$f^{-n_k}(q_k)=x_k\rightarrow x$
, we obtain
$$ \begin{align*} Dh^s_{p,x_k*}(\tilde v^s(h^{s^{-1}}_{p,x_k}(x_k)))\neq\pm Dh^u_{x,x_k*}(\tilde v^s(x)). \end{align*} $$
Since
$Dh^u$
preserves
$TW^u(p)$
, we obtain that
$Dh^s_{p,x_k*}(\tilde v^s(h^s_{x_k,p}(x_k)))\notin T_{x_k}W^u(p)$
, with
$x_k\in W^u(p)\cap W^s({\mathcal F}^c(p))$
, and this implies again that arbitrarily close to
$x_k$
(and thus close to x), there are transverse homoclinic intersection between
$W^s(p)$
and
$W^u(p)$
. This finishes the proof.
5 Proof of Theorem C
Remember that
$\phi :\mathbb T^4\rightarrow \mathbb R$
is a Hölder potential satisfying
$\sup (\phi )-\inf (\phi )<\log \unicode{x3bb} _B$
. For simplicity, we may assume
First, by the variation principle, there is a sequence of ergodic measures
$\mu _n$
of f such that
the last inequality comes from equation (7).
Again, by the variation principle, the pressure of the function
$\phi $
is
where the last inequality comes from the assumption that
$\phi>0$
in equation (19).
Thus, for any ergodic measure
$\mu $
with pressure sufficiently large, that is,
we have
As a consequence of Lemma 2.11,
$\mu $
is a hyperbolic measure with stable index
$2$
. By Lemma 2.7,
$\mu $
is homoclinically related to the atomic measure supported on a hyperbolic periodic point O. Since
$f\in {\mathcal U}$
, by Theorem A, all the hyperbolic periodic orbits with stable index
$2$
are homoclinically related, and as a consequence of Remark 1.11, all the hyperbolic ergodic measures with stable index
$2$
are homoclinically related. In particular, all the ergodic measures satisfying equation (20) are homoclinically related.
Thus, all equilibrium states for the Hölder potential
$\phi $
are homoclinically related, if they do exist. By Proposition 2.9, there exists at most one equilibrium state. The proof is complete.
Acknowledgements
We thank the anonymous referees for their helpful comments. C.L. was supported by NNSFC (grant nos. 12271538, 12071328, 11871487) and the Disciplinary Funds in CUFE. R.S. was partially supported by FONDECYT Regular 1230632 and MATH-AmSud 220029. J.Y. was partially supported by CNPq, FAPERJ, PRONEX, MATH-AmSud 220029 and NNSFC grant nos. 11871487, 12271538, and 12071202.
