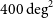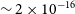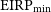1. Introduction
In this paper, we continue to report on our program to utilise the Murchison Widefield Array (MWA: Tingay et al. Reference Tingay2013; Wayth et al. Reference Wayth2018) in a Search for Extraterrestrial Intelligence (SETI) at low radio frequencies, over extremely wide fields of view.
In previous work, we have examined two survey fields, encompassing ![]() $400\,\textrm{deg}^{2}$
towards the Galactic Centre in the frequency range 103–133 MHz (Tingay et al. Reference Tingay, Tremblay, Walsh and Urquhart2016) and
$400\,\textrm{deg}^{2}$
towards the Galactic Centre in the frequency range 103–133 MHz (Tingay et al. Reference Tingay, Tremblay, Walsh and Urquhart2016) and ![]() $625\,\textrm{deg}^{2}$
towards the Galactic Anticentre direction in the frequency range of 99–122 MHz (Tingay, Tremblay, & Croft Reference Tingay, Tremblay and Croft2018). In these two survey fields, 45 and 22 exoplanets were known at the times of observation, respectively, and no candidate signals were detected above the observational detection limits, which were approximately
$625\,\textrm{deg}^{2}$
towards the Galactic Anticentre direction in the frequency range of 99–122 MHz (Tingay, Tremblay, & Croft Reference Tingay, Tremblay and Croft2018). In these two survey fields, 45 and 22 exoplanets were known at the times of observation, respectively, and no candidate signals were detected above the observational detection limits, which were approximately ![]() $4\,{\times}\,10^{13}$
and
$4\,{\times}\,10^{13}$
and ![]() $1\,{\times}\,10^{13}$
W for the closest exoplanets in the fields, respectively (assuming isotropic transmitters and a 10-kHz transmission bandwidth to calculate Effective Isotropic Radiated Power (EIRP)).
$1\,{\times}\,10^{13}$
W for the closest exoplanets in the fields, respectively (assuming isotropic transmitters and a 10-kHz transmission bandwidth to calculate Effective Isotropic Radiated Power (EIRP)).
A general improvement in our data processing techniques between the two sets of observations, and the fact that on average the known exoplanets towards the Galactic Anticentre are closer than those known towards the Galactic Centre, means that our upper limits on the EIRP for exoplanets towards the Galactic Anticentre are lower, in general. Tingay et al. (Reference Tingay, Tremblay and Croft2018) placed our results to that point in the context of the overall SETI endeavour and we refer the reader to that discussion and references therein for this context.
The MWA provides a unique facility to search for technosignatures at low radio frequencies, being highly sensitive, located at the radio-quiet Murchison Radio-astronomy Observatory (MRO), and having a very wide field-of-view (the surveyed areas noted above represent single MWA pointings). The Galactic Centre field survey we previously reported was placed in the context of past SETI surveys by Gray & Mooley (Reference Gray and Mooley2017), who show that the limits we achieved are highly competitive. In their analysis of ‘How Much SETI Has Been Done? Finding Needles in the n-dimensional Cosmic Haystack’, Wright et al. (Reference Wright, Kanodia and Lubar2018) examine an eight-dimensional parameter space for radio SETI and find our two previous surveys to have the highest searched fractions for this parameter space for single surveys, factors of approximately 2 and 10 greater than the next highest, respectively. However, the highest search fractions still sit at an order of ![]() $10^{-18}$
, indicating that only a vanishingly small fraction of the SETI parameter space has been covered thus far.
$10^{-18}$
, indicating that only a vanishingly small fraction of the SETI parameter space has been covered thus far.
While this conclusion may appear discouraging, cause for encouragement comes from the fact that SETI surveys can increasingly be performed effectively as commensal science in parallel with primary astrophysical investigations. This has been our approach using the MWA, whereby we utilise data collected and processed in wide field searches for low-frequency spectral lines (e.g. Tremblay et al. Reference Tremblay, Jones, Cunningham, Hurley-Walker, Jordan and Tingay2018). The FAST collaboration intends to complete commensal and dedicated SETI experiments, using a real-time data processing pipeline originally developed for the ![]() $SETI@Home$
platform to search for technosignatures from 1 to 1.5 GHz during normal science operations (Zhang et al. Reference Zhang2020; Li et al. Reference Li, Gajjar, Wang, Siemion, Zhang and Collaboration2020). Similar ideas exist for commensal searches being planned with MeerKAT (Gajjar et al. Reference Gajjar2019).
$SETI@Home$
platform to search for technosignatures from 1 to 1.5 GHz during normal science operations (Zhang et al. Reference Zhang2020; Li et al. Reference Li, Gajjar, Wang, Siemion, Zhang and Collaboration2020). Similar ideas exist for commensal searches being planned with MeerKAT (Gajjar et al. Reference Gajjar2019).
We continue this approach with the MWA here, adding a survey field centred on the Vela Supernova Remnant. In Section 2, we describe the observations and data processing, including increments in the quality of the data processing that lead to almost an order of magnitude improvement in our flux density sensitivity with commensurate improvements in our EIRP detection limits (for a fixed distance). In Section 3, we describe our results, examining the six known exoplanets in the Vela field as well as the full population of stellar systems in the field (millions of systems). In Section 4, we discuss our results and conclusions.
2. Observations and data processing
The MWA (Tingay et al. Reference Tingay2013) is a low-frequency interferometer operating between 70 and 300 MHz at the MRO in Western Australia. In 2018, the telescope was upgraded to the ‘Phase II’ array (Wayth et al. Reference Wayth2018), doubling the number of aperture array tiles from 128 to 256 and approximately doubling the maximum baseline from 3 to 5.5 km.
Observations of the Vela region took place between 2018 January 5 and 2018 January 23 for a total of 30 h, the details of which are summarised in Table 1. These observations were taken during the building and commissioning of the Phase II array and included 91 of the new 128 tiles. Of the 30 h of observation, 17 h were free from imaging artefacts likely caused due to the instrument being actively worked on during the day, while the observations were taken at night.
Table 1. MWA observing parameters

FWHM = Full Width at Half Maximum

Figure 1. Summary of the data processing pipeline from Figure 2 of Tremblay et al. (Reference Tremblay2017) used to create integrated spectral cubes with the MWA.
The MWA has an instantaneous bandwidth of 30.72 MHz that is distributed between 3072 ![]() $\times$
10 kHz fine frequency channels. Our data were processed following the procedure detailed in Tremblay et al. (Reference Tremblay2017) and Tremblay (Reference Tremblay2018) but a summary is provided here and in Figure 1. The bandpass and phase solutions were derived each night from a 2-min observation of Hydra A (a LINER galaxy with a flux density of 243 Jy at 160 MHz Kühr et al. Reference Kühr, Witzel, Pauliny-Toth and Nauber1981). The solutions were further refined by using self-calibration before they were applied to each 5-min observation of the Vela region field.
$\times$
10 kHz fine frequency channels. Our data were processed following the procedure detailed in Tremblay et al. (Reference Tremblay2017) and Tremblay (Reference Tremblay2018) but a summary is provided here and in Figure 1. The bandpass and phase solutions were derived each night from a 2-min observation of Hydra A (a LINER galaxy with a flux density of 243 Jy at 160 MHz Kühr et al. Reference Kühr, Witzel, Pauliny-Toth and Nauber1981). The solutions were further refined by using self-calibration before they were applied to each 5-min observation of the Vela region field.
For each of the 5-min observations, the fine frequency channels (10 kHz) are imaged at a rate of 100 fine channels per every 1.28 MHz coarse channel to avoid channels affected by aliasing. This means only 78% of the band is imaged. The Phase II configuration of the MWA used in these observations removed the compact core and had shortest baselines of 1.5 km. In order to obtain as much sensitivity to diffuse emission as possible, all images were created using a Briggs weighting of 0.5. This produced a field-of-view of ![]() $400\,\textrm{deg}^{2}$
and a synthesised beamwidth of 1
$400\,\textrm{deg}^{2}$
and a synthesised beamwidth of 1![]() $^{\prime}$
.
$^{\prime}$
.
In previous SETI surveys completed with the MWA towards the Galactic Centre and the Orion Molecular Cloud, only 4 and 3 h, respectively, of observations were obtained. In this survey, 17 h of total integration time is used to provide our deepest low-frequency survey, producing a mean spectral RMS (root mean squared) of ![]() $0.05\,\textrm{Jy beam}^{-1}$
across much of the field, in comparison to the previous
$0.05\,\textrm{Jy beam}^{-1}$
across much of the field, in comparison to the previous ![]() $0.35\,\textrm{Jy beam}^{-1}$
RMS.
$0.35\,\textrm{Jy beam}^{-1}$
RMS.
The MWA is situated in an RFI-protected environment but occasional intermittent interference occurs (Offringa et al. Reference Offringa2015; Sokolowski, Wayth, & Ellement Reference Sokolowski, Wayth and Ellement2017). Each 5-min observation was flagged using AOFlagger (Offringa et al. Reference Offringa2015) to remove strong sources of radio frequency interference (RFI) signals from the raw visibilities based on statistical methods. This is not expected to impact our science goals, as the chance of a real astronomical or signal from an ETI being strong enough to be flagged in a single 5-min observation is very small. It is estimated that this process removes less than 5–20% of the total visibilities, having little impact on an observation’s sensitivity. For these observations, after integrating each of the snapshot images, significant narrow-band RFI was detected in the commercial FM radio bands between 98 and 108 MHz. This left 64% of the band available for narrow-band signal searches.
These data are commensally searched for spectral line signals of an astrophysical nature, which will be reported in a separate publication (Tremblay et al. ApJ Submitted). An example of a typical spectrum with no significant signal, as seen towards HD 75289 b, is shown in Figure 2.
The source finding software Aegean (Hancock, Trott, & Hurley-Walker Reference Hancock, Trott and Hurley-Walker2018) is used to search each of the 2 400 (10 kHz) fine frequency channels independently for signals over a 5![]() $\sigma$
limit. Aegean works by fitting Gaussians to the pixel data and applies a correction for the backgroundFootnote a to calculate the flux density for potential sources. Any potential source is further evaluated based on various quality control checks, including but not limited to, ensuring the signal is greater than 5
$\sigma$
limit. Aegean works by fitting Gaussians to the pixel data and applies a correction for the backgroundFootnote a to calculate the flux density for potential sources. Any potential source is further evaluated based on various quality control checks, including but not limited to, ensuring the signal is greater than 5![]() $\sigma$
in both the spectral and image plane. Any remaining signals are cross-referenced to a combination of chemical databases and new chemical modelling reported in a future publication. Following this search, we found no signals of an unknown nature.
$\sigma$
in both the spectral and image plane. Any remaining signals are cross-referenced to a combination of chemical databases and new chemical modelling reported in a future publication. Following this search, we found no signals of an unknown nature.
3. Results
Utilising the processed data described in Section 2, we have access to the spectrum across our bandwidth at 10 kHz resolution, for every pixel in our ![]() $400\,\textrm{deg}^{2}$
field-of-view. Thus, as per our previous work (Tingay et al. Reference Tingay, Tremblay and Croft2018; Reference Tingay, Tremblay, Walsh and Urquhart2016), we can examine the spectrum at the locations of stellar systems with known exoplanets and search for narrow-band signals that may constitute technosignatures. We undertake this examination below in Section 3.1. Further, given that only a tiny fraction of the exoplanets in this field are known, we can also undertake a blind survey of all stellar systems in the field with known distances from Gaia (Bailer-Jones et al. Reference Bailer-Jones, Rybizki, Fouesneau, Mantelet and Andrae2018) and undertake the same search. We undertake this examination in Section 3.2, below.
$400\,\textrm{deg}^{2}$
field-of-view. Thus, as per our previous work (Tingay et al. Reference Tingay, Tremblay and Croft2018; Reference Tingay, Tremblay, Walsh and Urquhart2016), we can examine the spectrum at the locations of stellar systems with known exoplanets and search for narrow-band signals that may constitute technosignatures. We undertake this examination below in Section 3.1. Further, given that only a tiny fraction of the exoplanets in this field are known, we can also undertake a blind survey of all stellar systems in the field with known distances from Gaia (Bailer-Jones et al. Reference Bailer-Jones, Rybizki, Fouesneau, Mantelet and Andrae2018) and undertake the same search. We undertake this examination in Section 3.2, below.
To calculate the upper limit on the total EIRP, we use the equation:
where ![]() $\mbox{S}_{\textrm{rms}}$
is the RMS intensity value in
$\mbox{S}_{\textrm{rms}}$
is the RMS intensity value in ![]() $\textrm{Jy beam}^{-1}$
and R is the distance to the stellar system in pc. This assumes that the transmission bandwidth is matched to the MWA fine channel bandwidth of 10 kHz. For transmission bandwidths less than 10 kHz, the maximum EIRP estimates are increased by
$\textrm{Jy beam}^{-1}$
and R is the distance to the stellar system in pc. This assumes that the transmission bandwidth is matched to the MWA fine channel bandwidth of 10 kHz. For transmission bandwidths less than 10 kHz, the maximum EIRP estimates are increased by ![]() $\frac{10 kHz}{\Delta \nu_{t}}$
, where
$\frac{10 kHz}{\Delta \nu_{t}}$
, where ![]() $\Delta \nu_{t}$
is the transmission bandwidth. For example, a 10-Hz transmission bandwidth would cause our EIRP upper limits to be raised by a factor of 1000.
$\Delta \nu_{t}$
is the transmission bandwidth. For example, a 10-Hz transmission bandwidth would cause our EIRP upper limits to be raised by a factor of 1000.
Table 2. Known exoplanets in the survey field, from the exoplanet catalogue: http://exoplanet.eu/

aMass of planet times the sine of orbit inclination, in Jupiter masses.
bSpectral type of host star.
cRV = radial velocity; I = imaging; PT = primary transit.
dEquivalent Isotropic Radiated Power.

Figure 2. MWA spectrum for a data cube, with a total integration time of 17 h, used within this survey at the position of HD 75289 b. Some of the channels in the lower end of the band are affected by narrow-band RFI. The vertical shaded areas mark regions of known narrow-band RFI and the green region of the spectrum shows the top end of the FM band. Flagged channels are blanked out in the spectrum. The horizontal grey shaded region represents the ![]() $\pm1\sigma$
RMS value used in Table 2.
$\pm1\sigma$
RMS value used in Table 2.
3.1. Known exoplanets in the survey field
A search of our field-of-view in the Exosolar Planets Encyclopedia CatalogFootnote b (as of March 2020) returns six exoplanets hosted by five stellar systems. These exoplanets are listed in Table 2, including basic parameters of the exoplanets, their stellar host, and the radio observations. In no case were any narrow-band signals detected towards these objects in our observing band at or above a level of 5![]() $\sigma$
. As in our previous work, we assign upper limits to the EIRP based on the RMS of the measured spectrum, listed in Table 2.
$\sigma$
. As in our previous work, we assign upper limits to the EIRP based on the RMS of the measured spectrum, listed in Table 2.
3.2. Other stellar systems in the survey field
Given the small number of known exoplanets associated with the stellar systems in this field, it is likely that a vast number of exoplanets remain unknown. Thus, we examine the general limits we can derive for stars in this field. We do this by examining the Gaia catalogue, extracting the distances of stars within the field determined by their parallax measurements (Bailer-Jones et al. Reference Bailer-Jones, Rybizki, Fouesneau, Mantelet and Andrae2018). There are 10 355 066 such stars within the field-of-view for this survey. As no detections were made in the search discussed in Section 2, we utilise the RMS value as a function of position across our field and the coordinates and distances of the stars, to derive the EIRP upper limit histogram for all 10 355 066 stars with a distance smaller than 6 350 pc in Figure 3. As the distribution of distances is dominated by stars within the spiral arm of the Galaxy at 1.5–2.5 kpc, the EIRP upper limits are also very large, orders of magnitude larger than the lowest upper limits from our previous work.
To examine the most interesting part of this distribution, at low values of EIRP upper limit, we show the EIRP upper limit histogram for those stars within 30 and 50 pc in Figure 4. For the 10 closest stars, Table 3 lists the RMS and derived EIRP limits in more detail (excluding those systems referenced in Table 2).

Figure 3. Histogram of EIRP upper limits based on the distribution of stellar distances (set to a maximum of 6350 pc) from the Gaia catalogue.

Figure 4. Histogram of EIRP upper limits based on the distribution of distances from the Gaia catalogue, with a focus on sources with distances ![]() ${<}50$
and
${<}50$
and ![]() ${<}30\,\mbox{pc}$
.
${<}30\,\mbox{pc}$
.
Table 3. Gaia stellar systems in the survey field, from the Gaia DR2 release.

aEquivalent Isotropic Radiated Power.
4. Discussion and conclusion
The median distance for the six known exoplanet systems in the Vela field is 28.8 pc (treating HD 73526 b and c as a single system), compared to 50 pc for the 22 exoplanets examined by Tingay et al. (Reference Tingay, Tremblay and Croft2018) and ![]() $\approx$
2 kpc for the 45 exoplanets examined by Tingay et al. (Reference Tingay, Tremblay, Walsh and Urquhart2016). Coupled with the sensitivity improvements we obtained (gained from the increased integration time of 17 h compared to the previous 4 h) described in Section 2, the median EIRP upper limit from this work is therefore an order of magnitude better than the median upper limit from Tingay et al. (Reference Tingay, Tremblay and Croft2018). This represents continued improvement in our techniques and general upper limits. Our best upper limit from Table 3 of
$\approx$
2 kpc for the 45 exoplanets examined by Tingay et al. (Reference Tingay, Tremblay, Walsh and Urquhart2016). Coupled with the sensitivity improvements we obtained (gained from the increased integration time of 17 h compared to the previous 4 h) described in Section 2, the median EIRP upper limit from this work is therefore an order of magnitude better than the median upper limit from Tingay et al. (Reference Tingay, Tremblay and Croft2018). This represents continued improvement in our techniques and general upper limits. Our best upper limit from Table 3 of ![]() $6.2\,{\times}\,10^{12}$
W (not for a known exoplanet) approaches a 50% improvement on our best upper limit from Tingay et al. (Reference Tingay, Tremblay and Croft2018), still noting that an EIRP of
$6.2\,{\times}\,10^{12}$
W (not for a known exoplanet) approaches a 50% improvement on our best upper limit from Tingay et al. (Reference Tingay, Tremblay and Croft2018), still noting that an EIRP of ![]() $10^{12}$
W is high compared to the highest power transmitters on Earth at these frequencies (see Tingay et al. Reference Tingay, Tremblay, Walsh and Urquhart2016 for a discussion).
$10^{12}$
W is high compared to the highest power transmitters on Earth at these frequencies (see Tingay et al. Reference Tingay, Tremblay, Walsh and Urquhart2016 for a discussion).
Sheikh et al. (Reference Sheikh, Siemion, Enriquez, Price, Isaacson, Lebofsky, Gajjar and Kalas2020) recently completed an in-depth analysis of 20 stars within the Earth transit zone between 3.95–8 GHz with the NRAO Green Bank Telescope (GBT). They determined an EIRP of detectable narrow-band signals that ranged from 47 to ![]() $17590\,{\times}\,10^{9}$
W for stellar distances between 7 and 143 pc. These are similar distances to the stars we present in Table 3 for the nearby stars from Gaia in the Vela field, but our sample represents a much larger population of on-average closer sources. Sheikh et al. (Reference Sheikh, Siemion, Enriquez, Price, Isaacson, Lebofsky, Gajjar and Kalas2020) also convert their EIRP values to the fraction of signal capacity for the Aricebo Transmitter (
$17590\,{\times}\,10^{9}$
W for stellar distances between 7 and 143 pc. These are similar distances to the stars we present in Table 3 for the nearby stars from Gaia in the Vela field, but our sample represents a much larger population of on-average closer sources. Sheikh et al. (Reference Sheikh, Siemion, Enriquez, Price, Isaacson, Lebofsky, Gajjar and Kalas2020) also convert their EIRP values to the fraction of signal capacity for the Aricebo Transmitter (![]() $\mbox{L}_{A}$
). Their value of 0.033 for a star at 27 pc is a factor of two lower than for a star in our survey at the same distance (0.068), recognising the difference in frequency between the GBT and the MWA and the fact that the GBT has better frequency resolution than the MWA.
$\mbox{L}_{A}$
). Their value of 0.033 for a star at 27 pc is a factor of two lower than for a star in our survey at the same distance (0.068), recognising the difference in frequency between the GBT and the MWA and the fact that the GBT has better frequency resolution than the MWA.
For the first time, we obtain simultaneous upper limits on EIRP for in excess of 10 million stellar systems without known exoplanets, although the EIRP limits for the majority of distant systems are well above ![]() $10^{13}$
W. For any future exoplanet discoveries for systems in this field, the low-frequency EIRP upper limits are immediately available from our data.
$10^{13}$
W. For any future exoplanet discoveries for systems in this field, the low-frequency EIRP upper limits are immediately available from our data.
Seto & Kashiyama (Reference Seto and Kashiyama2020) completed an astrometric study of F-,G-, and K-type stars in Gaia Data Release 2 for interstellar communications, from the view point of the sender, and concluded that surveys like Gaia will be necessary to target these potential signals. Petigura, Marcy, & Howard (Reference Petigura, Marcy and Howard2013) suggest that approximately 20% of Galactic Sun-like stars could have Earth-sized planets in their habitable zones and Kipping (Reference Kipping2020) suggests that searching for technosignatures from stars with stellar types much earlier than our Sun may not be necessary, as life is unlikely to ever evolve. This means that matching SETI survey data to the Gaia survey is going to be an important approach for the future of SETI.
We compare our results to Figure 5 of Price et al. (Reference Price2020), in which the results of previous surveys are presented in a plane defined by minimum EIRP (![]() $\mbox{EIRP}_{\textrm{min}}$
) at the maximum stellar distance and Transmitter Rate, (
$\mbox{EIRP}_{\textrm{min}}$
) at the maximum stellar distance and Transmitter Rate, (![]() $\mbox{N}_{\textrm{star}}$
(
$\mbox{N}_{\textrm{star}}$
(![]() $\frac{\nu_{c}}{\nu_{tot}}))^{-1}$
, where
$\frac{\nu_{c}}{\nu_{tot}}))^{-1}$
, where ![]() $\mbox{N}_{\textrm{star}}$
is the total number of stars searched and
$\mbox{N}_{\textrm{star}}$
is the total number of stars searched and ![]() $\nu_{c}$
and
$\nu_{c}$
and ![]() $\nu_{tot}$
are the central frequency of the band (113.28 MHz) and the total bandwidth (30.72 MHz), respectively. For our survey using the Gaia catalogue, we see that our results sit below the most constraining limits set by prior work within this particular parameter space when using a distance of 1.7 kpc and a channel bandwidth of 10 kHz.
$\nu_{tot}$
are the central frequency of the band (113.28 MHz) and the total bandwidth (30.72 MHz), respectively. For our survey using the Gaia catalogue, we see that our results sit below the most constraining limits set by prior work within this particular parameter space when using a distance of 1.7 kpc and a channel bandwidth of 10 kHz.

Figure 5. Figure 5 from Price et al. (Reference Price2020) with our results for the Gaia catalogue survey (Section 3.2) shown for comparison. We report the results using a maximum RMS of ![]() $0.06\,\text{Jy beam}^{-1}$
and when we limit the distances to less than 50 pc, as per Figure 4 and for all stars less than 1.7 kpc. The value of 1.7 kpc is chosen as it is the distance to the Vela Molecular Cloud complex, a stellar-rich environment towards the Carina-Sagittarius spiral arm. The black ovals are the EIRP values per Equation (1) assuming a 10-kHz channel bandwidth and the red ovals are using the EIRP values assuming a transmission bandwidth of 10 Hz. These results span the diagonal grey line representing a fit between the previous most constraining data points for Transmitter Rate and
$0.06\,\text{Jy beam}^{-1}$
and when we limit the distances to less than 50 pc, as per Figure 4 and for all stars less than 1.7 kpc. The value of 1.7 kpc is chosen as it is the distance to the Vela Molecular Cloud complex, a stellar-rich environment towards the Carina-Sagittarius spiral arm. The black ovals are the EIRP values per Equation (1) assuming a 10-kHz channel bandwidth and the red ovals are using the EIRP values assuming a transmission bandwidth of 10 Hz. These results span the diagonal grey line representing a fit between the previous most constraining data points for Transmitter Rate and ![]() $\mbox{EIRP}_{\text{min}}$
at the most distant star when using the MWA channel bandwidth. The solid and dashed vertical lines represent the EIRP of the Arecibo planetary radar, and the total power from the Sun incident on the Earth, respectively.
$\mbox{EIRP}_{\text{min}}$
at the most distant star when using the MWA channel bandwidth. The solid and dashed vertical lines represent the EIRP of the Arecibo planetary radar, and the total power from the Sun incident on the Earth, respectively.
We also consider a different metric, utilising the method of Wright et al. (Reference Wright, Kanodia and Lubar2018) in order to calculate the ‘haystack fraction’ accessible to our observations of the Vela region. This metric takes into account the observational parameters without significant assumptions. We find the haystack fraction to be ![]() $\sim2\,{\times}\,10^{-16}$
, which is almost two orders of magnitude higher than the highest previous fraction listed in Wright et al. (Reference Wright, Kanodia and Lubar2018), which was for our previous observations of the Orion Molecular Cloud (Galactic Anticentre) field. Our new result yields the haystack fraction almost three orders of magnitude higher than the largest non-MWA survey listed by Wright et al. (Reference Wright, Kanodia and Lubar2018).
$\sim2\,{\times}\,10^{-16}$
, which is almost two orders of magnitude higher than the highest previous fraction listed in Wright et al. (Reference Wright, Kanodia and Lubar2018), which was for our previous observations of the Orion Molecular Cloud (Galactic Anticentre) field. Our new result yields the haystack fraction almost three orders of magnitude higher than the largest non-MWA survey listed by Wright et al. (Reference Wright, Kanodia and Lubar2018).
Recently, Westby & Conselice (Reference Westby and Conselice2020) described the so-called Strong Astrobiological Copernican scenario, in which life must arise in a system on timescales comparable to those experienced on Earth (4.5–5 Gyr) and posit on this basis that at least ![]() $36\pm^{175}_{32}$
civilisations capable of generating technosignatures exist in our Galaxy. The closest system to Earth would be
$36\pm^{175}_{32}$
civilisations capable of generating technosignatures exist in our Galaxy. The closest system to Earth would be ![]() $17\,000\pm^{33\,600}_{10\,000}$
lt-yr distant. The numbers are not large and represent a very small part of the haystack fraction parameter space, throwing into focus that SETI experiments will need to enter the statistical domain of Gaia-sized samples.
$17\,000\pm^{33\,600}_{10\,000}$
lt-yr distant. The numbers are not large and represent a very small part of the haystack fraction parameter space, throwing into focus that SETI experiments will need to enter the statistical domain of Gaia-sized samples.
Overall, our MWA surveys show the rapid progress that can currently be made in SETI at radio frequencies, using wide field and sensitive facilities, but also show that SETI surveys have a long way to go. The continued use of the MWA, and the future similar use of the SKA at much higher sensitivities, offers a mechanism to make significant cuts into the haystack fraction of Wright et al. (Reference Wright, Kanodia and Lubar2018), while maintaining a primary focus on astrophysical investigations, making excellent commensal use of these large-scale facilities.
4.1. Facilities
This scientific work makes use of the MRO, operated by CSIRO. We acknowledge the Wajarri Yamatji people as the traditional owners of the Observatory site. Support for the operation of the MWA is provided by the Australian Government (NCRIS), under a contract to Curtin University administered by Astronomy Australia Limited. Establishment of ASKAP, the MRO, and the Pawsey Supercomputing Centre are initiatives of the Australian Government, with support from the Government of Western Australia and the Science and Industry Endowment Fund.
4.2. Computer services
We acknowledge the Pawsey Supercomputing Centre which is supported by the Western Australian and Australian Governments. Access to Pawsey Data Storage Services is governed by a Data Storage and Management Policy. All-Sky Virtual Observatory (ASVO) has received funding from the Australian Commonwealth Government through the National eResearch Collaboration Tools and Resources (NeCTAR) Project, the Australian National Data Service, and the National Collaborative Research Infrastructure Strategy. This research has made use of NASA’s Astrophysics Data System Bibliographic Services.
4.3. Software
The following softwares were used in the creation of the data cubes:
aoflagger and cotter—Offringa et al. (Reference Offringa2015)
WSClean—Offringa et al. (Reference Offringa2014); Offringa & Smirnov (Reference Offringa and Smirnov2017)
Aegean—Hancock et al. (Reference Hancock, Trott and Hurley-Walker2018)
miriad—Sault, Teuben, & Wright (Reference Sault, Teuben, Wright, Shaw, Payne and Hayes1995)
TOPCAT—Taylor (Reference Taylor, Shopbell, Britton and Ebert2005)
Acknowledgements
We would like to thank Daniel Price (Swinburne University) for his insight and comments on this paper and Natasha Hurley-Walker for help with the continuum subtraction. We would also like to thank the anonymous reviewer for their helpful comments that significantly improved our manuscript.