1. Introduction
For a number field K, we define the Möbius function
![]() $\mu(\mathfrak{a}) = \mu_{K}(\mathfrak{a})$
assigning an integer to each integral ideal
$\mu(\mathfrak{a}) = \mu_{K}(\mathfrak{a})$
assigning an integer to each integral ideal
![]() $\mathfrak{a}$
, according to the rule
$\mathfrak{a}$
, according to the rule
 \begin{equation*} \mu(\mathfrak{p}^k) \;:\!=\; \begin{cases} 1 & \text{if $k = 0$} \\[5pt] -1 & \text{if $k = 1$} \\[5pt] 0 & \text{if $k \geq 2$} \end{cases}\end{equation*}
\begin{equation*} \mu(\mathfrak{p}^k) \;:\!=\; \begin{cases} 1 & \text{if $k = 0$} \\[5pt] -1 & \text{if $k = 1$} \\[5pt] 0 & \text{if $k \geq 2$} \end{cases}\end{equation*}
for prime ideals
![]() $\mathfrak{p}$
. This is extended multiplicatively by the unique factorisation of ideals. The summatory function of the Möbius function is the Mertens function
$\mathfrak{p}$
. This is extended multiplicatively by the unique factorisation of ideals. The summatory function of the Möbius function is the Mertens function
where
![]() $\mu_K(x) \;:\!=\; \sum_{N(\mathfrak{a}) = x} \mu(\mathfrak{a})$
is replaced with
$\mu_K(x) \;:\!=\; \sum_{N(\mathfrak{a}) = x} \mu(\mathfrak{a})$
is replaced with
![]() $({1}/{2}) \mu_K(x)$
if x is an integer. With this convention, the function
$({1}/{2}) \mu_K(x)$
if x is an integer. With this convention, the function
![]() $M_K(x)$
is expressed as the inverse Mellin transform of
$M_K(x)$
is expressed as the inverse Mellin transform of
![]() $1/s\zeta_K(s)$
via the formula
$1/s\zeta_K(s)$
via the formula
This relation can be seen as the definition of
![]() $M_K(x)$
as a matter of practical convenience.
$M_K(x)$
as a matter of practical convenience.
1·1. The naïve Mertens-type conjecture over a number field
For
![]() $K = \mathbb{Q}$
, the classical conjecture of Mertens [
Reference MertensMer97
] in 1897 asserts that
$K = \mathbb{Q}$
, the classical conjecture of Mertens [
Reference MertensMer97
] in 1897 asserts that
Knowing that the Riemann hypothesis is equivalent to the weaker statement that
![]() $M(x) = O(x^{1/2 + \varepsilon})$
for all
$M(x) = O(x^{1/2 + \varepsilon})$
for all
![]() $\varepsilon>0$
[
Reference TitchmarshTit86
, theorem 14·25(c)], this seemed to represent a viable avenue towards the Riemann hypothesis for the Riemann zeta function
$\varepsilon>0$
[
Reference TitchmarshTit86
, theorem 14·25(c)], this seemed to represent a viable avenue towards the Riemann hypothesis for the Riemann zeta function
![]() $\zeta(s)$
. Before the landmark work of Ingham [
Reference InghamIng42
] in 1942, preliminary calculations of Mertens and von Sterneck even compelled the hypothesis
$\zeta(s)$
. Before the landmark work of Ingham [
Reference InghamIng42
] in 1942, preliminary calculations of Mertens and von Sterneck even compelled the hypothesis
![]() $x^{-1/2}|M(x)|\;\leq {1}/{2}$
for sufficiently large x. Nevertheless, using lattice basis reduction algorithms, the conjecture was disproven by Odlyzko and te Riele [
Reference Odlyzko and te RieleOtR85
] in 1985, who obtained explicit bounds larger in absolute value than 1 for
$x^{-1/2}|M(x)|\;\leq {1}/{2}$
for sufficiently large x. Nevertheless, using lattice basis reduction algorithms, the conjecture was disproven by Odlyzko and te Riele [
Reference Odlyzko and te RieleOtR85
] in 1985, who obtained explicit bounds larger in absolute value than 1 for
![]() $x^{-1/2}M(x)$
on either side in the limit. The current record in this direction has been achieved by Hurst [
Reference HurstHur18
] in 2018, namely
$x^{-1/2}M(x)$
on either side in the limit. The current record in this direction has been achieved by Hurst [
Reference HurstHur18
] in 2018, namely
It is now common belief that
![]() $x^{-1/2}M(x)$
grows arbitrarily large in both directions, but this has not yet been proven unconditionally [
Reference Odlyzko and te RieleOtR85
]. Indeed, Ingham [
Reference InghamIng42
, theorem A] showed that, assuming the Riemann hypothesis and that the imaginary parts of the nontrivial zeros of
$x^{-1/2}M(x)$
grows arbitrarily large in both directions, but this has not yet been proven unconditionally [
Reference Odlyzko and te RieleOtR85
]. Indeed, Ingham [
Reference InghamIng42
, theorem A] showed that, assuming the Riemann hypothesis and that the imaginary parts of the nontrivial zeros of
![]() $\zeta(s)$
are
$\zeta(s)$
are
![]() $\mathbb{Q}$
-linearly independent, the claim is true. This work marked the first serious doubt regarding the Mertens conjecture until its subsequent disproof. In fact, preliminary computational support for the linear independence hypothesis is supplied in the proof of Best and Trudgian [
Reference Best and TrudgianBT15
], which builds upon a previous result of Bateman et al. [
Reference Bateman, Brown, Hall, Kloss and StemmlerBBH+71
].
$\mathbb{Q}$
-linearly independent, the claim is true. This work marked the first serious doubt regarding the Mertens conjecture until its subsequent disproof. In fact, preliminary computational support for the linear independence hypothesis is supplied in the proof of Best and Trudgian [
Reference Best and TrudgianBT15
], which builds upon a previous result of Bateman et al. [
Reference Bateman, Brown, Hall, Kloss and StemmlerBBH+71
].
Several mathematicians have investigated analogues of this conjecture in other settings, some achieving corresponding disproofs. Anderson [
Reference AndersonAnd79
] studied the case of cusp forms of sufficiently large weight
![]() $k \equiv 2 \pmod 4$
on the full modular group
$k \equiv 2 \pmod 4$
on the full modular group
![]() $\textrm{SL}_{2}(\mathbb{Z})$
. Grupp [
Reference GruppGru82
] generalised the work of Anderson to cusp forms of any even weight k. Humphries [
Reference HumphriesHum14
] considered Mertens-type conjectures for function fields of smooth projective curves over
$\textrm{SL}_{2}(\mathbb{Z})$
. Grupp [
Reference GruppGru82
] generalised the work of Anderson to cusp forms of any even weight k. Humphries [
Reference HumphriesHum14
] considered Mertens-type conjectures for function fields of smooth projective curves over
![]() $\mathbb{F}_q$
. Our work focuses on the case of number fields and seeks a disproof of the relevant conjecture in emulation of previous work.
$\mathbb{F}_q$
. Our work focuses on the case of number fields and seeks a disproof of the relevant conjecture in emulation of previous work.
Following the aforementioned works, it is most relevant to formulate a conjecture based on the limiting behaviour of the arithmetic function
![]() $M_K(x)$
. Let K be a number field, and write
$M_K(x)$
. Let K be a number field, and write
We now state the guiding question of our work.
Conjecture (The naïve Mertens-type conjectureover K).
![]() $-1\leq M_K^-\leq M_K^+\leq 1$
.
$-1\leq M_K^-\leq M_K^+\leq 1$
.
Although this is in some ways a naïve generalisation of the original Mertens conjecture, we have chosen 1 as the critical constant following tradition. Yet, it can be seen that this choice will be of strategic importance for our method.
A corresponding conclusion to that of Ingham’s theorem can be shown to hold for the function
![]() $M_K(x)$
(see conjecture 1·6, theorem 2·1, and lemma 2·4), which leads to the prediction that the naïve Mertens-type conjecture over K is indeed false for all K. Towards partial disproofs of the conjecture, the quadratic fields K are the most straightforward to consider and we give certain unconditional results.
$M_K(x)$
(see conjecture 1·6, theorem 2·1, and lemma 2·4), which leads to the prediction that the naïve Mertens-type conjecture over K is indeed false for all K. Towards partial disproofs of the conjecture, the quadratic fields K are the most straightforward to consider and we give certain unconditional results.
Theorem 1·1. We have the following statements:
-
(a) let K be an imaginary quadratic extension of
 $\mathbb{Q}$
, with the exception of
$\mathbb{Q}$
, with the exception of
 $K = \mathbb{Q}(\sqrt{-3})$
. Then the naïve Mertens-type conjecture over K is false;
$K = \mathbb{Q}(\sqrt{-3})$
. Then the naïve Mertens-type conjecture over K is false; -
(b) let K be a real quadratic extension of
 $\mathbb{Q}$
, with the exception of
$\mathbb{Q}$
, with the exception of
 $K = \mathbb{Q}(\sqrt{5})$
. Then the naïve Mertens-type conjecture over K is false.
$K = \mathbb{Q}(\sqrt{5})$
. Then the naïve Mertens-type conjecture over K is false.
Remark. While the basic statement
![]() $|M_K(x)|\;\leq x^{1/2}$
for all
$|M_K(x)|\;\leq x^{1/2}$
for all
![]() $x \geq 1$
is false for
$x \geq 1$
is false for
![]() $K = \mathbb{Q}(\sqrt{-3})$
and
$K = \mathbb{Q}(\sqrt{-3})$
and
![]() $K = \mathbb{Q}(\sqrt{5})$
(an easy computation demonstrates that
$K = \mathbb{Q}(\sqrt{5})$
(an easy computation demonstrates that
![]() $M_{\mathbb{Q}(\sqrt{-3})}(7) = -3$
and
$M_{\mathbb{Q}(\sqrt{-3})}(7) = -3$
and
![]() $M_{\mathbb{Q}(\sqrt{5})}(11) = -4$
), the methods of this paper are not immediately capable of demonstrating that the naïve Mertens-type conjecture fails for these fields (as this requires knowledge of limiting behaviour), unlike the other cases of the previous theorem. It is, however, likely that computations analogous to those used in [
Reference Odlyzko and te RieleOtR85
] to falsify the original Mertens conjecture would suffice for both of these quadratic fields as well.
$M_{\mathbb{Q}(\sqrt{5})}(11) = -4$
), the methods of this paper are not immediately capable of demonstrating that the naïve Mertens-type conjecture fails for these fields (as this requires knowledge of limiting behaviour), unlike the other cases of the previous theorem. It is, however, likely that computations analogous to those used in [
Reference Odlyzko and te RieleOtR85
] to falsify the original Mertens conjecture would suffice for both of these quadratic fields as well.
The techniques of the proof of Theorem 1·1 allow us to arrive at a similar result for general number fields of degree
![]() $n_K > 2$
. In what follows, the signature
$n_K > 2$
. In what follows, the signature
![]() $(r_1,r_2)$
of a number field K is the ordered pair of non-negative integers that encodes the number
$(r_1,r_2)$
of a number field K is the ordered pair of non-negative integers that encodes the number
![]() $r_1$
of real embeddings and
$r_1$
of real embeddings and
![]() $r_2$
of complex conjugate pairs of embeddings of K.
$r_2$
of complex conjugate pairs of embeddings of K.
Theorem 1·2. Fix a signature
![]() $(r_1,r_2)$
. There exists some
$(r_1,r_2)$
. There exists some
![]() $\mathcal{D} = \mathcal{D}_{r_1,2r_2} > 0$
depending only on
$\mathcal{D} = \mathcal{D}_{r_1,2r_2} > 0$
depending only on
![]() $(r_1,r_2)$
for which the naïve Mertens-type conjecture is false for every extension K of
$(r_1,r_2)$
for which the naïve Mertens-type conjecture is false for every extension K of
![]() $\mathbb{Q}$
of signature
$\mathbb{Q}$
of signature
![]() $(r_1,r_2)$
with absolute discriminant
$(r_1,r_2)$
with absolute discriminant
![]() $\textrm{D}_K > \mathcal{D}$
.
$\textrm{D}_K > \mathcal{D}$
.
We establish these results in Section 3.
1·2. Logarithmic limiting distributions
In order to study the Mertens function over a number field, we now define another object which serves as a chief interest of our work.
Definition 1·3. We say that a function
![]() $\vec{\phi}: [0,\infty) \rightarrow \mathbb{R}^{\ell}$
possesses a limiting distribution
$\vec{\phi}: [0,\infty) \rightarrow \mathbb{R}^{\ell}$
possesses a limiting distribution
![]() $\nu$
on
$\nu$
on
![]() $\mathbb{R}^{\ell}$
if
$\mathbb{R}^{\ell}$
if
![]() $\nu$
is a probability measure on
$\nu$
is a probability measure on
![]() $\mathbb{R}^{\ell}$
and
$\mathbb{R}^{\ell}$
and
for all bounded continuous real-valued functions f on
![]() $\mathbb{R}^{\ell}$
.
$\mathbb{R}^{\ell}$
.
Recent years have seen great refinements in the probabilistic methods used to study number-theoretic functions. The influential work of Rubinstein and Sarnak [ Reference Rubinstein and SarnakRS94 ] in establishing the existence of limiting distributions pertaining to various questions on Rényi–Shanks prime number races, with its extensive generalisations in the work of Ng [ Reference NgNg04 ], Humphries [ Reference HumphriesHum13 ], and Akbary–Ng–Shahabi [ Reference Akbary, Ng and ShahabiANS14 ], has seen wide applications to the summatory functions in number theory, including those of the Liouville function and the Möbius function. Pertaining to the classical Mertens function M(x), Ng [ Reference NgNg04 ] established that the function
possesses a limiting distribution
![]() $\nu$
on
$\nu$
on
![]() $\mathbb{R}$
, assuming the Riemann hypothesis for and the following conjecture of Gonek and Hejhal on the discrete moments of
$\mathbb{R}$
, assuming the Riemann hypothesis for and the following conjecture of Gonek and Hejhal on the discrete moments of
![]() $\zeta'(s)$
at the zeros:
$\zeta'(s)$
at the zeros:
where, with the convention
![]() $\rho = {1}/{2} + i\gamma$
,
$\rho = {1}/{2} + i\gamma$
,
 \begin{equation*} J_k(T) \;:\!=\; \sum_{\substack{0 < \gamma \leq T \\ \zeta(\frac{1}{2} + i\gamma) = 0}} |\zeta'(\rho)|^{2k}.\end{equation*}
\begin{equation*} J_k(T) \;:\!=\; \sum_{\substack{0 < \gamma \leq T \\ \zeta(\frac{1}{2} + i\gamma) = 0}} |\zeta'(\rho)|^{2k}.\end{equation*}
We prove the following generalisation of Ng’s result.
Theorem 1·4. Let K be an abelian number field. Assume the Riemann hypothesis for
![]() $\zeta_K(s)$
, and the following extension of (1·2):
$\zeta_K(s)$
, and the following extension of (1·2):
 \begin{equation} J_{-1}^K(T) \;:\!=\; \sum_{\substack{0 \leq \gamma \leq T \\ \zeta_K(\frac{1}{2} + i\gamma) = 0}} \frac{1}{|\zeta_K'(\rho)|^2} \ll_{\alpha} T^{1 + \alpha},\end{equation}
\begin{equation} J_{-1}^K(T) \;:\!=\; \sum_{\substack{0 \leq \gamma \leq T \\ \zeta_K(\frac{1}{2} + i\gamma) = 0}} \frac{1}{|\zeta_K'(\rho)|^2} \ll_{\alpha} T^{1 + \alpha},\end{equation}
for some
![]() $0 \leq \alpha < 2 - \sqrt{3}$
. Then the function
$0 \leq \alpha < 2 - \sqrt{3}$
. Then the function
possesses a limiting distribution
![]() $\nu_K$
on
$\nu_K$
on
![]() $\mathbb{R}$
:
$\mathbb{R}$
:
for all bounded continuous real-valued functions f on
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
This is proven in Section 4.
To be well-defined, the bound (1·3) implies that all the nontrivial zeros of
![]() $\zeta_K(s)$
are simple. This dictates, in consequence, the non-vanishing at
$\zeta_K(s)$
are simple. This dictates, in consequence, the non-vanishing at
![]() $s = {1}/{2}$
of
$s = {1}/{2}$
of
![]() $\zeta_K(s)$
, the sign of whose functional equation always prescribes at
$\zeta_K(s)$
, the sign of whose functional equation always prescribes at
![]() $s = {1}/{2}$
a zero of even multiplicity.
$s = {1}/{2}$
a zero of even multiplicity.
The validity of these suppositions is most transparent when
![]() $K/\mathbb{Q}$
is a Galois extension, due to Artin factorisation for the Dedekind zeta functions of such number fields, and is markedly different between abelian and non-abelian Galois extensions. Conjecturally, it emerges in the abelian case from the conventional hypotheses that no two Dirichlet L-functions share a nontrivial zero and that no Dirichlet L-function vanishes at the central point
$K/\mathbb{Q}$
is a Galois extension, due to Artin factorisation for the Dedekind zeta functions of such number fields, and is markedly different between abelian and non-abelian Galois extensions. Conjecturally, it emerges in the abelian case from the conventional hypotheses that no two Dirichlet L-functions share a nontrivial zero and that no Dirichlet L-function vanishes at the central point
![]() $s = {1}/{2}$
. Both of these assertions are weaker consequences of the Grand Simplicity Hypothesis for the Dirichlet L-functions (cf. [
Reference Rubinstein and SarnakRS94
]). The latter conjecture is remarkably well-studied, along with the work of Balasubramanian–Murty [
Reference Balasubramanian and Kumar MurtyBM92
] and Iwaniec–Sarnak [
Reference Iwaniec and SarnakIS99
] showing that
$s = {1}/{2}$
. Both of these assertions are weaker consequences of the Grand Simplicity Hypothesis for the Dirichlet L-functions (cf. [
Reference Rubinstein and SarnakRS94
]). The latter conjecture is remarkably well-studied, along with the work of Balasubramanian–Murty [
Reference Balasubramanian and Kumar MurtyBM92
] and Iwaniec–Sarnak [
Reference Iwaniec and SarnakIS99
] showing that
![]() $L({1}/{2},\chi_q) \neq 0$
for a positive proportion of the primitive characters
$L({1}/{2},\chi_q) \neq 0$
for a positive proportion of the primitive characters
![]() $\chi_q$
of any sufficiently large modulus q.
$\chi_q$
of any sufficiently large modulus q.
On the other hand, for non-abelian number fields, the simplicity hypothesis is known to be false unconditionally, with the zeta function of any such number field having infinitely many nontrivial zeros of multiplicity at least 2 (cf. [
Reference Hu, Kaneko, Martin and SchildkrautHKMS
]). By example, the non-vanishing at
![]() $s = {1}/{2}$
has also been disproven, with the earliest examples of number fields with
$s = {1}/{2}$
has also been disproven, with the earliest examples of number fields with
![]() $\zeta_K({1}/{2}) = 0$
known to Armitage and Serre (see Section 6 for further discussion). This renders an obstruction to any extension of Theorem 1·4 to the non-abelian case.
$\zeta_K({1}/{2}) = 0$
known to Armitage and Serre (see Section 6 for further discussion). This renders an obstruction to any extension of Theorem 1·4 to the non-abelian case.
The conjecture (1·2) is the special case
![]() $k = -1$
of a conjecture
$k = -1$
of a conjecture
![]() $J_{k}(T) \asymp T(\log T)^{(k+1)^2}$
that was first proposed independently by Gonek [
Reference GonekGon89
] and Hejhal [
Reference HejhalHej89
] for all
$J_{k}(T) \asymp T(\log T)^{(k+1)^2}$
that was first proposed independently by Gonek [
Reference GonekGon89
] and Hejhal [
Reference HejhalHej89
] for all
![]() $k \in {\mathbb {R}}$
in view of their examinations of the discrete moments
$k \in {\mathbb {R}}$
in view of their examinations of the discrete moments
![]() $J_{k}(T)$
. Gonek also predicted the asymptotic formula
$J_{k}(T)$
. Gonek also predicted the asymptotic formula
![]() $J_{-1}(T) \sim ({3}/{\pi^3})T$
and proved the bound
$J_{-1}(T) \sim ({3}/{\pi^3})T$
and proved the bound
![]() $J_{-1}(T) \gg T$
. It was subsequently proposed by Keating–Snaith [
Reference Keating and SnaithKS00
] that random matrix theoretic heuristics could be used in connection with conjectures about moments of the zeta function. In particular, they modeled the value distribution of
$J_{-1}(T) \gg T$
. It was subsequently proposed by Keating–Snaith [
Reference Keating and SnaithKS00
] that random matrix theoretic heuristics could be used in connection with conjectures about moments of the zeta function. In particular, they modeled the value distribution of
![]() $\zeta(s)$
near the critical line by the characteristic polynomial of a large unitary random matrix. Expanding upon this work, Hughes–Keating–O’Connell [
Reference Hughes, Keating and O’ConnellHKO00
] conjectured asymptotic formulae for all
$\zeta(s)$
near the critical line by the characteristic polynomial of a large unitary random matrix. Expanding upon this work, Hughes–Keating–O’Connell [
Reference Hughes, Keating and O’ConnellHKO00
] conjectured asymptotic formulae for all
![]() $J_{k}(T)$
,
$J_{k}(T)$
,
![]() $k > -{3}/{2}$
, giving explicit numerical constants depending on k. The random matrix approach has proven to produce reliable conjectures; for instance, the conjecture of Hughes–Keating–O’Connell in the case
$k > -{3}/{2}$
, giving explicit numerical constants depending on k. The random matrix approach has proven to produce reliable conjectures; for instance, the conjecture of Hughes–Keating–O’Connell in the case
![]() $k = -1$
agrees with that of Gonek. It is expected that similar heuristics would yield accurate conjectures for positive moments of Dedekind zeta functions as well (see [
Reference Gonek, Hughes and KeatingGHK07, Reference Bui, Gonek and MilinovichBGM15, Reference HeapHea21
]). They would also be useful in support of (1·3).
$k = -1$
agrees with that of Gonek. It is expected that similar heuristics would yield accurate conjectures for positive moments of Dedekind zeta functions as well (see [
Reference Gonek, Hughes and KeatingGHK07, Reference Bui, Gonek and MilinovichBGM15, Reference HeapHea21
]). They would also be useful in support of (1·3).
We argue in support of the conjecture in the equation (1·3) in Section 4. For now, we have not appealed to random matrix theory, instead relying on prior work and a series of generous but not unreasonable assumptions, by analogy with the case of the Riemann zeta function.
As a direct consequence of the arguments to be presented in Section 4, it behooves us to mention that Corollary 1·15 of Akbary–Ng–Shahabi [ Reference Akbary, Ng and ShahabiANS14 ] yields the following analogue of the weak Mertens conjecture as stated in [ Reference NgNg04 , theorem 1·3].
Theorem 1·5. With the same assumptions as in Theorem 1·4, we have
where
![]() $\beta = 2\sum_{\gamma > 0} |\rho \zeta_K'(\rho)|^{-2}$
. The assumption
$\beta = 2\sum_{\gamma > 0} |\rho \zeta_K'(\rho)|^{-2}$
. The assumption
![]() $J_{-1}^K(T) \ll_{\alpha} T^{1+\alpha}$
implies that the series defining
$J_{-1}^K(T) \ll_{\alpha} T^{1+\alpha}$
implies that the series defining
![]() $\beta$
is convergent.
$\beta$
is convergent.
In the spirit of the work of Rubinstein–Sarnak and Ng, the existence of a limiting distribution for
![]() $\phi_K(y)$
yields a number of consequences which are conditional on the following supplemental analogue of the linear independence for
$\phi_K(y)$
yields a number of consequences which are conditional on the following supplemental analogue of the linear independence for
![]() $\zeta(s)$
.
$\zeta(s)$
.
Conjecture 1·6. (Linear independence conjecture for
![]() $\zeta_K(s)$
). The multiset of the non-negative imaginary parts of the nontrivial zeros of
$\zeta_K(s)$
). The multiset of the non-negative imaginary parts of the nontrivial zeros of
![]() $\zeta_K(s)$
is linearly independent over the rationals.
$\zeta_K(s)$
is linearly independent over the rationals.
We remark that this conjecture encompasses the simplicity of the zeros of
![]() $\zeta_K(s)$
, as well as the non-vanishing of
$\zeta_K(s)$
, as well as the non-vanishing of
![]() $\zeta_K(s)$
at
$\zeta_K(s)$
at
![]() $s = {1}/{2}$
, and is hence a viable conjecture for a normal extension
$s = {1}/{2}$
, and is hence a viable conjecture for a normal extension
![]() $K/\mathbb{Q}$
only when the extension is abelian. Its principal use in the original work of Rubinstein–Sarnak is to obtain an expression for the Fourier transform of the limiting distribution. By [
Reference Akbary, Ng and ShahabiANS14
, corollary 1·3], the following is a direct consequence of Theorem 1·4.
$K/\mathbb{Q}$
only when the extension is abelian. Its principal use in the original work of Rubinstein–Sarnak is to obtain an expression for the Fourier transform of the limiting distribution. By [
Reference Akbary, Ng and ShahabiANS14
, corollary 1·3], the following is a direct consequence of Theorem 1·4.
Theorem 1·7. Let K be an abelian extension of
![]() $\mathbb{Q}$
. Assume the Riemann hypothesis for
$\mathbb{Q}$
. Assume the Riemann hypothesis for
![]() $\zeta_K(s)$
, that
$\zeta_K(s)$
, that
![]() $\zeta_K({1}/{2}) \neq 0$
, and that
$\zeta_K({1}/{2}) \neq 0$
, and that
![]() $J_{-1}^K(T) \ll T^{1+\alpha}$
for some
$J_{-1}^K(T) \ll T^{1+\alpha}$
for some
![]() $0 \leq \alpha < 2 - \sqrt{3}$
, and let
$0 \leq \alpha < 2 - \sqrt{3}$
, and let
![]() $\nu_K$
be the limiting distribution associated to
$\nu_K$
be the limiting distribution associated to
![]() $\phi_K(y)$
as in Theorem 1·4. Assume moreover Conjecture 1·6. Then the Fourier transform
$\phi_K(y)$
as in Theorem 1·4. Assume moreover Conjecture 1·6. Then the Fourier transform
of
![]() $\nu_K$
at
$\nu_K$
at
![]() $\xi \in \mathbb{R}$
exists and is equal to
$\xi \in \mathbb{R}$
exists and is equal to
 \begin{equation*} \widehat{\nu}_K(\xi) = \prod_{\substack{|\gamma| > 0 \\ \zeta_K(\rho) = 0}} \tilde J_0 \left( \frac{2 \xi}{|\rho \zeta_K'(\rho)|} \right),\end{equation*}
\begin{equation*} \widehat{\nu}_K(\xi) = \prod_{\substack{|\gamma| > 0 \\ \zeta_K(\rho) = 0}} \tilde J_0 \left( \frac{2 \xi}{|\rho \zeta_K'(\rho)|} \right),\end{equation*}
where
![]() $\tilde J_0(z)$
is the Bessel function
$\tilde J_0(z)$
is the Bessel function
This result can be used in pursuit of logarithmic density results: for instance, that the set of numbers
![]() $x \geq 1$
in the set
$x \geq 1$
in the set
![]() $P_{\beta} = \{x^{-1/2}|M_K(x)|\;\leq \beta\}$
has a logarithmic density, for certain
$P_{\beta} = \{x^{-1/2}|M_K(x)|\;\leq \beta\}$
has a logarithmic density, for certain
![]() $\beta > 0$
of interest.
$\beta > 0$
of interest.
Definition 1·8. For
![]() $P \subset [0, \infty)$
, set
$P \subset [0, \infty)$
, set
If the limit exists, we say that the logarithmic density of P is
![]() $\delta(P)$
.
$\delta(P)$
.
Following the arguments of [
Reference HumphriesHum13
, corollary 6·3, lemma 6·4], we deduce that the Fourier transform
![]() $\widehat{\nu}_K$
so constructed is symmetric and observes rapid decay as a function of
$\widehat{\nu}_K$
so constructed is symmetric and observes rapid decay as a function of
![]() $\xi$
. Hence,
$\xi$
. Hence,
![]() $\widehat{\nu}_K$
is absolutely continuous with respect to the Lebesgue measure on
$\widehat{\nu}_K$
is absolutely continuous with respect to the Lebesgue measure on
![]() $\mathbb{R}$
. After a logarithmic change of coordinates, this yields the following extension of the conclusion of Theorem 1·4 to characteristic functions of well-behaved sets.
$\mathbb{R}$
. After a logarithmic change of coordinates, this yields the following extension of the conclusion of Theorem 1·4 to characteristic functions of well-behaved sets.
Corollary 1·9. With the same assumptions as in Theorem 1·7,
for all Borel sets
![]() $B \subset \mathbb{R}$
with boundary of Lebesgue measure zero.
$B \subset \mathbb{R}$
with boundary of Lebesgue measure zero.
Thus, the set
![]() $P_{\beta} = \{x \geq 1 \mid |M_K(x)|\;\leq \beta \sqrt{x}\}$
has a logarithmic density, under the assumptions of RH, linear independence, and
$P_{\beta} = \{x \geq 1 \mid |M_K(x)|\;\leq \beta \sqrt{x}\}$
has a logarithmic density, under the assumptions of RH, linear independence, and
![]() $J_{-1}^K(T) \ll T^{1+\alpha}$
. See Section 7 for further discussion.
$J_{-1}^K(T) \ll T^{1+\alpha}$
. See Section 7 for further discussion.
2. Preliminaries
2·1. Notation and conventions
Throughout this paper, we use the following conventions:
-
(i) K is a number field;
-
(ii)
 $n_K = [K : {\mathbb {Q}}]$
;
$n_K = [K : {\mathbb {Q}}]$
; -
(iii)
 $r_1$
and
$r_1$
and
 $2r_2$
are the number of real and complex embeddings of K, respectively;
$2r_2$
are the number of real and complex embeddings of K, respectively; -
(iv)
 $\Delta_K$
is the discriminant of K;
$\Delta_K$
is the discriminant of K; -
(v)
 $\textrm{D}_K = \vert \Delta_K \vert$
is the absolute discriminant of K;
$\textrm{D}_K = \vert \Delta_K \vert$
is the absolute discriminant of K; -
(vi)
 $\zeta_K(s)$
is the Dedekind zeta function of K.
$\zeta_K(s)$
is the Dedekind zeta function of K.
Some theorems in this paper apply only to real or imaginary quadratic number fields. In these cases, we will specify any additional hypotheses on K. Otherwise, it is assumed that K is a general number field.
The Riemann hypothesis for
![]() $\zeta_K(s)$
will denote the conjecture that all nontrivial zeros of
$\zeta_K(s)$
will denote the conjecture that all nontrivial zeros of
![]() $\zeta_K(s)$
lie on the critical line
$\zeta_K(s)$
lie on the critical line
![]() $\textrm{Re}(s) = {1}/{2}$
. In light of this,
$\textrm{Re}(s) = {1}/{2}$
. In light of this,
![]() $\rho$
will always denote a nontrivial zero of
$\rho$
will always denote a nontrivial zero of
![]() $\zeta_K(s)$
with imaginary part
$\zeta_K(s)$
with imaginary part
![]() $\gamma$
.
$\gamma$
.
2·2. Analytic properties of Dedekind zeta functions
In this section, we provide some preliminary statements about Dedekind zeta functions that will be used in the proofs of each of our results. We start with the functional equation for
![]() $\zeta_K(s)$
.
$\zeta_K(s)$
.
Theorem 2·1. For any number field K, the Dedekind zeta function
![]() $\zeta_K(s)$
satisfies
$\zeta_K(s)$
satisfies
 \begin{equation*} \zeta_K(1-s)= \zeta_K(s) \left(\frac{\textrm{D}_K}{\pi^{n_K}2^{n_K}}\right)^{s-\frac{1}{2}} \left( \frac{\pi}{2} \right)^{\frac{r_1}{2}}\frac{\Gamma(s)^{r_2}}{(\sin \frac{\pi s}{2})^{r_1} \Gamma(1-s)^{r_1+r_2}}.\end{equation*}
\begin{equation*} \zeta_K(1-s)= \zeta_K(s) \left(\frac{\textrm{D}_K}{\pi^{n_K}2^{n_K}}\right)^{s-\frac{1}{2}} \left( \frac{\pi}{2} \right)^{\frac{r_1}{2}}\frac{\Gamma(s)^{r_2}}{(\sin \frac{\pi s}{2})^{r_1} \Gamma(1-s)^{r_1+r_2}}.\end{equation*}
This functional equation extends
![]() $\zeta_K$
to a meromorphic function on
$\zeta_K$
to a meromorphic function on
![]() $\mathbb C$
, which is analytic everywhere except for a simple pole at
$\mathbb C$
, which is analytic everywhere except for a simple pole at
![]() $s=1$
.
$s=1$
.
The Dedekind zeta function has trivial zeros of order
![]() $r_2$
at each negative odd integer and of order
$r_2$
at each negative odd integer and of order
![]() $r_1+r_2$
at each negative even integer, as well as a trivial zero of order
$r_1+r_2$
at each negative even integer, as well as a trivial zero of order
![]() $r_1+r_2-1$
at
$r_1+r_2-1$
at
![]() $s=0$
. It also possesses nontrivial zeros, each of which lies in the critical strip
$s=0$
. It also possesses nontrivial zeros, each of which lies in the critical strip
![]() $0 < \textrm{Re}(s) < 1$
. By the above functional equation and the reflection principle, these zeros are symmetric about
$0 < \textrm{Re}(s) < 1$
. By the above functional equation and the reflection principle, these zeros are symmetric about
![]() $\textrm{Re}(s) = {1}/{2}$
and the real line.
$\textrm{Re}(s) = {1}/{2}$
and the real line.
Next, we give a suitable upper bound, due to Chandrasekharan–Narasimhan, on the Dirichlet series coefficients for
![]() $\zeta_K(s)$
.
$\zeta_K(s)$
.
Lemma 2·2 (Chandrasekharan{Narasimhan [
Reference Chandrasekharan and NarasimhanCN63
, lemma 9]). Let K be any number field, and write in
![]() $\textrm{Re}(s) > 1$
,
$\textrm{Re}(s) > 1$
,
 \begin{equation*} \zeta_K(s) = \sum_{n=1}^\infty \frac{a_n}{n^s}.\end{equation*}
\begin{equation*} \zeta_K(s) = \sum_{n=1}^\infty \frac{a_n}{n^s}.\end{equation*}
Then
![]() $a_n$
is bounded by the coefficient
$a_n$
is bounded by the coefficient
![]() $b_n$
of
$b_n$
of
![]() $n^{-s}$
in
$n^{-s}$
in
![]() $\zeta(s)^{n_K}$
and there exists a constant C depending only on
$\zeta(s)^{n_K}$
and there exists a constant C depending only on
![]() $n_K$
such that
$n_K$
such that
The same holds for the Dirichlet series coefficients
![]() $a_n'$
of
$a_n'$
of
![]() $1/\zeta_K(s)$
.
$1/\zeta_K(s)$
.
Useful for our purposes will be an estimate for the number of nontrivial zeros of
![]() $\zeta_K(s)$
in unit intervals in the critical strip. Define
$\zeta_K(s)$
in unit intervals in the critical strip. Define
It is well known that
![]() $N(T+1) - N(T) \ll \log T$
in the case of
$N(T+1) - N(T) \ll \log T$
in the case of
![]() $K = \mathbb{Q}$
. An analogous result holds for any number field K.
$K = \mathbb{Q}$
. An analogous result holds for any number field K.
Lemma 2·3. For any
![]() $T\geq 0$
, we have that
$T\geq 0$
, we have that
![]() $N_K(T+1)-N_K(T)\ll \log D_K+n_K\log T$
.
$N_K(T+1)-N_K(T)\ll \log D_K+n_K\log T$
.
Proof. See for instance [
Reference Kadiri and NgKN12
] for suitable estimates of the quantity
![]() $N_K(T)$
.
$N_K(T)$
.
In the explicit formulae to follow in Section 4, we will also require the following result which gives good upper bounds for
![]() $1/\zeta_K(s)$
on certain horizontal lines near the critical strip. We note that it is conditional on the Riemann hypothesis for
$1/\zeta_K(s)$
on certain horizontal lines near the critical strip. We note that it is conditional on the Riemann hypothesis for
![]() $\zeta_K(s)$
,
$\zeta_K(s)$
,
Lemma 2·4. Assume that
![]() $\zeta_K(s)$
satisfies the Riemann hypothesis. Then there exists a constant
$\zeta_K(s)$
satisfies the Riemann hypothesis. Then there exists a constant
![]() $C > 0$
such that, for each positive integer
$C > 0$
such that, for each positive integer
![]() $n\geq 4$
, there exists some
$n\geq 4$
, there exists some
![]() $n\leq T_n<n+1$
such that
$n\leq T_n<n+1$
such that
for
![]() $-1\leq \sigma\leq 2$
. We denote by
$-1\leq \sigma\leq 2$
. We denote by
![]() $\mathcal{T} = \{T_n\}_{n=4}^\infty$
the sequence so constructed.
$\mathcal{T} = \{T_n\}_{n=4}^\infty$
the sequence so constructed.
This result is well known in the case
![]() $K = \mathbb{Q}$
(see [
Reference Montgomery and VaughanMV07
, theorem 13·22] or [
Reference TitchmarshTit86
, theorem 14·16]) and the proof for general K is mostly analogous. A complete proof can be found in Section 5.
$K = \mathbb{Q}$
(see [
Reference Montgomery and VaughanMV07
, theorem 13·22] or [
Reference TitchmarshTit86
, theorem 14·16]) and the proof for general K is mostly analogous. A complete proof can be found in Section 5.
2·3.
 $\Omega$
-type lemmas for
$\Omega$
-type lemmas for
 $M_K(x)$
and disproofs of the naïve Mertens-type conjecture in degenerate cases
$M_K(x)$
and disproofs of the naïve Mertens-type conjecture in degenerate cases
Fix any number field K. In this section, we provide various conditional
![]() $\Omega$
-type theorems for
$\Omega$
-type theorems for
![]() $M_K(x)$
which will reduce the unconditional disproofs in Section 3 to a number of conditional assumptions. The main result of this section is Theorem 2·10, which provides three cases in which the naïve Mertens-type conjecture is guaranteed to fail. Essential in the following proofs will be the following well-known method of Landau.
$M_K(x)$
which will reduce the unconditional disproofs in Section 3 to a number of conditional assumptions. The main result of this section is Theorem 2·10, which provides three cases in which the naïve Mertens-type conjecture is guaranteed to fail. Essential in the following proofs will be the following well-known method of Landau.
Lemma 2·5 (Landau [
Reference Montgomery and VaughanMV07
, theorem 15·1]). Suppose that A(x) is a bounded Riemann-integrable function in any finite interval
![]() $1 \leq x \leq X$
, and that
$1 \leq x \leq X$
, and that
![]() $A(x) \geq 0$
for all
$A(x) \geq 0$
for all
![]() $x > X_0$
. Let
$x > X_0$
. Let
![]() $\sigma_c$
denote the infimum of those
$\sigma_c$
denote the infimum of those
![]() $\sigma$
for which
$\sigma$
for which
![]() $\int_{X_0}^\infty A(x)x^{-\sigma}\, dx < \infty$
. Then the function
$\int_{X_0}^\infty A(x)x^{-\sigma}\, dx < \infty$
. Then the function
is analytic in the half-plane
![]() $\textrm{Re}(s) > \sigma_c$
, but not at the point
$\textrm{Re}(s) > \sigma_c$
, but not at the point
![]() $s = \sigma_c$
.
$s = \sigma_c$
.
We shall demonstrate that most cases in which zeros of
![]() $\zeta_K(s)$
behave contrary to conventional expectations (i.e. the Riemann hypothesis and simplicity of zeros) will degenerate into falsity of the naïve Mertens-type conjecture over K. One additional possible obstruction present in the case of Dedekind zeta functions, which is not so in the case of the Riemann zeta function, is the presence of nontrivial zeros on the real line. Let
$\zeta_K(s)$
behave contrary to conventional expectations (i.e. the Riemann hypothesis and simplicity of zeros) will degenerate into falsity of the naïve Mertens-type conjecture over K. One additional possible obstruction present in the case of Dedekind zeta functions, which is not so in the case of the Riemann zeta function, is the presence of nontrivial zeros on the real line. Let
 \begin{align*} &\Theta = \sup_{\zeta_K(\rho) = 0} \{ \textrm{Re}(\rho)\} = \max\{\Theta', \Theta''\},\quad \\[5pt] &\text{ where } \Theta' = \sup_{\substack{\zeta_K(\rho) = 0 \\ \rho \in (0,1)}} \rho, \quad \Theta'' = \sup_{\substack{\zeta_K(\rho) = 0 \\ \textrm{Im}(\rho) \neq 0}} \{ \textrm{Re}(\rho)\}.\end{align*}
\begin{align*} &\Theta = \sup_{\zeta_K(\rho) = 0} \{ \textrm{Re}(\rho)\} = \max\{\Theta', \Theta''\},\quad \\[5pt] &\text{ where } \Theta' = \sup_{\substack{\zeta_K(\rho) = 0 \\ \rho \in (0,1)}} \rho, \quad \Theta'' = \sup_{\substack{\zeta_K(\rho) = 0 \\ \textrm{Im}(\rho) \neq 0}} \{ \textrm{Re}(\rho)\}.\end{align*}
If no zero
![]() $\rho \in (0,1)$
exists, we set
$\rho \in (0,1)$
exists, we set
![]() $\Theta' = 0$
. In particular,
$\Theta' = 0$
. In particular,
![]() $\Theta \geq {1}/{2}$
and the Riemann hypothesis for
$\Theta \geq {1}/{2}$
and the Riemann hypothesis for
![]() $\zeta_K(s)$
is the statement
$\zeta_K(s)$
is the statement
![]() $\Theta = {1}/{2}$
. The following is our first degenerate case.
$\Theta = {1}/{2}$
. The following is our first degenerate case.
Proposition 2·6. If
![]() $\zeta_K(s)$
does not satisfy the Riemann hypothesis, and
$\zeta_K(s)$
does not satisfy the Riemann hypothesis, and
![]() $\Theta' < \Theta$
, then the naïve Mertens-type conjecture over K is false. More precisely,
$\Theta' < \Theta$
, then the naïve Mertens-type conjecture over K is false. More precisely,
![]() $M_K(x) = \Omega_{\pm}(x^{\Theta - \epsilon})$
for all
$M_K(x) = \Omega_{\pm}(x^{\Theta - \epsilon})$
for all
![]() $0 < \epsilon < \Theta - \Theta'$
.
$0 < \epsilon < \Theta - \Theta'$
.
Proof. Suppose that
![]() $M(x) < x^{\Theta - \epsilon}$
for all
$M(x) < x^{\Theta - \epsilon}$
for all
![]() $x > X_0(\epsilon)$
. Consider, in view of (1·1), the function
$x > X_0(\epsilon)$
. Consider, in view of (1·1), the function
Here the left-hand side has a pole at
![]() $\Theta - \epsilon$
, but is analytic for real
$\Theta - \epsilon$
, but is analytic for real
![]() $s > \Theta - \epsilon$
, since
$s > \Theta - \epsilon$
, since
![]() $\zeta_K(s)$
has no zeros to the right of
$\zeta_K(s)$
has no zeros to the right of
![]() $\Theta - \epsilon$
on the real line. The integrand of the right-hand side is non-negative for all
$\Theta - \epsilon$
on the real line. The integrand of the right-hand side is non-negative for all
![]() $x > X_0(\epsilon)$
. By an application of Lemma 2·5, the above identity holds for
$x > X_0(\epsilon)$
. By an application of Lemma 2·5, the above identity holds for
![]() $\textrm{Re}(s) > \Theta - \epsilon$
, and both sides are analytic in this half-plane. But by definition of
$\textrm{Re}(s) > \Theta - \epsilon$
, and both sides are analytic in this half-plane. But by definition of
![]() $\Theta$
, the function
$\Theta$
, the function
![]() $1/\zeta_K$
has poles with real part
$1/\zeta_K$
has poles with real part
![]() $> \Theta - \epsilon$
, which is a contradiction. Hence, we deduce that
$> \Theta - \epsilon$
, which is a contradiction. Hence, we deduce that
![]() $M(x) = \Omega_+(x^{\Theta - \epsilon})$
.
$M(x) = \Omega_+(x^{\Theta - \epsilon})$
.
To obtain the
![]() $\Omega_-$
estimate, we argue similarly using the identity
$\Omega_-$
estimate, we argue similarly using the identity
We then conclude that
![]() $M_K(x) = \Omega_{\pm}(x^{\Theta - \epsilon})$
. Specifically, this gives the falsity of the naïve Mertens-type conjecture over K, since
$M_K(x) = \Omega_{\pm}(x^{\Theta - \epsilon})$
. Specifically, this gives the falsity of the naïve Mertens-type conjecture over K, since
![]() $\Theta > {1}/{2}$
.
$\Theta > {1}/{2}$
.
If
![]() $\Theta' = \Theta$
, then since real zeros must be isolated, there is a zero at
$\Theta' = \Theta$
, then since real zeros must be isolated, there is a zero at
![]() $s = \Theta$
which prohibits the application of Lemma 2·5 in the proof above. In this case, we give a result in lieu of the previous proposition, which involves the elimination of the polar behaviour of
$s = \Theta$
which prohibits the application of Lemma 2·5 in the proof above. In this case, we give a result in lieu of the previous proposition, which involves the elimination of the polar behaviour of
![]() $1/s\zeta_K(s)$
at the real nontrivial zeros of
$1/s\zeta_K(s)$
at the real nontrivial zeros of
![]() $\zeta_K(s)$
. More precisely, there exist constants
$\zeta_K(s)$
. More precisely, there exist constants
![]() $c_{k,\alpha} \in \mathbb{C}$
,
$c_{k,\alpha} \in \mathbb{C}$
,
![]() $1 \leq k \leq m_{\alpha}$
, for each of the finitely many real zeros
$1 \leq k \leq m_{\alpha}$
, for each of the finitely many real zeros
![]() $\alpha \in (0,1)$
, such that the function
$\alpha \in (0,1)$
, such that the function
 \begin{equation} \frac{1}{s\zeta_K(s)} - \sum_{\substack{\zeta_K(\alpha) = 0 \\ \alpha \in (0,1)}} \sum_{k=1}^{m_\alpha} \frac{c_{k,\alpha}}{(s - \alpha)^k}\end{equation}
\begin{equation} \frac{1}{s\zeta_K(s)} - \sum_{\substack{\zeta_K(\alpha) = 0 \\ \alpha \in (0,1)}} \sum_{k=1}^{m_\alpha} \frac{c_{k,\alpha}}{(s - \alpha)^k}\end{equation}
is analytic on the segment (0, 1) on the real line, where
![]() $m_\alpha$
is the multiplicity of the zero at
$m_\alpha$
is the multiplicity of the zero at
![]() $\alpha$
. Upon this simplification, we may provide the following result.
$\alpha$
. Upon this simplification, we may provide the following result.
Proposition 2·7. Suppose that
![]() $\zeta_K(s)$
does not satisfy the Riemann hypothesis, and
$\zeta_K(s)$
does not satisfy the Riemann hypothesis, and
![]() $\Theta' = \Theta$
,
$\Theta' = \Theta$
,
![]() $\frac{1}{2} < \Theta'' \leq \Theta$
. Let
$\frac{1}{2} < \Theta'' \leq \Theta$
. Let
![]() $c_{k,\alpha}$
be as in the equation (2·1). Then for all
$c_{k,\alpha}$
be as in the equation (2·1). Then for all
![]() $0 < \epsilon < \Theta'' - {1}/{2}$
,
$0 < \epsilon < \Theta'' - {1}/{2}$
,
where
 \begin{equation} \tilde M_K(x) \;:\!=\; \sum_{\substack{\zeta_K(\alpha) = 0 \\ \alpha \in (0,1)}} \sum_{k=1}^{m_\alpha} \frac{c_{k,\alpha} x^\alpha (\log x)^{k-1}}{(k-1)!\!}.\end{equation}
\begin{equation} \tilde M_K(x) \;:\!=\; \sum_{\substack{\zeta_K(\alpha) = 0 \\ \alpha \in (0,1)}} \sum_{k=1}^{m_\alpha} \frac{c_{k,\alpha} x^\alpha (\log x)^{k-1}}{(k-1)!\!}.\end{equation}
In particular, the naïve Mertens-type conjecture over K is false.
Proof. Suppose that
![]() $M_K(x) - \tilde M_K(x) < x^{\Theta - \epsilon}$
for all
$M_K(x) - \tilde M_K(x) < x^{\Theta - \epsilon}$
for all
![]() $x > X_0(\epsilon)$
. Now
$x > X_0(\epsilon)$
. Now
 \begin{align*} \frac{1}{s-\Theta +\epsilon} - \frac{1}{s\zeta_K(s)} + \sum_{\substack{\zeta_K(\alpha) = 0 \\ \alpha \in (0,1)}} \sum_{k=1}^{m_\alpha} \frac{c_{k,\alpha}}{(s - \alpha)^k} = \int_1^\infty ( x^{\Theta - \epsilon} - M_K(x) + \tilde M_K(x))x^{-s-1}\, dx\end{align*}
\begin{align*} \frac{1}{s-\Theta +\epsilon} - \frac{1}{s\zeta_K(s)} + \sum_{\substack{\zeta_K(\alpha) = 0 \\ \alpha \in (0,1)}} \sum_{k=1}^{m_\alpha} \frac{c_{k,\alpha}}{(s - \alpha)^k} = \int_1^\infty ( x^{\Theta - \epsilon} - M_K(x) + \tilde M_K(x))x^{-s-1}\, dx\end{align*}
holds for all real
![]() $s > \Theta - \epsilon$
, and by Lemma 2·5 extends to
$s > \Theta - \epsilon$
, and by Lemma 2·5 extends to
![]() $\textrm{Re}(s) > \Theta - \epsilon$
. From here, the proof is similar to that of Proposition 2·6. For the last statement, note that
$\textrm{Re}(s) > \Theta - \epsilon$
. From here, the proof is similar to that of Proposition 2·6. For the last statement, note that
![]() $s = \Theta$
is one of the
$s = \Theta$
is one of the
![]() $\alpha$
in the sum
$\alpha$
in the sum
![]() $\tilde M_K(x)$
. Since
$\tilde M_K(x)$
. Since
![]() $\Theta > {1}/{2}$
, this sum surpasses the order of
$\Theta > {1}/{2}$
, this sum surpasses the order of
![]() $x^{1/2}$
, and since
$x^{1/2}$
, and since
![]() $M_K(x) - \tilde M_K(x)$
is oscillatory we deduce the falsity of the naïve Mertens-type conjecture over K.
$M_K(x) - \tilde M_K(x)$
is oscillatory we deduce the falsity of the naïve Mertens-type conjecture over K.
It remains to address the case where
![]() ${1}/{2} = \Theta'' < \Theta' = \Theta$
. We give the following auxiliary result, which is independent of RH.
${1}/{2} = \Theta'' < \Theta' = \Theta$
. We give the following auxiliary result, which is independent of RH.
Proposition 2·8. Suppose
![]() $\Theta$
,
$\Theta$
,
![]() $\Theta'$
,
$\Theta'$
,
![]() $\Theta''$
are as above, and that there is a non-real zero
$\Theta''$
are as above, and that there is a non-real zero
![]() $\rho$
of
$\rho$
of
![]() $\zeta_K$
of multiplicity
$\zeta_K$
of multiplicity
![]() $m \geq 1$
with
$m \geq 1$
with
![]() $\textrm{Re}(\rho) = \Theta''$
, say
$\textrm{Re}(\rho) = \Theta''$
, say
![]() $\rho = \Theta'' + i\gamma$
. Then
$\rho = \Theta'' + i\gamma$
. Then
where
![]() $\tilde M_K(x)$
is defined as in (2·2). More precisely,
$\tilde M_K(x)$
is defined as in (2·2). More precisely,
 \begin{equation*} \liminf_{x \rightarrow \infty} \frac{M_K(x) - \tilde M_K(x)}{x^{\Theta''}(\log x)^{m-1}} \leq -\frac{m}{|\rho \zeta_K^{(m)}(\rho)|}<\frac{m}{|\rho \zeta_K^{(m)}(\rho)|}\leq \limsup_{x \rightarrow \infty} \frac{M_K(x) - \tilde M_K(x)}{x^{\Theta''}(\log x)^{m-1}}.\end{equation*}
\begin{equation*} \liminf_{x \rightarrow \infty} \frac{M_K(x) - \tilde M_K(x)}{x^{\Theta''}(\log x)^{m-1}} \leq -\frac{m}{|\rho \zeta_K^{(m)}(\rho)|}<\frac{m}{|\rho \zeta_K^{(m)}(\rho)|}\leq \limsup_{x \rightarrow \infty} \frac{M_K(x) - \tilde M_K(x)}{x^{\Theta''}(\log x)^{m-1}}.\end{equation*}
Proof. Suppose that
![]() $M_K(x) - \tilde M_K(x) \leq cx^{\Theta''}(\log x)^{m-1}$
for all
$M_K(x) - \tilde M_K(x) \leq cx^{\Theta''}(\log x)^{m-1}$
for all
![]() $x > X_0$
. It suffices to prove that
$x > X_0$
. It suffices to prove that
![]() $c \geq m/|\rho \zeta_K^{(m)}(\rho)|$
. Consider the function
$c \geq m/|\rho \zeta_K^{(m)}(\rho)|$
. Consider the function
 \begin{align*} &\frac{c(m-1)!\!}{(s-\Theta'')^m} - \frac{1}{s \zeta_K(s)} + \sum_{\substack{\zeta_K(\alpha) = 0 \\ \alpha \in (0,1)}} \frac{c_{k,\alpha} x^{\alpha} (\log x)^{k-1}}{(k-1)!\!}\\[5pt] &\quad= \int_1^\infty (cx^{\Theta''}(\log x)^{m-1} - M_K(x) + \tilde M_K(x))x^{-s-1} \, dx \end{align*}
\begin{align*} &\frac{c(m-1)!\!}{(s-\Theta'')^m} - \frac{1}{s \zeta_K(s)} + \sum_{\substack{\zeta_K(\alpha) = 0 \\ \alpha \in (0,1)}} \frac{c_{k,\alpha} x^{\alpha} (\log x)^{k-1}}{(k-1)!\!}\\[5pt] &\quad= \int_1^\infty (cx^{\Theta''}(\log x)^{m-1} - M_K(x) + \tilde M_K(x))x^{-s-1} \, dx \end{align*}
for real
![]() $s > \Theta''$
. By Lemma 2·5, this can be extended to
$s > \Theta''$
. By Lemma 2·5, this can be extended to
![]() $\textrm{Re}(s) > \Theta''$
. Denote the function F(s). Then
$\textrm{Re}(s) > \Theta''$
. Denote the function F(s). Then
 \begin{align*} &F(s) + \frac{1}{2}e^{i\phi}F(s + i\gamma) + \frac{1}{2}e^{-i\phi}F(s - i \gamma) \\[5pt] &\quad = {\int_1^\infty (cx^{\Theta''}(\log x)^{m-1} - M_K(x) + \tilde M_K(x))(1 + \cos(\phi - \gamma \log x) x^{-s-1})\, dx}\end{align*}
\begin{align*} &F(s) + \frac{1}{2}e^{i\phi}F(s + i\gamma) + \frac{1}{2}e^{-i\phi}F(s - i \gamma) \\[5pt] &\quad = {\int_1^\infty (cx^{\Theta''}(\log x)^{m-1} - M_K(x) + \tilde M_K(x))(1 + \cos(\phi - \gamma \log x) x^{-s-1})\, dx}\end{align*}
for
![]() $\textrm{Re}(s) > \Theta''$
. On the right-hand side, the integral from 1 to
$\textrm{Re}(s) > \Theta''$
. On the right-hand side, the integral from 1 to
![]() $X_0$
is uniformly bounded, while the integral from
$X_0$
is uniformly bounded, while the integral from
![]() $X_0$
to
$X_0$
to
![]() $\infty$
is non-negative. Thus the
$\infty$
is non-negative. Thus the
![]() $\liminf$
of the right-hand side is bounded below as
$\liminf$
of the right-hand side is bounded below as
![]() $s \rightarrow \Theta^+$
. As a result, the coefficient of
$s \rightarrow \Theta^+$
. As a result, the coefficient of
![]() $(s - \Theta'')^{-m}$
in its Laurent series must be non-negative. On the other hand, the left-hand side has a pole of multiplicity m at
$(s - \Theta'')^{-m}$
in its Laurent series must be non-negative. On the other hand, the left-hand side has a pole of multiplicity m at
![]() $s = \Theta''$
, at which the Laurent series expansion contains a term
$s = \Theta''$
, at which the Laurent series expansion contains a term
![]() $(s - \Theta'')^{-m}$
with coefficient equal to
$(s - \Theta'')^{-m}$
with coefficient equal to
Choosing
![]() $\phi$
so that
$\phi$
so that
 \begin{equation*} e^{i\phi} = \frac{\rho \zeta_K^{(m)}(\rho)}{|\rho \zeta_K^{(m)}(\rho)|}.\end{equation*}
\begin{equation*} e^{i\phi} = \frac{\rho \zeta_K^{(m)}(\rho)}{|\rho \zeta_K^{(m)}(\rho)|}.\end{equation*}
Then the above is
![]() $(m-1)!\!(c - m/|\rho \zeta_K'(\rho)|)$
. This quantity must be non-negative, otherwise the left-hand side would tend to
$(m-1)!\!(c - m/|\rho \zeta_K'(\rho)|)$
. This quantity must be non-negative, otherwise the left-hand side would tend to
![]() $-\infty$
as
$-\infty$
as
![]() $s \rightarrow \Theta^+$
. Hence
$s \rightarrow \Theta^+$
. Hence
![]() $c \geq m/|\rho \zeta_K^{(m)}(\rho)|$
. The
$c \geq m/|\rho \zeta_K^{(m)}(\rho)|$
. The
![]() $\Omega_-$
case is similar.
$\Omega_-$
case is similar.
In the scenario where
![]() ${1}/{2} = \Theta'' < \Theta' = \Theta$
, we deduce from the previous proposition that the naïve Mertens-type conjecture is false over K. This completes the discussion under falsity of the Riemann hypothesis for
${1}/{2} = \Theta'' < \Theta' = \Theta$
, we deduce from the previous proposition that the naïve Mertens-type conjecture is false over K. This completes the discussion under falsity of the Riemann hypothesis for
![]() $\zeta_K(s)$
.
$\zeta_K(s)$
.
Turning to results that are instead conditional on the Riemann hypothesis for K, Proposition 2·8 in fact yields the following immediate corollary.
Corollary 2·9. Assume the Riemann hypothesis for
![]() $\zeta_K(s)$
, and that
$\zeta_K(s)$
, and that
![]() $\zeta_K(s)$
has a zero
$\zeta_K(s)$
has a zero
![]() $\rho = {1}/{2} + i\gamma$
,
$\rho = {1}/{2} + i\gamma$
,
![]() $\gamma > 0$
, of multiplicity
$\gamma > 0$
, of multiplicity
![]() $m \geq 1$
. Then
$m \geq 1$
. Then
where
![]() $\tilde M_K(x)$
defined as in (2·2) is the part corresponding to a possible zero at
$\tilde M_K(x)$
defined as in (2·2) is the part corresponding to a possible zero at
![]() $s = {1}/{2}$
.
$s = {1}/{2}$
.
Proof. In this case,
![]() ${1}/{2} = \Theta = \Theta''$
(and
${1}/{2} = \Theta = \Theta''$
(and
![]() $= \Theta'$
, if a real zero exists).
$= \Theta'$
, if a real zero exists).
Corollary 2·9 implies in particular that if
![]() $\zeta_K(s)$
satisfies the Riemann hypothesis, but possesses nontrivial zeros with multiplicity
$\zeta_K(s)$
satisfies the Riemann hypothesis, but possesses nontrivial zeros with multiplicity
![]() $m \geq 2$
(at
$m \geq 2$
(at
![]() $s = {1}/{2}$
or otherwise), then the naïve Mertens-type conjecture is false. Therefore, the only non-degenerate case of the naïve Mertens-type conjecture occurs when
$s = {1}/{2}$
or otherwise), then the naïve Mertens-type conjecture is false. Therefore, the only non-degenerate case of the naïve Mertens-type conjecture occurs when
![]() $\zeta_K(s)$
satisfies the Riemann hypothesis and has only simple nontrivial zeros (a priori none at
$\zeta_K(s)$
satisfies the Riemann hypothesis and has only simple nontrivial zeros (a priori none at
![]() $s = {1}/{2}$
).
$s = {1}/{2}$
).
The following theorem summarizes the results of this section.
Theorem 2·10. In the following special cases,
![]() $M_K(x)$
grows more quickly than
$M_K(x)$
grows more quickly than
![]() $\sqrt x$
.
$\sqrt x$
.
-
(a) If the Riemann hypothesis for
 $\zeta_K(s)$
fails with
$\zeta_K(s)$
fails with
 $\Theta=\Theta''>\Theta'$
, then for all
$\Theta=\Theta''>\Theta'$
, then for all
 $\epsilon > 0$
, If there is a zero
$\epsilon > 0$
, If there is a zero $$M_K(x)=\Omega_{\pm}(x^{\Theta - \epsilon}).$$
$$M_K(x)=\Omega_{\pm}(x^{\Theta - \epsilon}).$$
 $\Theta+i\gamma$
of
$\Theta+i\gamma$
of
 $\zeta_K(s)$
, then
$\zeta_K(s)$
, then
 $M_K(x)=\Omega_\pm(x^\Theta)$
.
$M_K(x)=\Omega_\pm(x^\Theta)$
.
-
(b) If the Riemann hypothesis for
 $\zeta_K(s)$
fails and
$\zeta_K(s)$
fails and
 $\Theta = \Theta'$
, then (in possibly only one direction).
$\Theta = \Theta'$
, then (in possibly only one direction). \begin{equation*} M_K(x) = \Omega(x^{\Theta}) \end{equation*}
\begin{equation*} M_K(x) = \Omega(x^{\Theta}) \end{equation*}
-
(c) If the Riemann hypothesis for
 $\zeta_K(s)$
holds but there is a zero
$\zeta_K(s)$
holds but there is a zero
 $\rho=1/2+i\gamma$
,
$\rho=1/2+i\gamma$
,
 $\gamma > 0$
, of multiplicity
$\gamma > 0$
, of multiplicity
 $m\geq1$
, then If
$m\geq1$
, then If $$M_K(x)=\Omega\left(\sqrt x(\log x)^{m-1}\right).$$
$$M_K(x)=\Omega\left(\sqrt x(\log x)^{m-1}\right).$$
 $\zeta_K({1}/{2})\neq 0$
, or if the multiplicity of the zero of
$\zeta_K({1}/{2})\neq 0$
, or if the multiplicity of the zero of
 $\zeta_K$
at
$\zeta_K$
at
 $s={1}/{2}$
is strictly less than m, then this
$s={1}/{2}$
is strictly less than m, then this
 $\Omega$
can be replaced with
$\Omega$
can be replaced with
 $\Omega_\pm$
.
$\Omega_\pm$
.
In particular, if
![]() $M_K(x)/\sqrt x$
is bounded (both above and below), then the Riemann hypothesis for
$M_K(x)/\sqrt x$
is bounded (both above and below), then the Riemann hypothesis for
![]() $\zeta_K(s)$
holds, and
$\zeta_K(s)$
holds, and
![]() $\zeta_K(s)$
has no multiple zero in the critical strip, thereby implying that
$\zeta_K(s)$
has no multiple zero in the critical strip, thereby implying that
![]() $\zeta_K(\frac12)\neq 0$
. We expand on the possibility of growth in only one direction in Section 6.
$\zeta_K(\frac12)\neq 0$
. We expand on the possibility of growth in only one direction in Section 6.
Corollary 2·11. If
![]() $K/{\mathbb {Q}}$
is Galois with non-abelian Galois group, then the naïve Mertens-type conjecture over K is false.
$K/{\mathbb {Q}}$
is Galois with non-abelian Galois group, then the naïve Mertens-type conjecture over K is false.
Proof. It is known that the Dedekind zeta function of a non-abelian Galois extension K of
![]() $\mathbb{Q}$
has infinitely many zeros of multiplicity
$\mathbb{Q}$
has infinitely many zeros of multiplicity
![]() $\geq 2$
in the critical strip (cf.[
Reference Hu, Kaneko, Martin and SchildkrautHKMS
]).
$\geq 2$
in the critical strip (cf.[
Reference Hu, Kaneko, Martin and SchildkrautHKMS
]).
2·4. The explicit formula for
 $M_K(x)$
$M_K(x)$
We now state the explicit formula for the Mertens function, which, in its compatibility with analytic methods, is essential to our applications. We must assume the Riemann hypothesis for
![]() $\zeta_K(s)$
and that it has no nontrivial multiple zeros. The error terms in our explicit formula are presented in different cases depending on their applicability to
$\zeta_K(s)$
and that it has no nontrivial multiple zeros. The error terms in our explicit formula are presented in different cases depending on their applicability to
![]() $x > 0$
; the generality of
$x > 0$
; the generality of
![]() $x>0$
is necessary for the unconditional results of Section 3, while more specific bounds for
$x>0$
is necessary for the unconditional results of Section 3, while more specific bounds for
![]() $x>1$
are necessary to prove the existence of a limiting distribution in Section 4.
$x>1$
are necessary to prove the existence of a limiting distribution in Section 4.
Proposition 2·12. Assume the Riemann hypothesis for
![]() $\zeta_K(s)$
, and that all nontrivial zeros of
$\zeta_K(s)$
, and that all nontrivial zeros of
![]() $\zeta_K(s)$
are simple. For any real
$\zeta_K(s)$
are simple. For any real
![]() $x>0$
and any
$x>0$
and any
![]() $T\in \mathcal T$
, where
$T\in \mathcal T$
, where
![]() $\mathcal T$
is as in Lemma 2·4,
$\mathcal T$
is as in Lemma 2·4,
 $$M_K(x)=\sum_{|\gamma|\leq T} \frac{x^\rho}{\rho\zeta_K'(\rho)}+\sum_{k=0}^\infty \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}+E(x,T),$$
$$M_K(x)=\sum_{|\gamma|\leq T} \frac{x^\rho}{\rho\zeta_K'(\rho)}+\sum_{k=0}^\infty \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}+E(x,T),$$
where for any
![]() $x>0$
,
$x>0$
,
![]() $E(x,T)=O_x(T^{1-\epsilon})$
for any
$E(x,T)=O_x(T^{1-\epsilon})$
for any
![]() $\epsilon$
, and for
$\epsilon$
, and for
![]() $x > 1$
we have
$x > 1$
we have
where C is as in Lemma 2·2. In addition, for
![]() $x > 1$
,
$x > 1$
,
 $$\sum_{k=0}^\infty \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}\ll (\log x)^{O(1)},$$
$$\sum_{k=0}^\infty \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}\ll (\log x)^{O(1)},$$
which in this case can be subsumed into the error term E(x,T).
We defer the proof of this formula to Section 5.
For the previous result and others to follow, we also require the following bound on the residues of
![]() ${x^s}/{s\zeta_K(s)}$
at the trivial zeros
${x^s}/{s\zeta_K(s)}$
at the trivial zeros
![]() $s = -k$
. The purpose of this bound is two-fold: it reveals dependence on k and x, which suffices already to prove the last statement in Proposition 2.12, and it clarifies dependence on
$s = -k$
. The purpose of this bound is two-fold: it reveals dependence on k and x, which suffices already to prove the last statement in Proposition 2.12, and it clarifies dependence on
![]() $r_1$
,
$r_1$
,
![]() $r_2$
, and
$r_2$
, and
![]() $D_K$
, which is crucial in our proof of Theorem 1·2.
$D_K$
, which is crucial in our proof of Theorem 1·2.
Lemma 2·13. Fix non-negative integers
![]() $r_1$
and
$r_1$
and
![]() $r_2$
, and let K be a number field with
$r_2$
, and let K be a number field with
![]() $r_1$
real embeddings and
$r_1$
real embeddings and
![]() $r_2$
complex conjugate pairs of embeddings. Then there exists some constant
$r_2$
complex conjugate pairs of embeddings. Then there exists some constant
![]() $c=c_{r_1,2r_2}$
such that, if
$c=c_{r_1,2r_2}$
such that, if
![]() $\zeta_K(s)$
has a zero at
$\zeta_K(s)$
has a zero at
![]() $s=-k$
for a positive integer k, then
$s=-k$
for a positive integer k, then
 $$\left|\textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}\right|\leq \frac{c(2\pi)^{kn_K}(\log (kx\textrm{D}_K))^{r_1 + r_2}}{kx^k\textrm{D}_K^{k+1/2}(k!\!)^{n_K}}.$$
$$\left|\textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}\right|\leq \frac{c(2\pi)^{kn_K}(\log (kx\textrm{D}_K))^{r_1 + r_2}}{kx^k\textrm{D}_K^{k+1/2}(k!\!)^{n_K}}.$$
In addition,
See Section 5 for the proof. Heavier consideration of the residue at
![]() $s = 0$
is necessary to prove Theorems 1·1 and 1·2, wherein dependence on
$s = 0$
is necessary to prove Theorems 1·1 and 1·2, wherein dependence on
![]() $n_K$
and
$n_K$
and
![]() $D_K$
will be significant.
$D_K$
will be significant.
3. Unconditional failure of the naïve Mertens-type conjecture
In light of Theorem 2·10, if
![]() $x^{-1/2}|M_K(x)|$
is bounded, then
$x^{-1/2}|M_K(x)|$
is bounded, then
![]() $\zeta_K(s)$
has no zeros off the line
$\zeta_K(s)$
has no zeros off the line
![]() $\textrm{Re}(s) = {1}/{2}$
and has only simple zeros. In this section, we describe some consequences of these assumptions, which lead to unconditional disproofs of the naïve Mertens-type conjecture for “most” number fields.
$\textrm{Re}(s) = {1}/{2}$
and has only simple zeros. In this section, we describe some consequences of these assumptions, which lead to unconditional disproofs of the naïve Mertens-type conjecture for “most” number fields.
3·1. The general result
In this section, we give a generic result about the limiting behaviour of
![]() $x^{-1/2}M_K(x)$
which holds unconditionally. We follow a method of Jurkat from [
Reference JurkatJur73
], using his main theorem directly in our application. In particular, Jurkat has identified a wide class of trigonometric series which are seen to share a key limiting property enjoyed by Bohr-almost periodic functions. By exploiting this property, we show
$x^{-1/2}M_K(x)$
which holds unconditionally. We follow a method of Jurkat from [
Reference JurkatJur73
], using his main theorem directly in our application. In particular, Jurkat has identified a wide class of trigonometric series which are seen to share a key limiting property enjoyed by Bohr-almost periodic functions. By exploiting this property, we show
![]() $x^{-1/2}M_K(x)$
approaches certain explicitly computable values infinitely often and arbitrarily closely.
$x^{-1/2}M_K(x)$
approaches certain explicitly computable values infinitely often and arbitrarily closely.
Definition 3·1. (cf. [
Reference JurkatJur73
]). A locally integrable function
![]() $f\;:\;{\mathbb {R}}\to{\mathbb {R}}$
is called almost periodic in a distributional sense (APD) if there is a Bohr-almost periodic function g so that
$f\;:\;{\mathbb {R}}\to{\mathbb {R}}$
is called almost periodic in a distributional sense (APD) if there is a Bohr-almost periodic function g so that
![]() $f = ({d^k}/{d^kx})g$
.
$f = ({d^k}/{d^kx})g$
.
Formally, this means f admits an expansion of the form
 \begin{equation} f(x) \sim \sum_{n=1}^\infty \textrm{Re}(a_n e^{i \lambda_n x}),\end{equation}
\begin{equation} f(x) \sim \sum_{n=1}^\infty \textrm{Re}(a_n e^{i \lambda_n x}),\end{equation}
where
![]() $0 < \lambda_n \nearrow \infty$
and
$0 < \lambda_n \nearrow \infty$
and
![]() $a_n$
are complex constants such that
$a_n$
are complex constants such that
 \begin{equation*} \sum_{n=1}^\infty \frac{|a_n|}{\lambda_n^k} < \infty\end{equation*}
\begin{equation*} \sum_{n=1}^\infty \frac{|a_n|}{\lambda_n^k} < \infty\end{equation*}
for some
![]() $k \in \mathbb{N}$
. When referring to an APD-function, we shall specify k.
$k \in \mathbb{N}$
. When referring to an APD-function, we shall specify k.
The notion of almost periodicity in a distributional sense is useful because such functions have easily-calculable limit points, as shown by the following main theorem of Jurkat.
Proposition 3·2 (Jurkat [
Reference JurkatJur73
, pp. 151[152]). Suppose
![]() $f\;:\;{\mathbb {R}}\to{\mathbb {R}}$
is an APD-function, and let L(f) denote the set of Lebesgue points of f. Then for any
$f\;:\;{\mathbb {R}}\to{\mathbb {R}}$
is an APD-function, and let L(f) denote the set of Lebesgue points of f. Then for any
![]() $t\in L(f)$
,
$t\in L(f)$
,
Moreover, all values of f at Lebesgue points are limit points of f.
The technical condition on Lebesgue points can be safely ignored for the remainder of this paper. The functions we work with are sufficiently well-behaved that the inclusion of their Lebesgue points does not change either limit.
For any real
![]() $x > 0$
, define
$x > 0$
, define
 \begin{equation}M_K^*(x)= - \sum_{k=0}^\infty \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}.\end{equation}
\begin{equation}M_K^*(x)= - \sum_{k=0}^\infty \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}.\end{equation}
(We remark that this carries a slightly different normalisation than Jurkat’s
![]() $M^*(x)$
, as he makes a few simplifications particular to the case
$M^*(x)$
, as he makes a few simplifications particular to the case
![]() $K={\mathbb {Q}}$
.) Motivated by Proposition 2·12, this is a “trivial completion” of
$K={\mathbb {Q}}$
.) Motivated by Proposition 2·12, this is a “trivial completion” of
![]() $M_K(x)$
, in the sense that, for
$M_K(x)$
, in the sense that, for
![]() $T\in\mathcal T$
(where
$T\in\mathcal T$
(where
![]() $\mathcal T$
is given by Lemma 2·4),
$\mathcal T$
is given by Lemma 2·4),
 \begin{equation}M_K(x)+M_K^*(x)=\sum_{|\gamma|\leq T}\frac{x^\rho}{\rho\zeta_K'(\rho)}+O_x\left(\frac1{T^{1-\epsilon}}\right)\end{equation}
\begin{equation}M_K(x)+M_K^*(x)=\sum_{|\gamma|\leq T}\frac{x^\rho}{\rho\zeta_K'(\rho)}+O_x\left(\frac1{T^{1-\epsilon}}\right)\end{equation}
for all
![]() $x>0$
, assuming the preconditions of Proposition 2·12 hold. We first show an analogue of Jurkat’s main theorem for number fields under these assumptions, as well as some more stringent assumptions.
$x>0$
, assuming the preconditions of Proposition 2·12 hold. We first show an analogue of Jurkat’s main theorem for number fields under these assumptions, as well as some more stringent assumptions.
The function
![]() $f\;:\; \mathbb{R} \rightarrow \mathbb{R}$
defined by
$f\;:\; \mathbb{R} \rightarrow \mathbb{R}$
defined by
is locally integrable. If we assume the Riemann hypothesis for
![]() $\zeta_K(s)$
and that all nontrivial zeros are simple, and let
$\zeta_K(s)$
and that all nontrivial zeros are simple, and let
![]() $T \rightarrow \infty$
along
$T \rightarrow \infty$
along
![]() $\mathcal{T}$
in the equation (3·3) above (with the necessary modifications for
$\mathcal{T}$
in the equation (3·3) above (with the necessary modifications for
![]() $M_K(e^y)$
if y is the logarithm of an integer), it furthermore has an expansion of the form in (3·1) with
$M_K(e^y)$
if y is the logarithm of an integer), it furthermore has an expansion of the form in (3·1) with
![]() $a_n = 2(\rho_n \zeta_K'(\rho_n))^{-1}$
,
$a_n = 2(\rho_n \zeta_K'(\rho_n))^{-1}$
,
![]() $\lambda_n = \gamma_n$
, where
$\lambda_n = \gamma_n$
, where
![]() $\gamma_n$
is the ordinate of the nth highest nontrivial zero
$\gamma_n$
is the ordinate of the nth highest nontrivial zero
![]() $\rho_n = {1}/{2} + i \gamma_n$
in the upper half plane. Here, the sum converges boundedly given this grouping of the terms. Assuming for now that there exists some constant
$\rho_n = {1}/{2} + i \gamma_n$
in the upper half plane. Here, the sum converges boundedly given this grouping of the terms. Assuming for now that there exists some constant
![]() $C > 0$
such that
$C > 0$
such that
the result of Lemma 2·3 implies that f is an APD-function with
![]() $k = 2$
. Hence, Proposition 3·2 functions produces the following.
$k = 2$
. Hence, Proposition 3·2 functions produces the following.
Proposition 3·3. Let K be a number field. Assume the Riemann hypothesis for
![]() $\zeta_K(s)$
, that all nontrivial zeros of
$\zeta_K(s)$
, that all nontrivial zeros of
![]() $\zeta_K(s)$
are simple, and that there exists some constant
$\zeta_K(s)$
are simple, and that there exists some constant
![]() $C > 0$
for which
$C > 0$
for which
for every nontrivial zero
![]() $\rho$
of
$\rho$
of
![]() $\zeta_K(s)$
. Then, for any
$\zeta_K(s)$
. Then, for any
![]() $x>0$
,
$x>0$
,
is a limit point of the function
![]() $x^{-1/2}M_K(x)$
.
$x^{-1/2}M_K(x)$
.
We now describe our major application of this result. Recall the definition
Lemma 3·4. Let K be any number field, and let
![]() $M_K^*(x)$
be as in (3·2).
$M_K^*(x)$
be as in (3·2).
-
(a) Unconditionally,
 $M_K^+-M_K^-\geq 1$
.
$M_K^+-M_K^-\geq 1$
. -
(b) If
 $M_K^*(1)>0$
(resp.
$M_K^*(1)>0$
(resp.
 $M_K^*(1) < -1$
), then the naïve Mertens-type conjecture for K fails infinitely often; in particular,
$M_K^*(1) < -1$
), then the naïve Mertens-type conjecture for K fails infinitely often; in particular,
 $M_K^+>1$
(resp.
$M_K^+>1$
(resp.
 $M_K^- < -1$
).
$M_K^- < -1$
).
Proof. If the Riemann hypothesis for
![]() $\zeta_K(s)$
is false, or
$\zeta_K(s)$
is false, or
![]() $\zeta_K(s)$
has a nontrivial zero of multiplicity greater than 1, then Theorem 2·10 implies that either
$\zeta_K(s)$
has a nontrivial zero of multiplicity greater than 1, then Theorem 2·10 implies that either
![]() $M_K^+=\infty$
or
$M_K^+=\infty$
or
![]() $M_K^-=-\infty$
, in which case both (a) and (b) follow. By the sign of the functional equation for
$M_K^-=-\infty$
, in which case both (a) and (b) follow. By the sign of the functional equation for
![]() $\zeta_K(s)$
in Theorem 2·1, any zero at
$\zeta_K(s)$
in Theorem 2·1, any zero at
![]() $s=1/2$
must be of even order, and thus any K with
$s=1/2$
must be of even order, and thus any K with
![]() $\zeta_K(1/2)=0$
is covered in the previous cases.
$\zeta_K(1/2)=0$
is covered in the previous cases.
In the case where the Riemann hypothesis holds and all nontrivial zeros are simple, we may apply Proposition 2·8 with
![]() $\Theta''=1/2$
and
$\Theta''=1/2$
and
![]() $m=1$
to obtain
$m=1$
to obtain
for any nontrivial zero
![]() $\rho$
of
$\rho$
of
![]() $\zeta_K(s)$
. If one of
$\zeta_K(s)$
. If one of
![]() $M_K^\pm$
is infinite, then (a) and (b) hold as before. Otherwise, if
$M_K^\pm$
is infinite, then (a) and (b) hold as before. Otherwise, if
![]() $M_K^\pm$
are both finite, then there is some constant C for which
$M_K^\pm$
are both finite, then there is some constant C for which
for every zero
![]() $\rho$
of
$\rho$
of
![]() $\zeta_K(s)$
. So, the preconditions of Proposition 3·3 hold, and we have for any x that
$\zeta_K(s)$
. So, the preconditions of Proposition 3·3 hold, and we have for any x that
is between
![]() $M_K^-$
and
$M_K^-$
and
![]() $M_K^+$
. In particular,
$M_K^+$
. In particular,
where limits to
![]() $1^-$
and
$1^-$
and
![]() $1^+$
denote approaching 1 from below and above, respectively. This inequality chain shows both (a) and (b).
$1^+$
denote approaching 1 from below and above, respectively. This inequality chain shows both (a) and (b).
3·2. Imaginary quadratic fields
In this subsection, we calculate and bound
![]() $M_K^*(x)$
explicitly for imaginary quadratic fields. We pick
$M_K^*(x)$
explicitly for imaginary quadratic fields. We pick
![]() $D>0$
such that
$D>0$
such that
![]() $-D$
is a negative fundamental discriminant and let
$-D$
is a negative fundamental discriminant and let
![]() $K={\mathbb {Q}}(\sqrt{-D})$
be the imaginary quadratic field with discriminant
$K={\mathbb {Q}}(\sqrt{-D})$
be the imaginary quadratic field with discriminant
![]() $-D$
. Let
$-D$
. Let
![]() $\chi_{-D}$
denote the odd quadratic character
$\chi_{-D}$
denote the odd quadratic character
![]() $\chi_{-D}(n)=\left({-D}/n\right)$
of conductor D, so that
$\chi_{-D}(n)=\left({-D}/n\right)$
of conductor D, so that
![]() $\zeta_K(s)=\zeta(s)L(s,\chi_{-D})$
. Using Theorem 2·1, we may compute
$\zeta_K(s)=\zeta(s)L(s,\chi_{-D})$
. Using Theorem 2·1, we may compute
 \begin{equation} M_K^*(x) \;:\!=\; \frac{2\pi}{L(1,\chi_{-D})D^{1/2}} + \sum_{k=1}^\infty \left( \frac{D}{4\pi^2} \right)^{-k - \frac{1}{2}}\frac{({-}1)^k x^{-k}}{k (k!\!)^2\zeta_K(k+1)}.\end{equation}
\begin{equation} M_K^*(x) \;:\!=\; \frac{2\pi}{L(1,\chi_{-D})D^{1/2}} + \sum_{k=1}^\infty \left( \frac{D}{4\pi^2} \right)^{-k - \frac{1}{2}}\frac{({-}1)^k x^{-k}}{k (k!\!)^2\zeta_K(k+1)}.\end{equation}
Via the class number formula of Dirichlet, the leading term of (3·4) is always positive. We show that, for
![]() $x = 1$
and sufficiently large D, it exceeds the other terms in absolute value.
$x = 1$
and sufficiently large D, it exceeds the other terms in absolute value.
Lemma 3·5. If
![]() $D>0$
and
$D>0$
and
![]() $-D$
is a fundamental discriminant, and
$-D$
is a fundamental discriminant, and
![]() $K={\mathbb {Q}}(\sqrt{-D})$
, then
$K={\mathbb {Q}}(\sqrt{-D})$
, then
 $$M_K^*(1)\geq \frac{2\pi}{D^{1/2}}\left(\frac1{\frac12\log D+\log\log D+2+\log 2}-\exp\left(\frac{4\pi^2}D\right)+1\right).$$
$$M_K^*(1)\geq \frac{2\pi}{D^{1/2}}\left(\frac1{\frac12\log D+\log\log D+2+\log 2}-\exp\left(\frac{4\pi^2}D\right)+1\right).$$
In particular, if
![]() $D>307$
, then
$D>307$
, then
![]() $M_K^*(1)>0$
.
$M_K^*(1)>0$
.
Proof. We begin by bounding from below the leading term of (3·4). The Euler product for
![]() $L(s,\chi_{-D})$
implies that it is positive for all real
$L(s,\chi_{-D})$
implies that it is positive for all real
![]() $s > 1$
, and hence
$s > 1$
, and hence
![]() $L(1,\chi_{-D}) > 0$
, knowing that it is nonzero. On the other hand,
$L(1,\chi_{-D}) > 0$
, knowing that it is nonzero. On the other hand,
where we have used partial summation and the Pólya–Vinogradov bound
![]() $\sqrt{D} \log D$
for the partial sums of the primitive character
$\sqrt{D} \log D$
for the partial sums of the primitive character
![]() $\chi_{-D}$
modulo D, as well as the bound
$\chi_{-D}$
modulo D, as well as the bound
![]() $1 + \log x$
for
$1 + \log x$
for
![]() $\sum_{n \leq x} \frac{1}{n}$
. Setting
$\sum_{n \leq x} \frac{1}{n}$
. Setting
![]() $N = 2\sqrt{D} \log D$
gives that
$N = 2\sqrt{D} \log D$
gives that
 \begin{equation}\frac{2\pi}{D^{1/2}L(1,\chi_{-D})}\geq \frac{2\pi}{D^{1/2}\left(\frac12\log D+\log\log D+2+\log 2\right)}.\end{equation}
\begin{equation}\frac{2\pi}{D^{1/2}L(1,\chi_{-D})}\geq \frac{2\pi}{D^{1/2}\left(\frac12\log D+\log\log D+2+\log 2\right)}.\end{equation}
Now, for any real
![]() $\sigma>1$
, we have
$\sigma>1$
, we have
![]() $\zeta_K(\sigma)>1$
by definition, so
$\zeta_K(\sigma)>1$
by definition, so
![]() $\zeta_K(k+1)^{-1}<1$
for every
$\zeta_K(k+1)^{-1}<1$
for every
![]() $k \geq 1$
. So, we have the bound
$k \geq 1$
. So, we have the bound
 \begin{align*} \left| \sum_{k=1}^\infty \left( \frac{D}{4\pi^2} \right)^{-k - \frac{1}{2}} \frac{(-1)^k}{k(k!\!)^2 \zeta_K(k+1)} \right| &\leq \frac{2\pi}{D^{1/2}} \sum_{k=1}^\infty \left( \frac{4\pi^2}{D} \right)^k \frac{1}{k (k!)^2\zeta_K(k+1)} \\[5pt] &\leq \frac{2\pi}{D^{1/2}} \sum_{k=1}^\infty \left( \frac{4\pi^2}{D} \right)^k \frac{1}{k!} \\[5pt] &\leq \frac{2\pi}{D^{1/2}} \left( \exp\left( \frac{4\pi^2}{D} \right) - 1 \right).\end{align*}
\begin{align*} \left| \sum_{k=1}^\infty \left( \frac{D}{4\pi^2} \right)^{-k - \frac{1}{2}} \frac{(-1)^k}{k(k!\!)^2 \zeta_K(k+1)} \right| &\leq \frac{2\pi}{D^{1/2}} \sum_{k=1}^\infty \left( \frac{4\pi^2}{D} \right)^k \frac{1}{k (k!)^2\zeta_K(k+1)} \\[5pt] &\leq \frac{2\pi}{D^{1/2}} \sum_{k=1}^\infty \left( \frac{4\pi^2}{D} \right)^k \frac{1}{k!} \\[5pt] &\leq \frac{2\pi}{D^{1/2}} \left( \exp\left( \frac{4\pi^2}{D} \right) - 1 \right).\end{align*}
Combining this bound with (3·5) gives the desired result.
Lemma 3·5 has the following immediate consequence via Lemma 3·4.
Theorem 3·6. Let K be an imaginary quadratic extension of
![]() $\mathbb{Q}$
with discriminant
$\mathbb{Q}$
with discriminant
![]() $-D$
such that
$-D$
such that
![]() $D > 307$
. Then the naïve Mertens-type conjecture over K, i.e. that
$D > 307$
. Then the naïve Mertens-type conjecture over K, i.e. that
![]() $|M_K(x)|\;\leq x^{1/2}$
, is false. In particular,
$|M_K(x)|\;\leq x^{1/2}$
, is false. In particular,
![]() $M_K^*(1) > 0$
, and if the Riemann hypothesis for
$M_K^*(1) > 0$
, and if the Riemann hypothesis for
![]() $\zeta_K(s)$
is true and all of its nontrivial zeros are simple, then
$\zeta_K(s)$
is true and all of its nontrivial zeros are simple, then
![]() $M_K^+ \geq 1 + M_K^*(1)$
.
$M_K^+ \geq 1 + M_K^*(1)$
.
By direct computation, we may address the smaller discriminants.
Table 1. Values of
![]() $M_K^*(1)$
for imaginary quadratic fields
$M_K^*(1)$
for imaginary quadratic fields
![]() $K = \mathbb{Q}(\sqrt{-D})$
of discriminant
$K = \mathbb{Q}(\sqrt{-D})$
of discriminant
![]() $-D$
,
$-D$
,
![]() $D \leq 307$
.
$D \leq 307$
.

Table 2. Given
![]() $K={\mathbb {Q}}(\sqrt{-D})$
for a fundamental discriminant
$K={\mathbb {Q}}(\sqrt{-D})$
for a fundamental discriminant
![]() $-D$
, the smallest positive integer n for which
$-D$
, the smallest positive integer n for which
![]() $M_K(n^+)+M_K^*(n)>n^{1/2}$
.
$M_K(n^+)+M_K^*(n)>n^{1/2}$
.
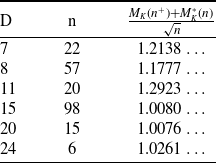
Theorem 3·7. Let K be an imaginary quadratic extension of
![]() $\mathbb{Q}$
with discriminant
$\mathbb{Q}$
with discriminant
![]() $-D$
such that
$-D$
such that
![]() $3<D \leq 307$
. Then the naïve Mertens-type conjecture over K is false, with
$3<D \leq 307$
. Then the naïve Mertens-type conjecture over K is false, with
![]() $M_K^+ > 1$
.
$M_K^+ > 1$
.
Proof. The values of
![]() $M_K^*(1)$
are tabulated in Table 1, where the sum has been computed up to threshold
$M_K^*(1)$
are tabulated in Table 1, where the sum has been computed up to threshold
![]() $k = 50$
. This implies the falsity of the naïve Mertens-type conjecture over K for all
$k = 50$
. This implies the falsity of the naïve Mertens-type conjecture over K for all
![]() $D \leq 307$
where
$D \leq 307$
where
since, via Lemma 3·4, we deduce from
![]() $M_K^*(1) > 0$
that
$M_K^*(1) > 0$
that
![]() $M_K^+ > 1$
. The procedure can be remedied for most of those exceptional values of
$M_K^+ > 1$
. The procedure can be remedied for most of those exceptional values of
![]() $-D$
by letting
$-D$
by letting
![]() $x \rightarrow n^+$
for different choices of positive integers n where
$x \rightarrow n^+$
for different choices of positive integers n where
as represented in Table 2 (we have taken the right-hand limits, as
![]() $n^{-1/2}M_K^*(n)$
is generally decreasing). This suffices to resolve all cases except for
$n^{-1/2}M_K^*(n)$
is generally decreasing). This suffices to resolve all cases except for
![]() $D = 3$
(the field
$D = 3$
(the field
![]() $K = \mathbb{Q}(\sqrt{-3})$
) and
$K = \mathbb{Q}(\sqrt{-3})$
) and
![]() $D = 4$
(the field
$D = 4$
(the field
![]() $K = \mathbb{Q}(i)$
).
$K = \mathbb{Q}(i)$
).
In order to resolve the case
![]() $D = 4$
, we appeal to a method originally due to Ingham [
Reference InghamIng42
, theorem 1] in examining the smoothed sums of
$D = 4$
, we appeal to a method originally due to Ingham [
Reference InghamIng42
, theorem 1] in examining the smoothed sums of
![]() $\sum_{|\gamma| <T} {e^{i\gamma t}}/{\rho \zeta_K'(\rho)}$
by a suitable kernel function f(y). In particular, we select the kernel function of Jurkat–Peyerimhoff (see [
Reference Jurkat and PeyerimhoffJP76, Reference Odlyzko and te RieleOtR85
]),
$\sum_{|\gamma| <T} {e^{i\gamma t}}/{\rho \zeta_K'(\rho)}$
by a suitable kernel function f(y). In particular, we select the kernel function of Jurkat–Peyerimhoff (see [
Reference Jurkat and PeyerimhoffJP76, Reference Odlyzko and te RieleOtR85
]),
 \begin{align*} f(y) = \begin{cases} (1 - y) \cos \pi y + \frac{1}{\pi} \sin \pi y &\text{ if } 0 \leq y \leq 1, \\[5pt] 0 &\text{ if } y \geq 1, \end{cases}\end{align*}
\begin{align*} f(y) = \begin{cases} (1 - y) \cos \pi y + \frac{1}{\pi} \sin \pi y &\text{ if } 0 \leq y \leq 1, \\[5pt] 0 &\text{ if } y \geq 1, \end{cases}\end{align*}
which produces the smoothed sum
 \begin{align} & h_{K,T}^*(t) = \sum_{|\gamma| < T} f\left( \frac{|\gamma|}{T} \right) \frac{e^{i \gamma y}}{\rho \zeta_K'(\rho)}\nonumber \\[5pt] &\quad = \sum_{|\gamma| < T} \left( \left( 1 - \frac{|\gamma|}{T} \right) \cos \left( \frac{\pi |\gamma|}{T} \right) + \frac{1}{\pi} \sin \left(\frac{\pi |\gamma|}{T} \right) \right) \frac{e^{i \gamma y}}{\rho \zeta_K'(\rho)}.\end{align}
\begin{align} & h_{K,T}^*(t) = \sum_{|\gamma| < T} f\left( \frac{|\gamma|}{T} \right) \frac{e^{i \gamma y}}{\rho \zeta_K'(\rho)}\nonumber \\[5pt] &\quad = \sum_{|\gamma| < T} \left( \left( 1 - \frac{|\gamma|}{T} \right) \cos \left( \frac{\pi |\gamma|}{T} \right) + \frac{1}{\pi} \sin \left(\frac{\pi |\gamma|}{T} \right) \right) \frac{e^{i \gamma y}}{\rho \zeta_K'(\rho)}.\end{align}
It holds for this sum that for
![]() $T > 0$
fixed,
$T > 0$
fixed,
and it follows from the fact that
![]() $h_{K,T}^*(t)$
is almost periodic that
$h_{K,T}^*(t)$
is almost periodic that
so it suffices to exhibit
![]() $T > 0$
and
$T > 0$
and
![]() $t \in \mathbb{R}$
for which
$t \in \mathbb{R}$
for which
![]() $h_{K,T}^*(t) > 1$
or
$h_{K,T}^*(t) > 1$
or
![]() $h_{K,T}^*(t) < -1$
.
$h_{K,T}^*(t) < -1$
.
A computation demonstrates that
![]() $h^*_{{\mathbb {Q}}(i), 600}(72.85) \leq -1.008$
and
$h^*_{{\mathbb {Q}}(i), 600}(72.85) \leq -1.008$
and
![]() $h^*_{{\mathbb {Q}}(i), 600}(-85.15) \geq 1.029$
. That is,
$h^*_{{\mathbb {Q}}(i), 600}(-85.15) \geq 1.029$
. That is,
![]() $M_K^- \leq -1.008 < 1.029 \leq M_K^+$
. This completes the proof.
$M_K^- \leq -1.008 < 1.029 \leq M_K^+$
. This completes the proof.
Combining Theorem 3·6 and Theorem 3·7 concludes the proof of Theorem 1·1(a).
3·3. Real quadratic fields
Next, we calculate and bound
![]() $M_K^*(x)$
explicitly for real quadratic fields. Pick a positive fundamental discriminant
$M_K^*(x)$
explicitly for real quadratic fields. Pick a positive fundamental discriminant
![]() $D>0$
and let
$D>0$
and let
![]() $K={\mathbb {Q}}(\sqrt{D})$
be the real quadratic field with discriminant D. Then
$K={\mathbb {Q}}(\sqrt{D})$
be the real quadratic field with discriminant D. Then
![]() $\zeta_K(s)=\zeta(s)L(s,\chi_D)$
, where
$\zeta_K(s)=\zeta(s)L(s,\chi_D)$
, where
![]() $\chi_D$
is the even quadratic character
$\chi_D$
is the even quadratic character
![]() $\chi_D(n)=\left(\frac Dn\right)$
of conductor D. We compute
$\chi_D(n)=\left(\frac Dn\right)$
of conductor D. We compute
 \begin{align} M_K^*(x) &= \frac{4}{L(1,\chi_D)D^{1/2}} \left( \log \left( \frac{xD}{4\pi^2} \right) - \gamma + \frac{L'}{L}(1,\chi_D) \right)\nonumber \\[5pt] &\quad + \frac{2}{D^{1/2}} {\sum_{k=1}^\infty \frac{\left(\frac{4\pi^2}{xD}\right)^{2k}}{k((2k)!\!)^2 \zeta_K(2k+1)} \left( \log \left( \frac{xD}{4\pi^2} \right) + \frac{1}{2k} + \frac{\zeta_K'}{\zeta_K}(2k+1) + 2 \frac{\Gamma'}{\Gamma}(2k+1)\! \right)\!.}\end{align}
\begin{align} M_K^*(x) &= \frac{4}{L(1,\chi_D)D^{1/2}} \left( \log \left( \frac{xD}{4\pi^2} \right) - \gamma + \frac{L'}{L}(1,\chi_D) \right)\nonumber \\[5pt] &\quad + \frac{2}{D^{1/2}} {\sum_{k=1}^\infty \frac{\left(\frac{4\pi^2}{xD}\right)^{2k}}{k((2k)!\!)^2 \zeta_K(2k+1)} \left( \log \left( \frac{xD}{4\pi^2} \right) + \frac{1}{2k} + \frac{\zeta_K'}{\zeta_K}(2k+1) + 2 \frac{\Gamma'}{\Gamma}(2k+1)\! \right)\!.}\end{align}
Here,
![]() $\gamma = 0.5772\ldots$
is Euler’s constant. The
$\gamma = 0.5772\ldots$
is Euler’s constant. The
![]() $L'/L$
,
$L'/L$
,
![]() $\zeta_K'/\zeta_K$
, and
$\zeta_K'/\zeta_K$
, and
![]() $\Gamma'/\Gamma$
terms arise (in contrast to (3·4)) since
$\Gamma'/\Gamma$
terms arise (in contrast to (3·4)) since
![]() $\zeta_K(s)$
has zeros of multiplicity two when K is real quadratic. We now only need to identify which D satisfy the estimate
$\zeta_K(s)$
has zeros of multiplicity two when K is real quadratic. We now only need to identify which D satisfy the estimate
![]() $M_K^*(1)>0$
. We first provide a bound on the
$M_K^*(1)>0$
. We first provide a bound on the
![]() $L'/L$
term that is particular to the case of real characters.
$L'/L$
term that is particular to the case of real characters.
Lemma 3·8. Let
![]() $\chi$
be a non-principal real primitive character of conductor D. Then
$\chi$
be a non-principal real primitive character of conductor D. Then
Proof. Recall [
Reference Montgomery and VaughanMV07
, corollary 10·18] for any Dirichlet character
![]() $\chi$
of conductor D the identity
$\chi$
of conductor D the identity
where
![]() $\kappa=({1-\chi(-1)})/2$
and
$\kappa=({1-\chi(-1)})/2$
and
![]() $\rho$
runs over all nontrivial zeros of
$\rho$
runs over all nontrivial zeros of
![]() $L(s,\chi)$
. Specifying to
$L(s,\chi)$
. Specifying to
![]() $s=1$
and
$s=1$
and
![]() $\chi = \overline{\chi}$
gives
$\chi = \overline{\chi}$
gives
Since
this gives
By grouping
![]() $\rho$
and
$\rho$
and
![]() $\overline\rho$
in the sum we have
$\overline\rho$
in the sum we have
 \begin{align*}\sum_\rho\frac1{\rho(1-\rho)}&=\frac12\sum_\rho\left(\frac1{\rho(1-\rho)}+\frac1{\overline\rho(1-\overline\rho)}\right)\\[5pt] &=\sum_\rho\frac{\textrm{Re}(\rho-\rho^2)}{|\rho|^2|1-\rho|^2}\\[5pt] &=\sum_\rho\frac{\beta(1-\beta)+\gamma^2}{|\rho|^2|1-\rho|^2}>0,\end{align*}
\begin{align*}\sum_\rho\frac1{\rho(1-\rho)}&=\frac12\sum_\rho\left(\frac1{\rho(1-\rho)}+\frac1{\overline\rho(1-\overline\rho)}\right)\\[5pt] &=\sum_\rho\frac{\textrm{Re}(\rho-\rho^2)}{|\rho|^2|1-\rho|^2}\\[5pt] &=\sum_\rho\frac{\beta(1-\beta)+\gamma^2}{|\rho|^2|1-\rho|^2}>0,\end{align*}
where
![]() $\rho=\beta+i\gamma$
and we have used
$\rho=\beta+i\gamma$
and we have used
![]() $0<\beta<1$
. This gives
$0<\beta<1$
. This gives
 \begin{align*}2\frac{L'}{L}(1,\chi)&=\gamma+2(1-\kappa)\log 2-\log\frac D\pi+\sum_\rho\frac1{\rho(1-\rho)}> \gamma+\log2\\[5pt] &\quad +\chi(-1)\log 2-\log\frac D\pi,\end{align*}
\begin{align*}2\frac{L'}{L}(1,\chi)&=\gamma+2(1-\kappa)\log 2-\log\frac D\pi+\sum_\rho\frac1{\rho(1-\rho)}> \gamma+\log2\\[5pt] &\quad +\chi(-1)\log 2-\log\frac D\pi,\end{align*}
as desired.
This allows us to establish the following result on
![]() $M_K^*(1)$
.
$M_K^*(1)$
.
Theorem 3·9. Let K be a real quadratic extension of
![]() $\mathbb{Q}$
with discriminant
$\mathbb{Q}$
with discriminant
![]() $D > 269$
. Then the naïve Mertens-type conjecture over K, i.e. that
$D > 269$
. Then the naïve Mertens-type conjecture over K, i.e. that
![]() $-1 \leq M_K^- \leq M_K^+ \leq 1$
, is false. In particular,
$-1 \leq M_K^- \leq M_K^+ \leq 1$
, is false. In particular,
![]() $M_K^*(1) > 0$
, and if the Riemann hypothesis for
$M_K^*(1) > 0$
, and if the Riemann hypothesis for
![]() $\zeta_K(s)$
is true and all of its nontrivial zeros are simple and not real, then
$\zeta_K(s)$
is true and all of its nontrivial zeros are simple and not real, then
![]() $M_K^+ \geq 1 + M_K^*(1)$
.
$M_K^+ \geq 1 + M_K^*(1)$
.
Proof. We begin by bounding the contribution of the infinite series in
![]() $M_K^*(1)$
. After dividing out by a factor of
$M_K^*(1)$
. After dividing out by a factor of
![]() $2/D^{1/2}$
, the series under consideration takes the form
$2/D^{1/2}$
, the series under consideration takes the form
 \begin{equation} \Sigma = \sum_{k=1}^\infty \left( \frac{4\pi^2}{D} \right)^{2k} \frac{1}{k ((2k)!\!)^2 \zeta_K(2k+1)} \left( \log\left( \frac{D}{4\pi^2} \right) + \frac{1}{2k} + \frac{\zeta_K'}{\zeta_K}(2k+1) + 2 \frac{\Gamma'}{\Gamma}(2k+1) \right).\end{equation}
\begin{equation} \Sigma = \sum_{k=1}^\infty \left( \frac{4\pi^2}{D} \right)^{2k} \frac{1}{k ((2k)!\!)^2 \zeta_K(2k+1)} \left( \log\left( \frac{D}{4\pi^2} \right) + \frac{1}{2k} + \frac{\zeta_K'}{\zeta_K}(2k+1) + 2 \frac{\Gamma'}{\Gamma}(2k+1) \right).\end{equation}
We note that
![]() $\zeta_K(2k + 1) \geq 1$
for all
$\zeta_K(2k + 1) \geq 1$
for all
![]() $k \geq 1$
, and by the triangle inequality,
$k \geq 1$
, and by the triangle inequality,
 \begin{align*} \left| \frac{\zeta_K'}{\zeta_K}(2k+1) \right| &= \left| \frac{\zeta'}{\zeta}(2k+1) + \frac{L'}{L}(2k+1,\chi_D) \right| \leq 2\sum_{n=1}^\infty \frac{\Lambda(n)}{n^{2k+1}} \\[5pt] &\leq 2\int_1^\infty \frac{\log x}{x^{2k+1}}\, dx = \frac{1}{2k^2}.\end{align*}
\begin{align*} \left| \frac{\zeta_K'}{\zeta_K}(2k+1) \right| &= \left| \frac{\zeta'}{\zeta}(2k+1) + \frac{L'}{L}(2k+1,\chi_D) \right| \leq 2\sum_{n=1}^\infty \frac{\Lambda(n)}{n^{2k+1}} \\[5pt] &\leq 2\int_1^\infty \frac{\log x}{x^{2k+1}}\, dx = \frac{1}{2k^2}.\end{align*}
We also have the following known identity for the digamma function:
 \begin{equation*} 2\frac{\Gamma'}{\Gamma}(2k + 1) = 2 \left( \sum_{n=1}^{2k} \frac{1}{n} - \gamma \right) \leq 2 \log(2k) + (2 - 2\gamma),\end{equation*}
\begin{equation*} 2\frac{\Gamma'}{\Gamma}(2k + 1) = 2 \left( \sum_{n=1}^{2k} \frac{1}{n} - \gamma \right) \leq 2 \log(2k) + (2 - 2\gamma),\end{equation*}
where
![]() $\gamma$
is Euler’s constant. Finally, we use these bounds to see that, for
$\gamma$
is Euler’s constant. Finally, we use these bounds to see that, for
![]() $D > 4\pi^2$
,
$D > 4\pi^2$
,
 \begin{align*} \Sigma &\leq \sum_{k=1}^\infty \left( \frac{4\pi^2}{D} \right)^{2k} \frac{1}{k ((2k)!\!)^2} \left( \log\left( \frac{D}{4\pi^2} \right) + \frac{1}{2k} + \frac{1}{2k^2} + 2 \log(2k) + (2 - 2\gamma) \right) \\[5pt] &\leq \left( \cosh\left( \frac{4\pi^2}{D} \right) - 1 \right) \left( \frac{1}{2}\log \left( \frac{D}{4\pi^2} \right) + \frac{1}{4} + \frac{1}{4} + \log 2 + (1 - \gamma) \right)\\[5pt] &= \left( \cosh \left( \frac{4\pi^2}{D} \right) - 1 \right) \left( \frac{1}{2} \log D +\frac 32-\log\pi -\gamma\right).\end{align*}
\begin{align*} \Sigma &\leq \sum_{k=1}^\infty \left( \frac{4\pi^2}{D} \right)^{2k} \frac{1}{k ((2k)!\!)^2} \left( \log\left( \frac{D}{4\pi^2} \right) + \frac{1}{2k} + \frac{1}{2k^2} + 2 \log(2k) + (2 - 2\gamma) \right) \\[5pt] &\leq \left( \cosh\left( \frac{4\pi^2}{D} \right) - 1 \right) \left( \frac{1}{2}\log \left( \frac{D}{4\pi^2} \right) + \frac{1}{4} + \frac{1}{4} + \log 2 + (1 - \gamma) \right)\\[5pt] &= \left( \cosh \left( \frac{4\pi^2}{D} \right) - 1 \right) \left( \frac{1}{2} \log D +\frac 32-\log\pi -\gamma\right).\end{align*}
We now turn our attention to the first term of
![]() $M_K^*(1)$
in (3·7). Upon dividing out by a factor of
$M_K^*(1)$
in (3·7). Upon dividing out by a factor of
![]() $2/D^{1/2}$
, we have
$2/D^{1/2}$
, we have
To this end, we recall the previously obtained bound from (3·5)
Finally, using Lemma 3·8 in the case of an even character, the problem reduces to finding the values D at which the inequality
 \begin{equation*} \frac{2 \left(\frac12\log D - \frac32\log\pi-\log2-\frac\gamma2\right)}{\frac{1}{2} \log D + \log \log D + 2 + \log 2} > \left( \cosh\left( \frac{4\pi^2}{D} \right) - 1 \right) \left( \frac{1}{2} \log D + \frac32-\gamma-\log\pi \right)\end{equation*}
\begin{equation*} \frac{2 \left(\frac12\log D - \frac32\log\pi-\log2-\frac\gamma2\right)}{\frac{1}{2} \log D + \log \log D + 2 + \log 2} > \left( \cosh\left( \frac{4\pi^2}{D} \right) - 1 \right) \left( \frac{1}{2} \log D + \frac32-\gamma-\log\pi \right)\end{equation*}
holds. This indeed holds for all
![]() $D > 269$
.
$D > 269$
.
By direct computation, we may address the smaller discriminants.
Table 3. Values of
![]() $M_K^*(1)$
for imaginary quadratic fields
$M_K^*(1)$
for imaginary quadratic fields
![]() $K = \mathbb{Q}(\sqrt{D})$
of discriminant D,
$K = \mathbb{Q}(\sqrt{D})$
of discriminant D,
![]() $D \leq 269$
.
$D \leq 269$
.
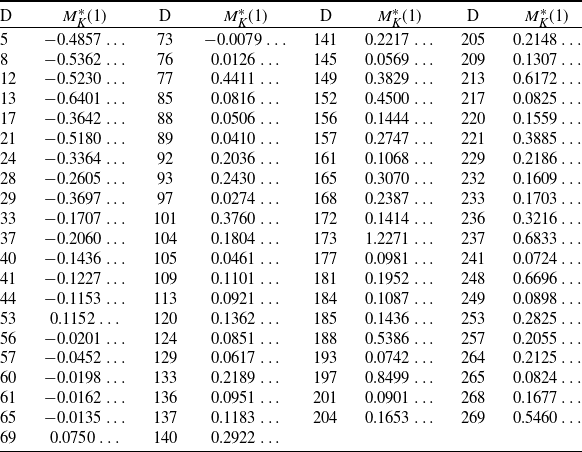
Table 4. Given
![]() $K={\mathbb {Q}}(\sqrt{-D})$
for a fundamental discriminant
$K={\mathbb {Q}}(\sqrt{-D})$
for a fundamental discriminant
![]() $-D$
, the smallest positive integer n for which
$-D$
, the smallest positive integer n for which
![]() $M_K(n^+)+M_K^*(n)>n^{1/2}$
.
$M_K(n^+)+M_K^*(n)>n^{1/2}$
.

Theorem 3·10. Let K be an real quadratic extension of
![]() $\mathbb{Q}$
with discriminant
$\mathbb{Q}$
with discriminant
![]() $5 < D \leq 269$
. Then the naïve Mertens-type conjecture over K is false, with
$5 < D \leq 269$
. Then the naïve Mertens-type conjecture over K is false, with
![]() $M_K^+ > 1$
.
$M_K^+ > 1$
.
Proof. As in the proof of Theorem 3·7, the values of
![]() $M_K^*(1)$
are tabulated in Table 3, where the sum has been computed up to threshold
$M_K^*(1)$
are tabulated in Table 3, where the sum has been computed up to threshold
![]() $k = 50$
. This implies the falsity of the naïve Mertens-type conjecture over K for all
$k = 50$
. This implies the falsity of the naïve Mertens-type conjecture over K for all
![]() $D \leq 269$
where
$D \leq 269$
where
Again, this can be remedied for most of the above discriminants by letting
![]() $x \rightarrow n^{+}$
for other positive integers n for which
$x \rightarrow n^{+}$
for other positive integers n for which
![]() $n^{-1/2}(M_K(n^{+})+ M_K^*(n)) > 1$
. These findings are presented in Table 4, which suffices to resolve all cases except for
$n^{-1/2}(M_K(n^{+})+ M_K^*(n)) > 1$
. These findings are presented in Table 4, which suffices to resolve all cases except for
![]() $D = 5$
(the field
$D = 5$
(the field
![]() ${\mathbb {Q}}(\sqrt{5})$
),
${\mathbb {Q}}(\sqrt{5})$
),
![]() $D = 8$
(the field
$D = 8$
(the field
![]() ${\mathbb {Q}}(\sqrt{2})$
), and
${\mathbb {Q}}(\sqrt{2})$
), and
![]() $D = 12$
(the field
$D = 12$
(the field
![]() ${\mathbb {Q}}(\sqrt{3})$
).
${\mathbb {Q}}(\sqrt{3})$
).
For these fields, we return to the means
![]() $h_{K,T}^*(t)$
as defined in (3·6). A computation shows that
$h_{K,T}^*(t)$
as defined in (3·6). A computation shows that
![]() $t = 17.32$
at
$t = 17.32$
at
![]() $T = 200$
suffices for
$T = 200$
suffices for
![]() $K = {\mathbb {Q}}(\sqrt{3})$
with a bound of
$K = {\mathbb {Q}}(\sqrt{3})$
with a bound of
![]() $M_K^+ > 1.027$
. Moreover,
$M_K^+ > 1.027$
. Moreover,
![]() $t = -24.64$
at
$t = -24.64$
at
![]() $T = 150$
suffices for
$T = 150$
suffices for
![]() $K = {\mathbb {Q}}(\sqrt{2})$
with a bound of
$K = {\mathbb {Q}}(\sqrt{2})$
with a bound of
![]() $M_K^+ > 1.049$
.
$M_K^+ > 1.049$
.
This concludes the proof of Theorem 1·1(b).
3·4. General number fields
In this subsection, we show that
![]() $M_K^*(1)>0$
for all number fields K with sufficiently large discriminant and fixed signature. In light of Lemma 3·4, this implies that the naïve Mertens-type conjecture is false for such K. We first show that the contribution of the residues at strictly negative integers is relatively small.
$M_K^*(1)>0$
for all number fields K with sufficiently large discriminant and fixed signature. In light of Lemma 3·4, this implies that the naïve Mertens-type conjecture is false for such K. We first show that the contribution of the residues at strictly negative integers is relatively small.
Lemma 3·11. Fix a signature
![]() $(r_1,r_2)$
, and consider a number field K with
$(r_1,r_2)$
, and consider a number field K with
![]() $r_1$
real embeddings,
$r_1$
real embeddings,
![]() $2r_2$
complex embeddings, and varying discriminant
$2r_2$
complex embeddings, and varying discriminant
![]() $\Delta_K$
of magnitude
$\Delta_K$
of magnitude
![]() $\textrm{D}_K$
. Then for all
$\textrm{D}_K$
. Then for all
![]() $x \geq 1$
,
$x \geq 1$
,
 $$\sum_{k=1}^\infty \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}\ll \frac{(\log(x\textrm{D}_K))^{n_K}}{x\textrm{D}_K^{3/2}}.$$
$$\sum_{k=1}^\infty \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}\ll \frac{(\log(x\textrm{D}_K))^{n_K}}{x\textrm{D}_K^{3/2}}.$$
Proof. Apply Lemma 2·13 and sum the results.
The remainder of this section will involve bounding the residue at
![]() $s=0$
. In our application, we are taking
$s=0$
. In our application, we are taking
![]() $x = 1$
, and it is easy to see that
$x = 1$
, and it is easy to see that
We first give a result about the Laurent series coefficients of
![]() $\zeta_K'(s)/\zeta_K(s)$
at
$\zeta_K'(s)/\zeta_K(s)$
at
![]() $s = 1$
.
$s = 1$
.
Lemma 3·12. Let K be a number field of fixed degree, and assume the Riemann hypothesis for
![]() $\zeta_K(s)$
. Then, for a fixed integer
$\zeta_K(s)$
. Then, for a fixed integer
![]() $j\geq 0$
,
$j\geq 0$
,
Proof. We mimic the proof of [
Reference Montgomery and VaughanMV07
, theorem 13·13]. Fix some real
![]() $x,y\geq 2$
, to be chosen later. Define
$x,y\geq 2$
, to be chosen later. Define
![]() $\Lambda^K(n)$
to be the coefficient of
$\Lambda^K(n)$
to be the coefficient of
![]() $n^{-s}$
in the Dirichlet series expansion of
$n^{-s}$
in the Dirichlet series expansion of
![]() $\zeta_K'(s)/\zeta_K(s)$
, and define
$\zeta_K'(s)/\zeta_K(s)$
, and define
 $$w(u)=w(x, y; u) \;:\!=\; \begin{cases} 1 & 1 \leq u \leq x \\[5pt] 1 - \frac{\log u/x}{\log y} & x \leq u \leq xy\\[5pt] 0 & u \geq xy.\end{cases}$$
$$w(u)=w(x, y; u) \;:\!=\; \begin{cases} 1 & 1 \leq u \leq x \\[5pt] 1 - \frac{\log u/x}{\log y} & x \leq u \leq xy\\[5pt] 0 & u \geq xy.\end{cases}$$
By Riesz summation ([ Reference Montgomery and VaughanMV07 , (5·20)]; cf. [ Reference Montgomery and VaughanMV07 , theorem 13·13]), we have
 \begin{equation}\sum_{n\leq xy}\frac{w(n)\Lambda^K(n)}{n^s}=-\frac{\zeta_K'(s)}{\zeta_K(s)}+\frac{(xy)^{1-s}-x^{1-s}}{(1-s)^2\log y}-\sum_\rho\frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y},\end{equation}
\begin{equation}\sum_{n\leq xy}\frac{w(n)\Lambda^K(n)}{n^s}=-\frac{\zeta_K'(s)}{\zeta_K(s)}+\frac{(xy)^{1-s}-x^{1-s}}{(1-s)^2\log y}-\sum_\rho\frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y},\end{equation}
where the sum runs over all zeros of
![]() $\zeta_K(s)$
, both trivial and nontrivial, and a zero of multiplicity m appears m times. Now, as the nontrivial zeros occur only at non-positive integers and with multiplicity bounded by
$\zeta_K(s)$
, both trivial and nontrivial, and a zero of multiplicity m appears m times. Now, as the nontrivial zeros occur only at non-positive integers and with multiplicity bounded by
![]() $n_K$
$n_K$
 \begin{equation}\left|\sum_{\rho\text{ trivial}}\frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y}\right|\leq n_K\sum_{k=0}^\infty \left|\frac{(xy)^{-k-s}-x^{-k-s}}{(k+s)^2\log y}\right|\ll \frac{2x^{-3/4}}{\log y},\end{equation}
\begin{equation}\left|\sum_{\rho\text{ trivial}}\frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y}\right|\leq n_K\sum_{k=0}^\infty \left|\frac{(xy)^{-k-s}-x^{-k-s}}{(k+s)^2\log y}\right|\ll \frac{2x^{-3/4}}{\log y},\end{equation}
where the last bound follows from
![]() $|s-1|\;\leq {1}/{4}$
. Also,
$|s-1|\;\leq {1}/{4}$
. Also,
 \begin{align*}\left|\sum_{\rho\text{ nontrivial}}\frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y}\right|&\leq 2\sum_{T=0}^\infty \sum_{T\leq \gamma<T+1}\frac{x^{1/2-\sigma}\left|y^{\rho-s}-1\right|}{\left|\frac12-\sigma+i(\gamma-t)\right|^2\log y}\\[5pt] &\leq \frac{4x^{-1/4}}{\log y}\sum_{T=0}^\infty \frac{N(T+1)-N(T)}{\frac1{16}+T^2}\ll \frac{x^{-1/4}\log\textrm{D}_K}{\log y},\end{align*}
\begin{align*}\left|\sum_{\rho\text{ nontrivial}}\frac{(xy)^{\rho-s}-x^{\rho-s}}{(\rho-s)^2\log y}\right|&\leq 2\sum_{T=0}^\infty \sum_{T\leq \gamma<T+1}\frac{x^{1/2-\sigma}\left|y^{\rho-s}-1\right|}{\left|\frac12-\sigma+i(\gamma-t)\right|^2\log y}\\[5pt] &\leq \frac{4x^{-1/4}}{\log y}\sum_{T=0}^\infty \frac{N(T+1)-N(T)}{\frac1{16}+T^2}\ll \frac{x^{-1/4}\log\textrm{D}_K}{\log y},\end{align*}
where we have used Lemma 2·3 in the last simplification. As a result,
 $$f(s)\;:\!=\; \frac{\zeta_K'(s)}{\zeta_K(s)}-\left[-\sum_{n\leq xy}\frac{w(n)\Lambda^K(n)}{n^s}+\frac{(xy)^{1-s}-x^{1-s}}{(1-s)^2\log y}\right]\ll O\left(\frac{x^{-1/4}\log\textrm{D}_K}{\log y}\right)$$
$$f(s)\;:\!=\; \frac{\zeta_K'(s)}{\zeta_K(s)}-\left[-\sum_{n\leq xy}\frac{w(n)\Lambda^K(n)}{n^s}+\frac{(xy)^{1-s}-x^{1-s}}{(1-s)^2\log y}\right]\ll O\left(\frac{x^{-1/4}\log\textrm{D}_K}{\log y}\right)$$
for
![]() $|s-1|\;\leq {1}/{4}$
. Now, the Taylor series expansion
$|s-1|\;\leq {1}/{4}$
. Now, the Taylor series expansion
 $$\frac{\zeta_K'(s)}{\zeta_K(s)}=-\frac1{s-1}+\sum_{j=0}^\infty \frac{a_j(s-1)^j}{j!\!},\qquad a_j=\lim_{s\to 1}\frac{d^j}{ds^j}\left(\frac1{s-1}+\frac{\zeta_K'(s)}{\zeta_K(s)}\right)$$
$$\frac{\zeta_K'(s)}{\zeta_K(s)}=-\frac1{s-1}+\sum_{j=0}^\infty \frac{a_j(s-1)^j}{j!\!},\qquad a_j=\lim_{s\to 1}\frac{d^j}{ds^j}\left(\frac1{s-1}+\frac{\zeta_K'(s)}{\zeta_K(s)}\right)$$
converges for
![]() $|s-1|\; < {1}/{2}$
, since
$|s-1|\; < {1}/{2}$
, since
![]() $\zeta_K(s)$
has no zeros strictly within distance
$\zeta_K(s)$
has no zeros strictly within distance
![]() ${1}/{2}$
of
${1}/{2}$
of
![]() $s=1$
. Furthermore, we have the expansions
$s=1$
. Furthermore, we have the expansions
 $$\sum_{n\leq xy}\frac{w(n)\Lambda^K(n)}{n^s}=\sum_{j=0}^\infty \frac{(s-1)^j}{j!\!}\sum_{n\leq xy}\frac{w(n)\Lambda^K(n)(-\log n)^j}{n}$$
$$\sum_{n\leq xy}\frac{w(n)\Lambda^K(n)}{n^s}=\sum_{j=0}^\infty \frac{(s-1)^j}{j!\!}\sum_{n\leq xy}\frac{w(n)\Lambda^K(n)(-\log n)^j}{n}$$
and
 $$\frac{(xy)^{1-s}-x^{1-s}}{(1-s)^2\log y}=-\frac1{s-1}+\sum_{j=0}^\infty \frac{(s-1)^j}{j!\!}\left(\frac{({-}1)^j\left(\log(xy)^{j+2}-(\log x)^{j+2}\right)}{(j+1)(j+2)\log y}\right).$$
$$\frac{(xy)^{1-s}-x^{1-s}}{(1-s)^2\log y}=-\frac1{s-1}+\sum_{j=0}^\infty \frac{(s-1)^j}{j!\!}\left(\frac{({-}1)^j\left(\log(xy)^{j+2}-(\log x)^{j+2}\right)}{(j+1)(j+2)\log y}\right).$$
Now, select
![]() $x=(\log\textrm{D}_K)^4$
and
$x=(\log\textrm{D}_K)^4$
and
![]() $y=e$
, so that
$y=e$
, so that
![]() $f(s)=O(1)$
. Writing
$f(s)=O(1)$
. Writing
 $$f(s)=\sum_{j=0}^\infty \frac{b_j(s-1)^j}{j!\!},$$
$$f(s)=\sum_{j=0}^\infty \frac{b_j(s-1)^j}{j!\!},$$
we have
for any
![]() $r\leq {1}/{4}$
, where
$r\leq {1}/{4}$
, where
![]() $\Gamma_r$
is a counterclockwise circular contour of radius r around 1. For fixed j and r, bounding the integrand in the second integral gives
$\Gamma_r$
is a counterclockwise circular contour of radius r around 1. For fixed j and r, bounding the integrand in the second integral gives
![]() $b_j=O(1)$
. So, recalling our choices of x and y and using partial summation gives
$b_j=O(1)$
. So, recalling our choices of x and y and using partial summation gives
 \begin{align*}a_j&=\sum_{n\leq xy}\frac{w(n)\Lambda^K(n)(-\log n)^j}{n}+\frac{({-}1)^j\left(\log(xy)^{j+2}-(\log x)^{j+2}\right)}{(j+1)(j+2)\log y}\\[5pt] &\quad +O(1)\ll(\log\log\textrm{D}_K)^{j+1}.\end{align*}
\begin{align*}a_j&=\sum_{n\leq xy}\frac{w(n)\Lambda^K(n)(-\log n)^j}{n}+\frac{({-}1)^j\left(\log(xy)^{j+2}-(\log x)^{j+2}\right)}{(j+1)(j+2)\log y}\\[5pt] &\quad +O(1)\ll(\log\log\textrm{D}_K)^{j+1}.\end{align*}
This completes the proof.
We are now ready to bound the residue at 0.
Lemma 3·13. In the same setting as Lemma 3·11,
 $$-\textrm{Res}_{s=0}\frac1{s\zeta_K(s)}=\frac{2^{r_1+r_2}\pi^{r_2}(\log\textrm{D}_K)^{r_1+r_2-1}}{\textrm{D}_K^{1/2}\lim_{s\to 1}{(s-1)\zeta_K(s)}}(1+o(1))\gg_{r_1,r_2} \frac{(\log\textrm{D}_K)^{-r_2}}{D_K^{1/2}}.$$
$$-\textrm{Res}_{s=0}\frac1{s\zeta_K(s)}=\frac{2^{r_1+r_2}\pi^{r_2}(\log\textrm{D}_K)^{r_1+r_2-1}}{\textrm{D}_K^{1/2}\lim_{s\to 1}{(s-1)\zeta_K(s)}}(1+o(1))\gg_{r_1,r_2} \frac{(\log\textrm{D}_K)^{-r_2}}{D_K^{1/2}}.$$
Proof. Write
Using the functional equation, we may write
 $$\frac{s^{r_1+r_2-1}}{\zeta_K(s)}=\left(\frac{2^{r_2}\pi^{n_K}}{\textrm{D}_K^{1/2}}\right)\left(\frac{\textrm{D}_K}{(2\pi)^{n_K}}\right)^s\left(\frac1{s\zeta_K(1-s)}\right)\left(\frac{s}{\sin\frac{\pi s}2}\right)^{r_1}\left(\frac s{\sin\pi s}\right)^{r_2}\left(\frac1{\Gamma(1-s)}\right)^{n_K}.$$
$$\frac{s^{r_1+r_2-1}}{\zeta_K(s)}=\left(\frac{2^{r_2}\pi^{n_K}}{\textrm{D}_K^{1/2}}\right)\left(\frac{\textrm{D}_K}{(2\pi)^{n_K}}\right)^s\left(\frac1{s\zeta_K(1-s)}\right)\left(\frac{s}{\sin\frac{\pi s}2}\right)^{r_1}\left(\frac s{\sin\pi s}\right)^{r_2}\left(\frac1{\Gamma(1-s)}\right)^{n_K}.$$
Define
 \begin{align*}f(s) &=\frac{s^{r_1+r_2-1}}{\zeta_K(s)}\\[5pt] g_1(s)&=s\log\left(\frac{\textrm{D}_K}{(2\pi)^{n_K}}\right)\\[5pt] g_2(s)&=\log(s\zeta_K(1-s))\\[5pt] g_3(s)&=\log s-\log\sin\frac{\pi s}2\\[5pt] g_4(s)&=\log s-\log\sin\pi s\\[5pt] g_5(s)&=\log\Gamma(1-s)\end{align*}
\begin{align*}f(s) &=\frac{s^{r_1+r_2-1}}{\zeta_K(s)}\\[5pt] g_1(s)&=s\log\left(\frac{\textrm{D}_K}{(2\pi)^{n_K}}\right)\\[5pt] g_2(s)&=\log(s\zeta_K(1-s))\\[5pt] g_3(s)&=\log s-\log\sin\frac{\pi s}2\\[5pt] g_4(s)&=\log s-\log\sin\pi s\\[5pt] g_5(s)&=\log\Gamma(1-s)\end{align*}
so that
 $$g(s)\;:\!=\;\log f(s)=\log\left(\frac{2^{r_2}\pi^{n_K}}{\textrm{D}_K^{1/2}}\right)+g_1(s)-g_2(s)+r_1g_3(s)+r_2g_4(s)-n_Kg_5(s).$$
$$g(s)\;:\!=\;\log f(s)=\log\left(\frac{2^{r_2}\pi^{n_K}}{\textrm{D}_K^{1/2}}\right)+g_1(s)-g_2(s)+r_1g_3(s)+r_2g_4(s)-n_Kg_5(s).$$
Since
![]() $f'(s)=g'(s)f(s)$
, we have via induction on j that
$f'(s)=g'(s)f(s)$
, we have via induction on j that
for some polynomial
![]() $P_j(t_1,\ldots,t_j)$
in j variables with positive integral coefficients, which is homogeneous of degree j when
$P_j(t_1,\ldots,t_j)$
in j variables with positive integral coefficients, which is homogeneous of degree j when
![]() $t_i$
is assigned degree i. In addition, the coefficient of
$t_i$
is assigned degree i. In addition, the coefficient of
![]() $t_1^j$
in
$t_1^j$
in
![]() $P_j(t_1,\ldots,t_j)$
is 1. We now bound the derivatives of g at 1.
$P_j(t_1,\ldots,t_j)$
is 1. We now bound the derivatives of g at 1.
For each
![]() $1\leq j\leq r_1+r_2-1$
, the derivatives
$1\leq j\leq r_1+r_2-1$
, the derivatives
![]() $g_i^{(j)}(s)$
for
$g_i^{(j)}(s)$
for
![]() $i\in\{3,4,5\}$
near
$i\in\{3,4,5\}$
near
![]() $s=0$
depend only on
$s=0$
depend only on
![]() $r_1$
and
$r_1$
and
![]() $r_2$
, so we can treat the terms corresponding to these
$r_2$
, so we can treat the terms corresponding to these
![]() $g_i$
as constants. This gives that, for
$g_i$
as constants. This gives that, for
![]() $j\geq 1$
,
$j\geq 1$
,
 $$g^{(j)}(s)=-g_2^{(j)}(s)+O(1)+\begin{cases}\log\textrm{D}_K&j=1\\[5pt] 0&j> 1.\end{cases}$$
$$g^{(j)}(s)=-g_2^{(j)}(s)+O(1)+\begin{cases}\log\textrm{D}_K&j=1\\[5pt] 0&j> 1.\end{cases}$$
Now, note that
so Lemma 3·12 shows that
![]() $g_2^{(j)}(0)\ll(\log\log\textrm{D}_K)^{j}$
for all
$g_2^{(j)}(0)\ll(\log\log\textrm{D}_K)^{j}$
for all
![]() $j\geq 1$
. This implies that, using the properties of
$j\geq 1$
. This implies that, using the properties of
![]() $P_j$
,
$P_j$
,
Also,
 $$\lim_{s\to 0}f(s)=\left(\frac{2^{r_2}\pi^{n_K}}{\textrm{D}_K^{1/2}}\right)\left(\lim_{s\to 0}\frac1{s\zeta_K(1-s)}\right)\left(\frac2\pi\right)^{r_1}\left(\frac1\pi\right)^{r_2}=-\frac{2^{r_1+r_2}\pi^{r_2}}{\textrm{D}_K^{1/2}}\lim_{s\to 1}\frac1{(s-1)\zeta_K(s)}.$$
$$\lim_{s\to 0}f(s)=\left(\frac{2^{r_2}\pi^{n_K}}{\textrm{D}_K^{1/2}}\right)\left(\lim_{s\to 0}\frac1{s\zeta_K(1-s)}\right)\left(\frac2\pi\right)^{r_1}\left(\frac1\pi\right)^{r_2}=-\frac{2^{r_1+r_2}\pi^{r_2}}{\textrm{D}_K^{1/2}}\lim_{s\to 1}\frac1{(s-1)\zeta_K(s)}.$$
By a theorem of Louboutin [ Reference LouboutinLou00a , theorem 1],
and is clearly positive. This gives the desired result.
Using this bound, we finish the proof that
![]() $M_K^*(1)>0$
for all sufficiently large
$M_K^*(1)>0$
for all sufficiently large
![]() $D_K$
.
$D_K$
.
Proof of Theorem 1·2. By Lemma 3·11,
 $$M_K^*(1)=-\textrm{Res}_{s=0}\frac1{s\zeta_K(s)}+O\left(\frac{(\log \textrm{D}_K)^{n_K}}{\textrm{D}_K^{3/2}}\right).$$
$$M_K^*(1)=-\textrm{Res}_{s=0}\frac1{s\zeta_K(s)}+O\left(\frac{(\log \textrm{D}_K)^{n_K}}{\textrm{D}_K^{3/2}}\right).$$
Now, Lemma 3·13 implies that the first term is positive, and that it grows at least as quickly as
For large
![]() $\textrm{D}_K$
depending on
$\textrm{D}_K$
depending on
![]() $r_1$
and
$r_1$
and
![]() $r_2$
, this outpaces the other terms, and so
$r_2$
, this outpaces the other terms, and so
![]() $M_K^*(1)>0$
. An application of Lemma 3·4 finishes the proof.
$M_K^*(1)>0$
. An application of Lemma 3·4 finishes the proof.
4. Proof of Theorem 1·4
In this section, we fix a number field K whose Dedekind zeta function satisfies the Riemann hypothesis and
![]() $J_{-1}^K(T) \ll_{\alpha} T^{1+\alpha}$
for some
$J_{-1}^K(T) \ll_{\alpha} T^{1+\alpha}$
for some
![]() $0 \leq \alpha < 2 - \sqrt{3}$
. We expect these hypotheses to hold for all K with
$0 \leq \alpha < 2 - \sqrt{3}$
. We expect these hypotheses to hold for all K with
![]() $K/{\mathbb {Q}}$
an abelian Galois extension, and provide support for the second condition later in this section.
$K/{\mathbb {Q}}$
an abelian Galois extension, and provide support for the second condition later in this section.
Ng [
Reference NgNg04
] demonstrates the existence of a limiting distribution for
![]() $e^{-y/2}M(e^y)$
by achieving bounds for the error term E(x,T) in the truncated explicit formula
$e^{-y/2}M(e^y)$
by achieving bounds for the error term E(x,T) in the truncated explicit formula
 $$M(x) = \sum_{|\gamma| \leq T} \frac{x^\rho}{\rho \zeta'(\rho)} + E(x,T)$$
$$M(x) = \sum_{|\gamma| \leq T} \frac{x^\rho}{\rho \zeta'(\rho)} + E(x,T)$$
for M(x). He then follows the method of Rubinstein–Sarnak [ Reference Rubinstein and SarnakRS94 ] to prove the existence of a limiting distribution by first constructing measures for the main term at height T, then bounding the error term E(x,T) to show that they converge to the desired probability measure.
Later work of Akbary–Ng–Shahabi in [ Reference Akbary, Ng and ShahabiANS14 ] allows for substantial generalisation of this method by proving that a more general class of functions of interest possess limiting distributions; we will use their framework in our proof. First, it requires the definition of a rather broad class of almost periodic functions.
Definition 4·1. Denote by
![]() $\mathbb {T}$
the class of all real-valued trigonometric polynomials
$\mathbb {T}$
the class of all real-valued trigonometric polynomials
 \begin{equation*} P_N(y) = \sum_{n=1}^N r_n e^{i \lambda_n y}, \quad y \in \mathbb{R}\end{equation*}
\begin{equation*} P_N(y) = \sum_{n=1}^N r_n e^{i \lambda_n y}, \quad y \in \mathbb{R}\end{equation*}
where
![]() $r_n \in \mathbb{C}$
and
$r_n \in \mathbb{C}$
and
![]() $\lambda_n \in \mathbb{R}$
. We say that a locally square-integrable function
$\lambda_n \in \mathbb{R}$
. We say that a locally square-integrable function
![]() $\phi \in L_{\text{loc}}^2([0,\infty))$
is
$\phi \in L_{\text{loc}}^2([0,\infty))$
is
![]() $B^2$
-almost periodic if for any
$B^2$
-almost periodic if for any
![]() $\epsilon > 0$
, there is a function
$\epsilon > 0$
, there is a function
![]() $f_\epsilon(y) \in \mathbb {T}$
such that
$f_\epsilon(y) \in \mathbb {T}$
such that
where
 \begin{equation*} \lVert \phi \rVert_{B^2} \;:\!=\; \left( \limsup_{Y \rightarrow \infty} \frac{1}{Y} \int_0^Y |\phi(y)|^2 \, dy \right)^{1/2}.\end{equation*}
\begin{equation*} \lVert \phi \rVert_{B^2} \;:\!=\; \left( \limsup_{Y \rightarrow \infty} \frac{1}{Y} \int_0^Y |\phi(y)|^2 \, dy \right)^{1/2}.\end{equation*}
All
![]() $B^2$
-almost periodic functions possess a limiting distribution [
Reference Akbary, Ng and ShahabiANS14
, theorem 2·9]. This allows for concrete descriptions of almost periodic functions in the line of Rubinstein–Sarnak, as well as the later Mertens-specific work of Ng.
$B^2$
-almost periodic functions possess a limiting distribution [
Reference Akbary, Ng and ShahabiANS14
, theorem 2·9]. This allows for concrete descriptions of almost periodic functions in the line of Rubinstein–Sarnak, as well as the later Mertens-specific work of Ng.
Theorem 4·2 (Akbary-Ng-Shahabi [
Reference Akbary, Ng and ShahabiANS14
, corollary 1·3]). Let
![]() $\phi:[0,\infty) \rightarrow \mathbb{R}$
be a scalar-valued function and let
$\phi:[0,\infty) \rightarrow \mathbb{R}$
be a scalar-valued function and let
![]() $y_0$
be such that
$y_0$
be such that
![]() $\phi$
is square-integrable on
$\phi$
is square-integrable on
![]() $[0,y_0]$
. Assume there exists a non-decreasing sequence of positive numbers
$[0,y_0]$
. Assume there exists a non-decreasing sequence of positive numbers
![]() $\{\lambda_n\}_{n \in \mathbb{N}}$
which tends to infinity, a sequence of complex numbers
$\{\lambda_n\}_{n \in \mathbb{N}}$
which tends to infinity, a sequence of complex numbers
![]() $\{r_n\}_{n \in \mathbb{N}}$
and a real constant c such that for
$\{r_n\}_{n \in \mathbb{N}}$
and a real constant c such that for
![]() $y \geq y_0$
,
$y \geq y_0$
,
 \begin{equation} \phi(y) = c + \textrm{Re}\left( \sum_{\lambda_n \leq X} r_n e^{i\lambda_n y} \right) + \mathcal{E}(y,X)\end{equation}
\begin{equation} \phi(y) = c + \textrm{Re}\left( \sum_{\lambda_n \leq X} r_n e^{i\lambda_n y} \right) + \mathcal{E}(y,X)\end{equation}
for any
![]() $X \geq X_0 > 0$
, where
$X \geq X_0 > 0$
, where
![]() $\mathcal{E}(y,X)$
satisfies
$\mathcal{E}(y,X)$
satisfies
Assume that
and that either
-
(a)
 $r_n \ll \lambda_n^{-\beta}$
for some
$r_n \ll \lambda_n^{-\beta}$
for some
 $\beta > {1}/{2}$
, or that
$\beta > {1}/{2}$
, or that -
(b) for some
 $0\leq \theta<3-\sqrt 3$
, (4·4)
$0\leq \theta<3-\sqrt 3$
, (4·4) \begin{equation} \sum_{\lambda_n \leq T} \lambda_n^2 |r_n|^2 \ll T^\theta. \end{equation}
\begin{equation} \sum_{\lambda_n \leq T} \lambda_n^2 |r_n|^2 \ll T^\theta. \end{equation}
Then
![]() $\phi(y)$
is a
$\phi(y)$
is a
![]() $B^2$
-almost periodic function and therefore possesses a limiting distribution.
$B^2$
-almost periodic function and therefore possesses a limiting distribution.
Therefore, to establish the existence of a logarithmic limiting distribution for
![]() $x^{-1/2}M_K(x)$
, it will suffice to provide a suitable expression for
$x^{-1/2}M_K(x)$
, it will suffice to provide a suitable expression for
as above with error small in the sense of (4·2), as well as to verify that (4·4) holds for some
![]() $\theta<3-\sqrt3$
. Our first step will be to extend the explicit formula (Proposition 2·12) for M(x) to all heights
$\theta<3-\sqrt3$
. Our first step will be to extend the explicit formula (Proposition 2·12) for M(x) to all heights
![]() $T\geq 2$
, assuming the analogue of the Gonek–Hejhal conjecture for K, as in (1·3).
$T\geq 2$
, assuming the analogue of the Gonek–Hejhal conjecture for K, as in (1·3).
Lemma 4·3. Assume the Riemann hypothesis for
![]() $\zeta_K(s)$
and that
$\zeta_K(s)$
and that
![]() $J_{-1}^K(T)\ll_\alpha T^{1+\alpha}$
. For
$J_{-1}^K(T)\ll_\alpha T^{1+\alpha}$
. For
![]() $x \geq 2$
and arbitrary
$x \geq 2$
and arbitrary
![]() $T \geq 2$
,
$T \geq 2$
,
 \begin{equation} M_K(x) = \sum_{|\gamma| \leq T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} + E(x,T),\end{equation}
\begin{equation} M_K(x) = \sum_{|\gamma| \leq T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} + E(x,T),\end{equation}
where
for any
![]() $\epsilon>0$
where the constant C is as in Lemma 2·2.
$\epsilon>0$
where the constant C is as in Lemma 2·2.
Proof. Suppose
![]() $T \geq 2$
satisfies
$T \geq 2$
satisfies
![]() $n \leq T \leq n+1$
for some positive integer n, and let
$n \leq T \leq n+1$
for some positive integer n, and let
![]() $T_n$
be as in Lemma 2·4. Suppose without loss of generality that
$T_n$
be as in Lemma 2·4. Suppose without loss of generality that
![]() $n \leq T_n \leq T \leq n+1$
. Proposition 2·12 gives that
$n \leq T_n \leq T \leq n+1$
. Proposition 2·12 gives that
 \begin{equation*} M_K(x) = \sum_{|\gamma| \leq T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} - \sum_{T_n \leq |\gamma| \leq T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} + E(x,T_n),\end{equation*}
\begin{equation*} M_K(x) = \sum_{|\gamma| \leq T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} - \sum_{T_n \leq |\gamma| \leq T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} + E(x,T_n),\end{equation*}
where
We use the assumption
![]() $J_{-1}^K(T)\ll T^{1 + \alpha}$
to bound the second sum. The Cauchy–Schwarz inequality gives that, under the Riemann hypothesis,
$J_{-1}^K(T)\ll T^{1 + \alpha}$
to bound the second sum. The Cauchy–Schwarz inequality gives that, under the Riemann hypothesis,
 \begin{equation*} \left| \sum_{T_n \leq |\gamma| \leq T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} \right| \leq x^{1/2} \left( \sum_{T_n \leq |\gamma| \leq T} \frac{1}{|\rho \zeta_K'(\rho)|^2} \right)^{1/2} \left( \sum_{T_n \leq |\gamma| \leq T} 1 \right)^{1/2}.\end{equation*}
\begin{equation*} \left| \sum_{T_n \leq |\gamma| \leq T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} \right| \leq x^{1/2} \left( \sum_{T_n \leq |\gamma| \leq T} \frac{1}{|\rho \zeta_K'(\rho)|^2} \right)^{1/2} \left( \sum_{T_n \leq |\gamma| \leq T} 1 \right)^{1/2}.\end{equation*}
Since
 $$\sum_{T_n\leq|\gamma|\leq T}\frac1{|\rho\zeta_K'(\rho)|^2}\ll \frac1{T^2}\sum_{T_n\leq|\gamma|\leq T}\frac1{|\zeta_K'(\rho)|^2}\ll \frac{J_{-1}^K(T)}{T^2}\ll T^{\alpha - 1},$$
$$\sum_{T_n\leq|\gamma|\leq T}\frac1{|\rho\zeta_K'(\rho)|^2}\ll \frac1{T^2}\sum_{T_n\leq|\gamma|\leq T}\frac1{|\zeta_K'(\rho)|^2}\ll \frac{J_{-1}^K(T)}{T^2}\ll T^{\alpha - 1},$$
and the number of zeros of
![]() $\zeta_K$
with ordinates between
$\zeta_K$
with ordinates between
![]() $T_n$
and T is
$T_n$
and T is
![]() $\ll \log T$
by Lemma 2·3,
$\ll \log T$
by Lemma 2·3,
 $$\left| \sum_{T_n \leq |\gamma| \leq T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} \right| \ll \left( \frac{x \log T}{T^{1 - \alpha}} \right)^{1/2},$$
$$\left| \sum_{T_n \leq |\gamma| \leq T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} \right| \ll \left( \frac{x \log T}{T^{1 - \alpha}} \right)^{1/2},$$
which is enough. The case
![]() $T \leq T_n$
is treated similarly; all that differs is the sign on the zeros with ordinates between T and
$T \leq T_n$
is treated similarly; all that differs is the sign on the zeros with ordinates between T and
![]() $T_n$
.
$T_n$
.
We are ready to establish the main theorem.
Proof of Theorem 1·4. Setting
![]() $x = e^y$
in Lemma 4·3, where
$x = e^y$
in Lemma 4·3, where
![]() $y \geq e$
, we may define
$y \geq e$
, we may define
 \begin{equation*} \phi_K(y) = e^{-\frac{y}{2}}M_K(e^y) = \sum_{|\gamma| \leq T} \frac{e^{i \gamma y}}{\rho \zeta_K'(\rho)} + \mathcal{E}(e^y,T),\end{equation*}
\begin{equation*} \phi_K(y) = e^{-\frac{y}{2}}M_K(e^y) = \sum_{|\gamma| \leq T} \frac{e^{i \gamma y}}{\rho \zeta_K'(\rho)} + \mathcal{E}(e^y,T),\end{equation*}
where
This is of the form required in Theorem 4·2; if we order the nontrivial zeros of
![]() $\zeta_K$
nondecreasingly by magnitude of ordinate (both with positive and negative ordinate) as
$\zeta_K$
nondecreasingly by magnitude of ordinate (both with positive and negative ordinate) as
![]() $\rho_n=1/2+i\gamma_n$
, then our definition of
$\rho_n=1/2+i\gamma_n$
, then our definition of
![]() $\phi_K(y)$
agrees with (4·1) with
$\phi_K(y)$
agrees with (4·1) with
As a result, we need only to verify (4·2), (4·3) and (4·4) for some
![]() $\theta<3-\sqrt 3$
. The second of these is implied by Lemma 2·3, and the third holds for
$\theta<3-\sqrt 3$
. The second of these is implied by Lemma 2·3, and the third holds for
![]() $\theta=1 + \alpha$
since
$\theta=1 + \alpha$
since
 $$\sum_{\lambda_n \leq T} \lambda_n^2 |r_n|^2 = \sum_{|\gamma|\leq T} \frac{4\gamma^2}{|\rho \zeta_K'(\rho)|^2}\ll J_{-1}^K(T) \ll T^{1+\alpha},$$
$$\sum_{\lambda_n \leq T} \lambda_n^2 |r_n|^2 = \sum_{|\gamma|\leq T} \frac{4\gamma^2}{|\rho \zeta_K'(\rho)|^2}\ll J_{-1}^K(T) \ll T^{1+\alpha},$$
using our assumption on
![]() $J_{-1}^K(T)$
, having chosen
$J_{-1}^K(T)$
, having chosen
![]() $0 \leq \alpha < 2 - \sqrt{3} = 0.2679\ldots$
. Finally, to verify (4·2), we first have, using the Cauchy–Schwarz inequality, that
$0 \leq \alpha < 2 - \sqrt{3} = 0.2679\ldots$
. Finally, to verify (4·2), we first have, using the Cauchy–Schwarz inequality, that
 \begin{equation*} \int_e^Y |\mathcal{E}(y,e^Y)|^2 \, dy \ll \int_e^Y \left( \frac{e^{\frac{2Cy}{\log y} + y} (\log y)^2}{e^{2Y}} + \frac{e^{y}}{e^{2Y(1-\epsilon)}} + \frac{Y}{e^{Y(1-\alpha)}} + e^{\frac{2Cy}{\log y} - y} \right) \, dy.\end{equation*}
\begin{equation*} \int_e^Y |\mathcal{E}(y,e^Y)|^2 \, dy \ll \int_e^Y \left( \frac{e^{\frac{2Cy}{\log y} + y} (\log y)^2}{e^{2Y}} + \frac{e^{y}}{e^{2Y(1-\epsilon)}} + \frac{Y}{e^{Y(1-\alpha)}} + e^{\frac{2Cy}{\log y} - y} \right) \, dy.\end{equation*}
The integral of the third term is bounded as
![]() $Y \rightarrow \infty$
when
$Y \rightarrow \infty$
when
![]() $\alpha < 2 - \sqrt{3}$
, and so is that of the second term when
$\alpha < 2 - \sqrt{3}$
, and so is that of the second term when
![]() $\epsilon< 1/2$
. Moreover, an application of L’Hôpital’s rule shows that the first and fourth terms are o(Y). This gives
$\epsilon< 1/2$
. Moreover, an application of L’Hôpital’s rule shows that the first and fourth terms are o(Y). This gives
as desired. We may conclude that
![]() $\phi_K(y)=e^{-y/2}M_K(e^y)$
possesses a limiting distribution by Theorem 4·2.
$\phi_K(y)=e^{-y/2}M_K(e^y)$
possesses a limiting distribution by Theorem 4·2.
4·1. Support for the conjecture (1·3)
By the discussion following the statement of Theorem 1·4, the picture is most transparent when
![]() $K/\mathbb{Q}$
is an abelian Galois extension. In this case, the irreducible characters on
$K/\mathbb{Q}$
is an abelian Galois extension. In this case, the irreducible characters on
![]() $\textrm{Gal}(K/\mathbb{Q})$
are all 1-dimensional, and therefore by abelian reciprocity the functions appearing in the Artin factorisation of
$\textrm{Gal}(K/\mathbb{Q})$
are all 1-dimensional, and therefore by abelian reciprocity the functions appearing in the Artin factorisation of
![]() $\zeta_K(s)$
are moreover distinct primitive Dirichlet L-functions, among them
$\zeta_K(s)$
are moreover distinct primitive Dirichlet L-functions, among them
![]() $\zeta(s)$
. Label the functions
$\zeta(s)$
. Label the functions
![]() $L_1(s),\ldots,L_n(s)$
, where
$L_1(s),\ldots,L_n(s)$
, where
![]() $L_1(s) = \zeta(s)$
, say, and
$L_1(s) = \zeta(s)$
, say, and
![]() $n = [K:\mathbb{Q}]$
. We assume the generalised Riemann hypothesis for the Dirichlet L-functions, simplicity of all nontrivial zeros (a priori none at
$n = [K:\mathbb{Q}]$
. We assume the generalised Riemann hypothesis for the Dirichlet L-functions, simplicity of all nontrivial zeros (a priori none at
![]() $s = {1}/{2}$
), and that no two Dirichlet L-functions share a nontrivial zero. Let
$s = {1}/{2}$
), and that no two Dirichlet L-functions share a nontrivial zero. Let
![]() $k \in \mathbb{R}$
. Then,
$k \in \mathbb{R}$
. Then,
 \begin{equation*} \sum_{\substack{0 < \gamma \leq T \\ \zeta_K(\frac{1}{2} + i\gamma) = 0}} |\zeta_K'(\rho)|^{2k} = \sum_{i=1}^n \sum_{\substack{0 < \gamma_i \leq T \\ L_i(\frac{1}{2} + i\gamma_i) = 0}} |L_i'(\rho)|^{2k} \,\prod_{j \neq i} |L_j(\rho)|^{2k},\end{equation*}
\begin{equation*} \sum_{\substack{0 < \gamma \leq T \\ \zeta_K(\frac{1}{2} + i\gamma) = 0}} |\zeta_K'(\rho)|^{2k} = \sum_{i=1}^n \sum_{\substack{0 < \gamma_i \leq T \\ L_i(\frac{1}{2} + i\gamma_i) = 0}} |L_i'(\rho)|^{2k} \,\prod_{j \neq i} |L_j(\rho)|^{2k},\end{equation*}
where we maintain the convention
![]() $\rho = {1}/{2} + i\gamma_i$
. Upon normalising the ith summand by the factor
$\rho = {1}/{2} + i\gamma_i$
. Upon normalising the ith summand by the factor
![]() $N_i(T) = \#\{0 \leq \gamma_i \leq T \mid L_i({1}/{2} + i \gamma_i) = 0 \}$
, we could anticipate that
$N_i(T) = \#\{0 \leq \gamma_i \leq T \mid L_i({1}/{2} + i \gamma_i) = 0 \}$
, we could anticipate that
 \begin{align*} & \frac{1}{N_i(T)} \sum_{\substack{0 < \gamma_i \leq T \\ L_i(\frac{1}{2} + i\gamma_i) = 0}} |L_i'(\rho)|^{2k} \,\prod_{j \neq i} |L_j(\rho)|^{2k} \\[5pt] &\phantom{\,\,\,\,}\asymp \left( \frac{1}{N_i(T)} \sum_{\substack{0 < \gamma_i \leq T \\ L_i(\frac{1}{2} + i \gamma_i) = 0}} |L_i'(\rho)|^{2k} \right) \prod_{j \neq i} \left(\frac{1}{ N_i(T)} \sum_{\substack{0 < \gamma_i \leq T \\ L_i(\frac{1}{2} + i\gamma_i) = 0}} |L_j(\rho)|^{2k} \right).\end{align*}
\begin{align*} & \frac{1}{N_i(T)} \sum_{\substack{0 < \gamma_i \leq T \\ L_i(\frac{1}{2} + i\gamma_i) = 0}} |L_i'(\rho)|^{2k} \,\prod_{j \neq i} |L_j(\rho)|^{2k} \\[5pt] &\phantom{\,\,\,\,}\asymp \left( \frac{1}{N_i(T)} \sum_{\substack{0 < \gamma_i \leq T \\ L_i(\frac{1}{2} + i \gamma_i) = 0}} |L_i'(\rho)|^{2k} \right) \prod_{j \neq i} \left(\frac{1}{ N_i(T)} \sum_{\substack{0 < \gamma_i \leq T \\ L_i(\frac{1}{2} + i\gamma_i) = 0}} |L_j(\rho)|^{2k} \right).\end{align*}
Noting its similarity to the sum
![]() $J_{k}(T)$
, and recalling the known asymptotic
$J_{k}(T)$
, and recalling the known asymptotic
![]() $N_i(T) \asymp T(\log T)$
(see [
Reference Montgomery and VaughanMV07
, theorem 14·5]), we may posit that
$N_i(T) \asymp T(\log T)$
(see [
Reference Montgomery and VaughanMV07
, theorem 14·5]), we may posit that
as in the case of the Riemann zeta function (cf. [ Reference GonekGon89 ]). Meanwhile, to address the inner sums
 \begin{equation*} \frac{1}{N_i(T)} \sum_{\substack{0 < \gamma_i \leq T \\ L_i(\frac{1}{2} + i\gamma_i) = 0}} |L_j(\rho)|^{2k},\end{equation*}
\begin{equation*} \frac{1}{N_i(T)} \sum_{\substack{0 < \gamma_i \leq T \\ L_i(\frac{1}{2} + i\gamma_i) = 0}} |L_j(\rho)|^{2k},\end{equation*}
where
![]() $j \neq i$
, it would be most favorable to impose some restriction on the proximity of the zeros
$j \neq i$
, it would be most favorable to impose some restriction on the proximity of the zeros
![]() $\gamma_i$
of
$\gamma_i$
of
![]() $L_i$
to lower values of the
$L_i$
to lower values of the
![]() $L_j$
; this is because we are taking
$L_j$
; this is because we are taking
![]() $k = -1$
. In this case, we expect that these normalised sums are
$k = -1$
. In this case, we expect that these normalised sums are
![]() $O_{\varepsilon}(T^\varepsilon)$
for all
$O_{\varepsilon}(T^\varepsilon)$
for all
![]() $\varepsilon > 0$
. This would suggest that
$\varepsilon > 0$
. This would suggest that
![]() $J_{-1}^K(T) \ll_{\alpha} T^{1 + \alpha}$
for all
$J_{-1}^K(T) \ll_{\alpha} T^{1 + \alpha}$
for all
![]() $\alpha > 0$
, which would be sufficient for Theorem 1·4. In fact, we believe that
$\alpha > 0$
, which would be sufficient for Theorem 1·4. In fact, we believe that
![]() $J_{-1}^K(T) \ll_K T$
holds for all abelian number fields K.
$J_{-1}^K(T) \ll_K T$
holds for all abelian number fields K.
5. Proofs of analytic results
In this section, we give proofs of some of the technical statements that we have used in prior sections.
5·1. Bounds in horizontal strips
In this section, we outline a proof of Lemma 2·4. This proof is heavily based on the proof of [
Reference Montgomery and VaughanMV07
, theorem 13·22], the corresponding statement for
![]() $K={\mathbb {Q}}$
. We will run through the intermediate statements needed for this result as it is proven in [
Reference Montgomery and VaughanMV07
], and in each step explain the necessary modifications in order to generalise to the setting of Dedekind zeta functions.
$K={\mathbb {Q}}$
. We will run through the intermediate statements needed for this result as it is proven in [
Reference Montgomery and VaughanMV07
], and in each step explain the necessary modifications in order to generalise to the setting of Dedekind zeta functions.
Lemma 5·1 (cf. [
Reference Montgomery and VaughanMV07
, corollary 10·5]). Suppose
![]() $-1 \leq \sigma \leq \frac{1}{2}$
. Then
$-1 \leq \sigma \leq \frac{1}{2}$
. Then
This follows from the reflection formula for Dedekind zeta functions and Stirling’s approximation. By the Hadamard product for the completed Dedekind zeta function, one gets the following formula for the logarithmic derivative of
![]() $\zeta_K$
.
$\zeta_K$
.
Lemma 5·2 (cf. [ Reference Montgomery and VaughanMV07 , lemma 12·1]). We have
 $$\frac{\zeta_K'(s)}{\zeta_K(s)} = -\left(\frac{1}{s} + \frac{1}{s-1}\right)+ \sum_{\vert \gamma - t \vert \leq 1}\left(\frac{1}{\rho} + \frac{1}{s - \rho}\right) + O(\log\tau)$$
$$\frac{\zeta_K'(s)}{\zeta_K(s)} = -\left(\frac{1}{s} + \frac{1}{s-1}\right)+ \sum_{\vert \gamma - t \vert \leq 1}\left(\frac{1}{\rho} + \frac{1}{s - \rho}\right) + O(\log\tau)$$
uniformly for
![]() $-1 \leq \sigma \leq 2$
, where
$-1 \leq \sigma \leq 2$
, where
![]() $\tau = |t| + 4$
.
$\tau = |t| + 4$
.
Define
![]() $\Lambda^K(n)$
to be, as in the proof of Lemma 3·12, such that
$\Lambda^K(n)$
to be, as in the proof of Lemma 3·12, such that
 $$\frac{\zeta_K'(s)}{\zeta_K(s)}=\sum_{n=1}^\infty \Lambda^K(n)n^{-s}.$$
$$\frac{\zeta_K'(s)}{\zeta_K(s)}=\sum_{n=1}^\infty \Lambda^K(n)n^{-s}.$$
We will use the bound
for all positive integers n in many of the following results. It may be proven by a simple consideration of the powers of prime ideals of
![]() $\mathcal{O}_K$
with given norm; for the upper bound, equality is reached for n a power of a prime p which splits completely in K. The first result needed for Lemma 2·4 is the following.
$\mathcal{O}_K$
with given norm; for the upper bound, equality is reached for n a power of a prime p which splits completely in K. The first result needed for Lemma 2·4 is the following.
Lemma 5·3 (cf. [ Reference Montgomery and VaughanMV07 , theorem 13·13]). Assume the Riemann hypothesis for K. Then
 $$\left \vert \frac{\zeta_K'(s)}{\zeta_K(s)}\right \vert \leq \sum_{n \leq (\log \tau)^2} \frac{\Lambda^K(n)}{n^\sigma} + O((\log \tau)^{2 - 2\sigma})$$
$$\left \vert \frac{\zeta_K'(s)}{\zeta_K(s)}\right \vert \leq \sum_{n \leq (\log \tau)^2} \frac{\Lambda^K(n)}{n^\sigma} + O((\log \tau)^{2 - 2\sigma})$$
uniformly for
![]() ${1}/{2} + {1}/{\log \log \tau} \leq \sigma \leq {3}/{2}$
,
${1}/{2} + {1}/{\log \log \tau} \leq \sigma \leq {3}/{2}$
,
![]() $\vert t \vert \;\geq 1$
.
$\vert t \vert \;\geq 1$
.
This lemma is proven essentially identically to the corresponding result from [ Reference Montgomery and VaughanMV07 ], and a proof along very similar lines is given in this paper for Lemma 3·12. In particular, the only modification to the proof in [ Reference Montgomery and VaughanMV07 ] that is needed results from the location and multiplicity of trivial zeros (see (3·10)). We remark that, in light of (5·1), this lemma implies the weaker bound
 \begin{equation}\left \vert \frac{\zeta_K'(s)}{\zeta_K(s)}\right \vert \leq n_K\sum_{n \leq (\log \tau)^2} \frac{\Lambda(n)}{n^\sigma} + O((\log \tau)^{2 - 2\sigma}),\end{equation}
\begin{equation}\left \vert \frac{\zeta_K'(s)}{\zeta_K(s)}\right \vert \leq n_K\sum_{n \leq (\log \tau)^2} \frac{\Lambda(n)}{n^\sigma} + O((\log \tau)^{2 - 2\sigma}),\end{equation}
in which a multiplicative constant is sacrificed for conceptual simplicity.
Lemma 5·4 (cf. [
Reference Montgomery and VaughanMV07
, corollary 13·16]). Assume the Riemann hypothesis for
![]() $\zeta_K(s)$
. Then, for
$\zeta_K(s)$
. Then, for
![]() $|t|\;\geq 1$
,
$|t|\;\geq 1$
,
 $$|\log\zeta_K(s)|\;\leq n_K\cdot\begin{cases} \log\frac1{\sigma-1}+O(\sigma-1) &\text{if } 1+\frac1{\log\log\tau}\leq\sigma\leq\frac32\\[5pt] \log\log\log\tau+O(1) &\text{if } 1-\frac1{\log\log\tau}\leq\sigma\leq1+\frac1{\log\log\tau}\\[5pt] \log\frac1{1-\sigma}+O\left(\frac{(\log \tau)^{2-2\sigma}}{(1-\sigma)\log\log\tau}\right) &\text{if } \frac12+\frac1{\log\log\tau}\leq\sigma\leq1-\frac1{\log\log\tau}. \end{cases}$$
$$|\log\zeta_K(s)|\;\leq n_K\cdot\begin{cases} \log\frac1{\sigma-1}+O(\sigma-1) &\text{if } 1+\frac1{\log\log\tau}\leq\sigma\leq\frac32\\[5pt] \log\log\log\tau+O(1) &\text{if } 1-\frac1{\log\log\tau}\leq\sigma\leq1+\frac1{\log\log\tau}\\[5pt] \log\frac1{1-\sigma}+O\left(\frac{(\log \tau)^{2-2\sigma}}{(1-\sigma)\log\log\tau}\right) &\text{if } \frac12+\frac1{\log\log\tau}\leq\sigma\leq1-\frac1{\log\log\tau}. \end{cases}$$
The proof of this corollary is identical to the proof of [
Reference Montgomery and VaughanMV07
, corollary 13·16], with (5·2) used in the place of [
Reference Montgomery and VaughanMV07
, theorem 13·13]. We also need two additional results about the zeros of
![]() $\zeta_K(s)$
, direct analogues of [
Reference Montgomery and VaughanMV07
, lemma 13·19] and [
Reference Montgomery and VaughanMV07
, lemma 13·20], with analogous proofs. Firstly, the bound in Lemma 5·3 can be used to show that
$\zeta_K(s)$
, direct analogues of [
Reference Montgomery and VaughanMV07
, lemma 13·19] and [
Reference Montgomery and VaughanMV07
, lemma 13·20], with analogous proofs. Firstly, the bound in Lemma 5·3 can be used to show that
a refinement of Lemma 2·3. Secondly, an application of Lemma 5·2 combined with the counting result from the preceding equation, shows that, for
![]() $|t|\;\geq 1$
and
$|t|\;\geq 1$
and
![]() $|\sigma-{1}/{2}|\;\leq {1}/{\log \log \tau}$
, then
$|\sigma-{1}/{2}|\;\leq {1}/{\log \log \tau}$
, then
 \begin{equation}\frac{\zeta_K'(s)}{\zeta_K(s)}=\sum_{|\gamma-t|\leq 1/\log\log\tau}\frac1{s-\rho}+O(\log\tau).\end{equation}
\begin{equation}\frac{\zeta_K'(s)}{\zeta_K(s)}=\sum_{|\gamma-t|\leq 1/\log\log\tau}\frac1{s-\rho}+O(\log\tau).\end{equation}
These results are enough to show Lemma 2·4 following the proof of [ Reference Montgomery and VaughanMV07 , theorem 13·22].
Proof of Lemma 2·4. Lemma 5·1 implies that we need only to consider
![]() ${1}/{2}<\sigma<2$
. From here, Lemma 5·4 shows the result for
${1}/{2}<\sigma<2$
. From here, Lemma 5·4 shows the result for
![]() $\sigma> {1}/{2}+{1}/{\log\log T}$
, and integrating (5·4) over a short horizontal segment gives a bound of the desired form, but in terms of the distances between T and various ordinates of the zeros of
$\sigma> {1}/{2}+{1}/{\log\log T}$
, and integrating (5·4) over a short horizontal segment gives a bound of the desired form, but in terms of the distances between T and various ordinates of the zeros of
![]() $\zeta_K(s)$
. Integrating this bound over
$\zeta_K(s)$
. Integrating this bound over
![]() $n\leq T<n+1$
for any n gives that the result holds on average, and thus for some fixed
$n\leq T<n+1$
for any n gives that the result holds on average, and thus for some fixed
![]() $T=T_n$
, as desired.
$T=T_n$
, as desired.
5·2. Bounds on residues at the trivial zeros
We now prove Lemma 2·13, following the method of the proof of Lemma 2·13.
Proof of Lemma 2·13. First, the residue at 0 can be written as
for some f independent of x with neither a pole nor a zero at
![]() $s=0$
. Evaluating the derivative explicitly yields that this residue is polylogarithmic in x, with exponent
$s=0$
. Evaluating the derivative explicitly yields that this residue is polylogarithmic in x, with exponent
![]() $r_1 + r_2 - 1$
.
$r_1 + r_2 - 1$
.
For
![]() $k>0$
, by Theorem 2·1, we write
$k>0$
, by Theorem 2·1, we write
where we have used the reflection formula
![]() $\Gamma(s)\Gamma(1-s) = \pi / \sin \pi s$
. At
$\Gamma(s)\Gamma(1-s) = \pi / \sin \pi s$
. At
![]() $s = -k$
, none of these terms are zero. The fourth term has a pole of order
$s = -k$
, none of these terms are zero. The fourth term has a pole of order
![]() $r_1$
if k is even, and the fifth term has a pole of order
$r_1$
if k is even, and the fifth term has a pole of order
![]() $r_2$
regardless. Define
$r_2$
regardless. Define
![]() $\epsilon$
to be 1 if k is even and 0 otherwise, so that
$\epsilon$
to be 1 if k is even and 0 otherwise, so that
![]() ${x^s}/{s\zeta_K(s)}$
has a pole of order
${x^s}/{s\zeta_K(s)}$
has a pole of order
![]() $r_1\epsilon+r_2$
at
$r_1\epsilon+r_2$
at
![]() $s=-k$
. Define
$s=-k$
. Define
 \begin{align*}f(s) &=\frac{(s+k)^{r_1\epsilon+r_2}x^s}{s\zeta_K(s)}\\[5pt] g_1(s)&=s\log\left(\frac{x\textrm{D}_K}{(2\pi)^{n_K}}\right)\\[5pt] g_2(s)&=\log(s\zeta_K(1-s))\\[5pt] g_3(s)&=\epsilon\log(s+k)-\log\sin\frac{\pi s}2\\[5pt] g_4(s)&=\log(s+k)-\log\sin\pi s\\[5pt] g_5(s)&=\log\Gamma(1-s)\end{align*}
\begin{align*}f(s) &=\frac{(s+k)^{r_1\epsilon+r_2}x^s}{s\zeta_K(s)}\\[5pt] g_1(s)&=s\log\left(\frac{x\textrm{D}_K}{(2\pi)^{n_K}}\right)\\[5pt] g_2(s)&=\log(s\zeta_K(1-s))\\[5pt] g_3(s)&=\epsilon\log(s+k)-\log\sin\frac{\pi s}2\\[5pt] g_4(s)&=\log(s+k)-\log\sin\pi s\\[5pt] g_5(s)&=\log\Gamma(1-s)\end{align*}
so that
 $$g(s)\;:\!=\;\log f(s)=\log\left(\frac{2^{r_2}\pi^{n_K}}{\textrm{D}_K^{1/2}}\right)+g_1(s)-g_2(s)+r_1g_3(s)+r_2g_4(s)-n_Kg_5(s),$$
$$g(s)\;:\!=\;\log f(s)=\log\left(\frac{2^{r_2}\pi^{n_K}}{\textrm{D}_K^{1/2}}\right)+g_1(s)-g_2(s)+r_1g_3(s)+r_2g_4(s)-n_Kg_5(s),$$
and so that
We may show that, for
![]() $\ell\leq n_K$
,
$\ell\leq n_K$
,
 \begin{align*}\left|g_1^{(\ell)}(k)\right|&\leq \log\left(\frac{xD_K}{(2\pi)^{n_K}}\right)\\[5pt] \left|g_2^{(\ell)}(k)\right|,\left|g_3^{(\ell)}(k)\right|,\left|g_4^{(\ell)}(k)\right|&\ll_{r_1,r_2} 1\\[5pt] \left|g_5^{(\ell)}(k)\right|&\ll \log k.\end{align*}
\begin{align*}\left|g_1^{(\ell)}(k)\right|&\leq \log\left(\frac{xD_K}{(2\pi)^{n_K}}\right)\\[5pt] \left|g_2^{(\ell)}(k)\right|,\left|g_3^{(\ell)}(k)\right|,\left|g_4^{(\ell)}(k)\right|&\ll_{r_1,r_2} 1\\[5pt] \left|g_5^{(\ell)}(k)\right|&\ll \log k.\end{align*}
This shows that
![]() $g^{(\ell)}(s)\ll_{r_1,r_2} \log(kx\textrm{D}_K)$
. In addition,
$g^{(\ell)}(s)\ll_{r_1,r_2} \log(kx\textrm{D}_K)$
. In addition,
 \begin{align*}\left|\lim_{s\to -k}f(s)\right|&=\left|\left(\frac{2^{r_2}\pi^{n_K}}{\textrm{D}_K^{1/2}}\right)\frac{\left(\frac{x\textrm{D}_K}{(2\pi)^{n_K}}\right)^{-k}}{\lim_{s\to -k}s\zeta_K(1-s)}\left(\frac 2\pi\right)^{\epsilon r_1}\left(\frac 1\pi\right)^{r_2}\frac1{k!^{n_K}}\right|\\[5pt] &\ll_{r_1,r_2}\frac{(2\pi)^{kn_K}}{x^k\textrm{D}_K^{k+1/2}k!^{n_K}}\cdot \frac{1}{\left|\lim_{s\to -k}s\zeta_K(1-s)\right|}\ll \frac{(2\pi)^{kn_K}}{kx^k\textrm{D}_K^{k+1/2}k!^{n_K}}.\end{align*}
\begin{align*}\left|\lim_{s\to -k}f(s)\right|&=\left|\left(\frac{2^{r_2}\pi^{n_K}}{\textrm{D}_K^{1/2}}\right)\frac{\left(\frac{x\textrm{D}_K}{(2\pi)^{n_K}}\right)^{-k}}{\lim_{s\to -k}s\zeta_K(1-s)}\left(\frac 2\pi\right)^{\epsilon r_1}\left(\frac 1\pi\right)^{r_2}\frac1{k!^{n_K}}\right|\\[5pt] &\ll_{r_1,r_2}\frac{(2\pi)^{kn_K}}{x^k\textrm{D}_K^{k+1/2}k!^{n_K}}\cdot \frac{1}{\left|\lim_{s\to -k}s\zeta_K(1-s)\right|}\ll \frac{(2\pi)^{kn_K}}{kx^k\textrm{D}_K^{k+1/2}k!^{n_K}}.\end{align*}
As in the proof of Lemma 3·13, since
![]() $f'(s)=g'(s)f(s)$
, we have that
$f'(s)=g'(s)f(s)$
, we have that
![]() $f^{(j)}(s)/f(s)$
is a polynomial of degree at most j in the first j derivatives of g. This finishes the proof.
$f^{(j)}(s)/f(s)$
is a polynomial of degree at most j in the first j derivatives of g. This finishes the proof.
5·3. Proof of the explicit formula
To prove Proposition 2·12, the explicit formula for
![]() $M_K(x)$
, we need a rather precise truncated form of Perron’s formula. This can be found by combining the statements of [
Reference TitchmarshTit86
, lemma 3·12] and [
Reference NgNg04
, lemma 2], and a similar result can be found in [
Reference Montgomery and VaughanMV07
, corollary 5·3].
$M_K(x)$
, we need a rather precise truncated form of Perron’s formula. This can be found by combining the statements of [
Reference TitchmarshTit86
, lemma 3·12] and [
Reference NgNg04
, lemma 2], and a similar result can be found in [
Reference Montgomery and VaughanMV07
, corollary 5·3].
Lemma 5·5. Suppose
![]() $f(s)=\sum_{n=1}^\infty a_nn^{-s}$
is absolutely convergent for
$f(s)=\sum_{n=1}^\infty a_nn^{-s}$
is absolutely convergent for
![]() $\textrm{Re}(s)>1$
, and let
$\textrm{Re}(s)>1$
, and let
![]() $\Phi(n)$
be a positive and non-decreasing function such that
$\Phi(n)$
be a positive and non-decreasing function such that
![]() $a_n\ll\Phi(n)$
. Assume that
$a_n\ll\Phi(n)$
. Assume that
 $$\sum_{n=1}^\infty \frac{|a_n|}{n^\sigma}=O\left(\frac1{(\sigma-1)^\alpha}\right)$$
$$\sum_{n=1}^\infty \frac{|a_n|}{n^\sigma}=O\left(\frac1{(\sigma-1)^\alpha}\right)$$
as
![]() $\sigma$
tends to 1 from above. Pick
$\sigma$
tends to 1 from above. Pick
![]() $w=u+iv$
and
$w=u+iv$
and
![]() $c>0$
such that
$c>0$
such that
![]() $u+c>1$
, and pick
$u+c>1$
, and pick
![]() $T>0$
. Then, for
$T>0$
. Then, for
![]() $x>0$
,
$x>0$
,
 \begin{equation*} \sum_{n \leq x}\frac{a_n}{n^w}=\frac1{2\pi i}\int_{c-iT}^{c+iT}f(w+s)\frac{x^s}sds+O\left(\frac{x^c}{T(u+c-1)^\alpha}+\frac{\Phi(2x)x^{1-u}\log x}{T}+E_1(x,T)\right),\end{equation*}
\begin{equation*} \sum_{n \leq x}\frac{a_n}{n^w}=\frac1{2\pi i}\int_{c-iT}^{c+iT}f(w+s)\frac{x^s}sds+O\left(\frac{x^c}{T(u+c-1)^\alpha}+\frac{\Phi(2x)x^{1-u}\log x}{T}+E_1(x,T)\right),\end{equation*}
where
if
![]() $x > 1$
, and, if N is the nearest integer to x (besides possibly x itself),
$x > 1$
, and, if N is the nearest integer to x (besides possibly x itself),
for any
![]() $x>0$
.
$x>0$
.
We now give a bound on the integral found in our application of Perron’s formula. This is done separately from the main proof of the explicit formula in order to elucidate the locations where the appropriate error terms arise.
Lemma 5·6. Fix a number field K, and let
![]() $\mathcal T$
be as in Lemma 2·4. For any
$\mathcal T$
be as in Lemma 2·4. For any
![]() $x>0$
,
$x>0$
,
![]() $0<T\in\mathcal T$
, and
$0<T\in\mathcal T$
, and
![]() $1<c \leq 2$
, write
$1<c \leq 2$
, write
 \begin{equation*}\frac1{2\pi i}\int_{c-iT}^{c+iT}\frac{x^s}{s\zeta_K(s)}ds= \sum_{|\gamma| < T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} + \sum_{k=0}^{\infty}\textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}+E_2(x,c,T).\end{equation*}
\begin{equation*}\frac1{2\pi i}\int_{c-iT}^{c+iT}\frac{x^s}{s\zeta_K(s)}ds= \sum_{|\gamma| < T} \frac{x^{\rho}}{\rho \zeta_K'(\rho)} + \sum_{k=0}^{\infty}\textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}+E_2(x,c,T).\end{equation*}
Then, for any
![]() $\epsilon>0$
,
$\epsilon>0$
,
![]() $E_2(x,c,T)=O_x(1/T^{1-\epsilon})$
. When
$E_2(x,c,T)=O_x(1/T^{1-\epsilon})$
. When
![]() $x>1$
,
$x>1$
,
![]() $E_2(x,c,T)=O(x^c/T^{1-\epsilon})$
uniformly.
$E_2(x,c,T)=O(x^c/T^{1-\epsilon})$
uniformly.
Proof. Pick a sufficiently large positive half-integer U (we will let
![]() $U\to \infty$
), and integrate around the rectangular contour with vertices
$U\to \infty$
), and integrate around the rectangular contour with vertices
![]() $c\pm iT$
and
$c\pm iT$
and
![]() $-U\pm iT$
. This gives
$-U\pm iT$
. This gives
 \begin{align}&\frac1{2\pi i}\int_{c-iT}^{c+iT}\frac{x^s}{s\zeta_K(s)}ds\nonumber \\[5pt] &=\sum_{|\gamma|<T}\frac{x^\rho}{\rho\zeta_K'(\rho)}+\sum_{k=0}^{\lfloor U\rfloor} \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}+\frac1{2\pi i}\left(\int_{c-iT}^{-U-iT}+\int_{-U-iT}^{-U+iT}+\int_{-U+iT}^{c+iT}\right)\frac{x^s}{s\zeta_K(s)}ds.\end{align}
\begin{align}&\frac1{2\pi i}\int_{c-iT}^{c+iT}\frac{x^s}{s\zeta_K(s)}ds\nonumber \\[5pt] &=\sum_{|\gamma|<T}\frac{x^\rho}{\rho\zeta_K'(\rho)}+\sum_{k=0}^{\lfloor U\rfloor} \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}+\frac1{2\pi i}\left(\int_{c-iT}^{-U-iT}+\int_{-U-iT}^{-U+iT}+\int_{-U+iT}^{c+iT}\right)\frac{x^s}{s\zeta_K(s)}ds.\end{align}
We first bound these integrals using the functional equation for
![]() $\zeta_K(s)$
(Theorem 2·1). First, we recall the identities and bounds
$\zeta_K(s)$
(Theorem 2·1). First, we recall the identities and bounds
 \begin{align*}\Gamma(s)\Gamma(1-s) &= \frac{\pi}{\sin \pi s}\\[5pt] \Gamma(s)^{-1}&\ll e^{\sigma-(\sigma-1/2)\log\sigma+\pi|t|/2}\\[5pt] |\sin\pi s|^{-1}&\ll e^{-\pi |t|}\\[5pt] \left|\sin\frac{\pi s}2\right|^{\pm 1}&\ll e^{\pm\pi |t|/2}\\[5pt] \zeta_K(s)^{-1}&\ll 1\text{ for }\sigma>2,\end{align*}
\begin{align*}\Gamma(s)\Gamma(1-s) &= \frac{\pi}{\sin \pi s}\\[5pt] \Gamma(s)^{-1}&\ll e^{\sigma-(\sigma-1/2)\log\sigma+\pi|t|/2}\\[5pt] |\sin\pi s|^{-1}&\ll e^{-\pi |t|}\\[5pt] \left|\sin\frac{\pi s}2\right|^{\pm 1}&\ll e^{\pm\pi |t|/2}\\[5pt] \zeta_K(s)^{-1}&\ll 1\text{ for }\sigma>2,\end{align*}
which hold for s bounded away from integers. As the paths of the three integrals in (5·6) always stay a distance of
![]() ${1}/{4}$
away from each integer, we have for s on such a path, and with real part not between
${1}/{4}$
away from each integer, we have for s on such a path, and with real part not between
![]() $-1$
and 2, that
$-1$
and 2, that
Thus, the middle integral is asymptotically at most
![]() $x^Ue^{-U\log U+O(U)}$
uniformly in x and T as
$x^Ue^{-U\log U+O(U)}$
uniformly in x and T as
![]() $U\to\infty$
. For the two horizontal integrals, we first bound the portion where
$U\to\infty$
. For the two horizontal integrals, we first bound the portion where
![]() $\textrm{Re}(s)$
runs from
$\textrm{Re}(s)$
runs from
![]() $-1$
to
$-1$
to
![]() $-U$
. Here, we may use (5·7). Since the integral in the right-hand side of
$-U$
. Here, we may use (5·7). Since the integral in the right-hand side of
converges as
![]() $U\to\infty$
, this is
$U\to\infty$
, this is
![]() $O(1/T)$
for fixed x, and for
$O(1/T)$
for fixed x, and for
![]() $x>1$
the dependence is
$x>1$
the dependence is
![]() $O(x^{-1})$
. As a result, we may write
$O(x^{-1})$
. As a result, we may write
 \begin{align*}&\frac1{2\pi i}\int_{c-iT}^{c+iT}\frac{x^s}{s\zeta_K(s)}ds\\[5pt] &=\sum_{|\gamma|<T}\frac{x^\rho}{\rho\zeta_K'(\rho)}+\sum_{k=0}^\infty \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}+\frac1{2\pi i}\left(\int_{c-iT}^{-1-iT}+\int_{-1+iT}^{c+iT}\right)\frac{x^s}{s\zeta_K(s)}ds+E_3(x,T),\end{align*}
\begin{align*}&\frac1{2\pi i}\int_{c-iT}^{c+iT}\frac{x^s}{s\zeta_K(s)}ds\\[5pt] &=\sum_{|\gamma|<T}\frac{x^\rho}{\rho\zeta_K'(\rho)}+\sum_{k=0}^\infty \textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}+\frac1{2\pi i}\left(\int_{c-iT}^{-1-iT}+\int_{-1+iT}^{c+iT}\right)\frac{x^s}{s\zeta_K(s)}ds+E_3(x,T),\end{align*}
where
![]() $E_3(x,T)=O_x(1/T)$
for
$E_3(x,T)=O_x(1/T)$
for
![]() $x > 0$
, and
$x > 0$
, and
![]() $E_3(x,T)=O(1/xT)$
for
$E_3(x,T)=O(1/xT)$
for
![]() $x>1$
. Finally, for the remaining integrals, we use the definition of
$x>1$
. Finally, for the remaining integrals, we use the definition of
![]() $\mathcal T$
. Since
$\mathcal T$
. Since
![]() $|\zeta_K(\sigma\pm iT)|^{-1}\ll T^\epsilon$
uniformly in
$|\zeta_K(\sigma\pm iT)|^{-1}\ll T^\epsilon$
uniformly in
![]() $-1\leq \sigma \leq 2$
for
$-1\leq \sigma \leq 2$
for
![]() $T\in\mathcal T$
and any
$T\in\mathcal T$
and any
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
for any s on one of our remaining line segments. This bounds our integrals by
![]() $\max(x^c,1/x)/T^{1-\epsilon}$
, which is enough.
$\max(x^c,1/x)/T^{1-\epsilon}$
, which is enough.
We are now ready to show the explicit formula for
![]() $M_K(x)$
.
$M_K(x)$
.
Proof of Proposition 2·12. First, note that
![]() $|\mu_K(n)|$
is bounded by the coefficient of
$|\mu_K(n)|$
is bounded by the coefficient of
![]() $n^{-s}$
in the Dirichlet series expansion of
$n^{-s}$
in the Dirichlet series expansion of
![]() $\zeta_K(s)$
. As a result,
$\zeta_K(s)$
. As a result,
 $$\sum_{n=1}^\infty \frac{|\mu_K(n)|}{n^\sigma}=O\left(\frac{1}{\sigma - 1}\right) \text{ as } \sigma \rightarrow 1^+,$$
$$\sum_{n=1}^\infty \frac{|\mu_K(n)|}{n^\sigma}=O\left(\frac{1}{\sigma - 1}\right) \text{ as } \sigma \rightarrow 1^+,$$
since the pole of
![]() $\zeta_K(s)$
at
$\zeta_K(s)$
at
![]() $s = 1$
is simple. Define
$s = 1$
is simple. Define
where C is as in Lemma 2·2, so that
![]() $\Phi(x)$
is positive, non-decreasing, and satisfies
$\Phi(x)$
is positive, non-decreasing, and satisfies
![]() $\mu_K(n)\ll \Phi(n)$
. Now, apply 5.5 to
$\mu_K(n)\ll \Phi(n)$
. Now, apply 5.5 to
![]() $f(s)=1/{\zeta_K(s)}$
,
$f(s)=1/{\zeta_K(s)}$
,
![]() $w=0$
,
$w=0$
,
![]() $\alpha=1$
,
$\alpha=1$
,
![]() $T>0$
, and with
$T>0$
, and with
![]() $1<c\leq 2$
to be chosen later. This gives
$1<c\leq 2$
to be chosen later. This gives
where
![]() $E_1(x,T)$
is as in the statement of Lemma 5·5. By Lemma 5·6, we have
$E_1(x,T)$
is as in the statement of Lemma 5·5. By Lemma 5·6, we have
 \begin{align*}M_K(x)&={\sum_{|\gamma|\leq T} \frac{x^\rho}{\rho\zeta_K'(\rho)}+\sum_{k=0}^{\infty}\textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}}\\[5pt] &+O\left(\frac{x^c}{T(c-1)}+\frac{\Phi(2x)x\log x}{T}+E_1(x,T)+E_2(x,c,T)\right).\end{align*}
\begin{align*}M_K(x)&={\sum_{|\gamma|\leq T} \frac{x^\rho}{\rho\zeta_K'(\rho)}+\sum_{k=0}^{\infty}\textrm{Res}_{s=-k}\frac{x^s}{s\zeta_K(s)}}\\[5pt] &+O\left(\frac{x^c}{T(c-1)}+\frac{\Phi(2x)x\log x}{T}+E_1(x,T)+E_2(x,c,T)\right).\end{align*}
This is enough to show our inequality on the error term when
![]() $x > 0$
, as each term in the above is asymptotically bounded by
$x > 0$
, as each term in the above is asymptotically bounded by
![]() $T^{-(1-\epsilon)}$
(any
$T^{-(1-\epsilon)}$
(any
![]() $1<c\leq2$
will suffice). When
$1<c\leq2$
will suffice). When
![]() $x > 1$
, we have
$x > 1$
, we have
Setting
![]() $c=1+(\log x)^{-1}$
gives
$c=1+(\log x)^{-1}$
gives
Finally, Lemma 2·13 implies that the sum of the residues at negative integers is convergent as a series in k, and its dependence on x is
![]() $O((\log x)^{r_1 + r_2})$
depending on K.
$O((\log x)^{r_1 + r_2})$
depending on K.
6. Speculations on one-sided growth of Mertens functions
We have mostly avoided the discussion of the fields K for which
![]() $\zeta_K(s)$
has nontrivial non-simple zeros. Although these fields are not problematic if the goal is to disprove the naïve Mertens-type conjecture over K, they pose a distinct challenge when trying to study properties like limiting distributions of normalisations of
$\zeta_K(s)$
has nontrivial non-simple zeros. Although these fields are not problematic if the goal is to disprove the naïve Mertens-type conjecture over K, they pose a distinct challenge when trying to study properties like limiting distributions of normalisations of
![]() $M_K(x)$
. In this setting, stronger hypotheses are needed. In this section, we posit and motivate a particularly strange property that Mertens functions of non-abelian number fields may satisfy.
$M_K(x)$
. In this setting, stronger hypotheses are needed. In this section, we posit and motivate a particularly strange property that Mertens functions of non-abelian number fields may satisfy.
Conjecture 6·1. There are infinitely many number fields K for which the Mertens function
![]() $M_K(x)$
changes sign only finitely many times.
$M_K(x)$
changes sign only finitely many times.
The heuristics behind this conjecture are covered in Section 6·3.
6·1. Complexities of non-abelian number fields
A main tool in studying the limiting distribution of
![]() $M_K(x)/\sqrt{x}$
is the explicit formula (Proposition 2·12). This formula was derived via Perron’s formula, which allows one to express
$M_K(x)/\sqrt{x}$
is the explicit formula (Proposition 2·12). This formula was derived via Perron’s formula, which allows one to express
![]() $M_K(x)$
as a sum of residues of
$M_K(x)$
as a sum of residues of
![]() ${x^s}/{s\zeta_K(s)}$
. If
${x^s}/{s\zeta_K(s)}$
. If
![]() $\rho$
is a simple zero of
$\rho$
is a simple zero of
![]() $\zeta_K(s)$
, then this residue has a particularly simple formula and is of order
$\zeta_K(s)$
, then this residue has a particularly simple formula and is of order
![]() $x^{1/2}$
as a function of x. However, if
$x^{1/2}$
as a function of x. However, if
![]() $\textrm{ord}_{s = \rho}\zeta_K(s) = n > 1$
, then this residue is a linear combination of terms
$\textrm{ord}_{s = \rho}\zeta_K(s) = n > 1$
, then this residue is a linear combination of terms
![]() $x^{1/2}(\log x)^k$
where
$x^{1/2}(\log x)^k$
where
![]() $k < n$
. In particular, the coefficients of these terms involve large positive and negative powers of higher derivatives of
$k < n$
. In particular, the coefficients of these terms involve large positive and negative powers of higher derivatives of
![]() $\zeta_K(x)$
, quantities whose moments are not well understood.
$\zeta_K(x)$
, quantities whose moments are not well understood.
Assuming some standard conjectures, the zeros of
![]() $\zeta_K(s)$
for a non-abelian number field K (with the possible exception of a zero at
$\zeta_K(s)$
for a non-abelian number field K (with the possible exception of a zero at
![]() $s = {1}/{2}$
) have multiplicity at most the largest dimension of an irreducible complex representation of
$s = {1}/{2}$
) have multiplicity at most the largest dimension of an irreducible complex representation of
![]() $\textrm{Gal}(K/{\mathbb {Q}})$
. This motivates the following question.
$\textrm{Gal}(K/{\mathbb {Q}})$
. This motivates the following question.
Question 6·2. If the largest irreducible representation of
![]() $\textrm{Gal}(K/{\mathbb {Q}})$
has dimension n, then does
$\textrm{Gal}(K/{\mathbb {Q}})$
has dimension n, then does
![]() $M_K(x)/(\sqrt x\log^{n-1}(x))$
have a limiting distribution?
$M_K(x)/(\sqrt x\log^{n-1}(x))$
have a limiting distribution?
Moreover, assume that the
![]() $\zeta_K(s)$
has a zero at
$\zeta_K(s)$
has a zero at
![]() $s = {1}/{2}$
of multiplicity larger than that of any other nontrivial zero. As described in Proposition 2·7, this term does not oscillate between large positive and negative values (like terms associated with non-real zeros), and will dominate all others in the explicit formula for
$s = {1}/{2}$
of multiplicity larger than that of any other nontrivial zero. As described in Proposition 2·7, this term does not oscillate between large positive and negative values (like terms associated with non-real zeros), and will dominate all others in the explicit formula for
![]() $M_K(x)$
. Hence, one may ask the following question.
$M_K(x)$
. Hence, one may ask the following question.
Question 6·3. If
![]() $\textrm{ord}_{s = {1}/{2}}\zeta_K(s) > \textrm{ord}_{s = \rho} \zeta_K(s)$
for all
$\textrm{ord}_{s = {1}/{2}}\zeta_K(s) > \textrm{ord}_{s = \rho} \zeta_K(s)$
for all
![]() $\rho \neq \frac{1}{2}$
, does
$\rho \neq \frac{1}{2}$
, does
![]() $M_K(x)$
change sign finitely many times?
$M_K(x)$
change sign finitely many times?
One may ask if such number fields satisfying the hypothesis of this question even exist. This is answered in the affirmative, assuming appropriate standard conjectures, by the work of Louboutin [ Reference LouboutinLou00b ].
It now remains to identify number fields K of interest, as well as give heuristic bounds on certain sums over zeros, which we turn to now. In what follows, it will be relevant to state the following assumptions on Artin L-functions, for a Galois extension of number fields
![]() $L/K$
:
$L/K$
:
Conjecture 6·4. (Artin holomorphy conjecture (AHC)). For any character
![]() $\chi$
of a nontrivial irreducible representation of
$\chi$
of a nontrivial irreducible representation of
![]() $\textrm{Gal}(L/K)$
, the function
$\textrm{Gal}(L/K)$
, the function
![]() $L(s,\chi,L/K)$
is holomorphic.
$L(s,\chi,L/K)$
is holomorphic.
Conjecture 6·5. (Simplicity hypothesis (
![]() $\text{SH}_{K/{\mathbb {Q}}}$
)). If
$\text{SH}_{K/{\mathbb {Q}}}$
)). If
![]() $\chi$
is an irreducible character of
$\chi$
is an irreducible character of
![]() $\textrm{Gal}(K/{\mathbb {Q}})$
, then the nontrivial zeros of
$\textrm{Gal}(K/{\mathbb {Q}})$
, then the nontrivial zeros of
![]() $L(s,\chi,K/{\mathbb {Q}})$
are simple.
$L(s,\chi,K/{\mathbb {Q}})$
are simple.
Conjecture 6·6 (Independence conjecture (
![]() $\text{IC}_{K/{\mathbb {Q}}}$
)). If
$\text{IC}_{K/{\mathbb {Q}}}$
)). If
![]() $\chi_1$
,
$\chi_1$
,
![]() $\chi_2$
are distinct irreducible characters of
$\chi_2$
are distinct irreducible characters of
![]() $\textrm{Gal}(K/{\mathbb {Q}})$
, then
$\textrm{Gal}(K/{\mathbb {Q}})$
, then
![]() $L(s,\chi_1,K/{\mathbb {Q}})$
and
$L(s,\chi_1,K/{\mathbb {Q}})$
and
![]() $L(s,\chi_2,K/{\mathbb {Q}})$
share no nontrivial zeros, except possibly for a zero at
$L(s,\chi_2,K/{\mathbb {Q}})$
share no nontrivial zeros, except possibly for a zero at
![]() $s={1}/{2}$
.
$s={1}/{2}$
.
6·2. Candidate number fields
The first appearance of a number field K satisfying
![]() $\zeta_K(\frac{1}{2}) = 0$
occurred in a paper of Armitage [
Reference ArmitageArm72
], who studied a degree 48 extension of
$\zeta_K(\frac{1}{2}) = 0$
occurred in a paper of Armitage [
Reference ArmitageArm72
], who studied a degree 48 extension of
![]() $\mathbb{Q}$
which had first appeared in a work of Serre [
Reference SerreSer71
]. Later, Serre (unpublished, see [
Reference NgNg00
, chapter 2]) discovered the simpler example
$\mathbb{Q}$
which had first appeared in a work of Serre [
Reference SerreSer71
]. Later, Serre (unpublished, see [
Reference NgNg00
, chapter 2]) discovered the simpler example
which is Galois with quaternionic Galois group
![]() $Q_8$
.
$Q_8$
.
In emulation of this latter construction, we identify as candidates for
![]() $\textrm{Gal}(K/\mathbb{Q})$
the following well-known class of groups to which
$\textrm{Gal}(K/\mathbb{Q})$
the following well-known class of groups to which
![]() $Q_8$
belongs. These groups possess convenient representation-theoretic properties, which allow control over the behaviour of
$Q_8$
belongs. These groups possess convenient representation-theoretic properties, which allow control over the behaviour of
![]() $\zeta_K(s)$
at
$\zeta_K(s)$
at
![]() $s={1}/{2}$
.
$s={1}/{2}$
.
Definition 6·7. Let
![]() $n \geq 2$
an integer. We define the dicyclic group
$n \geq 2$
an integer. We define the dicyclic group
![]() $Q_{4n}$
by the presentation
$Q_{4n}$
by the presentation
This is a solvable non-abelian group of order 4n.
In what follows, let
![]() $p \geq 3$
be an odd prime, and let
$p \geq 3$
be an odd prime, and let
![]() $N/\mathbb{Q}$
be a normal extension with Galois group
$N/\mathbb{Q}$
be a normal extension with Galois group
![]() $G = Q_{4p}$
, called a dicyclic number field of degree 4p. We recall the Galois theory of such fields, which in be found in the introduction to [
Reference LouboutinLou00b
].
$G = Q_{4p}$
, called a dicyclic number field of degree 4p. We recall the Galois theory of such fields, which in be found in the introduction to [
Reference LouboutinLou00b
].
If p is not totally ramified in
![]() $N/\mathbb{Q}$
, then by [
Reference LouboutinLou00b
, theorem 1], the root number
$N/\mathbb{Q}$
, then by [
Reference LouboutinLou00b
, theorem 1], the root number
![]() $W_{N/\mathbb{Q}}(\psi) = W_{N/L}(\chi)$
does not depend on
$W_{N/\mathbb{Q}}(\psi) = W_{N/L}(\chi)$
does not depend on
![]() $\chi$
but just on the field N, so either there are
$\chi$
but just on the field N, so either there are
![]() $(p-1)/2$
two-dimensional characters with root number
$(p-1)/2$
two-dimensional characters with root number
![]() $-1$
or there are none. Hence, assuming
$-1$
or there are none. Hence, assuming
![]() $\text{SH}_{N/{\mathbb {Q}}}$
, the order of the zero at
$\text{SH}_{N/{\mathbb {Q}}}$
, the order of the zero at
![]() $s = {1}/{2}$
of the Dedekind zeta function is either
$s = {1}/{2}$
of the Dedekind zeta function is either
![]() $p-1$
or zero. Moreover, there exist infinitely many examples of dicyclic fields N which produce either case. If p is totally ramified in
$p-1$
or zero. Moreover, there exist infinitely many examples of dicyclic fields N which produce either case. If p is totally ramified in
![]() $N/\mathbb{Q}$
, which can only occur when
$N/\mathbb{Q}$
, which can only occur when
![]() $p \equiv 1 \pmod{4}$
, and if
$p \equiv 1 \pmod{4}$
, and if
![]() $L = \mathbb{Q}(\sqrt{p})$
, then half of the
$L = \mathbb{Q}(\sqrt{p})$
, then half of the
![]() $(p-1)/2$
quaternionic characters have root number
$(p-1)/2$
quaternionic characters have root number
![]() $-1$
and half have root number
$-1$
and half have root number
![]() $+1$
. Hence, assuming
$+1$
. Hence, assuming
![]() $\text{SH}_{N/{\mathbb {Q}}}$
, the order of the zero at
$\text{SH}_{N/{\mathbb {Q}}}$
, the order of the zero at
![]() $s = {1}/{2}$
is
$s = {1}/{2}$
is
![]() $(p-1)/2$
.
$(p-1)/2$
.
Now that we have built up the multiplicity of the zero at
![]() $s = {1}/{2}$
, we invoke the conditions
$s = {1}/{2}$
, we invoke the conditions
![]() $\text{SH}_{N/{\mathbb {Q}}}$
and
$\text{SH}_{N/{\mathbb {Q}}}$
and
![]() $\text{IC}_{N/{\mathbb {Q}}}$
in order to tame the multiplicities of all the other nontrivial zeros. Equipped with these assumptions, the largest dimension of an irreducible representation of a dicyclic number field would be 2, so that all other zeroes besides
$\text{IC}_{N/{\mathbb {Q}}}$
in order to tame the multiplicities of all the other nontrivial zeros. Equipped with these assumptions, the largest dimension of an irreducible representation of a dicyclic number field would be 2, so that all other zeroes besides
![]() $s = {1}/{2}$
should have order at most 2.
$s = {1}/{2}$
should have order at most 2.
Theorem 6·8. Let
![]() $p \geq 3$
be a prime and let N be a dicyclic number field of order 4p. Assume
$p \geq 3$
be a prime and let N be a dicyclic number field of order 4p. Assume
![]() $\text{SH}_{N/{\mathbb {Q}}}$
.
$\text{SH}_{N/{\mathbb {Q}}}$
.
-
(a) If p is not totally ramified in
 $N/{\mathbb {Q}}$
, and
$N/{\mathbb {Q}}$
, and
 $W(\chi) = -1$
for all characters
$W(\chi) = -1$
for all characters
 $\chi$
on H of order 2p, then the order of the zero of
$\chi$
on H of order 2p, then the order of the zero of
 $\zeta_N(s)$
at
$\zeta_N(s)$
at
 $s = {1}/{2}$
is
$s = {1}/{2}$
is
 $p - 1$
.
$p - 1$
. -
(b) If p is totally ramified in
 $N/{\mathbb {Q}}$
, and
$N/{\mathbb {Q}}$
, and
 $L = {\mathbb {Q}}(\sqrt{p})$
, then the order of the zero of
$L = {\mathbb {Q}}(\sqrt{p})$
, then the order of the zero of
 $\zeta_N(s)$
at
$\zeta_N(s)$
at
 $s = {1}/{2}$
is
$s = {1}/{2}$
is
 $(p-1)/2$
.
$(p-1)/2$
.
Assuming moreover
![]() $\text{IC}_{N/{\mathbb {Q}}}$
, and for p sufficiently large, this order is higher than that of any other nontrivial zero.
$\text{IC}_{N/{\mathbb {Q}}}$
, and for p sufficiently large, this order is higher than that of any other nontrivial zero.
Moreover, there are infinitely many examples of N as in case (a) assuming
![]() $\text{SH}_{N/{\mathbb {Q}}}$
.
$\text{SH}_{N/{\mathbb {Q}}}$
.
6·3. Heuristics in support of one-sided growth of
 $M_K(x)$
$M_K(x)$
From now on, we shall specialise to the scenario of Theorem 6·8, where
![]() $K \;:\!=\; N$
. Hence, K is a dicyclic number field satisfying
$K \;:\!=\; N$
. Hence, K is a dicyclic number field satisfying
![]() $\text{SH}_{K/{\mathbb {Q}}}$
and
$\text{SH}_{K/{\mathbb {Q}}}$
and
![]() $\text{IC}_{K/{\mathbb {Q}}}$
, with the function
$\text{IC}_{K/{\mathbb {Q}}}$
, with the function
![]() $\zeta_K(s)$
having a zero of multiplicity
$\zeta_K(s)$
having a zero of multiplicity
![]() $\mu \geq 3$
at
$\mu \geq 3$
at
![]() $s = 1/2$
and all other nontrivial zeros of multiplicity equal to either 1 (simple) or 2 (double). In the notation of Proposition 2·12, for all
$s = 1/2$
and all other nontrivial zeros of multiplicity equal to either 1 (simple) or 2 (double). In the notation of Proposition 2·12, for all
![]() $T_n \in \mathcal{T}$
and
$T_n \in \mathcal{T}$
and
![]() $x > 1$
we have, under the Riemann hypothesis for
$x > 1$
we have, under the Riemann hypothesis for
![]() $\zeta_K(s)$
,
$\zeta_K(s)$
,
 \begin{equation} M_K(x) = \textrm{Res}_{s = 1/2} \frac{x^s}{s\zeta_K(s)} + \sum_{\substack{|\gamma| \leq T_n \\ \rho \text{ simple}}} \textrm{Res}_{s = \rho} \frac{x^s}{s\zeta_K(s)} +\sum_{\substack{|\gamma| \leq T_n \\ \rho \text{ double}}} \textrm{Res}_{s = \rho} \frac{x^s}{s\zeta_K(s)} + E(x,T_n).\end{equation}
\begin{equation} M_K(x) = \textrm{Res}_{s = 1/2} \frac{x^s}{s\zeta_K(s)} + \sum_{\substack{|\gamma| \leq T_n \\ \rho \text{ simple}}} \textrm{Res}_{s = \rho} \frac{x^s}{s\zeta_K(s)} +\sum_{\substack{|\gamma| \leq T_n \\ \rho \text{ double}}} \textrm{Res}_{s = \rho} \frac{x^s}{s\zeta_K(s)} + E(x,T_n).\end{equation}
As noted already, the leading term above grows one-sidedly in x as
![]() $x^{1/2}(\log x)^{\mu - 1}$
, so we seek to restrain the growth of the remaining terms. We have
$x^{1/2}(\log x)^{\mu - 1}$
, so we seek to restrain the growth of the remaining terms. We have
when
![]() $s = \rho$
is a simple and double zero, respectively. In the former case, one suitable bound would be a generalised form of (1·3) which is applicable to Dedekind zeta functions having nontrivial zeros of multiplicity, but which targets only the simple ones, namely
$s = \rho$
is a simple and double zero, respectively. In the former case, one suitable bound would be a generalised form of (1·3) which is applicable to Dedekind zeta functions having nontrivial zeros of multiplicity, but which targets only the simple ones, namely
 \begin{equation*} \sum_{\substack{0 < \gamma \leq T \\ \rho \text{ simple}}} \frac{1}{|\zeta_K'(\rho)|^2} \ll T,\end{equation*}
\begin{equation*} \sum_{\substack{0 < \gamma \leq T \\ \rho \text{ simple}}} \frac{1}{|\zeta_K'(\rho)|^2} \ll T,\end{equation*}
give or take the addition of a low power of
![]() $\log T$
to the right-hand side. In this case, we may replace the
$\log T$
to the right-hand side. In this case, we may replace the
![]() $T_n$
in the second term of (6·1) with any
$T_n$
in the second term of (6·1) with any
![]() $T > 0$
, upon inserting an additional error term of
$T > 0$
, upon inserting an additional error term of
A similar estimate pertaining to the double zeros,
 \begin{equation*} \sum_{\substack{0 < \gamma \leq T \\ \rho \text{ double}}} \frac{1}{|\zeta_K''(\rho)|^2} \ll T,\end{equation*}
\begin{equation*} \sum_{\substack{0 < \gamma \leq T \\ \rho \text{ double}}} \frac{1}{|\zeta_K''(\rho)|^2} \ll T,\end{equation*}
and an estimate of the form
 \begin{equation*} \sum_{\substack{0 < \gamma \leq T \\ \rho \text{ double}}} \frac{|\zeta_K'''(\rho)|}{|\rho||\zeta_K''(\rho)|^2} \ll (\log T)^a,\end{equation*}
\begin{equation*} \sum_{\substack{0 < \gamma \leq T \\ \rho \text{ double}}} \frac{|\zeta_K'''(\rho)|}{|\rho||\zeta_K''(\rho)|^2} \ll (\log T)^a,\end{equation*}
with a a reasonably small integer, would also come in handy, once again allowing for the replacement of
![]() $T_n$
with any
$T_n$
with any
![]() $T > 0$
in (6·1) in exchange for residual error terms. Finally, following the arguments in the proof of [
Reference NgNg04
, theorem 1] would produce the conclusion of Conjecture 6·1, assuming that the resulting contribution of extra powers of
$T > 0$
in (6·1) in exchange for residual error terms. Finally, following the arguments in the proof of [
Reference NgNg04
, theorem 1] would produce the conclusion of Conjecture 6·1, assuming that the resulting contribution of extra powers of
![]() $\log x$
has been smaller than
$\log x$
has been smaller than
![]() $(\log x)^{\mu - 1}$
.
$(\log x)^{\mu - 1}$
.
7. Conclusions and conjectures
In this paper, we have disproved the naïve Mertens-type conjecture for most number fields, and have conditionally shown the existence of limiting distributions for abelian number fields. There are, however, a number of questions prompted by our results.
First, as discussed in Section 6, it is possible that the Mertens function of certain non-abelian number fields may change sign only finitely many times – a surprising departure from the behaviour over
![]() $\mathbb{Q}$
. Furthermore, the question of existence of limiting distributions for non-abelian number fields was also posed.
$\mathbb{Q}$
. Furthermore, the question of existence of limiting distributions for non-abelian number fields was also posed.
We have also shown in Section 3 that for a fixed signature,
![]() $M_K^+ > 1$
for all but finitely many number fields given conventional assumptions on the zero structure of
$M_K^+ > 1$
for all but finitely many number fields given conventional assumptions on the zero structure of
![]() $\zeta_K(s)$
. This has been achieved by bounding from below the maxima of the function
$\zeta_K(s)$
. This has been achieved by bounding from below the maxima of the function
![]() $x^{-1/2}(M_K(x) + M_K^*(x))$
, which suffices for a disproof under the Riemann hypothesis and the simplicity of nontrivial zeros. As a companion to these findings, one may ask instead for upper bounds on the minima of this function, a question which pertains to
$x^{-1/2}(M_K(x) + M_K^*(x))$
, which suffices for a disproof under the Riemann hypothesis and the simplicity of nontrivial zeros. As a companion to these findings, one may ask instead for upper bounds on the minima of this function, a question which pertains to
![]() $M_K^-$
.
$M_K^-$
.
There are also several questions prompted by the existence of the limiting distributions
![]() $\nu_K$
(Theorem 1·4). Although the Mertens conjecture has been known to be false, numerical evidence suggests that the bound
$\nu_K$
(Theorem 1·4). Although the Mertens conjecture has been known to be false, numerical evidence suggests that the bound
![]() $|M_{{\mathbb {Q}}}(x)|\;\leq \sqrt x$
holds most of the time (in the sense of logarithmic density). Namely, if
$|M_{{\mathbb {Q}}}(x)|\;\leq \sqrt x$
holds most of the time (in the sense of logarithmic density). Namely, if
![]() $\nu_K$
is the logarithmic limiting distribution of
$\nu_K$
is the logarithmic limiting distribution of
![]() $x^{-1/2}M_K(x)$
as in Theorem 1·4, then preliminary computations suggest that
$x^{-1/2}M_K(x)$
as in Theorem 1·4, then preliminary computations suggest that
![]() $\nu_{{\mathbb {Q}}}([-1, 1]) \geq 0.99999993366$
(cf. [
Reference HumphriesHum14
]). Nevertheless, it has not yet been proven that
$\nu_{{\mathbb {Q}}}([-1, 1]) \geq 0.99999993366$
(cf. [
Reference HumphriesHum14
]). Nevertheless, it has not yet been proven that
![]() $\nu_{{\mathbb {Q}}}([-1, 1]) > 0$
. This motivates the following two questions.
$\nu_{{\mathbb {Q}}}([-1, 1]) > 0$
. This motivates the following two questions.
Question 7·1. How does
![]() $\nu_K([-1, 1])$
vary with K?
$\nu_K([-1, 1])$
vary with K?
Question 7·2. Let
![]() $\beta_K = \inf \{\alpha > 0 \mid \nu_K([-\alpha, \alpha]) \geq 0.5\}$
. How does
$\beta_K = \inf \{\alpha > 0 \mid \nu_K([-\alpha, \alpha]) \geq 0.5\}$
. How does
![]() $\beta_K$
vary with K?
$\beta_K$
vary with K?
In other words, is the statement
![]() $|M_K(x)|\;\leq \sqrt{x}$
correct more or less frequently as the degree and discriminant of K increase? Alternatively, one could study the asymptotic behaviour of the distributions
$|M_K(x)|\;\leq \sqrt{x}$
correct more or less frequently as the degree and discriminant of K increase? Alternatively, one could study the asymptotic behaviour of the distributions
![]() $\nu_K$
— in particular, the behaviour of its tails. In [
Reference NgNg04
, section 4·3], Ng shows (assuming some conjectures on
$\nu_K$
— in particular, the behaviour of its tails. In [
Reference NgNg04
, section 4·3], Ng shows (assuming some conjectures on
![]() $J_{-1}(T)$
and
$J_{-1}(T)$
and
![]() $J_{-1/2}(T)$
as in (1·2)) that there are constants
$J_{-1/2}(T)$
as in (1·2)) that there are constants
![]() $c_1, c_2$
so that
$c_1, c_2$
so that
In particular,
![]() $\nu_{\mathbb {Q}}([V, \infty)) > 0$
for all V, meaning
$\nu_{\mathbb {Q}}([V, \infty)) > 0$
for all V, meaning
![]() $M_{\mathbb {Q}}(x) > V\sqrt{x}$
a positive proportion of the time. That is, counterexamples to the Mertens conjecture over
$M_{\mathbb {Q}}(x) > V\sqrt{x}$
a positive proportion of the time. That is, counterexamples to the Mertens conjecture over
![]() ${\mathbb {Q}}$
have positive logarithmic density. One may ask how these asymptotics generalise to the settings of number fields. Thus, we pose the following two questions.
${\mathbb {Q}}$
have positive logarithmic density. One may ask how these asymptotics generalise to the settings of number fields. Thus, we pose the following two questions.
Question 7·3. For an abelian number field K, are there
![]() $c_1, c_2$
so that
$c_1, c_2$
so that
Question 7·4. If Question 7·3 is answered affirmatively, how should the constants vary with K?
Acknowledgements
We are deeply grateful to Peter Humphries for supervising this project and to Ken Ono for his valuable suggestions. We would also like to thank Winston Heap, David Lowry Duda and Micah Milinovich for helpful discussions. We are grateful for the generous support of the National Science Foundation (Grants DMS 2002265 and DMS 205118), National Security Agency (Grant H98230-21-1-0059), the Thomas Jefferson Fund at the University of Virginia, and the Templeton World Charity Foundation. This research was conducted as part of the 2021 Research Experiences for Undergraduates at the University of Virginia.



















