Introduction
Ice divides that are frozen to their beds maintain a unique stress regime; because surface slopes and shear stresses approach zero, ice is essentially in pure shear, and the effective deviatoric stress is low compared to elsewhere on the ice sheet. This stress regime poses a challenge for ice-dynamics modeling because the assumption in the shallow-ice approximation that longitudinal stresses are negligible is not valid. Yet, modeling the flow of ice near divides is crucial to examining the histories and possible futures of all ice sheets, including interpreting ice-core records and radar profiles.
The ways in which this ice-divide stress regime alters the ice flow pattern depend on the ice-sheet boundary conditions and the constitutive relation between stress and strain rate for ice (the flow law). Within two ice thicknesses of a divide, longitudinal stress can contribute as much as, or more than, bed-parallel shear stress to the effective deviatoric stress. According to Glen’s flow law for ice with a stress exponent n = 3, the effective viscosity is inversely proportional to the square of the deviatoric stress (Reference NyeNye, 1953; Reference GlenGlen, 1958). Thus, the region with the lowest deviatoric stress (near the bed at the divide) is more resistant to deformation than surrounding areas. Deformation is therefore concentrated in the softer ice nearer the surface; the velocity of ice particles along a flow path is slowed as they approach the deep resistant ice. Reference RaymondRaymond (1983) first described this special divide flow pattern and noted that the age/depth scale at a steady-state divide would be impacted by this flow pattern: with a uniform accumulation rate, ice of a particular age appears higher in the stratigraphic column at the divide than it does at flank sites. The special divide flow pattern has limited horizontal extent (blending into flank flowwithin one or two ice thicknesses of the divide), and leads to an arch in the isochrones, commonly called a′Raymond bump’.
Since Raymond’s initial analysis, several authors have expanded on this theory of divide flow by looking at perturbations to the flow field caused by different boundary conditions. Reference Nereson, Hindmarsh and RaymondNereson and others (1998b) explored the effects of changes in elevation of bounding ice streams, which can cause the divide to migrate. Reference HvidbergHvidberg (1996) included realistic thermal boundary conditions, and Reference Nereson and WaddingtonNereson and Waddington (2002) characterized isochrones and isotherms more fully under migrating divides. Reference Pettit, Jacobson and WaddingtonPettit and others (2003) and Reference Martín, Gudmundsson, Pritchard and GagliardiniMartín and others (2009a) modeled the effects of a sliding boundary condition at the base of the ice.
In addition to the boundary conditions, ice properties can also modify the special divide flow pattern. Conventionally, glaciologists have used Glen’s law, which describes ice as a power-law fluid (n = 3) constitutive relation between stress and strain rate, where dislocation creep is the dominant deformation mechanism. This theory has been successful at the relatively higher deviatoric stresses found in most valley glaciers and ice sheets. At low deviatoric stresses, however, the deformation mechanism probably shifts to a more linear mechanism such as diffusion creep or grain boundary sliding (e.g. Reference LangdonLangdon, 1996; Reference Goldsby and KohlstedtGoldsby and Kohlstedt, 2001). Reference Waddington, Raymond, Morse and HarrisonWaddington and others (1996) defined the crossover stress as the effective deviatoric stress at which the cubic and linear terms contribute equally to deformation. Reference MorseMorse (1997) estimated the crossover stress as 0.25 bar from surface velocities at Taylor Dome, Antarctica. Reference Pettit and WaddingtonPettit and Waddington (2003) summarized the theory behind this possible shift in flow mechanism, reformulated the flow law as a combination of a linear and a cubic term to allow for multiple deformation mechanisms (including different dependencies of ice properties on those mechanisms) and demonstrated the impacts of the linear term on ice-sheet surface and internal-layer shapes near ice divides. The crossover stress, which may depend on temperature, impurities and crystal size, is an intensive property of bulk polycrystalline ice (i.e. it does not depend on sample size or geometry) that has still not been rigorously measured because of the difficulties of isolating its effect on ice flow from that of crystal fabric (the pattern of preferred crystal orientation) and other ice properties. Our primary goal in this study was to determine the crossover stress using data and analysis of ice flow at Siple Dome, West Antarctica, using a model that includes the effect of the viscous anisotropy induced by a preferred crystal-orientation fabric. Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others (2007) and Reference Martín, Hindmarsh and NavarroMartín and others (2009b) showed that the crystal fabric can significantly modify the special divide flow pattern and can impact the interpretation of ice-core records for this site.
In this study, we used the model developed by Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others (2007) for divide flow, which includes a flow law that accounts for the effect of crystal fabric on deformation.
Siple Dome was chosen for this analysis because it has been studied extensively as the site of a recent US Antarctic Program deep-drilling project. In our study, we used available ice-core, surface-flow, mass-balance, borehole sonic-velocity and in situ vertical-strain data to constrain the flow-law parameters within a comprehensive finite-element model of ice flow near the divide.
The sonic-velocity and vertical-strain data were essential to this analysis. The vertical-strain instruments were adapted specifically for this study. We used data from two high-resolution custom instruments: fiber-optic displacement sensors developed by the University of California, San Diego (Reference ZumbergeZumberge and others, 2002), and wire strain meters developed by the University of Alaska, Fairbanks (Reference ElsbergElsberg and others, 2004). The sonic-velocity profile was measured by G. Lamorey. We converted it to express vertically oriented fabric through a method based on that of Reference ThorsteinssonThorsteinsson (2000).
We predicted strain rates and velocities using a finite-element flow model that incorporates specified geometry and ice properties as inputs. Given measured geometry and estimates of the ice properties, this flow model solves a forward problem. Through the corresponding inverse problem, we can infer the ice properties of interest (in this case the flow-law parameters) by comparing the measured depth profile of vertical-strain rate and measured horizontal surface velocities (including measurement uncertainties) with the respective model outputs. We focused our analysis on the measured vertical-strain-rate profile because this profile is more sensitive than horizontal surface velocities to ice rheology that varies with depth (horizontal surface velocities are responding to rheological properties that are integrated over the depth of the ice sheet). Furthermore, the velocities and vertical-strain-rate profiles depend only on the modern ice-sheet geometry and ice properties; unlike the shape of internal layers (which are often used for inferring ice-sheet dynamic behavior), which are based on past ice flow as well as the modern geometry and properties.
An Anisotropic Constitutive Law for Ice
Reference Pettit and WaddingtonPettit and Waddington (2003) developed a two-term flow law for isotropic ice that is simple to incorporate into ice flow models but can encompass a range of deformation behaviors, specifically the low-stress behavior seen near ice divides. This flow law is:
where ![]() and τij
are the strain-rate and deviatoric-stress tensors (i, j = 1, 2, 3),
and τij
are the strain-rate and deviatoric-stress tensors (i, j = 1, 2, 3), ![]() is the second invariant of the deviatoric-stress tensor, and
is the second invariant of the deviatoric-stress tensor, and
where
The associated effective viscosity, η eff, is:
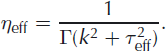
In this formulation, we incorporate processes that stiffen or soften the ice isotropically within Γo; therefore we call this the ‘isotropic flow-law coefficient’. The ‘isotropic enhancement factor’, E(z), combines all processes that affect the softness of ice isotropically (including a dimensionless enhancement factor due to crystal size) and A o represents a softness parameter for clean Holocene ice (A o is the same as the conventional temperature-independent softness parameter used in the n = 3 form of Glen’s law; units Pa−3s−1). Q is the activation energy for creep, T is the temperature and R is the gas constant.
In this formulation the ‘crossover stress’, k, is a threshold value of the effective deviatoric stress at which the linear and cubic terms contribute equally to the total strain rate. It is a property of the ice that can be described by:
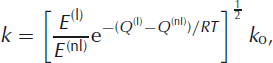
where superscripts (l) and (nl) refer to linear and nonlinear deformation mechanisms, respectively. As shown in this expression, the crossover stress depends on temperature only when the linear and nonlinear flow mechanisms have different activation energies, Q. Furthermore, the crossover stress also depends on impurities and other isotropic enhancement processes only when those processes are different for linear and nonlinear flow mechanisms. When k/τ eff ≪ 1, the conventional form of Glen’s law emerges.
This flow law does not, however, provide a straightforward way for incorporating the anisotropic deformation due to preferred crystal orientation, because, for anisotropic ice, one component of the stress tensor can induce strain rates in other components of the strain-rate tensor. Reference Placidi, Greve, Seddik and FariaPlacidi and others (2010) have designed the most comprehensive and successful model of anisotropic flow using the enhancement factor in Equation (3). Most other ice-sheet flow models which incorporate the effect of crystal fabric on flow use mathematically more complicated sets of assumptions that allow for fabric to induce deformation in directions different to the applied stress (e.g. Reference Mangeney, Califano and CastelnauMangeney and others, 1996; Reference CastelnauCastelnau and others, 1998; Reference Gödert and HutterGödert and Hutter, 1998; Reference Gillet-Chaulet, Gagliardini, Meyssonnier, Montagnat and CastelnauGillet-Chaulet and others, 2005, Reference Gillet-Chaulet, Gagliardini, Meyssonnier, Zwinger and Ruokolainen2006; Reference Morland and StaroszczykMorland and Staroszczyk, 2006; Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others, 2007). However, this makes large-scale flow models computer-processing intensive. The ability for fabric to induce deformation in directions different to the applied stress is often necessary because ice crystals have only two easy-slip systems, which are within the basal plane; deformation on other slip systems being >60 times harder (Reference Duval, Ashby and AndermanDuval and others, 1983). The easy slip on the basal plane makes deformation of a crystal similar to that of a deck of cards. As a result, an ice aggregate with crystal c-axes aligned in the same direction is much softer in simple shear parallel to the basal planes than an aggregate with randomly oriented crystals. Since crystals within an ice sheet are known to develop a preferred orientation as the ice sheet evolves (e.g. Reference AlleyAlley, 1992), incorporating deformation due to a preferred crystal fabric into a flow law may improve our ability to predict real ice-sheet behavior through models.
We used the same anisotropic flow law as Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others (2007), originally developed by Reference ThorsteinssonThorsteinsson (2001). Thorsteinsson’s flow law is based on the homogeneous stress assumption which states that the bulk deformation of the ice aggregate is the average deformation of all the crystals within the aggregate (Reference SachsSachs, 1928). Our model assumptions are similar to those of Reference Gödert and HutterGödert and Hutter (1998) and Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier (1999). The resolved shear stress on the basal plane of each crystal depends on its orientation relative to the applied stress. The resolved shear stress drives the deformation within the crystal. Thus, crystals with c-axes oriented in a direction nearly parallel to the applied stress have a smaller resolved shear stress in the basal planes and deform at a slower rate than crystals with c-axes oriented in a direction more perpendicular to the applied stress.
To build a flow law from this theory, Reference ThorsteinssonThorsteinsson (2001) used a statistical distribution of crystal orientations within an aggregate to determine the bulk deformation. The crystal fabric near an ice divide typically has a cluster of c-axes oriented vertically. This type of fabric can be described by a ‘cone angle’, the half-angle of a cone within which all crystals in an ideal block of ice are uniformly distributed. (In real ice, the distribution is not uniform and there are outliers; its cone angle is that of the ideal block of ice that produces the same bulk strain rate for a given bulk stress.) Thorsteinsson derived an analytical solution to describe the deformation of the bulk material for a given cone angle with a linear relation between the resolved shear stress and the strain rate on the basal plane (Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others, 2007). This bulk flow law, using the Sachs assumption of homogeneous stress (Reference SachsSachs, 1928), can be written:
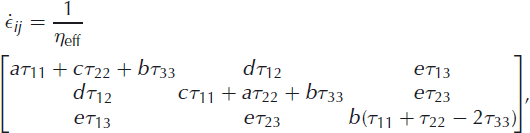
where coefficients a, b, c, d and e are given as functions of cone angle, α, (derived by Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others, 2007) and where η
eff is the bulk isotropic effective viscosity (Equation (4)). For plane strain, substituting velocity gradients for strain rates ![]() , the conservation laws of momentum and mass are:
, the conservation laws of momentum and mass are:
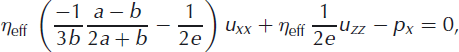
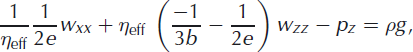
where
Note that in the Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others (2007) derivation, incompressibility (Equation (9)) was used to produce Equations (7) and (8). For an isotropic crystal fabric (cone angle α = 90°), a = 2/3, b = −1/3 and e = 1. For pure single-maximum fabric (α = 0°), α = 0, b = 0 and e = 5/2.
Compared to other anisotropic flow laws (e.g. Reference AzumaAzuma, 1994; Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others, 1996) this formulation generally under-predicts the magnitude of anisotropic enhancement (Reference ThorsteinssonThorsteinsson, 2001), which limits how successfully the model can predict observations. As defined, the unknown scalar parameters, E, cannot fully account for this model limitation. Furthermore, the Reference ThorsteinssonThorsteinsson (2001) flow law is based on a linear relation between deformation rate and resolved shear stress on the basal plane within a single crystal, which also limits its universal applicability for ice. We have assumed that the effects of these two limitations on this study are small compared to the magnitude of the anisotropic enhancement, for the following reason. The linear constitutive relation assumed by Thorsteinsson applies only to individual elements in the model domain. The relation we used to describe bulk effective viscosity, however, is a nonlinear flow law. As shown by Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others (2007), this combination of flow laws approximates the pattern of behavior due to crystal fabric of the fully nonlinear system without the mathematical complexity.
This model does not predict fabric evolution. Although crystal fabric is continually evolving in an ice sheet, the question posed here does not require the model results to be time-integrated. Instead, we use the flow law to relate the instantaneous stress field (imposed by the present geometry), the instantaneous strain-rate field (from in situ measurements) and the instantaneous crystal-orientation fabric (based on borehole measurements). As long as our extrapolation of the fabric data across the ice divide is realistic, the analysis we present here does not depend on the evolution of fabric.
Finite-Element Ice Flow Model
To study the flow at Siple Dome, we used a finite-element model similar to the ice-divide models developed by Reference RaymondRaymond (1983) and Reference HvidbergHvidberg (1996). Reference PettitPettit (2003) and Reference Pettit, Jacobson and WaddingtonPettit and others (2003, Reference Pettit, Thorsteinsson, Jacobson and Waddington2007) described other variations of this model. The assumptions for the present study include:
The ice deforms in plane strain; when the crystal fabric is anisotropic, this requires a three-dimensional stress field to keep the ice constrained to flow within the plane. This type of model best represents a ridge ice divide, such as Siple Dome (Reference Nereson, Waddington, Raymond and JacobsonNereson and others, 1996) or Roosevelt Island, West Antarctica, (Reference Conway, Hall, Denton, Gades and WaddingtonConway and others, 1999), where the primary deformation is perpendicular to the ridge line (see Fig. 1).
The temperature field is specified.
The present geometry is specified.
The upper surface is stress-free.
The horizontal-velocity profile on the flank boundary (at 30 ice thicknesses from the divide) carries away the integrated mass balance from the divide to the boundary, in order to satisfy global mass conservation for a steady-state ice sheet. Because our boundary is more than 20 ice thicknesses from the divide, the results for the region within 10 ice thicknesses of the divide are insensitive to the details of the horizontal-velocity profile on the flank boundary (Reference RaymondRaymond, 1983; Reference Schøtt, Waddington and RaymondSchøtt and others, 1992). In practice, we begin a model run with a laminar flow profile at the boundary. As velocities within the ice sheet are iteratively calculated, we update the shape of the horizontal-velocity profile at the boundary (while maintaining the flux) to account for the unique rheological properties of the anisotropic ice and the non-uniform temperature field. Ultimately, the model converges on a velocity solution with a more realistic shape for the horizontal-velocity profile at the boundary.
Ice rheology is described by the two-term isotropic flow law shown in Equations (1– 5) combined with Thorsteinsson’s anisotropic flow law, Equations (7– 9). The softness parameter, A o, is taken from Reference PatersonPaterson (1994), and variations from this standard softness are expressed through isotropic enhancement factors, E(z). The model is solved iteratively using the Jacobi method. Figure 2 shows a simplified flow chart of the nested iterations. First, an isotropic effective viscosity, η eff, is calculated for each element using Equations (1– 5), the momentum equations expressed in pressure and velocity fields, and the velocity field from the previous iteration (or initialized by using the shallow-ice approximation velocity field). Then this effective viscosity is substituted in Equations (7– 9), which are solved simultaneously over all elements for the new velocity field, given the fabric (cone angle) in each element. In Equations (7– 9), we assume that η eff and a–e are spatially uniform; they apply to individual finite elements in the model. The new velocity field is then used to calculate a new isotropic effective viscosity and the process is repeated to achieve convergence, defined as when the absolute change in velocity over successive iterations, summed over all elements, is below a tolerance of 0.5 × 10−3 m a−1.This two-step process allows us to combine the nonlinear bulk flow of ice based on Glen’s law with Thorsteinsson’s description of the effect of crystal fabric on flow based on linear crystal deformation rates.
The measured cone-angle profile at the divide is extrapolated to the flanks as a function of normalized height, z/H(x), where z is the height above the bed, x is distance from the divide and H is the ice thickness. This assumption is based on the idea that ice of similar age and depth has experienced similar strain history and therefore has developed similar fabric. Fabric develops through shear strain as it moves horizontally as well, which is not included in this assumption; therefore, the real distribution of fabric may have stronger fabric on the flanks than we assume in this model.
The model solves the flow equations on a 64 × 23 grid of nine-node quadratic elements for pressure and velocity fields. We use a finer grid near the divide and in regions where ice properties have strong gradients.
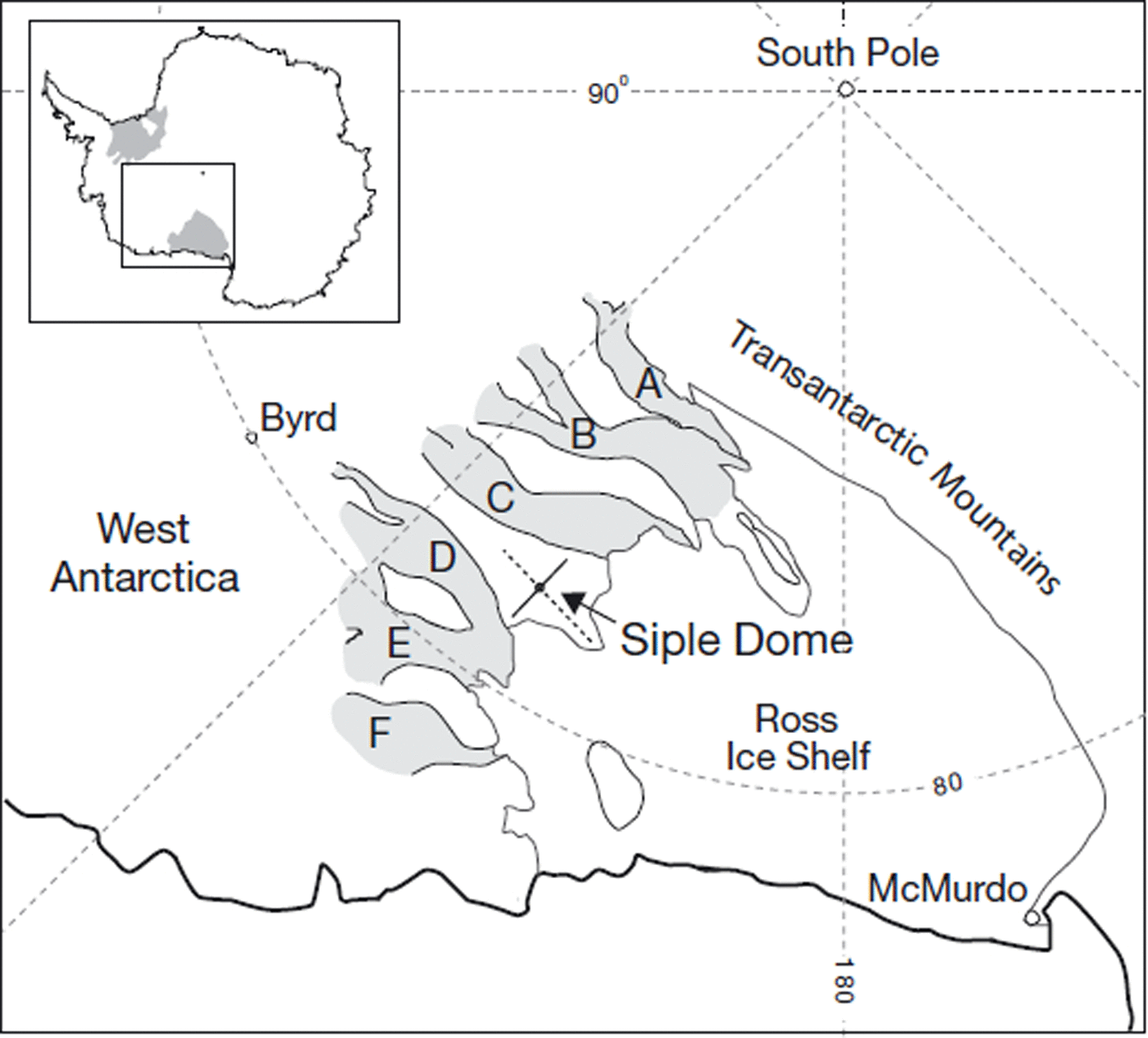
Fig. 1. The Siple Coast and the Ross Sea embayment, West Antarctica. Siple Dome is an inter-ice-stream ridge on the Siple Coast. Shaded regions represent Mercer Ice Stream (former Ice Stream A), Whillans Ice Stream (former Ice Stream B), Kamb Ice Stream (former Ice Stream C), Bindschadler Ice Stream (former Ice Stream D), MacAyeal Ice Stream (former Ice Stream E) and Echelmeyer Ice Stream (former Ice Stream F). The dot on Siple Dome approximately identifies the summit location, the dashed line is the ridge crest, and the solid line represents the cross section modeled here.
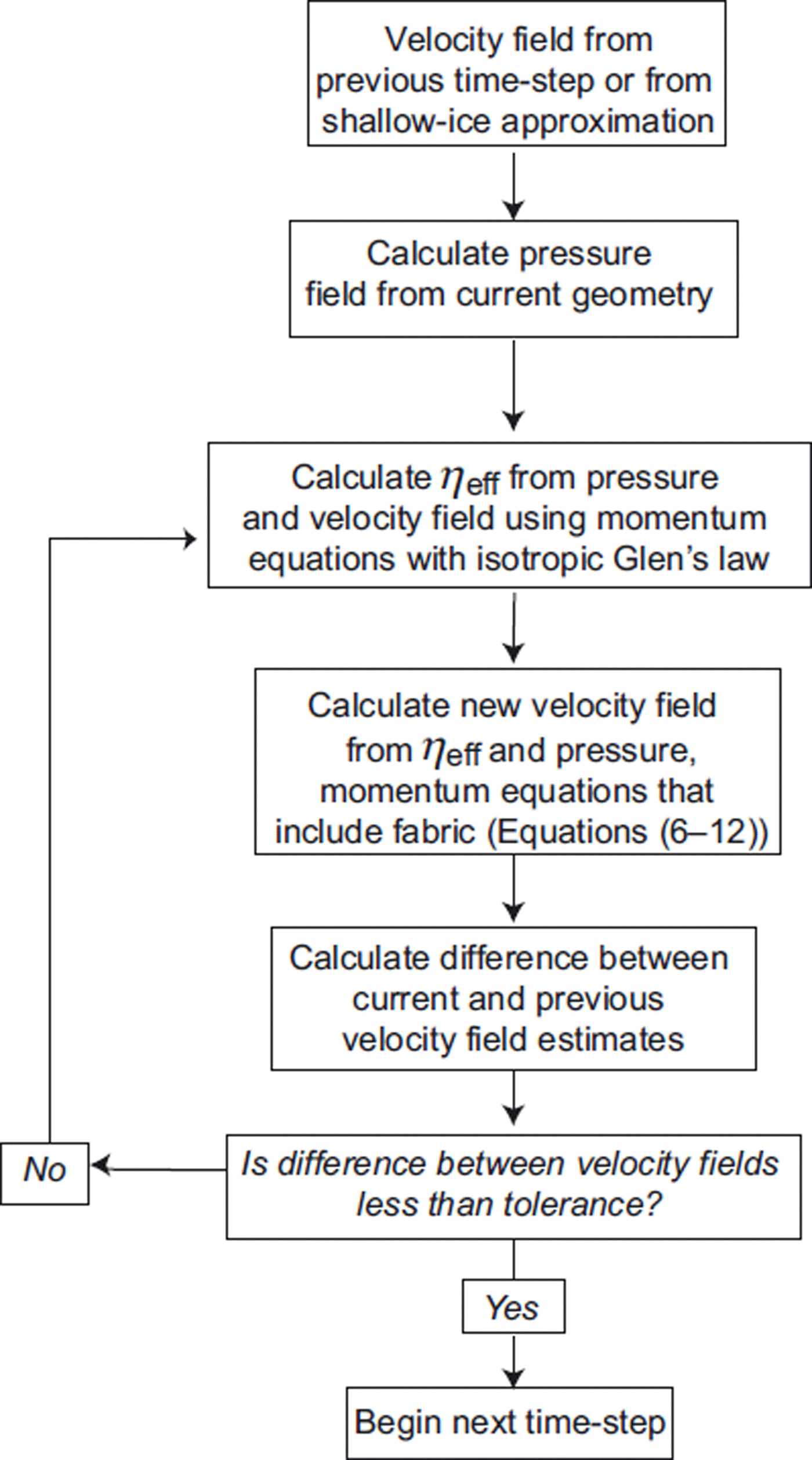
Fig. 2. A flow chart showing the nested loop used to calculate the effective viscosity and the influence of fabric on the flow. Note that in the models run for this inverse problem we do not use multiple time-steps. Instead we initiate the model with velocities calculated from the shallow-ice approximation and then iterate to a converged new velocity field. (For the isochrone calculations shown in Figure 9 we do evolve the ice sheet through multiple time-steps until it reaches a steady state, for comparison with internal layering from radar imagery.)
Siple Dome, West Antarctica
Siple Dome (81.65° S, 148.81° W) is a 1000 m thick ridge of slow-moving ice between Kamb and Bindschadler Ice Streams on the Siple Coast of West Antarctica (Fig. 1). The summit region has been in steady state for several thousand years (Reference Nereson and RaymondNereson and Raymond, 2001; Reference Pettit, Waddington, Nereson, Zumberge and HamiltonPettit and others, 2001; Reference PettitPettit, 2003) and it has been an elevated dome-like feature for much of the Holocene and possibly since the Last Glacial Maximum (Reference Nereson, Raymond, Jacobel and WaddingtonNereson and others, 2000). The internal structure, as imaged by ice-penetrating radar, shows a distinctive arch in the layers under the divide (Reference Raymond, Nereson, Gades, Conway, Jacobel and ScambosRaymond and others, 1995; Reference Scambos and NeresonScambos and Nereson, 1995; Reference Jacobel, Fisher and SundellJacobel and others, 1996). Assuming these layers represent the pattern of isochrones, this arch implies that nonlinear deformation mechanisms contribute significantly to the deformation (Reference RaymondRaymond, 1983). However, the characteristic deviatoric stress (as defined by Reference Waddington, Raymond, Morse and HarrisonWaddington and others, 1996; Reference Pettit and WaddingtonPettit and Waddington, 2003) is 0.2 bar, low enough that near-linear flow mechanisms may contribute measurably to the deformation. These characteristics make Siple Dome ideal for a study of the effects of rheological processes on divide flow.
In addition to the ice-core data available for Siple Dome, a surface strain network provides surface flow; snow pits, shallow cores and ice-penetrating radar provide spatial and temporal accumulation-rate patterns; instruments embedded in the ice provide vertical-strain measurements; and borehole sonic-velocity measurements provide crystal-fabric information. As described in detail below, we incorporated most of the available data into our analysis: the measured divide geometry, accumulation rates, borehole temperatures and sonic log provide inputs to the model, while the strain data (both on the surface and at depth) provide constraints on possible solutions.
Model inputs
Geometry
The surface topography along the cross section that we studied (the line across the dome in Fig. 1) was measured using GPS data (Reference Raymond, Nereson, Gades, Conway, Jacobel and ScambosRaymond and others, 1995; Reference Scambos and NeresonScambos and Nereson, 1995; Reference Nereson, Waddington, Raymond and JacobsonNereson and others, 1996). The bed topography came from ice-penetrating radar (Reference Raymond, Nereson, Gades, Conway, Jacobel and ScambosRaymond and others, 1995; Reference Jacobel, Fisher and SundellJacobel and others, 1996). Near the divide, flow appears to be parallel to the cross section (Reference NeresonNereson, 1998); we therefore assumed two-dimensional plane-strain flow.
Accumulation rate
The pattern of accumulation rate at Siple Dome is driven primarily by the topography. Storms generally approach from the north, oceanward, side of the divide, depositing more of their moisture on the north side, leaving the south side significantly drier (Reference BromwichBromwich, 1988). Reference Nereson, Raymond, Jacobel and WaddingtonNereson and others (2000) observed this trend in the pattern of radar-detected internal layers. They used a kinematic steady-state ice flow model to predict internal layer shapes as a function of a steady-state accumulation pattern across the dome. The accumulation pattern Reference Nereson, Raymond, Jacobel and WaddingtonNereson and others (2000) derived from radio-echo sounding (radar) images provides only relative accumulation rates. Even with a depth/age scale, extracting historical accumulation patterns is not straightforward (Reference WaddingtonWaddington and others, 2005). In our analysis, we used the Nereson accumulation pattern scaled to a point measurement of the modern 42 year average of 0.132 m a − 1 ice-equivalent accumulation rate at the divide, determined by Reference HamiltonHamilton (2002) based on gross-β analysis on a shallow core to detect nuclear bomb fallout layers from 1955.
Temperature
The temperature profile at Siple Dome was measured both in the deep borehole 500 m south of the summit by the US Geological Survey and the University of Washington (Reference MacGregor, Winebrenner, Conway, Matsuoka, Mayewski and ClowMacGregor and others, 2007) and in a hot-water-drilled borehole at the summit by the California Institute of Technology (Reference EngelhardtEngelhardt, 2004). Reference EngelhardtEngelhardt (2004) also measured a shorter profile to ∼300 m depth at the flank strain-gauge instrumentation site ∼7 km northeast (81.60° S, 148.69° W).
In a steady-state ice sheet, both advection and diffusion can contribute significantly to the temperature field if the Peclet number is large. As we described above, the vertical-velocity field near a divide is altered by low-stress behavior such that an arch forms in the isochrones. The process that produces this arch also produces an arch in the isotherms by affecting the advection term in the heat equation. We determined the temperature for our entire model cross section by adapting the two-dimensional steady-state advection/diffusion kinematic model of Reference Nereson and WaddingtonNereson and Waddington (2002) constrained by the measured temperature profile at the divide.
The Nereson–Waddington thermal model uses a kinematic velocity field based on the shape-function method of Reference ReehReeh (1988). The shape function for horizontal- and vertical-velocity smoothly varies from divide to flank, with divide and flank end-member profiles based on Dansgaard–Johnsen profiles (Reference Dansgaard and JohnsenDansgaard and Johnsen, 1969). We scaled the velocity field using vertical ice velocities at the surface, as derived from the local accumulation rate. We adjusted the bulk values of thermal conductivity, specific heat and geothermal flux in the model to best fit the measured temperature profile at the divide. We then applied these values to the entire ice-sheet cross section. We ultimately used 2.1 W m−1 K− 1 for conductivity, 1700 J kg − 1 K−1 for specific heat and 70 m W m−2 for the geothermal flux.
There are two primary sources of uncertainty in our thermal model. First, although the temperature field is dependent on the history of surface temperature and ice flow, we do not explicitly account for this. By best-fitting the model to the modern temperature profile, we minimize this uncertainty. Second, although Siple Dome has been neither thickening nor thinning in the late Holocene (Reference PettitPettit, 2003; Reference WaddingtonWaddington and others, 2005; Reference Price, Conway and WaddingtonPrice and others, 2007), there is evidence of slow divide migration in the recent past (Reference Nereson, Raymond, Waddington and JacobelNereson and others, 1998a). The range of possible migration speeds found by Reference Nereson, Raymond, Waddington and JacobelNereson and others (1998a) is 0.05–0.50 m a−1. We included a migration rate in the middle of this range (0.26 m a−1) in our calculation. The range of possible migration rates introduces some uncertainty in the temperature field.
The additional temperature measurements made by Reference EngelhardtEngelhardt (2004) on the flank provide one location with which to check our temperature calculation. All of our calculated temperatures in that location are less than 0.5°C from the measured values. We estimated, using the Arrhenius temperature relation in the flow law, that an uncertainty of 0.5°C would contribute an uncertainty of ±5% error in our strain-rate calculations.
Crystal size
Crystal size may be important where the crystals are small (Reference Cuffey, Thorsteinsson and WaddingtonCuffey and others, 2000b; Reference Goldsby and KohlstedtGoldsby and Kohlstedt, 2001). However, it is unclear whether crystal size is an independent factor or whether it is driven by impurity content and the strain-rate field (e.g. Reference Gow and WilliamsonGow and Williamson, 1976; Reference Alley, Perepezko and BentleyAlley and others, 1986a, Reference Alley, Perepezko and Bentleyb; Reference Jacka and LiJacka and Li, 1994; Reference De Bresser, Ter Heege and SpiersDe Bresser and others, 2001; Reference DurandDurand and others, 2006; Reference Iliescu and BakerIliescu and Baker, 2008). In this study, we assumed that crystal-size effects can be incorporated into the isotropic enhancement factors as a dimensionless crystal-size enhancement factor.
Crystal orientation
As preferred crystal orientation can alter local strain-rate patterns by up to an order of magnitude, crystal orientation is an important model input. We use observations of sonic velocity converted to cone angles to provide a profile of crystal fabric. Reference ThorsteinssonThorsteinsson (2000) describes the basic method for converting compressional wave velocity into cone angle, which relies on the assumption that viscous anisotropy can be directly related to elastic anisotropy and that the fabric can be well described by a single-maximum vertical preferred orientation.
The cone-angle profile is shown in Figure 3, along with crystal radius data (Reference DiPrinzio, Wilen, Alley, Fitzpatrick, Spencer and GowDiPrinzio and others, 2005), temperature (Reference EngelhardtEngelhardt, 2004) and calcium concentration (Reference MacGregor, Winebrenner, Conway, Matsuoka, Mayewski and ClowMacGregor and others, 2007) as a function of depth and age (Reference TaylorTaylor and others, 2004b). We include crystal size, temperature and calcium concentration in this plot to highlight the structural difference in the ice at different depths.
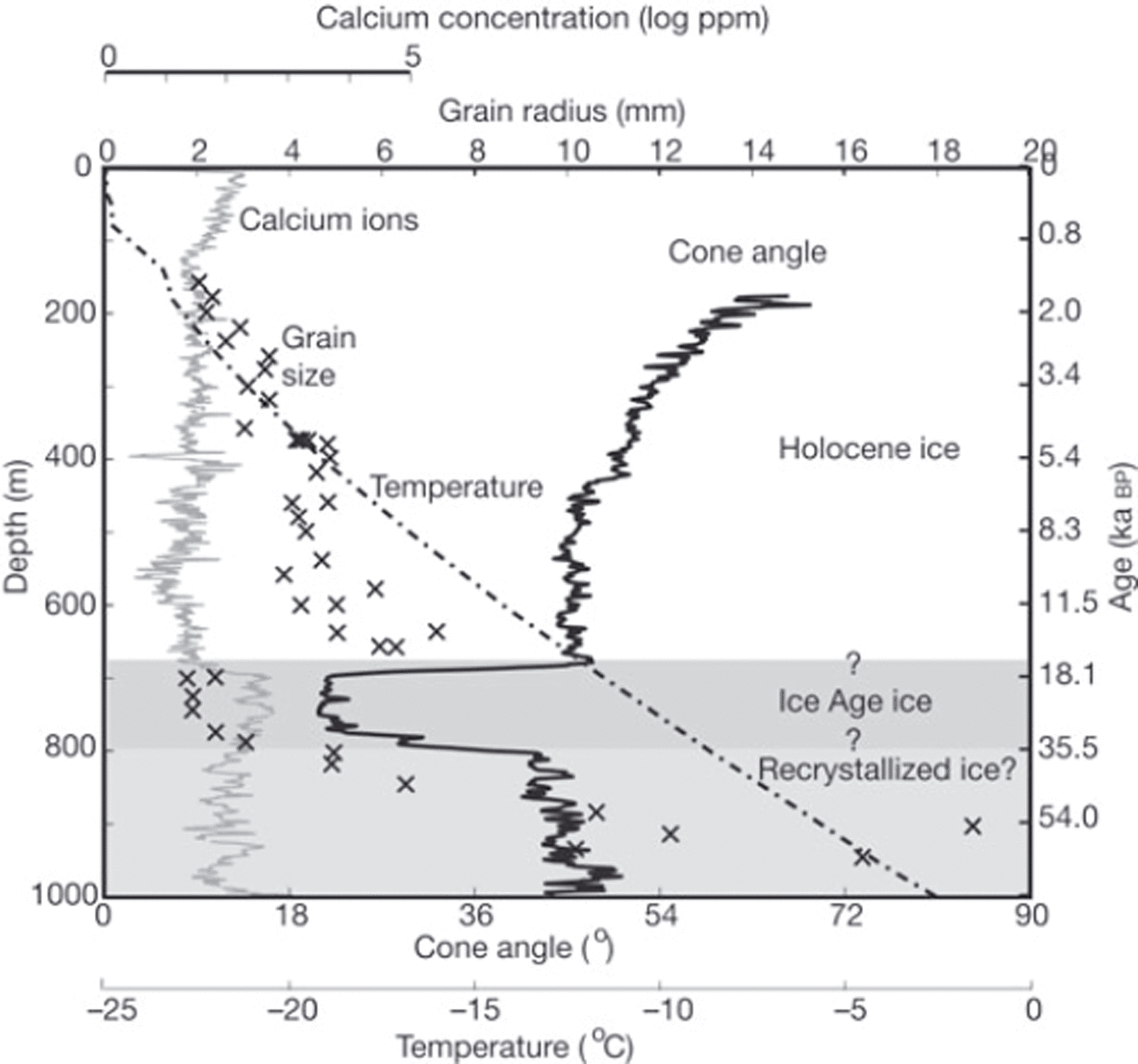
Fig. 3. The cone angle was derived from the sonic log of the borehole. Grain size was derived from thin sections of the ice core (Reference DiPrinzio, Wilen, Alley, Fitzpatrick, Spencer and GowDiPrinzio and others, 2005). Temperature is from a hot-water-drilled borehole at the summit (Reference EngelhardtEngelhardt, 2004). The calcium concentration is from ice-core samples (Reference MacGregor, Winebrenner, Conway, Matsuoka, Mayewski and ClowMacGregor and others, 2007). The approximate ages are given on the right vertical axis based on the combined timescale of Reference TaylorTaylor and others (2004a). Note the correspondence of the band of tight fabric with small grains between 700 and 800 m depth. Our assignment of Holocene, Wisconsin and recrystallized ice regions is an estimate based on ice properties.
The sonic log shows a distinct layer of extremely tight vertical fabric, bounded by large gradients in cone angle. The upper transition begins at 696 m (∼20 ka BP) and ends at 680 m (∼17.4 ka BP) when the crystal size abruptly increases and the calcium concentration jumps. An increase in crystal size is typical of the boundary between Holocene ice and deeper Ice Age ice (e.g. Reference PatersonPaterson, 1994, p.193); one theory suggests that Ice Age crystals are smaller because they initially grew more slowly due to lower temperatures (Reference Lipenkov, Barkov, Duval and PimientaLipenkov and others, 1989) and higher dust content (Reference PatersonPaterson, 1991). This theory provides one explanation as to why the transition to larger crystals and weaker fabric at Siple Dome is slightly deeper (earlier in time) than the transition to a warmer climate expressed by stable isotopes (Reference TaylorTaylor and others, 2004a). The offset can be explained if the warmer temperatures of the early Holocene affected crystal growth in the 10–20 m of Ice Age firn nearest the surface, but did not affect the dust concentration. This is possible, considering that the timescale for advection (![]() year for z = 20 m and
year for z = 20 m and ![]() ) is 1.5 orders of magnitude longer than the timescale for diffusion (∼ z
2
/K ≈ 13 years for a thermal diffusivity of K = 10−6 m2 s−1). In addition, the possibly lower accumulation rates during the Ice Age (Reference Spencer, Alley and FitzpatrickSpencer and others, 2006) would enhance this difference in timescales.
) is 1.5 orders of magnitude longer than the timescale for diffusion (∼ z
2
/K ≈ 13 years for a thermal diffusivity of K = 10−6 m2 s−1). In addition, the possibly lower accumulation rates during the Ice Age (Reference Spencer, Alley and FitzpatrickSpencer and others, 2006) would enhance this difference in timescales.
The deeper transition in the cone-angle profile occurs between 756 m (−10°C) and ∼805 m (−8°C). We identify this transition as the upper bound of dynamic recrystallization, which occurs as ice warms (typically above −10°C; Reference Weertman, Whalley, Jones and GoldWeertman, 1973).
In using the crystal fabric and other ice-core data in our ice flow analysis, we assume that the ice properties vary only with normalized depth. Realistically, there will be some variation in ice structure with distance from the divide, since ice properties are advected along particle paths. We, however, assume that horizontal variations in ice properties are small compared to vertical variations.
Chemical and physical impurities
Chemical and physical impurities affect the deformation rates (e.g. Reference PatersonPaterson, 1991; Reference Cuffey, Conway, Gades, Hallet, Raymond and WhitlowCuffey and others, 2000a), but the relations are complicated and often difficult to predict. We assume that flow enhancements due to impurity content are grain-scale isotropic effects that we can incorporate through the isotropic enhancement factors.
Data used to constrain model outputs
Our analysis is unique because we incorporate measurements of the vertical-strain-rate profile. We have data from two sites: the divide (81.65° S, 148.81° W) and a flank site (81.60° S, 148.69° W) 7 km to the northeast of the divide along the same flowline. We used two types of instruments: optical-fiber displacement sensors (effective gauge lengths 174 and 178 m) and wire-resistance strain gauges (gauge length 1 m).
Optical-fiber displacement sensors
The optical-fiber instruments, developed by Reference ZumbergeZumberge and others (2002), use a pair of dual-fiber-optic cables, one short and one long, to measure the total strain between the fiber end points. Each dual-fiber cable consists of a transmit fiber and a return fiber which are spliced together at the bottom. The cable is anchored at the surface and at depth, and the length of the fiber between anchors is measured using an electronic distance meter. The length of each cable is compared to the other cables, which have bottom anchors at different depths within the ice sheet. The effective gauge length for a pair of cables is the vertical distance between the bottom anchors. Within each cable, the fibers are housed in a stainless-steel sheath, so the fibers can move and deform freely except at the anchors.
At each of the two sites, cables were lowered into water-filled boreholes and allowed to freeze into the ice. Five 80 m cables were paired with five longer cables, whose lower anchors were spaced evenly with depth in the ice sheet. The fibers were pre-stretched with a 12 kg mass, allowing us to measure vertical compression of the ice. We monitored the length of each fiber using a specially adapted electronic distance meter during a few weeks each summer for 4 years. Subsequently, the data were corrected for temperature, optical/physical length ratio (Reference ZumbergeZumberge and others, 2002) and horizontal shearing of the boreholes (appendix C of Reference PettitPettit, 2003). From these data (Reference ZumbergeZumberge and others, 2002; Reference ElsbergElsberg and others, 2004) we determined the average annual strain rate at a series of depths, with an effective gauge length of 178 m at the divide and 174 m at the flank. The average strain rates over 4 years are shown as open (flank) and closed (divide) circles in Figure 4; the vertical bars indicate the effective gauge length. The horizontal dashed lines indicate uncertainties in the data, which are ∼3 × 10−6 to 9 × 10−6 a−1, as reported by Reference ZumbergeZumberge and others (2002).
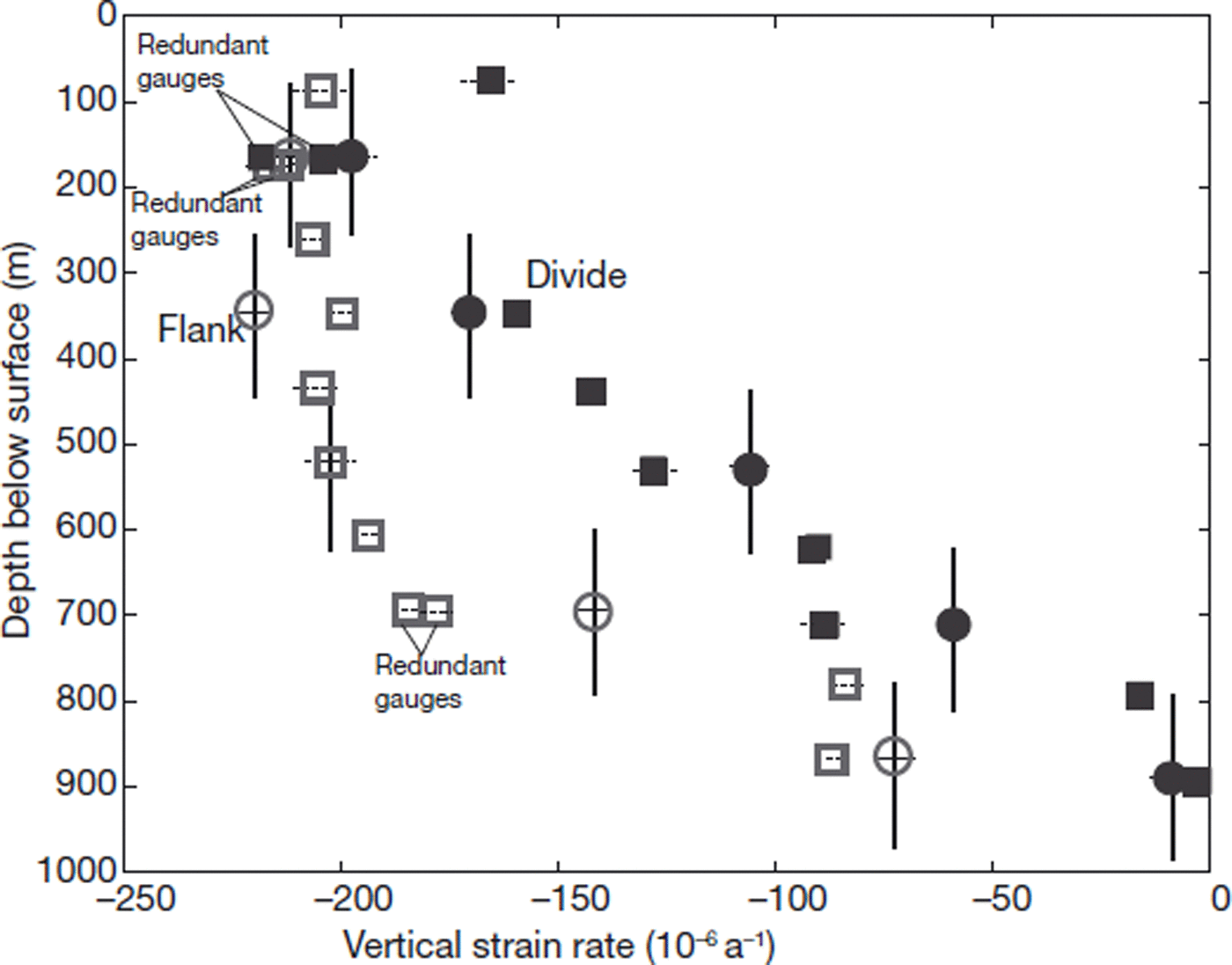
Fig. 4. Strain-rate data from the wire (squares) and fiber-optic (circles) instruments. The open symbols are flank-site measurements, while the closed symbols are divide measurements. The vertical bars represent the effective gauge length over which the fiber-optic instruments measured average vertical strain. The 1σ errors for the wire instruments are shown by horizontal dotted lines. The 1σ errors for the fiber instruments are shown by horizontal solid lines; however, these are often as small as the symbol. The three pairs of data points marked ‘Redundant gauges’ are pairs of wire gauges installed within 1 m of each other to observe the local variability of the ice. The spread of these data may be caused by rheological inhomogeneities in the ice on a scale of <10 m.
Wire-resistance strain gauges
The fiber-optic instruments measure average strain over depth intervals greater than 100 m. We compared these average strains with point measurements using 1 m long wire-resistance gauges developed by Reference ElsbergElsberg and others (2004). These instruments use a Wheatstone bridge configuration with one active wire that is 1 m long and in contact with the ice. The three other wires in the bridge are coiled inside the gauge housing. Similar to the installation of the fiber gauges, the active wires in these gauges were installed under tension to allow measurement of vertical compressive strains. A data logger on the surface recorded the voltage balance of the bridge every 30–90 min almost continuously for 4 years. Thus, as the fiber instruments measure strain rates averaged over time and space, the wire instruments are essentially point measurements of strain rate logged continuously. Although they exhibited some intriguing small-scale time-dependent fluctuations (Reference ElsbergElsberg and others, 2004), in this analysis we used the average strain rate over the 4 year experiment (after initial transients had dissipated). These data are shown as squares in Figure 4. The individual instrument uncertainties for the raw data are between 5 × 10−6 and 10 × 10−6 a−1. The data and uncertainties shown in the figure combine these instrument raw data with correction factors necessary for interpretation of the data as discussed below.
As these instruments measure strain over a short distance, they are sensitive to inhomogeneities in the ice on scales of decimeters to 10 m. The instruments may measure small-scale flow unrepresentative of larger ice volumes, particularly where there are large spatial gradients in ice properties. At three locations, we installed two instruments at the same depth (and within 10 m of each other horizontally) to observe this variability in the strain data. The results for each pair of redundant instruments are shown in Figure 4. Observations from thin sections suggest that structural variability exists (Reference DiPrinzio, Wilen, Alley, Fitzpatrick, Spencer and GowDiPrinzio and others, 2005), but this variability is difficult to quantify with the sparse data.
Three corrections are applied to the wire data. First, the correction for horizontal shear (appendix C of Reference PettitPettit, 2003) applies to the wires as well as the fibers; in general, this correction is larger for the wire instruments than it is for the fiber instruments. The difference in correction arises because most of the horizontal shearing occurs in the deeper part of the ice sheet. For the fiber cables, therefore, a small percentage of the total effective gauge length is affected, while for the wire instruments the entire instrument may be affected by shearing. The largest corrections correspond to the deepest four wire instruments.
Second, the raw wire strain-rate data show a systematic offset of ∼12% at the divide and 16% at the flank relative to the fiber strain-rate data. According to Reference ElsbergElsberg and others (2004), this is a result of unexpected coupling between the wire anchor and the bridge casing during the freeze-in process, that may increase the effective gauge length by 5–25%. In our study, we used their adjusted data. We assumed a random error in this correction factor of 2% and added it (in quadrature) to the overall uncertainty for the instruments.
The final correction involves only the uppermost wire and fiber instruments. Near the surface, the firn undergoes densification. Most, but not all, of this densification happens in the upper 80 m. Therefore, the wire instruments installed at 80 m depth recorded some measurable vertical-strain rate due to densification of the ice. Densification also affected the uppermost fiber gauge, but the error introduced is much smaller, because only the densification below 80 m affects the fiber-length measurement and that is small compared to the effective gauge length.
We calculated the rate of densification from a density profile measured by J. Fitzpatrick (personal communication, 2003) and the depth/age scale determined by Reference TaylorTaylor and others (2004b) using:
where ρ is the density at depth z and dz/dt is the downward velocity derived from the depth/age scale assuming steady state. To find the correction factor for each instrument, we averaged strain rate due to densification along the length of each gauge. This correction factor has a stronger gradient near the surface than it has deeper in the ice column. At 80 m depth (the depth of the highest gauge) it is also most sensitive to errors in the density profile, the depth/age scale and the depth and effective gauge length of the instrument. In Figure 4 we present the corrected data. It appears, however, that this calculation may have over-corrected the 80 m wire gauge at the divide by 20–30 × 10−6 a−1. It may also have over-corrected the flank 170 m instrument, but by a smaller amount. Because of the large uncertainty associated with this correction factor, we have given less weight to these data points in the inverse problem.
The Inverse Problem
Our goal in this study was to determine the crossover stress, k (Equation (5)), the effective deviatoric stress below which linear deformation mechanisms dominate. We modeled the stress field and strain-rate field in a cross section across Siple Dome, using geometry, accumulation rate, temperature field and ice properties as inputs. The ice flow law used in the model has an isotropic component and an anisotropic component. The isotropic component of the flow law includes a linear term and a nonlinear term. The anisotropic component describes the effect of vertically oriented c-axis crystal fabric.
Our model has four unknown flow-law parameters: the crossover stress, k, and three isotropic enhancement factors, one for each of the three layers shown in Figure 3 (Holocene ice, Ice Age ice and recrystallized ice). The crossover stress, k, determines the relative importance of the linear term in the flow law. As shown by Reference Pettit and WaddingtonPettit and Waddington (2003), the relative importance of the linear term influences the difference between the shape of the profiles of vertical-strain rate at the divide and the flank. If k ≪ τ eff, nonlinear mechanisms dominate deformation and the divide verticalstrain-rate profile has stronger curvature than the flank profile. If k ≫ τ eff, linear mechanisms dominate deformation and the divide and flank profiles have similar curvature. In this analysis, we assume k is spatially uniform, although, as defined in Equation (5), it can vary with temperature and other ice properties (Reference Pettit and WaddingtonPettit and Waddington, 2003).
Based on past studies of bulk ice properties (e.g. Reference PatersonPaterson, 1991), we expected that each layer shown in Figure 3 would have distinct rheological characteristics. Therefore, we defined a bulk isotropic flow-law coefficient, Γo in Equation (3), as EjA o (j = 1, 2, 3), where E 1 is for Holocene ice, E 2 is for Ice Age ice and E 3 is for recrystallized ice.
We used the value of A o (for clean, isotropic Holocene ice) recommended by Reference PatersonPaterson (1994), based on data from multiple studies. If the physical processes are well implemented in our model, and if Paterson’s average A o is a good representation of Holocene ice, then we would expect our model to fit the data best when E 1 ∼ 1. Although we term these flow-law coefficients ‘isotropic’, they do include some residual effects of crystal fabric that are not captured by the description of anisotropy within our flow law.
We determined the best values for these four flow-law parameters by matching the vertical-strain-rate profiles calculated by the model to the vertical-strain-rate profiles measured by the fiber-optic and wire instruments. We systematically explored the four-dimensional parameter space, beginning with a coarse grid that spanned the range expected for each parameter, and finishing with a fine grid to narrow in on the best-fitting parameter set.
We constrained the modeled vertical-strain-rate profiles to be smooth and to fit the observations to within the uncertainties. We chose a smooth vertical-strain-rate profile because in a real ice sheet strong gradients in the strain rate are moderated by redistribution of the stresses. In the tradeoff between these constraints, we relaxed the smoothness criteria to allow for some curvature where the strongest gradients in ice properties exist.
We chose the parameter set that best fitted the data to within the measurement uncertainties through minimizing a misfit function:
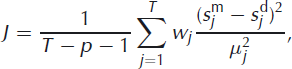
where T is the number of data points, p is the number of free model parameters (in this case p = 4) and ![]() and
and ![]() are the measured vertical-strain-rate data points and the corresponding model outputs, respectively. In this function, μj
are the uncertainties in the strain-rate measurements and wj
is a weighting function designed to give more weight to important data. Because the wire gauges are more sensitive to heterogeneity in the ice on a length scale much smaller than the finite-element mesh, we weighed these data less than the fiber data, which represent an average over a length scale larger than our mesh: we gave the wire data one-half the weight of the fiber data. Although we tested several weighting functions, we ultimately used wj
= 0 for the uppermost wire strain gauges because the firn densification process resulted in large variability that was difficult to quantify and was not related to ice properties. In this formulation, a misfit index less than 1 fits the data within 1 standard deviation of the instrument uncertainty. Because of the inherent heterogeneity of the ice on a scale smaller than our finite-element mesh, which our model is not capable of predicting, we do not expect our model to fit the data to this degree.
are the measured vertical-strain-rate data points and the corresponding model outputs, respectively. In this function, μj
are the uncertainties in the strain-rate measurements and wj
is a weighting function designed to give more weight to important data. Because the wire gauges are more sensitive to heterogeneity in the ice on a length scale much smaller than the finite-element mesh, we weighed these data less than the fiber data, which represent an average over a length scale larger than our mesh: we gave the wire data one-half the weight of the fiber data. Although we tested several weighting functions, we ultimately used wj
= 0 for the uppermost wire strain gauges because the firn densification process resulted in large variability that was difficult to quantify and was not related to ice properties. In this formulation, a misfit index less than 1 fits the data within 1 standard deviation of the instrument uncertainty. Because of the inherent heterogeneity of the ice on a scale smaller than our finite-element mesh, which our model is not capable of predicting, we do not expect our model to fit the data to this degree.
The observations that we used in the misfit calculation included not only the measured strain rates from both the fiber-optic and wire instruments, but also the difference in strain rate between the divide and the flank sites. It is this difference that is sensitive to the linear term in the flow law (Reference Waddington, Raymond, Morse and HarrisonWaddington and others, 1996; Reference Pettit and WaddingtonPettit and Waddington, 2003). The calculated horizontal velocities at the surface are much less sensitive to the ice rheological properties at depth in the ice sheet than is the strain-rate profile. We included velocity measurements in some misfit calculations, but not in those presented here; their impact on the choice of best models was negligible.
Results and Discussion
Figure 5 shows the misfit index for the four-dimensional parameter space in the region near the best-fitting parameter set. Each row of plots has a different crossover stress, k, and each column has a different Holocene enhancement factor, E 1. Each small plot is J(E 2,E 3), showing the misfit as a function of the Ice Age ice enhancement factor, E 2, and the recrystallized ice enhancement factor, E 3. Black regions indicate the best-fitting parameter sets, dark shading indicates parameter sets that fit the data less well, lightly shaded areas indicate parameter sets which do not fit the data, and white regions reflect no data.

Fig. 5. Misfit index describing the model results for the four-dimensional parameter space. Although we have explored the parameter space outside the range shown here, we show only the region near the best solution. Each row of plots has a different crossover stress (from 0.16 to 0.21 bar). Each column has a different Holocene enhancement factor, E 1 (1.2 to 1.8). Each small plot has the same values of the Ice Age enhancement factor, E 2 (0.07 to 0.22), on the horizontal axis and the recrystallized-ice enhancement factor, E 3 (0.05 to 0.25), on the vertical axis. Darker shading indicates better-fitting parameter sets. Lighter shading indicates parameter sets which do not fit the data well. White indicates no data.
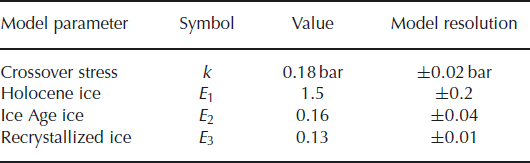
The pattern of dark areas shows the resolution of our model. With the uncertainties in our model, all of the parameter sets that produce misfit indices less than 2 are valid, in that they fit the data to within 2 standard deviations. In Table 1, we chose values for the best-fitting parameter set (identified by a star in Fig. 5), which is in the center of the cluster of valid parameter sets, on which to focus our discussion. It is important to reiterate here that this model accounts for deformation due to preferred crystal orientation explicitly using the cone angle. Therefore, E 1, E 2 and E 3 are isotropic enhancement factors that reflect softening or stiffening due to impurities, crystal size or other related effects. The enhancement factors only include the effect of crystal fabric as residuals not captured in our flow law. Because deformation rates in the shallower ice depend on the deformation rates in the deeper ice, the three enhancement factors are not independent in their effect on the misfit index. This interdependence explains the shape of the shaded area in the J(E 2, E 3) plots. For example, increasing the stiffness of the Ice Age ice layer, E 2, transmits more shear stress to the deeper recrystallized ice. In order to fit the data, therefore, the value of E 3 must also change to accommodate this higher stress yet keep the deformation rates within the measured values.
Table 1. Best-fit solution for the four model parameters. The rightmost column shows the range for which the misfit function is <2
The flank and divide strain-rate profiles for this best-fitting parameter set are shown in Figure 6. The profiles are generally smooth where there are no strong gradients in ice properties, but have strong curvature at the depths corresponding to the strong gradients in ice properties and the strong gradients in measurements of vertical-strain rate.
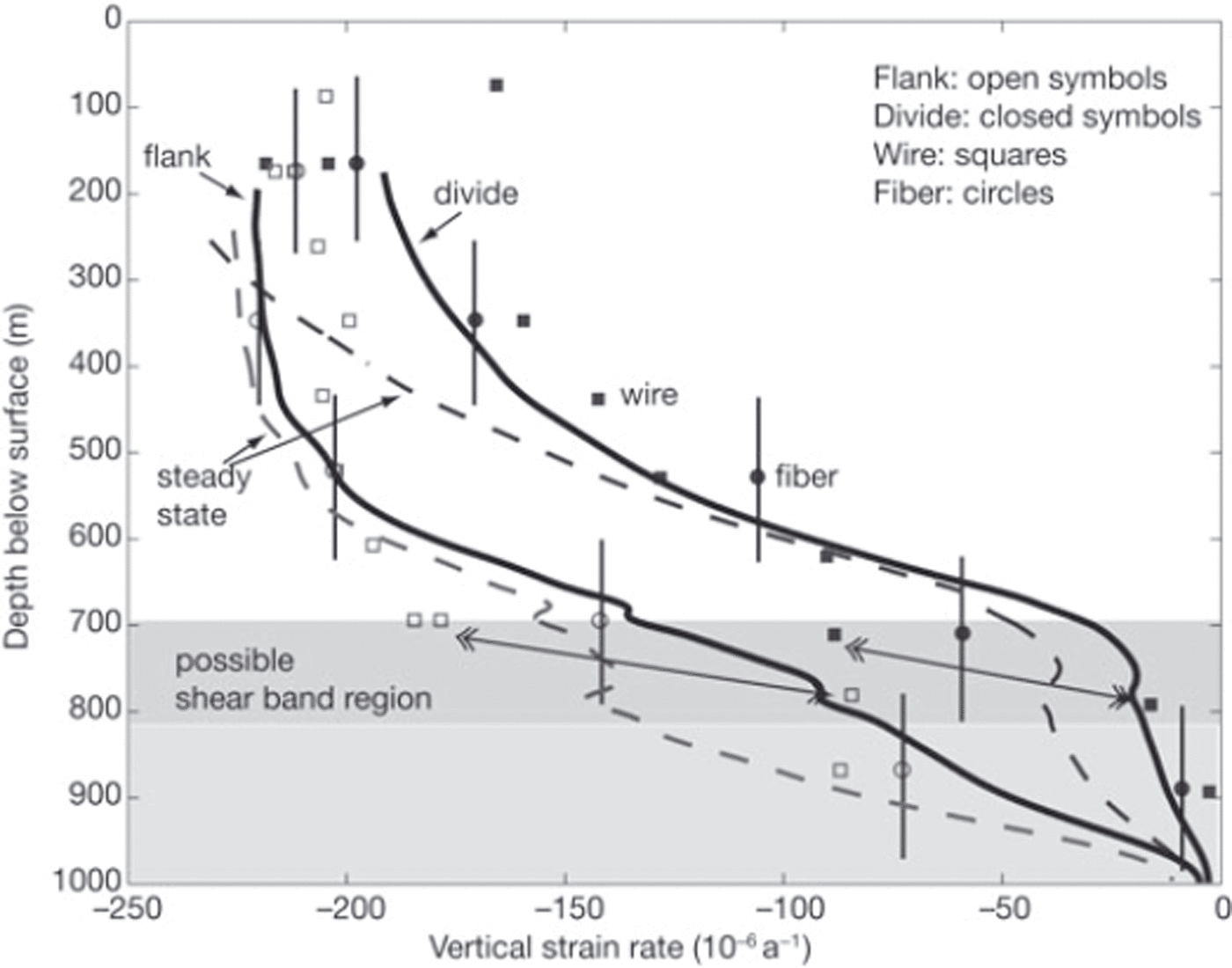
Fig. 6. Flank and divide strain-rate profiles for solution shown in Table 1. The data are from Figure 4. The thick solid curves are the best-fitting model results. The thin dashed curves result from the same solution parameters but the model was allowed to evolve until the surface profile was in balance with the accumulation rate derived from the radar internal layers. The three layers within the model are shown with the same shading as Figure 3. Within the Ice Age ice layer, the double-headed arrows show depths where the wire instruments indicate a very strong gradient in vertical-strain rate. This vertical gradient may signify the existence of a shear band.
Through most of the depth of the ice sheet, each profile follows the pattern expressed by the fiber data (vertical bars). The modeled profiles fit the wire data less well, most likely due to small-scale (<100 m) inhomogeneities in the ice. This conclusion is supported by the observation that the largest disagreements between the model and the wire data occur within the band of tight fabric (700–800 m deep), where the ice core shows variations in properties over short depth scales (<10 m). At both the flank and divide sites, there is a strong gradient in measured strain rate between the instruments placed ∼800 m deep and the instruments placed closer to 700 m deep. This strong gradient may signify the existence of a shear band. The effect of this shear band does not appear in the fiber data because the fiber data represent averages over spatial scales twice as large as the scale of the shear band.
In Figure 7 we show the sensitivity of the model to each unknown parameter, providing an indication of the influence of each parameter on the flow. In each plot, the heavy solid curves are the modeled strain-rate profiles for the best-fitting parameter set (Table 1). The dashed curves are the strain-rate profiles produced by the same model except for a ∼20% increase in one parameter, and the thin solid curve shows the results for a ∼20% decrease in one model parameter. Figure 7a shows that the vertical-strain-rate profile at the divide is much more sensitive to the crossover stress than is the flank profile: as k increases, the divide profile approaches the flank profile, while the flank profile changes little. For a divide in which τ eff ≪ k, the linear term in the flow law is relatively large; there is little difference between the divide and flank vertical-strain-rate profiles, and no arch develops in the isochrones (Reference Pettit and WaddingtonPettit and Waddington, 2003). Figure 7b shows that the upper part of the vertical-strain-rate profile (that within the Holocene ice layer) is most sensitive to changes in the Holocene ice enhancement factor, E 1. As shown in Figure 7c, the strain-rate profiles at all depths are least sensitive to the Ice Age ice enhancement factor, probably because that layer is thin relative to the rest of the ice sheet (∼10% of the thickness of the ice sheet) and it has a strong vertically oriented fabric, which stiffens the ice in the vertical direction and results in a small contribution from this layer to the total vertical strain the ice sheet experiences. The flank vertical-strain-rate profile is more sensitive than the divide to the softness of the deepest ice (Fig. 7d). This is a result of the much lower deviatoric compressive stress at the divide compared to the flank due to the nonlinearity of the flow law.
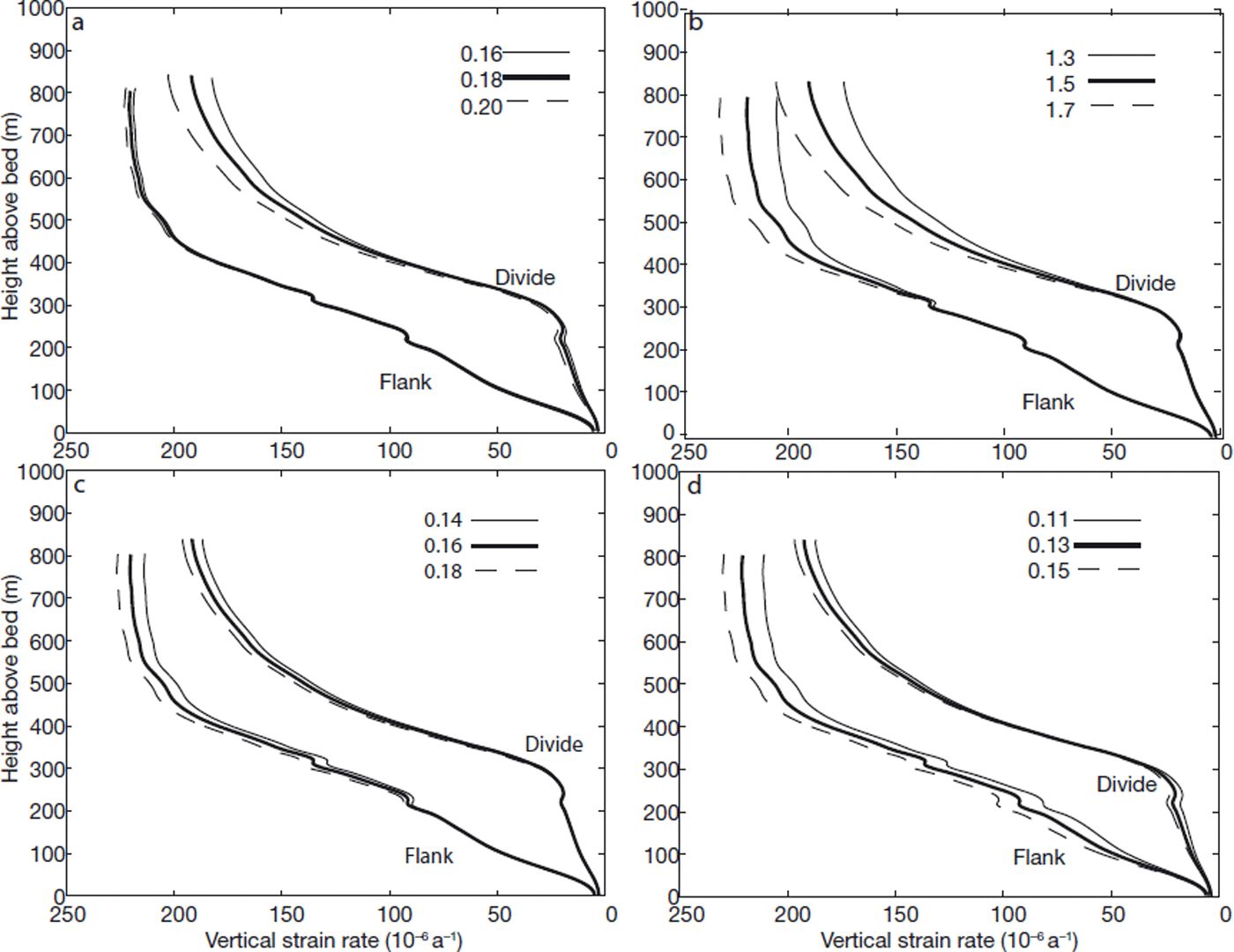
Fig. 7. Sensitivity of the model to each of the four unknown parameters. (a) The crossover stress, k. (b) Holocene ice isotropic enhancement factor, E 1. (c) Ice Age ice isotropic enhancement factor, E 2. (d) Recrystallized ice isotropic enhancement factor, E 3. Each plot shows the model output of vertical-strain rate as a function of depth for the divide and flank sites. The heavy solid curve is the model results using the best-fitting parameter set. The thin solid curve is a decrease in one parameter by ∼20%. The dashed curve shows the results from an increase in one parameter by ∼20%. Because the model is nonlinear, these are local sensitivities in the region near the best-fitting parameter set.
Considering these sensitivities, we can assess the ability of the model to predict the real strain-rate observations. Near the bed at the divide, the model predicts deformation rates larger than the measured values, while at the flank it predicts deformation rates smaller than the measured values. Decreasing the isotropic enhancement factor for the recrystallized ice layer, E 3, results in stiffer ice and smaller deformation rates at the divide, better fitting the divide data, but the model then fails to fit the data at depth at the flank or in the upper layers. This failure to fit the divide data and the flank data with the same model may be a result of our assumption that the measured ice fabric can be propagated downstream from the divide unchanged. An increase in magnitude of the effect of crystal fabric may be required for the model to fit all the data. The effect of crystal fabric leads to stiffer ice in the bottom layers at the divide (which is primarily experiencing vertical compression) and softer ice in the bottom layers at the flank (which is primarily experiencing horizontal shear). A strengthening of this effect could be driven by a strengthening of the crystal fabric (decreasing cone angle) as ice moves toward the flank. Such a strengthening of the fabric could occur as a result of the increase in bed-parallel shear stress and increasing shear strain with distance from the divide. Stronger flank fabric relative to the divide fabric will increase the difference in strain rate between the flank and the divide in the lowest layers and possibly result in a better-fitting model.
The different enhancement factors that we find in this analysis suggest a different mix of grain-scale deformation mechanisms for each ice type. A Holocene enhancement factor of E 1 = 1.5 implies that the upper part of the ice sheet is ∼50% softer than average Holocene ice as reviewed by Reference PatersonPaterson (1994). This discrepancy may result from the possibility that Paterson’s dataset includes data from ice that is not isotropic. The lower two layers have enhancements much less than 1, implying that the ice at depth is much stiffer than Holocene ice. The Ice Age ice in our best-fitting model is six times stiffer than the Holocene ice, yet the model still fails to fully capture the small vertical-strain rates thatwe measured. Reference Thorsteinsson, Waddington, Taylor, Alley and BlankenshipThorsteinsson and others (1999) separated the enhancement in bed-parallel shear deformation due to crystal fabric from that due to isotropic processes for the Dye 3 (Greenland) ice core (a flank site) and found that the Ice Age ice needed additional softening in bed-parallel shear to fit the borehole tilt data. Although these results are for different ice sheets, both model/data mismatches can be reduced by strengthening the effect of crystal fabric (making the ice softer in horizontal shear to match the Dye 3 data and stiffer in vertical compression to match the Siple Dome data). An isotropic process could not improve the model/data match at both sites. This suggests that either both models are underestimating the effect of crystal fabric on flow or that a different process may be acting to enhance the effect of crystal fabric.
In the deepest recrystallized ice our model requires a stiffness more than seven times that of Holocene ice to match the measured flank data, and yet the model still fails to capture the low vertical-strain rates at the divide. In this layer, too, another process must be acting to stiffen the ice. One possibility is that the large interlocking crystals in this ice may impede the migration of grain boundaries, creating ‘drag’ in the flow.
With only four adjustable parameters in our model, we are limited in how much detail we can infer about the flow. A more complete analysis would allow E(z) to be a function of depth and to be further split into a linear-term enhancement factor and a nonlinear-term enhancement factor. Resolving these functions, however, would require a much more extensive dataset.
In this analysis, the finite-element model calculates modern deformation rates based on present geometry and measured ice properties. This calculation does not involve evolution. Nor does it explicitly rely on an assumption of steady state. It is useful, however, to run the model using the best-fitting parameter set (Table 1) through time to allow the surface to evolve until the flow is in balance with the accumulation-rate pattern. The thin dashed curves in Figure 6 show this steady-state model result, and Figure 8 shows the corresponding horizontal- and vertical-velocity fields. The curves in Figure 6 are measurably different between the two models, particularly in the upper part of the ice sheet. This mismatch may imply a weakness in our assumptions that the dome is not thinning or thickening, that the accumulation pattern is realistic and unchanging through time, and that the divide flows primarily in plane strain (the first two assumptions apply only to the time-evolved version of the model, the third applies to both versions of the model). Without further data we cannot determine the dominant source of weakness in these assumptions.
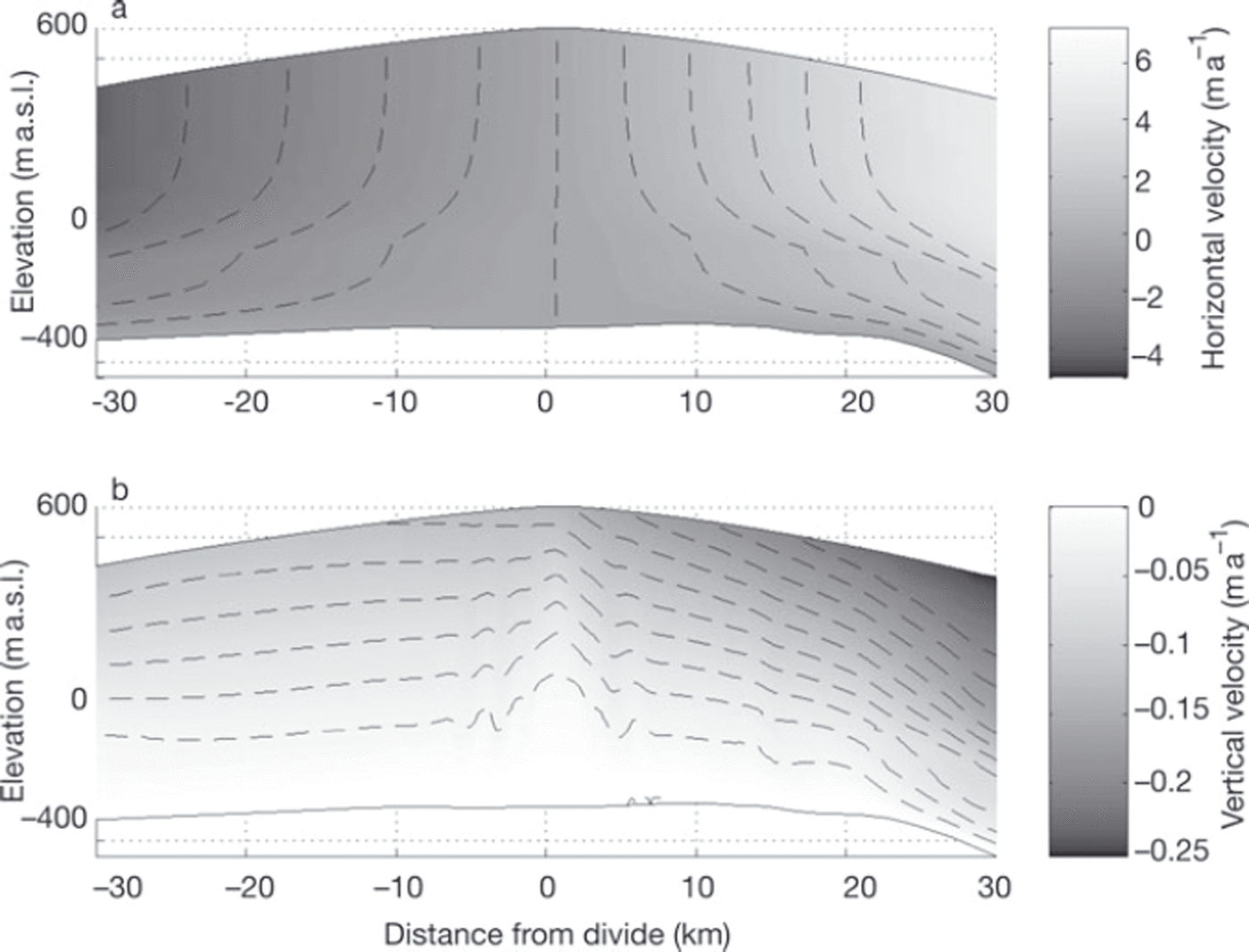
Fig. 8. Dashed curves show horizontal- (a) and vertical-velocity fields (b) from the steady-state solution using the best-fitting parameter set (Table 1). Bindschadler Ice Stream is to the right and Kamb Ice Stream is to the left. The dashed curves are velocity contours. Note the kink in the horizontal-velocity contours, which results from the false-bed effect.
Within the horizontal-velocity field (Fig. 8), the contours of equal velocity (dashed curves) each have a ‘kink’ at ∼700 m deep. This kink represents concentrated bed-parallel shearing in the Ice Age ice, due to strong preferred orientation of crystals. We call this concentrated shearing the ‘false-bed effect’ because a typical horizontal-velocity profile for an ice sheet concentrates shearing near the bed. At Siple Dome, however, the surface has adjusted to the presence of the soft layer, so that ice below the false bed experiences less bed-parallel shear stress and, therefore, deforms less than basal ice would in an ice sheet without a layer of highly oriented ice. Reference Russell-Head and BuddRussell-Head and Budd (1979) observed a similar effect at Law Dome, Antarctica, and Reference DurandDurand and others (2007) suggested the Dome C (Antarctica) flow pattern may be affected similarly by layered ice of different rheological characteristics.
In Figure 9 we plot the isochrones from the model in which we assume that Siple Dome has been in steady state since the deepest layer was deposited. These modeled layers are overlaid on the radar image of isochrones for Siple Dome. The history of Siple Dome is reflected in its internal-layer structure, so we expect some mismatch when comparing observed isochrones with modeled isochrones. The real history of Siple Dome includes migration of the divide (Reference Nereson, Raymond, Waddington and JacobelNereson and others, 1998a) and variation in past accumulation rates and surface elevations (Reference WaddingtonWaddington and others, 2005). Acknowledging this non-steady-state behavior, it is still valuable to compare the isochrones predicted by the steady-state model with those observed. In the upper half of the ice sheet, the arch in the predicted isochrones is generally broader, but has a similar amplitude to the observed arch. The observed layers are steeper on the northward side than the modeled steady-state layers. Reference Nereson and WaddingtonNereson and Waddington (2002) predicted this isochrone steepening in their study of migrating divides. At mid-depth, we have traced one of these layers in gray to show that the arch in the modeled isochrone has a significantly larger amplitude than the arch in the radar-imaged isochrone. One possible reason for this mismatch is that over the history of Siple Dome, the effect of crystal fabric has changed, most likely due to a change in the magnitude and shape of the cone-angle profile. Since the Ice Age, the gradient in cone angle at the Ice Age/Holocene transition has strengthened and the transition has moved deeper in the ice column.
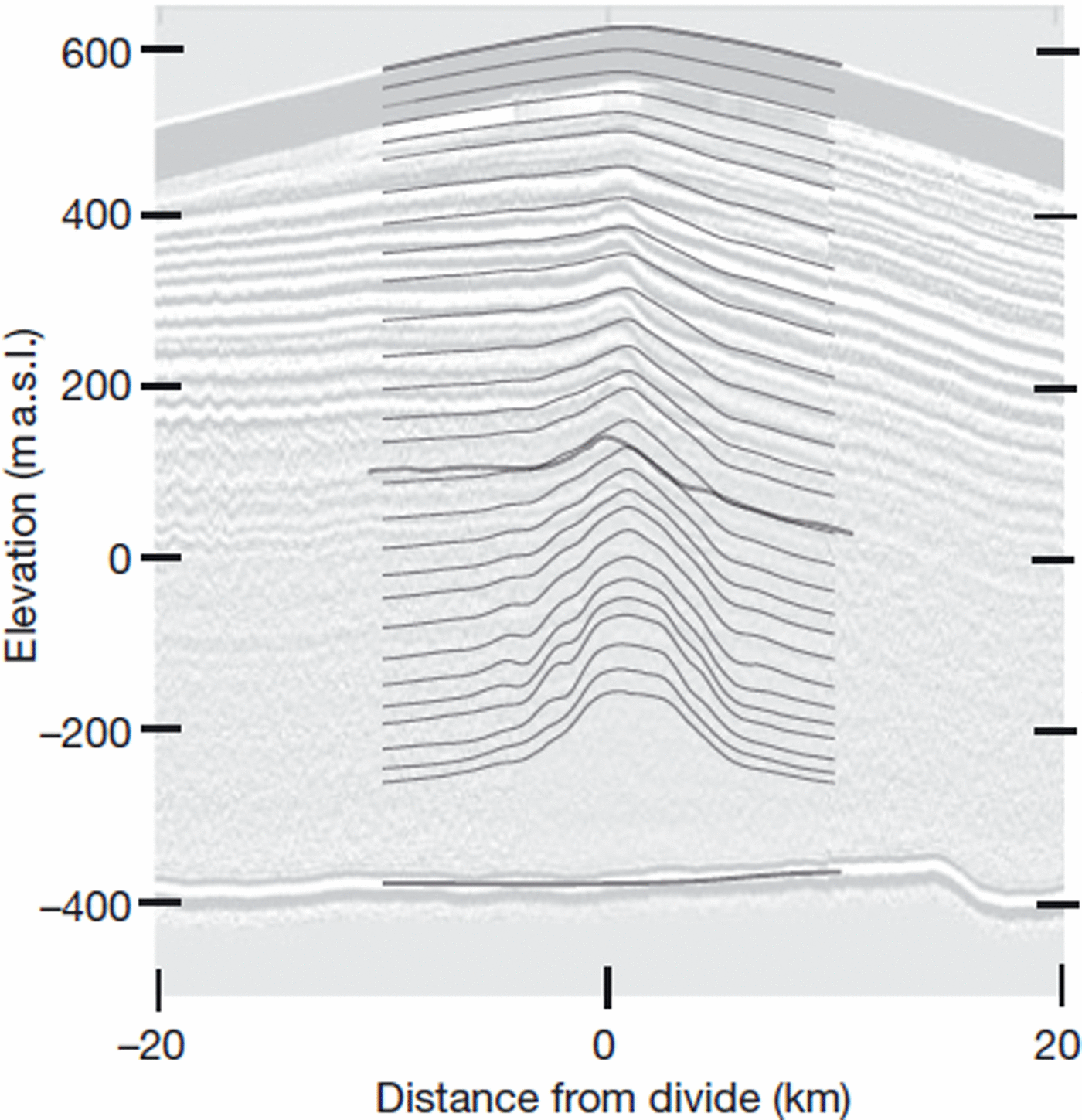
Fig. 9. Isochrones inferred for a steady-state ice sheet, using the best-fitting model parameters (Fig. 6) are overlaid on the ice-penetrating radar data of Reference Raymond, Nereson, Gades, Conway, Jacobel and ScambosRaymond and others (1995). One observed layer at mid-depth is traced as a slightly bolder line for comparison with the modeled layers.
The deeper layers, which will show the greatest effect of crystal fabric (Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others, 2007), were not detected continuously by radar and therefore cannot be compared.
Conclusions
The results of this analysis provide insight into the deformation of ice at low deviatoric stress. Reference Pettit and WaddingtonPettit and Waddington (2003) isolated the effect of a shift in flow mechanism at low deviatoric stress for an idealized divide based on the geometry of Siple Dome. Our initial goal in this study was to build on that work to determine the importance of a linear deformation mechanism in flow near a realistic ice divide, incorporating many measurements of ice properties and dynamics behavior at Siple Dome. This goal necessitated incorporating a flow law that includes the effect of crystal fabric, which Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others (2007) isolated for an idealized divide, again using Siple Dome as the basis of the model geometry.
We found that the flow pattern at Siple Dome (as defined by vertical-strain-rate measurements) does show influences of both linear and nonlinear deformation mechanisms. We found a crossover stress of k = 0.18 ± 0.02 bar best fits the observations at Siple Dome. Because the crossover stress is an intrinsic ice property, not specific to Siple Dome, this result implies that flow in ice sheets with a characteristic stress, ![]() (as defined by Reference Pettit and WaddingtonPettit and Waddington, 2003), less than or similar to 0.18 bar will be affected by linear deformation mechanisms.
(as defined by Reference Pettit and WaddingtonPettit and Waddington, 2003), less than or similar to 0.18 bar will be affected by linear deformation mechanisms.
A second conclusion from this work is that the flow pattern at Siple Dome is strongly dependent on the crystal fabric. A band of highly oriented fabric and small crystals exists at Siple Dome between ∼700 and 800 m depth. This band of highly oriented fabric affects the overall flow pattern in the ice sheet by concentrating bed-parallel shear several hundred meters above the bed, an effect we call the false-bed effect. Below 800 m the temperature exceeds −10°C and the ice is recrystallized, with large crystals and a broad single-maximum c-axis fabric that impedes easy bed-parallel shear in the deepest ice. The shift in fabric at ∼700 m depth occurs at the same depth as the Ice Age/Holocene transition. The band of highly oriented crystals consists entirely of Ice Age ice. This suggests there may be a strong correlation between fabric development and climate history.
Acknowledgements
We thank K. Taylor and all others who worked on Siple Dome for allowing us to use data from many different aspects of the deep ice core (especially L. Wilen, G. Lamorey, P. Mayewski and H. Engelhardt). We thank C. Raymond and H. Conway for comments and suggestions during the analysis stage. This work was funded by US National Science Foundation (NSF) grants OPP9615417, OPP0083132 and OPP0636996 to Waddington, OPP9615502 to Harrison, OPP9615454 to Zumberge and OPP 0636795 and an NSF Graduate Fellowship to Pettit.














