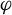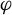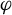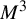1 Introduction
In this article, we adopt a homotopical approach in the investigation of non-singular Morse–Smale (NMS) flows on closed 3-manifolds by considering the unfolding of a spectral sequence of an NMS chain complex associated to it. Similar questions have been considered within other classes of dynamical systems, such as Morse–Smale flows with no periodic orbits [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3, Reference Bertolim, Lima, Mello, de Rezende and da Silveira4, Reference Lima, Mazoli Neto, de Rezende and da Silveira15], Morse–Bott flows [Reference Lima and de Rezende14], gradient flows associated to circle-valued Morse functions [Reference Lima, Mazoli Neto, de Rezende and da Silveira15] and Gutierrez–Sotomayor flows [Reference Lima, Raminelli and de Rezende16].
Based on results of Franks established in [Reference Franks9], we prove algebraic-dynamical correspondence theorems between the cancellations and reductions of periodic orbits in an NMS flow
![]() $\varphi $
and the differentials of a spectral sequence of a filtered NMS chain complex associated to
$\varphi $
and the differentials of a spectral sequence of a filtered NMS chain complex associated to
![]() $\varphi $
.
$\varphi $
.
Let
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
be two periodic orbits of an NMS flow
$\gamma _{k-1}$
be two periodic orbits of an NMS flow
![]() $\varphi $
, of indices k and
$\varphi $
, of indices k and
![]() $k-1$
, respectively. The orbits
$k-1$
, respectively. The orbits
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
can be cancelled if there exists an NMS flow
$\gamma _{k-1}$
can be cancelled if there exists an NMS flow
![]() ${\varphi }'$
in M that coincides with
${\varphi }'$
in M that coincides with
![]() $\varphi $
outside a neighborhood U of
$\varphi $
outside a neighborhood U of
![]() $W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and
$W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and
![]() ${\varphi }'$
has empty chain recurrent set in U. The orbits
${\varphi }'$
has empty chain recurrent set in U. The orbits
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
can be reduced if there exists an NMS flow
$\gamma _{k-1}$
can be reduced if there exists an NMS flow
![]() ${\varphi }'$
on M that coincides with
${\varphi }'$
on M that coincides with
![]() $\varphi $
outside a neighborhood U of
$\varphi $
outside a neighborhood U of
![]() $W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and the chain recurrent set of
$W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and the chain recurrent set of
![]() ${\varphi }'$
restricted to U is a unique periodic orbit
${\varphi }'$
restricted to U is a unique periodic orbit
![]() $\gamma '$
. More specifically, if
$\gamma '$
. More specifically, if
![]() $k=2$
,
$k=2$
,
![]() $\gamma '$
is a repelling periodic orbit and if
$\gamma '$
is a repelling periodic orbit and if
![]() $k=1$
,
$k=1$
,
![]() $\gamma '$
is an attracting periodic orbit. Local cancellations and reductions are described in more detail in §3.2. See Figure 1.
$\gamma '$
is an attracting periodic orbit. Local cancellations and reductions are described in more detail in §3.2. See Figure 1.

Figure 1 Flow cancellation and reduction in
![]() $S^3$
.
$S^3$
.
Let
![]() $ \Sigma (M^3)$
be the set of NMS flows on an orientable closed
$ \Sigma (M^3)$
be the set of NMS flows on an orientable closed
![]() $3$
-manifold
$3$
-manifold
![]() $M^3$
without heteroclinic trajectories between saddle periodic orbits. It follows that flows in
$M^3$
without heteroclinic trajectories between saddle periodic orbits. It follows that flows in
![]() $\Sigma (M^3)$
that undergo cancellations and reductions remain in
$\Sigma (M^3)$
that undergo cancellations and reductions remain in
![]() $\Sigma (M^3)$
.
$\Sigma (M^3)$
.
We say that
![]() $\varphi \in \Sigma (M^3)$
is a core flow if each inessential connection between two consecutive periodic orbits is part of a double inessential connection. Equivalently,
$\varphi \in \Sigma (M^3)$
is a core flow if each inessential connection between two consecutive periodic orbits is part of a double inessential connection. Equivalently,
![]() $\varphi \in \Sigma (M^3)$
is a core flow if pairs of consecutive periodic orbits in
$\varphi \in \Sigma (M^3)$
is a core flow if pairs of consecutive periodic orbits in
![]() $\varphi $
cannot be cancelled or reduced. See §3 for more details.
$\varphi $
cannot be cancelled or reduced. See §3 for more details.
Given
![]() $\varphi \in \Sigma (M^3)$
, one can associate it to a chain complex
$\varphi \in \Sigma (M^3)$
, one can associate it to a chain complex
![]() $(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
called an NMS chain complex, which will be defined in §3. In this work, we consider flows in
$(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
called an NMS chain complex, which will be defined in §3. In this work, we consider flows in
![]() $\Sigma (M^3)$
whose differentials
$\Sigma (M^3)$
whose differentials
![]() $\Delta ^{\mathrm {NMS}}$
are totally unimodular (TU) matrices, which is an essential technical hypothesis for obtaining cancellation results. Also, as a consequence of this hypothesis,
$\Delta ^{\mathrm {NMS}}$
are totally unimodular (TU) matrices, which is an essential technical hypothesis for obtaining cancellation results. Also, as a consequence of this hypothesis,
![]() $M^3$
is torsion free. See §3. Let
$M^3$
is torsion free. See §3. Let
One defines in
![]() $\Sigma (M^3)$
a partial order relation
$\Sigma (M^3)$
a partial order relation
![]() $<$
as follows: given
$<$
as follows: given
![]() $\varphi ,\phi \in \Sigma (M^3)$
,
$\varphi ,\phi \in \Sigma (M^3)$
,
![]() $\varphi <\phi $
if
$\varphi <\phi $
if
![]() $\phi $
is obtained from
$\phi $
is obtained from
![]() $\varphi $
by a cancellation or a reduction of a pair of periodic orbits and is extended by transitivity . Every totally ordered subset of
$\varphi $
by a cancellation or a reduction of a pair of periodic orbits and is extended by transitivity . Every totally ordered subset of
![]() $\mathcal {S}$
has a maximal element, which is a core flow in
$\mathcal {S}$
has a maximal element, which is a core flow in
![]() $\Sigma (M^3)$
. The set
$\Sigma (M^3)$
. The set
![]() $\mathcal {S}_{\varphi }=\{\phi \in \mathcal {S} \mid \varphi < \phi \}$
is the set of flows in
$\mathcal {S}_{\varphi }=\{\phi \in \mathcal {S} \mid \varphi < \phi \}$
is the set of flows in
![]() $\Sigma (M^3)$
that can be obtained from
$\Sigma (M^3)$
that can be obtained from
![]() $\varphi $
by performing cancellations and reductions of periodic orbits.
$\varphi $
by performing cancellations and reductions of periodic orbits.
Given
![]() $\varphi \in \mathcal {S}$
, the goal of this paper is to construct a family of NMS flows in
$\varphi \in \mathcal {S}$
, the goal of this paper is to construct a family of NMS flows in
![]() $\mathcal {S}_{\varphi }$
that takes
$\mathcal {S}_{\varphi }$
that takes
![]() $\varphi $
to a core flow through an algebraic procedure based on a spectral sequence analysis of the chain complex
$\varphi $
to a core flow through an algebraic procedure based on a spectral sequence analysis of the chain complex
![]() $(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
that is realized by using a spectral sequence algorithm. Spectral sequence algorithms are always filtration sensitive. Thus, the results obtained in §5 that use a spectral sequence algorithm will explore different types of filtrations as well as subclasses of
$(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
that is realized by using a spectral sequence algorithm. Spectral sequence algorithms are always filtration sensitive. Thus, the results obtained in §5 that use a spectral sequence algorithm will explore different types of filtrations as well as subclasses of
![]() $\mathcal {S}$
. Moreover, by requiring certain properties on the filtration and possibly on
$\mathcal {S}$
. Moreover, by requiring certain properties on the filtration and possibly on
![]() $M^3$
, the core flow
$M^3$
, the core flow
![]() $\varphi ^{\omega }$
reached by the algorithm minimizes the number of periodic orbits in
$\varphi ^{\omega }$
reached by the algorithm minimizes the number of periodic orbits in
![]() $\mathcal {S}_{\varphi }$
.
$\mathcal {S}_{\varphi }$
.
In §2, we present background material on NMS flows and an outline of the spectral sequence sweeping algorithm (SSSA).
In §3.1, we characterize topological-dynamical properties of the connections between periodic orbits for flows in
![]() $\Sigma (M^3)$
. These properties are essential for defining an NMS chain complex through a morsification process. In §3.2, this characterization is used to establish Theorems 3.11 and 3.12, which determine the conditions under which local cancellations and reductions of periodic orbits occur.
$\Sigma (M^3)$
. These properties are essential for defining an NMS chain complex through a morsification process. In §3.2, this characterization is used to establish Theorems 3.11 and 3.12, which determine the conditions under which local cancellations and reductions of periodic orbits occur.
In §4.1, we provide a proof that the SSSA applied to
![]() $\Delta ^{\tiny {NMS}}$
determines the modules
$\Delta ^{\tiny {NMS}}$
determines the modules
![]() $\mathcal {E}^r_p$
and induces the differentials
$\mathcal {E}^r_p$
and induces the differentials
![]() $d^r_p$
of the spectral sequence. This will be crucial in demonstrating the correspondence of the algebraic behavior of the modules and of the differentials in the spectral sequence with the dynamical cancellations and reductions of the periodic orbits of the flow. In §4.2, we prove Theorems 4.12 and 4.13 which characterize properties of the differentials of the spectral sequence under the hypothesis that the filtration is NMS-compatible.
$d^r_p$
of the spectral sequence. This will be crucial in demonstrating the correspondence of the algebraic behavior of the modules and of the differentials in the spectral sequence with the dynamical cancellations and reductions of the periodic orbits of the flow. In §4.2, we prove Theorems 4.12 and 4.13 which characterize properties of the differentials of the spectral sequence under the hypothesis that the filtration is NMS-compatible.
In §5, several algebraic-dynamical correspondence theorems are proved under different hypotheses either on the filtration or on the flow. In §5.1, by imposing restrictions on the filtration, we prove Theorems 5.1 and 5.2 which ensure that the unfolding of the spectral sequence provides a corresponding list of cancellations and reductions of periodic orbits that lead to a core flow. In §5.2, we consider flows in
![]() $\Sigma (M^3)$
that do not have pairs of cancelling periodic orbits. By requiring that the filtration satisfies the reduction ordering condition, Theorem 5.7 guarantees that the algebraic-dynamical correspondence obtained in Theorem 5.1 provides a corresponding list of reductions leading to a core flow that has the lowest number of attracting, saddle and repelling orbits in
$\Sigma (M^3)$
that do not have pairs of cancelling periodic orbits. By requiring that the filtration satisfies the reduction ordering condition, Theorem 5.7 guarantees that the algebraic-dynamical correspondence obtained in Theorem 5.1 provides a corresponding list of reductions leading to a core flow that has the lowest number of attracting, saddle and repelling orbits in
![]() $\mathcal {S}_{\varphi }$
. By removing the reduction ordering condition restriction, Theorem 5.8 still arrives at a core flow that does not need to have the minimal number of periodic orbits. In §5.3, we prove Theorem 5.15, which asserts that, given any flow
$\mathcal {S}_{\varphi }$
. By removing the reduction ordering condition restriction, Theorem 5.8 still arrives at a core flow that does not need to have the minimal number of periodic orbits. In §5.3, we prove Theorem 5.15, which asserts that, given any flow
![]() $\varphi \in \Sigma (S^3)$
whose differential is a TU matrix, all algebraic-dynamical correspondence theorems will lead to a core flow in
$\varphi \in \Sigma (S^3)$
whose differential is a TU matrix, all algebraic-dynamical correspondence theorems will lead to a core flow in
![]() $S_{\varphi }$
with exactly one repelling and one attracting periodic orbit.
$S_{\varphi }$
with exactly one repelling and one attracting periodic orbit.
Finally, in §6, we investigate NMS flows with heteroclinic connections between saddle periodic orbits. In Theorem 6.1, we prove a local reduction result between two saddle orbits.
2 Background
NMS flows have been studied by several authors who at first sought to answer the question of determining which manifolds admit these flows. Asimov proved in [Reference Asimov1] that, for a closed manifold
![]() $M^n$
,
$M^n$
,
![]() $n\neq 3$
, a necessary and sufficient condition is
$n\neq 3$
, a necessary and sufficient condition is
![]() $\chi (M)=0$
. This is not true in dimension three. Morgan proved in [Reference Morgan19] that an orientable closed prime 3-manifold admits an NMS flow if and only if it is a graph manifold. Moreover, as a result of Asimov’s and Morgan’s work, a manifold admits an NMS flow if and only if it admits a round handle decomposition. Later, Wada [Reference Wada23] characterized which classes of links could be realized as NMS flows on
$\chi (M)=0$
. This is not true in dimension three. Morgan proved in [Reference Morgan19] that an orientable closed prime 3-manifold admits an NMS flow if and only if it is a graph manifold. Moreover, as a result of Asimov’s and Morgan’s work, a manifold admits an NMS flow if and only if it admits a round handle decomposition. Later, Wada [Reference Wada23] characterized which classes of links could be realized as NMS flows on
![]() $S^3$
. Based on this work, Campos and Vindel [Reference Campos and Vindel5] found topological conditions for the existence of NMS flows on
$S^3$
. Based on this work, Campos and Vindel [Reference Campos and Vindel5] found topological conditions for the existence of NMS flows on
![]() $S^3$
without heteroclinic trajectories connecting saddle orbits. A nice survey on the classification of Morse–Smale systems, which includes NMS flows on 3-manifolds, can be found in [Reference Grines, Gurevich, Pochinka and Zhuzhoma12]. In [Reference Pochinka and Shubin20], Pochinka and Shubin characterize, up to topological equivalence, NMS flows on n-manifolds which admit exactly two periodic orbits. The aforementioned authors are mainly interested in the realization of NMS flows on closed manifolds.
$S^3$
without heteroclinic trajectories connecting saddle orbits. A nice survey on the classification of Morse–Smale systems, which includes NMS flows on 3-manifolds, can be found in [Reference Grines, Gurevich, Pochinka and Zhuzhoma12]. In [Reference Pochinka and Shubin20], Pochinka and Shubin characterize, up to topological equivalence, NMS flows on n-manifolds which admit exactly two periodic orbits. The aforementioned authors are mainly interested in the realization of NMS flows on closed manifolds.
Franks [Reference Franks8–Reference Franks11] adds a new perspective to this investigation by applying homotopical tools to the study of the structure of Morse–Smale flows on closed manifolds M by considering an associated CW-complex as well as the distinct attaching maps between cells and the connecting manifolds. Our work is inspired by this approach and will further bridge the gap between the topological-algebraic information of an NMS chain complex and the dynamics of an NMS flow.
In this section, we present some background material on NMS flows and provide a review of results on spectral sequences and on the sweeping algorithm introduced in [Reference Cornea, de Rezende and da Silveira6], which is used to recover the spectral sequence associated to a filtered chain complex.
2.1 NMS flows
A an NMS flow on an orientable smooth 3-manifold
![]() $M^3$
is a smooth flow with a chain recurrent set consisting of a finite number of hyperbolic periodic orbits that satisfies the transversality condition.
$M^3$
is a smooth flow with a chain recurrent set consisting of a finite number of hyperbolic periodic orbits that satisfies the transversality condition.
The index of a periodic orbit
![]() $\gamma $
is defined as the fiber dimension of the unstable bundle
$\gamma $
is defined as the fiber dimension of the unstable bundle
![]() $E^u$
over
$E^u$
over
![]() $\gamma $
. We say that a periodic orbit
$\gamma $
. We say that a periodic orbit
![]() $\gamma $
is untwisted if its unstable manifold
$\gamma $
is untwisted if its unstable manifold
![]() $W^u(\gamma )$
is orientable, that is,
$W^u(\gamma )$
is orientable, that is,
![]() $W^u(\gamma )$
is diffeomorphic to
$W^u(\gamma )$
is diffeomorphic to
![]() $S^1 \times \mathbb {R}^k$
, where k is the index of
$S^1 \times \mathbb {R}^k$
, where k is the index of
![]() $\gamma $
. The periodic orbit
$\gamma $
. The periodic orbit
![]() $\gamma $
of index k is twisted if its unstable manifold is non-orientable, that is,
$\gamma $
of index k is twisted if its unstable manifold is non-orientable, that is,
![]() $W^u(\gamma )$
is diffeomorphic to
$W^u(\gamma )$
is diffeomorphic to
![]() $\mathcal {M}\times \mathbb {R}^{k-1}$
, where
$\mathcal {M}\times \mathbb {R}^{k-1}$
, where
![]() $\mathcal {M}$
is an open Möebius strip.
$\mathcal {M}$
is an open Möebius strip.
In this work, we assume that the flow
![]() $\varphi $
has no twisted periodic orbits. Indeed, the results herein have the assumption that the differential of the chain complex associated to the flow is represented by a TU matrix, which is not the case when the flow has a twisted periodic orbit. This fact follows from results in [Reference Franks11, Reference Lima and de Rezende14].
$\varphi $
has no twisted periodic orbits. Indeed, the results herein have the assumption that the differential of the chain complex associated to the flow is represented by a TU matrix, which is not the case when the flow has a twisted periodic orbit. This fact follows from results in [Reference Franks11, Reference Lima and de Rezende14].
An untwisted periodic orbit
![]() $\gamma $
of index k is in standard form if there is a tubular neighborhood V of
$\gamma $
of index k is in standard form if there is a tubular neighborhood V of
![]() $\gamma $
with coordinates
$\gamma $
with coordinates
![]() $(\theta ,x,y) \in S^1\times \mathbb {R}^{k}\times \mathbb {R}^{n-k-1}$
such that the vector field has the form
$(\theta ,x,y) \in S^1\times \mathbb {R}^{k}\times \mathbb {R}^{n-k-1}$
such that the vector field has the form
 $$ \begin{align*} X= \dfrac{\partial}{\partial \theta} + \sum_{i=1}^k x_i\dfrac{\partial}{\partial x_i} - \sum_{j=1}^{n-k-1} y_j\dfrac{\partial}{\partial y_j}. \end{align*} $$
$$ \begin{align*} X= \dfrac{\partial}{\partial \theta} + \sum_{i=1}^k x_i\dfrac{\partial}{\partial x_i} - \sum_{j=1}^{n-k-1} y_j\dfrac{\partial}{\partial y_j}. \end{align*} $$
In [Reference Franks9], Franks shows that any Morse–Smale flow is topologically conjugate to a Morse–Smale flow whose periodic orbits are in standard form. See Figure 2.

Figure 2 Standard form of untwisted periodic orbits in dimension three.
The next result shows that a periodic orbit is, in a certain sense, interchangeable with a pair of rest points. See Figure 3.

Figure 3 Interchanging a periodic orbit with a pair of rest points.
Theorem 2.1. (Asimov [Reference Asimov1], Franks [Reference Franks10])
Suppose
![]() $\varphi $
is a Morse–Smale flow with rest points p and q of index
$\varphi $
is a Morse–Smale flow with rest points p and q of index
![]() $k+1$
and k, respectively, such that
$k+1$
and k, respectively, such that
![]() $W^u(p) \cap W^s(q)$
consists of two trajectories. Then
$W^u(p) \cap W^s(q)$
consists of two trajectories. Then
![]() $\varphi $
can be changed on any given neighborhood of the two trajectories from p to q in such a way as to eliminate the two critical points and replace them with:
$\varphi $
can be changed on any given neighborhood of the two trajectories from p to q in such a way as to eliminate the two critical points and replace them with:
-
(a) an untwisted periodic orbit of index k if
 $W^u(p) \cap W^s(q)$
consists of two trajectories with opposite signs; or
$W^u(p) \cap W^s(q)$
consists of two trajectories with opposite signs; or -
(b) a twisted periodic orbit if
 $W^u(p) \cap W^s(q)$
consists of two trajectories with the same sign.
$W^u(p) \cap W^s(q)$
consists of two trajectories with the same sign.
Franks’ next result shows the reverse construction, that is, the replacement of a periodic orbit of index k by two rest points of indices k and
![]() $k+1$
. See Figure 3.
$k+1$
. See Figure 3.
Theorem 2.2. (Franks [Reference Franks9])
Suppose
![]() $\varphi $
is a Morse–Smale flow on an orientable manifold M with a periodic orbit
$\varphi $
is a Morse–Smale flow on an orientable manifold M with a periodic orbit
![]() $\gamma $
of index k in standard form. Then, given a neighborhood U of
$\gamma $
of index k in standard form. Then, given a neighborhood U of
![]() $\gamma $
, there exists a Morse–Smale flow
$\gamma $
, there exists a Morse–Smale flow
![]() $\widetilde {\varphi }$
whose vector field agrees with that of
$\widetilde {\varphi }$
whose vector field agrees with that of
![]() $\varphi $
outside U and that has rest points p, q of indices
$\varphi $
outside U and that has rest points p, q of indices
![]() $k+1$
and k in U but no other chain recurrent points in U. For
$k+1$
and k in U but no other chain recurrent points in U. For
![]() $\widetilde {\varphi }$
,
$\widetilde {\varphi }$
,
![]() $W^u(p) \cap W^s(q)$
will consist of two trajectories with the same sign if
$W^u(p) \cap W^s(q)$
will consist of two trajectories with the same sign if
![]() $\gamma $
is twisted and opposite signs if
$\gamma $
is twisted and opposite signs if
![]() $\gamma $
is untwisted. Moreover, the unstable manifold for
$\gamma $
is untwisted. Moreover, the unstable manifold for
![]() $\gamma $
will be equal to
$\gamma $
will be equal to
![]() $W^u(p)\cup W^u(q)$
.
$W^u(p)\cup W^u(q)$
.
2.2 Spectral sequences and the sweeping algorithm for Morse complexes
In this subsection, we introduce a method that allows us to extract the modules and differentials of a spectral sequence of a filtered chain complex from its differential. This computation makes use of the sweeping algorithm that was introduced in [Reference Cornea, de Rezende and da Silveira6] and which will be described in this subsection.
In order to state a major theorem on spectral sequences, we make use of the following definitions.
Definition 2.3. Let
![]() $(C,\partial )$
be a chain complex and let
$(C,\partial )$
be a chain complex and let
![]() $F=\{F_{p}C\}$
be a filtration in
$F=\{F_{p}C\}$
be a filtration in
![]() $(C,\partial )$
.
$(C,\partial )$
.
-
(1) F is said to be an increasing filtration if there is a sequence of submodules
 $F_pC$
, for
$F_pC$
, for
 $p \in \mathbb {Z}$
, such that
$p \in \mathbb {Z}$
, such that
 $F_pC\subset F_{p+1}C$
. Moreover, the filtration must be compatible with the gradation of C, that is,
$F_pC\subset F_{p+1}C$
. Moreover, the filtration must be compatible with the gradation of C, that is,
 $F_pC$
is graded by
$F_pC$
is graded by
 $\{F_pC_q\}$
.
$\{F_pC_q\}$
. -
(2) F is said to be convergent if
 $\bigcap _p F_pC=0$
and
$\bigcap _p F_pC=0$
and
 $\cup F_{p}C=C$
.
$\cup F_{p}C=C$
. -
(3) F is finite if
 $F_pC=0$
for some p and
$F_pC=0$
for some p and
 $F_{p^{\prime }}C=C$
for some
$F_{p^{\prime }}C=C$
for some
 $p^{\prime }$
.
$p^{\prime }$
. -
(4) F is bounded below if, given q, there exists
 $p(q)$
such that
$p(q)$
such that
 $F_{p(q)}C_q=0$
.
$F_{p(q)}C_q=0$
.
The following theorem associates a spectral sequence to a filtered chain complex and can be found in [Reference Spanier22].
Theorem 2.4. Given a filtration F for the chain complex
![]() $(C,\partial )$
that is convergent and bounded below, there exists a convergent spectral sequence with
$(C,\partial )$
that is convergent and bounded below, there exists a convergent spectral sequence with
and
![]() $E^{\infty }$
is isomorphic to the module
$E^{\infty }$
is isomorphic to the module
![]() $GH_*(C)$
. The algebraic formulas for the modules are
$GH_*(C)$
. The algebraic formulas for the modules are
where
In [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3, Reference Bertolim, Lima, Mello, de Rezende and da Silveira4, Reference Cornea, de Rezende and da Silveira6], a spectral sequence analysis for a Morse chain complex
![]() $(C_{\ast }(f),\partial _{\ast })$
with a TU matrix
$(C_{\ast }(f),\partial _{\ast })$
with a TU matrix
![]() $\Delta $
associated to
$\Delta $
associated to
![]() $ \partial _{\ast }$
and a specific filtration induced by the flow
$ \partial _{\ast }$
and a specific filtration induced by the flow
![]() $\varphi _{f}$
was developed. The Morse chain complex describes the dynamics of a flow associated to a Morse–Smale function with no periodic orbits. Recall that
$\varphi _{f}$
was developed. The Morse chain complex describes the dynamics of a flow associated to a Morse–Smale function with no periodic orbits. Recall that
![]() $C(f)= \{C_{k}(f)\}$
is the
$C(f)= \{C_{k}(f)\}$
is the
![]() $\mathbb {Z}$
-module generated by the critical points of f and graded by their Morse index: that is,
$\mathbb {Z}$
-module generated by the critical points of f and graded by their Morse index: that is,
 $$ \begin{align*} C_{k}(f) := \bigoplus_{x \in \mathrm{Crit}_k(f)} \mathbb{Z} \langle x\rangle. \end{align*} $$
$$ \begin{align*} C_{k}(f) := \bigoplus_{x \in \mathrm{Crit}_k(f)} \mathbb{Z} \langle x\rangle. \end{align*} $$
The Morse boundary operator
![]() $\partial _{k}(x) : \mathcal {C}_{k}(f) \longrightarrow \mathcal {C}_{k-1}(f)$
is given on a generator x of
$\partial _{k}(x) : \mathcal {C}_{k}(f) \longrightarrow \mathcal {C}_{k-1}(f)$
is given on a generator x of
![]() $\mathcal {C}_{k}(f)$
by
$\mathcal {C}_{k}(f)$
by
 $$ \begin{align} \partial_k\langle x\rangle := \displaystyle\sum_{y \in \mathrm{Crit}_{k-1}(f)} n(x,y) \langle y\rangle , \end{align} $$
$$ \begin{align} \partial_k\langle x\rangle := \displaystyle\sum_{y \in \mathrm{Crit}_{k-1}(f)} n(x,y) \langle y\rangle , \end{align} $$
and it is extended to general chains by linearity, where
![]() $n(x,y)$
is the intersection number of x and y. The intersection number is defined for a pair
$n(x,y)$
is the intersection number of x and y. The intersection number is defined for a pair
![]() $x,y \in \mathrm {Crit}(f)$
such that
$x,y \in \mathrm {Crit}(f)$
such that
![]() $ind_{f} (x) - ind_{f} (y) = 1$
, as follows: a choice of orientations for the unstable manifolds
$ind_{f} (x) - ind_{f} (y) = 1$
, as follows: a choice of orientations for the unstable manifolds
![]() $W^{u}(x)$
and
$W^{u}(x)$
and
![]() $W^{u}(y)$
induces orientations on the connecting manifold
$W^{u}(y)$
induces orientations on the connecting manifold
![]() ${\mathcal M}_ {xy}$
through the isomorphism
${\mathcal M}_ {xy}$
through the isomorphism
where
![]() ${\mathcal V}_{{\mathcal M}_ {xy}}W^{s}(y)$
is the normal bundle of
${\mathcal V}_{{\mathcal M}_ {xy}}W^{s}(y)$
is the normal bundle of
![]() $W^{s}(y)$
restricted to
$W^{s}(y)$
restricted to
![]() ${\mathcal M}_{xy}$
. The orientation on
${\mathcal M}_{xy}$
. The orientation on
![]() ${\mathcal V}_{{\mathcal M}_{xy}}W^{s}(y)$
is determined by the orientation on a fiber
${\mathcal V}_{{\mathcal M}_{xy}}W^{s}(y)$
is determined by the orientation on a fiber
![]() ${\mathcal V}_{y}W^{s}(y)$
, which is given by the isomorphism
${\mathcal V}_{y}W^{s}(y)$
, which is given by the isomorphism
The moduli space between x and y is defined by
![]() ${{\mathcal M}}^{x}_{y}={\mathcal M}_{xy}\cap f^{-1}(a)$
, where a is a regular value of f such that
${{\mathcal M}}^{x}_{y}={\mathcal M}_{xy}\cap f^{-1}(a)$
, where a is a regular value of f such that
![]() $f(y)<a<f(x)$
. Given
$f(y)<a<f(x)$
. Given
![]() $u\in {{\mathcal M}}^{x}_{y}$
, the characteristic sign
$u\in {{\mathcal M}}^{x}_{y}$
, the characteristic sign
![]() $n_{u} $
of the orbit
$n_{u} $
of the orbit
![]() ${\mathcal O}(u)$
through u is defined by
${\mathcal O}(u)$
through u is defined by
![]() $[{\mathcal O}(u)]_{\mathrm {ind}} = n_u [\dot {u}]$
, where
$[{\mathcal O}(u)]_{\mathrm {ind}} = n_u [\dot {u}]$
, where
![]() $[\dot {u} ]$
and
$[\dot {u} ]$
and
![]() $[{\mathcal O}(u)]_{\mathrm {ind}}$
denote the orientations on
$[{\mathcal O}(u)]_{\mathrm {ind}}$
denote the orientations on
![]() $\mathcal {O}(u)$
induced by the flow and by
$\mathcal {O}(u)$
induced by the flow and by
![]() $\mathcal {M}_{xy}$
. The intersection number of x and y is defined by
$\mathcal {M}_{xy}$
. The intersection number of x and y is defined by
 $$ \begin{align*} n(x,y) = \displaystyle\sum_{u \in {{\mathcal M}}^{x}_{y}} n_u. \end{align*} $$
$$ \begin{align*} n(x,y) = \displaystyle\sum_{u \in {{\mathcal M}}^{x}_{y}} n_u. \end{align*} $$
The pair
![]() $(C_{\ast }(f),\partial _{\ast })$
is a chain complex, known as the Morse chain complex, and its homology coincides with the singular homology of the surface M. For more details see [Reference Weber24].
$(C_{\ast }(f),\partial _{\ast })$
is a chain complex, known as the Morse chain complex, and its homology coincides with the singular homology of the surface M. For more details see [Reference Weber24].
The filtration on
![]() $(C_{\ast }(f),\partial _{\ast })$
considered in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3, Reference Bertolim, Lima, Mello, de Rezende and da Silveira4, Reference Cornea, de Rezende and da Silveira6] is induced by the flow
$(C_{\ast }(f),\partial _{\ast })$
considered in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3, Reference Bertolim, Lima, Mello, de Rezende and da Silveira4, Reference Cornea, de Rezende and da Silveira6] is induced by the flow
![]() $\varphi _{f}$
. More specifically, given a finest Morse decomposition
$\varphi _{f}$
. More specifically, given a finest Morse decomposition
![]() $\{ M(p) \mid p\in P=\{1,\ldots , m \}, \ m = \# \mathrm {Crit}(f) \}$
such that there are distinct critical values
$\{ M(p) \mid p\in P=\{1,\ldots , m \}, \ m = \# \mathrm {Crit}(f) \}$
such that there are distinct critical values
![]() $c_p$
with
$c_p$
with
![]() $f^{-1}(c_p)\supset M(p)$
, we define a finest filtration on M by
$f^{-1}(c_p)\supset M(p)$
, we define a finest filtration on M by
since, for each
![]() $p\in P$
, there is only one singularity in
$p\in P$
, there is only one singularity in
![]() $F_p\setminus F_{p-1}$
.
$F_p\setminus F_{p-1}$
.
Whenever F is a finest filtration and the singularity in
![]() $F_p\setminus F_{p-1}$
has index k, then the only q such that
$F_p\setminus F_{p-1}$
has index k, then the only q such that
![]() $E^r_{p,q}$
is non-zero is
$E^r_{p,q}$
is non-zero is
![]() $q=k-p$
. Hence, in this case, we omit reference to q, that is,
$q=k-p$
. Hence, in this case, we omit reference to q, that is,
![]() $E^r_p$
is, in fact,
$E^r_p$
is, in fact,
![]() $E^r_{p,k-p}$
.
$E^r_{p,k-p}$
.
Note that
![]() $E^{\infty }$
does not determine
$E^{\infty }$
does not determine
![]() $H_*(C)$
completely, but
$H_*(C)$
completely, but
 $$ \begin{align*} E^{\infty}_{p,q}\approx GH_*(C)_{p,q}=\frac{F_pH_{p+q}(C)}{F_{p-1}H_{p+q}(C)}. \end{align*} $$
$$ \begin{align*} E^{\infty}_{p,q}\approx GH_*(C)_{p,q}=\frac{F_pH_{p+q}(C)}{F_{p-1}H_{p+q}(C)}. \end{align*} $$
However, it is a well-known fact that whenever
![]() $GH_*(C)_{p,q}$
is free and the filtration is bounded,
$GH_*(C)_{p,q}$
is free and the filtration is bounded,
 $$ \begin{align} \displaystyle\bigoplus_{p+q=k}GH_*(C)_{p,q}\approx H_{p+q}(C). \end{align} $$
$$ \begin{align} \displaystyle\bigoplus_{p+q=k}GH_*(C)_{p,q}\approx H_{p+q}(C). \end{align} $$
See [Reference Davis and Kirk7].
In [Reference Cornea, de Rezende and da Silveira6], where the spectral sequence associated to a Morse complex was considered in the setting of an n-dimensional manifold, for
![]() $n\geq 1$
, and computed over
$n\geq 1$
, and computed over
![]() $\mathbb {Z}$
, (3) is not necessarily true. However, a characterization theorem for primary pivots for TU differentials in dimension n, which states that the primary pivots are
$\mathbb {Z}$
, (3) is not necessarily true. However, a characterization theorem for primary pivots for TU differentials in dimension n, which states that the primary pivots are
![]() $\pm 1$
(Theorem 2.1) is proved in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira4]. As a consequence of this theorem and the fact that the differentials of the spectral sequence are induced by the primary pivots, whenever the differential is TU,
$\pm 1$
(Theorem 2.1) is proved in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira4]. As a consequence of this theorem and the fact that the differentials of the spectral sequence are induced by the primary pivots, whenever the differential is TU,
![]() $GH_*(C)_{p,q}$
is free for all p and q and thus (3) holds in the setting of a filtered Morse flow with a finest filtration.
$GH_*(C)_{p,q}$
is free for all p and q and thus (3) holds in the setting of a filtered Morse flow with a finest filtration.
2.2.1 Spectral Sequence Sweeping Algorithm—SSSA
The SSSA was introduced in [Reference Cornea, de Rezende and da Silveira6] for a chain complex with a finest filtration. It constructs recursively a family of matrices
![]() $\{\Delta ^r\}$
for
$\{\Delta ^r\}$
for
![]() $r\geq 0$
, where
$r\geq 0$
, where
![]() $\Delta ^0=\Delta $
, by considering at each stage the rth diagonal. It is shown in [Reference Cornea, de Rezende and da Silveira6] that this family of matrices, with marked entries called primary pivots and change of basis pivots, determines the spectral sequence
$\Delta ^0=\Delta $
, by considering at each stage the rth diagonal. It is shown in [Reference Cornea, de Rezende and da Silveira6] that this family of matrices, with marked entries called primary pivots and change of basis pivots, determines the spectral sequence
![]() $(E^r, d^r)$
.
$(E^r, d^r)$
.
For each fixed r and each non-zero entry
![]() $\Delta ^r_{i,j}$
in the rth diagonal of
$\Delta ^r_{i,j}$
in the rth diagonal of
![]() $\Delta ^r$
, the mark-up is carried out as follows.
$\Delta ^r$
, the mark-up is carried out as follows.
-
• If there is a primary pivot below
 $\Delta ^r_{i,j}$
, then it is left unmarked.
$\Delta ^r_{i,j}$
, then it is left unmarked. -
• If there is no primary pivot below and to the left of
 $\Delta ^r_{i,j}$
, then this entry is marked as a primary pivot.
$\Delta ^r_{i,j}$
, then this entry is marked as a primary pivot. -
• If there is no primary pivot below
 $\Delta ^r_{i,j}$
but there is a primary pivot to the left of it, then the entry is marked as a change of basis pivot.
$\Delta ^r_{i,j}$
but there is a primary pivot to the left of it, then the entry is marked as a change of basis pivot.
Whenever
![]() $\Delta ^r_{i,j}$
is marked as a change of basis pivot on the rth diagonal, then there exists a column, namely, the tth column
$\Delta ^r_{i,j}$
is marked as a change of basis pivot on the rth diagonal, then there exists a column, namely, the tth column
![]() $(t<j)$
, associated to a k-chain such that
$(t<j)$
, associated to a k-chain such that
![]() $\Delta ^r_{k_{i,t}}$
is a primary pivot. To construct the next matrix
$\Delta ^r_{k_{i,t}}$
is a primary pivot. To construct the next matrix
![]() $\Delta ^{r+1}$
, a change of basis is performed on
$\Delta ^{r+1}$
, a change of basis is performed on
![]() $\Delta ^{r}$
which zeroes out the entry
$\Delta ^{r}$
which zeroes out the entry
![]() $\Delta _{i,j}^{r}$
without introducing non-zero entries below the ith row, that is,
$\Delta _{i,j}^{r}$
without introducing non-zero entries below the ith row, that is,
![]() $\Delta ^{r}_{s,j}=0$
for
$\Delta ^{r}_{s,j}=0$
for
![]() $s>i$
. Since
$s>i$
. Since
![]() $\Delta $
is a TU matrix, the SSSA has primary pivots always equal to
$\Delta $
is a TU matrix, the SSSA has primary pivots always equal to
![]() $\pm 1$
as proved in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira4]. Hence, it is always possible to choose the particular change of basis which uses only the tth and the jth column of
$\pm 1$
as proved in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira4]. Hence, it is always possible to choose the particular change of basis which uses only the tth and the jth column of
![]() $\Delta ^r$
. In other words, we zero out the entry
$\Delta ^r$
. In other words, we zero out the entry
![]() $\Delta _{k_{i,j}}^{r}$
by adding or subtracting the tth column to or from the jth column of
$\Delta _{k_{i,j}}^{r}$
by adding or subtracting the tth column to or from the jth column of
![]() $\Delta ^{r}$
.
$\Delta ^{r}$
.
Let
![]() $k_1, k_2,\ldots $
be the columns of
$k_1, k_2,\ldots $
be the columns of
![]() $\Delta ^{r}$
that are associated to k chains. We denote by
$\Delta ^{r}$
that are associated to k chains. We denote by
![]() $\sigma _k^{k_{\ell },r}$
the k chain represented in the
$\sigma _k^{k_{\ell },r}$
the k chain represented in the
![]() $k_{\ell }$
th column of
$k_{\ell }$
th column of
![]() $\Delta ^r$
. Hence, the
$\Delta ^r$
. Hence, the
![]() $k_j$
th column of
$k_j$
th column of
![]() $\Delta ^{r+1}$
is
$\Delta ^{r+1}$
is
 $$ \begin{align} \sigma_k^{k_j,{r+1}}&=\underbrace{\sum_{\ell=1}^{j}c^{k_j,r}_{\ell}h_k^{k_{\ell}}}_{\sigma_k^{k_j,r}}\pm \underbrace{\sum_{\ell=1}^{t}c^{k_t,r}_{\ell}h_k^{k_{\ell}}}_{\sigma_k^{k_t,r}}\nonumber\\ &=c^{k_j,r+1}_{1}h_k^{k_1} +c^{k_j,r+1}_{2}h_k^{k_2}+\cdots +c^{k_j,r+1}_{j-1}h_k^{k_{j-1}}+ c^{k_j,r+1}_{j}h_k^{k_j},\end{align} $$
$$ \begin{align} \sigma_k^{k_j,{r+1}}&=\underbrace{\sum_{\ell=1}^{j}c^{k_j,r}_{\ell}h_k^{k_{\ell}}}_{\sigma_k^{k_j,r}}\pm \underbrace{\sum_{\ell=1}^{t}c^{k_t,r}_{\ell}h_k^{k_{\ell}}}_{\sigma_k^{k_t,r}}\nonumber\\ &=c^{k_j,r+1}_{1}h_k^{k_1} +c^{k_j,r+1}_{2}h_k^{k_2}+\cdots +c^{k_j,r+1}_{j-1}h_k^{k_{j-1}}+ c^{k_j,r+1}_{j}h_k^{k_j},\end{align} $$
where
![]() $c^{k_{\ell },r}\in \mathbb {Z}$
.
$c^{k_{\ell },r}\in \mathbb {Z}$
.
Therefore, the matrix
![]() $\Delta ^{r+1}$
has numerical values determined by the change of basis over
$\Delta ^{r+1}$
has numerical values determined by the change of basis over
![]() $\mathbb {Z}$
of
$\mathbb {Z}$
of
![]() $\Delta ^r$
. In particular, all the changes of basis pivots on the rth diagonal
$\Delta ^r$
. In particular, all the changes of basis pivots on the rth diagonal
![]() $\Delta ^r$
are zero in
$\Delta ^r$
are zero in
![]() $\Delta ^{r+1}$
.
$\Delta ^{r+1}$
.
It is easy to see that all
![]() $\Delta ^r$
are upper triangular and
$\Delta ^r$
are upper triangular and
![]() $\Delta ^r\circ \Delta ^r=0$
since they are recursively obtained from the initial connection matrix
$\Delta ^r\circ \Delta ^r=0$
since they are recursively obtained from the initial connection matrix
![]() $\Delta $
by specific changes of basis over
$\Delta $
by specific changes of basis over
![]() $\mathbb {Z}$
. Note that if the entry
$\mathbb {Z}$
. Note that if the entry
![]() $\Delta ^{r}_{p-r+1,p+1}$
has been identified by the SSSA as a primary pivot or a change of basis pivot, then the entries below it are all zero, that is,
$\Delta ^{r}_{p-r+1,p+1}$
has been identified by the SSSA as a primary pivot or a change of basis pivot, then the entries below it are all zero, that is,
![]() $\Delta ^{r}_{s,p+1}=0$
for all
$\Delta ^{r}_{s,p+1}=0$
for all
![]() $s>p-r+1$
.
$s>p-r+1$
.
In [Reference Cornea, de Rezende and da Silveira6], it is shown how the
![]() $\mathbb {Z}$
-modules
$\mathbb {Z}$
-modules
![]() $E^{r}_{p}$
are determined by the connection matrix
$E^{r}_{p}$
are determined by the connection matrix
![]() $\Delta $
. To do this, a formula for the module
$\Delta $
. To do this, a formula for the module
![]() $Z^{r}_{p,k-p}$
was established in terms of the
$Z^{r}_{p,k-p}$
was established in terms of the
![]() $\sigma _k^{r,j}$
determined by the SSSA. Let
$\sigma _k^{r,j}$
determined by the SSSA. Let
![]() $k_{\ell _{p}}$
be the rightmost
$k_{\ell _{p}}$
be the rightmost
![]() $h_k$
column such that
$h_k$
column such that
![]() $k_{\ell _{p}}\leq p+1$
, that is, the rightmost
$k_{\ell _{p}}\leq p+1$
, that is, the rightmost
![]() $h_k$
column in
$h_k$
column in
![]() $F_pC$
. Then
$F_pC$
. Then
 $$ \begin{align*}Z^{r}_{p,k-p}= \mathbb{Z}&[\mu^{k_{\ell_{p}},{r-p-1+k_{\ell_{p}}}}\sigma_k^{k_{\ell_{p}},{r-p-1+k_{\ell_{p}}}},\mu^{k_{\ell_{p}-1},{r-p-1+k_{\ell_{p}-1}}}\sigma_k^{k_{\ell_{p}-1},{r-p-1+k_{\ell_{p}-1}}},\ldots,\\&\quad\mu^{k_1,{r-p-1+k_1}}\sigma_k^{k_1,{r-p-1+k_1}}],\end{align*} $$
$$ \begin{align*}Z^{r}_{p,k-p}= \mathbb{Z}&[\mu^{k_{\ell_{p}},{r-p-1+k_{\ell_{p}}}}\sigma_k^{k_{\ell_{p}},{r-p-1+k_{\ell_{p}}}},\mu^{k_{\ell_{p}-1},{r-p-1+k_{\ell_{p}-1}}}\sigma_k^{k_{\ell_{p}-1},{r-p-1+k_{\ell_{p}-1}}},\ldots,\\&\quad\mu^{k_1,{r-p-1+k_1}}\sigma_k^{k_1,{r-p-1+k_1}}],\end{align*} $$
where
![]() $\mu ^{j,\zeta }=0$
whenever the primary pivot of the jth column is below the
$\mu ^{j,\zeta }=0$
whenever the primary pivot of the jth column is below the
![]() $(p-r+1)$
th row and
$(p-r+1)$
th row and
![]() $\mu ^{j,\zeta }=1$
otherwise. (Whenever
$\mu ^{j,\zeta }=1$
otherwise. (Whenever
![]() $j<0$
, we consider
$j<0$
, we consider
![]() $\sigma ^{i,j}_{k}=\sigma ^{i,0}_{k}$
.) Moreover, throughout the SSSA,
$\sigma ^{i,j}_{k}=\sigma ^{i,0}_{k}$
.) Moreover, throughout the SSSA,
![]() $\Delta $
induces the differentials
$\Delta $
induces the differentials
![]() $d^r_p$
in the spectral sequence. In fact, whenever
$d^r_p$
in the spectral sequence. In fact, whenever
![]() $E^{r}_{p}$
and
$E^{r}_{p}$
and
![]() $E^{r}_{p-r}$
are both non-zero, the map
$E^{r}_{p-r}$
are both non-zero, the map
![]() $d^r_p:E^{r}_{p}\to E^{r}_{p-r}$
is multiplication by the entry
$d^r_p:E^{r}_{p}\to E^{r}_{p-r}$
is multiplication by the entry
![]() $\Delta ^r_{p-r+1,p+1}$
which is either a primary pivot or a zero with a column of zero entries below it. Otherwise,
$\Delta ^r_{p-r+1,p+1}$
which is either a primary pivot or a zero with a column of zero entries below it. Otherwise,
![]() $d^r_p$
is zero. Since, in this case, the primary pivots are always equal to
$d^r_p$
is zero. Since, in this case, the primary pivots are always equal to
![]() $\pm 1$
, the non-zero
$\pm 1$
, the non-zero
![]() $d^r$
are always isomorphisms induced by primary pivots.
$d^r$
are always isomorphisms induced by primary pivots.
For a more detailed explanation of the SSSA as well as other sweeping algorithms, see [Reference Bertolim, Lima, Mello, de Rezende and da Silveira4].
3 Local behaviour of NMS flows
3.1 NMS chain complex
In this section, we consider a chain complex associated to an NMS flow
![]() $\varphi $
on a closed orientable 3-manifold and prove properties of its differential. We assume that
$\varphi $
on a closed orientable 3-manifold and prove properties of its differential. We assume that
![]() $\varphi $
has no heteroclinic trajectories connecting saddle orbits, that is, given two saddle periodic orbits
$\varphi $
has no heteroclinic trajectories connecting saddle orbits, that is, given two saddle periodic orbits
![]() $ \gamma _1^i $
and
$ \gamma _1^i $
and
![]() $\gamma _1^j$
,
$\gamma _1^j$
,
![]() $W^u(\gamma _1^i)\cap W^s(\gamma _1^j)$
is empty. The set of NMS flows satisfying this property is denoted by
$W^u(\gamma _1^i)\cap W^s(\gamma _1^j)$
is empty. The set of NMS flows satisfying this property is denoted by
![]() $\Sigma (M^3)$
. The next result shows that, for flows in
$\Sigma (M^3)$
. The next result shows that, for flows in
![]() $\Sigma (M^3)$
, the connecting manifold between periodic orbits has a nice behavior in the sense that, whenever
$\Sigma (M^3)$
, the connecting manifold between periodic orbits has a nice behavior in the sense that, whenever
![]() $W^u(\gamma _1)\cap W^s(\gamma _0)\neq \emptyset $
, each of its connected components is homeomorphic to a cylinder
$W^u(\gamma _1)\cap W^s(\gamma _0)\neq \emptyset $
, each of its connected components is homeomorphic to a cylinder
![]() $S^1 \times (0,1)$
. The dynamical behavior of these cylinders characterizes the differentials of the spectral sequence. As the spectral sequence unfolds, these differentials will play an important role in the construction of a continuation to a core NMS flow.
$S^1 \times (0,1)$
. The dynamical behavior of these cylinders characterizes the differentials of the spectral sequence. As the spectral sequence unfolds, these differentials will play an important role in the construction of a continuation to a core NMS flow.
Proposition 3.1. Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold,
$3$
-manifold,
![]() $\gamma _1$
is a saddle periodic orbit and
$\gamma _1$
is a saddle periodic orbit and
![]() $\gamma _0$
(respectively,
$\gamma _0$
(respectively,
![]() $\gamma _2$
) is an attracting (respectively, repelling) periodic orbit, such that
$\gamma _2$
) is an attracting (respectively, repelling) periodic orbit, such that
![]() $W^u(\gamma _1)\cap W^s(\gamma _0)$
(respectively,
$W^u(\gamma _1)\cap W^s(\gamma _0)$
(respectively,
![]() $W^u(\gamma _2)\cap W^s(\gamma _1)$
) is non-empty. Then each connected component of
$W^u(\gamma _2)\cap W^s(\gamma _1)$
) is non-empty. Then each connected component of
![]() $W^u(\gamma _1)\cap W^s(\gamma _0)$
(respectively,
$W^u(\gamma _1)\cap W^s(\gamma _0)$
(respectively,
![]() $W^u(\gamma _2)\cap W^s(\gamma _1)$
) is homeomorphic to
$W^u(\gamma _2)\cap W^s(\gamma _1)$
) is homeomorphic to
![]() $S^1 \times (0,1)$
.
$S^1 \times (0,1)$
.
Proof. Assume that
![]() $W^u(\gamma _1)\cap W^s(\gamma _0)$
is non-empty and let C be one of the connected components of
$W^u(\gamma _1)\cap W^s(\gamma _0)$
is non-empty and let C be one of the connected components of
![]() $W^{u}(\gamma _1)\setminus \{\gamma _1\}$
such that
$W^{u}(\gamma _1)\setminus \{\gamma _1\}$
such that
![]() $ W^s(\gamma _0)\cap C$
is also non-empty. Note that
$ W^s(\gamma _0)\cap C$
is also non-empty. Note that
![]() $W^s(\gamma _0)\cap C$
is an open set in C, since
$W^s(\gamma _0)\cap C$
is an open set in C, since
![]() $W^s(\gamma _0)$
is an open set in M. Also,
$W^s(\gamma _0)$
is an open set in M. Also,
![]() $W^s(\gamma _0)\cap C$
is a closed set in C. By the connectedness of C, it follows that
$W^s(\gamma _0)\cap C$
is a closed set in C. By the connectedness of C, it follows that
![]() $W^s(\gamma _0)\cap C$
must be equal to C.
$W^s(\gamma _0)\cap C$
must be equal to C.
Even though a non-empty connected component C of
![]() $W^u(\gamma _1)\cap W^s(\gamma _0)$
(respectively,
$W^u(\gamma _1)\cap W^s(\gamma _0)$
(respectively,
![]() $W^u(\gamma _2)\cap W^s(\gamma _1)$
) is always a cylinder, there are distinct embeddings of C into
$W^u(\gamma _2)\cap W^s(\gamma _1)$
) is always a cylinder, there are distinct embeddings of C into
![]() $W^s(\gamma _0)$
(respectively,
$W^s(\gamma _0)$
(respectively,
![]() $W^s(\gamma _2)$
).
$W^s(\gamma _2)$
).
A compressing disc for a surface F in a
![]() $3$
-manifold M is an embedded disc
$3$
-manifold M is an embedded disc
![]() $D \subset M$
that meets F along its boundary, that is,
$D \subset M$
that meets F along its boundary, that is,
![]() $D\cap F = \partial D$
. The compressing disc D is inessential if the curve
$D\cap F = \partial D$
. The compressing disc D is inessential if the curve
![]() $\partial D$
is trivial on F, that is, bounds a disc on F. Otherwise, D is essential. A surface
$\partial D$
is trivial on F, that is, bounds a disc on F. Otherwise, D is essential. A surface
![]() $F \subset M$
is called incompressible if it admits no essential compressing discs. Otherwise, it is called compressible. See [Reference Jaco13, Reference Matveev17].
$F \subset M$
is called incompressible if it admits no essential compressing discs. Otherwise, it is called compressible. See [Reference Jaco13, Reference Matveev17].
Definition 3.2. Let
![]() $\gamma _1$
be a saddle periodic orbit and let
$\gamma _1$
be a saddle periodic orbit and let
![]() $\gamma _0$
(respectively,
$\gamma _0$
(respectively,
![]() $\gamma _2$
) be an attracting (respectively, repelling) periodic orbit of
$\gamma _2$
) be an attracting (respectively, repelling) periodic orbit of
![]() $\varphi $
. Given C a connected component of
$\varphi $
. Given C a connected component of
![]() $W^u(\gamma _1)\cap W^s(\gamma _0)$
(
$W^u(\gamma _1)\cap W^s(\gamma _0)$
(
![]() $W^u(\gamma _2)\cap W^s(\gamma _1)$
), one says that C is an inessential connection if C is an incompressible surface in
$W^u(\gamma _2)\cap W^s(\gamma _1)$
), one says that C is an inessential connection if C is an incompressible surface in
![]() $W^s(\gamma _0)$
(respectively,
$W^s(\gamma _0)$
(respectively,
![]() $W ^u(\gamma _2)$
). Otherwise, one says that C is an essential connection.
$W ^u(\gamma _2)$
). Otherwise, one says that C is an essential connection.
In other words, if C is an incompressible surface in
![]() $W^s(\gamma _0)$
(respectively,
$W^s(\gamma _0)$
(respectively,
![]() $W^s(\gamma _2)$
), then there are only inessential compressing discs. If C is a compressible surface in
$W^s(\gamma _2)$
), then there are only inessential compressing discs. If C is a compressible surface in
![]() $W^s(\gamma _0)$
(respectively,
$W^s(\gamma _0)$
(respectively,
![]() $W^s(\gamma _2)$
), then there exists an essential compressing disc. See Figure 4.
$W^s(\gamma _2)$
), then there exists an essential compressing disc. See Figure 4.

Figure 4 Inessential cylinder of connections (left) and essential cylinder of connections (right).
Let U be a neighborhood of a periodic orbit
![]() $\gamma $
in a Morse–Smale flow
$\gamma $
in a Morse–Smale flow
![]() $\varphi $
such that U is disjoint from every other connected component of the recurrent set of
$\varphi $
such that U is disjoint from every other connected component of the recurrent set of
![]() $\varphi $
. A flow
$\varphi $
. A flow
![]() $\widetilde {\varphi }$
is a one step morsification of
$\widetilde {\varphi }$
is a one step morsification of
![]() $\varphi $
on U if:
$\varphi $
on U if:
-
(1)
 $\widetilde {\varphi }$
is a Morse–Smale flow;
$\widetilde {\varphi }$
is a Morse–Smale flow; -
(2)
 $\widetilde {\varphi }$
agrees with
$\widetilde {\varphi }$
agrees with
 $\varphi $
outside of U; and
$\varphi $
outside of U; and -
(3) U has two rest points
 $ p$
and q of index
$ p$
and q of index
 $k+1$
and k, where k is the index of the periodic orbit
$k+1$
and k, where k is the index of the periodic orbit
 $\gamma $
. There are exactly two orbits connecting p and q and there are no other rest points or periodic orbits in U. Finally,
$\gamma $
. There are exactly two orbits connecting p and q and there are no other rest points or periodic orbits in U. Finally,
 $W^u(\gamma )$
is equal to
$W^u(\gamma )$
is equal to
 $W^u(p) \cup W^u(q)$
and
$W^u(p) \cup W^u(q)$
and
 $W^s(\gamma )$
is equal to
$W^s(\gamma )$
is equal to
 $W^s(p) \cup W^s(q)$
. See Franks [Reference Franks9, Reference Franks10].
$W^s(p) \cup W^s(q)$
. See Franks [Reference Franks9, Reference Franks10].
Let
![]() $\mathcal {U} = \{U_1, U_2, \ldots , U_m\}$
be a collection of pairwise disjoint neighborhoods of the periodic orbits
$\mathcal {U} = \{U_1, U_2, \ldots , U_m\}$
be a collection of pairwise disjoint neighborhoods of the periodic orbits
![]() $\gamma ^1, \ldots , \gamma ^m$
in the Morse–Smale flow
$\gamma ^1, \ldots , \gamma ^m$
in the Morse–Smale flow
![]() $\varphi $
such that
$\varphi $
such that
![]() $\gamma ^i \subset U_i$
for
$\gamma ^i \subset U_i$
for
![]() $i = 1, \ldots , m$
and each
$i = 1, \ldots , m$
and each
![]() $U_i$
is disjoint from every other periodic orbit and every rest point of
$U_i$
is disjoint from every other periodic orbit and every rest point of
![]() $\varphi $
. A flow
$\varphi $
. A flow
![]() $\widetilde {\varphi }$
is a morsification of
$\widetilde {\varphi }$
is a morsification of
![]() $\varphi $
on
$\varphi $
on
![]() $\mathcal {U}$
if:
$\mathcal {U}$
if:
-
(1)
 $\widetilde {\varphi }$
is a Morse-Smale flow;
$\widetilde {\varphi }$
is a Morse-Smale flow; -
(2)
 $\widetilde {\varphi }$
agrees with
$\widetilde {\varphi }$
agrees with
 $\varphi $
outside of
$\varphi $
outside of
 $\bigcup _{i=1}^{m} U_i$
; and
$\bigcup _{i=1}^{m} U_i$
; and -
(3) in each
 $U_i$
,
$U_i$
,
 $\widetilde {\varphi }$
agrees with
$\widetilde {\varphi }$
agrees with
 $\widetilde {\varphi }_i$
, where
$\widetilde {\varphi }_i$
, where
 $\widetilde {\varphi }_i$
is a one step morsification of
$\widetilde {\varphi }_i$
is a one step morsification of
 $\varphi $
on
$\varphi $
on
 $U_i$
.
$U_i$
.
Whenever
![]() $\mathcal {U}$
contains a neighborhood of each periodic orbit of
$\mathcal {U}$
contains a neighborhood of each periodic orbit of
![]() $\varphi $
, for simplicity, we refer to
$\varphi $
, for simplicity, we refer to
![]() $\widetilde {\varphi }$
as a morsification of
$\widetilde {\varphi }$
as a morsification of
![]() $\varphi $
.
$\varphi $
.
Given a periodic orbit
![]() $\gamma _{k}$
of a Morse–Smale flow
$\gamma _{k}$
of a Morse–Smale flow
![]() $\varphi $
, denote by
$\varphi $
, denote by
![]() $h_{k}(\gamma _{k})$
and
$h_{k}(\gamma _{k})$
and
![]() $h_{k+1}(\gamma _{k})$
the index k and index
$h_{k+1}(\gamma _{k})$
the index k and index
![]() $k+1$
rest points corresponding to
$k+1$
rest points corresponding to
![]() $\gamma _{k}$
in a morsification
$\gamma _{k}$
in a morsification
![]() $\widetilde {\varphi }$
of
$\widetilde {\varphi }$
of
![]() $\varphi $
. Denote by
$\varphi $
. Denote by
![]() $\Gamma _{k}(\varphi )$
the set of all periodic orbits of index k of the flow
$\Gamma _{k}(\varphi )$
the set of all periodic orbits of index k of the flow
![]() $\varphi $
and denote by
$\varphi $
and denote by
![]() $\Gamma (\varphi ) = \Gamma _0(\varphi ) \cup \Gamma _1(\varphi ) \cup \Gamma _2(\varphi )$
the set of all periodic orbits.
$\Gamma (\varphi ) = \Gamma _0(\varphi ) \cup \Gamma _1(\varphi ) \cup \Gamma _2(\varphi )$
the set of all periodic orbits.
A natural chain complex that describes the dynamics of a Morse–Smale flow without periodic orbits is the Morse chain complex. In order to study the dynamics of an NMS flow
![]() $\varphi $
, we consider the Morse chain complex of a morsification
$\varphi $
, we consider the Morse chain complex of a morsification
![]() $\widetilde {\varphi }$
of
$\widetilde {\varphi }$
of
![]() $\varphi $
. More specifically, given periodic orbits
$\varphi $
. More specifically, given periodic orbits
![]() $\gamma $
,
$\gamma $
,
![]() $\beta $
, denote by
$\beta $
, denote by
![]() $n(h_k(\gamma ), h_{k-1}(\beta );\widetilde {\varphi })$
the intersection number between the unstable manifold of
$n(h_k(\gamma ), h_{k-1}(\beta );\widetilde {\varphi })$
the intersection number between the unstable manifold of
![]() $h_k(\gamma )$
and the stable manifold of
$h_k(\gamma )$
and the stable manifold of
![]() $h_{k-1}(\beta )$
with respect to
$h_{k-1}(\beta )$
with respect to
![]() $\widetilde {\varphi }$
. If it is clear from the context, we omit reference to
$\widetilde {\varphi }$
. If it is clear from the context, we omit reference to
![]() $\widetilde {\varphi }$
. The Morse group is the free
$\widetilde {\varphi }$
. The Morse group is the free
![]() $\mathbb {Z}$
-module
$\mathbb {Z}$
-module
![]() $C=C(\widetilde {\varphi })$
generated by the critical points of
$C=C(\widetilde {\varphi })$
generated by the critical points of
![]() $\widetilde {\varphi }$
and graded by the Morse index, that is,
$\widetilde {\varphi }$
and graded by the Morse index, that is,
![]() $C_{k}(\widetilde {\varphi }) = \mathbb {Z}[\mathrm {Crit}_k(\widetilde {\varphi })]$
. The boundary operator
$C_{k}(\widetilde {\varphi }) = \mathbb {Z}[\mathrm {Crit}_k(\widetilde {\varphi })]$
. The boundary operator
![]() $\partial $
of
$\partial $
of
![]() $\varphi $
on a generator
$\varphi $
on a generator
![]() $h_k(\gamma )$
is given by
$h_k(\gamma )$
is given by
 $$ \begin{align*} \partial_k : C_{k}(\widetilde{\varphi}) & \longrightarrow C_{k-1}(\widetilde{\varphi}) \nonumber \\ h_k(\gamma) & \longmapsto \sum_{\beta \in \Gamma_{k\!-\!1}(\varphi) \cup \Gamma_{k\!-\!2}(\varphi) }n(h_k(\gamma), h_{k-1}(\beta);\widetilde{\varphi}) h_{k-1}(\beta). \nonumber \end{align*} $$
$$ \begin{align*} \partial_k : C_{k}(\widetilde{\varphi}) & \longrightarrow C_{k-1}(\widetilde{\varphi}) \nonumber \\ h_k(\gamma) & \longmapsto \sum_{\beta \in \Gamma_{k\!-\!1}(\varphi) \cup \Gamma_{k\!-\!2}(\varphi) }n(h_k(\gamma), h_{k-1}(\beta);\widetilde{\varphi}) h_{k-1}(\beta). \nonumber \end{align*} $$
Note that
![]() $(C_{\ast }(\widetilde {\varphi }),\partial _{\ast })$
is a particular case of a connection matrix for a Morse decomposition of
$(C_{\ast }(\widetilde {\varphi }),\partial _{\ast })$
is a particular case of a connection matrix for a Morse decomposition of
![]() $(M,\varphi )$
, where each Morse set is a periodic orbit and the partial order is the flow order. This fact follows from the results in [Reference Lima and de Rezende14, Reference Salamon21]. Let
$(M,\varphi )$
, where each Morse set is a periodic orbit and the partial order is the flow order. This fact follows from the results in [Reference Lima and de Rezende14, Reference Salamon21]. Let
![]() $\Delta $
be the matrix corresponding to the map
$\Delta $
be the matrix corresponding to the map
![]() $\partial _{\ast }$
with respect to the basis of
$\partial _{\ast }$
with respect to the basis of
![]() $C_{\ast }(\widetilde {\varphi })$
given by
$C_{\ast }(\widetilde {\varphi })$
given by
![]() $h_{k}(\gamma )$
, for
$h_{k}(\gamma )$
, for
![]() $\gamma \in \Gamma (\varphi )$
and
$\gamma \in \Gamma (\varphi )$
and
![]() $k=0,1,2$
. The chain complex
$k=0,1,2$
. The chain complex
![]() $(C_{\ast }(\widetilde {\varphi }),\partial _{\ast })$
is said to be an NMS-chain complex for
$(C_{\ast }(\widetilde {\varphi }),\partial _{\ast })$
is said to be an NMS-chain complex for
![]() $(M,\varphi )$
. In this paper, we use the notation
$(M,\varphi )$
. In this paper, we use the notation
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
or
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
or
![]() $(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
whenever the morsification
$(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
whenever the morsification
![]() $\widetilde \varphi $
is clear from the context.
$\widetilde \varphi $
is clear from the context.
Recall that, in order for Smale’s cancellation theorem to hold, the intersection number between two singularities must be
![]() $\pm 1$
. Hence, it is natural to consider differentials
$\pm 1$
. Hence, it is natural to consider differentials
![]() $\Delta ^{\mathrm {NMS}}$
that are TU matrices and thus all entries are
$\Delta ^{\mathrm {NMS}}$
that are TU matrices and thus all entries are
![]() $0$
,
$0$
,
![]() $\pm 1$
. Later, this hypothesis will be instrumental in proving the cancellation theorems.
$\pm 1$
. Later, this hypothesis will be instrumental in proving the cancellation theorems.
Let
![]() $TUM(\varphi )$
be the class of morsifications
$TUM(\varphi )$
be the class of morsifications
![]() $\widetilde {\varphi }$
of
$\widetilde {\varphi }$
of
![]() $\varphi $
such that the differential
$\varphi $
such that the differential
![]() $\Delta ^{\mathrm {NMS}}$
of the Morse chain complex associated to
$\Delta ^{\mathrm {NMS}}$
of the Morse chain complex associated to
![]() $\widetilde {\varphi }$
is a TU matrix. In this paper, we consider flows
$\widetilde {\varphi }$
is a TU matrix. In this paper, we consider flows
![]() $\varphi $
such that
$\varphi $
such that
![]() $TUM(\varphi )\neq \emptyset $
.
$TUM(\varphi )\neq \emptyset $
.
The next theorem gives a correspondence between an inessential connection of an NMS flow
![]() $\varphi $
and the associated connections between the singularities of a morsification of
$\varphi $
and the associated connections between the singularities of a morsification of
![]() $\varphi $
.
$\varphi $
.
Theorem 3.3. Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold. Let
$3$
-manifold. Let
![]() $\gamma _0$
and
$\gamma _0$
and
![]() $\gamma _1$
(respectively,
$\gamma _1$
(respectively,
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
) be two periodic orbits of
$\gamma _2$
) be two periodic orbits of
![]() $\varphi $
and let
$\varphi $
and let
![]() $\widetilde {\varphi }\in TUM(\varphi )$
be a morsification of
$\widetilde {\varphi }\in TUM(\varphi )$
be a morsification of
![]() $\varphi $
on
$\varphi $
on
![]() $\mathcal {U}=\{U_1,U_2\}$
, where
$\mathcal {U}=\{U_1,U_2\}$
, where
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are two disjoint neighborhoods of
$U_2$
are two disjoint neighborhoods of
![]() $\gamma _0$
and
$\gamma _0$
and
![]() $\gamma _1$
(respectively,
$\gamma _1$
(respectively,
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
).
$\gamma _2$
).
-
(1) If
 $W^u(\gamma _1)\cap W^s(\gamma _0) $
(respectively,
$W^u(\gamma _1)\cap W^s(\gamma _0) $
(respectively,
 $W^u(\gamma _2)\cap W^s(\gamma _1) $
) has one connected component only, which is inessential, then there is a unique connection between
$W^u(\gamma _2)\cap W^s(\gamma _1) $
) has one connected component only, which is inessential, then there is a unique connection between
 $h_2(\gamma _1)$
and
$h_2(\gamma _1)$
and
 $h_1(\gamma _0)$
(respectively,
$h_1(\gamma _0)$
(respectively,
 $h_2(\gamma _2)$
and
$h_2(\gamma _2)$
and
 $h_1(\gamma _1)$
) in
$h_1(\gamma _1)$
) in
 $\widetilde {\varphi }$
.
$\widetilde {\varphi }$
. -
(2) If
 $W^u(\gamma _1)\cap W^s(\gamma _0) $
(respectively,
$W^u(\gamma _1)\cap W^s(\gamma _0) $
(respectively,
 $W^u(\gamma _2)\cap W^s(\gamma _1) $
) has two connected components where both are inessential connections, then the algebraic intersection number between
$W^u(\gamma _2)\cap W^s(\gamma _1) $
) has two connected components where both are inessential connections, then the algebraic intersection number between
 $h_2(\gamma _1)$
and
$h_2(\gamma _1)$
and
 $h_1(\gamma _0)$
(respectively,
$h_1(\gamma _0)$
(respectively,
 $h_2(\gamma _2)$
and
$h_2(\gamma _2)$
and
 $h_1(\gamma _1)$
) in
$h_1(\gamma _1)$
) in
 $\widetilde {\varphi }$
is zero.
$\widetilde {\varphi }$
is zero.
Proof. Let
![]() $\widetilde {\varphi }$
be a morsification of
$\widetilde {\varphi }$
be a morsification of
![]() $\varphi $
and let C be a connected component of
$\varphi $
and let C be a connected component of
![]() $W^u(\gamma _1)\cap W^s(\gamma _0)$
. The next two claims determine properties of the connecting orbits of
$W^u(\gamma _1)\cap W^s(\gamma _0)$
. The next two claims determine properties of the connecting orbits of
![]() $\widetilde {\varphi }$
in C.
$\widetilde {\varphi }$
in C.
Claim 1. If C is inessential, then
![]() $W^u(h_2(\gamma _1))\cap W^s(h_1(\gamma _0))\cap C\neq \emptyset $
in
$W^u(h_2(\gamma _1))\cap W^s(h_1(\gamma _0))\cap C\neq \emptyset $
in
![]() $\widetilde {\varphi }$
.
$\widetilde {\varphi }$
.
Suppose
![]() $W^u(h_2(\gamma _1))\cap W^s(h_1(\gamma _0))\cap C=\emptyset $
. Hence,
$W^u(h_2(\gamma _1))\cap W^s(h_1(\gamma _0))\cap C=\emptyset $
. Hence,
![]() $[W^u(h_1(\gamma _1))\cup W^u( h_2(\gamma _1))]\cap W^s(h_0(\gamma _0))\cap C = S^1\times (0,1)$
. There is a contractible neighborhood U of
$[W^u(h_1(\gamma _1))\cup W^u( h_2(\gamma _1))]\cap W^s(h_0(\gamma _0))\cap C = S^1\times (0,1)$
. There is a contractible neighborhood U of
![]() $h_0(\gamma _0)$
such that
$h_0(\gamma _0)$
such that
![]() $U\subset W^s(\gamma _0)$
and
$U\subset W^s(\gamma _0)$
and
Note that, given a non-contractible closed curve
![]() $\alpha $
in F, there is a disc
$\alpha $
in F, there is a disc
![]() $D $
in U such that
$D $
in U such that
![]() $\alpha $
is the boundary of D, that is,
$\alpha $
is the boundary of D, that is,
![]() $\partial {D}=\alpha $
. Hence, D is an essential compressing disc for F and the connection between
$\partial {D}=\alpha $
. Hence, D is an essential compressing disc for F and the connection between
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _0$
is an essential connection.
$\gamma _0$
is an essential connection.
Claim 2. If C is inessential, then all connections between
![]() $h_2(\gamma _1)$
and
$h_2(\gamma _1)$
and
![]() $h_1(\gamma _0)$
of
$h_1(\gamma _0)$
of
![]() $\widetilde {\varphi }$
in C have the same characteristic sign.
$\widetilde {\varphi }$
in C have the same characteristic sign.
In fact, the characteristic sign of an orbit connecting
![]() $h_2(\gamma _1)$
and
$h_2(\gamma _1)$
and
![]() $h_1(\gamma _0)$
is determined by two orientations: the orientation induced by the flow and the orientation on the connecting manifold
$h_1(\gamma _0)$
is determined by two orientations: the orientation induced by the flow and the orientation on the connecting manifold
![]() $\mathcal {M}_{h_2(\gamma _1)h_1(\gamma _0)}$
induced by the isomorphism (2). Either the orientation induced by the isomorphism (2) is compatible with the flow orientation for all orbits in
$\mathcal {M}_{h_2(\gamma _1)h_1(\gamma _0)}$
induced by the isomorphism (2). Either the orientation induced by the isomorphism (2) is compatible with the flow orientation for all orbits in
![]() $\mathcal {M}_{h_2(\gamma _1)h_1(\gamma _0)}\cap C$
or they are all not compatible. See Figure 5. Hence, all connecting orbits between
$\mathcal {M}_{h_2(\gamma _1)h_1(\gamma _0)}\cap C$
or they are all not compatible. See Figure 5. Hence, all connecting orbits between
![]() $h_2(\gamma _1)$
and
$h_2(\gamma _1)$
and
![]() $h_1(\gamma _0)$
in C have the same characteristic sign.
$h_1(\gamma _0)$
in C have the same characteristic sign.

Figure 5 Orientation of the connecting manifolds.
Case (1) follows from the claims above and the fact that
![]() $\Delta ^{\mathrm {NMS}}$
is a TU matrix.
$\Delta ^{\mathrm {NMS}}$
is a TU matrix.
In order to prove (2), let
![]() $C_1$
and
$C_1$
and
![]() $C_2$
be the connected components of
$C_2$
be the connected components of
![]() $W^u(\gamma _1)\cap W^s(\gamma _0)$
. The numbers of connecting orbits in
$W^u(\gamma _1)\cap W^s(\gamma _0)$
. The numbers of connecting orbits in
![]() $W^u(h_2(\gamma _1))\cap W^s(h_1(\gamma _0))\cap C_1$
and
$W^u(h_2(\gamma _1))\cap W^s(h_1(\gamma _0))\cap C_1$
and
![]() $W^u(h_2(\gamma _1))\cap W^s(h_1(\gamma _0))\cap C_2$
must be equal since, otherwise, there would be self-intersection in
$W^u(h_2(\gamma _1))\cap W^s(h_1(\gamma _0))\cap C_2$
must be equal since, otherwise, there would be self-intersection in
![]() $W^u(h_2(\gamma _1))$
. It follows that the intersection number
$W^u(h_2(\gamma _1))$
. It follows that the intersection number
![]() $n(h_2(\gamma _1),h_1(\gamma _0);\widetilde {\varphi })$
is a sum of an even number of
$n(h_2(\gamma _1),h_1(\gamma _0);\widetilde {\varphi })$
is a sum of an even number of
![]() $+1$
and
$+1$
and
![]() $-1$
and hence it must be an even number. Since
$-1$
and hence it must be an even number. Since
![]() $\widetilde {\varphi }\in TUM(\varphi )$
, then
$\widetilde {\varphi }\in TUM(\varphi )$
, then
![]() $n(h_2(\gamma _1),h_1(\gamma _0);\widetilde {\varphi })=0$
.
$n(h_2(\gamma _1),h_1(\gamma _0);\widetilde {\varphi })=0$
.
The proof with respect to the connections between a periodic orbits
![]() $\gamma _2$
and
$\gamma _2$
and
![]() $\gamma _1$
is completely analogous.
$\gamma _1$
is completely analogous.
Definition 3.4. Let C be an essential connected component of
![]() $W^u(\gamma _{i+1})\cap W^s(\gamma _i)$
, for
$W^u(\gamma _{i+1})\cap W^s(\gamma _i)$
, for
![]() $i=0,1$
. We say that C is
$i=0,1$
. We say that C is
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free if there exists a morsification
$h_1$
free if there exists a morsification
![]() $\widetilde {\varphi }\in TUM(\varphi )$
of
$\widetilde {\varphi }\in TUM(\varphi )$
of
![]() $\varphi $
such that
$\varphi $
such that
![]() $W^u(h_2(\gamma _{i+1}))\cap W^s(h_1(\gamma _i))\cap C=\emptyset $
in
$W^u(h_2(\gamma _{i+1}))\cap W^s(h_1(\gamma _i))\cap C=\emptyset $
in
![]() $\widetilde {\varphi }$
. In this case,
$\widetilde {\varphi }$
. In this case,
![]() $\widetilde {\varphi }$
is
$\widetilde {\varphi }$
is
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free in C. If
$h_1$
free in C. If
![]() $\widetilde {\varphi }\in TUM(\varphi )$
is
$\widetilde {\varphi }\in TUM(\varphi )$
is
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free in all essential connections of
$h_1$
free in all essential connections of
![]() $\varphi $
, then
$\varphi $
, then
![]() $\widetilde {\varphi }$
is said to be a
$\widetilde {\varphi }$
is said to be a
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free morsification. The class of
$h_1$
free morsification. The class of
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free morsifications of
$h_1$
free morsifications of
![]() $\varphi $
is denoted by
$\varphi $
is denoted by
![]() $FM(\varphi )$
.
$FM(\varphi )$
.
Corollary 3.5. Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold. Let
$3$
-manifold. Let
![]() $\gamma _0$
and
$\gamma _0$
and
![]() $\gamma _1$
(respectively,
$\gamma _1$
(respectively,
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
) be periodic orbits of
$\gamma _2$
) be periodic orbits of
![]() $\varphi $
and let
$\varphi $
and let
![]() $\widetilde {\varphi }\in TUM(\varphi )$
be a morsification of
$\widetilde {\varphi }\in TUM(\varphi )$
be a morsification of
![]() $\varphi $
on
$\varphi $
on
![]() $\mathcal {U}=\{U_1,U_2\}$
, where
$\mathcal {U}=\{U_1,U_2\}$
, where
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are disjoint neighborhoods of
$U_2$
are disjoint neighborhoods of
![]() $\gamma _0$
and
$\gamma _0$
and
![]() $\gamma _1$
(respectively,
$\gamma _1$
(respectively,
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
). If
$\gamma _2$
). If
![]() $W^u(\gamma _1)\cap W^s(\gamma _0) $
(respectively,
$W^u(\gamma _1)\cap W^s(\gamma _0) $
(respectively,
![]() $W^u(\gamma _2)\cap W^s(\gamma _1) $
) has two connected components, where one is an inessential connection and the other is a
$W^u(\gamma _2)\cap W^s(\gamma _1) $
) has two connected components, where one is an inessential connection and the other is a
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free essential connection, then there is a unique connection between
$h_1$
free essential connection, then there is a unique connection between
![]() $h_2(\gamma _1)$
and
$h_2(\gamma _1)$
and
![]() $h_1(\gamma _0)$
(respectively,
$h_1(\gamma _0)$
(respectively,
![]() $h_2(\gamma _2)$
and
$h_2(\gamma _2)$
and
![]() $h_1(\gamma _1)$
) in
$h_1(\gamma _1)$
) in
![]() $\widetilde {\varphi }$
.
$\widetilde {\varphi }$
.
Given periodic orbits
![]() $\gamma \in \Gamma _k(\varphi )$
and
$\gamma \in \Gamma _k(\varphi )$
and
![]() $\beta \in \Gamma _{k-1}(\varphi )$
, we denote by
$\beta \in \Gamma _{k-1}(\varphi )$
, we denote by
![]() $\Delta (\gamma ,\beta )$
the following submatrix of
$\Delta (\gamma ,\beta )$
the following submatrix of
![]() $\Delta ^{\mathrm {NMS}}$
.
$\Delta ^{\mathrm {NMS}}$
.
 $$ \begin{align*} \Delta(\gamma,\beta) = \left[ \begin{array}{@{}cc@{}} n(h_k(\gamma), h_{k-1}(\beta)) & n(h_{k+1}(\gamma), h_{k-1}(\beta)) \\ n(h_k(\gamma), h_{k}(\beta)) & n(h_{k+1}(\gamma), h_{k}(\beta)) \end{array} \right]\hspace{-2pt}. \end{align*} $$
$$ \begin{align*} \Delta(\gamma,\beta) = \left[ \begin{array}{@{}cc@{}} n(h_k(\gamma), h_{k-1}(\beta)) & n(h_{k+1}(\gamma), h_{k-1}(\beta)) \\ n(h_k(\gamma), h_{k}(\beta)) & n(h_{k+1}(\gamma), h_{k}(\beta)) \end{array} \right]\hspace{-2pt}. \end{align*} $$
We denote by
![]() $E_{ij}$
the
$E_{ij}$
the
![]() $2\times 2$
matrix having one non-zero entry only, namely, the entry
$2\times 2$
matrix having one non-zero entry only, namely, the entry
![]() $(i,j)$
, which is equal to one. Let I be the identity
$(i,j)$
, which is equal to one. Let I be the identity
![]() $2\times 2$
matrix and let
$2\times 2$
matrix and let
![]() $\widetilde {I}$
be the matrix
$\widetilde {I}$
be the matrix
 $$ \begin{align*} \left[ \begin{array}{cc} 1 & 0 \\ 0 & - 1 \end{array} \right].\end{align*} $$
$$ \begin{align*} \left[ \begin{array}{cc} 1 & 0 \\ 0 & - 1 \end{array} \right].\end{align*} $$
Proposition 3.6. Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, and let
$3$
-manifold, and let
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be the chain complex associated to a morsification
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be the chain complex associated to a morsification
![]() $\widetilde {\varphi }\in TUM(\varphi )$
of
$\widetilde {\varphi }\in TUM(\varphi )$
of
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $\gamma _0$
and
$\gamma _0$
and
![]() $\gamma _1$
(respectively,
$\gamma _1$
(respectively,
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
) be periodic orbits of
$\gamma _2$
) be periodic orbits of
![]() $\varphi $
such that
$\varphi $
such that
![]() $\widetilde {\varphi }$
is
$\widetilde {\varphi }$
is
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free in all essential connections between
$h_1$
free in all essential connections between
![]() $\gamma _0$
and
$\gamma _0$
and
![]() $\gamma _1$
(respectively,
$\gamma _1$
(respectively,
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
). Then the following hold.
$\gamma _2$
). Then the following hold.
-
(1)
 $\Delta (\gamma _1,\gamma _0)$
is an isomorphism if and only if there is a unique inessential cylinder of connections between the periodic orbits
$\Delta (\gamma _1,\gamma _0)$
is an isomorphism if and only if there is a unique inessential cylinder of connections between the periodic orbits
 $\gamma _1$
and
$\gamma _1$
and
 $\gamma _{0}$
. Analogously,
$\gamma _{0}$
. Analogously,
 $\Delta (\gamma _2,\gamma _1)$
is an isomorphism if and only if there is a unique inessential cylinder of connections between the periodic orbits
$\Delta (\gamma _2,\gamma _1)$
is an isomorphism if and only if there is a unique inessential cylinder of connections between the periodic orbits
 $\gamma _2$
and
$\gamma _2$
and
 $\gamma _{1}$
.
$\gamma _{1}$
. -
(2)
 $ \Delta (\gamma _1,\gamma _{0})= \pm E_{11}$
if and only if there is a unique essential cylinder of connections between
$ \Delta (\gamma _1,\gamma _{0})= \pm E_{11}$
if and only if there is a unique essential cylinder of connections between
 $\gamma _1$
and
$\gamma _1$
and
 $\gamma _{0}$
and there is an attracting periodic orbit
$\gamma _{0}$
and there is an attracting periodic orbit
 $\gamma _0^{\prime }\neq \gamma _{0}$
such that
$\gamma _0^{\prime }\neq \gamma _{0}$
such that
 $\Delta (\gamma _1,\gamma _{0}^{\prime }) $
is non-zero. Analogously,
$\Delta (\gamma _1,\gamma _{0}^{\prime }) $
is non-zero. Analogously,
 $ \Delta (\gamma _2,\gamma _{1})= \pm E_{22}$
if and only if there is a unique essential cylinder of connections between
$ \Delta (\gamma _2,\gamma _{1})= \pm E_{22}$
if and only if there is a unique essential cylinder of connections between
 $\gamma _1$
and
$\gamma _1$
and
 $\gamma _{2}$
and there is a repelling periodic orbit
$\gamma _{2}$
and there is a repelling periodic orbit
 $\gamma _2^{\prime }\neq \gamma _{2}$
such that
$\gamma _2^{\prime }\neq \gamma _{2}$
such that
 $\Delta (\gamma _2,\gamma _{1}^{\prime }) $
is non-zero.
$\Delta (\gamma _2,\gamma _{1}^{\prime }) $
is non-zero. -
(3)
 $ \Delta (\gamma _1,\gamma _{0})= \pm E_{22}$
if and only if
$ \Delta (\gamma _1,\gamma _{0})= \pm E_{22}$
if and only if
 $\gamma _1$
double connects with
$\gamma _1$
double connects with
 $\gamma _0$
through an inessential and an essential cylinder of connections. Analogously,
$\gamma _0$
through an inessential and an essential cylinder of connections. Analogously,
 $ \Delta (\gamma _2,\gamma _{1})= \pm E_{11}$
if and only if
$ \Delta (\gamma _2,\gamma _{1})= \pm E_{11}$
if and only if
 $\gamma _1$
double connects with
$\gamma _1$
double connects with
 $\gamma _2$
through an inessential and an essential cylinder of connections.
$\gamma _2$
through an inessential and an essential cylinder of connections.
Note that if
![]() $ \Delta (\gamma _k,\gamma _{k\!-\!1})$
is zero, for
$ \Delta (\gamma _k,\gamma _{k\!-\!1})$
is zero, for
![]() $k=1$
or
$k=1$
or
![]() $k=2$
, it does not necessarily mean that
$k=2$
, it does not necessarily mean that
![]() $W^u(\gamma _k)\cap W^s(\gamma _{k\!-\!1})$
is empty. For instance, this is the case when there are two inessential cylinders of connections between
$W^u(\gamma _k)\cap W^s(\gamma _{k\!-\!1})$
is empty. For instance, this is the case when there are two inessential cylinders of connections between
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $ \gamma _{k\!-\!1}$
. Also, if
$ \gamma _{k\!-\!1}$
. Also, if
![]() $\gamma ^1_k$
and
$\gamma ^1_k$
and
![]() $\gamma ^2_k$
are both attracting periodic orbits or are both repelling periodic orbits, then the associated map in the connection matrix is the null map.
$\gamma ^2_k$
are both attracting periodic orbits or are both repelling periodic orbits, then the associated map in the connection matrix is the null map.
Theorems 3.7 and 3.8 provide a characterization for the columns and rows of the differential
![]() $\Delta $
associated to an
$\Delta $
associated to an
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free morsification
$h_1$
free morsification
![]() $\widetilde {\varphi }$
of
$\widetilde {\varphi }$
of
![]() $\varphi $
. This characterization is done in terms of the matrices
$\varphi $
. This characterization is done in terms of the matrices
![]() $E_{ij}$
, I and
$E_{ij}$
, I and
![]() $\widetilde {I}$
.
$\widetilde {I}$
.
Theorem 3.7. (Column characterization of the differential matrix)
Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, and let
$3$
-manifold, and let
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be an NMS-chain complex such that
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be an NMS-chain complex such that
![]() $\widetilde {\varphi }\in TUM(\varphi )$
. Let
$\widetilde {\varphi }\in TUM(\varphi )$
. Let
![]() $\{\gamma _{0}^{\ell }\}_{\ell }$
be attracting periodic orbits of
$\{\gamma _{0}^{\ell }\}_{\ell }$
be attracting periodic orbits of
![]() $\varphi $
. Given a saddle periodic orbit
$\varphi $
. Given a saddle periodic orbit
![]() $\gamma _1$
, the maps
$\gamma _1$
, the maps
![]() $\Delta (\gamma _1,\gamma _0^{\ell })$
satisfy one of the following conditions.
$\Delta (\gamma _1,\gamma _0^{\ell })$
satisfy one of the following conditions.
-
(1)
 $\Delta (\gamma _1,\gamma _0^{\ell })$
is the null map for all
$\Delta (\gamma _1,\gamma _0^{\ell })$
is the null map for all
 $\ell $
.
$\ell $
. -
(2) There is
 ${\ell }_1$
such that
${\ell }_1$
such that
 $\Delta (\gamma _1,\gamma _0^{\ell _1})$
is the map
$\Delta (\gamma _1,\gamma _0^{\ell _1})$
is the map
 $\pm E_{22}$
and
$\pm E_{22}$
and
 $\Delta (\gamma _1,\gamma _0^{\ell })$
is the zero map for all
$\Delta (\gamma _1,\gamma _0^{\ell })$
is the zero map for all
 ${\ell }\neq {\ell }_{1}$
.
${\ell }\neq {\ell }_{1}$
. -
(3) There are
 ${\ell }_1,{\ell }_2$
such that the map
${\ell }_1,{\ell }_2$
such that the map
 $\Delta (\gamma _1,\gamma _0^{{\ell }_1})$
is either I,
$\Delta (\gamma _1,\gamma _0^{{\ell }_1})$
is either I,
 $\widetilde {I}$
or
$\widetilde {I}$
or
 $ E_{11}$
, the map
$ E_{11}$
, the map
 $\Delta (\gamma _1,\gamma _0^{{\ell }_2})$
is either
$\Delta (\gamma _1,\gamma _0^{{\ell }_2})$
is either
 $- I$
,
$- I$
,
 $- \widetilde {I}$
or
$- \widetilde {I}$
or
 $- E_{11}$
and
$- E_{11}$
and
 $\Delta (\gamma _1,\gamma _0^{\ell })$
is the zero map for all
$\Delta (\gamma _1,\gamma _0^{\ell })$
is the zero map for all
 ${\ell }\neq {\ell }_{1},{\ell }_{2}$
.
${\ell }\neq {\ell }_{1},{\ell }_{2}$
.
Proof. By Proposition 3.1,
![]() $\gamma _1$
connects with either one or two attracting periodic orbits. Hence, at most two maps
$\gamma _1$
connects with either one or two attracting periodic orbits. Hence, at most two maps
![]() $\Delta (\gamma _1,\gamma _0^{\ell })$
are non-zero.
$\Delta (\gamma _1,\gamma _0^{\ell })$
are non-zero.
Suppose that
![]() $\gamma _1$
connects with only one attracting periodic orbit
$\gamma _1$
connects with only one attracting periodic orbit
![]() $\gamma _{0}^{{\ell }_1}$
(see Figure 6). Then
$\gamma _{0}^{{\ell }_1}$
(see Figure 6). Then
![]() $h_{1}(\gamma _{1})$
double connects to an index
$h_{1}(\gamma _{1})$
double connects to an index
![]() $0$
critical point of
$0$
critical point of
![]() $\widetilde {\varphi }$
, which means that the column of
$\widetilde {\varphi }$
, which means that the column of
![]() $h_{1}(\gamma _{1})$
has only zero entries. On the other hand, the column corresponding to
$h_{1}(\gamma _{1})$
has only zero entries. On the other hand, the column corresponding to
![]() $h_{2}(\gamma _{1})$
is either a zero column or it has a unique non-zero entry in the row corresponding to
$h_{2}(\gamma _{1})$
is either a zero column or it has a unique non-zero entry in the row corresponding to
![]() $h_{1}(\gamma _{0}^{{\ell }_1})$
, which is
$h_{1}(\gamma _{0}^{{\ell }_1})$
, which is
![]() $\pm 1$
. Hence,
$\pm 1$
. Hence,
![]() $\Delta (\gamma _1,\gamma _0^{{\ell }_1})$
is the null map or
$\Delta (\gamma _1,\gamma _0^{{\ell }_1})$
is the null map or
![]() $\pm E_{22}$
.
$\pm E_{22}$
.

Figure 6 Double connection through an inessential and an essential cylinder of connections.
Suppose that
![]() $\gamma _1$
connects with two attracting periodic orbits
$\gamma _1$
connects with two attracting periodic orbits
![]() $\gamma _{0}^{{\ell }_1}$
and
$\gamma _{0}^{{\ell }_1}$
and
![]() $\gamma _{0}^{{\ell }_2}$
. Then
$\gamma _{0}^{{\ell }_2}$
. Then
![]() $h_{1}(\gamma _{1})$
connects with two index
$h_{1}(\gamma _{1})$
connects with two index
![]() $0$
critical points, namely,
$0$
critical points, namely,
![]() $h_0(\gamma _0^{{\ell }_1})$
and
$h_0(\gamma _0^{{\ell }_1})$
and
![]() $h_0(\gamma _0^{{\ell }_2})$
of
$h_0(\gamma _0^{{\ell }_2})$
of
![]() $\widetilde {\varphi }$
, and hence the column of
$\widetilde {\varphi }$
, and hence the column of
![]() $h_{1}(\gamma _{1})$
has exactly two non-zero entries,
$h_{1}(\gamma _{1})$
has exactly two non-zero entries,
![]() $+1$
and
$+1$
and
![]() $-1$
, corresponding to these connections. On the other hand, the column corresponding to
$-1$
, corresponding to these connections. On the other hand, the column corresponding to
![]() $h_{2}(\gamma _{1})$
is either a zero column or it has non-zero entries in the rows corresponding to
$h_{2}(\gamma _{1})$
is either a zero column or it has non-zero entries in the rows corresponding to
![]() $h_{1}(\gamma _{0}^{{\ell }_1})$
or
$h_{1}(\gamma _{0}^{{\ell }_1})$
or
![]() $h_{1}(\gamma _{0}^{{\ell }_2})$
. Hence,
$h_{1}(\gamma _{0}^{{\ell }_2})$
. Hence,
![]() $\Delta (\gamma _1,\gamma _0^{{\ell }_i})$
is the map
$\Delta (\gamma _1,\gamma _0^{{\ell }_i})$
is the map
![]() $\pm I$
,
$\pm I$
,
![]() $\pm \widetilde {I}$
or
$\pm \widetilde {I}$
or
![]() $\pm E_{11}$
for
$\pm E_{11}$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $\Delta (\gamma _1,\gamma _0^{{\ell }})$
is the null map for
$\Delta (\gamma _1,\gamma _0^{{\ell }})$
is the null map for
![]() $\ell \neq {\ell }_1,{\ell }_2$
.
$\ell \neq {\ell }_1,{\ell }_2$
.
Theorem 3.8. (Row characterization of the differential matrix)
Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, and let
$3$
-manifold, and let
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be an NMS-chain complex such that
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be an NMS-chain complex such that
![]() $\widetilde {\varphi }\in TUM(\varphi )$
. Let
$\widetilde {\varphi }\in TUM(\varphi )$
. Let
![]() $\{\gamma _{2}^{\ell }\}_{\ell }$
be the repelling periodic orbits of
$\{\gamma _{2}^{\ell }\}_{\ell }$
be the repelling periodic orbits of
![]() $\varphi $
. Given a saddle periodic orbit
$\varphi $
. Given a saddle periodic orbit
![]() $\gamma _1$
, the maps
$\gamma _1$
, the maps
![]() $\Delta (\gamma _2^{{\ell }},\gamma _1)$
satisfy one of the following conditions.
$\Delta (\gamma _2^{{\ell }},\gamma _1)$
satisfy one of the following conditions.
-
(1)
 $\Delta (\gamma _2^{{\ell }},\gamma _1)$
is the null map for all
$\Delta (\gamma _2^{{\ell }},\gamma _1)$
is the null map for all
 ${\ell }$
.
${\ell }$
. -
(2) There is
 ${\ell }_1$
such that
${\ell }_1$
such that
 $\Delta (\gamma _2^{{\ell }_1},\gamma _1)$
is the map
$\Delta (\gamma _2^{{\ell }_1},\gamma _1)$
is the map
 $\pm E_{11}$
and
$\pm E_{11}$
and
 $\Delta (\gamma _2^{{\ell }},\gamma _1)$
is the zero map for all
$\Delta (\gamma _2^{{\ell }},\gamma _1)$
is the zero map for all
 ${\ell }\neq {\ell }_{1}$
;
${\ell }\neq {\ell }_{1}$
; -
(3) There are
 ${\ell }_1,{\ell }_2$
such that the map
${\ell }_1,{\ell }_2$
such that the map
 $\Delta (\gamma _2^{{\ell }_1},\gamma _1)$
is either
$\Delta (\gamma _2^{{\ell }_1},\gamma _1)$
is either
 $ I$
,
$ I$
,
 $ \widetilde {I}$
or
$ \widetilde {I}$
or
 $ E_{22}$
, the map
$ E_{22}$
, the map
 $\Delta (\gamma _2^{{\ell }_2},\gamma _1)$
is either
$\Delta (\gamma _2^{{\ell }_2},\gamma _1)$
is either
 $- I$
,
$- I$
,
 $- \widetilde {I}$
or
$- \widetilde {I}$
or
 $- E_{22}$
and
$- E_{22}$
and
 $\Delta (\gamma _2^{{\ell }},\gamma _1)$
is the zero map for all
$\Delta (\gamma _2^{{\ell }},\gamma _1)$
is the zero map for all
 ${\ell }\neq {\ell }_{1},{\ell }_{2}$
.
${\ell }\neq {\ell }_{1},{\ell }_{2}$
.
Proof. The proof follows from the previous theorem by considering the reverse flow.
Note that, if
![]() $\gamma _2 \in \Gamma _2(\varphi )$
is a repelling periodic orbit and
$\gamma _2 \in \Gamma _2(\varphi )$
is a repelling periodic orbit and
![]() $\gamma _0 \in \Gamma _{0}(\varphi )$
is an attracting periodic orbit, the corresponding submatrix of
$\gamma _0 \in \Gamma _{0}(\varphi )$
is an attracting periodic orbit, the corresponding submatrix of
![]() $\Delta $
is
$\Delta $
is
 $$ \begin{align*} \Delta(\gamma_2,\gamma_0) = \left[ \begin{array}{@{}cc@{}} n(h_2(\gamma_2), h_{0}(\gamma_0)) & n(h_{3}(\gamma_2), h_{0}(\gamma_0)) \\ n(h_2(\gamma_2), h_{1}(\gamma_0)) & n(h_{3}(\gamma_2), h_{1}(\gamma_0)) \end{array} \right]\hspace{-2pt},\end{align*} $$
$$ \begin{align*} \Delta(\gamma_2,\gamma_0) = \left[ \begin{array}{@{}cc@{}} n(h_2(\gamma_2), h_{0}(\gamma_0)) & n(h_{3}(\gamma_2), h_{0}(\gamma_0)) \\ n(h_2(\gamma_2), h_{1}(\gamma_0)) & n(h_{3}(\gamma_2), h_{1}(\gamma_0)) \end{array} \right]\hspace{-2pt},\end{align*} $$
which is either a zero matrix or
![]() $\pm E_{21}$
.
$\pm E_{21}$
.
Example 3.9. Let
![]() $H_1$
and
$H_1$
and
![]() $H_2$
be two handlebodies. Consider
$H_2$
be two handlebodies. Consider
![]() $H_i\setminus D^3_i$
a handlebody minus a
$H_i\setminus D^3_i$
a handlebody minus a
![]() $3$
-ball in the interior of
$3$
-ball in the interior of
![]() $H_i$
, for
$H_i$
, for
![]() $i=1,2$
. Consider an NMS flow
$i=1,2$
. Consider an NMS flow
![]() $\varphi _1$
on the attractor
$\varphi _1$
on the attractor
![]() $H_1\setminus D^3_1$
transverse to the boundaries with two attracting periodic orbits
$H_1\setminus D^3_1$
transverse to the boundaries with two attracting periodic orbits
![]() $\gamma _0^1$
and
$\gamma _0^1$
and
![]() $\gamma _0^2$
and two saddle periodic orbits
$\gamma _0^2$
and two saddle periodic orbits
![]() $\gamma _1^3$
and
$\gamma _1^3$
and
![]() $\gamma _1^4$
. Similarly, consider an NMS flow
$\gamma _1^4$
. Similarly, consider an NMS flow
![]() $\varphi _2$
on the repeller
$\varphi _2$
on the repeller
![]() $H_2\setminus D^3_2$
transverse to the boundaries with one repelling periodic orbit
$H_2\setminus D^3_2$
transverse to the boundaries with one repelling periodic orbit
![]() $\gamma _2^6$
and one saddle periodic orbit
$\gamma _2^6$
and one saddle periodic orbit
![]() $\gamma _1^5$
. By gluing
$\gamma _1^5$
. By gluing
![]() $H_1\setminus D^3_1$
to
$H_1\setminus D^3_1$
to
![]() $H_2\setminus D^3_2$
via the identification of
$H_2\setminus D^3_2$
via the identification of
![]() $m_1$
with
$m_1$
with
![]() $\ell _2$
and
$\ell _2$
and
![]() $m_2$
with
$m_2$
with
![]() $\ell _1$
, one obtains
$\ell _1$
, one obtains
![]() $S^3\setminus \{D^3_1\cup D^3_2\}$
(see Figure 7). Now, by identifying the boundaries of
$S^3\setminus \{D^3_1\cup D^3_2\}$
(see Figure 7). Now, by identifying the boundaries of
![]() $D^3_1$
and
$D^3_1$
and
![]() $D^3_2$
, one obtains an NMS flow
$D^3_2$
, one obtains an NMS flow
![]() $\varphi $
on
$\varphi $
on
![]() $S^1\times S^2$
.
$S^1\times S^2$
.

Figure 7 NMS flow on
![]() $S^1\times S^2$
.
$S^1\times S^2$
.
Figure 8 shows the differential of an NMS-chain complex
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
associated to
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
associated to
![]() ${\varphi }$
, where
${\varphi }$
, where
![]() $\widetilde {\varphi }$
is a
$\widetilde {\varphi }$
is a
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free morsification of
$h_1$
free morsification of
![]() $\varphi $
.
$\varphi $
.

Figure 8 Differential
![]() $\Delta ^{\mathrm {NMS}}$
associated to
$\Delta ^{\mathrm {NMS}}$
associated to
![]() ${\varphi }$
.
${\varphi }$
.
3.2 Local cancellations and reductions of periodic orbits
The goal of this section is to determine sufficient conditions under which two periodic orbits in
![]() $\varphi \in \Sigma (M^3)$
can be cancelled or reduced.
$\varphi \in \Sigma (M^3)$
can be cancelled or reduced.
Definition 3.10. Let
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
be periodic orbits of an NMS flow
$\gamma _{k-1}$
be periodic orbits of an NMS flow
![]() $\varphi $
, of indices k and
$\varphi $
, of indices k and
![]() $k-1$
, respectively. The orbits
$k-1$
, respectively. The orbits
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
can be cancelled if there exists an NMS flow
$\gamma _{k-1}$
can be cancelled if there exists an NMS flow
![]() ${\varphi }'$
in M that coincides with
${\varphi }'$
in M that coincides with
![]() $\varphi $
outside a neighborhood U of
$\varphi $
outside a neighborhood U of
![]() $W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and
$W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and
![]() ${\varphi }'$
has empty chain recurrent set in U. The orbits
${\varphi }'$
has empty chain recurrent set in U. The orbits
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
can be reduced if there exists an NMS flow
$\gamma _{k-1}$
can be reduced if there exists an NMS flow
![]() ${\varphi }'$
on M that coincides with
${\varphi }'$
on M that coincides with
![]() $\varphi $
outside a neighborhood U of
$\varphi $
outside a neighborhood U of
![]() $W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and the chain recurrent set of
$W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and the chain recurrent set of
![]() ${\varphi }'$
restricted to U is a unique periodic orbit
${\varphi }'$
restricted to U is a unique periodic orbit
![]() $\gamma '$
.
$\gamma '$
.
Note that, if
![]() $k=2$
,
$k=2$
,
![]() $\gamma '$
is a repelling periodic orbit, and if
$\gamma '$
is a repelling periodic orbit, and if
![]() $k=1$
,
$k=1$
,
![]() $\gamma '$
is an attracting periodic orbit.
$\gamma '$
is an attracting periodic orbit.
Theorem 3.11. (Local cancellation of periodic orbits)
Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, and let
$3$
-manifold, and let
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be the NMS-chain complex such that
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be the NMS-chain complex such that
![]() $\widetilde {\varphi }\in TUM(\varphi )$
. Let
$\widetilde {\varphi }\in TUM(\varphi )$
. Let
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
be two periodic orbits of indices k and
$\gamma _{k-1}$
be two periodic orbits of indices k and
![]() $k-1$
, respectively, such that
$k-1$
, respectively, such that
![]() $\widetilde {\varphi }$
is
$\widetilde {\varphi }$
is
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free in an essential connection between
$h_1$
free in an essential connection between
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
. If the map
$\gamma _{k-1}$
. If the map
![]() $\Delta (\gamma _k,\gamma _{k\!-\!1})$
is an isomorphism, then there exists an NMS flow
$\Delta (\gamma _k,\gamma _{k\!-\!1})$
is an isomorphism, then there exists an NMS flow
![]() ${\varphi }'$
in M that coincides with
${\varphi }'$
in M that coincides with
![]() $\varphi $
outside a neighborhood U of
$\varphi $
outside a neighborhood U of
![]() $W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and
$W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and
![]() ${\varphi }'$
has empty chain recurrent set in U.
${\varphi }'$
has empty chain recurrent set in U.
Proof. Since
![]() $\Delta (\gamma _k,\gamma _{k\!-\!1})$
is an isomorphism, by Proposition 3.6, there is a unique inessential cylinder of connections between
$\Delta (\gamma _k,\gamma _{k\!-\!1})$
is an isomorphism, by Proposition 3.6, there is a unique inessential cylinder of connections between
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
.
$\gamma _{k-1}$
.
Let U be a neighborhood of
![]() $W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
that does not intersect any other periodic orbit of
$W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
that does not intersect any other periodic orbit of
![]() $\varphi $
.
$\varphi $
.
By the proof of Theorem 3.3, there is a unique orbit
![]() $u_1$
between
$u_1$
between
![]() $h_{k+1}(\gamma _{k})$
and
$h_{k+1}(\gamma _{k})$
and
![]() $h_{k}(\gamma _{k\!-\!1})$
, as well as, a unique orbit
$h_{k}(\gamma _{k\!-\!1})$
, as well as, a unique orbit
![]() $u_2$
between
$u_2$
between
![]() $h_{k}(\gamma _{k})$
and
$h_{k}(\gamma _{k})$
and
![]() $h_{k-1}(\gamma _{k\!-\!1})$
in the morsification
$h_{k-1}(\gamma _{k\!-\!1})$
in the morsification
![]() $\widetilde {\varphi }$
of
$\widetilde {\varphi }$
of
![]() $\varphi $
. Consider disjoint neighborhoods
$\varphi $
. Consider disjoint neighborhoods
![]() $V_i$
of
$V_i$
of
![]() $u_i$
, for
$u_i$
, for
![]() $i=1,2$
, such that
$i=1,2$
, such that
![]() $V_i\subset U$
. By Smale’s first cancellation theorem [Reference Milnor18], one may cancel
$V_i\subset U$
. By Smale’s first cancellation theorem [Reference Milnor18], one may cancel
![]() $h_{k+1}(\gamma _{k})$
and
$h_{k+1}(\gamma _{k})$
and
![]() $h_{k}(\gamma _{k\!-\!1})$
, resulting in a flow
$h_{k}(\gamma _{k\!-\!1})$
, resulting in a flow
![]() $\widetilde {\varphi }_1$
that coincides with
$\widetilde {\varphi }_1$
that coincides with
![]() $\widetilde {\varphi }$
outside
$\widetilde {\varphi }$
outside
![]() $V_1$
and has no critical points in
$V_1$
and has no critical points in
![]() $V_1$
. Note that, during this process of cancellation, the flow is not altered in
$V_1$
. Note that, during this process of cancellation, the flow is not altered in
![]() $V_2$
. Hence, there remains a unique orbit
$V_2$
. Hence, there remains a unique orbit
![]() $u_2$
between
$u_2$
between
![]() $h_{k}(\gamma _{k})$
and
$h_{k}(\gamma _{k})$
and
![]() $h_{k-1}(\gamma _{k\!-\!1})$
in
$h_{k-1}(\gamma _{k\!-\!1})$
in
![]() $\widetilde {\varphi }_1$
. Applying Smale’s first cancellation theorem once more to cancel
$\widetilde {\varphi }_1$
. Applying Smale’s first cancellation theorem once more to cancel
![]() $h_{k}(\gamma _{k})$
and
$h_{k}(\gamma _{k})$
and
![]() $h_{k-1}(\gamma _{k\!-\!1})$
, one obtains a flow
$h_{k-1}(\gamma _{k\!-\!1})$
, one obtains a flow
![]() $\widetilde {\varphi }_2$
that coincides with
$\widetilde {\varphi }_2$
that coincides with
![]() $\widetilde {\varphi }_1$
outside
$\widetilde {\varphi }_1$
outside
![]() $V_2$
and has no critical points in
$V_2$
and has no critical points in
![]() $V_2$
. By Theorem 2.1, one obtains a new NMS flow
$V_2$
. By Theorem 2.1, one obtains a new NMS flow
![]() $\varphi '$
with two fewer periodic orbits, which coincides with
$\varphi '$
with two fewer periodic orbits, which coincides with
![]() $\varphi $
outside U and has empty chain recurrent set in U.
$\varphi $
outside U and has empty chain recurrent set in U.
It follows from Theorem 3.11 that, given periodic orbits of
![]() $\varphi $
,
$\varphi $
,
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
, such that
$\gamma _{k-1}$
, such that
![]() $W^u(\gamma _k)\cap W^s(\gamma _{k-1})$
has only one connected component that is inessential, one can always perturb
$W^u(\gamma _k)\cap W^s(\gamma _{k-1})$
has only one connected component that is inessential, one can always perturb
![]() $\varphi $
in order to obtain a flow with two fewer periodic orbits. In this case, one says that the pair (
$\varphi $
in order to obtain a flow with two fewer periodic orbits. In this case, one says that the pair (
![]() $\gamma _k,\gamma _{k-1}$
) can be cancelled. See Figure 9.
$\gamma _k,\gamma _{k-1}$
) can be cancelled. See Figure 9.

Figure 9 Inessential cylinder of connections between an attracting and a saddle orbit (left) and their cancellation (right).
Theorem 3.12. (Local reduction of periodic orbits)
Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold and let
$3$
-manifold and let
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be an NMS-chain complex such that
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be an NMS-chain complex such that
![]() $\widetilde {\varphi }\in TUM(\varphi )$
. Let
$\widetilde {\varphi }\in TUM(\varphi )$
. Let
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
be periodic orbits of indices k and
$\gamma _{k-1}$
be periodic orbits of indices k and
![]() $k-1$
, respectively, such that
$k-1$
, respectively, such that
![]() $\widetilde {\varphi }$
is
$\widetilde {\varphi }$
is
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free in an essential connection between
$h_1$
free in an essential connection between
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
. If the map
$\gamma _{k-1}$
. If the map
![]() $ \Delta (\gamma _{1},\gamma _{0}) = \pm E_{22}$
(respectively,
$ \Delta (\gamma _{1},\gamma _{0}) = \pm E_{22}$
(respectively,
![]() $ \Delta (\gamma _{2},\gamma _{1})=\pm E_{11}$
), then there exists an NMS flow
$ \Delta (\gamma _{2},\gamma _{1})=\pm E_{11}$
), then there exists an NMS flow
![]() ${\varphi }'$
on M that coincides with
${\varphi }'$
on M that coincides with
![]() $\varphi $
outside a neighborhood U of
$\varphi $
outside a neighborhood U of
![]() $W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and the chain recurrent set of
$W^u(\gamma _k) \cap W^s(\gamma _{k-1})$
and the chain recurrent set of
![]() ${\varphi }'$
restricted to U is a unique attracting (respectively, repelling) periodic orbit.
${\varphi }'$
restricted to U is a unique attracting (respectively, repelling) periodic orbit.
Proof. Consider
![]() $k=1$
and assume that
$k=1$
and assume that
![]() $ \Delta (\gamma _{1},\gamma _{0}) = \pm E_{22}$
. By Proposition 3.6,
$ \Delta (\gamma _{1},\gamma _{0}) = \pm E_{22}$
. By Proposition 3.6,
![]() $\gamma _1$
double connects with
$\gamma _1$
double connects with
![]() $\gamma _0$
and there is a unique inessential cylinder of connections. By Theorem 3.3, there is a unique orbit u between
$\gamma _0$
and there is a unique inessential cylinder of connections. By Theorem 3.3, there is a unique orbit u between
![]() $h_{2}(\gamma _{1})$
and
$h_{2}(\gamma _{1})$
and
![]() $h_{1}(\gamma _{0})$
as well as two orbits
$h_{1}(\gamma _{0})$
as well as two orbits
![]() $v_1$
and
$v_1$
and
![]() $v_2$
between
$v_2$
between
![]() $h_{1}(\gamma _{1})$
and
$h_{1}(\gamma _{1})$
and
![]() $h_{0}(\gamma _{0})$
in the morsification
$h_{0}(\gamma _{0})$
in the morsification
![]() $\widetilde {\varphi }$
of
$\widetilde {\varphi }$
of
![]() $\varphi $
. Let U be a neighborhood of
$\varphi $
. Let U be a neighborhood of
![]() $W^u(\gamma _1) \cap W^s(\gamma _{0})$
that does not intersect any other periodic orbit of
$W^u(\gamma _1) \cap W^s(\gamma _{0})$
that does not intersect any other periodic orbit of
![]() $\varphi $
. Consider a neighborhood
$\varphi $
. Consider a neighborhood
![]() $V\subset U$
of u that does not intersect
$V\subset U$
of u that does not intersect
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. By Smale’s first cancellation theorem, one may cancel
$v_2$
. By Smale’s first cancellation theorem, one may cancel
![]() $h_{2}(\gamma _{1})$
and
$h_{2}(\gamma _{1})$
and
![]() $h_{1}(\gamma _{0})$
, resulting in a flow
$h_{1}(\gamma _{0})$
, resulting in a flow
![]() $\widetilde {\varphi }_1$
that coincides with
$\widetilde {\varphi }_1$
that coincides with
![]() $\widetilde {\varphi }$
outside V and has no critical points in V. Hence, there remain two orbits
$\widetilde {\varphi }$
outside V and has no critical points in V. Hence, there remain two orbits
![]() $v_1$
and
$v_1$
and
![]() $v_2$
between
$v_2$
between
![]() $h_{1}(\gamma _{1})$
and
$h_{1}(\gamma _{1})$
and
![]() $h_{0}(\gamma _{0})$
in
$h_{0}(\gamma _{0})$
in
![]() $\widetilde {\varphi }_1$
. Now apply the reverse morsification process (that is, Theorem 2.1) to obtain a new NMS flow
$\widetilde {\varphi }_1$
. Now apply the reverse morsification process (that is, Theorem 2.1) to obtain a new NMS flow
![]() $\varphi '$
that coincides with
$\varphi '$
that coincides with
![]() $\varphi $
outside U and such that the chain recurrent set restricted to U is exactly one attracting periodic orbit. The case when
$\varphi $
outside U and such that the chain recurrent set restricted to U is exactly one attracting periodic orbit. The case when
![]() $k=2$
is proved analogously.
$k=2$
is proved analogously.
It follows from Theorem 3.12 that, given periodic orbits of
![]() $\varphi $
,
$\varphi $
,
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
such that
$\gamma _{k-1}$
such that
![]() $W^u(\gamma _k)\cap W^s(\gamma _{k-1})$
has two connected components, where one is an inessential connection and the other is a
$W^u(\gamma _k)\cap W^s(\gamma _{k-1})$
has two connected components, where one is an inessential connection and the other is a
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free essential connection, one can always perturb
$h_1$
free essential connection, one can always perturb
![]() $\varphi $
in order to obtain a flow with one fewer periodic orbit. In this case, one says that the pair (
$\varphi $
in order to obtain a flow with one fewer periodic orbit. In this case, one says that the pair (
![]() $\gamma _k,\gamma _{k-1}$
) can be reduced. See Figure 10.
$\gamma _k,\gamma _{k-1}$
) can be reduced. See Figure 10.

Figure 10 Double connection between a saddle and an attracting orbit (left) and reduction to an attracting orbit (right).
3.3 Birth and death of connections
The first step towards understand the global behavior of the flow
![]() $\varphi '$
obtained from
$\varphi '$
obtained from
![]() $\varphi $
via the cancellation of the periodic orbits
$\varphi $
via the cancellation of the periodic orbits
![]() $\gamma _{1}$
and
$\gamma _{1}$
and
![]() $\gamma _{0}$
is to study the effect of the cancellation in terms of essential and inessential connections with the remaining periodic orbits such as
$\gamma _{0}$
is to study the effect of the cancellation in terms of essential and inessential connections with the remaining periodic orbits such as
![]() $\overline \gamma _{1}$
and
$\overline \gamma _{1}$
and
![]() $\overline \gamma _{0}$
.
$\overline \gamma _{0}$
.
Whenever the connection between
![]() $\overline \gamma _{1}$
and
$\overline \gamma _{1}$
and
![]() $\gamma _{0}$
and the connection between
$\gamma _{0}$
and the connection between
![]() $\gamma _{1}$
and
$\gamma _{1}$
and
![]() $\overline \gamma _{0}$
are both inessential connections in
$\overline \gamma _{0}$
are both inessential connections in
![]() $\varphi $
, then the corresponding connection between
$\varphi $
, then the corresponding connection between
![]() $\overline \gamma _{1}$
and
$\overline \gamma _{1}$
and
![]() $\overline \gamma _{0}$
in
$\overline \gamma _{0}$
in
![]() $\varphi '$
is an inessential connection. In fact, considering a morsification
$\varphi '$
is an inessential connection. In fact, considering a morsification
![]() $\widetilde \varphi \in TUM(\varphi )$
(see Figure 11(a)), the cancellations of corresponding pairs of critical points
$\widetilde \varphi \in TUM(\varphi )$
(see Figure 11(a)), the cancellations of corresponding pairs of critical points
![]() $(h_2(\gamma _1), h_1(\gamma _0))$
and
$(h_2(\gamma _1), h_1(\gamma _0))$
and
![]() $(h_1(\gamma _1),h_0(\gamma _0))$
give rise to the flow
$(h_1(\gamma _1),h_0(\gamma _0))$
give rise to the flow
![]() $\widetilde \varphi '$
(see Figure 11(b)). The new connections from
$\widetilde \varphi '$
(see Figure 11(b)). The new connections from
![]() $h_2(\overline \gamma _1)$
to
$h_2(\overline \gamma _1)$
to
![]() $h_1(\overline \gamma _0)$
and from
$h_1(\overline \gamma _0)$
and from
![]() $h_1(\overline \gamma _1)$
to
$h_1(\overline \gamma _1)$
to
![]() $h_0(\overline \gamma _0)$
characterize an inessential connection between
$h_0(\overline \gamma _0)$
characterize an inessential connection between
![]() $\overline \gamma _{1}$
and
$\overline \gamma _{1}$
and
![]() $\overline \gamma _{0}$
in the corresponding NMS flow
$\overline \gamma _{0}$
in the corresponding NMS flow
![]() $\varphi '$
.
$\varphi '$
.

Figure 11 Birth and death of flow lines within
![]() $\overline \gamma _{1}$
-
$\overline \gamma _{1}$
-
![]() $\gamma _{0}$
inessential and
$\gamma _{0}$
inessential and
![]() $\gamma _{1}$
-
$\gamma _{1}$
-
![]() $\overline \gamma _{0}$
inessential connections.
$\overline \gamma _{0}$
inessential connections.
On the other hand, whenever either the connection between
![]() $\overline \gamma _{1}$
and
$\overline \gamma _{1}$
and
![]() $\gamma _{0}$
or the connection between
$\gamma _{0}$
or the connection between
![]() $\gamma _{1}$
and
$\gamma _{1}$
and
![]() $\overline \gamma _{0}$
is an
$\overline \gamma _{0}$
is an
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free essential connection in
$h_1$
free essential connection in
![]() $\varphi $
, then a similar analysis shows that the corresponding connection in
$\varphi $
, then a similar analysis shows that the corresponding connection in
![]() $\varphi '$
is an
$\varphi '$
is an
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free essential connection. See Figures 12, 13, and 14.
$h_1$
free essential connection. See Figures 12, 13, and 14.

Figure 12 Birth and death of flow lines within
![]() $\overline \gamma _{1}$
-
$\overline \gamma _{1}$
-
![]() $\gamma _{0}$
essential and
$\gamma _{0}$
essential and
![]() $\gamma _{1}$
-
$\gamma _{1}$
-
![]() $\overline \gamma _{0}$
inessential connections.
$\overline \gamma _{0}$
inessential connections.

Figure 13 Birth and death of flow lines within
![]() $\overline \gamma _{1}$
-
$\overline \gamma _{1}$
-
![]() $\gamma _{0}$
inessential and
$\gamma _{0}$
inessential and
![]() $\gamma _{1}$
-
$\gamma _{1}$
-
![]() $\overline \gamma _{0}$
essential connections.
$\overline \gamma _{0}$
essential connections.

Figure 14 Birth and death of flow lines within
![]() $\overline \gamma _{1}$
-
$\overline \gamma _{1}$
-
![]() $\gamma _{0}$
essential and
$\gamma _{0}$
essential and
![]() $\gamma _{1}$
-
$\gamma _{1}$
-
![]() $\overline \gamma _{0}$
essential connections.
$\overline \gamma _{0}$
essential connections.
Note that the flow
![]() $\widetilde \varphi '$
can be chosen such that the transversality condition is satisfied and
$\widetilde \varphi '$
can be chosen such that the transversality condition is satisfied and
 $$ \begin{align*} n(h_{2}(\overline\gamma_{1}),h_{1}(\overline\gamma_{0});\widetilde\varphi') &= n(h_{2}(\overline\gamma_{1}),h_{1}(\overline\gamma_{0});\widetilde\varphi)\\ &\quad- \dfrac{n(h_{2}(\overline\gamma_{1}),h_{1}(\gamma_{0});\widetilde\varphi) }{n(h_{2}(\gamma_{1}),h_{1}(\gamma_{0});\widetilde\varphi) } n(h_{2}(\gamma_{1}),h_{1}(\overline\gamma_{0});\widetilde\varphi). \end{align*} $$
$$ \begin{align*} n(h_{2}(\overline\gamma_{1}),h_{1}(\overline\gamma_{0});\widetilde\varphi') &= n(h_{2}(\overline\gamma_{1}),h_{1}(\overline\gamma_{0});\widetilde\varphi)\\ &\quad- \dfrac{n(h_{2}(\overline\gamma_{1}),h_{1}(\gamma_{0});\widetilde\varphi) }{n(h_{2}(\gamma_{1}),h_{1}(\gamma_{0});\widetilde\varphi) } n(h_{2}(\gamma_{1}),h_{1}(\overline\gamma_{0});\widetilde\varphi). \end{align*} $$
Moreover, if C is an essential connected component of
![]() $W^u(\gamma _{1})\cap W^s(\gamma _0)$
in
$W^u(\gamma _{1})\cap W^s(\gamma _0)$
in
![]() $\varphi '$
, then the morsification
$\varphi '$
, then the morsification
![]() $\widetilde \varphi '$
of
$\widetilde \varphi '$
of
![]() $\varphi '$
is such that
$\varphi '$
is such that
![]() $W^u(h_2(\gamma _{1}))\cap W^s(h_1(\gamma _0))\cap C=\emptyset $
in
$W^u(h_2(\gamma _{1}))\cap W^s(h_1(\gamma _0))\cap C=\emptyset $
in
![]() $\widetilde \varphi '$
.
$\widetilde \varphi '$
.
The same analysis can be carried out to understand the global behavior of the flow obtained from
![]() $\varphi $
via the cancellation of the periodic orbits
$\varphi $
via the cancellation of the periodic orbits
![]() $\gamma _{2}$
and
$\gamma _{2}$
and
![]() $\gamma _{1}$
.
$\gamma _{1}$
.
The following proposition is a straightforward consequence of the analysis above.
Proposition 3.13. Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, and let
$3$
-manifold, and let
![]() $\gamma _{1}$
and
$\gamma _{1}$
and
![]() $\gamma _{0}$
(respectively,
$\gamma _{0}$
(respectively,
![]() $\gamma _{2}$
and
$\gamma _{2}$
and
![]() $\gamma _{1}$
) be periodic orbits in
$\gamma _{1}$
) be periodic orbits in
![]() $\varphi $
such that all essential connections from
$\varphi $
such that all essential connections from
![]() $\gamma _{1}$
(respectively,
$\gamma _{1}$
(respectively,
![]() $\gamma _{2}$
) to attracting (respectively, saddle) periodic orbits and all essential connections from saddle (respectively, repeller) periodic orbits to
$\gamma _{2}$
) to attracting (respectively, saddle) periodic orbits and all essential connections from saddle (respectively, repeller) periodic orbits to
![]() $\gamma _{0}$
(respectively,
$\gamma _{0}$
(respectively,
![]() $\gamma _{1}$
) are
$\gamma _{1}$
) are
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free connections. If
$h_1$
free connections. If
![]() $\varphi '$
is obtained from
$\varphi '$
is obtained from
![]() $\varphi $
by cancelling periodic orbits
$\varphi $
by cancelling periodic orbits
![]() $\gamma _{1}$
and
$\gamma _{1}$
and
![]() $\gamma _{0}$
(respectively,
$\gamma _{0}$
(respectively,
![]() $\gamma _{2}$
and
$\gamma _{2}$
and
![]() $\gamma _{1}$
), as in Theorem 3.11, then all essential connections that arise after the cancellation are
$\gamma _{1}$
), as in Theorem 3.11, then all essential connections that arise after the cancellation are
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free.
$h_1$
free.
4 Spectral sequences and filtrations for NMS complexes
The main goal in this paper is to retrieve dynamical information from the spectral sequence of a filtered chain complex associated to an NMS flow.
The SSSA was originally developed in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira4, Reference Cornea, de Rezende and da Silveira6] for a Morse chain complex with a finest filtration. In §4.1, we make use of the SSSA to retrieve algebraic information of a spectral sequence of an NMS chain complex. In §4.2, we present a special class of filtrations on an NMS chain complex.
4.1 SSSA for NMS complexes
Consider an NMS flow
![]() $\varphi $
on M. Let
$\varphi $
on M. Let
![]() $m_k$
be the cardinality of the set of all periodic orbits of index k of the flow
$m_k$
be the cardinality of the set of all periodic orbits of index k of the flow
![]() $\varphi $
, that is,
$\varphi $
, that is,
![]() $m_k=\# \Gamma _{k}(\varphi )$
. Also, let
$m_k=\# \Gamma _{k}(\varphi )$
. Also, let
![]() $m=m_0+m_1+m_2$
. Then, by Proposition 1.14 of [Reference Franks10], there exists a Lyapunov function
$m=m_0+m_1+m_2$
. Then, by Proposition 1.14 of [Reference Franks10], there exists a Lyapunov function
![]() $f:M\rightarrow \mathbb {R}$
for
$f:M\rightarrow \mathbb {R}$
for
![]() $\varphi $
such that:
$\varphi $
such that:
-
(1) given
 $\gamma ^s$
,
$\gamma ^s$
,
 $\gamma ^{t}$
in
$\gamma ^{t}$
in
 $\Gamma (\varphi )$
, then
$\Gamma (\varphi )$
, then
 $f(\gamma ^{s})\neq f(\gamma ^{t})$
, for all
$f(\gamma ^{s})\neq f(\gamma ^{t})$
, for all
 $s\neq t$
, where
$s\neq t$
, where
 $s,t\in \{1, \ldots , m\}$
; and
$s,t\in \{1, \ldots , m\}$
; and -
(2)
 $f(\gamma _{k})<f(\gamma _{k+1})$
for all
$f(\gamma _{k})<f(\gamma _{k+1})$
for all
 $k=0,1$
.
$k=0,1$
.
For each
![]() $p\in \{1, \ldots , m\}$
, let
$p\in \{1, \ldots , m\}$
, let
![]() $c_p:=f(\gamma ^p)$
. One can define a filtration on M by
$c_p:=f(\gamma ^p)$
. One can define a filtration on M by
where
![]() $\epsilon $
is sufficiently small so as to guarantee that there is only one periodic orbit
$\epsilon $
is sufficiently small so as to guarantee that there is only one periodic orbit
![]() $\gamma ^{p}$
in
$\gamma ^{p}$
in
![]() $\mathcal {F}_{p-1}\setminus \mathcal {F}_{p-2}$
, for each
$\mathcal {F}_{p-1}\setminus \mathcal {F}_{p-2}$
, for each
![]() $p\in \{1, \ldots , m\}$
(assume that
$p\in \{1, \ldots , m\}$
(assume that
![]() $\mathcal {F}_{-1}=\emptyset $
).
$\mathcal {F}_{-1}=\emptyset $
).
Throughout this paper, we consider the filtration
![]() $\mathcal {F}=\{\mathcal {F}_pC\}$
induced by
$\mathcal {F}=\{\mathcal {F}_pC\}$
induced by
![]() $\{\mathcal {F}_p\}$
on the NMS chain complex
$\{\mathcal {F}_p\}$
on the NMS chain complex
![]() $(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
associated to
$(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
associated to
![]() $\varphi $
.
$\varphi $
.
For each p, the chains generating
![]() $\mathcal {F}_pC$
that are not in
$\mathcal {F}_pC$
that are not in
![]() $ \mathcal {F}_{p-1}C$
are represented in the matrix
$ \mathcal {F}_{p-1}C$
are represented in the matrix
![]() $\Delta $
in columns
$\Delta $
in columns
![]() $2p+1$
and
$2p+1$
and
![]() $2p+2$
and are denoted by
$2p+2$
and are denoted by
![]() $h^{2p+1}_{k}(\gamma _k^{p+1})$
and
$h^{2p+1}_{k}(\gamma _k^{p+1})$
and
![]() $h^{2p+2}_{k+1}(\gamma _k^{p+1})$
, respectively (see Figure 15). To make reference to these generators, one uses the notation
$h^{2p+2}_{k+1}(\gamma _k^{p+1})$
, respectively (see Figure 15). To make reference to these generators, one uses the notation
![]() $\mathcal {F}_{p}C\setminus \mathcal {F}_{p-1}C=\{h^{2p+1}_{k}(\gamma _k^{p+1}) ,h^{2p+2}_{k+1}(\gamma _k^{p+1})\}$
.
$\mathcal {F}_{p}C\setminus \mathcal {F}_{p-1}C=\{h^{2p+1}_{k}(\gamma _k^{p+1}) ,h^{2p+2}_{k+1}(\gamma _k^{p+1})\}$
.

Figure 15 Filtration seen in the matrix
![]() $\Delta $
.
$\Delta $
.
Let
![]() $(\mathcal {E}^r_p,d^r_p)$
be the spectral sequence for
$(\mathcal {E}^r_p,d^r_p)$
be the spectral sequence for
![]() $(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
and a filtration
$(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
and a filtration
![]() $\mathcal {F}$
as defined above. The modules of the spectral sequence are given by
$\mathcal {F}$
as defined above. The modules of the spectral sequence are given by
where
Theorem 4.1. Given an NMS chain complex
![]() $(C^{\mathrm {NMS}}(\widetilde \varphi ),\Delta ^{\mathrm {NMS}})$
, where
$(C^{\mathrm {NMS}}(\widetilde \varphi ),\Delta ^{\mathrm {NMS}})$
, where
![]() $\widetilde \varphi \in TUM(\varphi )$
, and a filtration
$\widetilde \varphi \in TUM(\varphi )$
, and a filtration
![]() $\mathcal {F}$
, the SSSA applied to
$\mathcal {F}$
, the SSSA applied to
![]() $\Delta $
determines the modules
$\Delta $
determines the modules
![]() $\mathcal {E}^r_p$
and induces the differentials
$\mathcal {E}^r_p$
and induces the differentials
![]() $d^r_p$
of the spectral sequence.
$d^r_p$
of the spectral sequence.
The proof of this theorem follows from Theorems 4.3 and 4.6 in §4.1.1.
This algorithm produces a sequence of matrices
![]() $\{\Delta ^r\}$
. A consequence of Theorem 4.1 is that each differential
$\{\Delta ^r\}$
. A consequence of Theorem 4.1 is that each differential
![]() $d^{r}_{p}$
is induced by a submatrix of
$d^{r}_{p}$
is induced by a submatrix of
![]() $\Delta ^r$
, as in Corollary 4.7.
$\Delta ^r$
, as in Corollary 4.7.
As an important consequence of Theorem 4.1 and of a result proved in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira4], which states that primary pivots for TU matrices are
![]() $\pm 1$
, we have that, for NMS flows in
$\pm 1$
, we have that, for NMS flows in
![]() $ TUM (\varphi )$
, the non-zero differentials
$ TUM (\varphi )$
, the non-zero differentials
![]() $d^r_{p,q}$
of the associated spectral sequence are all isomorphisms and the modules
$d^r_{p,q}$
of the associated spectral sequence are all isomorphisms and the modules
![]() $E^r_{p,q}$
are all torsion free. In particular, the following result holds.
$E^r_{p,q}$
are all torsion free. In particular, the following result holds.
Corollary 4.2. The modules
![]() $E^{\infty }_{p,q}$
of the associated spectral sequence are free modules for all p and q.
$E^{\infty }_{p,q}$
of the associated spectral sequence are free modules for all p and q.
Thus, in this case,
![]() $GH_*(C)_{p,q}$
is free for all p and q and (3) holds: that is, the spectral sequence strongly converges to the homology of the NMS chain complex.
$GH_*(C)_{p,q}$
is free for all p and q and (3) holds: that is, the spectral sequence strongly converges to the homology of the NMS chain complex.
4.1.1 Proof of Theorem 4.1
In this section, we show how the modules
![]() $\mathcal {E}^r_p$
and the differentials
$\mathcal {E}^r_p$
and the differentials
![]() $d^r_p$
of the spectral sequence associated to a filtered NMS chain complex can be determined by the SSSA. It was shown in [Reference Cornea, de Rezende and da Silveira6] that the modules of the spectral sequence
$d^r_p$
of the spectral sequence associated to a filtered NMS chain complex can be determined by the SSSA. It was shown in [Reference Cornea, de Rezende and da Silveira6] that the modules of the spectral sequence
![]() $(E^r_p,d^r_p)$
associated to the finest filtration are determined by the SSSA. We use this fact to prove the following more general theorem.
$(E^r_p,d^r_p)$
associated to the finest filtration are determined by the SSSA. We use this fact to prove the following more general theorem.
Theorem 4.3. The SSSA determines the modules
![]() $\mathcal {E}^r_p$
.
$\mathcal {E}^r_p$
.
Proof. Note that the module
![]() $\mathcal {Z}^r_p$
consists of chains in
$\mathcal {Z}^r_p$
consists of chains in
![]() $\mathcal {F}_pC$
with boundary in
$\mathcal {F}_pC$
with boundary in
![]() $\mathcal {F}_{p-r}C$
. These chains are associated to all the columns of
$\mathcal {F}_{p-r}C$
. These chains are associated to all the columns of
![]() $\Delta $
to the left of and including the column
$\Delta $
to the left of and including the column
![]() $2p+2$
. Furthermore, since the boundary of the chains must be in
$2p+2$
. Furthermore, since the boundary of the chains must be in
![]() $\mathcal {F}_{p-r}C$
, we must consider columns or their linear combinations that have the property that the entries in rows
$\mathcal {F}_{p-r}C$
, we must consider columns or their linear combinations that have the property that the entries in rows
![]() $i>2(p-r)+2$
are all zeros. Hence, in terms of the finest filtration
$i>2(p-r)+2$
are all zeros. Hence, in terms of the finest filtration
![]() $\{F_p\}$
,
$\{F_p\}$
,
Analogously,
and
If there is a k-chain in
![]() $\mathcal {F}_i\setminus \mathcal {F}_{i-1}$
, then the column of
$\mathcal {F}_i\setminus \mathcal {F}_{i-1}$
, then the column of
![]() $\Delta $
associated to this chain, denoted by
$\Delta $
associated to this chain, denoted by
![]() $k_{i}$
, is
$k_{i}$
, is
![]() $2i+1$
or
$2i+1$
or
![]() $2i+2$
. Then, using the formula given in [Reference Cornea, de Rezende and da Silveira6], (5) and (6) we describe the modules
$2i+2$
. Then, using the formula given in [Reference Cornea, de Rezende and da Silveira6], (5) and (6) we describe the modules
![]() $\mathcal {Z}^r_{p,k-p}$
and
$\mathcal {Z}^r_{p,k-p}$
and
![]() $\mathcal {Z}^{r-1}_{p-1,k-(p-1)}$
in terms of the basis determined by
$\mathcal {Z}^{r-1}_{p-1,k-(p-1)}$
in terms of the basis determined by
![]() $\Delta $
in the SSSA: that is,
$\Delta $
in the SSSA: that is,
where
![]() $a=2(p-r)+2$
and, whenever there is no k-chain in
$a=2(p-r)+2$
and, whenever there is no k-chain in
![]() $\mathcal {F}_i\setminus \mathcal {F}_{i-1}$
,
$\mathcal {F}_i\setminus \mathcal {F}_{i-1}$
,
![]() $i=0,\ldots , P$
, the term
$i=0,\ldots , P$
, the term
![]() $\mu ^{k_{{i}},{k_{{i}}-a}}\sigma _k^{k_{{i}},{k_{{i}}-a}}$
is supressed. Note that, if there is no k-chain in
$\mu ^{k_{{i}},{k_{{i}}-a}}\sigma _k^{k_{{i}},{k_{{i}}-a}}$
is supressed. Note that, if there is no k-chain in
![]() $\mathcal {F}_p\setminus \mathcal {F}_{p-1}$
, then
$\mathcal {F}_p\setminus \mathcal {F}_{p-1}$
, then
![]() $\mathcal {Z}^r_{p,k-p}=\mathcal {Z}^{r-1}_{p-1,k-(p-1)}$
and
$\mathcal {Z}^r_{p,k-p}=\mathcal {Z}^{r-1}_{p-1,k-(p-1)}$
and
![]() $\mathcal {E}^r_{p,k-p}=0$
. Now suppose that there is a k-chain in
$\mathcal {E}^r_{p,k-p}=0$
. Now suppose that there is a k-chain in
![]() $\mathcal {F}_p\setminus \mathcal {F}_{p-1}$
. Consequently,
$\mathcal {F}_p\setminus \mathcal {F}_{p-1}$
. Consequently,
![]() $\mathcal {E}^{r}_{p,k-p}$
is isomorphic to a submodule of
$\mathcal {E}^{r}_{p,k-p}$
is isomorphic to a submodule of
![]() $\mathbb {Z}[\mu ^{k_{p},{k_{p}-a}}\sigma _k^{k_{p},{k_{p}-a}}].$
$\mathbb {Z}[\mu ^{k_{p},{k_{p}-a}}\sigma _k^{k_{p},{k_{p}-a}}].$
To determine
![]() $\mathcal {E}^{r}_{p,k-p}$
, we need to understand the module
$\mathcal {E}^{r}_{p,k-p}$
, we need to understand the module
![]() $\partial \mathcal {Z}^{r-1}_{p+r-1}$
. As we have seen, the module
$\partial \mathcal {Z}^{r-1}_{p+r-1}$
. As we have seen, the module
![]() $\mathcal {Z}^{r-1}_{p+r-1,(k+1)-(p+r-1)}$
is
$\mathcal {Z}^{r-1}_{p+r-1,(k+1)-(p+r-1)}$
is
 $$ \begin{align*} \mathbb{Z}&[\mu^{(k+1)_{{p+r-1}},(k+1)_{{p+r-1}}-(2p+2)}\sigma_{k+1}^{(k+1)_{{p+r-1}},{(k+1)_{{p+r-1}}-(2p+2)}}, \ldots,\\ &\quad\mu^{(k+1)_0,{(k+1)_0-(2p+2)}}\sigma_{k+1}^{(k+1)_0,{(k+1)_0-(2p+2)}}]. \end{align*} $$
$$ \begin{align*} \mathbb{Z}&[\mu^{(k+1)_{{p+r-1}},(k+1)_{{p+r-1}}-(2p+2)}\sigma_{k+1}^{(k+1)_{{p+r-1}},{(k+1)_{{p+r-1}}-(2p+2)}}, \ldots,\\ &\quad\mu^{(k+1)_0,{(k+1)_0-(2p+2)}}\sigma_{k+1}^{(k+1)_0,{(k+1)_0-(2p+2)}}]. \end{align*} $$
Since there is a unique k-chain in
![]() $\mathcal {F}_p\setminus \mathcal {F}_{p-1}$
that is in row
$\mathcal {F}_p\setminus \mathcal {F}_{p-1}$
that is in row
![]() $k_p$
, this formula is equivalent to
$k_p$
, this formula is equivalent to
and hence its boundary is
 $$ \begin{align*} \mathbb{Z}&[\mu^{(k+1)_{{p+r-1}},{(k+1)_{{p+r-1}}-k_p}}\partial\sigma_{k+1}^{(k+1)_{{p+r-1}},{(k+1)_{{p+r-1}}-k_p}}, \ldots,\\ &\quad \mu^{(k+1)_0,{(k+1)_0-k_p}}\partial\sigma_{k+1}^{(k+1)_0,{(k+1)_0-k_p}}]. \end{align*} $$
$$ \begin{align*} \mathbb{Z}&[\mu^{(k+1)_{{p+r-1}},{(k+1)_{{p+r-1}}-k_p}}\partial\sigma_{k+1}^{(k+1)_{{p+r-1}},{(k+1)_{{p+r-1}}-k_p}}, \ldots,\\ &\quad \mu^{(k+1)_0,{(k+1)_0-k_p}}\partial\sigma_{k+1}^{(k+1)_0,{(k+1)_0-k_p}}]. \end{align*} $$
If the column associated to
![]() $\sigma _{k+1}^{(k+1)_{\xi },{(k+1)_{\xi }-k_p}}$
has non-zero entries below the row
$\sigma _{k+1}^{(k+1)_{\xi },{(k+1)_{\xi }-k_p}}$
has non-zero entries below the row
![]() $k_{p}$
, then
$k_{p}$
, then
![]() $\mu ^{(k+1)_{\xi },{(k+1)_{\xi }-k_p}}=0$
. Hence, for each
$\mu ^{(k+1)_{\xi },{(k+1)_{\xi }-k_p}}=0$
. Hence, for each
![]() $\xi =0,\ldots , p+r-1$
, if
$\xi =0,\ldots , p+r-1$
, if
![]() $\mu ^{(k+1)_{\xi },{(k+1)_{\xi }-k_p}}=1$
, then
$\mu ^{(k+1)_{\xi },{(k+1)_{\xi }-k_p}}=1$
, then
 $$ \begin{align*} \partial\sigma_{k+1}^{(k+1)_{\xi},{(k+1)_{\xi}-k_p}}\ \ = \ \ \Delta^{(k+1)_{\xi}-k_p}_{k_{p},(k+1)_{\xi}}\sigma_k^{k_{p},(k+1)_{\xi}-k_p}+\underbrace{\ldots}_{\displaystyle\in \mathcal{Z}_{p-1}^{r-1}}.\end{align*} $$
$$ \begin{align*} \partial\sigma_{k+1}^{(k+1)_{\xi},{(k+1)_{\xi}-k_p}}\ \ = \ \ \Delta^{(k+1)_{\xi}-k_p}_{k_{p},(k+1)_{\xi}}\sigma_k^{k_{p},(k+1)_{\xi}-k_p}+\underbrace{\ldots}_{\displaystyle\in \mathcal{Z}_{p-1}^{r-1}}.\end{align*} $$
Since
![]() $\Delta ^{(k\!+\!1)_{\xi }\!-\!k_p}_{k_{{p}},(k\!+\!1)_{\xi }}=0$
whenever
$\Delta ^{(k\!+\!1)_{\xi }\!-\!k_p}_{k_{{p}},(k\!+\!1)_{\xi }}=0$
whenever
![]() $\xi <p$
, it follows that
$\xi <p$
, it follows that
![]() $\partial \mathcal {Z}^{r-1}_{p+r-1,(k+1)-(p+r-1)}$
is
$\partial \mathcal {Z}^{r-1}_{p+r-1,(k+1)-(p+r-1)}$
is
Using equations (7), (8) and (9), we obtain a formula for
![]() $\mathcal {E}^{r}_{p}$
in terms of the
$\mathcal {E}^{r}_{p}$
in terms of the
![]() $\sigma $
determined by the SSSA.
$\sigma $
determined by the SSSA.
Corollary 4.4. Each module
![]() $\mathcal {E}^{r}_{p,k-p}$
of the spectral sequence is either
$\mathcal {E}^{r}_{p,k-p}$
of the spectral sequence is either
![]() $0$
or
$0$
or
![]() $\mathbb {Z}[\sigma _k^{k_p,k_p-2(p-r)-2}]$
.
$\mathbb {Z}[\sigma _k^{k_p,k_p-2(p-r)-2}]$
.
Corollary 4.5. Each non-zero module
![]() $\mathcal {E}^{r}_{p}$
of the spectral sequence is either
$\mathcal {E}^{r}_{p}$
of the spectral sequence is either
We now want to prove that the differentials of the spectral sequence are induced by the matrices produced in the SSSA.
Theorem 4.6. Whenever the modules
![]() $\mathcal {E}^{r}_{p,k-p}$
and
$\mathcal {E}^{r}_{p,k-p}$
and
![]() $\mathcal {E}^{r}_{p-r,k-1-(p-r)}$
are non-zero, the differential
$\mathcal {E}^{r}_{p-r,k-1-(p-r)}$
are non-zero, the differential
![]() $d^{r}_{p,k-p}$
is induced by entry
$d^{r}_{p,k-p}$
is induced by entry
![]() $\Delta ^{k_p - (k-1)_{p-r}}_{(k-1)_{p-r},k_p}$
.
$\Delta ^{k_p - (k-1)_{p-r}}_{(k-1)_{p-r},k_p}$
.
Proof. By equations (7) and (9) in the proof of Theorem 4.3,
 $$ \begin{align*}\mathcal{E}^{r}_{p,k-p}&= \dfrac{\mathbb{Z}[\mu^{k_{{p}},{k_{{p}}-(k-1)_{p-r}}}\sigma_k^{k_{{p}},{k_{{p}}-(k-1)_{p-r}}}]+\mathcal{Z}_{p-1}^{r-1}}{\mathbb{Z}[\mu^{(k\!+\!1)_{\xi},(k\!+\!1)_{\xi}\!-\!k_p} \Delta^{(k\!+\!1)_{\xi}\!-\!k_p}_{k_{{p}},(k\!+\!1)_{\xi}} \sigma_k^{k_{p},(k\!+\!1)_{\xi}\!-\!k_p} ]_{{\xi=p,\ldots, p\!+\!r\!-\!1}}+ \mathcal{Z}_{p-1}^{r-1}}\\ & = \mathbb{Z}[\sigma_k^{k_{p},k_p-(k-1)_{p-r}}], \end{align*} $$
$$ \begin{align*}\mathcal{E}^{r}_{p,k-p}&= \dfrac{\mathbb{Z}[\mu^{k_{{p}},{k_{{p}}-(k-1)_{p-r}}}\sigma_k^{k_{{p}},{k_{{p}}-(k-1)_{p-r}}}]+\mathcal{Z}_{p-1}^{r-1}}{\mathbb{Z}[\mu^{(k\!+\!1)_{\xi},(k\!+\!1)_{\xi}\!-\!k_p} \Delta^{(k\!+\!1)_{\xi}\!-\!k_p}_{k_{{p}},(k\!+\!1)_{\xi}} \sigma_k^{k_{p},(k\!+\!1)_{\xi}\!-\!k_p} ]_{{\xi=p,\ldots, p\!+\!r\!-\!1}}+ \mathcal{Z}_{p-1}^{r-1}}\\ & = \mathbb{Z}[\sigma_k^{k_{p},k_p-(k-1)_{p-r}}], \end{align*} $$
and hence
![]() $[\mu ^{(k\!+\!1)_{\xi },(k\!+\!1)_{\xi }\!-\!k_p} \Delta ^{(k\!+\!1)_{\xi }\!-\!k_p}_{k_{{p}},(k\!+\!1)_{\xi }} \sigma _k^{k_{p},(k\!+\!1)_{\xi }\!-\!k_p} ]_{{\xi =p,\ldots , p\!+\!r\!-\!1}}=0$
. It follows that
$[\mu ^{(k\!+\!1)_{\xi },(k\!+\!1)_{\xi }\!-\!k_p} \Delta ^{(k\!+\!1)_{\xi }\!-\!k_p}_{k_{{p}},(k\!+\!1)_{\xi }} \sigma _k^{k_{p},(k\!+\!1)_{\xi }\!-\!k_p} ]_{{\xi =p,\ldots , p\!+\!r\!-\!1}}=0$
. It follows that
 $$ \begin{align*} \mathcal{E}^{r+1}_{p,k-p}= \dfrac{\mathbb{Z}[\mu^{k_{{p}},{k_{{p}}-(k-1)_{p-r-1}}}\sigma_k^{k_{{p}},{k_{{p}}-(k-1)_{p-r-1}}}]}{\mathbb{Z}[\mu^{(k\!+\!1)_{p+r},(k\!+\!1)_{p+r}\!-\!k_p} \Delta^{(k\!+\!1)_{p+r}\!-\!k_p}_{k_{{p}},(k\!+\!1)_{p+r}} \sigma_k^{k_{p},(k\!+\!1)_{p+r}\!-\!k_p} ]}. \end{align*} $$
$$ \begin{align*} \mathcal{E}^{r+1}_{p,k-p}= \dfrac{\mathbb{Z}[\mu^{k_{{p}},{k_{{p}}-(k-1)_{p-r-1}}}\sigma_k^{k_{{p}},{k_{{p}}-(k-1)_{p-r-1}}}]}{\mathbb{Z}[\mu^{(k\!+\!1)_{p+r},(k\!+\!1)_{p+r}\!-\!k_p} \Delta^{(k\!+\!1)_{p+r}\!-\!k_p}_{k_{{p}},(k\!+\!1)_{p+r}} \sigma_k^{k_{p},(k\!+\!1)_{p+r}\!-\!k_p} ]}. \end{align*} $$
Consider the map
![]() $\delta ^{r}_{p,k-p}: \mathcal {E}^{r}_{p,k-p}\to \mathcal {E}^{r}_{p-r,k-1-(p-r)}$
induced by multiplication by the entry
$\delta ^{r}_{p,k-p}: \mathcal {E}^{r}_{p,k-p}\to \mathcal {E}^{r}_{p-r,k-1-(p-r)}$
induced by multiplication by the entry
![]() $\Delta ^{k_p - (k-1)_{p-r}}_{(k-1)_{p-r},k_p}$
. We show that
$\Delta ^{k_p - (k-1)_{p-r}}_{(k-1)_{p-r},k_p}$
. We show that
 $$ \begin{align*} \mathcal{E}^{r+1}_{p,k-p}=\displaystyle\frac{\mathrm{Ker} \ \delta^{r}_{p,k-p}}{\mathrm{Im} \ \delta^{r}_{p+r,k+1-(p+r)}}. \end{align*} $$
$$ \begin{align*} \mathcal{E}^{r+1}_{p,k-p}=\displaystyle\frac{\mathrm{Ker} \ \delta^{r}_{p,k-p}}{\mathrm{Im} \ \delta^{r}_{p+r,k+1-(p+r)}}. \end{align*} $$
Note that, for column
![]() $k_p$
of
$k_p$
of
![]() $\Delta ^{k_{p}-2(p-r)}$
, one of the following two situations may occur.
$\Delta ^{k_{p}-2(p-r)}$
, one of the following two situations may occur.
(1) The non-zero entries of column
![]() $k_p$
are above row
$k_p$
are above row
![]() $2(p-r)$
: that is,
$2(p-r)$
: that is,
![]() $\sigma _k^{k_{p},k_{p}-2(p+r)}$
is a generator of
$\sigma _k^{k_{p},k_{p}-2(p+r)}$
is a generator of
![]() $\mathcal {Z}^{r+1}_{p,k-p}$
(that is,
$\mathcal {Z}^{r+1}_{p,k-p}$
(that is,
![]() $\mu ^{k_{p},k_{p}-2(p-r)}=1$
). In this case,
$\mu ^{k_{p},k_{p}-2(p-r)}=1$
). In this case,
![]() $\Delta ^{k_p - (k-1)_{p-r}}_{(k-1)_{p-r},k_p}=0$
and hence
$\Delta ^{k_p - (k-1)_{p-r}}_{(k-1)_{p-r},k_p}=0$
and hence
![]() $\mathrm {Ker} \ \delta ^{r}_{p,k-p}=0$
.
$\mathrm {Ker} \ \delta ^{r}_{p,k-p}=0$
.
(2) The non-zero entries of column
![]() $k_p$
are above row
$k_p$
are above row
![]() $2(p-r)+2$
and below row
$2(p-r)+2$
and below row
![]() $2(p-r)$
: that is, it has a primary pivot in row
$2(p-r)$
: that is, it has a primary pivot in row
![]() $(k-1)_{p-r}$
and hence
$(k-1)_{p-r}$
and hence
![]() $\sigma _k^{k_{p},k_{p}-(k-1)_{p-r}}$
is a generator of
$\sigma _k^{k_{p},k_{p}-(k-1)_{p-r}}$
is a generator of
![]() $\mathcal {Z}^r_{p,k-p}$
(
$\mathcal {Z}^r_{p,k-p}$
(
![]() $\mu ^{k_{p},k_{p}-(k-1)_{p-r}}=1$
) but
$\mu ^{k_{p},k_{p}-(k-1)_{p-r}}=1$
) but
![]() $\sigma _k^{k_{p},k_{p}-2(p-r)}$
is not a generator of
$\sigma _k^{k_{p},k_{p}-2(p-r)}$
is not a generator of
![]() $\mathcal {Z}^{r+1}_{p,k-p}$
(that is,
$\mathcal {Z}^{r+1}_{p,k-p}$
(that is,
![]() $\mu ^{k_{p},k_{p}-2(p-r)}=0$
). In this case,
$\mu ^{k_{p},k_{p}-2(p-r)}=0$
). In this case,
![]() $\Delta ^{k_p - (k-1)_{p-r}}_{(k-1)_{p-r},k_p}=\pm 1$
and hence
$\Delta ^{k_p - (k-1)_{p-r}}_{(k-1)_{p-r},k_p}=\pm 1$
and hence
![]() $\mathrm {Ker} \ \delta ^{r}_{p,k-p}=\mathbb {Z}[\sigma _k^{k_{p},k_{p}-2(p+r)} ]$
.
$\mathrm {Ker} \ \delta ^{r}_{p,k-p}=\mathbb {Z}[\sigma _k^{k_{p},k_{p}-2(p+r)} ]$
.
It follows that
![]() $\mathrm {Ker} \ \delta ^{r}_{p,k-p}=\mathbb {Z}[\mu ^{k_{p},k_{p}-2(p+r)}\sigma _k^{k_{p},k_{p}-2(p+r)} ]$
.
$\mathrm {Ker} \ \delta ^{r}_{p,k-p}=\mathbb {Z}[\mu ^{k_{p},k_{p}-2(p+r)}\sigma _k^{k_{p},k_{p}-2(p+r)} ]$
.
On the other hand, considering the map
![]() $\delta ^{r}_{p+r,k+1-(p+r)}: \mathcal {E}^{r}_{p+r,k+1-(p+r)}\to \mathcal {E}^{r}_{p,k-p}$
, where
$\delta ^{r}_{p+r,k+1-(p+r)}: \mathcal {E}^{r}_{p+r,k+1-(p+r)}\to \mathcal {E}^{r}_{p,k-p}$
, where
![]() $\mathcal {E}^{r}_{p+r,k+1-(p+r)}=0$
or
$\mathcal {E}^{r}_{p+r,k+1-(p+r)}=0$
or
we have that
Corollary 4.7. The differential
![]() $d^{r}_{p}: \mathcal {E}^{r}_{p,k-p}\oplus \mathcal {E}^{r}_{p,k-1-p}\to \mathcal {E}^{r}_{p-r,k-1-(p-r)}\oplus \mathcal {E}^{r}_{p-r}, {}_{k-2-(p-r)} $
is induced by the matrix
$d^{r}_{p}: \mathcal {E}^{r}_{p,k-p}\oplus \mathcal {E}^{r}_{p,k-1-p}\to \mathcal {E}^{r}_{p-r,k-1-(p-r)}\oplus \mathcal {E}^{r}_{p-r}, {}_{k-2-(p-r)} $
is induced by the matrix
 $$ \begin{align} \left(\begin{array}{cc} \Delta^r_{(k-2)_{p-r},(k-1)_p} & 0 \\ 0 & \Delta^r_{(k-1)_{p-r},k_p} \end{array} \right) \end{align} $$
$$ \begin{align} \left(\begin{array}{cc} \Delta^r_{(k-2)_{p-r},(k-1)_p} & 0 \\ 0 & \Delta^r_{(k-1)_{p-r},k_p} \end{array} \right) \end{align} $$
in the following sense.
4.2 NMS-compatible filtrations
In this section, we introduce filtrations on an NMS chain complex that are consistent with the underlying cancellations and reductions occurring in the global dynamics through a spectral sequence approach and establish some of their properties.
Definition 4.8. A filtration
![]() $\mathcal {F}$
for an NMS chain complex
$\mathcal {F}$
for an NMS chain complex
![]() $(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
is said to be an NMS-compatible filtration if, whenever one performs the sweeping algorithm to
$(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
is said to be an NMS-compatible filtration if, whenever one performs the sweeping algorithm to
![]() $\Delta ^{\mathrm {NMS}}$
, for each pair
$\Delta ^{\mathrm {NMS}}$
, for each pair
![]() $ \gamma _{k-1}^{p-r}$
and
$ \gamma _{k-1}^{p-r}$
and
![]() $ \gamma _{k}^{p}$
, the following conditions are satisfied.
$ \gamma _{k}^{p}$
, the following conditions are satisfied.
-
(SF1) If
 $\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})_{22} $
is a primary pivot, then
$\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})_{22} $
is a primary pivot, then
 $\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})_{11}$
is either a primary pivot or
$\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})_{11}$
is either a primary pivot or
 $\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})_{11}=0$
such that, for every
$\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})_{11}=0$
such that, for every
 $\ell \geq p-r$
,
$\ell \geq p-r$
,
 $\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{\ell })_{11} $
is not a change of basis pivot determined by a primary pivot
$\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{\ell })_{11} $
is not a change of basis pivot determined by a primary pivot
 $\pm E_{11}$
.
$\pm E_{11}$
. -
(SF2) If
 $\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})_{11} $
is a primary pivot, then
$\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})_{11} $
is a primary pivot, then
 $\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})_{22}$
is either a primary pivot or
$\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})_{22}$
is either a primary pivot or
 $\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})_{22}=0$
such, that for every
$\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})_{22}=0$
such, that for every
 $\ell \geq p-r$
,
$\ell \geq p-r$
,
 $\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{\ell })_{22} $
is not a change of basis pivot determined by a primary pivot
$\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{\ell })_{22} $
is not a change of basis pivot determined by a primary pivot
 $\pm E_{22}$
.
$\pm E_{22}$
.
Figure 16 SSSA for an NMS-compatible filtration:
 $\Delta ^2$
(top left),
$\Delta ^2$
(top left),
 $\Delta ^4$
(top right),
$\Delta ^4$
(top right),
 $\Delta ^6$
(bottom left),
$\Delta ^6$
(bottom left),
 $\Delta ^8$
(bottom right).
$\Delta ^8$
(bottom right).
Example 4.9. Consider the NMS chain complex
![]() $(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
of Example 3.9. Endowing
$(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
of Example 3.9. Endowing
![]() $(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
with the filtration
$(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
with the filtration
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathcal {F}_pC\setminus \mathcal {F}_{p-1}C= \{ h_{k}(\gamma _k^{p+1}) , h_{k+1}(\gamma _k^{p+1}) \}$
, the matrices
$\mathcal {F}_pC\setminus \mathcal {F}_{p-1}C= \{ h_{k}(\gamma _k^{p+1}) , h_{k+1}(\gamma _k^{p+1}) \}$
, the matrices
![]() $\Delta ^r$
produced by the SSSA are presented in Figure 16. The entries marked with red circles correspond to the differentials of the associated spectral sequence. Note that
$\Delta ^r$
produced by the SSSA are presented in Figure 16. The entries marked with red circles correspond to the differentials of the associated spectral sequence. Note that
![]() $\mathcal {F}$
satisfies (SF1) and (SF2) and hence it is an NMS-compatible filtration.
$\mathcal {F}$
satisfies (SF1) and (SF2) and hence it is an NMS-compatible filtration.
Not all filtrations of a chain complex are NMS-compatible filtrations (see the next example).
Example 4.10. Consider the same chain complex endowed with the following filtration:
![]() $\mathcal {F}_0C= \{ h_{0}(\gamma _0^{2}), h_{1}(\gamma _0^{2}) \}$
,
$\mathcal {F}_0C= \{ h_{0}(\gamma _0^{2}), h_{1}(\gamma _0^{2}) \}$
,
![]() $\mathcal {F}_1C\setminus \mathcal {F}_{0}C= \{ h_{0}(\gamma _0^{1}) , h_{1}(\gamma _0^{1}) \}$
,
$\mathcal {F}_1C\setminus \mathcal {F}_{0}C= \{ h_{0}(\gamma _0^{1}) , h_{1}(\gamma _0^{1}) \}$
,
![]() $\mathcal {F}_2C\setminus \mathcal {F}_{1}C= \{ h_{1}(\gamma _1^{3}) , h_{2}(\gamma _1^{3}) \}$
,
$\mathcal {F}_2C\setminus \mathcal {F}_{1}C= \{ h_{1}(\gamma _1^{3}) , h_{2}(\gamma _1^{3}) \}$
,
![]() $\mathcal {F}_3C\setminus \mathcal {F}_{2}C= \{ h_{1}(\gamma _1^{5}) , h_{2}(\gamma _1^{5}) \}$
,
$\mathcal {F}_3C\setminus \mathcal {F}_{2}C= \{ h_{1}(\gamma _1^{5}) , h_{2}(\gamma _1^{5}) \}$
,
![]() $\mathcal {F}_4C\setminus \mathcal {F}_{3}C=\! \{ h_{1}(\gamma _1^{4}) , h_{2}(\gamma _1^{4}) \}$
and
$\mathcal {F}_4C\setminus \mathcal {F}_{3}C=\! \{ h_{1}(\gamma _1^{4}) , h_{2}(\gamma _1^{4}) \}$
and
![]() $\mathcal {F}_5C\setminus \mathcal {F}_{4}C=\! \{ h_{1}(\gamma _2^{6}) , h_{2}(\gamma _2^{6}) \}$
. This filtration is not NMS-compatible, since it does not satisfy the SF1 condition. More specifically,
$\mathcal {F}_5C\setminus \mathcal {F}_{4}C=\! \{ h_{1}(\gamma _2^{6}) , h_{2}(\gamma _2^{6}) \}$
. This filtration is not NMS-compatible, since it does not satisfy the SF1 condition. More specifically,
![]() $\Delta ^{4}(\gamma _1^{3},\gamma _{0}^{2})_{22}$
is a primary pivot, but
$\Delta ^{4}(\gamma _1^{3},\gamma _{0}^{2})_{22}$
is a primary pivot, but
![]() $\Delta ^{4}(\gamma _1^{3},\gamma _{0}^{2})_{11}$
is an entry above a primary pivot and hence it is neither a primary pivot nor a zero entry. Moreover,
$\Delta ^{4}(\gamma _1^{3},\gamma _{0}^{2})_{11}$
is an entry above a primary pivot and hence it is neither a primary pivot nor a zero entry. Moreover,
![]() $\Delta ^{4}(\gamma _1^{5},\gamma _{0}^{1})_{22}$
is a primary pivot, but
$\Delta ^{4}(\gamma _1^{5},\gamma _{0}^{1})_{22}$
is a primary pivot, but
![]() $\Delta ^{4}(\gamma _1^{5},\gamma _{0}^{1})_{11}$
is a change of basis pivot determined by a primary pivot
$\Delta ^{4}(\gamma _1^{5},\gamma _{0}^{1})_{11}$
is a change of basis pivot determined by a primary pivot
![]() $- E_{11}$
. See Figure 17.
$- E_{11}$
. See Figure 17.

Figure 17 SSSA for a non-NMS-compatible filtration:
![]() $\Delta ^2$
(left) and
$\Delta ^2$
(left) and
![]() $\Delta ^4$
(right).
$\Delta ^4$
(right).
It is not known whether NMS-compatible filtrations always exist for a given NMS chain complex.
The next results show that NMS-compatible filtrations permit a characterization of non-zero differentials of the spectral sequence.
Proposition 4.11. Let
![]() $(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
be an NMS filtered chain complex, let
$(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
be an NMS filtered chain complex, let
![]() $\Delta ^{\mathrm {NMS}}$
be TU and let
$\Delta ^{\mathrm {NMS}}$
be TU and let
![]() $\mathcal {F}$
be an NMS-compatible filtration. Let
$\mathcal {F}$
be an NMS-compatible filtration. Let
![]() $\Delta ^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
be a submatrix of
$\Delta ^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
be a submatrix of
![]() $\Delta ^r$
that induces a non-zero differential
$\Delta ^r$
that induces a non-zero differential
![]() $d^r_p$
of the spectral sequence. Then
$d^r_p$
of the spectral sequence. Then
![]() $\Delta ^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
is one of the following matricesFootnote
1
, where the entries marked with circles are primary pivots and the entries marked with squares are change of basis pivots in the SSSA.
$\Delta ^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
is one of the following matricesFootnote
1
, where the entries marked with circles are primary pivots and the entries marked with squares are change of basis pivots in the SSSA.

Proof. As proved in Theorem 4.6, the non-zero differentials of the spectral sequence are induced by the pivots. Theorem 2.1 in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3] establishes that, whenever
![]() $\Delta ^{\mathrm {NMS}}$
is TU, the primary pivots are
$\Delta ^{\mathrm {NMS}}$
is TU, the primary pivots are
![]() $\pm 1$
. Hence, the differentials
$\pm 1$
. Hence, the differentials
![]() $d^{r}_{p,q}:E^r_{p,q}\to E^r_{p-r,q}$
associated to primary pivots are isomorphisms and the ones associated to change of basis pivots always correspond to zero maps. The result follows from Corollary 4.7 and the restrictions imposed by an NMS-compatible filtration.
$d^{r}_{p,q}:E^r_{p,q}\to E^r_{p-r,q}$
associated to primary pivots are isomorphisms and the ones associated to change of basis pivots always correspond to zero maps. The result follows from Corollary 4.7 and the restrictions imposed by an NMS-compatible filtration.
Theorem 4.12. Under the hypothesis of Proposition 4.11, a non-zero differential
![]() $d^r_p$
of the spectral sequence is multiplication by
$d^r_p$
of the spectral sequence is multiplication by
![]() $\pm I^{pp}$
,
$\pm I^{pp}$
,
![]() $\pm \widetilde {I}^{pp}$
,
$\pm \widetilde {I}^{pp}$
,
![]() $\pm E_{11}^p$
or
$\pm E_{11}^p$
or
![]() $\pm E_{22}^p$
.
$\pm E_{22}^p$
.
The last result characterizes the non-zero differentials
![]() $d^r_p$
induced by the submatrices
$d^r_p$
induced by the submatrices
![]() $\Delta ^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
corresponding to periodic orbits of consecutive indices. A non-zero differential induced by a submatrix
$\Delta ^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
corresponding to periodic orbits of consecutive indices. A non-zero differential induced by a submatrix
![]() $ \Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{0})$
corresponding to a repelling periodic orbit and an attracting periodic orbit is given by
$ \Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{0})$
corresponding to a repelling periodic orbit and an attracting periodic orbit is given by
![]() $\pm E_{21}^{p}$
.
$\pm E_{21}^{p}$
.
The next theorem is key in proving one of the main results of this paper, Theorem 5.1, since it is foundational in establishing dynamical results obtained in the next section.
Theorem 4.13. Let
![]() $(C^{\mathrm {{NMS}}},\Delta ^{\mathrm {{NMS}}})$
be an NMS filtered chain complex, let
$(C^{\mathrm {{NMS}}},\Delta ^{\mathrm {{NMS}}})$
be an NMS filtered chain complex, let
![]() $\Delta ^{\mathrm {NMS}}$
be TU and let
$\Delta ^{\mathrm {NMS}}$
be TU and let
![]() $\mathcal {F}$
be an NMS-compatible filtration. Then the matrices
$\mathcal {F}$
be an NMS-compatible filtration. Then the matrices
![]() $\Delta ^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
in the SSSA that induce non-zero differentials in the spectral sequence have the following properties.
$\Delta ^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
in the SSSA that induce non-zero differentials in the spectral sequence have the following properties.
-
(1) If
 $k=1$
, then
$k=1$
, then
 $\pm {I}^{pp}$
,
$\pm {I}^{pp}$
,
 $\pm \widetilde {I}^{pp}$
and
$\pm \widetilde {I}^{pp}$
and
 $\pm E_{22}^p$
never appear due to a change of basis determined by
$\pm E_{22}^p$
never appear due to a change of basis determined by
 $\pm E_{11}^p$
.
$\pm E_{11}^p$
. -
(2) If
 $k=2$
, then
$k=2$
, then
 $\pm {I}^{pp}$
,
$\pm {I}^{pp}$
,
 $\pm \widetilde {I}^{pp}$
and
$\pm \widetilde {I}^{pp}$
and
 $\pm E_{11}^p$
never appear due to a change of basis determined by
$\pm E_{11}^p$
never appear due to a change of basis determined by
 $\pm E_{22}^p$
.
$\pm E_{22}^p$
.
Proof. Let
![]() $k=1$
and let
$k=1$
and let
![]() $\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})$
be a matrix that induces a non-zero differential
$\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})$
be a matrix that induces a non-zero differential
![]() $d^r_p$
. Suppose that
$d^r_p$
. Suppose that
![]() $\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})$
appears owing to a change of basis determined by
$\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})$
appears owing to a change of basis determined by
![]() $\Delta ^{r}(\gamma ^t_1,\gamma ^{i}_{0})= \pm E_{11}^p$
, where
$\Delta ^{r}(\gamma ^t_1,\gamma ^{i}_{0})= \pm E_{11}^p$
, where
![]() $t<p$
and
$t<p$
and
![]() $i>p-r$
. By Theorem 3.7,
$i>p-r$
. By Theorem 3.7,
![]() $\Delta ^{p-i}(\gamma ^p_1,\gamma ^{i}_{0})$
must be either
$\Delta ^{p-i}(\gamma ^p_1,\gamma ^{i}_{0})$
must be either
![]() $ \pm E_{11}$
,
$ \pm E_{11}$
,
![]() $\pm {I}$
or
$\pm {I}$
or
![]() $\pm \widetilde {I}$
. Also,
$\pm \widetilde {I}$
. Also,
![]() $\Delta ^{p-i}(\gamma ^t_1,\gamma ^{p-r}_{0})$
is either
$\Delta ^{p-i}(\gamma ^t_1,\gamma ^{p-r}_{0})$
is either
![]() $ \pm E_{11}$
,
$ \pm E_{11}$
,
![]() $\pm {I}$
or
$\pm {I}$
or
![]() $\pm \widetilde {I}$
; in particular,
$\pm \widetilde {I}$
; in particular,
![]() $\Delta ^{p-i}(\gamma ^t_1,\gamma ^{p-r}_{0})_{11}=\pm 1$
. Therefore, by performing the corresponding change of basis, the column associated to
$\Delta ^{p-i}(\gamma ^t_1,\gamma ^{p-r}_{0})_{11}=\pm 1$
. Therefore, by performing the corresponding change of basis, the column associated to
![]() $h_2(\gamma ^p_1)$
remains unaltered during this change of basis and one has the following possibilities.
$h_2(\gamma ^p_1)$
remains unaltered during this change of basis and one has the following possibilities.
-
(a) If
 $\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})_{22}$
is zero, then
$\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})_{22}$
is zero, then
 $\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})$
is either null or
$\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})$
is either null or
 $\pm E_{11}$
.
$\pm E_{11}$
. -
(b) If
 $\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})_{22}$
is equal to
$\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})_{22}$
is equal to
 $\pm 1$
, then
$\pm 1$
, then
 $\Delta ^{p-i}(\gamma ^p_1,\gamma ^{p-r}_{0})_{11} =\pm 1$
, by Theorem 3.7. Thus, after the change of basis,
$\Delta ^{p-i}(\gamma ^p_1,\gamma ^{p-r}_{0})_{11} =\pm 1$
, by Theorem 3.7. Thus, after the change of basis,
 $\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})_{11}$
is zero, which means that
$\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})_{11}$
is zero, which means that
 $\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})$
is
$\Delta ^{r}(\gamma ^p_1,\gamma ^{p-r}_{0})$
is
 $\pm E_{22}^p$
, which contradicts (SF1).
$\pm E_{22}^p$
, which contradicts (SF1).
See Figure 18. Therefore,
![]() $\pm {I}^{pp}$
,
$\pm {I}^{pp}$
,
![]() $\pm \widetilde {I}^{pp}$
and
$\pm \widetilde {I}^{pp}$
and
![]() $\pm E_{22}^p$
never appear owing to a change of basis determined by
$\pm E_{22}^p$
never appear owing to a change of basis determined by
![]() $\pm E_{11}^p$
.
$\pm E_{11}^p$
.

Figure 18 Change of basis determined by
![]() $\pm E_{11}^p$
.
$\pm E_{11}^p$
.
Let
![]() $k=2$
and let
$k=2$
and let
![]() $\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})$
be a matrix that induces a non-zero differential
$\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})$
be a matrix that induces a non-zero differential
![]() $d^r_p$
. Suppose that
$d^r_p$
. Suppose that
![]() $\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})$
appears owing to a change of basis determined by
$\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})$
appears owing to a change of basis determined by
![]() $\Delta ^{r}(\gamma ^t_2,\gamma ^{i}_{1})= \pm E_{22}^p$
, where
$\Delta ^{r}(\gamma ^t_2,\gamma ^{i}_{1})= \pm E_{22}^p$
, where
![]() $t<p$
and
$t<p$
and
![]() $i>p-r$
. By Theorem 3.8,
$i>p-r$
. By Theorem 3.8,
![]() $\Delta ^{p-i}(\gamma ^p_2,\gamma ^{i}_{1})$
must be either
$\Delta ^{p-i}(\gamma ^p_2,\gamma ^{i}_{1})$
must be either
![]() $ \pm E_{22}$
,
$ \pm E_{22}$
,
![]() $\pm {I}$
or
$\pm {I}$
or
![]() $\pm \widetilde {I}$
and, analogously,
$\pm \widetilde {I}$
and, analogously,
![]() $\Delta ^{p-i}(\gamma ^t_2,\gamma ^{p-r}_{1})$
is either
$\Delta ^{p-i}(\gamma ^t_2,\gamma ^{p-r}_{1})$
is either
![]() $\pm E_{22}$
,
$\pm E_{22}$
,
![]() $\pm {I}$
or
$\pm {I}$
or
![]() $\pm \widetilde {I}$
; in particular,
$\pm \widetilde {I}$
; in particular,
![]() $\Delta ^{p-i}(\gamma ^t_2,\gamma ^{p-r}_{1})_{22}=\pm 1$
. Therefore, by performing the corresponding change of basis, the column associated to
$\Delta ^{p-i}(\gamma ^t_2,\gamma ^{p-r}_{1})_{22}=\pm 1$
. Therefore, by performing the corresponding change of basis, the column associated to
![]() $h_2(\gamma ^p_2)$
remains unaltered during this change of basis and one has the following possibilities.
$h_2(\gamma ^p_2)$
remains unaltered during this change of basis and one has the following possibilities.
-
(a) If
 $\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})_{11}$
is zero, then
$\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})_{11}$
is zero, then
 $\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})$
is either null or
$\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})$
is either null or
 $\pm E_{22}$
.
$\pm E_{22}$
. -
(b) If
 $\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})_{11}$
is equal to
$\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})_{11}$
is equal to
 $\pm 1$
, then
$\pm 1$
, then
 $\Delta ^{p-i}(\gamma ^p_2,\gamma ^{p-r}_{1})_{22} =\pm 1$
, by Theorem 3.8. Thus after the change of basis,
$\Delta ^{p-i}(\gamma ^p_2,\gamma ^{p-r}_{1})_{22} =\pm 1$
, by Theorem 3.8. Thus after the change of basis,
 $\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})_{22}$
is zero, which means that
$\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})_{22}$
is zero, which means that
 $\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})$
is
$\Delta ^{r}(\gamma ^p_2,\gamma ^{p-r}_{1})$
is
 $\pm E_{11}^p$
, which contradicts (SF2).
$\pm E_{11}^p$
, which contradicts (SF2).
See Figure 19. Therefore,
![]() $\pm {I}^{pp}$
,
$\pm {I}^{pp}$
,
![]() $\pm \widetilde {I}^{pp}$
and
$\pm \widetilde {I}^{pp}$
and
![]() $\pm E_{11}^p$
never appear owing to a change of basis determined by
$\pm E_{11}^p$
never appear owing to a change of basis determined by
![]() $\pm E_{22}^p$
.
$\pm E_{22}^p$
.
Note that the hypothesis of an NMS-compatible filtration is essential in Theorem 4.13 (see the next example).

Figure 19 Change of basis determined by
![]() $\pm E_{22}^p$
.
$\pm E_{22}^p$
.
Example 4.14. Consider the following filtration for the NMS chain complex given in Example 3.9:
![]() $\mathcal {F}_0C= \{ h_{0}(\gamma _0^{1}), h_{1}(\gamma _0^{1}) \}$
,
$\mathcal {F}_0C= \{ h_{0}(\gamma _0^{1}), h_{1}(\gamma _0^{1}) \}$
,
![]() $\mathcal {F}_1C\setminus \mathcal {F}_{0}C= \{ h_{0}(\gamma _0^{2}) , h_{1}(\gamma _0^{2}) \}$
,
$\mathcal {F}_1C\setminus \mathcal {F}_{0}C= \{ h_{0}(\gamma _0^{2}) , h_{1}(\gamma _0^{2}) \}$
,
![]() $\mathcal {F}_2C\setminus \mathcal {F}_{1}C= \{ h_{1}(\gamma _1^{4}) , h_{2}(\gamma _1^{4}) \}$
,
$\mathcal {F}_2C\setminus \mathcal {F}_{1}C= \{ h_{1}(\gamma _1^{4}) , h_{2}(\gamma _1^{4}) \}$
,
![]() $\mathcal {F}_3C\setminus \mathcal {F}_{2}C= \{ h_{1}(\gamma _1^{3}) , h_{2}(\gamma _1^{3}) \}$
,
$\mathcal {F}_3C\setminus \mathcal {F}_{2}C= \{ h_{1}(\gamma _1^{3}) , h_{2}(\gamma _1^{3}) \}$
,
![]() $\mathcal {F}_4C\setminus \mathcal {F}_{3}C= \{ h_{1}(\gamma _1^{5}) , h_{2}(\gamma _1^{5}) \}$
and
$\mathcal {F}_4C\setminus \mathcal {F}_{3}C= \{ h_{1}(\gamma _1^{5}) , h_{2}(\gamma _1^{5}) \}$
and
![]() $\mathcal {F}_5C\setminus \mathcal {F}_{4}C= \{ h_{1}(\gamma _2^{6}) , h_{2}(\gamma _2^{6}) \}$
. This filtration is not NMS-compatible, since it does not satisfy the SF1 condition in Definition 4.8. More specifically,
$\mathcal {F}_5C\setminus \mathcal {F}_{4}C= \{ h_{1}(\gamma _2^{6}) , h_{2}(\gamma _2^{6}) \}$
. This filtration is not NMS-compatible, since it does not satisfy the SF1 condition in Definition 4.8. More specifically,
![]() $\Delta ^{8}(\gamma _1^{5},\gamma _{0}^{1})_{22}$
is a primary pivot, but
$\Delta ^{8}(\gamma _1^{5},\gamma _{0}^{1})_{22}$
is a primary pivot, but
![]() $\Delta ^{8}(\gamma _1^{5},\gamma _{0}^{1})_{11}=0$
such that
$\Delta ^{8}(\gamma _1^{5},\gamma _{0}^{1})_{11}=0$
such that
![]() $\Delta ^{6}(\gamma _1^{5},\gamma _{0}^{2})_{11} $
is a change of basis pivot determined by a primary pivot
$\Delta ^{6}(\gamma _1^{5},\gamma _{0}^{2})_{11} $
is a change of basis pivot determined by a primary pivot
![]() $- E_{11}^p$
. Consequently,
$- E_{11}^p$
. Consequently,
![]() $E_{22}^p$
appeared owing to a change of basis determined by
$E_{22}^p$
appeared owing to a change of basis determined by
![]() $- E_{11}^p$
. See Figure 20.
$- E_{11}^p$
. See Figure 20.

Figure 20 Theorem 4.13 does not hold for non-NMS-compatible filtrations.
An additional requirement on an NMS-compatible filtration is reduction ordering.
Definition 4.15. Given a saddle periodic orbit
![]() $\gamma _1^{p}$
, one says that a filtration
$\gamma _1^{p}$
, one says that a filtration
![]() $\mathcal {F}$
satisfies the reduction ordering condition on a saddle
$\mathcal {F}$
satisfies the reduction ordering condition on a saddle
![]() $\gamma _1^{p}$
if, whenever
$\gamma _1^{p}$
if, whenever
![]() $\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})=\pm E_{22}^p$
(respectively,
$\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})=\pm E_{22}^p$
(respectively,
![]() $\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})=\pm E_{11}^p$
), then
$\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})=\pm E_{11}^p$
), then
![]() $\Delta ^{\ell -p}(\gamma _2^{\ell },\gamma _{1}^{p})$
(respectively,
$\Delta ^{\ell -p}(\gamma _2^{\ell },\gamma _{1}^{p})$
(respectively,
![]() $\Delta ^{p-r-\ell }(\gamma _1^{p-r},\gamma _{0}^{\ell })$
) is different from
$\Delta ^{p-r-\ell }(\gamma _1^{p-r},\gamma _{0}^{\ell })$
) is different from
![]() $\pm E_{11}^p$
(respectively,
$\pm E_{11}^p$
(respectively,
![]() $\pm E_{22}^p$
). If
$\pm E_{22}^p$
). If
![]() $\mathcal {F}$
satisfies the reduction ordering condition for all saddle periodic orbits, then one says that
$\mathcal {F}$
satisfies the reduction ordering condition for all saddle periodic orbits, then one says that
![]() $\mathcal {F}$
satisfies the reduction ordering condition.
$\mathcal {F}$
satisfies the reduction ordering condition.
For example, the filtration presented in Figure 20 does not satisfy the reduction ordering condition, since
![]() $\Delta ^{8}(\gamma _1^{4},\gamma _{0}^{1})= E_{22}^p$
and
$\Delta ^{8}(\gamma _1^{4},\gamma _{0}^{1})= E_{22}^p$
and
![]() $\Delta ^{6}(\gamma _2^{6},\gamma _{1}^{4})= E_{11}^p$
.
$\Delta ^{6}(\gamma _2^{6},\gamma _{1}^{4})= E_{11}^p$
.
Proposition 4.16. Let
![]() $(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
be an NMS chain complex, where
$(C^{\mathrm {NMS}},\Delta ^{\mathrm {NMS}})$
be an NMS chain complex, where
![]() $\Delta ^{\mathrm {NMS}}$
is a TU matrix.
$\Delta ^{\mathrm {NMS}}$
is a TU matrix.
-
(1) If
 $\Delta ^{r_0}(\gamma ^p_1,\gamma ^{p-r_0}_{0})=\pm E_{22}^p$
, then the entries of the row corresponding to
$\Delta ^{r_0}(\gamma ^p_1,\gamma ^{p-r_0}_{0})=\pm E_{22}^p$
, then the entries of the row corresponding to
 $h_1(\gamma ^{p}_1)$
and of the columns corresponding to
$h_1(\gamma ^{p}_1)$
and of the columns corresponding to
 $h_2(\gamma ^{\ell }_1)$
, for all
$h_2(\gamma ^{\ell }_1)$
, for all
 $\ell $
, are equal to zero in
$\ell $
, are equal to zero in
 $\Delta ^{r}$
for all r.
$\Delta ^{r}$
for all r. -
(2) If
 $\Delta ^{r_0}(\gamma ^p_2,\gamma ^{p-r_0}_{1})=\pm E_{11}^p$
then the entries of the column corresponding to
$\Delta ^{r_0}(\gamma ^p_2,\gamma ^{p-r_0}_{1})=\pm E_{11}^p$
then the entries of the column corresponding to
 $h_2(\gamma ^{p-r_0}_1)$
and of the rows corresponding to
$h_2(\gamma ^{p-r_0}_1)$
and of the rows corresponding to
 $h_1(\gamma ^{\ell }_1)$
, for all
$h_1(\gamma ^{\ell }_1)$
, for all
 $\ell $
, are equal to zero in
$\ell $
, are equal to zero in
 $\Delta ^{r}$
for all r.
$\Delta ^{r}$
for all r.
Proof. Let
![]() $\gamma _1^{{\ell }_1},\ldots , \gamma _1^{{\ell }_e}$
be the saddle periodic orbits of
$\gamma _1^{{\ell }_1},\ldots , \gamma _1^{{\ell }_e}$
be the saddle periodic orbits of
![]() $\varphi $
.
$\varphi $
.
(1) The entries in the row
![]() $2p-1$
and in the columns
$2p-1$
and in the columns
![]() $2\ell _1,\ldots , 2\ell _e$
are equal to zero in
$2\ell _1,\ldots , 2\ell _e$
are equal to zero in
![]() $\varphi $
since non-zero entries would correspond to connections between saddle periodic orbits. We will prove that the entries in the row
$\varphi $
since non-zero entries would correspond to connections between saddle periodic orbits. We will prove that the entries in the row
![]() $2p-1$
and in the columns
$2p-1$
and in the columns
![]() $2\ell _1,\ldots , 2\ell _e$
are equal to zero in
$2\ell _1,\ldots , 2\ell _e$
are equal to zero in
![]() $\Delta ^r$
for all r.
$\Delta ^r$
for all r.
Suppose there is a non-zero entry
![]() $\Delta ^r_{2p-1,2\ell _i}$
in the row
$\Delta ^r_{2p-1,2\ell _i}$
in the row
![]() $2p-1$
and the column
$2p-1$
and the column
![]() $2\ell _i$
. Note that
$2\ell _i$
. Note that
![]() $\Delta ^0_{2p-1,2\ell _i}=0$
. Moreover, under the SSSA,
$\Delta ^0_{2p-1,2\ell _i}=0$
. Moreover, under the SSSA,
![]() $\Delta ^r_{2p-1,2\ell _i}$
does not become non-zero owing to a change in row
$\Delta ^r_{2p-1,2\ell _i}$
does not become non-zero owing to a change in row
![]() $2p-1$
. In fact, since
$2p-1$
. In fact, since
![]() $\Delta ^{r_0}(\gamma ^p_1,\gamma ^{p-r_0}_{0})=\pm E_{22}^p$
, there can be no primary pivots in the column
$\Delta ^{r_0}(\gamma ^p_1,\gamma ^{p-r_0}_{0})=\pm E_{22}^p$
, there can be no primary pivots in the column
![]() $2p-1$
and the only rows that undergo changes are those whose corresponding column contains a primary pivot. Hence, by performing a backward analysis,
$2p-1$
and the only rows that undergo changes are those whose corresponding column contains a primary pivot. Hence, by performing a backward analysis,
![]() $\Delta ^r_{2p-1,2\ell _i}$
must have turned to
$\Delta ^r_{2p-1,2\ell _i}$
must have turned to
![]() $\pm 1$
owing to a change in columns: that is, there exist
$\pm 1$
owing to a change in columns: that is, there exist
![]() $j<i$
,
$j<i$
,
![]() $r_1<r$
such that
$r_1<r$
such that
![]() $\Delta ^{r_1}_{2p-1,2\ell _j}\neq 0$
.
$\Delta ^{r_1}_{2p-1,2\ell _j}\neq 0$
.
Repeating this procedure, after a finite number of steps we obtain a non-zero entry in
![]() $\Delta ^1$
that corresponds to a connection between saddle periodic orbits, which contradicts our hypothesis.
$\Delta ^1$
that corresponds to a connection between saddle periodic orbits, which contradicts our hypothesis.
(2) The entries in the column
![]() $2(p-r_0)$
and in the rows
$2(p-r_0)$
and in the rows
![]() $2\ell _1-1,\ldots , 2\ell _e-1$
are equal to zero in
$2\ell _1-1,\ldots , 2\ell _e-1$
are equal to zero in
![]() $\Delta $
, since non-zero entries would correspond to connections between saddle periodic orbits in
$\Delta $
, since non-zero entries would correspond to connections between saddle periodic orbits in
![]() $\varphi $
.
$\varphi $
.
Using a similar argument as in (1), we prove that these entries remain zero in the matrix
![]() $\Delta ^r$
for all r.
$\Delta ^r$
for all r.
5 Global dynamical cancellation and reduction of periodic orbits
It is proved in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3, Reference Bertolim, Lima, Mello, de Rezende and da Silveira4] that the algebraic cancellations of the modules
![]() $\mathcal {E}^r$
of a spectral sequence associated to a filtered Morse chain complex are in one-to-one correspondence with dynamical cancellations of singularities of a Morse flow.
$\mathcal {E}^r$
of a spectral sequence associated to a filtered Morse chain complex are in one-to-one correspondence with dynamical cancellations of singularities of a Morse flow.
The goal of this section is to construct an analogous correspondence between algebra and dynamics by means of cancellations and reductions of periodic orbits for an NMS flow. This correspondence is achieved through the algorithm SSSA presented in §4, which, applied to a filtered NMS chain complex, determines cancellations of periodic orbits as well as their reductions. As a result, one obtains a family of NMS flows where the last one is a core flow.
Recall that
![]() $\varphi \in \Sigma (M^3)$
is a core flow if each inessential connection between two consecutive periodic orbits is part of a double inessential connection. As a consequence, for each pair of consecutive periodic orbits
$\varphi \in \Sigma (M^3)$
is a core flow if each inessential connection between two consecutive periodic orbits is part of a double inessential connection. As a consequence, for each pair of consecutive periodic orbits
![]() $(\gamma _k, \gamma _{k-1})$
of a core flow, the following conditions cannot occur.
$(\gamma _k, \gamma _{k-1})$
of a core flow, the following conditions cannot occur.
-
(1) There is a unique inessential cylinder of connections between
 $\gamma _k$
and
$\gamma _k$
and
 $\gamma _{k-1}$
.
$\gamma _{k-1}$
. -
(2)
 $\gamma _k$
double connects with
$\gamma _k$
double connects with
 $\gamma _{k-1}$
through an inessential and an essential cylinder of connections.
$\gamma _{k-1}$
through an inessential and an essential cylinder of connections.
In other words, in a core flow, no pair of consecutive periodic orbits can be cancelled or reduced.
The choice of a filtration for a chain complex is key to establishing the order in which the cancellations and reductions take place within the flow. The ordering of cancellations and reductions of periodic orbits of a flow may produce topologically distinct flows. In fact, it may produce distinct core flows. See Remark 5.4.
In §5.1, we use the SSSA in an NMS-compatible filtered chain complex
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
, where
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
, where
![]() $\widetilde \varphi \in FM(\varphi )$
. It turns out that NMS-compatibility will be essential in establishing an algebraic-dynamical correspondence between the unfolding of the spectral sequence and the cancellation and reduction of periodic orbits within an associated NMS flow. More precisely, all the non-zero differentials of the associated spectral sequence via the SSSA will determine all cancellations and reductions of periodic orbits, which thus establishes in Theorem 5.1 a strong algebraic-dynamical correspondence. Furthermore, as the spectral sequence converges, one obtains a core flow as shown in Theorem 5.2.
$\widetilde \varphi \in FM(\varphi )$
. It turns out that NMS-compatibility will be essential in establishing an algebraic-dynamical correspondence between the unfolding of the spectral sequence and the cancellation and reduction of periodic orbits within an associated NMS flow. More precisely, all the non-zero differentials of the associated spectral sequence via the SSSA will determine all cancellations and reductions of periodic orbits, which thus establishes in Theorem 5.1 a strong algebraic-dynamical correspondence. Furthermore, as the spectral sequence converges, one obtains a core flow as shown in Theorem 5.2.
In §5.2, we explore NMS flows that have no pair of cancelling periodic orbits. In this case, we prove that any filtration on the corresponding chain complex is always NMS-compatible. Furthermore, if the filtration satisfies the reduction ordering condition, then we show in Theorem 5.7 that the core flow has the lowest number of attracting, repelling and saddle periodic orbits in
![]() $\mathcal {S}_{\varphi }$
. However, if it does not satisfy the the reduction ordering condition, then we show in Theorem 5.8, via an algorithm based on a spectral sequence analysis, that one arrives at a core flow at the expense of partially losing the algebraic-dynamical correspondence obtained in Theorem 5.1.
$\mathcal {S}_{\varphi }$
. However, if it does not satisfy the the reduction ordering condition, then we show in Theorem 5.8, via an algorithm based on a spectral sequence analysis, that one arrives at a core flow at the expense of partially losing the algebraic-dynamical correspondence obtained in Theorem 5.1.
In §5.3, we investigate in Corollary 5.12 the role of cancellations in an NMS flow in order to arrive at a core flow under arbitrary filtrations of the associated chain complex. We show in Theorem 5.15 that, in the case of
![]() $S^3$
, a core flow has precisely one attracting and one repelling periodic orbit.
$S^3$
, a core flow has precisely one attracting and one repelling periodic orbit.
5.1 Cancellations and reductions determined by a spectral sequence
In this section, one of the main results in this paper, Theorem 5.1, is proved. It establishes a correspondence between the dynamics of cancellations and reductions of periodic orbits in an NMS flow and the differentials of the spectral sequence of a filtered chain complex associated to the flow.
The hypothesis on the filtration of Theorem 5.1 will guarantee that, by following the unfolding of the associated spectral sequence, we can always dynamically perform corresponding cancellations and reductions in an NMS flow. First, one will require that
![]() $\mathcal {F}$
is an NMS-compatible filtration for
$\mathcal {F}$
is an NMS-compatible filtration for
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
. Second, one must ensure that the spectral sequence determines, at each stage, at most one cancellation or reduction of a given periodic orbit. This is precisely what is ensured by requiring that the filtration satisfies the reduction ordering condition. Recall that
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
. Second, one must ensure that the spectral sequence determines, at each stage, at most one cancellation or reduction of a given periodic orbit. This is precisely what is ensured by requiring that the filtration satisfies the reduction ordering condition. Recall that
![]() $FM(\varphi )$
is the class of
$FM(\varphi )$
is the class of
![]() $h_2-h_1$
free morsifications as in Definition 3.4.
$h_2-h_1$
free morsifications as in Definition 3.4.
Theorem 5.1. (Smale’s cancellation theorem via spectral sequence)
Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, such that
$3$
-manifold, such that
![]() $FM(\varphi )\neq \emptyset $
. Assume that there is an NMS-compatible filtration
$FM(\varphi )\neq \emptyset $
. Assume that there is an NMS-compatible filtration
![]() $\mathcal {F}$
for
$\mathcal {F}$
for
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
,
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
,
![]() $\widetilde {\varphi }\in FM(\varphi )$
satisfying the reduction ordering condition and let
$\widetilde {\varphi }\in FM(\varphi )$
satisfying the reduction ordering condition and let
![]() $(\mathcal {E}^r,d^r)$
be the spectral sequence associated to this filtered chain complex. Then the collection of matrices
$(\mathcal {E}^r,d^r)$
be the spectral sequence associated to this filtered chain complex. Then the collection of matrices
![]() $\{\Delta ^1,\ldots , \Delta ^{\omega }\}$
produced by the SSSA applied to
$\{\Delta ^1,\ldots , \Delta ^{\omega }\}$
produced by the SSSA applied to
![]() $\Delta ^{\mathrm {NMS}}$
determines a family of NMS flows
$\Delta ^{\mathrm {NMS}}$
determines a family of NMS flows
![]() $\{\varphi ^1,\ldots ,\varphi ^{\omega }\}\subset \mathcal {S}_{\varphi }$
on
$\{\varphi ^1,\ldots ,\varphi ^{\omega }\}\subset \mathcal {S}_{\varphi }$
on
![]() $M^3$
, where
$M^3$
, where
![]() $\varphi ^1=\varphi $
,
$\varphi ^1=\varphi $
,
![]() $\varphi ^r$
is obtained from
$\varphi ^r$
is obtained from
![]() $\varphi ^{r-1}$
by cancellations and reductions of periodic orbits corresponding to the differentials
$\varphi ^{r-1}$
by cancellations and reductions of periodic orbits corresponding to the differentials
![]() $d^r$
. More specifically, whenever
$d^r$
. More specifically, whenever
![]() $d^r_{p}$
is a non-zero differential:
$d^r_{p}$
is a non-zero differential:
-
(1) if
 $\Delta ^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
is equal to
$\Delta ^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
is equal to
 $ \pm I^{pp}$
or
$ \pm I^{pp}$
or
 $\pm \tilde {I}^{pp}$
, for
$\pm \tilde {I}^{pp}$
, for
 $k=1,2$
, then the pair
$k=1,2$
, then the pair
 $(\gamma ^{p}_k,\gamma ^{p-r}_{k-1})$
is cancelled;
$(\gamma ^{p}_k,\gamma ^{p-r}_{k-1})$
is cancelled; -
(2) if
 $\Delta ^{r}(\gamma _1^p,\gamma ^{p-r}_{0})$
is equal to
$\Delta ^{r}(\gamma _1^p,\gamma ^{p-r}_{0})$
is equal to
 $ \pm E_{22}^p$
, then the pair
$ \pm E_{22}^p$
, then the pair
 $(\gamma ^{p}_1,\gamma ^{p-r}_{0})$
is reduced; and
$(\gamma ^{p}_1,\gamma ^{p-r}_{0})$
is reduced; and -
(3) if
 $\Delta ^{r}(\gamma _2^p,\gamma ^{p-r}_{1})$
is equal to
$\Delta ^{r}(\gamma _2^p,\gamma ^{p-r}_{1})$
is equal to
 $ \pm E_{11}^p$
, then the pair
$ \pm E_{11}^p$
, then the pair
 $(\gamma ^{p}_2,\gamma ^{p-r}_{1})$
is reduced.
$(\gamma ^{p}_2,\gamma ^{p-r}_{1})$
is reduced.
Proof. By Theorem 4.12, a non-zero differential
![]() $d^r_p$
of the spectral sequence is multiplication by one of the matrices
$d^r_p$
of the spectral sequence is multiplication by one of the matrices
![]() $\pm E_{11}^p$
,
$\pm E_{11}^p$
,
![]() $\pm E_{22}^p$
,
$\pm E_{22}^p$
,
![]() $\pm I^{pp}$
or
$\pm I^{pp}$
or
![]() $\pm \widetilde {I}^{pp}$
.
$\pm \widetilde {I}^{pp}$
.
By Proposition 3.2 in [Reference Cornea, de Rezende and da Silveira6], whenever
![]() $\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})$
(respectively,
$\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})$
(respectively,
![]() $\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})$
) is equal to
$\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})$
) is equal to
![]() $\pm I^{pp}$
or
$\pm I^{pp}$
or
![]() $\pm \widetilde {I}^{pp}$
, then
$\pm \widetilde {I}^{pp}$
, then
![]() $\Delta ^{\ell -p}(\gamma _2^{\ell },\gamma _{1}^{p})$
(respectively,
$\Delta ^{\ell -p}(\gamma _2^{\ell },\gamma _{1}^{p})$
(respectively,
![]() $\Delta ^{p-r-\ell }(\gamma _1^{p-r},\gamma _{0}^{\ell })$
) never induces a non-zero differential, for any
$\Delta ^{p-r-\ell }(\gamma _1^{p-r},\gamma _{0}^{\ell })$
) never induces a non-zero differential, for any
![]() $\ell $
. Moreover, since
$\ell $
. Moreover, since
![]() $\mathcal {F}$
satisfies the reduction ordering condition, two reductions associated to the same saddle
$\mathcal {F}$
satisfies the reduction ordering condition, two reductions associated to the same saddle
![]() $\gamma _1^{p}$
never occur. Indeed, whenever
$\gamma _1^{p}$
never occur. Indeed, whenever
![]() $\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})=\pm E_{22}^p$
(respectively,
$\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})=\pm E_{22}^p$
(respectively,
![]() $\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})=\pm E_{11}^p$
), a non-zero differential induced by
$\Delta ^{r}(\gamma _2^{p},\gamma _{1}^{p-r})=\pm E_{11}^p$
), a non-zero differential induced by
![]() $\Delta ^{\ell -p}(\gamma _2^{\ell },\gamma _{1}^{p})$
(respectively,
$\Delta ^{\ell -p}(\gamma _2^{\ell },\gamma _{1}^{p})$
(respectively,
![]() $\Delta ^{p-r-\ell }(\gamma _1^{p-r},\gamma _{0}^{\ell })$
) never occurs.
$\Delta ^{p-r-\ell }(\gamma _1^{p-r},\gamma _{0}^{\ell })$
) never occurs.
Since
![]() $\mathcal {F}$
is an NMS-compatible filtration, one has that if
$\mathcal {F}$
is an NMS-compatible filtration, one has that if
![]() $k=1$
, then
$k=1$
, then
![]() $\pm {I}^{pp}$
,
$\pm {I}^{pp}$
,
![]() $\pm \widetilde {I}^{pp}$
and
$\pm \widetilde {I}^{pp}$
and
![]() $\pm E_{22}^p$
never appear to the right of
$\pm E_{22}^p$
never appear to the right of
![]() $\pm E_{22}^p$
; if
$\pm E_{22}^p$
; if
![]() $k=2$
, then
$k=2$
, then
![]() $\pm I^p$
,
$\pm I^p$
,
![]() $\pm \widetilde {I}^p$
,
$\pm \widetilde {I}^p$
,
![]() $\pm {I}^{pp}$
,
$\pm {I}^{pp}$
,
![]() $\pm \widetilde {I}^{pp}$
and
$\pm \widetilde {I}^{pp}$
and
![]() $\pm E_{11}^p$
never appear to the right of
$\pm E_{11}^p$
never appear to the right of
![]() $\pm E_{11}^p$
,
$\pm E_{11}^p$
,
![]() $\pm I^p$
or
$\pm I^p$
or
![]() $\pm \widetilde {I}^p$
.
$\pm \widetilde {I}^p$
.
As a consequence of these facts and Proposition 4.16, whenever the spectral sequence determines a cancellation or a reduction of a pair of periodic orbits, then no further cancellations or reductions of the resulting periodic orbit will occur determined by non-zero differentials.
Hence, given
![]() ${\Delta }^r$
, the matrix corresponding to the rth step of the SSSA, it is enough to prove the following.
${\Delta }^r$
, the matrix corresponding to the rth step of the SSSA, it is enough to prove the following.
-
(1) If
 ${\Delta }^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
is equal to
${\Delta }^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
is equal to
 $ \pm I^{pp}$
or
$ \pm I^{pp}$
or
 $\pm \tilde {I}^{pp}$
, then the connection between
$\pm \tilde {I}^{pp}$
, then the connection between
 $\gamma ^p_k$
and
$\gamma ^p_k$
and
 $\gamma ^{p-r}_{k-1}$
in the flow
$\gamma ^{p-r}_{k-1}$
in the flow
 $\varphi ^r$
is inessential. Hence, by Theorem 3.11, the pair
$\varphi ^r$
is inessential. Hence, by Theorem 3.11, the pair
 $(\gamma ^{p}_k,\gamma ^{p-r}_{k-1})$
is cancelled.
$(\gamma ^{p}_k,\gamma ^{p-r}_{k-1})$
is cancelled. -
(2) If
 ${\Delta }^{r}(\gamma _1^p,\gamma ^{p-r}_{0})$
is equal to
${\Delta }^{r}(\gamma _1^p,\gamma ^{p-r}_{0})$
is equal to
 $ \pm E_{22}^p$
, then the connection between
$ \pm E_{22}^p$
, then the connection between
 $\gamma ^p_1$
and
$\gamma ^p_1$
and
 $\gamma ^{p-r}_{0}$
in the flow
$\gamma ^{p-r}_{0}$
in the flow
 $\varphi ^r$
is a double connection with one inessential and one
$\varphi ^r$
is a double connection with one inessential and one
 $h_2$
-
$h_2$
-
 $h_1$
free essential connections. In this case, by Theorem 3.12, the pair
$h_1$
free essential connections. In this case, by Theorem 3.12, the pair
 $(\gamma ^{p}_1,\gamma ^{p-r}_{0})$
is reduced;
$(\gamma ^{p}_1,\gamma ^{p-r}_{0})$
is reduced; -
(3) if
 ${\Delta }^{r}(\gamma _2^p,\gamma ^{p-r}_{1})$
is equal to
${\Delta }^{r}(\gamma _2^p,\gamma ^{p-r}_{1})$
is equal to
 $ \pm E_{11}^p$
then the connection between
$ \pm E_{11}^p$
then the connection between
 $\gamma ^p_2$
and
$\gamma ^p_2$
and
 $\gamma ^{p-r}_{1}$
in the flow
$\gamma ^{p-r}_{1}$
in the flow
 $\varphi ^r$
is a double connection with one inessential and one
$\varphi ^r$
is a double connection with one inessential and one
 $h_2$
-
$h_2$
-
 $h_1$
free essential connections. In this case, by Theorem 3.12, the pair
$h_1$
free essential connections. In this case, by Theorem 3.12, the pair
 $(\gamma ^{p}_2,\gamma ^{p-r}_{1})$
is reduced.
$(\gamma ^{p}_2,\gamma ^{p-r}_{1})$
is reduced.
In [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3] it was shown that the row cancellation algorithm (RCA) reflects the dynamical behavior of a family of Morse flows that undergoes cancellations. Moreover, by Theorem 2.2 in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3], the primary pivots of both the SSSA and the RCA are the same. Therefore, one can consider the primary pivots detected via the RCA. Let
![]() $\{\widetilde {\Delta }^{r}\}_{r\geq 0}$
be the collection of matrices produced by applying the RCA to
$\{\widetilde {\Delta }^{r}\}_{r\geq 0}$
be the collection of matrices produced by applying the RCA to
![]() $\Delta ^{\mathrm {NMS}}$
.
$\Delta ^{\mathrm {NMS}}$
.
We show that the flow
![]() $\varphi ^r$
satisfies items (1–3) and, for every pair of periodic orbits
$\varphi ^r$
satisfies items (1–3) and, for every pair of periodic orbits
![]() $\gamma ^{\ell }_{k}, \gamma ^{i}_{k-1}$
of
$\gamma ^{\ell }_{k}, \gamma ^{i}_{k-1}$
of
![]() $\varphi ^r$
that were in
$\varphi ^r$
that were in
![]() $\varphi $
, there are the following possibilities for
$\varphi $
, there are the following possibilities for
![]() $\widetilde {\Delta }^{r}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})$
.
$\widetilde {\Delta }^{r}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})$
.
-
(a) It corresponds to the connections between
 $\gamma ^{\ell }_{k}, \gamma ^{i}_{k-1}$
in the flow
$\gamma ^{\ell }_{k}, \gamma ^{i}_{k-1}$
in the flow
 $\varphi ^r$
: that is,
$\varphi ^r$
: that is,
 $\widetilde {\Delta }^{r}_{11}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})= n(h_k(\gamma ^{\ell }_k), h_{k-1}(\gamma ^{i}_{k-1});\widetilde {\varphi ^r}) $
and
$\widetilde {\Delta }^{r}_{11}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})= n(h_k(\gamma ^{\ell }_k), h_{k-1}(\gamma ^{i}_{k-1});\widetilde {\varphi ^r}) $
and
 $\widetilde {\Delta }^{r}_{22}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})= n(h_{k+1}(\gamma ^{\ell }_k), h_{k}(\gamma ^{i}_{k-1});\widetilde {\varphi ^r}) $
.
$\widetilde {\Delta }^{r}_{22}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})= n(h_{k+1}(\gamma ^{\ell }_k), h_{k}(\gamma ^{i}_{k-1});\widetilde {\varphi ^r}) $
. -
(b)
 $k=1$
(respectively,
$k=1$
(respectively,
 $k=2$
) and it is generated by changes of basis caused by
$k=2$
) and it is generated by changes of basis caused by
 $\pm E_{11}^p$
(respectively,
$\pm E_{11}^p$
(respectively,
 $\pm E_{22}^p$
). More specifically, there is at least one change of basis pivot in the column of
$\pm E_{22}^p$
). More specifically, there is at least one change of basis pivot in the column of
 $h_1(\gamma ^{\ell })$
(respectively,
$h_1(\gamma ^{\ell })$
(respectively,
 $h_2(\gamma ^{\ell })$
) determined by a primary pivot in
$h_2(\gamma ^{\ell })$
) determined by a primary pivot in
 $\pm E_{11}^p$
(respectively,
$\pm E_{11}^p$
(respectively,
 $\pm E_{22}^p$
).
$\pm E_{22}^p$
).
The proof follows by induction on r. Assume that
![]() $\varphi ^{r-1}$
is well defined and satisfies items (1–3) and assertion (a) or (b). Define
$\varphi ^{r-1}$
is well defined and satisfies items (1–3) and assertion (a) or (b). Define
![]() $\varphi ^r$
as the flow obtained from
$\varphi ^r$
as the flow obtained from
![]() $\varphi ^{r-1}$
by cancelling and reducing the periodic orbits corresponding to the differentials
$\varphi ^{r-1}$
by cancelling and reducing the periodic orbits corresponding to the differentials
![]() $d^{r-1}$
, namely,
$d^{r-1}$
, namely,
![]() $\pm {I}^{pp}$
,
$\pm {I}^{pp}$
,
![]() $\pm \widetilde {I}^{pp}$
or
$\pm \widetilde {I}^{pp}$
or
![]() $\pm E_{22}^p$
, if
$\pm E_{22}^p$
, if
![]() $k=1$
;
$k=1$
;
![]() $\pm {I}^{pp}$
,
$\pm {I}^{pp}$
,
![]() $\pm \widetilde {I}^{pp}$
or
$\pm \widetilde {I}^{pp}$
or
![]() $\pm E_{11}^p$
, if
$\pm E_{11}^p$
, if
![]() $k=2$
.
$k=2$
.
Recall that, as shown in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3], the RCA corresponds to a morsified dynamics: that is,
![]() $\widetilde {\Delta }^{r}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})_{11}$
and
$\widetilde {\Delta }^{r}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})_{11}$
and
![]() $\widetilde {\Delta }^{r}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})_{22}$
correspond to connecting orbits in a Morse flow
$\widetilde {\Delta }^{r}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})_{22}$
correspond to connecting orbits in a Morse flow
![]() $\phi ^r$
obtained by cancelling the critical points corresponding to the non-zero differentials
$\phi ^r$
obtained by cancelling the critical points corresponding to the non-zero differentials
![]() $d^j$
for
$d^j$
for
![]() $1\leq j\leq r-1$
.
$1\leq j\leq r-1$
.
Assume that we are not in case (b). This implies that
![]() $\widetilde {\Delta }^{r}(\gamma ^{\ell }_1,\gamma ^{i}_{0})$
(respectively,
$\widetilde {\Delta }^{r}(\gamma ^{\ell }_1,\gamma ^{i}_{0})$
(respectively,
![]() $\widetilde {\Delta }^{r}(\gamma ^{\ell }_2,\gamma ^{i}_{1})$
) is not generated by changes of basis caused by
$\widetilde {\Delta }^{r}(\gamma ^{\ell }_2,\gamma ^{i}_{1})$
) is not generated by changes of basis caused by
![]() $\pm E_{11}^p$
(respectively,
$\pm E_{11}^p$
(respectively,
![]() $\pm E_{22}^p$
), that is, there are no change of basis pivots in the column of
$\pm E_{22}^p$
), that is, there are no change of basis pivots in the column of
![]() $h_1(\gamma ^{\ell })$
(respectively,
$h_1(\gamma ^{\ell })$
(respectively,
![]() $h_2(\gamma ^{\ell })$
) determined by a primary pivot in
$h_2(\gamma ^{\ell })$
) determined by a primary pivot in
![]() $E_{11}^p$
(respectively,
$E_{11}^p$
(respectively,
![]() $E_{22}^p$
). Then the connections between the critical points
$E_{22}^p$
). Then the connections between the critical points
![]() $h_0(\gamma ^i)$
,
$h_0(\gamma ^i)$
,
![]() $h_1(\gamma ^i)$
,
$h_1(\gamma ^i)$
,
![]() $h_1(\gamma ^{\ell })$
,
$h_1(\gamma ^{\ell })$
,
![]() $h_2(\gamma ^{\ell })$
(respectively,
$h_2(\gamma ^{\ell })$
(respectively,
![]() $h_1(\gamma ^i)$
,
$h_1(\gamma ^i)$
,
![]() $h_2(\gamma ^i)$
,
$h_2(\gamma ^i)$
,
![]() $h_2(\gamma ^{\ell })$
,
$h_2(\gamma ^{\ell })$
,
![]() $h_3(\gamma ^{\ell })$
) were not changed by cancellations that occurred in the Morse flow
$h_3(\gamma ^{\ell })$
) were not changed by cancellations that occurred in the Morse flow
![]() $\phi ^j$
but did not occur in the morsification
$\phi ^j$
but did not occur in the morsification
![]() $\widetilde {\varphi }^j$
of
$\widetilde {\varphi }^j$
of
![]() $\varphi ^j$
, for
$\varphi ^j$
, for
![]() $1\leq j\leq r-1$
. Hence,
$1\leq j\leq r-1$
. Hence,
![]() $\widetilde {\Delta }^{r}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})$
describes the connections in
$\widetilde {\Delta }^{r}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})$
describes the connections in
![]() $\widetilde {\varphi }^r$
and thus the connections between
$\widetilde {\varphi }^r$
and thus the connections between
![]() $\gamma ^{\ell }_{k}$
and
$\gamma ^{\ell }_{k}$
and
![]() $ \gamma ^{i}_{k-1}$
in
$ \gamma ^{i}_{k-1}$
in
![]() ${\varphi }^r$
proving (a). This proves that
${\varphi }^r$
proving (a). This proves that
![]() $\widetilde {\Delta }^{r}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})$
satisfies either (a) or (b).
$\widetilde {\Delta }^{r}(\gamma ^{\ell }_k,\gamma ^{i}_{k-1})$
satisfies either (a) or (b).
Suppose
![]() ${\Delta }^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
induces a non-zero differential and it is either
${\Delta }^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
induces a non-zero differential and it is either
![]() $\pm {I}^{pp}$
,
$\pm {I}^{pp}$
,
![]() $\pm \widetilde {I}^{pp}$
or
$\pm \widetilde {I}^{pp}$
or
![]() $\pm E_{22}^p$
, if
$\pm E_{22}^p$
, if
![]() $k=1$
, or
$k=1$
, or
![]() $\pm {I}^{pp}$
,
$\pm {I}^{pp}$
,
![]() $\pm \widetilde {I}^{pp}$
or
$\pm \widetilde {I}^{pp}$
or
![]() $\pm E_{11}^p$
, if
$\pm E_{11}^p$
, if
![]() $k=2$
. By Theorem 4.13, these entries are never generated by primary pivots
$k=2$
. By Theorem 4.13, these entries are never generated by primary pivots
![]() $\pm E_{11}^p$
, if
$\pm E_{11}^p$
, if
![]() $k=1$
, and
$k=1$
, and
![]() $\pm E_{22}^p$
, if
$\pm E_{22}^p$
, if
![]() $k=2$
. Therefore, it always corresponds to connections between
$k=2$
. Therefore, it always corresponds to connections between
![]() $\gamma ^{\ell }_{k}$
and
$\gamma ^{\ell }_{k}$
and
![]() $ \gamma ^{i}_{k-1}$
. The characterization of the connections in
$ \gamma ^{i}_{k-1}$
. The characterization of the connections in
![]() $\varphi ^r$
corresponding to
$\varphi ^r$
corresponding to
![]() ${\Delta }^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
follows from Propositions 3.6, 4.16 and 3.13.
${\Delta }^{r}(\gamma ^p_k,\gamma ^{p-r}_{k-1})$
follows from Propositions 3.6, 4.16 and 3.13.
The algebraic-dynamical correspondence follows by Theorems 3.11 and 3.12.
As a consequence of the definition of core flow, it follows that, given an NMS flow
![]() $\varphi $
in
$\varphi $
in
![]() $\Sigma (M^3)$
such that
$\Sigma (M^3)$
such that
![]() $FM(\varphi )\neq \emptyset $
, there is no pair of consecutive periodic orbits
$FM(\varphi )\neq \emptyset $
, there is no pair of consecutive periodic orbits
![]() $(\gamma _k, \gamma _{k-1})$
that can be cancelled or reduced.
$(\gamma _k, \gamma _{k-1})$
that can be cancelled or reduced.
In the next theorem, we show that following the unfolding of the spectral sequence and performing the cancellations and reductions determined therein, one arrives at a core flow. This is not always the case for filtrations that are not NMS-compatible or do not satisfy the reduction ordering condition.
Theorem 5.2. (Convergence to a core flow)
Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, such that
$3$
-manifold, such that
![]() $FM(\varphi )\neq \emptyset $
. Assume that there is an NMS-compatible filtration
$FM(\varphi )\neq \emptyset $
. Assume that there is an NMS-compatible filtration
![]() $\mathcal {F}$
for
$\mathcal {F}$
for
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
,
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
,
![]() $\widetilde {\varphi }\in FM(\varphi )$
satisfying the reduction ordering condition and let
$\widetilde {\varphi }\in FM(\varphi )$
satisfying the reduction ordering condition and let
![]() $(\mathcal {E}^r,d^r)$
be the spectral sequence associated to this filtered chain complex. Let
$(\mathcal {E}^r,d^r)$
be the spectral sequence associated to this filtered chain complex. Let
![]() $\varphi ^{\omega }$
be the last flow obtained when cancelling and reducing periodic orbits according to the non-zero differentials of
$\varphi ^{\omega }$
be the last flow obtained when cancelling and reducing periodic orbits according to the non-zero differentials of
![]() $(\mathcal {E}^r,d^r)$
. Then
$(\mathcal {E}^r,d^r)$
. Then
![]() $\varphi ^{\omega }$
is a core NMS flow and:
$\varphi ^{\omega }$
is a core NMS flow and:
-
(1) the number N of periodic orbits of
 $\varphi ^{\omega }$
is
$\varphi ^{\omega }$
is $\tfrac 12\sum _{i=0}^{3} \beta _{i} + \# \{\Delta ^{r}(\gamma _1,\gamma _0) = \pm \, E_{11}^p \mid r\geq 0\} + \# \{\Delta ^{r}(\gamma _2,\gamma _1) = \pm \, E_{22}^p \mid r\geq 0\} + \# \{\Delta ^{r} (\gamma _2,\gamma _0) = \pm \, E_{21}^p \mid r\geq 0\}; $
$\tfrac 12\sum _{i=0}^{3} \beta _{i} + \# \{\Delta ^{r}(\gamma _1,\gamma _0) = \pm \, E_{11}^p \mid r\geq 0\} + \# \{\Delta ^{r}(\gamma _2,\gamma _1) = \pm \, E_{22}^p \mid r\geq 0\} + \# \{\Delta ^{r} (\gamma _2,\gamma _0) = \pm \, E_{21}^p \mid r\geq 0\}; $
-
(2) the number of repelling periodic orbits of
 $\varphi ^{\omega }$
is
$\varphi ^{\omega }$
is
 $N_R = \beta _3 + \#\{\Delta ^{r}(\gamma _2,\gamma _1)=\pm E_{22}^p \mid r\geq 0\} $
;
$N_R = \beta _3 + \#\{\Delta ^{r}(\gamma _2,\gamma _1)=\pm E_{22}^p \mid r\geq 0\} $
; -
(3) the number of attracting periodic orbits of
 $\varphi ^{\omega }$
is
$\varphi ^{\omega }$
is
 $N_A = \beta _0 + \#\{\Delta ^{r}(\gamma _1,\gamma _0)=\pm E_{11}^p \mid r\geq 0\} $
; and
$N_A = \beta _0 + \#\{\Delta ^{r}(\gamma _1,\gamma _0)=\pm E_{11}^p \mid r\geq 0\} $
; and -
(4) the number of saddle periodic orbits of
 $\varphi ^{\omega }$
is
$\varphi ^{\omega }$
is
 $N_S = N - N_A - N_R $
.
$N_S = N - N_A - N_R $
.
Proof. Let
![]() $\widetilde {\varphi }$
be a morsification of
$\widetilde {\varphi }$
be a morsification of
![]() $\varphi $
in
$\varphi $
in
![]() $FM(\varphi )$
. By cancelling the critical points of
$FM(\varphi )$
. By cancelling the critical points of
![]() $\widetilde {\varphi }$
according to the non-zero differentials of the spectral sequences, one obtains a Morse flow
$\widetilde {\varphi }$
according to the non-zero differentials of the spectral sequences, one obtains a Morse flow
![]() $\phi ^{\omega }$
that has a zero Morse boundary operator, as shown in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3]. Since the spectral sequence converges to the homology of the chain complex
$\phi ^{\omega }$
that has a zero Morse boundary operator, as shown in [Reference Bertolim, Lima, Mello, de Rezende and da Silveira3]. Since the spectral sequence converges to the homology of the chain complex
![]() $(C^{\mathrm {NMS}}(\widetilde \varphi ),\Delta ^{\mathrm {NMS}})$
, which coincides with the homology of M, then
$(C^{\mathrm {NMS}}(\widetilde \varphi ),\Delta ^{\mathrm {NMS}})$
, which coincides with the homology of M, then
![]() ${\phi ^{\omega }}$
has a unique index k critical point corresponding to each generator of the kth singular homology of M.
${\phi ^{\omega }}$
has a unique index k critical point corresponding to each generator of the kth singular homology of M.
On the other hand, consider
![]() $\widetilde {\varphi ^{\omega }}$
, the morsification of
$\widetilde {\varphi ^{\omega }}$
, the morsification of
![]() ${\varphi ^{\omega }}$
. Note that there is no change in dynamics corresponding to the differentials
${\varphi ^{\omega }}$
. Note that there is no change in dynamics corresponding to the differentials
![]() $\Delta ^{\omega }(\gamma _2,\gamma _0) = \pm E_{21}^p$
and
$\Delta ^{\omega }(\gamma _2,\gamma _0) = \pm E_{21}^p$
and
![]() $\Delta ^{\omega }(\gamma _k,\gamma _{k-1})$
equal to
$\Delta ^{\omega }(\gamma _k,\gamma _{k-1})$
equal to
![]() $ \pm E_{11}^p$
for
$ \pm E_{11}^p$
for
![]() $k=1$
and equal to
$k=1$
and equal to
![]() $ \pm E_{22}^p$
for
$ \pm E_{22}^p$
for
![]() $k=2$
. Then the only non-zero columns of the Morse differential associated to the flow
$k=2$
. Then the only non-zero columns of the Morse differential associated to the flow
![]() $\widetilde {\varphi ^{\omega }}$
are the columns corresponding to
$\widetilde {\varphi ^{\omega }}$
are the columns corresponding to
![]() $\pm E_{21}^{p}$
,
$\pm E_{21}^{p}$
,
![]() $\pm E_{11}^p$
when
$\pm E_{11}^p$
when
![]() $k=1$
and
$k=1$
and
![]() $\pm E_{22}^p$
when
$\pm E_{22}^p$
when
![]() $k=2$
. Also, the NMS-compatible filtration
$k=2$
. Also, the NMS-compatible filtration
![]() $\mathcal {F}$
guarantees that there are no
$\mathcal {F}$
guarantees that there are no
![]() $\pm I$
,
$\pm I$
,
![]() $\pm \widetilde {I}$
and
$\pm \widetilde {I}$
and
![]() $\pm E_{22}$
when
$\pm E_{22}$
when
![]() $k=1$
(respectively,
$k=1$
(respectively,
![]() $\pm I$
,
$\pm I$
,
![]() $\pm \widetilde {I}$
and
$\pm \widetilde {I}$
and
![]() $\pm E_{11}$
when
$\pm E_{11}$
when
![]() $k=2$
) above primary pivots. Therefore, the NMS flow
$k=2$
) above primary pivots. Therefore, the NMS flow
![]() $\varphi ^{\omega }$
is a core flow.
$\varphi ^{\omega }$
is a core flow.
Moreover, the number of critical points of
![]() $\widetilde {\varphi ^{\omega }}$
is given by
$\widetilde {\varphi ^{\omega }}$
is given by
 $$ \begin{align*} \sum_{i=0}^{3} \beta_{i} \ + 2( \# \{\Delta^{r}(\gamma_1,\gamma_0)&=\pm E_{11}^p \mid r\geq 0\}+ \# \{\Delta^{r}(\gamma_2,\gamma_1)\\&=\pm E_{22}^p \mid r\geq 0\} +\# \{\Delta^{r}(\gamma_2,\gamma_0)=\pm E_{21}^p \mid r\geq 0\} ),\end{align*} $$
$$ \begin{align*} \sum_{i=0}^{3} \beta_{i} \ + 2( \# \{\Delta^{r}(\gamma_1,\gamma_0)&=\pm E_{11}^p \mid r\geq 0\}+ \# \{\Delta^{r}(\gamma_2,\gamma_1)\\&=\pm E_{22}^p \mid r\geq 0\} +\# \{\Delta^{r}(\gamma_2,\gamma_0)=\pm E_{21}^p \mid r\geq 0\} ),\end{align*} $$
Then the formulas for the number of periodic orbits of
![]() $\varphi ^{\omega }$
follow.
$\varphi ^{\omega }$
follow.
The next example illustrates Theorems 5.1 and 5.2.
Example 5.3. Returning to Example 3.9, consider the NMS flow
![]() $\varphi $
on
$\varphi $
on
![]() $S^1\times S^2$
, as in Figure 7. The differential
$S^1\times S^2$
, as in Figure 7. The differential
![]() $\Delta ^{\mathrm {NMS}}$
of the chain complex
$\Delta ^{\mathrm {NMS}}$
of the chain complex
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
endowed with the NMS-compatible filtration
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
endowed with the NMS-compatible filtration
![]() $\mathcal {F}_pC\setminus \mathcal {F}_{p-1}C= \{ h_{k}(\gamma _k^{p+1}) , h_{k+1}(\gamma _k^{p+1}) \}$
is shown in Figure 8. Note that this filtration satisfies the reduction ordering condition. In Figure 16, we represent the collection of matrices obtained by applying the SSSA to
$\mathcal {F}_pC\setminus \mathcal {F}_{p-1}C= \{ h_{k}(\gamma _k^{p+1}) , h_{k+1}(\gamma _k^{p+1}) \}$
is shown in Figure 8. Note that this filtration satisfies the reduction ordering condition. In Figure 16, we represent the collection of matrices obtained by applying the SSSA to
![]() $\Delta ^{\mathrm {NMS}}$
. By Theorem 5.1,
$\Delta ^{\mathrm {NMS}}$
. By Theorem 5.1,
-
•
 $\Delta ^{2}(\gamma _1^3,\gamma _0^2)=-\widetilde {I}^{pp}$
determines the cancellation of the pair
$\Delta ^{2}(\gamma _1^3,\gamma _0^2)=-\widetilde {I}^{pp}$
determines the cancellation of the pair
 $(\gamma _1^3,\gamma _0^2)$
;
$(\gamma _1^3,\gamma _0^2)$
; -
•
 $\Delta ^{4}(\gamma _2^6,\gamma _1^4)=E_{11}^{p}$
determines the reduction of the pair
$\Delta ^{4}(\gamma _2^6,\gamma _1^4)=E_{11}^{p}$
determines the reduction of the pair
 $(\gamma _2^6,\gamma _1^4)$
; and
$(\gamma _2^6,\gamma _1^4)$
; and -
•
 $\Delta ^{8}(\gamma _1^5,\gamma _0^1)=E_{22}^{p}$
determines the reduction of the pair
$\Delta ^{8}(\gamma _1^5,\gamma _0^1)=E_{22}^{p}$
determines the reduction of the pair
 $(\gamma _1^5,\gamma _0^1)$
.
$(\gamma _1^5,\gamma _0^1)$
.
The corresponding family of NMS flows obtained by cancelling and reducing periodic orbits following the unfolding of the spectral sequence is presented in Figure 21. The last flow
![]() $\varphi ^{\omega }$
is a core flow on
$\varphi ^{\omega }$
is a core flow on
![]() $S^1\times S^2$
.
$S^1\times S^2$
.

Figure 21 Family of NMS flows converging to a core flow.
Remark 5.4. When considering the dynamics of an NMS flow, it is clear that the choice of filtrations, an hence the order in which cancellations and reductions are performed, may produce different core flows. This can easily be seen in Example 5.3 by cancelling the pair
![]() $(\gamma ^5_1,\gamma ^1_0)$
and reducing the pair
$(\gamma ^5_1,\gamma ^1_0)$
and reducing the pair
![]() $(\gamma ^4_1,\gamma ^2_0)$
. One obtains a flow as in Figure 22, which is a core flow in
$(\gamma ^4_1,\gamma ^2_0)$
. One obtains a flow as in Figure 22, which is a core flow in
![]() $\mathcal {S}_{\varphi }$
and is different from the core flow obtained in the previous example.
$\mathcal {S}_{\varphi }$
and is different from the core flow obtained in the previous example.

Figure 22 A core flow on
![]() $S^1\times S^2.$
$S^1\times S^2.$
One can ask how much of the algebraic-dynamical information can be salvaged by considering more general filtrations. This will be answered in the next section.
5.2 Reductions determined by a spectral sequence under general filtrations
In this section, we develop a different strategy so as to consider more general filtrations that continue to allow us to obtain a core flow from a given NMS flow. The underlying assumption will be that the initial NMS flow has no pair of cancelling periodic orbits. In other words, we consider the special case of NMS flows such that each inessential connection is part of a double connection between two periodic orbits. More specifically, if a connected component of
![]() $W^{u}(\gamma _1) \cap W^{s}(\gamma _{0})$
(respectively,
$W^{u}(\gamma _1) \cap W^{s}(\gamma _{0})$
(respectively,
![]() $W^{u}(\gamma _2) \cap W^{s}(\gamma _{1})$
) is an inessential cylinder of connections, then
$W^{u}(\gamma _2) \cap W^{s}(\gamma _{1})$
) is an inessential cylinder of connections, then
![]() $W^{u}(\gamma _1) \cap W^{s}(\gamma _{0})$
(respectively,
$W^{u}(\gamma _1) \cap W^{s}(\gamma _{0})$
(respectively,
![]() $W^{u}(\gamma _2) \cap W^{s}(\gamma _{1})$
) is composed by two disjoint cylinders of connections. Consequently, the submatrices of the NMS differential corresponding to connections between saddles and attractors/repellers are not equal to either
$W^{u}(\gamma _2) \cap W^{s}(\gamma _{1})$
) is composed by two disjoint cylinders of connections. Consequently, the submatrices of the NMS differential corresponding to connections between saddles and attractors/repellers are not equal to either
![]() $\pm I$
or
$\pm I$
or
![]() $\pm \tilde {I}$
. The next result is the first step in this direction, since it proves that any filtration on an NMS complex in this setting is an NMS-compatible filtration.
$\pm \tilde {I}$
. The next result is the first step in this direction, since it proves that any filtration on an NMS complex in this setting is an NMS-compatible filtration.
Lemma 5.5. Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, such that
$3$
-manifold, such that
![]() $TUM(\varphi )\neq \emptyset $
and
$TUM(\varphi )\neq \emptyset $
and
![]() $\Delta $
the differential of an NMS complex associated to
$\Delta $
the differential of an NMS complex associated to
![]() $\varphi $
. If
$\varphi $
. If
![]() $\Delta (\gamma _k,\gamma _{k-1})$
,
$\Delta (\gamma _k,\gamma _{k-1})$
,
![]() $k=1,2$
, is neither
$k=1,2$
, is neither
![]() $ \pm I$
nor
$ \pm I$
nor
![]() $\pm \tilde {I}$
, for all periodic orbits
$\pm \tilde {I}$
, for all periodic orbits
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
, then any filtration is a NMS-compatible filtration.
$\gamma _{k-1}$
, then any filtration is a NMS-compatible filtration.
Proof. Given a filtration
![]() $\mathcal {F}$
for the NMS-chain complex associated to
$\mathcal {F}$
for the NMS-chain complex associated to
![]() $\varphi $
, let
$\varphi $
, let
![]() $\{\Delta ^r\}_{r\geq 0}$
be the matrices produced by the SSSA applied to
$\{\Delta ^r\}_{r\geq 0}$
be the matrices produced by the SSSA applied to
![]() $\Delta $
with respect to
$\Delta $
with respect to
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Firstly, we prove that, for each
![]() $r\geq 0$
,
$r\geq 0$
,
![]() $\Delta ^r(\gamma _k^{p},\gamma ^i_{k-1})$
is neither
$\Delta ^r(\gamma _k^{p},\gamma ^i_{k-1})$
is neither
![]() $ \pm I$
nor
$ \pm I$
nor
![]() $\pm \tilde {I}$
, for all periodic orbits
$\pm \tilde {I}$
, for all periodic orbits
![]() $\gamma _k^{p}$
,
$\gamma _k^{p}$
,
![]() $\gamma ^i_{k-1}$
, for
$\gamma ^i_{k-1}$
, for
![]() $k=1,2$
. The proof follows by induction on r. Suppose that
$k=1,2$
. The proof follows by induction on r. Suppose that
![]() $\Delta ^r$
does not have blocks
$\Delta ^r$
does not have blocks
![]() $ \pm I$
or
$ \pm I$
or
![]() $\pm \tilde {I}$
for
$\pm \tilde {I}$
for
![]() $r\leq r_0$
. Consider
$r\leq r_0$
. Consider
![]() $k=1$
(respectively,
$k=1$
(respectively,
![]() $k=2$
). If
$k=2$
). If
![]() $\Delta ^{r_0+1}(\gamma _k^{p},\gamma _{k-1}^i)\neq \Delta ^{r_0}(\gamma _k^{p},\gamma ^i_{k-1})$
, then there exist periodic orbits
$\Delta ^{r_0+1}(\gamma _k^{p},\gamma _{k-1}^i)\neq \Delta ^{r_0}(\gamma _k^{p},\gamma ^i_{k-1})$
, then there exist periodic orbits
![]() $\gamma _{k-1}^{p-r_{0}}$
and
$\gamma _{k-1}^{p-r_{0}}$
and
![]() $\gamma _{k}^{t}$
, for
$\gamma _{k}^{t}$
, for
![]() $i< t\leq p$
, such that
$i< t\leq p$
, such that
![]() $\Delta ^{r_0}(\gamma _k^{p},\gamma _{k-1}^{p-r_{0}})$
is equal to
$\Delta ^{r_0}(\gamma _k^{p},\gamma _{k-1}^{p-r_{0}})$
is equal to
![]() $\pm E_{11}^c$
(respectively,
$\pm E_{11}^c$
(respectively,
![]() $\pm E_{22}^c$
),
$\pm E_{22}^c$
),
![]() $\Delta ^{r_0}(\gamma _k^{t},\gamma _{k-1}^{p-r_{0}})$
is equal to
$\Delta ^{r_0}(\gamma _k^{t},\gamma _{k-1}^{p-r_{0}})$
is equal to
![]() $\pm E_{11} ^p$
(respectively,
$\pm E_{11} ^p$
(respectively,
![]() $\pm E_{22}^c$
) and
$\pm E_{22}^c$
) and
![]() $\Delta ^{r_0}(\gamma _k^{t},\gamma _{k-1}^{i})$
is equal to
$\Delta ^{r_0}(\gamma _k^{t},\gamma _{k-1}^{i})$
is equal to
![]() $\pm E_{11}$
(respectively,
$\pm E_{11}$
(respectively,
![]() $\pm E_{22}^c$
). By Theorem 3.7 (respectively, Theorem 3.8),
$\pm E_{22}^c$
). By Theorem 3.7 (respectively, Theorem 3.8),
![]() $\Delta ^{r_0}(\gamma _k^{p},\gamma _{k-1}^{i})$
is equal to
$\Delta ^{r_0}(\gamma _k^{p},\gamma _{k-1}^{i})$
is equal to
![]() $\pm E_{11}$
(respectively,
$\pm E_{11}$
(respectively,
![]() $\pm E_{22}^c$
) or it is a zero matrix, so
$\pm E_{22}^c$
) or it is a zero matrix, so
![]() $\Delta ^{r_0+1}(\gamma _k^{p},\gamma _{k-1}^{i})$
is equal to
$\Delta ^{r_0+1}(\gamma _k^{p},\gamma _{k-1}^{i})$
is equal to
![]() $\pm E_{11}$
(respectively,
$\pm E_{11}$
(respectively,
![]() $\pm E_{22}^c$
) or it is a zero matrix.
$\pm E_{22}^c$
) or it is a zero matrix.
Next, we prove that
![]() $\mathcal {F}$
is an NMS-compatible filtration.
$\mathcal {F}$
is an NMS-compatible filtration.
If
![]() $\Delta ^{r_0}(\gamma _1^{p},\gamma _{0}^{p-r_0})_{22} $
is a primary pivot, then
$\Delta ^{r_0}(\gamma _1^{p},\gamma _{0}^{p-r_0})_{22} $
is a primary pivot, then
![]() $\Delta ^{r_0}(\gamma _1^{p},\gamma _{0}^{p-r_0}) = \pm E_{22}$
, that is,
$\Delta ^{r_0}(\gamma _1^{p},\gamma _{0}^{p-r_0}) = \pm E_{22}$
, that is,
![]() $\Delta ^{r_0}(\gamma _1^{p},\gamma _{0}^{p-r_0})_{11}=0$
. Moreover, for every
$\Delta ^{r_0}(\gamma _1^{p},\gamma _{0}^{p-r_0})_{11}=0$
. Moreover, for every
![]() $\ell \geq p-r_0$
and
$\ell \geq p-r_0$
and
![]() $r \leq r_0$
,
$r \leq r_0$
,
![]() $\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{\ell }) $
is a null matrix, by Theorem 3.7, which is never a change of basis pivot. Hence, condition SF1 in Definition 4.8 is satisfied.
$\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{\ell }) $
is a null matrix, by Theorem 3.7, which is never a change of basis pivot. Hence, condition SF1 in Definition 4.8 is satisfied.
If
![]() $\Delta ^{r_0}(\gamma _2^{p},\gamma _{1}^{p-r_0})_{11} $
is a primary pivot, then
$\Delta ^{r_0}(\gamma _2^{p},\gamma _{1}^{p-r_0})_{11} $
is a primary pivot, then
![]() $\Delta ^{r_0}(\gamma _2^{p},\gamma _{1}^{p-r_0}) = \pm E_{11}$
, that is,
$\Delta ^{r_0}(\gamma _2^{p},\gamma _{1}^{p-r_0}) = \pm E_{11}$
, that is,
![]() $\Delta ^{r_0}(\gamma _2^{p},\gamma _{1}^{p-r_0})_{22}=0$
. Moreover, for every
$\Delta ^{r_0}(\gamma _2^{p},\gamma _{1}^{p-r_0})_{22}=0$
. Moreover, for every
![]() $\ell \leq p$
and
$\ell \leq p$
and
![]() $r\leq r_0$
, by Theorem 3.8,
$r\leq r_0$
, by Theorem 3.8,
![]() $\Delta ^{r}(\gamma _2^{\ell },\gamma _{1}^{p-r})$
is the null matrix. Hence,
$\Delta ^{r}(\gamma _2^{\ell },\gamma _{1}^{p-r})$
is the null matrix. Hence,
![]() $\Delta ^{r_0}(\gamma _2^{p},\gamma _{1}^{p-r_0})_{22}=0$
, for all
$\Delta ^{r_0}(\gamma _2^{p},\gamma _{1}^{p-r_0})_{22}=0$
, for all
![]() $r_0\leq r$
.
$r_0\leq r$
.
Remark 5.6. Note that submatrices
![]() $\Delta ^{r}(\gamma _1,\gamma _{0})=\pm E_{22}$
(respectively,
$\Delta ^{r}(\gamma _1,\gamma _{0})=\pm E_{22}$
(respectively,
![]() $\Delta ^{r}(\gamma _2,\gamma _{1})=\pm E_{11}$
) never appear owing to a change of basis determined by the SSSA. This follows from the fact that there are no blocks
$\Delta ^{r}(\gamma _2,\gamma _{1})=\pm E_{11}$
) never appear owing to a change of basis determined by the SSSA. This follows from the fact that there are no blocks
![]() $\Delta ^r(\gamma _k,\gamma _{k-1})$
,
$\Delta ^r(\gamma _k,\gamma _{k-1})$
,
![]() $k=1,2$
, equal to
$k=1,2$
, equal to
![]() $\pm I$
or
$\pm I$
or
![]() $\pm \tilde {I}$
and from Proposition 4.16. Hence, whenever
$\pm \tilde {I}$
and from Proposition 4.16. Hence, whenever
![]() $\Delta ^{r}(\gamma _1,\gamma _{0})=\pm E_{22}$
(respectively,
$\Delta ^{r}(\gamma _1,\gamma _{0})=\pm E_{22}$
(respectively,
![]() $\Delta ^{r}(\gamma _2,\gamma _{1})=\pm E_{11}$
), then
$\Delta ^{r}(\gamma _2,\gamma _{1})=\pm E_{11}$
), then
![]() $\Delta (\gamma _1,\gamma _{0})=\pm E_{22}$
(respectively,
$\Delta (\gamma _1,\gamma _{0})=\pm E_{22}$
(respectively,
![]() $\Delta (\gamma _2,\gamma _{1})=\pm E_{11}$
).
$\Delta (\gamma _2,\gamma _{1})=\pm E_{11}$
).
Of course, one may ask what happens if the filtration, in addition to being NMS-compatible, also satisfies the reduction ordering condition. Recall that different choices of filtrations may produce distinct numbers of periodic orbits in a core flow. However, this will not be the case here. The next result will guarantee that the number of periodic orbits in the core flow is unique.
Theorem 5.7. (Core flow with the lowest number of orbits in
 $\mathcal {S}_{\varphi }$
)
$\mathcal {S}_{\varphi }$
)
Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, such that
$3$
-manifold, such that
![]() $FM(\varphi )\neq \emptyset $
and
$FM(\varphi )\neq \emptyset $
and
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
is an NMS-chain complex, where
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
is an NMS-chain complex, where
![]() $\widetilde {\varphi }\in FM(\varphi )$
. Suppose that
$\widetilde {\varphi }\in FM(\varphi )$
. Suppose that
![]() $\Delta (\gamma _k,\gamma _{k-1})$
,
$\Delta (\gamma _k,\gamma _{k-1})$
,
![]() $k=1,2$
, is neither
$k=1,2$
, is neither
![]() $ \pm I$
nor
$ \pm I$
nor
![]() $\pm \tilde {I}$
, for all periodic orbits
$\pm \tilde {I}$
, for all periodic orbits
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
. Let
$\gamma _{k-1}$
. Let
![]() $\varphi ^{\omega }$
be the last flow obtained after all reductions are performed following the SSSA. If the filtration
$\varphi ^{\omega }$
be the last flow obtained after all reductions are performed following the SSSA. If the filtration
![]() $\mathcal {F}$
satisfies the reduction ordering condition, then
$\mathcal {F}$
satisfies the reduction ordering condition, then
![]() $\varphi ^{\omega }$
is a core flow and minimizes the total number of periodic orbits in
$\varphi ^{\omega }$
is a core flow and minimizes the total number of periodic orbits in
![]() $\mathcal {S}_{\varphi }$
. Moreover, the number of attracting, repelling and saddle periodic orbits of
$\mathcal {S}_{\varphi }$
. Moreover, the number of attracting, repelling and saddle periodic orbits of
![]() $\varphi ^{\omega }$
does not depend on the filtration.
$\varphi ^{\omega }$
does not depend on the filtration.
Proof. Let
![]() $\varphi ^{\omega }$
be the last flow obtained when reducing periodic orbits according to Theorem 5.1. Since the spectral sequence converges to the homology of M, for each fixed k, the number of primary pivots marked by the SSSA in columns associated to
$\varphi ^{\omega }$
be the last flow obtained when reducing periodic orbits according to Theorem 5.1. Since the spectral sequence converges to the homology of M, for each fixed k, the number of primary pivots marked by the SSSA in columns associated to
![]() $h_k$
chains does not depend on the filtration
$h_k$
chains does not depend on the filtration
![]() $\mathcal {F}$
. Consequently, the number of
$\mathcal {F}$
. Consequently, the number of
![]() $\Delta ^{r}(\gamma _1^{p+r},\gamma _{0}^{p})=\pm E_{11}^p$
(respectively,
$\Delta ^{r}(\gamma _1^{p+r},\gamma _{0}^{p})=\pm E_{11}^p$
(respectively,
![]() $\Delta ^{r}(\gamma _2^{p+r},\gamma _{1}^{p})=\pm E_{22}^p$
) is the same for any filtration. Moreover, by Remark 5.6, the number of
$\Delta ^{r}(\gamma _2^{p+r},\gamma _{1}^{p})=\pm E_{22}^p$
) is the same for any filtration. Moreover, by Remark 5.6, the number of
![]() $\Delta ^{r}(\gamma _1^{p+r},\gamma _{0}^{p})=\pm E_{22}^p$
(respectively,
$\Delta ^{r}(\gamma _1^{p+r},\gamma _{0}^{p})=\pm E_{22}^p$
(respectively,
![]() $\Delta ^{r}(\gamma _2^{p+r},\gamma _{1}^{p})=\pm E_{11}^p$
) corresponds to the number of rows (respectively, columns) that have at least one block
$\Delta ^{r}(\gamma _2^{p+r},\gamma _{1}^{p})=\pm E_{11}^p$
) corresponds to the number of rows (respectively, columns) that have at least one block
![]() $E_{22}$
(respectively,
$E_{22}$
(respectively,
![]() $E_{11}$
) in
$E_{11}$
) in
![]() $\Delta ^{\mathrm {NMS}}$
. Hence, the number of
$\Delta ^{\mathrm {NMS}}$
. Hence, the number of
![]() $\Delta ^{r}(\gamma _1^{p+r},\gamma _{0}^{p})=\pm E_{22}^p$
(respectively,
$\Delta ^{r}(\gamma _1^{p+r},\gamma _{0}^{p})=\pm E_{22}^p$
(respectively,
![]() $\Delta ^{r}(\gamma _2^{p+r},\gamma _{1}^{p})=\pm E_{11}^p$
) is the same for any filtration. Consequently, the number of
$\Delta ^{r}(\gamma _2^{p+r},\gamma _{1}^{p})=\pm E_{11}^p$
) is the same for any filtration. Consequently, the number of
![]() $\Delta ^{r}(\gamma _2^{p+r},\gamma _{0}^{p})=\pm E_{21}^p$
does not depend on the filtration.
$\Delta ^{r}(\gamma _2^{p+r},\gamma _{0}^{p})=\pm E_{21}^p$
does not depend on the filtration.
Since
![]() $\mathcal {F}$
satisfies the reduction ordering condition, by Lemma 5.5, it is an NMS-compatible filtration. It follows, from Theorem 5.2, that the number of attractor, repeller and saddle periodic orbits in
$\mathcal {F}$
satisfies the reduction ordering condition, by Lemma 5.5, it is an NMS-compatible filtration. It follows, from Theorem 5.2, that the number of attractor, repeller and saddle periodic orbits in
![]() $\varphi ^{\omega }$
is the same for any filtration.
$\varphi ^{\omega }$
is the same for any filtration.
The maximal number of reductions between saddles and an attracting (respectively, repelling) periodic orbit is the number of rows (respectively, columns) that have at least one block
![]() $E_{22}$
(respectively,
$E_{22}$
(respectively,
![]() $E_{11}$
) in
$E_{11}$
) in
![]() $\Delta ^{\mathrm {NMS}}$
. Therefore,
$\Delta ^{\mathrm {NMS}}$
. Therefore,
![]() $\varphi ^{\omega }$
minimizes the number of periodic orbits in
$\varphi ^{\omega }$
minimizes the number of periodic orbits in
![]() $\mathcal {S}_{\varphi }$
.
$\mathcal {S}_{\varphi }$
.
In order to establish a dynamical correspondence for the unfolding of the spectral sequence for more general filtrations under the hypothesis of Lemma 5.5, it is necessary to understand dynamically what occurs in the case when the filtration does not satisfy the reduction ordering condition. Indeed, if
![]() $\mathcal {F}$
does not satisfy the reduction ordering condition in
$\mathcal {F}$
does not satisfy the reduction ordering condition in
![]() $\gamma _1^p$
, then
$\gamma _1^p$
, then
![]() $\gamma _1^p$
double connects through an inessential connection and an
$\gamma _1^p$
double connects through an inessential connection and an
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free essential connection with an attracting and a repelling periodic orbit,
$h_1$
free essential connection with an attracting and a repelling periodic orbit,
![]() $\gamma _{0}^{p-{r_1}}$
and
$\gamma _{0}^{p-{r_1}}$
and
![]() $\gamma _2^{p+r_2}$
, respectively. There are two possible reductions that could be performed with
$\gamma _2^{p+r_2}$
, respectively. There are two possible reductions that could be performed with
![]() $\gamma _1^{p}$
, that is,
$\gamma _1^{p}$
, that is,
![]() $\Delta ^{r_1}(\gamma _1^{p},\gamma _{0}^{p-r_1})=\pm E_{22}^p$
and
$\Delta ^{r_1}(\gamma _1^{p},\gamma _{0}^{p-r_1})=\pm E_{22}^p$
and
![]() $\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})=\pm E_{11}^p$
. After one of these reductions is performed, the other one no longer corresponds to a reduction of the corresponding periodic orbits. Rather, it corresponds to a connection between an attractor and a repeller. An apparently reasonable dynamical understanding for this algebraic setting would be to perform one of the reductions and ignore the other one. However, this approach might not lead to a core flow.
$\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})=\pm E_{11}^p$
. After one of these reductions is performed, the other one no longer corresponds to a reduction of the corresponding periodic orbits. Rather, it corresponds to a connection between an attractor and a repeller. An apparently reasonable dynamical understanding for this algebraic setting would be to perform one of the reductions and ignore the other one. However, this approach might not lead to a core flow.
Thus far, we have shown that by considering a differential matrix that has no isomorphisms, that is, each inessential connection is part of a double connection between two periodic orbits, then every filtration for the associated chain complex is NMS-compatible. In order to circumvent the reduction ordering condition, the next theorem guarantees that, by making appropriate choices at each stage of the SSSA, one arrives at a core flow.
Theorem 5.8. Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, such that
$3$
-manifold, such that
![]() $FM(\varphi )\neq \emptyset $
and
$FM(\varphi )\neq \emptyset $
and
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
is an NMS-chain complex, where
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
is an NMS-chain complex, where
![]() $\widetilde {\varphi }\in FM(\varphi )$
. Assume that
$\widetilde {\varphi }\in FM(\varphi )$
. Assume that
![]() $\Delta (\gamma _k,\gamma _{k-1})$
is neither
$\Delta (\gamma _k,\gamma _{k-1})$
is neither
![]() $ \pm I$
nor
$ \pm I$
nor
![]() $\pm \tilde {I}$
, for all periodic orbits
$\pm \tilde {I}$
, for all periodic orbits
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
. Then, given any filtration
$\gamma _{k-1}$
. Then, given any filtration
![]() $\mathcal {F}$
for
$\mathcal {F}$
for
![]() $(C^{\mathrm {NMS}}(\widetilde \varphi ),\Delta ^{\mathrm {NMS}})$
, there exists an algorithm based on the spectral sequence that determines a family of NMS flows
$(C^{\mathrm {NMS}}(\widetilde \varphi ),\Delta ^{\mathrm {NMS}})$
, there exists an algorithm based on the spectral sequence that determines a family of NMS flows
![]() $\{\varphi ^1,\ldots ,\varphi ^{\omega }\}\subset \mathcal {S}_{\varphi }$
on
$\{\varphi ^1,\ldots ,\varphi ^{\omega }\}\subset \mathcal {S}_{\varphi }$
on
![]() $M^3$
, where
$M^3$
, where
![]() $\varphi ^1=\varphi $
,
$\varphi ^1=\varphi $
,
![]() $\varphi ^r$
is obtained from
$\varphi ^r$
is obtained from
![]() $\varphi ^{r-1}$
by reductions of periodic orbits determined by the differentials
$\varphi ^{r-1}$
by reductions of periodic orbits determined by the differentials
![]() $d^r$
of the spectral sequence. The last flow
$d^r$
of the spectral sequence. The last flow
![]() $\varphi ^{\omega }$
is a core NMS flow.
$\varphi ^{\omega }$
is a core NMS flow.
Proof. By Lemma 5.5,
![]() $\mathcal {F}$
is an NMS-compatible filtration. In the case when
$\mathcal {F}$
is an NMS-compatible filtration. In the case when
![]() $\mathcal {F}$
satisfies the reduction ordering condition, the result follows by Theorem 5.1. Suppose that
$\mathcal {F}$
satisfies the reduction ordering condition, the result follows by Theorem 5.1. Suppose that
![]() $\mathcal {F}$
does not satisfy the reduction ordering condition. In this case, one follows the algorithm stated below and the proof is an adaptation of the proof of Theorem 5.1.
$\mathcal {F}$
does not satisfy the reduction ordering condition. In this case, one follows the algorithm stated below and the proof is an adaptation of the proof of Theorem 5.1.
Let
![]() $\{ \Delta ^{r}\}_{r\geq 0}$
be the collection of matrices produced by the SSSA applied to
$\{ \Delta ^{r}\}_{r\geq 0}$
be the collection of matrices produced by the SSSA applied to
![]() $\Delta ^{\mathrm {NMS}}$
. The steps described below must be applied for each fixed r in increasing order.
$\Delta ^{\mathrm {NMS}}$
. The steps described below must be applied for each fixed r in increasing order.
(1) If
![]() $\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})=\pm E_{11}^p$
(respectively,
$\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})=\pm E_{11}^p$
(respectively,
![]() $\Delta ^{r}(\gamma _{2}^{p+r},\gamma _1^{p})=\pm E_{22}^p$
), then the flow remains unaltered.
$\Delta ^{r}(\gamma _{2}^{p+r},\gamma _1^{p})=\pm E_{22}^p$
), then the flow remains unaltered.
(2) If
![]() $\mathcal {F}$
satisfies the reduction ordering condition in
$\mathcal {F}$
satisfies the reduction ordering condition in
![]() $\gamma _1^p\kern-0.2pt$
, then whenever
$\gamma _1^p\kern-0.2pt$
, then whenever
![]() $\Delta ^{\kern-0.1pt r}\kern-1pt(\gamma _1^{p},\gamma _{0}^{p-r}){=} \pm E_{22}^p$
(respectively,
$\Delta ^{\kern-0.1pt r}\kern-1pt(\gamma _1^{p},\gamma _{0}^{p-r}){=} \pm E_{22}^p$
(respectively,
![]() $\Delta ^{r}(\gamma _{2}^{p+r},\gamma _1^{p})=\pm E_{11}^p$
), perform a reduction of the periodic orbits
$\Delta ^{r}(\gamma _{2}^{p+r},\gamma _1^{p})=\pm E_{11}^p$
), perform a reduction of the periodic orbits
![]() $\gamma _1^p$
and
$\gamma _1^p$
and
![]() $\gamma _0^{p-r}$
(respectively,
$\gamma _0^{p-r}$
(respectively,
![]() $\gamma _2^{p+r}$
).
$\gamma _2^{p+r}$
).
(3) If
![]() $\mathcal {F}$
does not satisfy the reduction ordering condition in
$\mathcal {F}$
does not satisfy the reduction ordering condition in
![]() $\gamma _1^{p}$
, that is, there are
$\gamma _1^{p}$
, that is, there are
![]() $r_1$
and
$r_1$
and
![]() $r_2$
such that
$r_2$
such that
![]() $\Delta ^{r_1}(\gamma _1^{p},\gamma _{0}^{p-r_1})=\pm E_{22}^p$
and
$\Delta ^{r_1}(\gamma _1^{p},\gamma _{0}^{p-r_1})=\pm E_{22}^p$
and
![]() $\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})=\pm E_{11}^p$
, where
$\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})=\pm E_{11}^p$
, where
![]() $ \gamma _{0}^{p-r_1}$
and
$ \gamma _{0}^{p-r_1}$
and
![]() $\gamma _2^{p+r_2}$
are, respectively, attracting and repelling periodic orbits, then proceed as follows.
$\gamma _2^{p+r_2}$
are, respectively, attracting and repelling periodic orbits, then proceed as follows.
(3.1) If
![]() $r_1\leq r_2$
:
$r_1\leq r_2$
:
-
(a) and there exists
 $\ell _0>p$
such that
$\ell _0>p$
such that
 $\Delta ^{\ell _0-p+r_1}(\gamma _1^{\ell _0},\gamma _{0}^{p-r_1})=\pm E_{22}$
and
$\Delta ^{\ell _0-p+r_1}(\gamma _1^{\ell _0},\gamma _{0}^{p-r_1})=\pm E_{22}$
and
 $\Delta ^{r}(\gamma _2^{s},\gamma _1^{\ell _0})\neq \pm E_{11}^{p}$
, for all r and
$\Delta ^{r}(\gamma _2^{s},\gamma _1^{\ell _0})\neq \pm E_{11}^{p}$
, for all r and
 $\gamma _2^{s}$
, then perform a reduction of the periodic orbits
$\gamma _2^{s}$
, then perform a reduction of the periodic orbits
 $\gamma _1^{\ell _0}$
and
$\gamma _1^{\ell _0}$
and
 $\gamma _0^{p-r_1}$
(in this case, one says that there was a replacement of reductions); on the
$\gamma _0^{p-r_1}$
(in this case, one says that there was a replacement of reductions); on the
 $r_2$
th step, perform a reduction of the periodic orbits
$r_2$
th step, perform a reduction of the periodic orbits
 $\gamma _{1}^{p}$
and
$\gamma _{1}^{p}$
and
 $\gamma _2^{p+r_2}$
corresponding to
$\gamma _2^{p+r_2}$
corresponding to
 $\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})=\pm E_{11}^p$
;
$\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})=\pm E_{11}^p$
; -
(b) otherwise, perform a reduction of the orbits
 $\gamma _1^{p}$
and
$\gamma _1^{p}$
and
 $\gamma _{0}^{p-r_1}$
. Moreover:
$\gamma _{0}^{p-r_1}$
. Moreover:-
(i) if there exists
 $\ell _1<p$
such that
$\ell _1<p$
such that
 $\Delta ^{p+r_2-\ell _1}(\gamma _2^{p+r_2},\gamma _{1}^{\ell _1})=\pm E_{11}$
and
$\Delta ^{p+r_2-\ell _1}(\gamma _2^{p+r_2},\gamma _{1}^{\ell _1})=\pm E_{11}$
and
 $\Delta ^{r}(\gamma _1^{\ell _1}, \gamma _0^s)\neq \pm E_{22}^{p}$
, for all r and s, then perform a reduction of the periodic orbits
$\Delta ^{r}(\gamma _1^{\ell _1}, \gamma _0^s)\neq \pm E_{22}^{p}$
, for all r and s, then perform a reduction of the periodic orbits
 $\gamma _1^{\ell _1}$
and
$\gamma _1^{\ell _1}$
and
 $\gamma _2^{p+r_2}$
;
$\gamma _2^{p+r_2}$
; -
(ii) otherwise, the flow remains unaltered and
 $\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})$
is said to be a persistent differential.
$\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})$
is said to be a persistent differential.
-
(3.2) If
![]() $r_2 < r_1$
:
$r_2 < r_1$
:
-
(a) and there exists
 $\ell _0<p$
such that
$\ell _0<p$
such that
 $\Delta ^{p+r_2-\ell _0}(\gamma _2^{p+r_2},\gamma _{1}^{\ell _0})=\pm E_{11}$
and
$\Delta ^{p+r_2-\ell _0}(\gamma _2^{p+r_2},\gamma _{1}^{\ell _0})=\pm E_{11}$
and
 $\Delta ^{r}(\gamma _1^{\ell _0}, \gamma _0^s)\neq \pm E_{22}^{p}$
, for all r and s, then perform a reduction of the periodic orbits
$\Delta ^{r}(\gamma _1^{\ell _0}, \gamma _0^s)\neq \pm E_{22}^{p}$
, for all r and s, then perform a reduction of the periodic orbits
 $\gamma _1^{\ell _0}$
and
$\gamma _1^{\ell _0}$
and
 $\gamma _2^{p+r_2}$
(in this case, one says that there was a replacement of reductions); on the
$\gamma _2^{p+r_2}$
(in this case, one says that there was a replacement of reductions); on the
 $r_1$
th step, perform a reduction of the periodic orbits
$r_1$
th step, perform a reduction of the periodic orbits
 $\gamma _{1}^{p}$
and
$\gamma _{1}^{p}$
and
 $\gamma _0^{p-r_1}$
corresponding to
$\gamma _0^{p-r_1}$
corresponding to
 $\Delta ^{r_1}(\gamma _1^{p},\gamma _{0}^{p-r_1})=\pm E_{22}^p$
;
$\Delta ^{r_1}(\gamma _1^{p},\gamma _{0}^{p-r_1})=\pm E_{22}^p$
; -
(b) otherwise, perform a reduction of the orbits
 $\gamma _1^{p}$
and
$\gamma _1^{p}$
and
 $\gamma _{2}^{p+r_2}$
. Moreover:
$\gamma _{2}^{p+r_2}$
. Moreover:-
(i) if there exists
 $\ell _1>p$
such that
$\ell _1>p$
such that
 $\Delta ^{\ell _1-p+r_1}(\gamma _{1}^{\ell _1},\gamma _0^{p-r_1})=\pm E_{22}$
and
$\Delta ^{\ell _1-p+r_1}(\gamma _{1}^{\ell _1},\gamma _0^{p-r_1})=\pm E_{22}$
and
 $\Delta ^{r}(\gamma _2^s,\gamma _1^{\ell _1})\neq \pm E_{11}^{p}$
, for all r and s, then perform a reduction of the periodic orbits
$\Delta ^{r}(\gamma _2^s,\gamma _1^{\ell _1})\neq \pm E_{11}^{p}$
, for all r and s, then perform a reduction of the periodic orbits
 $\gamma _1^{\ell _1}$
and
$\gamma _1^{\ell _1}$
and
 $\gamma _0^{p-r_1}$
;
$\gamma _0^{p-r_1}$
; -
(ii) otherwise, the flow remains unaltered and
 $\Delta ^{r_1}(\gamma _1^{p},\gamma _{0}^{p-r_1})=\pm E_{22}^p$
is said to be a persistent differential.
$\Delta ^{r_1}(\gamma _1^{p},\gamma _{0}^{p-r_1})=\pm E_{22}^p$
is said to be a persistent differential.
-
It remains to prove that the correspondence between algebra and dynamics can be achieved through this algorithm.
By Remark 5.6, if
![]() $\Delta ^{r}(\gamma _1,\gamma _{0})=\pm E_{22}$
(respectively,
$\Delta ^{r}(\gamma _1,\gamma _{0})=\pm E_{22}$
(respectively,
![]() $\Delta ^{r}(\gamma _2,\gamma _{1})=\pm E_{11}$
), then
$\Delta ^{r}(\gamma _2,\gamma _{1})=\pm E_{11}$
), then
![]() $\Delta (\gamma _1,\gamma _{0})=\pm E_{22}$
(respectively,
$\Delta (\gamma _1,\gamma _{0})=\pm E_{22}$
(respectively,
![]() $\Delta (\gamma _2,\gamma _{1})=\pm E_{11}$
). Hence, it corresponds to a double connection, one inessential connection and one
$\Delta (\gamma _2,\gamma _{1})=\pm E_{11}$
). Hence, it corresponds to a double connection, one inessential connection and one
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free essential connection in
$h_1$
free essential connection in
![]() $\varphi $
.
$\varphi $
.
Suppose that we are in case (2). Since
![]() $\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})=\pm E_{22}^p$
(respectively,
$\Delta ^{r}(\gamma _1^{p},\gamma _{0}^{p-r})=\pm E_{22}^p$
(respectively,
![]() $\Delta ^{r}(\gamma _{0}^{p+r},\gamma _1^{p})=\pm E_{11}^p$
), then there are no blocks
$\Delta ^{r}(\gamma _{0}^{p+r},\gamma _1^{p})=\pm E_{11}^p$
), then there are no blocks
![]() $\pm E_{22}^p$
(respectively,
$\pm E_{22}^p$
(respectively,
![]() $\pm E_{11}^p$
),
$\pm E_{11}^p$
),
![]() $\pm E_{22}^c$
(respectively,
$\pm E_{22}^c$
(respectively,
![]() $\pm E_{11}^c$
) in the rows and columns associated to
$\pm E_{11}^c$
) in the rows and columns associated to
![]() $\gamma _{0}^{p-r}$
(respectively,
$\gamma _{0}^{p-r}$
(respectively,
![]() $\gamma _2$
) in
$\gamma _2$
) in
![]() $\Delta ^{\ell }$
for
$\Delta ^{\ell }$
for
![]() $0 \leq \ell \leq r-1$
. Moreover, there are no blocks
$0 \leq \ell \leq r-1$
. Moreover, there are no blocks
![]() $\pm E_{22}^p$
(respectively,
$\pm E_{22}^p$
(respectively,
![]() $\pm E_{11}^p$
) in the rows associated to
$\pm E_{11}^p$
) in the rows associated to
![]() $\gamma _1$
and, since
$\gamma _1$
and, since
![]() $\mathcal {F}$
satisfies the reduction ordering condition, there are no blocks
$\mathcal {F}$
satisfies the reduction ordering condition, there are no blocks
![]() $\pm E_{11}^p$
(respectively,
$\pm E_{11}^p$
(respectively,
![]() $\pm E_{22}^p$
) in the columns associated to
$\pm E_{22}^p$
) in the columns associated to
![]() $\gamma _1$
. Hence, both
$\gamma _1$
. Hence, both
![]() $\gamma _0$
and
$\gamma _0$
and
![]() $\gamma _1$
are still periodic orbits in
$\gamma _1$
are still periodic orbits in
![]() $\varphi ^r$
and the connections between them were not altered until step r. Therefore,
$\varphi ^r$
and the connections between them were not altered until step r. Therefore,
![]() $\Delta ^{r}(\gamma _1,\gamma _{0})$
(respectively,
$\Delta ^{r}(\gamma _1,\gamma _{0})$
(respectively,
![]() $\Delta ^{r}(\gamma _2,\gamma _{1}$
) corresponds to a double connection, one inessential connection and one
$\Delta ^{r}(\gamma _2,\gamma _{1}$
) corresponds to a double connection, one inessential connection and one
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free essential connection in
$h_1$
free essential connection in
![]() $\varphi ^r$
. By Theorem 3.12, the pair
$\varphi ^r$
. By Theorem 3.12, the pair
![]() $(\gamma _1,\gamma _{0})$
(respectively,
$(\gamma _1,\gamma _{0})$
(respectively,
![]() $(\gamma _2,\gamma _{1})$
) may be reduced.
$(\gamma _2,\gamma _{1})$
) may be reduced.
Suppose that we are in case (3.1). As in case (2),
![]() $\Delta ^{r_1}(\gamma _1^{p},\gamma _{0}^{p-r_1})=\pm E_{22}^p$
(respectively,
$\Delta ^{r_1}(\gamma _1^{p},\gamma _{0}^{p-r_1})=\pm E_{22}^p$
(respectively,
![]() $\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})=\pm E_{11}^p$
) corresponds to a double connection, one inessential connection and one
$\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})=\pm E_{11}^p$
) corresponds to a double connection, one inessential connection and one
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free essential connection in
$h_1$
free essential connection in
![]() $\varphi ^{r_1}$
(respectively,
$\varphi ^{r_1}$
(respectively,
![]() $\varphi ^{r_2}$
) and, by Theorem 3.12, the pair
$\varphi ^{r_2}$
) and, by Theorem 3.12, the pair
![]() $(\gamma _1,\gamma _{0})$
(respectively,
$(\gamma _1,\gamma _{0})$
(respectively,
![]() $(\gamma _2,\gamma _{1})$
) may be reduced. It remains to prove that, in case (a) (respectively, (b(i))),
$(\gamma _2,\gamma _{1})$
) may be reduced. It remains to prove that, in case (a) (respectively, (b(i))),
![]() $\Delta ^{\ell _0-p+r_1}(\gamma _1^{\ell _0},\gamma _{0}^{p-r_1})=\pm E_{22}$
(respectively,
$\Delta ^{\ell _0-p+r_1}(\gamma _1^{\ell _0},\gamma _{0}^{p-r_1})=\pm E_{22}$
(respectively,
![]() $\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})=\pm E_{11}^p$
) corresponds to a double connection, one inessential connection and one
$\Delta ^{r_2}(\gamma _2^{p+r_2},\gamma _{1}^{p})=\pm E_{11}^p$
) corresponds to a double connection, one inessential connection and one
![]() $h_2$
-
$h_2$
-
![]() $h_1$
free essential connection in
$h_1$
free essential connection in
![]() $\varphi ^{r_1}$
(respectively,
$\varphi ^{r_1}$
(respectively,
![]() $\varphi ^{r_2}$
). In fact, by Remark 5.6, this is the only non-zero block in the columns (respectively, rows) associated to
$\varphi ^{r_2}$
). In fact, by Remark 5.6, this is the only non-zero block in the columns (respectively, rows) associated to
![]() $\gamma _1^{\ell _0}$
(respectively,
$\gamma _1^{\ell _0}$
(respectively,
![]() $\gamma _1^{\ell _1}$
and
$\gamma _1^{\ell _1}$
and
![]() $\gamma _2^{p+r_2}$
) in
$\gamma _2^{p+r_2}$
) in
![]() $\Delta ^r$
for all r. Hence, both
$\Delta ^r$
for all r. Hence, both
![]() $\gamma _0^{p-r_1}$
and
$\gamma _0^{p-r_1}$
and
![]() $\gamma _1^{\ell _0}$
(respectively,
$\gamma _1^{\ell _0}$
(respectively,
![]() $\gamma _1^{\ell _1}$
and
$\gamma _1^{\ell _1}$
and
![]() $\gamma _2^{p+r_2}$
) are still periodic orbits in
$\gamma _2^{p+r_2}$
) are still periodic orbits in
![]() $\varphi ^{r_1}$
(respectively,
$\varphi ^{r_1}$
(respectively,
![]() $\varphi ^{r_2}$
) and the connections between them were not altered until step
$\varphi ^{r_2}$
) and the connections between them were not altered until step
![]() $r_1$
(respectively,
$r_1$
(respectively,
![]() $r_2$
). By Theorem 3.12, the pair
$r_2$
). By Theorem 3.12, the pair
![]() $(\gamma _1^{\ell _0},\gamma _{0}^{p-r_1})$
(respectively,
$(\gamma _1^{\ell _0},\gamma _{0}^{p-r_1})$
(respectively,
![]() $(\gamma _2^{p+r_2},\gamma _{1}^{\ell _1})$
) may be reduced. Whenever these reductions are performed, they correspond to replacements of reductions. Moreover, apart from the differential corresponding to replaced reductions and the persistent differentials, all the remaining ones correspond to dynamical reductions.
$(\gamma _2^{p+r_2},\gamma _{1}^{\ell _1})$
) may be reduced. Whenever these reductions are performed, they correspond to replacements of reductions. Moreover, apart from the differential corresponding to replaced reductions and the persistent differentials, all the remaining ones correspond to dynamical reductions.
Case 3.2 is analogous.
If
![]() $\mathcal {F}$
does not satisfy the reduction ordering condition in
$\mathcal {F}$
does not satisfy the reduction ordering condition in
![]() $\gamma _1^{p_1}, \ldots , \gamma _1^{p_f}$
, the arguments above hold for each one of the saddles. Moreover, by Proposition 3.2 in [Reference Cornea, de Rezende and da Silveira6], the changes in dynamics and algebra that happen with
$\gamma _1^{p_1}, \ldots , \gamma _1^{p_f}$
, the arguments above hold for each one of the saddles. Moreover, by Proposition 3.2 in [Reference Cornea, de Rezende and da Silveira6], the changes in dynamics and algebra that happen with
![]() $\gamma _1^{p_i}$
do not interfere with the changes that happen with
$\gamma _1^{p_i}$
do not interfere with the changes that happen with
![]() $\gamma _1^{p_j}$
. By the algorithm above, the differential corresponding to the flow
$\gamma _1^{p_j}$
. By the algorithm above, the differential corresponding to the flow
![]() $\varphi ^{\omega }$
is such that, for every saddle
$\varphi ^{\omega }$
is such that, for every saddle
![]() $\gamma _1$
,
$\gamma _1$
,
![]() $ \Delta (\gamma _1,\gamma _{0})$
(respectively,
$ \Delta (\gamma _1,\gamma _{0})$
(respectively,
![]() $ \Delta (\gamma _2,\gamma _{1})$
) is never equal to
$ \Delta (\gamma _2,\gamma _{1})$
) is never equal to
![]() $\pm E_{22}$
(respectively,
$\pm E_{22}$
(respectively,
![]() $ \pm E_{11}$
). In other words,
$ \pm E_{11}$
). In other words,
![]() $\gamma _1$
does not double connect with
$\gamma _1$
does not double connect with
![]() $\gamma _0$
(respectively,
$\gamma _0$
(respectively,
![]() $\gamma _2$
) through an inessential and an essential cylinder of connections. Therefore,
$\gamma _2$
) through an inessential and an essential cylinder of connections. Therefore,
![]() $\varphi ^{\omega }$
is a core flow.
$\varphi ^{\omega }$
is a core flow.

Figure 23 A flow on
![]() $S^1\times S^2.$
$S^1\times S^2.$
Corollary 5.9. Under the hypothesis of Theorem 5.8:
-
(1) the number N of period orbits of
 $\varphi ^{\omega }$
is
$\varphi ^{\omega }$
is  $$ \begin{align*} \kern-6pt N &= \displaystyle \frac{1}{2}\sum_{i=0}^{3} \beta_{i} \ + \ \# \{\Delta^{r}(\gamma_1,\gamma_0)\!=\!\pm E_{11}^p \mid r\geq 0\}\ + \ \# \{\Delta^{r}(\gamma_2,\gamma_1)\!=\!\pm E_{22}^p \mid r\geq 0\}\\& \quad + \displaystyle \# \{\Delta^{r}(\gamma_2,\gamma_0)\!=\!\pm E_{21}^p \mid r\geq 0\}+ \# \{ \mbox{persistent differentials} \pm E_{11}^p \mbox{ and } \pm E_{22}^p\}; \end{align*} $$
$$ \begin{align*} \kern-6pt N &= \displaystyle \frac{1}{2}\sum_{i=0}^{3} \beta_{i} \ + \ \# \{\Delta^{r}(\gamma_1,\gamma_0)\!=\!\pm E_{11}^p \mid r\geq 0\}\ + \ \# \{\Delta^{r}(\gamma_2,\gamma_1)\!=\!\pm E_{22}^p \mid r\geq 0\}\\& \quad + \displaystyle \# \{\Delta^{r}(\gamma_2,\gamma_0)\!=\!\pm E_{21}^p \mid r\geq 0\}+ \# \{ \mbox{persistent differentials} \pm E_{11}^p \mbox{ and } \pm E_{22}^p\}; \end{align*} $$
-
(2) the number of repelling periodic orbits of
 $\varphi ^{\omega }$
is
$\varphi ^{\omega }$
is
 $N_R = \beta _3 + \#\{\Delta ^{r}(\gamma _2,\gamma _1)=\pm E_{22}^p \mid r\geq 0\} $
;
$N_R = \beta _3 + \#\{\Delta ^{r}(\gamma _2,\gamma _1)=\pm E_{22}^p \mid r\geq 0\} $
; -
(3) the number of attracting periodic orbits of
 $\varphi ^{\omega }$
is
$\varphi ^{\omega }$
is
 $N_A = \beta _0 + \#\{\Delta ^{r}(\gamma _1,\gamma _0)=\pm E_{11}^p \mid r\geq 0\} $
; and
$N_A = \beta _0 + \#\{\Delta ^{r}(\gamma _1,\gamma _0)=\pm E_{11}^p \mid r\geq 0\} $
; and -
(4) the number of saddle periodic orbits of
 $\varphi ^{\omega }$
is
$\varphi ^{\omega }$
is
 $N_S = N - N_A - N_R $
.
$N_S = N - N_A - N_R $
.
The next exampleFootnote 2 illustrates Theorem 5.8 by performing reductions determined by the differentials of the associated spectral sequence obtaining a core flow. We choose a filtration which does not satisfy the reduction ordering condition.
Example 5.10. Consider the NMS flow
![]() $S^1\times S^2$
given in Figure 23 with the following filtration:
$S^1\times S^2$
given in Figure 23 with the following filtration:
![]() $\mathcal {F}_0C= \{ h_{0}(\gamma _0^{1}), h_{1}(\gamma _0^{1}) \}$
,
$\mathcal {F}_0C= \{ h_{0}(\gamma _0^{1}), h_{1}(\gamma _0^{1}) \}$
,
![]() $\mathcal {F}_1C\setminus \mathcal {F}_{0}C= \{ h_{1}(\gamma _1^{2}) , h_{2}(\gamma _1^{2}) \}$
,
$\mathcal {F}_1C\setminus \mathcal {F}_{0}C= \{ h_{1}(\gamma _1^{2}) , h_{2}(\gamma _1^{2}) \}$
,
![]() $\mathcal {F}_2C\setminus \mathcal {F}_{1}C= \{ h_{1}(\gamma _1^{3}) , h_{2}(\gamma _1^{3}) \}$
and
$\mathcal {F}_2C\setminus \mathcal {F}_{1}C= \{ h_{1}(\gamma _1^{3}) , h_{2}(\gamma _1^{3}) \}$
and
![]() $\mathcal {F}_3C\setminus \mathcal {F}_{2}C= \{ h_{2}(\gamma _2^{4}) , h_{3}(\gamma _2^{4}) \}$
. By applying the SSSA to
$\mathcal {F}_3C\setminus \mathcal {F}_{2}C= \{ h_{2}(\gamma _2^{4}) , h_{3}(\gamma _2^{4}) \}$
. By applying the SSSA to
![]() $\Delta ^{\mathrm {NMS}}$
, one obtains the collection of matrices in Figure 24 where the differentials of the spectral sequence are represented with marked entries. The differentials of the spectral sequence are induced by
$\Delta ^{\mathrm {NMS}}$
, one obtains the collection of matrices in Figure 24 where the differentials of the spectral sequence are represented with marked entries. The differentials of the spectral sequence are induced by
![]() $\Delta ^{2}(\gamma _1^2,\gamma _0^2)=E_{22}^{p}$
and
$\Delta ^{2}(\gamma _1^2,\gamma _0^2)=E_{22}^{p}$
and
![]() $\Delta ^{4}(\gamma _2^4,\gamma _1^1)=E_{11}^{p}$
. Note that the filtration does not satisfy the reduction ordering condition in
$\Delta ^{4}(\gamma _2^4,\gamma _1^1)=E_{11}^{p}$
. Note that the filtration does not satisfy the reduction ordering condition in
![]() $\gamma ^2_1$
. Following step 3.1 of the proof of Theorem 5.8, instead of performing the reduction of the pair
$\gamma ^2_1$
. Following step 3.1 of the proof of Theorem 5.8, instead of performing the reduction of the pair
![]() $(\gamma _1^2,\gamma _0^1)$
indicated by the differential
$(\gamma _1^2,\gamma _0^1)$
indicated by the differential
![]() $\Delta ^{2}(\gamma _1^2,\gamma _0^1)=E_{22}^{p}$
, one performs a reduction of the pair
$\Delta ^{2}(\gamma _1^2,\gamma _0^1)=E_{22}^{p}$
, one performs a reduction of the pair
![]() $(\gamma _1^3,\gamma _0^1)$
, which corresponds to
$(\gamma _1^3,\gamma _0^1)$
, which corresponds to
![]() $\Delta ^{4}(\gamma _1^3,\gamma _0^1)=E_{22}^{c}$
. By reducing the pair
$\Delta ^{4}(\gamma _1^3,\gamma _0^1)=E_{22}^{c}$
. By reducing the pair
![]() $(\gamma _2^4,\gamma ^2_1)$
, one obtains the flow as in Figure 25, which is a core flow.
$(\gamma _2^4,\gamma ^2_1)$
, one obtains the flow as in Figure 25, which is a core flow.

Figure 24 Matrices determined by the SSSA.

Figure 25 A core flow on
![]() $S^1\times S^2.$
$S^1\times S^2.$
Remark 5.11. Note that, if we follow the reduction order determined by the spectral sequence, after performing the reduction of the pair
![]() $(\gamma ^2_1,\gamma ^1_0)$
, the differential
$(\gamma ^2_1,\gamma ^1_0)$
, the differential
![]() $\Delta ^{4}(\gamma _2^4,\gamma _1^2)=E_{11}^{p}$
will not correspond to a reduction, since the orbit
$\Delta ^{4}(\gamma _2^4,\gamma _1^2)=E_{11}^{p}$
will not correspond to a reduction, since the orbit
![]() $\gamma _1^2$
was already reduced with
$\gamma _1^2$
was already reduced with
![]() $\gamma _0^1$
. This example shows that if the replacement of step 3.1 of Theorem 5.8 is not implemented, then we may not obtain a core flow.
$\gamma _0^1$
. This example shows that if the replacement of step 3.1 of Theorem 5.8 is not implemented, then we may not obtain a core flow.
5.3 Minimality and the role of cancellations
In the previous sections minimality results were obtained either by imposing a hypothesis on the filtrations, as in §5.1, or by imposing restrictions on the NMS flow and consequently on the differential of the chain complex associated to it, as in §5.2.
Recall that Theorem 5.1 guarantees that by establishing a correspondence between dynamical cancellations and reductions of an NMS flow and algebraic cancellations of an associated spectral sequence under the hypothesis of an NMS-compatible filtration satisfying the reduction ordering property, one arrives at a core flow.
On the other hand, Theorem 5.8 also arrives at a core flow but does not require any hypothesis on the filtration
![]() $\mathcal {F}$
. One achieves this by restricting the differential
$\mathcal {F}$
. One achieves this by restricting the differential
![]() $\Delta ^{\mathrm {NMS}}$
of a filtered NMS-chain complex
$\Delta ^{\mathrm {NMS}}$
of a filtered NMS-chain complex
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
so that all differentials
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
so that all differentials
![]() $d^r_p$
of the associated spectral sequence are not isomorphisms. Dynamically this implies that there are no cancelling pairs of periodic orbits in the associated NMS flow and this provides a new algebraic-dynamical background with the presence of persistent differentials.
$d^r_p$
of the associated spectral sequence are not isomorphisms. Dynamically this implies that there are no cancelling pairs of periodic orbits in the associated NMS flow and this provides a new algebraic-dynamical background with the presence of persistent differentials.
Thus, it is clear from the above results that cancellations and the order in which they are performed, determined by the filtration, play an important role in arriving at a core flow and, in some cases, arriving at one in which the number of periodic orbits are minimized.
In this section, we prove Corollary 5.12, which considers an NMS flow
![]() $\varphi $
and an associated chain complex with an arbitrary filtration, and we apply the spectral sequence algorithm to obtain a family of NMS flows, the last of which is maximal in
$\varphi $
and an associated chain complex with an arbitrary filtration, and we apply the spectral sequence algorithm to obtain a family of NMS flows, the last of which is maximal in
![]() $\mathcal {S}_{\varphi }$
. Since the filtration is arbitrary, one cannot use Theorem 5.1 and, since isomorphisms may be present, one cannot use Theorem 5.8. The proof is partially based on a spectral sequence analysis, and thus the algebraic-dynamical correspondence is weaker in Corollary 5.12. We also prove Theorem 5.15, which shows that, on the
$\mathcal {S}_{\varphi }$
. Since the filtration is arbitrary, one cannot use Theorem 5.1 and, since isomorphisms may be present, one cannot use Theorem 5.8. The proof is partially based on a spectral sequence analysis, and thus the algebraic-dynamical correspondence is weaker in Corollary 5.12. We also prove Theorem 5.15, which shows that, on the
![]() $3$
-sphere, following the unfolding of the spectral sequence one always obtains an NMS flow with one attracting and one repelling periodic orbit.
$3$
-sphere, following the unfolding of the spectral sequence one always obtains an NMS flow with one attracting and one repelling periodic orbit.
Corollary 5.12. Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, such that
$3$
-manifold, such that
![]() $FM(\varphi )\neq \emptyset $
and let
$FM(\varphi )\neq \emptyset $
and let
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be an NMS complex where
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be an NMS complex where
![]() $\widetilde {\varphi }\in FM(\varphi )$
. Then there exists a periodic orbit reduction and cancellation algorithm using the pair
$\widetilde {\varphi }\in FM(\varphi )$
. Then there exists a periodic orbit reduction and cancellation algorithm using the pair
![]() $(\varphi ,\mathcal {F}) $
as input, based on spectral sequences, that determines a family of NMS flows
$(\varphi ,\mathcal {F}) $
as input, based on spectral sequences, that determines a family of NMS flows
![]() $\{\varphi ^1,\ldots , \varphi ^{\omega }\}$
on
$\{\varphi ^1,\ldots , \varphi ^{\omega }\}$
on
![]() $M^3$
, where
$M^3$
, where
![]() $\varphi ^1=\varphi $
,
$\varphi ^1=\varphi $
,
![]() $\varphi ^{r-1}<\varphi ^r$
and
$\varphi ^{r-1}<\varphi ^r$
and
![]() $\varphi ^{\omega }$
is a core flow.
$\varphi ^{\omega }$
is a core flow.
Proof. The proof is carried out in two steps. In the first step, we perform cancellations detected in the NMS differential in order to obtain a flow where each inessential connection is part of a double connection between two periodic orbits. To do this, we cancel pairs of periodic orbits in an increasing order of gaps in the filtration, as follows.
-
(I.1) Let
 $\varphi ^1=\varphi $
. If
$\varphi ^1=\varphi $
. If
 $\gamma _1^{p}$
and
$\gamma _1^{p}$
and
 $\gamma _{0}^{p-r}$
(respectively,
$\gamma _{0}^{p-r}$
(respectively,
 $\gamma _{2}^{p+r}$
and
$\gamma _{2}^{p+r}$
and
 $\gamma _1^{p}$
) are two periodic orbits with gap
$\gamma _1^{p}$
) are two periodic orbits with gap
 $r\geq 1$
in
$r\geq 1$
in
 $\mathcal {F}$
such that
$\mathcal {F}$
such that
 $\Delta (\gamma _1^{p}, \gamma _{0}^{p-r};\varphi ^r)$
(respectively,
$\Delta (\gamma _1^{p}, \gamma _{0}^{p-r};\varphi ^r)$
(respectively,
 $\Delta (\gamma _{2}^{p+r},\gamma _1^{p};\varphi ^r)$
) is equal to
$\Delta (\gamma _{2}^{p+r},\gamma _1^{p};\varphi ^r)$
) is equal to
 $\pm I$
or
$\pm I$
or
 $\pm \widetilde {I}$
, by Theorem 3.11, cancel the pair of periodic orbits
$\pm \widetilde {I}$
, by Theorem 3.11, cancel the pair of periodic orbits
 $\gamma _1^{p}$
and
$\gamma _1^{p}$
and
 $ \gamma _{0}^{p-r}$
(respectively,
$ \gamma _{0}^{p-r}$
(respectively,
 $\gamma _{2}^{p+r}$
and
$\gamma _{2}^{p+r}$
and
 $\gamma _1^{p}$
).
$\gamma _1^{p}$
). -
(I.2) Let
 $\varphi ^{r+1}$
be the the resulting flow. By Proposition 3.13, FM(
$\varphi ^{r+1}$
be the the resulting flow. By Proposition 3.13, FM(
 $\varphi ^{r+1})\neq \emptyset $
. Let
$\varphi ^{r+1})\neq \emptyset $
. Let
 $(C^{\mathrm {NMS}}(\widetilde \varphi ^{r+1}),\Delta ^{\mathrm {NMS}}(\widetilde \varphi ^{r+1}))$
, where
$(C^{\mathrm {NMS}}(\widetilde \varphi ^{r+1}),\Delta ^{\mathrm {NMS}}(\widetilde \varphi ^{r+1}))$
, where
 $\widetilde \varphi ^{r+1}\in FM(\varphi ^{r+1})$
is the associated chain complex endowed with the induced filtration
$\widetilde \varphi ^{r+1}\in FM(\varphi ^{r+1})$
is the associated chain complex endowed with the induced filtration
 $\mathcal {F}$
.
$\mathcal {F}$
. -
(I.3) Repeat (I.1) and (I.2) for all gaps r.
Denote by
![]() $\varphi ^{\prime }$
the last flow obtained in the first part. By Proposition 3.13, FM(
$\varphi ^{\prime }$
the last flow obtained in the first part. By Proposition 3.13, FM(
![]() $\varphi ^{\prime })\neq \emptyset $
. After the pre-processing steps outlined previously, one obtains a chain complex associated to
$\varphi ^{\prime })\neq \emptyset $
. After the pre-processing steps outlined previously, one obtains a chain complex associated to
![]() $\varphi '$
, such that the submatrices
$\varphi '$
, such that the submatrices
![]() $\Delta (\gamma _k,\gamma _{k-1})$
of the differential
$\Delta (\gamma _k,\gamma _{k-1})$
of the differential
![]() $\Delta ^{\mathrm {NMS}}(\varphi ^{\prime })$
for all periodic orbits
$\Delta ^{\mathrm {NMS}}(\varphi ^{\prime })$
for all periodic orbits
![]() $\gamma _k$
and
$\gamma _k$
and
![]() $\gamma _{k-1}$
are never isomorphisms, neither
$\gamma _{k-1}$
are never isomorphisms, neither
![]() $ \pm I$
nor
$ \pm I$
nor
![]() $\pm \tilde {I}$
. The second step consists of performing reductions of pairs of periodic orbits of
$\pm \tilde {I}$
. The second step consists of performing reductions of pairs of periodic orbits of
![]() $\varphi '$
, following the algorithm presented in the proof of Theorem 5.8.
$\varphi '$
, following the algorithm presented in the proof of Theorem 5.8.
Example 5.13. Consider the NMS flow given in Example 5.3 with the non-NMS- compatible filtration presented in Figure 20. The first step is to cancel, in an increasing order of gaps in the filtration, the inessential connections detected by the NMS differential. In this case, the entry
![]() $\Delta (\gamma _1^3,\gamma _0^2)=-\widetilde {I}$
determines the cancellation of the pair
$\Delta (\gamma _1^3,\gamma _0^2)=-\widetilde {I}$
determines the cancellation of the pair
![]() $(\gamma _1^3,\gamma _0^2)$
. After this cancellation has been performed, one obtains a flow
$(\gamma _1^3,\gamma _0^2)$
. After this cancellation has been performed, one obtains a flow
![]() $\varphi '$
where there are no more possible cancellations of periodic orbits. The chain complex associated to
$\varphi '$
where there are no more possible cancellations of periodic orbits. The chain complex associated to
![]() $\varphi '$
enriched with the induced filtration is presented in Figure 26. Now, apply Theorem 5.8 to this matrix:
$\varphi '$
enriched with the induced filtration is presented in Figure 26. Now, apply Theorem 5.8 to this matrix:
![]() $\Delta ^{4}(\gamma _2^6,\gamma _1^4)=E_{11}^{p}$
determines the reduction of the pair
$\Delta ^{4}(\gamma _2^6,\gamma _1^4)=E_{11}^{p}$
determines the reduction of the pair
![]() $(\gamma _2^6,\gamma _1^4)$
and
$(\gamma _2^6,\gamma _1^4)$
and
![]() $\Delta ^{4}(\gamma _1^5,\gamma _0^1)=E_{22}^{p}$
determines the reduction of the pair
$\Delta ^{4}(\gamma _1^5,\gamma _0^1)=E_{22}^{p}$
determines the reduction of the pair
![]() $(\gamma _1^5,\gamma _0^1)$
. In this case, note that the core flow obtained is the one with the least number of periodic orbits in
$(\gamma _1^5,\gamma _0^1)$
. In this case, note that the core flow obtained is the one with the least number of periodic orbits in
![]() $S^1\times S^2$
.
$S^1\times S^2$
.

Figure 26 Differential of the chain complex associated to
![]() $\varphi '$
obtained after the pre-processing steps.
$\varphi '$
obtained after the pre-processing steps.
The next example suggests that, given an NMS flow
![]() $\varphi $
on
$\varphi $
on
![]() $M^3$
, in general, different filtrations of an associated chain complex may lead to core flows with different numbers of periodic orbits in
$M^3$
, in general, different filtrations of an associated chain complex may lead to core flows with different numbers of periodic orbits in
![]() $\mathcal {S}_{\varphi }$
.
$\mathcal {S}_{\varphi }$
.
Example 5.14. Let
![]() $(C,\Delta )$
be a chain complex where the modules are given by
$(C,\Delta )$
be a chain complex where the modules are given by
![]() $C_0=\mathbb {Z}[ h_{0}(\gamma _0^{1}), h_{0}(\gamma _0^{2})]$
,
$C_0=\mathbb {Z}[ h_{0}(\gamma _0^{1}), h_{0}(\gamma _0^{2})]$
,
![]() $C_1=\mathbb {Z}[h_{1}(\gamma _0^{1}), h_{1}(\gamma _0^{2}), h_{1}(\gamma _1^{3}), h_{1}(\gamma _1^{4}), h_{1}(\gamma _1^{5})]$
,
$C_1=\mathbb {Z}[h_{1}(\gamma _0^{1}), h_{1}(\gamma _0^{2}), h_{1}(\gamma _1^{3}), h_{1}(\gamma _1^{4}), h_{1}(\gamma _1^{5})]$
,
![]() $C_2=\mathbb {Z}[h_{2}(\gamma _1^{3}), h_{2}(\gamma _1^{4}), h_{2}(\gamma _1^{5}), h_{2}(\gamma _2^{6})]$
and
$C_2=\mathbb {Z}[h_{2}(\gamma _1^{3}), h_{2}(\gamma _1^{4}), h_{2}(\gamma _1^{5}), h_{2}(\gamma _2^{6})]$
and
![]() $C_3=\mathbb {Z}[h_{3}(\gamma _2^{6})]$
, and the non-zero differentials on the generators are given by
$C_3=\mathbb {Z}[h_{3}(\gamma _2^{6})]$
, and the non-zero differentials on the generators are given by
![]() $\partial _1( h_{1}(\gamma _1^{3}))= -h_{0}(\gamma _0^{1})+ h_{0}(\gamma _0^{2}) $
,
$\partial _1( h_{1}(\gamma _1^{3}))= -h_{0}(\gamma _0^{1})+ h_{0}(\gamma _0^{2}) $
,
![]() $\partial _1( h_{1}(\gamma _1^{5}))= -h_{0}(\gamma _0^{1})+ h_{0}(\gamma _0^{2}) $
,
$\partial _1( h_{1}(\gamma _1^{5}))= -h_{0}(\gamma _0^{1})+ h_{0}(\gamma _0^{2}) $
,
![]() $\partial _2( h_{2}(\gamma _1^{3}))= h_{1}(\gamma _0^{2}) $
,
$\partial _2( h_{2}(\gamma _1^{3}))= h_{1}(\gamma _0^{2}) $
,
![]() $\partial _2( h_{2}(\gamma _1^{4}))= h_{1}(\gamma _0^{2}) $
,
$\partial _2( h_{2}(\gamma _1^{4}))= h_{1}(\gamma _0^{2}) $
,
![]() $\partial _2( h_{2}(\gamma _1^{5}))= h_{1}(\gamma _0^{2}) $
,
$\partial _2( h_{2}(\gamma _1^{5}))= h_{1}(\gamma _0^{2}) $
,
![]() $\partial _2( h_{2}(\gamma _2^{6}))= h_{1}(\gamma _0^{1}) $
.
$\partial _2( h_{2}(\gamma _2^{6}))= h_{1}(\gamma _0^{1}) $
.
Endowing
![]() $(C,\Delta )$
with the filtration
$(C,\Delta )$
with the filtration
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathcal {F}_pC\setminus \mathcal {F}_{p-1}C= \{ h_{k}(\gamma _k^{p+1}), h_{k+1} (\gamma _k^{p+1}) \}$
, the matrices
$\mathcal {F}_pC\setminus \mathcal {F}_{p-1}C= \{ h_{k}(\gamma _k^{p+1}), h_{k+1} (\gamma _k^{p+1}) \}$
, the matrices
![]() $\Delta ^r$
produced by the SSSA are presented in Figure 27. The entries marked with circles correspond to the differentials of the associated spectral sequence. Note that
$\Delta ^r$
produced by the SSSA are presented in Figure 27. The entries marked with circles correspond to the differentials of the associated spectral sequence. Note that
![]() $\mathcal {F}$
is an NMS-compatible filtration that satisfies the reduction ordering condition.
$\mathcal {F}$
is an NMS-compatible filtration that satisfies the reduction ordering condition.

Figure 27 SSSA applied to
![]() $\Delta $
endowed with
$\Delta $
endowed with
![]() $\mathcal {F}'$
.
$\mathcal {F}'$
.
Consider the alternative filtration
![]() $\mathcal {F}'$
on
$\mathcal {F}'$
on
![]() $(C,\Delta )$
given by
$(C,\Delta )$
given by
![]() $\mathcal {F}^{\prime }_0C= \{ h_{0}(\gamma _0^{1}), h_{1}(\gamma _0^{1}) \}$
,
$\mathcal {F}^{\prime }_0C= \{ h_{0}(\gamma _0^{1}), h_{1}(\gamma _0^{1}) \}$
,
![]() $\mathcal {F}^{\prime }_1C\setminus \mathcal {F}^{\prime }_{0}C\kern1.3pt{=}\kern1.3pt \{ h_{0}(\gamma _0^{2}) , h_{1}(\gamma _0^{2}) \}$
,
$\mathcal {F}^{\prime }_1C\setminus \mathcal {F}^{\prime }_{0}C\kern1.3pt{=}\kern1.3pt \{ h_{0}(\gamma _0^{2}) , h_{1}(\gamma _0^{2}) \}$
,
![]() $\mathcal {F}^{\prime }_2C\setminus \mathcal {F}^{\prime }_{1}C\kern1.3pt{=}\kern1.3pt \{ h_{1}(\gamma _1^{4}) , h_{2}(\gamma _1^{4}) \}$
,
$\mathcal {F}^{\prime }_2C\setminus \mathcal {F}^{\prime }_{1}C\kern1.3pt{=}\kern1.3pt \{ h_{1}(\gamma _1^{4}) , h_{2}(\gamma _1^{4}) \}$
,
![]() $\mathcal {F}^{\prime }_3C\setminus \mathcal {F}^{\prime }_{2}C\kern1.3pt{=}\kern1.3pt \{ h_{1}(\gamma _1^{3}) , h_{2}(\gamma _1^{3}) \}$
,
$\mathcal {F}^{\prime }_3C\setminus \mathcal {F}^{\prime }_{2}C\kern1.3pt{=}\kern1.3pt \{ h_{1}(\gamma _1^{3}) , h_{2}(\gamma _1^{3}) \}$
,
![]() $\mathcal {F}^{\prime }_4C\setminus \mathcal {F}^{\prime }_{3}C= \{ h_{1}(\gamma _1^{5}) , h_{2}(\gamma _1^{5}) \}$
and
$\mathcal {F}^{\prime }_4C\setminus \mathcal {F}^{\prime }_{3}C= \{ h_{1}(\gamma _1^{5}) , h_{2}(\gamma _1^{5}) \}$
and
![]() $\mathcal {F}^{\prime }_5C\setminus \mathcal {F}^{\prime }_{4}C= \{ h_{2}(\gamma _2^{6}) , h_{3}(\gamma _2^{6}) \}$
that is also NMS-compatible and satisfies the reduction ordering condition. Applying the SSSA to
$\mathcal {F}^{\prime }_5C\setminus \mathcal {F}^{\prime }_{4}C= \{ h_{2}(\gamma _2^{6}) , h_{3}(\gamma _2^{6}) \}$
that is also NMS-compatible and satisfies the reduction ordering condition. Applying the SSSA to
![]() $\Delta ^{\mathrm {NMS}}$
endowed with the filtration
$\Delta ^{\mathrm {NMS}}$
endowed with the filtration
![]() $\mathcal {F}'$
, one obtains a different collection of matrices, as shown in Figure 28.
$\mathcal {F}'$
, one obtains a different collection of matrices, as shown in Figure 28.

Figure 28 SSSA applied to
![]() $\Delta $
endowed with
$\Delta $
endowed with
![]() $\mathcal {F}'$
.
$\mathcal {F}'$
.
However, the next theorem proves that, for NMS flows on
![]() $S^3$
, every filtration leads to the same core flow.
$S^3$
, every filtration leads to the same core flow.
Theorem 5.15. Let
![]() $\varphi $
be an NMS flow in
$\varphi $
be an NMS flow in
![]() $\Sigma (M^3)$
, where
$\Sigma (M^3)$
, where
![]() $M^3$
is an orientable closed
$M^3$
is an orientable closed
![]() $3$
-manifold, and assume that
$3$
-manifold, and assume that
![]() $ TUM(\varphi ) \neq \emptyset $
. If
$ TUM(\varphi ) \neq \emptyset $
. If
![]() $\varphi $
is core flow in
$\varphi $
is core flow in
![]() $S^3$
, then
$S^3$
, then
![]() $\varphi $
has only one attracting periodic orbit and one repelling periodic orbit.
$\varphi $
has only one attracting periodic orbit and one repelling periodic orbit.
Proof. Suppose that
![]() $\varphi $
is a core flow in
$\varphi $
is a core flow in
![]() $S^3$
that has more than two periodic orbits. Then
$S^3$
that has more than two periodic orbits. Then
![]() $\varphi $
has at least one saddle periodic orbit, namely,
$\varphi $
has at least one saddle periodic orbit, namely,
![]() $\gamma _1$
. Note that, in an NMS flow on
$\gamma _1$
. Note that, in an NMS flow on
![]() $S^3$
, the two connections between a saddle periodic orbit and attractors (respectively, repellers) cannot be both essential connections since this would create a level surface homeomorphic to a sphere
$S^3$
, the two connections between a saddle periodic orbit and attractors (respectively, repellers) cannot be both essential connections since this would create a level surface homeomorphic to a sphere
![]() $S^2$
.
$S^2$
.
Let
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be an NMS complex, where
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
be an NMS complex, where
![]() $\widetilde \varphi \in TUM(\varphi )$
. Since
$\widetilde \varphi \in TUM(\varphi )$
. Since
![]() $\varphi $
is a core flow, it follows, from Theorem 3.7, that
$\varphi $
is a core flow, it follows, from Theorem 3.7, that
![]() $\Delta (\gamma _1,\gamma _0^{\ell })$
is the null map for all
$\Delta (\gamma _1,\gamma _0^{\ell })$
is the null map for all
![]() $\ell $
and, from Theorem 3.8, that
$\ell $
and, from Theorem 3.8, that
![]() $\Delta (\gamma _2^{\ell },\gamma _1)$
is the null map for all
$\Delta (\gamma _2^{\ell },\gamma _1)$
is the null map for all
![]() $\ell $
. Consequently,
$\ell $
. Consequently,
![]() $H_2(C^{\mathrm {NMS}}(\widetilde \varphi ),\Delta ^{\mathrm {NMS}})$
must be non-zero, which contradicts the fact that
$H_2(C^{\mathrm {NMS}}(\widetilde \varphi ),\Delta ^{\mathrm {NMS}})$
must be non-zero, which contradicts the fact that
![]() $S^3$
is simply connected. Hence,
$S^3$
is simply connected. Hence,
![]() $\varphi $
is the NMS flow that has only one attracting periodic orbit and one repelling periodic orbit.
$\varphi $
is the NMS flow that has only one attracting periodic orbit and one repelling periodic orbit.

Figure 29 An NMS flow on the
![]() $3$
-sphere.
$3$
-sphere.

Figure 30 NMS differential matrix.
Example 5.16. Consider an NMS flow on
![]() $S^3$
, as shown in Figure 29. The differential
$S^3$
, as shown in Figure 29. The differential
![]() $\Delta ^{\mathrm {NMS}}$
of the chain complex
$\Delta ^{\mathrm {NMS}}$
of the chain complex
![]() $(C^{\mathrm {NMS}}(\widetilde \varphi ),\Delta ^{\mathrm {NMS}})$
endowed with the NMS-compatible filtration
$(C^{\mathrm {NMS}}(\widetilde \varphi ),\Delta ^{\mathrm {NMS}})$
endowed with the NMS-compatible filtration
![]() $\mathcal {F}_pC\setminus \mathcal {F}_{p-1}C= \{ h_{k}(\gamma _k^{p+1}) \ , \ h_{k+1}(\gamma _k^{p+1}) \}$
is shown in Figure 30. First, the cancellations of the pairs
$\mathcal {F}_pC\setminus \mathcal {F}_{p-1}C= \{ h_{k}(\gamma _k^{p+1}) \ , \ h_{k+1}(\gamma _k^{p+1}) \}$
is shown in Figure 30. First, the cancellations of the pairs
![]() $(\gamma _1^4,\gamma _0^2)$
and
$(\gamma _1^4,\gamma _0^2)$
and
![]() $(\gamma _2^7,\gamma _1^5)$
are performed in an increasing order of the gaps in the filtration. Let
$(\gamma _2^7,\gamma _1^5)$
are performed in an increasing order of the gaps in the filtration. Let
![]() $\varphi '$
be the resulting flow in which there are no more possible cancellations of periodic orbits to be performed. See Figure 31. The chain complex associated to
$\varphi '$
be the resulting flow in which there are no more possible cancellations of periodic orbits to be performed. See Figure 31. The chain complex associated to
![]() $\varphi '$
enriched with the induced filtration is presented in Figure 32. Now, apply Theorem 5.8 to this matrix. Thus,
$\varphi '$
enriched with the induced filtration is presented in Figure 32. Now, apply Theorem 5.8 to this matrix. Thus,
![]() $\Delta ^{2}(\gamma _1^3,\gamma _0^1)=E_{22}^{p}$
determines the reduction of the pair
$\Delta ^{2}(\gamma _1^3,\gamma _0^1)=E_{22}^{p}$
determines the reduction of the pair
![]() $(\gamma _1^3,\gamma _0^1)$
. At the end of this process, the final flow is a core flow in
$(\gamma _1^3,\gamma _0^1)$
. At the end of this process, the final flow is a core flow in
![]() $S^3$
.
$S^3$
.

Figure 31 A core flow on
![]() $S^3$
.
$S^3$
.

Figure 32 Matrix determined by the SSSA.
6 Final remarks
In this work, we proved results on cancellations and reductions of periodic orbits in an NMS flow on a closed
![]() $3$
-manifold with the restriction that there are no heteroclinic trajectories connecting saddle periodic orbits. A natural course of action at this point is to consider NMS flows without this restriction. The great challenge in this new setting is to understand the effect of broken cylinder connections of the flow on the dynamics of cancellations and reductions as well as the algebraic interpretation of these connections within the unfolding of the spectral sequence.
$3$
-manifold with the restriction that there are no heteroclinic trajectories connecting saddle periodic orbits. A natural course of action at this point is to consider NMS flows without this restriction. The great challenge in this new setting is to understand the effect of broken cylinder connections of the flow on the dynamics of cancellations and reductions as well as the algebraic interpretation of these connections within the unfolding of the spectral sequence.
Fortunately, with the tools introduced in this work, we manage to salvage a local result for NMS flows with saddle-saddle connections.
Theorem 6.1. (Local reduction for heteroclinic trajectories connecting saddle periodic orbits)
Let
![]() $\varphi $
be an NMS flow on
$\varphi $
be an NMS flow on
![]() $M^3$
and let
$M^3$
and let
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma ^{\prime }_{1}$
be saddle periodic orbits. If
$\gamma ^{\prime }_{1}$
be saddle periodic orbits. If
![]() $W^u(\gamma ^{\prime }_1) \cap W^s(\gamma _{1})$
is a single orbit, then there exists an NMS flow
$W^u(\gamma ^{\prime }_1) \cap W^s(\gamma _{1})$
is a single orbit, then there exists an NMS flow
![]() ${\varphi }'$
on M that coincides with
${\varphi }'$
on M that coincides with
![]() $\varphi $
outside a neighborhood U of
$\varphi $
outside a neighborhood U of
![]() $W^u(\gamma ^{\prime }_1) \cap W^s(\gamma _{1})$
and the chain recurrent set of
$W^u(\gamma ^{\prime }_1) \cap W^s(\gamma _{1})$
and the chain recurrent set of
![]() ${\varphi }'$
restricted to U is a unique saddle periodic orbit.
${\varphi }'$
restricted to U is a unique saddle periodic orbit.
Proof. Since
![]() $W^u(\gamma ^{\prime }_1) \cap W^s(\gamma _{1})$
is a single orbit, there is a unique orbit between
$W^u(\gamma ^{\prime }_1) \cap W^s(\gamma _{1})$
is a single orbit, there is a unique orbit between
![]() $h_{2}(\gamma _{1})$
and
$h_{2}(\gamma _{1})$
and
![]() $h_{1}(\gamma ^{\prime }_{1})$
in the morsification
$h_{1}(\gamma ^{\prime }_{1})$
in the morsification
![]() $\widetilde {\varphi }$
of
$\widetilde {\varphi }$
of
![]() $\varphi $
. Let u be the single orbit between the singularities
$\varphi $
. Let u be the single orbit between the singularities
![]() $h_{2}(\gamma _{1})$
and
$h_{2}(\gamma _{1})$
and
![]() $h_{1}(\gamma ^{\prime }_{1})$
in the morsification
$h_{1}(\gamma ^{\prime }_{1})$
in the morsification
![]() $\widetilde {\varphi }$
. Consider a neighborhood V of u such that
$\widetilde {\varphi }$
. Consider a neighborhood V of u such that
![]() $V \subset U$
. By Smale’s first cancellation theorem, one may cancel
$V \subset U$
. By Smale’s first cancellation theorem, one may cancel
![]() $h_{2}(\gamma _{1})$
and
$h_{2}(\gamma _{1})$
and
![]() $h_{1}(\gamma ^{\prime }_{1})$
, which results in a flow
$h_{1}(\gamma ^{\prime }_{1})$
, which results in a flow
![]() $\widetilde {\varphi }_1$
that coincides with
$\widetilde {\varphi }_1$
that coincides with
![]() $\widetilde {\varphi }$
outside V and has no critical points in V. Note that, during this process of cancellation, the flow is not altered outside V. Moreover, in
$\widetilde {\varphi }$
outside V and has no critical points in V. Note that, during this process of cancellation, the flow is not altered outside V. Moreover, in
![]() $\widetilde {\varphi }_1$
, there are two flow lines between
$\widetilde {\varphi }_1$
, there are two flow lines between
![]() $h_{1}(\gamma _{1})$
and
$h_{1}(\gamma _{1})$
and
![]() $h_{2}(\gamma ^{\prime }_{1})$
with opposite characteristic signs. Now, by reversing the morsification process (see Theorem 2.1), one obtains a new NMS flow
$h_{2}(\gamma ^{\prime }_{1})$
with opposite characteristic signs. Now, by reversing the morsification process (see Theorem 2.1), one obtains a new NMS flow
![]() $\varphi '$
with a saddle periodic orbit in U that coincides with
$\varphi '$
with a saddle periodic orbit in U that coincides with
![]() $\varphi $
outside U.
$\varphi $
outside U.
For motivational purposes, consider the following example of an NMS flow on
![]() $S^3$
with heteroclinic trajectories connecting saddle orbits.
$S^3$
with heteroclinic trajectories connecting saddle orbits.
Example 6.2. Consider an NMS flow
![]() $\varphi $
on
$\varphi $
on
![]() $S^3$
as presented in Figure 7 of [Reference Campos and Vindel5]. The differential
$S^3$
as presented in Figure 7 of [Reference Campos and Vindel5]. The differential
![]() $\Delta ^{\mathrm {NMS}}$
of the associated chain complex
$\Delta ^{\mathrm {NMS}}$
of the associated chain complex
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
is shown in Figure 33(a). Performing a reduction of the saddle periodic orbits
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
is shown in Figure 33(a). Performing a reduction of the saddle periodic orbits
![]() $\gamma _1^2$
and
$\gamma _1^2$
and
![]() $\gamma _1^3$
corresponding to
$\gamma _1^3$
corresponding to
![]() $\Delta (\gamma _1^3,\gamma _1^2)=E_{12}$
produces a new periodic orbit
$\Delta (\gamma _1^3,\gamma _1^2)=E_{12}$
produces a new periodic orbit
![]() $\gamma _1^{\ast }$
. The differential of the complex of the new flow is shown in Figure 33(b). Performing a second reduction of the saddle periodic orbit
$\gamma _1^{\ast }$
. The differential of the complex of the new flow is shown in Figure 33(b). Performing a second reduction of the saddle periodic orbit
![]() $\gamma _1^{\ast }$
and the attracting periodic orbit
$\gamma _1^{\ast }$
and the attracting periodic orbit
![]() $\gamma _0^1$
, produces a new attracting periodic orbit
$\gamma _0^1$
, produces a new attracting periodic orbit
![]() $\gamma _0^{\ast }$
. The differential of the complex of the resulting flow is shown in Figure 33(c) and corresponds to a core flow on
$\gamma _0^{\ast }$
. The differential of the complex of the resulting flow is shown in Figure 33(c) and corresponds to a core flow on
![]() $S^3$
.
$S^3$
.

Figure 33 Reductions and corresponding differentials.
Note that, in this particular example, if one attempts to follow the algebra of the SSSA dynamically for
![]() $(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
endowed with the filtration
$(C^{\mathrm {NMS}}(\widetilde {\varphi }),\Delta ^{\mathrm {NMS}})$
endowed with the filtration
![]() $\mathcal {F}_0C= \{ h_{0}(\gamma _0^{1}), h_{1}(\gamma _0^{1}) \}$
,
$\mathcal {F}_0C= \{ h_{0}(\gamma _0^{1}), h_{1}(\gamma _0^{1}) \}$
,
![]() $\mathcal {F}_1C\setminus \mathcal {F}_{0}C= \{ h_{1}(\gamma _1^{2}) , h_{2}(\gamma _1^{2}) \}$
,
$\mathcal {F}_1C\setminus \mathcal {F}_{0}C= \{ h_{1}(\gamma _1^{2}) , h_{2}(\gamma _1^{2}) \}$
,
![]() $\mathcal {F}_2C\setminus \mathcal {F}_{1}C= \{ h_{1}(\gamma _1^{3}) , h_{2}(\gamma _1^{3}) \}$
and
$\mathcal {F}_2C\setminus \mathcal {F}_{1}C= \{ h_{1}(\gamma _1^{3}) , h_{2}(\gamma _1^{3}) \}$
and
![]() $\mathcal {F}_3C\setminus \mathcal {F}_{2}C= \{ h_{2}(\gamma _2^{4}) , h_{3}(\gamma _2^{4}) \}$
, the reductions under
$\mathcal {F}_3C\setminus \mathcal {F}_{2}C= \{ h_{2}(\gamma _2^{4}) , h_{3}(\gamma _2^{4}) \}$
, the reductions under
![]() $E_{22}^p$
and
$E_{22}^p$
and
![]() $E_{11}^p$
are performed as determined in Theorem 5.1. See Figure 34.
$E_{11}^p$
are performed as determined in Theorem 5.1. See Figure 34.

Figure 34 Differentials
![]() $E_{22}^p$
,
$E_{22}^p$
,
![]() $E_{11}^p$
and
$E_{11}^p$
and
![]() $E_{12}^p$
.
$E_{12}^p$
.
The differential
![]() $\Delta ^1(\gamma _1^2,\gamma _0^1)=E_{22}^p$
determines a reduction of the periodic orbits
$\Delta ^1(\gamma _1^2,\gamma _0^1)=E_{22}^p$
determines a reduction of the periodic orbits
![]() $\gamma _1^2$
and
$\gamma _1^2$
and
![]() $\gamma _0^1$
producing a new periodic orbit
$\gamma _0^1$
producing a new periodic orbit
![]() $\gamma _0^{\prime }$
. The differential
$\gamma _0^{\prime }$
. The differential
![]() $\Delta ^1(\gamma _2^4,\gamma _1^3)=E_{11}^p$
determines a reduction of the periodic orbits
$\Delta ^1(\gamma _2^4,\gamma _1^3)=E_{11}^p$
determines a reduction of the periodic orbits
![]() $\gamma _2^4$
and
$\gamma _2^4$
and
![]() $\gamma _1^3$
producing a new periodic orbit
$\gamma _1^3$
producing a new periodic orbit
![]() $\gamma _2^{\prime }$
. Note that the differential
$\gamma _2^{\prime }$
. Note that the differential
![]() $\Delta ^2(\gamma _1^3,\gamma _1^2)=E_{12}^p$
, which initially corresponded to a heteroclinic trajectory between the saddle periodic orbits
$\Delta ^2(\gamma _1^3,\gamma _1^2)=E_{12}^p$
, which initially corresponded to a heteroclinic trajectory between the saddle periodic orbits
![]() $\gamma _1^3$
and
$\gamma _1^3$
and
![]() $\gamma _1^2$
, does not determine a reduction and hence it plays a similar role to a persistent differential described in Theorem 5.8. The resulting flow is a core flow on
$\gamma _1^2$
, does not determine a reduction and hence it plays a similar role to a persistent differential described in Theorem 5.8. The resulting flow is a core flow on
![]() $S^3$
.
$S^3$
.
This example raises several questions for future investigation. What is the dynamical characterization of the differential of an NMS-chain complex associated to an NMS flow with several saddle-saddle connections? Under what conditions are we able to perform cancellations and redutions within an NMS flow with saddle-saddle connections corresponding to the differentials of an associated spectral sequence in order to obtain a core flow? Finally, results analogous to Theorems 5.1, 5.7 and 5.8 in the case of NMS flows with heteroclinic trajectories connecting saddle periodic orbits are still open problems.
The main difficulties reside in understanding the effect of the broken cylinder connections in the reduction and cancellation processes and the fact that Smale’s second cancellation theorem does not hold in dimension three.
Acknowledgements
We would like to acknowledge and thank U. Hryniewicz for the opportunity to exchange ideas regarding the depth of the contributions to the present work. D. V. S. Lima was supported by FAPESP under grants 2020/11326-8 and 2016/24707-4. K. A. de Rezende was partially supported by CNPq under grant 305649/2018-3 and by FAPESP under grants 2016/24707-4 and 2018/13481-0. M. R. da Silveira was partially supported by FAPESP under grants 2016/24707-4 and 2018/13481-0.