Lagrangian and augmented Lagrangian methods for nondifferentiableoptimization problems that arise from the total bounded variation formulation of image restoration problems are analyzed. Conditional convergence of theUzawa algorithm and unconditional convergence of the first order augmentedLagrangian schemes are discussed. A Newton type method based on an activeset strategy defined by means of the dual variables is developed andanalyzed. Numerical examples for blocky signals and images perturbedby very high noise are included.

In this paper we consider the numerical computation of the optimal costfunction associated to the problem that consists in finding the minimum ofthe maximum of a scalar functional on a trajectory. We present anapproximation method for the numerical solution which employs bothdiscretization on time and on spatial variables. In this way, we obtain afully discrete problem that has unique solution. We give an optimal estimatefor the error between the approximated solution and the optimal costfunction of the original problem. Also, numerical examples are presented.

We propose a two point subdivision scheme with parameters to draw curves that satisfy Hermite conditions at both ends of [a,b]. We build three functions f,p and s on dyadic numbers and, using infinite products of matrices, we prove that, under assumptions on the parameters, these functions can be extended by continuity on [a,b], with f'=p and f''=s .

We give results for the approximation of a laminate withvarying volume fractions for multi-well energy minimizationproblems modeling martensitic crystals thatcan undergo either an orthorhombicto monoclinic or a cubic to tetragonal transformation. We construct energy minimizing sequences of deformations which satisfythe corresponding boundary condition, and we establish a series of error bounds in terms of the elastic energyfor the approximation of the limiting macroscopicdeformation and the simply laminated microstructure.Finally, we give results for the corresponding finite element approximation of the laminate with varying volume fractions.

In this paper, a multi-parameter error resolutiontechnique is applied into a mixed finite element method for theStokes problem. By using this technique and establishing a multi-parameter asymptotic error expansion for the mixed finite element method, an approximation of higheraccuracy is obtained by multi-processor computers in parallel.

In this paper we present a novel exponentially fitted finite elementmethod with triangular elements for the decoupled continuity equations in the drift-diffusion model of semiconductor devices.The continuous problem is first formulated as a variational problem using a weighted inner product. A Bubnov-Galerkinfinite element method with a set of piecewise exponential basis functions is then proposed. The method is shown to be stable and can be regarded asan extension to two dimensions of the well-known Scharfetter-Gummel method.Error estimates for the approximate solution and its associated flux are given. These h-order error bounds depend on some first-order seminorms of the exact solution, the exact fluxand the coefficient function of the convection terms.A method is also proposed for the evaluation of terminal currentsand it is shown that the computed terminal currents are convergent andconservative.

The initial-boundary value problem of two-dimensionalincompressible fluid flow in stream function form is considered.A prediction-correction Legendre spectral scheme is proposed, which iseasy to be performed.The numerical solution possesses the accuracy of second-order in time and higher order in space. Thenumerical experiments show the high accuracy of this approach.

We prove existence (uniqueness is easy) of a weak solution to a boundary value problem for an equation like $(v-1)^+_t = v_{xx} + F(v)_x$ where the function $F: \Bbb R\rightarrow\Bbb R$ is onlysupposed to be locally lipschitz continuous. In order to replace the lack of compactness in t on v<1, we use nonlinear semigroup theory.

In this paper, we study some finite volume schemes for the nonlinear hyperbolic equation ${u_t}(x,t)+\mbox{div}F(x,t,u(x,t))=0$ 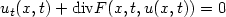with the initial condition $u_{0}\in{L^\infty}(\mathbb{R}^N)$ 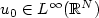. Passing to the limit in these schemes, we prove the existence of an entropy solution $u\in{L^infty}(\mathbb{R}^N\times\mathbb{R}_+)$ 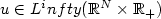. Proving also uniqueness, we obtain the convergence of the finite volume approximation to the entropy solution in $L^p_{loc}(\mathbb{R}^N\times\mathbb{R}_+)$ 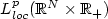, 1 ≤ p ≤ +∞. Furthermore, if ${u_0}\in {L^\infty}\cap\mbox{BV}_{loc}(\mathbb{R}^N)$ 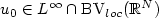, we show that $u\in\mbox{BV}_{loc}(\mathbb{R}^N\times\mathbb{R}_+)$ 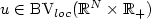, which leads to an “ $h^{\frac{1}{4}}$ 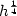” error estimate between the approximate and the entropy solutions (where h defines the size of the mesh).

This work deals with a system of nonlinear parabolic equations arisingin turbulence modelling. The unknowns are the N components of the velocityfield u coupled with two scalar quantities θ and φ. The systempresents nonlinear turbulent viscosity $A(\theta,\varphi)$ and nonlinearsource terms of the form $\theta^2|\nabla u|^2$ and $\theta\varphi|\nabla u|^2$ lying in L 1. Some existence results are shown in this paper, including $L^\infty$ -estimates and positivity for both θ and φ.

The Navier–Stokes equations are approximated by means ofa fractional step, Chorin–Temam projection method; the time derivativeis approximated by a three-level backward finite difference, whereasthe approximation in space is performed by a Galerkin technique.It is shown that the proposed scheme yields an errorof ${\cal O}(\delta t^2 + h^{l+1})$ for the velocity in the norm of l 2(L2(Ω)d), where l ≥ 1 isthe polynomial degree of the velocity approximation. It is also shownthat the splitting error of projection schemes based on theincremental pressure correction is of ${\cal O}(\delta t^2)$ independent of theapproximation order of the velocity time derivative.

This note deals with the approximation, by a P 1 finite element method with numerical integration,of solution curves of a semilinear problem. Because of both mixed boundary conditions and geometrical properties of the domain, some of the solutions do not belong to H 2. So, classical results for convergence lead to poor estimates. We show how to improve such estimates with the use of weighted Sobolev spaces together with a mesh“a priori adapted” to the singularity. For the H 1 or L 2-norms,we achieve optimal results.

We show that Boltzmann's collision operator can be written explicitlyin divergence and double divergence forms. These conservativeformulations may be of interest for both theoretical and numericalpurposes. We give an application to the asymptotics of grazing collisions.