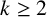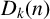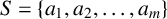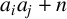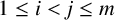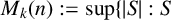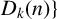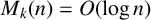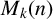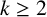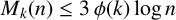1 Introduction
Given a nonzero integer n, we say a set of natural numbers
![]() $S=\{a_1,a_2,\ldots , a_m\}$
is a Diophantine m-tuple with property
$S=\{a_1,a_2,\ldots , a_m\}$
is a Diophantine m-tuple with property
![]() $D(n)$
if
$D(n)$
if
![]() $a_ia_j +n$
is a perfect square for
$a_ia_j +n$
is a perfect square for
![]() $1\leq i<j\leq m$
. Diophantus first studied such sets of numbers and found the quadruple
$1\leq i<j\leq m$
. Diophantus first studied such sets of numbers and found the quadruple
![]() $\{1,33,68,105\}$
with property
$\{1,33,68,105\}$
with property
![]() $D(256)$
. The first
$D(256)$
. The first
![]() $D(1)$
-quadruple
$D(1)$
-quadruple
![]() $\{1,3,8,120\}$
was discovered by Fermat, and this was later generalised by Euler who found an infinite family of quadruples with property
$\{1,3,8,120\}$
was discovered by Fermat, and this was later generalised by Euler who found an infinite family of quadruples with property
![]() $D(1)$
, namely,
$D(1)$
, namely,
where
![]() $ab + 1 = r^2$
. In fact, any
$ab + 1 = r^2$
. In fact, any
![]() $D(1)$
-triple can be extended to a Diophantine quadruple [Reference Arkin, Hoggatt and Straus1]. In 1969, using Baker’s theory of linear forms in the logarithms of algebraic numbers and a reduction method based on continued fractions, Baker and Davenport [Reference Baker and Davenport2] proved that Fermat’s example is the only extension of
$D(1)$
-triple can be extended to a Diophantine quadruple [Reference Arkin, Hoggatt and Straus1]. In 1969, using Baker’s theory of linear forms in the logarithms of algebraic numbers and a reduction method based on continued fractions, Baker and Davenport [Reference Baker and Davenport2] proved that Fermat’s example is the only extension of
![]() $\{1,3,8\}$
with property
$\{1,3,8\}$
with property
![]() $D(1)$
. In 2004, Dujella [Reference Dujella10], using similar methods, proved that there are no
$D(1)$
. In 2004, Dujella [Reference Dujella10], using similar methods, proved that there are no
![]() $D(1)$
-sextuples and there are only finitely many
$D(1)$
-sextuples and there are only finitely many
![]() $D(1)$
-quintuples, if any. The nonexistence of
$D(1)$
-quintuples, if any. The nonexistence of
![]() $D(1)$
-quintuples was finally settled in
$D(1)$
-quintuples was finally settled in
![]() $2019$
by He et al. in [Reference He, Togbé and Ziegler15].
$2019$
by He et al. in [Reference He, Togbé and Ziegler15].
In general, there are
![]() $D(n)$
-quintuples for
$D(n)$
-quintuples for
![]() $n\neq 1$
. For example,
$n\neq 1$
. For example,
are Diophantine quintuples satisfying property
![]() $D(256)$
. There are also examples of
$D(256)$
. There are also examples of
![]() $D(n)$
-sextuples, but no
$D(n)$
-sextuples, but no
![]() $D(n)$
-septuple is known. So, it is natural to study the size of the largest m-tuple with property
$D(n)$
-septuple is known. So, it is natural to study the size of the largest m-tuple with property
![]() $D(n)$
. Define
$D(n)$
. Define
In 2004, Dujella [Reference Dujella9] showed that
where C is an absolute constant. He also showed that for
![]() $n>10^{100}$
, one can choose
$n>10^{100}$
, one can choose
![]() $C=8.37$
. This constant was improved by Becker and Murty [Reference Becker and Murty3], who showed that for any n,
$C=8.37$
. This constant was improved by Becker and Murty [Reference Becker and Murty3], who showed that for any n,
 $$ \begin{align} M_n \leq 2.6071 \log |n| + \mathcal{O}\left(\frac{\log |n|}{(\log\log |n|)^2}\right). \end{align} $$
$$ \begin{align} M_n \leq 2.6071 \log |n| + \mathcal{O}\left(\frac{\log |n|}{(\log\log |n|)^2}\right). \end{align} $$
Our goal is to study this problem when squares are replaced by higher powers.
Definition 1.1 (Generalised Diophantine m-tuples)
Fix a natural number
![]() $k\geq 2$
. A set of natural numbers
$k\geq 2$
. A set of natural numbers
![]() $S=\{a_1,a_2,\ldots , a_m\}$
satisfies property
$S=\{a_1,a_2,\ldots , a_m\}$
satisfies property
![]() $D_k(n)$
if
$D_k(n)$
if
![]() $a_ia_j +n$
is a kth power for
$a_ia_j +n$
is a kth power for
![]() $1\leq i<j\leq m$
.
$1\leq i<j\leq m$
.
For each nonzero integer n, define
For
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $m\geq 3$
, we can apply the celebrated theorem of Faltings [Reference Faltings12] to deduce that a superelliptic curve of the form
$m\geq 3$
, we can apply the celebrated theorem of Faltings [Reference Faltings12] to deduce that a superelliptic curve of the form
has only finitely many rational points and a fortiori, finitely many integral points. Therefore, a set S satisfying property
![]() $D_k(n)$
must be finite. When
$D_k(n)$
must be finite. When
![]() $n=1$
, Bugeaud and Dujella [Reference Bugeaud and Dujella6] showed that
$n=1$
, Bugeaud and Dujella [Reference Bugeaud and Dujella6] showed that
In other words, the size of
![]() $D_k(1)$
-tuples is bounded by
$D_k(1)$
-tuples is bounded by
![]() $3$
for large enough k. In the general case, for any
$3$
for large enough k. In the general case, for any
![]() $n \neq 0$
and
$n \neq 0$
and
![]() $k \geq 3$
, Bérczes et al. [Reference Bérczes, Dujella, Hajdu and Luca5] obtained upper bounds for
$k \geq 3$
, Bérczes et al. [Reference Bérczes, Dujella, Hajdu and Luca5] obtained upper bounds for
![]() $M_k(n)$
. In particular, they showed that for
$M_k(n)$
. In particular, they showed that for
![]() $k\geq 5$
,
$k\geq 5$
,
Dixit et al. [Reference Dixit, Kim and Murty8] improved these bounds on
![]() $M_k(n)$
for large n and a fixed k. Define
$M_k(n)$
for large n and a fixed k. Define
Then, for
![]() $k\geq 3$
, as
$k\geq 3$
, as
![]() $n\to \infty $
,
$n\to \infty $
,
The purpose of this paper is to make the implied constants in (1.2) explicit. In [Reference Dixit, Kim and Murty8], the bounds for
![]() $M_k(n)$
were proved under the further assumption that
$M_k(n)$
were proved under the further assumption that
![]() $n>0$
. As remarked in [Reference Dixit, Kim and Murty8], this assumption is not necessary, but an argument was not provided. We begin by proving the bounds (1.2) for all nonzero integers n.
$n>0$
. As remarked in [Reference Dixit, Kim and Murty8], this assumption is not necessary, but an argument was not provided. We begin by proving the bounds (1.2) for all nonzero integers n.
Theorem 1.2. Let
![]() $k \geq 3$
be an integer. Then the following statements hold as
$k \geq 3$
be an integer. Then the following statements hold as
![]() $|n| \to \infty $
.
$|n| \to \infty $
.
-
(1) For
 $L \geq 3$
, where the implied constant depends on k and L, but is independent of n.
$L \geq 3$
, where the implied constant depends on k and L, but is independent of n. $$ \begin{align*}M_k(n, L) \ll 1,\end{align*} $$
$$ \begin{align*}M_k(n, L) \ll 1,\end{align*} $$
-
(2) Moreover,
where the implied constant depends on k. $$ \begin{align*}M_k(n) \ll \log |n|,\end{align*} $$
$$ \begin{align*}M_k(n) \ll \log |n|,\end{align*} $$
We next state our main theorem, which is an effective version of Theorem 1.2.
Theorem 1.3. Let
![]() $k \geq 3$
be a positive integer. Then the following statements hold.
$k \geq 3$
be a positive integer. Then the following statements hold.
-
(a) For
 $L \geq 3$
, (1.3)
$L \geq 3$
, (1.3) $$ \begin{align} M_k(n, L) \leq 2^{28} \log (2k) \log (2 \log (2k)) + 14. \end{align} $$
$$ \begin{align} M_k(n, L) \leq 2^{28} \log (2k) \log (2 \log (2k)) + 14. \end{align} $$
-
(b) Suppose n and k vary such that as
 $|n|\to \infty $
and
$|n|\to \infty $
and
 $k = o(\log \log |n|)$
, then where
$k = o(\log \log |n|)$
, then where $$ \begin{align*} M_k(n) \leq 3 \, \phi(k)\, \log |n| + \mathcal{O} \bigg(\frac{ (\phi(k))^2\log |n|}{\log \log |n|}\bigg), \end{align*} $$
$$ \begin{align*} M_k(n) \leq 3 \, \phi(k)\, \log |n| + \mathcal{O} \bigg(\frac{ (\phi(k))^2\log |n|}{\log \log |n|}\bigg), \end{align*} $$
 $\phi (n)$
denotes the Euler totient function.
$\phi (n)$
denotes the Euler totient function.
Remark 1.4. (a) It is possible to replace
![]() $14$
on the right-hand side of (1.3) with a smaller positive integer for large values of k.
$14$
on the right-hand side of (1.3) with a smaller positive integer for large values of k.
(b) For a fixed
![]() $k>2$
, Theorem 1.3(b) gives
$k>2$
, Theorem 1.3(b) gives
 $$ \begin{align*} M_k(n) \leq 3 \, \phi(k) \, \log |n| + \mathcal{O}\bigg(\frac{\log |n|}{\log\log |n|}\bigg) \quad \mbox{as } |n|\to \infty. \end{align*} $$
$$ \begin{align*} M_k(n) \leq 3 \, \phi(k) \, \log |n| + \mathcal{O}\bigg(\frac{\log |n|}{\log\log |n|}\bigg) \quad \mbox{as } |n|\to \infty. \end{align*} $$
For
![]() $k=2$
, this upper bound is very close to the best known upper bound due to Becker and Murty which is given by (1.1).
$k=2$
, this upper bound is very close to the best known upper bound due to Becker and Murty which is given by (1.1).
(c) Theorem 1.3 holds in a slightly more general setting for Diophantine tuples with property
![]() $D_k(n)$
in the ring of integers of the kth cyclotomic field
$D_k(n)$
in the ring of integers of the kth cyclotomic field
![]() $\mathbb {Q}(\zeta _k)$
. In that case, we replace the Legendre symbol by the power residue symbol and follow the same method as in the proof of Theorem 1.3.
$\mathbb {Q}(\zeta _k)$
. In that case, we replace the Legendre symbol by the power residue symbol and follow the same method as in the proof of Theorem 1.3.
2 Preliminaries
In this section, we develop the necessary tools to prove our main theorems.
2.1 Gallagher’s larger sieve
In 1971, Gallagher [Reference Gallagher13] discovered an elementary sieve inequality which he called the larger sieve. We refer the reader to [Reference Cojocaru and Murty7] for the general discussion and record the result in a form applicable to our context.
Theorem 2.1. Let N be a natural number and
![]() $\mathcal {S}$
a subset of
$\mathcal {S}$
a subset of
![]() $\{1,2,\ldots , N\}$
. Let
$\{1,2,\ldots , N\}$
. Let
![]() ${\mathcal P}$
be a set of primes. For each prime
${\mathcal P}$
be a set of primes. For each prime
![]() $p \in {\mathcal P}$
, let
$p \in {\mathcal P}$
, let
![]() $\mathcal {S}_p=\mathcal {S} \pmod {p}$
. For
$\mathcal {S}_p=\mathcal {S} \pmod {p}$
. For
![]() $1<Q\leq N$
,
$1<Q\leq N$
,
 $$ \begin{align*} |\mathcal{S}|\leq \frac{\sum_{p\leq Q, p\in {\mathcal P}} \log p - \log N}{\sum_{p\leq Q, p \in {\mathcal P}} \dfrac{\log p}{|\mathcal{S}_p|}-\log N}, \end{align*} $$
$$ \begin{align*} |\mathcal{S}|\leq \frac{\sum_{p\leq Q, p\in {\mathcal P}} \log p - \log N}{\sum_{p\leq Q, p \in {\mathcal P}} \dfrac{\log p}{|\mathcal{S}_p|}-\log N}, \end{align*} $$
where the summations are over primes
![]() $p\leq Q, p \in {\mathcal P}$
, and the inequality holds provided the denominator is positive.
$p\leq Q, p \in {\mathcal P}$
, and the inequality holds provided the denominator is positive.
2.2 A quantitative Roth’s theorem
There are several quantitative results counting exceptions in Roth’s celebrated theorem on Diophantine approximations. We will use the following result due to Evertse [Reference Evertse11]. For an algebraic number
![]() $\xi $
of degree r, we define the (absolute) height by
$\xi $
of degree r, we define the (absolute) height by
 $$ \begin{align*}H(\xi):= \bigg( a\prod_{i=1}^r \max(1, |\xi^{(i)}|)\bigg)^{1/r}, \end{align*} $$
$$ \begin{align*}H(\xi):= \bigg( a\prod_{i=1}^r \max(1, |\xi^{(i)}|)\bigg)^{1/r}, \end{align*} $$
where
![]() $\xi ^{(i)}$
for
$\xi ^{(i)}$
for
![]() $1\leq i\leq r$
are the conjugates of
$1\leq i\leq r$
are the conjugates of
![]() $\xi $
(over
$\xi $
(over
![]() $\mathbb {Q}$
) and a is the positive integer such that
$\mathbb {Q}$
) and a is the positive integer such that
 $$ \begin{align*}a\prod_{i=1}^r (x-\xi^{(i)}) \end{align*} $$
$$ \begin{align*}a\prod_{i=1}^r (x-\xi^{(i)}) \end{align*} $$
has rational integer coefficients with greatest common divisor equal to 1.
Theorem 2.2. Let
![]() $\alpha $
be a real algebraic number of degree r over
$\alpha $
be a real algebraic number of degree r over
![]() $\mathbb {Q}$
and
$\mathbb {Q}$
and
![]() $0 <\kappa \leq 1$
. The number of rational numbers
$0 <\kappa \leq 1$
. The number of rational numbers
![]() $p/q$
satisfying
$p/q$
satisfying
![]() $\max (|p|,|q|) \geq \max (H(\alpha ), 2)$
and
$\max (|p|,|q|) \geq \max (H(\alpha ), 2)$
and
 $$ \begin{align*} \bigg|\alpha - \frac{p}{q} \bigg| \leq \frac{1}{\max (|p|,|q|)^{2+\kappa}} \end{align*} $$
$$ \begin{align*} \bigg|\alpha - \frac{p}{q} \bigg| \leq \frac{1}{\max (|p|,|q|)^{2+\kappa}} \end{align*} $$
is at most
2.3 Vinogradov’s theorem
The following bound on character sums was proved by Vinogradov (see [Reference Vinogradov16]).
Lemma 2.3. Let
![]() $\chi \pmod q$
be a nontrivial Dirichlet character and n an integer such that
$\chi \pmod q$
be a nontrivial Dirichlet character and n an integer such that
![]() $(n,q)=1$
. If
$(n,q)=1$
. If
![]() $\mathcal {A} \subseteq (\mathbb {Z}/q\mathbb {Z})^*$
and
$\mathcal {A} \subseteq (\mathbb {Z}/q\mathbb {Z})^*$
and
![]() $\mathcal {B} \subseteq (\mathbb {Z}/q\mathbb {Z})^* \cup \{0\}$
, then
$\mathcal {B} \subseteq (\mathbb {Z}/q\mathbb {Z})^* \cup \{0\}$
, then
The original method of Vinogradov gives the bound on the right-hand side of the inequality as
![]() $ \sqrt {2q |\mathcal {A}| |\mathcal {B}|}$
. However, the above bound holds and a short proof can be found in [Reference Becker and Murty3, Proposition 2.5].
$ \sqrt {2q |\mathcal {A}| |\mathcal {B}|}$
. However, the above bound holds and a short proof can be found in [Reference Becker and Murty3, Proposition 2.5].
2.4 Bounds for primes in arithmetic progression
Let
![]() $Q,k,a$
be positive integers with
$Q,k,a$
be positive integers with
![]() $(a,k)=1$
. Denote by
$(a,k)=1$
. Denote by
![]() $\theta (Q;k,a)$
the sum of the logarithms of the primes
$\theta (Q;k,a)$
the sum of the logarithms of the primes
![]() ${p \equiv a \pmod k}$
with
${p \equiv a \pmod k}$
with
![]() $p \leq Q$
, that is,
$p \leq Q$
, that is,
 $$ \begin{align*} \theta(Q;k,a) := \sum_{\substack{p \equiv a \bmod k \\ p \text{ prime} \leq Q}} \log p. \end{align*} $$
$$ \begin{align*} \theta(Q;k,a) := \sum_{\substack{p \equiv a \bmod k \\ p \text{ prime} \leq Q}} \log p. \end{align*} $$
The following bound on
![]() $\theta (Q;k,a)$
was obtained by Bennet et al. in [Reference Bennett, Martin, O’Bryant and Rechnitzer4, Theorem 1.2].
$\theta (Q;k,a)$
was obtained by Bennet et al. in [Reference Bennett, Martin, O’Bryant and Rechnitzer4, Theorem 1.2].
Theorem 2.4. For
![]() $k \geq 3$
and
$k \geq 3$
and
![]() $(a, k) = 1$
,
$(a, k) = 1$
,
 $$ \begin{align*} \bigg |\theta (Q; k, a) - \frac{Q}{\phi(k)} \bigg| < \frac{1}{160} \frac{Q}{\log Q} \end{align*} $$
$$ \begin{align*} \bigg |\theta (Q; k, a) - \frac{Q}{\phi(k)} \bigg| < \frac{1}{160} \frac{Q}{\log Q} \end{align*} $$
for all
![]() $Q \geq Q_0 (k)$
, where
$Q \geq Q_0 (k)$
, where
 $$ \begin{align*} Q_0(k) = \begin{cases} 8 \cdot 10^9 & \text{if } 3 \leq k \leq 10^5, \\ \exp(0.03\sqrt{k}\log^3 k) & \text{if }k> 10^5. \end{cases} \end{align*} $$
$$ \begin{align*} Q_0(k) = \begin{cases} 8 \cdot 10^9 & \text{if } 3 \leq k \leq 10^5, \\ \exp(0.03\sqrt{k}\log^3 k) & \text{if }k> 10^5. \end{cases} \end{align*} $$
2.5 Gap principle
The next two lemmas are variations of a gap principle of Gyarmati [Reference Gyarmati14].
Lemma 2.5 [Reference Dixit, Kim and Murty8, Lemma 2.4]
Let
![]() $k\geq 2$
. Suppose that
$k\geq 2$
. Suppose that
![]() $a,b,c,d$
are positive integers such that
$a,b,c,d$
are positive integers such that
![]() $a<b$
and
$a<b$
and
![]() $c<d$
. Suppose further that
$c<d$
. Suppose further that
are perfect kth powers. Then,
An immediate corollary of this lemma shows that ‘large’ elements of any set with property
![]() $D_k(n)$
have ‘super-exponential growth’.
$D_k(n)$
have ‘super-exponential growth’.
Corollary 2.6 [Reference Dixit, Kim and Murty8, Corollary 2]
Let
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $m\geq 5$
. Suppose that
$m\geq 5$
. Suppose that
![]() $n^3 \leq a_1 < a_2 < \cdots < a_m$
and the set
$n^3 \leq a_1 < a_2 < \cdots < a_m$
and the set
![]() $\{ a_1, a_2,\ldots , a_m\}$
has property
$\{ a_1, a_2,\ldots , a_m\}$
has property
![]() $D_k(n)$
. Then
$D_k(n)$
. Then
![]() $a_{2+3j} \geq a_2^{(k-1)^{j}}$
provided
$a_{2+3j} \geq a_2^{(k-1)^{j}}$
provided
![]() $1\leq j \leq (m-2)/3$
.
$1\leq j \leq (m-2)/3$
.
A modification of the proof of Lemma 2.5 yields a gap principle for negative values of n.
Lemma 2.7. For
![]() $n> 0$
and natural numbers
$n> 0$
and natural numbers
![]() $a,b,c,d$
such that
$a,b,c,d$
such that
![]() $n^3 \leq a < b < c < d$
,
$n^3 \leq a < b < c < d$
,
Proof. Since
![]() $(ac-n)(bd-n) = abcd-n(ac+bd)+n^2$
, it is enough to prove that
$(ac-n)(bd-n) = abcd-n(ac+bd)+n^2$
, it is enough to prove that
Also, since
![]() $a \geq n^3$
and
$a \geq n^3$
and
![]() $c> n^3$
, for all cases other than
$c> n^3$
, for all cases other than
![]() $n=1, a=1, b=2, c=3$
,
$n=1, a=1, b=2, c=3$
,
 $$ \begin{align*} abcd &\geq 4n bd\\ &\geq 2nbd +2nac\\ &\geq 2nbd+2nac-2n^2, \end{align*} $$
$$ \begin{align*} abcd &\geq 4n bd\\ &\geq 2nbd +2nac\\ &\geq 2nbd+2nac-2n^2, \end{align*} $$
where the first inequality is obvious as
![]() $a \geq n^3$
and
$a \geq n^3$
and
![]() $c \geq n^3+2$
. This gives the desired result. For the case
$c \geq n^3+2$
. This gives the desired result. For the case
![]() $n=1, a=1, b=2, c=3$
, since
$n=1, a=1, b=2, c=3$
, since
![]() $d> c$
, clearly
$d> c$
, clearly
We are now ready to prove the following analogue of Lemma 2.5.
Lemma 2.8. Let
![]() $n> 0$
and
$n> 0$
and
![]() $k \geq 2$
. Suppose that
$k \geq 2$
. Suppose that
![]() $a,b,c,d$
are positive integers such that
$a,b,c,d$
are positive integers such that
![]() $n^3 \leq a < b < c < d$
. Suppose further that
$n^3 \leq a < b < c < d$
. Suppose further that
![]() $ac - n, bc-n, ad-n, bd-n$
are perfect kth powers. Then,
$ac - n, bc-n, ad-n, bd-n$
are perfect kth powers. Then,
Proof. Since
![]() $(b-a)(d-c)>0$
, we have
$(b-a)(d-c)>0$
, we have
![]() $bd + ac> ad + bc$
and it is easily seen that
$bd + ac> ad + bc$
and it is easily seen that
As
![]() $(ac-n)(bd-n)$
and
$(ac-n)(bd-n)$
and
![]() $(ad-n)(bc-n)$
are both perfect kth powers,
$(ad-n)(bc-n)$
are both perfect kth powers,
 $$ \begin{align*} (ad-n)(bc-n) &\geq [((ac-n)(bd-n))^{1/k} + 1]^k\\ &\geq (ac-n)(bd-n) + k((ac-n)(bd-n))^{k-1/k}\\ &\geq (ac-n)(bd-n) + k\bigg(\frac{abcd}{2}\bigg)^{k-1/k}, \end{align*} $$
$$ \begin{align*} (ad-n)(bc-n) &\geq [((ac-n)(bd-n))^{1/k} + 1]^k\\ &\geq (ac-n)(bd-n) + k((ac-n)(bd-n))^{k-1/k}\\ &\geq (ac-n)(bd-n) + k\bigg(\frac{abcd}{2}\bigg)^{k-1/k}, \end{align*} $$
where the last inequality follows from Lemma 2.7. Thus,
Since
![]() $bd> ad + bc - ac > 0$
, we have
$bd> ad + bc - ac > 0$
, we have
![]() $bd+ac-ad-bc < bd$
and hence,
$bd+ac-ad-bc < bd$
and hence,
Therefore,
which proves the lemma.
This enables us to prove super-exponential growth for large elements of a set with
![]() $D_k(n)$
, when
$D_k(n)$
, when
![]() $n<0$
.
$n<0$
.
Corollary 2.9. Let
![]() $k \geq 3$
. If
$k \geq 3$
. If
![]() $n^3 \leq a < b < c < d < e$
are natural numbers such that the set
$n^3 \leq a < b < c < d < e$
are natural numbers such that the set
![]() $\{a,b,c,d,e\}$
has property
$\{a,b,c,d,e\}$
has property
![]() $D_k(-n)$
, then
$D_k(-n)$
, then
![]() $e \geq b^{k-1}$
.
$e \geq b^{k-1}$
.
Proof. From Lemma 2.8,
Therefore,
Using induction on the previous corollary, we deduce the following corollary.
Corollary 2.10. Let
![]() $k \geq 3$
and
$k \geq 3$
and
![]() $m \geq 5$
. Suppose that
$m \geq 5$
. Suppose that
![]() $n^3 \leq a_1 < a_2 < \cdots < a_m$
and the set
$n^3 \leq a_1 < a_2 < \cdots < a_m$
and the set
![]() $\{a_1, a_2, \ldots , a_m\}$
has property
$\{a_1, a_2, \ldots , a_m\}$
has property
![]() $D_k(-n)$
. Then we have
$D_k(-n)$
. Then we have
![]() $a_{2+3j} \geq a_2^{(k-1)^j}$
provided
$a_{2+3j} \geq a_2^{(k-1)^j}$
provided
![]() $1 \leq j \leq (m-2)/3$
.
$1 \leq j \leq (m-2)/3$
.
3 Proof of the main theorems
3.1 Proof of Theorem 1.2
We first prove Theorem 1.2. The proof follows a similar method to [Reference Dixit, Kim and Murty8].
Let n be a positive integer,
![]() $m = M_k (-n)$
and
$m = M_k (-n)$
and
![]() $S = \{a_1, a_2, a_3, \ldots , a_m\}$
be a generalised m-tuple with the property
$S = \{a_1, a_2, a_3, \ldots , a_m\}$
be a generalised m-tuple with the property
![]() $D_k(-n)$
. Suppose
$D_k(-n)$
. Suppose
![]() $n^L < a_1 < a_2 < \cdots < a_m$
for some
$n^L < a_1 < a_2 < \cdots < a_m$
for some
![]() $L \geq 3$
. Consider the system of equations
$L \geq 3$
. Consider the system of equations
 $$ \begin{align} \begin{split} a_1 x -n = u^k, \\ a_2 x -n = v^k. \end{split} \end{align} $$
$$ \begin{align} \begin{split} a_1 x -n = u^k, \\ a_2 x -n = v^k. \end{split} \end{align} $$
Clearly,
![]() $x=a_i$
for
$x=a_i$
for
![]() $i \geq 3$
are solutions to this system. Also,
$i \geq 3$
are solutions to this system. Also,
Let
![]() $\alpha := (a_1/a_2)^{1/k}$
and
$\alpha := (a_1/a_2)^{1/k}$
and ![]() . Then, we have the following two lemmas analogous to those proved in [Reference Dixit, Kim and Murty8]. The proof of the first lemma is identical to the proof of [Reference Dixit, Kim and Murty8, Lemma 3.1].
. Then, we have the following two lemmas analogous to those proved in [Reference Dixit, Kim and Murty8]. The proof of the first lemma is identical to the proof of [Reference Dixit, Kim and Murty8, Lemma 3.1].
Lemma 3.1. Let
![]() $k \geq 3$
be odd. Suppose
$k \geq 3$
be odd. Suppose
![]() $u, v$
satisfy the system of equations (3.1). Let
$u, v$
satisfy the system of equations (3.1). Let

Then, for
![]() $n> 2^{1/(L-1)}c(k)^{-1/(L-1)}$
,
$n> 2^{1/(L-1)}c(k)^{-1/(L-1)}$
,
Lemma 3.2. Let
![]() $(u_i, v_i)$
denote distinct pairs that satisfy the system of equations (3.1) with
$(u_i, v_i)$
denote distinct pairs that satisfy the system of equations (3.1) with
![]() $v_{i+1}> v_i$
. For
$v_{i+1}> v_i$
. For
![]() $n> 2^{1/(L-1)}c(k)^{-1/(L-1)}$
and
$n> 2^{1/(L-1)}c(k)^{-1/(L-1)}$
and
![]() $i\geq 14$
,
$i\geq 14$
,
 $$ \begin{align*} \bigg|\frac{u}{v} - \alpha\bigg| < \frac{1}{v_i^{k-1/2}} \quad \mbox{and} \quad v_i> a_2^4. \end{align*} $$
$$ \begin{align*} \bigg|\frac{u}{v} - \alpha\bigg| < \frac{1}{v_i^{k-1/2}} \quad \mbox{and} \quad v_i> a_2^4. \end{align*} $$
Proof. From Lemma 3.1,
![]() $|{u_i}/{v_i} - \alpha | < {a_2}/{2v_i^k}$
. Thus, we need to show
$|{u_i}/{v_i} - \alpha | < {a_2}/{2v_i^k}$
. Thus, we need to show
![]() $a_2 < 2v_i^{1/2}$
for
$a_2 < 2v_i^{1/2}$
for
![]() $i> 14$
. Since
$i> 14$
. Since
![]() $v_i^k = a_2 a_i - n$
, we have
$v_i^k = a_2 a_i - n$
, we have
![]() $v_i \geq a_i^{1/k}$
. By Corollary 2.10,
$v_i \geq a_i^{1/k}$
. By Corollary 2.10,
![]() $a_{2+3j} \geq a_2^{(k-1)^j}$
, so that
$a_{2+3j} \geq a_2^{(k-1)^j}$
, so that
![]() $v_{2+3j} \geq a_2^{(k-1)^j/k}$
. We choose a positive integer
$v_{2+3j} \geq a_2^{(k-1)^j/k}$
. We choose a positive integer
![]() $j_0$
such that
$j_0$
such that
![]() $(k-1)^{j_0}> 4k$
. Since
$(k-1)^{j_0}> 4k$
. Since
![]() $k \geq 3$
, we can take
$k \geq 3$
, we can take
![]() $j_0=4$
. As
$j_0=4$
. As
![]() $2+3j_0 = 14$
, we have
$2+3j_0 = 14$
, we have
![]() $v_i \geq v_{14}> a_2^4$
for all
$v_i \geq v_{14}> a_2^4$
for all
![]() $i \geq 14$
. This completes the proof.
$i \geq 14$
. This completes the proof.
For larger values of k, the number
![]() $14$
in the above lemma can be improved to
$14$
in the above lemma can be improved to
![]() $2 + 3 j_0$
, where
$2 + 3 j_0$
, where
![]() $j_0$
satisfies the condition
$j_0$
satisfies the condition
![]() $(k-1)^{j_0}> 4k$
.
$(k-1)^{j_0}> 4k$
.
Proof of Theorem 1.2
Now, assume that
![]() $(u_1,v_1), (u_2, v_2), \ldots , (u_m,v_m)$
satisfy the system of equations (3.1) with
$(u_1,v_1), (u_2, v_2), \ldots , (u_m,v_m)$
satisfy the system of equations (3.1) with
By Lemma 3.2, for
![]() $14 \leq i \leq m$
,
$14 \leq i \leq m$
,
 $$ \begin{align*} \bigg|\frac{u}{v} - \alpha\bigg| < \frac{1}{v_i^{k-1/2}} \leq \frac{1}{v_i^{2.5}}, \end{align*} $$
$$ \begin{align*} \bigg|\frac{u}{v} - \alpha\bigg| < \frac{1}{v_i^{k-1/2}} \leq \frac{1}{v_i^{2.5}}, \end{align*} $$
as
![]() $k \geq 3$
. Since
$k \geq 3$
. Since
![]() $\alpha =(a_1/a_2)^{1/k} < 1$
and
$\alpha =(a_1/a_2)^{1/k} < 1$
and
![]() $\max (u_i, v_i) = v_i$
, from Theorem 2.2, the number of such
$\max (u_i, v_i) = v_i$
, from Theorem 2.2, the number of such
![]() $v_i$
is
$v_i$
is
![]() $\mathcal {O} (\log k \,\log \log k)$
. This proves Theorem 1.2.
$\mathcal {O} (\log k \,\log \log k)$
. This proves Theorem 1.2.
3.2 Proof of Theorem 1.3
Let
![]() $m = M_k (n)$
and
$m = M_k (n)$
and
![]() $S = \{a_1, a_2, a_3, \ldots , a_m\}$
be a generalised m-tuple with the property
$S = \{a_1, a_2, a_3, \ldots , a_m\}$
be a generalised m-tuple with the property
![]() $D_k(n)$
. Suppose
$D_k(n)$
. Suppose
![]() $|n|^L < a_1 < a_2 < \cdots < a_m$
for some
$|n|^L < a_1 < a_2 < \cdots < a_m$
for some
![]() $L \geq 3$
. We consider the system of equations
$L \geq 3$
. We consider the system of equations
 $$ \begin{align} \begin{split} a_1 x +n = u^k, \\ a_2 x +n = v^k. \end{split} \end{align} $$
$$ \begin{align} \begin{split} a_1 x +n = u^k, \\ a_2 x +n = v^k. \end{split} \end{align} $$
As before,
![]() $x=a_i$
for
$x=a_i$
for
![]() $i \geq 3$
are solutions to this system. The statements of Lemmas 3.1 and 3.2 hold for all nonzero integers n. For
$i \geq 3$
are solutions to this system. The statements of Lemmas 3.1 and 3.2 hold for all nonzero integers n. For
![]() $n>0$
, this was proved in [Reference Dixit, Kim and Murty8].
$n>0$
, this was proved in [Reference Dixit, Kim and Murty8].
Proof of Theorem 1.3(a)
Let
![]() $(u_1,v_1), \ldots , (u_m,v_m)$
satisfy the system of equations (3.2) with
$(u_1,v_1), \ldots , (u_m,v_m)$
satisfy the system of equations (3.2) with
![]() $v_i> \max (a_2^{1/k}, 2) \geq \max (H(\alpha ), 2)$
. By Lemma 3.2, for
$v_i> \max (a_2^{1/k}, 2) \geq \max (H(\alpha ), 2)$
. By Lemma 3.2, for
![]() $14 \leq i \leq m$
,
$14 \leq i \leq m$
,
 $$ \begin{align*} \bigg |\frac{u_i}{v_i} - \alpha \bigg| \leq \frac{1}{v_i^{k-1/2}} \leq \frac{1}{v_i^{2.5}}, \end{align*} $$
$$ \begin{align*} \bigg |\frac{u_i}{v_i} - \alpha \bigg| \leq \frac{1}{v_i^{k-1/2}} \leq \frac{1}{v_i^{2.5}}, \end{align*} $$
as
![]() $k \geq 3$
. Since
$k \geq 3$
. Since
![]() $\alpha = (a_1/a_2)^{1/k} < 1$
and
$\alpha = (a_1/a_2)^{1/k} < 1$
and
![]() $\max (u_i, v_i) = v_i$
, applying Theorem 2.2 with
$\max (u_i, v_i) = v_i$
, applying Theorem 2.2 with
![]() $\kappa = 0.5$
shows that the number of
$\kappa = 0.5$
shows that the number of
![]() $v_i$
satisfying the above inequality is
$v_i$
satisfying the above inequality is
So, for
![]() $k \geq 3$
, the total number of solutions is at most
$k \geq 3$
, the total number of solutions is at most
Proof of Theorem 1.3(b)
Let
![]() $S = \{a_1, a_2, \ldots , a_m\}$
be a generalised Diophantine m-tuple with property
$S = \{a_1, a_2, \ldots , a_m\}$
be a generalised Diophantine m-tuple with property
![]() $D_k(n)$
such that each
$D_k(n)$
such that each
![]() $a_i \leq |n|^3$
. Since
$a_i \leq |n|^3$
. Since
![]() $M_k (n;3)$
has a finite bound depending on k, it is enough to prove the statement for
$M_k (n;3)$
has a finite bound depending on k, it is enough to prove the statement for
![]() $|S|$
. We shall apply Gallagher’s larger sieve with primes
$|S|$
. We shall apply Gallagher’s larger sieve with primes
![]() $p \leq Q$
satisfying
$p \leq Q$
satisfying
![]() $p \equiv 1 \pmod k$
. Let
$p \equiv 1 \pmod k$
. Let
![]() $\mathcal {P}$
be the set of all primes
$\mathcal {P}$
be the set of all primes
![]() $p \equiv 1\pmod k$
. For all such primes
$p \equiv 1\pmod k$
. For all such primes
![]() $p \in \mathcal {P}$
, there exists a Dirichlet character
$p \in \mathcal {P}$
, there exists a Dirichlet character
![]() $\chi \, (\mathrm {mod\, } p)$
of order k.
$\chi \, (\mathrm {mod\, } p)$
of order k.
Denote by
![]() $S_p$
the image of
$S_p$
the image of
![]() $S \pmod p$
for a given prime p. For
$S \pmod p$
for a given prime p. For
![]() $p\in \mathcal {P}$
, applying Lemma 2.3 with
$p\in \mathcal {P}$
, applying Lemma 2.3 with
![]() $\mathcal {A} = \mathcal {B} = S_p$
and
$\mathcal {A} = \mathcal {B} = S_p$
and
![]() $\chi \, (\mathrm {mod\, } p)$
a character of order k,
$\chi \, (\mathrm {mod\, } p)$
a character of order k,
 $$ \begin{align*} |S_p|(|S_p| - 1) \leq \sum_{a \in S_p-\{0\}} \sum_{b \in S_p} \chi(ab+n) + |S_p| \leq \sqrt{p} |S_p| + |S_p|. \end{align*} $$
$$ \begin{align*} |S_p|(|S_p| - 1) \leq \sum_{a \in S_p-\{0\}} \sum_{b \in S_p} \chi(ab+n) + |S_p| \leq \sqrt{p} |S_p| + |S_p|. \end{align*} $$
Thus,
Take
![]() $N = |n|^3$
. Since
$N = |n|^3$
. Since
![]() $a_i \leq |n|^3$
, applying Theorem 2.1 yields
$a_i \leq |n|^3$
, applying Theorem 2.1 yields
 $$ \begin{align*} |S| \leq \frac{\sum_{p\in \mathcal{P}, p \leq Q } \log p- \log N}{\sum_{p\in \mathcal{P}, p \leq Q } \dfrac{\log p}{|S_p|}-\log N}. \end{align*} $$
$$ \begin{align*} |S| \leq \frac{\sum_{p\in \mathcal{P}, p \leq Q } \log p- \log N}{\sum_{p\in \mathcal{P}, p \leq Q } \dfrac{\log p}{|S_p|}-\log N}. \end{align*} $$
By Theorem 2.4,
 $$ \begin{align*} \sum_{\substack{p \leq Q \\ p \equiv 1 \mathrm{mod\, } k}} \log p = \frac{Q}{\phi(k)} + \mathcal{O} \bigg(\frac{Q}{\log Q}\bigg), \end{align*} $$
$$ \begin{align*} \sum_{\substack{p \leq Q \\ p \equiv 1 \mathrm{mod\, } k}} \log p = \frac{Q}{\phi(k)} + \mathcal{O} \bigg(\frac{Q}{\log Q}\bigg), \end{align*} $$
when
![]() $Q> Q_0(k)$
. As in Section 2.4,
$Q> Q_0(k)$
. As in Section 2.4,
![]() $\theta (Q;k,1) = \sum _{p \leq Q, p \equiv 1 \mathrm {mod\, } k} \log p$
. We take
$\theta (Q;k,1) = \sum _{p \leq Q, p \equiv 1 \mathrm {mod\, } k} \log p$
. We take
![]() $f(t) = {1}/{(\sqrt t+2)}$
. By partial summation,
$f(t) = {1}/{(\sqrt t+2)}$
. By partial summation,
 $$ \begin{align} \sum_{\substack{p \leq Q \\ p \equiv 1 \mathrm{mod\, } k}} f(p) \log p = \theta (Q;k,1) f(Q) - \int_{2}^{Q} \theta (t;k,1) f'(t) \,dt. \end{align} $$
$$ \begin{align} \sum_{\substack{p \leq Q \\ p \equiv 1 \mathrm{mod\, } k}} f(p) \log p = \theta (Q;k,1) f(Q) - \int_{2}^{Q} \theta (t;k,1) f'(t) \,dt. \end{align} $$
The right-hand side is equal to
 $$ \begin{align*}\frac{Q}{\phi(k) (\sqrt{Q}+2)} + \mathcal{O}\bigg(\frac{\sqrt{Q}}{\log Q}\bigg) + \frac{1}{\phi(k)} \bigg(\int_{2}^{Q} \frac{t}{2(\sqrt{t}+2)^2 \sqrt{t}} \,dt\bigg) + \mathcal{O} \bigg(\int_{2}^{Q} \frac{1}{\sqrt{t} \log t} \,dt\bigg).\end{align*} $$
$$ \begin{align*}\frac{Q}{\phi(k) (\sqrt{Q}+2)} + \mathcal{O}\bigg(\frac{\sqrt{Q}}{\log Q}\bigg) + \frac{1}{\phi(k)} \bigg(\int_{2}^{Q} \frac{t}{2(\sqrt{t}+2)^2 \sqrt{t}} \,dt\bigg) + \mathcal{O} \bigg(\int_{2}^{Q} \frac{1}{\sqrt{t} \log t} \,dt\bigg).\end{align*} $$
The three terms above can be estimated as
 $$ \begin{align*} \frac{Q}{\phi(k) (\sqrt{Q}+2)} &= \frac{\sqrt{Q}}{\phi(k)} + \mathcal{O}(1),\\ \frac{1}{\phi(k)} \bigg(\int_{2}^{Q} \frac{t}{2(\sqrt{t}+2)^2 \sqrt{t}} \,dt\bigg) &= \frac{\sqrt{Q}}{\phi(k)} + \mathcal{O}(\log Q),\\ \mathcal{O} \bigg(\int_{2}^{Q} \frac{1}{\sqrt{t} \log t} \,dt\bigg) &= \mathcal{O}\bigg(\frac{\sqrt{Q}}{\log Q}\bigg). \end{align*} $$
$$ \begin{align*} \frac{Q}{\phi(k) (\sqrt{Q}+2)} &= \frac{\sqrt{Q}}{\phi(k)} + \mathcal{O}(1),\\ \frac{1}{\phi(k)} \bigg(\int_{2}^{Q} \frac{t}{2(\sqrt{t}+2)^2 \sqrt{t}} \,dt\bigg) &= \frac{\sqrt{Q}}{\phi(k)} + \mathcal{O}(\log Q),\\ \mathcal{O} \bigg(\int_{2}^{Q} \frac{1}{\sqrt{t} \log t} \,dt\bigg) &= \mathcal{O}\bigg(\frac{\sqrt{Q}}{\log Q}\bigg). \end{align*} $$
Putting this together in (3.3) yields
 $$ \begin{align*} \sum_{\substack{p \leq Q \\ p \equiv 1 \mathrm{mod\, } k}} \frac{\log p}{\sqrt{p}+2} = \frac{2 \sqrt{Q}}{\phi(k)} + \mathcal{O} \bigg(\frac{\sqrt{Q}}{\log Q}\bigg). \end{align*} $$
$$ \begin{align*} \sum_{\substack{p \leq Q \\ p \equiv 1 \mathrm{mod\, } k}} \frac{\log p}{\sqrt{p}+2} = \frac{2 \sqrt{Q}}{\phi(k)} + \mathcal{O} \bigg(\frac{\sqrt{Q}}{\log Q}\bigg). \end{align*} $$
Thus,
 $$ \begin{align*} |S| \leq \frac{\dfrac{Q}{\phi(k)} + \mathcal{O}\bigg(\dfrac{Q}{\log Q}\bigg) - \log N}{\dfrac{2 \sqrt{Q}}{\phi(k)} + \mathcal{O}\bigg(\dfrac{\sqrt{Q}}{\log Q}\bigg) - \log N}. \end{align*} $$
$$ \begin{align*} |S| \leq \frac{\dfrac{Q}{\phi(k)} + \mathcal{O}\bigg(\dfrac{Q}{\log Q}\bigg) - \log N}{\dfrac{2 \sqrt{Q}}{\phi(k)} + \mathcal{O}\bigg(\dfrac{\sqrt{Q}}{\log Q}\bigg) - \log N}. \end{align*} $$
Choose
![]() $Q=(\phi (k) \log N)^2$
. Note that the condition
$Q=(\phi (k) \log N)^2$
. Note that the condition
![]() $Q> Q_0(k)$
is the same as
$Q> Q_0(k)$
is the same as
 $$ \begin{align} \log N> \frac{\exp(0.015 \sqrt{k} (\log k)^3) }{ \phi(k)}. \end{align} $$
$$ \begin{align} \log N> \frac{\exp(0.015 \sqrt{k} (\log k)^3) }{ \phi(k)}. \end{align} $$
Since
![]() $k = o(\log \log |n|)$
, (3.4) holds for N large enough. Now, for both the numerator and the denominator, divide by
$k = o(\log \log |n|)$
, (3.4) holds for N large enough. Now, for both the numerator and the denominator, divide by
![]() $\log N$
to get
$\log N$
to get
 $$ \begin{align} |S| \leq \frac{\phi(k)\log N -1 + \mathcal{O} \bigg(\dfrac{Q}{\log N \log Q}\bigg)}{1 + \mathcal{O}\bigg(\dfrac{\sqrt{Q}}{\log N \log Q}\bigg)}. \end{align} $$
$$ \begin{align} |S| \leq \frac{\phi(k)\log N -1 + \mathcal{O} \bigg(\dfrac{Q}{\log N \log Q}\bigg)}{1 + \mathcal{O}\bigg(\dfrac{\sqrt{Q}}{\log N \log Q}\bigg)}. \end{align} $$
Because
![]() $k=o(\log \log N)$
, it is easy to see that
$k=o(\log \log N)$
, it is easy to see that
 $$ \begin{align*} \frac{\sqrt{Q}}{\log N \log Q} = \frac{\phi(k)}{2\log \phi(k) + 2\log \log N} = o(1). \end{align*} $$
$$ \begin{align*} \frac{\sqrt{Q}}{\log N \log Q} = \frac{\phi(k)}{2\log \phi(k) + 2\log \log N} = o(1). \end{align*} $$
Hence, from (3.5),
 $$ \begin{align*} |S| &\leq \frac{\phi(k)\log N + \mathcal{O} \bigg(\dfrac{(\phi(k))^2\log N}{\log \log N}\bigg)}{1 + \mathcal{O}\bigg(\dfrac{\phi(k)}{\log \log N}\bigg)}. \end{align*} $$
$$ \begin{align*} |S| &\leq \frac{\phi(k)\log N + \mathcal{O} \bigg(\dfrac{(\phi(k))^2\log N}{\log \log N}\bigg)}{1 + \mathcal{O}\bigg(\dfrac{\phi(k)}{\log \log N}\bigg)}. \end{align*} $$
As
![]() $\mathcal {O}({\phi (k)}/{\log \log N}) = o(1) $
, it follows that
$\mathcal {O}({\phi (k)}/{\log \log N}) = o(1) $
, it follows that
 $$ \begin{align*} \frac{1}{1 + \mathcal{O}\bigg(\dfrac{\phi(k)}{\log \log N}\bigg)}=1 + \mathcal{O}\bigg(\frac{\phi(k)}{\log \log N}\bigg). \end{align*} $$
$$ \begin{align*} \frac{1}{1 + \mathcal{O}\bigg(\dfrac{\phi(k)}{\log \log N}\bigg)}=1 + \mathcal{O}\bigg(\frac{\phi(k)}{\log \log N}\bigg). \end{align*} $$
So, we obtain
 $$ \begin{align*} |S| &\leq \phi(k)\log N + \mathcal{O} \bigg(\frac{(\phi(k))^2\log N}{\log \log N}\bigg). \end{align*} $$
$$ \begin{align*} |S| &\leq \phi(k)\log N + \mathcal{O} \bigg(\frac{(\phi(k))^2\log N}{\log \log N}\bigg). \end{align*} $$
Since
![]() $N=|n|^3$
and
$N=|n|^3$
and
![]() $M_k(n) := \text {sup}\{|S|\}$
, we conclude that
$M_k(n) := \text {sup}\{|S|\}$
, we conclude that
 $$ \begin{align*} M_k(n) \leq 3 \, \phi(k) \, \log |n| + \mathcal{O} \bigg(\frac{(\phi(k))^2 \log |n|}{\log \log |n|}\bigg) \end{align*} $$
$$ \begin{align*} M_k(n) \leq 3 \, \phi(k) \, \log |n| + \mathcal{O} \bigg(\frac{(\phi(k))^2 \log |n|}{\log \log |n|}\bigg) \end{align*} $$
as required.
Acknowledgements
We thank Professor Alain Togbé for his question regarding effective versions of the bounds in [Reference Dixit, Kim and Murty8] during the second author’s talk in the Leuca 2022 conference, which motivated this paper. We are grateful to Professor Ram Murty and Dr. Seoyoung Kim for helpful comments on an earlier version of this paper. We also thank the referee for detailed and helpful comments on the paper.