2.1. Decomposition-based simulation of the turbulence–wave system

The wave and turbulent motions are described by the incompressible Navier–Stokes equations as

(2.1)$$\begin{gather} \frac{\partial \boldsymbol{U}}{\partial t} + (\boldsymbol{U}\boldsymbol{\cdot}\boldsymbol{\nabla})\boldsymbol{U} =-\frac{1}{\rho}\boldsymbol{\nabla} P + \nu\boldsymbol{\nabla}^2 \boldsymbol{U} - \boldsymbol{\nabla} \boldsymbol{\cdot} {\tau}^{SGS}, \end{gather}$$

(2.2)$$\begin{gather}\boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{U} = 0. \end{gather}$$

In the above equations, $\boldsymbol {U}$ is the total flow velocity, $P$ is the dynamic pressure, $\rho$ is the water density and $\nu$ is the kinematic viscosity. The flow is modelled by large-eddy simulation, i.e. the above flow variables and equations are filtered to resolve only grid-scale structures, and ${\tau }^{SGS}$ is the subgrid-scale stress that accounts for the effect of unresolved small-scale motions. We remark that, in this study, we mainly focus on the wave effect on turbulence and, therefore, the Coriolis and stratification effects are neglected.

Then, we decompose the flow velocity $\boldsymbol {U}$ into a potential part $\boldsymbol {u}_\phi$ and a rotational part $\boldsymbol {u}$, inspired by the Helmholtz theorem, as

(2.3)\begin{equation} \boldsymbol{U} = \boldsymbol{u}_\phi + \boldsymbol{u}. \end{equation}

The potential part can be associated with a velocity potential $\phi$ as $\boldsymbol {u}_\phi =\boldsymbol {\nabla }\phi$, and $\phi$ satisfies the Laplace equation:

(2.4)\begin{equation} \nabla^2 \phi = 0. \end{equation}

By subtracting $\boldsymbol {u}_\phi$ from (2.1) and (2.2), we obtain the governing equations for the rotational part $\boldsymbol {u}$:

(2.5)$$\begin{gather} \frac{\partial \boldsymbol{u}}{\partial t} + (\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla})\boldsymbol{u} =-\boldsymbol{u}_\phi\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u} - \boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u}_\phi -\frac{1}{\rho}\boldsymbol{\nabla} p + \nu\boldsymbol{\nabla}^2 \boldsymbol{u} - \boldsymbol{\nabla}\boldsymbol{\cdot} \tau^{SGS}, \end{gather}$$

(2.6)$$\begin{gather}\boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{u} = 0. \end{gather}$$

Since the wave motions are predominantly irrotational, while turbulence is characterised by vortices or rotational motions, we assume that $\boldsymbol {u}_\phi$ represents wave motions and that $\boldsymbol {u}$ corresponds to current and turbulence motions. Notably, treating the irrotational and rotational parts of the flow as waves and turbulence, respectively, is mainly for physical interpretation, while the Helmholtz decomposition does not imply the natures of the two parts. However, this interpretation is supported by the fact that most ocean wave theories are based on the irrotational flow assumption (Mei, Stiassnie & Yue Reference Mei, Stiassnie and Yue2005). Moreover, this interpretation is adopted by Craik & Leibovich (Reference Craik and Leibovich1976) for the derivation of CL formulations, where the wave motions are assumed to be irrotational and the vorticity equations are used to describe the current and turbulence motions. We note that the Helmholtz decomposition has also been widely applied to the analyses of various free-surface flow problems, such as the decay of viscous waves (Lamb Reference Lamb1932) and the interaction of vortex tubes with a free surface (Dommermuth Reference Dommermuth1993). Additionally, this decomposition approach is useful for studying the effect of one known component on another component (Joseph Reference Joseph2006), which aligns with the aim of the present study to investigate the wave effect on turbulence.

In (2.5), it is important to highlight the terms $-\boldsymbol {u}_\phi \boldsymbol {\cdot }\boldsymbol {\nabla }\boldsymbol {u} - \boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {\nabla }\boldsymbol {u}_\phi$, which arise from the decomposition of the advection term in the original (2.1). These terms account for the coupling between the irrotational and rotational parts. Since the irrotational and rotational parts are associated with the wave and turbulence motions, respectively, these two terms represent the wave effect on turbulence.

At the water surface described by $z=\eta (x,y)$, where $\eta$ denotes the surface elevation, $x$ and $y$ denote the horizontal coordinates and $z$ denotes the vertical coordinate, the balance of stress leads to the following dynamic boundary conditions:

(2.7a–c)\begin{equation} {\boldsymbol{n}} \boldsymbol{\cdot} \boldsymbol{\sigma} \boldsymbol{\cdot} {\boldsymbol{n}}^{\mathrm{T}} = 0, \quad {\boldsymbol{t}}_x \boldsymbol{\cdot} \boldsymbol{\sigma} \boldsymbol{\cdot} {\boldsymbol{n}}^{\mathrm{T}} = \tau_x, \quad {\boldsymbol{t}}_y \boldsymbol{\cdot} \boldsymbol{\sigma} \boldsymbol{\cdot} {\boldsymbol{n}}^{\mathrm{T}} = \tau_y, \end{equation}

where $\boldsymbol {\sigma } = -P \boldsymbol {I}+\rho \nu (\boldsymbol {\nabla } \boldsymbol {U}+\boldsymbol {\nabla }\boldsymbol {U}^\mathrm {T})$ is the stress tensor and $\boldsymbol {I}$ denotes the identity tensor. The boundary condition (2.7a) describes the stress balance with the normal force applied by the air on the water surface and $\boldsymbol {n}$ denotes the surface-normal unit vector defined as

(2.8)\begin{equation} {\boldsymbol{n}} = \frac{{(-\eta_x, -\eta_y, 1)}}{C_0}, \end{equation}

where $\eta _x$ and $\eta _y$ denote the derivatives $\eta _x=\partial \eta /\partial x$ and $\eta _y=\partial \eta /\partial y$, respectively. The term $C_0$, defined as $C_0={(\eta _x^2 + \eta _y^2 + 1)}^{1/2}$, normalises the vector to a unit length. Here, the air-side normal stress is set to zero. Equations (2.7b) and (2.7c) state that the tangential shear stresses imposed by the air on the surface are $\tau _x$ and $\tau _y$ in the $\boldsymbol {t}_x$ and $\boldsymbol {t}_y$ directions, respectively, where ${\boldsymbol {t}}_x$ and ${\boldsymbol {t}}_y$ are the surface tangential unit vectors defined as

(2.9a,b)\begin{equation} {\boldsymbol{t}}_x = \frac{(1, 0, \eta_x)}{\sqrt{1+\eta_x^2}}, \quad {\boldsymbol{t}}_y = \frac{(0, 1, \eta_y)}{\sqrt{1+\eta_y^2}}. \end{equation}

The no-penetration condition of the surface leads to the free-surface kinematic boundary condition, which can be used to describe the evolution of $\eta (x,y)$ as follows:

(2.10)\begin{equation} \frac{\partial \eta}{\partial t} - \boldsymbol{U}\boldsymbol{\cdot} (-\eta_x, -\eta_y, 1) = 0.\end{equation}

The boundary conditions above also need to be determined for $\boldsymbol {u}_\phi$ and $\boldsymbol {u}$. First, since turbulence in the ocean mixed layer is typically much weaker than wave motions, we adopt the assumption that free-surface motions are mainly driven by wave motions or the irrotational velocity $\boldsymbol {u}_\phi$. In other words, we assume that the turbulence-induced surface fluctuations are much smaller than the wave elevations. This assumption is similar to that used by the CL formulation, in which the wave is undisturbed by turbulence and current. This assumption is further supported by the simulations of the Langmuir circulations under a progressive wave conducted by Xuan et al. (Reference Xuan, Deng and Shen2019), who reported that the turbulence-induced surface fluctuation is less than $1.2$ % of the wave amplitude. Under this assumption, we obtain the following decomposed kinematic boundary conditions for $\boldsymbol {u}_\phi$ and $\boldsymbol {u}$:

(2.11)$$\begin{gather} \frac{\partial \eta}{\partial t} - C_0 {\boldsymbol{n}}\boldsymbol{\cdot} \boldsymbol{u}_\phi = 0, \end{gather}$$

(2.12)$$\begin{gather}{\boldsymbol{n}}\boldsymbol{\cdot} \boldsymbol{u} = 0. \end{gather}$$

The normal stress balance (2.7a) can be written as an evolution equation for the velocity potential at the wave surface $\phi |_{z=\eta }$ (Dommermuth Reference Dommermuth1993). In the present study, we neglect the turbulence effect on the wave, which is consistent with the assumption we use for the kinematic boundary condition. We also neglect the viscous dissipation of the wave, considering the short-term evolution of the wave packet in the simulation set-up (see § 2.2). These assumptions lead to the following evolution equation for $\phi$ that governs $\boldsymbol {u}_\phi$:

(2.13)\begin{equation} \frac{\partial \phi}{\partial t} + \frac{1}{2}{|\boldsymbol{\nabla}\phi|}^2 + g\eta = 0, \quad \text{at } z=\eta. \end{equation}

With the above assumptions, the wave evolution becomes independent of the turbulence simulation. As a result, the tangential stress balance for $\boldsymbol {u}$ can be computed from (2.7b,c) as follows:

(2.14a,b)\begin{equation} {\boldsymbol{t}}_x\boldsymbol{\cdot} \boldsymbol{\sigma}_u \boldsymbol{\cdot} {\boldsymbol{n}}^{\mathrm{T}} = \tau^r_x, \quad {\boldsymbol{t}}_y\boldsymbol{\cdot} \boldsymbol{\sigma}_u \boldsymbol{\cdot} {\boldsymbol{n}}^{\mathrm{T}} = \tau^r_y. \end{equation}

Here, $\tau ^r_x$ and $\tau ^r_y$ are the stresses excluding the contributions from the irrotational velocity, defined as

(2.15a,b)\begin{equation} \tau^r_x = \tau_x - {\boldsymbol{t}}_x\boldsymbol{\cdot} \boldsymbol{\sigma}_{u_\phi} \boldsymbol{\cdot} {\boldsymbol{n}}^{\mathrm{T}}, \quad \tau^r_y = \tau_y - {\boldsymbol{t}}_y\boldsymbol{\cdot} \boldsymbol{\sigma}_{u_\phi} \boldsymbol{\cdot} {\boldsymbol{n}}^{\mathrm{T}}, \end{equation}

where $\boldsymbol {\sigma }_u=-p\boldsymbol {I}+\rho \nu (\boldsymbol {\nabla } \boldsymbol {u} + \boldsymbol {\nabla }\boldsymbol {u}^\mathrm {T})$ and $\boldsymbol {\sigma }_{u_\phi }=-p\boldsymbol {I}+\rho \nu (\boldsymbol {\nabla } \boldsymbol {u}_\phi + \boldsymbol {\nabla }\boldsymbol {u}_\phi ^\mathrm {T})$, with $\boldsymbol {u}_\phi$ being a known quantity when solving $\boldsymbol {u}$.

As discussed above, the rotational field $\boldsymbol {u}$ described by (2.5) and (2.6) is bounded by the wave surface. Solving this system would traditionally require a boundary-fitted grid, as in Hodges & Street (Reference Hodges and Street1999) and Xuan & Shen (Reference Xuan and Shen2019), which is computationally expensive, especially for complex wave surface elevations such as the wave packet in the present problem. To reduce the simulation cost, we employ the Taylor expansion to approximate the boundary conditions using quantities on a flat plane $z=0$. The surface velocity at $z=\eta$ can be expressed using the Taylor series as

(2.16)\begin{equation} {u_i |}_{z=\eta} = {u_i |}_{z=0} + \sum_{l=1}^{M}{\frac{\eta^l}{l!}\left.\frac{\partial^l u_i}{\partial z^l}\right|}_{z=0} + O(\eta^{M+1}).\end{equation}

Here, we truncate the Taylor expansion at $M=1$ to derive a first-order approximation of the boundary conditions (see Appendix A for detailed formulations of the boundary conditions). In this way, the boundary conditions become dependent on the values at $z=0$, which enables the solution of the rotational velocity $\boldsymbol {u}$ in a rectangular box rather than a wavy domain. As a result, the computational cost is reduced because the computation of the metric coefficients arising from a boundary-fitted grid is no longer needed. We note that the accuracy of this boundary approximation depends on the higher-order terms that are omitted, with the leading-order error being proportional to $(\eta /\delta )^{M+1}$, where $\delta$ represents a characteristic length scale related to the velocity gradient $\partial ^l u_i/\partial z^l$. Following the assumption made by Craik & Leibovich (Reference Craik and Leibovich1976) and Leibovich (Reference Leibovich1977) that the length scale $\delta$ is proportional to the inverse of the wavenumber $k^{-1}$, the magnitude of the error term is $O(\alpha ^{M+1})$, where $\alpha$ is the wave steepness. Our validation case based on the comparison between the present method and the boundary-fitted-grid method, which is detailed below, indicates that the first-order approximation can effectively capture the wave boundary effect. This approximation can be naturally applied to waves with multiple components, provided that the wave slope remains moderate. Therefore we anticipate that this approach can be used to simulate flows under more complex wave fields, such as broadband sea waves. However, for wave fields with higher steepness, a higher-order approximation might be necessary, which exceeds the scope of this study and is a direction for future research.

In the present study, a large-eddy simulation solver (Deng et al. Reference Deng, Yang, Xuan and Shen2019, Reference Deng, Yang, Xuan and Shen2020; Deng, Yang & Shen Reference Deng, Yang and Shen2022) is adapted to solve the governing equations (2.5) and (2.6) with the boundary conditions (2.12) and (2.14a,b) for $\boldsymbol {u}$. The Fourier pseudo-spectral method is employed in the discretisation of the horizontal directions, and the finite-difference method is employed in the vertical direction. The solver is advanced in time using a second-order Adam–Bashforth method with the fractional-step method to enforce the incompressibility condition (Kim & Moin Reference Kim and Moin1985).

The potential wave flow determined by the boundary conditions (2.11) and (2.13) is solved using the HOS method (Dommermuth & Yue Reference Dommermuth and Yue1987; West et al. Reference West, Brueckner, Janda, Milder and Milton1987), which employs the Zakharov formulation (Zakharov Reference Zakharov1968) to describe the nonlinear wave evolution. This method has been widely applied for predicting phase-resolved nonlinear waves due to its accuracy and efficiency (see e.g. Hao & Shen Reference Hao and Shen2020). The details of the HOS method and the validations are given in Dommermuth & Yue (Reference Dommermuth and Yue1987).

To validate the accuracy of the numerical method to capture turbulence–wave interaction dynamics, we use the proposed method to simulate Langmuir circulations under a monochromatic wave train and compare the results with those obtained by the boundary-fitted-grid method. The detailed validation set-up and result comparisons are presented in Appendix C. The results obtained by our proposed method agree well with the results predicted by the boundary-fitted-grid method in terms of both the depth variation and wave-phase variation in the turbulence statistics. These results indicate that the proposed method can effectively capture the dominant turbulence–wave interaction dynamics with wave-phase dependency resolved.

It is worth noting that, although the decomposition results in two systems to simulate, both systems are simulated using efficient numerical methods. Therefore, the overall numerical method is still substantially cheaper than solving a unified system on a deforming boundary-fitted grid. The HOS method is formulated using surface variables, i.e. the surface elevation $\eta =\eta (x,y)$ and the surface potential $\phi _s=\phi (x,y; z=\eta )$, and does not solve a fully three-dimensional wave velocity field. Therefore, its computational cost scales with the horizontal grid size. For the rotational motions, a three-dimensional field is required to capture complex turbulence structures. However, using a rectangular domain, facilitated by the approximated boundary conditions based on the Taylor expansion, has a significantly lower computational cost than does using a boundary-fitted-grid method.

Finally, we remark that the proposed approach, although solved in a rectangular domain, is fundamentally different from the rigid-lid approximation used in the CL formulation. First, the CL formulation is based on wave-phase averaging, wherein the vortex force term represents the averaged effect of the wave on turbulence. This is in contrast to the coupling term in (2.5), which depends on the phase-resolved wave orbital motions and represents the instantaneous effect of the wave motions on turbulence. We note that the wave coupling term in (2.5) can be reformulated using the cross product of $\boldsymbol {u}_\phi$ and $\boldsymbol {\omega }$, as detailed in Appendix B. However, this alternative formulation fundamentally differs from the vortex force in the CL formulation in terms of the time scales resolved, despite their superficial similarity. It is worth noting that previous studies using wave-phase-resolved methods have shown that motions with time scales shorter than the wave period, which are unresolved in the CL formulation, can exert appreciable influences on motions with longer time scales (Zhou Reference Zhou1999; Xuan et al. Reference Xuan, Deng and Shen2020; Xuan & Shen Reference Xuan and Shen2022). In other words, these unresolved time scales in the CL formulation can lead to quantitative differences in turbulence statistics. Second, the flat surface of the CL formulation is a result of using the wave-phase-averaging formulation. In other words, the wave elevation is removed by averaging. In our proposed method, the approximated boundary conditions based on Taylor expansions about the flat plane $z=0$ still account for the effects associated with the wave elevation. This can be seen in the validation results of the wave-phase variation in the Reynolds stress (figure 20) presented in Appendix C. Both features are essential for retaining phase-related information in the simulation of turbulence–wave interactions and providing a more accurate representation of physical processes compared with the CL formulation.

2.2. Simulation parameters

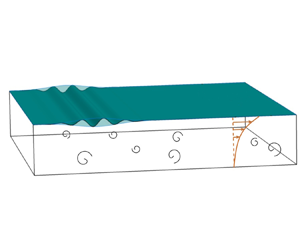
Figure 1 illustrates the simulation set-up, depicting a turbulent flow field influenced by an incoming Gaussian wave packet. We first simulate the base flow without waves, which is a fully developed turbulence boundary layer forced by a constant shear stress at the surface representing the effect of wind-driven shear. A free-slip boundary condition is applied at the bottom boundary, mimicking an ocean surface boundary layer base with weak shear (Belcher et al. Reference Belcher2012). To ensure that the turbulent flow reaches an equilibrium state, we apply a uniform adverse pressure gradient $\partial p/\partial x=\tau _0/H$ to balance the surface momentum flux from the wind shear $\tau _0$, where $H$ is the boundary layer depth. In this study, we neglect the Coriolis effect to focus only on the turbulence and wave effects. Although the Coriolis effect is insignificant in coastal settings with a no-slip bottom (Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007; Grosch & Gargett Reference Grosch and Gargett2016), which is related to the dynamics of Langmuir supercells (Gargett et al. Reference Gargett, Wells, Tejada-Martínez and Grosch2004), the Coriolis force does influence momentum balance in the open ocean. Our set-up uses the pressure gradient to balance the wind shear, facilitating our analysis of turbulence–wave dynamics without the rotational effect. This set-up has been employed in studying turbulence–wave interactions in the context of Langmuir turbulence by Xuan et al. (Reference Xuan, Deng and Shen2020). The base flow is simulated with a moderate Reynolds number $Re_\tau =u_* H/\nu = 2000$. The simulated flow condition with a moderate Reynolds number could be directly relevant to small-scale turbulence–wave interactions, e.g. Langmuir circulations of length scales $O(10\ {\rm cm})$ (see the discussions in Xuan et al. (Reference Xuan, Deng and Shen2020)). These small-scale circulations naturally arise from the interactions of gravity–capillary waves with underlying turbulence, e.g. after wind starts blowing over an initially quiescent water (Melville et al. Reference Melville, Shear and Veron1998; Veron & Melville Reference Veron and Melville2001; Tejada-Martínez et al. Reference Tejada-Martínez, Hafsi, Akan, Juha and Veron2020). The Reynolds number in a realistic ocean surface boundary layer is higher. Although it would be desirable to perform simulations at larger Reynolds numbers, which can be crucial for a realistic ocean boundary layer with interplays of other forces including the Coriolis and buoyancy forces, it is worth noting that low- and moderate-Reynolds-number flows can still provide valuable insights into higher-Reynolds-number dynamics. Xuan et al. (Reference Xuan, Deng and Shen2019) compared the wave-phase-resolved simulations of Langmuir turbulence at $Re_\tau =2000$ with those at $Re_\tau =500$ and found that the fundamental turbulence–wave interaction mechanisms remain consistent across different Reynolds numbers. Therefore, the present set-up is appropriate for capturing the dominant turbulence structures and the associated turbulence–wave interaction dynamics.

Figure 1. Sketch of the problem set-up: turbulence interacting with a Gaussian wave packet.

We then add the wave packet into the simulation and enable the turbulence–wave coupling described in § 2.1. The wave packet is initialised by the wave elevation $\eta$ and surface potential $\phi _s$ according to the linear wave theory as

(2.17)$$\begin{gather} \eta(x,t)|_{t=0} = A_0(x)\cos (k_0 x), \end{gather}$$

(2.18)$$\begin{gather}\phi_s(x,t)|_{t=0} = A_0(x) \omega_0 k_0^{-1} \sin (k_0 x). \end{gather}$$

This corresponds to a carrier wave with wavenumber $k_0$ and angular frequency $\omega _0$ bounded by an initial envelope $A_0(x)$. The envelope $A_0(x)$ is a Gaussian shape given by

(2.19)\begin{equation} {A_0(x) = a_0 \exp \left(-{\frac{{(x - x_0)}^2}{2\chi^2}}\right),} \end{equation}

where $a_0$ is the amplitude of the packet, $x_0$ is the initial centre of the packet and $\chi$ is the bandwidth of the Gaussian packet. The carrier wavelength is set to $k_0 H=12$ and the carrier wave satisfies the deep-water wave condition. Following van den Bremer & Taylor (Reference van den Bremer and Taylor2016), we characterise the wave packet with two dimensionless parameters: a steepness parameter $\alpha$ defined as $\alpha =a_0 k_0$ and a bandwidth parameter $\epsilon$ defined as $\epsilon ={(k_0 \chi )}^{-1}$. Wave packets with different carrier wave steepnesses are considered, including $\alpha =a_0 k_0 =0.12$, $0.09$ and $0.06$, and the three cases are denoted as ${W}_{12}$, ${W}_{09}$ and ${W}_{06}$, respectively. We set the bandwidth parameter to $\epsilon =0.13$ to ensure a relatively small dispersion (van den Bremer & Taylor Reference van den Bremer and Taylor2016). Here, we use the friction velocity at the water surface, $u_*=\sqrt {\tau _0/\rho }$, as the characteristic velocity. The Froude number, defined as $Fr=u_*/\sqrt {gH}$, affects the characteristic velocity of the wave motion and is set to $3.74 \times 10^{-4}$. This Froude number is chosen such that the resulting wave packet has a fast propagation velocity compared with the underlying turbulent flow and can exert strong straining on turbulence. Based on the linear wave theory, the phase velocity of the carrier wave and the group velocity of the wave packet are $c_0=\sqrt {g/k_0}={(Fr\sqrt {k_0 H})}^{-1} u_*=772 u_*$ and $c_g=c_0/2=386 u_*$, respectively. Notably, the mean current velocity of a developed shear-driven boundary layer, which typically reaches a maximum of $O(20 u_*)$ at the surface where the driving stress is applied, is negligibly small compared with the wave packet propagation. In other words, the mean current advection of turbulence is expected to be nearly stationary compared to the wave packet passage. The ratios between the maximum wave orbital straining magnitude within the wave packet $a_0 k_0^2 c_0$ and the characteristic turbulence large-eddy strain rate $u_*/H$ are $1112$, $834$ and $556$ for cases ${W}_{12}$, ${W}_{09}$ and ${W}_{06}$, respectively, indicating that the wave straining effect is much stronger than the shear effect. To estimate the cumulative effect of the wave on turbulence compared with that of the shear straining, we compute the turbulence Langmuir number ${La}_t =\sqrt {u_*/U_s}$, where we use the maximum surface Stokes drift of the wave packet $U_s=\alpha ^2 c_0$ as the characteristic Stokes drift velocity. We obtain ${La}_t=0.3$, $0.4$ and $0.6$ for the three cases, respectively, which fall within the Langmuir regime where the cumulative wave forcing effect is dominant (Li, Garrett & Skyllingstad Reference Li, Garrett and Skyllingstad2005). Furthermore, we note that the Froude number $Fr=3.74 \times 10^{-4}$ selected falls within a range typical of oceanic conditions. For example, this could correspond to a friction velocity $u_*=8 \times 10^{-3}\ \text {m}\ \text {s}^{-1}$ and a mixed layer depth of $47$ m. The domain size is set to $L_x \times L_y \times H = 6{\rm \pi} H \times 2{\rm \pi} H \times H$. The domain is discretised by a grid of size $512 \times 256 \times 112$. To obtain the statistics of turbulence modified by the wave packet, we perform ensemble simulations of the wave packet propagating through the turbulence field using different initial instants. The wave field is maintained the same across different ensemble runs. For each case, $30$ ensemble runs are carried out.

4.1. Enstrophy

The enstrophy quantifies the strength of turbulence vorticity fluctuations. Figure 2 shows the three components of the packet-scale mean enstrophy, $\widehat {\omega '^2_i}$, near the surface. We find that the variations in $\widehat {\omega '^2_i}$ are qualitatively similar across all considered cases, and the primary difference lies in the magnitude of changes. This is because the imposed wave packets have the same characteristic length scales, i.e. the carrier wavenumber $k_0$ and bandwidth $\chi$, while the wave amplitudes vary. Therefore, only the results for case ${W}_{12}$ are presented. The quantitative differences among the cases, particularly the effect of the wave steepness, are discussed later in this section. First, we note that the streamwise and spanwise vortices are dominant and are related to the quasi-streamwise vortices and the head of the hairpin vortices, which are the predominant structures in a shear-driven boundary layer (Jeong et al. Reference Jeong, Hussain, Schoppa and Kim1997; Wu & Christensen Reference Wu and Christensen2006). In contrast to a no-slip boundary condition, vertical vortices are allowed to attach to the free surface. Therefore, $\widehat {\omega '^2_z}$ is non-zero at the surface (Shen et al. Reference Shen, Zhang, Yue and Triantafyllou1999). Figure 2 clearly shows that the turbulence vortices are influenced by the wave packet and that the strengths of the enstrophy components change during the passage of the wave packet.

Figure 2. Contours of the packet-following average of the enstrophy components: (a) $\widehat {\omega '^2_x}/{(u_*^2/\nu )}^2$, (b) $\widehat {\omega '^2_y}/{(u_*^2/\nu )}^2$ and (c) $\widehat {\omega '^2_z}/{(u_*^2/\nu )}^2$, where $u_*^2/\nu$ is the mean shear at the surface. The dashed lines at the top of the panels illustrate the shape of the wave envelope. The arrow within the envelope indicates the direction of the wave group velocity $c_g$. Correspondingly, the right and left sides are the leading and trailing edges of the packet, respectively. Case ${W}_{12}$ is shown.

Figure 3 shows the ratio of the enstrophy components to their values at each depth under the leading edge of the wave packet to provide a clearer view of the relative change in the vorticity strength. All three components of enstrophy show enhancement below the wave packet core, followed by a decrease, creating an intensity bump below the packet core. This intensity bump is caused by the kinematic disturbances by the wave elevation. We take the spanwise enstrophy component, $\widehat {\omega _y'^2}$, which exhibits the most significant influence, as an example. We note that $\omega _y' = \partial u'/\partial z - \partial w'/\partial x$ and thus $\widehat {\omega _y'^2}$ is contributed by the variances of $\partial u'/\partial z$ and $\partial w'/\partial x$ and their cross-correlation. A comparison among the three contributions reveals that $(\partial u'/\partial z)^2$ accounts for approximately $80\,\%$ of the near-surface $\widehat {\omega _y'^2}$ around the wave packet core ($k_0 z > -0.5$ and $-\chi < x' < \chi$). As the wave packet core approaches, the wave amplitude increases and the stretching and compression of spanwise vortices in the vertical direction intensify with the increasing surface fluctuations, leading to strong variations in $\partial u'/\partial z$, and consequently in $\widehat {\omega _y'^2}$ under the packet core. At the trailing edge of the wave packet, with the decreasing wave surface fluctuation amplitude, the disturbances in vorticity fluctuations caused by the wave surface diminish rapidly. In a fully developed shear-driven boundary layer, $u'$ is the strongest among the three velocity components, therefore $\partial u'/\partial z$ exhibits the greatest influence and $\widehat {\omega _y'^2}$ shows the largest intensity bump under the packet core. By comparison, the intensity bumps in the streamwise and spanwise enstrophy components are relatively weak. For the streamwise vorticity fluctuations, variations in $\partial w'/\partial z$ predominantly contribute to the observed increase in $\widehat {\omega '^2_x}$ at the wave packet core. For $\widehat {\omega '^2_z}$, the increase can be attributed to the forward and backward tilting of surface-connected vertical vortices as different wave phases pass.

Figure 3. Relative variation in the enstrophy components compared with their undisturbed values at the leading edge of the wave packet ($x'=3\chi$): (a) $\widehat {\omega '^2_x}/\widehat {\omega '^2_x}|_{x'=3\chi }$, (b) $\widehat {\omega '^2_y}/\widehat {\omega '^2_y}|_{x'=3\chi }$ and (c) $\widehat {\omega '^2_z}/\widehat {\omega '^2_z}|_{x'=3\chi }$. The dashed lines at the top of the panels illustrate the shape of the wave envelope. The arrow within the envelope indicates the direction of the wave group velocity $c_g$. Correspondingly, the right and left sides are the leading and trailing edges of the packet, respectively. Case ${W}_{12}$ is shown.

Figure 4 plots the relative increases in the enstrophy, $\Delta \widehat {\omega '^2_i}/\widehat {\omega '^2_i}|_{x'=3\chi }$, at fixed depths for cases with different steepness $\alpha = a_0 k_0$ (${W}_{12}$, ${W}_{09}$ and ${W}_{06}$; see § 2.2), where $\Delta \widehat {\omega '^2_i}$ denotes the change from leading edge of the wave packet, defined as $\vphantom{\widehat {\omega '^2_i}^{12}}\Delta \widehat {\omega '^2_i} = \widehat {\omega '^2_i} - \widehat {\omega '^2_i}|_{x'=3\chi }$. In figure 4, two depths, $k_0 z=-0.5$ and $k_0 z = -0.8$, are plotted as examples, but the following observations apply to all depths unless otherwise stated. After the wave packet core passes and the strong disturbances caused by the wave elevation subside quickly, the three enstrophy components are still considerably enhanced compared with their initial values at the leading edge for all cases considered, indicating that the modification of turbulence by the wave packet persists.

Figure 4. Relative increase in the enstrophy components at fixed depths, $k_0 z = -0.5$ (——–) and $k_0 z =-0.8$ (– – –), for cases ${W}_{12}$ ($\alpha =0.12$, $\bullet$), ${W}_{09}$ ($\alpha =0.09$, $\blacksquare$) and ${W}_{06}$ ($0.06$, $\blacktriangledown$): (a) $\Delta \widehat {\omega _x'^2}/\widehat {\omega _x'^2}|_{x'=3\chi }\vphantom{\widehat {\omega '^2_i}^{12}}$, (b) $\Delta \widehat {\omega _y'^2}/\widehat {\omega _y'^2}|_{x'=3\chi }$ and (c) $\Delta \widehat {\omega _z'^2}/\widehat {\omega _z'^2}|_{x'=3\chi }$.

To understand the changes in turbulence vorticity after the wave packet passes, the vertical profiles of $\Delta \widehat {\omega '^2_i}/\widehat {\omega '^2_i}|_{x'=3\chi }$ at the trailing edge of the wave packet ($x'=-3\chi$) are plotted in figure 5. It is evident from the figure that the turbulence vorticity fluctuations in all three directions are enhanced, and the streamwise vorticity is enhanced the most at the trailing edge. For example, in case ${W}_{12}$, at the trailing edge ($x'=-3\chi$), the relative increase in $\widehat {\omega '^2_x}$ reaches $30\,\%$ at $k_0 z=-0.3$. By comparison, the final enhancements of $\widehat {\omega '^2_y}$ and $\widehat {\omega '^2_z}$ at the trailing edge relative to the leading edge are weaker, with the peak relative increases being less than $20\,\%$. Among the three cases, the vertical variations of $\Delta \widehat {\omega '^2_i}/\widehat {\omega '^2_i}|_{x'=3\chi }$ at the trailing edge are similar. The wave effect is most prominent near the surface, consistent with the contours shown in figures 2 and 3. Away from the surface, e.g. below $z < 2k_0^{-1}$, the turbulence vorticity intensity is changed much less.

Figure 5. Vertical profiles of the relative changes in the enstrophy components at the trailing edge ($x'=-3\chi$) compared with the leading edge ($x'=3\chi$) for cases ${W}_{12}$ ($\alpha =0.12$, $\bullet$), ${W}_{09}$ ($\alpha =0.09$, $\blacksquare$) and ${W}_{06}$ ($\alpha =0.06$, $\blacktriangledown$): (a) $\Delta \widehat {\omega '^2_x}/\widehat {\omega '^2_x}|_{x'=3\chi }$, (b) $\Delta \widehat {\omega '^2_y}/\widehat {\omega '^2_y}|_{x'=3\chi }$ and (c) $\Delta \widehat {\omega '^2_z}/\widehat {\omega '^2_z}|_{x'=3\chi }$.

We further quantify the overall intensification of the enstrophy components by evaluating a vertical integration as

(4.1)\begin{equation} \Delta \varOmega_i = \int_{D}^0 \Delta\widehat{\omega'^2_i} \,\mathrm{d}z = \int_{D}^0 (\widehat{\omega'^2_i}|_{x'=-3\chi} - \widehat{\omega'^2_i}|_{x'=3\chi} ) \,\mathrm{d}z, \end{equation}

where the depth $D$ from which the integration starts is set to $D = -2 k_0^{-1}$ considering that the changes in the enstrophy are negligible below this depth (figure 5). The normalised integrated changes for cases ${W}_{12}$, ${W}_{09}$ and ${W}_{06}$ are listed in table 1, which confirms our observation that the streamwise vortices are enhanced more significantly than the other two components.

Table 1. Relative changes in the enstrophy components integrated from $k_0 z=-2.0$ to the surface after the passage of the wave packet.

Figures 4 and 5, along with table 1, indicate that the relative changes in the enstrophy increase with the wave steepness $\alpha =a_0 k_0$, both during the packet passage and for the final effect after the packet passes. We find that the variation in the streamwise enstrophy component, $\widehat {\omega '^2_x}$, approximately scales with $\alpha ^2$, as shown by the collapse of curves in figure 6. The normalisation with the steepness squared is also applied to the integrated changes in the streamwise enstrophy components, as listed in table 1. The integrated relative $\widehat {\omega '^2_x}$ enhancement, when normalised by $\alpha ^2$, becomes comparable, further confirming that the leading-order changes induced by the wave packet in the streamwise vorticity fluctuations are proportional to $\alpha ^2$. However, such a relationship is not observed for the spanwise and vertical enstrophy components.

Figure 6. Normalised relative changes in the streamwise enstrophy, $\Delta \widehat {\omega '^2_x}/\widehat {\omega '^2_x}|_{x'=3\chi }$, for cases ${W}_{12}$ ($\alpha =0.12$, $\bullet$), ${W}_{09}$ ($\alpha =0.09$, $\blacksquare$) and ${W}_{06}$ ($\alpha =0.06$, $\blacktriangledown$). (a) Variation along the wave packet at fixed depths, $k_0 z = -0.5$ (——–) and $k_0 z =-0.8$ (– – –). (b) Vertical profiles of the changes at the trailing edge ($x'=-3\chi )$ compared with at the leading edge ($x'=3\chi$).

The fact that the streamwise vortices have the largest enhancement is to some extent consistent with the prediction by the CL theory (Craik & Leibovich Reference Craik and Leibovich1976) or the analysis based on the wave-phase-resolved simulation of Langmuir turbulence interacting with a monochromatic wave (Xuan et al. Reference Xuan, Deng and Shen2019), i.e. the surface wave cumulatively tilts vertical vortices to enhance the streamwise vortices. This effect of the surface wave is considered related to the generation of elongated quasi-streamwise vortices in Langmuir turbulence. The enhancement of the streamwise vortices is also reported in laboratory experiments of grid turbulence interacting with a passing wave group (Smeltzer et al. Reference Smeltzer, Rømcke, Hearst and Ellingsen2023), consistent with the prediction of isotropic turbulence distortion by a surface wave using the rapid distortion theory (Teixeira & Belcher Reference Teixeira and Belcher2002). Smeltzer et al. (Reference Smeltzer, Rømcke, Hearst and Ellingsen2023) also found that the streamwise enstrophy enhancement increases with the wave steepness, consistent with our data. In the present study, the base flow is a fully developed shear-driven boundary layer, and therefore the turbulence–wave interactions are not expected to be quantitatively comparable to other types of flows. However, the trend of the overwhelming enhancement of streamwise vortices suggests that the streamwise vorticity enhancement is a universal feature of turbulence–wave interactions. Considering the relations of streamwise vortices with vertical and spanwise turbulent motions, we expect that the vertical and spanwise Reynolds normal stresses will also exhibit strong enhancement. On the other hand, given that the vertical vortices near the surface boundary are mostly related to spanwise variations in streamwise velocity fluctuations, known as high-speed and low-speed streaks (Jeong et al. Reference Jeong, Hussain, Schoppa and Kim1997), we expect that the moderate enhancement of vertical vortices would be associated with a slight increase in streamwise velocity fluctuations. The detailed statistics of the Reynolds normal stresses are discussed next.

4.2. Reynolds normal stresses

The mean Reynolds normal stresses in the packet-following frame $\widehat {u'^2_i}$ for case ${W}_{12}$ are plotted in figure 7. Here, case ${W}_{12}$ is used as the representative case for the qualitative discussions of the wave packet effect on $\widehat {u'^2_i}$ because cases ${W}_{09}$ and ${W}_{06}$ share similar characteristics. The quantitative differences among the cases are discussed in detail later in this section.

Figure 7. Contours of the packet-following average of the Reynolds normal stresses: (a) $\widehat {u'^2}$, (b) $\widehat {v'^2}$ and (c) $\widehat {w'^2}$. The dashed lines at the top of the panels illustrate the shape of the wave envelope. The arrow within the envelope indicates the direction of the wave group velocity $c_g$. Correspondingly, the right and left sides are the leading and trailing edges of the packet, respectively. Case ${W}_{12}$ is shown.

We can observe the relation $\widehat {u'^2} > \widehat {v'^2} > \widehat {w'^2}$, which is characteristic of a fully developed turbulent boundary layer driven by shear forcing. Due to the free-surface kinematic boundary condition (2.12), the vertical fluctuations are suppressed near the surface (Shen et al. Reference Shen, Zhang, Yue and Triantafyllou1999). From the variations in contour levels and shapes, all three components of the Reynolds normal stresses exhibit a strong dependence on the wave packet location. Consistent with the results of the enstrophy components in § 4.1, the disturbance in the Reynolds normal stresses persists at the trailing edge of the wave packet ($x'=-3\chi$), confirming that the wave packet induces cumulative changes in turbulence. Specifically, all three velocity fluctuations experience varying degrees of enhancement, suggesting a net energy transfer from the waves to turbulence.

To further quantify the turbulence enhancement effect of the wave packet, we calculate the relative changes in the Reynolds normal stresses by normalising them by their values at each depth under the leading edge of the wave packet, i.e. $\widehat {u'^2_i}/\widehat {u'^2_i}|_{x'=3\chi }$. The contours of these ratios are presented in figure 8. It is shown that the vertical velocity fluctuations undergo the most substantial increase among the three components. Notably, by the moment the wave packet has passed, i.e. at the trailing edge $x'=-3\chi$, $\widehat {w'^2}$ increases as much as $45\,\%$. The increase in the spanwise velocity fluctuations is less pronounced than that in the vertical velocity fluctuations but can still reach approximately $24\,\%$ after the passage of the wave packet. By comparison, the change in the streamwise velocity fluctuations is relatively small, less than $10\,\%$ at the trailing edge.

Figure 8. Relative variation in the Reynolds normal stresses compared with their undisturbed values at the leading edge of the wave packet ($x'=3\chi$): (a) $\widehat {u'^2}/\widehat {u'^2}|_{x'=3\chi }$, (b) $\widehat {v'^2}/\widehat {v'^2}|_{x'=3\chi }$ and (c) $\widehat {w'^2}/\widehat {w'^2}|_{x'=3\chi }$. The dashed lines at the top of the panels illustrate the shape of the wave envelope. The arrow within the envelope indicates the direction of the wave group velocity $c_g$. Correspondingly, the right and left sides are the leading and trailing edges of the packet, respectively. Case ${W}_{12}$ is shown.

The wave effect differs by velocity components, not only in terms of the enhancement ratio but also in terms of the depth dependence. As evident in figures 7 and 8, the enhancement effect is most pronounced near the surface. Due to the near-surface enhancement, the peak of $\widehat {w'^2}$ shifts towards the surface after the wave packet passes, as shown in figure 7(c). Because both the undisturbed $\widehat {u'^2}$ and $\widehat {v'^2}$ are stronger near the surface, the enhancement by the wave does not alter their peak depths. The depths that the wave can influence also differ by component. The vertical velocity fluctuations are affected not only in the near-surface region but also away from the surface, with an increase of more than $10\,\%$ at $k_0 z=-1$ (figure 8c). The deep influence of the wave on $\widehat {w'^2}$ is also evident in figure 7(c), in which we can observe a considerable change in the contour shapes of $\widehat {w'^2}$. By comparison, the wave impact on $\widehat {v'^2}$ is more localised near the surface and relatively weak below $k_0 z = -1$ (figure 8b). The weak wave effect on $\widehat {u'^2}$ is also confined to the near-surface region. Given that the length scales of turbulent coherent structures usually increase with distance from the boundary, we expect that the wave packet may influence some relatively large-scale structures associated with $w'$, which is further discussed in § 4.3.

Figure 9 shows the relative variation in the Reynolds normal stresses at fixed depths, $\Delta \widehat {u'^2_i}/\widehat {u'^2_i}|_{x'=3\chi }$, for cases with different steepness $\alpha =a_0 k_0$ (${W}_{12}$, ${W}_{09}$ and ${W}_{06}$), where $\Delta \widehat {u'^2_i}$ denotes the change in the Reynolds normal stresses, defined as $\Delta \widehat {u'^2_i} = \widehat {u'^2_i} - \widehat {u'^2_i}|_{x'=3\chi }$. Here, $\Delta \widehat {u'^2_i}$ at two depths, $k_0 z =-0.5$ and $k_0 z=-0.8$, are plotted as examples. At all depths, the turbulence enhancement increases with the steepness $\alpha$. We find that the changes in Reynolds normal stresses can be approximately normalised by $\alpha ^2$. Figures 10 and 11 show the along-packet variations and the vertical profiles of $\Delta \widehat {u'^2_i}/(\alpha ^2 \widehat {u'^2_i}|_{x'=3\chi })$. In both figures, the curves of $\Delta \widehat {w'^2}/(\alpha ^2 \widehat {w'^2}|_{x'=3\chi })$ and $\Delta \widehat {v'^2}/(\alpha ^2 \widehat {v'^2}|_{x'=3\chi })$ collapse, indicating that such scaling works well for the vertical and spanwise Reynolds normal stresses at different depths throughout the passage of the wave packet. As analysed in § 4.1, the scaling with $\alpha ^2$ is also observed for the streamwise enstrophy. Considering that the streamwise vorticity fluctuation $\omega _x'$ is related to the gradients of $w'$ and $v'$, the observed $\alpha ^2$ scaling law is consistent across these turbulence statistics. The behaviour of the streamwise Reynolds normal stress deviates from the proposed scaling. As shown in figures 10 and 11, after applying the $\alpha ^2$ normalisation, the variations in $\Delta \widehat {u'^2}$ are not monotonically dependent on $\alpha$, suggesting that the wave steepness may not be the only parameter for scaling the variation behaviour of streamwise velocity fluctuations. Since the gradients of $u'$ are related to the spanwise and vertical vorticity, this deviation is also consistent with our findings that the changes in the spanwise and vertical enstrophy components do not follow the $\alpha ^2$ scaling law.

Figure 9. Relative increase in the Reynolds normal stresses at fixed depths, $k_0 z = -0.5$ (——–) and $k_0 z =-0.8$ (– – –), for cases ${W}_{12}$ ($\alpha =0.12$, $\bullet$), ${W}_{09}$ ($\alpha =0.09$, $\blacksquare$) and ${W}_{06}$ ($0.06$, $\blacktriangledown$): (a) $\Delta \widehat {u'^2}/\widehat {u'^2}|_{x'=3\chi }$, (b) $\Delta \widehat {v'^2}/\widehat {v'^2}|_{x'=3\chi }$ and (c) $\Delta \widehat {w'^2}/\widehat {w'^2}|_{x'=3\chi }$.

Figure 10. Relative increase in the Reynolds normal stresses at fixed depths, $k_0 z = -0.5$ (——–) and $k_0 z =-0.8$ (– – –), normalised by $\alpha ^2$, for cases ${W}_{12}$ ($\alpha =0.12$, $\bullet$), ${W}_{09}$ ($\alpha =0.09$, $\blacksquare$) and ${W}_{06}$ ($0.06$, $\blacktriangledown$): (a) $\Delta \widehat {u'^2}/(\alpha ^2\widehat {u'^2}|_{x'=3\chi })$, (b) $\Delta \widehat {v'^2}/(\alpha ^2\widehat {v'^2}|_{x'=3\chi })$ and (c) $\Delta \widehat {w'^2}/(\alpha ^2\widehat {w'^2}|_{x'=3\chi })$.

Figure 11. Normalised vertical profiles of the changes in the Reynolds normal stresses at the trailing edge ($x'=-3\chi$) compared with at the leading edge ($x'=3\chi$) for cases ${W}_{12}$ ($\alpha =0.12$, ——–), ${W}_{09}$ ($\alpha =0.09$, – – –) and ${W}_{06}$ ($\alpha =0.06$, — $\cdot$ —): (a) $\Delta \widehat {u'^2}/(\alpha ^2\widehat {u'^2}|_{x'=3\chi })$, (b) $\Delta \widehat {v'^2}/(\alpha ^2\widehat {v'^2}|_{x'=3\chi })$ and (c) $\Delta \widehat {w'^2}/(\alpha ^2\widehat {w'^2}|_{x'=3\chi })$.

To further quantify the overall intensification of turbulence, we examine the integrated changes in the Reynolds normal stresses near the surface, defined as

(4.2)\begin{equation} \Delta E_i = \int_D^0 \Delta\widehat{u'^2_i} \,\mathrm{d}z = \int_D^0 (\widehat{u'^2_i}|_{x'=-3\chi} - \widehat{u'^2_i}|_{x'=3\chi} ) \,\mathrm{d}z. \end{equation}

Here, the depth from which we compute the integration is set to $D=-2k_0^{-1}$. This depth captures most of the regions influenced by the wave, as shown in figures 7, 8 and 11. The normalised integrated changes in the Reynolds normal stresses for cases ${W}_{12}$, ${W}_{09}$ and ${W}_{06}$ are listed in table 2. The increase in the integrated Reynolds normal stress exhibits consistent behaviour as discussed above, i.e. the relative increase in the vertical fluctuations is the largest among the three velocity components. Also listed in table 2 is the relative change normalised by $\alpha ^2$. The normalisation significantly reduces the difference in the enhancement ratio among the cases. The results indicate that the leading-order wave effect on the turbulence enhancement, particularly the enhancement of spanwise and vertical turbulence kinetic energy, is proportional to $\alpha ^2$.

Table 2. Relative changes in the Reynolds normal stresses integrated from $k_0 z=-2.0$ to the surface after the passage of the wave packet for the streamwise component $\mathcal {E}_u=\Delta E_u/E_u\vert_{x'=3\chi }$, spanwise component $\mathcal {E}_v = \Delta E_v/E_v\vert_{x'=3\chi }$ and vertical component $\mathcal {E}_w = \Delta E_w/E_w\vert_{x'=3\chi }$.

It can also be observed from figures 9 and 10 that the most significant changes in $\widehat {u'^2_i}$ occur approximately between $x'=\chi$ and $x'=-\chi$, especially for $\widehat {v'^2}$ and $\widehat {w'^2}$, indicating that the direct effect of the wave forcing on turbulence is most active around the core of the wave packet. Notably, this range ($-\chi < x' <\chi$) corresponds to only a small number of wave periods. With the bandwidth parameter $\epsilon =(k_0\chi )^{-1}=0.13$ (see § 2.2), $\chi$ is approximately equal to $1.22\lambda$ with $\lambda$ being the wavelength of the carrier wave. Since the group speed of the wave packet is twice the phase speed of the carrier wave, the time that the wave envelope takes to propagate for a width of $2\chi$ is approximately five wave periods. Compared with the large-eddy turnover time of the turbulence boundary layer, which is $O(H/u_*)$, this duration is only $0.0033 H/u_*$, indicating that the wave packet acts on turbulence for a significantly shorter time than the characteristic time scale of large eddies. We note again that during this relatively short period, the vertical fluctuations are enhanced by as much as $45\,\%$ (figure 8c). This result indicates that a passing wave packet can rapidly exert a substantial impact on the turbulence underneath.

In the present study, we simulate the changes to a fully developed surface shear-driven turbulence boundary layer impacted by an incoming wave packet. This idealised set-up is designed to reveal the unsteady evolution of turbulence that is initially in an equilibrium state but without wave effects, i.e. not Langmuir turbulence. Previous studies on the unsteady turbulence–wave interactions were based on different set-ups, such as the modification of isotropic turbulence (Teixeira & Belcher Reference Teixeira and Belcher2002; Smeltzer et al. Reference Smeltzer, Rømcke, Hearst and Ellingsen2023) and the co-development of the turbulence and waves under wind shear (Melville et al. Reference Melville, Shear and Veron1998; Veron & Melville Reference Veron and Melville2001; Tejada-Martínez et al. Reference Tejada-Martínez, Hafsi, Akan, Juha and Veron2020). Therefore, exact quantitative agreement with existing studies is not anticipated. However, we find that our results share similar characteristics with the previous research, with some statistics aligning within the same order of magnitude as earlier predictions or observations. First, we compare our results with the theoretical prediction of the changes in isotropic turbulence by a constant-amplitude progressive wave train obtained by Teixeira & Belcher (Reference Teixeira and Belcher2002). Using the rapid distortion theory, Teixeira & Belcher (Reference Teixeira and Belcher2002) showed that the vertical component of the Reynolds normal stresses can be enhanced three times after ten wave periods for a wave train with wave steepness $\alpha =0.2$. The exact rate of increase was not provided, but an estimation can be made based on figure 7 in Teixeira & Belcher (Reference Teixeira and Belcher2002), which indicates that the change is approximately linear with time. Therefore, we estimate the increase in the vertical Reynolds normal stress to be $1.5$ after five wave periods. Since the relative change is proportional to $\alpha ^2$, the prediction given by the rapid distortion theory, when scaled to match our ${W}_{12}$ with $\alpha =0.12$, roughly corresponds to a $54\,\%$ increase. This estimated increase rate aligns with our simulation data, which show an increase of $45\,\%$. This comparison suggests that the rapid distortion theory may capture the leading-order effect during the initial stage of the turbulence–wave interaction. However, we note that there still exist some differences between the predictions obtained via rapid distortion theory and our results. Although the streamwise velocity fluctuation intensity is the least influenced among the three velocity components, the theory predicts that the streamwise fluctuations weaken as the wave propagates. This prediction is in contrast to our results, where the streamwise velocity fluctuations still exhibit a minor increase. This difference is likely because the flow in the present set-up with a wind shear-driven turbulent flow and a transient wave packet is different from the isotropic turbulence interacting with a monochromatic wave studied by Teixeira & Belcher (Reference Teixeira and Belcher2002). Savelyev, Maxeiner & Chalikov (Reference Savelyev, Maxeiner and Chalikov2012) investigated the turbulence evolution under the influence of a passing wave packet using wave tank experiments and large-eddy simulations. They observed an increase in the surface kinetic energy, i.e. the streamwise and spanwise velocity fluctuations. The surface spanwise velocity fluctuations were found to grow faster than the streamwise component, as shown in their figure 5, which aligns with our simulation data where $\widehat {v'^2}$ is more enhanced than $\widehat {u'^2}$. Interestingly, they also noted that the surface streamwise velocity fluctuations can either increase or decrease, and they attributed these behaviours to the difference in the initial turbulence conditions. This result supports our conjecture that pre-existing turbulence can influence the outcomes of turbulence–wave interactions.

4.3. Spectra of the turbulence fluctuations

In this section, to elucidate the contributions to the change in the Reynolds normal stress from different length scales, the spectra of the turbulence velocity fluctuations are analysed. Specifically, we focus on the change in the spectra before and after the passage of the wave packet to understand how surface waves influence turbulence structures at various scales. Here we analyse the energy spectra with respect to spanwise scales considering that $y$ is the homogeneous direction. The spectra at spanwise wavenumbers $k_y$ can be computed as $\varPhi _i(x, k_y, z) = U^*_i U_i$, where $U_i$ denotes the Fourier coefficients of turbulence velocity fluctuations $u'_i$ and $U^*_i$ denotes its complex conjugate. Hereafter, we use case ${W}_{12}$ as the representative case for discussions about the length scales of turbulence structures influenced by the wave packet because the affected length scales are similar among various cases.

We first look at the spectra of the most impacted velocity component, $w'$. Figure 12(a,b) shows the pre-multiplied spectra of $w'$ as functions of $\lambda _y/H$ and $k_0 z$ at the leading edge ($x'=3\chi$) and the trailing edge ($x'=-3\chi$) of the wave packet. The pre-multiplied spectrum $k_y\varPhi _w$ accounts for the logarithmic scale used in the plots and represents the energy density per logarithmic wavenumber, i.e. per $\log {k_y}$, or equivalently, per $\log {\lambda _y}$. After the wave packet passes, the peak in the energy density shifts closer to the surface, indicating a significant near-surface enhancement that changes the depth where the maximum $\widehat {w'^2}$ occurs, consistent with the behaviour of $\widehat {w'^2}$ described earlier (figure 7c). Furthermore, the energy spectra indicate that $w'$ becomes dominated by smaller-scale fluctuations. In figure 12(c), the ratio of the spectra after and before the wave packet passage is plotted to directly quantify the enhancement at different scales and depths. These results confirm that near the surface, the enhancement effect is the strongest for small-scale structures. The enhancement of small-scale vertical fluctuations can also be observed in the supplementary movie, which shows that the regions of positive and negative $w'$, intensified after the wave packet passes, mostly exhibit narrow spanwise length scales. While the intensification of near-surface small-scale $w'$ structures is the most prominent, the near-surface effect extends over at least a decade of spanwise scales, reaching up to $\lambda _y \sim H$. This result suggests that the wave packet can affect turbulence structures with large spanwise length scales comparable to the boundary layer depth. Additionally, as one moves away from the surface, the most amplified scales become increasingly larger, supporting the conjecture in § 4.2 that the deep impact of the wave packet on $w'$ is related to larger-scale structures.

Figure 12. Pre-multiplied energy spectrum of vertical velocity fluctuations $w'$ with respect to the spanwise wavelength $\lambda _y$ at (a) the leading edge ($x'=3\chi$) and (b) the trailing edge ($x'=-3\chi$) of the wave packet. (c) The ratio between the spectra at the trailing edge and the leading edge. Case ${W}_{12}$ is plotted.

Figure 13 shows the pre-multiplied spectra of the spanwise velocity fluctuations $v'$. Similar to the vertical velocity fluctuations, the spanwise velocity fluctuations are enhanced near the surface across a wide range of scales, as evidenced by figure 13(c). Close to the surface (approximately above $k_0 z > -0.3$), the most enhanced scale near the surface is found around $\lambda _y \sim 0.2 H$, which is slightly larger than that for $w'$. The influence extends to large-scale motions with $\lambda _y\sim H$ but is more localised near the surface than is $w'$. Slightly away from the surface (at $k_0 z = -0.5$), an enhancement at smaller scales can be observed. The overall enhancement effect on $v'$ at different scales is weaker than that on $w'$, consistent with the observations of $\widehat {v'^2}$ in § 4.2.

Figure 13. Pre-multiplied spectrum of spanwise velocity fluctuations $v'$ with respect to the spanwise wavelength $\lambda _y$ at (a) the leading edge ($x'=3\chi$) and (b) the trailing edge ($x'=-3\chi$) of the wave packet. (c) The ratio between the spectra at the trailing edge and the leading edge. Case ${W}_{12}$ is shown.

Figure 14 shows the pre-multiplied energy spectra of the streamwise velocity fluctuations $u'$. In the near-surface region, characteristic double peaks occur, which is associated with the separation of large-scale motions from smaller-scale turbulence motions near the boundary in high-Reynolds-number flows (Hutchins & Marusic Reference Hutchins and Marusic2007). Consistent with the earlier findings in § 4.2 that $\widehat {u'^2}$ experiences the least impact from the wave packet among the three velocity components, the pre-multiplied spectra shown in figure 14 demonstrate that most scales are only slightly affected. The observed enhancement in $\widehat {u'^2}$ is mostly attributed to small-to-mid scales $\lambda _y < 0.3h$. Additionally, we can observe weak yet distinct enhancement at large spanwise scales $\lambda _y \sim H$. This result further supports that the wave packet can affect large-scale turbulent coherent structures.

Figure 14. Pre-multiplied spectrum of streamwise velocity fluctuations $u'$ with respect to the spanwise wavelength $\lambda _y$ at (a) the leading edge ($x'=3\chi$) and (b) the trailing edge ($x'=-3\chi$) of the wave packet. (c) The ratio between the spectra at the trailing edge and the leading edge. Case ${W}_{12}$ is shown.

In summary, the passage of a wave packet is found to induce considerable changes in turbulence, intensifying turbulence fluctuations in all three velocity components, which suggests the transfer of energy from the wave to turbulence. The wave impact on the three velocity components follows the order $w' > v' > u'$, in terms of both the enhancement magnitude and the depth of influence. This observation aligns with our findings for the enstrophy components, where the streamwise vorticity fluctuations experience the most significant enhancement, correlating with the intensification of $w'$ and $v'$. We also find that the enhancement of vertical and spanwise Reynolds normal stresses $\widehat {u'^2_i}$ is approximately proportional to the square of the wave steepness $\alpha ^2$. Furthermore, we find that the variation in the Reynolds normal stresses occurs rapidly within approximately five wave periods in the cases considered. Spectral analysis reveals that the wave packet enhances the near-surface vertical velocity fluctuations at small scales. We note that the appearance of small-scale near-surface streamwise vortices and the associated spanwise alternating vertical velocity fluctuations were observed in laboratory experiments (Melville et al. Reference Melville, Shear and Veron1998; Veron & Melville Reference Veron and Melville2001) and numerical simulations (Li & Garrett Reference Li and Garrett1993; Tejada-Martínez et al. Reference Tejada-Martínez, Hafsi, Akan, Juha and Veron2020) of an initially quiescent flow after the wind started to blow on the surface. The subsequent growth and merging of vortices were considered related to the spin-up and formation of larger-scale Langmuir circulations. In addition to small-scale structures, the present results suggest that surface waves can influence coherent structures at larger scales too. For example, for vertical velocity fluctuations, medium scales rather than small scales are enhanced away from the surface. Moreover, we observe structures with a spanwise scale $\lambda _y \sim h$ in the energy spectra, implying that the wave packet may trigger the generation of large-scale structures. These observations suggest that existing turbulent coherent structures in turbulent flows may be modified by waves. Since the enhanced length scales vary by the velocity components and depth, the underlying mechanisms at different length scales are likely to be different and therefore are analysed next in § 5.