2 Target design and experimental setup

The target design, which models the astrophysical scale, is shown in Figure 1. It is composed of a pusher playing the role of the accreted matter, and an obstacle modelling the white dwarf photosphere. The two parts are separated by a vacuum zone and fixed on a plastic support. The main difference from previous POLAR targets is the absence of the tube.

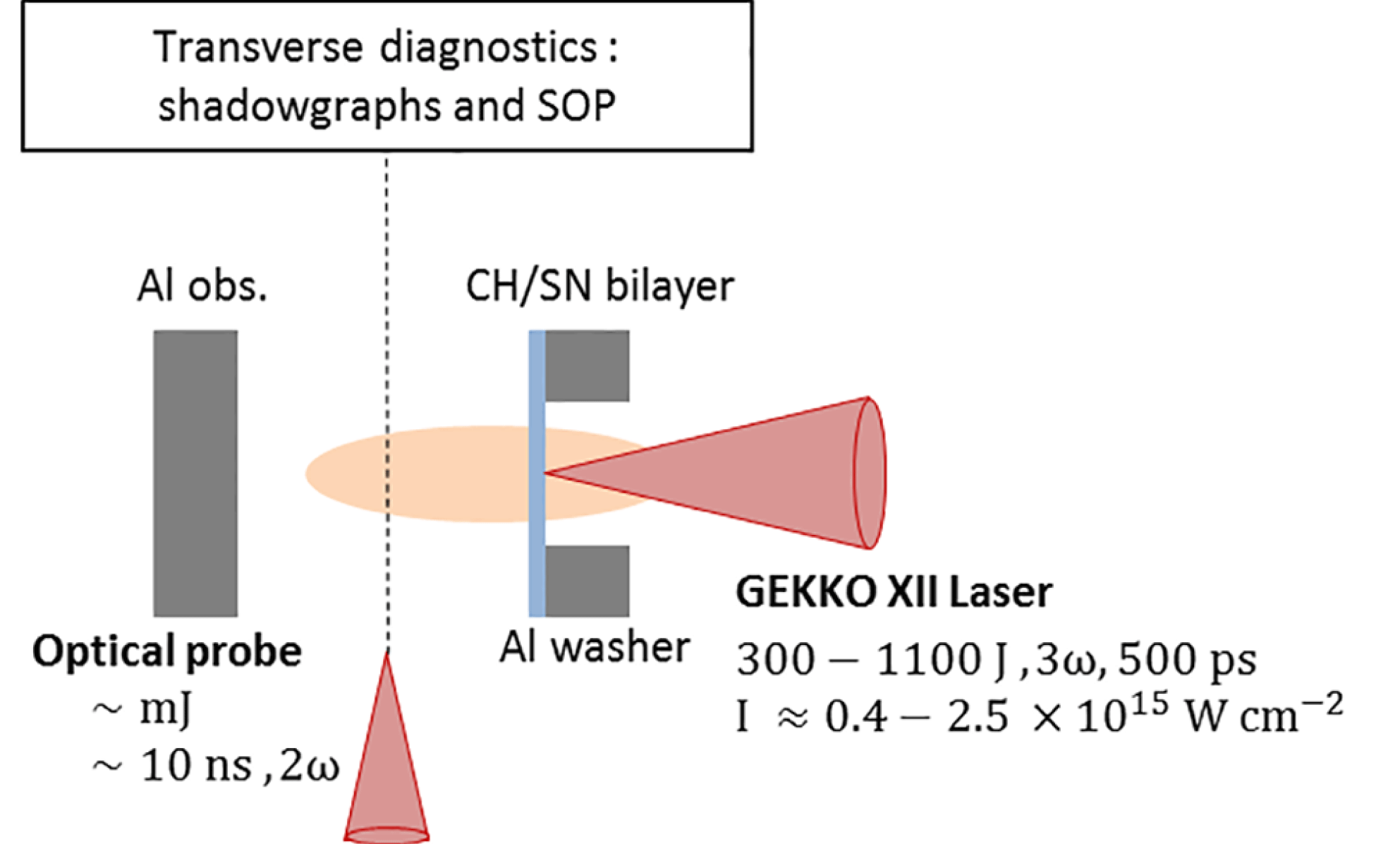
Figure 1. Target’s schematic. The laser comes from the right and it interacts with the pusher. A plasma is created due to the interaction between the laser and the pusher. This supersonic plasma expands in the vacuum and impacts an obstacle. This leads to the creation of a reverse shock.

The pusher is composed of a $25~\unicode[STIX]{x03BC}\text{m}$ thick plastic layer ( $1.29~\text{g}\cdot \text{cm}^{-3}$ ), which converts laser energy into kinetic energy by rocket effect^{[Reference Atzeni and Meyer-ter-Vehn21]}, and a $4~\unicode[STIX]{x03BC}\text{m}$ thick tin layer, which has two important roles: it protects the obstacle against X-ray radiation produced by the hot coronal plasma and increases the radiative properties of the target. All these layers are stuck to an aluminium washer.

Experiments were performed on the GEKKO XII facility. Depending on the chosen laser configuration, the energy delivered to the target can range from 300 J to 1100 J at $3\unicode[STIX]{x1D714}$ wavelength, with a Gaussian focal spot of around $350{-}400~\unicode[STIX]{x03BC}\text{m}$ full width at half maximum and a Gaussian pulse width of 500 ps. The associated intensities can vary from $4\times 10^{14}~\text{W}\cdot \text{cm}^{-2}$ to $2.5\times 10^{15}~\text{W}\cdot \text{cm}^{-2}$ on the target. Seven optical diagnostics methods (1D and 2D streaked optical pyrometer [SOP], 1D and 2D shadowgraphies and interferometry) have been implemented to probe the incoming plasma and the post-shock region. An optical probe beam ( ${\sim}$ mJ, $2\unicode[STIX]{x1D714}$ and 10 ns duration) has been installed in the perpendicular direction to the incoming flow propagation direction. Transverse optical pyrometry (SOP) diagnostics images the self-emission from the incoming flow and the reverse shock structure. In addition, shadowgraphy diagnostics records the global shape of the plasma and interferometers enable inference of the electron density of the flow. Streak cameras record the incoming flow expansion and propagation in vacuum, and the radiation flux emission as a function of time.

We compare experimental results with one-dimensional (1D) and two-dimensional (2D) numerical simulations performed with the CEA laser radiation hydrodynamic arbitrary Lagrangian–Eulerian (ALE scheme) code FCI2^{[Reference Schurtz, Nicolaï and Busquet22]}. We use the multi-group diffusion model ( $100$ groups), which allows one to reproduce the GEKKO XII regime, and the laser–matter interaction is modelled by a ray tracing algorithm^{[Reference Busschaert, Falize, Loupias, Michaut, Ravasio, Pelka, Yurchak and Koenig23]}. The typical longitudinal and radial resolutions of the simulations are around $0.5~\unicode[STIX]{x03BC}\text{m}$ .

To illustrate the experimental principle and the dynamics of the plasma flow, a 1D numerical simulation result is shown in Figure 2. We present the density evolution as a function of time. The plasma, created by the laser–pusher interaction, expands in the vacuum. Then, the supersonic plasma flow impacts an aluminium solid obstacle leading to the formation of a radiative reverse shock, which can be analysed with laser diagnostics. At the same time, a transmitted shock is created in the obstacle. The radiative properties of the post-shock region are proportional to the charge number $Z$ ^{[Reference Busschaert, Falize, Loupias, Michaut, Ravasio, Pelka, Yurchak and Koenig23]}, which justifies the use of a high- $Z$ layer, here the tin layer, to increase radiative effects. Despite the obvious simplicity of the target design, the studied physical processes (collision of an expanding plasma flow with an obstacle and formation of a radiative reverse shock) are relatively hydrodynamical complex issues where high-energy radiation can play a fundamental role.

To study the density and the temperature evolutions in the vacuum, two distances between the pusher and the obstacle, labelled $l_{\text{vac}}$ , are considered: 2.5 mm and 3.5 mm. Indeed, the density ( $\unicode[STIX]{x1D70C}_{\text{flow}}\propto l_{\text{vac}}^{-1}$ ) and the temperature ( $T_{\text{flow}}\propto [l_{\text{vac}}]^{1-\unicode[STIX]{x1D6FE}}$ , considering an adiabatic flow) of the expanding plasma are inversely proportional to powers of the distance to travel.

Figure 2. Spatial evolution of the density as a function of time extracted from 1D simulation performed with FCI2 code. The position axis is horizontal, whereas the time evolution is the vertical axis. The laser deposits 600 J on the target, and it comes from the right. The distance to the obstacle is 3.5 mm.

3 Laboratory accretion plasma

3.1 Plasma flow generation and propagation

First, it is necessary to characterize the plasma structure and dynamics before the collision since the reverse shock depends on the physical properties of the incident flow. A typical image from shadowgraphy diagnostics is presented in Figure 3. The length of the flow is 1.6 mm around 7 ns before the collision and its radial expansion is $860~\unicode[STIX]{x03BC}\text{m}$ for a laser energy of 836 J.

Figure 3. 2D snapshot shadowgraphy obtained at 13 ns after the laser drive of the incident plasma flow.

We compare these values with a 2D axisymmetrical numerical simulation. The density and temperature maps of the incident flow around 10 ns before the collision obtained by simulation are presented in Figure 4. Due to the absence of the tube, the Sn plasma expands in vacuum by creating a bubble around the CH plasma. The contact discontinuity between Sn and CH layers can be observed in Figure 4(b), which confirms the bubble structure of the flow. The velocity of the high- $Z$ radial bubble expansion can be evaluated to about $20~\text{km}\,\cdot \,\text{s}^{-1}$ , which corresponds to the transverse kinetic energy lost for the propagation. The dimensions of the flow obtained by simulations (Figure 4(a)) are compatible with those of the experimental data in Figure 3. Moreover a collimation effect is induced by Sn expanding plasma stuck on the washer, which creates an important pressure gradient located at the internal radius of the aluminium washer. The expanding plasma is due to the propagation of thermal waves created by the interaction of laser with matter, where electrons transport energy. This structure generates an analogue nozzle geometry. This effect induces a hydrodynamic collimation of the flow visible both in experimental data (see Figure 3) and simulation (see Figure 4).

Figure 4. (a) Density and (b) temperature maps of the incident flow around 10 ns before the collision extracted from 2D FCI2 simulation.

In the shadowgraphy, a low-density plasma is observed. It is confirmed in the 2D snapshot interferometry (Figure 5(a)) where we can observe strong perturbations of the fringes around the plasma flow. These irregularities are due to lower plasma expansion ahead of the flow. The electronic density of this low-density matter is presented in Figure 5(b). It has been calculated assuming a cylindrical symmetry using Neutrino softwareFootnote ¹ . The iso-density curves at $10^{18}$ , $10^{19}$ and $10^{20}~\text{cm}^{-3}$ extracted from 2D simulations are added to the experimental electronic density (see the black lines in Figure 5(b)). In spite of some disparities due to large errors in the determination of the fringe shifts, a global agreement is found between the experimental and numerical plasma shapes.

Figure 5. (a) 2D snapshot interferometry obtained at 11 ns after the laser drive of the incident flow compared with (b) the associated electronic density. The experimental electronic density is compared to iso-density curves at $10^{18}$ , $10^{19}$ and $10^{20}~\text{cm}^{-3}$ extracted from 2D simulations (black lines).

From 1D transverse shadowgraphy and 1D self-emission diagnostics, we can infer the expansion velocity that is of prime importance to the radiative properties of the post-shock region as we will see later. Typical images are presented respectively in Figures 6 and 7. The plasma created by the laser comes from the right. The position is relative to the obstacle position, whereas the vertical axis presents the time evolution. The mean velocity of the incoming flow is $115~\text{km}\cdot \text{s}^{-1}$ with a collision time of about 20 ns.

Figure 6. 1D shadowgraphy used to determine the velocity of the incident flow. The plasma created by the laser comes from the right. The position is relative to the obstacle position, whereas the vertical axis presents the time evolution.

Figure 7. 1D self-emission (SOP). The plasma created by the laser comes from the right. The position is relative to the obstacle position, whereas the vertical axis presents the time evolution. The CH flow position (white dotted line), the reverse shock position (white line) and the 10 eV iso-contour (black line) extracted from 2D simulations are added.

We can notice that the incoming flow position is slightly overestimated with the SOP diagnostics ( $\!v_{\text{flow}}\!\,=\!\,125~\text{km}\,\cdot \,\text{s}^{-1}\!$ ) compared to the shadowgraphy ( $v_{\text{flow}}=105~\text{km}\,\cdot \,\text{s}^{-1}$ ). The plasma density, probed by the shadowgraphies, is close to the critical density $n_{e}\sim n_{c}\sim 10^{21}~\text{cm}^{-3}$ , whereas the radiation is emitted by a lower density zone with $n_{e}<10^{20}~\text{cm}^{-3}$ in front of the flow. The flow lengths determined by 2D shadowgraphy snapshots are added on the 1D shadowgraphy presented in Figure 6 (red points). Good agreement is found between the 1D and 2D shadowgraphies. In the 2D FCI2 simulations, the plasma flow at lower density and at about 5 eV propagates at ${\sim}130~\text{km}\cdot \text{s}^{-1}$ , whereas at about $n_{c}$ , it propagates at a lower velocity, ${\sim}100~\text{km}\cdot \text{s}^{-1}$ . Good agreement is found for the impact time and for the velocity of the plasma flow. The simulation forecasts a hypersonic incident flow with an internal Mach number around $14$ . During the expansion of the incident flow, the obstacle is heated before the collision due to the high-energy radiation coming from the coronal plasma. The expansion velocity of the obstacle is about $15~\text{km}\cdot \text{s}^{-1}$ as shown in Figure 6. This does not disturb the collision and the generation of the reverse shock.

Figure 8 summarizes the different plasma flow velocities determined from the experimental data as a function of the laser energy achieved at the GEKKO XII facility. The errors are associated with the uncertainties in the plasma position determination from the diagnostics, which are linked to the uncertainties of the plasma velocities. We compared the plasma flow velocities extracted from 2D simulations (black triangles and diamonds) to the 1D shadowgraphy (blue squares) and the 1D SOP (red points). The SOP velocities (red points) are compared to velocities of the iso-temperature curve at 5 eV in the incident flow at different laser energies (black triangles). Then the shadowgraphy velocities (blue points) are correlated with the velocities of the iso-density curve at $n_{c}$ density (black diamonds). A good agreement is obtained between experimental and numerical data for the two types of flow.

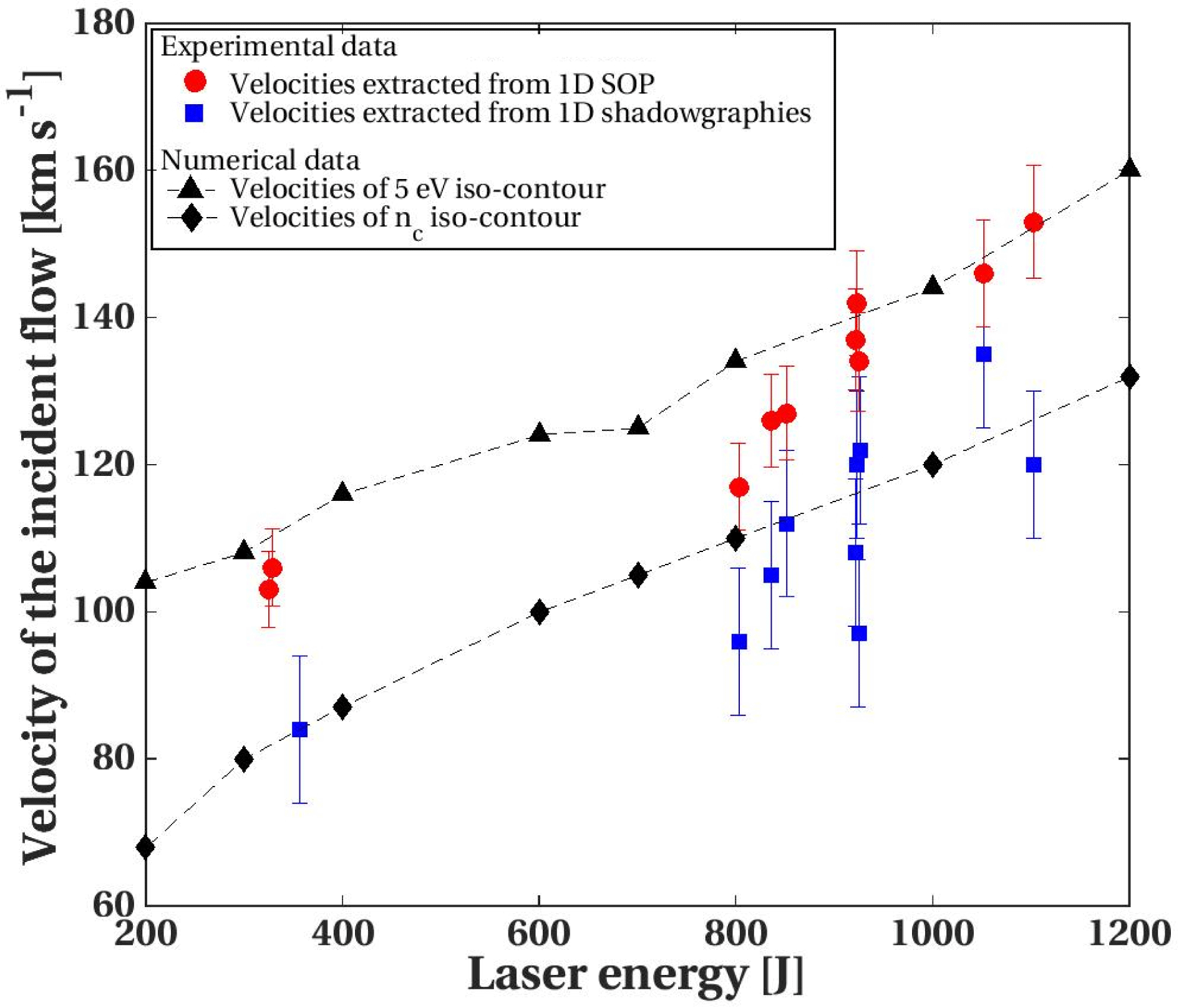
Figure 8. Experimental velocities of the incident flow as functions of the laser energy extracted from the 1D shadowgraphies (blue squares) and from the 1D SOP (red points). They are compared to velocities extracted from 2D simulations: velocities of the iso-temperature curve at 5 eV (black triangles) and velocities of the iso-density curve at $n_{c}$ density (black diamonds).

3.2 Reverse shock structure

The plasma impacts the obstacle at about 20 ns (see Figures 6 and 7) leading to the formation of a reverse shock and a transmitted shock in the obstacle (see Figure 2). Based on the Rankine–Hugoniot conditions for a strong shock, the typical post-shock temperature can be expressed as a function of the incoming flow velocity, $v_{\text{flow}}$ , and the material characteristics (the atomic number $A$ and the charge number $Z$ ): $T_{\text{ps}}\propto [A/(Z+1)](v_{\text{flow}})^{2}$ . Consequently the post-shock temperature is about $T_{\text{ps}}\sim 40~\text{eV}$ . When the flow impacts the obstacle, a radiative flash (heat wave) is generated and observed both in simulations (see Figure 9(a)) and SOP diagnostics (see Figure 7, at 20 ns). The spatial extension of this emission structure is proportional to the Rosseland mean free path of the pre-shock matter ( $L_{R}\propto \unicode[STIX]{x1D706}_{R}(\unicode[STIX]{x1D70C}_{\text{flow}},T_{\text{flow}})$ ). This leads to the creation of a radiative structure upstream of the shock.

From the 2D simulation, we can determine that the reverse shock propagates into the Sn incoming flow at a slow velocity ( $v_{\text{shock}}\sim 5~\text{km}\cdot \text{s}^{-1}$ ) due to the density increase in the post-shock region. With only optical diagnostics, it is not possible to exhibit the position of the reverse shock on experimental data. To probe its structure and its position, X-ray radiographies are necessary. However, the visible emitting region in SOP figures proves that the radiative structure is sustained by a reverse shock as shown by the 2D simulations (see Figure 7). Indeed without the presence of the reverse shock, the strong emission generated on impact would decrease rapidly, which is not the case here. We define the extension of the radiative structure as the heat zone higher than about 10 eV. The positions of the reverse shock (white line) and the radiative structure (iso-curve at 10 eV in black line) determined from simulations are compared with experimental data extracted from the 1D SOP diagnostics in Figure 7. The simulation can reproduce the dynamics of the emission region. At the CH arrival at about 10 ns after the impact, the reverse shock accelerates at $25~\text{km}\cdot \text{s}^{-1}$ . The radiative structure persists until the reverse shock catches up with it, which confirms that this particular structure is not a radiative precursor. After 20 ns following the collision, the emission region and the post-shock region are mixed (see Figure 9(b)).

Figure 9. Density and temperature maps of the incident flow extracted from 2D numerical simulation around (a) 5 ns and (b) 20 ns after the collision. Just after the collision, the reverse shock is not propagated, whereas a radiative flash is clearly visible in the impact zone. Around 20 ns after the collision, the reverse shock has caught up with the radiative structure.

The reverse shock structure depends strongly on the laser parameters and the distance to the obstacle. This is due to the fact that the temperatures of the accretion flow and the post-shock region increase with the laser energy, which strengthens the radiative effects. However the distance of the obstacle decreases the density and the temperature of both the expanding plasma and the post-shock structure because of the longer relaxation in the vacuum.

4 Similarity properties

Table 1. Similarity properties of four typical shots at different laser energies and different distances from the obstacle. Values are extracted from the 2D simulations performed with the FCI2 code.

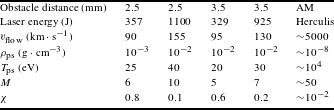
The similarity properties are presented in Table 1. In order to evaluate the hydrodynamic parameters of the post-shock region, the quantities are estimated when the reverse shock is located at $200~\unicode[STIX]{x03BC}\text{m}$ from the obstacle, according to the simulations. The characteristic parameters (plasma flow velocity $v_{\text{flow}}$ , post-shock density $\unicode[STIX]{x1D70C}_{\text{ps}}$ and temperature $T_{\text{ps}}$ ) and the cooling parameter are compared with the data from the polar prototype AM Herculis star in high-state accretion^{[Reference Gänsicke, Beuermann and de Martino24]}. The Mach number ( $M$ ) of the reverse shock is defined as $(v_{\text{flow}}-v_{\text{shock}})/c_{s,\text{ps}}$ . The cooling parameter ( $\unicode[STIX]{x1D712}$ ) in the post-shock region characterizes the balance between the radiative processes and the hydrodynamics in the radiative zone^{[Reference Falize, Michaut and Bouquet12]}, and then the astrophysical relevance of such laboratory targets. In such a process where radiation effects are of some relevance, the cooling parameter offers a qualitative hydrodynamic scaling. However, the atomic physics processes might only be partially addressed by such a macroscopic dimensionless number. The cooling parameter is defined as the ratio between the cooling time and the dynamical time in the post-shock region. The dynamical time is defined as the ratio of the length of the post-shock region to the sound velocity. The cooling time is determined as the ratio of the internal energy density to the emissivity of the medium. Due to the relatively low temperature and high density of the laboratory plasma compared to the astrophysical regime, the plasma emissivity is not due to the bremsstrahlung cooling. Thus the laboratory emissivity of the medium is given by $\unicode[STIX]{x1D716}\sim \unicode[STIX]{x1D705}_{P}\unicode[STIX]{x1D70E}T^{4}$ , where $\unicode[STIX]{x1D705}_{P}$ and $\unicode[STIX]{x1D70E}$ are respectively the Planck mean opacity and the Stefan–Boltzmann constant.

The targets achieve a cooling parameter below 1, $\unicode[STIX]{x1D712}\sim 0.1{-}1$ , which implies that the cooling losses start to play a role in the structure of the post-shock region. The increase of the obstacle distance decreases the density and the temperature of the expanding flow, which cools the post-shock region as shown in Section 3. Consequently, the increase of the obstacle distance increases the cooling parameter. By increasing the laser energy, the cooling parameter can reach $0.1$ . In these laboratory conditions, although the cooling parameter is below 1, the radiative losses play a role in the evolution of the plasma but do not dominate the dynamics as in the astrophysical regime ( $\unicode[STIX]{x1D712}\lesssim 10^{-2}$ ). The GEKKO XII facility allows us to achieve a radiative regime similar to that achieved at the LULI2000 facility^{[Reference Falize, Loupias, Ravasio, Gregory, Dizière, Koenig, Michaut, Cavet, Barroso, Leidinger, Ribeyre, Breil, Takabe, Sakawa, Kuramitsu, Morita, Woolsey, Nazarov and Pikuz16, Reference Falize, Ravasio, Loupias, Dizière, Gregory, Michaut, Busschaert, Cavet and Koenig17]} for low-energy configuration ( $\unicode[STIX]{x1D712}\sim 1$ ) and that achieved at the Orion facility^{[Reference Cross, Gregori, Foster, Graham, Bonnet-Bidaud, Busschaert, Charpentier, Danson, Doyle, Drake, Fyrth, Gumbrell, Koenig, Krauland, Kuranz, Loupias, Michaut, Mouchet, Patankar, Skidmore, Spindloe, Tubman, Woolsey, Yurchak and Falize18]} at high-energy configuration ( $\unicode[STIX]{x1D712}\sim 0.1$ ) (see Figure 10). The intermediate energies allow us to reach new radiative hydrodynamic regimes ( $\unicode[STIX]{x1D712}\sim 0.1{-}0.5$ ), not studied yet. The velocities, associated with the range of laser energies used in the GEKKO XII facility, measured with the SOP and the shadowgraphy diagnostics, vary from 90 to $160~\text{km}\cdot \text{s}^{-1}$ for the different types of target designs. The obtained radiative regime links and fills the gap between the LULI2000 and Orion regimes as shown in Figure 10. In order to achieve a similar regime at the laboratory scale, the scaling laws point out that the incident flow must reach about $300~\text{km}\cdot \text{s}^{-1}$ and the post-shock medium must be dominated by the bremsstrahlung losses with $\unicode[STIX]{x1D712}\sim 10^{-2}$ . These conditions are illustrated by the horizontal line in Figure 10. Targets used in intermediate laser facilities, such as the GEKKO XII laser facility, cannot reach a similar astrophysical regime. Thus, these experimental regimes should be accessible in megajoule laser facilities such as the Laser Megajoule and the National Ignition Facility.

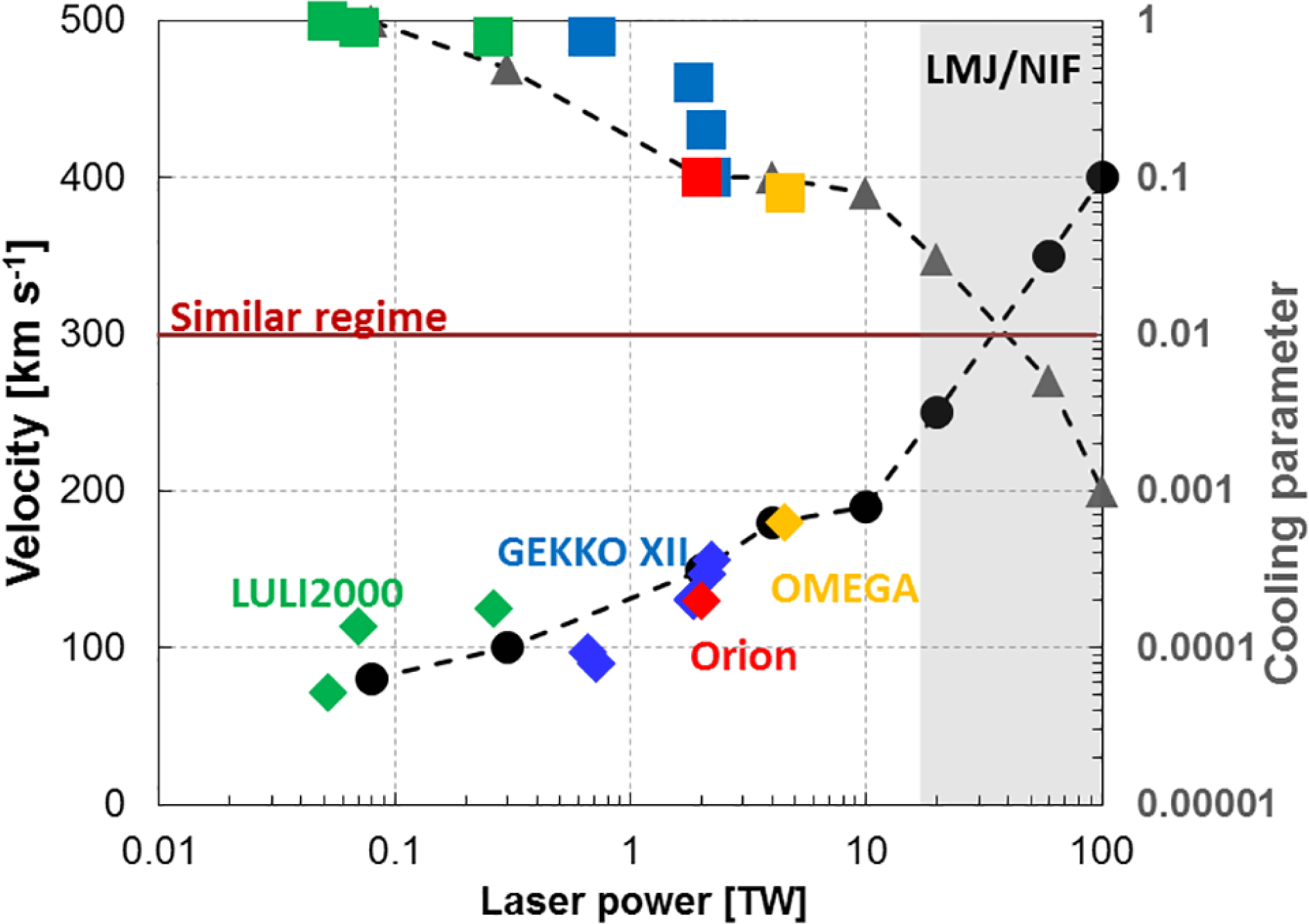
Figure 10. Velocities and cooling parameters in the POLAR project as a function of the laser power. Simulations are presented by dotted black lines. Experimental results obtained with intermediate laser facilities are displayed by coloured dots. The results obtained with GEKKO XII are presented by blue dots.