Introduction
Highly disparate constitutive relations have been proposed for sediment deformation beneath glaciers (e.g. Reference Alley, Blankenship, Bentley and RooneyAlley and others, 1987; Reference Boulton and HindmarshBoulton and Hindmarsh, 1987; Reference KambKamb, 1991). None has gained widespread acceptance due to a lack of reliable field measurements and appropriately configured laboratory experiments.
Reference Blake, Clarke and GérinBlake and others (1992) presented novel down-hole techniques for the measurement of shear strain in a subglacial sediment layer. As a complement to deformation measurements, continuous measurements of the shear stress that ice exerts on the upper surface of such a layer are needed. Estimates based on glacier geometry are unsatisfactory, as they yield only spatial and temporal averages. Thus, as an alternative, efforts have been directed at measuring the sediment strength by inserting an instrument into sediment at the bottom of a borehole. Reference Humphrey, Kamb, Fahnestock and EngelhardtHumphrey and others (1993) and Reference Fischer and ClarkeFischer and Clarke (1994) determined the force on a long cylinder fixed at the base of a borehole and ploughing through the deforming bed. By assuming that the sediment deformed as an ideal plastic, they arrived at estimates of the yield strength. They also considered a Newtonian viscous rheology and were able to estimate the apparent viscosity of the sediment.
Any technique for measuring the strength of sediment beneath glaciers should ideally satisfy a number of criteria, some of which are quite restrictive:
-
1. The technique should draw upon extensive theoretical and empirical developments from geotechnical engineering on in-situ testing of sediment.
-
2. Any assumed rheology for the sediment should explicitly include the important influence of effective pressure on strength.
-
3. The measurement should be made in sediment some distance from the base of the borehole. Steep gradients in effective normal stress are expected beneath the edges of the borehole because the ice-overburden pressure there is zero and because the pore pressure there is likely to be perturbed. These problems make standard down-hole methods for measuring sediment strength, such as penetrometer and vane-shear tests, undesirable, particularly when the borehole diameter is a significiant fraction of the sediment-layer thickness.
-
4. The measuring device should not perturb the ambient pore-water pressure in the sediment, or alternatively, if the pore pressure is perturbed, it should be measured or estimated and factored into the data reduction.
Here, a technique is presented that, to a large extent, satisfies these criteria. Initial results are reported that are part of a more comprehensive data set on basal till deformation gathered at Storglaciären. The till is considered to be a granular material in which resistance to deformation is controlled by intergranular friction. This is a particularly good assumption for the till beneath Storglaciären, which contains little clay and consists mostly of coarse silt and fine sand, like most tills developed on crystalline bedrock in Scandinavia and North America (Reference Dreimanis, Vagners and GoldthwaitDreimanis and Vagners, 1971; Reference Scott and LeggetScott, 1976; Reference JorgesenJorgesen, 1977; Reference HaroldsenHaroldsen, 1981).
Method
Instrument design
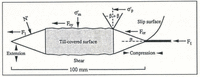
As in other studies (Reference Humphrey, Kamb, Fahnestock and EngelhardtHumphrey and others, 1993; Reference Fischer and ClarkeFischer and Clarke, 1994), we sought to measure till strength by dragging an object through the till and measuring the force on the object. Our device (Fig. 1), hereafter referred to as a “dragometer”, consists of a steel cylinder with conical ends, dubbed the “fish”, that is dragged through the till by a 1.9 m long steel pipe. The fish is 100 mm long and 19 mm [3/4 in] in diameter (Fig. 2). A flexible, vinyl-covered aircraft cable with a diameter of 1.6 mm [1/16 in] runs from the fish up through the bottom of the pipe to a load cell that is housed in a separate module in the pipe’s upper end. The module is filled with mineral oil to prevent penetration of water into the load cell. The pipe and fish are lowered down a borehole and driven into the bed with a percussion hammer and insertion tube similar to that used by Reference Blake, Clarke and GérinBlake and others (1992) (Fig. 1a). After insertion, the hammer and tube are withdrawn leaving the pipe and fish embedded in the till. Eventually, owing to the glacier motion, the pipe jams in the bottom of the borehole. After several days of bed deformation, probably together with sliding at the ice—till interface, the cable becomes taut and the fish begins moving through the till (Fig. 1b). The instrument is calibrated by fixing the pipe horizontally and hanging weights on the cable at a right-angle to the pipe axis.

Fig. 1. Sketch of dragometer; (a) immediately after insertion and (b) in operation.

Fig. 2. Cross-section of fish moving from left to right through till. Slip surfaces lie approximately parallel to surface defined by β. Other parameters are discussed in the text and Appendix.
The cable length was adjusted so that the fish was dragged 100 mm behind the base of the pipe, which was 19 mm in diameter. This length was sufficient to position the fish beneath the ice, rather than beneath the borehole, but was short enough to provide an acceptably small time between insertion and the beginning of the experiment. Whether this distance was large enough to insure that the disturbance caused by the ploughing pipe did not significantly affect the force on the fish is assessed later.
Theory
It is well established that granular materials have a yield strength, τ, at which they begin to deform irrecoverably. This strength is typically expressed by the Coulomb failure criterion:
where c is the cohesion, ϕ is the angle of internal friction, σ′ is the effective normal stress (the difference between the total normal stress and the pore pressure) acting on the zone of failure. Dilation of sediment as it begins to shear results in a reduction of the apparent friction angle. This effect is complemented by the alignment of platy clay minerals during shearing. After shearing displacements that vary from several millimeters to several meters, the sediment volume and friction angle become steady (e.g. Reference SkemptonSkempton, 1985). At this point, the sediment is said to have reached its residual state and to have a residual friction angle, ϕr . There is no cohesion in the residual state (Reference MitchellMitchell, 1976, p. 313; Reference HeadHead, 1982, p. 532). It is this residual strength of the deforming sediment that we wish to measure.
The shear stress supported along a shear plane through the sediment depends on the friction between grains and the extent of grain interlocking (Reference Lambe and WhitmanLambe and Whitman, 1969, p. 130). In order to simulate this friction and interlocking, till from beneath Storglaciären, excluding grains larger than 2 mm, was cemented to the cylindrical part of the fish (Fig. 2). Therefore, the shear force supported by the cylinder sides divided by the surface area of the cylinder should approximate the till’s residual strength.
A significant fraction of the total (measured) force on the fish, however, is exerted on its leading end. Thus, the partitioning of the force between the leading cone and the sides of the fish must be determined. This problem has been studied extensively by engineers concerned with calibration of cone penetrometers. Such instruments are used in drillholes to provide estimates of the mechanical properties of on-and offshore sediments (see Reference Ruiter, Verruijt, Beringen and de LeeuwRuiter (1982) for a review).
The force on the leading end depends on a number of factors, and no single theory yet addresses all of these without some empiricism. Most importantly, it depends on the composition and rheology of the till. The till rheology is complicated by the compressibility of granular materials and the influence of the effective normal stress. In addition, forces measured in penetrometer tests depend sensitively on the penetrometer roughness (Reference Durgunoglu, Mitchell and BromsDurgunoglu and Mitchell, 1974).
Consistent with studies of cone penetration, we assume that the sediment behaves as a Coulomb plastic material. Like an ideal (Mises) plastic, the strength is independent of the deformation rate. In addition, the strength is explicitly formulated in terms of the effective normal stress (Equation (1)). This model is well suited to studies of sediment deformation in which intergranular friction provides most or all of the resistance to deformation in the residual state. Indeed, it is the classic model on which most geotechnical work and many models of landslide behaviour are based (e.g. Reference Savage and SmithSavage and Smith, 1986; Reference Baum and FlemingBaum and Fleming, 1991).
Consider deformation around the leading cone as the fish ploughs forward (Fig. 2). There is a zone of compression where plastic deformation occurs. Empirical studies show that the shape and size of this zone vary with grain-size distribution, sediment consolidation, cone roughness and cone angle, α. The angle β defines a surface that lies approximately parallel to slip surfaces within the zone of compression. Experiments with cones, plates and piles indicate that it varies from +15° in compressible, fine sediment to −30° in compact, coarsegrained sediment (Reference Janbu, Senneset and BromsJanbu and Senneset, 1974; Reference Senneset, Janbu, Chaney and DemarsSenneset and Janbu, 1985). We will assume that β = +15° because basal tills should be compressible in the residual state and are typically dominated by silt and fine sand, like the till beneath Storglaciären.
The force, F c, on the leading end is given by
where A c is the cross-sectional area of the cone, σ′p is the effective stress in the direction of the fish axis, C a is called the “attraction” and is equal to c/ tan ϕ r and N F is a bearing-capacity factor (Janbu and Senneset, 1974; Reference Senneset, Janbu, Svano, Verruijt, Beringen and de LeeuwSenneset and others, 1982; Reference Senneset, Janbu, Chaney and DemarsSenneset and Janbu, 1985). A simple expression for N F in plane strain that agrees reasonably well with experiments using cones, plates and piles is

(Reference Janbu, Senneset and BromsJanbu and Senneset, 1974). For deforming till in its residual state, ϕ = ϕ r, and there is no cohesion, so C a should be zero. Thus, substituting Equation (3) into Equation (2), the bed-parallel force on the leading cone for till in the residual state, F cr, is given by

The force supported parallel to the roughened sides of the cylindrical part of the fish, F cy, is given by

where A cy is the surface area of the cylinder, and σ′ m is the mean effective normal stress acting on the cylinder.
A good approximation is to neglect the force, F 1, on the trailing cone (Appendix), leaving the total bed-parallel force, F t, equal to the sum of Equations (4) and (5). Effective stresses in the till are probably not isotropic, but without information to the contrary, it is assumed that σ′ = σ′ p = σ′ m. Dividing Equation (5) by the sum of Equations (4) and (5) gives the fraction of the total force on the fish that is supported along its sides, κ:

Using κ and the measured value of F t, the residual strength, τr, and the effective normal stress can be determined from
Figure 3 illustrates how κ varies through the potential range of residual friction angle.

Fig. 3. κ as a function of residual friction angle.
To some extent, ϕ r can be estimated from the sediment composition. For example, for sediment that contains less than 25% clay, ϕ r should typically be greater than 20° (Reference SkemptonSkempton, 1985). A better alternative is to measure ϕ r in laboratory tests. We conducted a series of drained direct-shear tests (Reference HeadHead, 1982, p. 509–71) on till collected from the bed of Storglaciären. The test yielded a peak friction angle of 31° and a cohesion of 5 kPa. Although the geometry of the test cell limited the shearing displacement to about 80 mm, the samples contained no clay and were normally consolidated. Under these conditions, there is generally no post-peak reduction in strength observed in experiments carried out to large strains (Reference Lambe and WhitmanLambe and Whitman, 1969; Reference SkemptonSkempton, 1985). Thus, a good assumption is that ϕ r = 31°, which yields κ = 0.30.
Excess pore pressure
Our technique, as well as others (Reference Humphrey, Kamb, Fahnestock and EngelhardtHumphrey and others, 1993; Reference Fischer and ClarkeFischer and Clarke, 1994), is only appropriate when subglacial sediment is sufficiently permeable that compression in front of the ploughing object does not result in pore pressure in excess of hydrostatic pressure. In practice, during cone-penetration tests on impermeable sediments such as clay and silt, excess pore pressure does tend to develop adjacent to the cone and shaft, and this may weaken the sediment by an order of magnitude (e.g. Reference Campanella, Robertson and GillespieCampanella and others, 1983; Reference Senneset, Janbu, Chaney and DemarsSenneset and Janbu, 1985). The standard rate of cone penetration in such tests, however, is 0.02 ms−1 (Reference Campanella, Robertson and GillespieCampanella and others, 1983), which is orders of magnitude faster than rates of glacier sliding. It is, therefore, uncertain whether excess pore pressure might develop in till adjacent to the fish.
In order to investigate this problem, we follow scaling arguments by Reference RudnickiRudnicki (1984) and Reference Iverson and LaHusenIverson and LaHusen (1989) and calculate a dimensionless parameter, R, which depends on the relative rates at which the grain skeleton is compressed and at which pore pressure diffusively dissipates:
Here, k is the hydraulic permeability of the till, V is the fish velocity relative to the till, χ is the till compressibility, μ is the dynamic viscosity of water at 0°C (1.78 × 10−3 Pa s) and δ is a characteristic length, equal to the diameter of the zone of compression in front of the fish. R is the ratio of the time-scale for generation of excess pore pressure to the time-scale for diffusive pore-pressure equilibration across δ(δ/V to δ 2 μχ/k). Thus, when R is sufficiently large, significant excess pore pressure should not develop.
Such scaling arguments are most useful if the threshold value or range of values for R can be determined from experiments in which all relevant parameters are known. Reference Campanella, Robertson and GillespieCampanella and others (1983) presented the results of a cone-penetration test on a silty clay in which the rate of cone penetration was systematically varied and excess pore pressure was recorded by a transducer in the cone. Their data suggest that significant excess pore pressure developed at a velocity of the order of 10−4 m s−1. Other parameters were k = 8 × 10−16 m2, δ ∼ 0.05 m and μ = 1.1 × 10−3 Pa s. They did not report the sediment compressibility; a reasonable range is 10−16 − 10−8 Pa−1 (Reference Freeze and CherryFreeze and Cherry, 1979, p.55; Reference HeadHead, 1982, p.683). Inserting these values in Equation (8) yields a threshold range for R of 0.15–15. Thus, a good assumption is that when R >> 15 excess pore pressure should not develop ahead of the fish.
Empirical studies of sediment deformation beneath cone penetrometers (e.g. Reference Malyshev, Lavisin and BromsMalyshev and Lavisin, 1974; Reference Koumoto, Kaku, Verruijt, Beringen and de LeeuwKoumoto and Kaku, 1982) suggest that δ = 0.02 m is a good approximation for our fish. Several tests with a falling-head permeameter on till samples collected from beneath Storglaciären yielded k = 1.3 × 10−14m2. V cannot exceed the surface velocity, which on Storglaciären seldom exceeds 0.1 m d−1 during the summer. The compressibility of the till beneath the glacier has not been measured; we choose a maximum value of 1 × 10−6 Pa−1 in order to minimize R. Using these values in Equation (8) shows that R exceeds 315 for experiments on the till beneath Storglaciären, indicating that pore pressure adjacent to the fish did not exceed hydrostatic pressure.
However, on glaciers with less permeable subglacial sediment and higher sliding velocities, the time-scales for the generation and dissipation of excess pore pressure may be of the same order. For example, for the sediment beneath Ice Stream B, Antarctica, k = 2 × 10−16 m2, and V may approach 2.3 m d−1 (Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990). In this case, R ranges from 0.21 to 21 for 10−6 > χ > 10−8 Pa−1. Therefore, excess pore pressure may develop and would need to be measured or estimated.
Laboratory tests
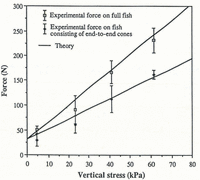
In an effort to evaluate the theory, laboratory tests were conducted in which the fish was dragged through till collected from Storglaciären. The till was dry and was confined within a 0.28 m × 0.14 m × 0.16 m box. A normal stress was exerted on the upper surface of the till by a platen loaded with weights, while the fish was dragged horizontally along the long dimension of the box. A second fish consisting of end-to-end cones was also used to study forces on the fish ends alone. Results from 16 experiments with each fish type are plotted in Figure 4.

Fig. 4. Experimental and theoretical values for force on full fish and force on fish consisting of end-to-end cones, as a function of vertical stress. Each experimental value is the mean of four measurements. Error bars show ±1 standard deviation.
The experimental conditions differed from those at a glacier bed in several ways. In the experiments, the till was not deforming independently of the fish motion, and thus it was not necessarily in the residual state. Therefore, cohesive forces may have been operating in the zone of compression in front of the fish. Along the fish sides, no cohesion was expected because minute particles responsible for cohesive forces should have been effectively submerged in the epoxy resin used for cementation. The theoretical force on the full fish, therefore, was calculated by adding Equations (2) and (5). A further complication is that effective stresses were not isotropic in the experiments. It is well established that when sediment is loaded vertically in confined compression for the first time, the horizontal stress σh is less than the vertical stress σv. A relation that fits most experimental values was suggested by Reference JákyJáky (1944) (in Reference Lambe and WhitmanLambe and Whitman 1969, p. 127):
This relation was used to determine
The theory approximates the measured force on the fish relatively well (Fig. 4). Although the laboratory till was dry, its behavior would not be significantly different if it were water-saturated, but drained well enough so that excess pore pressure did not develop (Reference Lambe and WhitmanLambe and Whitman, 1969, p. 295). Thus, these experiments demonstrate that the theory adequately approximates the total force on the fish and the force on the fish ends. Therefore, values of κ calculated from Equation (6) can be used with some confidence in Equations (7) to estimate the residual strength and local effective normal stress from the measured force on the fish.
Results From Storglaciären
The dragometer was used to study the residual strength of till beneath 95 m of ice in the ablation area of Storglaciären. Tiltmeters inserted in this till demonstrate that it is actively shearing (Reference Iverson, Jansson, Hooke and HansonIverson and others, 1992). Prior to installing the instrument, a penetrometer was driven into the till, which yielded a minimim till thickness of 0.35 m. The depth of fish emplacement is difficult to determine accurately due to possible settling of the insertion assembly into the till prior to hammering. However, the penetration caused by hammering can be measured with a precision of approximately 0.01 m. This measurement indicated an initial minimum depth of travel for the fish of 0.06 m.
The raw data (Fig. 5) show that the signal from the dragometer changed immediately after insertion. This is partly a temperature-related effect caused by submerging the load cell in water at 0°C. Some of the change probably reflects tension on the cell resulting from friction between sediment and the cable. The cable was observed to fall out of the end of the pipe under its own weight as the dragometer was prepared for insertion. Thus, a fraction of the exposed cable may have tightened due to friction along its length prior to tightening of the full cable length. Assuming a friction coefficient of 1.0 and an effective normal stress on the full cable length of 100 kPa yields friction equivalent to about 0.35 mV in Figure 5.

Fig. 5. Dragometer signal. Rapid increase on 15 July 1992 is inferred to be when cable became taut and fish began ploughing through till.
Four days after insertion, there was a rapid increase in the load-cell signal (Fig. 5). The increase is inferred to represent the tightening of the cable as the fish began to be dragged through the till. If this is correct, the relative velocity between the fish and the basal ice would have had to have been about 26 mm d−1 over this 4 d period, a speed that is consistent with the mean surface velocity, 42 mm d−1. The difference between these speeds presumably reflects deformation of ice and especially till.
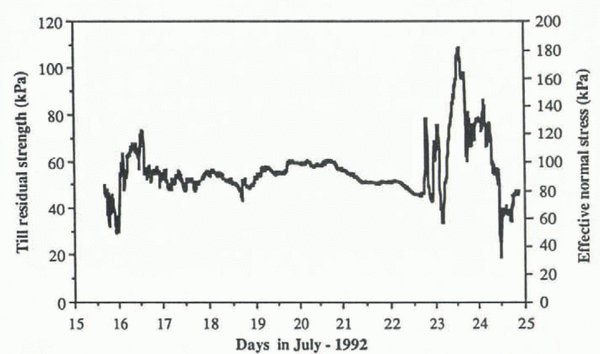
The signal was converted to a force, F t, which was then substituted into Equations (7) to obtain the residual strength and the effective normal stress on the till (Fig. 6). κ was calculated using a residual friction angle of 31° and β = 15°.

Fig. 6. Residual strength of till and effective normal stress calculated from measured force on fish.
The average residual strength of the sediment over the period of the measurement was approximately 55 kPa. This is about 60% of the winter basal shear stress, calculated from the driving stress by measuring lateral and longitudinal strain rates and applying a force-balance model for the area just up-glacier from the site of the experiment (Reference Hooke, Calla, Holmlund, Nilsson and StroevenHooke and others, 1989). The unsteady character of the record is similar to records obtained with cone penetrometers (e.g. Reference McNeilan, Bugno, Chaney and DemarsMcNeilan and Bungo, 1985; Reference Senneset, Janbu, Chaney and DemarsSenneset and Janbu, 1985). We interpret these apparent variations in strength, together with changes in the rate of shear strain measured in the till nearby and sub-hourly variations in glacier-surface velocity (unpublished work of B. Hanson), in a second paper in preparation.
Discussion and Conclusions
Like other in-situ determinations of the mechanical properties of basal till (Reference Humphrey, Kamb, Fahnestock and EngelhardtHumphrey and others, 1993; Reference Fischer and ClarkeFischer and Clarke, 1994), ours requires that a specific till rheology be chosen. Numerous empricial studies of cone penetration through sand, silt and clay demonstrate that the Coulomb plastic model is reasonable (e.g. Reference Durgunoglu, Mitchell and BromsDurgunoglu and others, 1974; Reference McNeilan, Bugno, Chaney and DemarsMcNeilan and Bungo, 1985; Reference Senneset, Janbu, Chaney and DemarsSenneset and Janbu, 1985). In contrast, there is no comparable empiricial support for assuming Newtonian viscous flow around inclusions in granular materials, the other end member of the range of potential rheological behaviors that has been suggested for till deformation around inclusions (Reference Humphrey, Kamb, Fahnestock and EngelhardtHumphrey and others, 1993; Reference Fischer and ClarkeFischer and Clarke, 1994). Studies of cone penetration also permit us to account approximately for several factors that are difficult to consider theoretically, including the grain-size distribution and the sediment compressibility. These factors are embodied in the angle β in Equation (6) (Reference Senneset, Janbu, Chaney and DemarsSenneset and Janbu, 1985).
Nevertheless, measurements of shear deformation that are distributed across significant thicknesses of subglacial till (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987; Reference Blake, Clarke and GérinBlake and others, 1992; Reference Humphrey, Kamb, Fahnestock and EngelhardtHumphrey and others, 1993) suggest that till layers as a whole exhibit some viscous behavior. Owing to the wide range of grain-sizes, it is possible that localized deformation adjacent to the fish is essentially plastic, but that on a larger scale shear stresses exerted by the glacier sole induce deformation that is, to some extent, viscous. However, we cannot rule out the possibility that local till deformation around the fish was also viscous. In this case, the force on the fish would have depended on its speed relative to the till.
It is important to consider whether the pipe that drags the fish disturbs the till sufficiently to influence the measurement. Although the fish trailed the pipe by about five pipe diameters, it is possible that the original porosity of the till was not fully recovered from this disturbance when sampled by the fish. This would be a major concern if the till were not independently deforming. However, because the till was presumably dilated and in its residual state prior to the deformation induced by the pipe, we anticipate that this effect was minor.
Another consideration is that the fish may have traveled at variable depths in the till during the experiment. This could be caused by vertical motion of the ice or a change in the angle of the pipe in the borehole. Thus, the fish could have sampled different layers within the till, or in the worst case, could have lodged at the ice–till interface. We believe that the latter situation was unlikely, owing to the large amount of glacier uplift or pipe rotation required to lift the fish to glacier sole, 0.06 m or 20°, respectively.
The results from Storglaciären suggest that the basal till supports ∼55kPa. Reference Fischer and ClarkeFischer and Clarke (1994) determined a yield strength of 48–57 kPa for the deforming till beneath Trapridge Glacier. In contrast with these values, Reference Humphrey, Kamb, Fahnestock and EngelhardtHumphrey and others (1993) obtained a yield strength of 5.5 kPa for the sediment beneath Columbia Glacier by analyzing the deformation of a drill stem that was stuck at the base of a borehole. The difference in sediment strength could potentially be a function of differing sediment permeabilities related to composition. Less permeable sediment would allow the maintenance of higher pore-water pressures, thereby reducing strength. Alternatively, the lower strength may have resulted from excess pore pressure induced by the drill stem. The sliding velocity of Columbia Glacier is 3–4 m d−1, and the till permeability is not known. If δ in Equation (8) is 0.034 m, equal to the diameter of the drill stem, and the sediment compressibility is constrained as before, then the time-scales for loading of sediment in front of the stem and pore-pressure dissipation are of the same order (R = 1) if till permeabilities range from 3 × 10−15 to 3 × 10−7m2. These permeabilities are at the center of the range of values for till provided by Reference Freeze and CherryFreeze and Cherry (1979, p. 29). Thus, excess pore pressure induced by the drill stem cannot be precluded.
The difference between the strength of the till beneath Storglaciären and the winter basal shear stress could be due to several factors. For example, in the upper part of the ablation area, force-balance calculations indicate that the basal shear stress decreases during periods of high velocity during the summer (Reference Hooke, Calla, Holmlund, Nilsson and StroevenHooke and others, 1989). These periods are associated with high water inputs to the glacier, suggesting that the effective pressure on the till may be reduced during such periods. A second possible explanation is that the glacier may be supported, in part, by bedrock bumps. Occasionally, we are unable to penetrate or sample the bed, indicating that some subglacial bedrock is indeed free of till. In contrast with results from the upper ablation area, force-balance calculations for the lower ablation area (Reference Hooke, Calla, Holmlund, Nilsson and StroevenHooke and others, 1989), slightly up-glacier from the site of the present experiment, showed that the basal shear stress increased during periods of high velocity. This apparent viscous behavior is consistent with sliding over rigid bumps on the bed. It may also be significant that the dragometer experiment and the measurements used for input to the force-balance calculation were made during different years and at slightly different locations in the ablation area.
An obvious improvement in the dragometer would be the installation of a miniature pore-pressure transducer within the fish. Such transducers are standard in many cone penetrometers (Reference Ruiter, Verruijt, Beringen and de LeeuwRuiter, 1982) and greatly increase the quality of data gathered in poorly drained sediments. The leads for the transducer would require connecting the fish to the load cell with a thin armored electrical cable rather than an aircraft cable. We plan to test this modification in future experiments on Storglaciären.
Acknowledgements
This research was supported by the U.S. National Science Foundation (grant DPP-8822156) and by the Swedish Natural Resources Research Council. We would be remiss if we did not acknowledge our debt to G. Clarke and his students whose imaginative instrumentation for the in-situ study of subglacial till has inspired our efforts. We thank E. Blake, U. Fischer, R. Iverson and J. Walder for helpful reviews of the manuscript.
The accuracy of references in the text and in this list is the responsibility of the authors, to whom queries should be addressed.
Appendix
The bed-parallel force on the leeward cone, Fu is negligible relative to F cr. F 1 depends on the stress that till exerts normal to the cone surface, N′. The bed-parallel component of N′ pushes forward on the fish, and friction between the till and cone surface provides resistance. Balancing these forces gives
where A cs is the surface area of the cone and tan ϕ s is the friction coefficient for till sliding over steel. To maximize F 1 assume that N′ = σ′m = σ′p. Dividing by Equation (4) then yields a maximum estimate for F 1/F cr:

Simple experiments in which a loaded steel plate was dragged across till from Storglaciären yielded ϕ 2 = 28°. A cs/A c = 2.8 and N F = 15 (Equation (3) with ϕ = ϕ r = 31° and β = 15°). Thus, F 1/F cr < 0.03.