Published online by Cambridge University Press: 13 January 2023
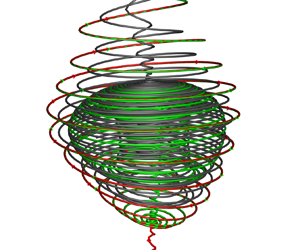
The spatial structure and time evolution of tornado-like vortices in a three-dimensional cavity are studied by topological analysis and numerical simulation. The topology theory of the unsteady vortex in the rectangular coordinate system (Zhang, Zhang & Shu, J. Fluid Mech., vol. 639, 2009, pp. 343–372) is generalized to the curvilinear coordinate system. Two functions  $\lambda (q_1,t)$ and
$\lambda (q_1,t)$ and  $q(q_1,t)$ are obtained to determine the topology structure of the sectional streamline pattern in the cross-section perpendicular to the vortex axis and the meridional plane, respectively. The spiral direction of the sectional streamlines in the cross-section perpendicular to the vortex axis depends on the sign of
$q(q_1,t)$ are obtained to determine the topology structure of the sectional streamline pattern in the cross-section perpendicular to the vortex axis and the meridional plane, respectively. The spiral direction of the sectional streamlines in the cross-section perpendicular to the vortex axis depends on the sign of  $\lambda (q_1,t)$. The types of critical points in the meridional plane depend on the sign of
$\lambda (q_1,t)$. The types of critical points in the meridional plane depend on the sign of  $q(q_1,t)$. The relation between the critical points of the streamline pattern in the meridional plane and that in the cross-section perpendicular to the vortex axis is set up. The flow in a three-dimensional rectangular cavity is numerically simulated by solving the three-dimensional Navier–Stokes equations using high-order numerical methods. The spatial structures and the time evolutions of the tornado-like vortices in the cavity are analysed with our topology theory. Both the bubble type and spiral type of vortex breakdown are observed. They have a close relationship with the vortex structure in the cross-section perpendicular to the vortex axis. The bubble-type breakdown has a conical core and the core is non-axisymmetric in the sense of topology. A criterion for the bubble type and the spiral type based on the spatial structure characteristic of the two breakdown types is provided.
$q(q_1,t)$. The relation between the critical points of the streamline pattern in the meridional plane and that in the cross-section perpendicular to the vortex axis is set up. The flow in a three-dimensional rectangular cavity is numerically simulated by solving the three-dimensional Navier–Stokes equations using high-order numerical methods. The spatial structures and the time evolutions of the tornado-like vortices in the cavity are analysed with our topology theory. Both the bubble type and spiral type of vortex breakdown are observed. They have a close relationship with the vortex structure in the cross-section perpendicular to the vortex axis. The bubble-type breakdown has a conical core and the core is non-axisymmetric in the sense of topology. A criterion for the bubble type and the spiral type based on the spatial structure characteristic of the two breakdown types is provided.