Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-24T11:19:14.106Z Has data issue: false hasContentIssue false
  • English
  • Français

A deterministic gradient-based approach to avoid saddle points

Part of: Parabolic equations and systems Applications - Dynamical systems and ergodic theory Artificial intelligence (68Txx)

Published online by Cambridge University Press:  09 November 2022

L. M. Kreusser Open the ORCID record for L. M. Kreusser [Opens in a new window] ,
S. J. Osher  and
B. Wang
L. M. Kreusser*
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK
S. J. Osher
Affiliation:
Department of Mathematics, University of California, Los Angeles, CA 90095, USA
B. Wang
Affiliation:
Department of Mathematics, Scientific Computing and Imaging Institute, University of Utah, Salt Lake City, UT 84112, USA
*
*Corresponding author. E-mail: lmk54@bath.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Loss functions with a large number of saddle points are one of the major obstacles for training modern machine learning (ML) models efficiently. First-order methods such as gradient descent (GD) are usually the methods of choice for training ML models. However, these methods converge to saddle points for certain choices of initial guesses. In this paper, we propose a modification of the recently proposed Laplacian smoothing gradient descent (LSGD) [Osher et al., arXiv:1806.06317], called modified LSGD (mLSGD), and demonstrate its potential to avoid saddle points without sacrificing the convergence rate. Our analysis is based on the attraction region, formed by all starting points for which the considered numerical scheme converges to a saddle point. We investigate the attraction region’s dimension both analytically and numerically. For a canonical class of quadratic functions, we show that the dimension of the attraction region for mLSGD is 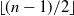$\lfloor (n-1)/2\rfloor$, and hence it is significantly smaller than that of GD whose dimension is 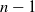$n-1$.

Keywords

Deterministic algorithmgradient-based methodssaddle pointsattraction regionLaplacian smoothing

MSC classification

Primary: 65K10: Optimization and variational techniques 90C26: Nonconvex programming, global optimization
Secondary: 35K91: Semilinear parabolic equations with Laplacian, bi-Laplacian or poly-Laplacian 37N40: Dynamical systems in optimization and economics 68T05: Learning and adaptive systems
Type
Papers
Information
European Journal of Applied Mathematics , Volume 34 , Issue 4 , August 2023 , pp. 738 - 757
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agarwal, N., Allen-Zhu, Z., Bullins, B., Hazan, E. & Ma, T. (2017) Finding approximate local minima faster than gradient descent. In: Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2017, Association for Computing Machinery, New York, NY, USA, pp. 1195–1199.CrossRefGoogle Scholar
Bengio, Y. (2009) Learning deep architectures for AI. Found. Trends Mach. Learn. 2(1), 1–127.CrossRefGoogle Scholar
Carmon, Y. & Duchi, J. C. (2019) Gradient descent finds the cubic-regularized nonconvex Newton step. SIAM J. Optim. 29(3), 2146–2178.CrossRefGoogle Scholar
Curtis, F. E. & Robinson, D. P. (2019) Exploiting negative curvature in deterministic and stochastic optimization. Math. Program. 176(1), 69–94.CrossRefGoogle Scholar
Curtis, F. E., Robinson, D. P. & Samadi, M. (2014) A trust region algorithm with a worst-case iteration complexity of $\mathcal{O}(\epsilon^{-3/2})$ for nonconvex optimization. Math. Program. 162, 1–32.CrossRefGoogle Scholar
Dauphin, Y. N., Pascanu, R., Gulcehre, C., Cho, K., Ganguli, S. & Bengio, Y. (2014) Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. In: Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence and K. Q. Weinberger (editors), Advances in Neural Information Processing Systems 27, Curran Associates, Inc., pp. 2933–2941.Google Scholar
Du, S., Jin, C., Lee, J. D., Jordan, M. I., Poczos, B. & Singh, A. (2017) Gradient descent can take exponential time to escape saddle points. In Advances in Neural Information Processing Systems (NIPS 2017).Google Scholar
Ge, R. (2016) Escaping from saddle points.Google Scholar
Ge, R., Huang, F., Jin, C. & Yuan, Y. (2015) Escaping from saddle points — online stochastic gradient for tensor decomposition. In: P. Grünwald, E. Hazan and S. Kale (editors), Proceedings of Machine Learning Research, Vol. 40, Paris, France, 03–06 Jul 2015, PMLR, pp. 797–842.Google Scholar
Ge, R., Huang, F., Jin, C. & Yuan, Y. (2015) Escaping from saddle points – online stochastic gradient for tensor decomposition. In: Conference on Learning Theory (COLT 2015).Google Scholar
He, K., Zhang, X., Ren, S. & Sun, J. (2016) Deep residual learning for image recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778.CrossRefGoogle Scholar
Iqbal, M., Rehman, M. A., Iqbal, N. & Iqbal, Z. (2020) Effect of Laplacian smoothing stochastic gradient descent with angular margin softmax loss on face recognition. In: I. S. Bajwa, T. Sibalija and D. N. A. Jawawi (editors), Intelligent Technologies and Applications, Springer Singapore, Singapore, pp. 549–561.CrossRefGoogle Scholar
Jin, C., Ge, R., Netrapalli, P., Kakade, S. & Jordan, M. I. (2017) How to escape saddle points efficiently. In: Proceedings of the 34th International Conference on Machine Learning (ICML 2017).Google Scholar
Jin, C., Netrapalli, P. & Jordan, M. I. (2018) Accelerated gradient descent escapes saddle points faster than gradient descent. In: Conference on Learning Theory (COLT 2018).Google Scholar
Lee, J. D., Panageas, I., Piliouras, G., Simchowitz, M., Jordan, M. I. & Recht, B. (2019) First-order methods almost always avoid strict saddle points. Math. Program. 176(1–2), 311–337.CrossRefGoogle Scholar
Lee, J. D., Simchowitz, M., Jordan, M. I. & Recht, B. (2016) Gradient descent only converges to minimizers. In: V. Feldman, A. Rakhlin and O. Shamir (editors), Proceedings of Machine Learning Research, Vol. 49, Columbia University, New York, New York, USA, 23–26 Jun 2016, PMLR, pp. 1246–1257.Google Scholar
Levy, K. Y. (2016) The power of normalization: faster evasion of saddle points. arXiv:1611.04831.Google Scholar
Liang, Z., Wang, B., Gu, Q., Osher, S. & Yao, Y. (2020) Exploring private federated learning with Laplacian smoothing. arXiv:2005.00218.Google Scholar
Liu, M. & Yang, T. (2017) On noisy negative curvature descent: competing with gradient descent for faster non-convex optimization. arXiv:1709.08571.Google Scholar
Martens, J. (2010) Deep learning via Hessian-free optimization. In: Proceedings of the 27th International Conference on International Conference on Machine Learning, ICML’10, Omnipress, Madison, WI, USA, pp. 735–742.Google Scholar
Nesterov, Y. (1998) Introductory Lectures on Convex Programming Volume I: Basic Course. Lecture Notes.Google Scholar
Nesterov, Y. & Polyak, B. T. (2006) Cubic regularization of newton method and its global performance. Math. Program. 108(1), 177–205.CrossRefGoogle Scholar
Nocedal, J. & Wright, S. (2006) Numerical Optimization. Springer Series in Operations Research and Financial Engineering, Springer-Verlag New York.Google Scholar
Osher, S., Wang, B., Yin, P., Luo, X., Pham, M. & Lin, A. (2018) Laplacian smoothing gradient descent. arXiv:1806.06317.Google Scholar
Paternain, S., Mokhtari, A. & Ribeiro, A. (2019) A Newton-based method for nonconvex optimization with fast evasion of saddle points. SIAM J. Optim. 29(1), 343–368.CrossRefGoogle Scholar
Rumelhart, D. E., Hinton, G. E. & Williams, R. J. (1998) Learning representations by back-propagating errors. Cognit. Model 323, 533–536.Google Scholar
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bernstein, M., Berg, A. C. & Fei-Fei, L. (2015) Imagenet large scale visual recognition challenge. Int. J. Comput. Vision 115(3), 211–252 323, 533–536.10.1007/s11263-015-0816-yCrossRefGoogle Scholar
Sun, J., Qu, Q. & Wright, J. (2018) A geometric analysis of phase retrieval. Found. Comput. Math. 18(5), 1131–1198.CrossRefGoogle Scholar
Ul Rahman, J., Ali, A., Rehman, M. & Kazmi, R. (2020) A unit softmax with Laplacian smoothing stochastic gradient descent for deep convolutional neural networks. In: I. S. Bajwa, T. Sibalija and D. N. A. Jawawi (editors), Intelligent Technologies and Applications. Springer Singapore, Singapore, pp. 162–174.CrossRefGoogle Scholar
Vapnik, V. (1992) Principles of risk minimization for learning theory. In: Advances in Neural Information Processing Systems, pp. 831–838.Google Scholar
Wang, B., Gu, Q., Boedihardjo, M., Wang, L., Barekat, F. & Osher, S. J. (2020) DP-LSSGD: a stochastic optimization method to lift the utility in privacy-preserving ERM. In: Mathematical and Scientific Machine Learning. PMLR, pp. 328–351.Google Scholar
Wang, B., Nguyen, T. M., Bertozzi, A. L., Baraniuk, R. G. & Osher, S. J. (2020) Scheduled restart momentum for accelerated stochastic gradient descent. arXiv:2002.10583.Google Scholar
Wang, B., Zou, D., Gu, Q. & Osher, S. (2020) Laplacian smoothing stochastic gradient Markov Chain Monte Carlo. SIAM J. Sci. Comput. 43, A26–A53.Google Scholar