1. INTRODUCTION
Satellite observations of surface elevation and velocity changes of the ice sheets show widespread dynamic thinning of outlet glaciers and ice streams in Greenland and West Antarctica (e.g. Pritchard and others, Reference Pritchard, Arthern, Vaughan and Edwards2009; Shepherd and others, Reference Shepherd2012). Many of these changes are attributed to the acceleration of the flow of grounded ice, increased ice discharge through the grounding line and subsequent grounding line retreat (e.g. Mouginot and others, Reference Mouginot, Rignot and Scheuchl2014; Rignot and others, Reference Rignot, Mouginot, Morlighem, Seroussi and Scheuchl2014).
In a steady state, the ice discharge through the grounding line balances the mass accumulated at the surface upstream of the grounding line. The position of the grounding line depends on several factors, including the accumulation rate, bed elevation and basal shear stress (Schoof, Reference Schoof2007a; Tsai and others, Reference Tsai, Stewart and Thompson2015). Establishing conditions that determine whether a grounding line position is stable (i.e. under small perturbations it returns to its original location) or unstable (i.e. small perturbations lead to its unstoppable advance or retreat) is a longstanding problem in glaciology (Hughes, Reference Hughes1973; Mercer, Reference Mercer1978).
The bed slope has been identified as the main control on the stability of grounding lines of unconfined marine ice sheets, i.e. ice sheets which rest on the bed below sea level. Weertman (Reference Weertman1974) and Thomas and Bentley (Reference Thomas and Bentley1978) were the first to hypothesise that grounding lines of marine ice sheets on beds that deepen towards the interior of ice sheets (‘retrograde’ beds) are unstable. While their arguments were based on simplified representations of the ice flow through the transition from the grounded ice sheet to the floating ice shelf, they correctly deduced that the stability of the grounding line is determined by the gradient of the flux at the grounding line, which in turn is determined by the bed slope at the grounding line.
In a stable steady state, the downstream flux gradient at the grounding line must exceed the accumulation rate. In this case, a downstream perturbation of the grounding line from the steady-state position leads to a negative net mass balance, forcing the grounding line to retreat back to its original position. Similarly, perturbing the grounding line in the upstream direction leads to a positive net mass balance, causing the grounding line to advance back to the steady state. Conversely, if the downstream gradient of the steady-state ice flux is less than the accumulation rate, then an advance will lead to a positive mass balance and runaway advance. These heuristic mass-balance arguments have been confirmed by linear stability analyses (Wilchinsky, Reference Wilchinsky2009; Schoof, Reference Schoof2012). Thus, the ice flux at the grounding line allows us to determine the grounding line steady-state position and its stability.
Early numerical studies of the grounding line behaviour in configurations with retrograde slopes found both stable and unstable behaviour (Hindmarsh, Reference Hindmarsh1993, Reference Hindmarsh1996; Dupont and Alley, Reference Dupont and Alley2005; Hindmarsh, Reference Hindmarsh:2006). The ambiguity of these results is partly due to the need for stable numerical algorithms and high spatial resolutions in the vicinity of the grounding line to ensure consistent results (Vieli and Payne, Reference Vieli and Payne2005; Durand and others, Reference Durand, Gagliardini, Zwinger, Le Meur and Hindmarsh2009b; Gladstone and others, Reference Gladstone, Payne and Cornford2012; Pattyn and others, Reference Pattyn2012) and partly due to inconsistent mathematical formulations of the grounding line boundary conditions. By using matched asymptotic expansions to determine the ice flux through the grounding line of an unconfined marine ice sheet, Schoof (Reference Schoof2007a) eliminated this ambiguity. The results of his analysis confirm the original results by Weertman (Reference Weertman1974). Schoof (Reference Schoof2007a) found that the ice flux at the grounding line depends on local ice and bed properties and on the grounding line ice thickness. The latter is solely determined by the bed elevation as a result of Archimedes’ principle. Therefore, both the grounding line position and its stability can be determined from the local bed elevation and its slope. Schoof (Reference Schoof:2007b) illustrated that this dependence on local bed properties can lead to hysteresis behaviour of grounding lines on beds with overdeepenings similar to those in the West Antarctic.
Many existing studies investigating grounding line dynamics focus on laterally unconfined marine ice sheets that transition into freely floating ice shelves (e.g. Nowicki and Wingham, Reference Nowicki and Wingham2008; Durand others, Reference Durand, Gagliardini, de Fleurian, Zwinger and Le Meur2009a; Tsai and others, Reference Tsai, Stewart and Thompson2015). In this case, the ice-shelf extent and configuration do not affect the grounded ice sheet and its dynamics can be modelled independently of the ice shelf (MacAyeal and Barcilon, Reference MacAyeal and Barcilon1988). This is, however, a significant simplification, and observations suggest that ice-shelf mass loss has the potential to trigger grounding line retreat (e.g. Rignot and others, Reference Rignot, Casassa, Gogieneni, Rivera and Thomas2004; Scambos and others, Reference Scambos, Bohlander, Shuman and Skvarca2004; Shepherd and others, Reference Shepherd, Wingham and Rignot:2004; Shepherd and Wingham, Reference Shepherd and Wingham2007; Jacobs and other, Reference Jacobs, Jenkins, Giulivi and Dutrieux2011; Pritchard and others, Reference Pritchard2012).
Recent numerical studies of laterally confined marine ice sheets confirm that confined ice shelves can affect grounding line behaviour by reducing the stress at the grounding line (e.g. MacAyeal and others, Reference MacAyeal1996; Goldberg and others, Reference Goldberg, Holland and Schoof2009; Gagliardini and others, Reference Gagliardini, Durand, Zwinger, Hindmarsh and Le Meur:2010; Katz and Worster, Reference Katz and Worster:2010; Jamieson and others, Reference Jamieson2012). In laterally confined ice shelves, lateral shear stresses provide resistance to the grounded ice flow through the so-called buttressing effect – a reduction of the net stress at the grounding line (Paterson, Reference Paterson1994). Numerical studies found that in the presence of buttressing, stable grounding lines on upwards sloping beds are possible (Dupont and Alley, Reference Dupont and Alley2005; Gudmundsson and others, Reference Gudmundsson, Krug, Durand, Favier and Gagliardini2012; Gudmundsson, Reference Gudmundsson2013). Similar to laterally unconfined configurations, numerical simulations of confined marine ice-sheet geometries are challenging. Solutions are highly sensitive to the grid resolution at the grounding line, and to the numerical schemes used to track grounding line migration.
To date, analytic studies of confined marine ice sheets have mainly focused on the ice shelf, in particular on identifying the boundary layer structure of confined ice shelves and/or on deriving solutions of the ice velocity in the downstream parts of the ice shelf (e.g. Hindmarsh, Reference Hindmarsh2012; Pegler and others, Reference Pegler, Kowal, Hasenclever and Worster2013; Wearing and others, Reference Wearing, Hindmarsh and Worster2015; Pegler, Reference Pegler2016). This has led to the development of models that parameterise the effect of buttressing in laterally integrated ‘flow-line’ models (Dupont and Alley, Reference Dupont and Alley2005; Hindmarsh, Reference Hindmarsh2012; Pegler, Reference Pegler2016). Here, we build on these analytic approaches to derive an explicit expression for the backstress at the grounding line of buttressed marine ice sheets. By combining these new results with the boundary layer solution developed in Schoof (Reference Schoof2007a), we then extend the results by Schoof (Reference Schoof2007a) to account for buttressing and derive an expression for the ice flux at the grounding line for laterally confined ice-stream/ice-shelf systems. We compare our analytic results with numerical simulations of a laterally confined version of the MISMIP 1a experiment (Pattyn and others, Reference Pattyn2012). Finally, we investigate the dependence of grounding line dynamics on conditions at the calving front and on geometric parameters such as ice-shelf width and length.
This paper is organised as follows: Section 2 describes the model. The derivation of steady-state solutions for the ice-shelf component of the model is presented in Section 3. These solutions provide the backstress at the grounding line, and can be used to determine an expression for the flux through the grounding line (Section 4). These analytic results are confirmed by comparison with numerical simulations in Section 5. We discuss our results in Section 6. Readers not interested in the details of the derivation of the ice flux expression can skip Sections 3 and 4.
2. THE MODEL
2.1 Ice flow
We consider a steady-state marine ice sheet flowing in the x-direction in a channel of constant width W (Fig. 1). At the grounding line, x = x g, the ice sheet starts to float, forming an ice shelf of length L s which terminates at the calving front x = x c. We use a vertically and laterally integrated flow model of an ice-stream/ice-shelf system. This model has been widely used in the glaciological literature, e.g. Morland (Reference Morland, Van der Veen and Oerlemans1987); MacAyeal (Reference MacAyeal1989); Dupont and Alley (Reference Dupont and Alley2005); Pattyn and others (Reference Pattyn, Huyghe, De Brabander and De Smedt2006); Nick and others (Reference Nick, Vieli, Howat and Joughin2009); Hindmarsh (Reference Hindmarsh2012); Pegler (Reference Pegler2016):
 $$\eqalign{0 = & {\kern 1pt} 2\displaystyle{\partial \over {\partial x}}\left( {A^{ - 1/n}h{\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert} ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}}} \right) - \Lambda h \vert u \vert ^{\,p - 1}u - C \vert u \vert ^{m - 1}u \cr & - \rho gh\displaystyle{{\partial (h + b)} \over {\partial x}},\quad {\rm if}\;0 \le x \le x_{\rm g},{\kern 1pt} h \ge \displaystyle{{\rho _{\rm w}} \over \rho} b,} $$
$$\eqalign{0 = & {\kern 1pt} 2\displaystyle{\partial \over {\partial x}}\left( {A^{ - 1/n}h{\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert} ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}}} \right) - \Lambda h \vert u \vert ^{\,p - 1}u - C \vert u \vert ^{m - 1}u \cr & - \rho gh\displaystyle{{\partial (h + b)} \over {\partial x}},\quad {\rm if}\;0 \le x \le x_{\rm g},{\kern 1pt} h \ge \displaystyle{{\rho _{\rm w}} \over \rho} b,} $$ $$\eqalign{0 = & {\kern 1pt} 2\displaystyle{\partial \over {\partial x}}\left( {A^{ - 1/n}h{\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert} ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}}} \right) - \Lambda h \vert u \vert ^{\,p - 1}u \cr & - \rho \left( {1 - \displaystyle{\rho \over {\rho _{\rm w}}}} \right)gh\displaystyle{{\partial h} \over {\partial x}}\quad {\rm if}\;x_{\rm g} \lt x \lt x_{\rm c},{\kern 1pt} h \lt \displaystyle{{\rho _{\rm w}} \over \rho} b.} $$
$$\eqalign{0 = & {\kern 1pt} 2\displaystyle{\partial \over {\partial x}}\left( {A^{ - 1/n}h{\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert} ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}}} \right) - \Lambda h \vert u \vert ^{\,p - 1}u \cr & - \rho \left( {1 - \displaystyle{\rho \over {\rho _{\rm w}}}} \right)gh\displaystyle{{\partial h} \over {\partial x}}\quad {\rm if}\;x_{\rm g} \lt x \lt x_{\rm c},{\kern 1pt} h \lt \displaystyle{{\rho _{\rm w}} \over \rho} b.} $$u(x) is the ice velocity, h(x) is the ice thickness, b(x) is the bed elevation (negative below sea level and positive above sea level), A −1/n is the temperature-dependent part of the viscosity, here taken to be constant, ρ and ρ w are the densities of ice and water, respectively, g is the acceleration due to gravity, C and m are basal sliding parameters, and Λ and ![]() $p \in (0,{\kern 1pt} 1)$ are lateral drag parameters.
$p \in (0,{\kern 1pt} 1)$ are lateral drag parameters.

Fig. 1. Geometry of the model. (a) Plan view and (b) cross-section. We consider a marine ice sheet of constant width W flowing in the positive x-direction. An ice shelf forms at the grounding line x g, the calving front is located at x c = x g + L s, with L s the length of the ice shelf.
A number of different formulations have been proposed to parameterise lateral drag:
 $$\Lambda = \left\{ {\matrix{ {\displaystyle{{2(n + {1)}^{1/n}} \over {A^{1/n}W^{1/n + 1}}}} \hfill & \matrix{{\rm with}\;p = \displaystyle{1 \over n} \hfill \cr \quad ({\rm Hindmarsh},{\rm 2012)}, \hfill} \hfill \cr {\displaystyle{{2{\left( {1 + n/2} \right)}^{1/n}} \over {A^{1/n}W^{1/n + 1}}}} \hfill & \matrix{{\rm with}\;p = \displaystyle{1 \over n} \hfill \cr \quad ({\rm Pegler},{\rm 2016)}, \hfill} \hfill \cr {\displaystyle{{c_{\rm l}} \over W}} \hfill & \matrix{{\rm with}\;p = 1 \hfill \cr \quad (\hbox{Sergienko and others, } 20{\rm 13)}. \hfill} \hfill \cr}} \right.$$
$$\Lambda = \left\{ {\matrix{ {\displaystyle{{2(n + {1)}^{1/n}} \over {A^{1/n}W^{1/n + 1}}}} \hfill & \matrix{{\rm with}\;p = \displaystyle{1 \over n} \hfill \cr \quad ({\rm Hindmarsh},{\rm 2012)}, \hfill} \hfill \cr {\displaystyle{{2{\left( {1 + n/2} \right)}^{1/n}} \over {A^{1/n}W^{1/n + 1}}}} \hfill & \matrix{{\rm with}\;p = \displaystyle{1 \over n} \hfill \cr \quad ({\rm Pegler},{\rm 2016)}, \hfill} \hfill \cr {\displaystyle{{c_{\rm l}} \over W}} \hfill & \matrix{{\rm with}\;p = 1 \hfill \cr \quad (\hbox{Sergienko and others, } 20{\rm 13)}. \hfill} \hfill \cr}} \right.$$Hindmarsh (Reference Hindmarsh2012) derived his expression for the centre-line velocity u(x) assuming that the lateral shear stress increases linearly from the ice-shelf centre to its margin. Using similar assumptions Pegler (Reference Pegler2016) obtained a qualitatively similar expression, but for u(x) the width-integrated velocity. Sergienko and others (Reference Sergienko, Goldberg and Little2013), in contrast, use p = 1 and Λ ~ W −1 to account for the possibility of sliding along the ice-shelf side walls. We do not choose a specific expression for Λ and p at this point, but leave them in their general form for now. Where we explicitly give values, we use Hindmarsh's formula (2)1 to calculate Λ.
The steady-state form of mass conservation is
where ![]() $\dot a$ is the net surface and basal mass balance of the ice sheet (positive for accumulation), and
$\dot a$ is the net surface and basal mass balance of the ice sheet (positive for accumulation), and ![]() $\dot m$ the net surface and basal mass balance of the ice shelf (positive for accumulation/freeze-on). For simplicity, we assume
$\dot m$ the net surface and basal mass balance of the ice shelf (positive for accumulation/freeze-on). For simplicity, we assume ![]() $\dot m$ to be constant. However, all derivations can be straightforwardly extended to spatially variable
$\dot m$ to be constant. However, all derivations can be straightforwardly extended to spatially variable ![]() $\dot a$ and
$\dot a$ and ![]() $\dot m$.
$\dot m$.
Boundary conditions are specified at the ice divide at x = 0 and at the calving front x = x c
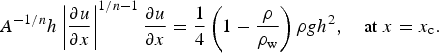 $$A^{ - 1/n}h\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}} = \displaystyle{1 \over 4}\left( {1 - \displaystyle{\rho \over {\rho _{\rm w}}}} \right)\rho gh^2,\quad {\rm at}\;x = x_{\rm c}.$$
$$A^{ - 1/n}h\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}} = \displaystyle{1 \over 4}\left( {1 - \displaystyle{\rho \over {\rho _{\rm w}}}} \right)\rho gh^2,\quad {\rm at}\;x = x_{\rm c}.$$Additionally, we require the ice thickness, velocity and extensional stress to be continuous across the grounding line at x g. Note that this model is only well-posed if the calving front position is directly or indirectly specified, for example through an extra condition on the ice-shelf length or ice thickness at the calving front. Since we are interested in steady-state ice shelves, the calving front position is constant in either scenario.
In the analysis described below, we first consider the dynamics of the ice shelf separately from the grounded ice sheet. We then use these results together with the continuity conditions on stress and ice thickness at the ice-stream/ice-shelf junction – the grounding line – to determine the steady-state behaviour of a confined ice-stream/ice-shelf system. This approach allows us to explicitly determine the backstress and ice flux at the grounding line, and to investigate grounding line stability for different geometric configurations and lateral-shear conditions.
3. ICE-SHELF SOLUTIONS
In this Section, we investigate the behaviour of the ice shelf and determine the stress at the grounding line τ g, defined as
 $$\tau _{\rm g} = 2A^{ - 1/n}h\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}}\quad \quad {\rm at}\;x = x_{\rm g}.$$
$$\tau _{\rm g} = 2A^{ - 1/n}h\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}}\quad \quad {\rm at}\;x = x_{\rm g}.$$First, we non-dimensionalise the governing equations for an ice shelf in steady state (Section 3.1). This provides us with two non-dimensional groups that determine the ice-shelf state: the ratio between extensional stress and driving stress scales (η) and a non-dimensional buttressing strength (β), the ratio between lateral shear stress and driving stress scales. For a linearised version of the buttressing term (p = 1 and β>0, (2)3), it is possible to obtain an exact solution for τ g and hence q g. We summarise these results in Section 3.2 to illustrate our approach. In the limit of strongly buttressed ice shelves (β ≫ η), it is possible to obtain an approximate solution for τ g for general values of the buttressing term with matched asymptotic expansions. We derive this solution in Section 3.3.
3.1 Non-dimensionalisation of the ice shelf
By non-dimensionalising (1a)–(4c), we aim to simplify these equations as much as possible and reduce the number of free parameters to a minimum. We choose as characteristic length scale [x]s the ice-shelf length L s = x c − x g and set x = [x]sx* + x g. This leads to non-dimensional ice-shelf domain reaching from x* = 0 (the grounding line) to x* = 1 (the calving front). Moreover, we consider the ice thickness h g and the ice flux q g at the grounding line as given scales and identify [h]s = h g and [u]s[h]s = q g with u g = q g/h g the velocity at the grounding line. We set x = [x]sx* + x g, u = [u]su*, h = [h]sh*, as well as ![]() $\dot m^* = \dot mL_{\rm s}/q_{\rm g}$. This leads to two non-dimensional parameters
$\dot m^* = \dot mL_{\rm s}/q_{\rm g}$. This leads to two non-dimensional parameters
 $$\eta = \displaystyle{{4A^{ - 1/n}h_{\rm g}u_{\rm g}^{1/n} L_{\rm s}^{ - 1/n}} \over {\rho g(1 - \rho /\rho _{\rm w})h_{\rm g}^2}}, \quad \beta = 2\displaystyle{{\Lambda h_{\rm g}u_{\rm g}^p L_{\rm s}} \over {\rho g(1 - \rho /\rho _{\rm w})h_{\rm g}^2}} $$
$$\eta = \displaystyle{{4A^{ - 1/n}h_{\rm g}u_{\rm g}^{1/n} L_{\rm s}^{ - 1/n}} \over {\rho g(1 - \rho /\rho _{\rm w})h_{\rm g}^2}}, \quad \beta = 2\displaystyle{{\Lambda h_{\rm g}u_{\rm g}^p L_{\rm s}} \over {\rho g(1 - \rho /\rho _{\rm w})h_{\rm g}^2}} $$which describe the entire dynamics of the system. The parameter η is the ratio between the scale of the extensional stress at the grounding line and the scale of the driving stress at the grounding line and β is the ratio between the scale of the lateral shear stress at the grounding line and the scale of the driving stress at the grounding line. Characteristic values of these parameters for Petermann glacier (North-West Greenland), with L s = 65 km, W = 15 km, h g = 500 m, u g = 1000 m/year, and the parameters listed in table 1, are η ≈ 0.8 and β ≈ 3.6. For Pine Island (West Antarctica), with L s = 55 km, W = 40 km, h g = 750 m and u g = 1500 m/year, they are η ≈ β ≈ 0.6. It is important to note that this non-dimensionalisation does not change the dynamics of the ice-shelf system (see, e.g. Holmes, Reference Holmes2009; Fowler, Reference Fowler2011), it merely reformulates the mathematical problem in a way that is convenient for a solution with matched asymptotic expansions.
Table 1. List of parameters with their value, where applicable

The non-dimensional versions of the ice-shelf stress balance (1b) and the mass balance (3) are (with the asterisks discarded)
 $$\displaystyle{\partial \over {\partial x}}\left( {\eta h{\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert} ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}}} \right) - \beta h \vert u \vert ^{\,p - 1}u - 2h\displaystyle{{\partial h} \over {\partial x}} = 0,$$
$$\displaystyle{\partial \over {\partial x}}\left( {\eta h{\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert} ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}}} \right) - \beta h \vert u \vert ^{\,p - 1}u - 2h\displaystyle{{\partial h} \over {\partial x}} = 0,$$The boundary conditions (4b) and (4c) are
 $$\eta h\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}} = h^2\quad {\rm at}\;x = 1.$$
$$\eta h\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}} = h^2\quad {\rm at}\;x = 1.$$With these boundary conditions, (7b) can be easily integrated:
One advantage of the scaling introduced here is a considerable simplification of the boundary conditions and dimensions of the domain. All information about the ice-shelf length, thickness and flux at the grounding line is now contained in the non-dimensional parameters β and η. The ratio β/η equals the ratio between the scales of the lateral shear stress and the extensional stress (6), so η ≪ β corresponds to the parameter regime where we expect lateral shear stresses to balance most of the driving stress. Therefore, we refer to this parameter regime (η ≪ β) as the limit of strong buttressing.
3.2. Exact solution
To illustrate the general idea underlying the derivations in this paper, we start by considering the linear parameterisation of the lateral shear term with p = 1 and (2)3. In this case, it is possible to obtain an expression for the stress at the grounding line by integrating (7a) with (9) (Pegler, Reference Pegler2016)
 $$\tau _0 = 1 - \beta \int\limits_0^1 {hu{\rm d}x = 1 - \beta} \left( {1 + \displaystyle{{\dot m} \over 2}} \right)\quad {\rm for}\;p = 1.$$
$$\tau _0 = 1 - \beta \int\limits_0^1 {hu{\rm d}x = 1 - \beta} \left( {1 + \displaystyle{{\dot m} \over 2}} \right)\quad {\rm for}\;p = 1.$$This expression is valid for ![]() $ - 1 \le \dot m \le 2/\beta - 2$. The lower bound arises from the requirement that the ice flux is non-negative. The upper bound on
$ - 1 \le \dot m \le 2/\beta - 2$. The lower bound arises from the requirement that the ice flux is non-negative. The upper bound on ![]() $\dot m$ (or alternatively β) is a requirement that the backstress at the grounding line has to be non-negative as well.
$\dot m$ (or alternatively β) is a requirement that the backstress at the grounding line has to be non-negative as well.
In dimensional form, the stress (10) can be written as
with
the grounding line stress of unbuttressed marine ice sheets and
Schoof (Reference Schoof:2007b) states that if buttressing changes the unbuttressed stress at the grounding line by a factor of Θ < 1, i.e. τ g = τ g,0 × Θ, then this changes the flux at the grounding line by a factor of Θn/(m+1), i.e.
where
 $$q_{{\rm g},0} = \left( {\displaystyle{{A{(\rho g)}^{n + 1}(1 - \rho /\rho _w)} \over {4^nC}}} \right)^{1/(m + 1)}h_{\rm g}^{(3 + m + n)/(m + 1)} $$
$$q_{{\rm g},0} = \left( {\displaystyle{{A{(\rho g)}^{n + 1}(1 - \rho /\rho _w)} \over {4^nC}}} \right)^{1/(m + 1)}h_{\rm g}^{(3 + m + n)/(m + 1)} $$is the ice flux of unconfined and hence unbuttressed marine ice sheets (Schoof, Reference Schoof2007a). For the linear case considered here, this means that the ice flux at the grounding line can be written as
 $$\eqalign{q_{\rm g} = & \left( {\displaystyle{{A{(\rho g)}^{n + 1}(1 - \rho /\rho _w)} \over {4^nC}}} \right)^{1/(m + 1)}h_{\rm g}^{(3 + m + n)/(m + 1)} \cr & \times \left( {1 - \displaystyle{{2\Lambda L_{\rm s}(q_{\rm g} + 1/2\dot mL_{\rm s})} \over {\rho g(1 - \rho /\rho _{\rm w})h_{\rm g}^2}}} \right)^{n/(m + 1)}.} $$
$$\eqalign{q_{\rm g} = & \left( {\displaystyle{{A{(\rho g)}^{n + 1}(1 - \rho /\rho _w)} \over {4^nC}}} \right)^{1/(m + 1)}h_{\rm g}^{(3 + m + n)/(m + 1)} \cr & \times \left( {1 - \displaystyle{{2\Lambda L_{\rm s}(q_{\rm g} + 1/2\dot mL_{\rm s})} \over {\rho g(1 - \rho /\rho _{\rm w})h_{\rm g}^2}}} \right)^{n/(m + 1)}.} $$There are several important things we can learn from this simple solution. First, Θ ≤ 1, so buttressing always reduces the ice flux through the grounding line. Secondly, the amount by which the ice flux is reduced depends itself on the ice flux through the grounding line, and finally, the ice flux also depends on the ice-shelf geometry through the ice-shelf length L s and width W (hidden in Λ (2)). We discuss these properties in detail in Section 5.
For p = 1/n < 1, it is not straightforward to integrate h|u|1/n−1u. To derive Θ, we therefore construct an approximate solution using matched asymptotic expansions (Hinch, Reference Hinch1991; Holmes, Reference Holmes2013) based on the assumption that η ≪ β. This corresponds to the limit of strong buttressing where the extensional stresses are small compared to the lateral shear stresses in the ice shelf (see (6)).
3.3. Asymptotic solutions
In this section, we construct solutions for the velocity field in strongly buttressed ice shelves by using matched asymptotic expansions (see for example chapter 5 of Hinch (Reference Hinch1991) or chapter 2 of Holmes (Reference Holmes2013)). In this approach, we assume the perturbation parameter η to be small (for a discussion of this assumption see Section 3.4). If η ≪ 1, then the solutions u and h can be expanded in terms of η, e.g. u = u (0) + ηu (1) + O(η 2). This allows us to neglect terms of O(η) in the main part of the ice shelf, termed the ‘outer’ region, and we can derive a simplified ‘outer’ solution in this part of the ice shelf. However, this outer solution cannot satisfy the boundary conditions at the grounding line, where the extensional stress becomes non-negligible. To satisfy these boundary conditions, we introduce a boundary layer at the grounding line in which we rescale the ice-shelf equations. Solution of these rescaled boundary layer equations leads to the so-called ‘inner’ solution. Finally, by matching the inner and outer solution, we can then construct an approximate solution (called a ‘composite solution’ in the literature on matched asymptotic expansions) valid in the entire shelf. We can use this composite solution to determine the stress at the grounding line τ g. The remainder of this section describes the construction of the composite velocity solution for ice shelves that exhibit a boundary layer structure. Readers not interested in technical details of the derivation can proceed to Section 3.4 where the main results are summarised.
We start by deriving the outer solution (h (0) and u (0)), obtained by neglecting terms of O(η) in the momentum balance (7a) and assuming that η ≪ β ~ 1:
with the boundary conditions
Keeping in mind that ![]() $uh = 1 + \dot mx$, (17a) is really just a first-order equation in either u (0) or h (0), and we proceed by solving for the velocity u (0). Note that we have two boundary conditions for u (0) (h (0) = 0 is the same as requiring u (0) → ∞), but (17a) is only a first-order differential equation. Therefore, we can only expect to satisfy one of the boundary conditions.
$uh = 1 + \dot mx$, (17a) is really just a first-order equation in either u (0) or h (0), and we proceed by solving for the velocity u (0). Note that we have two boundary conditions for u (0) (h (0) = 0 is the same as requiring u (0) → ∞), but (17a) is only a first-order differential equation. Therefore, we can only expect to satisfy one of the boundary conditions.
The velocity and flux should be non-negative (![]() $u^{(0)} \ge 0,1 + \dot mx \ge 0)$, so that (17a) can be integrated to obtain (Pegler, Reference Pegler2016)
$u^{(0)} \ge 0,1 + \dot mx \ge 0)$, so that (17a) can be integrated to obtain (Pegler, Reference Pegler2016)
 $$u^{(0)}(x) = \displaystyle{{1 + \dot mx} \over {{\left( {h_{1,{\rm butt}}^{\,p + 1} + \beta /(2\dot m)\left[ {{(1 + \dot m)}^{\,p + 1} - {(1 + \dot mx)}^{\,p + 1}} \right]} \right)}^{1/(p + 1)}}},$$
$$u^{(0)}(x) = \displaystyle{{1 + \dot mx} \over {{\left( {h_{1,{\rm butt}}^{\,p + 1} + \beta /(2\dot m)\left[ {{(1 + \dot m)}^{\,p + 1} - {(1 + \dot mx)}^{\,p + 1}} \right]} \right)}^{1/(p + 1)}}},$$which satisfies the calving front boundary condition (17c) if h 1,butt = 0. This leads to an infinite leading order velocity at the calving front at x = 1. However, this excludes the possibility of later investigating the effect of ice-thickness-based calving laws (e.g. Nick and others, Reference Nick, Vieli, Howat and Joughin2009). One way to include a non-zero ice thickness at the calving front is to follow Pegler (Reference Pegler2016), who determines h 1,butt by applying the boundary condition (8b) instead of (17c). This leads to (Pegler, Reference Pegler2016)
 $$h_{1,{\rm butt}} = \left[ {\eta ^n\displaystyle{\beta \over 2}{(1 + \dot m)}^{\,p + 1}} \right]^{1/(2 + n + p)}.$$
$$h_{1,{\rm butt}} = \left[ {\eta ^n\displaystyle{\beta \over 2}{(1 + \dot m)}^{\,p + 1}} \right]^{1/(2 + n + p)}.$$As discussed in Pegler (Reference Pegler2016), this matches the ice thickness at the calving front obtained by numerical solution of (7a) and (8b) to an error of < 2%, and leads to a better match between numerically calculated velocity fields in the main part of the ice shelf and (18). We show in the Supplementary material (Section S1) that this approach is consistent with the introduction of a boundary layer at the calving front.
The outer solution (18) does not satisfy the boundary conditions (8a) at x = 0, which requires us to introduce a boundary layer by rescaling of the downstream coordinate with x = η nX (e.g. Holmes, Reference Holmes2013). To distinguish the ice thickness and velocity in the boundary layer from the outer variables we denote these with H and U, respectively. With these definitions, we obtain from (7) and (8) the boundary layer equations (neglecting terms of O(η n) as we again assume that a series expansion of u and h in terms of η is possible):
 $$\displaystyle{\partial \over {\partial X}}\left( {H{\left \vert {\displaystyle{{\partial U} \over {\partial X}}} \right \vert} ^{1/n - 1}\displaystyle{{\partial U} \over {\partial X}}} \right) - 2H\displaystyle{{\partial H} \over {\partial X}} = 0,$$
$$\displaystyle{\partial \over {\partial X}}\left( {H{\left \vert {\displaystyle{{\partial U} \over {\partial X}}} \right \vert} ^{1/n - 1}\displaystyle{{\partial U} \over {\partial X}}} \right) - 2H\displaystyle{{\partial H} \over {\partial X}} = 0,$$with the boundary conditions
and the matching conditions
We can integrate (20a) to obtain
 $$\tau _0 - H\left \vert {\displaystyle{{\partial U} \over {\partial X}}} \right \vert ^{1/n - 1}\displaystyle{{\partial U} \over {\partial X}} = 1 - H^2,$$
$$\tau _0 - H\left \vert {\displaystyle{{\partial U} \over {\partial X}}} \right \vert ^{1/n - 1}\displaystyle{{\partial U} \over {\partial X}} = 1 - H^2,$$where τ 0 is the non-dimensional version of the extensional stress at the grounding line τ g:
 $$\tau _0 = H\left \vert {\displaystyle{{\partial U} \over {\partial X}}} \right \vert ^{1/n - 1}\displaystyle{{\partial U} \over {\partial X}} = \eta h\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}}\quad {\rm at}\;X = x = 0,$$
$$\tau _0 = H\left \vert {\displaystyle{{\partial U} \over {\partial X}}} \right \vert ^{1/n - 1}\displaystyle{{\partial U} \over {\partial X}} = \eta h\left \vert {\displaystyle{{\partial u} \over {\partial x}}} \right \vert ^{1/n - 1}\displaystyle{{\partial u} \over {\partial x}}\quad {\rm at}\;X = x = 0,$$which we aim to determine here. Using H = 1/U (20b), we can rewrite (21) as
 $$\left \vert {\displaystyle{{\partial U} \over {\partial X}}} \right \vert ^{1/n - 1}\displaystyle{{\partial U} \over {\partial X}} = \displaystyle{1 \over U} - U(1 - \tau _0).$$
$$\left \vert {\displaystyle{{\partial U} \over {\partial X}}} \right \vert ^{1/n - 1}\displaystyle{{\partial U} \over {\partial X}} = \displaystyle{1 \over U} - U(1 - \tau _0).$$This leads to the integral equation
 $$\int\limits_0^X {{\rm d}{X}^{\prime} = \int\limits_1^U {\displaystyle{{V^n{\rm d}V} \over {{[1 - (1 - \tau _0)V^2]}^n}},}} $$
$$\int\limits_0^X {{\rm d}{X}^{\prime} = \int\limits_1^U {\displaystyle{{V^n{\rm d}V} \over {{[1 - (1 - \tau _0)V^2]}^n}},}} $$which determines the boundary layer velocity U implicitly.
For n > 0, the solution of (24) can be written as
 $$X = \displaystyle{1 \over {(n + 1)}}\left[ {U^{1 + n}{\kern 1pt} _2F_1\left( {n,\displaystyle{{n + 1} \over 2};\displaystyle{{n + 3} \over 2};(1 - \tau _0)U^2} \right)} \right]_1^U, $$
$$X = \displaystyle{1 \over {(n + 1)}}\left[ {U^{1 + n}{\kern 1pt} _2F_1\left( {n,\displaystyle{{n + 1} \over 2};\displaystyle{{n + 3} \over 2};(1 - \tau _0)U^2} \right)} \right]_1^U, $$where 2 F 1(a, b;c;x) is the hypergeometric function, and the subscript and superscript denote the lower and upper integration limits. There is no closed form expression for the inverse of the hypergeometric function for an arbitrary value of n, which would allow us to explicitly give U = f −1(X). However, for the typically assumed value of n = 3, we can write U = f −1(X) as (Abramowitz and Stegun, Reference Abramowitz and Stegun1964)
 $$U = \displaystyle{1 \over {\sqrt {1 - \tau _0}}} \left[ {\left( {\displaystyle{{1 + Y} \over Y}} \right)\left( {1 + \sqrt {\displaystyle{1 \over {1 + Y}}}} \right)} \right]^{1/2}$$
$$U = \displaystyle{1 \over {\sqrt {1 - \tau _0}}} \left[ {\left( {\displaystyle{{1 + Y} \over Y}} \right)\left( {1 + \sqrt {\displaystyle{1 \over {1 + Y}}}} \right)} \right]^{1/2}$$with ![]() $Y = 4(1 - \tau _0)^2X + (1 - 2\tau _0)/\tau _0^2 $.
$Y = 4(1 - \tau _0)^2X + (1 - 2\tau _0)/\tau _0^2 $.
The extensional stress at the grounding line (τ 0) must be determined by matching the solutions for the boundary layer velocity U and the outer solution u (0) (18), i.e. from the condition U ~ u (0) for X → ∞, x → 0, (20d)1 (Holmes, Reference Holmes2013). For n = 3, we can use (26) to determine U ~ (1 − τ 0)−1/2 for X → ∞. For an arbitrary n, we can exploit the fact that the right-hand side of (24) has a pole at U = (1 − τ 0)−1/2, which determines the limiting behaviour for X → ∞ (a vertical pole in the inverse function turns into a horizontal pole in the forward function). Thus,
which has to match the asymptotic behaviour of the outer solution u (0) (18) as x → 0:
 $$u^{(0)} \to \left( {h_{1,{\rm butt}}^{\,p + 1} + \displaystyle{\beta \over {2\dot m}}[(1 + \dot m)^{\,p + 1} - 1]} \right)^{ - 1/(\,p + 1)}\quad {\rm as}\;x \to 0.$$
$$u^{(0)} \to \left( {h_{1,{\rm butt}}^{\,p + 1} + \displaystyle{\beta \over {2\dot m}}[(1 + \dot m)^{\,p + 1} - 1]} \right)^{ - 1/(\,p + 1)}\quad {\rm as}\;x \to 0.$$Hence, the matching condition (20d)1 becomes
 $$\eqalign{(1 -& \tau _0)^{ - 1/2}{\rm \sim} \left( {h_{1,{\rm butt}}^{\,p + 1} + \displaystyle{\beta \over {2\dot m}}[(1 + \dot m)^{\,p + 1} - 1]} \right)^{ - 1/(\,p + 1)} \cr & {\rm as}\;X \to \infty, x \to 0,}$$
$$\eqalign{(1 -& \tau _0)^{ - 1/2}{\rm \sim} \left( {h_{1,{\rm butt}}^{\,p + 1} + \displaystyle{\beta \over {2\dot m}}[(1 + \dot m)^{\,p + 1} - 1]} \right)^{ - 1/(\,p + 1)} \cr & {\rm as}\;X \to \infty, x \to 0,}$$which provides us with an expression for the stress at the grounding line τ 0
 $$\tau _0 = 1 - \left( {h_{1,{\rm butt}}^{\,p + 1} + \displaystyle{\beta \over {2\dot m}}[(1 + \dot m)^{\,p + 1} - 1]} \right)^{2/(\,p + 1)}$$
$$\tau _0 = 1 - \left( {h_{1,{\rm butt}}^{\,p + 1} + \displaystyle{\beta \over {2\dot m}}[(1 + \dot m)^{\,p + 1} - 1]} \right)^{2/(\,p + 1)}$$with h 1,butt given by (19). At this point, we have all the information we need to determine the ice flux at the grounding line.
Finally, it is possible to obtain the composite velocity field through the superposition of the inner solution U (25) and the outer solution u (0) (18) minus the overlap term (1 − τ 0)−1/2 shared by both solutions (e.g. Holmes, Reference Holmes2013):
For n = 3, this yields
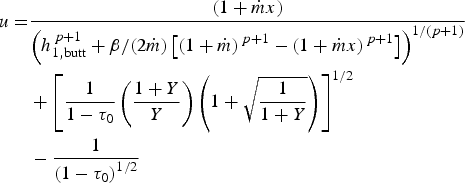 $$\eqalign{u = & \displaystyle{{(1 + \dot mx)} \over {{\left( {h_{1,{\rm butt}}^{\,p + 1} + \beta /(2\dot m)\left[ {{(1 + \dot m)}^{\,p + 1} - {(1 + \dot mx)}^{\,p + 1}} \right]} \right)}^{1/(p + 1)}}} \cr & + \left[ {\displaystyle{1 \over {1 - \tau _0}}\left( {\displaystyle{{1 + Y} \over Y}} \right)\left( {1 + \sqrt {\displaystyle{1 \over {1 + Y}}}} \right)} \right]^{1/2} \cr & - \displaystyle{1 \over {{(1 - \tau _0)}^{1/2}}}} $$
$$\eqalign{u = & \displaystyle{{(1 + \dot mx)} \over {{\left( {h_{1,{\rm butt}}^{\,p + 1} + \beta /(2\dot m)\left[ {{(1 + \dot m)}^{\,p + 1} - {(1 + \dot mx)}^{\,p + 1}} \right]} \right)}^{1/(p + 1)}}} \cr & + \left[ {\displaystyle{1 \over {1 - \tau _0}}\left( {\displaystyle{{1 + Y} \over Y}} \right)\left( {1 + \sqrt {\displaystyle{1 \over {1 + Y}}}} \right)} \right]^{1/2} \cr & - \displaystyle{1 \over {{(1 - \tau _0)}^{1/2}}}} $$with ![]() $Y = 4\eta ^{ - 3}(1 - \tau _0)^2x + (1 - 2\tau _0)/\tau _0^2. $ In Fig. 2, we compare the composite solution (30) with numerical solutions obtained by solving the unsimplified non-dimensional ice-shelf equations (7a) and (8b) for either different values of η and β fixed, or η fixed and β varying. In both cases, the match between the composite and numerical solutions improves as the ratio β/η increases. This is not surprising since β/η ≫ 1 is the limit for which the solutions derived here are valid. As η is reduced, the boundary layer at the grounding line becomes more pronounced (see inset a 1). Conversely, increasing β leads to steeper velocity gradients towards the calving front (see panel (b)).
$Y = 4\eta ^{ - 3}(1 - \tau _0)^2x + (1 - 2\tau _0)/\tau _0^2. $ In Fig. 2, we compare the composite solution (30) with numerical solutions obtained by solving the unsimplified non-dimensional ice-shelf equations (7a) and (8b) for either different values of η and β fixed, or η fixed and β varying. In both cases, the match between the composite and numerical solutions improves as the ratio β/η increases. This is not surprising since β/η ≫ 1 is the limit for which the solutions derived here are valid. As η is reduced, the boundary layer at the grounding line becomes more pronounced (see inset a 1). Conversely, increasing β leads to steeper velocity gradients towards the calving front (see panel (b)).
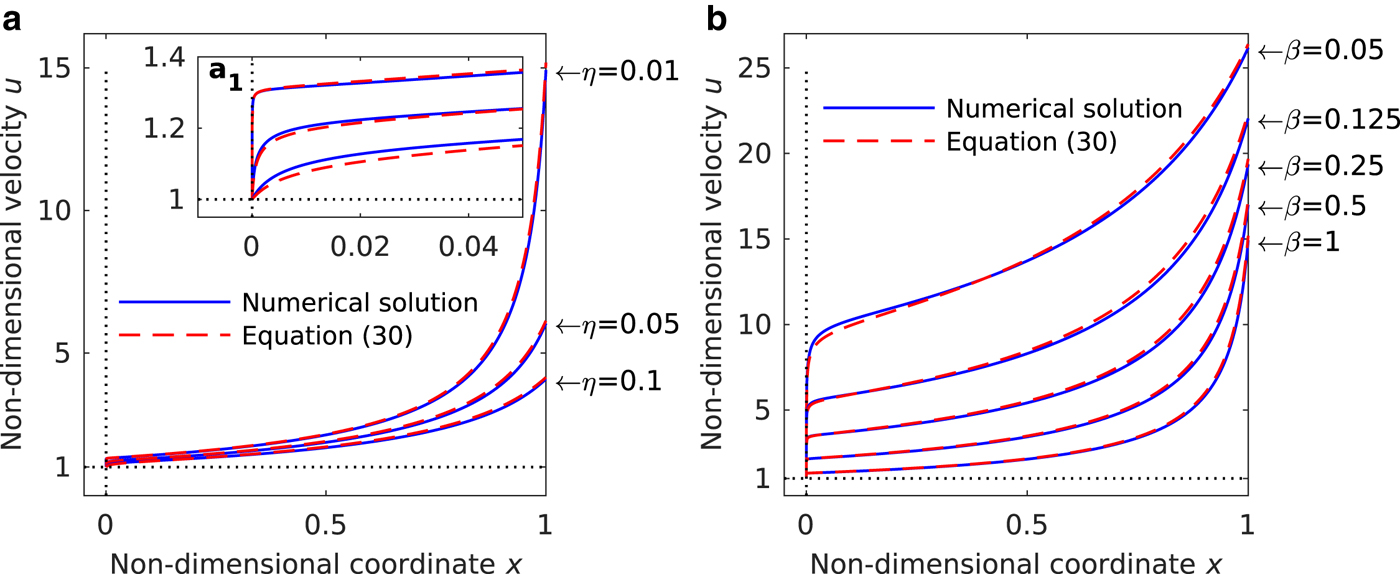
Fig. 2. Velocity profiles in the ice shelf. Panel (a) shows a comparison of numerical solutions and composite solutions u (30) in the ice shelf for different η as indicated, and ![]() $n = 1/p = 3,\dot m = 0,\beta = 1$. The grounding line is located at x = 0, the calving front is located at x = 1. Note that the boundary layer at the grounding line becomes more pronounced as η decreases and that the match between numerical and composite solution improves as η decreases (see inset panel a 1). Panel (b) shows a comparison of numerical solutions and composite solutions in the ice shelf for different β as indicated, and
$n = 1/p = 3,\dot m = 0,\beta = 1$. The grounding line is located at x = 0, the calving front is located at x = 1. Note that the boundary layer at the grounding line becomes more pronounced as η decreases and that the match between numerical and composite solution improves as η decreases (see inset panel a 1). Panel (b) shows a comparison of numerical solutions and composite solutions in the ice shelf for different β as indicated, and ![]() $n = 1/p = 3,\dot m = 0,\eta = 10^{ - 2}$. Numerical solutions are obtained by direct solution of the unsimplified equations (7a) and (8b) with Matlab ODE solvers and a shooting method.
$n = 1/p = 3,\dot m = 0,\eta = 10^{ - 2}$. Numerical solutions are obtained by direct solution of the unsimplified equations (7a) and (8b) with Matlab ODE solvers and a shooting method.
3.4 Analysis of the ice-shelf solution
In the last section, we have exploited the boundary layer structure of strongly buttressed ice shelves to derive solutions for the velocity (30) and the stress at the grounding line (28) for a non-linear lateral shear stress term (p < 1 in (2)). The flow in the main part of the ice shelf can be described by a leading order balance between the lateral shear stress and driving stress (Hindmarsh, Reference Hindmarsh2012), and its solution (18) has previously been derived in Pegler (Reference Pegler2016). The main difference between our ice-shelf solution and the solutions considered in Pegler (Reference Pegler2016) and Hindmarsh (Reference Hindmarsh2012) is that we explicitly introduce a boundary layer at the grounding line which ensures that the boundary conditions at the grounding line are satisfied. The existence of this boundary layer is noted in Pegler (Reference Pegler2016), who also discusses its properties. Solution of the leading order equations in this boundary layer allows us to determine the backstress at the grounding line τ 0 by using matched asymptotic expansions (Hinch, Reference Hinch1991; Holmes, Reference Holmes2013), which provides us with an avenue to determine the ice flux at the grounding line through (14).
The boundary layer treatment of the ice-shelf equations at the grounding line and the derivation of the backstress τ 0 relies on the assumption that η is small and that terms of O(η) can be neglected in the main part of the ice shelf. The size of η is determined by the ice-shelf properties (see (6)) and it is not guaranteed that η ≪ 1. We therefore validate our equation for the grounding line stress (28) by comparing it with numerical solutions of the unsimplified non-dimensional ice-shelf equations (7a) to (8b) obtained with Matlab ODE solvers together with a shooting method to determine the correct grounding line stress τ 0. Figure 3 shows numerical and asymptotic solutions of the grounding line stress τ 0 (28) for different values of the non-dimensional viscosity η (panel a) and accumulation rate ![]() $\dot m$ (panel (b)). There is good agreement between the asymptotic and the numerical solutions for η ≤ 10−2. Note that there is a viscosity-dependence of τ 0 which decreases for η → 0, i.e. τ 0 converges to a viscosity-independent value as η → 0, the limit where lateral shear stresses balance most of the driving stress. Note also that the asymptotic solutions appear to remain valid all the way up to β = 0.
$\dot m$ (panel (b)). There is good agreement between the asymptotic and the numerical solutions for η ≤ 10−2. Note that there is a viscosity-dependence of τ 0 which decreases for η → 0, i.e. τ 0 converges to a viscosity-independent value as η → 0, the limit where lateral shear stresses balance most of the driving stress. Note also that the asymptotic solutions appear to remain valid all the way up to β = 0.
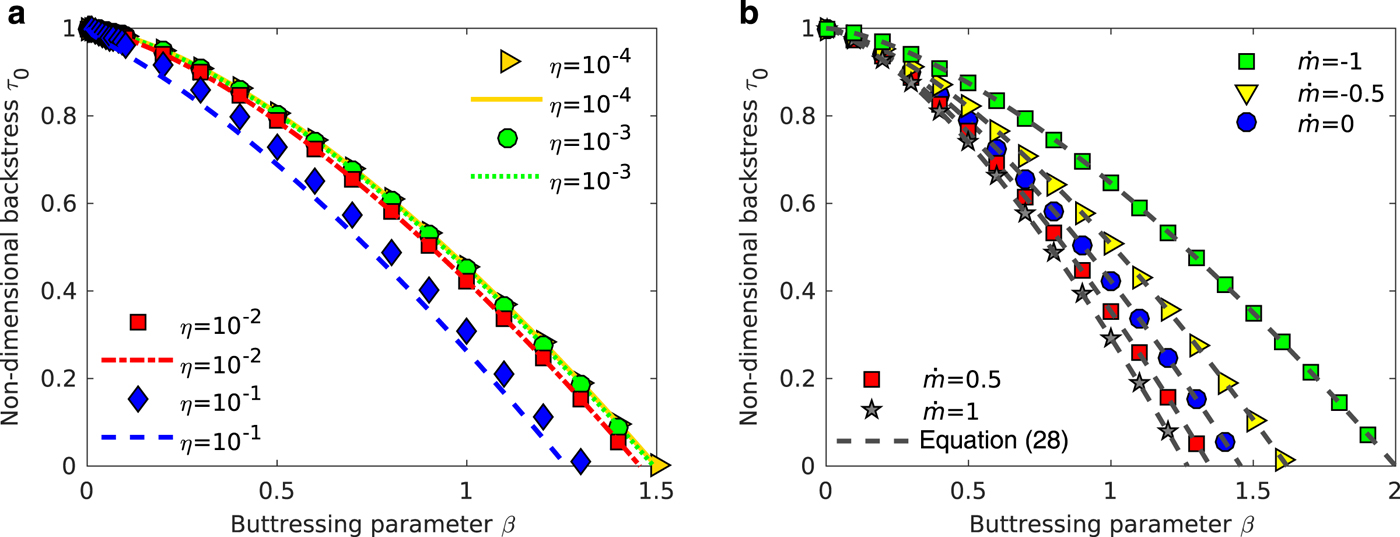
Fig. 3. Comparison of asymptotic solutions and numerical solutions of the stress at the grounding line. Markers are numerical solutions obtained by solving the unsimplified non-dimensional problem (7a) to (8b) with Matlab ODE solvers and a shooting method, lines are the asymptotic solution (28). (a) Non-dimensional backstress τ 0 vs the buttressing parameter β for ![]() $\dot m = 0$ and different values of η, as indicated in the legend. Note that
$\dot m = 0$ and different values of η, as indicated in the legend. Note that ![]() $[(1 + \dot m)^{p + 1} - 1]/\dot m = p + 1$ at
$[(1 + \dot m)^{p + 1} - 1]/\dot m = p + 1$ at ![]() $\dot m = 0$. (b) Non-dimensional backstress τ 0 vs the buttressing parameter β, for different accumulation rates and η = 10−2. p = 1/n = 1/3 for all calculations.
$\dot m = 0$. (b) Non-dimensional backstress τ 0 vs the buttressing parameter β, for different accumulation rates and η = 10−2. p = 1/n = 1/3 for all calculations.
The asymptotic solution captures this viscosity dependence via the expression for the ice thickness at the calving front h 1,butt (19). This is qualitatively different from the linearised case for p = 1, where the exact formula (10) predicts that the stress τ 0 is independent of the viscosity and the ice thickness at the calving front. However, this also implies that the boundary layer solution (28) agrees with the exact solution for p = 1 (10) in the limit of η → 0 (where h 1,butt → 0) only.
We have explicitly included the term h 1,butt (19) in our expression of the grounding line stress (28) in order to later test calving laws that are based on the ice thickness at the calving front. However, we expect h 1,butt (19) to provide a valid approximation for the ice thickness at the calving front for η ≪ β ~ 1 only, as this is the limit in which the outer solution was derived. This is confirmed by a comparison of (19) with numerical solutions of (7) and (8) for constant η but different values of β and either ![]() $\dot m = 0$ or
$\dot m = 0$ or ![]() $\dot m = 1$ in Fig. 4 (for
$\dot m = 1$ in Fig. 4 (for ![]() $\dot m = - 1$ the ice thickness at the calving front is zero: h c = h c,butt = 0). Figure 4 illustrates that h 1,butt and the numerical solution of the ice thickness at the calving front only agree for
$\dot m = - 1$ the ice thickness at the calving front is zero: h c = h c,butt = 0). Figure 4 illustrates that h 1,butt and the numerical solution of the ice thickness at the calving front only agree for ![]() $\beta /\eta \mathop \gt \limits_ \approx 1.$. For
$\beta /\eta \mathop \gt \limits_ \approx 1.$. For ![]() $\beta /\eta \mathop \lt \limits_ \approx 1, {h_{1,{\rm butt}}}$ decreases with decreasing β, while the numerical solution converges towards the value for the calving front ice thickness of unbuttressed ice shelves (Van der Veen, Reference Van der Veen1983, referenced as (32) below).
$\beta /\eta \mathop \lt \limits_ \approx 1, {h_{1,{\rm butt}}}$ decreases with decreasing β, while the numerical solution converges towards the value for the calving front ice thickness of unbuttressed ice shelves (Van der Veen, Reference Van der Veen1983, referenced as (32) below).

Fig. 4. Comparison of the different solutions for the non-dimensional ice thickness at the calving front, plotted against the buttressing strength β/η for non-dimensional accumulation ![]() $\dot m = 0$ and
$\dot m = 0$ and ![]() $\dot m = 1$. h 1,butt is the asymptotic solution for buttressed ice shelves (19), h 1,unbutt is the exact solution for unconfined ice shelves (32), h 1 is the approximate solution (31), and numerical results are obtained by solving the unsimplified non-dimensional ice shelf Eqns (7a) to (8b). η = 10−2, n = 1/p = 3.
$\dot m = 1$. h 1,butt is the asymptotic solution for buttressed ice shelves (19), h 1,unbutt is the exact solution for unconfined ice shelves (32), h 1 is the approximate solution (31), and numerical results are obtained by solving the unsimplified non-dimensional ice shelf Eqns (7a) to (8b). η = 10−2, n = 1/p = 3.
This deviation does not affect the prediction of the backstress at the grounding line and the flux at the grounding line unless the ice thickness at the grounding line is explicitly set by a calving law. In this case, we approximate the ice thickness at the calving front with
where h 1,butt is given by (19) and h 1,unbutt is given by (Van der Veen, Reference Van der Veen1983)
 $$h_{1,{\rm unbutt}} = \displaystyle{{(1 + \dot m)} \over {{(1 + 1/(\eta ^n\dot m)[{(1 + \dot m)}^{n + 1} - 1])}^{1/(n + 1)}}}.$$
$$h_{1,{\rm unbutt}} = \displaystyle{{(1 + \dot m)} \over {{(1 + 1/(\eta ^n\dot m)[{(1 + \dot m)}^{n + 1} - 1])}^{1/(n + 1)}}}.$$Note that (31) is an approximation which is chosen purely heuristically because of its simplicity and because it correctly reproduces the asymptotic behaviour for β/η ≫ 1 and β/η ≪ 1. Therefore, we cannot expect to correctly match the transition between these two asymptotic limits, which is apparent for the solutions plotted in Fig. 4. However, as we will see in Section 5, h 1 is a useful tool for interpreting grounding line positions. In the Supplementary material, we compare (31) with an exact solution for the special case of n = p = 1 and ![]() $\dot m = 0$, which is derived in Pegler (Reference Pegler2016).
$\dot m = 0$, which is derived in Pegler (Reference Pegler2016).
Requiring the stress at the grounding line (28) to be positive constraints β:
Two other conditions – a positive ice-shelf length, and a positive ice thickness at the calving front, which should also be less than the ice thickness at the grounding line (0 ≤ h 1 < 1) – provide constraints on the maximum net mass loss over the ice shelf ![]() $ - \dot mL_{\rm s}$. This mass loss must be equal or less than the ice flux at the grounding line:
$ - \dot mL_{\rm s}$. This mass loss must be equal or less than the ice flux at the grounding line:
The dimensional forms of the derived expressions are the following: the extensional stress τ g is
with τ g,0 given by (12) and
 $$\Theta _{{\rm general}} = \left( {1 - {\left[ {\displaystyle{{h_{{\rm c},{\rm butt}}^{\,p + 1}} \over {h_{\rm g}^{\,p + 1}}} + \Lambda \displaystyle{{{(q_{\rm g} + \dot mL_{\rm s})}^{\,p + 1} - q_{\rm g}^{\,p + 1}} \over {\rho g(1 - \rho /\rho _{\rm w})\dot mh_{\rm g}^{\,p + 1}}}} \right]}^{2/(p + 1)}} \right)$$
$$\Theta _{{\rm general}} = \left( {1 - {\left[ {\displaystyle{{h_{{\rm c},{\rm butt}}^{\,p + 1}} \over {h_{\rm g}^{\,p + 1}}} + \Lambda \displaystyle{{{(q_{\rm g} + \dot mL_{\rm s})}^{\,p + 1} - q_{\rm g}^{\,p + 1}} \over {\rho g(1 - \rho /\rho _{\rm w})\dot mh_{\rm g}^{\,p + 1}}}} \right]}^{2/(p + 1)}} \right)$$(note that for ![]() $\dot m = 0$ we have
$\dot m = 0$ we have ![]() $[(q_{\rm g} + \dot mL_{\rm s})^{p + 1} - q_{\rm g}^{p + 1} ]/ \dot m = (p + 1)q_{\rm g}^p L_{\rm s} $). In contrast to the unbuttressed case, where the grounding line stress τ g,0 (12) depends only on the ice thickness at the grounding line h g and local ice and bed properties, the buttressed stress also depends on the length of the ice shelf L s, the ice flux at the grounding line q g, the accumulation/melt rate on the shelf
$[(q_{\rm g} + \dot mL_{\rm s})^{p + 1} - q_{\rm g}^{p + 1} ]/ \dot m = (p + 1)q_{\rm g}^p L_{\rm s} $). In contrast to the unbuttressed case, where the grounding line stress τ g,0 (12) depends only on the ice thickness at the grounding line h g and local ice and bed properties, the buttressed stress also depends on the length of the ice shelf L s, the ice flux at the grounding line q g, the accumulation/melt rate on the shelf ![]() $\dot m$ and the width of the ice shelf W through Λ (Eqn (2)). Additionally, the grounding line stress depends on h c,butt, given by (19)
$\dot m$ and the width of the ice shelf W through Λ (Eqn (2)). Additionally, the grounding line stress depends on h c,butt, given by (19)
 $$h_{{\rm c},{\rm butt}} = \left[ {\Lambda \displaystyle{{{(4A^{ - 1/n})}^n} \over {{((1 - \rho /\rho _{\rm w})\rho g)}^{n + 1}}}{(q_{\rm g} + \dot mL_{\rm s})}^{\,p + 1}} \right]^{1/(2 + n + p)}.$$
$$h_{{\rm c},{\rm butt}} = \left[ {\Lambda \displaystyle{{{(4A^{ - 1/n})}^n} \over {{((1 - \rho /\rho _{\rm w})\rho g)}^{n + 1}}}{(q_{\rm g} + \dot mL_{\rm s})}^{\,p + 1}} \right]^{1/(2 + n + p)}.$$In the limit of strong buttressing, h c,butt corresponds to the ice thickness at the calving front h c (Pegler, Reference Pegler2016), which we approximate by (31)
 $$\eqalign{h_{\rm c} = & \left[ {h_{{\rm c},{\rm butt}}^{2 + n + p} {\rm erf}\left( {\displaystyle{1 \over 2}\Lambda u_{\rm g}^{\,p - 1/n} L_{\rm s}^{1 + 1/n} A^{1/n}} \right)} \right. \cr & + \left. {h_{{\rm c},{\rm unbutt}}^{2 + n + p} {\rm erfc}\left( {\displaystyle{1 \over 2}\Lambda u_{\rm g}^{\,p - 1/n} L_{\rm s}^{1 + 1/n} A^{1/n}} \right)} \right]^{1/(2 + n + p)},} $$
$$\eqalign{h_{\rm c} = & \left[ {h_{{\rm c},{\rm butt}}^{2 + n + p} {\rm erf}\left( {\displaystyle{1 \over 2}\Lambda u_{\rm g}^{\,p - 1/n} L_{\rm s}^{1 + 1/n} A^{1/n}} \right)} \right. \cr & + \left. {h_{{\rm c},{\rm unbutt}}^{2 + n + p} {\rm erfc}\left( {\displaystyle{1 \over 2}\Lambda u_{\rm g}^{\,p - 1/n} L_{\rm s}^{1 + 1/n} A^{1/n}} \right)} \right]^{1/(2 + n + p)},} $$with h c,unbutt the calving front ice thickness of an unconfined ice shelf from (32):
 $$\eqalign{h_{{\rm c},{\rm unbutt}} = & \left( {q_{\rm g} + \dot mL_{\rm s}} \right) \times \bigg[\left( {\displaystyle{{q_{\rm g}} \over {h_{\rm g}}}} \right)^{n + 1} + A\left( {\displaystyle{{\rho g} \over 4}\left( {1 - \displaystyle{\rho \over {\rho _{\rm w}}}} \right)} \right)^n \cr & \times \left. {\displaystyle{1 \over {\dot m}}\left( {{(q_{\rm g} + \dot mL_{\rm s})}^{n + 1} - q_{\rm g}^{n + 1}} \right)} \right]^{ - 1/(n + 1)}.} $$
$$\eqalign{h_{{\rm c},{\rm unbutt}} = & \left( {q_{\rm g} + \dot mL_{\rm s}} \right) \times \bigg[\left( {\displaystyle{{q_{\rm g}} \over {h_{\rm g}}}} \right)^{n + 1} + A\left( {\displaystyle{{\rho g} \over 4}\left( {1 - \displaystyle{\rho \over {\rho _{\rm w}}}} \right)} \right)^n \cr & \times \left. {\displaystyle{1 \over {\dot m}}\left( {{(q_{\rm g} + \dot mL_{\rm s})}^{n + 1} - q_{\rm g}^{n + 1}} \right)} \right]^{ - 1/(n + 1)}.} $$Note that the ice thickness at the calving front h c,butt (35) directly depends on the flux at the grounding line. If the net accumulation over the shelf is zero ![]() $(\dot m = 0)$ the calving front ice thickness and the flux at the grounding line appear to be explicitly linked:
$(\dot m = 0)$ the calving front ice thickness and the flux at the grounding line appear to be explicitly linked: ![]() $h_{{\rm c},{\rm butt}}{\rm \sim} q_{\rm g}^{(1 + p)/(2 + n + p)} $. We will discuss the implications of this in Section 5.
$h_{{\rm c},{\rm butt}}{\rm \sim} q_{\rm g}^{(1 + p)/(2 + n + p)} $. We will discuss the implications of this in Section 5.
As outlined in Section 3.2, we can now use (34b) to determine the ice flux at the grounding line from (14), i.e.
without having to solve the grounding line problem considered in (Schoof, Reference Schoof2007a). This accomplishes the goal of this section, even though the resulting expression for q g is relatively complicated (we explicitly write it out in (44)).
4. THE ICE FLUX AT THE GROUNDING LINE IN THE LIMIT OF STRONG BUTTRESSING
In this section, we consider steady-state solutions for the grounded ice-stream part of the marine-based ice-stream/ice-shelf system in order to derive a simplified ice-flux expression. This is possible in the limit of strong buttressing. In this limit, it is not necessary to solve the boundary layer problem considered in Schoof (Reference Schoof2007a) because the leading order problem is well posed.
The derived expression for the backstress at the grounding line (34) allows us to focus on the momentum- and mass balance of the laterally confined ice stream using the stress as a boundary condition at the grounding line. Following Schoof (Reference Schoof2007a), we non-dimensionalise the momentum- and mass-balance equations and corresponding boundary conditions (1a), (3), (4a) and (4b), and (34) and (35) with the scales [x] = L 0, C[u]m = ρg[h]2/[x], and [u][h]/[x] = [a], and put ![]() $x = [x]\tilde x,h = [h]\tilde h,b = [h]\tilde b,u = [u]\tilde u$. This leads to two non-dimensional groups
$x = [x]\tilde x,h = [h]\tilde h,b = [h]\tilde b,u = [u]\tilde u$. This leads to two non-dimensional groups
Additionally, we introduce δ = 1 − ρ/ρ w. (34) was derived under the assumption η ≪ β, where η and β are the two non-dimensional groups defined in (6). ε and Λ are directly related to η and β through:
 $$\varepsilon = \eta \displaystyle{{\delta {\tilde h}_{\rm g}\tilde L_{\rm s}^{1/n}} \over {8({\tilde u}_{\rm g})^{1/n}}},\;\lambda = \beta \displaystyle{\delta \over 2}\displaystyle{{\delta {\tilde h}_{\rm g}} \over {\tilde u_{\rm g}^p {\tilde L}_{\rm s}}}.$$
$$\varepsilon = \eta \displaystyle{{\delta {\tilde h}_{\rm g}\tilde L_{\rm s}^{1/n}} \over {8({\tilde u}_{\rm g})^{1/n}}},\;\lambda = \beta \displaystyle{\delta \over 2}\displaystyle{{\delta {\tilde h}_{\rm g}} \over {\tilde u_{\rm g}^p {\tilde L}_{\rm s}}}.$$The condition η < β therefore corresponds to
 $$\varepsilon {\rm \ll} \displaystyle{{\tilde L_{\rm s}^{1 + 1/n}} \over {\tilde u_{\rm g}^{1/n - p}}} \lambda $$
$$\varepsilon {\rm \ll} \displaystyle{{\tilde L_{\rm s}^{1 + 1/n}} \over {\tilde u_{\rm g}^{1/n - p}}} \lambda $$implying either a very narrow (λ ~ Λ ~ W −(1/n+1) large) or a very long ice shelf (L s large), or a fast sliding glacier with thin ice at the grounding line (ε → 0).
With the non-dimensional groups (39) and assuming ε ≪ λ ~ 1, we obtain a simplified ice-sheet model from (1a), (3)–(4b) and (34) by neglecting terms of O(ε)
 $$\left. {\matrix{ { - \vert \tilde u \vert ^{m - 1}\tilde u - \lambda \tilde h \vert \tilde u \vert ^{\,p - 1}\tilde u - \tilde h\displaystyle{{\partial (\tilde h + \tilde b)} \over {\partial \tilde x}} = 0} \hfill \cr {\displaystyle{{\partial (\tilde u\tilde h)} \over {\partial \tilde x}} = \dot a} \hfill \cr {\tilde h \ge \displaystyle{{ - \tilde b(\tilde x)} \over {1 - \delta }}} \hfill \cr } \!\! } \right\} \tilde x \in (0,\tilde x_{\rm g}).$$
$$\left. {\matrix{ { - \vert \tilde u \vert ^{m - 1}\tilde u - \lambda \tilde h \vert \tilde u \vert ^{\,p - 1}\tilde u - \tilde h\displaystyle{{\partial (\tilde h + \tilde b)} \over {\partial \tilde x}} = 0} \hfill \cr {\displaystyle{{\partial (\tilde u\tilde h)} \over {\partial \tilde x}} = \dot a} \hfill \cr {\tilde h \ge \displaystyle{{ - \tilde b(\tilde x)} \over {1 - \delta }}} \hfill \cr } \!\! } \right\} \tilde x \in (0,\tilde x_{\rm g}).$$The boundary conditions at the ice divide are
and the boundary conditions at the grounding line are
 $$\left.\matrix{ {\tilde h} = {\displaystyle{ - {\tilde b}({\tilde x})} \over \displaystyle{1 - \delta}}, \hfill \cr {\tilde h}^{\,p + 1} = {\displaystyle{\lambda \over \delta}} \displaystyle{{({\tilde q} + {\dot m}{\tilde L}_{\rm s})^{\,p + 1} - {\tilde q}^{\,p + 1}} \over {\dot m}}}\right\}\quad {\rm at}\;{\tilde x} = {\tilde x}_{\rm g},$$
$$\left.\matrix{ {\tilde h} = {\displaystyle{ - {\tilde b}({\tilde x})} \over \displaystyle{1 - \delta}}, \hfill \cr {\tilde h}^{\,p + 1} = {\displaystyle{\lambda \over \delta}} \displaystyle{{({\tilde q} + {\dot m}{\tilde L}_{\rm s})^{\,p + 1} - {\tilde q}^{\,p + 1}} \over {\dot m}}}\right\}\quad {\rm at}\;{\tilde x} = {\tilde x}_{\rm g},$$where we neglected terms of O(εn(p+1)/(2+n+p)), which includes the scaled version of h c,butt (35) in the stress condition at the grounding line (34). We also defined ![]() $\tilde q = \tilde u\tilde h$.
$\tilde q = \tilde u\tilde h$.
In the limit ε ≪ λ ~ 1 we are interested in here, equation (42c) shows that we can now obtain a relationship between the ice thickness at the grounding line ![]() $\tilde h(\tilde x_{\rm g})$ and the ice flux
$\tilde h(\tilde x_{\rm g})$ and the ice flux ![]() $\tilde q(\tilde x_{\rm g})$ at the grounding line without recourse to a boundary layer problem. Physically, this is the limit where the leading order stress balance at the grounding line is between the driving stress and the lateral shear stress. By solving (42c) for
$\tilde q(\tilde x_{\rm g})$ at the grounding line without recourse to a boundary layer problem. Physically, this is the limit where the leading order stress balance at the grounding line is between the driving stress and the lateral shear stress. By solving (42c) for ![]() $\tilde q(x_{\rm g})$, we have now obtained an expression for the ice flux at the grounding line valid in the limit of strong buttressing.
$\tilde q(x_{\rm g})$, we have now obtained an expression for the ice flux at the grounding line valid in the limit of strong buttressing.
Note that for λ = 0, (42a)–(42c) are the same equations as those considered in Schoof (Reference Schoof2007a). Condition (42c)2 then becomes ![]() $\tilde h \to 0$, and we have two conditions for the ice thickness at the grounding line, while the ice flux at the grounding line is undetermined. Therefore, we are missing a flux boundary condition to solve (42a)–(42c). Schoof (Reference Schoof2007a) determines this flux condition by introducing a boundary layer at the grounding line, which in our case yields (38) with Θgeneral given by (34b).
$\tilde h \to 0$, and we have two conditions for the ice thickness at the grounding line, while the ice flux at the grounding line is undetermined. Therefore, we are missing a flux boundary condition to solve (42a)–(42c). Schoof (Reference Schoof2007a) determines this flux condition by introducing a boundary layer at the grounding line, which in our case yields (38) with Θgeneral given by (34b).
5. GROUNDING LINE DYNAMICS IN THE PRESENCE OF BUTTRESSING
5.1 Simplified marine ice-sheet model
Using the results of the previous sections, a simplified model for steady-state marine ice sheets can be considered in lieu of the full problem (1)–(4c). The momentum balance (1a) and mass balance (3) of the grounded ice sheet are simplified per (42a) (see also Schoof, Reference Schoof2007a)
 $$\hskip-4pt \left. {\matrix{ { - C \vert u \vert ^{m - 1}u - \Lambda h \vert u \vert ^{\,p - 1}u - \rho gh\displaystyle{{\partial (h + b)} \over {\partial x}} = 0} \hfill \cr {\displaystyle{{\partial (uh)} \over {\partial x}} = \dot a} \hfill \cr {h \ge - \displaystyle{{\rho _{\rm w}} \over \rho} b} \hfill \cr}}\!\! \right\}x \in (0,x_{\rm g})$$
$$\hskip-4pt \left. {\matrix{ { - C \vert u \vert ^{m - 1}u - \Lambda h \vert u \vert ^{\,p - 1}u - \rho gh\displaystyle{{\partial (h + b)} \over {\partial x}} = 0} \hfill \cr {\displaystyle{{\partial (uh)} \over {\partial x}} = \dot a} \hfill \cr {h \ge - \displaystyle{{\rho _{\rm w}} \over \rho} b} \hfill \cr}}\!\! \right\}x \in (0,x_{\rm g})$$with the boundary conditions at ice divide and grounding line from (42b)and (42c):
The effect of an ice shelf is captured by the implicit expression for the ice flux at the grounding line q g (38) with (34b):
 $$\eqalign{q_{\rm g} = & \left( {\displaystyle{{A{(\rho g)}^{n + 1}{\left( {1 - \rho /\rho _{\rm w}} \right)}^n} \over {4^nC}}} \right)^{1/(m + 1)}h_{\rm g}^{(3 + m + n)/(m + 1)} \cr & \times \left( {1 - {\left[ {\displaystyle{{h_{{\rm c},{\rm butt}}^{\,p + 1}} \over {h_{\rm g}^{\,p + 1}}} + \Lambda \displaystyle{{{(q_{\rm g} + \dot mL_{\rm s})}^{\,p + 1} - q_{\rm g}^{\,p + 1}} \over {\rho g\left( {1 - \rho /\rho _{\rm w}} \right)\dot mh_{\rm g}^{\,p + 1}}}} \right]}^{2/(p + 1)}} \right)^{n/(m + 1)}} $$
$$\eqalign{q_{\rm g} = & \left( {\displaystyle{{A{(\rho g)}^{n + 1}{\left( {1 - \rho /\rho _{\rm w}} \right)}^n} \over {4^nC}}} \right)^{1/(m + 1)}h_{\rm g}^{(3 + m + n)/(m + 1)} \cr & \times \left( {1 - {\left[ {\displaystyle{{h_{{\rm c},{\rm butt}}^{\,p + 1}} \over {h_{\rm g}^{\,p + 1}}} + \Lambda \displaystyle{{{(q_{\rm g} + \dot mL_{\rm s})}^{\,p + 1} - q_{\rm g}^{\,p + 1}} \over {\rho g\left( {1 - \rho /\rho _{\rm w}} \right)\dot mh_{\rm g}^{\,p + 1}}}} \right]}^{2/(p + 1)}} \right)^{n/(m + 1)}} $$q g now depends not only on the ice thickness at the grounding line, but also on the length of the ice shelf L s, the width W of the ice shelf through Λ in (2), and h c,butt (35).
For strongly buttressed ice shelves, we can replace (44) with the dimensional version of (42c):
There are two noteworthy special cases of (45): if there is zero net accumulation, we get
 $$q_{\rm g} = \left( {\displaystyle{{\rho g(1 - \rho /\rho _{\rm w})} \over {(\,p + 1)\Lambda L_{\rm s}}}} \right)^{1/p}h_{\rm g}^{1 + 1/p}, \quad {\rm if}\;\dot m = 0$$
$$q_{\rm g} = \left( {\displaystyle{{\rho g(1 - \rho /\rho _{\rm w})} \over {(\,p + 1)\Lambda L_{\rm s}}}} \right)^{1/p}h_{\rm g}^{1 + 1/p}, \quad {\rm if}\;\dot m = 0$$as ![]() $[(q_{\rm g} + \dot mL_{\rm s})^{p + 1} - q_{\rm g}^{p + 1} ]/\dot m = (p + 1)q_{\rm g}^p L_s$ at
$[(q_{\rm g} + \dot mL_{\rm s})^{p + 1} - q_{\rm g}^{p + 1} ]/\dot m = (p + 1)q_{\rm g}^p L_s$ at ![]() $\dot m = 0$. Alternatively, if all the mass of the ice shelf is lost through melting, that is in the absence of calving, we have
$\dot m = 0$. Alternatively, if all the mass of the ice shelf is lost through melting, that is in the absence of calving, we have ![]() $L_{\rm s} = q_{\rm g}/( - \dot m)$ and obtain
$L_{\rm s} = q_{\rm g}/( - \dot m)$ and obtain
 $$q_{\rm g} = \left[ {\rho g\left( {1 - \displaystyle{\rho \over {\rho _{\rm w}}}} \right)\displaystyle{{ - \dot m} \over \Lambda}} \right]^{1/(p + 1)}h_{\rm g},\quad {\rm if}\left\{ {\matrix{ {\dot m \lt 0,} \hfill \cr {L_{\rm s} = \displaystyle{{q_{\rm g}} \over {( - \dot m)}}.} \hfill \cr}} \right.$$
$$q_{\rm g} = \left[ {\rho g\left( {1 - \displaystyle{\rho \over {\rho _{\rm w}}}} \right)\displaystyle{{ - \dot m} \over \Lambda}} \right]^{1/(p + 1)}h_{\rm g},\quad {\rm if}\left\{ {\matrix{ {\dot m \lt 0,} \hfill \cr {L_{\rm s} = \displaystyle{{q_{\rm g}} \over {( - \dot m)}}.} \hfill \cr}} \right.$$We write (46a) and (46b) out here as these explicit expressions for the ice flux are easier to understand than their more complicated implicit counterparts. In particular, we can see from (46a) and (46b) that in the limit of strong buttressing, the ice flux at the grounding line is again a function of the ice thickness at the grounding line, and that the exponent on the ice thickness strongly depends on the mechanism through which the ice shelf loses its mass (i.e. q g ∝ h 1+1/p for calving only, q g ∝ h g for melting only). In contrast to the unbuttressed case (compare (15)), q g is independent of the properties of the ice sheet, which are represented by the sliding parameters C and m in the unbuttressed flux (15). Instead, the strongly buttressed flux (46) depends only on the ice-shelf width W (which is somewhat hidden in the expression of Λ), the ice-shelf length L s and/or net accumulation term ![]() $\dot m$. This is also true for the more general case of mixed ice-shelf calving and melting, see (45). We therefore expect the dynamics of strongly buttressed marine ice sheets to be governed by the ice-shelf properties, as also suggested from the analysis of laboratory studies in Pegler and others (Reference Pegler, Kowal, Hasenclever and Worster2013) and Kowal and others (Reference Kowal, Pegler and Worster2016).
$\dot m$. This is also true for the more general case of mixed ice-shelf calving and melting, see (45). We therefore expect the dynamics of strongly buttressed marine ice sheets to be governed by the ice-shelf properties, as also suggested from the analysis of laboratory studies in Pegler and others (Reference Pegler, Kowal, Hasenclever and Worster2013) and Kowal and others (Reference Kowal, Pegler and Worster2016).
In the next section, we use (43)–(45) to confirm these initial observations and to investigate how buttressing affects the position of the grounding line. As a test case, we choose a laterally confined version of the MISMIP experiment 1a (Pattyn and others, Reference Pattyn2012) with the ice-stream/ice-shelf system flowing in a channel of constant width W and the bed elevation given by
In the case of a constant accumulation rate ![]() $\dot a$, we can solve (43a)2 to obtain
$\dot a$, we can solve (43a)2 to obtain
Together with the flux expressions (44) or (45), this allows us to directly determine the grounding line position x g. Additionally, we assume that the rate of mass gain of the ice shelf ![]() $(\dot m)$ equals the rate of mass gain of the ice sheet
$(\dot m)$ equals the rate of mass gain of the ice sheet ![]() $(\dot m = \dot a)$. All other parameters are listed in table 1.
$(\dot m = \dot a)$. All other parameters are listed in table 1.
With the flux expressions (44) and (45), we now have three different methods to determine steady-state grounding line positions of buttressed marine ice sheets:
For the numerical solution, we use the finite element solver Comsol at a resolution that is sufficiently high such that further refinement of the numerical grid does not change the numerical results. To obtain the semi-analytical solutions with (44) or (45), we have to solve the algebraic Eqn (47). While this is significantly faster than solving the system of differential Eqns (1)–(4c), a numerical algorithm is still necessary to solve these non-linear equations. We use a Newton method to determine x g up to a relative accuracy of 10−8.
5.2 The effect of calving on the grounding line position
In the unbuttressed MISMIP experiments, it is not necessary to prescribe a calving law as the ice shelf can be excluded from the momentum balance in accordance with (15). In the buttressed case, however, computing the grounding line flux q g from (44) or (45) requires a condition on either L s (length of the ice shelf), x c (position of the calving front), or h c (ice thickness at the calving front), and prescription of the lateral drag term Λ. Here, we determine Λ from the ice-shelf width W with the formula provided by Hindmarsh (Reference Hindmarsh2012), Eqn (3)1.
Figures 5–7 illustrate how different calving laws affect steady-state grounding line position as the ice-shelf width is reduced and buttressing increases. Figure 5 shows steady-state grounding line positions for different ice-shelf widths with a prescribed ice-shelf length L s = 750 km. Figure 6 shows results with a prescribed calving front x c = 3000 km, i.e. we use L s = x c − x g in (44) and (45). Figure 7 shows results with a prescribed calving front thickness h c = 250 m.
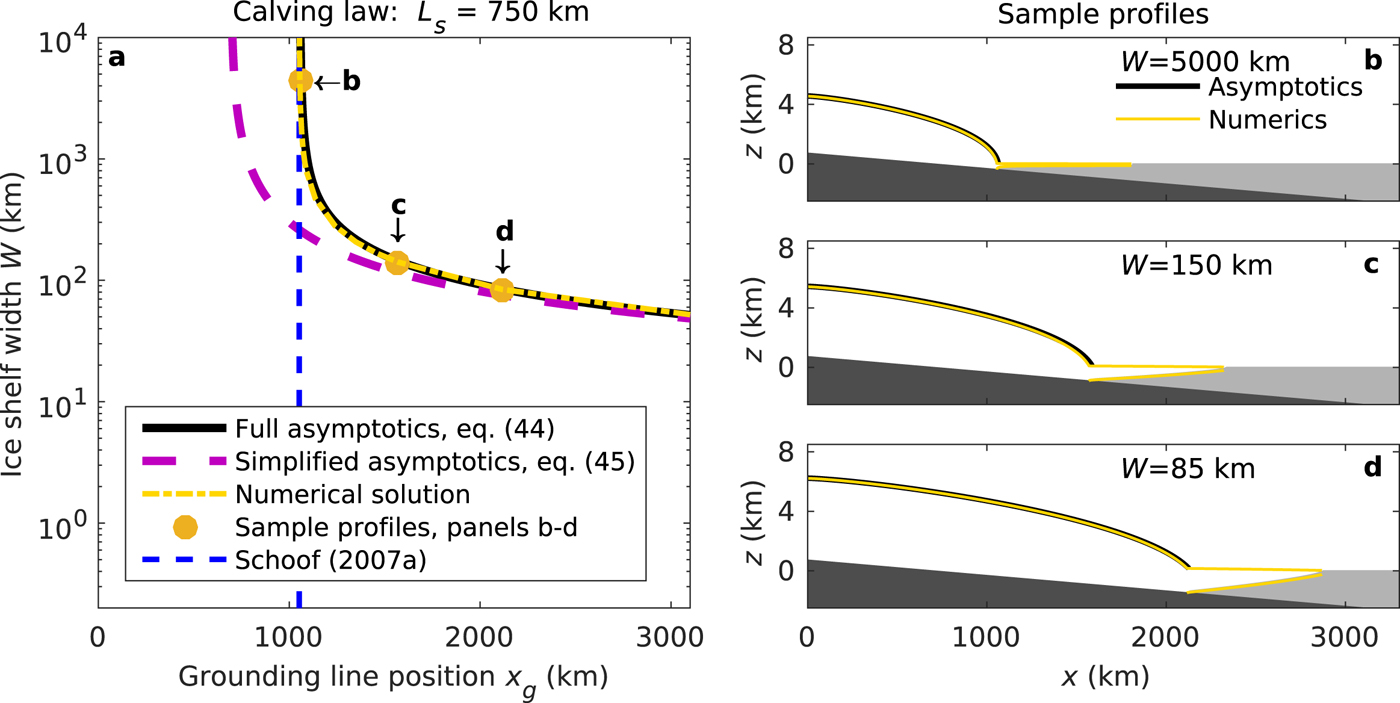
Fig. 5. Comparison of asymptotic and numerical results for MISMIP experiment 1a (Pattyn and others, Reference Pattyn2012) with additional buttressing. Panel (a) shows ice-shelf width W vs grounding line position x g for a fixed ice-shelf length of L s = 750 km, and panels (b) and (d) show corresponding ice-sheet profiles. Numerical results are obtained by solving the unsimplified model (1)–(4c) numerically with Comsol. The asymptotic grounding line positions are obtained by solving ![]() $\dot ax_{\rm g} = q_{\rm g}$ (47) with q g given by (44) and (45), respectively. The asymptotic profiles are calculated by additionally integrating (43a)–(43c). Note that the ice shelf is only plotted for the numerical solutions, as it can be excluded from the asymptotics.
$\dot ax_{\rm g} = q_{\rm g}$ (47) with q g given by (44) and (45), respectively. The asymptotic profiles are calculated by additionally integrating (43a)–(43c). Note that the ice shelf is only plotted for the numerical solutions, as it can be excluded from the asymptotics.
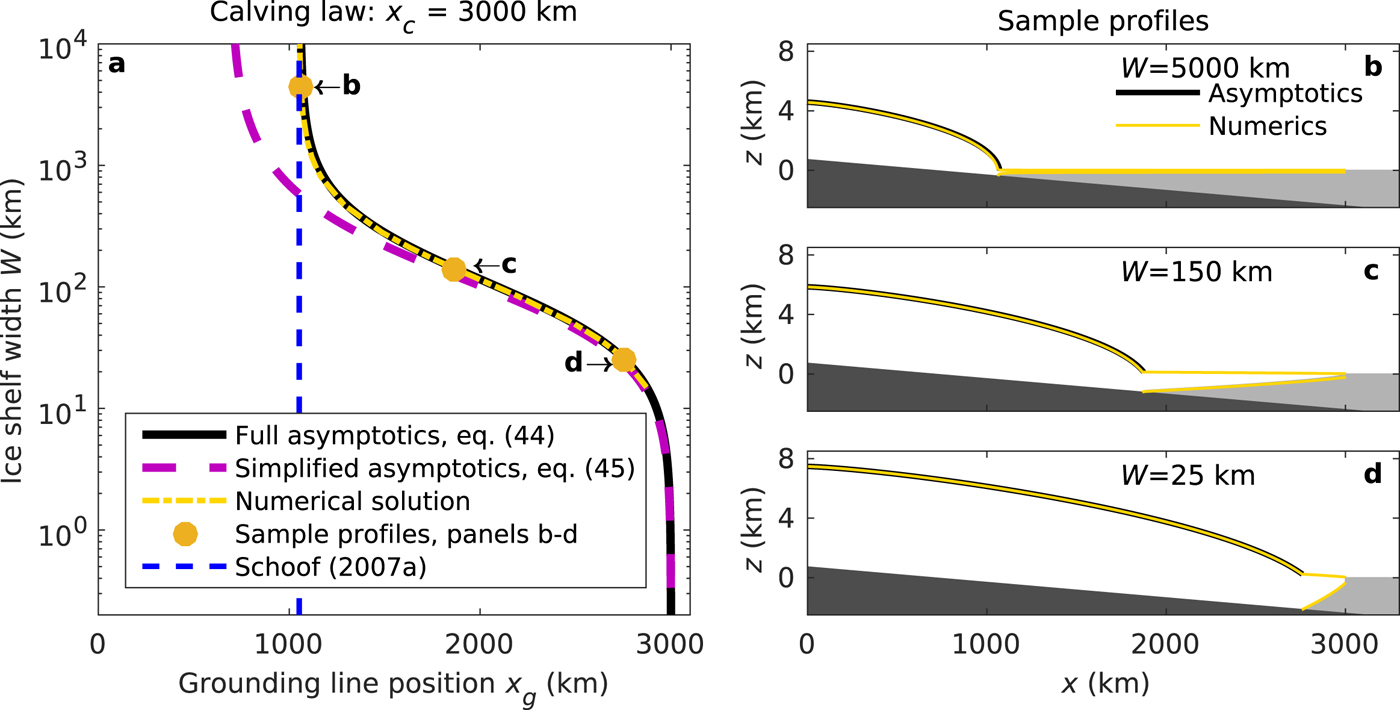
Fig. 6. Same as Fig. 5 but for a fixed calving front position at x c = 3000 km: panel a shows ice-shelf width W vs grounding line position x g, and panels (b) and (d) show corresponding ice-sheet profiles. Numerical results are obtained by solving the unsimplified model (1)–(4c) numerically with Comsol. The asymptotic grounding line positions are obtained by solving ![]() $\dot ax_g = q_g$ (47) with q g given by (44) and (45), respectively. The asymptotic profiles are calculated by additionally integrating (43a)–(43c). Note that the ice shelf is only plotted for the numerical solutions, as it can be excluded from the asymptotics.
$\dot ax_g = q_g$ (47) with q g given by (44) and (45), respectively. The asymptotic profiles are calculated by additionally integrating (43a)–(43c). Note that the ice shelf is only plotted for the numerical solutions, as it can be excluded from the asymptotics.
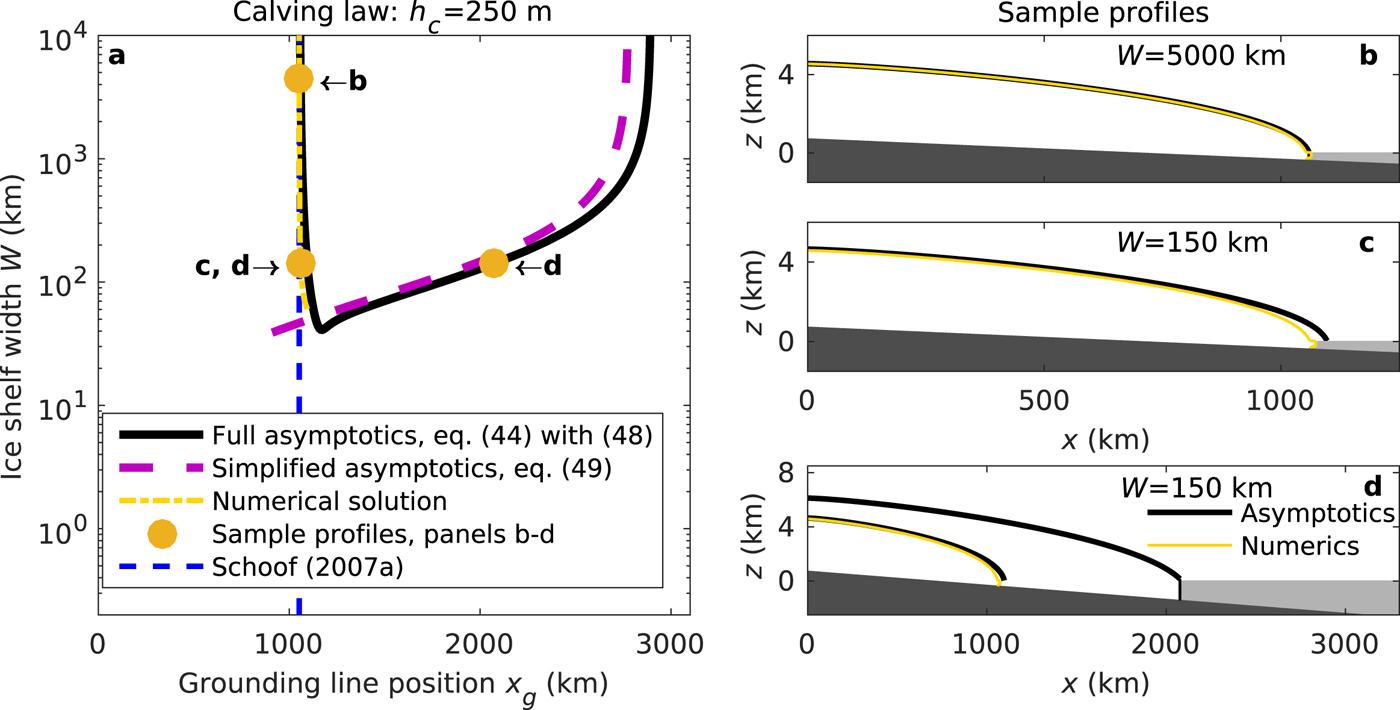
Fig. 7. Same as Fig. 5 but with calving if ice thickness at the calving front h c is below 250 m. Panel a shows ice-shelf width W vs grounding line position x g, and panels (b)–(d) show corresponding ice-sheet profiles. Numerical results are obtained by solving the unsimplified model (1)–(4c) numerically with Comsol. The asymptotic grounding line positions are obtained by solving ![]() $\dot ax_{\rm g} = q_{\rm g}$ (47) with q g given by (44) and (49), respectively. The asymptotic profiles are calculated by additionally integrating (43a)–(43c). Note that the ice shelf is only plotted for the numerical solutions, as it can be excluded from the asymptotics, and that no numerical solution exists for the profile with a grounding line at x g ≈ 2100 km, as this solution is unstable (see Fig. 8).
$\dot ax_{\rm g} = q_{\rm g}$ (47) with q g given by (44) and (49), respectively. The asymptotic profiles are calculated by additionally integrating (43a)–(43c). Note that the ice shelf is only plotted for the numerical solutions, as it can be excluded from the asymptotics, and that no numerical solution exists for the profile with a grounding line at x g ≈ 2100 km, as this solution is unstable (see Fig. 8).
For an infinitely wide marine ice sheet (W → ∞) the solutions of the asymptotic model (44) with a fixed ice-shelf length (Fig. 5a) and with a fixed calving front position (Fig. 6a) converge to the solution for unbuttressed marine ice sheets by Schoof (Reference Schoof2007a). Decreasing the width leads to grounding line advance, which continues indefinitely for the case of a fixed ice-shelf length. Conversely, the fixed calving front position leads to the grounding line asymptotically approaching the calving front position as the ice-shelf width decreases. Comparison of the full asymptotic solutions (44) with numerical solutions of the unsimplified model (1a)–(4c) obtained with the finite-element solver Comsol shows < 2% difference of grounding line positions at any computed point (yellow dashed lines in Figs 5a, 6a, respectively).
For these two cases (x c = const. and L s = const., Figs 5, 6, respectively), the grounding line positions predicted by the simplified asymptotic model (45) qualitatively follow the results of the full asymptotic model, but deviate significantly towards the unbuttressed limit (for W → ∞). Results with the simplified flux converge to the full asymptotic solution and the numerical solution for ![]() $W\mathop \lt \limits_ \approx 50$, which is consistent with the limit of strong buttressing, the limit for which we derived the simplified flux expression. As (45) only depends on ice-shelf properties, these results confirm that in the limit of strong buttressing, the position of the grounding line is determined by the ice-shelf dynamics only.
$W\mathop \lt \limits_ \approx 50$, which is consistent with the limit of strong buttressing, the limit for which we derived the simplified flux expression. As (45) only depends on ice-shelf properties, these results confirm that in the limit of strong buttressing, the position of the grounding line is determined by the ice-shelf dynamics only.
Use of a calving model that prescribes calving when the ice thickness at the calving front is below a certain threshold requires us to solve (47) with (44) and (36), as we apply the boundary condition by prescribing h c. With (2)1, (36) can be written as
 $$\eqalign{h_{\rm c} = & \left[ {h_{{\rm c},{\rm unbutt}}^{2 + n + p} {\rm erfc}\left( {{(n + 1)}^{1/n}L_{\rm s}^{1 + 1/n} /W^{1 + 1/n}} \right)} \right. \cr & + \left. {h_{{\rm c},{\rm butt}}^{2 + n + p} {\rm erf}\left( {{(n + 1)}^{1/n}L_{\rm s}^{1 + 1/n} /W^{1 + 1/n}} \right)} \right]^{1/(2 + n + p)},} $$
$$\eqalign{h_{\rm c} = & \left[ {h_{{\rm c},{\rm unbutt}}^{2 + n + p} {\rm erfc}\left( {{(n + 1)}^{1/n}L_{\rm s}^{1 + 1/n} /W^{1 + 1/n}} \right)} \right. \cr & + \left. {h_{{\rm c},{\rm butt}}^{2 + n + p} {\rm erf}\left( {{(n + 1)}^{1/n}L_{\rm s}^{1 + 1/n} /W^{1 + 1/n}} \right)} \right]^{1/(2 + n + p)},} $$which converges to h c,unbutt (37) for W → ∞ and to h c,butt (35) for W ≪ L s.
Equation (44) with (47) and (48) implicitly provides the ice flux at the grounding line. In the limit of strong buttressing, we can again obtain an explicit equation for the grounding line flux by combining (45) with (35):
 $$\eqalign{q_{\rm g} = & \left( {\displaystyle{{\rho g(1 - \rho /\rho _{\rm w})} \over \Lambda}} \right)^{1/(p + 1)} \cr & \times \left[ {{\left( {\displaystyle{{\rho g} \over 4}\left( {1 - \displaystyle{\rho \over {\rho _{\rm w}}}} \right)} \right)}^nAh_{{\rm c},{\rm butt}}^{2 + n + p} - \dot mh_{\rm g}^{\,p + 1}} \right]^{1/(p + 1)}} $$
$$\eqalign{q_{\rm g} = & \left( {\displaystyle{{\rho g(1 - \rho /\rho _{\rm w})} \over \Lambda}} \right)^{1/(p + 1)} \cr & \times \left[ {{\left( {\displaystyle{{\rho g} \over 4}\left( {1 - \displaystyle{\rho \over {\rho _{\rm w}}}} \right)} \right)}^nAh_{{\rm c},{\rm butt}}^{2 + n + p} - \dot mh_{\rm g}^{\,p + 1}} \right]^{1/(p + 1)}} $$and applying the boundary condition directly to h c,butt, i.e. h c,butt = 250 m. As we discuss in Section 3.4, h c,butt (35) is the ice thickness at the calving front of strongly buttressed ice shelves. To obtain physically plausible solutions from (49), we also require that the ice thickness at the grounding line is greater or equal to the ice thickness at the calving front (h g ≥ h c) and that the ice-shelf length remains non-negative (L s ≥ 0). In writing (49), we have eliminated the ice-shelf length, but it can be calculated from (45).
Note that (49) predicts that the ice flux at the grounding line decreases with increasing ice thickness at the grounding line if there is net accumulation on the ice shelf ![]() $(\dot m \gt 0)$, the case we consider here, and we discuss the implications of this for the stability of grounding line positions below. Conversely, for net melting on the ice shelf
$(\dot m \gt 0)$, the case we consider here, and we discuss the implications of this for the stability of grounding line positions below. Conversely, for net melting on the ice shelf ![]() $(\dot m \lt 0)$, (49) predicts that the ice flux at the grounding line increases with increasing ice thickness. This suggests that melting can directly alter the stability of grounding lines, at least when a thickness-based calving law is used. We will explore these dynamics in future publications.
$(\dot m \lt 0)$, (49) predicts that the ice flux at the grounding line increases with increasing ice thickness. This suggests that melting can directly alter the stability of grounding lines, at least when a thickness-based calving law is used. We will explore these dynamics in future publications.
In the case of a prescribed ice thickness at the calving front (h c = 250 m), the grounding line positions predicted by the asymptotic solutions (44) and (48) are qualitatively different from the two examples discussed above. We now find two branches, which connect at a minimum width W min below which no steady-state positions are possible. On one of these branches, grounding line positions converge to the position of an unbuttressed marine ice sheet by Schoof (Reference Schoof2007a) for W → ∞, and grounding line positions slightly advance downstream for decreasing ice-shelf widths. On the second branch, grounding line positions retreat for decreasing ice-shelf widths. The simplified asymptotic model (49) only reproduces the behaviour of the second branch. Conversely, numerically we only find steady-state positions along the first branch on which grounding lines advance for decreasing ice-shelf widths. If we decrease W beyond W min in the numerical model, the grounding line advances to the end of the computational domain, which confirms that no solutions exist for W < W min.
To capture both branches in Fig. 7a, we have to rely on the ice thickness approximation (48), which we have given in an ad hoc manner in Section 3.4. In the Supplementary material (Section S2), we therefore consider the special case of ![]() $m = n = p = 1,\dot m = 0$. In this limit, an exact solution for the ice thickness at the calving front exists (Pegler, Reference Pegler2016), and we can use this exact expression for h c to confirm the robustness of the results observed here. Note that we were able to capture the dynamics of the other two calving laws considered above with our derived expression for the ice flux alone even in the limit of W → ∞. These two cases converge to the unbuttressed limit by Schoof (Reference Schoof2007a) because Λ ∝ W −(1+1/n) appears in both terms that reduce the unbuttressed flux through the grounding line in (44) (h c,butt ∝ Λ, see (35)). Consequently, these terms vanish for W → ∞. However, if we directly set the calving front ice thickness through h c,butt, then we retain a non-zero flux reduction at the grounding line, which prevents us from reproducing the unbuttressed limit. This is also the reason why the simplified flux expression (49) only predicts grounding line positions along one of the branches in Fig. 7.
$m = n = p = 1,\dot m = 0$. In this limit, an exact solution for the ice thickness at the calving front exists (Pegler, Reference Pegler2016), and we can use this exact expression for h c to confirm the robustness of the results observed here. Note that we were able to capture the dynamics of the other two calving laws considered above with our derived expression for the ice flux alone even in the limit of W → ∞. These two cases converge to the unbuttressed limit by Schoof (Reference Schoof2007a) because Λ ∝ W −(1+1/n) appears in both terms that reduce the unbuttressed flux through the grounding line in (44) (h c,butt ∝ Λ, see (35)). Consequently, these terms vanish for W → ∞. However, if we directly set the calving front ice thickness through h c,butt, then we retain a non-zero flux reduction at the grounding line, which prevents us from reproducing the unbuttressed limit. This is also the reason why the simplified flux expression (49) only predicts grounding line positions along one of the branches in Fig. 7.
The fact that the numerical model only confirms the existence of grounding line positions on one of the branches in Fig. 7 motivates us to consider the stability of the solutions in Fig. 7 next. Steady states are possible where the ice flux q g matches the integrated accumulation ![]() $\dot ax$ (47) and this condition is satisfied by all solutions plotted in Figs 5–7. If we do not impose this condition, then we can plot the grounding line flux q g for all potential steady-state positions x g. The stability of a steady state can then be inferred from comparison of the flux gradient with the accumulation rate (Schoof, Reference Schoof2012):
$\dot ax$ (47) and this condition is satisfied by all solutions plotted in Figs 5–7. If we do not impose this condition, then we can plot the grounding line flux q g for all potential steady-state positions x g. The stability of a steady state can then be inferred from comparison of the flux gradient with the accumulation rate (Schoof, Reference Schoof2012):
 $$\eqalign{& {\rm if}\displaystyle{{\partial q_{\rm g}} \over {\partial x}}\; \gt \dot a:\;\hbox{stable steady state} \cr & {\rm if}\displaystyle{{\partial q_{\rm g}} \over {\partial x}}\; \lt \dot a:\;\hbox{unstable steady state}.} $$
$$\eqalign{& {\rm if}\displaystyle{{\partial q_{\rm g}} \over {\partial x}}\; \gt \dot a:\;\hbox{stable steady state} \cr & {\rm if}\displaystyle{{\partial q_{\rm g}} \over {\partial x}}\; \lt \dot a:\;\hbox{unstable steady state}.} $$At a stable steady state, the flux increases more than the net accumulation in the downstream direction. Therefore a downstream perturbation of the grounding line position leads to a net mass deficit. This causes the ice sheet to thin and the grounding line to retreat back to its original position. Conversely, at an unstable steady state, the net accumulation increases in a downstream direction while the flux decreases so that a downstream perturbation from this steady state leads to a mass surplus and a runaway advance.
For W = 150 km (the width of the steady states marked with (c) and (d) in Fig. 7a), two intersections of the integrated flux (yellow dashed line in Fig. 8) with the boundary layer solution (black line) exist; these are marked with yellow circles. According to (50), the state at x g ≈ 1100 km is stable, while the state at x g ≈ 2100 km is unstable. This is confirmed by our numerical results, which only find the stable steady state. If we initialise time-dependent calculations from the unstable branch, grounding lines either advance to the end of the computational domain or retreat to the stable branch. The existence of two branches in Fig. 7a, one stable and one unstable, is typical for a saddle-node bifurcation (Strogatz, Reference Strogatz2014).
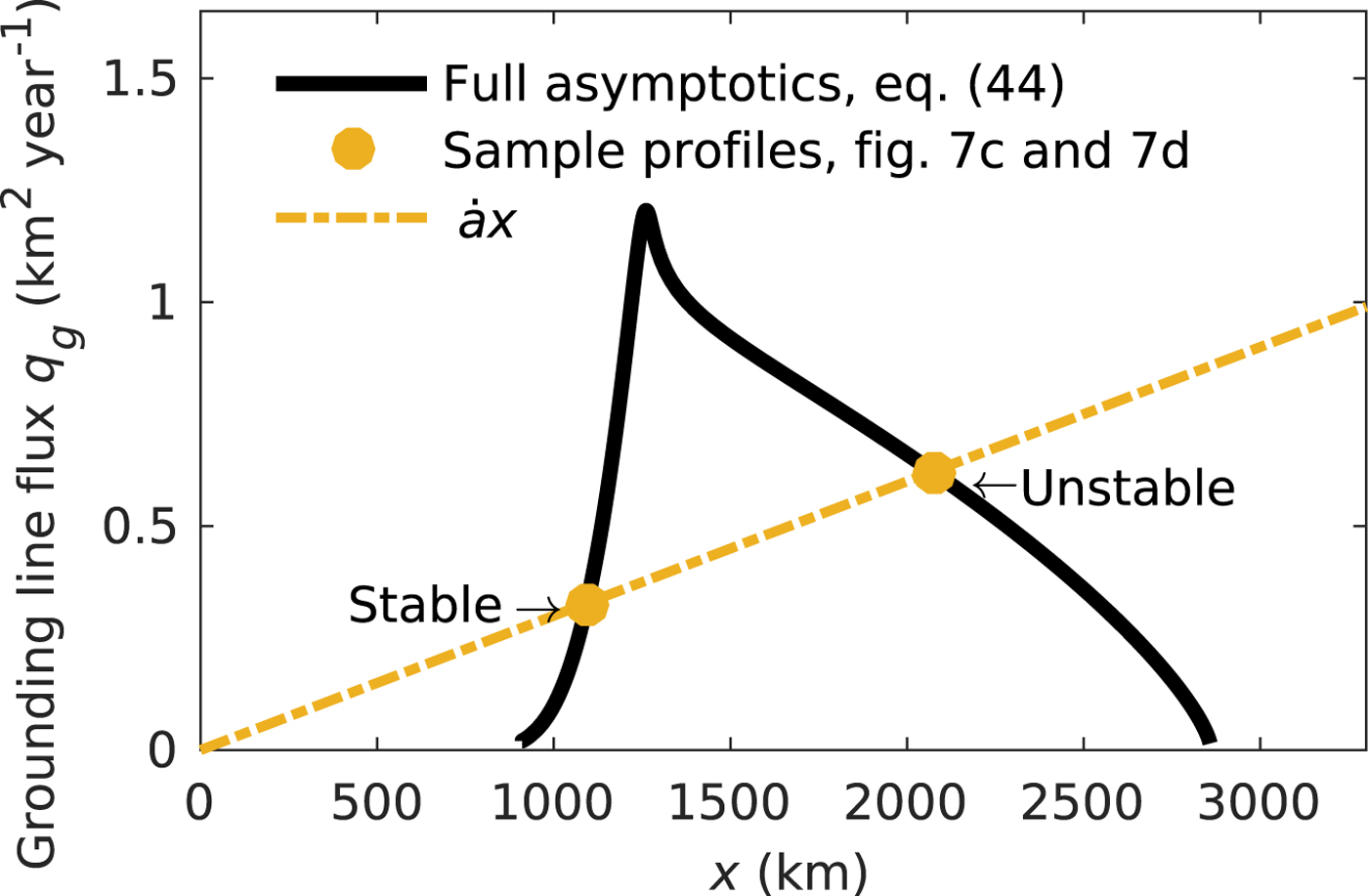
Fig. 8. Ice flux at the grounding line flux q g vs downstream position x for W = 150 km and a fixed calving front thickness of h c = 250 m. Plotted are the ice flux predicted by the full flux expression (45) (black line) and the integrated accumulation ![]() $\dot ax_{\rm g}$ (dash-dotted yellow line). Possible steady states are at the intersection of the integrated accumulation
$\dot ax_{\rm g}$ (dash-dotted yellow line). Possible steady states are at the intersection of the integrated accumulation ![]() $\dot ax$ and the grounding line flux (yellow dots). The steady state at x ≈ 1100 km is stable, the steady state at x ≈ 2100 km is unstable (compare Eqn (50)).
$\dot ax$ and the grounding line flux (yellow dots). The steady state at x ≈ 1100 km is stable, the steady state at x ≈ 2100 km is unstable (compare Eqn (50)).
Comparison of Fig. 7d with Figs 5c, 6c illustrates that in the presence of buttressing, different calving laws lead to very different grounding line dynamics. Each of these panels shows ice-sheet profiles at an ice-shelf width of W = 150 km, with stable grounding line positions located at x g ≈ 1000, x g ≈ 2000, and x g ≈ 2800 km, and an unstable grounding line position located at x g ≈ 2100 km.
6. DISCUSSION AND CONCLUSIONS
The objective of this study is to derive an expression for the ice flux at the grounding line of buttressed marine ice sheets. To this end, we derive an asymptotic solution for the extensional stress at the grounding line (34) of buttressed marine ice shelves in Section 3. This allows us to determine the implicit expression (44) for the ice flux at the grounding line by combining previous results obtained by Schoof (Reference Schoof2007a) with ice-shelf solutions from Hindmarsh (Reference Hindmarsh2012) and Pegler (Reference Pegler2016) via a boundary layer treatment. The implicit ice-flux expression (44) can be simplified to the explicit formulae (46a), (46b) and (49) for strongly buttressed ice shelves.
One of the advantages of the ice-flux solutions derived here is that they allow us to determine the position and stability of grounding lines from a system of algebraic equations. The model thereby provides an efficient tool to investigate the effects of buttressing, calving laws and changes in external (e.g. atmospheric and oceanic) forcings on grounding line stability. Comparison of the grounding line positions predicted by the flux expression (44) with numerically calculated grounding line positions shows a close agreement between the two approaches (Section 5). The results for different calving laws suggest that steady-state configurations of laterally confined marine ice-stream/ice-shelf systems are markedly different from those of unconfined marine ice sheets (e.g. Schoof, Reference Schoof2007a).
Buttressing reduces the ice flux through the grounding line, leading to steady-state grounding line positions downstream of the unbuttressed case. We find that the calving front boundary condition (the calving law) strongly controls the location and stability of the grounding line. In the MISMIP 1a test case, a configuration with a fixed ice-shelf length leads to an advance of the grounding line as the width of the ice-stream/ice-shelf system is reduced. For a configuration with a fixed calving front position, the grounding line asymptotically approaches the calving front position as the width of the ice-stream/ice-shelf is reduced. Alternatively, for a MISMIP 1a configuration with the fixed ice thickness at the calving front, we find a saddle-node bifurcation in the grounding line position as a function of the ice stream width. In this case, if the width of the marine ice sheet is larger than a critical width W min, both stable and unstable grounding line positions exist. For this calving law, steady-state grounding line positions obtained with time-dependent numerical models will therefore depend on the assumed initial conditions: either the grounding line achieves a stable steady-state position, or it advances indefinitely. However, if the width of the marine ice sheet is less than the critical width W min, no steady-state grounding line position exists.
These results illustrate that buttressing forges a link between calving front dynamics and grounding line dynamics. In contrast to the ice flux at the grounding line of unconfined marine ice sheets, which is a purely local function of the bed elevation at the grounding line (Schoof, Reference Schoof2007a), the ice flux at the grounding line of confined marine ice sheets is also a function of non-local ice-shelf properties. Consequently, knowledge of the bed slope alone is not sufficient to predict the stability of grounding lines of confined marine ice sheets. The example of a fixed ice thickness at the calving front illustrates that confined marine ice sheets are not necessarily unconditionally stable on downwards sloping beds. Conversely, confined marine ice sheets are not necessarily unstable on upward sloping beds. This has also been found by numerical studies (Gudmundsson, Reference Gudmundsson2013), and suggests that the concept of marine ice-sheet instability may not be applicable to confined marine ice sheets. We will investigate this further in a separate study.
Given the strong influence the calving law exerts on grounding line dynamics, it is possible that the results of past numerical studies of marine ice-sheet dynamics have depended on the assumed calving law used in these studies, and future studies should investigate this sensitivity. In the absence of a unifying calving law, choosing realistic calving-front boundary conditions is challenging, and many different formulations have been suggested in the literature. We have considered conditions that are determined by geometric parameters – a prescribed calving front position, a prescribed ice-shelf length, and a prescribed ice thickness at the calving front. These boundary conditions are widely used in numerical studies. For example, Dupont and Alley (Reference Dupont and Alley2005) and Gudmundsson and others (Reference Gudmundsson, Krug, Durand, Favier and Gagliardini2012) use a prescribed calving front position, Gagliardini and others (Reference Gagliardini, Durand, Zwinger, Hindmarsh and Le Meur:2010) use a constant ice-shelf length, and Van der Veen (Reference Van der Veen1996) and Vieli and others (Reference Vieli, Funk and Blatter2001) use a prescribed ice thickness at the calving front. The latter condition is also used in studies relying on a crevasse-depth condition and in calving laws based on extensional stresses at the calving front (Benn and others, Reference Benn, Warren and Mottram2007; Alley and others, Reference Alley2008; Nick and others, Reference Nick, Van der Veen, Vieli and Benn2010), albeit indirectly through the stress balance condition at the calving front (4c).
In the process of deriving (44) and (45), we have made several simplifying assumptions: we use a width- and depth-integrated model which parameterises some stress components in the momentum-balance equation and neglects others altogether (Morland, Reference Morland, Van der Veen and Oerlemans1987; MacAyeal, Reference MacAyeal1989; Hindmarsh, Reference Hindmarsh2012; Pegler, Reference Pegler2016). While analytical and numerical studies show that taking higher-order stresses into account does not qualitatively alter the behaviour of unconfined marine ice sheets (Nowicki and Wingham, Reference Nowicki and Wingham2008; Durand and others, Reference Durand, Gagliardini, de Fleurian, Zwinger and Le Meur2009a; Schoof, Reference Schoof2011), it is not clear whether the same conclusions can be extended to buttressed marine ice sheets. In particular, numerical studies suggest that across-flow variations of topography cannot be resolved in sufficient detail by flow-band models (Sergienko, Reference Sergienko2012). Moreover, ice rises are known to stabilise the flow of grounded ice (Goldberg and others, Reference Goldberg, Holland and Schoof2009; Favier and others, Reference Favier, Gagliardini, Durand and Zwinger2012), but it is unclear whether their effects can be included in flow-line models. Hence, future studies should verify whether the conclusions drawn here for flow-line models with parameterised buttressing also hold in models that explicitly resolve the across-flow direction.
Our approximation of the ice thickness at the calving front (48) is based on an ad hoc superposition of the two asymptotic limits of strong buttressing and no buttressing. While this superposition allows us to understand numerical results obtained with the unsimplified underlying model and qualitatively matches those results, it must inevitably fail in the transition between the two asymptotic limits it connects. A better representation of h c which can be used instead of (48) is clearly desirable, and should be addressed in future work.
The strongest assumption that we have made is that the marine ice sheet is in a steady state. Neither present-day nor paleo ice sheets have ever achieved a steady state, and observations show that ice shelves and grounding lines evolve on a variety of timescales (e.g. Rignot and Jacobs, Reference Rignot and Jacobs2002; Jenkins and others, Reference Jenkins2010; Shepherd and others, Reference Shepherd2010; Paolo and others, Reference Paolo, Fricker and Padman2015). These dynamics, their timescales, and possible trajectories of ice-sheet evolution remain topics of future research.
SUPPLEMENTARY MATERIAL
The supplementary material for this article can be found at https://doi.org/10.1017/jog.2018.30
ACKNOWLEDGEMENTS
M.H. was funded by the Princeton AOS Postdoctoral and Visiting Scientist Program. O.S. is supported by NOAA NA13OAR4310097 and NSF-GEOP/ANT1246151 grants. We thank Duncan Wingham, the associate editor Ralf Greve and two anonymous reviewers for constructive comments that greatly improved the quality of this manuscript.













