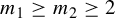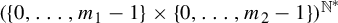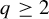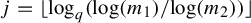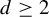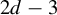1. Introduction
For the reader’s convenience we summarize a list of commonly used symbols in Appendix A. Let
$m_1 \geq m_2 \geq 2$
and
$q \geq 2$
be integers. Let
$\Omega $
be a closed subset of
$$ \begin{align*} \Sigma_{m_1,m_2} = (\mathcal{A}_1 \times \mathcal{A}_2)^{\mathbb{N}^*}, \end{align*} $$
where
$\mathcal {A}_1 = \{0,\ldots ,m_1-1\}$
and
$\mathcal {A}_2 = \{0,\ldots ,m_2-1\}$
. We can associate to
$\Omega $
a closed subset of the torus
$\mathbb {T}^2$
by considering
$\psi (\Omega )$
, where
$\psi $
is the coding map defined as
$$ \begin{align*} \psi : (x_k,y_k)_{k=1}^{\infty} \in \Sigma_{m_1,m_2} \longmapsto \bigg( \sum_{k=1}^{\infty} \frac{x_k}{m_1^k}, \sum_{k=1}^{\infty} \frac{y_k}{m_2^k} \bigg) \in \mathbb{T}^2. \end{align*} $$
Let
$\sigma $
be the standard shift map on
$\Sigma _{m_1,m_2}$
and
$\pi $
be the projection on the second coordinate. Closed subsets of
$\Sigma _{m_1,m_2}$
that are
$\sigma $
-invariant are sent through
$\psi $
to closed subsets of
$\mathbb {T}^2$
that are invariant under the diagonal endomorphism of
$\mathbb {T}^2$
;
$$ \begin{align*} (x,y) \in \mathbb{T}^2 \longmapsto (m_1 x, m_2 x). \end{align*} $$
Classical examples of such subsets are Sierpiński carpets. Given
$$ \begin{align*} \emptyset \neq A \subset \{0,\ldots,m_1-1\} \times \{0,\ldots,m_2-1\}, \end{align*} $$
consider
$$ \begin{align*} \Omega = \{(x,y) = (x_k,y_k)_{k=1}^{\infty} \in \Sigma_{m_1,m_2} : \text{for all } k \geq 1, \ (x_k,y_k) \in A\}. \end{align*} $$
Then
$\psi (\Omega )$
is a Sierpiński carpet. In this case,
$\psi (\Omega )$
is the attractor of the iterated function system made of the contractions
$f_{(i,j)} : (x,y) \in \mathbb {T}^2 \mapsto ( ({x+i})/{m_1}, ({y+j})/{m_2} )$
with
$(i,j) \in A$
. When
$m_1 = m_2 = m$
, we obtain a self-similar fractal and it is well-known that
$$ \begin{align*} \dim_{\mathrm{H}}(\psi(\Omega)) = \dim_{\mathrm{M}}(\psi(\Omega)) = \frac{\log(\# A)}{\log(m)}, \end{align*} $$
where
$\dim _{\mathrm {H}}$
and
$\dim _{\mathrm {M}}$
denote the Hausdorff and Minkowski (also called box-counting) dimensions, respectively. See, for example, [Reference Falconer3, Ch. 2]. More generally, as proved in [Reference Furstenberg7], if
$\Omega $
is a closed shift-invariant subset of
$\Sigma _{m,m}$
, then we have
$$ \begin{align*} \dim_{\mathrm{H}}(\psi(\Omega)) = \dim_{\mathrm{M}}(\psi(\Omega)) = \frac{h (\sigma|_{\Omega})}{\log(m)}, \end{align*} $$
where h stands for the topological entropy. McMullen [Reference McMullen10] and Bedford [Reference Bedford1] independently computed the Hausdorff and Minkowski dimensions of general Sierpiński carpets when
$m_1> m_2$
, which we assume from now on. Furthermore, the Hausdorff and Minkowski dimensions of Sierpiński sponges, defined as the generalization of Sierpiński carpets in all dimensions, were later computed in [Reference Kenyon and Peres8].
Let
$$ \begin{align*} \gamma = \frac{\log(m_2)}{\log(m_1)} \end{align*} $$
and
$$ \begin{align*} L: n \in \mathbb{N}^* \longmapsto \bigg\lceil \frac{n}{\gamma} \bigg\rceil. \end{align*} $$
We need the following metric on
$\Sigma _{m_1,m_2}$
: for
$(x,y)$
and
$(u,v)$
in
$\Sigma _{m_1,m_2}$
let
$$ \begin{align*} \begin{split} &d((x_k,y_k)_{k=1}^{\infty}, (u_k,v_k)_{k=1}^{\infty}) \\ &\quad= \max (m_1^{-\min \{k \geq 0: (x_{k+1},y_{k+1}) \neq (u_{k+1},v_{k+1})\}}, \ m_1^{-\gamma \min \{k \geq 0: y_{k+1} \neq v_{k+1} \}}). \end{split} \end{align*} $$
This metric allows us to consider ‘quasi-squares’ as defined by McMullen when computing the dimensions of Sierpiński carpets. It is easy to see that for
$(x,y) \in \Sigma _{m_1,m_2}$
the balls centered at
$(x,y)$
are
$$ \begin{align*} B_n(x,y) = B_{m_1^{-n}}(x,y)& = \{(u,v) \in \Sigma_{m_1,m_2}: u_k = x_k \text{ for all } 1 \leq k \leq n \\ &\quad \, \,\text{and} \ v_k = y_k \text{ for all } 1 \leq k \leq L(n)\}. \end{align*} $$
Using this metric on
$\Sigma _{m_1,m_2}$
the Hausdorff and Minkowski dimensions of
$\Omega $
are then equal to those of
$\psi (\Omega )$
. Thus, from now on we only work on the symbolic space. In this paper, our goal is to compute the Hausdorff and Minkowski dimensions of more general carpets that are not shift invariant. More precisely, given an arbitrary closed subset
$\Omega $
of
$\Sigma _{m_1,m_2}$
we consider
$$ \begin{align*} X_{\Omega} = \{ (x_k,y_k)_{k=1}^{\infty} \in \Sigma_{m_1,m_2}: (x_{i q^{\ell}},y_{i q^{\ell}})_{\ell=0}^{\infty} \in \Omega \ \text{for all} \ i, \ q \nmid i\}. \end{align*} $$
Such sets were studied in [Reference Kenyon, Peres and Solomyak9], where the authors restricted their work to the one-dimensional case: they computed the Hausdorff and Minkowski dimensions of sets defined by
$$ \begin{align*} \{ (x_k)_{k=1}^{\infty} \in \{0,\ldots,m-1\}^{\mathbb{N}^*}: (x_{i q^{\ell}})_{\ell=0}^{\infty} \in \Omega \ \text{for all} \ i, \ q \nmid i\}, \end{align*} $$
where
$\Omega $
is an arbitrary closed subset of
$\{0,\ldots ,m-1\}^{\mathbb {N}^*}$
. It is easily seen that this case covers the situation where
$m_1 = m_2$
in our setting. Their interest in these sets was prompted by the computation of the Minkowski dimension of the ‘multiplicative golden mean shift’
$$ \begin{align*} \bigg\{x = \sum_{k=1}^{\infty} \frac{x_k}{2^k}: x_k \in \{0,1\} \ \text{and} \ x_k x_{2k} = 0 \ \text{for all} \ k \geq 1\bigg\} \end{align*} $$
done in [Reference Fan, Liao and Ma4]. We aim to give formulas for
$\dim _{\mathrm {H}}(X_{\Omega })$
and
$\dim _{\mathrm {M}}(X_{\Omega })$
in the two-dimensional case, and then in all dimensions. Note that if
$\Omega $
is shift-invariant, then
$X_{\Omega }$
is invariant under the action of any integer
$r \in \mathbb {N}^*$
$$ \begin{align*} (x_k,y_k)_{k=1}^{\infty} \longmapsto (x_{rk},y_{rk})_{k=1}^{\infty}. \end{align*} $$
For example, as in the case of dimension one, we can consider subshifts of finite type on
$\Sigma _{m_1,m_2}$
. To do so, let
$D = \{(0,0),(0,1), \ldots ,(0,m_2-1),(1,0),(1,1),\ldots ,(1,m_2-1),\ldots ,(m_1-1,0),(m_1-1,1),\ldots ,(m_1-1,m_2-1)\}$
and let A be an
$m_1 m_2$
-sized square matrix indexed by
$D \times D$
with entries in
$\{0,1\}$
. Then we define
$$ \begin{align*} \Sigma_A = \{ (x_k,y_k)_{k=1}^{\infty} \in \Sigma_{m_1,m_2}: A((x_k,y_k),(x_{k+1},y_{k+1})) = 1, \ k \geq 1 \}, \end{align*} $$
and
$$ \begin{align*} X_A = X_{\Sigma_A} = \{ (x_k,y_k)_{k=1}^{\infty} \in \Sigma_{m_1,m_2}: A((x_k,y_k),(x_{qk},y_{qk})) = 1, \ k \geq 1 \}. \end{align*} $$
Figure 1 Approximation of order four of the set
$X_A$
for
$m_1 = 3$
,
$m_2 = 2$
,
$q=2$
, and A a circulant matrix whose first row is
$(1,0,0,1,0,0)$
.
Figure 2 Approximation of order six of the set
$X_A$
for
$m_1 = 3$
,
$m_2 = 2$
,
$q=2$
, and A a circulant matrix whose first row is
$(1,0,0,1,0,0)$
.
See Figures 1 and 2 for some illutration of an example of such sets. Note that further generalizations of the sets considered in [Reference Kenyon, Peres and Solomyak9] were studied in [Reference Peres, Schmeling, Seuret and Solomyak12], in the one-dimensional case as well.
This paper is organized as follows. In §2, we focus on the two-dimensional situation. We first introduce in §2.1 a particular class of measures on
$X_{\Omega }$
. We show that these measures are exact dimensional and we compute their Hausdorff dimensions. This class of measures is the same as that considered in [Reference Kenyon, Peres and Solomyak9], but in our case the parameter
$j = \lfloor \log _q ( {\log (m_1)}/{\log (m_2)} ) \rfloor $
comes into play when studying their local dimension. Indeed, this parameter plays a crucial role in the definition of generalized cylinders whose masses are used to study the mass of balls under the metric d. In §2.2, out of curiosity, we study under which condition the Ledrappier–Young formula (where the entropies of invariant measures are replaced by their entropy dimensions) can hold for these measures, which are not shift-invariant in general.
In §§2.3–2.5, we compute the Hausdorff and Minkowski dimensions of
$X_{\Omega }$
, using a variational principle over the class of measures we studied earlier. We show that there exists a unique Borel probability measure which allows us to bound
$\dim _{\mathrm {H}}(X_{\Omega })$
both from below and from above.
Then, in §3, we extend our results to the general multidimensional case. The combinatorics involved there become significantly more complex, as the study of the local dimension of the measures of interest invokes some generalized cylinders which depend in a subtle way on a collection of
$2d-3$
parameters.
Finally, Appendix B introduces several lemmas used throughout our proofs.
2. The two-dimensional case
2.1. The measures
$\mathbb {P}_{\mu }$
and their dimensions
Throughout the paper we use the notation
if
$m \leq n$
are integers.
To compute
$\dim _{\mathrm {H}}(X_{\Omega })$
, we use the classical strategy of stating a variational principle over a certain class of Borel probability measures
$\mathbb {P}_{\mu }$
on
$X_{\Omega }$
defined below, that is, we show that
$$ \begin{align*} \dim_{\mathrm{H}}(X_{\Omega}) = \max_{\mathbb{P}_{\mu}} \dim_{\mathrm{H}}(\mathbb{P}_{\mu}). \end{align*} $$
To do so, we use the following classical facts (for a proof, see [Reference Falconer3, Proposition 2.3]).
Theorem 2.1. Let
$\mu $
be a finite Borel measure on
$\Sigma _{m_1,m_2}$
and let
$A \subset \Sigma _{m_1,m_2}$
such that
$\mu (A)> 0$
.
-
• If
$\liminf _{n \rightarrow \infty } -({\log _{m_1}(\mu (B_n(x)))}/{n}) \geq D$
for
$\mu $
-almost all x, then
$\dim _{\mathrm {H}}(\mu ) \geq D$
. -
• If
$\liminf _{n \rightarrow \infty } -({\log _{m_1}(\mu (B_n(x)))}/{n}) \leq D$
for
$\mu $
-almost all x, then
$\dim _{\mathrm {H}}(\mu ) \leq D$
. -
• If
$\liminf _{n \rightarrow \infty } -({\log _{m_1}(\mu (B_n(x)))}/{n}) \leq D$
for all
$x \in A$
, then
$\dim _{\mathrm {H}}(A) \leq D$
.
For
$p,\ell \in \mathbb {N}$
and
$u \in (\{0,\ldots ,m_1-1\} \times \{0,\ldots ,m_2-1\})^p \times \{0,\ldots ,m_2-1\}^{\ell }$
, define the generalized cylinder
$$ \begin{align*} [u] = \{(x,y) \in \Sigma_{m_1,m_2}: ((x,y)|_p, \pi(\sigma^p((x,y))|_{\ell})) = u\}, \end{align*} $$
where
$(x,y)|_p = (x_1,y_1) \cdots (x_p,y_p)$
and
$\pi ((x,y)|_p) = y|_p$
, and set
$$ \begin{align*} \mathrm{Pref}_{p,\ell}(\Omega) &= \{u \in (\{0,\ldots,m_1-1\}\\ &\quad\times \{0,\ldots,m_2-1\})^p \times \{0,\ldots,m_2-1\}^{\ell}: \Omega \cap [u] \neq \varnothing\}. \end{align*} $$
For
$(x,y) \in \Sigma _{m_1,m_2}$
,
$n \geq 1$
and i an integer such that
$q \nmid i$
, we define
$$ \begin{align*} (x,y)|_{J_i^n} = (x_i,y_i) (x_{qi},y_{qi}) \cdots (x_{q^r i},y_{q^r i}) \end{align*} $$
if
$q^r i \leq n < q^{r+1} i$
. Let
$\mu $
be a Borel probability measure on
$\Omega $
. Following [Reference Kenyon, Peres and Solomyak9] we define
$\mathbb {P}_{\mu }$
on the semi-algebra of cylinder sets of
$\Sigma _{m_1,m_2}$
by
$$ \begin{align*} \mathbb{P}_{\mu}([(x,y)|_n]) = \prod_{\substack{i \leq n \\ q \nmid i}} \mu ([(x,y)|_{J_i^n}] ). \end{align*} $$
This is a well-defined pre-measure. Indeed it is easy to see that
$\mathbb {P}_{\mu }([(k,l)]) = \mu ([(k,l)])$
for
$(k,l) \in \mathcal {A}_1 \times \mathcal {A}_2$
, and for
$n+1 = q^r i$
with
$q \nmid i$
,
$$ \begin{align*}\frac{\mathbb{P}_{\mu}( [(x_1,y_1) \cdots (x_n,y_n) (x_{n+1},y_{n+1}) ])}{\mathbb{P}_{\mu}( [(x_1,y_1) \cdots (x_n,y_n) ] )} = \frac{\mu([(x_i,y_1) (x_{qi},y_{qi}) \cdots (x_{q^r i},y_{q^r i}) ])}{\mu ([(x_i,y_1) (x_{qi},y_{qi}) \cdots (x_{q^{r-1} i},y_{q^{r-1} i}) ] )}, \end{align*} $$
whence
$$ \begin{align*} \mathbb{P}_{\mu}( [(x_1,y_1) \cdots (x_n,y_n) ]) = \sum_{(i,j) \in \mathcal{A}_1 \times \mathcal{A}_2} \mathbb{P}_{\mu}( [(x_1,y_1) \cdots (x_n,y_n) (i,j) ]). \end{align*} $$
Denote also by
$\mathbb {P}_{\mu }$
the extension of
$\mathbb {P}_{\mu }$
to a Borel probability measure on
$(\Sigma _{m_1,m_2},\mathcal {B} (\Sigma _{m_1,m_2} ) )$
. By construction,
$\mathbb {P}_{\mu }$
is supported on
$X_{\Omega }$
, since
$\Omega $
is a closed subset of
$\Sigma _{m_1,m_2}$
and, hence,
$$ \begin{align*} \Omega = \bigcap_{k=1}^{\infty} \bigcup_{u \in \mathrm{Pref}_{k,0}(\Omega)} [u]. \end{align*} $$
Let us now introduce some further notation. For all
$k \geq 1$
, we consider the finite partitions of
$\Omega $
defined by
$$ \begin{align*}\alpha^1_k = \{\Omega \cap [u]: u \in \mathrm{Pref}_{0,k}(\Omega)\} \end{align*} $$
and
$$ \begin{align*} \alpha^2_k = \{\Omega \cap [u]: u \in \mathrm{Pref}_{k,0}(\Omega)\}. \end{align*} $$
For a Borel probability measure
$\mu $
on
$\Omega $
and a finite measurable partition
$\mathcal {P}$
on
$\Omega $
, denote by
$H^{\mu }_{m_2}(\mathcal {P})$
the
$\mu $
-entropy of the partition, with the base-
$m_2$
logarithm:
$$ \begin{align*} H^{\mu}_{m_2}(\mathcal{P}) = - \sum_{C \in \mathcal{P}} \mu(C) \log_{m_2} \mu(C). \end{align*} $$
Let j be the unique non-negative integer such that
$$ \begin{align*} q^j \leq \frac{1}{\gamma} = \frac{\log(m_1)}{\log(m_2)} < q^{j+1}. \end{align*} $$
Note that for all
$n \geq 1$
large enough, we have
$$ \begin{align*} q^j n \leq L(n) < q^{j+1} n. \end{align*} $$
Theorem 2.2. Let
$\mu $
be a Borel probability measure on
$\Omega $
. Then
$\mathbb {P}_{\mu }$
is exact dimensional and we have
$$ \begin{align*} \dim_{\mathrm{H}}(\mathbb{P}_{\mu}) &= (q-1)^2 \sum_{p=1}^j \frac{H^{\mu}_{m_2}(\alpha^1_p)}{q^{p+1}} + (q-1)(q^{j+1} \gamma - 1) \sum_{p=j+1}^{\infty} \frac{H^{\mu}_{m_2}(\alpha^2_{p-j} \lor \alpha^1_p)}{q^{p+1}} \\ &\quad+ (q-1)(1-q^j \gamma) \sum_{p=j+1}^{\infty} \frac{H^{\mu}_{m_2}(\alpha^2_{p-j-1} \lor \alpha^1_p)}{q^p}. \end{align*} $$
Proof. Our method is inspired by the calculation of
$\dim _{\mathrm {H}}(\mathbb {P}_{\mu })$
in [Reference Kenyon, Peres and Solomyak9]. The strategy of the proof is the same, nevertheless the computations will be more involved, owing to the fact that the
$\mathbb {P}_{\mu }$
-mass of a ball for the metric d is a product of
$\mu $
-masses of generalized cylinders rather than standard ones as in [Reference Kenyon, Peres and Solomyak9].
Let
$\ell \geq j+1$
. We first show that for
$\mathbb {P}_{\mu }$
-almost all
$(x,y) \in X_{\Omega }$
we have
$$ \begin{align*} \liminf_{n \rightarrow \infty} \frac{-\log_{m_1}(\mathbb{P}_{\mu}(B_{n}(x,y)))}{n} &\geq (q-1)^2 \sum_{p=1}^j \frac{H^{\mu}_{m_2}(\alpha^1_p)}{q^{p+1}} \\ &\quad+ (q-1)(q^{j+1} \gamma - 1) \sum_{p=j+1}^{\ell} \frac{H^{\mu}_{m_2}(\alpha^2_{p-j} \lor \alpha^1_p)}{q^{p+1}} \\ &\quad+ (q-1)(1-q^j \gamma) \sum_{p=j+1}^{\ell} \frac{H^{\mu}_{m_2}(\alpha^2_{p-j-1} \lor \alpha^1_p)}{q^p}, \end{align*} $$
and
$$ \begin{align*} \limsup_{n \rightarrow \infty} \frac{-\log_{m_1}(\mathbb{P}_{\mu}(B_{n}(x,y)))}{n} &\leq (q-1)^2 \sum_{p=1}^j \frac{H^{\mu}_{m_2}(\alpha^1_p)}{q^{p+1}} \\ &\quad+ (q-1)(q^{j+1} \gamma - 1) \sum_{p=j+1}^{\ell} \frac{H^{\mu}_{m_2}(\alpha^2_{p-j} \lor \alpha^1_p)}{q^{p+1}} \\ &\quad+ (q-1)(1-q^j \gamma) \sum_{p=j+1}^{\ell} \frac{H^{\mu}_{m_2}(\alpha^2_{p-j-1} \lor \alpha^1_p)}{q^k} \\ &\quad+ \frac{(\ell+1) \log_{m_2}(m_1 m_2)}{q^{\ell}}. \end{align*} $$
Letting
$\ell \rightarrow \infty $
will yield the desired equality (cf. Theorem 2.1). To check these, we can restrict ourselves to
$n = q^{\ell } r$
,
$r \in \mathbb {N}$
. Indeed, if
$q^{\ell } r \leq n < q^{\ell } (r+1)$
, then
$$ \begin{align*} \frac{-\log_{m_1}(\mathbb{P}_{\mu}(B_n(x,y)))}{n} \geq \frac{-\log_{m_1}(\mathbb{P}_{\mu}(B_{q^{\ell} r}(x,y)))}{q^{\ell} (r+1)} \geq \frac{r}{r+1} \frac{-\log_{m_1}(\mathbb{P}_{\mu}(B_{q^{\ell} r}(x,y)))}{q^{\ell} r}, \end{align*} $$
which gives
$$ \begin{align*} \liminf_{n \rightarrow \infty} \frac{-\log_{m_1}(\mathbb{P}_{\mu}(B_{n}(x,y)))}{n} = \liminf_{r \rightarrow \infty} \frac{-\log_{m_1}(\mathbb{P}_{\mu}(B_{q^{\ell} r}(x,y)))}{q^{\ell} r}. \end{align*} $$
The
$\limsup $
is dealt with similarly.
As proved in [Reference Kenyon, Peres and Solomyak9] we have
$$ \begin{align*} &\lim_{n\rightarrow \infty} \frac{-\log_{m_1} (\mathbb{P}_{\mu} ([(x,y)|_n]))}{n} \\ &\quad = (q-1)^2 \sum_{p=1}^{\infty} \frac{H^{\mu}_{m_1}(\alpha^2_p)}{q^{p+1}} \ \text{for} \ \mathbb{P}_{\mu}-\text{almost all} \ (x,y) \in X_{\Omega}. \end{align*} $$
Note that
$$ \begin{align*} \mathbb{P}_{\mu}(B_n(x,y)) = \sum_{x^{\prime}_{n+1},\ldots,x^{\prime}_{L(n)}} \mathbb{P}_{\mu} ( [(x_1,y_1)\cdots(x_n,y_n) (x^{\prime}_{n+1},y_{n+1})\cdots (x^{\prime}_{L(n)},y_{L(n)})] ), \end{align*} $$
the sum being taken over all
$x^{\prime }_{n+1},\ldots ,x^{\prime }_{L(n)}$
such that
$$ \begin{align*} [(x_1,y_1)\cdots(x_n,y_n)(x^{\prime}_{n+1},y_{n+1})\cdots (x^{\prime}_{L(n)},y_{L(n)})] \cap X_{\Omega} \neq \emptyset. \end{align*} $$
Let
$$ \begin{align*} i \in{\kern2pt}\bigg]\frac{L(n)}{q^{\ell}},L(n)\bigg] = \bigsqcup_{p=1}^{\ell} \bigg]\frac{L(n)}{q^{p}},\frac{L(n)}{q^{p-1}}\bigg] \end{align*} $$
such that
$q \nmid i$
. Note that if
$i \in \, ]{L(n)}/{q^{p}},{L(n)}/{q^{p-1}}]$
then the word
$(x,y)|_{J_i^{L(n)}}$
is of length p. Recall that j is defined by
$q^j \leq {1}/{\gamma } < q^{j+1}$
. Suppose
$j \geq 1$
. If
$1 \leq p \leq j$
, then
${L(n)}/{q^p} \geq n$
, so
$$ \begin{align*} \bigg]\frac{L(n)}{q^p},\frac{L(n)}{q^{p-1}} \bigg] \subset \ ]n,L(n)]. \end{align*} $$
If
$j+1 \leq p \leq \ell $
and
$\ell $
is large enough, then
${n}/{q^{p-j-1}} \in \, ]{L(n)}/{q^p},{L(n)}/{q^{p-1}}]$
, thus we can partition
$$ \begin{align*} \bigg]\frac{L(n)}{q^p},\frac{L(n)}{q^{p-1}}\bigg] = \bigg]\frac{L(n)}{q^p},\frac{n}{q^{p-j-1}}\bigg] \bigsqcup \bigg]\frac{n}{q^{p-j-1}}, \frac{L(n)}{q^{p-1}}\bigg]. \end{align*} $$
In the case where
$i \in \, ]{n}/{q^{p-j-1}}, {L(n)}/{q^{p-1}}]$
we have
$$ \begin{align*} q^{p-j-2} i \leq n < q^{p-j-1} i \leq q^{p-1} i \leq L(n) < q^p i, \end{align*} $$
and if
$i \in \, ]{L(n)}/{q^p},{n}/{q^{p-j-1}}]$
, then
$$ \begin{align*} q^{p-j-1} i \leq n < q^{p-j} i \leq q^{p-1} i \leq L(n) < q^p i. \end{align*} $$
If
$j=0$
, then
$$ \begin{align*} i \in{\kern2pt}\bigg]\frac{n}{q^{p-1}}, \frac{L(n)}{q^{p-1}}\bigg] \Longrightarrow q^{p-2} i \leq n < q^{p-1} i \leq L(n) < q^p i \end{align*} $$
$$ \begin{align*} i \in{\kern2pt}\bigg]\frac{L(n)}{q^p},\frac{n}{q^{p-1}}\bigg] \Longrightarrow q^{p-1} i \leq n \leq L(n) < q^p i. \end{align*} $$
Thus, for any j we have
$$ \begin{align*} &\mathbb{P}_{\mu}(B_n(x,y)) = \bigg[ \prod_{p=1}^j \prod_{\substack{i \in{\kern2pt}\big] \frac{L(n)}{q^p},\frac{L(n)}{q^{p-1}} \big] \\ q \nmid i}} \mu ( [y_i , \ldots, y_{q^{p-1} i} ] ) \bigg] \\ &\boldsymbol{\cdot} \bigg[ \prod_{p=j+1}^{\ell} \bigg( \prod_{\substack{i \in{\kern2pt}\big]\frac{n}{q^{p-j-1}},\frac{L(n)}{q^{p-1}} \big] \\ q \nmid i}} \mu ( [(x_i,y_i) \cdots (x_{q^{p-j-2} i}, y_{q^{p-j-2} i}) y_{q^{p-j-1} i} , \ldots, y_{q^{p-1} i} ] ) \bigg) \\ &\boldsymbol{\cdot} \bigg(\prod_{\substack{i \in{\kern2pt}\big]\frac{L(n)}{q^{p}},\frac{n}{q^{p-j-1}} \big] \\ q \nmid i}} \mu ( [(x_i,y_i) \cdots (x_{q^{p-j-1} i}, y_{q^{p-j-1} i}) y_{q^{p-j} i} , \ldots, y_{q^{p-1} i} ] ) \bigg) \bigg] \boldsymbol{\cdot} D_n(x,y), \end{align*} $$
with
$D_n(x,y)$
being the product of the remaining quotients (words beginning with
$(x_i,y_i)$
with
$i \leq {L(n)}/{q^{\ell }}$
). Here we used the notion of generalized cylinders we defined earlier:
$$ \begin{align*} &\mu ( [y_i , \ldots, y_{q^{p-1} i} ] ) = \sum_{x^{\prime}_i,\ldots,x^{\prime}_{q^{p-1} i}} \mu ( [(x^{\prime}_i,y_i) \cdots (x^{\prime}_{q^{p-1} i},y_{q^{p-1} i}) ] ),\\ &\mu ( [(x_i,y_i) \cdots (x_{q^{p-j-2} i}, y_{q^{p-j-2} i}) y_{q^{p-j-1} i} , \ldots, y_{q^{p-1} i} ] ) \\ &{={\kern-2pt}} \sum_{x^{\prime}_{q^{p{-}j{-}1} i},{\ldots},x^{\prime}_{q^{p{-}1} i}}{\kern-2pt}\mu ( [(x_i{\kern-1pt},{\kern-1.7pt}y_i){\cdots}(x_{q^{p{-}j{-}2} i}{\kern-1pt},{\kern-1.7pt}y_{q^{p{-}j{-}2} i}) (x^{\prime}_{q^{p{-}j{-}1} i}{\kern-1pt},{\kern-1.7pt}y_{q^{p{-}j{-}1} i}){\cdots}(x^{\prime}_{q^{p{-}1} i}{\kern-1pt},{\kern-1.7pt}y_{q^{p{-}1} i}) ] ), \\ & \mu ( [(x_i,y_i) \cdots (x_{q^{p-j-1} i}, y_{q^{p-j-1} i}) y_{q^{p-j} i} , \ldots, y_{q^{p-1} i} ] ) \\ &{=} \sum_{x^{\prime}_{q^{p-j} i},\ldots,x^{\prime}_{q^{p-1} i}} \mu ( [(x_i,y_i) \cdots (x_{q^{p-j-1} i}, y_{q^{p-j-1} i}) (x^{\prime}_{q^{p-j} i}, y_{q^{p-j} i}) \cdots (x^{\prime}_{q^{p-1} i},y_{q^{p-1} i}) ] ), \end{align*} $$
the sums being taken over the cylinders that intersect
$\Omega $
. If
$(u_n),(v_n) \in (\mathbb {R}^*)^{\mathbb {N}^*}$
, we say that
$u_n \sim v_n$
if
$({u_n}/{v_n}) \rightarrow 1$
as
$n \rightarrow \infty $
. Here we have
$$ \begin{align*} \begin{aligned} \# \bigg\{i \in{\kern2pt}\bigg]\frac{L(n)}{q^{p}},\frac{L(n)}{q^{p-1}}\bigg] : q \nmid i \bigg\} & \sim \frac{(q-1)^2 n}{\gamma q^{p+1}}, \\ \# \bigg\{i \in{\kern2pt}\bigg]\frac{n}{q^{p-j-1}},\frac{L(n)}{q^{p-1}}\bigg] : q \nmid i \bigg\} & \sim \frac{n (q-1)(1-q^j \gamma)}{\gamma q^p}, \\ \# \bigg\{ i \in{\kern2pt}\bigg] \frac{L(n)}{q^p},\frac{n}{q^{p-j-1}} \bigg] : q \nmid i \bigg\} & \sim \frac{n (q-1) (q^{j+1} \gamma - 1)}{\gamma q^{p+1}}. \end{aligned} \end{align*} $$
Note that for
$i \kern-2pt\in \, ]{n}/{q^{p-j-1}},{L(n)}/{q^{p-1}} ]$
,
$q \nmid i$
the random variables
$$ \begin{align*} Y_{i,n,p} : (x,y) \in X_{\Omega} \longmapsto &- \log_{m_1} (\mu ( [(x_i,y_i) \cdots\\&\ (x_{q^{p-j-2} i}, y_{q^{p-j-2} i}) y_{q^{p-j-1} i} , \ldots, y_{q^{p-1} i} ] ) ) \end{align*} $$
are independent and identically distributed and uniformly bounded, with expectation being
$H^{\mu }_{m_1}(\alpha ^2_{p-j-1} \lor \alpha ^1_p)$
. Fixing
$j+1 \leq p \leq l$
and letting
$n = q^{\ell } r, r \rightarrow \infty $
, we can use Lemma B.2 to obtain that for
$\mathbb {P}_{\mu }$
-almost all
$(x,y) \in X_{\Omega }$
$$ \begin{align*} \frac{\gamma q^p}{n (q-1)(1-q^j \gamma)} \sum_{\substack{i \in{\kern2pt}\big]\frac{n}{q^{p-j-1}},\frac{L(n)}{q^{p-1}}\big] \\ q \nmid i}} Y_{i,n,p}(x,y) \underset{r \rightarrow \infty}{\longrightarrow} H^{\mu}_{m_1}(\alpha^2_{p-j-1} \lor \alpha^1_p). \end{align*} $$
Thus,
$$ \begin{align*} \begin{split} &\sum_{p=j+1}^ \ell\frac{(q-1)(1-q^j \gamma)}{\gamma q^p} \sum_{\substack{i \in{\kern2pt}\big]\frac{n}{q^{p-j-1}},\frac{L(n)}{q^{p-1}}\big ] \\ q \nmid i}} \frac{\gamma q^p Y_{i,n,p}(x,y)}{n (q-1)(1-q^j \gamma)} \\ & \quad \underset{r \rightarrow \infty}{\longrightarrow} (q-1)(1-q^j \gamma) \sum_{p=j+1}^{\ell} \frac{H^{\mu}_{m_2}(\alpha^2_{p-j-1} \lor \alpha^1_p)}{q^p}. \end{split} \end{align*} $$
Similarly, if we define
$$ \begin{align*} Z_{i,n,p} : (x,y) \longmapsto - \log_{m_1}(\mu ( [y_i , \ldots, y_{q^{p-1} i} ] ) ), \end{align*} $$
the expectation of which is
$H^{\mu }_{m_1}(\alpha ^1_p)$
, for
$\mathbb {P}_{\mu }$
-almost all
$(x,y) \in X_{\Omega }$
we have
$$ \begin{align*} \frac{\gamma q^{p+1}}{n (q-1)^2} \sum_{\substack{i \in{\kern2pt}\big] \frac{L(n)}{q^p},\frac{L(n)}{q^{p-1}}\big] \\ q \nmid i}} Z_{i,n,p}(x,y) \underset{r \rightarrow \infty}{\longrightarrow} H^{\mu}_{m_1}(\alpha^1_p), \end{align*} $$
hence,
$$ \begin{align*} \sum_{p=1}^j \frac{(q-1)^2}{\gamma q^{p+1}} \sum_{\substack{i \in{\kern2pt}\big] \frac{L(n)}{q^p},\frac{L(n)}{q^{p-1}} \big] \\ q \nmid i}} \frac{\gamma q^{p+1} Z_{i,n,p}(x,y)}{n (q-1)^2} \underset{r \rightarrow \infty}{\longrightarrow} (q-1)^2 \sum_{p=1}^j \frac{H^{\mu}_{m_2}(\alpha^1_p)}{q^{p+1}}. \end{align*} $$
The third term is treated in a similar manner. We have, thus, proved the first inequality. Now it remains to prove the second inequality using
$D_n(x,y)$
. It is easily seen that there exists
$C \geq 0$
such that for all
$b> a > 0$
$$ \begin{align*} \bigg|\# \{i \in \mathbb{N} \cap ]a,b] : q \nmid i\} - \frac{q-1}{q} (b-a) \bigg| \leq C. \end{align*} $$
Thus, the number of letters in
$\mathcal {A}_1 \times \mathcal {A}_2$
appearing in the words of the developed
$D_n(x,y)$
is
$$ \begin{align} d_n &:= L(n) - \sum_{p=1}^{\ell} \# \bigg\{i \in \mathbb{N} \cap \bigg]\frac{L(n)}{q^p},\frac{L(n)}{q^{p-1}}\bigg] : q \nmid i\bigg\} p \nonumber \\ &\leq L(n) - \sum_{p=1}^{\ell} \frac{(q-1)^2 L(n) p}{q^{p+1}} + \frac{\ell(\ell+1)}{2} C \nonumber \\ &= \frac{L(n)}{q^{\ell}} \bigg[(\ell+1)-\frac{\ell}{q} \bigg] + \frac{\ell(\ell+1)}{2} C \nonumber \\ &\leq \frac{(\ell+1) L(n)}{q^{\ell}} + \frac{\ell(\ell+1)}{2} C. \end{align} $$
On the other hand
$$ \begin{align*} d_n \geq L(n) - \sum_{p=1}^{\ell} \frac{(q-1)^2 L(n) p}{q^{p+1}} - \frac{\ell(\ell+1)}{2} C \geq r \bigg[(\ell+1)-\frac{\ell}{q} \bigg] - \frac{\ell(\ell+1)}{2} C, \end{align*} $$
so
$\sum _{r=1}^{\infty } 2^{-d_{q^{\ell } r}} < +\infty $
. Define
$$ \begin{align*} S_n = \{(x,y) \in X_{\Omega} : D_n(x,y) \leq (2 m_1 m_2)^{-d_n} \}. \end{align*} $$
Clearly
$\mathbb {P}_{\mu }(S_n) \leq 2^{-d_n}$
, so
$\mathbb {P}_{\mu } (\bigcap _{N \geq 1} \bigcup _{r=N}^{\infty } S_{q^{\ell } r} ) = 0$
, using Borel–Cantelli lemma. Hence, for
$\mathbb {P}_{\mu }$
-almost all
$(x,y) \in X_{\Omega }$
there exists
$N(x,y)$
such that
$(x,y) \notin S_n$
for all
$n=q^{\ell } r \geq N(x,y)$
. For such
$(x,y)$
and
$n \geq N(x,y)$
, using (1), we have
$$ \begin{align*} \frac{-\log_{m_1}(D_n(x,y))}{n} &\leq \frac{d_n \log_{m_1}(2 m_1 m_2)}{n} \\ &\leq \frac{(\ell+1) L(n) \log_{m_1}(2 m_1 m_2)}{n q^{\ell}} + \frac{\ell(\ell+1) \log_{m_1}(2 m_1 m_2)}{2n}. \end{align*} $$
Thus,
$$ \begin{align*} \limsup_{r \rightarrow \infty} \frac{-\log_{m_1}(D_{q^{\ell} r}(x,y))}{q^{\ell} r} \leq \frac{(\ell+1) \log_{m_2}(2 m_1 m_2)}{q^{\ell}}. \end{align*} $$
Finally, for such
$(x,y)$
we get the second desired inequality.
2.2. Study of the validity of the Ledrappier–Young formula
Here, we discuss the validity of the Ledrappier–Young formula in our context. Recall that for a shift-invariant ergodic measure
$\mu $
on
$\Sigma _{m_1,m_2}$
, the Ledrappier–Young formula is (see [Reference Kenyon and Peres8, Lemma 3.1] for a proof)
$$ \begin{align*} \dim_{\mathrm{H}}(\mu) = \frac{1}{\log(m_1)} h_{\mu}(\sigma) + \bigg(\frac{1}{\log(m_2)}-\frac{1}{\log(m_1)}\bigg) h_{\pi_* \mu}(\tilde{\sigma}), \end{align*} $$
where
$\tilde {\sigma }$
is the standard shift map on
$\Sigma _{m_2}$
,
$\pi $
is the projection on the second coordinate, and
$h_{\mu }(\sigma )$
is the entropy of
$\mu $
with respect to
$\sigma $
. This can be rewritten as
$$ \begin{align} \dim_{\mathrm{H}}(\mu) = \frac{1}{\log(m_1)} \dim_{\mathrm{e}}(\mu) + \bigg(\frac{1}{\log(m_2)}-\frac{1}{\log(m_1)}\bigg) \dim_{\mathrm{e}}(\pi_* \mu), \end{align} $$
where for any Borel probability measure
$\nu $
on
$\Sigma _{m_1,m_2}$
,
$\dim _{\mathrm {e}}(\nu )$
denotes, whenever it exists, its entropy dimension defined by
$$ \begin{align*} \dim_{\mathrm{e}}(\nu) = \lim_{n\rightarrow \infty} -\frac{1}{n} \sum_{u \in (\mathcal{A}_1 \times \mathcal{A}_2)^n} \nu([u]) \log (\nu ([u])), \end{align*} $$
and where
$\dim _{\mathrm {e}}(\pi _*\nu )$
is defined similarly. We show that this fails to hold for
$\mathbb {P}_{\mu }$
in general. This is expected because
$\mathbb {P}_{\mu }$
is not shift-invariant in general. However, we give a sufficient condition on
$\mu $
for
$\mathbb {P}_{\mu }$
to satisfy (2.4).
Let
$(\nu ^y)_{y \in \pi (\Sigma _{m_1,m_2})}$
be the
$\pi _* \nu $
-almost everywhere uniquely determined disintegration of the Borel probability measure
$\nu $
on
$\Sigma _{m_1,m_2}$
with respect to
$\pi $
. Each
$\nu ^y$
is a Borel probability measure on
$\Sigma _{m_1,m_2}$
supported on
$\pi ^{-1}(\{y\})$
, which can be computed using the formula
$$ \begin{align*} &\nu^y([x|_n] \times \{y\})\\ &\quad= \lim_{p \rightarrow \infty} \frac{\nu ([(x_1,y_1) \cdots (x_n,y_n) y_{n+1} , \ldots, y_p] )}{\pi_* \nu ([y_1 , \ldots, y_p ] )} \quad \text{for } \pi_* \nu \text{-almost all} \ y \in \pi(\Sigma_{m_1,m_2}). \end{align*} $$
For some basics on the notion of disintegrated measure we advise [Reference Oliveira and Viana11] to the reader.
Proposition 2.3. Let
$\mu $
be a Borel probability measure on
$\Omega $
. Then
$\pi _*(\mathbb {P}_{\mu })$
is exact dimensional. Moreover,
$\mathbb {P}_{\mu }^y$
is exact dimensional for
$\pi _*(\mathbb {P}_{\mu }) \text {-almost all} \ y \in \pi (X_{\Omega })$
, and we have
$$ \begin{align*} \underset{y \sim \pi_*(\mathbb{P}_{\mu})}{\mathrm{essinf}} \dim_{\mathrm{e}}(\mathbb{P}_{\mu}^y) = \underset{y \sim \pi_*(\mathbb{P}_{\mu})}{\mathrm{esssup}} \dim_{\mathrm{e}}(\mathbb{P}_{\mu}^y). \end{align*} $$
Finally,
$$ \begin{align*} \dim_{\mathrm{e}}(\pi_*(\mathbb{P}_{\mu})) + \underset{y \sim \pi_*(\mathbb{P}_{\mu})}{\mathrm{essinf}} \dim_{\mathrm{e}}(\mathbb{P}_{\mu}^y) \leq \dim_{\mathrm{e}}(\mathbb{P}_{\mu}), \end{align*} $$
with equality if and only if for all
$p \geq 1$
, for all
$I \in \alpha ^2_p$
, the map
$y \in \pi (I) \mapsto \mu ^y(I)$
is
$\pi _* \mu $
-almost surely constant.
Proof. First note that for
$(x,y) \in \Sigma _{m_1,m_2}$
$$ \begin{align*} \pi_*(\mathbb{P}_{\mu}) ([y_1 , \ldots, y_n ]) &= \sum_{x_1,\ldots,x_n} \prod_{\substack{i \leq n \\ q \nmid i}} \mu ([(x,y)|_{J_i^n}] )\\ &= \prod_{\substack{i \leq n \\ q \nmid i}} \sum_{x_i, \ldots, x_{q^r i}} \mu ( [(x,y)|_{J_i^n}] ) = \mathbb{P}_{\pi_* \mu} ([y_1 , \ldots, y_n ]). \end{align*} $$
Thus,
$\pi _*(\mathbb {P}_{\mu })$
is a Borel probability measure supported on
$\pi (X_{\Omega }) = X_{\pi (\Omega )}$
, which is equal to
$\mathbb {P}_{\pi _* \mu }$
. Thus, using the one-dimensional case studied in [Reference Kenyon, Peres and Solomyak9] we easily obtain that
$\pi _*(\mathbb {P}_{\mu })$
is exact dimensional with
$$ \begin{align*} \dim_{\mathrm{e}}(\pi_*(\mathbb{P}_{\mu})) = (q-1)^2 \sum_{p=1}^{\infty} \frac{H^{\mu}(\alpha^1_p)}{q^{p+1}}. \end{align*} $$
Now we study
$\mathbb {P}_{\mu }^y$
. First observe that for i such that
$q \nmid i$
, the map
$$ \begin{align*} \phi_i : y \in \pi(X_{\Omega}) \longmapsto y|_{J_i} = (y_{q^{\ell} i})_{\ell=0}^{\infty} \in \pi(\Omega) \end{align*} $$
is measure-preserving, that is,
$(\phi _i)_*(\mathbb {P}_{\pi _* \mu }) = \pi _* \mu $
. Let
$p \geq n \geq 1$
. For
$(x,y) \in X_{\Omega }$
we have
$$ \begin{align*} &\frac{\mathbb{P}_{\mu} ([(x_1,y_1) \cdots (x_n,y_n) y_{n+1} , \ldots, y_p ])}{\mathbb{P}_{\pi_* \mu}([y_1 , \ldots, y_p])} \\[6pt] &\quad= \frac{\prod \limits_{\substack{i \leq p \\ q \nmid i}} \sum \limits_{x^{\prime}_{q^k i}, \ldots, x^{\prime}_{q^{\ell} i}} \mu ( [(x_i,y_i) \cdots (x_{q^{k-1} i},y_{q^{k-1} i}) (x^{\prime}_{q^{k} i},y_{q^{k} i}) \cdots (x^{\prime}_{q^{\ell} i},y_{q^{\ell} i}) ] )}{\prod \limits_{\substack{i \leq p \\ q \nmid i}} \sum \limits_{x^{\prime}_i, \ldots, x^{\prime}_{q^{\ell} i}} \mu ( [(x^{\prime}_i,y_i) \cdots (x^{\prime}_{q^{\ell} i},y_{q^{\ell} i} ) ] )} \\[6pt] &\quad= \prod\limits_{\substack{i \leq n \\ q \nmid i}} \frac{\mu ([(x_i,y_i) \cdots (x_{q^{k-1} i},y_{q^{k-1} i}) y_{q^k i} , \ldots, y_{q^{\ell} i} ] )}{\pi_* \mu ( [ y_i , \ldots, y_{q^{\ell} i} ] )}, \end{align*} $$
where
$q^{k-1} i \leq n < q^k i \leq q^{\ell } i \leq p < q^{\ell +1} i$
. Using the remark above and letting
$p \rightarrow \infty $
we deduce that for
$\pi _*(\mathbb {P}_{\mu }) \text {-almost all} \ y$
$$ \begin{align*} (\mathbb{P}_{\mu})^y ([x|_n] \times \{y\}) = \prod\limits_{\substack{i \leq n \\ q \nmid i}} \mu^{y|_{J_i}}([x|_{J_i^n} ] \times \{y|_{J_i}\} ). \end{align*} $$
We use the
$\mathbb {P}_{\mu }$
-almost everywhere defined independent and identically distributed random variables
$$ \begin{align*} X_{i,n} : (x,y) \in X_{\Omega} \longmapsto -\log(\mu^{y|_{J_i}} ( [x|_{J_i^n}] \times \{y|_{J_i}\}) \ \text{for} \ q \nmid i \end{align*} $$
whose expectation is
$$ \begin{align*} &- \int_{\pi(X_{\Omega})} \bigg( \int_{\pi^{-1}(\tilde{y})} \log (\mu^{\tilde{y}|_{J_i}} ( [x|_{J_i^n}] \times \{\tilde{y}|_{J_i}\}) )\, d(\mathbb{P}_{\mu}^{\tilde{y}})(x,y) \bigg)\, d(\pi_*(\mathbb{P}_{\mu}))(\tilde{y}) \\ &\quad= \int_{\pi(X_{\Omega})} H^{\mu^{\tilde{y}|_{J_i}}} (\Delta_p (\Omega_{\tilde{y}|_{J_i}}))\, d(\pi_*(\mathbb{P}_{\mu}))(\tilde{y}) \\ &\quad= \int_{\pi(\Omega)} H^{\mu^y} (\Delta_p (\Omega_{y}))\, d(\pi_*\mu)(y), \end{align*} $$
where
$\Omega _y = \pi ^{-1}(\{y\}) \cap \Omega $
and
$\Delta _p$
is the partition of
$\Omega _y$
into cylinders of length p on the first coordinate x, if
$x|_{J_i^n}$
is of length p. Using again the same reasoning as in the one-dimensional case when computing
$\dim _{\mathrm {H}}(\mathbb {P}_{\mu })$
(see [Reference Kenyon, Peres and Solomyak9]), we get that for
$\pi _*(\mathbb {P}_{\mu }) \text {-almost all} \ y$
,
$\mathbb {P}_{\mu }^y$
is exact dimensional and
$$ \begin{align*} \dim_{\mathrm{e}}(\mathbb{P}_{\mu}^y) = (q-1)^2 \sum_{p=1}^{\infty} \int_{\pi(\Omega)} \frac{H^{\mu^y}(\Delta_p (\Omega_{y}))}{q^{p+1}}\, d(\pi_*\mu)(y). \end{align*} $$
Now we have
$$ \begin{align*} \begin{split} &\int_{\pi(\Omega)} H^{\mu^y}(\Delta_p (\Omega_{y})) \, d(\pi_*\mu)(y) \\ &= - \int_{\pi(\Omega)} \sum_{I \in \theta_p(\Omega_y)} \mu^y(I) \log(\mu^y(I)) \, d(\pi_*\mu)(y) \\ &= - \sum_{I \in \alpha^2_p} \int_{\pi(\Omega)} \mu^y(I \cap \pi^{-1}(\{y\})) \log(\mu^y(I \cap \pi^{-1}(\{y\}))) \, d(\pi_*\mu)(y) \\ &= - \sum_{I \in \alpha^2_p} \int_{\pi(I)} \mu^y(I) \log(\mu^y(I)) \, d(\pi_*\mu)(y) \\ &\leq - \sum_{I \in \alpha^2_p} \pi_* \mu(\pi(I)) \bigg(\!\int_{\pi(I)} \frac{\mu^y(I)}{\pi_* \mu(\pi(I))} \, d(\pi_*\mu)(y)\! \bigg) \log \bigg(\!\int_{\pi(I)} \frac{\mu^y(I)}{\pi_* \mu(\pi(I))} \, d(\pi_*\mu)(y) \!\bigg) \\ &= - \sum_{I \in \alpha^2_p} \mu(I) \log \bigg(\frac{\mu(I)}{\pi_* \mu(\pi(I))} \bigg) \\ &= H^{\mu}(\alpha^2_p|\alpha^1_p), \end{split} \end{align*} $$
using Jensen’s inequality. The function
$x \in [0,1] \mapsto -x\log (x)$
being strictly concave, this is a strict inequality unless for all
$p \geq 1$
, for all
$I \in \alpha ^2_p$
, the map
$y \in \pi (I) \mapsto \mu ^y(I)$
is
$\pi _* \mu $
-almost surely constant.
Using Lemma B.4 we obtain the following result.
Corollary 2.4. If, for all
$p \geq 1$
, for all
$I \in \alpha ^2_p$
, the map
$y \in \pi (I) \mapsto \mu ^y(I)$
is almost surely constant, then
$\mathbb {P}_{\mu }$
satisfies the Ledrappier–Young formula:
$$ \begin{align*} \dim_{\mathrm{H}}(\mathbb{P}_{\mu}) = \frac{1}{\log(m_1)} \dim_{\mathrm{e}}(\mathbb{P}_{\mu}) + \bigg(\frac{1}{\log(m_2)}-\frac{1}{\log(m_1)}\bigg) \dim_{\mathrm{e}} (\pi_* (\mathbb{P}_{\mu})). \end{align*} $$
This sufficient condition is equivalent to saying that for all
$p \geq 1$
, for all
$I = [(x_1,y_1) \cdots (x_p,y_p)] \in \alpha ^2_p$
, for
$\pi _* \mu $
-almost all
$y \in \pi (I)$
we have
$$ \begin{align*} \mu^y(I) = \frac{\mu(I)}{\pi_*\mu(\pi(I))} = \frac{\mu ([(x_1,y_1) \cdots (x_p,y_p)] )}{\mu ([y_1 , \ldots, y_p] )}. \end{align*} $$
For instance, this is clearly satisfied when
$\mu $
is an inhomogeneous Bernoulli product on
$\Omega $
. In this case
$\mathbb {P}_{\mu }$
is not shift-invariant in general. However, we can easily build examples where the equality in Corollary 2.4 does not hold.
Example 2.5. Suppose that
$j=0$
. Then there exists
$\Omega $
and
$\mu $
a Borel probability measure on
$\Omega $
such that
$$ \begin{align*} \dim_{\mathrm{H}}(\mathbb{P}_{\mu}) < \frac{1}{\log(m_1)} \dim_{\mathrm{e}}(\mathbb{P}_{\mu}) + \bigg(\frac{1}{\log(m_2)}-\frac{1}{\log(m_1)}\bigg) \dim_{\mathrm{e}}(\pi_*(\mathbb{P}_{\mu})). \end{align*} $$
Indeed, using the property
$H^{\mu }(\alpha ^2_{p-1} \lor \alpha ^1_p) = H^{\mu }(\alpha ^1_p|\alpha ^2_{p-1}) + H^{\mu }(\alpha ^2_{p-1})$
we have
$$ \begin{align*} \dim_{\mathrm{H}}(\mathbb{P}_{\mu}) = (q-1)^2 \sum_{p=1}^{\infty} \frac{H^{\mu}_{m_1}(\alpha^2_p)}{q^{p+1}} + (q-1)(1-\gamma) \sum_{p=1}^{\infty} \frac{H^{\mu}_{m_2}(\alpha^1_p|\alpha^2_{p-1})}{q^{p}} \end{align*} $$
and
$$ \begin{align*} \begin{split} &\frac{1}{\log(m_1)} \dim_{\mathrm{e}}(\mathbb{P}_{\mu}) + \bigg(\frac{1}{\log(m_2)}-\frac{1}{\log(m_1)}\bigg) \dim_{\mathrm{e}}(\pi_*(\mathbb{P}_{\mu})) \\ &\quad= (q-1)^2 \sum_{p=1}^{\infty} \frac{H^{\mu}_{m_1}(\alpha^2_p)}{q^{p+1}} + (q-1)^2 \bigg(\frac{1}{\log(m_2)}-\frac{1}{\log(m_1)}\bigg) \sum_{p=1}^{\infty} \frac{H^{\mu}(\alpha^1_p)}{q^{p+1}}. \end{split} \end{align*} $$
It is then enough to choose
$\Omega $
and
$\mu $
such that:
-
•
$H^{\mu }(\alpha ^1_1) = 0$
; -
•
$H^{\mu }(\alpha ^1_p | \alpha ^2_{p-1}) = 0$
for all
$p \geq 2$
; -
•
$H^{\mu }(\alpha ^1_p)> 0$
for
$p \geq 2$
.
Such
$\Omega $
and
$\mu $
yield the desired example.
2.3. Lower bound for
$\dim _{\mathrm {H}}(X_{\Omega })$
We are now interested in maximizing
$\dim _{\mathrm {H}}(\mathbb {P}_{\mu })$
over all Borel probability measures
$\mu $
on
$\Omega $
. We define first the jth tree of prefixes of
$\Omega $
, which is a directed graph
$\Gamma _j(\Omega )$
whose set of vertices is
$\bigcup _{k=0}^{\infty } \mathrm{Pref}_{k,j}(\Omega )$
, where
$\mathrm{Pref}_{0,j}(\Omega ) = \{\varnothing \}$
. There is a directed edge from a prefix
$$ \begin{align*} u = (x_1,y_1) \cdots (x_k,y_k) y_{k+1} , \ldots, y_{k+j} \end{align*} $$
to another one v if
$$ \begin{align*} v = (x_1,y_1) \cdots (x_k,y_k) (x_{k+1},y_{k+1}) y_{k+2} , \ldots, y_{k+j} y_{k+j+1} \end{align*} $$
for some
$x_{k+1} \in \{0,\ldots ,m_1-1\}$
and
$y_{k+j+1} \in \{0,\ldots ,m_2-1\}$
. Moreover there is an edge from
$\varnothing $
to every
$u \in \mathrm{Pref}_{1,j}(\Omega )$
. Then
$\Gamma _j(\Omega )$
is a tree with its outdegree being bounded by
$m_1 m_2$
(except the first edges from
$\varnothing $
, which can be more numerous). The following result is an analog of [Reference Kenyon, Peres and Solomyak9, Lemma 2.1].
Lemma 2.6. Let
$u \in \mathrm {Pref}_{1,j}(\Omega )$
and
$\Gamma _{u,j}(\Omega )$
be the tree of followers of u in
$\Gamma _j(\Omega )$
. Let
$V_{u,j}(\Omega )$
be its set of vertices. Then there exists a unique vector
$t = t(u) \in [1,m_2^{{2}/({\gamma (q-1)})}]^{V_{u,j}(\Omega )}$
such that for all
$(x_1,y_1) \cdots (x_k,y_k) y_{k+1} , \ldots , y_{k+j} \in V_{u,j}(\Omega )$
$$ \begin{align} t_{(x_1,y_1) \cdots (x_k,y_k) y_{k+1} , \ldots, y_{k+j}}^{q^{j+1} \gamma} = \sum_{y^{\prime}_{k+j+1}} \bigg( \sum_{x^{\prime}_{k+1}} t_{(x_1,y_1) \cdots (x_k,y_k) (x^{\prime}_{k+1},y_{k+1}) y_{k+2} , \ldots, y_{k+j} y^{\prime}_{k+j+1}} \bigg)^{q^j \gamma}, \end{align} $$
the sums being taken over the followers of
$(x_1,y_1) \cdots (x_k,y_k) y_{k+1} , \ldots , y_{k+j}$
in
$\Gamma _{u,j}(\Omega )$
.
Proof. Let
$Z = [1,m_2^{{2}/({\gamma (q-1)})}]^{V_{u,j}(\Omega )}$
and
$F : Z \rightarrow Z$
be given by
$$ \begin{align*} &F(z_{(x_1,y_1) \cdots (x_k,y_k) y_{k+1} , \ldots, y_{k+j}})\\ &\quad= \bigg(\sum_{y^{\prime}_{k+j+1}} \bigg( \sum_{x^{\prime}_{k+1}} z_{(x_1,y_1) \cdots (x_k,y_k) (x^{\prime}_{k+1},y_{k+1}) y_{k+2} , \ldots, y_{k+j} y^{\prime}_{k+j+1}} \bigg)^{q^j \gamma} \bigg)^{{1}/{q^{j+1} \gamma}}. \end{align*} $$
We can see that F is monotone for the pointwise partial order
$\leq $
, defined as
$$ \begin{align*} z \leq z' \Leftrightarrow \text{ for all } v \in V_{u,j}(\Omega), \ z_v \leq z^{\prime}_v \end{align*} $$
for
$z,z' \in Z$
. Indeed, because
$q^j \gamma $
,
${1}/{q^{j+1} \gamma } \geq 0$
we have
$$ \begin{align*} z \leq z' \Longrightarrow F(z) \leq F(z'). \end{align*} $$
Denote by
$1$
the constant function equal to
$1$
over Z. Then
$1 \leq F(1) \leq F^2(1) \leq \cdots $
, so by compactness
$(F^n(1))_{n \geq 1}$
has a pointwise limit t, which is a fixed point of F. Let us now verify the uniqueness. Suppose that t and
$t'$
are two fixed points of F and that t is not smaller than
$t'$
for
$\leq $
(without loss of generality). Let
$$ \begin{align*} \omega = \inf \{ \xi> 1, \ t \leq \xi t' \}. \end{align*} $$
Clearly,
$\omega \leq m_2^{{2}/{\gamma (q-1)}}$
, and by continuity we have
$t \leq \omega t'$
, so
$\omega> 1$
. Now
$$ \begin{align*} t = F(t) \leq F(\omega t') = \omega^{{1}/{q}} F(t') = \omega^{{1}/{q}} t', \end{align*} $$
contradicting the definition of
$\omega $
.
Furthermore, we define
$$ \begin{align*} t_{\varnothing} = \sum_{y^{\prime}_1} \bigg( \sum_{y^{\prime}_2} \bigg( \cdots \bigg( \sum_{y^{\prime}_{j+1}} \bigg( \sum_{x^{\prime}_1} t_{(x^{\prime}_1,y^{\prime}_1) y^{\prime}_2 , \ldots, y^{\prime}_{j+1}} \bigg)^{q^j \gamma} \bigg)^{{1}/{q}} \cdots \bigg)^{{1}/{q}} \bigg)^{{1}/{q}}. \end{align*} $$
Proposition 2.7. For
$u = (x_1,y_1) \cdots (x_k,y_k) y_{k+1} , \ldots , y_{k+j} \in \mathrm{Pref}_{k,j}(\Omega )$
define
$$ \begin{align*} \begin{split} &\mu([u]) = \frac{t_{(x_1,y_1) y_2 , \ldots, y_{j+1}} (\sum_{x^{\prime}_1} t_{(x^{\prime}_1,y_1) y_2 , \ldots, y_{j+1}} )^{q^j \gamma-1}}{t_{\varnothing}} \\ &\boldsymbol{\cdot}\prod_{p=0}^{j-1} \bigg(\sum_{y^{\prime}_{j+1-p}} \bigg( \sum_{y^{\prime}_{j+2-p}} \bigg({\cdots}\bigg(\sum_{y^{\prime}_{j+1}}\bigg(\sum_{x^{\prime}_1} t_{(x^{\prime}_1,y_1) y_2 , \ldots, y_{j-p} y^{\prime}_{j+1-p} , \ldots, y^{\prime}_{j+1}} \bigg)^{q^j \gamma} \bigg)^{{1}/{q}}{\cdots}\bigg)^{{1}/{q}} \bigg)^{{1}/{q}} \bigg)^{({1-q})/{q}} \\ &\boldsymbol{\cdot} \prod_{p=2}^k \frac{t_{(x_1,y_1) \cdots (x_p,y_p) y_{p+1} , \ldots, y_{p+j}} (\sum_{x^{\prime}_p} t_{(x_1,y_1) \cdots (x^{\prime}_p,y_p) y_{p+1} , \ldots, y_{p+j}} )^{q^j \gamma-1}}{t_{(x_1,y_1) \cdots (x_{p-1},y_{p-1}) y_{p} , \ldots, y_{p-1+j}}^{q^{j+1} \gamma}}, \end{split} \end{align*} $$
where there are
$p+2$
sums and p exponents
${1}/{q}$
in each term of the first product. This defines a Borel probability measure on
$\Omega $
such that
$\mathbb {P}_{\mu }$
is the unique optimal measure, that is, such that
$\dim _{\mathrm {H}}(\mathbb {P}_{\mu })$
is maximal over all Borel probability measures
$\mu $
on
$\Omega $
. Moreover, we have
$\dim _{\mathrm {H}}(\mathbb {P}_{\mu }) = ({q-1})/{q} \log _{m_2}(t_{\varnothing })$
. Using Theorem 2.1 we deduce that
$$ \begin{align*} \dim_{\mathrm{H}}(X_{\Omega}) \geq \frac{q-1}{q} \log_{m_2}(t_{\varnothing}). \end{align*} $$
Proof. Let
$$ \begin{align*} \begin{split} S(\Omega,\mu) &= (q-1)^2 \sum_{p=1}^j \frac{H^{\mu}_{m_2}(\alpha^1_p)}{q^{p+1}} + (q-1)(1-q^j \gamma) \sum_{p=j+1}^{\infty} \frac{H^{\mu}_{m_2}(\alpha^2_{p-j-1} \lor \alpha^1_p)}{q^p} \\[6pt] &\quad+ (q-1)(q^{j+1} \gamma-1) \sum_{p=j+1}^{\infty} \frac{H^{\mu}_{m_2}(\alpha^2_{p-j} \lor \alpha^1_p)}{q^{p+1}}. \end{split} \end{align*} $$
We try to optimize
$S(\Omega ,\mu )$
over all Borel probability measures
$\mu $
on
$\Omega $
. Let
$S(\Omega ) = \max _{\mu } S(\Omega ,\mu )$
. Recall that for some measurable partitions
$\mathcal {P},\mathcal {Q}$
of
$\Omega $
we have
$$ \begin{align*}H^{\mu}_{m_2}(\mathcal{P}|\mathcal{Q}) = \sum_{Q \in \mathcal{Q}} \bigg( - \sum_{P \in \mathcal{P}} \mu(P|Q) \log_{m_2}(\mu(P|Q)) \bigg) \mu(Q). \end{align*} $$
Let
$p \geq j+2$
. We have
$$ \begin{align*}H^{\mu}_{m_2}(\alpha^2_{p-j-1} \lor \alpha^1_p) = H^{\mu}_{m_2}(\alpha^2_{p-j-1} \lor \alpha^1_p|\alpha^2_1 \lor \alpha^1_{j+1}) + H^{\mu}_{m_2}(\alpha^2_1 \lor \alpha^1_{j+1}) \end{align*} $$
and
$$ \begin{align*}H^{\mu}_{m_2}(\alpha^2_{p-j} \lor \alpha^1_p) = H^{\mu}_{m_2}(\alpha^2_{p-j} \lor \alpha^1_p|\alpha^2_1 \lor \alpha^1_{j+1}) + H^{\mu}_{m_2}(\alpha^2_1 \lor \alpha^1_{j+1}). \end{align*} $$
Moreover,
$$ \begin{align*} \begin{split} &H^{\mu}_{m_2}(\alpha^2_{p-j-1} \lor \alpha^1_p|\alpha^2_1 \lor \alpha^1_{j+1}) \\[6pt] &\quad= \sum_{x_1,y_1,y_2,\ldots,y_{j+1}} \theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}} H^{\mu_{(x_1,y_1)y_2 , \ldots, y_{j+1}}}_{m_2}(\alpha^2_{p-j-2} \lor \alpha^1_{p-1} (\Omega_{(x_1,y_1)y_2 , \ldots, y_{j+1}})) \end{split} \end{align*} $$
and
$$ \begin{align*} \begin{split} &H^{\mu}_{m_2}(\alpha^2_{p-j} \lor \alpha^1_p|\alpha^2_1 \lor \alpha^1_{j+1}) \\[6pt] &\quad= \sum_{x_1,y_1,y_2,\ldots,y_{j+1}} \theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}} H^{\mu_{(x_1,y_1) y_2 , \ldots, y_{j+1}}}_{m_2}(\alpha^2_{p-j-1} \lor \alpha^1_{p-1}(\Omega_{(x_1,y_1)y_2 , \ldots, y_{j+1}})), \end{split} \end{align*} $$
where
$$ \begin{align*}\theta_{(x_1,y_1)y_2 , \ldots, y_{j+1}} = \mu([(x_1,y_1)y_2 , \ldots, y_{j+1}]),\end{align*} $$
and
$H_{m_2}^{\mu _{(x_1,y_1) y_2, \ldots , y_{j+1}}}(\alpha ^2_{p-j-2} \lor \alpha ^1_{p-1}(\Omega _{(x_1,y_1) y_2 , \ldots , y_{j+1}}))$
is the entropy of the partition of
$\Omega _{(x_1,y_1) y_2 , \ldots , y_{j+1}}$
, the follower set of
$(x_1,y_1)$
in
$\Omega $
with
$y_2 , \ldots , y_{j+1}$
being fixed, with respect to
$\mu _{(x_1,y_1)y_2 , \ldots , y_{j+1}}$
which is the normalized measure induced by
$\mu $
on
$\Omega _{(x_1,y_1) y_2 , \ldots , y_{j+1}}$
. Then
$$ \begin{align*} \begin{split} S(\Omega,\mu) &= (q-1)^2 \sum_{p=1}^j \frac{H^{\mu}_{m_2}(\alpha^1_p)}{q^{p+1}}\\[6pt] &\quad+ \frac{(q-1)(1-q^j \gamma)}{q^{j+1}} H^{\mu}_{m_2}(\alpha^1_{j+1}) + \frac{\gamma (q-1)}{q} H^{\mu}_{m_2}(\alpha^2_1 \lor \alpha^1_{j+1}) \\[6pt] &\quad+ \frac{1}{q} \sum_{x_1,y_1,y_2,\ldots,y_{j+1}} \theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}} S (\Omega_{(x_1,y_1) y_2 , \ldots, y_{j+1}},\mu_{(x_1,y_1) y_2 , \ldots, y_{j+1}}). \end{split} \end{align*} $$
Observe that the measure is completely determined by the knowledge of
$\theta _{(x_1,y_1) y_2 , \ldots , y_{j+1}}$
and
$\mu _{(x_1,y_1) y_2 , \ldots , y_{j+1}}$
for all
$(x_1,y_1) y_2 , \ldots , y_{j+1}$
. The optimization problems on
$\Omega _{(x_1,y_1) y_2 , \ldots , y_{j+1}}$
being independent, we obtain
$$ \begin{align*} \begin{split} S(\Omega) &= \max_{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}} (q-1)^2 \sum_{p=1}^j \frac{H^{\mu}_{m_2}(\alpha^1_p)}{q^{p+1}} + \frac{(q-1)(1-q^j \gamma)}{q^{j+1}} H^{\mu}_{m_2}(\alpha^1_{j+1}) \\[6pt] &\quad+ \frac{\gamma (q-1)}{q} H^{\mu}_{m_2}(\alpha^2_1 \lor \alpha^1_{j+1}) \\[6pt] &\quad+ \frac{1}{q} \sum_{x_1,y_1,y_2,\ldots,y_{j+1}} \theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}} S (\Omega_{(x_1,y_1) y_2 , \ldots, y_{j+1}}). \end{split} \end{align*} $$
After factorizing, we have
$$ \begin{align*} S(\Omega) &= \max \frac{q-1}{q} \bigg( H^{\mu}_{m_2}(\beta_1) + \frac{1}{q} \sum_{y_1} \theta_{y_1} \bigg( -\sum_{y_2} \frac{\theta_{y_1 y_2}}{\theta_{y_1}} \log_{m_2} \bigg(\frac{\theta_{y_1 y_2}}{\theta_{y_1}} \bigg) \\ &\quad+ \frac{1}{q} \sum_{y_2} \frac{\theta_{y_1 y_2}}{\theta_{y_1}} \bigg(-\sum_{y_3} \frac{\theta_{y_1 y_2 y_3}}{\theta_{q_1 y_2}} \log_{m_2} \bigg(\frac{\theta_{y_1 y_2 y_3}}{\theta_{q_1 y_2}} \bigg) \\ &\quad+ \frac{1}{q} \sum_{y_3} \frac{\theta_{y_1 y_2 y_3}}{\theta_{y_1 y_2}} \bigg( \cdots + q^j \gamma \sum_{y_{j+1}} \frac{\theta_{y_1 , \ldots, y_{j+1}}}{\theta_{y_1 , \ldots, y_j}}\\ &\quad\quad \bigg( -\sum_{x_1} \frac{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}}{\theta_{y_1 , \ldots, y_{j+1}}} \log_{m_2} \bigg(\frac{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}}{\theta_{y_1 , \ldots, y_{j+1}}} \bigg) \\ &\quad+ \frac{1}{\gamma (q-1)} \sum_{x_1} \frac{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}}{\theta_{y_1 , \ldots, y_{j+1}}} S ( \Omega_{(x_1,y_1) y_2 , \ldots, y_{j+1}} ) \bigg) \cdots \bigg) \bigg) \bigg) \bigg). \end{align*} $$
We can now recursively optimize these quantities. First fix
$y_1, \ldots , y_{j+1}$
. To optimize the last part of the above expression of
$S(\Omega )$
, we use Lemma B.1 and we obtain
$$ \begin{align*}\frac{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}}{\theta_{y_1 , \ldots, y_{j+1}}} = \frac{m_2^{{S ( \Omega_{(x_1,y_1) y_2 , \ldots, y_{j+1}})}/{\gamma (q-1)}}}{\sum_{x^{\prime}_1} m_2^{{S ( \Omega_{(x^{\prime}_1,y_1) y_2 , \ldots, y_{j+1}} )}/{\gamma(q-1)}}} \end{align*} $$
and
$$ \begin{align*} \begin{split} &-\sum_{x_1} \frac{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}}{\theta_{y_1 , \ldots, y_{j+1}}} \log_{m_2} \bigg(\frac{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}}{\theta_{y_1 , \ldots, y_{j+1}}} \bigg)\\ &+ \frac{1}{\gamma (q-1)} \sum_{x_1} \frac{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}}{\theta_{y_1 , \ldots, y_{j+1}}} S ( \Omega_{(x_1,y_1) y_2 , \ldots, y_{j+1}} )\\ &\quad = \log_{m_2} \bigg(\sum_{x_1} m_2^{{S ( \Omega_{(x_1,y_1) y_2 , \ldots, y_{j+1}} )}/{\gamma(q-1)}} \bigg). \end{split} \end{align*} $$
Using again Lemma B.1, we obtain
${\theta _{y_1 , \ldots , y_{j+1}}}/{\theta _{y_1 , \ldots , y_j}}$
, and so on. This gives us the weights
$\theta _{(x_1,y_1) y_2 , \ldots , y_{j+1}}$
, which are equal to
$$ \begin{align*} \begin{split} &\frac{z_{(x_1,y_1) y_2 , \ldots, y_{j+1}} (\sum_{x^{\prime}_1} z_{(x^{\prime}_1,y_1) y_2 , \ldots, y_{j+1}} )^{q^j \gamma-1}}{z_{\varnothing}} \\ &\quad\boldsymbol{\cdot} \prod_{p=0}^{j-1} \bigg(\sum_{y^{\prime}_{j+1-p}} \bigg( \sum_{y^{\prime}_{j+2-p}} \bigg( \cdots \\ &\qquad\bigg(\sum_{y^{\prime}_{j+1}}\bigg(\sum_{x^{\prime}_1} z_{(x^{\prime}_1,y_1) y_2 , \ldots, y_{j-p} y^{\prime}_{j+1-p} , \ldots, y^{\prime}_{j+1}} \bigg)^{q^j \gamma} \bigg)^{{1}/{q}} \cdots \bigg)^{{1}/{q}} \bigg)^{{1}/{q}} \bigg)^{({1-q})/{q}}, \end{split} \end{align*} $$
where
$z_{(x_1,y_1) y_2 , \ldots , y_{j+1}} = m_2^{{S (\Omega _{(x_1,y_1) y_2 , \ldots , y_{j+1}})}/{\gamma (q-1)}}$
and
$z_{\varnothing } = m_2^{{q S(\Omega )}/({q-1})}$
. In particular, we obtain
$$ \begin{align*}z_{\varnothing} = \sum_{y^{\prime}_1} \bigg( \sum_{y^{\prime}_2} \bigg( \cdots \bigg( \sum_{y^{\prime}_{j+1}} \bigg( \sum_{x^{\prime}_1} z_{(x^{\prime}_1,y^{\prime}_1) y^{\prime}_2 , \ldots, y^{\prime}_{j+1}} \bigg)^{q^j \gamma} \bigg)^{{1}/{q}} \cdots \bigg)^{{1}/{q}} \bigg)^{{1}/{q}}. \end{align*} $$
Now let us consider
$\Omega _u$
for fixed
$u = (x_1,y_1) y_2 , \ldots , y_{j+1} \in \mathrm{Pref}_{1,j}(\Omega )$
. The optimization problem is now analogous on this tree, but simpler: we now have to optimize the quantity
$$ \begin{align*} \begin{split} &\frac{(q-1)(1-q^j \gamma)}{q^{j+1}} H^{\mu_{(x_1,y_1)y_2 , \ldots, y_{j+1}}}_{m_2} (\alpha^1_{j+1} (\Omega_{(x_1,y_1)y_2 , \ldots, y_{j+1}} ) ) \\ &\quad+ \frac{\gamma (q-1)}{q} H^{\mu_{(x_1,y_1)y_2 , \ldots, y_{j+1}}}_{m_2} (\alpha^2_1 \lor \alpha^1_{j+1} (\Omega_{(x_1,y_1)y_2 , \ldots, y_{j+1}} ) ) \\ &\quad+ \frac{1}{q} \sum_{x_2,y_{j+2}} \frac{\theta_{(x_1,y_1)(x_2,y_2) y_3 , \ldots, y_{j+2}}}{\theta_{(x_1,y_1)y_2 , \ldots, y_{j+1}}} S (\Omega_{(x_1,y_1)(x_2,y_2) y_3 , \ldots, y_{j+2}} ), \end{split} \end{align*} $$
which is after factorization
$$ \begin{align*} \begin{split} \frac{q-1}{q^{j+1}} \bigg( &\!-\!\sum_{y_{j+2}} \frac{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+2}}}{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}} \log_{m_2}\bigg(\frac{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+2}}}{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}}\bigg) \\ &+ q^j \gamma \sum_{y_{j+2}} \frac{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+2}}}{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}} \bigg(\!-\!\sum_{x_2} \frac{\theta_{(x_1,y_1)(x_2,y_2) y_3 , \ldots, y_{j+2}}}{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+2}}}\\ &\quad\quad \log_{m_2} \bigg(\frac{\theta_{(x_1,y_1)(x_2,y_2) y_3 , \ldots, y_{j+2}}}{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+2}}} \bigg) \\ &+ \frac{1}{\gamma (q-1)} \sum_{x_2} \frac{\theta_{(x_1,y_1)(x_2,y_2) y_3 , \ldots, y_{j+2}}}{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+2}}} S (\Omega_{(x_1,y_1)(x_2,y_2) y_3 , \ldots, y_{j+2}} ) \bigg) \bigg). \end{split} \end{align*} $$
This gives the weights
$$ \begin{align*}\frac{\theta_{(x_1,y_1)(x_2,y_2) y_3 , \ldots, y_{j+2}}}{\theta_{(x_1,y_1) y_2 , \ldots, y_{j+1}}} = \frac{z_{(x_1,y_1)(x_2,y_2) y_3 , \ldots, y_{j+2}} (\sum_{x^{\prime}_2} z_{(x_1,y_1)(x^{\prime}_2,y_2) y_3 , \ldots, y_{j+2}} )^{q^j \gamma-1}}{z_{(x_1,y_1) y_2 , \ldots, y_{j+1}}^{q^{j+1} \gamma}},\end{align*} $$
with
$$ \begin{gather*} z_{(x_1,y_1)(x_2,y_2) y_3 , \ldots, y_{j+2}} = m_2^{{S (\Omega_{(x_1,y_1)(x_2,y_2) y_3 , \ldots, y_{j+2}})}/{\gamma (q-1)}},\\ z_{(x_1,y_1) y_2 , \ldots, y_{j+1}} = m_2^{{S (\Omega_{(x_1,y_1) y_2 , \ldots, y_{j+1}})}/{\gamma (q-1)}} \end{gather*} $$
and
$$ \begin{align*} z_{(x_1,y_1) y_2 , \ldots, y_{j+1}}^{q^{j+1} \gamma} = \sum_{y^{\prime}_{j+2}} \bigg( \sum_{x^{\prime}_{2}} z_{(x_1,y_1) (x^{\prime}_2,y_2) y_3 , \ldots, y^{\prime}_{j+2}} \bigg)^{q^j \gamma}. \end{align*} $$
This is exactly (3) at the root of the graph
$\Gamma _{u,j}(\Omega )$
. The problem being the same at each vertex for
$\Gamma _{u,j}(\Omega )$
, for all
$u \in \mathrm{Pref}_{1,j}(\Omega )$
, we can repeat the argument for the entire graphs. We also obtain the given formula for the optimal measure from the form of all optimal probability vectors that we found. The solutions
$z = z(u)$
of the systems (3) which we obtain in this way are in
$[1,m_2^{{2}/{\gamma (q-1)}} ]^{V_{u,j}(\Omega )}$
, thus we have
$z(u) = t(u)$
for all u (indeed, for all
$k \geq 1$
, for all
$v \in \mathrm{Pref}_{k,j}(\Omega )$
, for all
$\mu $
on
$\Omega _v$
we have
$\dim _{\mathrm {H}}(\mathbb {P}_{\mu }) \leq 2$
, thus
$S(\Omega _v) \leq 2$
).
2.4. Upper bound for
$\dim _{\mathrm {H}}(X_{\Omega })$
Theorem 2.8. Let
$\mu $
be the Borel probability measure on
$\Omega $
defined in the last theorem, and let
$\mathbb {P}_{\mu }$
be the corresponding Borel probability measure on
$X_{\Omega }$
. Let
$(x,y) \in X_{\Omega }$
. Then
$$ \begin{align*}\liminf_{n \rightarrow \infty} \frac{-\log_{m_2}(\mathbb{P}_{\mu}(B_n(x,y)))}{L(n)} \leq \frac{q-1}{q} \log_{m_2}(t_{\varnothing}), \end{align*} $$
from which we deduce that
$\dim _{\mathrm {H}}(X_{\Omega })=(({q-1})/{q}) \log _{m_2}(t_{\varnothing })$
.
Proof. Recall that
$$ \begin{align*} &-\log_{m_2}(\mathbb{P}_{\mu}(B_n(x,y))) \\ &\quad=- \sum_{\substack{i,\ q \nmid i \\ i \leq L(n)}} \log_{m_2} ( \mu ([(x_i,y_i) (x_{q i},y_{q i}) \cdots (x_{q^{k-1} i},y_{q^{k-1} i}) y_{q^{k} i} , \ldots, y_{q^{\ell} i} ] ) ), \end{align*} $$
where k and
$\ell $
are determined by
$i < qi < \cdots < q^{k-1} i \leq n < q^{k} i < \cdots < q^{\ell } i \leq L(n) < q^{\ell +1} i$
in each term of the sum.
Suppose first that
$j=1$
for the sake of simplicity. We have
$$ \begin{align*} \begin{split} &\mu ([(x_1,y_1) \cdots (x_k,y_k) y_{k+1}] )\\ &\quad= \frac{t_{(x_1,y_1) y_2} (\sum_{x^{\prime}_1} t_{(x^{\prime}_1,y_1) y_2} )^{q \gamma-1} (\sum_{y^{\prime}_2} ( \sum_{x^{\prime}_1} t_{(x^{\prime}_1,y_1) y^{\prime}_2} )^{q \gamma} )^{({1-q})/{q}}}{t_{\varnothing}} \\ &\qquad\boldsymbol{\cdot} \prod_{p=2}^k \frac{t_{(x_1,y_1) \cdots (x_p,y_p) y_{p+1}} (\sum_{x^{\prime}_p} t_{(x_1,y_1) \cdots (x^{\prime}_p,y_p) y_{p+1}} )^{q \gamma-1}}{t_{(x_1,y_1) \cdots (x_{p-1},y_{p-1}) y_p}^{q^2 \gamma}}, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} &\mu ([(x_1,y_1) \cdots (x_{k-1},y_{k-1}) y_k y_{k+1}] )\\ &\quad= \frac{t_{(x_1,y_1) y_2} (\sum_{x^{\prime}_1} t_{(x^{\prime}_1,y_1) y_2} )^{q \gamma-1} (\sum_{y^{\prime}_2} ( \sum_{x^{\prime}_1} t_{(x^{\prime}_1,y_1) y^{\prime}_2} )^{q \gamma} )^{({1-q})/{q}}}{t_{\varnothing}} \\ &\qquad\boldsymbol{\cdot} \prod_{p=2}^{k-1} \frac{t_{(x_1,y_1) \cdots (x_p,y_p) y_{p+1}} (\sum_{x^{\prime}_p} t_{(x_1,y_1) \cdots (x^{\prime}_p,y_p) y_{p+1}} )^{q \gamma-1}}{t_{(x_1,y_1) \cdots (x_{p-1},y_{p-1}) y_p}^{q^2 \gamma}} \\ &\qquad\boldsymbol{\cdot} \frac{(\sum_{x^{\prime}_k} t_{(x_1,y_1) \cdots (x^{\prime}_k,y_k) y_{k+1}} )^{q \gamma}}{t^{q^2 \gamma}_{(x_1,y_1) \cdots (x_{k-1},y_{k-1}) y_k}} \end{split} \end{align*} $$
for
$k \geq 2$
,
$$ \begin{align*}\mu ([y_1 y_2 ] ) = \frac{ (\sum_{x^{\prime}_1} t_{(x^{\prime}_1,y_1) y_2} )^{q \gamma} (\sum_{y^{\prime}_2} ( \sum_{x^{\prime}_1} t_{(x^{\prime}_1,y_1) y^{\prime}_2} )^{q \gamma} )^{({1-q})/{q}}}{t_{\varnothing}}, \end{align*} $$
and
$$ \begin{align*}\mu ([y_1 ] ) = \frac{ (\sum_{y^{\prime}_2} ( \sum_{x^{\prime}_1} t_{(x^{\prime}_1,y_1) y^{\prime}_2} )^{q \gamma} )^{{1}/{q}}}{t_{\varnothing}}. \end{align*} $$
For each positive integer
$\kappa \leq L(n)$
, we can write
$\kappa = q^r i$
with
$q \nmid i$
for some unique
$(r,i)$
. Now, developing the product
$\mathbb {P}_{\mu }(B_n(x,y))$
, we pick up:
-
•
${1}/{t_{\varnothing }}$
for each
$i \leq L(n)$
such that
$q \nmid i$
; -
•
$t_{(x_i,y_i) \cdots (x_{q^r i},y_{q^r i}) y_{q^{r+1} i}}$
for each
$\kappa = q^r i \leq n$
; -
•
${1}/{t_{(x_i,y_i) \cdots (x_{q^r i},y_{q^r i}) y_{q^{r+1} i}}^{q^2 \gamma }}$
for each
$\kappa \leq \lfloor {L(n)}/{q^2} \rfloor $
, that is, because for these
$\kappa $
we have
$q^2 \kappa = q^{r+2} i \leq L(n)$
, and for
$\kappa> \lfloor {L(n)}/{q^2} \rfloor $
we have
$q^2 \kappa \geq q^2 \lfloor {L(n)}/{q^2} \rfloor + q^2> L(n)$
; -
•
$(\sum _{x^{\prime }_{q^r i}} t_{(x_i,y_i) \cdots (x^{\prime }_{q^r i},y_{q^r i}) y_{q^{r+1} i}} )^{q\gamma - 1}$
for each
$\kappa \leq n$
; -
•
$(\sum _{x^{\prime }_{q^r i}} t_{(x_i,y_i) \cdots (x^{\prime }_{q^r i},y_{q^r i}) y_{q^{r+1} i}} )^{q\gamma }$
for each
$n < \kappa \leq \lfloor {L(n)}/{q} \rfloor $
; -
•
$(\sum _{y^{\prime }_{qi}} ( \sum _{x^{\prime }_i} t_{(x^{\prime }_i,y_i) y^{\prime }_{qi}} )^{q \gamma } )^{({1-q})/{q}}$
for each
$i \leq \lfloor {L(n)}/{q} \rfloor $
such that
$q \nmid i$
; -
•
$(\sum _{y^{\prime }_{qi}} ( \sum _{x^{\prime }_i} t_{(x^{\prime }_i,y_i) y^{\prime }_{qi}} )^{q \gamma } )^{{1}/{q}}$
for each
$\lfloor {L(n)}/{q} \rfloor < i \leq L(n)$
such that
$q \nmid i$
.
Thus, if we define
$$ \begin{align*} R(\kappa) = \log_{m_2} (t_{(x_i,y_i) (x_{qi},y_{qi}) \cdots (x_{q^r i},y_{q^r i}) y_{q^{r+1} i}} ) \end{align*} $$
for
$\kappa = q^r i$
with
$q \nmid i$
,
$$ \begin{align*} \tilde{R}(\kappa) = \log_{m_2} \bigg(\sum_{x^{\prime}_{q^r i}} t_{(x_i,y_i) (x_{qi},y_{qi}) \cdots (x^{\prime}_{q^r i},y_{q^r i}) y_{q^{r+1} i}} \bigg)\end{align*} $$
for
$\kappa = q^r i$
with
$q \nmid i$
, and
$$ \begin{align*} u^1_n = \frac{1}{n} \sum_{\kappa=1}^n R(\kappa), \quad u^2_n = \frac{1}{n} \sum_{\kappa=1}^n \tilde{R}(\kappa), \end{align*} $$
$$ \begin{align*} u^3_n = \frac{1}{n} \sum_{i \leq n, \ q \nmid i} \log_{m_2} \bigg(\sum_{y^{\prime}_{qi}} \bigg(\sum_{x^{\prime}_i} t_{(x^{\prime}_i,y_i) y^{\prime}_{qi}} \bigg)^{q \gamma} \bigg), \end{align*} $$
we obtain
Getting back to the general case, let us define
$j+2$
sequences as follows. At first, set
$$ \begin{align*}u^1_n = \frac{1}{n} \sum_{\kappa=1}^n R(\kappa), \quad u^2_n = \frac{1}{n} \sum_{\kappa=1}^n \tilde{R}(\kappa), \end{align*} $$
where
$$ \begin{align*} R(\kappa) = \log_{m_2} (t_{(x_i,y_i) (x_{qi},y_{qi}) \cdots (x_{q^r i},y_{q^r i}) y_{q^{r+1} i} , \ldots, y_{q^{r+j} i}} ) \end{align*} $$
if
$\kappa = q^r i$
with
$q \nmid i$
, and
$$ \begin{align*} \tilde{R}(\kappa) = \log_{m_2} \bigg(\sum_{x^{\prime}_{q^r i}} t_{(x_i,y_i) (x_{qi},y_{qi}) \cdots (x^{\prime}_{q^r i},y_{q^r i}) y_{q^{r+1} i} , \ldots, y_{q^{r+j} i}} \bigg) \end{align*} $$
if
$\kappa = q^r i$
with
$q \nmid i$
. Then, for
$3 \leq k \leq j+2$
let
$$ \begin{align*} u^k_n &= \frac{1}{n} \sum_{i \leq n, \ q \nmid i} \log_{m_2} \bigg(\sum_{y^{\prime}_{q^{j+3-k} i}} \bigg( \sum_{y^{\prime}_{q^{j+4-k} i}} \bigg( \cdots \\ &\qquad\bigg(\sum_{y^{\prime}_{q^j i}} \bigg(\sum_{x^{\prime}_i} t_{(x^{\prime}_i,y_i) y_{qi} , \ldots, y^{\prime}_{q^{j} i}} \bigg)^{q^j \gamma} \bigg)^{{1}/{q}} \cdots \bigg)^{{1}/{q}} \bigg)^{{1}/{q}} \bigg), \end{align*} $$
where there are exactly
$k-1$
sums and
$k-3$
exponents
${1}/{q}$
in each
$\log _{m_2}$
term. It is easy to see that all these sequences are non-negative, bounded, with
$$ \begin{align*} \text{for all } 1 \leq k \leq j+2, \quad \lim_{n \rightarrow \infty} u^k_{n+1} - u^k_n = 0. \end{align*} $$
Let
$\epsilon> 0$
. Using the definition of
$\mu $
we can obtain the following expression for n large enough, which will be justified when studying the case
$d \geq 2$
To conclude we now use Lemma B.3 and then let
$\epsilon \rightarrow 0$
.
Example 2.9. If
$\Omega $
is a Sierpiński carpet, then clearly
$X_{\Omega } = \Omega $
. Using uniqueness in Theorem 2.6 we deduce that the values
$t_{(x_1,y_1) y_2 , \ldots , y_{j+1}}$
do not depend on
$x_1$
and
$y_1$
. We call them
$t_{y_2 , \ldots , y_{j+1}}$
. Equation (3) now reduces to
$$ \begin{align*} t_{y_2 , \ldots, y_{j+1}}^{q^{j+1} \gamma} = N(y_2)^{q^j \gamma} \sum_{y_{j+2}} t_{y_3 , \ldots, y_{j+2}}^{q^j \gamma}, \end{align*} $$
where
$N(y_2) = \# \{x_2, \ (x_2,y_2) \in A\}$
. Thus,
$$ \begin{align*} \sum_{y_{j+1}} t_{y_2 , \ldots, y_{j+1}}^{q^j \gamma} = N(y_2)^{q^{j-1} \gamma} \sum_{y_{j+1}} \bigg( \sum_{y_{j+2}} t_{y_3 , \ldots, y_{j+2}}^{q^j \gamma} \bigg)^{{1}/{q}}, \end{align*} $$
and so on. After having summed on the different coordinates we obtain
$$ \begin{align*} \sum_{y_2} \bigg( \sum_{y_3} \bigg( \cdots \bigg( \sum_{y_j} \bigg( \sum_{y_{j+1}} t_{y_2 , \ldots, y_{j+1}}^{q^j \gamma} \bigg)^{{1}/{q}} \bigg)^{{1}/{q}} \cdots \bigg)^{{1}/{q}} \bigg)^{{1}/{q}} = \bigg( \sum_{y_2} N(y_2)^{\gamma} \bigg)^{{q}/({q-1})}. \end{align*} $$
Thus, finally,
$t_{\varnothing } = ( \sum _{y_2} N(y_2)^{\gamma } )^{{q}/({q-1})}$
and
$\dim _{\mathrm {H}}(X_{\Omega }) = \log _{m_2} ( \sum _{y_2} N(y_2)^{\gamma } )$
, which is as expected in the McMullen formula. In addition, we check that the maximizing measure is the Bernoulli product measure used by McMullen.
Example 2.10. Let
$q=2$
,
$m_1=3$
,
$m_2=2$
, and
$D = \{(0,0),(0,1),(1,0),(1,1),(2,0), (2,1)\}$
. We have
$j=0$
. Let
$$ \begin{align*} A = \begin{pmatrix} 0 & 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 & 0 \\ \end{pmatrix} \end{align*} $$
be a
$0$
–
$1$
matrix indexed by
$D \times D$
. Let
$$ \begin{align*} X_A = \{(x_k,y_k)_{k=1}^{\infty} \in \Sigma_{3,2}, \ A((x_k,y_k),(x_{2k},y_{2k}))=1, \ k \geq 1 \}. \end{align*} $$
We look for the solutions t of the systems of equations described in Lemma 2.6. Using uniqueness we know that
$$ \begin{align*} t_{(0,0)} = t_{(0,1)} = t_{(1,0)} = t_{(2,0)}, \quad t_{(1,1)} = t_{(2,1)}. \end{align*} $$
Moreover
$$ \begin{gather*} t_{(0,0)}^{\gamma q} = (t_{(1,0)} + t_{(2,0)})^{\gamma} + (t_{(0,1)} + t_{(1,1)} + t_{(2,1)})^{\gamma} = 2^{\gamma} t_{(0,0)}^{\gamma} + (t_{(0,0)} + 2 t_{(1,1)} )^{\gamma} , \\ t_{(1,1)}^{\gamma q} = (t_{(0,0)} + t_{(1,0)} + t_{(2,0)})^{\gamma} + t_{(0,1)}^{\gamma} = (3^{\gamma} + 1) t_{(0,0)}^{\gamma}, \end{gather*} $$
thus,
$t_{(0,0)}^{\gamma q} = 2^{\gamma } t_{(0,0)}^{\gamma } + (t_{(0,0)} + 2 (3^{\gamma }+1)^{{1}/{\gamma q}} t_{(0,0)}^{{1}/{q}} )^{\gamma }$
. Finally, we have
$$ \begin{align*} t_{\varnothing} &= (t_{(1,0)} + t_{(1,0)} + t_{(2,0)})^{\gamma} + (t_{(0,1)} + t_{(1,1)} + t_{(2,1)})^{\gamma}\\ &= 3^{\gamma} t_{(0,0)}^{\gamma} + (t_{(0,0)} + 2 (3^{\gamma}+1)^{{1}/{\gamma q}}\, t_{(0,0)}^{{1}/{q}} )^{\gamma}. \end{align*} $$
Using Scilab we obtain
$t_{(0,0)} \simeq 7.1446$
, thus
$\dim _{\mathrm {H}} y(X_A) = \tfrac 12 \log _2(t_{\varnothing }) \simeq 1.878$
.
2.5. The Minkowski dimension of
$X_{\Omega }$
Theorem 2.11. We have
$$ \begin{align*} \begin{split} \dim_{\mathrm{M}}(X_{\Omega}) &= (q-1)^2 \sum_{p=1}^j \frac{\log_{m_2}(|\mathrm{Pref}_{0,p}(\Omega)|)}{q^{p+1}}\\ &\quad+ (q-1)(1-q^j \gamma) \sum_{p=j+1}^{\infty} \frac{\log_{m_2}(|\mathrm{Pref}_{p-j-1,j+1}(\Omega)|)}{q^p}\\ &\quad+ (q-1)(q^{j+1} \gamma-1) \sum_{p=j+1}^{\infty} \frac{\log_{m_2}(|\mathrm{Pref}_{p-j,j}(\Omega)|)}{q^{p+1}}. \end{split} \end{align*} $$
Proof. Recall that, by definition,
$$ \begin{align*} \underline{\dim}_{\mathrm{M}}(X_{\Omega}) = \liminf_{n\rightarrow \infty} \frac{\log_{m_1}(\mathrm{Pref}_{n,L(n)-n}(X_{\Omega}))}{n}. \end{align*} $$
We can again fix
$\ell \geq j+1$
and take
$n = q^{\ell } r$
with
$r \rightarrow \infty $
in this
$\liminf $
. Now using the computations used in the proof of Theorem 2.2 we obtain
$$ \begin{align*} \begin{split} &\log_{m_1}(\mathrm{Pref}_{n,L(n)-n}(X_{\Omega}))\\ &\quad\geq \sum_{p=1}^j \# \bigg\{i \in{\kern2pt}\bigg]\frac{L(n)}{q^{p}},\frac{L(n)}{q^{p-1}}\bigg] : q \nmid i \bigg\} \log_{m_1}(|\mathrm{Pref}_{0,p}(\Omega)|) \\ &\qquad + \sum_{p=j+1}^{\ell} \# \bigg\{i \in{\kern2pt}\bigg]\frac{n}{q^{p-j-1}},\frac{L(n)}{q^{p-1}}\bigg] : q \nmid i \bigg\} \log_{m_1}(|\mathrm{Pref}_{p-j-1,j+1}(\Omega)|) \\ &\qquad + \sum_{p=j+1}^{\ell} \# \bigg\{ i \in{\kern2pt}\bigg] \frac{L(n)}{q^p},\frac{n}{q^{p-j-1}} \bigg] : q \nmid i \bigg\} \log_{m_1}(|\mathrm{Pref}_{p-j,j}(\Omega)|). \end{split} \end{align*} $$
On the other hand,
$$ \begin{align*} \begin{split} &\log_{m_1}(\mathrm{Pref}_{n,L(n)-n}(X_{\Omega}))\\ &\quad\leq \sum_{p=1}^j \# \bigg\{i \in{\kern2pt}\bigg]\frac{L(n)}{q^{p}},\frac{L(n)}{q^{p-1}}\bigg] : q \nmid i \bigg\} \log_{m_1}(|\mathrm{Pref}_{0,p}(\Omega)|) \\ &\qquad + \sum_{p=j+1}^{\ell} \# \bigg\{i \in{\kern2pt}\bigg]\frac{n}{q^{p-j-1}},\frac{L(n)}{q^{p-1}}\bigg] : q \nmid i \bigg\} \log_{m_1}(|\mathrm{Pref}_{p-j-1,j+1}(\Omega)|) \\ &\qquad + \sum_{p=j+1}^{\ell} \# \bigg\{ i \in{\kern2pt}\bigg] \frac{L(n)}{q^p},\frac{n}{q^{p-j-1}} \bigg] : q \nmid i \bigg\} \log_{m_1}(|\mathrm{Pref}_{p-j,j}(\Omega)|) \\ &\qquad+ \log_{m_1}(m_1 m_2) d_n \end{split} \end{align*} $$
by putting arbitrary digits in the remaining places (
$d_n$
being defined in (1)). Remember that
$d_n \leq {(\ell +1) L(n)}/{q^{\ell }}+ C ({\ell (\ell +1)}/{2})$
. By letting
$r \rightarrow \infty $
we obtain
$$ \begin{align*} \begin{split} \underline{\dim}_{\mathrm{M}}(X_{\Omega}) &\geq (q-1)^2 \sum_{p=1}^j \frac{\log_{m_2}(|\mathrm{Pref}_{0,p}(\Omega)|)}{q^{p+1}}\\ &\quad+ (q-1)(1-q^j \gamma) \sum_{p=j+1}^{\ell} \frac{\log_{m_2}(|\mathrm{Pref}_{p-j-1,j+1}(\Omega)|)}{q^p}\\ &\quad+ (q-1)(q^{j+1} \gamma-1) \sum_{p=j+1}^{\ell} \frac{\log_{m_2}(|\mathrm{Pref}_{p-j,j}(\Omega)|)}{q^{p+1}} \end{split} \end{align*} $$
and
$$ \begin{align*} \begin{split} \overline{\dim}_{\mathrm{M}}(X_{\Omega}) &\leq (q-1)^2 \sum_{p=1}^j \frac{\log_{m_2}(|\mathrm{Pref}_{0,p}(\Omega)|)}{q^{p+1}}\\ &\quad+ (q-1)(1-q^j \gamma) \sum_{p=j+1}^{\ell} \frac{\log_{m_2}(|\mathrm{Pref}_{p-j-1,j+1}(\Omega)|)}{q^p}\\ &\quad+ (q-1)(q^{j+1} \gamma-1) \sum_{p=j+1}^{\ell} \frac{\log_{m_2}(|\mathrm{Pref}_{p-j,j}(\Omega)|)}{q^{p+1}} \\ &\quad+ \log_{m_2}(m_1 m_2) \frac{\ell+1}{q^{\ell}}. \end{split} \end{align*} $$
As
$\ell $
is arbitrary, the proof is complete.
Proposition 2.12. We have
$\dim _{\mathrm {M}}(X_{\Omega }) = \dim _{\mathrm {H}}(X_{\Omega })$
if and only if the following four conditions are satisfied:
-
• the tree
$\Gamma _{j}(\Omega )$
is spherically symmetric; -
•
$\# \{x_1 : (x_1,y_1) y_2 , \ldots , y_{j+1} \in \mathrm{Pref}_{1,j}(\Omega ) \}$
does not depend on
$y_1 , \ldots , y_{j+1} \in \mathrm{Pref}_{0,j+1}(\Omega )$
; -
• for
$1 \leq p \leq j$
,
$\# \{y_{p+1} : y_1 , \ldots , y_{p+1} \in \mathrm{Pref}_{0,p+1}(\Omega ) \}$
does not depend on
$y_1 , \ldots , y_p \in \mathrm{Pref}_{0,p}(\Omega )$
; -
• for
$p \geq 2$
,
$\# \{x_p : (x_1,y_1) \cdots (x_p,y_p) y_{p+1} , \ldots , y_{p+j} \in \mathrm{Pref}_{p,j}(\Omega ) \}$
does not depend on
$(x_1,y_1) \cdots (x_{p-1},y_{p-1}) y_p , \ldots , y_{p+j} \in \mathrm{Pref}_{p-1,j}(\Omega )$
.
Proof. Compare the formulas in Theorems 2.2 and 2.11. We have
$$ \begin{align*} H^{\mu}_{m_{2}}(\alpha^{2}_{p-j} \lor \alpha^{1}_{p}) \leq \log_{m_{2}} ( | \mathrm{Pref}_{p-j,j} (\Omega) | ), \end{align*} $$
with equality if and only if every [u] for
$u \in \mathrm{Pref}_{p-j,j}(\Omega )$
has equal measure
$\mu $
, and similar results for
$H^{\mu }_{m_2}(\alpha ^1_p)$
and
$H^{\mu }_{m_2}(\alpha ^2_{p-j-1} \lor \alpha ^1_p)$
. Now, the expression of
$\mu $
in Proposition 2.7 and uniqueness in Lemma 2.6 give the conditions we stated.
3. Generalization to the higher dimensional cases
We are now trying to compute
$\dim _{\mathrm {H}} y(\mathbb {P}_{\mu })$
in any dimension
$d \geq 2$
. Here
$\Omega $
is now a closed subset of
$$ \begin{align*} \Sigma_{m_1,\ldots,m_d} = (\mathcal{A}_1 \times \cdots \times \mathcal{A}_d)^{\mathbb{N}^*}, \end{align*} $$
where
$m_1 \geq \cdots \geq m_d \geq 2$
and
$\mathcal {A}_i = \{0,\ldots ,m_i-1\}$
. We define
$$ \begin{align*} \gamma_i = \frac{\log(m_{i})}{\log(m_{i-1})} \end{align*} $$
and
$$ \begin{align*} L_i : n \in \mathbb{N} \mapsto \bigg\lceil \frac{n}{\gamma_i} \bigg\rceil \end{align*} $$
for
$2 \leq i \leq d$
(
$L_1$
being the identity on
$\mathbb {N}$
). We can again define the Borel probability measures
$\mathbb {P}_{\mu }$
on
$X_{\Omega }$
as in the two-dimensional case. For
$(x^1,\ldots ,x^d) \in X_{\Omega }$
we need to compute
$\mathbb {P}_{\mu }(B_n(x^1,\ldots ,x^d))$
, where
$$ \begin{align*} B_n(x^1,\ldots,x^d) &= \{(u^1,\ldots,u^d) \in \Sigma_{m_1,\ldots,m_d} : \text{for all } 1 \leq k \leq d, \\ &\qquad \text{for all } 1 \leq i\leq (L_k \circ \cdots \circ L_1)(n), \ u^k_i = x^k_i \}. \end{align*} $$
3.1. Computation of
$\dim _{\mathrm {H}}(\mathbb {P}_{\mu })$
for three-dimensional sponges
First suppose that
$d=3$
, as the computation of
$\dim _{\mathrm {H}}(\mathbb {P}_{\mu })$
in this case helps to better understand the general one. Let
$j_2,j_3$
be the unique non-negative integers such that
$q^{j_2} \leq ({1}/{\gamma _2}) < q^{j_2+1}$
and
$q^{j_3} \leq ({1}/{\gamma _3}) < q^{j_3+1}$
. Now we obtain two cases: either
$q^{j_2+j_3} \leq ({1}/{\gamma _2 \gamma _3}) < q^{j_2+j_3+1}$
or
$q^{j_2+j_3+1} \leq ({1}/{\gamma _2 \gamma _3}) < q^{j_2+j_3+2}$
. Suppose we are in the first case. In this case, for all n large enough, we have
$q^{j_2}n \leq L_2(n) < q^{j_2+1}n$
,
$q^{j_3}n \leq L_3(n) < q^{j_3+1}n$
, and
$q^{j_2+j_3}n \leq L_3(L_2(n)) < q^{j_2+j_3+1}n$
. In order to compute
$\dim _{\mathrm {H}}y(\mathbb {P}_{\mu })$
we now use the same method as in Proposition 2.2. For
$n = q^{\ell } r$
with
$\ell $
fixed we can write
$$ \begin{align*} \bigg]\frac{L_3(L_2(n))}{q^{\ell}},L_3(L_2(n))\bigg] = \bigsqcup_{p=1}^{\ell} \bigg]\frac{L_3(L_2(n))}{q^p},\frac{L_3(L_2(n))}{q^{p-1}}\bigg]. \end{align*} $$
We now have, for all r large enough:
-
•
$1 \leq p \leq j_3 \Longrightarrow ]{L_3(L_2(n))}/{q^p},{L_3(L_2(n))}/{q^{p-1}}] \subset ] L_2(n), L_3(L_2(n)) ]$
; -
•
$j_3+1 \leq p \leq j_3+j_2 \Longrightarrow ]{L_3(L_2(n))}/{q^p},{L_3(L_2(n))}/{q^{p-1}}] \subset ] n, L_3(L_2(n)) ]$
; we have
${L_2(n)}/{q^{p-j_3-1}} \in \, ]{L_3(L_2(n))}/{q^p}, {L_3(L_2(n))}/{q^{p-1}}]$
and
$$ \begin{align*} &i \in{\kern2pt}\bigg]\frac{L_3(L_2(n))}{q^p}, \frac{L_2(n)}{q^{p-j_3-1}} \bigg]\\[6pt] &\quad \Longrightarrow n < i \leq q^{p-j_3-1} i \leq L_2(n) < q^{p-j_3} i q^{p-1} i \leq L_3(L_2(n)) < q^p i, \end{align*} $$
$$ \begin{align*} &i \in{\kern2pt}\bigg] \frac{L_2(n)}{q^{p-j_3-1}}, \frac{L_3(L_2(n))}{q^{p-1}} \bigg] \\[6pt] &\quad\Longrightarrow n < i \leq q^{p-j_3-2} i \leq L_2(n) < q^{p-j_3-1} i \leq q^{p-1} i \leq L_3(L_2(n)) < q^p i; \end{align*} $$
-
• for
$j_3+j_2+1 \leq p \leq \ell $
we have
${L_2(n)}/{q^{p-j_3-1}}, {n}/{q^{p-j_2-j_3-1}} \in \, ]{L_3(L_2(n))}/{q^p}, {L_3(L_2(n))}/{q^{p-1}}]$
and
${n}/{q^{p-j_2-j_3-1}} \leq {L_2(n)}/{q^{p-j_3-1}}$
, thus if
$i \in \, ]{L_3(L_2(n))}/{q^p}, {n}/{q^{p-j_2-j_3-1}} ]$
, then if
$$ \begin{align*}q^{p-j_2-j_3-1} i &\leq n < q^{p-j_2-j_3} i \leq q^{p-j_3-1} i \leq L_2(n) < q^{p-j_3} i\\ &\leq q^{p-1} i \leq L_3(L_2(n)) < q^p i, \end{align*} $$
$i \in \, ]{n}/{q^{p-j_2-j_3-1}},{L_2(n)}/{q^{p-j_3-1}}]$
, then and if
$$ \begin{align*} q^{p-j_2-j_3-2} i &\leq n < q^{p-j_2-j_3-1} i \leq q^{p-j_3-1} i \leq L_2(n) < q^{p-j_3} i\\ &\leq q^{p-1} i \leq L_3(L_2(n)) < q^p i, \end{align*} $$
$i \in \, ]{L_2(n)}/{q^{p-j_3-1}}, {L_3(L_2(n))}/{q^{p-1}}]$
, then
$$ \begin{align*} q^{p-j_2-j_3-2} i &\leq n < q^{p-j_2-j_3-1} i \leq q^{p-j_3-2} i \leq L_2(n) < q^{p-j_3-1} i\\ &\leq q^{p-1} i \leq L_3(L_2(n)) < q^p i. \end{align*} $$
Denote by
$\alpha ^3_p$
,
$\alpha ^2_p$
, and
$\alpha ^1_p$
the partitions of
$\Omega $
into cylinders of length p along all three coordinates, the second and the third coordinates, and the third coordinate, respectively. Using the same approach as in the two-dimensional case, we can obtain
$$ \begin{align*} \begin{split} \dim_{\mathrm{H}}(\mathbb{P}_{\mu}) &= (q-1)^2 \sum_{p=1}^{j_3} \frac{H^{\mu}_{m_3}(\alpha^1_p)}{q^{p+1}} + (q-1)(\gamma_3 q^{j_3+1}-1) \sum_{p=j_3+1}^{j_2+j_3} \frac{H^{\mu}_{m_3}(\alpha^2_{p-j_3} \lor \alpha^1_p)}{q^{p+1}} \\ &\quad+ (q-1)(1-\gamma_3 q^{j_3}) \sum_{p=j_3+1}^{j_2+j_3} \frac{H^{\mu}_{m_3}(\alpha^2_{p-j_3-1} \lor \alpha^1_p)}{q^{p}} \\ &\quad+ (q-1)(\gamma_2 \gamma_3 q^{j_2+j_3+1}-1) \sum_{p=j_2+j_3+1}^{\infty} \frac{H^{\mu}_{m_3}(\alpha^3_{p-j_2-j_3} \lor \alpha^2_{p-j_3} \lor \alpha^1_p)}{q^{p+1}} \\ &\quad+ (q-1)(\gamma_3 q^{j_3} - \gamma_2 \gamma_3 q^{j_2 + j_3}) \sum_{p=j_2+j_3+1}^{\infty} \frac{H^{\mu}_{m_3}(\alpha^3_{p-j_2-j_3-1} \lor \alpha^2_{p-j_3} \lor \alpha^1_p)}{q^{p}} \\ &\quad+ (q-1) (1-\gamma_3 q^{j_3}) \sum_{p=j_2+j_3+1}^{\infty} \frac{H^{\mu}_{m_3}(\alpha^3_{p-j_2-j_3-1} \lor \alpha^2_{p-j_3-1} \lor \alpha^1_p)}{q^{p}}. \end{split} \end{align*} $$
If we suppose now that
$q^{j_2+j_3+1} \leq {1}/{\gamma _2 \gamma _3} < q^{j_2+j_3+2}$
, we have
${L_2(n)}/{q^{p-j_3-1}} \leq {n}/{q^{p-j_2-j_3-2}}$
for n large enough and we obtain
$$ \begin{align} &\dim_{\mathrm{H}}(\mathbb{P}_{\mu}) = (q-1)^2 \sum_{p=1}^{j_3} \frac{H^{\mu}_{m_3}(\alpha^1_p)}{q^{p+1}} + (q-1)(\gamma_3 q^{j_3+1}-1) \sum_{p=j_3+1}^{j_2+j_3+1} \frac{H^{\mu}_{m_3}(\alpha^2_{p-j_3} \lor \alpha^1_p)}{q^{p+1}} \nonumber\\ &\qquad+ (q-1)(1-\gamma_3 q^{j_3}) \sum_{p=j_3+1}^{j_2+j_3+1} \frac{H^{\mu}_{m_3}(\alpha^2_{p-j_3-1} \lor \alpha^1_p)}{q^{p}} \nonumber\\[-29pt]\notag \\\notag\\ &\qquad+ (q-1)(\gamma_3 q^{j_3+1}-1) \sum_{p=j_2+j_3+2}^{\infty} \frac{H^{\mu}_{m_3}(\alpha^3_{p-j_2-j_3-1} \lor \alpha^2_{p-j_3} \lor \alpha^1_p)}{q^{p+1}} \nonumber\\ &\qquad+ (q-1)(\gamma_2 \gamma_3 q^{j_2+j_3+1} - \gamma_3 q^{j_3}) \sum_{p=j_2+j_3+2}^{\infty} \frac{H^{\mu}_{m_3}(\alpha^3_{p-j_2-j_3-1} \lor \alpha^2_{p-j_3-1} \lor \alpha^1_p)}{q^{p}}\nonumber \\ &\qquad+ (q-1) (1- \gamma_2 \gamma_3 q^{j_2+j_3+1}) \sum_{p=j_2+j_3+2}^{\infty} \frac{H^{\mu}_{m_3}(\alpha^3_{p-j_2-j_3-2} \lor \alpha^2_{p-j_3-1} \lor \alpha^1_p)}{q^{p}}. \end{align} $$
In the next subsection we adopt a more general point of view to avoid this dichotomy case.
3.2. Results in any dimension
We now return to the general case, by first introducing some notation and making a few observations before stating the theorems. Let
$I \subset \mathbb {N}^*$
and
be finite sets. If
$x \in \Omega $
and
$(x^k_i)_{\substack {i \in I \\ k \in K}}$
is a finite set of coordinates of x (the upper index corresponding to the ‘geometric’ coordinate and the lower index being the digit), we define the generalized cylinder
$$ \begin{align*} [(x^k_i)_{\substack{i \in I \\ k \in K}}] = \{y \in \Omega : y^k_i = x^k_i \text{ for all } i \in I, \text{ for all } k \in K\}. \end{align*} $$
For some arbitrary coordinate functions
we also define
$$ \begin{align*} \mathrm{Pref}_{\chi_1,\ldots,\chi_N}(\Omega) = \{(\chi_1(x),\ldots,\chi_N(x)) : x \in \Omega\}. \end{align*} $$
For all
, let
$j_t \in \mathbb {N}$
such that
$$ \begin{align*} q^{j_t} \leq \frac{1}{\gamma_{t}} < q^{j_t+1}. \end{align*} $$
There is a unique sequence of integers
$(n_{t})_{2 \leq t \leq d}$
such that
Let
$$ \begin{align*} p_t = j_d+j_{d-1}+\cdots+j_{t+1}+n_{t+1}. \end{align*} $$
The sequence
$(n_t)$
takes its values in
and is non-decreasing; moreover,
$n_d = 0$
and
$n_{t} \in \{n_{t+1},n_{t+1}+1\}$
for
$2 \leq t \leq d-1$
. The integers
$j_t$
,
, and
$n_t$
,
, are the
$2d-3$
parameters mentioned in the introduction. Thus, we obtain that for all n large enough, for
,
and
$$ \begin{align*} \frac{L_d \circ \cdots \circ L_1(n)}{q^p} \geq L_{s-1} \circ \cdots \circ L_1(n), \end{align*} $$
with
$p_0 = \ell $
and
$L_0(n) = 0$
. If
, then
$$ \begin{align*} \frac{L_d \circ \cdots \circ L_1(n)}{q^p} \geq L_{d-1} \circ \cdots \circ L_1(n). \end{align*} $$
For
let
be the unique permutation such that the sequence
is non-decreasing for all n large enough and all p. We define
$$ \begin{align*} I^{s,s-1}_p = \bigg]\frac{L_d \circ \cdots \circ L_1(n)}{q^p}, \frac{L_{\sigma_s(s)} \circ \cdots \circ L_1(n)}{q^{p-p_{\sigma_s(s)}-1}} \bigg], \end{align*} $$
$$ \begin{align*} I^{s,t}_p = \bigg]\frac{L_{\sigma_s(t)} \circ \cdots \circ L_1(n)}{q^{p-p_{\sigma_s(t)}-1}} , \frac{L_{\sigma_s(t+1)} \circ \cdots \circ L_1(n)}{q^{p-p_{\sigma_s(t+1)}-1}} \bigg] \end{align*} $$
for
and
$$ \begin{align*}I^{s,d-1}_p = \bigg]\frac{L_{\sigma_s(d-1)} \circ \cdots \circ L_1(n)}{q^{p-p_{\sigma_s(d-1)}-1}} , \frac{L_d \circ \cdots \circ L_1(n)}{q^{p-1}} \bigg]. \end{align*} $$
We use the partitions
$$ \begin{align*}\bigg] \frac{L_d \circ \cdots \circ L_1(n)}{q^p}, \frac{L_d \circ \cdots \circ L_1(n)}{q^{p-1}} \bigg] = \bigsqcup_{t=s-1}^{d-1} I^{s,t}_p \end{align*} $$
for all
. Observe that for
$i \in \, ] {L_d \circ \cdots \circ L_1(n)}/{q^p}, {L_d \circ \cdots \circ L_1(n)}/ {q^{p-1}} ]$
such that
$q \nmid i$
we have
$$ \begin{align*}q^{p-p_k-2} i \leq L_{k} \circ \cdots \circ L_1(n) < q^{p-p_k} i\end{align*} $$
for all
. Hence, for
, either
$$ \begin{align*}q^{p-p_k-2} i \leq L_{k} \circ \cdots \circ L_1(n) < q^{p-p_k-1} i \end{align*} $$
or
$$ \begin{align*} q^{p-p_k-1} i \leq L_{k} \circ \cdots \circ L_1(n) < q^{p-p_k} i. \end{align*} $$
Moreover, if
$i \in I_p^{s,t}$
, then
$$ \begin{align*} \begin{split} &\frac{L_{\sigma_s(s)} \circ \cdots \circ L_1(n)}{q^{p-p_{\sigma_s(s)}-1}} \leq \cdots \leq \frac{L_{\sigma_s(t)} \circ \cdots \circ L_1(n)}{q^{p-p_{\sigma_s(t)}-1}} < i \leq \\ & \frac{L_{\sigma_s(t+1)} \circ \cdots \circ L_1(n)}{q^{p-p_{\sigma_s(t+1)}-1}} \leq \cdots \leq \frac{L_{\sigma_s(d-1)} \circ \cdots \circ L_1(n)}{q^{p-p_{\sigma_s(d-1)}-1}}. \end{split} \end{align*} $$
For
and
let
be defined by
$p^{s,t}_{k} = p_k+1$
if
, and
$p^{s,t}_k = p_k$
otherwise. Then we have
Thus, the
$\mathbb {P}_{\mu }$
-mass of an arbitrary ‘quasi-cube’ is
$$ \begin{align} \mathbb{P}_{\mu}(B_n(x^1, \ldots, x^d)) &= \bigg(\prod_{p=1}^{j_d} \prod_{\substack{i \in{\kern2pt}\big]\frac{L_d \circ \cdots \circ L_1(n)}{q^p}, \frac{L_d \circ \cdots \circ L_1(n)}{q^{p-1}} \big]\\ q \nmid i}} \mu ( [x_i^d \cdots x^d_{q^{p-1}i} ] ) \bigg) \nonumber\\[6pt] &\quad\boldsymbol{\cdot} \ \prod_{s=2}^{d-1} \ \bigg( \prod_{p=p_s+1}^{p_{s-1}} \ \prod_{t=s-1}^{d-1} \ \prod_{\substack{i \in I^{s,t}_p \\[3pt] q \nmid i}} \mu (C^{s,t}_{p,i}(x)) \bigg) \nonumber\\[6pt] &\quad\boldsymbol{\cdot} \bigg(\prod_{p=p_{1}+1}^{\ell} \ \prod_{t=0}^{d-1} \ \prod_{\substack{i \in I^{1,t}_p \\[3pt] q \nmid i}} \mu (C^{1,t}_{p,i}(x)) \bigg) \boldsymbol{\cdot} D_n(x^1,\ldots,x^d), \end{align} $$
where
$$ \begin{align*} \begin{split} C^{s,t}_{p,i}(x) =&\bigg[ \bigg(x_i^{s},\ldots,x_i^d\bigg) \cdots \bigg(x_{q^{p-p_s^{s,t}-1} i}^{s},\ldots,x_{q^{p-p_s^{s,t}-1} i}^d\bigg) \bigg] \\[8pt] &\cap \bigg[\bigg(x_{q^{p-p_s^{s,t}} i}^{s+1},\ldots,x_{q^{p-p_{s}^{s,t}} i}^d\bigg) \cdots \bigg(x_{q^{p-p_{s+1}^{s,t}-1} i}^{s+1},\ldots,x_{q^{p-p_{s+1}^{s,t}-1} i}^d\bigg) \bigg] \cap \cdots \\[8pt] &\cap \bigg[ \bigg(x^{d-1}_{q^{p-p_{d-2}^{s,t}} i}, x^{d}_{q^{p-p_{d-2}^{s,t}} i}\bigg) \cdots \bigg(x^{d-1}_{q^{p-p_{d-1}^{s,t}-1} i}, x^{d}_{q^{p-p_{d-1}^{s,t}-1} i}\bigg) \bigg]\cap \cdots \\[8pt] & \cap \bigg[ x^d_{q^{p-p_{d-1}^{s,t}} i} \ \cdots \ x^d_{q^{p-1}i} \bigg] \end{split} \end{align*} $$
and
$D_n(x^1,\ldots ,x^d)$
is the residual term. Note that
$C^{s,t}_{p,i}(x)$
can also be compactly written as
$$ \begin{align*} \begin{split} &[\pi^s(x)_i , \ldots, \pi^s(x)_{q^{p-p_s^{s,t}-1} i}] \cap [\pi^{s+1}(x)_{q^{p-p_s^{s,t}} i} , \ldots, \pi^{s+1}(x)_{q^{p-p_{s+1}^{s,t}-1} i}] \cap \cdots \\[6pt] &\cap [\pi^d(x)_{q^{p-p_{d-1}^{s,t}} i} , \ldots, \pi^d(x)_{q^{p-1}i}], \end{split} \end{align*} $$
using the projections
$\pi ^k : x \mapsto (x^k,\ldots ,x^d)$
for
.
Now, for all
$p \geq 1$
, we define
and
$$ \begin{align*}\delta^{s,d-1}_{p} = \lim_{n \rightarrow \infty} \frac{\# \{i \in I^{s,s}_p : q \nmid i \}}{L_d \circ \cdots \circ L_1(n)} = \frac{(1-q^{p_{\sigma_s(d-1)}} \prod_{i=\sigma_s(d-1)+1}^d \gamma_i)(q-1)}{q^p}. \end{align*} $$
Moreover, denote by
$\alpha ^k_p$
the partition of
$\Omega $
into cylinders of length p along the last k coordinates for
. Finally, let
$$ \begin{align*}\widetilde{H}_{s,p}^{\mu} = \sum_{t=s-1}^{d-1} \delta^{s,t}_p H^{\mu}_{m_d} (\alpha^{1}_p \lor \alpha^2_{p-p^{s,t}_{d-1}} \lor \alpha^3_{p-p^{s,t}_{d-2}} \lor \cdots \lor \alpha^{d-s+1}_{p-p^{s,t}_{s}}) \end{align*} $$
for
.
Theorem 3.1. The Borel probability measure
$\mathbb {P}_{\mu }$
is exact dimensional and its dimension is
$$ \begin{align*}S(\Omega,\mu) = \bigg(\sum_{p=1}^{j_d} \widetilde{H}_{d,p}^{\mu} \bigg) + \bigg(\sum_{s=2}^{d-1} \ \sum_{p=p_{s}+1}^{p_{s-1}} \widetilde{H}_{s,p}^{\mu} \bigg) + \sum_{p=p_{1}+1}^{\infty} \widetilde{H}_{1,p}^{\mu}. \end{align*} $$
Proof. We use exactly the same method as in the proof of Theorem 2.2, using the computation of
$\mathbb {P}_{\mu }(B_n(x^1,\ldots ,x^d))$
above, the different families of independent and identically distributed random variables
$$ \begin{align*} \{ Y^{s,t}_{p,i} : x \in X_{\Omega} \mapsto -\log(\mu(C^{s,t}_{p,i}(x)))\}_{i\in I_p^{s,t}} \end{align*} $$
whose expectations are
$H^{\mu }_{m_d} \Big(\alpha ^{1}_p \lor \alpha ^2_{p-p^{s,t}_{d-1}} \lor \alpha ^3_{p-p^{s,t}_{d-2}} \lor \cdots \lor \alpha ^{d-s+1}_{p-p^{s,t}_{s}}\Big)$
, respectively, and Theorem 2.1 and Lemma B.2 repeatedly. We then show again that the residual term
$D_n(x^1,\ldots ,x^d)$
, which is larger than or equal to the
$\mathbb {P}_{\mu }$
-mass of those points in
$X_{\Omega }$
which share the same symbolic coordinates as x for those indices j which do not appear in the cylinders of the forme
$C^{s,t}_{p,i}(x)$
with
$p \leq \ell $
, is
$\mathbb {P}_{\mu }$
-almost always negligible. To this end, we use, as in the proof of Theorem 2.2, the Borel–Cantelli lemma and the set
$$ \begin{align*}S_n = \{(x^1,\ldots,x^d) \in X_{\Omega} : D_n(x^1,\ldots,x^d) \leq (2 m_1 m_2 \ldots m_d)^{-d_n}\}, \end{align*} $$
where the exponent
$$ \begin{align*}d_n = L_d \circ \cdots \circ L_1(n) - \sum_{p=1}^{\ell} \#\bigg\{ i \in \mathbb{N} \cap \bigg] \frac{L_d \circ \cdots \circ L_1(n)}{q^p},\frac{L_d \circ \cdots \circ L_1(n)}{q^{p-1}} \!\bigg] : q \nmid i \bigg\} p \end{align*} $$
can likewise easily be controlled.
We can again optimize this quantity following the method we used in the two-dimensional case, by conditioning all the entropy terms appearing in the third part of this expression for
$p \geq p_{1}+2$
by the finest partition appearing in the term
$\widetilde {H}_{1,p_{1}+1}^{\mu }$
. We know that for all s we have
$$ \begin{align} \begin{split} &t \leq t' \Longrightarrow \text{ for all } k, \ p_k^{s,t} \leq p_k^{s,t'},\\ &t < t' \Longrightarrow \text{ there exists } k, \ p_k^{s,t} < p_k^{s,t'}, \end{split} \end{align} $$
so this partition is that appearing in the
$t=0$
term, that is,
$$ \begin{align*} \begin{split} \alpha &= \alpha^1_{p_{1}+1} \lor \alpha^2_{p_{1}+1-p_{d-1}^{1,0}} \lor \alpha^3_{p_{1}+1-p_{d-2}^{1,0}} \lor \cdots \lor \alpha^d_{p_{1}+1-p_{1}^{1,0}}\\ &= \alpha^1_{p_{1}+1} \lor \alpha^2_{p_{1}+1-p_{d-1}} \lor \alpha^3_{p_{1}+1-p_{d-2}} \lor \cdots \lor \alpha^d_{1}. \end{split} \end{align*} $$
If C is a cylinder of this partition in
$\Omega $
, denote by
$\Omega _C$
,
$\theta _C$
, and
$\mu _C$
the associate rooted set at
$C \in \alpha $
in
$\Omega $
, its
$\mu $
-mass and the normalized measure induced on it, respectively. As, for
$p \geq p_{1}+2$
and
, we can write
$$ \begin{align*} \begin{split} &H^{\mu}_{m_d} (\alpha^{1}_p \lor \alpha^2_{p-p^{1,t}_{d-1}} \lor \alpha^3_{p-p^{1,t}_{d-2}} \lor \cdots \lor \alpha^{d}_{p-p^{1,t}_{1}}) \\ &\quad= H^{\mu}_{m_d}(\alpha) + H^{\mu}_{m_d} (\alpha^{1}_p \lor \alpha^2_{p-p^{1,t}_{d-1}} \lor \alpha^3_{p-p^{1,t}_{d-2}} \lor \cdots \lor \alpha^{d}_{p-p^{1,t}_{1}} | \alpha )\\ &\quad= H^{\mu}_{m_d}(\alpha) + \sum_{C \in \mathcal{C}} \theta_C H^{\mu_C}_{m_d} (\alpha^{1}_{p-1} \lor \alpha^2_{p-p^{1,t}_{d-1}-1} \lor \alpha^3_{p-p^{1,t}_{d-2}-1} \lor \cdots \lor \alpha^{d}_{p-p^{1,t}_{1}-1}(\Omega_C) ), \end{split} \end{align*} $$
we obtain
$$ \begin{align} S(\Omega,\mu) &= \sum_{p=1}^{j_d} \widetilde{H}_{d,p}^{\mu} + \sum_{s=2}^{d-1} \ \sum_{p=p_s+1}^{p_{s-1}} \widetilde{H}_{s,p}^{\mu} \nonumber\\ &\quad+ \sum_{t=1}^{d-1} \delta^{1,t}_{p_{1}+1} H^{\mu}_{m_d} (\alpha^1_{p_{1}+1} \lor \alpha^2_{p_{1}+1-p_{d-1}^{1,t}} \lor \cdots \lor \alpha^d_{p_{1}+1-p_{1}^{1,t}} ) \nonumber\\ &\quad+ \bigg(\delta_{p_{1}+1}^{1,0}+\sum_{p=p_{1}+2}^{\infty} \ \sum_{t=0}^{d-1} \delta_p^{1,t}\bigg) H^{\mu}_{m_d}(\alpha) + \frac{1}{q} \sum_{C \in \mathcal{C}} \theta_C S(\Omega_C,\mu_C). \end{align} $$
Now we can obtain the unique optimal measure as in the proof of Theorem 2.7 by getting the
$q_C$
with a recursive reasoning and repeating the argument for the entire suitable graphs. To make things clearer and to highlight the fact that the structure of the optimal measure is similar to that appearing in the two-dimensional case, we introduce now the unique sequence of coordinate functions
$(\chi _i)_{i \geq 1}$
such that if we reorder the partitions of
$\Omega $
appearing in the expression of
$\dim _{\mathrm {H}}({\mathbb {P}_{\mu }})$
above as an increasing sequence
$\beta _1 \leq \beta _2 \leq \cdots $
(the symbol
$\leq $
corresponding there to the ‘finer than’ partial order) we have
$$ \begin{align*}H^{\mu}(\beta_i) = -\int_{\Omega} \log_{m_d} (\mu ( [\chi_1(x), \ldots, \chi_i(x)])) \, d \mu(x) \end{align*} $$
for all
$i \geq 1$
. Here we used a slight generalization of the notion of cylinders we defined at the beginning of §3.2, allowing ourselves to use any family
of coordinates of x and not necessarily a product. This order is exactly the following (using again facts (6)):
$$ \begin{align*} &\alpha^1_1 \leq \cdots \leq \alpha^1_{p_{d-1}} \leq \alpha^1_{p_{d-1}+1} \lor \alpha^2_{p_{d-1}+1-p_{d-1}^{d-1,d-1}} \leq \alpha^1_{p_{d-1}+1} \lor \alpha^2_{p_{d-1}+1-p_{d-1}^{d-1,d-2}} \\ &\leq\alpha^1_{p_{d-1}+2}{{\kern-1.5pt}\lor{\kern-1.5pt}}\alpha^2_{p_{d-1}+2-p_{d-1}^{d-1,d-1}}{{\kern-1.5pt}\leq{\kern-1.5pt}}\alpha^1_{p_{d-1}+2}{{\kern-1.5pt}\lor{\kern-1.5pt}}\alpha^2_{p_{d-1}+2-p_{d-1}^{d-1,d-2}}{{\kern-1.5pt}\leq{\kern-1.5pt}}{{\kern-3pt}\cdots{\kern-3pt}}{{\kern-1.5pt}\leq{\kern-1.5pt}}\alpha^1_{p_{d-2}}{{\kern-1.5pt}\lor{\kern-1.5pt}}\alpha^2_{p_{d-2}-p_{d-1}^{d-1,d-1}} \\ &\leq\alpha^1_{p_{d-2}} \lor \alpha^2_{p_{d-2}-p_{d-1}^{d-1,d-2}} \leq \cdots \leq \alpha^1_{p_2+1} \lor \alpha^{2}_{p_2+1-p_{d-1}^{2,d-1}} \lor \cdots \lor \alpha^{d-1}_{p_2+1-p_2^{2,d-1}} \leq \cdots \\ &\leq \alpha^1_{p_2+1} \lor \alpha^{2}_{p_2+1-p_{d-1}^{2,1}} \lor \cdots \lor \alpha^{d-1}_{p_2+1-p_2^{2,1}} \leq \cdots \leq \alpha^1_{p_1} \lor \alpha^{2}_{p_1-p_{d-1}^{2,d-1}} \lor \cdots \lor \alpha^{d-1}_{p_1-p_2^{2,d-1}}\\ &\leq \cdots \leq \alpha^1_{p_1} \lor \alpha^{2}_{p_1-p_{d-1}^{2,1}} \lor \cdots \lor \alpha^{d-1}_{p_1-p_2^{2,1}} \leq \alpha^1_{p_1+1} \lor \alpha^2_{p_1+1-p_{d-1}^{1,d-1}} \lor \cdots \lor \alpha^d_{p_1+1-p_1^{1,d-1}}\\ &\leq \cdots \leq \alpha^1_{p_1+1} \lor \alpha^2_{p_1+1-p_{d-1}^{1,0}} \lor \cdots \lor \alpha^d_{p_1+1-p_1^{1,0}} = \alpha \leq \alpha^1_{p_1+2} \lor \alpha^2_{p_1+2-p_{d-1}^{1,d-1}} \lor \cdots \\ &\lor\alpha^d_{p_1+2-p_1^{1,d-1}} \leq \cdots \leq \alpha^1_{p_1+2} \lor \alpha^2_{p_1+2-p_{d-1}^{1,0}} \lor \cdots \lor \alpha^d_{p_1+2-p_1^{1,0}} \leq \cdots. \end{align*} $$
For example, when
$d=3$
and
$\dim _{\mathrm {H}}({\mathbb {P}_{\mu }})$
is given by (4), this sequence is given by
$$ \begin{align*}(\chi_i)_{i \geq 1} = (x^3_1, \ldots, x^3_{j_3},x^3_{j_3+1},x^2_1,x^3_{j_3+2},x^2_2,\ldots,x^3_{j_2+j_3+2},x^1_1,x^2_{j_2+2},\ldots ). \end{align*} $$
We also denote by
the sequence of real factors giving weights to the N entropies in
$S(\Omega ,\mu )$
(see (7)) when being reordered that way. Let
$$ \begin{align*} N = p_{1} + 1 + \sum_{k=1}^{d-1} (p_{1} + 1 - p_k) \end{align*} $$
be the number of coordinates
$\chi _i$
appearing in the partition
$\alpha $
distinguished above. Finally, for
$(X_1,\ldots ,X_N) \in \mathrm{Pref}_{\chi _1,\ldots ,\chi _N}(\Omega )$
let
$\Gamma _{(X_1,\ldots ,X_N)}(\Omega )$
be the directed graph whose set of vertices is
$(X_1,\ldots ,X_N) \cup \bigcup _{\ell =1}^{\infty } \mathrm{Pref}_{\chi _1,\ldots ,\chi _{N+\ell d}}(\Omega )$
, and where for all
$\ell \geq 0$
there is a directed edge from
$u = X_1 , \ldots , X_{N+\ell d}$
to another one v if and only if
$v = X_1 , \ldots , X_{N+\ell d} X_{N+\ell d +1} , \ldots , X_{N+(\ell +1)d}$
for some
$X_i$
,
.
Theorem 3.2. Let
$\omega _1 = \sum _{i=1}^N \delta _i$
,
$\omega _k = {\sum _{i=k}^N \delta _i}/{\sum _{i=k-1}^N \delta _i}$
for
$2 \leq k \leq N$
and
$\omega _{N+1} = {1}/{q \delta _N}$
. For all
$(X_1,\ldots ,X_N) \in \mathrm{Pref}_{\chi _1,\ldots ,\chi _N}(\Omega )$
there is a unique vector
$t \in [1,m_d^{\omega _{N+1} d}]^{\Gamma _{(X_1,\ldots ,X_N)}(\Omega )}$
such that for all
$\ell \geq 0$
and
$(X_1,\ldots ,X_{N+\ell d}) \in \Gamma _{(X_1,\ldots ,X_N)}(\Omega )$
we have
$$ \begin{align*} &(t_{X_1 , \ldots, X_{N+\ell d}})^{{1}/({\tilde{\omega}_{N-d+1} \omega_{N+1}})}\\ &\quad= \sum_{X^{\prime}_{N+\ell d+1}} \bigg( \sum_{X^{\prime}_{N+\ell d+2}} \bigg( \cdots \bigg( \sum_{X^{\prime}_{N+(\ell+1)d}} t_{X_1 , \ldots, X^{\prime}_{N+(\ell+1)d}} \bigg)^{\omega_N} \cdots \bigg)^{\omega_{N-d+3}} \bigg)^{\omega_{N-d+2}}, \end{align*} $$
where
$\tilde {\omega }_{N-d+1} = \omega _1 \omega _2 \ldots \omega _{N-d+1}$
. Moreover, if we define
$$ \begin{align*}t_{\varnothing} = \sum_{X^{\prime}_1} \bigg( \sum_{X^{\prime}_2} \bigg( \cdots \bigg( \sum_{X^{\prime}_{N-1}} \bigg( \sum_{X^{\prime}_N} t_{X^{\prime}_1 , \ldots, X^{\prime}_N} \bigg)^{\omega_N} \bigg)^{\omega_{N-1}} \cdots \bigg)^{\omega_3} \bigg)^{\omega_2}, \end{align*} $$
the unique Borel probability measure maximizing
$S(\Omega ,\mu )$
is defined for all
$\ell \geq 0$
by
$$ \begin{align} \begin{split} & \mu ( [X_1 , \ldots, X_{N+\ell d}]) \\ & = \frac{t_{X_1 , \ldots, X_N}}{t_{\varnothing}} \prod_{p=2}^{N} \bigg(\sum_{X^{\prime}_{p}} \bigg( \sum_{X^{\prime}_{p+1}} \bigg( \cdots \bigg(\sum_{X^{\prime}_{N-1}} \bigg(\sum_{X^{\prime}_N} t_{X_1 \cdots X_{p-1} X^{\prime}_p \cdots X^{\prime}_N} \bigg)^{\omega_N} \bigg)^{\omega_{N-1}} \cdots \bigg)^{\omega_{p+2}} \bigg)^{\omega_{p+1}} \bigg)^{\omega_{p}-1} \\ &\quad\boldsymbol{\cdot} \prod_{k=1}^{\ell} t_{X_1{\cdots}X_{N+kd}} \ t_{X_1{\cdots}X_{N+(k-1)d}}^{-({1}/{\tilde{\omega}_{N-d+1} \omega_{N+1}})} \\ &\quad\boldsymbol{\cdot} \prod_{p=2}^d\bigg(\sum_{X^{\prime}_{N+(k-1)d+p}}{\kern-3pt}\bigg({\cdots} \bigg(\sum_{X^{\prime}_{N+kd}} t_{X_1 \cdots X^{\prime}_{N+kd}} \bigg)^{\omega_N}{\cdots}\bigg)^{\omega_{N-d+p+1}} \bigg)^{\omega_{N-d+p}-1} \\[-24pt] \end{split} \end{align} $$
and its Hausdorff dimension is equal to
$\omega _1 \log _{m_d}(t_{\varnothing })$
.
Proof. The existence and uniqueness of t are checked using a fixed point theorem as in Lemma 2.6. We obtain with this notation that
$$ \begin{align*} \begin{split} S(\Omega,\mu) &= \sum_{i=1}^N \delta_i H^{\mu}_{m_d}(\beta_i) + \frac{1}{q} \sum_{X_1,\ldots,X_N} \theta_{X_1 , \ldots, X_N} S(\Omega_{X_1 , \ldots, X_N},\mu_{X_1 , \ldots, X_N})\\ &= \omega_1 \bigg( H^{\mu}_{m_d}(\beta_1) + \omega_2 \sum_{X_1} \theta_{X_1} \bigg( -\sum_{X_2} \frac{\theta_{X_1 X_2}}{\theta_{X_1}} \log_{m_d} \bigg(\frac{\theta_{X_1 X_2}}{\theta_{X_1}} \bigg) \\ &\quad+ \omega_3 \sum_{X_2} \frac{\theta_{X_1 X_2}}{\theta_{X_1}} \bigg(-\sum_{X_3} \frac{\theta_{X_1 X_2 X_3}}{\theta_{X_1 X_2}} \log_{m_d} \bigg(\frac{\theta_{X_1 X_2 X_3}}{\theta_{X_1 X_2}} \bigg) \\ &\quad+ \omega_4 \sum_{X_3} \frac{\theta_{X_1 X_2 X_3}}{\theta_{X_1 X_2}} \bigg( \cdots + \omega_{N} \!\sum_{X_{N-1}} \frac{\theta_{X_1 , \ldots, X_{N-1}}}{\theta_{X_1 , \ldots, X_{N-2}}} \bigg( \!-\!\sum_{X_{N}} \frac{\theta_{X_1 , \ldots, X_{N}}}{\theta_{X_1 , \ldots, X_{N-1}}} \log_{m_d} \\ &\quad\quad \bigg(\frac{\theta_{X_1 , \ldots, X_{N}}}{\theta_{X_1 , \ldots, X_{n-1}}} \bigg)+ \omega_{N+1} \sum_{X_N} \frac{\theta_{X_1 , \ldots, X_{N}}}{\theta_{X_1 , \ldots, X_{N-1}}} S (\Omega_{X_1 , \ldots, X_N},\mu_{X_1 , \ldots, X_N} ) \bigg) \cdots \bigg) \bigg) \bigg) \bigg). \end{split} \end{align*} $$
Optimizing this expression as before, we get that
$\theta _{X_1, \ldots , X_N}$
equals
$$ \begin{align*} &\frac{z_{X_1, \ldots,X_N}}{z_{\varnothing}} \prod_{p=2}^{N} \bigg(\!\sum_{X^{\prime}_{p}} \bigg( \!\sum_{X^{\prime}_{p+1}} \bigg( \cdots\\ &\quad \bigg(\!\sum_{X^{\prime}_{N-1}} \bigg(\!\sum_{X^{\prime}_N} z_{X_1, \ldots, X_{p-1} X^{\prime}_p, \ldots, X^{\prime}_N} \bigg)^{\omega_N} \bigg)^{\omega_{N-1}} \cdots \bigg)^{\omega_{p+2}} \bigg)^{\omega_{p+1}} \bigg)^{\omega_{p}-1}, \end{align*} $$
where
$z_{X_1, \ldots , X_N} = m_d^{\omega _{N+1} S (\Omega _{X_1, \ldots , X_N} )}$
and
$z_{\varnothing } = m_d^{{S(\Omega )}/{\omega _1}}$
. It remains to optimize the conditional measures on the subtrees
$\Omega _{X_1, \ldots , X_N}$
, by maximizing the expression
$S (\Omega _{X_1, \ldots , X_N},\mu _{X_1, \ldots , X_N} )$
which is equal to
$$ \begin{align*} &\sum_{i=N-d+1}^N \delta_i H^{\mu_{X_1 , \ldots, X_N}}_{m_d} (\beta_i (\Omega_{X_1 , \ldots, X_N} ) )\\[6pt] &\qquad + \frac{1}{q} \sum_{X_{N+1},\ldots,X_{N+d}} \frac{\theta_{X_1 , \ldots, X_{N+d}}}{\theta_{X_1 , \ldots, X_N}} S ( \Omega_{X_1 , \ldots, X_{N+d}},\mu_{X_1 , \ldots, X_{N+d}} ) \\[6pt] &\quad=\widetilde{\omega}_{N-d+1} \bigg(-\sum_{X_{N+1}} \frac{\theta_{X_1 , \ldots, X_{N+1}}}{\theta_{X_1 , \ldots, X_N}} \log_{m_d} \bigg(\frac{\theta_{X_1 , \ldots, X_{N+1}}}{\theta_{X_1 , \ldots, X_N}} \bigg) \\[6pt] &\qquad+ \omega_{N-d+2} \sum_{X_{N+1}} \frac{\theta_{X_1 , \ldots, X_{N+1}}}{\theta_{X_1 , \ldots, X_N}} \bigg( \cdots \\[6pt] &\qquad+ \omega_{N} \sum_{X_{N+d-1}} \frac{\theta_{X_1 , \ldots, X_{N+d-1}}}{\theta_{X_1 , \ldots, X_{N+d-2}}} \bigg( -\sum_{X_{N+d}} \frac{\theta_{X_1 , \ldots, X_{N+d}}}{\theta_{X_1 , \ldots, X_{N+d-1}}} \log_{m_d} \bigg(\frac{\theta_{X_1 , \ldots, X_{N+d}}}{\theta_{X_1 , \ldots, X_{N+d-1}}} \bigg) \\[6pt] &\qquad+ \omega_{N+1} \sum_{X_{N+d}} \frac{\theta_{X_1 , \ldots, X_{N+d}}}{\theta_{X_1 , \ldots, X_{N+d-1}}} S(\Omega_{X_1 , \ldots, X_{N+d}},\mu_{X_1 , \ldots, X_{N+d}}) \bigg) \cdots \bigg) \bigg) \end{align*} $$
and repeating the argument for the entire graphs. This yields the desired results.
Theorem 3.3. Let
$\mu $
be the Borel probability measure on
$\Omega $
defined in the last theorem, and let
$\mathbb {P}_{\mu }$
be the corresponding probability measure on
$X_{\Omega }$
. Let
$x \in X_{\Omega }$
. Then
$$ \begin{align*}\liminf_{n \rightarrow \infty} \frac{-\log_{m_d}(\mathbb{P}_{\mu}(B_n(x)))}{L_d \circ \cdots \circ L_1(n)} \leq \omega_1 \log_{m_d}(t_{\varnothing}). \end{align*} $$
Using Theorem 2.1, we deduce that
$$ \begin{align*}\dim_{\mathrm{H}}(X_{\Omega}) = \omega_1 \log_{m_d}(t_{\varnothing}) = \frac{q-1}{q} \log_{m_d}(t_{\varnothing}). \end{align*} $$
Proof. Let
$\Lambda (n) = \bigcup _{k=1}^d \{({L_k \circ \cdots \circ L_1(n)}/{q^r}) : r \in \mathbb {N} \}$
. We can reorder the elements of
$\Lambda (n)$
as the following increasing sequence:
$$ \begin{align*} \begin{split} &L_d \circ \cdots \circ L_1(n) \geq \frac{L_d \circ \cdots \circ L_1(n)}{q} \geq \cdots \geq \frac{L_d \circ \cdots \circ L_1(n)}{q^{p_{d-1}}} \geq L_{d-1} \circ \cdots \circ L_1(n) \\ & \quad \geq\frac{L_d \circ \cdots \circ L_1(n)}{q^{p_{d-1}+1}} \geq \frac{L_{d-1} \circ \cdots \circ L_1(n)}{q} \geq \cdots \geq \frac{L_{d-1} \circ \cdots \circ L_1(n)}{q^{p_{d-2}-p_{d-1}-1}} \\ &\quad \geq\frac{L_d \circ \cdots \circ L_1(n)}{q^{p_{d-2}}} \geq \frac{L_{\sigma_{d-2}(d-1)} \circ \cdots \circ L_1(n)}{q^{p_{d-2}-p_{\sigma_{d-2}(d-1)}}} \geq \frac{L_{\sigma_{d-2}(d-2)} \circ \cdots \circ L_1(n)}{q^{p_{d-2}-p_{\sigma_{d-2}(d-2)}}} \\ &\quad \geq\frac{L_d \circ \cdots \circ L_1(n)}{q^{p_{d-2}+1}} \geq \cdots \geq \frac{L_{\sigma_{d-2}(d-1)} \circ \cdots \circ L_1(n)}{q^{p_{d-3}-p_{\sigma_{d-2}(d-1)}-1}} \geq \frac{L_{\sigma_{d-2}(d-2)} \circ \cdots \circ L_1(n)}{q^{p_{d-3}-p_{\sigma_{d-2}(d-2)}-1}} \\ &\quad \geq \frac{L_d \circ \cdots \circ L_1(n)}{q^{p_{d-3}}} \geq \cdots \geq \frac{L_d \circ \cdots \circ L_1(n)}{q^{p_{1}}} \geq \frac{L_{\sigma_{1}(d-1)} \circ \cdots \circ L_1(n)}{q^{p_{1}-p_{\sigma_{1}(d-1)}}} \geq \cdots \\ &\quad \geq \frac{L_{\sigma_{1}(1)} \circ \cdots \circ L_1(n)}{q^{p_{1}-p_{\sigma_{1}(1)}}} \geq \frac{L_d \circ \cdots \circ L_1(n)}{q^{p_{1}+1}} \geq \frac{L_{\sigma_{1}(d-1)} \circ \cdots \circ L_1(n)}{q^{p_{1}-p_{\sigma_{1}(d-1)}+1}} \geq \cdots\\ & \quad \geq \frac{L_{\sigma_{1}(1)} \circ \cdots \circ L_1(n)}{q^{p_{1}-p_{\sigma_{1}(1)}+1}} \geq \frac{L_d \circ \cdots \circ L_1(n)}{q^{p_{1}+2}} \geq \cdots. \end{split} \end{align*} $$
We denote this sequence by
$$ \begin{align*}\phi_0(n) = L_d \circ \cdots \circ L_1(n) \geq \phi_1(n) \geq \phi_2(n) \geq \cdots,\end{align*} $$
which is valid for all n. Observe that
$\phi _N(n) \kern-1pt =\kern-1pt ({L_d \circ \cdots \circ L_1(n)})/{q^{p_{1}+1}}\kern-1pt$
. We now fix
$n \kern-1pt\geq\kern-1pt 1$
. Let
$S \geq 0$
be the unique integer such that we have
$$ \begin{align*}\phi_S(n) < 1 \leq \phi_{S-1}(n) \leq \cdots \leq \phi_0(n). \end{align*} $$
We can write
$S = N + Md +R$
, with
$M \geq 0$
and
. Recall formula (5). With this notation, we obtain that
$$ \begin{align} \mathbb{P}_{\mu}(B_n(x)) = \prod_{k=1}^S \ \prod_{\substack{\phi_k(n) < i \leq \phi_{k-1}(n) \\ q \nmid i}} \mu ( [ \chi_1 (x|_{J_i} ) \cdots \chi_k(x|_{J_i} ) ] ). \end{align} $$
Now, for all
$1 \leq k \leq N-1$
, we have
$$ \begin{align} &\mu ( [ \chi_1 (x|_{J_i} ) \cdots \chi_k(x|_{J_i} ) ] ) \nonumber\\ &\ \ = \frac{1}{t_{\varnothing}} \prod_{p=2}^k \bigg(\! \sum_{\chi_p(x|_{J_i})'} \cdots \bigg(\!\sum_{\chi_N (x|_{J_i})'} t_{\chi_1 (x|_{J_i}) \cdots \chi_{p-1}(x|_{J_i}) \chi_p(x|_{J_i})' \cdots \chi_N (x|_{J_i})'} \bigg)^{\omega_N} \cdots \bigg)^{\omega_p-1} \nonumber\\ & \ \ \quad\boldsymbol{\cdot} \bigg(\sum_{\chi_{k+1}(x|_{J_i})'} \cdots \bigg( \sum_{\chi_N(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{k}(x|_{J_i}) \chi_{k+1}(x|_{J_i})' \cdots \chi_N(x|_{J_i})'} \bigg)^{\omega_N} \cdots \bigg)^{\omega_{k+1}}. \end{align} $$
If
$R=0$
then
$$ \begin{align*} \begin{split} &\mu ( [ \chi_1 (x|_{J_i} ) \cdots \chi_{N+Md}(x|_{J_i} ) ] ) \\ &= \mu ( [ \chi_1 (x|_{J_i} ) \cdots \chi_N(x|_{J_i} ) ] ) \boldsymbol{\cdot} \prod_{r=1}^{M} \bigg[t_{\chi_1 (x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})} \ t_{\chi_1(x|_{J_i}) \cdots \chi_{N+(r-1)d}(x|_{J_i})}^{-({1}/{\tilde{\omega}_{N-d+1} \omega_{N+1}})} \\ &\quad\prod_{p=2}^d\bigg(\sum_{\chi_{N+(r-1)d+p}(x|_{J_i})'} \bigg( \cdots \bigg(\sum_{\chi_{N+rd}(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})'} \bigg)^{\omega_N} \cdots \bigg)^{\omega_{N-d+p+1}} \bigg)^{\omega_{N-d+p}-1}\bigg], \end{split} \end{align*} $$
and if
, then
$$ \begin{align} \begin{split} &\mu ( [ \chi_1 (x|_{J_i} ) \cdots \chi_{N+Md+R}(x|_{J_i} ) ] ) \\ &= \mu ( [ \chi_1 (x|_{J_i} ) \cdots \chi_N(x|_{J_i} ) ] ) \boldsymbol{\cdot} \prod_{r=1}^{M} \bigg[t_{\chi_1 (x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})} \ t_{\chi_1(x|_{J_i}) \cdots \chi_{N+(r-1)d}(x|_{J_i})}^{-({1}/{\tilde{\omega}_{N-d+1} \omega_{N+1}})} \\ &\prod_{p=2}^d\!\bigg(\!\sum_{\chi_{N+(r-1)d+p}(x|_{J_i})'} \bigg( \cdots \bigg(\!\sum_{\chi_{N+rd}(x|_{J_i})'} \!t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})'} \bigg)^{\omega_N} \cdots \bigg)^{\omega_{N-d+p+1}} \bigg)^{\omega_{N-d+p}-1}\bigg] \\ &\boldsymbol{\cdot} t_{\chi_1(x|_{J_i}) \ldots \chi_{N+Md}(x|_{J_i})}^{-({\tilde{\omega}_{N-d+1} \omega_{N+1}})^{-1}} \\ &\boldsymbol{\cdot} \prod_{p=2}^{R} \bigg(\sum_{\chi_{N+Md+p}(x|_{J_i})'} \bigg({\cdots{\kern0.5pt}}\bigg(\sum_{\chi_{N+(M+1)d}(x|_{J_i})'} t_{\chi_1(x|_{J_i}){{\kern-3pt}\cdots}\chi_{N+(M+1)d}(x|_{J_i})'} \bigg)^{\omega_N} \cdots \bigg)^{\omega_{N-d+p+1}} \bigg)^{\omega_{N-d+p}-1} \\ &\boldsymbol{\cdot} \bigg(\!\sum_{\chi_{N+Md+R+1}(x|_{J_i})'} \cdots \bigg(\! \sum_{\chi_{N+(M+1)d}(x|_{J_i})'} \!t_{\chi_1(x|_{J_i}) \cdots \chi_{N+(M+1)d}(x|_{J_i})'} \bigg)^{\omega_N} \cdots \!\bigg)^{\omega_{N-d+R+1}}. \end{split} \end{align} $$
Observe that for
and
$r \in \mathbb {N}$
we have
$\phi _{N-k+rd}(n) = {\phi _{N-k}(n)}/{q^r}$
. Thus, for
and
$r \in \mathbb {N}$
$$ \begin{align} \phi_{N-k+rd}(n) < i \leq \phi_{N-k+rd-1}(n) \Longleftrightarrow \phi_{N-k}(n) < q^r i \leq \phi_{N-k-1}(n). \end{align} $$
Now we can develop the expression (9) of
$\mathbb {P}_{\mu }(B_n(x))$
and group together the terms with the same number of sums. We obtain
$t_{\varnothing }^{-1}$
for all
$1 \leq i \leq \phi _0(n)$
such that
$q \nmid i$
; using property (12) we obtain
$$ \begin{align*}\prod\limits_{r=0}^M \ \prod\limits_{\substack{1 \leq i \leq \phi_{N+rd-1}(n) \\ q \nmid i}} t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})} = \prod\limits_{\substack{\kappa = q^r i \leq \phi_{N-1}(n) \\ q \nmid i}} t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})},\end{align*} $$
and
$$ \begin{align*}\prod\limits_{r=0}^M \ \prod\limits_{\substack{1 \leq i \leq \phi_{N+rd}(n) \\ q \nmid i}} t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})}^{-(\tilde{\omega}_{N-d+1} \omega_{N+1})^{-1}} = \prod\limits_{\substack{\kappa = q^r i \leq \phi_{N}(n) \\ q \nmid i}} t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})}^{-(\tilde{\omega}_{N-d+1} \omega_{N+1})^{-1}};\end{align*} $$
we gather the product of terms coming from (10) with
to obtain
$$ \begin{align*} \begin{split} &\prod\limits_{k=1}^{N-d} \prod\limits_{\phi_k(n) < i \leq \phi_{k-1}(n)} \bigg(\sum_{\chi_{k+1}(x|_{J_i})'} \cdots \bigg( \sum_{\chi_N(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{k}(x|_{J_i}) \chi_{k+1}(x|_{J_i})' \cdots \chi_N(x|_{J_i})'} \bigg)^{\omega_N} \cdots \bigg)^{\omega_{k+1}} \\[8pt] &= \prod_{p=d+1}^{N} \ \prod_{\substack{\phi_{N-p+1}(n) < i \leq \phi_{N-p}(n) \\ q \nmid i}} \ \bigg(\sum_{\chi_{N-p+2}(x|_{J_i})'} \cdots \bigg(\sum_{\chi_{N}(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{N}(x|_{J_i})'} \bigg)^{\omega_N} \cdots \bigg)^{\omega_{N-p+2}}; \end{split} \end{align*} $$
and, similarly,
$$ \begin{align*} \begin{split} &\prod\limits_{k=N-d+1}^{N-1} \prod\limits_{\phi_k(n) < i \leq \phi_{k-1}(n)} \bigg(\sum_{\chi_{k+1}(x|_{J_i})'}{\cdots{\kern0.5pt}}\bigg( \sum_{\chi_N(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{k}(x|_{J_i}) \chi_{k+1}(x|_{J_i})' \cdots \chi_N(x|_{J_i})'} \bigg)^{\omega_N}{\cdots}\bigg)^{\omega_{k+1}}\\[8pt] &= \prod\limits_{p=2}^{d} \ \prod\limits_{\substack{\phi_{N-p+1}(n) < i \leq \phi_{N-p}(n) \\ q \nmid i}} \ \bigg(\sum_{\chi_{N-p+2}(x|_{J_i})'} \cdots \bigg(\sum_{\chi_{N}(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{N}(x|_{J_i})'} \bigg)^{\omega_N} \cdots \bigg)^{\omega_{N-p+2}}, \end{split} \end{align*} $$
that we combine with
$$ \begin{align*} \begin{split} &\prod\limits_{k=0}^M \prod\limits_{R=1}^{d-1} \prod\limits_{\substack{\phi_{N+kd+R}(n) < i \leq \phi_{N+kd+R-1}(n) \\[-1pt] q \nmid i}} \bigg(\sum\limits_{\chi_{N+kd+R+1}(x|_{J_i})'}{{\kern-3.7pt}\cdots{\kern0.5pt}}\bigg( \sum\limits_{\chi_{N+(k+1)d}(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{N+(M+1)d}(x|_{J_i})'} \bigg)^{\omega_N}{{\kern-3.7pt}\cdots}\bigg)^{\omega_{N-d+R+1}} \\[8pt]&= \prod\limits_{r=1}^{M+1} \prod\limits_{p=2}^d \prod\limits_{\substack{\phi_{N+rd-p+1}(n) < i \leq \phi_{N+rd-p}(n) \\[-1pt] q \nmid i}} \bigg(\sum_{\chi_{N+rd-p+2}(x|_{J_i})'}{\cdots{\kern0.5pt}}\bigg(\sum_{\chi_{N+rd}(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})'} \bigg)^{\omega_N}{\cdots}\bigg)^{\omega_{N-p+2}}, \end{split} \end{align*} $$
to obtain
$$ \begin{align*} \begin{split} \prod_{p=2}^{d} \ \prod_{\substack{\phi_{N-p+1}(n) < \kappa = q^r i \leq \phi_{N-p}(n) \\ q \nmid i}} \! \bigg(\sum_{\chi_{N+rd-p+2}(x|_{J_i})'} {{\kern-3pt}\cdots{\kern0.5pt}} \bigg(\sum_{\chi_{N+rd}(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})'} \bigg)^{\omega_N} {{\kern-3pt}\cdots} \bigg)^{\omega_{N-p+2}}; \end{split} \end{align*} $$
finally, we combine in a similar way, all the remaining terms from the products (11) and (10) and obtain
$$ \begin{align*} \begin{split} &\!\prod_{p=2}^{d} \, \prod_{\substack{\kappa = q^r i \leq \phi_{N-p+1}(n)\\ q \nmid i}} \! \bigg(\sum_{\chi_{N+rd-p+2}(x|_{J_i})'} {{\kern-5.2pt}\cdots{\kern0.5pt}}\bigg(\sum_{\chi_{N+rd}(x|_{J_i})'} {\kern-3pt} t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})'} \bigg)^{\!\omega_N}{{\kern-5.2pt}\cdots}\bigg)^{\!\omega_{N-p+2}-1} \\[8pt] &\quad \boldsymbol{\cdot} \prod_{p=d+1}^{N} \ \prod_{\substack{i \leq \phi_{N-p+1}(n) \\ q \nmid i}} \ \bigg(\sum_{\chi_{N-p+2}(x|_{J_i})'} \cdots \bigg(\sum_{\chi_{N}(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{N}(x|_{J_i})'} \bigg)^{\omega_N}\! \cdots \bigg)^{\omega_{N-p+2}-1}\!. \end{split} \end{align*} $$
Thus,
For
$\kappa = q^r i$
with
$q \nmid i$
, let
$$ \begin{align*} \begin{split} R_1(\kappa) &= \log_{m_d}(t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})}),\\ R_2(\kappa) &= \log_{m_d} \bigg(\sum_{\chi_{N+rd}(x|_{J_i})'} t_{\chi_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})'}\bigg), \end{split} \end{align*} $$
and for
, let
$$ \begin{align*}R_{p}(\kappa) = \log_{m_d} \bigg(\!\sum_{\chi_{N+rd-p+2}(x|_{J_i})'} \!\bigg(\! \cdots \bigg(\!\sum_{\chi_{N+rd}(x|_{J_i})'} t_{X_1(x|_{J_i}) \cdots \chi_{N+rd}(x|_{J_i})'} \bigg)^{\omega_N} \cdots \bigg)^{\omega_{N-p+3}}\bigg). \end{align*} $$
For
and
$n \geq 1$
, let
$$ \begin{align*}u^p_n = \frac{1}{n} \sum_{\kappa=1}^n R_p(\kappa), \end{align*} $$
and for
, let
$$ \begin{align*}u^p_n = \frac{1}{n} \sum_{i \leq n, \ q \nmid i} \log_{m_d} \bigg(\sum_{\chi_{N-p+2}(x|_{J_i})'} \bigg( \cdots \bigg(\sum_{\chi_{N}(x|_{J_i})'} \!t_{\chi_1(x|_{J_i}) \cdots \chi_{N}(x|_{J_i})'} \bigg)^{\omega_N} \cdots \bigg)^{\omega_{N-p+3}} \bigg). \end{align*} $$
This gives us N bounded sequences. We can now write
Furthermore, some basic recursive computations give us the values of the exponents
$$ \begin{align*} \begin{split} \omega_1 &= \sum_{p=1}^{j_d} \delta_p^{d,d-1} + \sum_{s=2}^{d-1} \sum_{p=p_s+1}^{p_{s-1}} \sum_{t=s-1}^{d-1} \delta_p^{s,t} + \sum_{p=p_1+1}^{\infty} \sum_{t=0}^{d-1} \delta_p^{1,t} = \frac{q-1}{q} \\[4pt] &= \lim\limits_{n \rightarrow \infty} \frac{\# \{i \leq L_d \circ \cdots \circ L_1(n) : q \nmid i \}}{L_d \circ \cdots \circ L_1(n)}, \end{split} \end{align*} $$
$$ \begin{align*} \omega_2 &= \frac{\omega_1-\delta_1}{\omega_1} = \lim\limits_{n \rightarrow \infty} \frac{\# \{i \leq {L_d \circ \cdots \circ L_1(n)}/{q} : q \nmid i \}}{\# \{i \leq L_d \circ \cdots \circ L_1(n) : q \nmid i \}} = \frac{1}{q}, \hspace{1.9pc} \\[4pt]\omega_3 &= \frac{\omega_1 - \delta_1 - \delta_2}{\omega_1-\delta_1} = \frac{1}{q}, \end{align*} $$
$$ \begin{align*} \hspace{-6.3pc} \omega_4 = \cdots = \omega_{p_{d-1}+2} = \frac{1}{q}, \quad \omega_{p_{d-1}+3} = \gamma_d q^{p_{d-1}}, \end{align*} $$
$$ \begin{align*} \omega_{p_{d-1}+4} = \frac{1}{\gamma_d q^{p_{d-1}+1}}, \ldots , \!\quad\! \omega_k = \frac{\omega_1 - \sum\nolimits_{i=1}^{k-1} \delta_i}{\omega_1 - \sum\nolimits_{i=1}^{k-2} \delta_i} = \lim\limits_{n \rightarrow \infty} \frac{\# \{i \leq \phi_{k-1}(n) : q \nmid i \}}{\# \{i \leq \phi_{k-2}(n) : q \nmid i \}}, \ \ \ldots \end{align*} $$
$$ \begin{align*} \omega_N = q^{p_{\sigma_1(1)}-p_{\sigma_1(2)}} \frac{\prod_{i=\sigma_1(1)+1}^d \gamma_i}{\prod_{i=\sigma_1(2)+1}^d \gamma_i}, \quad \omega_{N+1} = \frac{q^{p_1-p_{\sigma_1(1)}}}{(q-1) \prod_{\sigma_1(1)+1}^d \gamma_i}. \end{align*} $$
This yields
$$ \begin{align*} (\tilde{\omega}_{N-d+1} \omega_{N+1})^{-1} = q^{p_{\sigma_1(1)}+1} \prod_{i=\sigma_1(1)+1}^d \gamma_i \end{align*} $$
and the asymptotic equivalences
$$ \begin{align*} \lfloor\phi_{N-1}(n)\rfloor \sim (\tilde{\omega}_{N-d+1} \omega_{N+1})^{-1} \lfloor \phi_N(n)\rfloor, \end{align*} $$
$$ \begin{align*} \lfloor\phi_{k+1}(n)\rfloor \sim \omega_{k+2} \lfloor\phi_k(n)\rfloor \end{align*} $$
for all
, when
$n \rightarrow +\infty $
. We conclude by again using Lemma B.3.
Theorem 3.4. For
$n_1,\ldots ,n_d \in \mathbb {N}$
let
We have
$$ \begin{align*} \begin{split} \dim_{\mathrm{M}}(X_{\Omega}) &= \sum_{p=1}^{j_d} \delta_p^{d,d-1} |\mathrm{Pref}_{0,\ldots,0,p}(\Omega)| \\ &\quad+ \sum_{s=2}^{d-1} \ \sum_{p=p_s+1}^{p_{s-1}} \ \sum_{t=s-1}^{d-1} \delta_p^{s,t} |\mathrm{Pref}_{0,\ldots,0,p-p_s^{s,t},p_s^{s,t}-p_{s+1}^{s,t},\ldots,p_{d-2}^{s,t}-p_{d-1}^{s,t},p_{d-1}^{s,t}}(\Omega)| \\ &\quad+ \sum_{p=p_1+1}^{\infty} \ \sum_{t=0}^{d-1} \delta^{1,t}_p |\mathrm{Pref}_{p-p_1^{1,t},p_1^{1,t}-p_{2}^{1,t},\ldots,p_{d-2}^{1,t}-p_{d-1}^{1,t},p_{d-1}^{1,t}}(\Omega)|. \end{split} \end{align*} $$
Proof. The proof follows the same path as in the two-dimensional case. We leave it to the reader, along with the characterization of the equality case with the Hausdorff dimension.
A Appendix. Notation
B Appendix
Lemma B.1. Let
$p_1,\ldots ,p_m \geq 0$
with
$\sum _{i=1}^m p_1 = 1$
, and let
$q_1,\ldots ,q_m \in \mathbb {R}$
. Then
$$ \begin{align*}\sum_{i=1}^m p_i (-\log(p_i)+q_i) \leq \log \bigg( \sum_{i=1}^m e^{q_i} \bigg), \end{align*} $$
with equality if and only if
$p_i = {e^{q_i}}/{\sum _{j=1}^m e^{q_j}}$
for all i.
Proof. See [Reference Falconer3, Corollary 1.5].
Lemma B.2. Let
$(\Omega , \mathcal {F}, \mathbb {P})$
be a probability space,
$(m_n) \in (\mathbb {N}^*)^{\mathbb {N}^*}$
be a strictly increasing sequence such that
$\sum _{n=1}^{\infty } ({1}/{m_n^2}) < +\infty $
and for all
$n \geq 1$
let
be a family of independent centered random variables on
$(\Omega , \mathcal {F}, \mathbb {P})$
. Assume that there exists
$K \geq 0$
such that
Then
$({1}/{m_n}) \sum _{i=1}^{m_n} X_{i,n} \xrightarrow [n \rightarrow \infty ]{\text {a.s.}} 0$
.
Proof. Fix
$n \geq 1$
. We have
$$ \begin{align*} \begin{split} \mathbb{E} \bigg[ \bigg(\sum_{i=1}^{m_n} X_{i,n} \bigg)^4 \bigg] &= \mathbb{E} \bigg[ \sum_{i=1}^{m_n} X_{i,n}^4 + 6 \sum_{i<j} X_{i,n}^2 X_{j,n}^2 \bigg] \\ &\leq m_n K + 3 m_n (m_n-1) K \\ &\leq 3 K m_n^2 \end{split} \end{align*} $$
by using independence and Jensen’s inequality. Now
$\sum _{n=1}^{\infty } ( ({1}/{m_n}) \sum _{i=1}^{m_n} X_{i,n} )^4$
is a well-defined random variable taking values in
$\mathbb {R}^+ \cup \{+\infty \}$
. Moreover, by the monotone convergence theorem
$$ \begin{align*}\mathbb{E} \bigg[\sum_{n=1}^{\infty} \bigg( \frac{1}{m_n} \sum_{i=1}^{m_n} X_{i,n} \bigg)^4 \bigg] = \sum_{n=1}^{\infty} \frac{1}{m_n^4} \mathbb{E} \bigg[ \bigg(\sum_{i=1}^{m_n} X_{i,n} \bigg)^4 \bigg] \leq 3K \sum_{n=1}^{\infty} \frac{1}{m_n^2} < +\infty. \end{align*} $$
Thus,
$\sum _{n=1}^{\infty } ( ({1}/{m_n}) \sum _{i=1}^{m_n} X_{i,n} )^4 < +\infty $
almost surely and
$({1}/{m_n}) \sum _{i=1}^{m_n} X_{i,n} \xrightarrow [n \rightarrow \infty ]{\text {a.s.}} 0$
.
Lemma B.3. Let
$p \in \mathbb {N}^*$
and for
$1 \leq j \leq p$
let
$(u^j_n) \in \mathbb {R}^{\mathbb {N}}$
be p bounded sequences with
$$ \begin{align*}\lim_{n \rightarrow \infty} u^j_{n+1} - u^j_n = 0. \end{align*} $$
For
let
$\phi _j, \psi _j : \mathbb {N} \rightarrow \mathbb {N}$
be such that
$$ \begin{align*} &\text{there exists } c_j,r_j> 0, \text{ there exists } A_j,B_j \in \mathbb{N}, \text{ for all } n, \\ &\quad|\phi_j(n) - \lceil r_j n \rceil| \leq A_j \quad \text{and} \quad |\psi_j(n) - \lceil c_j n \rceil| \leq B_j. \end{align*} $$
Then, we have
$$ \begin{align*}\liminf_{n \rightarrow \infty} \sum_{j=1}^p (u^j_{ \phi_j (n) } - u^j_{ \psi_j (n) } ) \leq 0. \end{align*} $$
Proof. Observe that for all j and n we have
$\lceil r_j n \rceil \in \{\phi _j(n) + k, \ |k| \leq A_j\} $
and
$\lceil c_j n \rceil \in \{\psi _j(n) + k, \ |k| \leq B_j\}$
. Thus,
$$ \begin{align*}|u^j_{\phi_j(n)}-u^j_{\lceil r_j n \rceil}| \leq \max_{|k| \leq A_j} |u^j_{\phi_j(n)}-u^j_{\phi_j(n)+k}| \underset{n\to \infty}{\longrightarrow} 0 \end{align*} $$
using the hypothesis on
$u^j$
above. Similarly,
$|u^j_{\psi _j(n)}-u^j_{\lceil c_j n \rceil }| \underset {n\to \infty }{\longrightarrow } 0$
. Now, conclude with [Reference Feng and Huang6, Lemma 5.4] or [Reference Kenyon and Peres8, Lemma 4.1].
Lemma B.4. Let
$\mu $
be a Borel probability measure on
$\Sigma _{m_1,m_2}$
. Suppose that
$\mu $
is exact dimensional with respect to the metric
$$ \begin{align*}\tilde{d}((x_k,y_k)_{k=1}^{\infty},(u_k,v_k)_{k=1}^{\infty}) = e^{-\min \{k \geq 1, \ (x_k,y_k) \neq (u_k,v_k)\}}, \end{align*} $$
with dimension
$\delta $
. Denote by
$\delta _2$
the lower Hausdorff dimension of
$\pi _* \mu $
with respect to the metric induced by
$\tilde {d}$
, and let
$\underline {\delta _1}$
and
$\overline {\delta _1}$
be the essential infimum and the essential supremum of the lower Hausdorff dimensions of the conditional measures
$\mu ^y$
with respect to
$\tilde {d}$
again, where
$\mu _y$
is obtained from the disintegration of
$\mu $
with respect to
$\pi _* \mu $
. Then, with respect to the metric d, for
$\mu $
-almost every point z, we have
$$ \begin{align*}\frac{\overline{\delta_1}}{\log(m_1)} + \frac{\delta_2}{\log(m_2)} &\leq \underline{\dim}_{\mathrm{loc}}(\mu,z)\leq \overline{\dim}_{\mathrm{loc}}(\mu,z) \\&\leq \frac{\delta}{\log(m_2)} - \bigg(\frac{1}{\log(m_2)} - \frac{1}{\log(m_1)} \bigg) \underline{\delta_1}. \end{align*} $$
Thus, if
$\underline {\delta _1} = \overline {\delta _1}$
and
$\delta = \underline {\delta _1} + \delta _2$
, then
$\mu $
is exact dimensional with respect to d.
Proof. The first inequality follows from the proof of a result of Marstrand (see [Reference Falconer2, Theorem 5.8]), whereas the second inequality can be deduced from the proof of [Reference Feng and Hu5, Theorem 2.11].
