2. Simulation Setup

In this study, two-dimensional simulations are carried out with PIC codes named EPOCH [Reference Arber, Bennett and Brady29]. The size of the simulation domain is $x\times y=100{\lambda }_0\times 40{\lambda }_0$ , and it is divided into 5000 × 2000 cells, where λ ₀ is the vacuum laser wavelength. The grid mesh spacing is enough to resolve the minimum characteristic scale of the problem. The left boundary conditions of fields are so-called simple-laser, the top, bottom, and right conditions of fields, and the boundaries of particles are all open. A p-polarized laser pulse with wavelength of ${\lambda }_0=1.0\mathrm{\mu m}$ and waist 1.5 μm is incident from the left boundary of the simulation domain. It is focused to a focal spot at a distance of 6 μm from the left boundary. The laser pulse has a Gaussian spatial profile, and the pulse duration is 20T ₀, where $T_0=3.3fs$ is the laser period. The peak intensity is 2.2 × 10²¹W/cm², corresponding to the normalized vector potential a ₀ = 40.

The NCD plasma target consisted of electrons and fully ionized hydrogen. Its left boundary is placed at x = 6 μm, that is, the laser is focused at the front of the target. The length of the target between both ends is 50λ ₀, and the left end extends to the transverse boundaries of the simulation region. The density is $n_0=1.6n_c$ , where $n_c=m_e{\omega }_0^2/4\pi e^2$ is the critical density, m_e is the electron mass, and e is the unit charge, respectively. It has been confirmed that the acceleration effectiveness has a strong dependence on the target thickness and density for a given laser power, which is based on a simple analytical model for the behavior of the EM wave inside a waveguide. Thus, the target parameters in our simulations follow the optimum condition for MVA acceleration $n_e/n_c=\sqrt{8\pi P/P_c}{\left(K{L}_p/L_{ch}\right)}^{3/2}$ according to previous works [Reference Bulanov, Bychenkov and Chvykov22, Reference Zhao, Jiao and Xie27], where $L_p=c\tau$ is the laser pulse length, τ is the laser pulse duration, K = 1/10 is the geometrical factor for 2D cases, P is the laser power, $P_c=2m_e^2{c}^5/e^2=17GW$ is the critical power for relativistic self-focusing, n_e is the electron number density, and c is the speed of light in vacuum. A hollow high-Z metal cone, which is open at both ends, is used to confine near-critical plasmas. The high-Z cone is composed of uniform aluminum plasmas with a thickness of 1.0μm, which has the same longitudinal length with the NCD plasma target. For the convenience of computation, the electron density of the high-Z cone is set to be $45n_c$ . The target configuration is shown in Figure 1. The gap size of the cone tip d is equal to the diameter of the laser focal spot.

Figure 1: Scheme of target. The near-critical density plasma (gray) is confined in a hollow high-Z metal cone (red).

3. Simulation Results

The density profiles of proton and electron, the longitudinal electric field, the z-component of magnetic field, and the currents in x-axis direction at obvious vortex structure formation stage are presented to illustrate the MVA process. With the same setup including the laser and plasma parameters, the simulation of conventional MVA with a uniform rectangle target is performed as a comparison. The time-averaged electric field E_x and magnetic field B_z in conical target case are shown in Figures 2(a) and 2(b). The electric field and magnetic field are normalized by $m_e{\omega }_{0}c/e$ and $m_e{\omega }_0/e$ , respectively. It is clear that the electric field and magnetic field are located at the rear side of the target in uniform rectangle target case, however, near the end of the cone in conical target case.

Figure 2: Snapshots of the time-averaged electric field E_x ((a), (d)) normalized by $m_e{\omega }_{0}c/e$ , the z-component of magnetic field B_z, ((b), (e)) normalized by $m_e{\omega }_0/e$ and currents in x-axis direction J_x, and ((c), (f)) normalized by ecn_c at t = 85T ₀ for the conical target (top) and the uniform rectangle target (bottom).

As shown in Figures 2(c) and 2(f), the current density along the central axis of the channel is approximately equal to the return current flowing in the walls of the channel, which can screen the magnetic field outside the channel. The electromagnetic energy is perfectly confined inside the self-generated channel, as discussed in previous studies [Reference Park, Bulanov and Bin30]. The self-generated magnetic field plays an important role in proton acceleration by the MVA mechanism. It can be clearly seen that the growth of the electric field is related to the expansion of the magnetic field. The magnetic field pushes out electrons causing a long-living positively charged region and induces a longitudinal electric field. This structure moves together with the expanding dipole vortex. The resulting charge-separation electric field will accelerate and collimate ions from the thin filament. As mentioned in [Reference Nakamura, Bulanov, Esirkepov and Kando19], the electric field moves together with the expanding magnetic dipole vortex, and the background ions located ahead of the electric field are reflected by the moving potential and gain velocity which is roughly twice the velocity of vortex. It is easy to notice the approximately similar distributions pattern between self-generated magnetic field B_z and electric field E_x. By comparison, the magnetic field in conical target is attached the cone wall, and the electric field is more concentrated. In the density profile of proton, a proton filament is produced along the laser axis behind the cone tip gap.

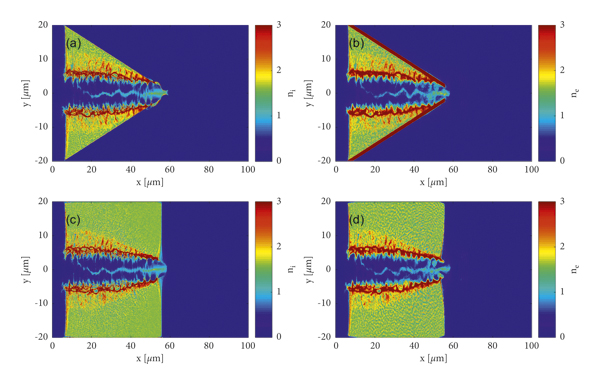
Figure 3 shows the electron and proton density profile of two cases at t = 85T ₀, which are normalized by n_c. The laser pulse passes through plasma and creates a channel in both electron and ion density. There forms a thin proton filament along the central axis. The protons from the filamentation get acceleration by the longitudinal quasistatic electric field. It can be seen that the density of filament near the cone tip is higher than that in the rear of uniform rectangle target.

Figure 3: Snapshots of ion density (a) and electron density (b) for the conical target and ion density (c) and electron density (d) for the uniform rectangle target at t = 85T ₀ MVA, which are normalized by n_c.

The snapshots of phase space of protons in the uniform rectangle target and the conical target at t = 160T ₀ are shown in Figure 4. The phase plot of proton displays a ramp momentum distribution, which indicates that the acceleration of the proton occurs behind the target. As shown in Figure 4(a), it can be noted that the maximum proton momentum in conical target reaches $0.68m_{p}c$ and the corresponding proton energy is approximately 220MeV, which is consistent with the cutoff energy of the energy spectrum shown in Figure 5. The maximum proton momentum in uniform rectangle target is $0.6m_{p}c$ in Figure 4(b), obviously lower than that in conical target. The difference of both cases approaches about 10%.

Figure 4: Snapshots of phase space (p_x − x) of protons in the conical target (a) and the uniform rectangle target (b) at t = 160T ₀. The momentum is normalized by $m_{p}c$ , where m_p is the proton mass, and c is the speed of light in vacuum.

Figure 5: The proton energy spectra of the conical target with different gap sizes (d = 5.0, 3.0, 2.0, 1.0, 0.5μm) and the uniform rectangle targets (r target) at the final stage t = 160T ₀.

In Figure 6, angular divergence is displayed between these two cases. The r target represents the uniform rectangle target and the c target represents the conical target. Such a narrow angular dispersion is the typical characteristic feature of MVA, which makes it possible to get a promising candidate for an ion source for hadron cancer therapy [Reference Bulanov, Esarey and Schroeder31]. Apparently, the angular distribution of proton beams from conical target is more concentrated to the central axis. Meanwhile, the number of protons within 0.1π divergence angle in the conical target is larger than that in the uniform rectangle target. It is evident that the confinement effect of conical target helps to improve the collimation of proton beams.

Figure 6: The angle distributions (with respect to the laser axis) of protons in the uniform rectangle target (r target) and the conical target (c target) at t = 160T ₀.

Finally, in order to investigate the effect of different gap sizes of cone tip to MVA, our simulations are carried out for several cases corresponding d = 5.0, 3.0, 2.0, 1.0, 0.5μm, in which the gap size is of the order of the diameter of the laser focal spot size. The energy spectra of accelerated protons in different cases are shown in Figure 5. It can be clearly seen that the proton cutoff energy in the conical target is higher than that in the rectangle target. However, as the gap width decreases from 3.0μm to 0.5μm, the cutoff energy decreases. Obviously, smaller gap sizes of cone tip do not mean more enhanced MVA. It can be explained that small gap may make against the formation of plasmas channel, and thus, MVA would be affected. Therefore, it is suggested that gap size of cone tip prefers to be the size of the laser focal spot.

4. Summary

The effects of a NCD plasma with a conical target or a uniform rectangle target on the MVA mechanism are studied in this study. The simulations are carried out for a tightly focused high-intensity laser pulse interaction with near-critical density plasma inside a hollow conical target. The results prove that the conical guiding structure is helpful for the generation of high-energy protons. For typical laser and plasma parameters, the magnetic vortex structure forms at the density gradient and induces charge-separation electric field between electrons and protons to accelerate protons to a peak energy of 220 MeV. It also shows the enhancement of magnetic vortex acceleration on the collimation and cutoff energy of proton beams. By using conical target, the near-critical density plasmas are confined in a high-Z cone. The electric field and magnetic field at the rear side of the target get more localized. As a result, the accelerated protons get more collimated and more energetic. Besides, the optimal gap size of conical target tip is supposed to match the size of the laser focal spot in order to improve MVA.