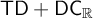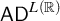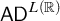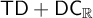1. Introduction
There are two known proofs that
$\mathsf {TD}+\mathsf {DC}_{\mathbb {R}}$
imply
$\mathsf {AD}^{L(\mathbb {R})}$
both due to Woodin. The later proof involves proving the stronger result of Suslin determinacy from Turing determinacy +
$\mathsf {DC}_{\mathbb {R}}$
directly [Reference Hugh Woodin1]. Combining that with Kechris and Woodin’s theorem that Suslin determinacy in
$L(\mathbb {R})$
implies
$\mathsf {AD}^{L(\mathbb {R})}$
[Reference Kechris and Hugh Woodin2], the desired result becomes an immediate corollary.
Woodin’s original proof uses an early version of the core model induction (CMI) technique. Through the work of many set theorists, the CMI has been developed into a proper framework for proving determinacy results from non-large cardinal hypotheses such as generic elementary embeddings, forcing axioms, and the failure of fine-structural combinatorial principles. The technique as it is understood in
$L(\mathbb {R})$
-like models (i.e.,
$L(\mathbb {R}^g)$
where
$\mathbb {R}^g$
are the reals of a symmetric collapse) can be seen as an inductive method by which one proves
$J_\alpha (\mathbb {R})\models \mathsf {AD}$
for all
$\alpha $
. An introduction to this as well as all terminology used in this paper can be found in Schindler and Steel’s book [Reference Schindler and Steel7].
This paper aims to prove that
$\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$
implies
$\mathsf {AD}^{L(\mathbb {R})}$
using modern perspectives on the core model induction in
$L(\mathbb {R})$
. The key lemma is a modification of a well-known theorem of Kechris and Solovay to work in the
$\mathsf {TD}$
context. Utilizing the proof of the witness dichotomy it is sufficient to just prove the
$J\mapsto M_1^{\#,J}$
step of the core model induction.
2. Rough background
2.1. Determinacy
Given some
$A\subseteq \omega ^\omega $
the Gale–Stewart game
$G_\omega (A)$
is defined to be the perfect information game where two players
$\mathbf {I}$
and
$\mathbf {II}$
take turns playing digits
$x_n\in \omega $
for
$\omega $
turns as written:
This results in the infinite sequence
$x = (x_0,x_1,\ldots )\in \omega ^\omega $
. We say that
$\mathbf {I}$
wins if
$x\in A$
, otherwise we say
$\mathbf {II}$
wins. A player is said to have a winning strategy provided they can ensure themselves a win regardless of how their opponent plays. A game
$G_\omega (A)$
is determined if a player has a winning strategy.
Definition 2.1. The axiom of determinacy
$\mathsf {AD}$
states that for every
$A\subseteq \omega ^\omega $
,
$G_\omega (A)$
is determined.
One of the earliest remarkable consequences of
$\mathsf {AD}$
is Martin’s cone theorem. We say that
$\mathbf A\subseteq \mathcal D$
is a cone if there is some
$\mathbf {x}\in \mathcal D$
such that
$\mathbf A = \{\mathbf {a}\mid \mathbf {a}\geq _{\mathcal {D}}\mathbf x\}$
.
Theorem 2.2 [Reference Martin4]
Assume
$\mathsf {AD}$
. Suppose that
$\mathbf A\subseteq \mathcal D$
. Then either
$\mathbf A$
or
$\mathbf A^c$
contains a Turing cone.
Proof Consider the set
$A = \{x\in \mathbb {R}\mid [x]_T\in \mathbf A\}$
. As this is a set of reals it’s determined, so assume that player I has a winning strategy
$\sigma $
. Then for any
$x\geq _T\sigma $
we have that
$x\equiv _T\sigma *x\in A$
. Therefore,
$\{x\mid x\geq _T\sigma \}\subseteq A$
and
$\{\mathbf x\mid \mathbf x\geq _{\mathcal {D}}[\sigma ]_T\}\subseteq \mathbf A$
. If player II has a winning strategy
$\tau $
, then there is an almost identical argument that
$\mathbf A^c$
contains a Turing cone above
$[\tau ]_T$
.
The axiom of Turing determinacy (
$\mathsf {TD}$
) is the isolation of the consequence of this theorem, e.g., that every set of Turing degrees contains or is disjoint from a cone.
2.2. Core model theory
The core model theory required in a core model induction is largely summarized by the
$K^J$
existence dichotomy. This is a straightforward generalization of the typical K existence dichotomy to a hierarchy of relativized mice. These relativized mice, called hybrid mice, abstract the use of the rudimentary closure to take a one step in the constructibility hierarchy to the use of some “model operator” J with similar enough properties. Examples of model operators include:
-
•
$x\mapsto \text {rud}(x\cup \{x\})$
; -
• Mouse operators, e.g., the sharp operator, the one Woodin cardinal operator;
-
• Hybrid mouse operators, e.g., term-relation hybrid mouse operators from self-justifying systems, strategy hybrid mouse operators.
For an exposition of operator mice in the style of this paper one can read either Chapter 1 of [Reference Schindler and Steel7] or Sections 2.1–2.3 of [Reference Wilson11]. For the sake of this paper, the full definition of a mouse operator is not that important.
An important property all model operators of interest have is that they “condense well.” Condensing well is a technical condition ensuring that one can develop a fine structure for structures built in terms of J, i.e., one can perform background constructions relativized to J that behave in the same manner as they do with the rudimentary closure. In particular, J condensing well implies that the models constructed in a
$K^{c,J}$
construction are J-premice and there is a relativized core model theory.
Theorem 2.3. (
$K^J$
existence dichotomy)
Let
$\Omega $
be a measurable cardinal. Let J be a model operator with real parameter z on
$H_\Omega $
which condenses well. Let
$\mathcal P$
be countable model with parameter z and let
$K^{c,J}(\mathcal P) = K^{c,J}(\mathcal P)|\Omega $
. Then the following statements are true
$:$
-
1. If the
$K^{c,J}(\mathcal P)$
construction reaches
$M_1^{\#,J}(\mathcal P)$
, then
$M_1^{\#,J}(\mathcal P)$
is
$(\omega ,\Omega ,\Omega +1)$
-iterable via the unique strategy guided by
$J^\#$
, i.e., the sharp for
$L^{J}$
. -
2. If the
$K^{c,J}(\mathcal P)$
construction does not reach
$M_1^{\#,J}(\mathcal P)$
, then
$K^{c,J}(\mathcal P)$
is
$(\omega ,\Omega , \Omega +1)$
-iterable. This implies that
$K^J(\mathcal P)$
exists and is
$(\omega ,\Omega ,\Omega +1)$
-iterable via the unique strategy guided by
$J^\#$
.
In this case, the “true”
$K^J(\mathcal P)$
is defined as in [Reference Steel9], the only real change being that one has to relativize all notions considered there to the model operator J.
All model operators encountered in the core model induction condense well. Additional properties possessed by all model operators encountered in the core model induction are that they relativize well and determine themselves on generic extensions.
Definition 2.4. We say that a model operator J relativizes well if there is a formula
$\varphi (x,y,z)$
such that for any
$\mathcal N,\mathcal N'$
models such that
$\mathcal N\in |\mathcal N'|$
and
$\mathcal {M}$
a J-premouse with base model
$\mathcal N'$
such that
$\mathcal {M}\models \mathsf {ZFC}^-$
, then
$J(\mathcal N)\in \mathcal M$
and
$J(\mathcal N)$
is the unique
$x\in |\mathcal M|$
such that
$\varphi (x,\mathcal N,J(\mathcal N'))$
.
Definition 2.5. We say that J determines itself on generic extensions if there is a formula
$\phi (x,y,z)$
and some parameter
$c\in HC$
such that for any countable transitive structure
$\mathcal M$
satisfying
$\mathsf {ZFC}^-$
containing c and closed under J, for any generic extension
$\mathcal M[g]$
of
$\mathcal M$
in V,
$J\cap \mathcal M[g]\in M[g]$
and is definable via
$b = J(a)$
iff
$\mathcal M[g]\models \phi (c,a,b)$
.
3. Kechris–Solovay theorem
The following is our primary lemma which is a modification on a theorem of Kechris and Solovay [Reference Kechris and Solovay3]. Given a set of ordinals S,
$\mathsf {OD}_S$
-Turing determinacy (i.e.,
$\mathsf {OD}_S$
-
$\mathsf {TD}$
) is the assertion that every set of Turing degrees ordinal definable with S as an additional parameter contains or is disjoint from a Turing cone.
Lemma 3.1. Assume
$\mathsf {\mathsf {TD}}$
. For any set of ordinals S, on a Turing cone
$\mathcal C$
the following holds for
$x\in \mathcal C$
:
$$ \begin{align*}L[S,x]\models\mathsf{OD}_{{S}}\text{-}\mathsf{\mathsf{TD}}.\end{align*} $$
Proof Assume for a contradiction that there is no cone of reals on which
$L[S,x]\models \mathsf {OD}_{S}\text {-}\mathsf {\mathsf {TD}}$
. Then we can define, on a cone
$\mathcal C$
, the map
$x\mapsto A_x$
where
$A_x$
is the least
$\mathsf {OD}_{S}^{L[S,x]} \equiv _T$
-invariant subset of
$\mathbb R$
which doesn’t contain a Turing cone and whose complement does not contain a Turing cone in
$L[S,x]$
. Notice that
$A_x$
only depends on the S-constructibility degree of x.
It is clear from the last observation that the set
$\{x\in \mathbb R\mid x\in A_x\}$
is
$\equiv _T$
-invariant and is well-defined on
$\mathcal C$
. Suppose that this set contains a Turing cone
$\mathcal C'$
. Consider some arbitrary
$y\in \mathcal C\cap \mathcal C'$
, if
$w\geq _{T} z\geq _{T} y$
and
$w\in L[S,z]$
then we have that
$w\in A_w = A_z$
. So
$A_z$
contains a Turing cone in
$L[S,z]$
. We reach a similar conclusion if we assume that
$\{x\in \mathbb R\mid x\not \in A_x\}$
contains a Turing cone. Contradiction.
Ordinal (Turing) determinacy has the following well-known consequence:
Corollary 3.2.
$\mathsf {\mathsf {HOD}}_{{S}}^{L[S,x]}\models \text {" }\omega _1^{L[S,x]}\text { is measurable"}$
for a cone of x.
Proof outline
This proof is standard, but for the sake of completeness it will be sketched. We work inside
$L[S,x]$
and assume that
$\mathsf {OD}_{S}\text {-}\mathsf {\mathsf {TD}}$
holds. Let f be the function
$f : x\mapsto \omega _1^x$
which maps x to the least x-admissible ordinal, then we can define
$\mu $
as the pushforward of the cone filter under f, i.e.,
$A\in \mu $
iff
$f^{-1}(A)\text { contains a Turing cone}$
. Clearly
$\mu $
is countably closed and, by assumption,
$\mu $
restricts to an ultrafilter on
$P(\omega _1)\cap \mathsf {OD}_S$
. The cone measure and the map f are both definable, so
$\mathsf {\mathsf {HOD}}_{S}\cap \mu \in \mathsf {\mathsf {HOD}}_{S}$
witnesses that
$\omega _1^{V}$
is measurable in
$\mathsf {\mathsf {HOD}}_S$
.
4. The existence of
$M_1^\#$
The following consequences of
$\Delta ^1_2$
-
$\mathsf {\mathsf {TD}}$
are proven by modifying the analogous arguments from
$\Delta ^1_2$
-
$\mathsf {Det}$
in a similar fashion to the core argument of Theorem 3.1 then verifying that nothing breaks. As the modifications are relatively straightforward the proofs will not be included.
-
• (Martin) Assume
$\Delta ^1_2$
-
$\mathsf {TD + DC}$
, then
$\Pi ^1_2\text {-}\mathsf {\mathsf {TD}}$
. -
• (Kechris–Solovay) Assume
$\Delta ^1_2$
-
$\mathsf {TD + DC}$
, then for any real y, on a Turing cone
$x\in \mathcal C$
the following holds for
$x\in \mathcal C$
:
$$ \begin{align*}L[x,y]\models\mathsf{OD}_{{y}}\text{-}\mathsf{TD}.\end{align*} $$
-
• (Consequence of Kechris–Woodin [Reference Kechris and Hugh Woodin2]) Assume
$\Delta ^1_2$
-
$\mathsf {TD {\kern-1pt}+{\kern-1pt} DC}$
and
$(\forall x{\kern-1pt}\in{\kern-1pt} \mathbb {R}) x^\#\text { exists}$
, then
$\operatorname {Th}(L[x])$
is fixed on a Turing cone.
We can utilize these three observations to prove the first step in our induction from a weaker hypothesis.
Theorem 4.1. Assume
$\Delta ^1_2$
-
$\mathsf {TD + DC}$
and
$(\forall x\in \mathbb {R})\: x^\#\text { exists}$
, then
$M_1^\#$
exists and is
$\omega _1$
-iterable.
Proof Utilizing lemma 3.1 we have that
$L[x]\models \mathsf {OD}\text {-}\mathsf {\mathsf {TD}}$
on a Turing cone. Let x be the base of such a cone and fix the least x-indiscernible
$i^x_0 < \omega _1^V$
. The measure U on
$i^x_0$
given by
$x^\#$
is sufficient for the construction of the Steel core model K (as described in CMIP [Reference Steel9]) in
$L[x]$
below
$i^x_0$
. Suppose that the
$K^c$
construction below
$i^x_0$
in
$L[x]$
does not reach an
$M_1$
-like premouse, then there is a U-measure one set of
$\alpha < i_0$
we have that
$L[x]\models (\alpha ^+)^K = \alpha ^+$
. Select such an
$\alpha $
and let
$z = \left <x,g\right>$
where g is
$L[x]$
-generic for
$Coll(\omega ,\alpha )$
. Working in
$L[z]$
, K exists, is inductively definable, and
$\omega _1$
is a successor cardinal in K. As
$z\geq _T x$
we have that
$L[z]\models \mathsf {OD}\text {-}\mathsf {\mathsf {TD}}$
; therefore,
$HOD^{L[z]}\models \omega _1\text { is measurable}$
. But as
$K^{L[z]}\subseteq HOD^{L[z]}$
we have a contradiction. Therefore we have that the
$K^c$
construction of
$L[x]$
below
$i^x_0$
reaches an
$M_1$
-like premouse on a cone.
Utilizing the limit branch construction described in Theorem 4.16 of HOD as a Core Model [Reference Steel and Hugh Woodin10] there is an
$\omega _1$
-iterable
$M_1^{\#}$
.
Note that by [Reference Neeman5], the
$\omega _1$
-iterability of
$M_1^\#$
is enough to prove
$\Delta ^1_2$
-determinacy. So in fact we get an equivalence of
$\Delta ^1_2\text{-}\mathsf {TD}$
and
$\Delta ^1_2$
-determinacy under
$\mathsf {ZF+DC}$
.
5. The
$J\mapsto M^{\#,J}_1$
step
Following this point on the argument is identical to that of Steel and Schindler. But I will rewrite it (practically verbatim) for the sake of completeness. For the rest of this argument we will assume
$\mathsf {ZF} + \mathsf {TD} + \mathsf {DC} + V = L(\mathbb {R})$
. Recall that every (hybrid) model operator considered in the core model induction relativizes well and determines itself on generic extensions.
Theorem 5.1. Let
$a\in \mathbb {R}$
and let J be a (hybrid) model operator that condenses well, relativizes well, and determines itself on generic extensions, and suppose that
$$ \begin{align*}W_x = \left(K^{c,J}(a)\right)^{\mathsf{\mathsf{HOD}}_{a}^{L^{J^{\#}}[x]}}\end{align*} $$
constructed with height
$\omega _1^V$
exists for a cone of x. Then there is a cone of x such that
$W_x$
cannot be
$\omega _1^V+1$
iterable above a inside
$\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[x]}$
.
Proof Assume for a contradiction that this is not the case. Then there is a cone
$\mathcal {C}$
such that for all
$x\in \mathcal C$
we have
$L^{J^{\#}}[a,x] = L^{J^{\#}}[x]$
and
$$ \begin{align*}\omega_1^{L^{J^{\#}}[x]}\text{ is measurable in }\mathsf{\mathsf{HOD}}_{a}^{L^{J^{\#}}[x]}\end{align*} $$
and so we can isolate
$K^{J}_x = \left (K^{ J}(a)\right )^{\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[x]}}$
. Furthermore, we can assume that any element of
$\mathcal {C}$
can compute the code for the parameter c which witnesses that J determines itself on generic extensions. Fixing some
$x\in \mathcal C$
we will write
$K^{ J}$
for
$K^{ J}_x$
.
Claim 5.2. The universe of
$L^{J^{\#}}[x]$
is a size
${<}{\omega}_1^V$
forcing extension of
$\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
.
Proof The observation we want to make is that
$L^{J^{\#}}[x]$
is the result of adding x to
$\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
via Vopenka forcing. Suppose that
$\mathbb {V}$
is the Vopenka forcing and
$\tau $
is a name for x, then as
$\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
is
$J^\#$
-closed and contains the parameter c, it contains
$L^{J^{\#}}(\mathbb {V},\tau ,c)$
as an inner model. Letting
$g\in L^{J^{\#}}[x]$
be generic such that
$\tau _g = x$
, we have that
$x\in L^{J^{\#}}(\mathbb {V},\tau ,a)[g]$
. Using that
$J^\#$
determines itself on generic extensions and relativizes well, we can then reconstruct
$L^{J^{\#}}[x]$
inside
$L^{J^{\#}}(\mathbb {V},\tau ,a)[g]$
. So the universe of
$\mathsf {HOD}^{L^{J^{\#}}[x]}_{a,x}$
and
$L^{J^{\#}}[x]$
are identical. The Vopenka forcing to add a real over
$\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
is of size
$<\omega _1^V$
as
$\omega _1^V$
is inaccessible in
$L^{J^{\#}}[x]$
.
By cheapo covering and the claim we can choose some
$\lambda < \omega _1^V$
above the size of the forcing such that
$$ \begin{align*}\lambda^{+K^{ J}} = \lambda^{+\mathsf{HOD}^{L^{J^{\#}}[x]}_{a}} = \lambda^{+L^{J^{\#}}[x]}.\end{align*} $$
Let
$g\in V$
be
$Col(\omega ,\lambda )$
-generic over
$L^{J^{\#}}[x]$
and let
$y\in V$
be a real coding
$(g,x)$
. As J determines itself on generic extensions we have that
$L^{J^{\#}}[y] = L^{J^{\#}}[x][g]$
. Therefore,
$$ \begin{align*}\omega_1^{L^{J^{\#}}[y]} = \lambda^{+K^{J}} = \lambda^{+L^{J^{\#}}[x]}.\end{align*} $$
As
$y\in \mathcal C$
we have that
$$ \begin{align*}\omega_1^{L^{J^{\#}}[y]}\text{ is measurable in }\mathsf{\mathsf{HOD}}^{L^{J^{\#}}[y]}_{a}.\end{align*} $$
We reach a contradiction if we can demonstrate the following claim:
Claim 5.3.
$K^{ J}\in \mathsf {\mathsf {HOD}}^{L^{J^{\#}}[y]}_{a}$
.
Proof This claim is a verification that the proofs in Chapter 5 of CMIP [Reference Steel9] work given that J condenses well.
$K^{ J}$
is still fully iterable inside
$L^{J^{\#}}[y]$
because it has no Woodin cardinals (above a) and J condenses well so its strategy is guided by
$J^\#$
. This implies that
$K^{ J}$
is still the core model above a of
$L^{J^{\#}}[y]$
, i.e., it is the common transitive collapse of
$Def(W,S)$
for any
$W,S$
such that W is an
$\omega _1^V$
-iterable
$ J$
-weasel and
$\omega _1^V$
is S-thick. Using this characterization we can conclude that
$K^{ J}\in \mathsf {\mathsf {HOD}}^{L^{J^{\#}}[y]}_{a}$
.
Utilizing this theorem we wish to show
$\forall \alpha \;W^*_\alpha $
. Suppose that for some fixed critical
$\alpha $
,
$W_\alpha ^*$
holds, we wish to show that
$W^*_{\alpha +1}$
holds. By the witness dichotomy (Theorem 3.6.1 of [Reference Schindler and Steel7]) this means that we need to see that for all
$n<\omega $
,
$J^n_\alpha $
is total on
$\mathbb {R}$
. Suppose that
$\mathbb {R}$
is closed under
$J = J^n_\alpha $
. To utilize Theorem 5.1 we first need to close
$\mathbb {R}$
under
$J^\#$
. As we’re assuming
$\mathsf {DC}$
the Martin measure ultrapower is well-founded, so as J relativizes well we have that
$Ult(L^{J},\mu _{Tu}) = L^{J}$
and
$J^\#$
exists (a full proof along these lines can be found in Theorem 28 of [Reference Steel and Zoble8]). One could avoid the use of
$\mathsf {DC}$
by instead working inside
$\mathsf {HOD}^{L^{J}[x]}$
and utilizing the measurable cardinal on
$\omega _1^{L^{J}[x]}$
.
Now we can show that
$\mathbb {R}$
is closed under
$J^{n+1}_\alpha $
. Let us fix
$a\in \mathbb {R}$
. By Theorem 5.1, for any (hybrid) model operator J which relatives well and determines itself on generic extensions there is a cone of b on which
$$ \begin{align*}W_b = \left(K^{c, J}(a)\right)^{\mathsf{\mathsf{HOD}}_{a}^{L^{J^{\#}}[b]}}\end{align*} $$
cannot be
$\omega _1^V+1$
iterable inside
$\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[b]}$
. Let b lie in this cone, by applying the
$K^J$
existence dichotomy internal to
$\mathsf {HOD}_{a}^{L^{J^{\#}}[b]}$
we must have that the
$K^{c,J}(a)$
construction reaches
$M_1^{J,\#}(a)$
and
$M_1^{J,\#}(a)$
is
$\omega _1+1$
iterable in
$\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[b]}$
. In summary, we can define the following map on a cone:
$$ \begin{align*}b\mapsto (M_1^{J,\#}(a))^{\mathsf{HOD}_{a}^{L^{J^{\#}}[b]}}.\end{align*} $$
Consider the map
$f:\mathcal D\to \mathbb {R}$
given by
$$ \begin{align*}[b]\mapsto\text{the master code for }(M_1^{J,\#}(a))^{\mathsf{HOD}_{a}^{L^{J^{\#}}[b]}}.\end{align*} $$
By
$\mathsf {\mathsf {TD}}$
, for each
$n<\omega $
the set
$\{b\in \mathbb {R} : n\in f([b])\}$
either contains a cone or is disjoint from a cone. Let
$n\in \mathcal P$
iff
$n\in f([b])$
on a cone, then by countable choice for the reals
$f([b]) = \mathcal {P}$
on a cone.
One can see that
$\mathcal P$
is
$\omega _1$
iterable in V: if
$\mathcal T$
is a countable tree on
$\mathcal P$
of limit length, then the good branch through
$\mathcal T$
is the one picked by the strategies of
$\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[b]}$
on a cone. Turing determinacy allows us to extend this to an
$\omega _1+1$
-iteration strategy using the measurability of
$\omega _1$
; therefore,
$\mathcal P$
is the actual
$M_1^{J,\#}(a)$
. From this, the map
$a\mapsto J^{n+1}_\alpha (a) := M_1^{J,\#}(a)$
can be defined.
Note 5.4. Given a model operator J, in The Core Model Induction [Reference Schindler and Steel7] the operators
$J^{n}$
are defined as
$M^{J,\#}_n$
. This is not literally equal but intertranslatable with the hierarchy where
$J^{n+1} = M^{J^n,\#}_1$
as utilized above.
Note 5.5. The strongest choice principle necessary in the above argument is
$\mathsf {CC}_{\mathbb {R}}$
(which follows from
$\mathsf {TD}$
[Reference Peng and Yu6]); however, the assumption
$L(\mathbb {R})\models \mathsf {\mathsf {DC}}$
seems to be necessary for the guts of the core model induction. In particular, it’s used in both the Kechris–Woodin transfer theorem and in the A-iterability proof.
Acknowledgements
The author would like to thank Woodin for giving permission to write up this result. He would also like to thank Schindler and Steel for reading over the proof and giving several helpful suggestions.
