1 Introduction
Nowadays, research activities in the field of plasma-based particle acceleration are shifting from the investigation of fundamental processes aimed at understanding and optimizing the acceleration mechanism, to the actual practical implementation of such promising technologies. For example, laser wake-field acceleration (LWFA) is foreseen as being implemented in user-oriented facilities to deliver high-quality GeV electron bunches[Reference Walker, Alesini, Alexandrova, Anania, Andreev, Andriyash, Aschikhin, Assmann, Audet, Bacci, Barna, Beaton, Beck, Beluze, Bernhard, Bielawski, Bisesto, Boedewadt, Brandi, Bringer, Brinkmann, Bründermann, Büscher, Bussmann, Bussolino, Chance, Chanteloup, Chen, Chiadroni, Cianchi, Clarke, Cole, Couprie, Croia, Cros, Dale, Dattoli, Delerue, Delferriere, Delinikolas, Dias, Dorda, Ertel, Ferran Pousa, Ferrario, Filippi, Fils, Fiorito, Fonseca, Galimberti, Gallo, Garzella, Gastinel, Giove, Giribono, Gizzi, Grüner, Habib, Haefner, Heinemann, Hidding, Holzer, Hooker, Hosokai, Irman, Jaroszynski, Jaster-Merz, Joshi, Kaluza, Kando, Karger, Karsch, Khazanov, Khikhlukha, Knetsch, Kocon, Koester, Kononenko, Korn, Kostyukov, Labate, Lechner, Leemans, Lehrach, Li, Li, Libov, Lifschitz, Litvinenko, Lu, Maier, Malka, Manahan, Mangles, Marchetti, Marocchino, Martinez de la Ossa, Martins, Massimo, Mathieu, Maynard, Mehrling, Molodozhentsev, Mosnier, Mostacci, Mueller, Najmudin, Nghiem, Nguyen, Niknejadi, Osterhoff, Papadopoulos, Patrizi, Pattathil, Petrillo, Pocsai, Poder, Pompili, Pribyl, Pugacheva, Romeo, Rossi, Roussel, Sahai, Scherkl, Schramm, Schroeder, Schwindling, Scifo, Serafini, Sheng, Silva, Silva, Simon, Sinha, Specka, Streeter, Svystun, Symes, Szwaj, Tauscher, Thomas, Thompson, Toci, Tomassini, Vaccarezza, Vannini, Vieira, Villa, Wahlström, Walczak, Weikum, Welsch, Wiemann, Wolfenden, Xia, Yabashi, Yu, Zhu and Zigler1, Reference Toth, Evans, Gonsalves, Kirkpatrick, Magana, Mannino, Mao, Nakamura, Riley, Steinke, Sipla, Syversrud, Ybarrolaza and Leemans2] which are typically obtained from multiple laser-plasma stages (for example, injectors and accelerators), and should be suitable for injection in a free-electron laser (FEL). Also, beam-driven plasma wake-field acceleration is considered as a suitable candidate for 1 GeV injectors in compact FEL facilities[Reference Ferrario, Alesini, Anania, Artioli, Bacci, Bartocci, Bedogni, Bellaveglia, Biagioni, Bisesto, Brandi, Brentegani, Broggi, Buonomo, Campana, Campogiani, Cannaos, Cantarella, Cardelli, Carpanese, Castellano, Castorina, Catalan Lasheras, Chiadroni, Cianchi, Cimino, Ciocci, Cirrincione, Cirrone, Clementi, Coreno, Corsini, Croia, Curcio, Costa, Curatolo, Cuttone, Dabagov, Dattoli, DAuria, Debrot, Diomede, Drago, Di Giovenale, Di Mitri, Di Pirro, Esposito, Faiferri, Ficcadenti, Filippi, Frasciello, Gallo, Ghigo, Giannessi, Giribono, Gizzi, Grudiev, Guiducci, Koester, Incremona, Iungo, Labate, Latina, Licciardi, Lollo, Lupi, Manca, Marcelli, Marini, Marocchino, Marongiu, Martinelli, Masciovecchio, Mastino, Michelotti, Milardi, Minicozzi, Mira, Morante, Mostacci, Nguyen, Pagnutti, Pellegrino, Petralia, Petrillo, Piersanti, Pioli, Polese, Pompili, Pusceddu, Ricci, Ricci, Rochow, Romeo, Rosenzweig, Rossetti Conti, Rossi, Rotundo, Sabbatini, Sabia, Sans Plannell, Schulte, Scifo, Scuderi, Serafini, Spataro, Stecchi, Stella, Shpakov, Stellato, Turco, Vaccarezza, Vacchi, Vannozzi, Variola, Vescovi, Villa, Wuensch, Zigler and Zobov3].
In this context the definition and deployment of appropriate diagnostic tools for efficient and reliable monitoring of the main process parameters are of paramount importance to fulfill the goal of a functional user-oriented facility. In fact, robust and possibly real-time diagnostic tools are needed for the implementation of the adequate control procedures that are necessary to achieve long-term stable operation of the accelerator.
Concerning the LWFA stages, one of the fundamental parameters is the particle number density in the gas used as the target medium and the free-electron density in the plasma thereby created. The gas can either be pre-ionized to form a plasma[Reference Hooker, Brunetti, Esarey, Gallacher, Geddes, Gonsalves, Jaroszynski, Kamperidis, Kneip, Krushelnick, Leemans, Mangles, Murphy, Nagler, Najmudin, Nakamura, Norreys, Panasenko, Rowlands-Rees, Schroeder, Tóth and Trines4] or photo-ionized by the initial part of the main high-intensity ultra-short driving laser pulse itself[Reference Palla, Baffigi, Brandi, Fulgentini, Koester, Labate, Londrillo and Gizzi5].
Here, an overview is given of existing optical diagnostics suitable for neutral gas and free-electron number density measurements in laser-plasma accelerator stages (LPA). Both interferometry, in its various configurations, and optical emission spectroscopy (OES), specifically Stark broadening and Raman shift measurements, are discussed. These techniques are analyzed, aimed at their implementation as robust and reliable diagnostics. The sensitivity (that is, the lowest density value that can be reliably measured) and ease of implementation and operation are considered.
All interferometric methods require an appropriate optical line of sight through the sample. In the case of a freely expanding gas jet, interferometry is easy to implement, whereas in the case of confined samples (for example, gas cells and square cross-section capillaries), flat optical side windows are necessary to provide the optical path for transverse interferometry[Reference Hooker, Brunetti, Esarey, Gallacher, Geddes, Gonsalves, Jaroszynski, Kamperidis, Kneip, Krushelnick, Leemans, Mangles, Murphy, Nagler, Najmudin, Nakamura, Norreys, Panasenko, Rowlands-Rees, Schroeder, Tóth and Trines4, Reference Gonsalves, Rowlands-Rees, Broks, van der Mullen and Hooker6–Reference Hooker8]. If a transverse line of sight is not present (as in cylindrical capillaries), then longitudinal interferometry must be adopted, resulting in an average density value along the main laser beam propagation direction.
In contrast, optical emission spectroscopy does not require a line of sight through the sample, thus making it easy to implement[Reference Qin, Li, Liu, Liu, Yu, Wang, Qi, Zhang, Fang, Feng, Wu, Ke, Chen, Wang, Li and Xu9]. OES can be performed both longitudinally or transversely to the main laser beam and, if imaging spectrometers are used, information on the space-dependent density can be obtained from a single measurement.
Both pure gases and gas mixtures[Reference Mirzaie, Li, Zeng, Hafz, Chen, Li, Zhu, Liao, Sokollik, Liu, Ma, Chen, Sheng and Zhang10] have been used in laser-plasma acceleration studies, with a very promising medium to obtain high-quality GeV electron bunches being hydrogen[Reference Hooker, Brunetti, Esarey, Gallacher, Geddes, Gonsalves, Jaroszynski, Kamperidis, Kneip, Krushelnick, Leemans, Mangles, Murphy, Nagler, Najmudin, Nakamura, Norreys, Panasenko, Rowlands-Rees, Schroeder, Tóth and Trines4, Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Tóth, Daniels, Mittelberger, Bulanov, Vay, Geddes and Esarey11]. Therefore, we consider hydrogen gas here, with densities in the range
![]() $10^{17}{-}10^{19}~\text{cm}^{-3}$
being well suited for LWFA. In general, the number density of free electrons in the plasma can be estimated from measurements of the neutral particle number density[Reference Kononenko, Lopes, Cole, Kamperidis, Mangles, Najmudin, Osterhoff, Poder, Rusby, Symes, Warwick, Wood and Palmer12]. Full ionization of a hydrogen molecule creates a pair of free electrons, and a straightforward relation exists between the neutral hydrogen density and the free-electron density. Thus, estimation and, ultimately, control of the electron density can be implemented through the measurement of the molecular particle density within the target. In the case of a pre-formed plasma – for example, discharged gas-filled capillaries[Reference Schroeder, Benedetti, Esarey, van Tilborg and Leemans13] – a measurement of the actual plasma density has to be performed since, due to plasma dynamics[Reference Hooker, Brunetti, Esarey, Gallacher, Geddes, Gonsalves, Jaroszynski, Kamperidis, Kneip, Krushelnick, Leemans, Mangles, Murphy, Nagler, Najmudin, Nakamura, Norreys, Panasenko, Rowlands-Rees, Schroeder, Tóth and Trines4, Reference Schroeder, Benedetti, Esarey, van Tilborg and Leemans13], the local plasma density along the propagation path of the main laser beam is actually different from the background plasma density value obtained by assuming full ionization of the gas.
$10^{17}{-}10^{19}~\text{cm}^{-3}$
being well suited for LWFA. In general, the number density of free electrons in the plasma can be estimated from measurements of the neutral particle number density[Reference Kononenko, Lopes, Cole, Kamperidis, Mangles, Najmudin, Osterhoff, Poder, Rusby, Symes, Warwick, Wood and Palmer12]. Full ionization of a hydrogen molecule creates a pair of free electrons, and a straightforward relation exists between the neutral hydrogen density and the free-electron density. Thus, estimation and, ultimately, control of the electron density can be implemented through the measurement of the molecular particle density within the target. In the case of a pre-formed plasma – for example, discharged gas-filled capillaries[Reference Schroeder, Benedetti, Esarey, van Tilborg and Leemans13] – a measurement of the actual plasma density has to be performed since, due to plasma dynamics[Reference Hooker, Brunetti, Esarey, Gallacher, Geddes, Gonsalves, Jaroszynski, Kamperidis, Kneip, Krushelnick, Leemans, Mangles, Murphy, Nagler, Najmudin, Nakamura, Norreys, Panasenko, Rowlands-Rees, Schroeder, Tóth and Trines4, Reference Schroeder, Benedetti, Esarey, van Tilborg and Leemans13], the local plasma density along the propagation path of the main laser beam is actually different from the background plasma density value obtained by assuming full ionization of the gas.
For the numerical estimates of the interferometric phase shifts given in this work, the fundamental and second harmonic of a Ti:sapphire laser, at 800 nm and 400 nm, respectively, are considered as probe beams. However, the calculations can easily be extended to other gases and different probe beam wavelengths. If gases other than hydrogen are considered there still exists a direct relationship between the neutral gas number density and the background free-electron density in the plasma, which can be estimated by evaluating the degree of ionization using well-known photo-ionization models[Reference Palla, Baffigi, Brandi, Fulgentini, Koester, Labate, Londrillo and Gizzi5]. For instance, helium is another gas suitable for obtaining high-quality 1 GeV electron beams from LWFA[Reference Kim, Pathak, Pae, Lifschitz, Syllá, Shin, Hojbota, Lee, Sung, Lee, Guillaume, Thaury, Nakajima, Vieira, Silva, Malka and Nam14, Reference Hafz, Jeong, Choi, Lee, Pae, Kulagin, Sung, Yu, Hong, Hosokai, Cary, Ko and Lee15], in which more energy is necessary to get full ionization (two electrons per atom) compared to hydrogen molecules. If other lasers are used, the numerical values reported can be scaled easily by considering the wavelength-dependent index of refraction.
2 Interferometric methods
With interferometry, the density of a neutral gas or a plasma is evaluated by measurement of the phase shift acquired by an optical probe beam when passing through the sample relative to a known reference phase. The refractive index
![]() $\unicode[STIX]{x1D702}(n)$
of the sample is in fact dependent on the particle number density
$\unicode[STIX]{x1D702}(n)$
of the sample is in fact dependent on the particle number density
![]() $n$
, with the refractivity
$n$
, with the refractivity
![]() $\unicode[STIX]{x1D702}(n)-1$
actually being proportional to the particle number density
$\unicode[STIX]{x1D702}(n)-1$
actually being proportional to the particle number density
![]() $n_{g}$
in a gas and of free electrons
$n_{g}$
in a gas and of free electrons
![]() $n_{e}$
in a plasma. For neutral atoms/molecules, as from the Lorentz–Lorenz equation[Reference Born and Wolf16], the refractivity can be expressed as
$n_{e}$
in a plasma. For neutral atoms/molecules, as from the Lorentz–Lorenz equation[Reference Born and Wolf16], the refractivity can be expressed as
![]() $\unicode[STIX]{x1D702}_{g}(\unicode[STIX]{x1D706},n_{g})-1=[\unicode[STIX]{x1D702}_{0}(\unicode[STIX]{x1D706})-1]\times n_{g}/n_{0}$
, where
$\unicode[STIX]{x1D702}_{g}(\unicode[STIX]{x1D706},n_{g})-1=[\unicode[STIX]{x1D702}_{0}(\unicode[STIX]{x1D706})-1]\times n_{g}/n_{0}$
, where
![]() $\unicode[STIX]{x1D706}$
is the wavelength of the light and the reference value
$\unicode[STIX]{x1D706}$
is the wavelength of the light and the reference value
![]() $\unicode[STIX]{x1D702}_{0}(\unicode[STIX]{x1D706})$
is the refractive index at a specific number density
$\unicode[STIX]{x1D702}_{0}(\unicode[STIX]{x1D706})$
is the refractive index at a specific number density
![]() $n_{0}$
. The Loschmidt constant
$n_{0}$
. The Loschmidt constant
![]() $2.69\times 10^{19}~\text{cm}^{-3}$
, being the particle number density of a perfect gas at standard temperature and pressure (STP: 273.15 K and 1 atm), is typically used as a reference value. In an underdense plasma the refractivity is
$2.69\times 10^{19}~\text{cm}^{-3}$
, being the particle number density of a perfect gas at standard temperature and pressure (STP: 273.15 K and 1 atm), is typically used as a reference value. In an underdense plasma the refractivity is
![]() $\unicode[STIX]{x1D702}_{e}(n_{e},\unicode[STIX]{x1D706})-1=-\frac{n_{e}e^{2}\unicode[STIX]{x1D706}^{2}}{8\unicode[STIX]{x1D70B}^{2}m_{e}\unicode[STIX]{x1D716}_{0}c^{2}}$
, where
$\unicode[STIX]{x1D702}_{e}(n_{e},\unicode[STIX]{x1D706})-1=-\frac{n_{e}e^{2}\unicode[STIX]{x1D706}^{2}}{8\unicode[STIX]{x1D70B}^{2}m_{e}\unicode[STIX]{x1D716}_{0}c^{2}}$
, where
![]() $e$
is the electron charge,
$e$
is the electron charge,
![]() $m_{e}$
is the electron mass,
$m_{e}$
is the electron mass,
![]() $\unicode[STIX]{x1D716}_{0}$
is the vacuum permittivity and
$\unicode[STIX]{x1D716}_{0}$
is the vacuum permittivity and
![]() $c$
is the speed of light.
$c$
is the speed of light.
In general, the phase acquired by a light beam when passing through a sample of length
![]() $L$
is
$L$
is
![]() $\unicode[STIX]{x1D719}=\frac{2\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}}\int _{L}\unicode[STIX]{x1D702}(l,\unicode[STIX]{x1D706})\,\text{d}l=\frac{2\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}}\times L\times \overline{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706})}$
, where
$\unicode[STIX]{x1D719}=\frac{2\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}}\int _{L}\unicode[STIX]{x1D702}(l,\unicode[STIX]{x1D706})\,\text{d}l=\frac{2\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}}\times L\times \overline{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706})}$
, where
![]() $\overline{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706})}$
is the average refractive index along the geometrical path. Therefore, with an interferometric measurement the information acquired is related to the line-integrated particle density.
$\overline{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706})}$
is the average refractive index along the geometrical path. Therefore, with an interferometric measurement the information acquired is related to the line-integrated particle density.
To retrieve the actual density value from interferometric measurements, some assumptions on the spatial density distribution of the sample have to be made. There are two typical cases: cylindrically symmetric samples (for example, pulsed gas jets from circular nozzles) and non-cylindrically symmetric samples (for example, pulsed gas jets with rectangular nozzles). For the simplest case of cylindrically symmetric samples the well-known Abel inversion method is used, which allows one to extract the actual value of the radially dependent density from line-integrated measurements along several chords[Reference Brandi and Giammanco17, Reference Park, Baldis and Chen18]. In the case of non-cylindrically symmetric targets, multiple measurements along different lines of sight are necessary to implement a 3D tomographic reconstruction procedure[Reference Couperusa, Köhlera, Wolterink, Jochmann, Zarinia, Bastiaens, Boller, Irman and Schramma19, Reference Adelmann, Hermann, Ischebeck, Kaluza, Locans, Sauerwein and Tarkeshian20]. Finally, in the case of homogeneous samples, such as uniformly filled gas cells, the density is actually given by the average density measured by means of interferometry[Reference Brandi, Giammanco, Conti, Syllá, Lambert and Gizzi21].
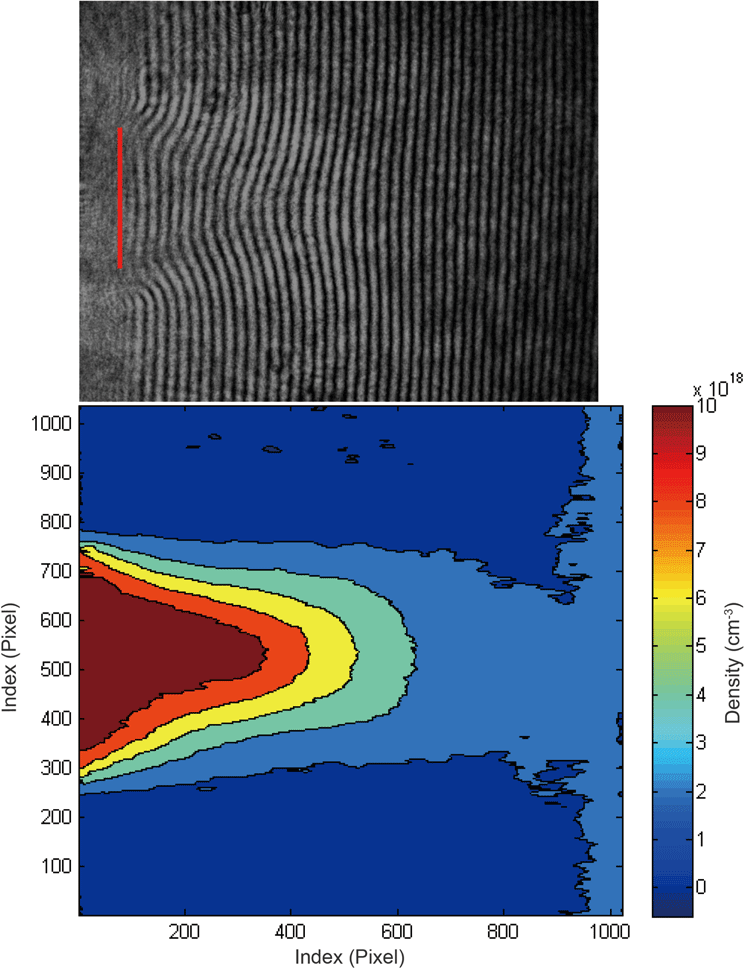
An interferometric measurement can be performed over a extended area of the plasma using an optical imaging system and camera as the light detector to acquire an image (the so-called interferogram), which enables 2D mapping of the line-integrated density over the light beam cross-section. In such a case, a numerical analysis of the interferogram is necessary to extract the actual phase shift using a phase-retrieval algorithm comprising phase-unwrapping procedures. Such measurements allow one to obtain an actual 2D map of the density, which is necessary to understand and monitor physical phenomena in ultra-fast laser–plasma interactions, especially during alignment and tuning of the LPA stages. As an example of a 2D measurement, in Figure 1 an interferogram of a supersonic gas jet in vacuum acquired by a Nomarski interferometer is shown, along with the density map retrieved from a phase-retrieval algorithm. Conversely, a 1D measurement of the average density along the laser beam path in the sample is performed when the intensity over the entire light beam cross-section is acquired using a photodiode or a photomultiplier tube (PMT) as the light detector. These 1D measurements are much faster and require less intense data analysis than the 2D measurements, making them potentially more suitable during LPA operation (for example, to monitor in real time the particle number density in the interaction region).
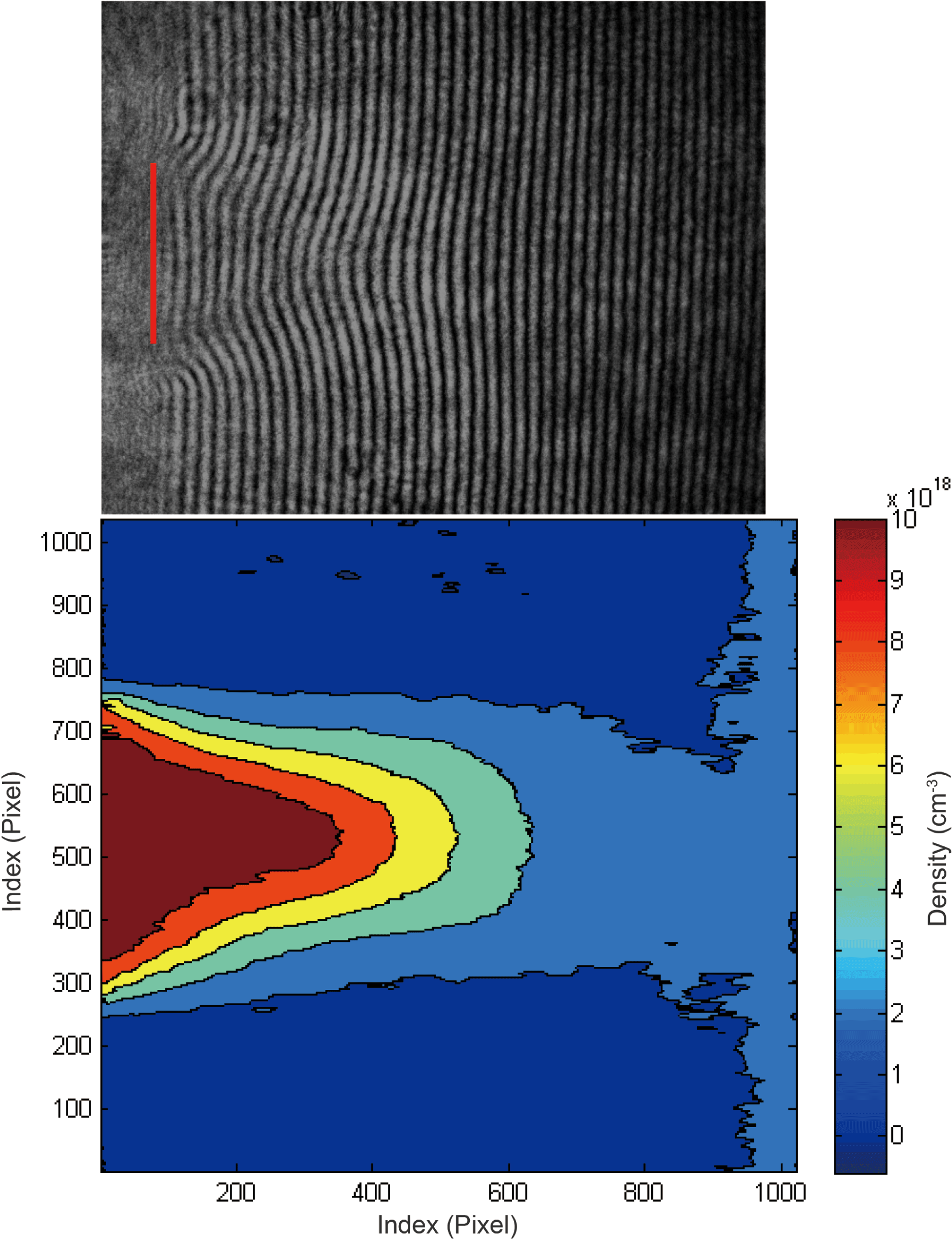
Figure 1. Upper panel: interferogram of a pulsed gas jet in vacuum with a rectangular orifice acquired by means of a Nomarski interferometer; lower panel: corresponding average density map obtained with a phase-retrieval algorithm[Reference Tomassini, Borghesi, Galimberti, Giulietti, Giulietti, Willi and Gizzi22].
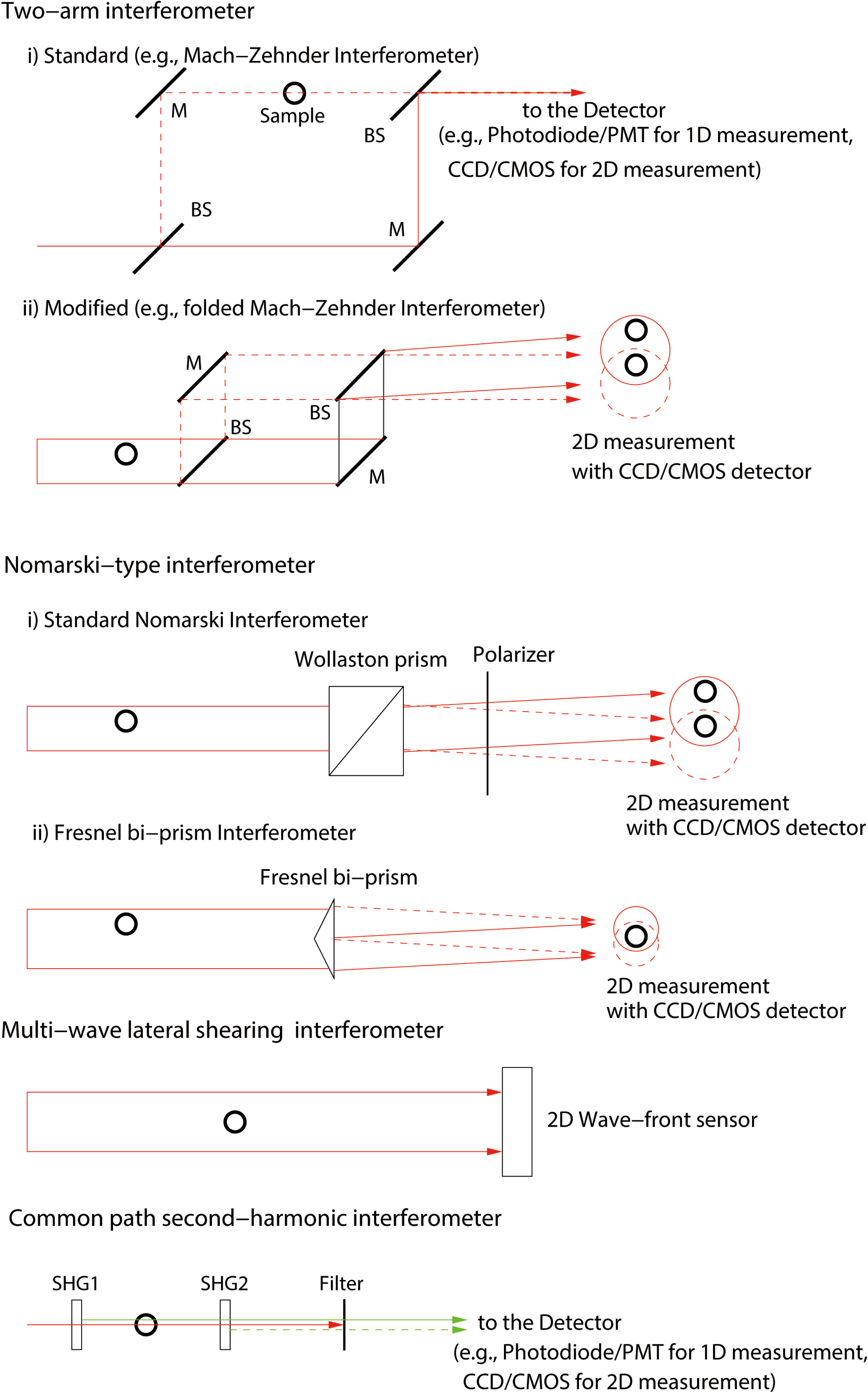
Figure 2. Schematic representation of the most common interferometers used for density measurements in laser-plasma accelerators; M, mirror; BS, beam splitter; SHG, second-harmonic generation unit. Optical elements used for imaging, such as lenses, are omitted for clarity.
The main interferometric methods used to measure the particle density in LPA targets are schematically summarized in Figure 2 and discussed in the following.
2.1 Two-arm interferometers
In a two-arm interferometer (TAI) the phase shift is measured relative to the phase of a reference optical beam not passing through the sample but typically through a vacuum where the refractive index value is unity. The measured phase shift is then given by
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D719}_{\text{TAI}}(\unicode[STIX]{x1D706})=\frac{2\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D706}}\int _{L}[\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706})-1]\,\text{d}l$
. Two-arm interferometry can be implemented in two main configurations, depending on the optical design adopted.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D719}_{\text{TAI}}(\unicode[STIX]{x1D706})=\frac{2\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D706}}\int _{L}[\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706})-1]\,\text{d}l$
. Two-arm interferometry can be implemented in two main configurations, depending on the optical design adopted.
I Standard TAI, such as Mach–Zehnder interferometers, where the light beam is split into two distinct beams following different geometrical paths, called the reference and measurement arms, which are then recombined and interfere[Reference Uhm, Jang, Kim and Suk7, Reference Gizzi, Galimberti, Giulietti, Giulietti, Koester, Labate, Tomassini, Martin, Ceccotti, De Oliveira and Monot23, Reference Aniculaesei, Kim, Yoo, Oh and Nam24].
II Modified TAIs, also called two-arm folded, where the light beam is split into two parts after passing through the sample, and interference takes place between the part of the beam that has passed through the sample and the part of the beam not passing through the sample[Reference Park, Baldis and Chen18, Reference Feister, Nees, Morrison, Frische, Orban, Chowdhury and Roquemore25]. This method provides good control on the fringe spacing and image formation.
The standard TAIs suffer from a very high susceptibility to environmental conditions (for example, mechanical vibration and temperature changes) while the folded TAI is relatively more robust against environmental conditions due to the more compact size of the two-arm section. The typical sensitivity of an ultra-fast imaging TAI can be hundredths of a fringe (
![]() ${\sim}$
0.1 rad). To achieve better sensitivity, on the order of a few millradians, special care has to be taken during the measurement by making use of a probe beam with very good quality, active mechanical stabilization and averaging[Reference Couperusa, Köhlera, Wolterink, Jochmann, Zarinia, Bastiaens, Boller, Irman and Schramma19]. The latter may hamper implementation of TAIs for real-time measurement and online monitoring applications. However, TAIs may find applications for the characterization, alignment and optimization of LPA stages due to their versatility.
${\sim}$
0.1 rad). To achieve better sensitivity, on the order of a few millradians, special care has to be taken during the measurement by making use of a probe beam with very good quality, active mechanical stabilization and averaging[Reference Couperusa, Köhlera, Wolterink, Jochmann, Zarinia, Bastiaens, Boller, Irman and Schramma19]. The latter may hamper implementation of TAIs for real-time measurement and online monitoring applications. However, TAIs may find applications for the characterization, alignment and optimization of LPA stages due to their versatility.
Besides time-domain measurements, also spectral-domain interferometry has been implemented in TAIs for the measurement of the free-electron density in discharged capillaries using ultra-fast laser pulses[Reference van Tilborg, Daniels, Gonsalves, Schroeder, Esarey and Leemans26, Reference Daniels, van Tilborg, Gonsalves, Schroeder, Benedetti, Esarey and Leemans27]. These measurements are based on the density-dependent group velocity of an ultra-short laser pulse when propagating in a plasma channel[Reference Schroeder, Benedetti, Esarey, van Tilborg and Leemans13]. Specifically, the group velocity delay between a laser pulse propagating in vacuum and a laser pulse propagating through the plasma inside the discharged capillary actually depends on the mismatch of the group index of refraction due to the free electrons. However, such a two-arm configuration poses serious challenges which prevent its use in monitoring discharged capillary-based LPA for high-quality accelerators in user-oriented facilities. This limitation can be overcome by instead adopting spectral-domain second-harmonic interferometry, as will be discussed later.
2.2 Nomarski-type interferometers
These are similar in principle to the modified TAI, and the phase measured is exactly the same (reference beam in vacuum and signal beam over the object), but they have a somewhat easier setup, being a quasi-common-path configuration with minimal geometrical separation between the two interfering parts of the beam. Typical configurations are as follows.
I Standard Nomarski interferometer, where the two interfering beams are separated by means of a Wollaston beam splitter and interference is recorded after a polarizer[Reference Kalal, Slezak, Martinkova and Rhee28–Reference Gamucci, Galimberti, Giulietti, Gizzi, Labate, Petcu, Tomassini and Giulietti30].
II Fresnel bi-prism interferometer, which is based on the use of a Fresnel bi-prism that allows one to overlap directly two different parts of the same input beam[Reference Gao, Hafz, Li, Mirzaie, Li and Ain31].
2.3 Multi-wave lateral shearing interferometer
A versatile and robust method to measure phase variations across a light beam is based on the use of wavefront (WF) sensors (for example, the quadri-wave lateral shearing interferometer[Reference Chanteloup32]). This instrument measures the phase difference between two adjacent points of the light beam cross-section by means of a wavefront detector. In fact this method is sensitive to phase gradients of the beam cross-section along two orthogonal directions, and the actual 2D map of the phase is retrieved by analyzing the data with specific software. Finally, the phase shift of interest is calculated by subtracting the phase map of an undisturbed beam acquired in a separate measurement without the sample[Reference Mollica, Syllá, Flacco, Bourgeois, Wattellier and Malka33]. It can be considered a single-arm configuration, since interference takes place only at the detector, and is therefore a very robust method allowing for easy installation with a phase sensitivity which is stated to be
![]() ${<}$
2 nm (that is,
${<}$
2 nm (that is,
![]() ${<}$
30 mrad at 400 nm)[34]. A value of 11 mrad has actually been estimated as the root-mean-square over 188 acquisitions using 400 nm laser light[Reference Plateau, Matlis, Geddes, Gonsalves, Shiraishi, Lin, van Mourik and Leemans35]. It must be noted that a single-acquisition value has not been reported to our best knowledge, so a conservative value of 30 mrad at 400 nm is assumed here.
${<}$
30 mrad at 400 nm)[34]. A value of 11 mrad has actually been estimated as the root-mean-square over 188 acquisitions using 400 nm laser light[Reference Plateau, Matlis, Geddes, Gonsalves, Shiraishi, Lin, van Mourik and Leemans35]. It must be noted that a single-acquisition value has not been reported to our best knowledge, so a conservative value of 30 mrad at 400 nm is assumed here.
Of note, the wavefront of a laser beam, and the density information contained therein, can be extracted also by numerical beam intensity analysis of standard 2D images from a camera, with a phase resolution of about 80 mrad[Reference Chessa, Galimberti, Danson, Giulietti, Giulietti and Gizzi36]. However, the numerical analysis involves multiple images for this approach to be effective, thus limiting its applicability for real-time measurements, but it could be suitable for offline tuning and optimization of LPA stages.
2.4 Second-harmonic interferometer
Another kind of interferometric approach for the measurement of particle density in optically dispersive samples (for example, neutral gas or plasma) is based on the so-called second-harmonic interferometer (SHI), also known as the dispersion interferometer. The SHI has a fully common-path configuration and is sensitive to the phase difference acquired by the fundamental and second-harmonic beams when passing collinearly through the sample[Reference Hopf, Tomita and Al-Jumaily37, Reference Alum, Kovalchuk and Ostrovskaia38]. The measured phase shift is given by
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D719}_{\text{SHI}}=\frac{4\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}}\int _{L}\unicode[STIX]{x0394}\unicode[STIX]{x1D702}(l,\unicode[STIX]{x1D706})\,\text{d}l=\frac{4\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}}L\overline{\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D706})$
, where
$\unicode[STIX]{x0394}\unicode[STIX]{x1D719}_{\text{SHI}}=\frac{4\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}}\int _{L}\unicode[STIX]{x0394}\unicode[STIX]{x1D702}(l,\unicode[STIX]{x1D706})\,\text{d}l=\frac{4\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}}L\overline{\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D706})$
, where
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706}/2)$
. It is a very robust method against mechanical vibrations and environmental conditions in general, and it can reach a phase sensitivity of less then 1 mrad for 1D measurements without requiring any vibration mitigation system[Reference Brandi and Giammanco39]. Although 2D measurements using the SHI method have been demonstrated[Reference Jobes and Bretz40, Reference Abraham, Minoshima and Matsumoto41], there is no quantitative data available in the literature regarding the sensitivity of the imaging SHI. Here, we assume a conservative value of 10 mrad for quadrature detection[Reference Brandi and Giammanco39, Reference Brandi and Giammanco42]. To date, SHIs have mostly been developed and applied to monitor the free-electron density in magnetically confined large plasma machines[Reference Brandi, Giammanco, Harris, Roche, Trask and Wessel43, Reference Drachev, Krasnikov and Bagryansky44]. Recently, due to their versatility and robustness, SHIs have been successfully applied also for the characterization and monitoring of gas targets for LWFA (namely discharged gas-filled capillaries[Reference van Tilborg, Gonsalves, Esarey, Schroeder and Leemans45, Reference van Tilborg, Gonsalves, Esarey, Schroeder and Leemans46] and gas cells[Reference Brandi, Giammanco, Conti, Syllá, Lambert and Gizzi21, Reference Brandi, Marsili, Giammanco, Syllà and Gizzi47]).
$\unicode[STIX]{x0394}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706})-\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706}/2)$
. It is a very robust method against mechanical vibrations and environmental conditions in general, and it can reach a phase sensitivity of less then 1 mrad for 1D measurements without requiring any vibration mitigation system[Reference Brandi and Giammanco39]. Although 2D measurements using the SHI method have been demonstrated[Reference Jobes and Bretz40, Reference Abraham, Minoshima and Matsumoto41], there is no quantitative data available in the literature regarding the sensitivity of the imaging SHI. Here, we assume a conservative value of 10 mrad for quadrature detection[Reference Brandi and Giammanco39, Reference Brandi and Giammanco42]. To date, SHIs have mostly been developed and applied to monitor the free-electron density in magnetically confined large plasma machines[Reference Brandi, Giammanco, Harris, Roche, Trask and Wessel43, Reference Drachev, Krasnikov and Bagryansky44]. Recently, due to their versatility and robustness, SHIs have been successfully applied also for the characterization and monitoring of gas targets for LWFA (namely discharged gas-filled capillaries[Reference van Tilborg, Gonsalves, Esarey, Schroeder and Leemans45, Reference van Tilborg, Gonsalves, Esarey, Schroeder and Leemans46] and gas cells[Reference Brandi, Giammanco, Conti, Syllá, Lambert and Gizzi21, Reference Brandi, Marsili, Giammanco, Syllà and Gizzi47]).
Specifically, spectral-domain (SD) second-harmonic interferometry[Reference Wilson, Jiang, Aktsipetrov, Mishina and Downer48] has been adopted instead of spectral-domain TAI to monitor the density inside a discharged gas-filled capillary, due to the much easier implementation and much higher stability of the common-path configuration compared to the two-arm design[Reference van Tilborg, Gonsalves, Esarey, Schroeder and Leemans45]. In an SD SHI, the spectral interference takes place between the second-harmonic pulse generated before the sample and the time-delayed second-harmonic pulse generated after the fundamental pulse has propagated through the sample. The time delay
![]() $\unicode[STIX]{x0394}T$
between the two second-harmonic ultra-short pulses arises from the different group velocities in the sample at the fundamental and second-harmonic wavelengths, which is proportional to the density. In terms of phase, the pulse envelope slippage due to the plasma is
$\unicode[STIX]{x0394}T$
between the two second-harmonic ultra-short pulses arises from the different group velocities in the sample at the fundamental and second-harmonic wavelengths, which is proportional to the density. In terms of phase, the pulse envelope slippage due to the plasma is
![]() $\frac{4\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}}c\unicode[STIX]{x0394}T$
, where
$\frac{4\unicode[STIX]{x1D70B}}{\unicode[STIX]{x1D706}}c\unicode[STIX]{x0394}T$
, where
![]() $\unicode[STIX]{x1D706}$
is the fundamental laser wavelength. The time delay is estimated by measuring the modulation period
$\unicode[STIX]{x1D706}$
is the fundamental laser wavelength. The time delay is estimated by measuring the modulation period
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D708}$
in the frequency spectrum of the two interfering pulses (
$\unicode[STIX]{x0394}\unicode[STIX]{x1D708}$
in the frequency spectrum of the two interfering pulses (
![]() $\unicode[STIX]{x0394}T=1/\unicode[STIX]{x0394}\unicode[STIX]{x1D708}$
). For laser pulses propagating in a discharged gas-filled capillary with a near-match guided configuration typical for LPA, the relation between the time delay
$\unicode[STIX]{x0394}T=1/\unicode[STIX]{x0394}\unicode[STIX]{x1D708}$
). For laser pulses propagating in a discharged gas-filled capillary with a near-match guided configuration typical for LPA, the relation between the time delay
![]() $\unicode[STIX]{x0394}T$
and the average on-axis plasma density
$\unicode[STIX]{x0394}T$
and the average on-axis plasma density
![]() $n_{e}$
can be approximated very well by assuming free propagation in a plasma with an average density
$n_{e}$
can be approximated very well by assuming free propagation in a plasma with an average density
![]() $n_{e}$
[Reference van Tilborg, Gonsalves, Esarey, Schroeder and Leemans45], resulting in the same phase shift as a function of the electron density (see Table 1). When applying SD interferometry, also the spectral phase of the modulated frequency spectrum can be measured. It is noted that, given a linear response of the plasma, the phase shift due to the different group velocities (group delay) and the phase shift due to the different phase velocities (spectral phase shift) have the same magnitude but opposite sign. Recently, sensitivities of 2.85 rad in group-delay measurements and of 63 mrad for spectral phase measurements have been demonstrated[Reference van Tilborg, Gonsalves, Esarey, Schroeder and Leemans46].
$n_{e}$
[Reference van Tilborg, Gonsalves, Esarey, Schroeder and Leemans45], resulting in the same phase shift as a function of the electron density (see Table 1). When applying SD interferometry, also the spectral phase of the modulated frequency spectrum can be measured. It is noted that, given a linear response of the plasma, the phase shift due to the different group velocities (group delay) and the phase shift due to the different phase velocities (spectral phase shift) have the same magnitude but opposite sign. Recently, sensitivities of 2.85 rad in group-delay measurements and of 63 mrad for spectral phase measurements have been demonstrated[Reference van Tilborg, Gonsalves, Esarey, Schroeder and Leemans46].
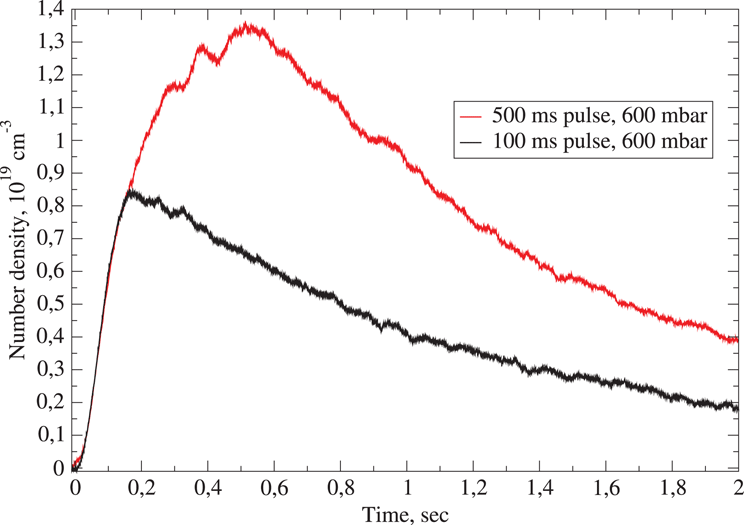
The use of a continuous-wave (CW) laser-based SHI has been successfully demonstrated for high-resolution real-time monitoring of the gas density inside a gas flow cell placed in a vacuum chamber[Reference Brandi, Giammanco, Conti, Syllá, Lambert and Gizzi21, Reference Brandi, Marsili, Giammanco, Syllà and Gizzi47]. As an example, Figure 3 reports the results of real-time measurements by a CW 1064 nm second-harmonic interferometer of the Ar gas number density inside a pulsed gas flow cell specifically developed for LWFA (SourceLAB, Model SL-ALC). The measurement is performed transversely over a length of 35 mm for a backing pressure of 600 mbar (1 bar
![]() $=$
100 kPa) and for gas pulse lengths of 100 ms and 500 ms.
$=$
100 kPa) and for gas pulse lengths of 100 ms and 500 ms.

Figure 3. Real-time measurements of the Ar gas number density inside a pulsed gas flow cell by an SHI at 1064 nm: black curve, pulse length 100 ms; red curve, pulse length 500 ms. Backing Ar pressure 600 mbar.
A specific issue common to all time-domain interferometric measurements is related to the periodic evolution of the intensity pattern with alternating minima and maxima in the detected light intensity, which gives rise to so-called fringes. This fact implies that measurements of a phase shift that spans multiple fringes may become indeterminate when retrieving the absolute phase shift from the measured intensity data. Typically, this issue is addressed during the data analysis with specific phase-unwrapping protocols. There are two basic requirements for such phase-unwrapping protocols to be effective. First, the presence of a reference data point with known phase shift, typically zero, with respect to which all other phase shifts are referred. In 2D measurements such data can be a pixel or an area of the image where the two interfering beams have the exact same phase, while in 1D measurements the reference value is typically obtained from the data acquired before the event under investigation has started or by waiting until its completion. Second, the measurements have to resolve all fringes. In 2D measurements this means that the spatial gradient of the phase to be measured must be small enough to avoid fringe jumps between two adjacent pixels of the detector[Reference Gizzi, Giulietti, Giulietti, Afshar-Rad, Biancalana, Chessa, Danson, Schifano, Viana and Willi49]. In 1D measurements, the detector has to be fast enough to accurately follow the evolution in time of the interference signal in order to count the number of fringes[Reference Ju and Cros50].
Table 1. Expected phase shifts in TAIs and SHIs for both hydrogen gas and free electrons at 800 nm and 400 nm wavelengths, with
![]() $L$
expressed in cm,
$L$
expressed in cm,
![]() $n_{g}$
in
$n_{g}$
in
![]() $10^{19}~\text{cm}^{-3}$
and
$10^{19}~\text{cm}^{-3}$
and
![]() $n_{e}$
in
$n_{e}$
in
![]() $10^{17}~\text{cm}^{-3}$
. Note that for SHI the fundamental wavelength used is indicated, while the phase is actually measured at its second harmonic, i.e., 400 nm.
$10^{17}~\text{cm}^{-3}$
. Note that for SHI the fundamental wavelength used is indicated, while the phase is actually measured at its second harmonic, i.e., 400 nm.

When the measured phase shift is small enough to stay within a half-fringe so that it can be determined unambiguously, i.e.,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D719}<\unicode[STIX]{x1D70B}$
, then fringe jumps are avoided and phase-tracking or phase-unwrapping protocols are not necessary, enhancing the phase measurement sensitivity and speed, and allowing for more robust real-time monitoring. As an example, the maximum density shown in Figure 3 corresponds to approximately 0.5 bar pressure at room temperature, which would result in a
$\unicode[STIX]{x0394}\unicode[STIX]{x1D719}<\unicode[STIX]{x1D70B}$
, then fringe jumps are avoided and phase-tracking or phase-unwrapping protocols are not necessary, enhancing the phase measurement sensitivity and speed, and allowing for more robust real-time monitoring. As an example, the maximum density shown in Figure 3 corresponds to approximately 0.5 bar pressure at room temperature, which would result in a
![]() ${\sim}27$
rad phase shift (
${\sim}27$
rad phase shift (
![]() ${>}$
4 fringes) in a TAI[Reference Bideau-Mehu, Guern, Abjean and Johannin-Gilles51], while the phase shift read by the SHI is
${>}$
4 fringes) in a TAI[Reference Bideau-Mehu, Guern, Abjean and Johannin-Gilles51], while the phase shift read by the SHI is
![]() ${<}1$
rad[Reference Velsko and Eimerl52], thus sub-fringe, allowing for a real-time measurement.
${<}1$
rad[Reference Velsko and Eimerl52], thus sub-fringe, allowing for a real-time measurement.
It is highlighted that a time delay measurement in SD interferometry is inherently immune to the fringe-jump issue, and can be applied to measure plasma densities over relatively long distances, which would result in a signal spanning many fringes in a time-domain measurement. As an example, when adopting SD second-harmonic interferometry to measure the electron density in gas discharged capillary[Reference van Tilborg, Gonsalves, Esarey, Schroeder and Leemans46] the group-delay measurement is used to determine the number of fringes, thanks to a sub-fringe phase resolution of 2.85 rad, while the simultaneous determination of the spectral phase allows one to achieve an overall 63 mrad phase resolution over multiple fringes.
2.5 Phase-shift estimates
The actual relation between the measured phase shift and the particle density is different in the case of neutral particles in a gas or free electrons in a plasma. The values of the refractivity of hydrogen at STP for the fundamental and second-harmonic wavelengths of a Ti:sapphire laser are
![]() $\unicode[STIX]{x1D702}(800)=1.374\times 10^{-4}$
and
$\unicode[STIX]{x1D702}(800)=1.374\times 10^{-4}$
and
![]() $\unicode[STIX]{x1D702}(400)=1.426\times 10^{-4}$
, respectively[Reference Peck and Hung53], thus
$\unicode[STIX]{x1D702}(400)=1.426\times 10^{-4}$
, respectively[Reference Peck and Hung53], thus
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D702}(800)=\unicode[STIX]{x1D702}(400)-\unicode[STIX]{x1D702}(800)=52\times 10^{-7}$
. So, based on these values and on the known equation for the plasma refractive index as a function of wavelength and electron density, the expected phase shifts can be evaluated and are reported in Table 1. The wavelength reported for SHI is the fundamental wavelength used, while the reported phase refers to the detected second harmonic, i.e., 400 nm wavelength. It is noted that the phase to be measured by Nomarski-type interferometers is actually the same as for the TAI.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D702}(800)=\unicode[STIX]{x1D702}(400)-\unicode[STIX]{x1D702}(800)=52\times 10^{-7}$
. So, based on these values and on the known equation for the plasma refractive index as a function of wavelength and electron density, the expected phase shifts can be evaluated and are reported in Table 1. The wavelength reported for SHI is the fundamental wavelength used, while the reported phase refers to the detected second harmonic, i.e., 400 nm wavelength. It is noted that the phase to be measured by Nomarski-type interferometers is actually the same as for the TAI.
The wavefront sensor measures only the gradient of the density, and therefore there is no straightforward analytical relation between the measured quantity and the density which is determined from the phase extracted by dedicated software. A comparison between similar measurements performed with both wavefront-based sensors and a modified TAI revealed a difference in the absolute value of the measured density of 10%–20%[Reference Plateau, Matlis, Geddes, Gonsalves, Shiraishi, Lin, van Mourik and Leemans35]. Indeed, a 15 nm accuracy is stated for the instrument[34], i.e., 0.24 rad at 400 nm, which can explain the deviation of the absolute value found with respect to the modified TAI measurement. Thus, the WF-sensor-based instrument requires an accurate calibration before being used for the absolute measurement of density. For comparison, the SHI employing quadrature detection can reach an absolute accuracy of 1% or less for 1D measurements[Reference Brandi and Giammanco39].

Figure 4. Interferometric capability for neutral hydrogen density measurements. For each methodology considered, the wavelength used and the measured phase are shown. For SHI, the fundamental wavelength used is reported, while the phase shift refers to the actually detected second-harmonic wavelength, i.e., 400 nm. The solid lines correspond to the smallest measurable phase, indicated in the legend, while the dashed lines correspond to measurements within half-fringe.
In Figures 4 and 5 the capabilities of the various interferometric methods are shown graphically for neutral hydrogen and free electrons, respectively: the full lines represent the lower detection limit set by the sensitivity, while the dashed lines represent the upper limit for measurement within a single fringe, i.e.,
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D719}<\unicode[STIX]{x1D70B}$
. Of course a fringe jump allows one to overcome this upper limit, but at the expense of higher uncertainty in time-domain measurements. As discussed, fringe jumps are not an issue in spectral-domain interferometry, thanks to simultaneous group-delay and spectral phase measurements. In Figure 5 the capabilities in terms of the phase of both group-delay and spectral phase measurements are reported separately.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D719}<\unicode[STIX]{x1D70B}$
. Of course a fringe jump allows one to overcome this upper limit, but at the expense of higher uncertainty in time-domain measurements. As discussed, fringe jumps are not an issue in spectral-domain interferometry, thanks to simultaneous group-delay and spectral phase measurements. In Figure 5 the capabilities in terms of the phase of both group-delay and spectral phase measurements are reported separately.
Interferometry is usually performed transversely to the main laser beam. In such a case, the plasma length covered by the interferometer light beam lies between
![]() $10~\unicode[STIX]{x03BC}\text{m}$
(roughly the dimensions of the main laser beam spot) and hundreds of
$10~\unicode[STIX]{x03BC}\text{m}$
(roughly the dimensions of the main laser beam spot) and hundreds of
![]() $\unicode[STIX]{x03BC}\text{m}$
. The transverse neutral gas length can range from
$\unicode[STIX]{x03BC}\text{m}$
. The transverse neutral gas length can range from
![]() ${\sim}$
mm typical for pulsed jets[Reference Brandi and Giammanco17] to tens of millimeters in gas flow cells[Reference Brandi, Giammanco, Conti, Syllá, Lambert and Gizzi21, Reference Aniculaesei, Kim, Yoo, Oh and Nam24, Reference Audet, Desforges, Maitrallain, Dobosz Dufrénoy, Bougeard, Maynard, Lee, Hansson, Aurand, Persson, Gallardo González, Monot, Wahlström, Lundh and Cros54].
${\sim}$
mm typical for pulsed jets[Reference Brandi and Giammanco17] to tens of millimeters in gas flow cells[Reference Brandi, Giammanco, Conti, Syllá, Lambert and Gizzi21, Reference Aniculaesei, Kim, Yoo, Oh and Nam24, Reference Audet, Desforges, Maitrallain, Dobosz Dufrénoy, Bougeard, Maynard, Lee, Hansson, Aurand, Persson, Gallardo González, Monot, Wahlström, Lundh and Cros54].
For neutral hydrogen measurements, from Figure 4 it is evident that both the SHI and the WF-based sensors are capable of measuring low density values, even for few millimeters path. The 1D measurement with the SHI allows very fast monitoring of the neutral hydrogen density (acquisition time
![]() ${\sim}1~\unicode[STIX]{x03BC}\text{s}$
) and can be implemented as a sensor in closed-loop gas flow regulation systems. This is very important when gas cells are used. In fact, repetitive shots of the high-power main laser beam will eventually modify the cell’s orifice, usually of hundreds of microns diameter, altering the gas flow dynamics and therefore the actual gas number density inside the cell for a pre-set backing pressure[Reference Kononenko, Lopes, Cole, Kamperidis, Mangles, Najmudin, Osterhoff, Poder, Rusby, Symes, Warwick, Wood and Palmer12]. Online regulation of such a gas supply system is therefore necessary in order to achieve a stable and reproducible laser-plasma acceleration process. The 1D measurement with the SHI can achieve a sensitivity of
${\sim}1~\unicode[STIX]{x03BC}\text{s}$
) and can be implemented as a sensor in closed-loop gas flow regulation systems. This is very important when gas cells are used. In fact, repetitive shots of the high-power main laser beam will eventually modify the cell’s orifice, usually of hundreds of microns diameter, altering the gas flow dynamics and therefore the actual gas number density inside the cell for a pre-set backing pressure[Reference Kononenko, Lopes, Cole, Kamperidis, Mangles, Najmudin, Osterhoff, Poder, Rusby, Symes, Warwick, Wood and Palmer12]. Online regulation of such a gas supply system is therefore necessary in order to achieve a stable and reproducible laser-plasma acceleration process. The 1D measurement with the SHI can achieve a sensitivity of
![]() ${<}$
1 mrad, therefore enabling the measurement of densities of about
${<}$
1 mrad, therefore enabling the measurement of densities of about
![]() $10^{17}~\text{cm}^{-3}$
over a 1 mm length[Reference Brandi and Giammanco39]. The WF sensor is indeed suitable for 2D mapping, starting at a few
$10^{17}~\text{cm}^{-3}$
over a 1 mm length[Reference Brandi and Giammanco39]. The WF sensor is indeed suitable for 2D mapping, starting at a few
![]() $10^{17}~\text{cm}^{-3}$
and few millimeters in length. As per the higher values of density and medium length, all the methods can measure within a single fringe for millimeter-sized sample with densities up to
$10^{17}~\text{cm}^{-3}$
and few millimeters in length. As per the higher values of density and medium length, all the methods can measure within a single fringe for millimeter-sized sample with densities up to
![]() $10^{19}~\text{cm}^{-3}$
, except the TAI interferometer at 400 nm.
$10^{19}~\text{cm}^{-3}$
, except the TAI interferometer at 400 nm.

Figure 5. Interferometric capability for free-electron density measurements. For each methodology considered the wavelength used and the measured phase are shown. For SHI, the fundamental wavelength used is reported, while the phase shift refers to the actually detected second-harmonic wavelength, i.e., 400 nm. The solid lines correspond to the smallest measurable phase, indicated in the legend, while the dashed lines correspond to measurements within half-fringe, except for group delay measurements with the SHI.
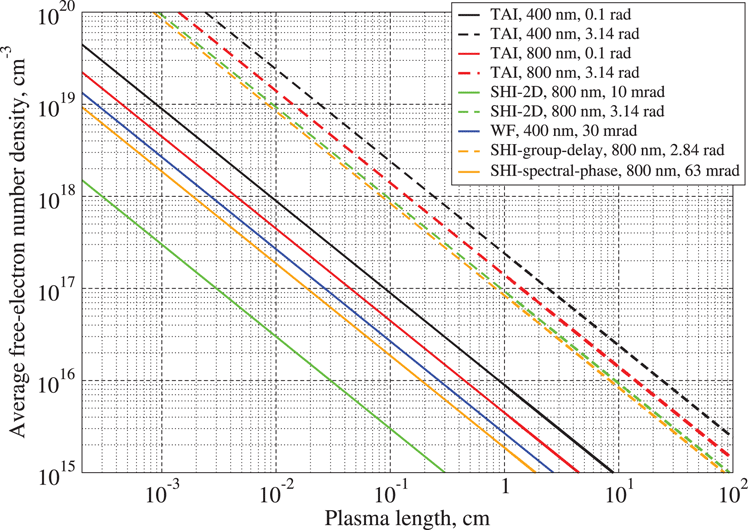
For free-electron density measurements, Figure 5 shows that only the imaging SHI with 10 mrad sensitivity would be suitable to measure the lowest free-electron density in the range of few
![]() $10^{17}~\text{cm}^{-3}$
for a plasma length
$10^{17}~\text{cm}^{-3}$
for a plasma length
![]() ${<}100~\unicode[STIX]{x03BC}\text{m}$
. However, such an instrument has not been tested yet and further development is necessary to assess the actual sensitivity achievable with the imaging SHI. An ultra-fast probe beam has to be used to monitor the free electrons during laser–plasma interactions. Ultra-fast SHI has been presented in the literature[Reference Brandi and Giammanco42, Reference Minoshirna and Matsumoto55], but more development is necessary to establish a femtosecond version of the SHI. The WF-sensor-based instrument is suitable for the measurement of free-electron densities
${<}100~\unicode[STIX]{x03BC}\text{m}$
. However, such an instrument has not been tested yet and further development is necessary to assess the actual sensitivity achievable with the imaging SHI. An ultra-fast probe beam has to be used to monitor the free electrons during laser–plasma interactions. Ultra-fast SHI has been presented in the literature[Reference Brandi and Giammanco42, Reference Minoshirna and Matsumoto55], but more development is necessary to establish a femtosecond version of the SHI. The WF-sensor-based instrument is suitable for the measurement of free-electron densities
![]() ${>}10^{18}~\text{cm}^{-3}$
with plasma paths longer than hundreds of
${>}10^{18}~\text{cm}^{-3}$
with plasma paths longer than hundreds of
![]() $\unicode[STIX]{x03BC}\text{m}$
, and it can work readily with ultra-fast light sources[Reference Plateau, Matlis, Geddes, Gonsalves, Shiraishi, Lin, van Mourik and Leemans35]. In Figure 5 the capability of SD second-harmonic interferometry is also reported. High-sensitivity spectral phase measurements, combined with group-delay measurements over multiple fringes, are ideal candidates as diagnostics to monitor the electron density inside gas discharged capillaries with relatively large line-integrated densities.
$\unicode[STIX]{x03BC}\text{m}$
, and it can work readily with ultra-fast light sources[Reference Plateau, Matlis, Geddes, Gonsalves, Shiraishi, Lin, van Mourik and Leemans35]. In Figure 5 the capability of SD second-harmonic interferometry is also reported. High-sensitivity spectral phase measurements, combined with group-delay measurements over multiple fringes, are ideal candidates as diagnostics to monitor the electron density inside gas discharged capillaries with relatively large line-integrated densities.
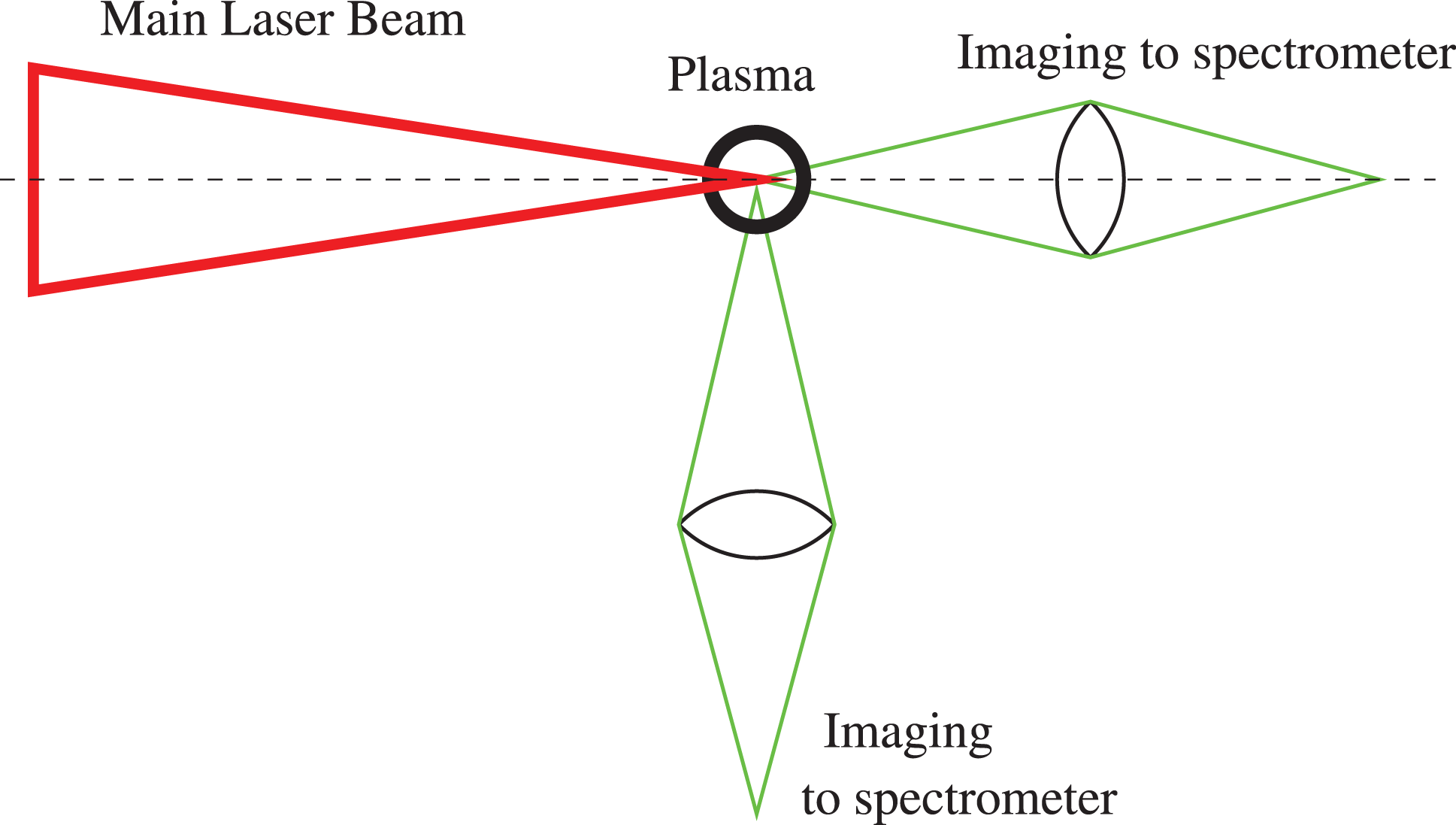
Figure 6. Schematic of the Stark broadening measurement setup, showing both longitudinal and transverse configurations.
Table 2. Qualitative comparison of interferometric methods.

The advantages and disadvantages (pros and cons) of each interferometric method are summarized in Table 2.
3 Optical emission spectroscopy
All interferometric methods require an appropriate optical line of sight through the sample. In the case of a freely expanding gas jet, interferometry is easy to implement, whereas in the case of confined samples (for example, gas cells, capillaries and tubes), flat optical side windows are necessary to provide the optical path for transverse interferometry. This issue must be considered when designing the actual geometry of the accelerator stage. When a straight optical path through the sample is not available (for example, cylindrical capillary or tubes) optical emission spectroscopy can be considered as a means to monitor the density. Specifically, Stark broadening of hydrogen emission lines and wavelength-shifted Raman scattering of the main laser beam will be considered here.
3.1 Stark broadening
Spectroscopic investigation of hydrogen emission lines (for example,
![]() $\text{H}_{\unicode[STIX]{x1D6FC}}$
at 656.3 nm and
$\text{H}_{\unicode[STIX]{x1D6FC}}$
at 656.3 nm and
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}$
at 486.1 nm) may be implemented to monitor the free electron density with a relatively simple approach[Reference Griem56]. In fact, the electron density can be estimated from the broadening of the hydrogen emission lines as
$\text{H}_{\unicode[STIX]{x1D6FD}}$
at 486.1 nm) may be implemented to monitor the free electron density with a relatively simple approach[Reference Griem56]. In fact, the electron density can be estimated from the broadening of the hydrogen emission lines as
where
![]() $n_{e}$
is in
$n_{e}$
is in
![]() $\text{cm}^{-3}$
and
$\text{cm}^{-3}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D706}_{1/2}$
, the full width at half-maximum of the Stark-broadened spectral line, in ångstroms. The data analysis in this case depends (slightly) on the actual electron temperature via the tabulated parameter
$\unicode[STIX]{x0394}\unicode[STIX]{x1D706}_{1/2}$
, the full width at half-maximum of the Stark-broadened spectral line, in ångstroms. The data analysis in this case depends (slightly) on the actual electron temperature via the tabulated parameter
![]() $\unicode[STIX]{x1D6FC}_{1/2}$
[Reference Griem56], and therefore a measurement (or at least a reliable estimate) of the electron temperature may be necessary in parallel with Stark broadening measurements. Remarkably, the plasma temperature can be estimated from the spectroscopic measurement via the ratio of the emission line to the background underlying continuum[Reference Gonsalves, Liu, Bobrova, Sasorov, Pieronek, Daniels, Antipov, Butler, Bulanov, Waldron, Mittelberger and Leemans57, Reference Daniels, Gonsalves, Pieronek, Benedetti, van Tilborg, Schroeder and Leemans58]. Stark broadening measurements can be performed both longitudinally[Reference Gautam and Parigger59–Reference Jang, Kim, Nam, Jang and Suka63] and transversely[Reference Qin, Li, Liu, Liu, Yu, Wang, Qi, Zhang, Fang, Feng, Wu, Ke, Chen, Wang, Li and Xu9, Reference Ashkenazy, Kipper and Caner64, Reference Flih, Oks and Vitel65], as shown schematically in Figure 6. Spatially resolved emission spectroscopy can be implemented using an imaging spectrometer, and measurements on the nanosecond time scale can be achieved using a fast camera[Reference Oh, Uhm, Kang, Lee and Suk66]. For example, Stark broadening of
$\unicode[STIX]{x1D6FC}_{1/2}$
[Reference Griem56], and therefore a measurement (or at least a reliable estimate) of the electron temperature may be necessary in parallel with Stark broadening measurements. Remarkably, the plasma temperature can be estimated from the spectroscopic measurement via the ratio of the emission line to the background underlying continuum[Reference Gonsalves, Liu, Bobrova, Sasorov, Pieronek, Daniels, Antipov, Butler, Bulanov, Waldron, Mittelberger and Leemans57, Reference Daniels, Gonsalves, Pieronek, Benedetti, van Tilborg, Schroeder and Leemans58]. Stark broadening measurements can be performed both longitudinally[Reference Gautam and Parigger59–Reference Jang, Kim, Nam, Jang and Suka63] and transversely[Reference Qin, Li, Liu, Liu, Yu, Wang, Qi, Zhang, Fang, Feng, Wu, Ke, Chen, Wang, Li and Xu9, Reference Ashkenazy, Kipper and Caner64, Reference Flih, Oks and Vitel65], as shown schematically in Figure 6. Spatially resolved emission spectroscopy can be implemented using an imaging spectrometer, and measurements on the nanosecond time scale can be achieved using a fast camera[Reference Oh, Uhm, Kang, Lee and Suk66]. For example, Stark broadening of
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}$
allows the local electron density with values
$\text{H}_{\unicode[STIX]{x1D6FD}}$
allows the local electron density with values
![]() ${<}10^{17}~\text{cm}^{-3}$
to be determined with a medium-resolution spectrometer. An experimental study comparing transverse TAI and longitudinal Stark broadening measurements of
${<}10^{17}~\text{cm}^{-3}$
to be determined with a medium-resolution spectrometer. An experimental study comparing transverse TAI and longitudinal Stark broadening measurements of
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}$
[Reference Jang, Kim, Nam, Jang and Suka63] has demonstrated very good agreement between the two measurement methods.
$\text{H}_{\unicode[STIX]{x1D6FD}}$
[Reference Jang, Kim, Nam, Jang and Suka63] has demonstrated very good agreement between the two measurement methods.
3.2 Raman scattering
Measurement of the Raman scattering of the main laser beam photons due to the plasma can give information on the local free-electron density[Reference Pathak, Zhidkov, Hosokai and Kodama67]. In fact, the frequency of the Raman scattered signal
![]() $\unicode[STIX]{x1D714}_{R}$
is shifted compared to the original laser frequency,
$\unicode[STIX]{x1D714}_{R}$
is shifted compared to the original laser frequency,
![]() $\unicode[STIX]{x1D714}_{L}$
by the plasma frequency
$\unicode[STIX]{x1D714}_{L}$
by the plasma frequency
![]() $\unicode[STIX]{x1D714}_{p}$
, i.e.,
$\unicode[STIX]{x1D714}_{p}$
, i.e.,
![]() $\unicode[STIX]{x1D714}_{R}=\unicode[STIX]{x1D714}_{L}-\unicode[STIX]{x1D714}_{p}$
, so that the free-electron density can be estimated as
$\unicode[STIX]{x1D714}_{R}=\unicode[STIX]{x1D714}_{L}-\unicode[STIX]{x1D714}_{p}$
, so that the free-electron density can be estimated as
where
![]() $n_{e}$
is expressed in
$n_{e}$
is expressed in
![]() $10^{19}~\text{cm}^{-3}$
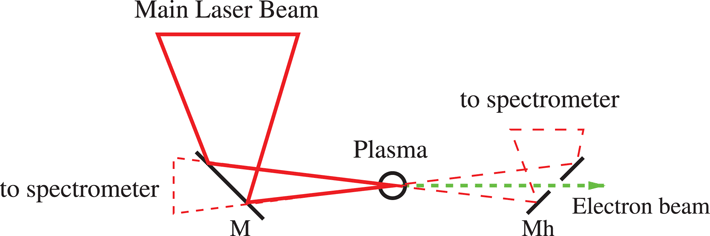
and the wavelength in nanometers[Reference Kaganovich, Hafizi, Palastro, Ting, Helle, Chen, Jones and Gordon68]. Raman scattering can be measured in the forward or backward directions compared to the main laser beam, as schematically shown in Figure 7. The implementation of forward scattering measurements in LWFA experiments requires the use of a mirror with a hole in the center such that the Raman radiation is reflected while the electron bunch can propagate undisturbed[Reference Nam, Kim, Lee, Jang and Suk69], whereas the backward measurement can be performed mainly at wavelengths outside the reflectivity range of the main laser beam mirror[Reference Kaganovich, Hafizi, Palastro, Ting, Helle, Chen, Jones and Gordon70].
$10^{19}~\text{cm}^{-3}$
and the wavelength in nanometers[Reference Kaganovich, Hafizi, Palastro, Ting, Helle, Chen, Jones and Gordon68]. Raman scattering can be measured in the forward or backward directions compared to the main laser beam, as schematically shown in Figure 7. The implementation of forward scattering measurements in LWFA experiments requires the use of a mirror with a hole in the center such that the Raman radiation is reflected while the electron bunch can propagate undisturbed[Reference Nam, Kim, Lee, Jang and Suk69], whereas the backward measurement can be performed mainly at wavelengths outside the reflectivity range of the main laser beam mirror[Reference Kaganovich, Hafizi, Palastro, Ting, Helle, Chen, Jones and Gordon70].

Figure 7. Schematic of the Raman scattering measurement setup, showing both backward and forward configurations. M, mirror, Mh, mirror with a hole in the center to let the electron beam through.
An experimental study comparing the free-electron density inside a 15-mm-long discharged gas-filled capillary measured by TAI and estimated by the frequency shift between the original TW level main laser wavelength and the forward-scattered Raman light has indicated a good agreement between the two diagnostics up to
![]() $10^{19}~\text{cm}^{-3}$
[Reference Nam, Kim, Lee, Jang and Suk69]. However, strong discrepancies in the Raman-based measurement can occur above
$10^{19}~\text{cm}^{-3}$
[Reference Nam, Kim, Lee, Jang and Suk69]. However, strong discrepancies in the Raman-based measurement can occur above
![]() $10^{19}~\text{cm}^{-3}$
[Reference Kaganovich, Hafizi, Palastro, Ting, Helle, Chen, Jones and Gordon70]. On the other hand, densities
$10^{19}~\text{cm}^{-3}$
[Reference Kaganovich, Hafizi, Palastro, Ting, Helle, Chen, Jones and Gordon70]. On the other hand, densities
![]() ${<}10^{18}~\text{cm}^{-3}$
are difficult to quantify by this methodology since the wavelength shift and the scattered light intensity may be too low to be accurately measured, due also to the spurious light from the high-intensity main laser beam. So, this methodology is indeed interesting for high-quality LPA due to its relatively simple implementation, but would be useful mainly for free-electron densities in the range
${<}10^{18}~\text{cm}^{-3}$
are difficult to quantify by this methodology since the wavelength shift and the scattered light intensity may be too low to be accurately measured, due also to the spurious light from the high-intensity main laser beam. So, this methodology is indeed interesting for high-quality LPA due to its relatively simple implementation, but would be useful mainly for free-electron densities in the range
![]() $10^{18}$
–
$10^{18}$
–
![]() $10^{19}~\text{cm}^{-3}$
.
$10^{19}~\text{cm}^{-3}$
.
Besides forward and backward Raman scattering, it is worth noting that the measurement of side Raman scattering of the main laser pulse interacting with the plasma can also provide a monitor of the electron number density[Reference Thomas, Mangles, Najmudin, Kaluza, Murphy and Krushelnick71]. A systematic experimental investigation of the spatial–spectral properties of the side emission scattered out of the polarization plane of the drive intense laser pulse during LWFA has shown a correlation between the wavelength shift of the Stokes line of Raman side scattering and the electron number density[Reference Cole72]. In the specific case, a detailed analysis of the recorded spectral shifts as a function of the electron number density, measured independently by interferometry in the range
![]() $10^{18}{-}10^{19}~\text{cm}^{-3}$
, revealed a very good agreement with relativistic stimulated Raman scattering theory in plasmas at a high laser intensity, demonstrating the feasibility of Raman side scattering measurements as a density diagnostic tool. From a practical point of view, side Raman scattering measurements, being somehow easier to implement than forward and backward scattering measurements, could provide an online monitor of the accelerator performance as well as a density monitor during alignment, optimization and operation of an LPA once it is calibrated by means of other methodologies (for example, interferometry).
$10^{18}{-}10^{19}~\text{cm}^{-3}$
, revealed a very good agreement with relativistic stimulated Raman scattering theory in plasmas at a high laser intensity, demonstrating the feasibility of Raman side scattering measurements as a density diagnostic tool. From a practical point of view, side Raman scattering measurements, being somehow easier to implement than forward and backward scattering measurements, could provide an online monitor of the accelerator performance as well as a density monitor during alignment, optimization and operation of an LPA once it is calibrated by means of other methodologies (for example, interferometry).
4 Conclusions
For LPA stages in the range 0.1–1 GeV (for example, injector in multi-stage systems) the corresponding electron density is in the range from a few
![]() $10^{17}~\text{cm}^{-3}$
up to a few
$10^{17}~\text{cm}^{-3}$
up to a few
![]() $10^{18}~\text{cm}^{-3}$
(lower density
$10^{18}~\text{cm}^{-3}$
(lower density
![]() $\rightarrow$
higher energy), and target configuration may be mm-long gas jets or gas flow cells. The 2D SHI potentially has the capability of accurate diagnostics for the electron density in the low density range, but further development is necessary to validate the ultra-fast and 2D imaging configuration. At higher density and/or greater plasma lengths the WF-sensor-based instrument provides a good solution for 2D mapping with ultra-fast resolution. Concerning neutral gas density measurements in the range
$\rightarrow$
higher energy), and target configuration may be mm-long gas jets or gas flow cells. The 2D SHI potentially has the capability of accurate diagnostics for the electron density in the low density range, but further development is necessary to validate the ultra-fast and 2D imaging configuration. At higher density and/or greater plasma lengths the WF-sensor-based instrument provides a good solution for 2D mapping with ultra-fast resolution. Concerning neutral gas density measurements in the range
![]() $10^{17}{-}10^{19}~\text{cm}^{-3}$
, 1D SHI provides a ready solution for real-time monitoring, while the WF sensor is suitable for 2D mapping.
$10^{17}{-}10^{19}~\text{cm}^{-3}$
, 1D SHI provides a ready solution for real-time monitoring, while the WF sensor is suitable for 2D mapping.
For LPA stage(s) requiring greater acceleration lengths to reach electron energies of several GeV, plasma channels with densities in the range
![]() $10^{17}{-}10^{19}~\text{cm}^{-3}$
provide adequate target structures. In this context, small-diameter plasma channels created with a laser pre-pulse in gas cells are open structures that can allow transverse interferometry: at lower density only the ultra-fast 2D SHI may be useful, while at higher density the WF-sensor-based instrument may be adequate. However, this LPA configuration is difficult to control, involving two separate laser beams, and may pose serious challenges when adopted in user-oriented high-quality accelerators.
$10^{17}{-}10^{19}~\text{cm}^{-3}$
provide adequate target structures. In this context, small-diameter plasma channels created with a laser pre-pulse in gas cells are open structures that can allow transverse interferometry: at lower density only the ultra-fast 2D SHI may be useful, while at higher density the WF-sensor-based instrument may be adequate. However, this LPA configuration is difficult to control, involving two separate laser beams, and may pose serious challenges when adopted in user-oriented high-quality accelerators.
Concerning plasma channels created by a discharge in a capillary, they do not allow for transverse interferometry unless a square capillary cross-section is used. Then, Stark broadening/Raman scattering measurements and/or longitudinal interferometry may be adopted. Significantly, spectral-domain second-harmonic interferometry has recently been demonstrated to be an elegant and suitable methodology to monitor discharged gas-filled capillaries longitudinally. Combining simultaneous group-delay and spectral phase measurements, a high phase resolution has been achieved in measurements spanning multiple fringes.
TAI interferometers are in general less suitable for implementation during operation and they may be more useful during alignment/tuning of the system due to their well-established use in research laboratories.
Acknowledgements
This work received support from the European Unions Horizon 2020 research and innovation program under Grant Agreement No. 653782-EuPRAXIA, and the MIUR-funded Italian research Network ELI-Italy.