1. Introduction
High power solid-state laser facilities for Inertial Confinement Fusion (ICF) employ thousands of large optical components, including amplifiers, polarizing films, electro-optical switches, lenses, and mirrors[Reference Trummer, Foley and Shaw1–Reference Qiao, Kalb, Guardalben, King, Canning and Kelly3]. These components usually possess large sizes and weights; some of them have diameters larger than half a meter and weigh up to hundreds of kilogram. The performance of these components is easily influenced by material non-uniformity, manufacturing errors, assembly stresses, and temperature changes[Reference Williams, Auerbach and Henesian4]. For example, while the surfaces of large-aperture lenses can be accurately manufactured, their large weight and size cause deformations due to gravity, and assembly stress formed during installation may introduce remarkable changes in their shapes[Reference Williams, Auerbach, Henesian, Lawson, Renard and Sacks5]. These variations, in turn, introduce significant aberrations to the passing laser beam. Wavefront distortion causes irregular malformation of far-field beams and reduction of the through-hole efficiency of spatial filtering; the frequency doubling efficiency is also substantially decreased, leading to serious degradation in the performance of the entire facility[Reference Van Wonterghem, Salmon and Wilcox6]. Low frequency wavefront distortion changes the spatial distribution of the focal spot[Reference Williams, Auerbach and Henesian4], whereas high frequency wavefront distortion, which results from the noise of phase perturbation, may lead to self-focusing inside the optical components and generate serious material damage[Reference Bespalov and Talanov7]. Extremely accurate techniques are necessary in laser beam sensing and optical component measurement to satisfy the requirements of ICF systems for laser beam wavefronts. High precision measurements of optical components and laser beams are important endeavors in ICF research.
Wavefronts in high power lasers possess two distinguishing features. First, the laser beam to be measured is pulsed, which makes extraction of phase information using conventional phase-shifting techniques difficult. Second, the space for pulse synchronization and wave shaping optics inside the laser driver system is insufficient. An ideal phase measurement technique for an ICF system should feature high spatial resolution, high accuracy, simple setup, and rapid data acquisition. Given that most of the commonly used devices for wavefront measurement are unable to satisfy all of these requirements simultaneously and that the number of phase measurement techniques applicable to an ICF system is limited, several measurement techniques must be used in combination to obtain the required accuracy.
First, the current paper presents a general discussion on the wavefront measurement techniques applicable in ICF systems. Second, three traditional measurement methods, namely the Hartmann–Shack wavefront sensor, interferometry, and the knife-edge test, as well as their advantages and disadvantages, are discussed. Third, the development of Coherent Diffraction Imaging (CDI) and its application in high power laser systems is introduced in detail. Fourth, some newly developed techniques including the Ptychographical Iterative Engine (PIE) and Phase Modulation (PM) are introduced; some of their applications and potential applications in the field of high power laser systems are also demonstrated.

Figure 1. Schematic of a Hartmann–Shack sensor.

Figure 2. Overview of an OMEGA EP, showing the relative location of the main laser beam and the sample beam used by diagnostics for on-shot measurement of the laser properties. The FSD wavefront sensor is one of many laser diagnostics that characterize the sample beam (from Ref. [Reference Bromage, Bahk, Irwin, Kwiatkowski, Pruyne, Millecchia, Moore and Zuegel10]).

Figure 3. FSD measurements using the OPCPA front end (by Bromage). (a) Raw Hartmann–Shack image with inset showing the spots formed by each lenslet, (b) fluence (normalized), and (c) wavefront (in units of waves) (from Ref. [Reference Bromage, Bahk, Irwin, Kwiatkowski, Pruyne, Millecchia, Moore and Zuegel10]).

Figure 4. Same-shot measurements of a focal spot using the FSD and FSM (by Bromage) and the diffraction-limited (DL) spot, which are calculated by setting the wavefront error to zero. (a–c) Linear scale plots; (d–f) logarithmic scale plots. The circles contain 80% of the energy (from Ref. [Reference Bromage, Bahk, Irwin, Kwiatkowski, Pruyne, Millecchia, Moore and Zuegel10]).

Figure 5. Testing results of an ICF system. (a) Radial shearing interferogram with spatial PM, (b) phase of the tested laser wavefront, and (c) amplitude of the tested laser wavefront (from Ref. [Reference Liu, Yang, Weng, Zhang, Chen and Qin14]).
2. Traditional methods of phase measurement
Commonly used phase measurement techniques for ICF systems include the Hartmann–Shack wavefront sensor, interferometry, and the knife-edge technique, all of which are well-developed and commercialized techniques. The Hartmann–Shack wavefront sensor is used to detect online wavefronts and realize feedback control because of its high data acquisition speed and rapid computational processing. Interferometry is used to evaluate the properties of the optical elements. The knife-edge technique, which features the simplest structure among the three phase measurement techniques, is used to evaluate the characteristics of optics qualitatively. Apart from these traditional measurement techniques, the CDI method, which was developed for X-ray and electron beam imaging, is also used in some special cases and has shown significant advantages in high power lasers.
2.1. Hartmann–Shack wavefront sensor
The Hartmann–Shack wavefront sensor is mainly composed of a micro-lens array and a CCD camera (Figure 1). The focal spot array of an ideal plane wave is used as the reference pattern when a deformed wavefront is measured, and the focal spots of the deformed wavefront shift from that of the reference beam. The spot deviation of ![]() $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\Delta y$ in the
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\Delta y$ in the ![]() $y$ direction is related to the slope of the deformed wavefront:
$y$ direction is related to the slope of the deformed wavefront:
where ![]() $f$ is the focal length of the lenslet. In this way, the wavefront distortion is converted to the spot offsets at the CCD sensor plane, and the phase map of the wavefront can be generated by integrating the calculated slope.
$f$ is the focal length of the lenslet. In this way, the wavefront distortion is converted to the spot offsets at the CCD sensor plane, and the phase map of the wavefront can be generated by integrating the calculated slope.
The most remarkable advantages of the Hartmann–Shack sensor are its simple structure and rapid data processing; these merits allow the use of the sensor in measurement of dynamic wavefronts[Reference Brennan and Wittich8], evaluation of laser beam quality, and realization of closed-loop wavefront control in combination with adaptive optics[Reference Saad and Martin9]. However, given its limited number of micro-lenses, low resolution is an inherent disadvantage of the Hartmann–Shack sensor. Most commercial Hartmann–Shack sensors have a limited number of micro-lenses. As such, only the low frequency components of the wavefront can be measured, which results in low accuracy measurements.
In OMEGA EP system, a Hartmann–Shack sensor of ![]() $133 \times 133$ lenslets is applied to set up a focal spot diagnostic (FSD) system to measure a lower energy sample of the main beam that is attenuated and down-collimated to a more convenient beam size (
$133 \times 133$ lenslets is applied to set up a focal spot diagnostic (FSD) system to measure a lower energy sample of the main beam that is attenuated and down-collimated to a more convenient beam size (![]() $12\ \mathrm{mm}\times 12\ \mathrm{mm}$). Stretched pulses (250 mJ, 8 nm square spectrum, 5 Hz) are amplified using a multipass Nd:glass amplifier and compressed by a tiled-grating compressor, then 99.5% of the compressed pulse energy is reflected by a diagnostic pickoff mirror and the remainder is transmitted as a sample beam for the laser diagnostics package. The Hartmann–Shack sensor is positioned at an image plane conjugate to the fourth compressor grating, as shown in Figure 2. A local wavefront gradient as high as 15 mrad can be measured[Reference Bromage, Bahk, Irwin, Kwiatkowski, Pruyne, Millecchia, Moore and Zuegel10]. The FSD is qualified using a sequence of experiments designed to compare measurements made by the FSD and focal-spot microscope (FSM). Figure 3 shows some of the measurement results of the FSD wavefront sensor in these experiments; wave-plate throttles are set so that
$12\ \mathrm{mm}\times 12\ \mathrm{mm}$). Stretched pulses (250 mJ, 8 nm square spectrum, 5 Hz) are amplified using a multipass Nd:glass amplifier and compressed by a tiled-grating compressor, then 99.5% of the compressed pulse energy is reflected by a diagnostic pickoff mirror and the remainder is transmitted as a sample beam for the laser diagnostics package. The Hartmann–Shack sensor is positioned at an image plane conjugate to the fourth compressor grating, as shown in Figure 2. A local wavefront gradient as high as 15 mrad can be measured[Reference Bromage, Bahk, Irwin, Kwiatkowski, Pruyne, Millecchia, Moore and Zuegel10]. The FSD is qualified using a sequence of experiments designed to compare measurements made by the FSD and focal-spot microscope (FSM). Figure 3 shows some of the measurement results of the FSD wavefront sensor in these experiments; wave-plate throttles are set so that ![]() $400\, \mu \mathrm{J}$ of the 100 mJ front end is focused in the target chamber, which provides enough energy for the FSD wavefront sensor and is not too high for the FSM. The image plane for this sensor is the last of the four tiled gratings inside the compressor. Figure 3(a) illustrates the raw data of the Hartmann–Shack sensor, Figure 3(b) shows the measured fluence of the near-field, and Figure 3(c) shows the corresponding measured wavefront. The performance of this system is evaluated by comparing its measurement results with those of the FSM system, which can be assumed to be correct. Figures 4(a) and (b) indicate the distributions of the focal spot measured using the FSD and FSM systems, respectively. Given the finite spatial resolution of the FSD wavefront sensor (
$400\, \mu \mathrm{J}$ of the 100 mJ front end is focused in the target chamber, which provides enough energy for the FSD wavefront sensor and is not too high for the FSM. The image plane for this sensor is the last of the four tiled gratings inside the compressor. Figure 3(a) illustrates the raw data of the Hartmann–Shack sensor, Figure 3(b) shows the measured fluence of the near-field, and Figure 3(c) shows the corresponding measured wavefront. The performance of this system is evaluated by comparing its measurement results with those of the FSM system, which can be assumed to be correct. Figures 4(a) and (b) indicate the distributions of the focal spot measured using the FSD and FSM systems, respectively. Given the finite spatial resolution of the FSD wavefront sensor (![]() $133\times 133$ lenslets), the wavefront cannot be captured accurately and the fine details of the focal spot cannot be faithfully represented; however, the encircled energies of these two measurements show good agreement. Figures 4(d) and (e) show the spot distributions in logarithmic scales to demonstrate their difference more clearly.
$133\times 133$ lenslets), the wavefront cannot be captured accurately and the fine details of the focal spot cannot be faithfully represented; however, the encircled energies of these two measurements show good agreement. Figures 4(d) and (e) show the spot distributions in logarithmic scales to demonstrate their difference more clearly.
The Hartmann–Shack sensor is also used at National Ignition Facility (NIF)[Reference Zacharias, Beer, Bliss, Burkhart, Cohen, Sutton, Van Atta, Winters, Salmon, Latta, Stolz, Pigg and Arnold2] for phase measurements, where the beam passes though a micro-lens array and is focused on a CCD. A hexagonal lens array of 77 micro-lenses is used to form the focal spot array and a measurement accuracy of ![]() $0.1\lambda $ is achieved at 1.053 mm in the offline test.
$0.1\lambda $ is achieved at 1.053 mm in the offline test.
In most cases, measurements obtained using the Hartmann–Shack sensor present the closest real wavefront, but the resolution and accuracy of this technique are significantly lower than those obtained from interferometry.

Figure 6. Designed and measured surfaces of a CPP with 380 mm diameter (from Ref. [Reference Wen, Shi, Yan, Zhang, Yang and Wang18]).
2.2. Interferometry
2.2.1. Traditional interferometry
Interferometry is a classic method to determine phase distributions and detect wavefronts. The light wave to be measured initially interferes with a regular spherical or planar reference wave to generate interference fringe patterns, and the resultant phase distribution is extracted from the recorded fringes using various methods, including phase shifting and fringe carriers. Given that interferometry is remarkably sensitive to environmental turbulence, such as mechanical vibration and air fluence, the interferometer must be installed on a vibration-isolated table inside a room at constant temperature and humidity to achieve high accuracy. Using the phase-shift technique and high resolution CCD, the highest measurement accuracy of interferometry can reach ![]() $\lambda /1000$ in theory. Although the accuracy of interferometry is significantly higher than that of other techniques, its setup complexity and high requirement on its working environment limit its application in high power laser systems.
$\lambda /1000$ in theory. Although the accuracy of interferometry is significantly higher than that of other techniques, its setup complexity and high requirement on its working environment limit its application in high power laser systems.
Interferometers used in high power lasers must possess large apertures because the diameters of large optical elements can reach up to half a meter. Given the difficulties associated with fabricating large reference standard mirrors and the related optical components, the cost of an interferometer increases drastically with its diameter, and its requirements on the working environment become more difficult to satisfy. To detect the machining quality of optical elements used at NIF, VEECO (USA) developed seven large Fizeau interferometers with diameters of up to 610 mm[Reference Ai, Knowiden and Lamb11]; the highest measurement precision of these instruments reached ![]() $\lambda /10$ (PV) and the measurement repeatability depended on the test surface gradient. The interferometer applied by the French Atomic Energy Commission (CEA) has a diameter of 800 mm and is the largest interferometer ever reported. In addition to optical element measurements, the Fizeau laser interferometer is also used in adjusting the optical alignment[Reference Williams, Auerbach and Henesian4].
$\lambda /10$ (PV) and the measurement repeatability depended on the test surface gradient. The interferometer applied by the French Atomic Energy Commission (CEA) has a diameter of 800 mm and is the largest interferometer ever reported. In addition to optical element measurements, the Fizeau laser interferometer is also used in adjusting the optical alignment[Reference Williams, Auerbach and Henesian4].
Interferometers are capable of performing phase measurement with high accuracy and can meet the requirements of most high power laser applications in terms of resolution and aperture size. However, the use of interferometers to detect wavefronts online is difficult because of their complex structure and complicated environmental requirements.
2.2.2. Shearing interferometry
The reference standard mirror used in classic interferometry must be fabricated at an accuracy one order higher than that for a common optical element. Fabrication of a large reference mirror that is suitable for use in high power lasers remains challenging. Shearing interferometers do not need an accurate reference standard mirror; they possess simple structures, strong anti-interference abilities, and stable stripes. In theory, shearing interferometers are a good alternative to traditional interferometers for measuring the quality of optical elements and light beam wavefronts. Shearing interferometers can be classified into lateral and radial shearing interferometers. Given that two orthogonal shearing interferograms at precise displacements in the ![]() $x$ and
$x$ and ![]() $y$ directions are necessary for lateral shearing interferometers, the wavefront retrieval process is markedly complex and error prone. Although the cross-grating lateral shearing interferometer has been proposed to test the density distribution of deuterium–tritium (DT) ice in ICF experiments and the root-mean-square error has been found to be
$y$ directions are necessary for lateral shearing interferometers, the wavefront retrieval process is markedly complex and error prone. Although the cross-grating lateral shearing interferometer has been proposed to test the density distribution of deuterium–tritium (DT) ice in ICF experiments and the root-mean-square error has been found to be ![]() ${<}\lambda /15$[Reference Ling, Liu, Sun, Yang and Cheng12] in theory, no experimental result has yet been reported. The radial shearing interferometer introduces radially symmetric shearing by interfering with the wavefront with an expanded copy of itself[Reference Malacara13]. The wavefronts are measured with high precision without setting special reference light beams. The radial shearing interferometer is also sensitive to mechanical vibrations and disturbances in the environment. The accuracy of radial shearing interferometers is better than that of Zygo interferometers in the comparison made by Liu[Reference Liu, Yang, Weng, Zhang, Chen and Qin14], yielding an error of
${<}\lambda /15$[Reference Ling, Liu, Sun, Yang and Cheng12] in theory, no experimental result has yet been reported. The radial shearing interferometer introduces radially symmetric shearing by interfering with the wavefront with an expanded copy of itself[Reference Malacara13]. The wavefronts are measured with high precision without setting special reference light beams. The radial shearing interferometer is also sensitive to mechanical vibrations and disturbances in the environment. The accuracy of radial shearing interferometers is better than that of Zygo interferometers in the comparison made by Liu[Reference Liu, Yang, Weng, Zhang, Chen and Qin14], yielding an error of ![]() ${<}1/1000\, \lambda $ in computer simulations. Figure 5 shows practical testing results from a 1064 nm pulse laser using a radial shearing interferometer in the ICF system.
${<}1/1000\, \lambda $ in computer simulations. Figure 5 shows practical testing results from a 1064 nm pulse laser using a radial shearing interferometer in the ICF system.
Given that shearing interferometers measure the phase variance and that the measured phase map indicates the differential distribution of the wavefront, these instruments are not as intuitive as classic interferometers. Complicated imaging processing and wavefront reconstruction algorithms are necessary to retrieve the wavefront from the differential data, thereby limiting the applications of shearing interferometers.
2.2.3. Subaperture stitching method
In classical interferometry, the elements to be measured are imaged by a CCD camera. Thus, the resolution is ![]() $L/N$, where
$L/N$, where ![]() $L$ is the size of the element to be measured and
$L$ is the size of the element to be measured and ![]() $N$ is the pixel number of the CCD camera. The spatial resolution of a 400 mm diameter element and a CCD with
$N$ is the pixel number of the CCD camera. The spatial resolution of a 400 mm diameter element and a CCD with ![]() $2048\ \mathrm{pixels}\times 2048\ \mathrm{pixels}$ is approximately
$2048\ \mathrm{pixels}\times 2048\ \mathrm{pixels}$ is approximately ![]() $195\ \mu \mathrm{m}$, which is too low for most high power laser applications. Subaperture stitching interferometers can measure the large optical components of various subapertures, after which the measurements are stitched together to obtain a high resolution. This measurement method has been used to measure large optical elements with sizes of up to
$195\ \mu \mathrm{m}$, which is too low for most high power laser applications. Subaperture stitching interferometers can measure the large optical components of various subapertures, after which the measurements are stitched together to obtain a high resolution. This measurement method has been used to measure large optical elements with sizes of up to ![]() $800\ \mathrm{mm}\times 400\ \mathrm{mm}$ at Laser Méga Joule and NIF[Reference Wolfe, Downie and Lawson15–Reference Bray17]. Wen[Reference Wen, Shi, Yan, Zhang, Yang and Wang18] successfully measured a continuous phase plate (CPP) using the subaperture stitching method, the global least squares method, and the image fusion technique. Figure 6 shows the designed and measured CPP surfaces (380 mm diameter). The original stitching method only detects low order components of the surface by fitting polynomials to non-overlapping subapertures[Reference Thunen and Kwon19, Reference Chow and Lawrence20]; by contrast, the stitching method of overlapping subapertures and connecting interferograms minimizes the error of connection down to
$800\ \mathrm{mm}\times 400\ \mathrm{mm}$ at Laser Méga Joule and NIF[Reference Wolfe, Downie and Lawson15–Reference Bray17]. Wen[Reference Wen, Shi, Yan, Zhang, Yang and Wang18] successfully measured a continuous phase plate (CPP) using the subaperture stitching method, the global least squares method, and the image fusion technique. Figure 6 shows the designed and measured CPP surfaces (380 mm diameter). The original stitching method only detects low order components of the surface by fitting polynomials to non-overlapping subapertures[Reference Thunen and Kwon19, Reference Chow and Lawrence20]; by contrast, the stitching method of overlapping subapertures and connecting interferograms minimizes the error of connection down to ![]() $\lambda /20$[Reference Otsubo, Okada and Tsujiuchi21].
$\lambda /20$[Reference Otsubo, Okada and Tsujiuchi21].
The use of subaperture stitching interferometers significantly reduces cost and increases spatial resolution[Reference Chen, Li, Dai and Zheng22] and measurement accuracy[Reference Fleig, Dumas, Murphy and Forbes23]. However, the subaperture stitching method possesses inherent disadvantages. First, this method requires a high quality standard mirror, which is difficult to fabricate. Second, error transfer and the unstable solution are unavoidable sources of errors, which make it difficult to obtain sufficiently high measurement accuracy. In addition, the subaperture stitching interferometer detection process is time consuming, and the requirements of environmental stability are remarkably complicated.
2.3. Knife-edge test method
2.3.1. Traditional Foucault method
The knife-edge method was proposed by Foucault in 1858[Reference Malacara13]. The geometric principle of the knife-edge test is shown in Figure 7, where ![]() $\mathit{AA}'$ is an ideal spherical surface with center
$\mathit{AA}'$ is an ideal spherical surface with center ![]() $o$. When a point source is placed at
$o$. When a point source is placed at ![]() $o$, the light from
$o$, the light from ![]() $o$ to
$o$ to ![]() $\mathit{AA}'$ coincides with the normal direction of the corresponding surface element and the reflected light returns to
$\mathit{AA}'$ coincides with the normal direction of the corresponding surface element and the reflected light returns to ![]() $o$. When the knife-edge cuts the reflected beam from right to left, the mirror is observed behind the knife-edge. When the knife-edge is located at position 1, the shadow on
$o$. When the knife-edge cuts the reflected beam from right to left, the mirror is observed behind the knife-edge. When the knife-edge is located at position 1, the shadow on ![]() $\mathit{AA}'$ darkens from right to left, i.e., the shadow and knife-edge move in the same direction. The entire field is bright if the knife-edge has not met point
$\mathit{AA}'$ darkens from right to left, i.e., the shadow and knife-edge move in the same direction. The entire field is bright if the knife-edge has not met point ![]() $o$ and when the knife-edge is located at position 2, which is at the center of the sphere;
$o$ and when the knife-edge is located at position 2, which is at the center of the sphere; ![]() $\mathit{AA}'$ darkens immediately when the knife-edge first cuts through point
$\mathit{AA}'$ darkens immediately when the knife-edge first cuts through point ![]() $o$. When the knife-edge cuts the light at position 3, the shadow on
$o$. When the knife-edge cuts the light at position 3, the shadow on ![]() $\mathit{AA}'$ darkens from left to right, which is opposite to the moving direction of the knife-edge. This method is sensitive to slopes rather than heights, and only one direction can be measured at a single orientation of the knife-edge.
$\mathit{AA}'$ darkens from left to right, which is opposite to the moving direction of the knife-edge. This method is sensitive to slopes rather than heights, and only one direction can be measured at a single orientation of the knife-edge.

Figure 7. Geometric principle of the knife-edge test.
Given that only qualitative measurements can be realized by the traditional Foucault test method, a digitized Foucault tester (Figure 8) is used for quantitative measurements.
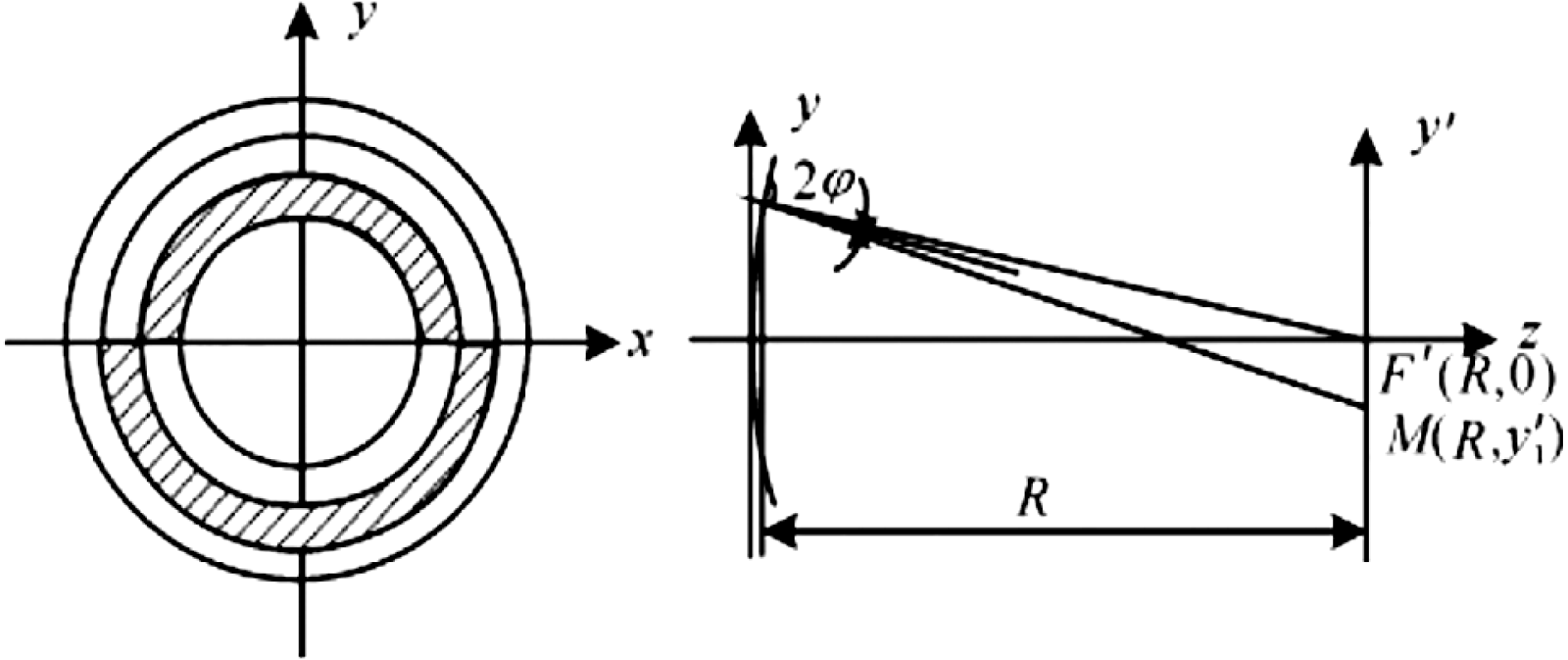
Figure 8. Principle of a digitized Foucault tester.
When a point source is located at the center of a spherical mirror, the returning beam focuses on the same position as the point source if the mirror under testing possesses an ideal spherical surface. When defects are present on the surface of the mirror, the returning beam deviates from the focal point and reaches a new location. The angle by which it departs from the ideal position can be calculated as follows:
where ![]() $n$ is the refractive index of air and
$n$ is the refractive index of air and ![]() $\Delta \omega (x,y)$ is the wave aberration. The deviation of the returning beam from the ideal position
$\Delta \omega (x,y)$ is the wave aberration. The deviation of the returning beam from the ideal position ![]() $E_{x}$ and
$E_{x}$ and ![]() $E_{y}$ can be calculated from the location of the knife-edge, and the wave aberration of the mirror can be obtained using
$E_{y}$ can be calculated from the location of the knife-edge, and the wave aberration of the mirror can be obtained using
where ![]() $E_{x}=R\varphi _{x}$,
$E_{x}=R\varphi _{x}$, ![]() $E_{y}=R\varphi _{y}$, and
$E_{y}=R\varphi _{y}$, and ![]() $R$ is the radius of curvature.
$R$ is the radius of curvature.
The performance of the digitized Foucault test method has been compared with that of interferometry[Reference Vandenberg, Humbel and Wertheimer24, Reference Yuan and Wu25]; when the air turbulence is totally eliminated, the precision of the former is comparable with that of the latter. Foucault testers have been used in nonlinear measurement of wavefront sensorless adaptive optics systems[Reference Song, Vdovin, Fraanje, Schitter and Verhaegen26] as well as in measurements of mid-frequency surface errors in ICF[Reference Xuan, Li, Song and Xie27]. However, given that the Foucault tester has strict testing environment requirements, even slight turbulence in the optical path may cause remarkable image distortion and affect the final test results. Thus, significant improvements are needed to enable the use of this method in high power laser applications.
3. CDI technology and its applications
3.1. Development of CDI
CDI is a phase-retrieval method based on computer iterative calculations. The original purpose of CDI is imaging of the wave phase using X-rays and electron beams when high quality optics are unavailable. Given its outstanding advantages, which include simple setup, compact structure, and low environmental requirements, CDI has been used in high power laser systems to measure wavefronts and predict focus.
The principle of CDI was first developed by Hoppe in the 1970s and then improved by Fienup. The main theories include the Gerchberg–Saxton (G–S) algorithm, the error-reduction algorithm, and the input–output algorithm[Reference Fienup28]. These algorithms have been widely used in X-ray and electron imaging[Reference Zuo, Vartanyants, Gao, Zhang and Nagahara29, Reference Williams, Quiney, Dhal, Tran, Nugent, Peele, Paterson and de Jonge30]. The traditional CDI method suffers from disadvantages with respect to viewing field, convergence speed, and reliability. To overcome these disadvantages, Rodenburg[Reference Rodenburg and Faulkner31] proposed an improved phase retrieval algorithm called PIE, which used a Wegener filter-like algorithm to reconstruct images iteratively from a set of diffraction patterns and extended it to an extended PIE (ePIE) algorithm to obtain an accurate model of the illumination and specimen functions simultaneously. PIE and ePIE are promising algorithms for imaging using X-rays[Reference Weierstall, Chen, Spence, Howells, Isaacson and Panepucci32, Reference Chapman33], electron beams[Reference Hüe, Rodenburg, Maiden, Sweeney and Midgley34, Reference Humphry, Kraus, Hurst, Maiden and Rodenburg35], and visible light[Reference Osherovich, Shechtman, Szameit, Sidorenko, Bullkich, Gazit, Shoham, Kley, Zibulevsky, Yavneh, Eldar, Cohen and Segev36, Reference Szameit, Shechtman, Osherovich, Bullkich, Sidorenko, Dana, Steiner, Kley, Gazit, Cohen-Hyams, Shoham, Zibulevsky, Yavneh, Eldar, Cohen and Segev37]. Given that the CDI algorithms can directly measure the phase distribution of a laser beam from the recorded diffraction intensity, they are often used in various high power laser applications, including wavefront detection, large optical element measurement, and FSDs.
3.2. Applications of traditional CDI
The wavefront of a high power laser system is easily distorted because of the high complexity of the system, which contains thousands of optical elements. The wavefront of the laser beam is difficult to control because it involves routing tasks of all of the ICF facilities. However, most of the commonly used measurement techniques do not satisfy the requirements for accurate online measurement because of the compact structure and limited inner space of CDI. In 2000, CDI was first used to measure the phase of high power laser beams[Reference Matsuoka and Yamakawa38]. The intensity of the laser beam at two different planes vertical to the optical axis were recorded, and the Fresnel phase-retrieval algorithm based on the G–S algorithm and the Fienup phase-retrieval algorithm was used to reconstruct the complex amplitudes of these two recording planes. Figure 9 shows the experimental results, where the first two images from the left of each row indicate the laser intensities at the two recording planes; the third image provides the measured phase distribution of the laser beam.

Figure 9. Measured intensity distributions (image 1 and image 2) and reconstructed wavefronts of 100 fs pulses at different output power levels (from Ref. [Reference Matsuoka and Yamakawa38]).

Figure 10. Experimental arrangement used for phase retrieval measurements (from Ref. [Reference Brady and Fienup39]).
In 2006 Brady and Fienup[Reference Brady and Fienup39] measured a concave spherical mirror using the CDI method (setup shown in Figure 10), where a He–Ne laser was filtered by a microscope objective and a pinhole placed near the center of curvature of the concave spherical mirror was used as the illumination beam; the intensity distributions of the resulting diffraction spots were measured using a CCD mounted on a computer-controlled translation stage, which could accurately shift along the optical axis. The measurement results are shown in Figure 11, where the images in the top row are the recorded diffraction intensities and the images in the bottom row are the obtained surface shapes. However, the accuracy of these results is not ensured because the element is not measured independently using an instrument with sufficient accuracy. The diameter of the optical elements used in the high power laser system is up to half a meter, and numerous optical elements possess large surface curvatures. Given that the common interferometer or Hartmann–Shack sensor is incapable of measuring large phase slopes, the measurement of the complex reflectance or transmittance of these large elements is fairly challenging, but CDI method can be used to solve this problem.
Knowledge of the focus is important in conducting physical experiments. The focal spots of a high power laser system can be highly structured because of the complexity of the facility, which contains hundreds of optical surfaces. However, measurement of the focus field varies significantly[Reference Zacharias, Beer, Bliss, Burkhart, Cohen, Sutton, Van Atta, Winters, Salmon, Latta, Stolz, Pigg and Arnold2, Reference Kessler, Bunkenburg, Huang, Kozlov and Meyerhofer40] because direct measurement of the focus is impossible at extreme intensities. Multiple focal-plane spatial phase retrieval for a chirped-pulse-amplification laser was demonstrated by Bahk in 2008[Reference Bahk, Bromage, Zuegel and Fienup41, Reference Bahk, Bromage, Begishev, Mileham, Stoeckl, Storm and Zuegel42]. The wavefront measured by phase retrieval is used to predict focal spots at high energies via separate measurement of the differential wavefront changes. Comparison of the measured and the predicted focal spots is shown in Figure 12, where the directly measured focal spot is shown in Figure 12(a); this spot agrees well morphologically with the predicted focal spot shown in Figure 12(b). The application of phase retrieval helps to extend the capability of FSDs for high intensity lasers beyond conventional direct wavefront measurements.
In 2010, the CDI algorithm was used to form a FSD to predict the focus of an OMEGA EP laser at the University of Rochester’s Laboratory for Laser Energetics[Reference Kruschwitz, Bahk, Bromage, Irwin, Moore, Waxer, Zuegel and Kelly43]. The short-pulse diagnostic package contained a FSD which received a sampled beam downstream and a far-field CCD camera imaging the far-field intensity of the sample beam. The phase was initially retrieved from the sample beam to remove the differential piston uncertainty. Using a dense quasi-Newton downhill search algorithm to modify the optimization parameters for the subsequent iterations, the FSD prediction improved significantly compared with the initial FSD prediction, with the correlations for the diagnostic and target beams increased from ![]() $0.87\pm 0.04$ and
$0.87\pm 0.04$ and ![]() $0.82\pm 0.04$ to
$0.82\pm 0.04$ to ![]() $0.96\pm 0.01$ and
$0.96\pm 0.01$ and ![]() $0.87\pm 0.02$, respectively. The error in the transfer wavefront measurement was then measured by CDI using the data recorded in the FSM. The correlation between the FSD prediction and the direct FSM measurement was improved to
$0.87\pm 0.02$, respectively. The error in the transfer wavefront measurement was then measured by CDI using the data recorded in the FSM. The correlation between the FSD prediction and the direct FSM measurement was improved to ![]() $0.93\pm 0.02$ using the corrected transfer wavefront. Using the measured complex amplitude and transfer function, the focal spot of the main laser beam inside the chamber could be accurately predicted.
$0.93\pm 0.02$ using the corrected transfer wavefront. Using the measured complex amplitude and transfer function, the focal spot of the main laser beam inside the chamber could be accurately predicted.
This diagnostic method was evaluated on the OMEGA EP laser beam over a population of 175 shots to illustrate its reliability and stability; the evaluation was conducted for approximately 18 months from 2010 to 2012[Reference Kruschwitz, Bahk, Bromage and Irwin44]. Figure 13(a) shows the frequency of cross-correlation values between the FSD and the far-field CCD. A significant improvement in performance was obtained after the phase-retrieved corrections were applied; the mean cross-correlation increased from 0.83 to 0.96. Figure 13(b) shows the results of more stringent testing of the FSD measurement accuracy; the cross-correlation values (reliability ![]() ${>} 0.9$ with
${>} 0.9$ with ![]() ${>}95{\%}$ probability) between the measurements of FSD and FSM are also indicated. These diagnostics are used as a key tool for focal spot checking in the OMEGA EP laser.
${>}95{\%}$ probability) between the measurements of FSD and FSM are also indicated. These diagnostics are used as a key tool for focal spot checking in the OMEGA EP laser.
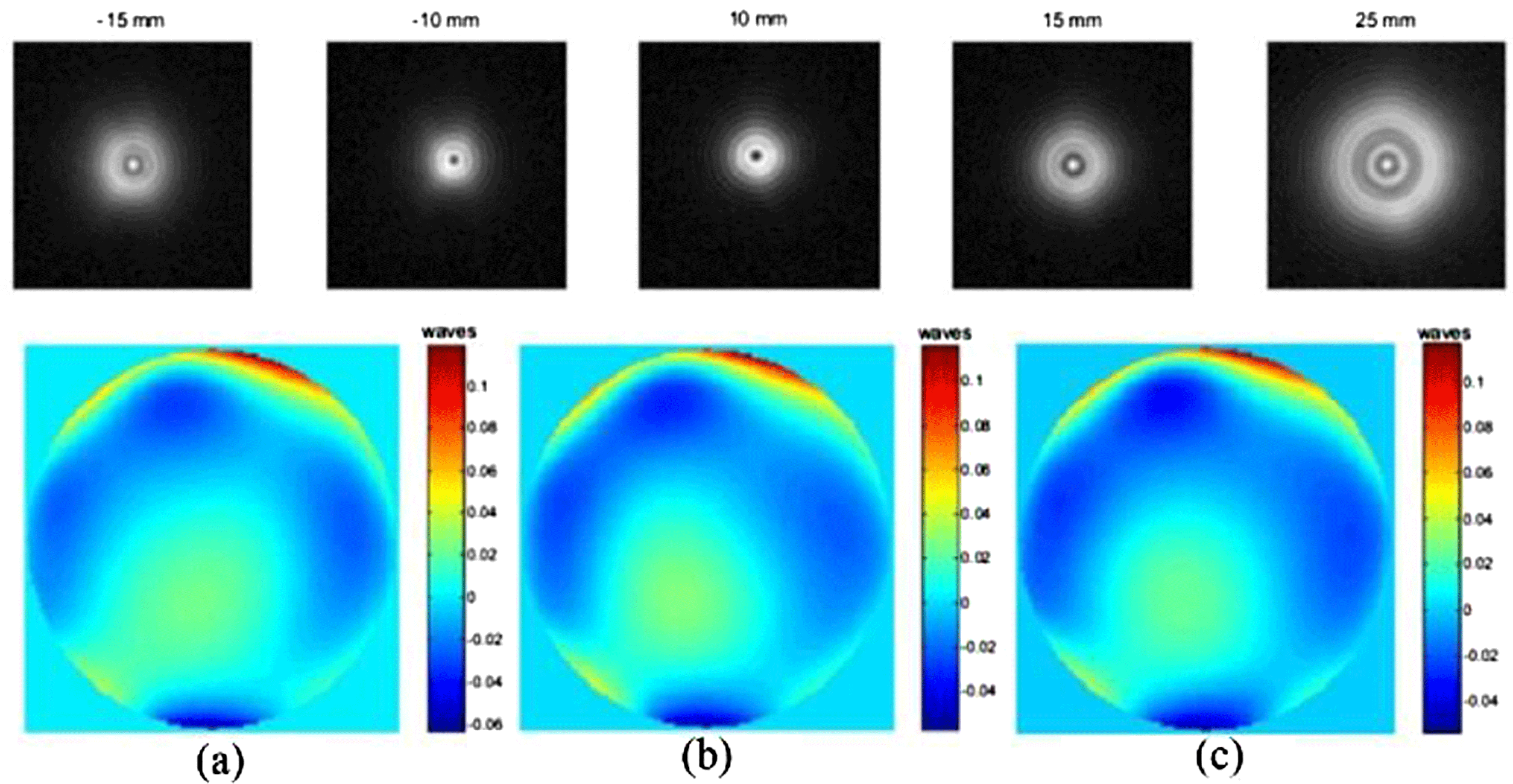
Figure 11. Recovered phases obtained by Brady and Fienup (from Ref. [Reference Brady and Fienup39]).

Figure 12. Linear scale comparison of the directly measured focal spot (a) in the presence of an aberrator with the focal spots calculated with and without the use ((b) and (c), respectively) of the transfer wavefront obtained from phase retrieval (from Ref. [Reference Bahk, Bromage, Begishev, Mileham, Stoeckl, Storm and Zuegel42]).

Figure 13. Histograms illustrating the effects of phase-retrieval improvements on a large population of measurements. (a) Sample beam focal-spot accuracy showing cross-correlation between the FSD prediction and the far-field CCD measurement. (b) Main-beam focal-spot accuracy showing cross-correlation between the FSD prediction and the FSM measurement (from Ref. [Reference Kruschwitz, Bahk, Bromage and Irwin44]).
4. PIE and its application
PIE is a newly developed CDI method proposed by Rodenburg in 2004 to overcome the disadvantages of traditional CDI[Reference Williams, Quiney, Dhal, Tran, Nugent, Peele, Paterson and de Jonge30]. Although PIE has been successfully used in electron and X-ray imaging, its high power laser applications have not been explored.
4.1. Basic principles
For clarity, the principles of PIE and ePIE are outlined in Figure 14; details can be found in the relevant literature[Reference Rodenburg and Faulkner31, Reference Faulkner and Rodenburg45]. The object ![]() $O$(x, y) under the illumination
$O$(x, y) under the illumination ![]() $P$(x, y) can accurately shift across the optical axis; a set of diffraction patterns
$P$(x, y) can accurately shift across the optical axis; a set of diffraction patterns ![]() $I_{\mathrm{n}}$(x, y) is recorded by the CCD downstream of the object when the object is scanned to a series of positions (Figure 15). Iterative calculations are performed between the object and the recording planes to retrieve the complex transmittance of the object and the complex amplitude of the illumination via the following procedure.
$I_{\mathrm{n}}$(x, y) is recorded by the CCD downstream of the object when the object is scanned to a series of positions (Figure 15). Iterative calculations are performed between the object and the recording planes to retrieve the complex transmittance of the object and the complex amplitude of the illumination via the following procedure.
(1) The exit field at the current position ![]() $R_{i}$ is calculated with two random guesses for
$R_{i}$ is calculated with two random guesses for ![]() $P_{n,g} \left (r \right )$ and
$P_{n,g} \left (r \right )$ and ![]() $O_{n,g} \left ({r-R_{i}}\right )$
$O_{n,g} \left ({r-R_{i}}\right )$
where the subscript ![]() $n$ represents the
$n$ represents the ![]() $n$th iteration.
$n$th iteration.
(2) The wavefunction in the data recording plane is calculated from the Fourier transform of ![]() $\Psi _{n,g} \left ({r,R_{i}}\right )$:
$\Psi _{n,g} \left ({r,R_{i}}\right )$:
(3) The amplitude of ![]() $\Psi _{n,g}({r,R_{i} })$ is replaced by the square root of
$\Psi _{n,g}({r,R_{i} })$ is replaced by the square root of ![]() $I_{n}(x, y)$:
$I_{n}(x, y)$:
(4) The guess is updated at the exit field by inverse Fourier transform:
(5) The functions ![]() $P(r)$ and
$P(r)$ and ![]() $O(r, R_{i})$ are updated with the following formulas:
$O(r, R_{i})$ are updated with the following formulas:
 $$\begin{eqnarray} \label {eq6} O_{\mathrm {new}}(r,R_{i}) &=& O_{g,n} (r,R_{i}) + \frac {|P_{n}(r)|}{|P_{n}(r)|_{\max }} \frac {P_{n}^{\ast }(r)}{[|P_{n}(r)|^{2}+\alpha ]} \\ && \times \, [{\Psi _{c,n} ({r, R_{i} } )-P_{n}(r)\cdot O({r,R_{i}})} ],\end{eqnarray}$$
$$\begin{eqnarray} \label {eq6} O_{\mathrm {new}}(r,R_{i}) &=& O_{g,n} (r,R_{i}) + \frac {|P_{n}(r)|}{|P_{n}(r)|_{\max }} \frac {P_{n}^{\ast }(r)}{[|P_{n}(r)|^{2}+\alpha ]} \\ && \times \, [{\Psi _{c,n} ({r, R_{i} } )-P_{n}(r)\cdot O({r,R_{i}})} ],\end{eqnarray}$$ $$\begin{eqnarray} P_{\mathrm {new}}(r) &=& P(r)+\frac {|{O({r,R_{i} } )}|}{| {O({r,R_{i}})}|_{\max } }\frac {O^{\ast }({r,R_{i}})}{[{|{O({r,R_{i} })}|^{2}+\alpha }]} \\ && \times \,[{\Psi _{c,n} (r, R_{i})-P_{n}(r )\cdot O(r,R_{i})}]. \end{eqnarray}$$
$$\begin{eqnarray} P_{\mathrm {new}}(r) &=& P(r)+\frac {|{O({r,R_{i} } )}|}{| {O({r,R_{i}})}|_{\max } }\frac {O^{\ast }({r,R_{i}})}{[{|{O({r,R_{i} })}|^{2}+\alpha }]} \\ && \times \,[{\Psi _{c,n} (r, R_{i})-P_{n}(r )\cdot O(r,R_{i})}]. \end{eqnarray}$$Steps 1 to 5 are repeated until satisfactory images are generated.

Figure 14. Principles of PIE and ePIE (from Ref. [Reference Wang, Liu and Veetil46]).

Figure 15. Diffraction patterns with the illumination beam in overlapping positions.

Figure 16. Experimental setup of the phase detection for large-aperture optical elements.

Figure 17. (a) Manufactured CPP, (b) CPP design value, (c) measurement result of a Zygo interferometer, (d) wrapped phase of the measured modulation function, (e) unwrapped phase of the measured modulation function, and (f) the measured result and designed value along the horizontal lines of (b) and (e) (from Ref. [Reference Wang, Liu and Veetil46]).
4.2. Measurement of the transmittance of a large optical element with the use of ePIE
Illumination on the specimen in Figure 16 can be measured with the use of ePIE, and this property provides a new method for measuring the complex transmittance of large optical elements used in high power laser applications[Reference Wang, Liu and Veetil46]. Practical measurement was conducted to illustrate the feasibility of this method by CPP, which is a key element in ICF systems that smoothens the laser beam to ensure an ideal focal spot with a highly irregular surface profile[Reference Haynam, Wegner, Auerbach, Bowers, Dixit, Erbert, Heestand, Henesian, Hermann and Jancaitis47, Reference Neauport, Ribeyre, Daurios, Valla, Lavergne, Beau and Videau48]. The optical setup used is shown in Figure 16. The wavefront ![]() $\varphi _{0}(x, y)$ of the light leaving the convergent lens can be measured using the ePIE algorithm when the CPP is removed (Figure 16); the wavefront
$\varphi _{0}(x, y)$ of the light leaving the convergent lens can be measured using the ePIE algorithm when the CPP is removed (Figure 16); the wavefront ![]() $\varphi _{1}(x,y)$ of the light leaving the CPP can also be measured. By subtracting
$\varphi _{1}(x,y)$ of the light leaving the CPP can also be measured. By subtracting ![]() $\varphi _{0}{(x,y)}$ from
$\varphi _{0}{(x,y)}$ from ![]() $\varphi _{1}{(x, y)}$, the PM of the CPP is obtained.
$\varphi _{1}{(x, y)}$, the PM of the CPP is obtained.
Figure 17(a) shows a photograph of the manufactured CPP plate with approximately 31 cm diameter. Figure 17(b) shows the design value of the surface profile. Figure 17(c) shows the measurement result obtained using a Zygo interferometer, where the black areas indicate invalid measurements. The slope of the surface profile is very steep at these black areas and the interference fringes are too dense to resolve, resulting in the existence of these immeasurable areas. As such, the measurement result cannot indicate the real surface profile of the CPP. Figure 17(d) shows the wrapped phase of the measured PM function and Figure 17(e) shows the corresponding unwrapped phase distribution. The aperture of the measurement is 28 cm, which is decided by the parallel beam illuminating the CPP. The values along the vertical lines in Figures 17(b) and (e) are plotted in Figure 17(f), and the maximum difference between the measured and designed values is approximately 2.1 rad. This research illustrates that ePIE is a promising technique for measuring large optical elements.

Figure 18. Schematic of the PM technique. (a) Basic principle and (b) experimental setup.

Figure 19. Experimental results of PM. (a) Reconstructed phase, (b) reconstructed modulus, (c) predicted focal spot with the PM technique, and (d) the measured focal spot.
4.3. PM technique and its potential application
The data acquisition time of ePIE is several minutes; thus, it cannot be used to measure dynamic wavefronts. To overcome this disadvantage, Zhang proposed the PM method[Reference Zhang and Rodenburg49]. The basic principle and the experimental setup of the phase modulation technique are shown in Figures 18(a) and (b).
The modulator with a designed transmission function is located between the entrance and detector domains, while the entrance plane is the focal plane of the incident wave to be measured. As one frame of the diffraction pattern is recorded, the illumination on the modulator plane can be iteratively reconstructed at high accuracy. This method features a very simple structure and short data acquisition time; thus, it is suitable for FSDs and laser plasma imaging, where the laser beam is pulsed and most of the common techniques do not work well. Proof of concept is demonstrated by measuring a seriously distorted convergent He–Ne laser beam; Figures 19(a) and (b) show the reconstructed phase and modulus of the field incident on the phase modulator. Figures 19(c) and (d) show the predicted and measured focal spots; the difference between the two focal spots is difficult to distinguish with the naked eye. The details of this research will be reported in a separate paper.
Summary
The use of several traditional phase measurement methods to measure the wavefront in high power laser applications was evaluated; their advantages, disadvantages, and applications were also discussed. As a classical technique, interferometry features the highest accuracy and resolution among the techniques studied. However, in most cases, interferometry is only used to measure the static properties of optical elements because of its complex structure and critical environmental requirements. The Hartmann–Shack wavefront sensor shows high measurement speed and may be used to realize feedback wavefront control. However, this sensor cannot detect high frequency components. CDI techniques have been increasingly adopted in high power laser applications and are to be considered as promising techniques in special cases. CDI techniques are based on principles that are entirely different from those of traditional techniques and were developed particularly for imaging using short-wavelength radiation.
Acknowledgement
This research is supported by the One Hundred Talents Project of the Chinese Academy of Sciences, China (Grant No. 1204341-XR0).





















